Does Relativity Rule over Quantum or Vice Versa?

The harmonization of quantum theory with special relativity is highly nontrivial. Even though quantum field theory has been constructed the tension between quantum theory and relativity persists for many fundamental reasons. For example an open conceptual problem in relativistic quantum theory concerns the relation between measurement and causality. Now it is well known fact that conventional account of ideal measurement can lead to superluminal signaling [1,2,3,4,5,6,7,8]. In this letter, we will encounter such a situation while interpreting two-photon interference. When two indistinguishable photons combined at a beam splitter, they behave in an interesting way [9]. For example, when two indistinguishable photons are brought together at a 50/50 beam splitter whose output ports are monitored by two photon-counting detectors, only two photons can be detected together in one of the detectors at a time. The other possibility where each of the photons detected at a different detector (coincidence detection) cannot be seen. There are two ways to produce such a coincidence: either both photons are reflected (r-r) or both are transmitted (t-t) by the beam splitter. the two-photon amplitudes for double reflection (r-r) and double transmission (t-t) are indistinguisable and has opposite sign. So, they can cancel each other completely if a 50/50 beam splitter is used. This cancellation means that the two photons of a pair cannot both be reflected or both be transmitted. Thus, they cannot end up at different detectors. If the two detectors are monitored in coincidence, there will be a complete lack of coincidence counts due to this destructive interference. This effect is known as Hong-Ou-Mandel (HOM) interference [9,10,11,12,13,14,15,16], named after Chung Ki Hong, Zhe Yu Ou and Leonard Mandel, who experimentally verified the effect in 1987.

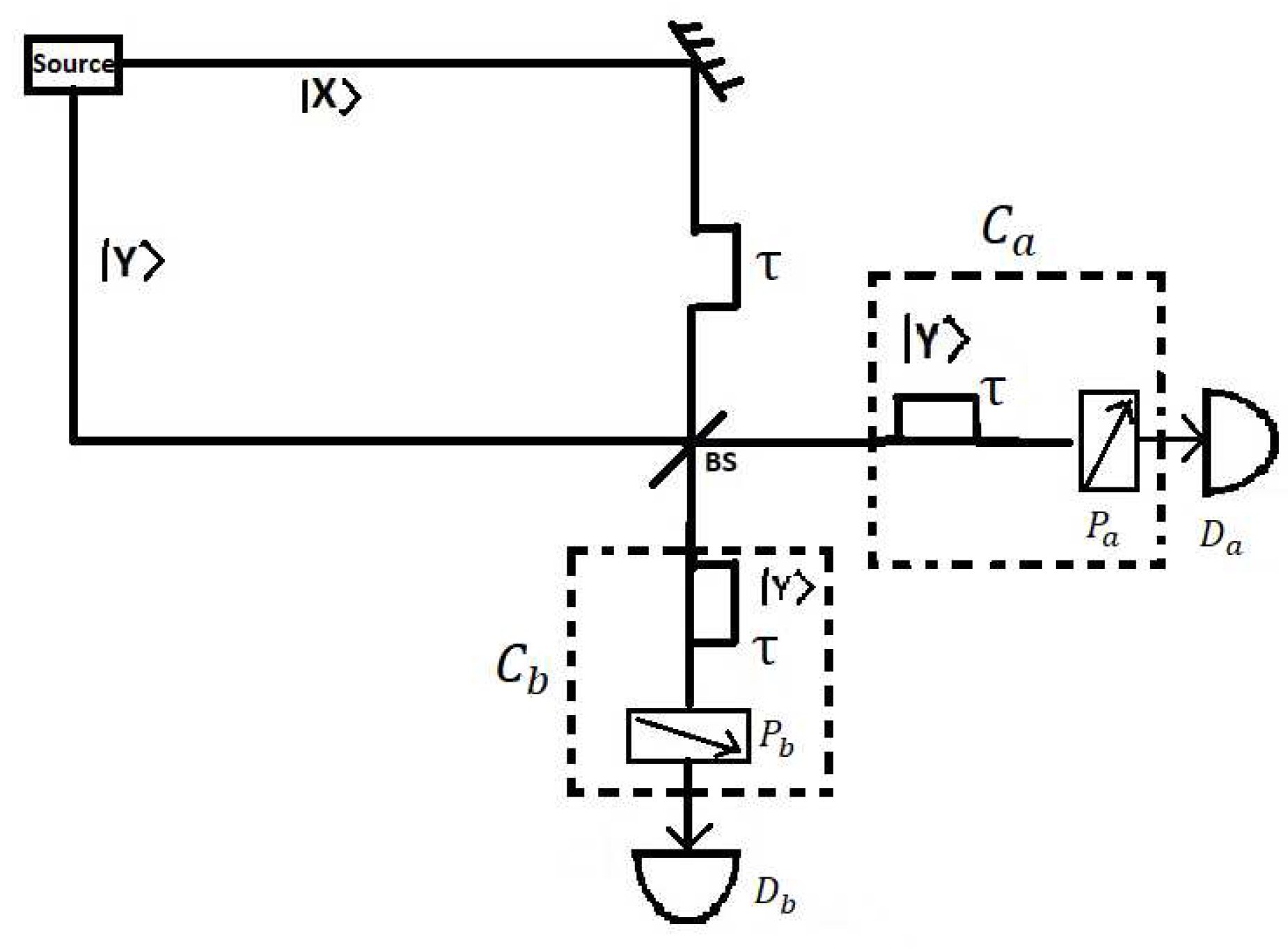
Two-photon interference effects can be observed even when one starts with two distinguishable photons with orthogonal polarisation or the optical paths in the interferometer have very different lengths, and the photons do not arrive at the beam splitter at the same time [17]. In these cases one has to somehow compensate for the delay and polarization after the beam splitter in such a way that the detector firing times do not provide any information concerning which of the two-photon alternative amplitudes led to the coincidence detection. What is important is the indistinguishability of the r-r and t-t amplitudes. Suppose before arrival at beam splitter the |X> polarized signal photon takes a path of delay $\tau$ (Figure 1). After the beam splitter the compensators requires the |Y> polarized idler photons to take a same path of relative delay $\tau$ compared to the |X> polarized signal photons. The polarizers $P_a$ and $P_b$ are oriented at angles $\theta ={45}^o$ with respect to |X> to make the amplitudes indistinguisable. As a result there will be a complete lack of coincidence counts due to destructive interference.

In this research letter we present a protocol using the postponed compensation HOM interferometer that allows superluminal signaling. After that, by critically examining it from the perspective of special relativity, we make two propositions to deal with paradoxical situations. Then we propose experiments for confirmation.

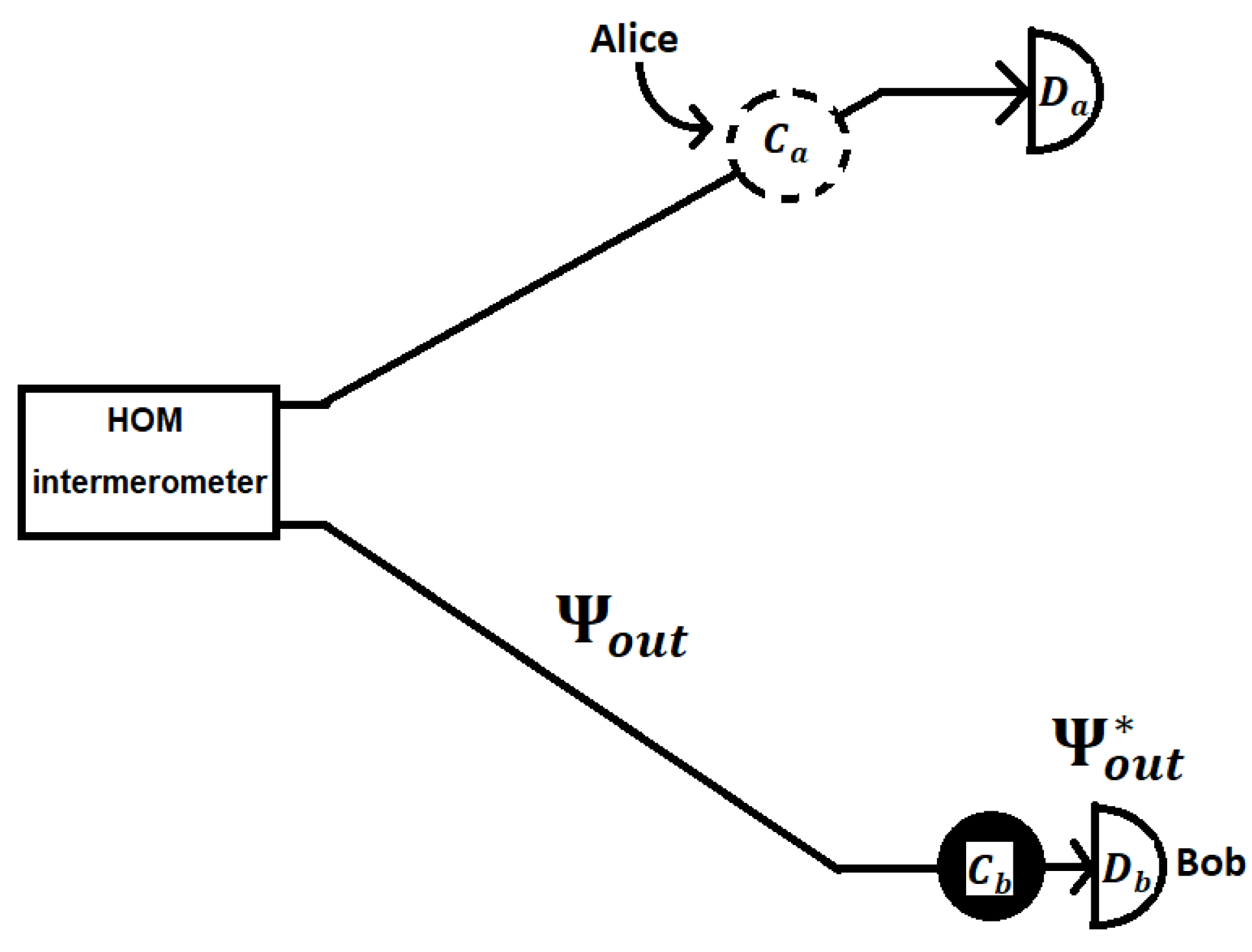
The basic idea of the superluminal signaling experiment can be seen in Figure 2 and Figure 3. Suppose compensator package $C_a$ and $C_b$ include polarizers also. Consider two observers, Alice and Bob, each are situated in one of the output mode of the interferometer where the detectors are $D_a$ and $D_b$. Alice and Bob are located near $C_a$ and $D_b$ respectively. Alice has freedom to make decision about whether she will put the compensator $C_a$ in place or not. But Bob has no such freedom. The compensator of the output mode b $C_b$ is fixed. Bob always measures with detector $D_b$ after compensation of $C_b$. Both $C_a$ and $C_b$ is necessary to make the amplitudes corresponding to r-r and t-t case indistinguisable. Now suppose $C_a$ and $D_a$ operates at time $t_a$ and $t_a+\delta$ respectively and $C_b$ and $D_b$ operates at time $t_b$ and $t_b+\delta$ respectively, where $t_b>t_a$. Without the compensator of Alice $C_a\left(t_a\right)$ in place, photon amplitudes after operation of $C_b\left(t_b\right)$ are still distinguisable and the complete output state after the operation of $C_b$ can be written as following where ${\widehat{a}}_X^{†}$, ${\widehat{a}}_Y^{†}$, ${\widehat{b}}_X^{†}$ and ${\widehat{a}}_Y^{†}$ are bosonic creation operators in beam splitter modes, a and b, respectively. In addition to being identified by their respective beam splitter modes, the photons may have different polarization, labeled by X and Y, that determine how distinguishable they are. ${\widehat{P}}_b$ is the operator corresponding to polarizer $P_b$. From Eq.(1) one can obtain that Bob measures two photons at the detector $D_b$ with probability $\frac{1}{16}$.

Now with the compensator of Alice $C_a\left(t_a\right)$ in place, r-r and t-t amplitudes after operation of $C_b\left(t_b\right)$ become indistinguishable. The complete output state after the operation $C_b\left(t_b\right)$ can be written as following From Eq.(3) one can obtain that Bob receives two photons at the detector $D_b$ with probability ${\left|\frac{1}{2\sqrt{2}}\right|}^2=\frac{1}{8}$, which is different from the previous case. Hence Alice can send signal to Bob instantaneously (in the limit $(t_b-t_a)\to 0$ and $\delta \to 0$).

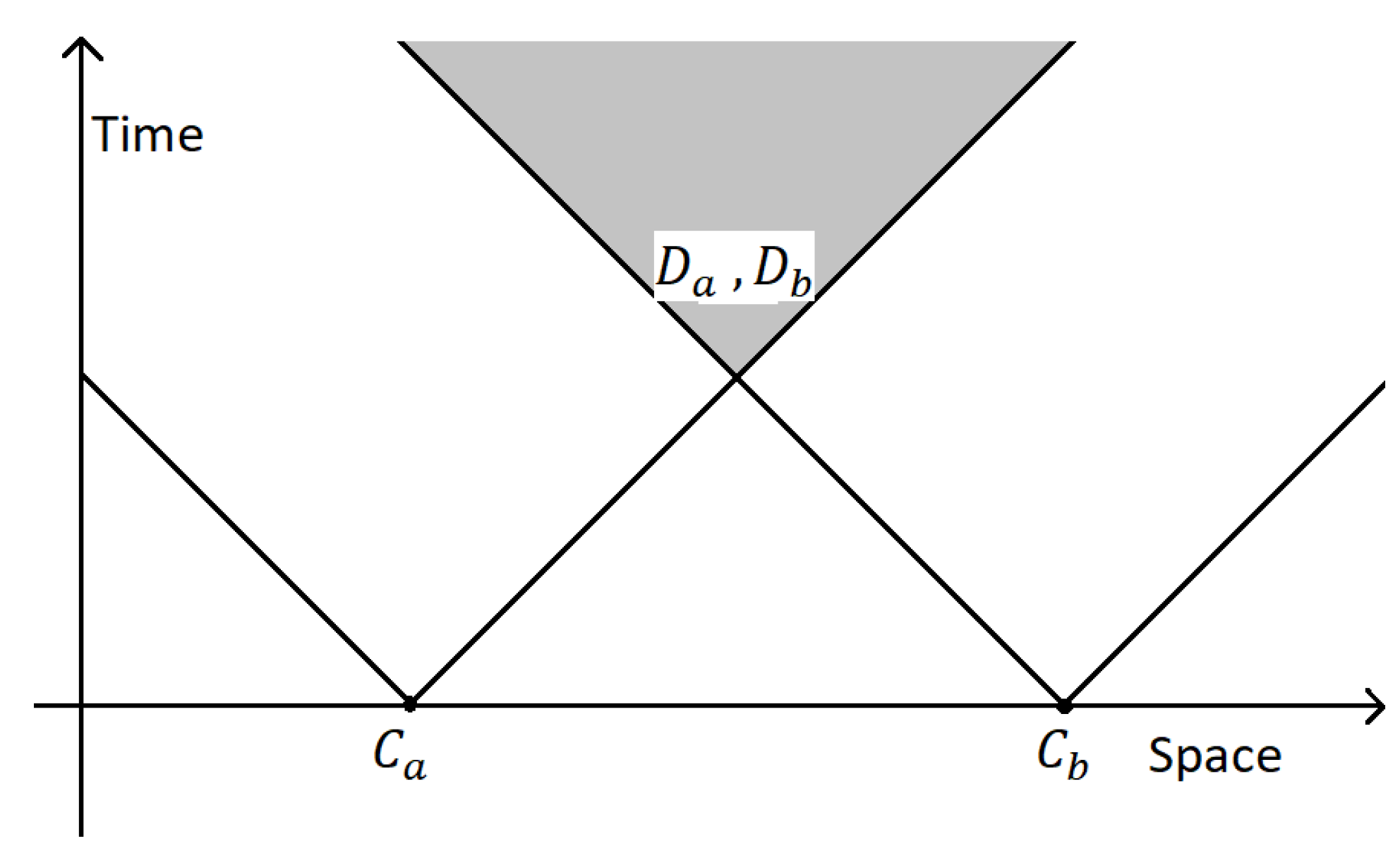
Now suppose space-time cordinates of $C_a$ and $C_b$ are $(t_a,x_a,y_a,z_a)$ and $(t_b,x_b,y_b,z_b)$ respectively. If $C_a$ and $C_b$ are spacelike separated then square of the space-time distance $S^2(C_a,C_b)=-c^2{(t_a-t_b)}^2+{(x_a-x_b)}^2+{(y_a-y_b)}^2+{(z_a-z_b)}^2$, will be greater than zero. Unlike timelike-separated events, the time order of spacelike-separated events may change for different Lorentz frames. So, in some Lorentz frames, the signal is sent by Alice at a later time than it arrives at Bob. As a result causality is violated. But the important question is whether the phenomenon would allow us to pick out a particular Lorentz frame as holding a privileged position in nature: if so, then a fundamental relativity principle will be violated. There are possible Lorentz frames where operation of $C_b$ will occure before $C_a$, which implies that in those frames $D_b$ measures $|{\psi }_{out}^{*}>$ even though the amplitudes are still distinguisable and quantum rules are violated. So, some reference frame holds special privilege and violates relativistic invariance principle. There is no doubt that if superluminal signaling is possible a paradoxical situation will arise. And on this point, it should be noted that no experimental work has yet been done to the best of our knowledge to test whether superluminal signaling in this way is possible or not. In this regard, we give two propositions whose validity can be proved only through experiment.

Proposition 1: Modification of quantum rules are necessary, so that it does not violate Lorentz invariance.

Proposition 2: Quantum rules are correct, and it is relativity which needs modification so that it can be reconciled with quantum rules.

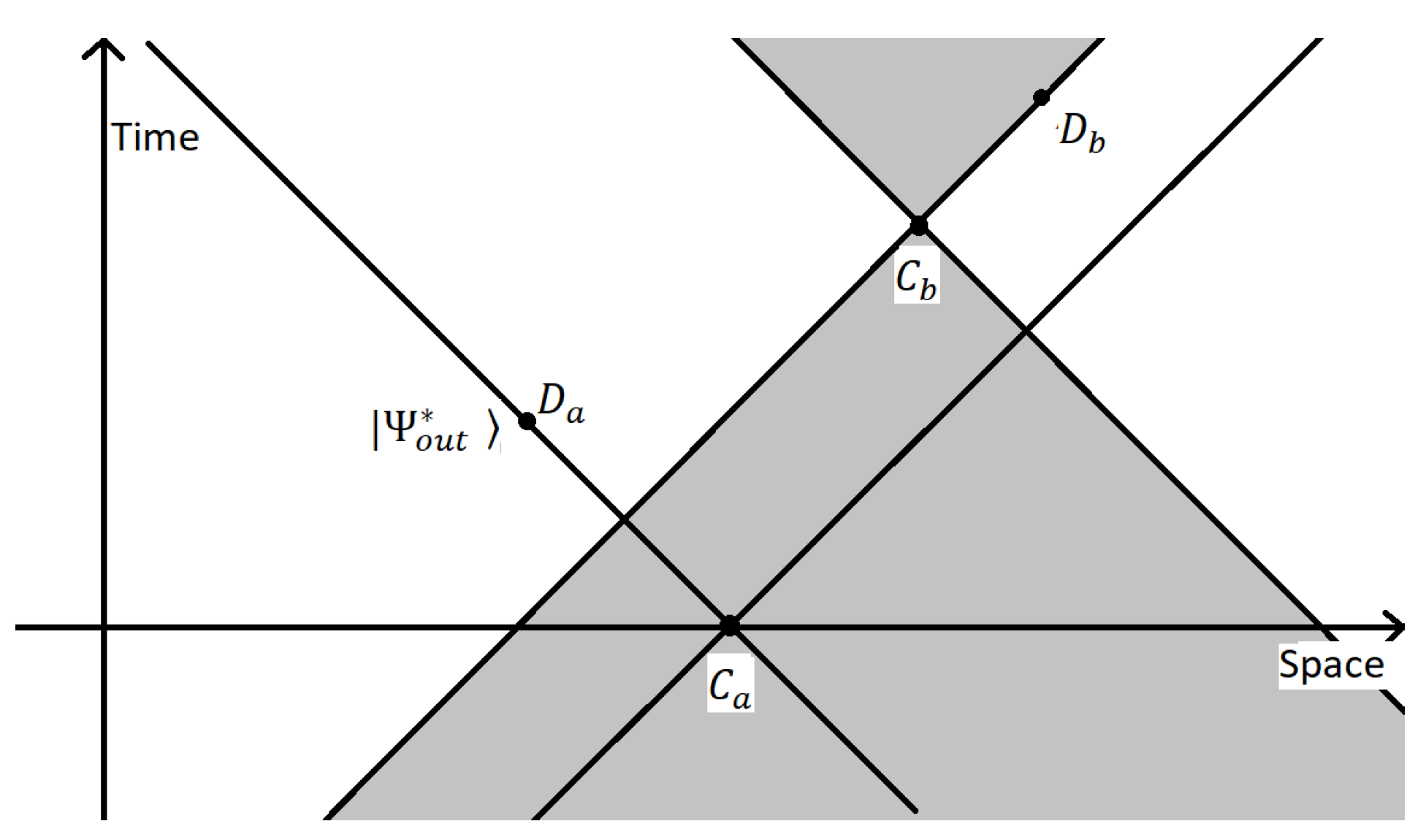
Let us discuss proposition 1. Based on the experimental findings so far, one can modify the quantum rules in the following way. One has to assume that indistinguishability of r-r and t-t amplitudes are necessary but not a sufficient condition for interference. Even though the r-r and t-t amplitudes are indistinguishable in a particular Lorentz frame, it is not enough for the occurrence of $|{\psi }_{out}^{*}>$ in that frame. $|{\psi }_{out}^{*}>$ will only occur when the amplitudes become indistinguishable with respect to every possible Lorentz frames before the measurment either at $D_a$ or $D_b$. It is possible only if the spacetime distances $S(C_a,D_b)$ and $S(C_b,D_a)$ are timelike (Figure 5). This situation retains the relativity principle fully: no Lorentz frame is intrinsically preferred over any other. Even though signaling is possible in such a setup, it is not superluminal because Alice and Bob are timelike separated.

So, going in line of proposition 1 one must conclude that indistinguishability of amplitudes with respect to a particular reference frame is not the condition for interference to occur in that frame, instead indistinguishability of amplitudes with respect to every possible Lorentz frame is the necessary condition for interference.

On the other hand proposition 2 implies the existence of a privileged frame which is not in line with the spirit of relativity. It should be stressed that there is also no empirical evidence implying its absence. There is another possibility which also goes with proposition 2 is that spacetime geometry should be modified to include quantum nonlocality in such a way that it can reclaim the nonexistence of a privileged frame.

Till now, no experimental study has been reported where the compensations and detections in the output modes (frequency, delay, or both) have been carried out in such a way that one can decide which proposition is true. So, these propositions need experimental verification. One has to perform postponed compensation two photon interference experiment in such a way that Alice and Bob are strictly spacelike isolated. If interference does not occur in that setup, then one must change it so that the indistinguishability of the r-r and t-t amplitudes for every possible Lorentz frame can be assured.

In the context of the present work, it should be noted that some earlier papers [1,2] showed the existence of quantities represented by bounded self-adjoint operators, the measurement of which would allow superluminal signaling.

For example consider Alice and Bob, each equipped with a two-state quantum system. Bob starts with |0>, and Alice selects either |0> or |1> at time $t_0$. Thus the initial state is either |00> or |10>. Now suppose a partial measurement $\epsilon$ projects onto the following orthonormal basis ${|0>}_A\otimes {|0>}_B$, ${|0>}_A\otimes {|1>}_B$, ${|1>}_A\otimes {|\mathrm{+}>}_B$ and ${|1>}_A\otimes {|->}_B$. Where $|\mathrm{\pm }>=\frac{1}{\sqrt{2}}(|0>\pm |1>)$. At time $t_0+\delta t$, measurement $\epsilon$ is made on the system. If Alice began with state |0>, then Bob will obtain |0> with certainty. But if Alice prepared her particle in |1>, then the initial state can be written as there is a $50\%$ chance that Bob will obtain |1>. Thus if such a measurement is possible, it would appear that Alice can signal Bob instantaneously (in the limit $\delta t\to 0)$. Now suppose $\epsilon ={\epsilon }_A\otimes {\epsilon }_B$. The authors in [1] argued that either one has to conclude that to realize such situation Bob’s action ${\epsilon }_A$ must be in the forward light cone of Alice’s action ${\epsilon }_B$ or relativistic quantum theory tolerates a much more restricted selection of observables than the full set of Hermitian operators. But in the caption of Figure 6 we have argued that timelike separation of $C_a$ and $C_b$ can not ensure relativistic invariance. The same logic can also be applied for ${\epsilon }_A$ and ${\epsilon }_B$. [3,4,5,6,7,8] have shown many such situations in quantum theory where conventional account of ideal measurement leads to superluminal signaling when straightforwardly applied. The previous studies implies that the most general, logically consistent, application of the quantum measurement framework to observables in spacetime, is problematic. Since there was no way to decide by any experiment, only guesses have been made. For example, it has been conjectured that either the class of observables that may be measured is restricted by causal constraints or the constituent systems must be brought into causal contact to realize such measurements. It has been realized that constructing a complete and causality-respecting measurement model of quantum theory is highly nontrivial. In the present research letter we have proposed an experiment by which this issue can be resolved.

We have shown that rules of quantum theory corresponding to two photon interference supports superluminal signaling and it violates principle of relativistic invariance. To solve this paradox we make two propositons.

According to propositon 1 quantum physics needs revision. Relative indistinguishability (indistinguishability for a particular reference frame) of the amplitudes is not the condition for interference as quantum theory suggests but absolute indistinguishability (indistinguishability for all possible Lorentz frames) is. So, relativity rules over quantum.

On the other hand proposition 2 implies that it is relativity which needs reassessment not quantum theory. In this regard it should be noted that even though causality and relativistic invariance are violated in bohmian mechanics [18], it yields the standard quantum predictions generally associated with the Copenhagen interpretation. Reassessment of relativistic spacetime structure will further motivates such investigations. So, from the perspective of proposition 2, one can say that ruantum rules over relativity.

Ultimately, only experiment can decide whether relativity rules over quantum or vice versa.