Submitted:
29 January 2023
Posted:
30 January 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. The energy polynomials
- (1)
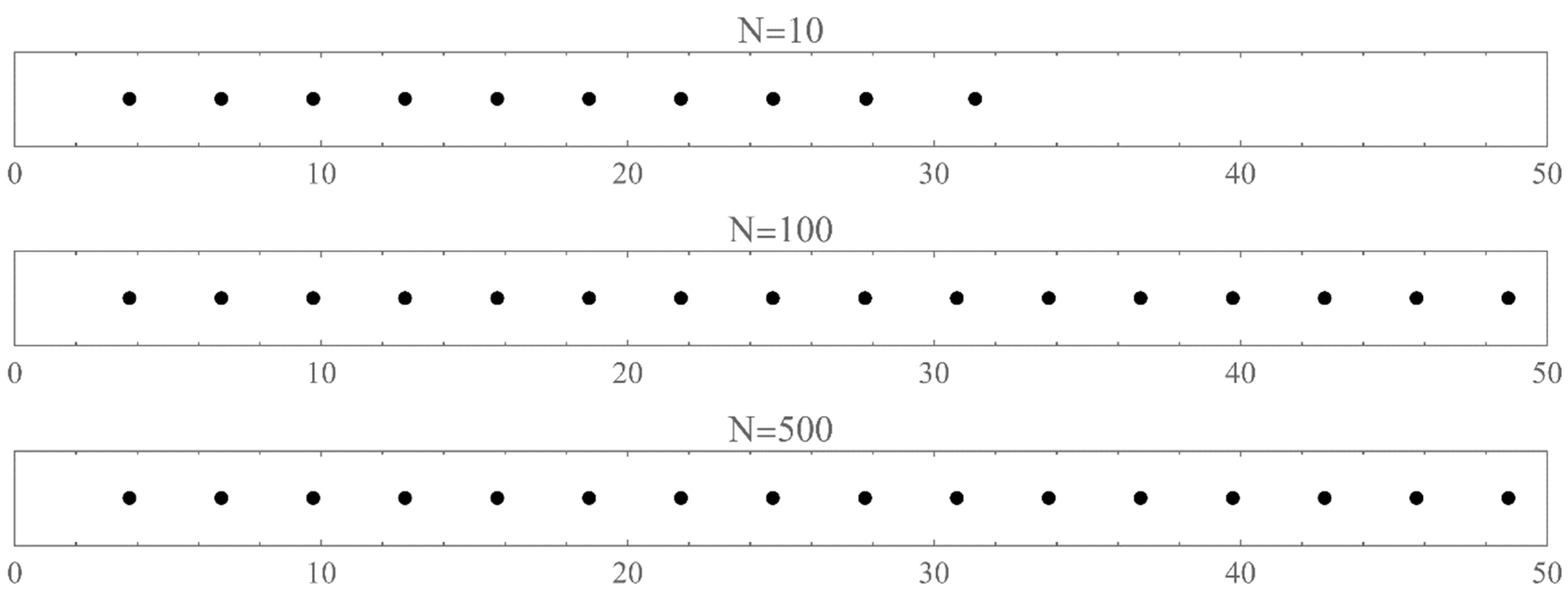
- The set of energies that satisfy: . That is, is an asymptotic zero for all energy polynomials in the limit of infinite (large enough) degrees [12].
- (2)
- The set of eigenvalues of the tridiagonal matrix (7) that lie outside the energy bands and do not change significantly (within the desired accuracy) if we vary the size of the matrix around a large enough size [13].
- (3)
3. Problems in the infinite domain
3.1. Problem I
3.2. Problem II
3.3. Problem III
3.4. Problem IV
4. Problems in the semi-infinite domain
4.1. Problem V
4.2. Problem VI
5. Conclusion
Author Contributions
Funding
Acknowledgements
Conflict of Interest
Appendix: Partial Solutions

| N | Left Boundaries | Right Boundaries |
|---|---|---|
| 10 20 50 100 200 |
-0.959493 -0.988831 -0.998103 -0.999516 -0.999878 |
0.959493 0.988831 0.998103 0.999516 0.999878 |

| N | Left Boundaries | Right Boundaries | ||
|---|---|---|---|---|
| 20 50 100 200 400 |
-0.926138 -0.973840 -0.988118 -0.994550 -0.997467 |
-0.105799 -0.034724 -0.014908 -0.006517 -0.002915 |
1.105799 1.034724 1.014908 1.006517 1.002915 |
1.926138 1.973840 1.988118 1.994550 1.997467 |

| N | Left Boundaries | Right Boundaries | ||
|---|---|---|---|---|
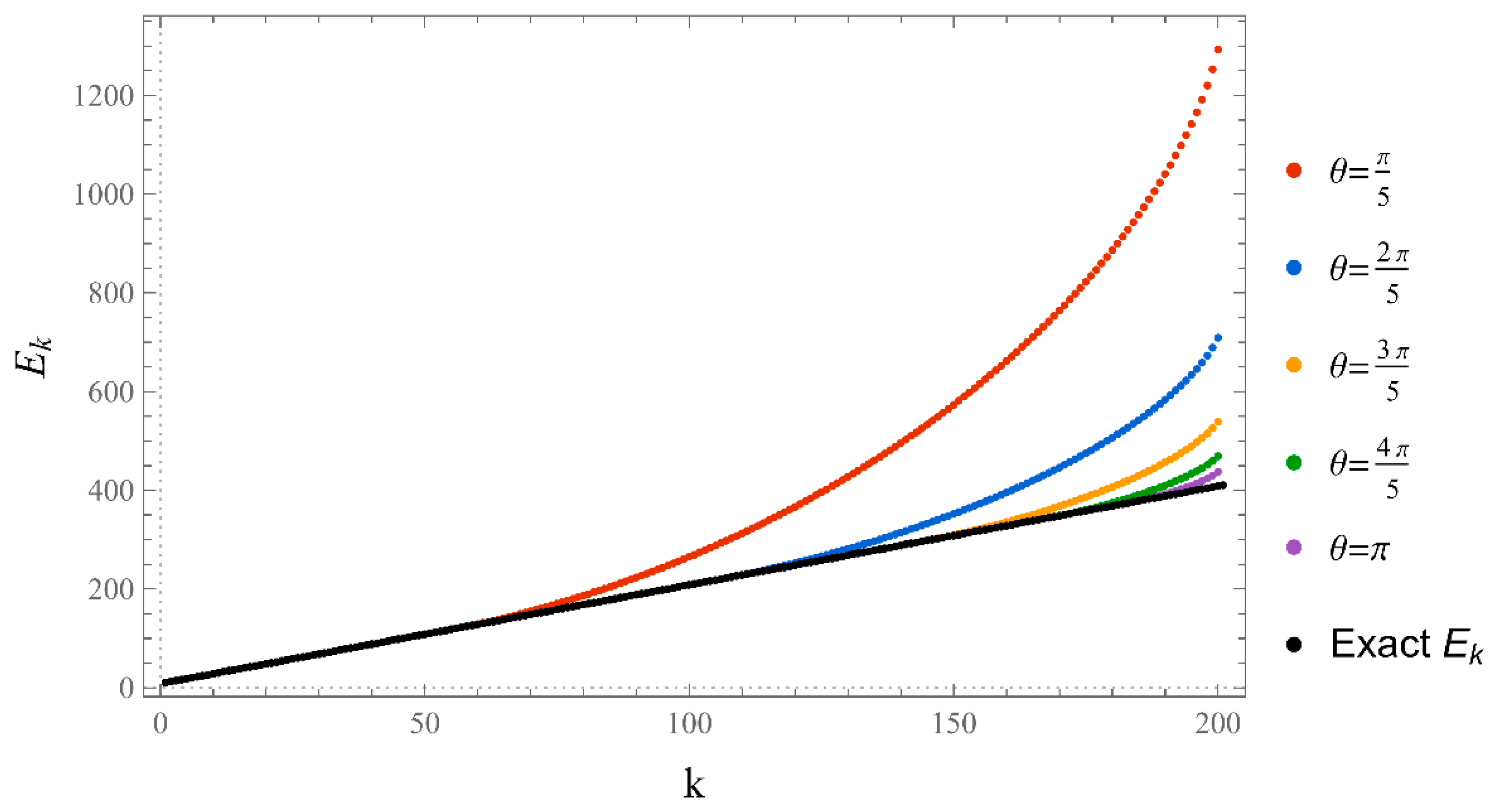
| 20 | -2.61667 | -1.02433 | 2.02433 | 3.61667 |
| 50 | -2.65286 | -0.81445 | 1.81445 | 3.65286 |
| 100 | -2.65775 | -0.760255 | 1.76026 | 3.65775 |
| 200 | -2.6601 | -0.737958 | 1.73796 | 3.6601 |
| 300 | -2.6609 | -0.731469 | 1.73147 | 3.6609 |
| Exact | -2.66228 | -0.720656 | 1.72066 | 3.66228 |


| N | Gap Boundaries | |
|---|---|---|
| 20 | -2.54592 | 3.54592 |
| 50 | -2.25155 | 3.25155 |
| 100 | -2.13357 | 3.13357 |
| 200 | -2.06917 | 3.06917 |
| 300 | -2.04672 | 3.04672 |
| Exact | -2.00000 | 3.00000 |




References
- Lev Vaidman, Role of potentials in the Aharonov-Bohm effect, Phys. Rev. A 86 (2012) 040101(R). [CrossRef]
- D. Alhaidari, Formulation of quantum mechanics without potential function, Quant. Phys. Lett. 4 (2015) 51. [CrossRef]
- D. Alhaidari and M. E. H. Ismail, Quantum mechanics without potential function, J. Math. Phys. 56 (2015) 072107.
- D. Alhaidari and T. J. Taiwo, Wilson-Racah Quantum System, J. Math. Phys. 58 (2017) 022101.
- D. Alhaidari, Reconstructing the potential function in a formulation of quantum mechanics based on orthogonal polynomials, Commun. Theor. Phys. 68 (2017) 711.
- D. Alhaidari and Y.-T. Li, Quantum systems associated with the Hahn and continuous Hahn polynomials, Rep. Math. Phys. 82 (2018) 285. [CrossRef]
- D. Alhaidari, Representation of the quantum mechanical wavefunction by orthogonal polynomials in the energy and physical parameters, Commun. Theor. Phys. 72 (2020) 015104.
- M. E. H. Ismail, Classical and Quantum orthogonal polynomials in one variable, paperback edition (Cambridge University press, 2009).
- T. S. Chihara, An Introduction to Orthogonal Polynomials (Dover, 2011).
- One can write the orthogonality (6) in a compact form as , where and .
- H. Bahlouli, A. D. Alhaidari and M. S. Abdelmonem, Phys. Lett. A 367 (2007) 162; and references therein.
- If for a particular value of the energy, for all n (not only asymptotically) then is not the energy of a bound state. In fact, this property makes the energy polynomials non-orthogonal. If we remove this zero by defining then the polynomials will form a true orthogonal sequence of energy polynomials.
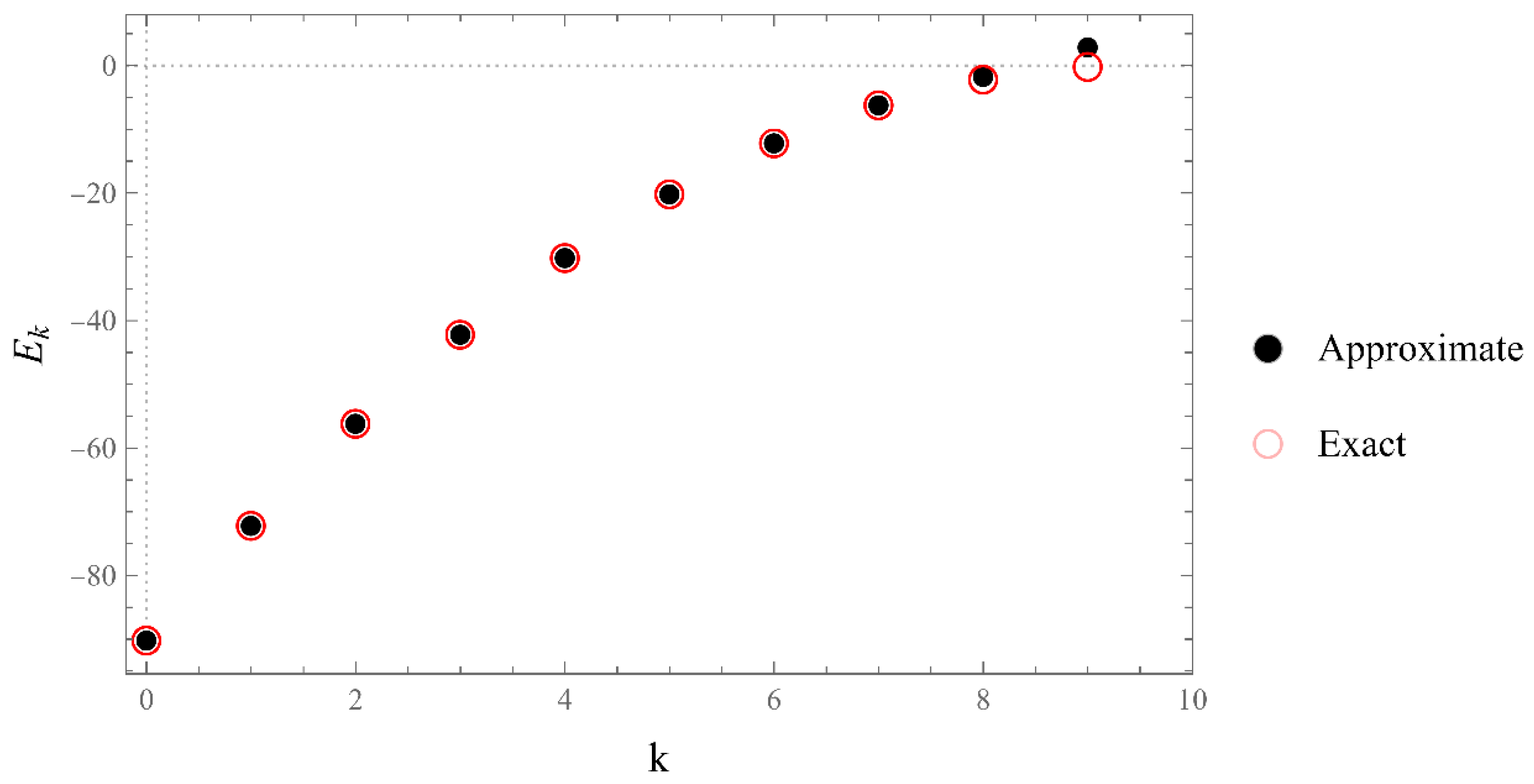
- It may happen that an eigenvalue of the matrix (7), which lies isolated outside the energy bands or in an energy gap, does not correspond to a bound state. It is advisable that one evaluates the polynomial at all such eigenvalues and performs the test .
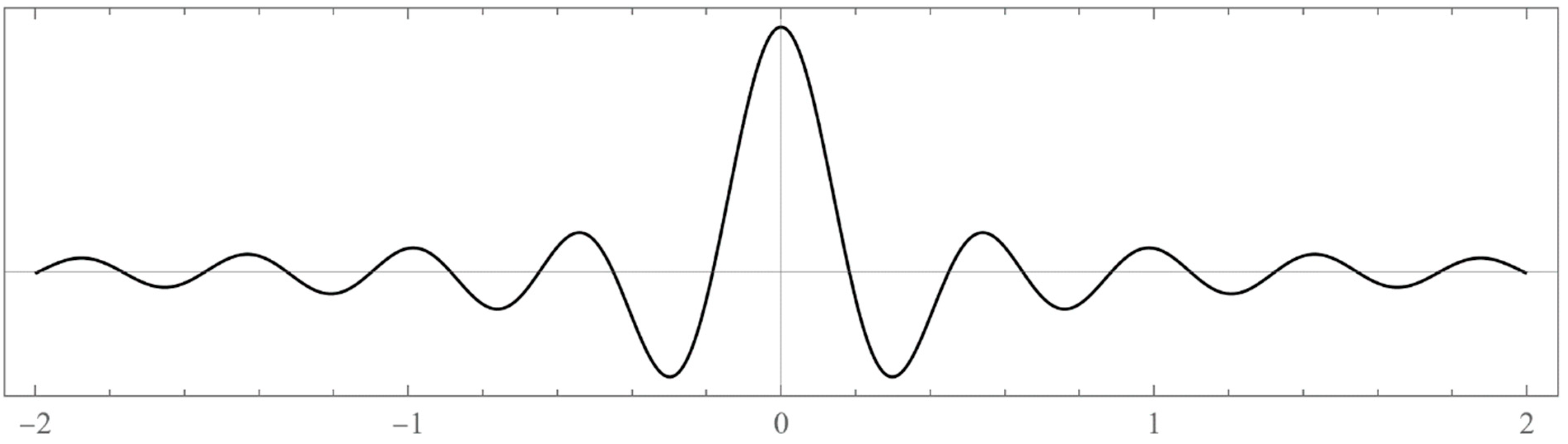
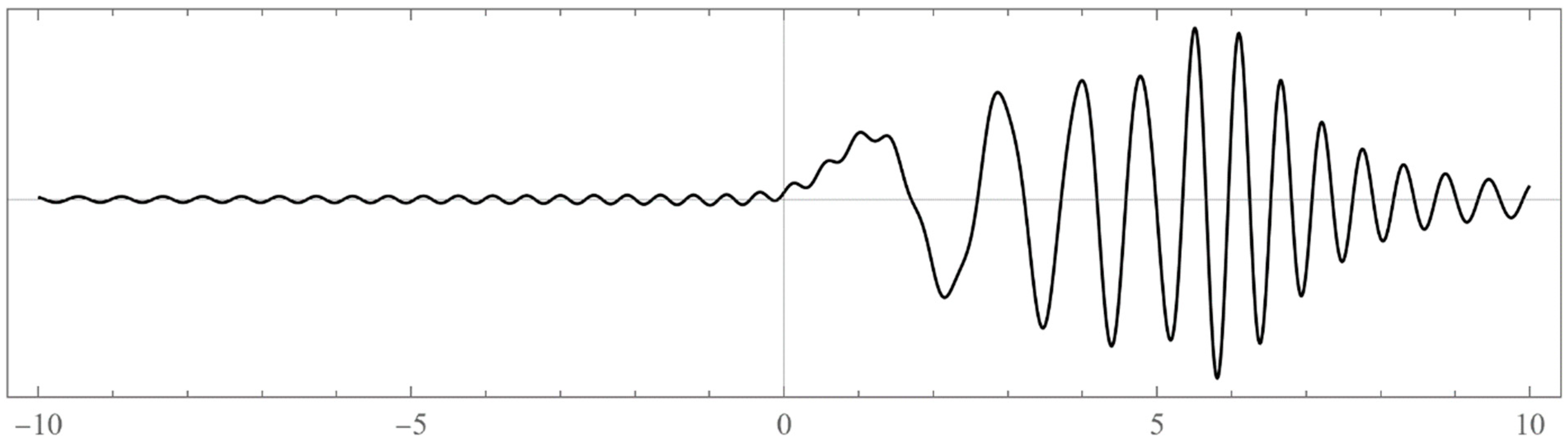
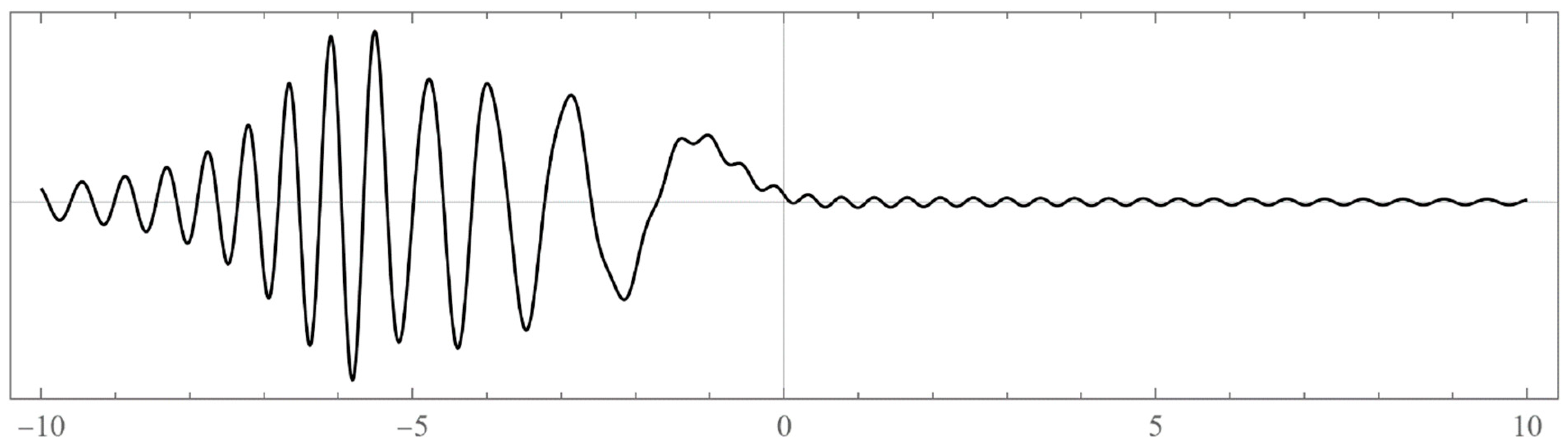
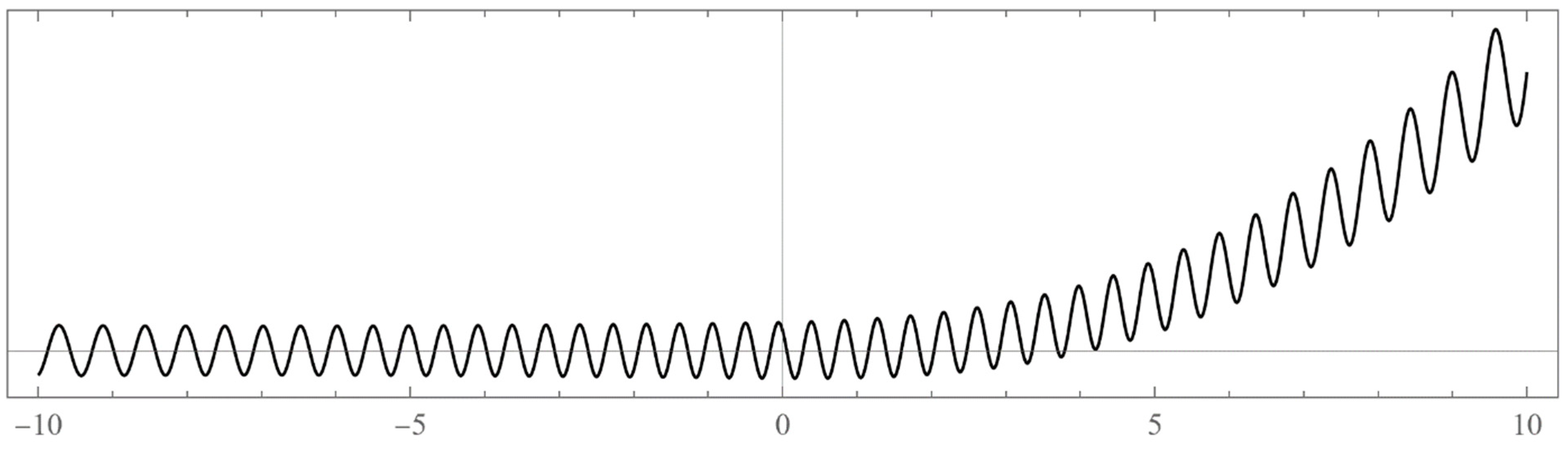
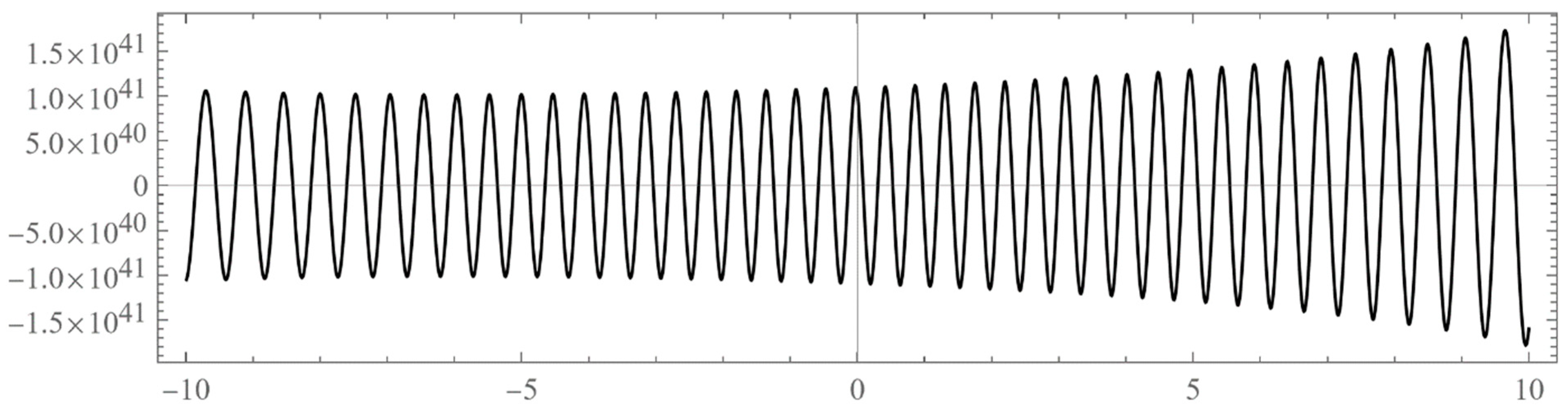
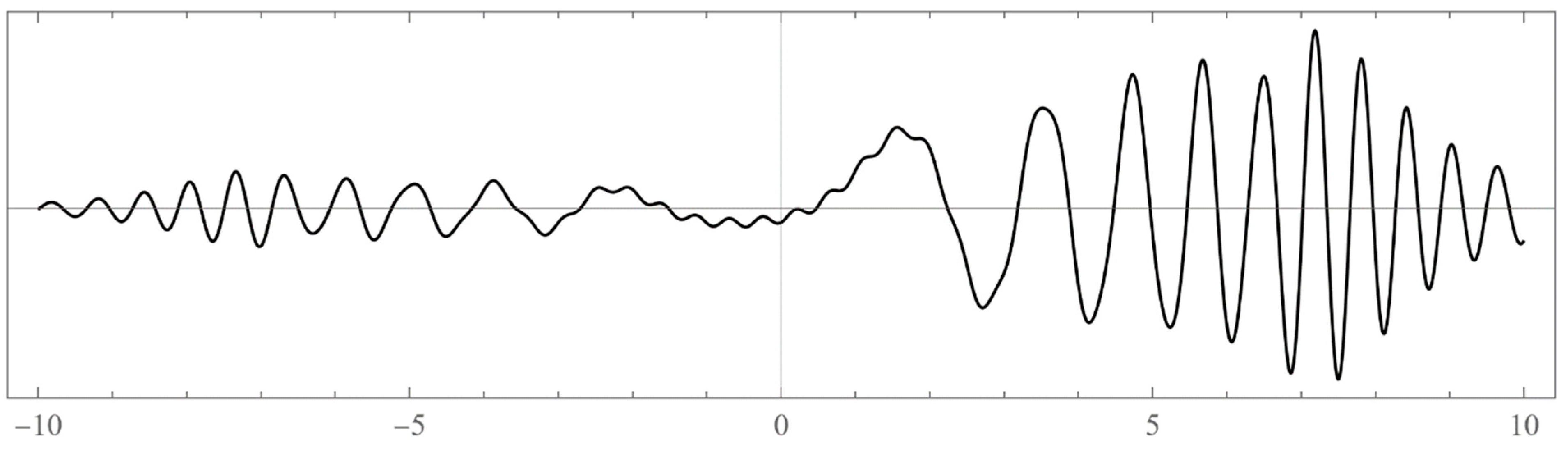
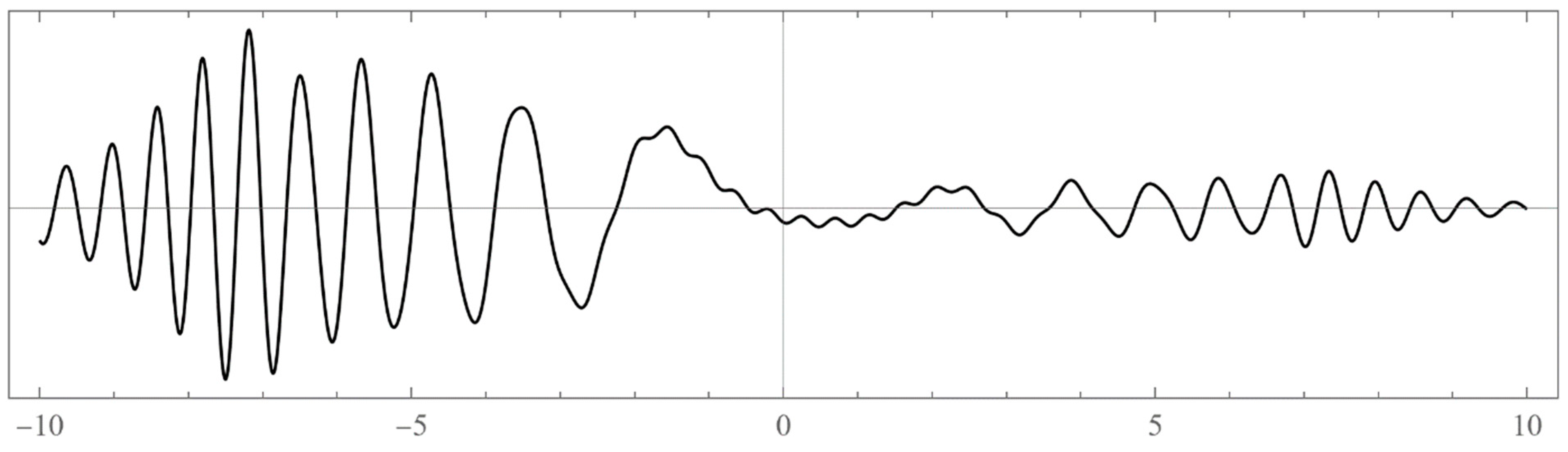
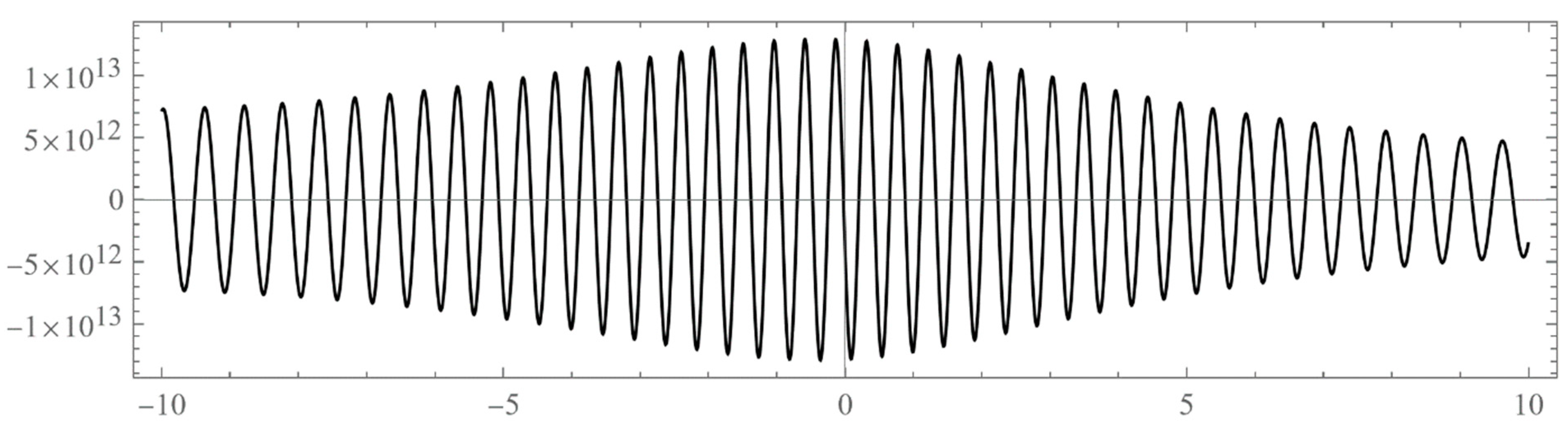
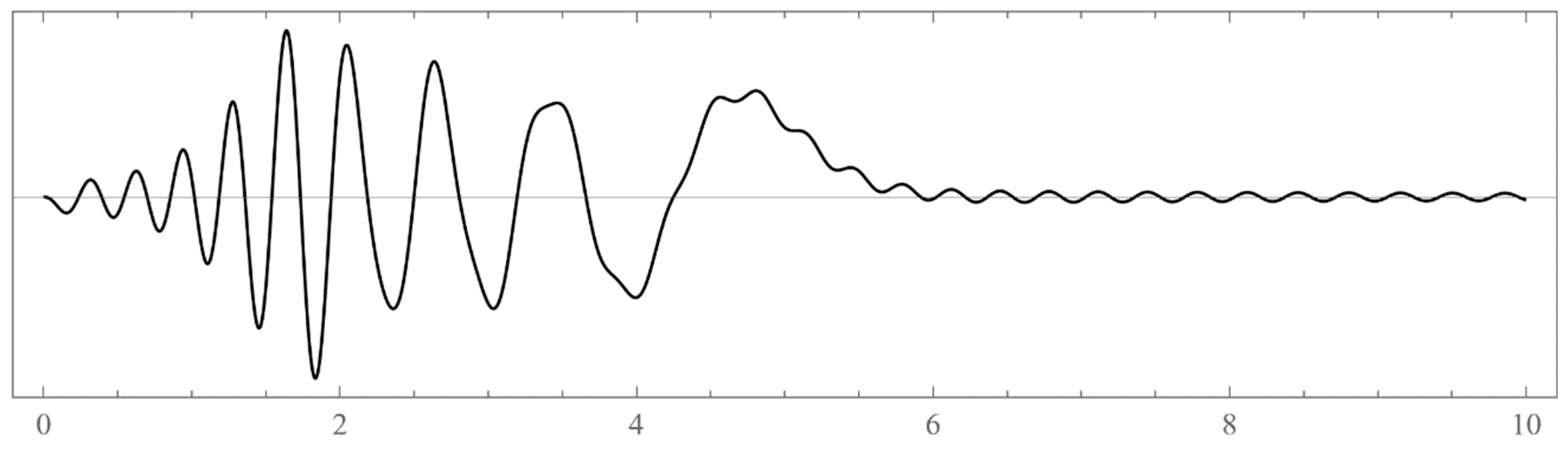
- Typically, these asymptotics take the form , where and are positive real parameters, is the weight function, is an entire function, and is the scattering phase shift. If then . As an illustration, we plot as a function of n for a fixed E from within the bands in Problem II and verify the oscillatory behavior of the asymptotics (we take, for example, ). We also show that the asymptotics in fact vanishes at the energy .
- A. D. Alhaidari, Density of states engineering: normalized energy density of states band structure using the tridiagonal representation approach, Can. J. Phys. 96 (2018) 275-286.
- R. Koekoek, P. A. Lesky and R. F. Swarttouw, Hypergeometric Orthogonal Polynomials and Their q-Analogues (Springer, 2010).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





