Submitted:
06 August 2024
Posted:
07 August 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
1.1. Heuristics for Completing Quantum Mechanics
1.1.1. Expectation Function for Non-Commuting Observables Cannot Be Linear
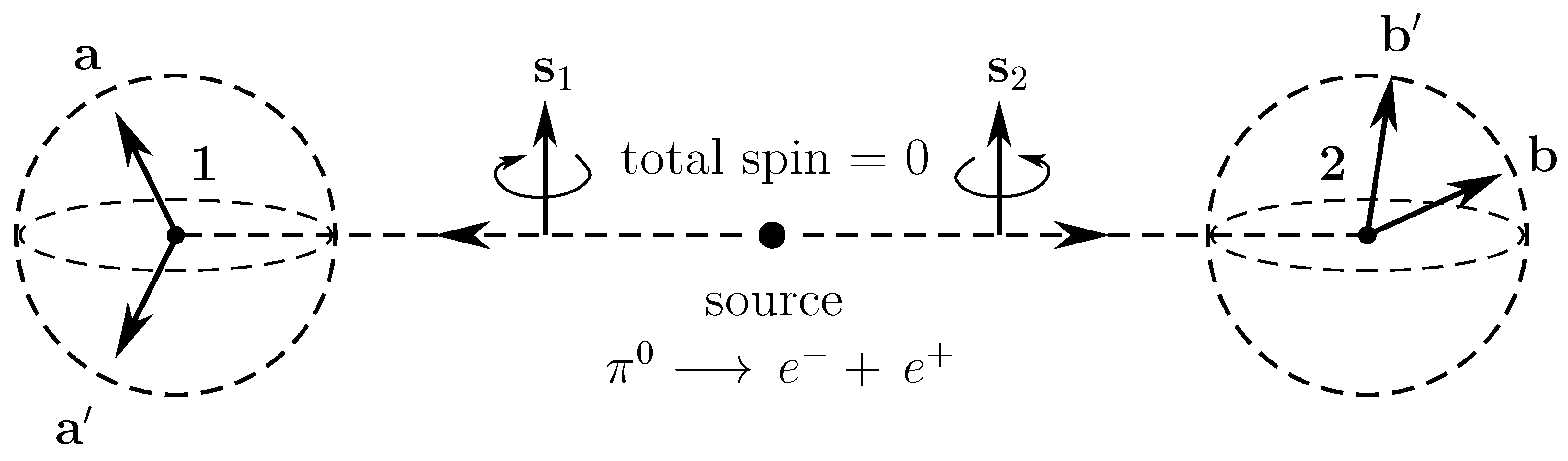
1.2. Special Case of the Singlet State and EPR-Bohm Observables
Apart from the hidden variables , the result of Alice depends only on the measurement context , chosen freely by Alice, regardless of Bob’s actions [1]. And, likewise, apart from the hidden variables , the result of Bob depends only on the measurement context , chosen freely by Bob, regardless of Alice’s actions. In particular, the function does not depend on or and the function does not depend on or . Moreover, the hidden variables do not depend on either , , , or [11].
1.3. Mathematical Core of Bell’s Theorem
1.3.1. Standard derivation of the Bell-CHSH inequalities (26)
1.3.2. Converse Derivation of the Additivity (23) by assuming (26)
1.4. Additivity of Expectation Values (23) Is An Unjustified Assumption, Equivalent to the Thesis to Be Proven
1.5. Additivity of expectation values is respected by quantum states
1.6. Additivity of Expectation Values Does Not Hold for Dispersion-Free States
1.7. Oversight and Circular Reasoning in the GHZ Variant of Bell’s Theorem
1.7.1. Expectation Functions for Non-Commuting Observables Cannot Be Multiplicative
1.7.2. Four-Particle Greenberger–Horne–Zeilinger State and the Associated Observables
1.7.3. Illegitimate Use of Multiplicative Expectation Functions and Eigenvalues in [20]
1.7.4. Correction of the Sign Mistake in the Derivation of Equation (16) in [20]
1.8. Hardy’s Variant of Bell’s Theorem in Not “a Proof of Non-Locality”
1.9. Conclusion: Bell’s Theorem Assumes Its Conclusion (petitio principii)
Appendix A Dynamical Equivalence of Quantum Mechanical Description and Einstein’s Description
Appendix B Demonstration of Linearity of the Expectation Function ψ,λ|Ω(c)|ψ,λ Assumed in (23)
Appendix C Separating the Commuting and Non-Commuting Parts of the Summed Operator (40)

Appendix D Establishing bounds on the magnitude of the vector n defined in (uid52)
References
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics. 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Einstein, A. Quantum mechanics and reality. Dialectica. 1948, 2, 320–324. [Google Scholar] [CrossRef]
- Von Neumann, J. 1955 Mathematical Foundations of Quantum Mechanics. Princeton, NJ: Princeton University Press.
- Coleman, S.; Mandula, J. All possible symmetries of the S matrix. Physical Review. 1967, 159, 1251–1256. [Google Scholar] [CrossRef]
- Christian, J. Bell’s theorem versus local realism in a quaternionic model of physical space. IEEE Access. 2019, 7, 133388–133409. [Google Scholar] [CrossRef]
- Christian, J. 2007 Disproof of Bell’s theorem by Clifford algebra valued local variables. [CrossRef]
- Christian, J. 2014 Disproof of Bell’s Theorem: Illuminating the Illusion of Entanglement. Second Edition. Boca Raton, Florida: Brwonwalker Press.
- Christian, J. Macroscopic observability of spinorial sign changes under 2π rotations. Int. J. Theor. Phys. 2015, 54, 20–46. [Google Scholar] [CrossRef]
- Christian, J. 2017 Oversights in the respective theorems of von Neumann and Bell are homologous.
- Christian, J. Quantum correlations are weaved by the spinors of the Euclidean primitives. R. Soc. Open Sci. 2018, 5, 180526. [Google Scholar] [CrossRef] [PubMed]
- Christian, J. Dr. Bertlmann’s socks in the quaternionic world of ambidextral reality. IEEE Access. 2020, 8, 191028–191048. [Google Scholar] [CrossRef]
- Christian, J. Reply to “Comment on `Dr. Bertlmann’s socks in the quaternionic world of ambidextral reality.” IEEE Access. 2021, 9, 72161–72171. [Google Scholar] [CrossRef]
- Christian, J. Reply to “Comment on `Bell’s theorem versus local realism in a quaternionic model of physical space. ” IEEE Access. 2022, 10, 14429–14439. [Google Scholar] [CrossRef]
- Christian, J. 2022 Local origins of quantum correlations rooted in geometric algebra.
- Christian, J. Symmetric derivation of singlet correlations in a quaternionic 3-sphere model. Int. J. Theor. Phys. 2024, 63, 126. [Google Scholar] [CrossRef]
- Christian, J. Response to ‘Comment on “Quantum correlations are weaved by the spinors of the Euclidean primitives. ”’ R. Soc. Open Sci. 2022, 9, 220147. [Google Scholar] [CrossRef] [PubMed]
- Clauser, J.F.; Shimony, A. Bell’s theorem: Experimental tests and implications. Rep. Prog. Phys. 1978, 41, 1881–1927. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 10, 880–884. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A. Experimental consequences of objective local theories. Phys. Rev. D. 1974, 10, 526–535. [Google Scholar] [CrossRef]
- Greenberger, D.M.; Horne, M.A.; Shimony, A.; Zeilinger, A. Bell’s theorem without inequalities. Am. J. Phys. 1990, 58, 1131–1143. [Google Scholar] [CrossRef]
- Hardy, L. Nonlocality for two particles without inequalities for almost all entangled states. Phys. Rev. Lett. 1993, 71, 1665–1668. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Christian, J. 2009 Disproofs of Bell, GHZ, and Hardy type theorems and the illusion of entanglement. (doi:10.48550/arXiv.0904.4259); Reproduced as Chapter 6 in Ref. [7]. [CrossRef]
- Bell, J.S. On the problem of hidden variables in quantum mechanics. Rev. Mod. Phys. 1966, 38, 447–452. [Google Scholar] [CrossRef]
- Gudder, S. On hidden-variable theories. Journal of Mathematical Physics. 1970, 11, 431–436. [Google Scholar] [CrossRef]
- Robertson, H.P. The uncertainty principle. Phys. Rev. 1929, 34, 163–164. [Google Scholar] [CrossRef]
- Belinfante, F.J. 1973 A Survey of Hidden-Variables Theories. New York, NY: Pergamon Press.
- Gleason, A.M. Measures on the closed subspaces of a Hilbert space. J. Math. Mech. 1957, 6, 885–893. [Google Scholar] [CrossRef]
- Shimony, A. Contextual hidden variables theories and Bell’s inequalities. Brit. J. Phil. Sci. 1984, 35, 25–45. [Google Scholar] [CrossRef]
- Hermann, G. 1935 Die naturphilosophischen Grundlagen der Quantenmechanik. Abhandlungen der Fries’schen Schule 6, 75–152 (doi.org/10.1007/978-3-658-16241-2_12) — For English translation, see Chapter 15 of “Grete Hermann – Between Physics and Philosophy”, Crull E. and Bacciagaluppi G., eds., Springer, 2016, 239–278. [CrossRef]
- Bohm, D. 1951 Quantum Theory. Englewood Cliffs, NJ: Prentice-Hall. pp 614–623.
- Mermin, N.D.; Schack, R. Homer nodded: von Neumann’s surprising oversight. Found. Phys. 2018, 48, 1007–1020. [Google Scholar] [CrossRef]
- Bohm, D.; Bub, J. A proposed solution of the measurement problem in quantum mechanics by a hidden variable theory. Rev. Mod. Phys. 1966, 38, 453–469. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




