Bell's Theorem Begs the Question

1. Introduction

Bell’s theorem [1] is an impossibility argument (or “proof”) that claims that no locally causal and realistic hidden variable theory envisaged by Einstein [2] that could “complete” quantum theory can reproduce all of the predictions of quantum theory. But some such claims of impossibility in physics are known to harbor unjustified assumptions. In this paper, I show that Bell’s theorem against locally causal hidden variable theories is no exception. It is no different, in this respect, from von Neumann’s theorem against all hidden variable theories [3], or the Coleman-Mandula theorem overlooking the possibilities of supersymmetry [4]. The implicit and unjustified assumptions underlying the latter two theorems seemed so innocuous to many that they escaped notice for decades. By contrast, Bell’s theorem has faced skepticism and challenges by many from its very inception (cf. footnote 1 in [5]), including by me [5,6,7,8,9,10,11,12,13,14,15,16], because it depends on a number of questionable implicit and explicit physical assumptions that are not difficult to recognize [10,16]. In what follows, I bring out one such assumption and demonstrate that Bell’s theorem is based on a circular argument [9]. It unjustifiably assumes the additivity of expectation values for dispersion-free states of hidden variable theories for non-commuting observables involved in the Bell-test experiments [17], which is tautologous to assuming the bounds of $\pm 2$ on the Bell-CHSH sum of expectation values. Its premises thus assume in a different guise what it sets out to prove. Once this oversight is ameliorated from Bell’s argument, the local-realistic bounds on the Bell-CHSH sum of expectation values work out to be $\pm 2\sqrt{2}$ instead of $\pm 2$, thereby mitigating the conclusion of Bell’s theorem. As a result, what is ruled out by the Bell-test experiments is not local realism but the additivity of expectation values, which does not hold for non-commuting observables in dispersion-free states of hidden variable theories to begin with.

2. Heuristics for completing quantum mechanics

The goal of any hidden variable theory [3,18,19] is to reproduce the statistical predictions encoded in the quantum states $|\psi \rangle \in \mathcal{H}$ of physical systems using hypothetical dispersion-free states $|\psi ,\lambda ):=\left\{\right|\psi \rangle ,\lambda \}\in \mathcal{H}\otimes \mathcal{L}$ that have no inherent statistical character, where the Hilbert space $\mathcal{H}$ is extended by the space $\mathcal{L}$ of hidden variables $\lambda$, which are hypothesized to “complete” the states of the physical systems as envisaged by Einstein [2]. If the values of $\lambda \in \mathcal{L}$ can be specified in advance, then the results of any measurements on a given physical system are uniquely determined.

To appreciate this, recall that expectation value of the square of any self-adjoint operator $\Omega \in \mathcal{H}$ in a normalized quantum mechanical state $|\psi \rangle$ and the square of the expectation value of $\Omega$ will not be equal to each other in general:

$$\langle \psi \left|{\Omega }^2\right|\psi \rangle \ne {〈\psi \left|\Omega \right|\psi 〉}^2.$$

(1)

This gives rise to inherent statistical uncertainty in the value of $\Omega$, indicating that the state $|\psi \rangle$ is not dispersion-free:

$$\Delta \Omega =\sqrt{\langle \psi \left|\right\{\Omega -{\langle \psi |\Omega |\psi \rangle \}}^2|\psi \rangle }\ne 0.$$

(2)

By contrast, in a normalized dispersion-free state $|\psi ,\lambda )$ of hidden variable theories formalized by von Neumann [3], the expectation value of $\Omega$, by hypothesis, is equal to one of its eigenvalues $\omega \left(\lambda \right)$, determined by the hidden variables$\lambda$,

$$\left(\psi ,\lambda |\Omega |\psi ,\lambda \right)=\omega \left(\lambda \right)⟺\Omega |\psi ,\lambda )=\omega \left(\lambda \right)|\psi ,\lambda ),$$

(3)

so that a measurement of $\Omega$ in the state $\left|\psi ,\lambda \right)$ would yield the result $\omega \left(\lambda \right)$ with certainty. How this can be accomplished in a dynamical theory of measurement process remains an open question [18]. But accepting the hypothesis (3) implies

$$(\psi ,\lambda |{\Omega }^2|\psi ,\lambda )={(\psi ,\lambda |\Omega |\psi ,\lambda )}^2.$$

(4)

Consequently, unlike in a quantum sate $|\psi \rangle$, in a dispersion-free state $|\psi ,\lambda )$ observables $\Omega$ have no inherent uncertainty:

$$\Delta \Omega =\sqrt{(\psi ,\lambda |{\{\Omega -\left(\psi ,\lambda |\Omega |\psi ,\lambda \right)\}}^2|\psi ,\lambda )}=0.$$

(5)

The expectation value of $\Omega$ in the quantum state $|\psi \rangle$ can then be recovered by integrating over the hidden variables$\lambda$:

$$〈\psi |\Omega |\psi 〉={\int }_{\mathcal{L}}\left(\psi ,\lambda |\Omega |\psi ,\lambda \right)p\left(\lambda \right)d\lambda ={\int }_{\mathcal{L}}\omega \left(\lambda \right)p\left(\lambda \right)d\lambda ,$$

(6)

where $p\left(\lambda \right)$ denotes the normalized probability distribution over the space $\mathcal{L}$ of thus hypothesized hidden variables. The quantum mechanical dispersion (2) in the measured value of the observer $\Omega$ can thus be interpreted as due to thedistribution $p\left(\lambda \right)$ in the values of the hidden variables $\lambda$ over the statistical ensemble of the physical systems measured.

As it stands, this prescription amounts to assignment of unique eigenvalues $\omega \left(\lambda \right)$ to all observables $\Omega$ simultaneously, regardless of whether they are actually measured. In other words, according to (6) every physical quantity of a given system represented by $\Omega$ would possess a unique preexisting value, irrespective of any measurements being performed. The prescription (6) thus mathematically encodes Einstein’s conception of realism. In [2], Einstein explained his point of view in terms of the position and momentum of a free particle as follows: “The (free) particle really has a definite position and a definite momentum, even if they cannot both be ascertained by measurement in the same individual case [as in quantum mechanics]. According to this point of view, the $\psi$-function represents an incomplete description of the real state of affairs.” The acceptance of this point of view — Einstein continued — “would lead to an attempt toobtain a complete description of the real state of affairs as well as the incomplete one (my emphasis), and to discover physical laws for such a description.” Accordingly, the left-hand side of the first equality in (6) provides the incomplete description of the system and its right-hand side provides the complete one, with all possible statements one can make about the system encoded in the expectation values of the observables being measured in the states of the system [3].

In Section 2 of [18], Bell works out an instructive example to illustrate how the prescription (6) works for a system of two-dimensional Hilbert space. It fails, however, for Hilbert spaces of dimensions greater than two, because in higher dimensions degeneracies prevent simultaneous assignments of unique eigenvalues to all observables in dispersion-free states $\left|\psi ,\lambda \right)$ dictated by the ansatz (3), giving contradictory values for the same physical quantities. This was proved independently by Bell [18], Kochen and Specker [20], and Belinfante [21], as a corollary to Gleason’s theorem [22,23].

These proofs – known as the Kochen-Specker theorem – do not exclude contextual hidden variable theories in which the complete state $|\psi ,\lambda )$ of a system assigns unique values to physical quantities only relative to experimental contexts [19,23]. If we denote the observables as $\Omega \left(c\right)$ with c being the environmental contexts of their measurements, then thenon-contextual prescription (6) can be easily modified to accommodate contextual hidden variable theories as follows:

$$〈\psi |\Omega (c\left)\right|\psi 〉={\int }_{\mathcal{L}}\left(\psi ,\lambda |\Omega (c\left)\right|\psi ,\lambda \right)p\left(\lambda \right)d\lambda ={\int }_{\mathcal{L}}\omega (c,\lambda )p\left(\lambda \right)d\lambda .$$

(7)

Each observable $\Omega \left(c\right)$ is still assigned a unique eigenvalue $\omega (c,\lambda )$, but now determined cooperatively by the complete state $|\psi ,\lambda )$ of the system and the state c of its environmental contexts. Consequently, even though some of its features are no longer intrinsic to the system, contextual hidden variable theories do not have the inherent statistical character of quantum mechanics, because outcome of an experiment is a cooperative effect just as it is in classical physics [23].Therefore, such theories interpret quantum entanglement at the level of the complete state $|\psi ,\lambda )$ only epistemically.

For our purposes here, it is also important to recall that in the Hilbert space formulation of quantum mechanics [3] the correspondence between observables and Hermitian operators is one-to-one. Moreover, a sum $\tilde{\Omega }\left(\tilde{c}\right)={\sum }_{i=1}^n{\Omega }_i\left(c_i\right)$ of several observables such as ${\Omega }_1\left(c_1\right),{\Omega }_2\left(c_2\right),{\Omega }_3\left(c_3\right),\cdots ,{\Omega }_n\left(c_n\right)$ is also an observable representing a physical quantity, and consequently the sum of the expectation values of ${\Omega }_i\left(c_i\right)$ is the expectation value of the summed operator $\tilde{\Omega }\left(\tilde{c}\right)$,

$$\sum _{i=1}^n〈\psi |{\Omega }_i\left(c_i\right)|\psi 〉=\langle \psi |\left[\sum _{i=1}^n{\Omega }_i\left(c_i\right)\right]|\psi \rangle ,$$

(8)

regardless of whether the observables are simultaneously measurable or mutually commutative [18]. The question then is, since within any contextual hidden variable theory characterized by (7) all of the observables ${\Omega }_i\left(c_i\right)$ and their sum $\tilde{\Omega }\left(\tilde{c}\right)$ are assigned unique eigenvalues ${\omega }_i(c_i,\lambda )$ and $\tilde{\omega }(\tilde{c},\lambda )$, respectively, would these eigenvalues satisfy the equality

$$\sum _{i=1}^n\left[{\int }_{\mathcal{L}}{\omega }_i(c_i,\lambda )p\left(\lambda \right)d\lambda \right]\stackrel{?}{=}{\int }_{\mathcal{L}}\left[\sum _{i=1}^n{\omega }_i(c_i,\lambda )\right]p\left(\lambda \right)d\lambda$$

(9)

in dispersion-free states $|\psi ,\lambda )$ of physical systems in analogy with the linear quantum mechanical relation (8) above? The answer is: Not in general, because the eigenvalue $\tilde{\omega }(\tilde{c},\lambda )$ of the summed operator $\tilde{\Omega }\left(\tilde{c}\right)$ is not equal to the sum ${\sum }_{i=1}^n{\omega }_i(c_i,\lambda )$ of eigenvalues ${\omega }_i(c_i,\lambda )$ for given $\lambda$, unless the constituent observables ${\Omega }_i\left(c_i\right)$ are mutually commutative. In other words, $\tilde{\omega }(\tilde{c},\lambda )\ne {\sum }_{i=1}^n{\omega }_i(c_i,\lambda )$ in general, and therefore the correct counterpart of relation (8) is not (9) but

$$\sum _{i=1}^n\left[{\int }_{\mathcal{L}}{\omega }_i(c_i,\lambda )p\left(\lambda \right)d\lambda \right]={\int }_{\mathcal{L}}\tilde{\omega }(\tilde{c},\lambda )p\left(\lambda \right)d\lambda .$$

(10)

As Bell points out in Section 3 of [18], the linear relation (8) is an unusual property of quantum mechanical states $|\psi \rangle$. There is no reason to demand it individually of the dispersion-free states $|\psi ,\lambda )$, whose function is to reproduce themeasurable features of quantum systems only when averaged over, as in (7). There is no reason why the value of $\Omega \left(c\right)$should not be determined by some nonlinear function $\left(\psi ,\lambda |\Omega (c\left)\right|\psi ,\lambda \right)$. I will come back to this issue in Section 5.

In [18], Bell explains this non-linearity using spin components of a spin-$\frac{1}{2}$ particle. Suppose we make a measurement of the component ${\sigma }_x$ of the spin with a Stern-Gerlach magnet suitably oriented in $\mathrm{I}{\mathrm{R}}^3$. That would yield an eigenvalue $s_x$ of ${\sigma }_x$ as a result. However, if we wish to measure the component ${\sigma }_y$ of the spin, then that would require a different orientation of the magnet in $\mathrm{I}{\mathrm{R}}^3$, and would give a different eigenvalue, $s_y$ of ${\sigma }_y$, as a result. Moreover, a measurement of the sum of the x- and y-components of the spin, ${\sigma }_x+{\sigma }_y$, would again require a very different orientation of the magnet in $\mathrm{I}{\mathrm{R}}^3$. Therefore, the result obtained as an eigenvalue of the summed operators ${\sigma }_x+{\sigma }_y$ will not be the sum $s_x+s_y$ of an eigenvalue of the operator ${\sigma }_x$ added linearly to an eigenvalue of the operator ${\sigma }_y$. Indeed, the eigenvalues of ${\sigma }_x$ and ${\sigma }_y$ are both $\pm 1$, while the eigenvalues of ${\sigma }_x+{\sigma }_y$ are $\pm \sqrt{2}$, so a linear relation cannot hold. As Bell points outin [18], the additivity of expectation values $\langle \psi |{\sigma }_x|\psi \rangle +\langle \psi |{\sigma }_y|\psi \rangle =\langle \psi |{\sigma }_x+{\sigma }_y|\psi \rangle$ is a rather unusual property of the quantum states $|\psi \rangle$. The linearity of it is effectuated in quantum mechanics by promoting observable quantities to self-adjoint operators [24]. It does not hold for the dispersion-free states $|\psi ,\lambda )$ of hidden variable theories in general because the eigenvalues of non-commuting observables such as ${\sigma }_x$ and ${\sigma }_y$ do not add linearly, as we noted above. Consequently, the additivity relation (8) that holds for quantum states would not hold for the dispersion-free states.

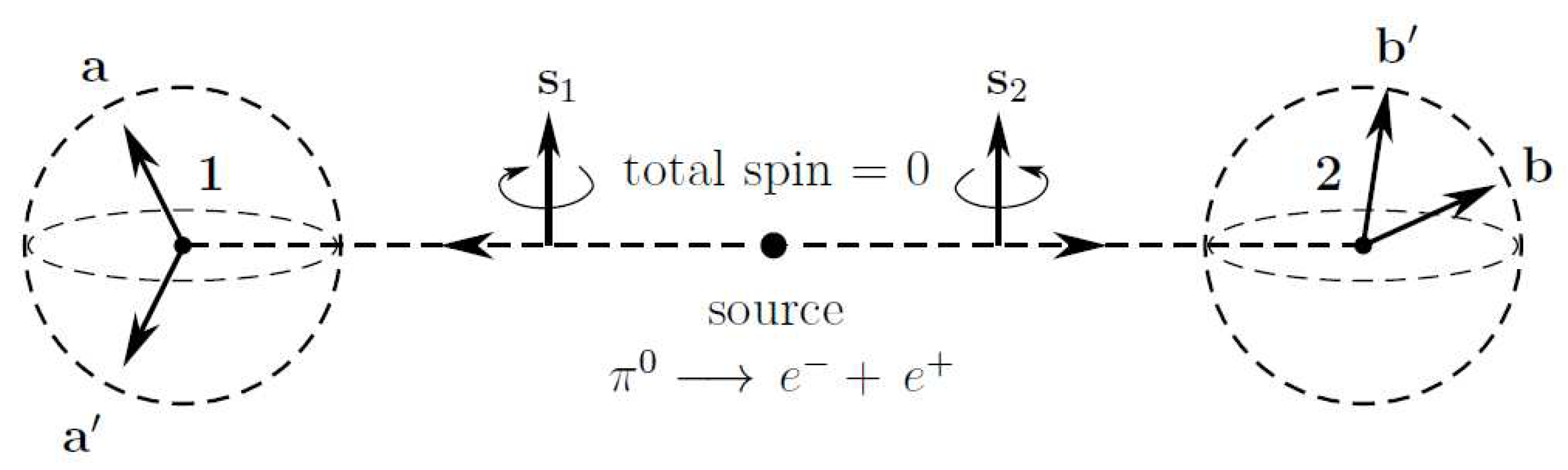
3. Special case of the singlet state and EPR-Bohm observables

Now, the proof of Bell’s famous theorem [1] is based on Bohm’s spin version of the EPR’s thought experiment [25], which involves an entangled pair of spin-$\frac{1}{2}$ particles emerging from a source and moving freely in opposite directions, with particles 1 and 2 subject, respectively, to spin measurements along independently chosen unit directions $\mathbf{a}$ and $\mathbf{b}$ by Alice and Bob, who are stationed at a spacelike separated distance from each other (see Figure 1). If initially the pair has vanishing total spin, then the quantum mechanical state of the system is described by the entangled singlet state

$$|\Psi \rangle =\frac{1}{\sqrt{2}}\left\{{|\mathbf{k},+\rangle }_1{\otimes |\mathbf{k},-\rangle }_2{-|\mathbf{k},-\rangle }_1\otimes {|\mathbf{k},+\rangle }_2\right\},$$

(11)

where $\mathbf{k}$ is an arbitrary unit vector in $\mathrm{I}{\mathrm{R}}^3$ and

$$\sigma ·\mathbf{k}|\mathbf{k},\pm \rangle =\pm |\mathbf{k},\pm \rangle$$

(12)

defines quantum mechanical eigenstates in which the two fermions have spins “up” or “down” in the units of $\hslash =2$, with $\sigma$ being the Pauli spin “vector” $({\sigma }_x,{\sigma }_y,{\sigma }_z)$. Once the state (11) is prepared, the observable $\Omega \left(c\right)$ of interest is

$$\Omega \left(c\right)={\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b},$$

(13)

whose possible eigenvalues are

$$\omega (c,\lambda )=\mathcal{A}\mathcal{B}(\mathbf{a},\mathbf{b},\lambda )=\pm 1,$$

(14)

where $\mathcal{A}=\pm 1$ and $\mathcal{B}=\pm 1$ are the results of spin measurements made jointly by Alice and Bob along their randomly chosen detector directions $\mathbf{a}$ and $\mathbf{b}$. In the singlet state (11), the joint observable (13) predicts sinusoidal correlations $\langle \Psi |{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}|\Psi \rangle =-\mathbf{a}·\mathbf{b}$ between the values of the spins observed about the freely chosen contexts $\mathbf{a}$ and $\mathbf{b}$ [6].

For locally contextual hidden variable theories there is a further requirement that the results of local measurements must be describable by functions that respect local causality, as first envisaged by Einstein [2] and later formulated mathematically by Bell [1]. It can be satisfied by requiring that the eigenvalue $\omega (c,\lambda )$ of the observable $\Omega \left(c\right)$ in (13) representing the joint result $\mathcal{A}\mathcal{B}(\mathbf{a},\mathbf{b},\lambda )=\pm 1$ is factorizable as $\omega (c,\lambda )={\omega }_1(c_1,\lambda ){\omega }_2(c_2,\lambda )$, or in Bell’s notation as

$$\mathcal{A}\mathcal{B}(\mathbf{a},\mathbf{b},\lambda )=\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda ),$$

(15)

with the factorized functions $\mathcal{A}(\mathbf{a},\lambda )=\pm 1$ and $\mathcal{B}(\mathbf{b},\lambda )=\pm 1$ satisfying the following condition of local causality:

Apart from the hidden variables $\lambda$, the result $\mathcal{A}=\pm 1$ of Alice depends only on the measurement context $\mathbf{a}$, chosen freely by Alice, regardless of Bob’s actions [1]. And, likewise, apart from the hidden variables $\lambda$, the result $\mathcal{B}=\pm 1$ of Bob depends only on the measurement context $\mathbf{b}$, chosen freely by Bob, regardless of Alice’s actions. In particular, the function $\mathcal{A}(\mathbf{a},\lambda )$ does not depend on $\mathbf{b}$ or $\mathcal{B}$ and the function $\mathcal{B}(\mathbf{b},\lambda )$ does not depend on $\mathbf{a}$ or $\mathcal{A}$. Moreover, the hidden variables $\lambda$ do not depend on either $\mathbf{a}$, $\mathbf{b}$, $\mathcal{A}$, or $\mathcal{B}$ [11].

The expectation value $\mathcal{E}(\mathbf{a},\mathbf{b})$ of the joint results in the dispersion-free state $|\psi ,\lambda )$ should then satisfy the condition

$$\langle \Psi |{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}|\Psi \rangle =\mathcal{E}(\mathbf{a},\mathbf{b}):={\int }_{\mathcal{L}}\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )p\left(\lambda \right)d\lambda ,$$

(16)

where the hidden variables $\lambda$ originate from a source located in the overlap of the backward light cones of Alice and Bob, and the normalized probability distribution $p\left(\lambda \right)$ is assumed to remain statistically independent of the contexts $\mathbf{a}$ and $\mathbf{b}$ so that $p\left(\lambda \right|\mathbf{a},\mathbf{b})=p(\lambda )$, which is a reasonable assumption. In fact, relaxing this assumption to allow $p\left(\lambda \right)$ to depend on $\mathbf{a}$ and $\mathbf{b}$ introduces a form of non-locality, as explained by Clauser and Horne in footnote 13 of [26]. Then, since $\mathcal{A}(\mathbf{a},\lambda )=\pm 1$ and $\mathcal{B}(\mathbf{b},\lambda )=\pm 1$, their product $\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )=\pm 1$, setting the following bounds on $\mathcal{E}(\mathbf{a},\mathbf{b})$:

$$-1⩽\mathcal{E}(\mathbf{a},\mathbf{b})⩽+1.$$

(17)

These bounds are respected not only by local hidden variable theories but also by quantum mechanics and experiments.

4. Mathematical core of Bell’s theorem

By contrast, at the heart of Bell’s theorem is a derivation of the bounds of $\pm 2$ on an ad hoc sum of the expectation values $\mathcal{E}(\mathbf{a},\mathbf{b})$ of local results $\mathcal{A}(\mathbf{a},\lambda )$ and $\mathcal{B}(\mathbf{b},\lambda )$, recorded at remote observation stations by Alice and Bob, from four different sub-experiments involving measurements of non-commuting observables such as ${\sigma }_1·\mathbf{a}$ and ${\sigma }_1·{\mathbf{a}}^{\prime }$ [1,17]:

$$\mathcal{E}(\mathbf{a},\mathbf{b})+\mathcal{E}(\mathbf{a},{\mathbf{b}}^{\prime })+\mathcal{E}({\mathbf{a}}^{\prime },\mathbf{b})-\mathcal{E}({\mathbf{a}}^{\prime },{\mathbf{b}}^{\prime }).$$

(18)

Alice can freely choose a detector direction $\mathbf{a}$ or ${\mathbf{a}}^{\prime }$, and likewise Bob can freely choose a detector direction $\mathbf{b}$ or ${\mathbf{b}}^{\prime }$, to detect, at a space-like distance from each other, the spins of fermions they receive from the common source. Then, from (17), we can immediately read off the upper and lower bounds on the combination (18) of expectation values:

$$-4⩽\mathcal{E}(\mathbf{a},\mathbf{b})+\mathcal{E}(\mathbf{a},{\mathbf{b}}^{\prime })+\mathcal{E}({\mathbf{a}}^{\prime },\mathbf{b})-\mathcal{E}({\mathbf{a}}^{\prime },{\mathbf{b}}^{\prime })⩽+4.$$

(19)

4.0.1. Standard derivation of the Bell-CHSH inequalities (23) 

The next step in Bell’s derivation of the bounds $\pm 2$ instead of $\pm 4$ is the assumption of the additivity of expectation values:

$$\begin{array}{cc}\hfill & \mathcal{E}(\mathbf{a},\mathbf{b})+\mathcal{E}(\mathbf{a},{\mathbf{b}}^{\prime })+\mathcal{E}({\mathbf{a}}^{\prime },\mathbf{b})-\mathcal{E}({\mathbf{a}}^{\prime },{\mathbf{b}}^{\prime })\hfill \\ \hfill & ={\int }_{\mathcal{L}}\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )p\left(\lambda \right)d\lambda +{\int }_{\mathcal{L}}\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )p\left(\lambda \right)d\lambda \hfill \\ \hfill & +{\int }_{\mathcal{L}}\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )p\left(\lambda \right)d\lambda -{\int }_{\mathcal{L}}\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )p\left(\lambda \right)d\lambda \hfill \\ \hfill & ={\int }_{\mathcal{L}}\left\{\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )+\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )+\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )-\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )\right\}p\left(\lambda \right)d\lambda .\hfill \end{array}$$

(20)

We will have much to discuss about this seemingly harmless mathematical step employing the built-in linear additivity of integrals. I will demonstrate in SectionSection 5 that, far from being harmless, it is, in fact, an unjustified assumption that harbors a profound mistake of assuming the very thesis of the theorem to be proven, just as von Neumann’s theorem did [9,18,24,27,28]. It assumes, without proof, that linear additivity of integrals leading to (20) can be meaningfully applied, not only to the eigenvalues of commuting observables but also to the eigenvalues of non-commuting observables that cannot be measured simultaneously. But, as we saw in the paragraph following equation (10), this assumption is quite mistaken. However, if we overlook this mistake and accept equality (20), then the bounds of $\pm 2$ on the Bell-CHSHcombination (18) of expectation values are not difficult to work out by rewriting the integrand on its right-hand side as

$$\mathcal{A}(\mathbf{a},\lambda )\left\{\mathcal{B}(\mathbf{b},\lambda )+\mathcal{B}({\mathbf{b}}^{\prime },\lambda )\right\}+\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\left\{\mathcal{B}(\mathbf{b},\lambda )-\mathcal{B}({\mathbf{b}}^{\prime },\lambda )\right\}.$$

(21)

Since $\mathcal{B}(\mathbf{b},\lambda )=\pm 1$, if $|\mathcal{B}(\mathbf{b},\lambda )+\mathcal{B}({\mathbf{b}}^{\prime },\lambda )|=2$, then $|\mathcal{B}(\mathbf{b},\lambda )-\mathcal{B}({\mathbf{b}}^{\prime },\lambda )|=0$, and vice versa. Consequently, since $\mathcal{A}(\mathbf{a},\lambda )=\pm 1$, the integrand (21) is bounded by $\pm 2$ and the absolute value of the last integral in (20) does not exceed2:

$$-2⩽{\int }_{\mathcal{L}}\left\{\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )+\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )+\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )-\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )\right\}p\left(\lambda \right)d\lambda ⩽+2.$$

(22)

Therefore, the equality (20) implies that the absolute value of the combination of expectation values is bounded by 2:

$$-2⩽\mathcal{E}(\mathbf{a},\mathbf{b})+\mathcal{E}(\mathbf{a},{\mathbf{b}}^{\prime })+\mathcal{E}({\mathbf{a}}^{\prime },\mathbf{b})-\mathcal{E}({\mathbf{a}}^{\prime },{\mathbf{b}}^{\prime })⩽+2.$$

(23)

But since the bounds on (18) predicted by quantum mechanics and observed in experiments are $\pm 2\sqrt{2}$, Bell concludes that no local and realistic theory envisaged by Einstein can reproduce the statistical predictions of quantum mechanics. In particular, contextual hidden variable theories specified by (7) that respect the factorizability (15) are not viable.

In many derivations of (23) in the literature, factorized probabilities of observing binary measurement results are employed rather than measurement results themselves I have used in (15) in my derivation following Bell [1,17]. But employing probabilities would only manage to obfuscate the logical flaw in Bell’s argument I intend to bring out here.

4.0.2. Converse derivation of the additivity (20) by assuming (23) 

Now, it is not difficult to demonstrate the converse of the above derivation in which the additivity of expectation values (20) is derived by assuming the stringent bounds of $\pm 2$ on the sum (18). Employing (16), (18) can be writtenas

$${\int }_{\mathcal{L}}\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )p\left(\lambda \right)d\lambda +{\int }_{\mathcal{L}}\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )p\left(\lambda \right)d\lambda +{\int }_{\mathcal{L}}\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )p\left(\lambda \right)d\lambda -{\int }_{\mathcal{L}}\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )p\left(\lambda \right)d\lambda .$$

(24)

Since each product $\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )$ in the above integrals is equal to $\pm 1$, each of the four integrals is bounded by $\pm 1$:

$$-1⩽{\int }_{\mathcal{L}}\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )p\left(\lambda \right)d\lambda ⩽+1.$$

(25)

Thus the sum of four integrals in (24) is bounded by $\pm 4$, not $\pm 2$. However, we started with (23), which contends that the sum of integrals in (24) is bounded by $\pm 2$. But the only way to reduce the bounds on (24) from $\pm 4$ to $\pm 2$ without compromising the independence of the results $\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )$, etc., or of their averages appearing in the sum (24), orviolating the rules of anti-derivatives, is by equating the sum of integrals in (24) to the following integral of the sum:

$${\int }_{\mathcal{L}}\left\{\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )+\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )+\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )-\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )\right\}p\left(\lambda \right)d\lambda .$$

(26)

To be sure, we can easily reduce the bounds on the sum in (24) from $\pm 4$ to $\pm 2$, for example, by setting the last two integrals in it equal to each other, with the minus sign between them. That would reduce (24) to a sum of only the first two integrals, which is then easily seen to be bounded by $\pm 2$ using (25). But to achieve this, we have compromised the independence of at least the last two sub-ensemble averages, which is not permitted by the conditions adhered to in Bell’s argument. Similarly, again as an example, we can set the results themselves in the last two integrals in (24) equal to each other: $\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )=\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )$. That would again reduce (24) to the sum of only the first two integrals, which is then easily seen to be bounded by $\pm 2$ using (25). But we have again compromised the independence of the last two results to achieve this, which is not permitted. One can also easily reduce the bounds on (24) from $\pm 4$ to $\pm 2$ by violating some of the rules of anti-derivatives, or of statistical averages, etc., as an extreme measure, but that again amounts to forfeiting the game from the start. Thus, the only admissible means of reducing the bounds on (24) from $\pm 4$ to $\pm 2$ is by using the standard rules of anti-derivatives that allow us to equate the sum ofintegrals appearing in (24) to the integral (26) of the sum of eigenvalues, which, as we saw in (22), is bounded by $\pm 2$.

We have thus derived the additivity of expectation values (20) by imposing the bounds of $\pm 2$ on the Bell-CHSH sum (18) as our starting assumption. Therefore, given the previous derivation that led us to (23) by assuming (20) and the current derivation that led us to (20) by assuming (23), we have proved that the assumption (20) of the additivity of expectation values is tautologous to assuming the bounds of $\pm 2$ on the Bell-CHSH sum (18) of expectation values.

5. Additivity of expectation values (20) is an unjustified assumption, equivalent to the thesis to be proven

The key step that led us to the bounds of $\pm 2$ on (18) that are more restrictive than $\pm 2\sqrt{2}$ is the step (20) of the linear additivity of expectation values. In what follows, I will demonstrate that this step is, in fact, an unjustified assumption, equivalent to the main thesis of the theorem to be proven, just as it is in von Neumann’s now discredited theorem [9,18,24,27,28]. But this fact is obscured by the seemingly innocuous built-in linear additivity of integrals used in step (20). However, as we noted around (10) and will be further demonstrated in Section 7, the built-in linear additivity of integrals is physically meaningful only for simultaneously measurable or commuting observables [24,27]. It is, therefore, not legitimate to invoke it at step (20) without proof. Step (20) would be valid also in classical physics in which the value of a sum of observable quantities would be the same as the sum of the values each quantity would take separately, because, unlike in quantum mechanics, they would all be simultaneously measurable, yielding only sharp values. Perhaps for this reason it is usually not viewed as an assumption but mistaken for a benign mathematical step. It is also sometimes claimed to be necessitated by Einstein’s requirement of realism [2]. But I will soon explain why it is a much overlooked unjustified assumption, and demonstrate in Section 7 that, far from being required by realism, the right-hand side of step (20), in fact, contradicts realism, which requires that every observable of a physical system,including any sums of observables, must be assigned a correct eigenvalue, quantifying one of its preexisting properties.

Moreover, realism has already been adequately accommodated by the very definition of the local functions $\mathcal{A}(\mathbf{a},\lambda )$ and $\mathcal{B}(\mathbf{b},\lambda )$ and their counterfactual juxtaposition on the left-hand side of (20), as contextually existing properties of the system. Evidently, while a result in only one of the four expectation values corresponding to a sub-experiment that appears on the left-hand side of (20) can be realized in a given run of a Bell-test experiment, the remaining three results appearing on that side are realizable at least counterfactually, thus fulfilling the requirement of realism [9]. Therefore, the requirement of realism does not necessitate the left-hand side of (20) to be equated with its right-hand side in the derivation of (23). Realism requires definite results $\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )$ to exist as eigenvalues only counterfactually, not allfour at once, as they are written on the right-hand side of (20). What is more, as we will soon see, realism implicit in the prescription (7) requires the quantity (21) to be a correct eigenvalue of the summed operator (37), but it is not.

On the other hand, given the assumption $p\left(\lambda \right|\mathbf{a},\mathbf{b})=p(\lambda )$ of statistical independence and the additivity property of anti-derivatives, mathematically the equality (20) follows at once because of the linearity built into the integrals, provided we adopt a double standard for additivity: we reject (20) for von Neumann’s theorem as Bell did in [18], but accept it unreservedly for Bell’s theorem [9,24]. The binary properties of the functions $\mathcal{A}(\mathbf{a},\lambda )$ and $\mathcal{B}(\mathbf{b},\lambda )$ then immediately lead us to the bounds of $\pm 2$ on (18). But, as we saw above, assuming the bounds of $\pm 2$ on (18) leads, conversely, to the assumption (20) of additivity of expectation values. Thus, assuming the additivity of expectation values (20) is mathematically equivalent to assuming the bounds of $\pm 2$ on the Bell-CHSH sum (18). In other words, Bell’s argument presented in Section 4 assumes its conclusion (23) in the guise of assumption (20), by implicitly assuming that the expectation functions $(\Psi ,\lambda |\Omega \left(c\right)|\Psi ,\lambda )$ determining the eigenvalues $\omega (c,\lambda )$ of $\Omega \left(c\right)$ are linear [28]:

$$\tilde{\omega }(\tilde{c},\lambda )=(\Psi ,\lambda |\left[\sum _{i=1}^4{\Omega }_i\left(c_i\right)\right]|\Psi ,\lambda )=\sum _{i=1}^4(\Psi ,\lambda |{\Omega }_i\left(c_i\right)|\Psi ,\lambda )=\sum _{i=1}^4{\omega }_i(c_i,\lambda ).$$

(27)

But, as explained by Bohm and Bub in [28] (see Appendix A below), this assumed linearity of $(\Psi ,\lambda |\Omega \left(c\right)|\Psi ,\lambda )$ is unreasonably restrictive for dispersion-free states $|\Psi ,\lambda )$, because the observables defined in (13) are not simultaneously measurable. However, it allows us to reduce the following correct relation within quantum mechanics as well as hidden variable theories,

$$\sum _{i=1}^4\left[{\int }_{\mathcal{L}}(\Psi ,\lambda |{\Omega }_i\left(c_i\right)|\Psi ,\lambda )p\left(\lambda \right)d\lambda \right]={\int }_{\mathcal{L}}(\Psi ,\lambda |\left[\sum _{i=1}^4{\Omega }_i\left(c_i\right)\right]|\Psi ,\lambda )p\left(\lambda \right)d\lambda ,$$

(28)

to the relation

$$\sum _{i=1}^4\left[{\int }_{\mathcal{L}}(\Psi ,\lambda |{\Omega }_i\left(c_i\right)|\Psi ,\lambda )p\left(\lambda \right)d\lambda \right]={\int }_{\mathcal{L}}\left[\sum _{i=1}^4(\Psi ,\lambda |{\Omega }_i\left(c_i\right)|\Psi ,\lambda )\right]p\left(\lambda \right)d\lambda ,$$

(29)

which is the same as assumption (20), albeit written in a more general notation. The equality (28), on the other hand, is equivalent to the quantum mechanical relation (30) discussed below, which can be verified using the prescription (7).The same equality (28) is also valid for hidden variable theories, because it does not make the mistake of relying on the linearity assumption (27). This can be verified also using (7) and the ansatz (3). Thus, the innocuous-looking linear additivity of integrals in assumption (20), while mathematically correct, is neither innocent nor physically reasonable.

It is not difficult to understand why appealing to the built-in linear additivity of anti-derivatives is not as innocent or physically reasonable as it may seem. In fact, for non-commuting observables that are not simultaneously measurable, justification of (20) or (29) by appealing to the built-in linear additivity of integrals leads to incorrect equality between unequal physical quantities. The reasons for this were recognized by Grete Hermann [24] some three decades before the formulation of Bell’s theorem [1], as part of her insightful criticism of von Neumann’s alleged theorem [3,27]. As she explained in [24], we are not concerned here with classical physics in which all observable quantities are simultaneously measurable yielding only sharp values, and therefore the value of a sum of observable quantities is nothing other than the sum of the values each of those quantities would separately take. Consequently, in classical physics, the averages of such values over individual initial states $\lambda$ of the system can also be meaningfully added linearly, just as assumed in step (20) or (29), because there is no scope for any contradiction between the averages obtained by evaluating the left-hand side and the right-hand side of these equations. Therefore, in classical physics linear additivity of expectation values remains consistent with the built-in linear additivity of anti-derivatives. However, the same cannot be assumed without proof for the dispersion-free states $|\psi ,\lambda )$ of hidden variable theories, because, in that case, the values of the observable quantities are eigenvalues of the corresponding quantum mechanical operators dictated by the ansatz (3), and, as we noted above and toward the end of Section 2, the eigenvalue $\tilde{\omega }(\tilde{c},\lambda )$ of the summed observable $\tilde{\Omega }\left(\tilde{c}\right)$ is not equal to the sum ${\sum }_{i=1}^n{\omega }_i(c_i,\lambda )$ of the eigenvalues ${\omega }_i(c_i,\lambda )$ of ${\Omega }_i\left(c_i\right)$, unless the observables ${\Omega }_i\left(c_i\right)$ constituting the sum $\tilde{\Omega }\left(\tilde{c}\right)$ are simultaneously measurable. Thus, an important step in the proof of (23) is missing. A necessary step that would prove the consistency of the built-in linear additivity of anti-derivatives with the non-additivity of expectation values for the non-commuting observables. In equation (40) of SectionSection 7 below we will see the difference between the eigenvalue of the summed operator and the sum of individual eigenvalues explicitly. It will demonstrate how, in hidden variable theories equation (20) or (29) involving averages of eigenvalues ends up equating unequal averages of physical quantities in general. It will thereby prove that, while valid in classical physics and for simultaneously measurable observables, equation (20) or (29) is not valid for hidden variable theories in general. Insisting otherwise thus amounts to assuming the validity of this equation without proof, despite the contrary evidence just presented [24]. That, in turn, amounts to assuming the very thesis to be proven — namely, the bounds of $\pm 2$ on the Bell-CHSH sum (18). Consequently, the onlycorrect meaning assignable to (20) or (23) is that it is valid only in classical physics and/or for commuting observables.

Sometimes assumption (20) is justified on statistical grounds. It is argued that the four sub-experiments appearing on the left-hand side of (20) with different experimental settings $\{\mathbf{a},\mathbf{b}\}$, $\{\mathbf{a},{\mathbf{b}}^{\prime }\}$, etc. can be performed independently of each other, on possibly different occasions, and then the resulting averages are added together at a later time for statistical analysis. If the number of experimental runs for each pair of settings is sufficiently large, then, theoretically, the sum of the four averages appearing on the left-hand side of (20) are found not to exceed the bounds of $\pm 2$, thus justifying the equality (20). This can be easily verified in numerical simulations (see Ref. [27] cited in [13]). However,this heuristic argument is not an analytical proof of the bounds. What it implicitly neglects to take into account by explicitly assuming that the four sub-experiments can be performed independently, is that the sub-experiments involve mutually exclusive pairs of settings such as $\{\mathbf{a},\mathbf{b}\}$ and $\{\mathbf{a},{\mathbf{b}}^{\prime }\}$ in physical space, and thus involve non-commuting observables that cannot be measured simultaneously [9]. Unless the statistical analysis takes this physical fact into account, it cannot be claimed to have any relevance for the Bell-test experiments [16]. For ignoring this physical fact amounts to incorrectly assuming that the spin observables ${\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}$, etc. are mutually commuting, and thus simultaneously measurable, for which assumption (20) is indeed valid, as demonstrated below in Section 7 (see the discussion around (43)). On the other hand, when the non-commutativity of the observables involved in the sub-experiments is taken into account in numerical simulations, the bounds on (18) turn out to be $\pm 2\sqrt{2}$, as shown in [10,11] and Ref. [27] cited in [13]. In other words, such a statistical argument is simply assumption (20) in disguise.

Another important point to recognize here is that the above derivation of the stringent bounds of $\pm 2$ on (18) for a locally causal dispersion-free counterpart $|\Psi ,\lambda )$ of the quantum mechanical singlet state (11) must comply with the heuristics of the contextual hidden variable theories we discussed in Section 2. If it does not, then the bounds of $\pm 2$ cannot be claimed to have any relevance for the viability of local hidden variable theories [23]. Therefore, as discussed in Section 2, in a contextual hidden variable theory all of the observables ${\Omega }_i\left(c_i\right)$ of any physical system, including their sum $\tilde{\Omega }\left(\tilde{c}\right)={\sum }_{i=1}^n{\Omega }_i\left(c_i\right)$, which also represents a physical quantity in the Hilbert space formulation of quantum mechanics [3] whether or not it is observed, must be assigned unique eigenvalues ${\omega }_i(c_i,\lambda )$ and $\tilde{\omega }(\tilde{c},\lambda )$, respectively, in the dispersion-free states $|\psi ,\lambda )$ of the system, regardless of whether these observables are simultaneously measurable. In particular, while the summed observable (37) discussed below is never observed in the Bell-test experiments, realism nevertheless requires it to be assigned a unique eigenvalue in accordance with the ansatz (3) and the prescription (7).

6. Additivity of expectation values is respected by quantum states

Now, within quantum mechanics, expectation values do add in analogy with the equality (20) assumed by Bell for local hidden variable theories [3,18]. In quantum mechanics, the statistical predictions of which any hidden variable theory is obliged to reproduce, the joint results $\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )$ observed by Alice and Bob would be eigenvalues of the operators ${\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}$, and the linearity in the rules of Hilbert space quantum mechanics ensures that these operators satisfy the additivity of expectation values. Thus, for any quantum state $|\psi \rangle$, the following equality holds:

$$\begin{array}{cc}\hfill \langle \psi |{\sigma }_1·\mathbf{a}& \otimes {\sigma }_2·\mathbf{b}|\psi \rangle +\langle \psi |{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·{\mathbf{b}}^{\prime }|\psi \rangle +\langle \psi |{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·\mathbf{b}|\psi \rangle -\langle \psi |{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·{\mathbf{b}}^{\prime }|\psi \rangle \hfill \\ \hfill & =\langle \psi |{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}+{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·{\mathbf{b}}^{\prime }+{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·\mathbf{b}-{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·{\mathbf{b}}^{\prime }|\psi \rangle .\hfill \end{array}$$

(30)

The linearity of this equation has been achieved by promoting observable quantities to Hermitian operators [3,24]. Any local hidden variable theory is then obliged to reproduce the predictions of both sides of this equation. Comparing equations (20) and (30), the equality between the two sides of (20) seems reasonable, even physically. Furthermore, since the condition (16) for any hidden variable theory obliges us to set the four terms on the left-hand side of (30) as

$$\begin{array}{cc}\hfill \langle \Psi |{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}|\Psi \rangle & ={\int }_{\mathcal{L}}\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )p\left(\lambda \right)d\lambda ,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill \langle \Psi |{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·{\mathbf{b}}^{\prime }|\Psi \rangle & ={\int }_{\mathcal{L}}\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )p\left(\lambda \right)d\lambda ,\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \langle \Psi |{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·\mathbf{b}|\Psi \rangle & ={\int }_{\mathcal{L}}\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )p\left(\lambda \right)d\lambda ,\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill \mathrm{and}\langle \Psi |{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·{\mathbf{b}}^{\prime }|\Psi \rangle & ={\int }_{\mathcal{L}}\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )p\left(\lambda \right)d\lambda ,\hfill \end{array}$$

(34)

it may seem reasonable that, given the quantum mechanical equality (30), any hidden variable theory should satisfy

$$\begin{array}{cc}\hfill \langle \Psi \left|\tilde{\Omega }\left(\tilde{c}\right)\right|\Psi \rangle & =\langle \Psi |{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}+{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·{\mathbf{b}}^{\prime }+{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·\mathbf{b}-{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·{\mathbf{b}}^{\prime }|\Psi \rangle \hfill \\ \hfill & ={\int }_{\mathcal{L}}\{\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )+\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )\hfill \\ \hfill & +\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )-\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )\}p\left(\lambda \right)d\lambda ,\hfill \end{array}$$

(35)

adhering to the prescription (7), which would then justify equality (20). Since hidden variable theories are required to satisfy the prescription (7), should not they also reproduce equation (35)? The answer to this is not straightforward.

7. Additivity of expectation values does not hold for dispersion-free states

The problem with equation (35) is that, while the joint results $\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )$, etc. appearing on the left-hand side of equation (20) are possible eigenvalues of the products of spin operators ${\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}$, etc., their summation

$$\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )+\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )+\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )-\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )$$

(36)

appearing as the integrand on the right-hand side of equation (35) or (20) is not an eigenvalue of the summed operator

$$\tilde{\Omega }\left(\tilde{c}\right)={\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}+{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·{\mathbf{b}}^{\prime }+{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·\mathbf{b}-{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·{\mathbf{b}}^{\prime },$$

(37)

because the spin operators ${\sigma }_1·\mathbf{a}$ and ${\sigma }_1·{\mathbf{a}}^{\prime }$, etc., and therefore ${\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}$, etc., do not commute with each other:

$$\begin{array}{cc}\hfill \left[{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b},{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·{\mathbf{b}}^{\prime }\right]& =2\sigma ·\left\{\left(\mathbf{a}\times {\mathbf{b}}^{\prime }\right)\times \left(\mathbf{a}\times \mathbf{b}\right)\right\}\hfill \\ \hfill & \ne 0\mathrm{if}{\mathbf{b}}^{\prime }\ne \mathbf{b}\ne \mathbf{a}.\hfill \end{array}$$

(38)

Consequently, equation (35) would hold within any hidden variable theory only if the operators ${\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}$, etc. were commuting operators. As we discussed, this is well known from the famous criticisms of von Neumann’s theorem against hidden variable theories [9,18,24,27]. While the equality (20) of the sum of expectation values with the expectation value of the sum is respected in quantum mechanics, it does not hold for hidden variable theories [18]. Nor does local realism necessitate the linear additivity (27) of eigenvalues for individual dispersion-free states $|\Psi ,\lambda )$.

This problem, however, suggests its own resolution. We can work out the correct eigenvalue $\tilde{\omega }(\tilde{c},\lambda )$ of the summed operator (37), at least formally, as I have worked out in Appendix B below. The correct version of equation (35) is then

$$\langle \Psi |{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}+{\sigma }_1·\mathbf{a}\otimes {\sigma }_2·{\mathbf{b}}^{\prime }+{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·\mathbf{b}-{\sigma }_1·{\mathbf{a}}^{\prime }\otimes {\sigma }_2·{\mathbf{b}}^{\prime }|\Psi \rangle ={\int }_{\mathcal{L}}\tilde{\omega }(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime },\lambda )p\left(\lambda \right)d\lambda ,$$

(39)

where

$$\tilde{\omega }=\pm \sqrt{{\left\{\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )+\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )+\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )-\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )\right\}}^2+(\Psi ,\lambda |\tilde{\Theta }|\Psi ,\lambda )\ne 0}$$

(40)

is the correct eigenvalue of the summed operator (37), with its non-commuting part separated out as the operator

$$\tilde{\Theta }(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime })=2\sigma ·\mathbf{n}(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime }),$$

(41)

where the vector

$$\begin{array}{cc}\hfill \mathbf{n}(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime })=\{\left(\mathbf{a}\times {\mathbf{b}}^{\prime }\right)\times \left(\mathbf{a}\times \mathbf{b}\right)& +\left({\mathbf{a}}^{\prime }\times \mathbf{b}\right)\times \left(\mathbf{a}\times \mathbf{b}\right)+\left({\mathbf{a}}^{\prime }\times \mathbf{b}\right)\times \left(\mathbf{a}\times {\mathbf{b}}^{\prime }\right)\hfill \\ \hfill & -\left({\mathbf{a}}^{\prime }\times {\mathbf{b}}^{\prime }\right)\times \left(\mathbf{a}\times \mathbf{b}\right)-\left({\mathbf{a}}^{\prime }\times {\mathbf{b}}^{\prime }\right)\times \left({\mathbf{a}}^{\prime }\times \mathbf{b}\right)\hfill \\ \hfill & -\left({\mathbf{a}}^{\prime }\times {\mathbf{b}}^{\prime }\right)\times \left(\mathbf{a}\times {\mathbf{b}}^{\prime }\right)\}.\hfill \end{array}$$

(42)

The details of how this separation is accomplished using (38) can be found in Appendix B below. From (40), it is now easy to appreciate that the additivity of expectation values (20) assumed by Bell can hold only if the expectation value $(\Psi ,\lambda |\tilde{\Theta }|\Psi ,\lambda )=\pm 2\left|\right|\mathbf{n}\left|\right|$ of the non-commuting part within the eigenvalue $\tilde{\omega }(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime },\lambda )$ of the summed operator (37) is zero. But that is possible only if the operators ${\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}$, etc. constituting the sum (37) commute with eachother. In general, if the operators ${\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}$, etc. in (37) do not commute with each other, then we would have

$$\tilde{\omega }(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime },\lambda )\ne \mathcal{A}(\mathbf{a},\lambda )\mathcal{B}(\mathbf{b},\lambda )+\mathcal{A}(\mathbf{a},\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda )+\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}(\mathbf{b},\lambda )-\mathcal{A}({\mathbf{a}}^{\prime },\lambda )\mathcal{B}({\mathbf{b}}^{\prime },\lambda ).$$

(43)

But the operators ${\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}$, etc. indeed do not commute with each other, because the pairs of directions $\{\mathbf{a},{\mathbf{a}}^{\prime }\}$, etc. in (37) are mutually exclusive directions in $\mathrm{I}{\mathrm{R}}^3$. Therefore, the additivity of expectation values assumed at step (20) in the derivation of (23) is unjustifiable. Far from being necessitated by realism, it actually contradicts realism.

Since three of the four results appearing in the expression (36) can be realized only counterfactually, their summation in (36) cannot be realized even counterfactually [9]. Thus, in addition to not being a correct eigenvalue of the summed operator (37) as required by the prescription (7) for hidden variable theories, the quantity appearing in (36) is, in fact, an entirely fictitious quantity, with no counterpart in any possible world, apart from in the trivial case when all observables are commutative. By contrast, the correct eigenvalue (40) of the summed operator (37) can be realized at least counterfactually because it is a genuine eigenvalue of that operator, thereby satisfying the requirement of realism correctly, in accordance with the prescription (7) for hidden variable theories. Using (40), all five of the observables appearing on both sides of the quantum mechanical equation (30) can be assigned unique and correct eigenvalues [9].

Once this oversight is ameliorated, it is not difficult to show that the conclusion of Bell’s theorem no longer follows. For then, using the correct eigenvalue (40) of (37) instead of (36) on the right-hand side of (20), we have the equation

$$\mathcal{E}(\mathbf{a},\mathbf{b})+\mathcal{E}(\mathbf{a},{\mathbf{b}}^{\prime })+\mathcal{E}({\mathbf{a}}^{\prime },\mathbf{b})-\mathcal{E}({\mathbf{a}}^{\prime },{\mathbf{b}}^{\prime })={\int }_{\mathcal{L}}\tilde{\omega }(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime },\lambda )p\left(\lambda \right)d\lambda$$

(44)

instead of (20), which implements local realism correctly on both of its sides, as required by the prescription (7) we discussed in Section 2. This equation (44) is thus the correct dispersion-free counterpart of the equivalence (30) for the quantum mechanical expectation values [9]. It can reduce to Bell’s assumption (20) only when the expectation value $(\Psi ,\lambda |\tilde{\Theta }|\Psi ,\lambda )$ of the non-commuting part within the eigenvalue $\tilde{\omega }(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime },\lambda )$ of the summed operator (37) happens to be vanishing. It thus expresses the correct relationship (28) among the expectation values for the singlet state (11) in the local hidden variable framework considered by Bell [1]. Recall again from the end of Section 2 that the quantum mechanical relation (30) is an unusual property of the quantum states $|\psi \rangle$. As Bell stressed in [18], “[t]here is no reason to demand it individually of the hypothetical dispersion free states, whose function it is to reproduce the measurable peculiarities of quantum mechanics when averaged over.” Moreover, in Section V of [9] I have demonstrated that the bounds on the right-hand side of (44) are $\pm 2\sqrt{2}$ instead of $\pm 2$. An alternative derivation of these bounds follows from the magnitude $\left|\right|\mathbf{n}\left|\right|$ of the vector defined in (42), which, as proved in Appendix C below, is bounded by 2, and thereforethe eigenvalue $\pm 2\left|\right|\mathbf{n}\left|\right|$ of the operator (41) obtained as its expectation value $(\Psi ,\lambda |\tilde{\Theta }|\Psi ,\lambda )$ is bounded by $\pm 4$, giving

$$-4⩽(\Psi ,\lambda |\tilde{\Theta }(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime })|\Psi ,\lambda )⩽+4.$$

(45)

Substituting these into (40), together with the bounds of $\pm 2$ we worked out before on the commuting part (36), gives

$$-2\sqrt{2}⩽\tilde{\omega }(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime },\lambda )⩽+2\sqrt{2},$$

(46)

which is constrained to be real despite the square root in the expression (40) because the operator (37) is Hermitian. Consequently, we obtain the following Tsirel’son’s bounds in the dispersion-free state, on the right-hand side of (44):

$$-2\sqrt{2}⩽{\int }_{\mathcal{L}}\tilde{\omega }(\mathbf{a},{\mathbf{a}}^{\prime },\mathbf{b},{\mathbf{b}}^{\prime },\lambda )p\left(\lambda \right)d\lambda ⩽+2\sqrt{2}.$$

(47)

Given the correct relation (44) between expectation values instead of the flawed assumption (20), we thus arrive at

$$-2\sqrt{2}⩽\mathcal{E}(\mathbf{a},\mathbf{b})+\mathcal{E}(\mathbf{a},{\mathbf{b}}^{\prime })+\mathcal{E}({\mathbf{a}}^{\prime },\mathbf{b})-\mathcal{E}({\mathbf{a}}^{\prime },{\mathbf{b}}^{\prime })⩽+2\sqrt{2}.$$

(48)

Since the bounds of $\pm 2\sqrt{2}$ we have derived on the Bell-CHSH sum of expectation values are the same as those predicted by quantum mechanics and observed in the Bell-test experiments, the conclusion of Bell’s theorem is mitigated. What is ruled out by these experiments is not local realism but the assumption of the additivity of expectation values, which does not hold for non-commuting observables in dispersion-free states of any hidden variable theories to begin with.

It is also instructive to note that the intermediate bounds $\pm 2\sqrt{2}$ on the Bell-CHSH sum (18), instead of the extreme bounds $\pm 2$ or $\pm 4$, follow in the above derivation of (48) as a consequence of the geometry of physical space [5,6]. Thus, what is brought out in it is the oversight of the non-commutative or Clifford-algebraic attributes of the physical space in Bell’s derivation of the bounds $\pm 2$ in (23). Indeed, it is evident from Appendix C below that the geometry of physical space imposes the bounds $0⩽\left|\right|\mathbf{n}\left|\right|⩽2$ on the magnitude of the vector (42), which, in turn, lead us to the bounds $\pm 2\sqrt{2}$ in (48). This is in sharp contrast with the traditional view of these bounds as due to non-local influences,stemming from a failure of the locality condition (15). But in the derivation of (48) above, the condition (15) is strictly respected. Therefore, the strength of the bounds $\pm 2\sqrt{2}$ in (48) is a consequence — not of non-locality or non-reality, but of the geometry of physical space [5,6]. Non-locality or non-reality is necessitated only if one erroneously insists on linear additivity (20) of eigenvalues of non-commuting observables for each individual dispersion-free state $|\Psi ,\lambda )$.

8. Conclusion: Bell’s theorem assumes its conclusion (petitio principii)

Let me reiterate the main points discussed above. Together, they demonstrate that Bell’s theorem begs the question.

(1) The first point is that the derivation in Section 4 of the bounds of $\pm 2$ on (18) for the dispersion-free counterpart $|\Psi ,\lambda )$ of the singlet state (11) must comply with the heuristics of the contextual hidden variable theories discussed in Section 2. Otherwise, the stringent bounds of $\pm 2$ cannot be claimed to have any relevance for hidden variable theories. This requires compliance with the prescription (7) that equates the quantum mechanical expectation values with theirhidden variable counterparts for all observables, including any sums of observables, pertaining to the singlet system.

(2) The most charitable view of the equality (20) is that it is an assumption, over and above those of locality, realism, and all other auxiliary assumptions required for deriving the inequalities (23), because it is valid only for commuting observables. Far from being required by realism, it contradicts realism, because it fails to assign the correct eigenvalue (40) to the summed observable (37) as its realistic counterpart, as required by the prescription (7). Realism requiresthat all observables, including their sums, must be assigned unique eigenvalues, regardless of whether they are observed.

(3) Expectation values in dispersion-free states of hidden variable theories do not add linearly for observables that are not simultaneously measurable. And yet, Bell assumed linear additivity (20) within a local hidden variable model. Conversely, in the light of the heuristics of contextual hidden variable theories we discussed in Section 2, assuming (20)is equivalent to assuming that the spin observables ${\sigma }_1·\mathbf{a}\otimes {\sigma }_2·\mathbf{b}$, etc. commute with each other, but they do not.

(4) When the correct eigenvalue (40) is assigned to the summed operator (37) replacing the incorrect step (20), the bounds on Bell-CHSH sum (18) work out to be $\pm 2\sqrt{2}$ instead of $\pm 2$, thus mitigating the conclusion of Bell’s theorem.

(5) As we proved in Section 4, the assumption (20) of the additivity of expectation values is equivalent to assuming the strong bounds of $\pm 2$ on Bell-CHSH sum (18) of expectation values. In other words, (20) and (23) are tautologous.

(6) For observables that are not simultaneously measurable or commuting, the built-in linear additivity of integrals in step (20) or (29) leads to incorrect equality between averages of unequal physical quantities. Therefore, the view that this step is a harmless mathematical step is mistaken. It is, in fact, an unjustified assumption that is equivalent to the very thesis of the theorem to be proven, and is valid only in classical physics and/or for commuting observables.

The first four points above invalidate assumption (20), and thus inequalities (23) on physical grounds, and the lasttwo demonstrate that Bell’s theorem assumes its conclusion in a different guise, and is thus invalid on logical grounds.

Bell’s theorem is useful, however, for ruling out classical local theories. By relying on the assumption (20), which is valid for classical theories [24], it proves that no classical local theory can reproduce all of the predictions of quantummechanics. But no serious hidden variable theories I am aware of have ever advocated returning to classical physics [19].

In this paper, I have focused on a formal or logical critique of Bell’s theorem. Elsewhere [10,14,16], I have developed a comprehensive local-realistic framework for understanding quantum correlations in terms of the geometry of the spatial part of one of the well-known solutions of Einstein’s field equations of general relativity — namely, that of a quaternionic 3-sphere — taken as a physical space within which we are confined to perform Bell-test experiments. Thisframework is based on Clifford algebra and thus explicitly takes the non-commutativity of observables into account. It thus shows, constructively, that contextually local hidden variable theories are not ruled out by Bell-test experiments. Since, as we discussed in Section 3, the formal proof of Bell’s theorem is based on the entangled singlet state (11), in [5,6,8,11,12,13,15] I have reproduced the correlations predicted by (11) as a special case within the local-realistic framework proposed in [10,14,16]. I especially recommend the calculations presented in [8] and [15], which also discuss a macroscopic experiment that would be able to falsify the 3-sphere hypothesis I have proposed in these publications.