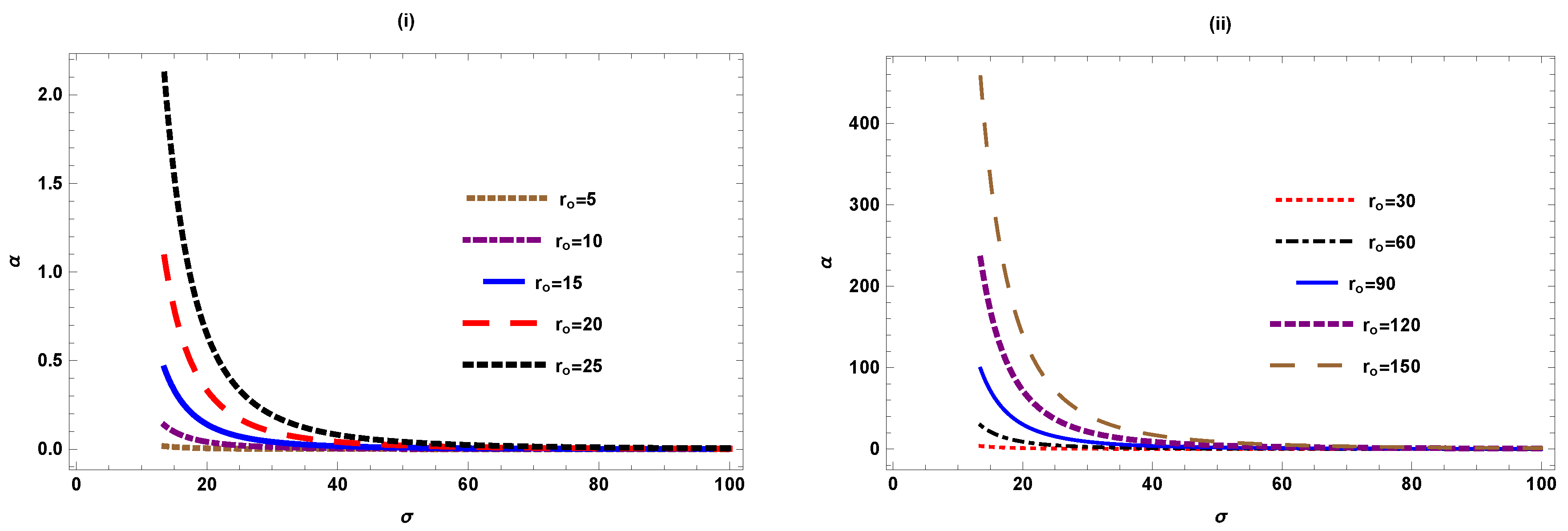Prerpints.org logo
Preprint
Article

Light Deflection by Traversable Wormhole in a Curvature-Coupled Antisymmetric Background Field

This version is not peer-reviewed.

Submitted:

28 February 2023

Posted:

28 February 2023

Read the latest preprint version here

Abstract
This paper is devoted to study the gravitational lensing for Curvature-coupled antisymmetric wormhole solution to compute the bending angle of light by utilizing the Gibbons and Werner technique. To achieve this, we find the Gaussian optical curvature and then apply Gauss-Bonnet theorem in the weak field limits. We also study the effects of plasma as well as dark matter mediums on the bending angle. Moreover, we analyze the graphical behaviour of the deflection angle $\alpha$ with respect to the impact parameter $\sigma$ and minimal radius $r_{0}$ in non-plasma and plasma mediums. We examine that deflection angle shows direct relation with $r_{0}$ such that large values of $r_{0}$ gives large deflection angle and small values of $r_{0}$ gives small deflection angle. For impact parameter $\sigma$, deflection angle $\alpha$ shows inverse relation. Additionally, we derive the deflection angle of light by using Keeton and Petters method and compare with the previous results.
Keywords: 
General Relativity
;  
Gravitational lensing
;  
Dark Matter
;  
Gauss-Bonnet Theorem
;  
Plasma Medium
;  
Wormhole
Subject: 
Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

Wormhole (WH) solutions were first discovered by Flamm in the background of General Relativity, in 1916 [1]. Generally, just like black holes (BHs), WHs seem as a practical solutions to the Einstein’s field equations. Schwarzschild metric [2] is the most simple solution to Einstein’s field equation, because it describes gravitational field around a mass which is static and spherically symmetric. For sufficiently high density, the solution defines a BH, named as Schwarzschild BH. Flamm found that Einstein equations additionally give another solution which is referred as white hole. These both BH and white hole solutions, describing distinct regions of spacetime, which are joined with the help of a tube called “spacetime tube". In 1935, Einstein and Rosen [3] investigated the concept of inter-universe connections. The main purpose of their investigation was to recognize the elementary charged particles in terms of spacetime tube penetrated by lines of electromagnetic force. These spacetime pathways have been known as “Einstein-Rosen Bridges". Later, in 1957, Wheeler named these bridges as “WHs". [4].
Later on, it was Morris and Thorne [5], who introduced the term traversable WH in 1988, where the basic factor is the exploded condition of throat of a WH. Traversable WHs with no horizons permit two way travelling by joining two distinct regions of spacetime in Lorentzian geometry. It is possible to travel from one universe to other through a traversable WH [6–14]. Morris, Thorne and Yurtsever’s [6] established flat traversable WH with exotic matter which do not fulfil the null energy conditions and they also proved that traversable WHs can be made stable by using Casimir effect. In 1989, another type of traversable WH was introduced by Matt-Visser, called the thin shell WH [1]. This type of WH is created by joining two spacetimes to form a geodesically complete manifolds with a shell located at the joining interface. Chetouani and Clement [15] identified deflection of light by Ellis WH [16] for the first time. Strong and weak deflection limit by Ellis WHs has been recently investigated by Tsukamoto [17,18,19]. Nakajima and Asada [20] studied the gravitational lensing by Ellis WH. Bhattachary and Potapov used different methods to calculate the deflection angle of Ellis spacetime, such as direct method of integration, perturbation method, invariant angle method [21]. Cuyubamba et al. show that there is no stable wormholes in Einstein-dilaton-Gauss-Bonnet theory [22].
In 19 t h century, Einstein’s theory of General Relativity envision that when light emitted by distant objects such as massive galaxies, passes through the heavy objects in space, the gravitational pull of these heavy objects bends the light from its path. This phenomenon is called “Gravitational Lensing" (GL). The study of GL has been growing continuously from almost last two decades [23]. Gravitational lensing plays a vital role in investigating the existence of WHs. Gravity is a force to be considered with lensing can be used as an investigation to distinguish between WHs and BHs. Due to the significance of this problem, numerous articles, including [24–91], had been studied GL of BHs and also WHs.
Recently, Gibbons and Werner discovered new technique to compute the bending angle of light by using Gauss-Bonnet theorem (GBT) to the optical geometry [93]. In GBT, we use the D R space bounded by a light beam and circular boundary curve C r in the focus area where photon beam intersects both light source and viewer. It is presume that both light source as well the viewer is coordinated at a distance from the focus area. At the weak field limits, the GBT provides the given conditional mathematical expression as [93]
∫ ∫ D R K d S + ∮ ∂ D R k d t + ∑ i θ i = 2 π X ( D R ) ,
where, K indicates the Gaussian optical curvature, d S is a surface element of optical geometry and D R is a region accommodates the light ray source, the referential of the observer and the len’s center. For simplicity, we suppose that as long as radial distance R → ∞ [94], the sum of the external angles θ i becomes π for the observer. The asymptotic deflection angle can be calculated as [93]:
∫ ∫ D R K d S + ∮ ∂ D R k d t = π ,
where, D ∞ indicates the infinite domain bounded by the ray of photon. Werner took a step forward by extending this method to stationary BHs [94]. In Einstein-Maxwell-dilation theory, the bending angle of light can also be computed for charged WHs by using GBT and rotating monopole spacetime [96–99]. Furthermore, Sakalli and Övgün pointed out the bending angle of Rindler modified Schwarzschild BH at infrared area [100].
The standard model of astronomy says that the Universe is composed of 27 % of dark matter and 68 % of dark energy [101], although the remaining is baryonic matter. Though dark matter can not be directly able to detect, observational evidence for its existence can be found in abundance. There are many dark matter applicants, such as weakly interacting massive particles (WIMPs), super-WIMPs, axions, and sterile neutrinos [102]. It has been suggested that dark matter is a compound, like dark atom model, which we are investigating here by using light deviation. The dark matter, although suppressed, usually interacts with the electromagnetic field [103,104], so that the object in the center must have objects that cannot sense the moving photon due to the reflection indicator based on frequencies. Refractive index controls the speed at which a wave propagates through a medium. Dark matter particles are not electrically charged, but can be paired with other particles with a virtual magnetic charge, and can also pair with photons. To find the amplitude of dark matter dissipation into two photons, we must first calculate the amplitude of the dispersion. One can find a refractive index of light, where the real part is related to the speed of diffusion. For this purpose, we take the refractive index as [73,104]
n ( ω ) = 1 + β A 0 + A 2 ω 2 .
Here ω is the frequency of photon. It is observed here that β = ρ 0 4 m 2 ω 2 , where ρ 0 is the mass density of scattered particles of dark matter, while A 0 = − 2 ε 2 e 2 and A 2 j ≥ 0 .
The effect of GL is a global effect, where multiple rays intersect between the light source and the observer. Therefor, the deflection angle can be found accurately at weak field limits. In this paper, we investigate the deflection angle of Curvature-coupled antisymmetric WH by using GBT in the existence of different mediums such as plasma, non-plasma and dark matter. We shall also calculate the deflection angle by using another method introduced by Keeton and Petters [105] called “Keeton and Petters" method.
This paper is arranged as: In Section 2 , we discuss about the Curvature-coupled antisymmetric traversable WH. In Section 3 , we calculate the bending angle of light using Gauss-Bonnet theorem for WH in non-plasma medium. In Section 4 , we discuss the graphical behaviour of deflection angle in plasma medium. In Section 5 we investigate the impact of plasma medium on GL. In Section 6 , we analyze the graphical behaviour of bending angle in the existence of plasma medium. In Section 7 , we investigate the effect of dark matter medium on deflection angle of curvature-coupled antisymmetric traversable WH. In Section 8 , we calculate the bending angle of light using Keeton and Petters method. Lastly, in Section 9 , we discuss our results.

2. Curvature-Coupled Antisymmetric Traversable Wormhole

If we look through the properties of a traversable WH solution we find out the metric is spherically symmetric and does not depend on time. The reason of taking it spherical is just to simplify our calculations. In physics, a WH is a hypothetical topological feature of spacetime that is primarily a “shortcut" through space and time. It permits travelling from one universe to another. It takes very limited and short time for a traveller to pass through the WH. A traveller experience slightly small gravitational force inside a WH. Until now, no one has been able to prove the existence of WHs experimentally, while this is only a mathematical concept.
The Morris Throne geometry shows a static and spherically symmetric WH solution which is described by [6,106]
d s 2 = − e 2 Φ ( r ) d t 2 + 1 − Ω ( r ) r − 1 d r 2 + r 2 ( d θ 2 + sin 2 θ d ϕ 2 ) .
Here, Ω ( r ) is called the shape function of WH and Φ ( r ) is called redshift function, which is finite everywhere to avoid the singularities. Furthermore, for a traversable WH, some additional conditions are required on Φ ( r ) and Ω ( r ) . One of theses conditions is the existence of minimal radius: ( Ω ( r 0 ) = r 0 ) , where r = r 0 is the radius of the traversable WH’s throat. Another significant requirement is the flare-out condition at the throat: Ω ( r ) < 1 , while Ω ′ ( r 0 ) < 1 . Also, there must be very small tidal gravitational forces which means | Φ | ≪ 1 . For the further work, we will neglect the tidal forces assuming Φ ( r ) = 0 . The solution of shape function is given by [107]
Ω ( r ) = 1 1 + ( 1 − 2 λ ) ω − 2 λ ω r + ( 1 + ω ) r 0 ( r 0 r ) 1 − λ ω ( 1 − λ ) ω ,
where ω is the real parameter which has no dimension and λ is an affine parameter. Anyone can see that the radial metric g r r = ( 1 − Ω ( r ) r ) − 1 component diverges at r = r 0 , which is normal for any WH. To avoid the complexity in calculations, one can simplify the expression in Eq.(2) by using λ = 3 and ω = − 1 3 . Using these values, the shape function can be expressed as:
1 − Ω ( r ) r = 1 4 − 1 4 ( r 0 r ) 3
Now, the spacetime metric can be written in the general form as
d s 2 = − g t t d t 2 + g r r d r 2 + r 2 d θ 2 + r 2 sin 2 θ d ϕ 2 ,
for WH with the configuration g t t = − 1 and g r r = ( 1 − Ω ( r ) r ) − 1 .

3. Bending Angle in Non-plasma Medium

In this section, we analyze the deflection angle of Curvature-coupled antisymmetric WH. Using the Eq.(4) the optical path can be described by using null geodesic condition d s 2 = 0 , we can write the optical path metric as
d t 2 = g ¯ i j d x i d x j = g ¯ r r d r 2 + g ¯ ϕ ϕ d ϕ 2 .
By setting the metric into the equatorial plane with ( θ = π 2 ) . The corresponding expression is
d t 2 = d r 2 1 − Ω ( r ) r + r 2 d ϕ 2 .
The geodesic curvature is defined by [93]
K ( C R ) = | ∇ C R C R | ,
by taking the radial component of the Eq.(7), one can write.
( ∇ C R C R ) r = C R ϕ ( ∂ ϕ C R r ) + Γ ϕ ϕ r ( C R ϕ ) 2 ,
where Γ ϕ ϕ r is the Christoffel symbol representing the optical path of Eq.(6), which results in
Γ ϕ ϕ r = 1 2 g ¯ r r ∂ g ¯ ϕ ϕ ∂ r = − r 1 − ( r r 0 ) 2 1 − 2 λ .
Assuming radial distance so large that it results in infinity, r ≡ R → ∞ . As C R does not depends on ϕ then the only last term of the Eq.(8) plays a part along with the term C R = 1 R . Hence the expression Eq.(7) becomes
lim R → ∞ K ( C R ) = lim R → ∞ | ∇ C R C R | = 1 − ( R r 0 ) 2 1 − 2 λ R → 1 R .
Remembering that R = c o n s t a n t , from Eq.(6), we get
d t = R d ϕ .
By using Eqs.(6) and (11), we obtain the following expression [93]
∫ ∫ D ∞ K d S + ∫ 0 π + α 1 R R d ϕ = π .
The Gaussian curvature can be defined as
K = R i c c i − s c a l a r 2 .
Now by using Eq.(6), one can calculate the non-zero Christofell symbols as
Γ r r r = 3 r 0 3 2 r 0 3 r − 2 r 4 , Γ ϕ ϕ r = r 0 3 − r 3 4 r 2 , Γ r ϕ r = 1 r ,
Using Eq.(14), we can compute the Gaussian Curvature as
K = 3 r 0 3 8 r 5 .
We can see that K depends on two parameters, radial coordinate r and minimal radius of the throat of WH r 0 . As we are working in weak gravitational field limits, it is useful for us to apply GBT to compute the deflection angle. We apply the GBT to the region D R stated as
∫ ∫ D R K d S + ∮ ∂ D R k d t = π ,
where the term d S is surface element and calculated as
d S = g ¯ r r d r d ϕ = 2 r d r d ϕ + O [ r ] 3
As the light rays come from a source at infinity up to such radial distance, the rays becomes nearly straight. So, we can use the straight line approximation r = σ sin ( ϕ ) , where σ is the impact parameter
α = − ∫ 0 π ∫ σ sin ( ϕ ) ∞ K d S ,
By substituting the values of Gaussian curvature and d S , we simplify our expression to the obtain deflection angle α in non-plasma medium, i.e,
α = r 0 3 3 σ 3
The obtained expression shows that the deflection angle α for curvature-coupled antisymmetric WH depends on two parameters, impact parameter σ and minimal radius of throat of the WH r 0 . We analyze that α has direct relation with the minimal radius of the throat of WH r 0 as the increase in r 0 gives large deflection angle and decrease in r 0 gives small deflection angle. For impact parameter σ , the deflection angle α shows inverse relation as its value decreases with the increase in σ and vice-versa.

4. Graphical Behaviour of α in Non-Plasma Medium

In the following sections, we observe the graphical behaviour of bending angle of light in non-plasma medium. We also signify the impact of minimal radius r 0 and impact parameter σ on the deflection angle.

4.1. Deflection angle α versus impact parameter σ

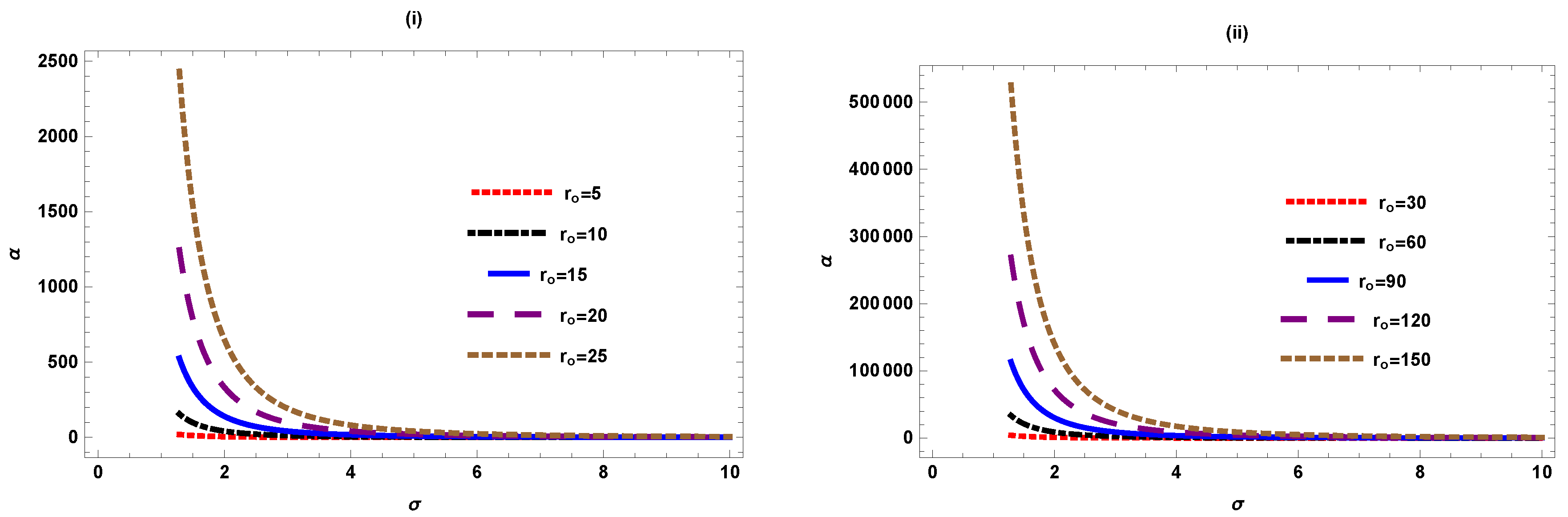
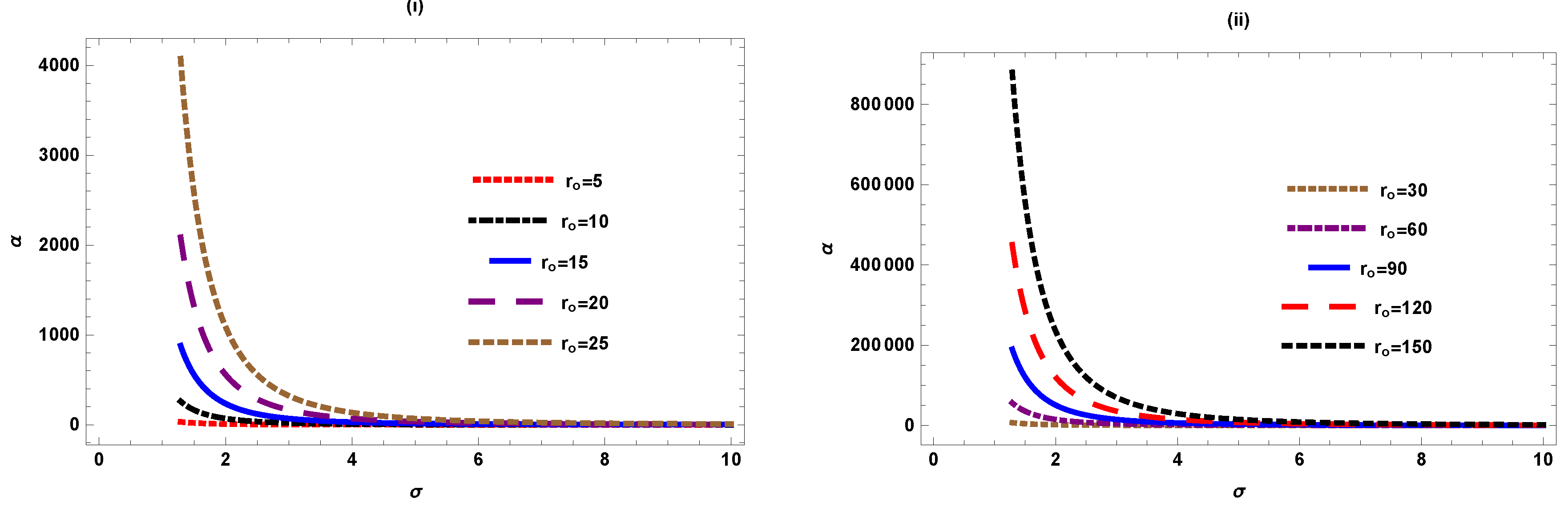
Figure 1 shows the graphical behaviour of deflection angle α w.r.t impact parameter σ by varying r 0 when 0 ≤ σ ≤ 10 . Figure (i) consists of small values of r 0 and figure (ii) consists of larger values of r 0 for the same values of σ . We find that for the small values of r 0 , angle approaches to zero as σ ⟶ 1 . We notice that as we increase the value of r 0 , the deflection angle increases asymptotically with the decrease in σ . For the large value of r 0 , the graph shows similar behaviour.
Preprints 69258 g001
Figure 1. α versus σ ( 0 ≤ σ ≤ 10 ).
Figure 1. α versus σ ( 0 ≤ σ ≤ 10 ).
Preprints 69258 g001
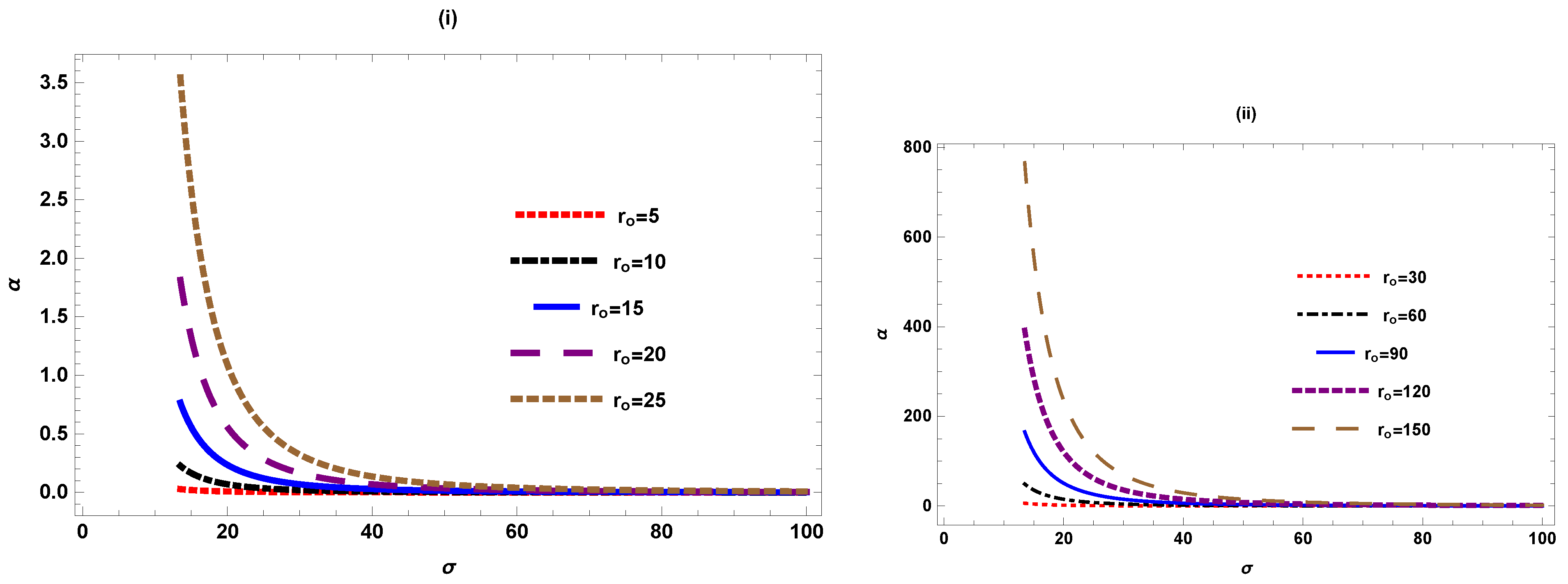
Figure 2 shows the graphical behaviour of deflection angle α w.r.t impact parameter σ when 0 ≤ σ ≤ 100 . We noticed that the deflection angle decreases when r 0 → 0 and σ → ∞ and shows the same behaviour for the small and larger values of r 0 .
Preprints 69258 g002
Figure 2. α versus σ ( 0 ≤ σ ≤ 100 ).
Figure 2. α versus σ ( 0 ≤ σ ≤ 100 ).
Preprints 69258 g002

4.2. Deflection angle α versus minimal radius r 0

We observe the graphical behaviour of the deflection angle α w.r.t the minimal radius r 0 by varying the values of σ as well as r 0 .
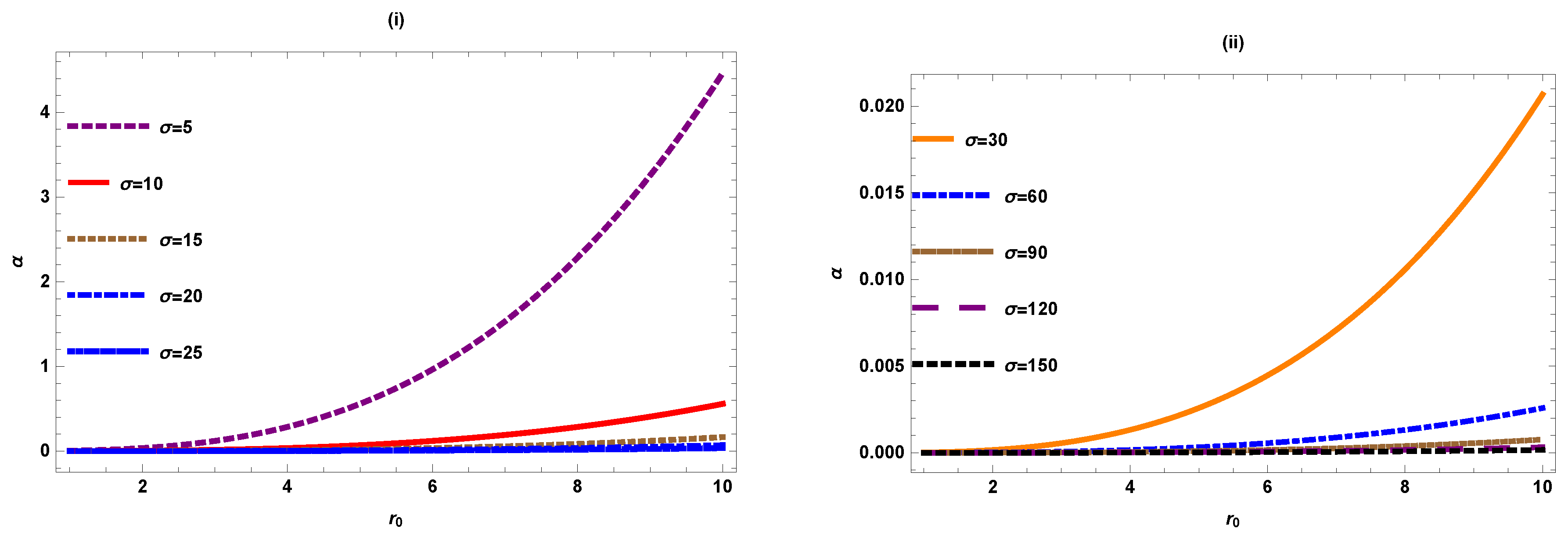
Figure 3 shows the behaviour of deflection angle α w.r.t the minimal radius r 0 for varying values of σ when 0 ≤ r 0 ≤ 10 . We notice that in figure (i), the deflection angle decreases gradually and approaches to zero as we increase the value of σ ( σ → ∞ , the deflection angle approaches to zero). In fig (ii), for larger values of σ and using the same value of r 0 , the graph shows similar behaviour.
Preprints 69258 g003
Figure 3. α versus r 0 ( 0 ≤ r 0 ≤ 10 ).
Figure 3. α versus r 0 ( 0 ≤ r 0 ≤ 10 ).
Preprints 69258 g003
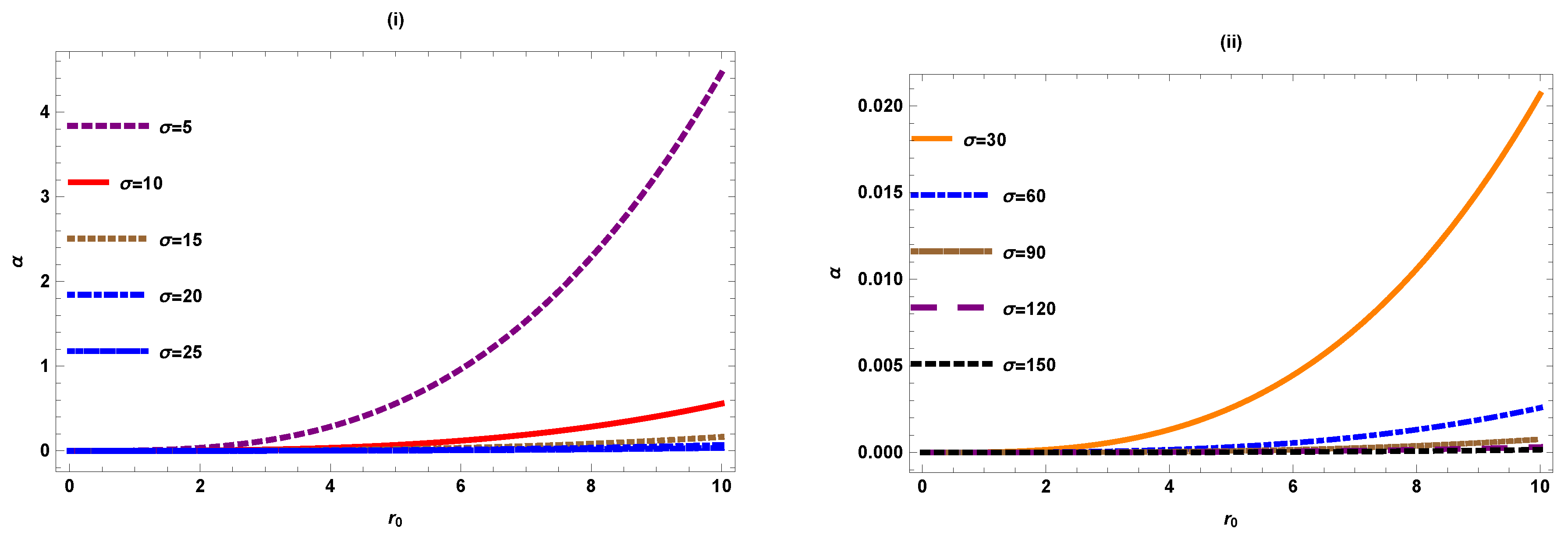
Figure 4 shows the behaviour of deflection angle α w.r.t the minimal radius r 0 when 0 ≤ r 0 ≤ 100 . We notice that the deflection angle shows similar behaviour for small and larger values of σ . We observe that as r 0 increases, α increases with the small value of impact parameter σ . For large σ , as r 0 increases, the angle shows slightly different behaviour than zero angle.
Preprints 69258 g004
Figure 4. α versus r 0 ( 0 ≤ r 0 ≤ 100 ).
Figure 4. α versus r 0 ( 0 ≤ r 0 ≤ 100 ).
Preprints 69258 g004

5. Bending Angle in Plasma Medium

This part is mainly devoted to examine the gravitational lensing of curvature-coupled antisymmetric WH in the presence of plasma medium. For this purpose, the refractive index n for plasma medium is described as [43]
n ( r ) = 1 − ω e 2 ( r ) ω ∞ 2 ( r ) f ( r ) ,
where f ( r ) = 1 − Ω ( r ) r . In refractive index n ( r ) , ω e represents the plasma frequency of electron while ω ∞ denotes the frequency of photon which is noticed by an observer at infinity. The optical metric in plasma medium can be defined as
d t 2 = g l m o p t d x l d x m = n 2 ( r ) d r 2 1 − Ω ( r ) r + r 2 d ϕ 2 ,
Using Eq.(21), we calculate the non-zero Christofell symbols as
Γ r r r = 3 r 0 3 ( ( r 0 3 − r 3 ) ω e 2 − 4 r 3 ω ∞ 2 ) 8 r 4 ( r 3 − r 0 3 ) ω ∞ 2 ,
Γ ϕ ϕ r = ( r 0 3 − r 3 ) ( ( r 0 3 + 2 r 3 ) ω e 2 + 8 r 3 ω ∞ 2 ) ( ( r 0 3 − r 3 ) ω e 2 − 4 r 3 ω ∞ 2 ) 128 r 8 ω ∞ 4 ,
Γ r ϕ r = ( ( r 0 3 + 2 r 63 ) ω e 2 + 8 r 3 ω ∞ 2 ) ( ( r 0 3 − r 3 ) ω e 2 − 4 r 3 ω ∞ 2 ) 32 r 4 ω ∞ 4 .
By using the Christofell symbols obtained above, one can find the Gaussian Curvature (16). The calculated Gaussian Curvature in plasma medium can be written as
K = − 3 r 0 3 8 r 3 + 15 r 0 12 ω e 6 1027 r 14 ω ∞ 6 − 9 r 0 9 ω e 6 512 r 11 ω ∞ 6 − 9 r 0 6 ω e 6 1024 r 8 ω ∞ 6 + 3 r 0 3 ω e 6 256 r 5 ω ∞ 6 − 21 r 0 9 ω e 4 128 r 11 ω ∞ 4 + 3 r 0 6 ω e 4 16 r 8 ω ∞ 9 − 3 r 0 3 ω e 4 128 r 5 ω ∞ 4 + 33 r 0 6 ω e 2 14 r 8 ω ∞ 2 − 3 r 0 3 ω e 2 8 r 5 ω ∞ 2 .
By using GBT (18), we calculate the deflection in plasma medium as
α = r 0 3 3 σ 3 + r 0 3 ω e 2 4 σ 3 ω ∞ 2 .
If we remove the plasma effect, we observe that the obtained expression for deflection angle (23) will convert into deflection angle obtained in non-plasma medium. The deflection angle α depends on two parameters, impact parameter σ and the minimal radius of throat of the WH r 0 .

6. Graphical Behaviour of α in Plasma Medium

This section is based on the explanation of the graphical analysis of deflection angle for curvature-coupled antisymmetric WH solution in plasma medium. For this purpose, we analyze the deflection angle with respect to the impact parameter σ and the minimal radius r 0 .
Note: When we use ω e ω ∞ = 10 − 1 , for the sake of simplification, the graph of plasma medium gives the same behaviour as non-plasma medium. Therefor, to get the significant results of graphical behaviour in plasma medium, we set ω e ω ∞ = 0.9 .

6.1. Deflection angle α versus impact parameter σ

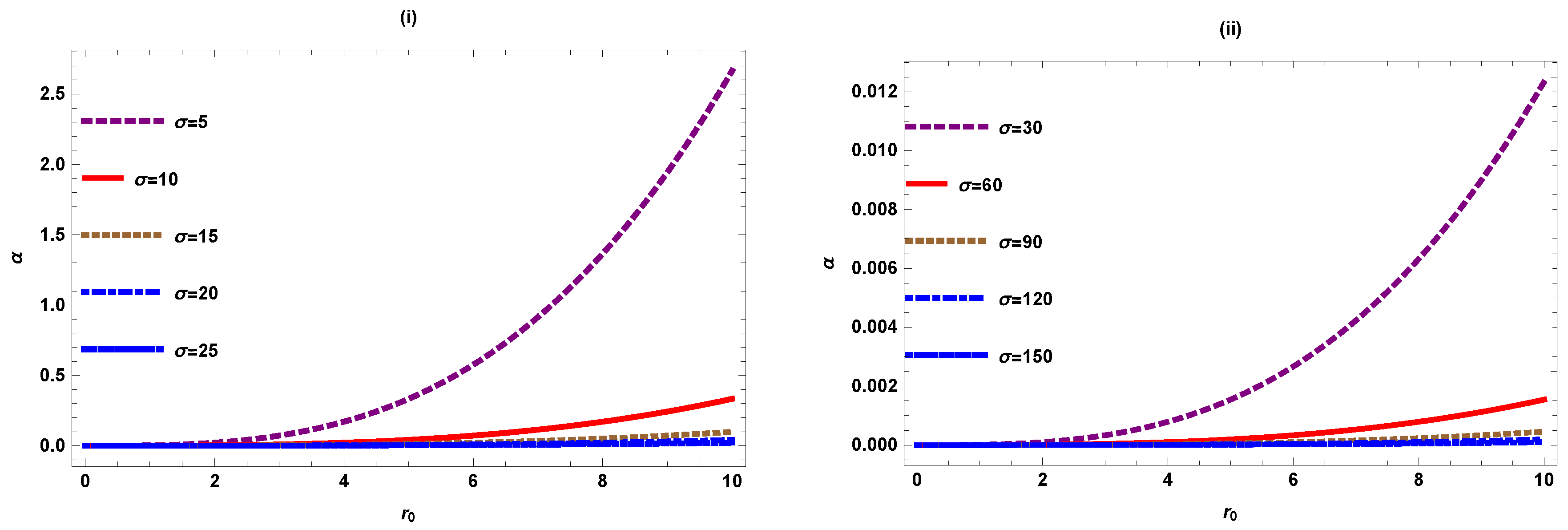
Figure 5 shows the graphical behaviour of deflection angle α w.r.t impact parameter σ by varying r 0 when 0 ≤ σ ≤ 10 in the presence of plasma medium. We observe that the graph of α increases asymptotically as we increase the value of r 0 with the decrease in impact parameter σ . For plasma medium, we observe that graph gives higher range than given in figure (5) for non-plasma medium.
Preprints 69258 g005
Figure 5. α versus σ ( 0 ≤ σ ≤ 10 ).
Figure 5. α versus σ ( 0 ≤ σ ≤ 10 ).
Preprints 69258 g005
Figure 6 shows the graphical behaviour of α w.r.t σ when 0 ≤ σ ≤ 100 . We noticed that behaviour of deflection angle changes as we change the value of σ such that graph increases as r 0 → ∞ and σ → 0 . We can see that the range of graph is greater than the figure(2) because of the plasma effect.
Preprints 69258 g006
Figure 6. α versus σ ( 0 ≤ σ ≤ 100 ).
Figure 6. α versus σ ( 0 ≤ σ ≤ 100 ).
Preprints 69258 g006

6.2. Deflection angle α versus minimal radius r 0

We observe the graphical behaviour of angle of deflection angle α with regards to the minimal radius r 0 for different values of σ and r 0 in plasma medium.
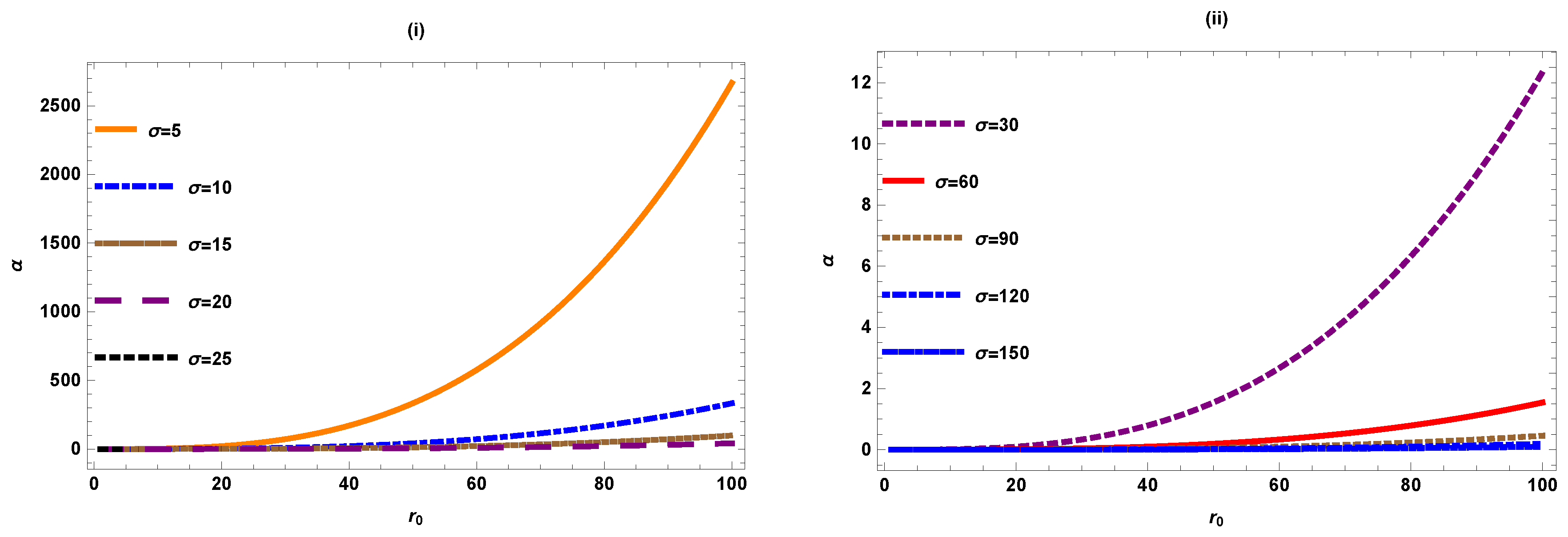
Figure 7 shows the behaviour of deflection angle w.r.t the minimal radius r 0 for varying the values of σ when 0 ≤ r 0 ≤ 10 . Figure(i) shows behaviour for smaller σ and fig(ii) shows behaviour for larger σ . We observed that deflection shows same behaviour for larger and smaller values of σ such that it gradually decreases and approaches to zero as we increase the value of σ using the same value of r 0 . This graph of deflection angle gives higher range as compared to figure (3) due to the effect of plasma.
Preprints 69258 g007
Figure 7. α versus r 0 ( 0 ≤ r 0 ≤ 10 ).
Figure 7. α versus r 0 ( 0 ≤ r 0 ≤ 10 ).
Preprints 69258 g007
Figure 8 shows the behaviour of α w.r.t r 0 when 0 ≤ r 0 ≤ 100 . We noticed that the graph shows same behaviour for the larger and small values of σ but it changes when we change r 0 and shows direct relation. The graph of α decreases when σ → ∞ and r 0 → 0 . We also observe that range of graph is higher than the figure(4) for the presence of plasma medium.
Preprints 69258 g008
Figure 8. α versus r 0 ( 0 ≤ r 0 ≤ 100 ).
Figure 8. α versus r 0 ( 0 ≤ r 0 ≤ 100 ).
Preprints 69258 g008

7. Deflection Angle by using Keeton and Petters Method

Keeton and Petters [105] originate an approximate form of GL with the help of spherically symmetric lenses up-to post-post-Newtonian (PPN). They have developed a practical framework for computing modifications in general asymptotically flat metric theory of gravity. The goal is to use the PPN corrections up-to the third order to illustrate how to deal with the lensing in computing gravity theories. The Keeton and Petters method gives calculations of observable quantities which are physically relevant because of its essentially coordinate independence. The spacetime geometry is supposed to be stable, non-linear, spherically symmetric and quadratically Minkowski
d s 2 = − E ( r ) d t 2 + F ( r ) d r 2 + G ( r ) d Ω 2 ,
here d Ω 2 represents the standard unit metric. The metric is flat in the absence of lens and we make natural mathematical suppositions that E, F and G all are positive in the outside region of the lens from where the light rays pass. The curvature-coupled WH solution takes the form of (24) presented as
d s 2 = − d t 2 + d r 2 1 − Ω ( r ) r ,
having metric functions E ( r ) = 1 and
F ( r ) = 1 1 − Ω ( r ) r ,
Using the solution of the shape function in Eq.(26), the expression can be written as
F ( r ) = 1 1 4 1 − r 0 r 3 .
We compare the coefficients of the extended form of metric function with the coefficients of standard form of general metric in a PPN series up to third order given in [108] to find the PPN coefficients. Then, we get the value of the coefficients of PPN metric as
a 1 = 0 , a 2 = 0 , a 3 = 0 , b 1 = 0 , b 2 = 0 , b 3 = 1 4 .
Now, we calculate the coefficients in the extended form of the deflection angle. The extended form of the light deflection angle follows as [105]
a ( b ) = A 1 a b + A 2 a b 2 + A 3 a b 3 + O a b 4 .
We take r 0 = a and r = b . The coefficients of bending angle in Eq.(29) can be defined as
A 1 = 2 ( a 1 + b 1 ) A 2 = 2 a 1 2 − a 2 + a 1 b 1 + b 2 − b 1 2 4 π , A 3 = 2 3 ( 35 a 1 3 + 15 a 1 2 b 1 − 3 a 1 ( 10 a 2 + b 1 2 − 4 b 2 ) + 6 a 3 + b 1 3 − 6 a 2 b 1 − 4 b 1 b 2 + 8 b 3 ) .
By utilizing above equations, we can determine the only value of the coefficient is
A 3 = 4 3 .
After substituting this value of the coefficient, we obtain the required deflection angle given as follows
α = 4 r 0 3 3 σ 3 .

8. Deflection Angle in Dark Matter Medium

In this section, we examine the effect of dark matter medium on the deflection angle of urvature-coupled antisymmetric WH. For this purpose, we use the refractive index for dark matter medium as [73,104]
n ( ω ) = 1 + β A 0 + A 2 ω 2 .
The 2-dimensional optical geometry of the curvature-coupled antisymmetric WH is
d t 2 = n 2 d r 2 1 − Ω ( r ) r + r 2 d ϕ 2 .
Using Eq.(33), we can calculate the Christoffel symbols as
Γ r r r = 3 r 0 3 2 ( r 0 3 r − r 4 ) , Γ ϕ ϕ r = r 0 3 − r 3 4 r 2 , Γ r ϕ r = 1 r .
We calculate the Gaussian Curvature K (13) by using above mentioned Christofell symbols
K = 3 r 0 3 8 r 5 ( 1 + β A 0 + A 2 ω 2 ) 2 .
Using GBT (16), one can compute the deflection angle for curvature-coupled antisymmetric WH in dark matter medium which is given by
α ≈ r 0 3 3 σ 3 ( 1 + β A 0 + A 2 ω 2 ) 2 + 2 r 0 3 β A 0 3 σ 3 ( 1 + β A 0 + A 2 ω 2 ) 2 + O ( σ 4 , r 0 4 )
In the above expression, the term O ( σ 4 , r 0 4 ) describes that we only consider the third order of impact parameter σ and minimal radius r 0 also ignore the higher order terms. We analyze that deflection angle obtained in dark matter medium for curvature-coupled antisymmetric WH is larger compared to deflection angle without dark matter medium. If we neglect the effect of dark matter in the Eq.(35), the deflection angle α converts into the angle in non-plasma medium.

9. Conclusion

In brief, the investigation of WHs by studying the GL is the most practical way to certify them in Cosmology. In this paper, we determined the deflection angle of Curvature-coupled antisymmetric WH solution in the presence of different mediums such as plasma, non-plasma and dark matter in weak field approximation using the latest technique introduced by Gibbons and Werner. For this purpose, we have determined optical curvature. Later, we applied GBT and derived value of deflection angle for Curvature-coupled antisymmetric WH solution in non-plasma Eq.(19), plasma Eq.(23) and dark matter medium Eq.(35). We observed that if we remove the effect of plasma and dark matter, the obtained expressions reduce into non-plasma expression. Furthermore, we have also calculated the deflection angle using Keeton and Petters method. To do so, first, we calculated the coefficients of PPN metric by comparing the extended metric function with standard PPN metric. Later on, we have determined the coefficients of the and obtained the deflection angle and again by comparing them with general form of Schwarzschild metric to get final results given in Eq.(31), where the deflection angle depends on A i ’s.
Later on, we have discussed the graphical behaviour of deflection angle in the presence of non-plasma and plasma medium.
  • We observe that graph of deflection angle α w.r.t σ increases asymptotically with the increase in minimal radius r 0 and decrease in impact parameter σ .
  • Graph of α gives same behaviour for the larger and small values of r 0 but changes its behaviour of change in σ .
  • Graph of deflection angle α w.r.t minimal radius r 0 decreases when σ → ∞ and r 0 → 0 .
  • The graphs of α have gives same behaviour but higher range as compared to the graph of α in non-plasma medium due to the presence of plasma medium.
Form the obtained results for deflection angle of light for Curvature-coupled antisymmetric WH solution, we observed that deflection angle α depends on two parameters, impact parameter σ and minimal radius r 0 . The deflection angle shows direct relation with r 0 which means that WH with greater radius of its throat bends the light passing by it at greater angle and a WH with smaller radius of throat has the less gravitational pull and bends the light at smaller angle. For the impact parameter σ , the deflection angle showed inverse relation which says that greater value of σ gives smaller deflection angle and vice-versa.

Acknowledgments

A. Ö. and R. P. would like to acknowledge networking support by the COST Action CA18108 - Quantum gravity phenomenology in the multi-messenger approach (QG-MM).

References

  1. M. Visser, Lorentzian Wormholes: From Einstein to Hawking (American Institute of Physics, New York, 1996).
  2. K. Schwarzschild, “On the gravitational field of a mass point according to Einstein’s theory,” Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys. ) 1916, 189-196 (1916) [arXiv:physics/9905030 [physics]].
  3. A. Einstein and N. Rosen, “The Particle Problem in the General Theory of Relativity,” Phys. Rev. 48, 73-77 (1935).
  4. J. A. Wheeler, “Geons,” Phys. Rev. 97, 511-536 (1955).
  5. M. S. Morris and K. S. Thorne, “Wormholes in space-time and their use for interstellar travel: A tool for teaching general relativity,” Am. J. Phys. 56, 395-412 (1988).
  6. M. S. Morris, K. S. Thorne and U. Yurtsever, “Wormholes, Time Machines, and the Weak Energy Condition,” Phys. Rev. Lett. 61, 1446-1449 (1988).
  7. S. Ansoldi and E. I. Guendelman, “Universes out of almost empty space,” Prog. Theor. Phys. 120, 985-993 (2008).
  8. S. Bahamonde, D. Benisty and E. I. Guendelman, “Linear potentials in galaxy halos by Asymmetric Wormholes,” Universe 4, no.11, 112 (2018).
  9. S. Ansoldi, Z. Merali and E. I. Guendelman, “From Black Holes to Baby Universes: Exploring the Possibility of Creating a Cosmos in the Laboratory,” Bulg. J. Phys. 45, no.2, 203-220 (2018).
  10. E. Guendelman, E. Nissimov, S. Pacheva and M. Stoilov, “Einstein-Rosen ”Bridge” Revisited and Lightlike Thin-Shell Wormholes,” Bulg. J. Phys. 44, no.1, 084-097 (2017).
  11. E. I. Guendelman, A. Kaganovich, E. Nissimov and S. Pacheva, “Einstein-Rosen ’Bridge’ Needs Lightlike Brane Source,” Phys. Lett. B 681, 457-462 (2009).
  12. E. I. Guendelman, “Wormholes and the construction of compactified phases,” Gen. Rel. Grav. 23, 1415-1419 (1991).
  13. E. I. Guendelman and D. A. Owen, “Universe creation entropy and extra dimensions,” Gen. Rel. Grav. 21, 201-210 (1989).
  14. M. Visser, “Wormholes, Baby Universes and Causality,” Phys. Rev. D 41, 1116 (1990).
  15. L. Chetouani, L., G. Clement, “Geometrical optics in the Ellis geometry,” Gen Relat Gravit 16, 111–119 (1984).
  16. H. G. Ellis, “Ether flow through a drainhole - a particle model in general relativity,” J. Math. Phys. 14, 104-118 (1973).
  17. N. Tsukamoto and T. Harada, “Light curves of light rays passing through a wormhole,” Phys. Rev. D 95, no.2, 024030 (2017).
  18. N. Tsukamoto, T. Harada and K. Yajima, “Can we distinguish between black holes and wormholes by their Einstein ring systems?,” Phys. Rev. D 86, 104062 (2012).
  19. N. Tsukamoto and T. Harada, “Signed magnification sums for general spherical lenses,” Phys. Rev. D 87, no.2, 024024 (2013).
  20. K. Nakajima and H. Asada, “Deflection angle of light in an Ellis wormhole geometry,” Phys. Rev. D 85, 107501 (2012).
  21. A. Bhattacharya and A. A. Potapov, “Bending of light in Ellis wormhole geometry,” Mod. Phys. Lett. A 25, 2399-2409 (2010).
  22. M. A. Cuyubamba, R. A. Konoplya and A. Zhidenko, “No stable wormholes in Einstein-dilaton-Gauss-Bonnet theory,” Phys. Rev. D 98, no.4, 044040 (2018).
  23. J. Wambsganss, “Gravitational lensing in astronomy,” Living Rev. Rel. 1, 12 (1998).
  24. F. Atamurotov, A. Abdujabbarov and B. Ahmedov, “Shadow of rotating non-Kerr black hole,” Phys. Rev. D 88, no.6, 064004 (2013).
  25. V. Bozza, “Gravitational lensing in the strong field limit,” Phys. Rev. D 66, 103001 (2002).
  26. A. Övgün, “Light deflection by Damour-Solodukhin wormholes and Gauss-Bonnet theorem,” Phys. Rev. D 98, no.4, 044033 (2018).
  27. K. Jusufi and A. Övgün, “Gravitational Lensing by Rotating Wormholes,” Phys. Rev. D 97, no.2, 024042 (2018).
  28. K. S. Virbhadra and G. F. R. Ellis, “Schwarzschild black hole lensing,” Phys. Rev. D 62, 084003 (2000).
  29. K. S. Virbhadra and G. F. R. Ellis, “Gravitational lensing by naked singularities,” Phys. Rev. D 65, 103004 (2002).
  30. K. S. Virbhadra, D. Narasimha and S. M. Chitre, “Role of the scalar field in gravitational lensing,” Astron. Astrophys. 337, 1-8 (1998).
  31. K. S. Virbhadra and C. R. Keeton, “Time delay and magnification centroid due to gravitational lensing by black holes and naked singularities,” Phys. Rev. D 77, 124014 (2008).
  32. K. S. Virbhadra, “Relativistic images of Schwarzschild black hole lensing,” Phys. Rev. D 79, 083004 (2009).
  33. N. Tsukamoto and Y. Gong, “Extended source effect on microlensing light curves by an Ellis wormhole,” Phys. Rev. D 97, no.8, 084051 (2018).
  34. P. K. F. Kuhfittig, “Gravitational lensing of wormholes in the galactic halo region,” Eur. Phys. J. C 74, no.99, 2818 (2014).
  35. A. Övgün,, K. Jusufi and I. Sakalli, “Gravitational lensing under the effect of Weyl and bumblebee gravities: Applications of Gauss–Bonnet theorem,” Annals Phys. 399, 193-203 (2018).
  36. N. Tsukamoto, “Strong deflection limit analysis and gravitational lensing of an Ellis wormhole,” Phys. Rev. D 94, no.12, 124001 (2016).
  37. A. Övgün, İ. Sakallı and J. Saavedra, “Shadow cast and Deflection angle of Kerr-Newman-Kasuya spacetime,” JCAP 10, 041 (2018).
  38. A. Övgün, İ. Sakallı and J. Saavedra, “Weak gravitational lensing by Kerr-MOG black hole and Gauss–Bonnet theorem,” Annals Phys. 411, 167978 (2019).
  39. A. Övgün and İ. Sakallı, “Testing generalized Einstein–Cartan–Kibble–Sciama gravity using weak deflection angle and shadow cast,” Class. Quant. Grav. 37, no.22, 225003 (2020).
  40. W. Javed, M. B. Khadim, A. Övgün and J. Abbas, “Weak gravitational lensing by stringy black holes,” Eur. Phys. J. Plus 135, no.3, 314 (2020).
  41. K. Jusufi, A. Övgün, J. Saavedra, Y. Vásquez and P. A. González, “Deflection of light by rotating regular black holes using the Gauss-Bonnet theorem,” Phys. Rev. D 97, no.12, 124024 (2018).
  42. M. Sereno and F. De Luca, “Analytical Kerr black hole lensing in the weak deflection limit,” Phys. Rev. D 74, 123009 (2006).
  43. G. Crisnejo and E. Gallo, “Weak lensing in a plasma medium and gravitational deflection of massive particles using the Gauss-Bonnet theorem. A unified treatment,” Phys. Rev. D 97, no.12, 124016 (2018).
  44. W. Javed, R. Babar and A. Övgün, “The effect of the Brane-Dicke coupling parameter on weak gravitational lensing by wormholes and naked singularities,” Phys. Rev. D 99, no.8, 084012 (2019).
  45. A. Övgün, “Weak field deflection angle by regular black holes with cosmic strings using the Gauss-Bonnet theorem,” Phys. Rev. D 99, no.10, 104075 (2019).
  46. A. Övgün, “Deflection Angle of Photons through Dark Matter by Black Holes and Wormholes Using Gauss–Bonnet Theorem,” Universe 5, no.5, 115 (2019).
  47. A. Övgün, G. Gyulchev and K. Jusufi, “Weak Gravitational lensing by phantom black holes and phantom wormholes using the Gauss-Bonnet theorem,” Annals Phys. 406, 152-172 (2019).
  48. İ. Çimdiker, D. Demir and A. Övgün, “Black hole shadow in symmergent gravity,” Phys. Dark Univ. 34, 100900 (2021).
  49. W. Javed, M. B. Khadim and A. Övgün, “Weak gravitational lensing by Bocharova–Bronnikov–Melnikov–Bekenstein black holes using Gauss–Bonnet theorem,” Eur. Phys. J. Plus 135, no.7, 595 (2020).
  50. Z. Li and A. Övgün, “Finite-distance gravitational deflection of massive particles by a Kerr-like black hole in the bumblebee gravity model,” Phys. Rev. D 101, no.2, 024040 (2020).
  51. W. Javed, J. Abbas and A. Övgün, “Deflection angle of photon from magnetized black hole and effect of nonlinear electrodynamics,” Eur. Phys. J. C 79, no.8, 694 (2019).
  52. W. Javed, j. Abbas and A. Övgün, “Effect of the Hair on Deflection Angle by Asymptotically Flat Black Holes in Einstein-Maxwell-Dilaton Theory,” Phys. Rev. D 100, no.4, 044052 (2019).
  53. Y. Kumaran and A. Övgün, “Deriving weak deflection angle by black holes or wormholes using Gauss-Bonnet theorem,” Turk. J. Phys. 45, no.5, 247-267 (2021).
  54. Z. Li, G. Zhang and A. Övgün, “Circular Orbit of a Particle and Weak Gravitational Lensing,” Phys. Rev. D 101, no.12, 124058 (2020).
  55. W. Javed, J. Abbas, Y. Kumaran and A. Övgün, “Weak deflection angle by asymptotically flat black holes in Horndeski theory using Gauss-Bonnet theorem,” Int. J. Geom. Meth. Mod. Phys. 18, no.01, 2150003 (2021).
  56. R. C. Pantig and A. Övgün, “Dark matter effect on the weak deflection angle by black holes at the center of Milky Way and M87 galaxies,” Eur. Phys. J. C 82, no.5, 391 (2022).
  57. R. C. Pantig and A. Övgün, “Dehnen halo effect on a black hole in an ultra-faint dwarf galaxy,” JCAP 08, no.08, 056 (2022).
  58. R. C. Pantig, P. K. Yu, E. T. Rodulfo and A. Övgün, “Shadow and weak deflection angle of extended uncertainty principle black hole surrounded with dark matter,” Annals of Physics 436, 168722 (2022).
  59. A. Uniyal, R. C. Pantig and A. Övgün, “Probing a nonlinear electrodynamics black hole with thin accretion disk, shadow and deflection angle with M87* and Sgr A* from EHT,” [arXiv:2205.11072 [gr-qc]].
  60. R. C. Pantig and A. Övgün, “Testing dynamical torsion effects on the charged black hole’s shadow, deflection angle and greybody with M87* and Sgr A* from EHT,” [arXiv:2206.02161 [gr-qc]].
  61. J. Rayimbaev, R. C. Pantig, A. Övgün, A. Abdujabbarov and D. Demir, “Quasiperiodic oscillations, weak field lensing and shadow cast around black holes in Symmergent gravity,” [arXiv:2206.06599 [gr-qc]].
  62. G. Mustafa, F. Atamurotov, I. Hussain, S. Shaymatov and A. Övgün, “Shadows and gravitational weak lensing by the Schwarzschild black hole in the string cloud background with quintessential field,” [arXiv:2207.07608 [gr-qc]].
  63. X. M. Kuang and A. Övgün, “Strong gravitational lensing and shadow constraint from M87* of slowly rotating Kerr-like black hole,” [arXiv:2205.11003 [gr-qc]].
  64. W. Javed, S. Riaz and A. Övgün, “Weak Deflection Angle and Greybody Bound of Magnetized Regular Black Hole,” Universe 8, no.5, 262 (2022).
  65. E. F. Eiroa, G. E. Romero and D. F. Torres, “Reissner-Nordstrom black hole lensing,” Phys. Rev. D 66, 024010 (2002).
  66. C. R. Keeton, C. S. Kochanek and E. E. Falco, “The Optical properties of gravitational lens galaxies as a probe of galaxy structure and evolution,” Astrophys. J. 509, 561-578 (1998).
  67. R. C. Pantig, L. Mastrototaro, G. Lambiase and A. Övgün, “Shadow, lensing and neutrino propagation by dyonic ModMax black holes,” [arXiv:2208.06664 [gr-qc]].
  68. M. Sharif and S. Iftikhar, “Strong gravitational lensing in non-commutative wormholes,” Astrophys. Space Sci. 357, no.1, 85 (2015).
  69. R. Shaikh and S. Kar, “Gravitational lensing by scalar-tensor wormholes and the energy conditions,” Phys. Rev. D 96, no.4, 044037 (2017).
  70. S. N. Sajadi and N. Riazi, “Gravitational lensing by multi-polytropic wormholes,” Can. J. Phys. 98, no.11, 1046-1054 (2020).
  71. R. C. Pantig and E. T. Rodulfo, “Weak deflection angle of a dirty black hole,” Chin. J. Phys. 66, 691-702 (2020).
  72. W. Javed, R. Babar and A. Övgün, “Effect of the dilaton field and plasma medium on deflection angle by black holes in Einstein-Maxwell-dilaton-axion theory,” Phys. Rev. D 100, no.10, 104032 (2019).
  73. A. Övgün, “Weak Deflection Angle of Black-bounce Traversable Wormholes Using Gauss-Bonnet Theorem in the Dark Matter Medium,” Turk. J. Phys. 44, no.5, 465-471 (2020).
  74. Y. Kumaran and A. Övgün, “Weak Deflection Angle of Extended Uncertainty Principle Black Holes,” Chin. Phys. C 44, no.2, 025101 (2020).
  75. A. Övgün, Y. Kumaran, W. Javed and J. Abbas, “Effect of Horndeski theory on weak deflection angle using the Gauss–Bonnet theorem,” Int. J. Geom. Meth. Mod. Phys. 2250192 (2022).
  76. M. Okyay and A. Övgün, “Nonlinear electrodynamics effects on the black hole shadow, deflection angle, quasinormal modes and greybody factors,” JCAP 01, no.01, 009 (2022).
  77. W. Javed, J. Abbas and A. Övgün, “Effect of the Quintessential Dark Energy on Weak Deflection Angle by Kerr-Newmann Black Hole,” Annals Phys. 418, 168183 (2020).
  78. W. Javed, A. Hamza and A. Övgün, “Effect of nonlinear electrodynamics on the weak field deflection angle by a black hole,” Phys. Rev. D 101, no.10, 103521 (2020).
  79. T. K. Dey and S. Sen, “Gravitational lensing by wormholes,” Mod. Phys. Lett. A 23, 953-962 (2008).
  80. H. Asada, “Gravitational lensing by exotic objects,” Mod. Phys. Lett. A 32, no.34, 1730031 (2017).
  81. C. M. Yoo, T. Harada and N. Tsukamoto, “Wave Effect in Gravitational Lensing by the Ellis Wormhole,” Phys. Rev. D 87, 084045 (2013).
  82. N. Tsukamoto, T. Harada and K. Yajima, “Can we distinguish between black holes and wormholes by their Einstein ring systems?,” Phys. Rev. D 86, 104062 (2012).
  83. W. Javed, I. Hussain and A. Övgün, “Weak deflection angle of Kazakov–Solodukhin black hole in plasma medium using Gauss–Bonnet theorem and its greybody bonding,” Eur. Phys. J. Plus 137, no.1, 148 (2022).
  84. H. El Moumni, K. Masmar and A. Övgün, “Weak deflection angle of light in two classes of black holes in nonlinear electrodynamics via Gauss–Bonnet theorem,” Int. J. Geom. Meth. Mod. Phys. 19, no.06, 2250094 (2022).
  85. A. Belhaj, H. Belmahi, M. Benali and H. Moumni El, “Light Deflection by Rotating Regular Black Holes with a Cosmological Constant,” [arXiv:2204.10150 [gr-qc]].
  86. A. Belhaj, H. Belmahi, M. Benali and H. El Moumni, “Light deflection angle by superentropic black holes,” Int. J. Mod. Phys. D 31, no.07, 2250054 (2022).
  87. A. Belhaj, M. Benali, A. El Balali, H. El Moumni and S. E. Ennadifi, “Deflection angle and shadow behaviors of quintessential black holes in arbitrary dimensions,” Class. Quant. Grav. 37, no.21, 215004 (2020).
  88. Z. Li, G. Zhang and A. Övgün, “Circular Orbit of a Particle and Weak Gravitational Lensing,” Phys. Rev. D 101, no.12, 124058 (2020).
  89. W. Javed, M. Aqib and A. Övgün, “Effect of the magnetic charge on weak deflection angle and greybody bound of the black hole in Einstein-Gauss-Bonnet gravity,” Phys. Lett. B 829, 137114 (2022).
  90. W. Javed, A. Hamza and A. Övgün, “Weak Deflection Angle and Shadow by Tidal Charged Black Hole,” Universe 7, no.10, 385 (2021).
  91. W. Javed, M. B. Khadim and A. Övgün, “Weak gravitational lensing by Einstein-nonlinear-Maxwell–Yukawa black hole,” Int. J. Geom. Meth. Mod. Phys. 17, no.12, 2050182 (2020).
  92. K. K. Nandi, Y. Z. Zhang and A. V. Zakharov, “Gravitational lensing by wormholes,” Phys. Rev. D 74, 024020 (2006).
  93. G. W. Gibbons and M. C. Werner, “Applications of the Gauss-Bonnet theorem to gravitational lensing,” Class. Quant. Grav. 25, 235009 (2008).
  94. A. Ishihara, Y. Suzuki, T. Ono and H. Asada, “Finite-distance corrections to the gravitational bending angle of light in the strong deflection limit,” Phys. Rev. D 95, no.4, 044017 (2017).
  95. M. C. Werner, “Gravitational lensing in the Kerr-Randers optical geometry,” Gen. Rel. Grav. 44, 3047-3057 (2012).
  96. K. Jusufi, M. C. Werner, A. Banerjee and A. Övgün, “Light Deflection by a Rotating Global Monopole Spacetime,” Phys. Rev. D 95, no.10, 104012 (2017).
  97. P. Goulart, “Phantom wormholes in Einstein–Maxwell-dilaton theory,” Class. Quant. Grav. 35, no.2, 025012 (2018).
  98. K. Jusufi, A. Övgün and A. Banerjee, “Light deflection by charged wormholes in Einstein-Maxwell-dilaton theory,” Phys. Rev. D 96, no.8, 084036 (2017).
  99. K. Jusufi, I. Sakallı and A. Övgün, “Effect of Lorentz Symmetry Breaking on the Deflection of Light in a Cosmic String Spacetime,” Phys. Rev. D 96, no.2, 024040 (2017).
  100. I. Sakalli and A. Övgün,, “Hawking Radiation and Deflection of Light from Rindler Modified Schwarzschild Black Hole,” EPL 118, no.6, 60006 (2017).
  101. Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. 2013, 208, 19. [CrossRef]
  102. J. L. Feng, “Dark Matter Candidates from Particle Physics and Methods of Detection,” Ann. Rev. Astron. Astrophys. 48, 495-545 (2010).
  103. D. C. Latimer, “Dispersive Light Propagation at Cosmological Distances: Matter Effects,” Phys. Rev. D 88, 063517 (2013).
  104. D. C. Latimer, “Anapole dark matter annihilation into photons,” Phys. Rev. D 95, no.9, 095023 (2017).
  105. C. R. Keeton and A. O. Petters, “Formalism for testing theories of gravity using lensing by compact objects. I. Static, spherically symmetric case,” Phys. Rev. D 72, 104006 (2005).
  106. M. S. Morris and K. S. Thorne, “Wormholes in space-time and their use for interstellar travel: A tool for teaching general relativity,” Am. J. Phys. 56, 395-412 (1988).
  107. R. V. Maluf and C. R. Muniz, “Exact solution for a traversable wormhole in a curvature-coupled antisymmetric background field,” Eur. Phys. J. C 82, no.5, 445 (2022).
  108. C. R. Keeton and A. O. Petters, “Formalism for testing theories of gravity using lensing by compact objects. II. Probing post-post-Newtonian metrics,” Phys. Rev. D 73, 044024 (2006).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

416

Views

144

Comments

1

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated