Submitted:
15 August 2023
Posted:
16 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Wormhole in Einstein-bumblebee gravity with an antisymmetric tensor
3. Weak deflection angle in Non-plasma Medium
4. Deflection angle in Plasma Medium
5. Conclusion
Acknowledgments
References
- M. Visser, Lorentzian Wormholes: From Einstein to Hawking (American Institute of Physics, New York, 1996).
- K. Schwarzschild, “On the gravitational field of a mass point according to Einstein’s theory,” Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys. ) 1916, 189-196 (1916) [arXiv:physics/9905030 [physics]].
- A. Einstein and N. Rosen, “The Particle Problem in the General Theory of Relativity,” Phys. Rev. 48, 73-77 (1935).
- J. A. Wheeler, “Geons,” Phys. Rev. 97, 511-536 (1955).
- M. S. Morris and K. S. Thorne, “Wormholes in space-time and their use for interstellar travel: A tool for teaching general relativity,” Am. J. Phys. 56, 395-412 (1988).
- M. S. Morris, K. S. M. S. Morris, K. S. Thorne and U. Yurtsever, “Wormholes, Time Machines, and the Weak Energy Condition,” Phys. Rev. Lett. 61, 1446-1449 (1988).
- F. Rahaman, N. F. Rahaman, N. Paul, A. Banerjee, S. S. De, S. Ray and A. A. Usmani, “The Finslerian wormhole models,” Eur. Phys. J. C 76, no.5, 246 (2016).
- F. Rahaman, T. F. Rahaman, T. Manna, R. Shaikh, S. Aktar, M. Mondal and B. Samanta, “Thin accretion disks around traversable wormholes,” Nucl. Phys. B 972, 115548 (2021).
- F. Rahaman, K. N. F. Rahaman, K. N. Singh, R. Shaikh, T. Manna and S. Aktar, “Shadows of Lorentzian traversable wormholes,” Class. Quant. Grav. 38, no.21, 215007 (2021).
- F. Rahaman, S. F. Rahaman, S. Sarkar, K. N. Singh and N. Pant, “Generating functions of wormholes,” Mod. Phys. Lett. A 34, no.01, 1950010 (2019).
- P. K. F. Kuhfittig, “Traversable wormholes sustained by an extra spatial dimension,” Phys. Rev. D 98, no.6, 064041 (2018).
- P. K. F. Kuhfittig, “Wormholes admitting conformal Killing vectors and supported by generalized Chaplygin gas,” Eur. Phys. J. C 75, no.8, 357 (2015).
- P. K. F. Kuhfittig, “Accounting for exotic matter and the extreme radial tension in Morris–Thorne wormholes of embedding class one,” Eur. Phys. J. C 81, no.8, 778 (2021).
- P. K. F. Kuhfittig, “Accounting for the large radial tension in Morris–Thorne wormholes,” Eur. Phys. J. Plus 135, no.6, 510 (2020).
- P. K. F. Kuhfittig and V. D. Gladney, “Seeking connections between wormholes, gravastars, and black holes via noncommutative geometry,” Mod. Phys. Lett. A 35, no.09, 2050059 (2019).
- P. K. F. Kuhfittig, “Thin-shell wormholes from Kiselev black holes,” Turk. J. Phys. 43, no.2, 213-220 (2019).
- S. Ansoldi and E. I. Guendelman, “Universes out of almost empty space,” Prog. Theor. Phys. 120, 985-993 (2008).
- S. Bahamonde, D. S. Bahamonde, D. Benisty and E. I. Guendelman, “Linear potentials in galaxy halos by Asymmetric Wormholes,” Universe 4, no. 2018. [Google Scholar]
- S. Ansoldi, Z. S. Ansoldi, Z. Merali and E. I. Guendelman, “From Black Holes to Baby Universes: Exploring the Possibility of Creating a Cosmos in the Laboratory,” Bulg. J. Phys. 45, no.2, 203-220 (2018).
- E. Guendelman, E. E. Guendelman, E. Nissimov, S. Pacheva and M. Stoilov, “Einstein-Rosen ”Bridge” Revisited and Lightlike Thin-Shell Wormholes,” Bulg. J. Phys. 44, no.1, 084-097 (2017).
- E. I. Guendelman, A. E. I. Guendelman, A. Kaganovich, E. Nissimov and S. Pacheva, “Einstein-Rosen ’Bridge’ Needs Lightlike Brane Source,” Phys. Lett. B 681, 457-462 (2009).
- E. I. Guendelman, “Wormholes and the construction of compactified phases,” Gen. Rel. Grav. 23, 1415-1419 (1991).
- E. I. Guendelman and D. A. Owen, “Universe creation entropy and extra dimensions,” Gen. Rel. Grav. 1989; 21.
- M. Visser, “Wormholes, Baby Universes and Causality,” Phys. Rev. D 41, 1116 (1990).
- L. Chetouani, L., G. L. Chetouani, L., G. Clement, “Geometrical optics in the Ellis geometry,” Gen Relat Gravit 16, 111–119 (1984).
- H. G. Ellis, “Ether flow through a drainhole - a particle model in general relativity,” J. Math. Phys. 14, 104-118 (1973).
- N. Tsukamoto and T. Harada, “Light curves of light rays passing through a wormhole,” Phys. Rev. D 95, no.2, 024030 (2017).
- N. Tsukamoto, T. N. Tsukamoto, T. Harada and K. Yajima, “Can we distinguish between black holes and wormholes by their Einstein ring systems?,” Phys. Rev. D 86, 104062 (2012).
- N. Tsukamoto and T. Harada, “Signed magnification sums for general spherical lenses,” Phys. Rev. D 87, no.2, 024024 (2013).
- K. Nakajima and H. Asada, “Deflection angle of light in an Ellis wormhole geometry,” Phys. Rev. D 85, 107501 (2012).
- A. Bhattacharya and A. A. Potapov, “Bending of light in Ellis wormhole geometry,” Mod. Phys. Lett. A 25, 2399-2409 (2010).
- M. A. Cuyubamba, R. A. M. A. Cuyubamba, R. A. Konoplya and A. Zhidenko, “No stable wormholes in Einstein-dilaton-Gauss-Bonnet theory,” Phys. Rev. D 98, no. 0440. [Google Scholar]
- J. Wambsganss, “Gravitational lensing in astronomy,” Living Rev. Rel. 1, 12 (1998).
- F. Atamurotov, A. F. Atamurotov, A. Abdujabbarov and B. Ahmedov, “Shadow of rotating non-Kerr black hole,” Phys. Rev. D 88, no.6, 064004 (2013).
- V. Bozza, “Gravitational lensing in the strong field limit,” Phys. Rev. D 66, 103001 (2002).
- A. Övgün, “Light deflection by Damour-Solodukhin wormholes and Gauss-Bonnet theorem,” Phys. Rev. D 98, no.4, 044033 (2018).
- K. Jusufi and A. Övgün, “Gravitational Lensing by Rotating Wormholes,” Phys. Rev. D 97, no.2, 024042 (2018).
- K. S. Virbhadra and G. F. R. Ellis, “Schwarzschild black hole lensing,” Phys. Rev. D 62, 084003 (2000).
- K. S. Virbhadra and G. F. R. Ellis, “Gravitational lensing by naked singularities,” Phys. Rev. D 65, 103004 (2002).
- K. S. Virbhadra, D. K. S. Virbhadra, D. Narasimha and S. M. Chitre, “Role of the scalar field in gravitational lensing,” Astron. Astrophys. 337, 1-8 (1998).
- K. S. Virbhadra and C. R. Keeton, “Time delay and magnification centroid due to gravitational lensing by black holes and naked singularities,” Phys. Rev. D 77, 124014 (2008).
- K. S. Virbhadra, “Relativistic images of Schwarzschild black hole lensing,” Phys. Rev. D 79, 083004 (2009).
- N. Tsukamoto and Y. Gong, “Extended source effect on microlensing light curves by an Ellis wormhole,” Phys. Rev. D 97, no.8, 084051 (2018).
- P. K. F. Kuhfittig, “Gravitational lensing of wormholes in the galactic halo region,” Eur. Phys. J. C 74, no.99, 2818 (2014).
- A. Övgün,, K. Jusufi and I. Sakalli, “Gravitational lensing under the effect of Weyl and bumblebee gravities: Applications of Gauss–Bonnet theorem,” Annals Phys. 399, 193-203 (2018).
- N. Tsukamoto, “Strong deflection limit analysis and gravitational lensing of an Ellis wormhole,” Phys. Rev. D 94, no.12, 124001 (2016).
- A. Övgün, İ. Sakallı and J. Saavedra, “Shadow cast and Deflection angle of Kerr-Newman-Kasuya spacetime,” JCAP 10, 041 (2018).
- A. Övgün, İ. Sakallı and J. Saavedra, “Weak gravitational lensing by Kerr-MOG black hole and Gauss–Bonnet theorem,” Annals Phys. 411, 167978 (2019).
- A. Övgün and İ. Sakallı, “Testing generalized Einstein–Cartan–Kibble–Sciama gravity using weak deflection angle and shadow cast,” Class. Quant. Grav. 37, no.22, 225003 (2020).
- W. Javed, M. B. W. Javed, M. B. Khadim, A. Övgün and J. Abbas, “Weak gravitational lensing by stringy black holes,” Eur. Phys. J. Plus 135, no.3, 314 (2020).
- K. Jusufi, A. K. Jusufi, A. Övgün, J. Saavedra, Y. Vásquez and P. A. González, “Deflection of light by rotating regular black holes using the Gauss-Bonnet theorem,” Phys. Rev. D 97, no.12, 124024 (2018).
- M. Sereno and F. De Luca, “Analytical Kerr black hole lensing in the weak deflection limit,” Phys. Rev. D 74, 123009 (2006).
- G. Crisnejo and E. Gallo, “Weak lensing in a plasma medium and gravitational deflection of massive particles using the Gauss-Bonnet theorem. A unified treatment,” Phys. Rev. D 97, no.12, 124016 (2018).
- W. Javed, R. W. Javed, R. Babar and A. Övgün, “The effect of the Brane-Dicke coupling parameter on weak gravitational lensing by wormholes and naked singularities,” Phys. Rev. D 99, no.8, 084012 (2019).
- A. Övgün, “Weak field deflection angle by regular black holes with cosmic strings using the Gauss-Bonnet theorem,” Phys. Rev. D 99, no.10, 104075 (2019).
- A. Övgün, “Deflection Angle of Photons through Dark Matter by Black Holes and Wormholes Using Gauss–Bonnet Theorem,” Universe 5, no.5, 115 (2019).
- A. Övgün, G. A. Övgün, G. Gyulchev and K. Jusufi, “Weak Gravitational lensing by phantom black holes and phantom wormholes using the Gauss-Bonnet theorem,” Annals Phys. 406, 152-172 (2019).
- İ. Çimdiker, D. İ. Çimdiker, D. Demir and A. Övgün, “Black hole shadow in symmergent gravity,” Phys. Dark Univ. 34, 100900 (2021).
- W. Javed, M. B. W. Javed, M. B. Khadim and A. Övgün, “Weak gravitational lensing by Bocharova–Bronnikov–Melnikov–Bekenstein black holes using Gauss–Bonnet theorem,” Eur. Phys. J. Plus 135, no.7, 595 (2020).
- Z. Li and A. Övgün, “Finite-distance gravitational deflection of massive particles by a Kerr-like black hole in the bumblebee gravity model,” Phys. Rev. D 101, no.2, 024040 (2020).
- W. Javed, J. W. Javed, J. Abbas and A. Övgün, “Deflection angle of photon from magnetized black hole and effect of nonlinear electrodynamics,” Eur. Phys. J. C 79, no.8, 694 (2019).
- W. Javed, j. W. Javed, j. Abbas and A. Övgün, “Effect of the Hair on Deflection Angle by Asymptotically Flat Black Holes in Einstein-Maxwell-Dilaton Theory,” Phys. Rev. D 100, no.4, 044052 (2019).
- Y. Kumaran and A. Övgün, “Deriving weak deflection angle by black holes or wormholes using Gauss-Bonnet theorem,” Turk. J. Phys. 45, no.5, 247-267 (2021).
- Z. Li, G. Z. Li, G. Zhang and A. Övgün, “Circular Orbit of a Particle and Weak Gravitational Lensing,” Phys. Rev. D 101, no.12, 124058 (2020).
- W. Javed, J. W. Javed, J. Abbas, Y. Kumaran and A. Övgün, “Weak deflection angle by asymptotically flat black holes in Horndeski theory using Gauss-Bonnet theorem,” Int. J. Geom. Meth. Mod. Phys. 18, no.01, 2150003 (2021).
- R. C. Pantig and A. Övgün, “Dark matter effect on the weak deflection angle by black holes at the center of Milky Way and M87 galaxies,” Eur. Phys. J. C 82, no.5, 391 (2022).
- R. C. Pantig and A. Övgün, “Dehnen halo effect on a black hole in an ultra-faint dwarf galaxy,” JCAP 08, no.08, 056 (2022).
- R. C. Pantig, P. K. R. C. Pantig, P. K. Yu, E. T. Rodulfo and A. Övgün, “Shadow and weak deflection angle of extended uncertainty principle black hole surrounded with dark matter,” Annals of Physics 436, 168722 (2022).
- A. Uniyal, R. C. A. Uniyal, R. C. Pantig and A. Övgün, “Probing a nonlinear electrodynamics black hole with thin accretion disk, shadow and deflection angle with M87* and Sgr A* from EHT,” Physics of the Dark Universe 40 (2023) 101178.
- R. C. Pantig and A. Övgün, “Testing dynamical torsion effects on the charged black hole’s shadow, deflection angle and greybody with M87* and Sgr A* from EHT,” Annals Phys. 448, 169197 (2023).
- J. Rayimbaev, R. C. J. Rayimbaev, R. C. Pantig, A. Övgün, A. Abdujabbarov and D. arXiv:2206.06599 [gr-qc]].
- G. Mustafa, F. G. Mustafa, F. Atamurotov, I. Hussain, S. Shaymatov and A. Övgün, “Shadows and gravitational weak lensing by the Schwarzschild black hole in the string cloud background with quintessential field,” Chin. Phys. C 46, no.12, 125107 (2022).
- X. M. Kuang and A. Övgün, “Strong gravitational lensing and shadow constraint from M87* of slowly rotating Kerr-like black hole,” Annals Phys. 447, 169147 (2022).
- W. Javed, S. W. Javed, S. Riaz and A. Övgün, “Weak Deflection Angle and Greybody Bound of Magnetized Regular Black Hole,” Universe 8, no.5, 262 (2022).
- E. F. Eiroa, G. E. E. F. Eiroa, G. E. Romero and D. F. Torres, “Reissner-Nordstrom black hole lensing,” Phys. Rev. D 66, 024010 (2002).
- C. R. Keeton, C. S. C. R. Keeton, C. S. Kochanek and E. E. Falco, “The Optical properties of gravitational lens galaxies as a probe of galaxy structure and evolution,” Astrophys. J. 509, 561-578 (1998).
- R. C. Pantig, L. R. C. Pantig, L. Mastrototaro, G. Lambiase and A. Övgün, “Shadow, lensing and neutrino propagation by dyonic ModMax black holes,” Eur. Phys. J. C 82, no.12, 1155 (2022).
- M. Sharif and S. Iftikhar, “Strong gravitational lensing in non-commutative wormholes,” Astrophys. Space Sci. 357, no.1, 85 (2015).
- R. Shaikh and S. Kar, “Gravitational lensing by scalar-tensor wormholes and the energy conditions,” Phys. Rev. D 96, no.4, 044037 (2017).
- S. N. Sajadi and N. Riazi, “Gravitational lensing by multi-polytropic wormholes,” Can. J. Phys. 98, no.11, 1046-1054 (2020).
- R. C. Pantig and E. T. Rodulfo, “Weak deflection angle of a dirty black hole,” Chin. J. Phys. 66, 691-702 (2020).
- W. Javed, R. W. Javed, R. Babar and A. Övgün, “Effect of the dilaton field and plasma medium on deflection angle by black holes in Einstein-Maxwell-dilaton-axion theory,” Phys. Rev. D 100, no.10, 104032 (2019).
- A. Övgün, “Weak Deflection Angle of Black-bounce Traversable Wormholes Using Gauss-Bonnet Theorem in the Dark Matter Medium,” Turk. J. Phys. 44, no.5, 465-471 (2020).
- Y. Kumaran and A. Övgün, “Weak Deflection Angle of Extended Uncertainty Principle Black Holes,” Chin. Phys. C 44, no.2, 025101 (2020).
- A. Övgün, Y. A. Övgün, Y. Kumaran, W. Javed and J. Abbas, “Effect of Horndeski theory on weak deflection angle using the Gauss–Bonnet theorem,” Int. J. Geom. Meth. Mod. Phys. 2250192 (2022).
- M. Okyay and A. Övgün, “Nonlinear electrodynamics effects on the black hole shadow, deflection angle, quasinormal modes and greybody factors,” JCAP 01, no.01, 009 (2022).
- W. Javed, J. W. Javed, J. Abbas and A. Övgün, “Effect of the Quintessential Dark Energy on Weak Deflection Angle by Kerr-Newmann Black Hole,” Annals Phys. 418, 168183 (2020).
- W. Javed, A. W. Javed, A. Hamza and A. Övgün, “Effect of nonlinear electrodynamics on the weak field deflection angle by a black hole,” Phys. Rev. D 101, no.10, 103521 (2020).
- T. K. Dey and S. Sen, “Gravitational lensing by wormholes,” Mod. Phys. Lett. A 23, 953-962 (2008).
- H. Asada, “Gravitational lensing by exotic objects,” Mod. Phys. Lett. A 32, no.34, 1730031 (2017).
- C. M. Yoo, T. C. M. Yoo, T. Harada and N. Tsukamoto, “Wave Effect in Gravitational Lensing by the Ellis Wormhole,” Phys. Rev. D 87, 084045 (2013).
- N. Tsukamoto, T. N. Tsukamoto, T. Harada and K. Yajima, “Can we distinguish between black holes and wormholes by their Einstein ring systems?,” Phys. Rev. D 86, 104062 (2012).
- W. Javed, I. W. Javed, I. Hussain and A. Övgün, “Weak deflection angle of Kazakov–Solodukhin black hole in plasma medium using Gauss–Bonnet theorem and its greybody bonding,” Eur. Phys. J. Plus 137, no.1, 148 (2022).
- H. El Moumni, K. H. El Moumni, K. Masmar and A. Övgün, “Weak deflection angle of light in two classes of black holes in nonlinear electrodynamics via Gauss–Bonnet theorem,” Int. J. Geom. Meth. Mod. Phys. 19, no.06, 2250094 (2022).
- A. Belhaj, H. A. Belhaj, H. Belmahi, M. Benali and H. arXiv:2204.10150 [gr-qc]].
- A. Belhaj, H. A. Belhaj, H. Belmahi, M. Benali and H. El Moumni, “Light deflection angle by superentropic black holes,” Int. J. Mod. Phys. D 31, no.07, 2250054 (2022).
- A. Belhaj, M. A. Belhaj, M. Benali, A. El Balali, H. El Moumni and S. E. Ennadifi, “Deflection angle and shadow behaviors of quintessential black holes in arbitrary dimensions,” Class. Quant. Grav. 37, no.21, 215004 (2020).
- Z. Li, G. Z. Li, G. Zhang and A. Övgün, “Circular Orbit of a Particle and Weak Gravitational Lensing,” Phys. Rev. D 101, no.12, 124058 (2020).
- W. Javed, M. W. Javed, M. Aqib and A. Övgün, “Effect of the magnetic charge on weak deflection angle and greybody bound of the black hole in Einstein-Gauss-Bonnet gravity,” Phys. Lett. B 829, 137114 (2022).
- W. Javed, A. W. Javed, A. Hamza and A. Övgün, “Weak Deflection Angle and Shadow by Tidal Charged Black Hole,” Universe 7, no.10, 385 (2021).
- W. Javed, M. B. W. Javed, M. B. Khadim and A. Övgün, “Weak gravitational lensing by Einstein-nonlinear-Maxwell–Yukawa black hole,” Int. J. Geom. Meth. Mod. Phys. 17, no.12, 2050182 (2020).
- C. R. Keeton and A. O. Petters, “Formalism for testing theories of gravity using lensing by compact objects. I. Static, spherically symmetric case,” Phys. Rev. D 72, 104006 (2005).
- K. K. Nandi, Y. Z. K. K. Nandi, Y. Z. Zhang and A. V. Zakharov, “Gravitational lensing by wormholes,” Phys. Rev. D 74, 024020 (2006).
- G. W. Gibbons and M. C. Werner, “Applications of the Gauss-Bonnet theorem to gravitational lensing,” Class. Quant. Grav. 25, 235009 (2008).
- A. Ishihara, Y. A. Ishihara, Y. Suzuki, T. Ono and H. Asada, “Finite-distance corrections to the gravitational bending angle of light in the strong deflection limit,” Phys. Rev. D 95, no.4, 044017 (2017).
- M. C. Werner, “Gravitational lensing in the Kerr-Randers optical geometry,” Gen. Rel. Grav. 44, 3047-3057 (2012).
- K. Jusufi, M. C. K. Jusufi, M. C. Werner, A. Banerjee and A. Övgün, “Light Deflection by a Rotating Global Monopole Spacetime,” Phys. Rev. D 95, no.10, 104012 (2017).
- P. Goulart, “Phantom wormholes in Einstein–Maxwell-dilaton theory,” Class. Quant. Grav. 35, no.2, 025012 (2018).
- K. Jusufi, A. K. Jusufi, A. Övgün and A. Banerjee, “Light deflection by charged wormholes in Einstein-Maxwell-dilaton theory,” Phys. Rev. D 96, no.8, 084036 (2017).
- K. Jusufi, I. K. Jusufi, I. Sakallı and A. Övgün, “Effect of Lorentz Symmetry Breaking on the Deflection of Light in a Cosmic String Spacetime,” Phys. Rev. D 96, no.2, 024040 (2017).
- I. Sakalli and A. Övgün,, “Hawking Radiation and Deflection of Light from Rindler Modified Schwarzschild Black Hole,” EPL 118, no.6, 60006 (2017).
- V. A. Kostelecky and S. Samuel, “Spontaneous Breaking of Lorentz Symmetry in String Theory,” Phys. Rev. D 39, 683 (1989).
- V. A. Kostelecky and R. Potting, “CPT and strings,” Nucl. Phys. B 359, 545-570 (1991).
- D. Colladay and V. A. Kostelecky, “CPT violation and the standard model,” Phys. Rev. D 55, 6760-6774 (1997).
- D. Colladay and V. A. Kostelecky, “Lorentz violating extension of the standard model,” Phys. Rev. D 58, 116002 (1998).
- V. A. Kostelecky, “Gravity, Lorentz violation, and the standard model,” Phys. Rev. D 69, 105009 (2004).
- V. A. Kostelecky and N. Russell, “Data Tables for Lorentz and CPT Violation,” Rev. Mod. Phys. 83, 11-31 (2011).
- V. A. Kostelecky and R. Lehnert, “Stability, causality, and Lorentz and CPT violation,” Phys. Rev. D 63, 065008 (2001).
- V. A. Kostelecky, R. V. A. Kostelecky, R. Lehnert and M. J. Perry, “Spacetime - varying couplings and Lorentz violation,” Phys. Rev. D 68, 123511 (2003).
- R. Lehnert, “Threshold analyses and Lorentz violation,” Phys. Rev. D 68, 085003 (2003).
- R. Casana, A. R. Casana, A. Cavalcante, F. P. Poulis and E. B. Santos, “Exact Schwarzschild-like solution in a bumblebee gravity model,” Phys. Rev. D 97, no.10, 104001 (2018).
- A. Delhom, T. A. Delhom, T. Mariz, J. R. Nascimento, G. J. Olmo, A. Y. Petrov and P. J. Porfírio, “Spontaneous Lorentz symmetry breaking and one-loop effective action in the metric-affine bumblebee gravity,” JCAP 07, no.07, 018 (2022).
- A. Delhom, J. R. A. Delhom, J. R. Nascimento, G. J. Olmo, A. Y. Petrov and P. J. Porfírio, “Metric-affine bumblebee gravity: classical aspects,” Eur. Phys. J. C 81, no.4, 287 (2021).
- A. F. Santos, A. Y. A. F. Santos, A. Y. Petrov, W. D. R. Jesus and J. R. Nascimento, “Gödel solution in the bumblebee gravity,” Mod. Phys. Lett. A 30, no.02, 1550011 (2015).
- C. Ding and X. Chen, “Slowly rotating Einstein-bumblebee black hole solution and its greybody factor in a Lorentz violation model,” Chin. Phys. C 45, no.2, 025106 (2021).
- R. V. Maluf and J. C. S. Neves, “Black holes with a cosmological constant in bumblebee gravity,” Phys. Rev. D 103, no.4, 044002 (2021).
- B. Altschul, Q. G. B. Altschul, Q. G. Bailey and V. A. Kostelecky, “Lorentz violation with an antisymmetric tensor,” Phys. Rev. D 81, 065028 (2010).
- L. A. Lessa, J. E. G. L. A. Lessa, J. E. G. Silva, R. V. Maluf and C. A. S. Almeida, “Modified black hole solution with a background Kalb–Ramond field,” Eur. Phys. J. C 80, no.4, 335 (2020).
- L. A. Lessa, R. L. A. Lessa, R. Oliveira, J. E. G. Silva and C. A. S. Almeida, “Traversable wormhole solution with a background Kalb–Ramond field,” Annals Phys. 433, 168604 (2021).
- M. S. Morris and K. S. Thorne, “Wormholes in space-time and their use for interstellar travel: A tool for teaching general relativity,” Am. J. Phys. 56, 395-412 (1988).
- R. V. Maluf and C. R. Muniz, “Exact solution for a traversable wormhole in a curvature-coupled antisymmetric background field,” Eur. Phys. J. C 82, no.5, 445 (2022).
- C. R. Keeton and A. O. Petters, “Formalism for testing theories of gravity using lensing by compact objects. II. Probing post-post-Newtonian metrics,” Phys. Rev. D 73, 044024 (2006).
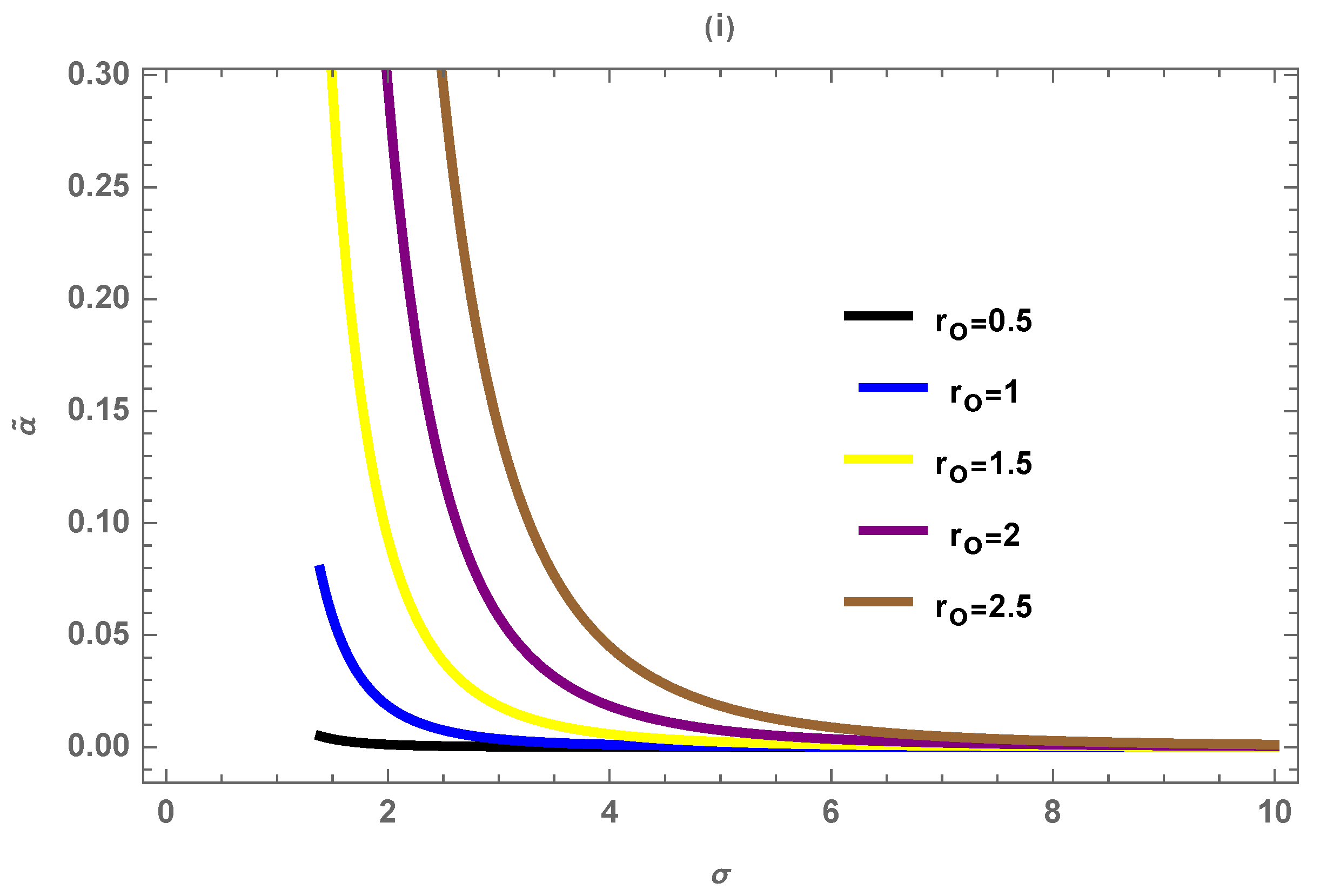
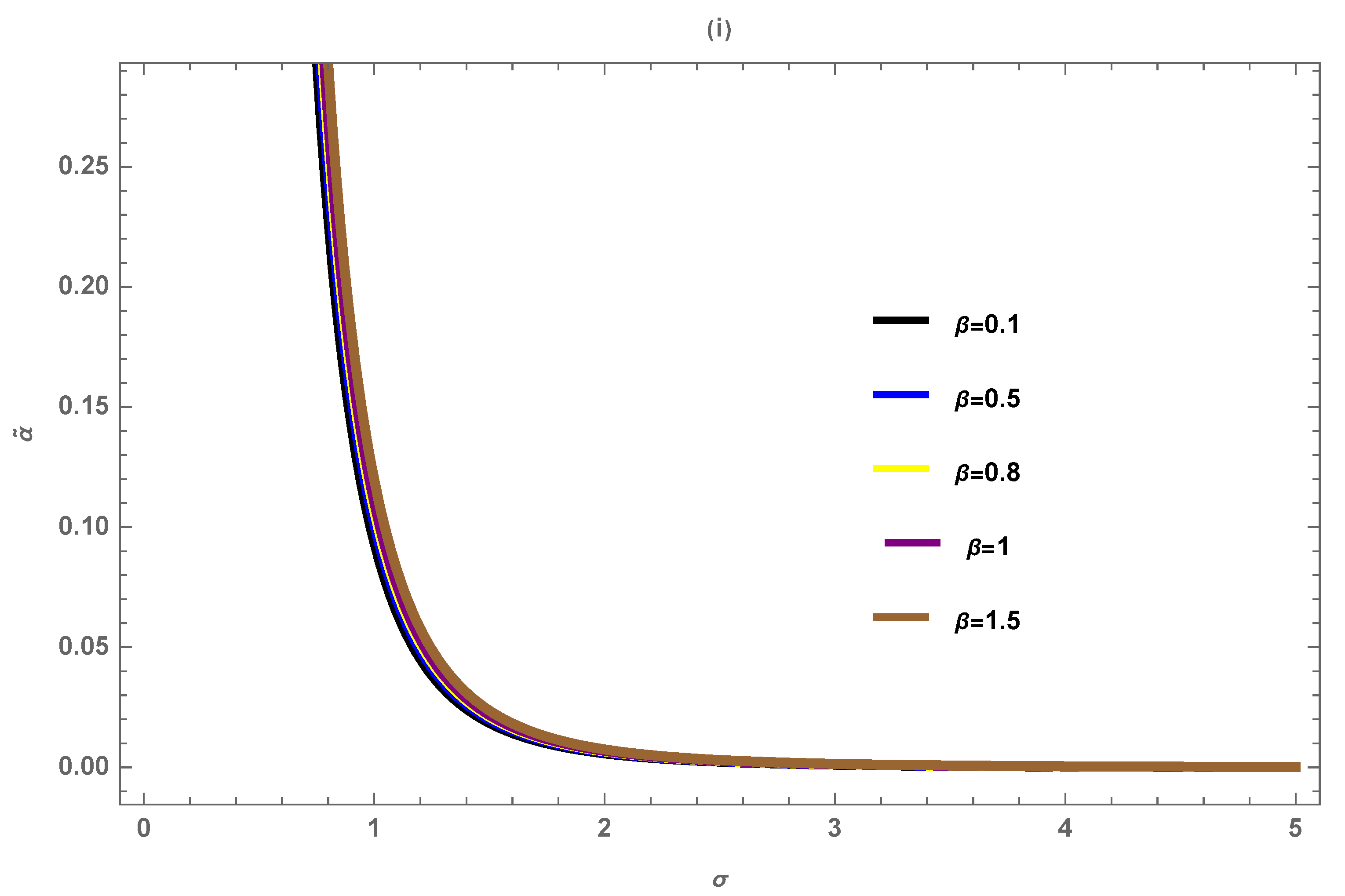
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




