Reflection of Light as a Mechanical Phenomenon Applied to the Michelson Interferometer with Light from the Sun

1. Introduction

The reflection of light as a mechanical phenomenon [1,2,3] considers the speed of light independent from its moving source and its reflection similar to a ball by a mirror in motion. This study continues with emission, propagation, and reflection of light as mechanical phenomena in inertial frames [4], observation of a star’s orbit [5], a general consideration of light reflection [6,7], and here with the reflection of light applied to the Miller experiment [8,9].

The emission, propagation, and reflection of light in inertial frames [4] conclude that physics phenomena in an inertial frame can be studied in any other inertial frame considered at relative rest. Here, the Sun’s frame at relative rest replaces the absolute frame for physics studies in Earth’s inertial frame. Thus, the Sun is a fixed light source for Earth, and Earth may be considered an inertial frame in the Sun’s frame at relative rest at the time of an experiment. The light from the Sun travels at the constant speed $c$ in any direction in the Sun’s frame at relative rest.

The reflection of light as a mechanical phenomenon applied to Michelson’s interferometer with a particular geometry [1,2] predicts zero fringe shift, and to a geometry [3] close to that presented in the Michelson-Morley experiment [10] offers $0.40\times {10}^{-4}$ fringe shift and greater for other geometries. Michelson’s derivation predicts a $0.40$ fringe shift.

This paper applies the theoretical derivation [1,2] and numerical calculation [3] to Miller’s experiments. Unlike the Tomaschek experiments [11], the fringe shifts in Miller’s experiments are predictable.

The reflection of light as a mechanical phenomenon [1,2,5] based on the elastic collision of balls with a wall in motion at the limit when the mass of balls converges to zero offers the equation

$$c_{ra}=c_s+v_i+v_r$$

(1)

In Equation (1), $c_{ra}$ is the speed of a reflected wavefront of a ray of light by a mirror in motion, $c_s$ is the wavefront speed from the source or a mirror as a source, $v_i$ is the mirror speed in the opposite direction of the incident wavefront from the source, and $v_r$ is the mirror speed in the direction of the reflected wavefront. Here, these speeds are in the Sun’s frame at relative rest. The mirror moves in one unique observable direction with speed $v$. However, regarding the light wavefront, as far as the collision effect is concerned, it has multiple directions of $v_i$ and $v_r$ at the moment of collision according to the mirror inclinations. Speeds $v_i$ and $v_r$ are projections of $v$ in their corresponding directions.

Another form of Equation (1) is

$$c_{ra}=c_s+v\cos a+v\cos b$$

(2)

In Equation (2), the speeds $v\cos a$ and $v\cos b$ replace $v_i$ and $v_r$ in Equation (1), respectively. Angle $a$ corresponds to the opposite direction of the incident wavefront, and angle $b$ to the direction of the reflected wavefront. These angles are measured from the direction of velocity vector $v$, originating at the point of collision. The directions of $v_i$ and $v_r$ are outward from the point of collision.

Michelson [10] derives the fringe shift in the space filled with ether. Consequently, the speed of light from a source before and after reflection is the constant $c$. The study of light reflection as a mechanical phenomenon [1,2,5] occurs in a vacuum. Like a ball in an elastic collision with a wall, the wavefront speed changes after reflection by a moving mirror. Therefore, the difference between these two approaches is the reflection of light by a moving mirror.

2. Interferometer on the Earth’s Equator

2.1. General considerations

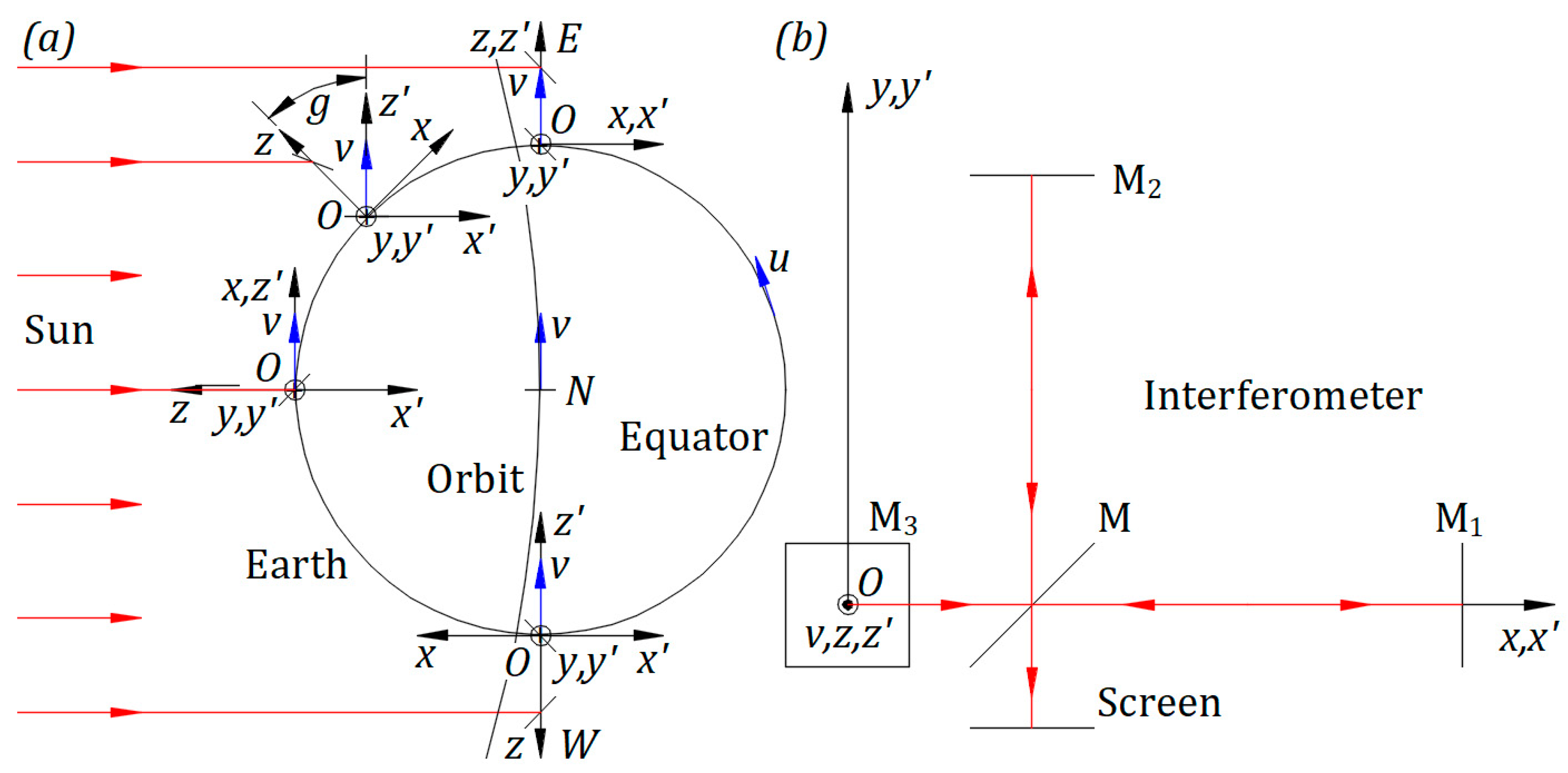
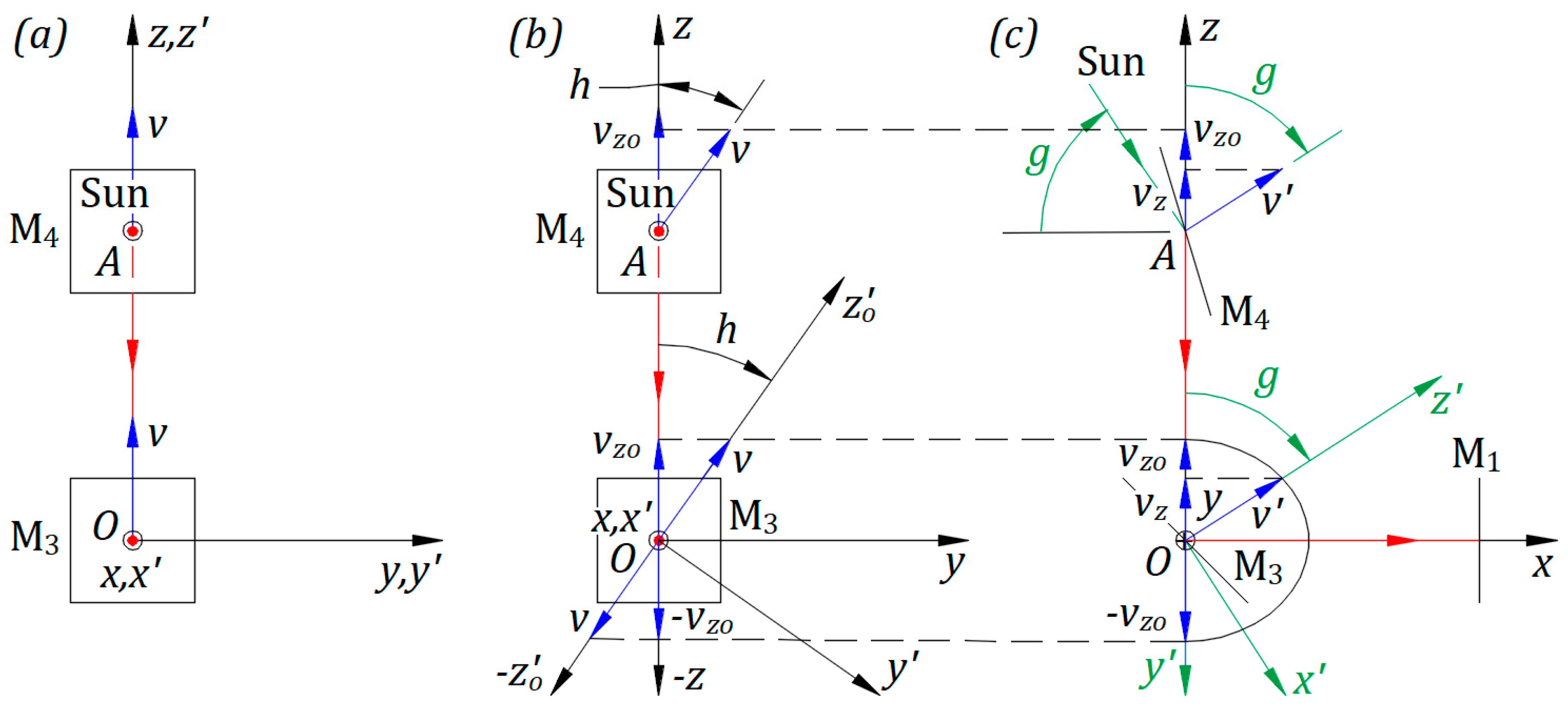
The following drawings illustrate a way to bring the light from the Sun to a modified Michelson interferometer. For simplicity, Earth’s axis has no tilt.

Figure 1(a) illustrates Earth's equatorial circle, Earth's revolving orbit around the Sun, and the center of the Sun and Earth in the same plane. The North Pole is outward, and the South Pole is inward, perpendicular to the paper plane.

An observer in the Sun’s frame at relative rest also perceives the physics phenomena as a local observer in Earth’s inertial frame. The observer’s location is on the North side of the Equator.

Figure 1(b) illustrates the Michelson interferometer at 6 am, as seen from the top side of Figure 1(a). Mirrors M₁, M₂, M₃, and beam splitter M belong to the instrument. Mirror M₃ replaces the instrument’s source of light.

The cartesian frame $Oxyz$, fixed to the instrument, originates at point $O$ of M₃. Axis $Ox$ is on the horizontal line, and axis $Oz$ is perpendicular to Earth’s local surface. Plane $Oxy$ is parallel to Earth’s local surface and perpendicular to the local Earth’s radius. At 6 am, the revolving velocity $v$ of Earth coincides with $Oz$.

The interferometer is in plane $Oxy$. It rotates counterclockwise around $Oz$ with an angle $f$ measured from $Ox$. The initial position of the instrument is when direction $O{M}_1$ coincides with $Ox$ for $f=0°$, as shown in Figure 1(b).

In the Sun’s frame at relative rest, a vector velocity $v$ in the direction $Oz\text{'}$ of the cartesian frame $Ox\text{'}y\text{'}z\text{'}$ is attached permanently to the origin $O$ of $Oxyz$. Earth’s spin changes the origin position $O$ of $Oxyz$ and $Ox\text{'}y\text{'}z\text{'}$; different from $Oxyz$, $Ox\text{'}y\text{'}z\text{'}$ keeps its axes’ directions fixed in the Sun’s frame at relative rest.

The instrument on the Equator belongs to a local Meridian. The Equator's start position can be defined when: the local Meridian of the instrument is at 6 am, frames $Oxyz$ and $Ox\mathrm{\text{'}}y\mathrm{\text{'}}z\mathrm{\text{'}}$ coincide, and the device is at the initial position, as illustrated in Figure 1(b).

In the Sun’s frame at relative rest, the center of the Sun, Earth’s orbit, and the Equator’s circle are always in the same plane. Planes $Oxz$ and $Ox\mathrm{\text{'}}z\mathrm{\text{'}}$ belong to Equator’s plane. Plane $Oxy$ is parallel to Earth’s local surface and perpendicular to Equator’s plane. Axes $Oy$ and $Oy\mathrm{\text{'}}$ are overlapping from 6 am to 6 pm.

Earth’s spin changes the position of $Oxyz$. At the same time, in plane $Oxz$, axis $Oz\mathrm{\text{'}}$ rotates clockwise around $Oy\mathrm{\text{'}}$, keeping the directions of $Ox\mathrm{\text{'}}y\mathrm{\text{'}}z\mathrm{\text{'}}$ unchanged. $Oz\mathrm{\text{'}}$ with the vector velocity $v$ at $O$ makes the angle $g$ measured from $Oz$.

Figure 1(a) indicates the position of the interferometer at 6 am, which is the Equator's start position, corresponding to $g=0°$. Earth’s spin brings the interferometer to an angle $g$ between 6 am and 6 pm, to $g=90°$ at noon, and $g=180°$ at 6 pm.

2.2. Interferometer on the Equator at 6 am, noon, and 6 pm

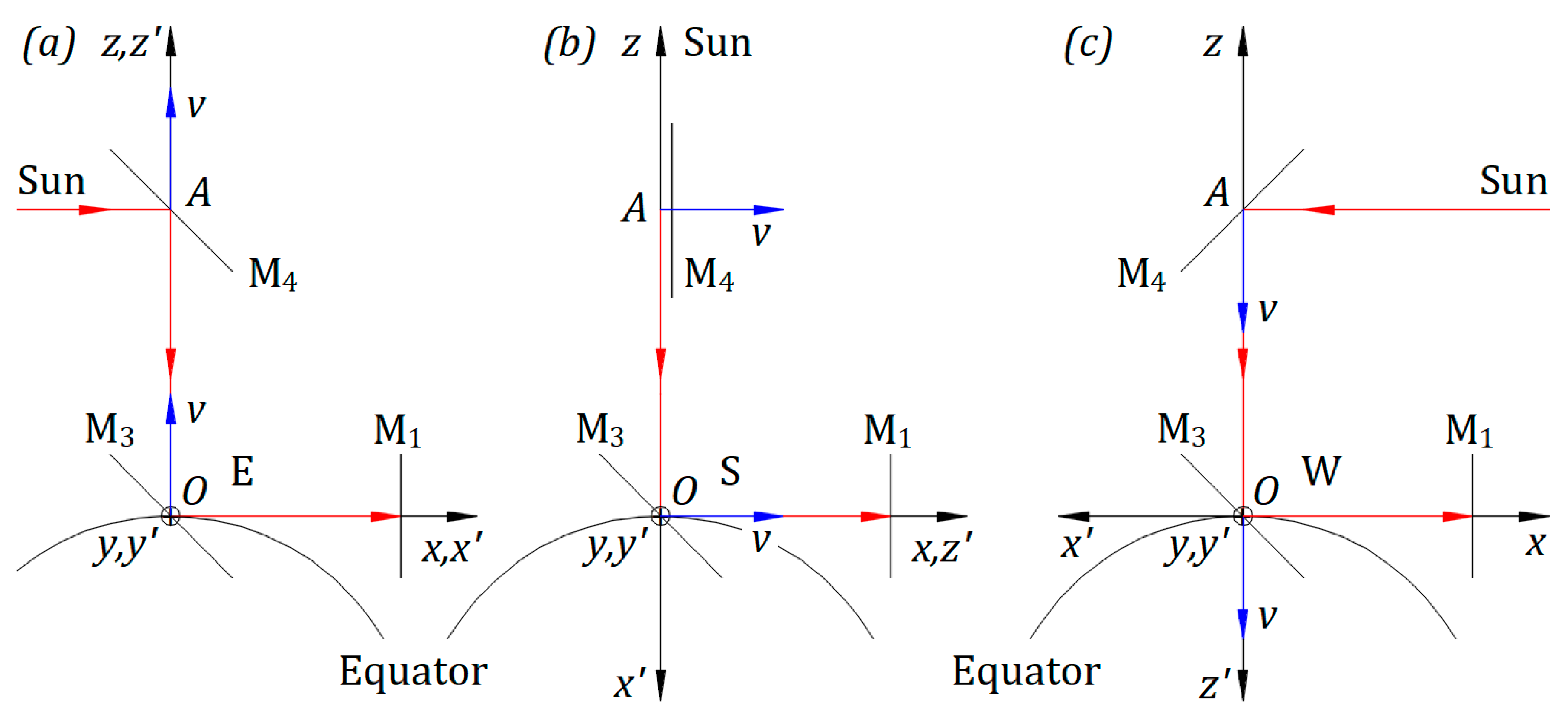
Figure 2(a) depicts the Equator's start position at 6 am for $g=0°$. Earth’s spin brings the interferometer at noon, as illustrated in Figure 2(b) for $g=90°$, at 6 pm, as presented in Figure 2(c) for $g=180°$, and in general, at a time between 6 am and 6 pm, as shown in Figure 3(a) for an angle $g$.

Point $A$ belongs to mirror M₄ and to axis $Oz$. Mirror M₄, axis $Oz$, mirror M₃, and interferometer form a solid structure. Mirror M₄ rotates at the Equator around an axis through point $A$ perpendicular to $Oxz$. At the North Pole around axis $Oz$. And between the Equator and the North Pole around both. M₄ stays fixed while the interferometer rotates $360°$ around axis $Oz$.

Considering that the Sun emits parallel rays of light in the direction from the Sun’s center toward Earth’s center, only these rays are reflected by M₄ in the opposite direction to $Oz$ toward M₃. The incident rays from the Sun are perpendicular to $v$ at any location on Earth.

In Figure 2(a), point $A$ of M₄ reflects the ray of light toward $O$ with the speed $c_{ra}$ given by Equation (2), $c_{ra}=c_s+v\cos a+v\cos b=c+v\cos 90°+v\cos 180°=c-v$.

The ray reflected at $O$ along $Ox$ and $O{\mathrm{M}}_1$ for $f=0°$ has the speed $c_{f=0°}=c_s+v\cos a+v\cos b$. With $c_s=c_{ra}$, $c_{f=0°}=\left(c-v\right)+v\cos 0°+v\cos 90°=c$.

The projection of $v$ on $Oz$ is $v_z=v$. The rays reflected by M₃ drift transversal opposite to velocity $v_z$.

In Figure 2(b), the light from the Sun travels perpendicular to $Ox$; therefore, no need for mirror M₄. At this position, M₄ rotates $180°$ around $Oz$ to continue reflecting rays for $90°<g\le 180°$.

The ray reflected at $O$ along $Ox$ and $O{\mathrm{M}}_1$ for $f=0°$ has, according to Equation (2), the speed $c_{f=0°}=c_s+v\cos a+v\cos b=c+v\cos 90°+v\cos 0°=c+v$.

The projection of $v$ on $Oz$ is zero. Thus, there is no transversal drift on rays reflected at M₃.

Figure 2(c) shows the device at 6 pm. Point $A$ of M₄ reflects the ray of light toward $O$ with the speed $c_{ra}$ given by Equation (2), $c_{ra}=c_s+v\cos a+v\cos b=c+v\cos 90°+v\cos 0°=c+v$.

The ray reflected at $O$ along $Ox$ and $O{\mathrm{M}}_1$ for $f=0°$ has the speed $c_{f=0°}=c_s+v\cos a+v\cos b=c_{ra}+v\cos 180°+v\cos 90°=\left(c+v\right)-v=c$.

The projection of $v$ on $Oz$ is $v_z=-v$. The rays reflected by M₃ drift transversal opposite to velocity $v_z$.

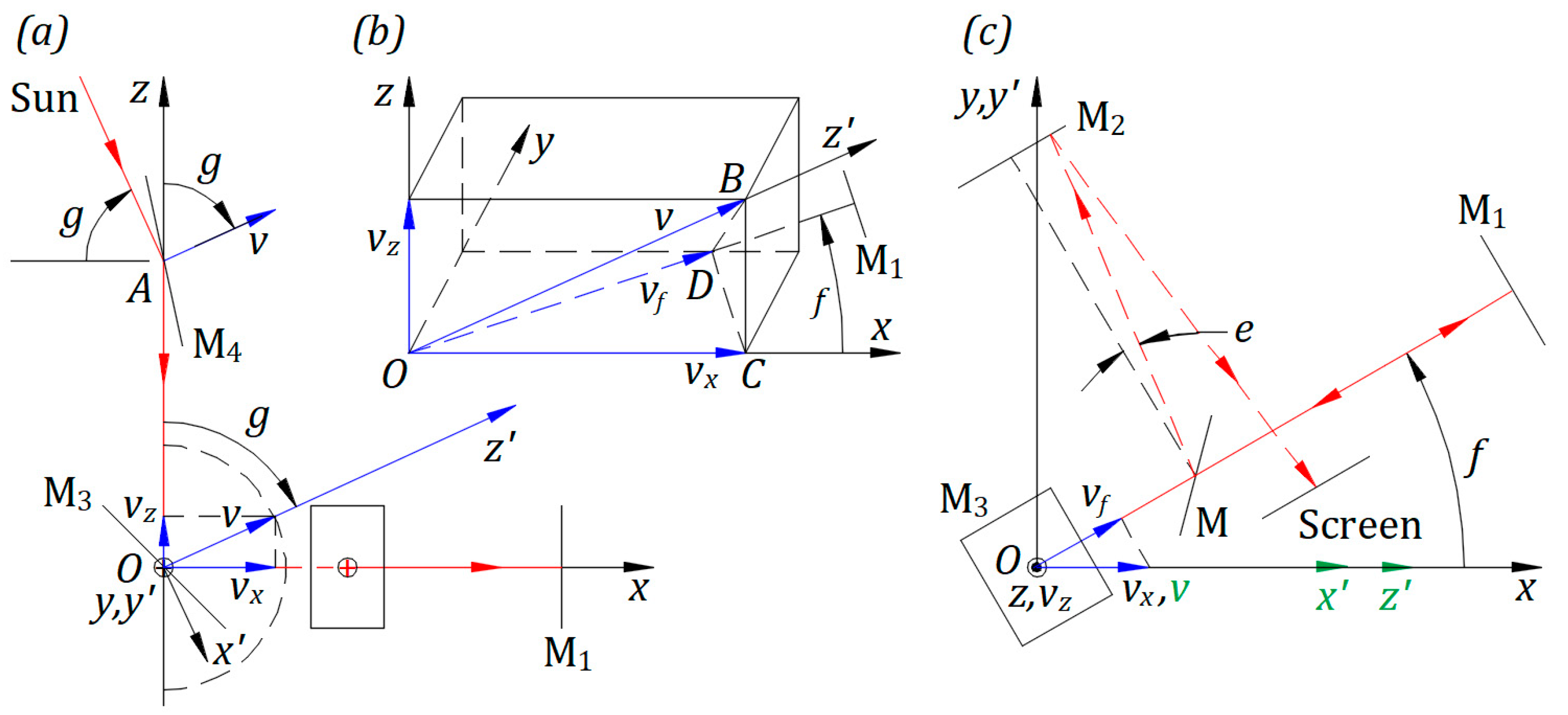
2.3. Interferometer on the Equator at an angle g

Figure 3(a) presents the instrument between 6 am and 6 pm when $Oz\text{'}$ makes an angle $g$ measured from $Oz$. To reflect the rays in the direction $AO$, M₄ rotates around the axis through point $A$ and perpendicular to $Oxz$. Angle $g$ has an opposite direction to Earth’s spin.

From 6 am to 6 pm for $0°\le g\le 180°$, projection of $v$ on $Oz$ is the transversal speed of the instrument in the Sun’s frame at relative rest

$$v_z=v\cos g$$

(3)

Projection of $v$ on $Ox$ is the longitudinal speed of the instrument in the Sun’s frame at relative rest $v_x=v\cos (90°-g)$, then

$$v_x=v\sin g$$

(4)

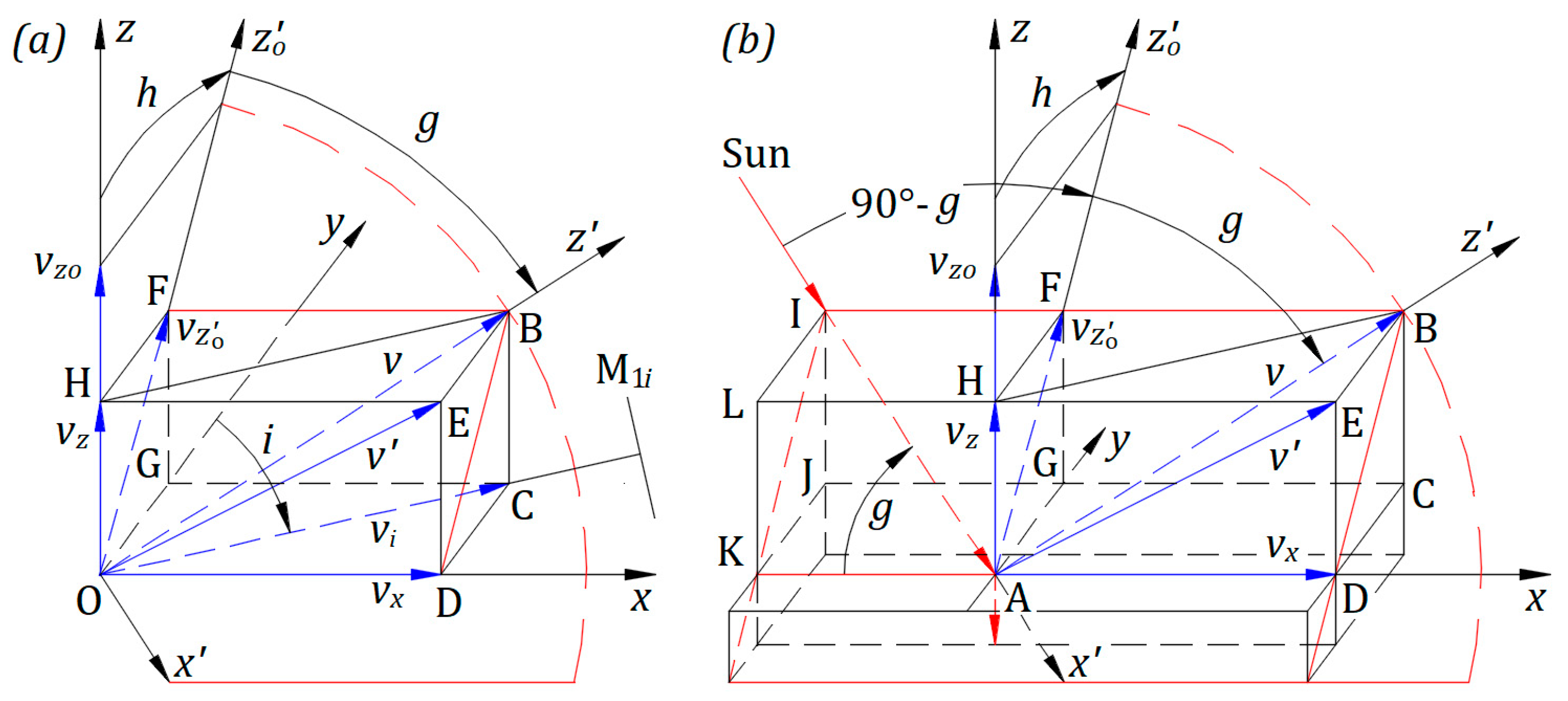
Figure 3(b) is a detail at point $O$ in a three-dimensional view when the instrument is at an angle $f$ from $Ox$. $OBC$ and $BCD$ planes and their intersection along $BC$ are perpendicular to $Oxy$, and $BD$ is perpendicular to $O{\mathrm{M}}_1$. Therefore, $OD$ is perpendicular to plane $BCD$, and $CD$ is perpendicular to $OD$. Thus, the projections of $v$ and $v_x$ on $O{\mathrm{M}}_1$ are identical to $OD=v_f$; with $v_x$ from Equation (4),

$$v_f=v_x\cos f$$

(5)

Figure 3(c) illustrates the top side view of Figure 3(a) with the interferometer rotated by an angle $f$ from $Ox$. For the geometry presented in Ref. [3], reflected rays by beam splitter M travel as illustrated at an angle $e$ from the perpendicular line to M₂. $Ox\text{'}$, $Oz\text{'}$ and $v$ in green indicate that they are not in plane $Oxy$.

Point $A$ of M₄ reflects the ray of light toward $O$ with the speed $c_{ra}=c_s+v\cos a+v\cos b=c+v\cos 90°+v\cos (180°+g)$ that gives the equation

$$c_{ra}=c-v\cos g$$

(6)

The ray from $A$ reflected at $O$ along $Ox$, employing Equation (2), has the speed $c_{f=0°}=c_{ra}+v\cos a+v\cos b$. With $c_{ra}$ from Equation (6) and $v_x$ from Equation (4), $c_{f=0°}=\left(c-v\cos g\right)+v\cos g+v\sin g$ yields the equation

$$c_{f=0°}=c+v_x$$

(7)

The reflected speed of light at $O$ along $O{\mathrm{M}}_1$ at an angle $f$ is $c_f=c_{ra}+v\cos a+v\cos b=\left(c-v\cos g\right)+v\cos g+v_x\cos f)$, therefore,

$$c_f=c+v_x\cos f$$

(8)

3. The Interferometer on the North Pole

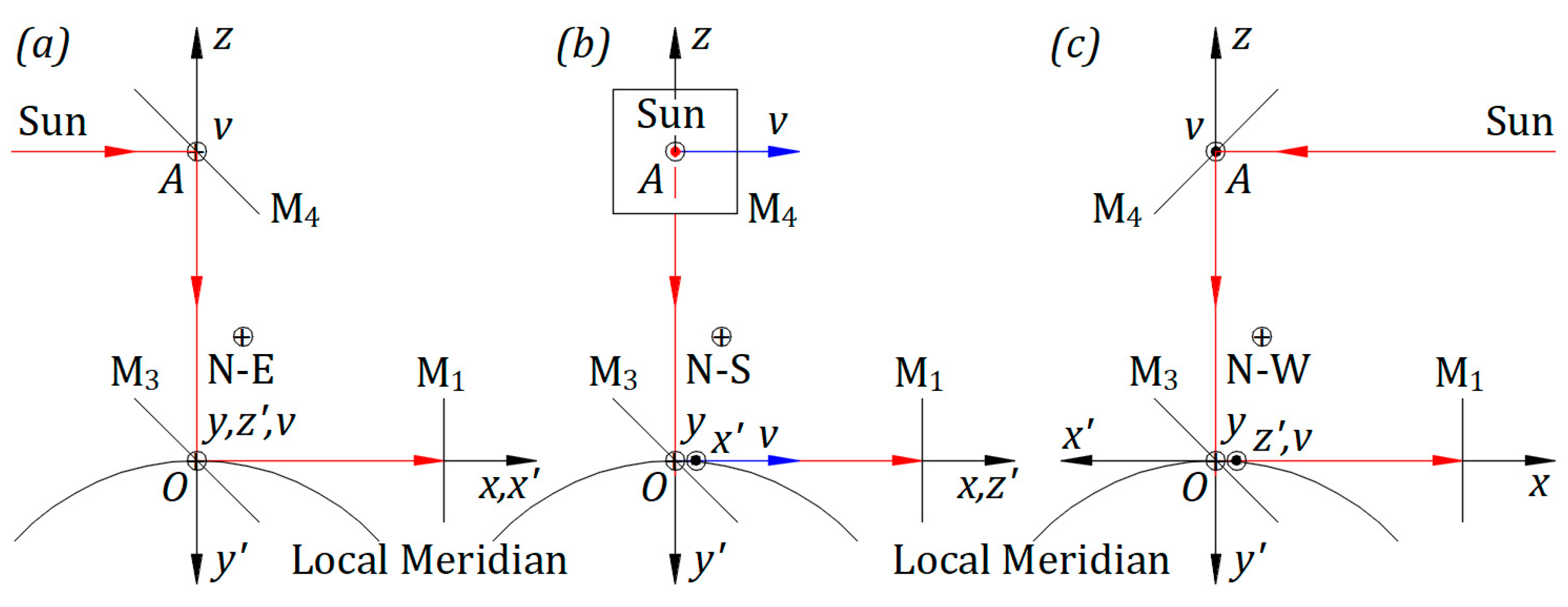
The solid structure, illustrated in Figure 2(a), brought from the Equator at 6 am along the local Meridian at the North Pole, looks like in Figure 4(a). From the Equator to the North Pole, the frame $Oxyz$ rotates $90°$ in the Sun’s frame at relative rest. In plane $Oyz$, $Oz\mathrm{\text{'}}$ rotates $90°$ around $Ox\mathrm{\text{'}}$ from $Oz$ to $Oy$; after rotation, $Oz\mathrm{\text{'}}$ has the same direction as $Oy$. Planes $Oxy$ and $Ox\mathrm{\text{'}}z\mathrm{\text{'}}$ coincide and are parallel to Equator’s plane. Axis $Oy\mathrm{\text{'}}$ is perpendicular to Equator’s plane.

Earth’s spin rotates $Oxyz$ in the Sun’s frame at relative rest. In plane $Oxy$, $Oz\mathrm{\text{'}}$ rotates around fixed $Oy\mathrm{\text{'}}$ from $Oy$ at 6 am at angle $g=0°$, as illustrated in Figure 4(a), to $Ox$ at noon at angle $g=90°$, as in Figure 4(b), and to $-Oy$ at 6 pm at angle $g=180°$, as in Figure 4(c). At the North Pole, mirror M₄ rotates only around $Oz$.

4. Interferometer on a Latitude

The right side view of Figure 2(a), ignoring M₁, is as in Figure 5(a). Moving the solid structure from the Equator toward the North Pole, $Oxyz$ rotates in the Sun’s frame at relative rest. Velocity $v$ with its axis $Oz\text{'}$ rotates in plane $Oyz$ around $Ox\text{'}$ with angle $h$ measured from axis $Oz$, as visualized in Figure 5(b). For $h=0°$, the interferometer is at the Equator, and for $h=90°$ at the North Pole. In the rotation on a Meridian, from the Equator to the North Pole, Mirror M₄ stays fixed.

In Figure 5(b), we can define the Latitude's start position at the intersection of the local Meridian with the local Latitude at 6 am. $Oz\text{'}$ is marked with index o for angle $g$ $=0°$, $O{z}_{\mathrm{o}}^{\text{'}}$ , and is in plane $Oyz$ making an angle $h$ measured from $Oz$.

Plane $Ox\text{'}z\text{'}$ is parallel, and axis $Oy\text{'}$ is perpendicular to Equator’s plane here and at any location on Earth. Plane $Oxy$ is parallel, and the axis $Oz$ is perpendicular to Earth’s local surface as on any place on Earth. $Oxz$ and $Ox\text{'}z\text{'}$ are perpendicular to plane $Oyz$ and intersect along $Ox$.

Earth’s spin rotates the frame $Oxyz$ on the Latitude from 6 am to 6 pm. At the same time, velocity $v$ with its axis $Oz\text{'}$ rotates around fixed axis $Oy\text{'}$ from $O{z}_{\mathrm{o}}^{\text{'}}$ at 6 am for angle $g=0°$ to $Ox$ at noon for $g=90°$ and to $-O{z}_{\mathrm{o}}^{\text{'}}$ at 6 pm for $g=180°$. Thus, on a Meridian, angle $g$ is identical when the instrument is on different Latitudes to that at the Equator. On a Latitude, mirror M₄ rotates around both axes to capture only the parallel rays from the Sun.

The view from the opposite direction of $Oy\mathrm{\text{'}}$ shows vector $v$ with its axis $Oz\mathrm{\text{'}}$ rotating from 6 am to 6 pm on a semicircle with origin at $O$ and radius $v$. The semicircle is in plane $Ox\mathrm{\text{'}}z\mathrm{\text{'}}$. Any angle $h$ yields an identical image. The semicircle is identical to that in Figure 3(a), illustrated in a dashed line in plane $Oxz$.

The view from the opposite direction of $Oy$ sees the semicircle projection of the vector $v$ as a semi-ellipse in plane $Oxz$, as illustrated in Figure 5(c). The projection points of this semi-ellipse on $Oz$ represent the speeds $v_z$ for angles $g$.

Figure 5(c) is the left side view of Figure 5 (b) for an angle $g$ measured from $O{z}_{\mathrm{o}}^{\mathrm{\text{'}}}$. The projection of the velocity $v$ that belongs to $Oz\mathrm{\text{'}}$ on plane $Oxz$ is $v\mathrm{\text{'}}$. $Ox\mathrm{\text{'}}$, $Oy\mathrm{\text{'}}$, and $Oz\mathrm{\text{'}}$ axes are depicted in green to indicate that they are not in plane $Oxz$; $Ox\mathrm{\text{'}}$ is in the front, and $Oy\mathrm{\text{'}}$ and $Oz\mathrm{\text{'}}$ are in the back of plane $Oxz$.

Planes $Oxz$ and $Ox\mathrm{\text{'}}z\mathrm{\text{'}}$ intersect along $Ox$. $Ox\mathrm{\text{'}}$ coincides with $Ox$ only at $g=0°$. Axis $Oz\mathrm{\text{'}}$ rotates in the back of plane $Oxz$ from $O{z}_{\mathrm{o}}^{\mathrm{\text{'}}}$ at the Latitude’s start position when it is behind $Oz$ for $g=0°$ to plane $Oxz$ coinciding with $Ox$ for $g=90°$. Then $Oz\mathrm{\text{'}}$ rotates in front of plane $Oxz$ to $-O{z}_{\mathrm{o}}^{\mathrm{\text{'}}}$ for $g=180°$, above $-Oz$. $Ox\mathrm{\text{'}}$ rotates in front of plane $Oxz$ from $Ox$ for $g=0°$ to above $-Oz$ for $g=90°$, then to $-Ox$ for $g=180°$.

Figure 6(a) offers a three-dimensional visualization of the mechanical velocities at point $O$ of Figure 5(c). Axis $O{z}_{\mathrm{o}}^{\mathrm{\text{'}}}$ is in plane $Oyz$. Rectangular $ODEH$ belongs to $Oxz$, $ODCG$ to $Oxy$, and $OGFH$ to $Oyz$. The speed $v$ is along axis $Oz\mathrm{\text{'}}$. Index $i$ for ${\mathrm{M}}_{1i}$ indicates that mirror M₁ location corresponds to angles $i$ defined below. Velocities $v$ and $v_{z_{\mathrm{o}}^{\mathrm{\text{'}}}}$ belong to rectangular $ODBF$ of the plane in red; $v_x$ and $v_i$ to plane $Oxy$.

The projection of $v$ on $Oz$ at the Latitude’s start position offers the equation

$$v_{z\mathrm{o}}=v\cos h$$

(9)

The projection of $v$ on $O{z}_{\mathrm{o}}^{\mathrm{\text{'}}}$ is $OF=v_{z_{\mathrm{o}}^{\mathrm{\text{'}}}}$, therefore,

$$v_{z_{\mathrm{o}}^{\mathrm{\text{'}}}}=v\cos g$$

(10)

The projection of $v_{z_{\mathrm{o}}^{\mathrm{\text{'}}}}$ on $Oz$, $v_z=v_{z_{\mathrm{o}}^{\mathrm{\text{'}}}}\cos h$, is also the projection of $v$ on $Oz$. Employing Equation (10),

$$v_z=v\cos h\cos g$$

(11)

$v_z$ is the transversal speed of the instrument in the Sun’s frame at relative rest.

The projection of $v$ on $Ox$ is $v_x=v\cos (90°-g)$, therefore,

$$v_x=v\sin g$$

(12)

$BC=OH=v_z$. From triangle $OBC$, the longitudinal velocity of the instrument in the Sun’s frame at relative rest has the magnitude of $v_i=\sqrt{v^2-v_z^2}$ that with $v_z$ from Equation (11) yields the equation

$$v_i=v\sqrt{1-{\left(\cos h\cos g\right)}^2}$$

(13)

In triangle $OCG$, $\sin i=GC/v_i=v_x/v_i$, then

$$i={\sin }^{-1}\left(v_x/v_i\right)$$

(14)

Angle $i$ indicates the interferometer's initial position direction $O{\mathrm{M}}_{1i}$ when $O{\mathrm{M}}_1$ and $v_i$ directions coincide.

Figure 6(b) offers a three-dimensional visualization of the mechanical velocities at point $A$ of Figure 5(c). At $A$, we can attach the same frame as at $O$, $Axyz$, and $Ax\mathrm{\text{'}}y\mathrm{\text{'}}z\mathrm{\text{'}}$. Axis $A{z}_0^{\mathrm{\text{'}}}$ is in plane $Ayz$. Velocities $v$ and $v_{z_{\mathrm{o}}^{\mathrm{\text{'}}}}$ belong to rectangular $BDKI$ with its sides in red, which belongs to $Ax\mathrm{\text{'}}z\mathrm{\text{'}}$. The ray from the Sun travels in this plane along the line $IA$. Point $A$ of M₄ reflects it towards $O$. M₄ must be adjusted with both axes to reflect the incident ray at $A$ along $Ax\mathrm{\text{'}}$’s direction towards $O$.

The ray of light reflected at $A$ toward $O$ has the speed $c_{ra}=c_s+v\cos a+v\cos b=c+v\cos 90°-v_z$ that gives the equation

$$c_{ra}=c-v_z$$

(15)

From Figure 6(a), the speed of light reflected in the direction ${\mathrm{M}}_{1i}$ for angle $i$, $c_i=c_{ra}+v\cos a+v\cos b=\left(c-v_z\right)+v_z+v_i$, offers the equation

$$c_i=c+v_i$$

(16)

Equation (16) corresponds to Equation (7) when the interferometer is on the Equator.

For the same reason as in Figure 3(b), the projections of $v$ and $v_i$ along $O{\mathrm{M}}_1$ are identical for any angle $f$ measured from ${\mathrm{M}}_{1i}$. The speed of light reflected at $O$ in the direction of $O{\mathrm{M}}_1$ for an angle $f$ measured from ${\mathrm{M}}_{1i}$ is $c_{if}=c_{ra}+v\cos a+v\cos b=\left(c-v_z\right)+v_z+v_i\cos f$ that yield the equation

$$c_{if}=c+v_i\cos f$$

(17)

Equation (17) corresponds to Equation (8) when the interferometer is on the Equator.

5. Conclusions

With the assumption that the transversal velocity of the interferometer $v_z$ does not affect the fringe shift, Michelson derivation does not agree with Miller’s experiments at Mount Wilson in 1921 and 1025 and with those at Cleveland laboratory in 1924. The derivation based on the reflection of light as a mechanical phenomenon does not agree with Miller’s experiments at Mount Wilson but agrees with experiments at Cleveland laboratory with sunlight and laboratory sources.

When the local meridian is at noon, from the Equator to the North Pole, there is no transversal speed for the instrument, and the numerical calculation yields zero fringe shift. Miller observed fringe shifts at Mount Wilson for these positions as well. Therefore, a derivation considering the transversal speed should not affect the fringe shift for these positions and is not likely for any position of the instrument on Earth.

For any angle $f$, the speed of light $c_{if}=c+v_i\cos f$, and the longitudinal speed of the interferometer is $v_i\cos f$. Thus, the speed of light within the interferometer is $c$, which could explain why the fringe shift is zero or undetectable.

The Tomaschek experiment [11] may display a fringe shift if the star's velocity in the Universe is different from that of the Sun. The light from a star arrives on Earth, no matter the distance from the star to the Sun, with two components: the emitted velocity $c$ and the star's velocity [4,5]. The fringe shift depends on the difference of star and Sun velocities. Experiments consist of trials and observations with different stars without any expectations. Nevertheless, the theoretical derivation is more complex, even if we know the star's velocity to the Sun.

However, regardless of the outcome of a complete theoretical derivation, the contradictory results observed at Mount Wilson and the Cleveland laboratory leave this subject open to theoretical and experimental challenges.

Ref. [3] offers zero fringe shift for $e=0$ rad, $0.40\times {10}^{-4}$ for aberration angle $e=0.0001$ rad, and greater than $0.40\times {10}^{-4}$ for an angle $e$ beyond the aberration angle. We chose a geometry for theoretical derivation and calculation of the fringe shift, but an experiment yields a fringe shift according to an unknown geometry. The author expected this study to predict Miller's observations at the Mount Wilson and Cleveland laboratory because different actual geometries of the interferometer's light paths, which imply different angles $e$, could explain the observations at the two locations.