Only in Natural Concepts Does Nature Disclose Her Secrets

1. Introduction

Today’s concepts of space and time were coined by Albert Einstein. In SR, space and time are merged into a flat spacetime described by the Minkowski metric. SR is often presented in Minkowski spacetime [3]. Predicting the lifetime of muons [4] is one example that supports SR. In GR, a curved spacetime is described by the Einstein tensor. The deflection of starlight [5] and the high accuracy of GPS [6] are two examples that support GR. Quantum field theory [7] unifies classical field theory, SR, and QM but not GR.

The two postulates of ER: (1) All energy moves through Euclidean spacetime (ES) at the speed of light $c$. Mathematically, ES is 4D Euclidean space. Physically, only three axes are spatial. (2) The laws of physics have the same form in each observer’s view. His view is created by orthogonally projecting ES to his proper space and to his proper time. In SR, these two projections are called an observer’s “coordinate space” and “coordinate time”, but they are assembled to a non-Euclidean spacetime. In ER, these two projections span a Euclidean spacetime. My first postulate is stronger than the second SR postulate: $c$ is both absolute and universal. My second postulate refers to each observer’s view rather than to inertial frames. On top, I use natural concepts: Proper space/time (pure distance) replace coordinate space/time. Curved worldlines in flat ES replace curved spacetime. “Wavematters” (pure energy, see Section 5.13) replace particle/electromagnetic wave. To improve readability, my observers are male. To make up for it, Mother Nature is female.

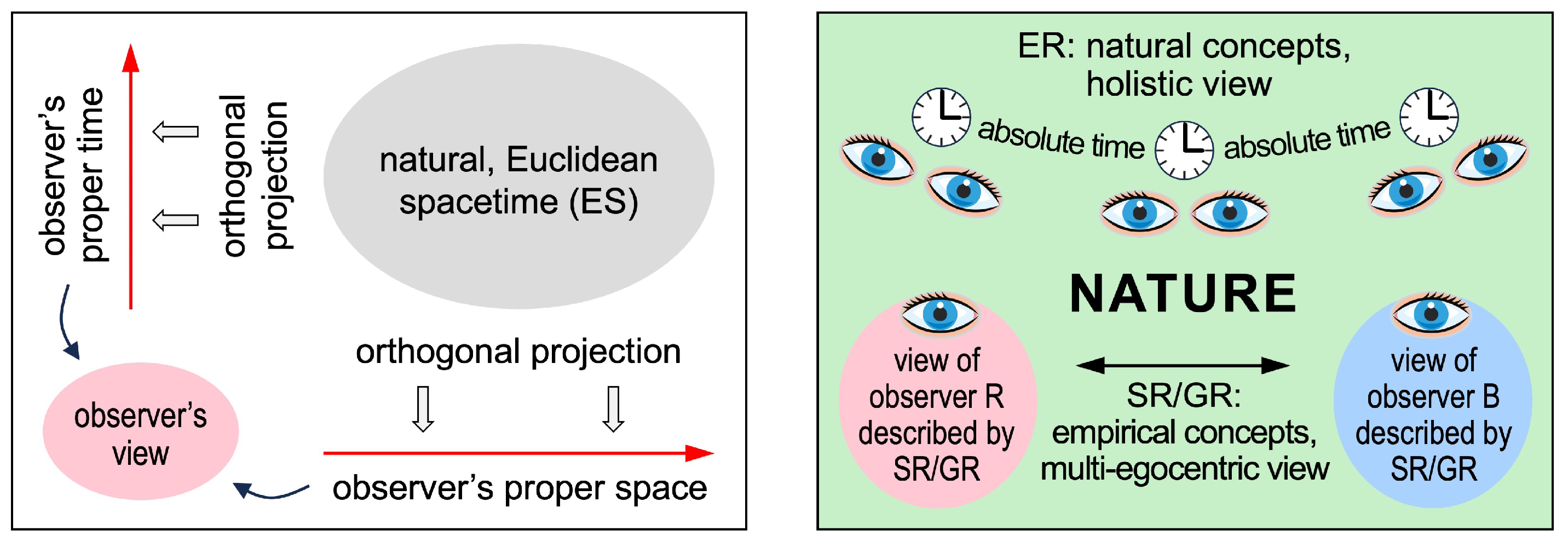
Figure 1 left illustrates that an observer’s view is created by orthogonally projecting ES (see Section 4 for orthogonal projections). Figure 1 right illustrates that there are two approaches to describing nature. ER describes her in natural concepts and tells us how an observer’s view is created. SR/GR describe nature in empirical concepts and tell us how the view of an observer R relates to the view of an observer B. There is absolute time in ER only. Because of different concepts, we must not play SR/GR off against ER. ER does not compete with SR/GR. So, what is ER good for? ER solves mysteries that are rooted in ES.

In 1969, Newburgh and Phipps [8] pioneered ER. Montanus [9] added a constraint: A pure time interval must be a pure time interval for all observers. According to Montanus [10], this constraint is required to avoid the twin paradox and a “character paradox” (confusion of photons, particles, antiparticles). I show that the constraint is obsolete. Whatever is proper time for me, it may be one axis of proper space for you. There is no twin paradox if we take cosmic time as the parameter. There is no “character paradox” if we take the 4D vector “flow of proper time” into account (see Section 3). Montanus was mistaken in assuming that only antiparticles would feature a reversed flow of proper time. An observed object’s proper time can flow backward with respect to the observer without its physical charges being reversed (see Section 5.15). Montanus calculated the precession of Mercury’s perihelion in ER [10] and other relativistic effects [11]. He failed to set up Maxwell’s equations and a wave equation in ER because of a missing minus sign [10].

Almeida [12] studied geodesics in ES. Gersten [13] showed that the Lorentz transformation can be interpreted as an SO(4) rotation. van Linden maintains a website about ER (https://euclideanrelativity.com/). Most physicists reject ER because dark energy and non-locality make cosmology and QM work, the SO(4) symmetry of ES seems to exclude waves, and paradoxes seem to arise. This paper marks a turning point. I disclose an issue in SR/GR. I explain why ES does not exclude waves. I avoid paradoxes by projecting ES.

It is instructive to contrast Newton’s physics, Einstein’s physics, and ER. In Newton’s physics, all energy moves through 3D Euclidean space as a function of independent time. There is no speed limit for matter. In Einstein’s physics, all energy moves through a non-Euclidean spacetime. The 3D speed of matter is $v_{3\mathrm{D}}<c$. In ER, all energy moves through ES. The 4D speed of all energy is $c$. Newton’s physics [14] shaped Kant’s philosophy [15]. I am convinced that ER will trigger a reformation of physics and philosophy.

2. Disclosing an Issue in Special and General Relativity

The fourth coordinate in SR is an observer’s coordinate time $t$. In § 1 of SR, Einstein gives an instruction for synchronizing clocks at the points P and Q. At $t_{\mathrm{P}}$, a light pulse is sent from P to Q. At $t_{\mathrm{Q}}$, it is reflected at Q. At $t_{\mathrm{P}}^{*}$, it is back at P. The clocks synchronize if

$$t_{\mathrm{Q}}-t_{\mathrm{P}}=t_{\mathrm{P}}^{\mathrm{*}}-t_{\mathrm{Q}}.$$

(1)

In § 3 of SR, Einstein derives the Lorentz transformation. The coordinates $x_1,x_2,x_3,t$ of an event in a system K are transformed to the coordinates $x_1^{\text{'}},x_2^{\text{'}},x_3^{\text{'}},t^{\text{'}}$ in K’ by

$$x_1^{\mathrm{\text{'}}}=\gamma \left(x_1-v_{3\mathrm{D}}t\right),$$

(2a)

$$x_2^{\mathrm{\text{'}}}=x_2,x_3^{\mathrm{\text{'}}}=x_3,$$

(2c)

$$t^{\mathrm{\text{'}}}=\gamma (t-v_{3\mathrm{D}}{x}_1/c^2),$$

(2c)

where K’ moves relative to K in $x_1$ at the constant speed $v_{3\mathrm{D}}$ and $\gamma =(1-v_{3\mathrm{D}}^2/c^2{)}^{-0.5}$ is the Lorentz factor. Mathematically, Equations (2a–c) are correct: They transform the coordinates from K to K’. There are covariant equations that transform the coordinates from K’ to K. Physically, there is an issue in SR and also in GR: The empirical concepts of SR/GR fail to solve fundamental mysteries. There are coordinate-free formulations of both SR [16] and GR [17], but there is no absolute time in SR/GR and thus no “holistic view” (I repeat the definition: universal for all objects at the same instant in time). The view in SR/GR is multi-egocentric: SR/GR work for all observers, but each observer’s view is egocentric. All observers’ views taken together do not make a holistic view because they still do not provide absolute time. Without absolute time, observers will not always agree on what is past and what is future. Physics paid a high price for dismissing absolute time: ER restores absolute time (see Section 3) and solves 15 fundamental mysteries (see Section 5). Thus, the issue is real.

The issue in SR/GR is not about making wrong predictions. It has much in common with the issue in the geocentric model: In either case, there is no holistic view. Geocentrism is the egocentric view of mankind. In the old days, it was natural to believe that all celestial bodies would orbit Earth. Only astronomers wondered about the retrograde loops of some planets and claimed that Earth orbits the sun. In modern times, engineers have improved rulers and clocks. Today, it is natural to believe that it would be fine to describe nature as accurately as possible but in the empirical concepts of one or more observers. The human brain is smart, but it often takes itself as the center/measure of everything.

The analogy of SR/GR to the geocentric model is not perfect: Heliocentrism and geocentrism exclude each other, whereas ER and SR/GR complement each other. Even so, the analogy is close: (1) After a transformation in SR/GR (or after choosing another center of the Universe), the view is again egocentric (or else geocentric). (2) Retrograde loops make geocentrism work, but heliocentrism declares retrograde loops obsolete. Dark energy and non-locality make cosmology and QM work, but ER declares dark energy and non-locality obsolete. (3) The geocentric model was a dogma in the old days. SR/GR are dogmata today. Have physicists not learned from history? Does history repeat itself?

3. The Physics of Euclidean Relativity

ER cannot be derived from measurement instructions because the proper coordinates of other objects cannot be measured. We start with the Minkowski metric of SR:

$${c^2\mathrm{d}\tau }^2={c^2\mathrm{d}t}^2-\mathrm{d}{x}_1^2-\mathrm{d}{x}_2^2-\mathrm{d}{x}_3^2,$$

(3)

where $\mathrm{d}\tau$ is an infinitesimal distance in proper time $\tau$, whereas $\mathrm{d}t$ and ${\mathrm{d}x}_i$ ($i=1,2,3$) are infinitesimal distances in an observer’s coordinate space $x_1,x_2,x_3$ and coordinate time $t$. Coordinate spacetime $x_1,x_2,x_3,t$ is empirical because its four coordinates are construed by an observer and thus not immanent in rulers and clocks. Rulers measure proper length. Clocks measure proper time. We introduce ER by defining its Euclidean metric:

$${c^2\mathrm{d}\theta }^2=\mathrm{d}{d}_1^2+\mathrm{d}{d}_2^2+\mathrm{d}{d}_3^2+\mathrm{d}{d}_4^2,$$

(4)

where $\mathrm{d}\theta$ is an infinitesimal distance in cosmic time $\theta$, whereas all ${\mathrm{d}d}_i$ ($i=1,2,3$) and ${\mathrm{d}d}_4=c\mathrm{d}\tau$ are infinitesimal “pure distances”. Now the role of proper time $\tau$ is reversed: The new fourth coordinate is proper time $\tau$; the new invariant is absolute, cosmic time $\theta$; the new metric tensor is the identity matrix. I choose the symbol $\theta$ because the initial of the Greek letter theta is “t” as in “time”. I prefer the indices 1–4 to 0–3 to stress the full symmetry in all four coordinates. Any object’s proper space $d_1,d_2,d_3$ and its proper time $\tau$ span $d_1,d_2,d_3,d_4$ (ES) with $d_4=c\tau$. Euclidean spacetime is natural because its four coordinates $d_{\mu }$ ($\mu =1,2,3,4$) are measured by and are thus immanent in rulers and clocks. Intrinsic rulers and clocks of all objects measure out natural spacetime! Do not confuse Equation (4) with a Wick rotation [18], where $t$ is imaginary and $\tau$ is the invariant.

Each object is free to label the axes of ES (observers are objects too). We assume that it labels the axis of its current 4D motion as $d_4$. Since it does not move in its proper space, it moves in the $d_4$ axis at the speed $c$ (first postulate). Because of length contraction at the speed $c$ (see Section 4), the $d_4$ axis disappears for itself and is experienced as proper time. Objects moving in the $d_4^{\text{'}}$ axis at the speed $c$ experience the $d_4^{\text{'}}$ axis as proper time. Each object experiences its 4D motion as proper time. For each object, there is a 4D vector “flow of proper time” $\mathit{\tau }$. Information is lost if the 4D vector $\mathit{\tau }$ is ignored, as in SR/GR.

$$\tau =d_4/c,{\tau }^{\mathrm{\text{'}}}=d_4^{\mathrm{\text{'}}}/c,$$

(5)

$$\mathit{\tau }=d_4\mathit{u}/c^2,{\mathit{\tau }}^{\mathbf{\text{'}}}=d_4^{\mathrm{\text{'}}}{\mathit{u}}^{\mathbf{\text{'}}}/c^2,$$

(6)

where $\mathit{u}$ is an object’s 4D velocity in ES. Speed is not defined as $v_i={\mathrm{d}x}_i/\mathrm{d}t$ ($i=1,2,3$) but as $u_{\mu }=\mathrm{d}{d}_{\mu }/\mathrm{d}\theta$ ($\mu =1,2,3,4$). Thus, Equation (4) is nothing but my first postulate:

$$u_1^2+u_2^2+u_3^2+u_4^2=c^2.$$

(7)

It is instructive to contrast three concepts of time. $t$ is a subjective measure of time: An observer uses his clock as the master clock. $\tau$ is an objective measure of time: Clocks measure $\tau$ independently of observers. $\theta$ is the total distance covered in ES (length of a worldline) divided by $c$. By taking $\theta$ as the parameter, all observers agree on what is past and what is future. Since $\theta$ is absolute, there is no twin paradox in ER. Twins are the same age in cosmic time. A finite $c$ implies that there is no coordinate “absolute time”. Physicists are not yet aware that a finite $c$ is compatible with a parameter “absolute time”.

Different concepts disable a unification of SR/GR and ER. SR describes nature in the empirical concepts $x_1\left(\tau \right),x_2\left(\tau \right),x_3\left(\tau \right),t\left(\tau \right)$, where $\tau$ is some evolution parameter and $t$ is coordinate time. GR is locally equivalent to SR. ER describes nature in the natural concepts $d_1\left(\theta \right),d_2\left(\theta \right),d_3\left(\theta \right),d_4\left(\theta \right)$, where $\theta$ is the “cosmic evolution parameter” and $d_4$ relates to proper time. Only in proper coordinates can we access ES, but the proper coordinates of other objects cannot be measured. In Section 6, I explain why this is fine.

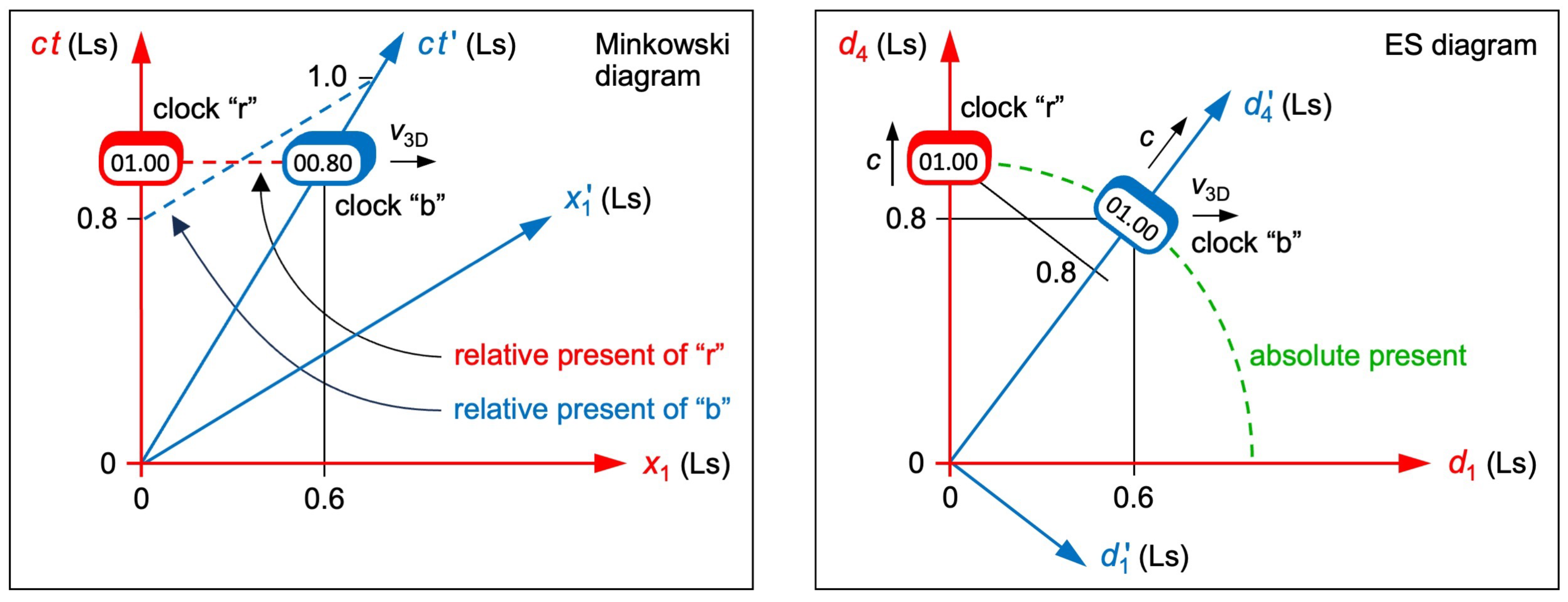
We consider two identical clocks “r” (red clock) and “b” (blue clock). In SR, “r” moves in the $ct$ axis. Clock “b” starts at $x_1=0$ and moves in the $x_1$ axis at a constant speed of $v_{3\mathrm{D}}=0.6c$. Figure 2 left shows the instant when either clock moved 1.0 Ls (light seconds) in $ct$. Clock “b” moved 0.6 Ls in $x_1$ and 0.8 Ls in $c{t}^{\text{'}}$. It displays “0.8”. In ER, “r” moves in the $d_4$ axis. Figure 2 right shows the instant when either clock moved 1.0 s in its proper time, which is equal to cosmic time for either clock. Both clocks display “1.0”.

We now assume that an observer R (or B) moves with clock “r” (or else “b”). In SR and only from the perspective of R, clock “b” is at $c{t}^{\text{'}}=0.8\mathrm{L}\mathrm{s}$ when “r” is at $ct=1.0\mathrm{L}\mathrm{s}$ (see Figure 2 left). Thus, “b” is slow with respect to “r” in $t^{\text{'}}$ (of B). In ER and independently of observers, clock “b” is at $d_4=0.8\mathrm{L}\mathrm{s}$ when “r” is at $d_4=1.0\mathrm{L}\mathrm{s}$ (see Figure 2 right). Thus, “b” is slow with respect to “r” in $d_4$ (of R). In SR and ER, “b” is slow with respect to “r”, but time dilation occurs in different axes. Experiments do not disclose the axis in which a clock is slow. This is why both SR and ER describe time dilation correctly—if they yield the same Lorentz factor. This is the case (see Section 4). Note that there is a difference regarding clock synchronization: In SR, R is able to synchronize clock “b” to his clock “r” (same value of $ct$ in Figure 2 left). If he does, these clocks are not synchronized for B. In ER, clocks with the same 4D vector $\mathit{\tau }$ are always synchronized, whereas clocks with different $\mathit{\tau }$ and ${\mathit{\tau }}^{\mathit{\text{'}}}$ are never synchronized (different values of $d_4$ in Figure 2 right).

But why does ER provide a holistic view? Well, Equation (4) is fully symmetric in all four $d_{\mu }$. They are “pure distances” because ES itself does not distinguish between “spatial” and “temporal”. Only objects/observers experience three axes as spatial and one as temporal. R and B experience different axes as temporal. This is why Figure 2 left works for R but not for B: A second Minkowski diagram is required, where $x_1^{\text{'}}$ and $c{t}^{\text{'}}$ are orthogonal. Here the view is multi-egocentric. In contrast, Figure 2 right works for R and for B at once (at the same cosmic time): Not only are $d_1$ and $d_4$ orthogonal but also $d_1^{\text{'}}$ and $d_4^{\text{'}}$. ES is independent of observers and thus absolute. Here the view is universal and thus holistic.

What about waves in ES? I admit that regarding waves I was on the wrong track for three years. I was misled by editors who insisted that the SO(4) symmetry of ES is incompatible with waves. Meanwhile, I realized: All objects moving through ES—we call them “wavematters”—are waves, but they propagate and oscillate as a function of the parameter time $\theta$ and not of the coordinate time $t$. To see this, we rearrange Equation (4):

$${c^2\mathrm{d}\theta }^2-\mathrm{d}{d}_1^2-\mathrm{d}{d}_2^2-\mathrm{d}{d}_3^2=\mathrm{d}{d}_4^2={c^2\mathrm{d}\tau }^2.$$

(4*)

The metric in Equation (4∗) is Minkowskian. It is compatible with waves propagating and oscillating as a function of $\theta$. Since Equations (4) and (4∗) are equivalent, we interpret wavematters as waves propagating through and oscillating in ES as a function of $\theta$. In an observer’s view, wavematters reduce to wave packets or else to particles (see Section 5.13).

4. Geometric Effects in Euclidean Relativity

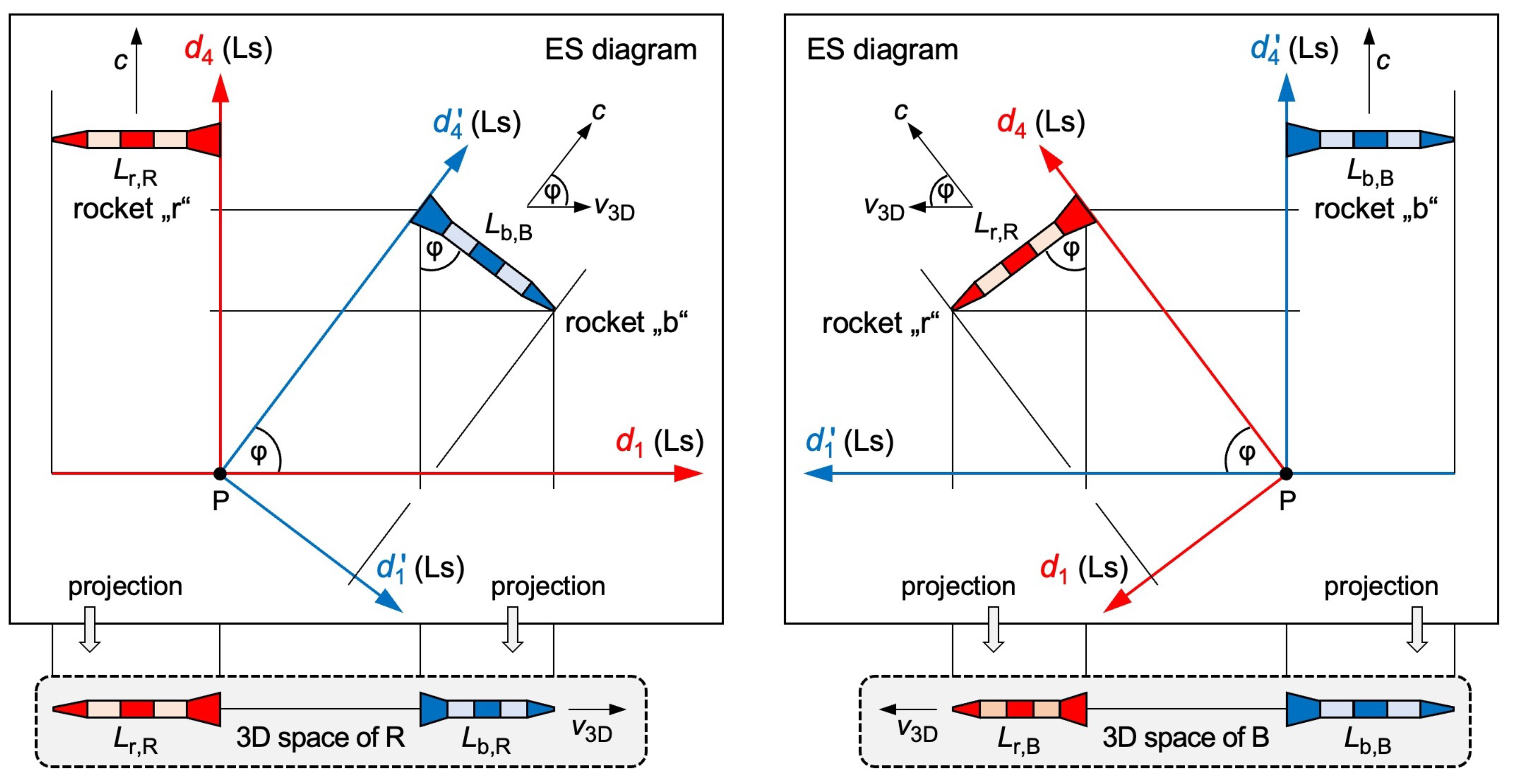
We consider two identical rockets “r” (red rocket) and “b” (blue rocket). Let observer R (or B) be in the rear end of “r” (or else “b”). The 3D space of R (or B) is spanned by $d_1,d_2,d_3$ (or else $d_1^{\text{'}},d_2^{\text{'}},d_3^{\text{'}}$). We use “3D space” as a synonym of proper space. The proper time of R (or B) relates to $d_4$ (or else $d_4^{\text{'}}$) according to Equation (5). Both rockets start at the same point P and at the same cosmic time ${\theta }_0$. They move relative to each other at the constant speed $v_{3\mathrm{D}}$. R and B are free to label the axis of relative motion in 3D space. R (or B) labels it as $d_1$ (or else $d_1^{\text{'}}$). The ES diagrams in Figure 3 must fulfill my two postulates and the initial conditions (same P, same ${\theta }_0$). This is achieved by rotating the red and the blue frame with respect to each other. Do not confuse ES diagrams with Minkowski diagrams. In ES diagrams, objects maintain proper length and clocks display proper time. To improve readability, a rocket’s width is drawn in $d_4$ (or $d_4^{\text{'}}$) although it is in the $d_2,d_3$ plane (or else $d_2^{\text{'}},d_3^{\text{'}}$ plane).

We now assume that $N$ rockets “${\mathrm{r}}_i$” are launched from P at the same cosmic time ${\theta }_0$, where “${\mathrm{r}}_1$” is equal to “r”. We also assume: The 4D vector ${\mathit{\tau }}_i$ of “${\mathrm{r}}_i$” ($2\le i\le N$) is rotated with respect to ${\mathit{\tau }}_{i-1}$ of “${\mathrm{r}}_{i-1}$” by $\pi /2-\phi$. This implies that “${\mathrm{r}}_i$” recedes from “${\mathrm{r}}_{i-1}$” in the 3D space of “${\mathrm{r}}_{i-1}$” at the speed $v_{3\mathrm{D}}$. If $N(\pi /2-\phi )>\pi /2$, some rockets move backward in $d_4$. If one rocket “${\mathrm{r}}_i$” rotates by $\pi$, it stands still in the 3D space of “${\mathrm{r}}_1$” and its 4D vector ${\mathit{\tau }}_i$ is reversed with respect to the 4D vector ${\mathit{\tau }}_1$ of “${\mathrm{r}}_1$”. This example shows that ER does not compete with SR. Our assumptions are not valid in SR: There is no “same cosmic time ${\theta }_0$” and no 4D vector $\mathit{\tau }$ in SR. We can draw all “${\mathrm{r}}_i$” in a Minkowski diagram (launched at the same coordinate time), but our example is outside the scope of SR.

Up next, we verify: (1) Rotating the red and the blue frame with respect to each other causes length contraction. (2) The fact that proper time flows in different 4D directions for R and for B causes time dilation. Let $L_{\mathrm{b},\mathrm{R}}$ (or $L_{\mathrm{b},\mathrm{B}}$) be the length of rocket “b” for observer R (or else B). In a first step, we project “b” in Figure 3 left to the $d_1$ axis:

$${\sin }^2\phi +{\cos }^2\phi =(L_{\mathrm{b},\mathrm{R}}/L_{\mathrm{b},\mathrm{B}}{)}^2+(v_{3\mathrm{D}}/c{)}^2=1,$$

(8)

$$L_{\mathrm{b},\mathrm{R}}={\gamma }^{-1}{L}_{\mathrm{b},\mathrm{B}}(\mathrm{l}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h} \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}),$$

(9)

where $\gamma =(1-v_{3\mathrm{D}}^2/c^2{)}^{-0.5}$ is the same Lorentz factor as in SR. For R, rocket “b” contracts to $L_{\mathrm{b},\mathrm{R}}$. Despite the Euclidean metric, we calculate the same $\gamma$ as in SR. We now ask: Which distances will R observe in $d_4$? We rotate “b” until it serves as a ruler for R in $d_4$. In his 3D space, this ruler contracts to zero: The $d_4$ axis disappears for R because of length contraction at the speed $c$. In a second step, we project “b” in Figure 3 left to the $d_4$ axis:

$${\sin }^2\phi +{\cos }^2\phi =(d_{4,\mathrm{B}}/d_{4,\mathrm{B}}^{\mathrm{\text{'}}}{)}^2+(v_{3\mathrm{D}}/c{)}^2=1,$$

(10)

$$d_{4,\mathrm{B}}={{\gamma }^{-1}d}_{4,\mathrm{B}}^{\mathrm{\text{'}}},$$

(11)

where $d_{4,\mathrm{B}}$ (or $d_{4,\mathrm{B}}^{\text{'}}$) is the distance that B moved in $d_4$ (or else $d_4^{\text{'}}$). With $d_{4,\mathrm{B}}^{\text{'}}=d_{4,\mathrm{R}}$ (R and B cover the same distance in ES but in different 4D directions), we calculate

$$d_{4,\mathrm{R}}=\gamma d_{4,\mathrm{B}}(\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e} \mathrm{d}\mathrm{i}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}),$$

(12)

where $d_{4,\mathrm{R}}$ is the distance that R moved in $d_4$. Equations (9) and (12) tell us: $\gamma$ is recovered in ER if we project ES to the axes $d_1$ and $d_4$ of an observer. This result is significant: It tells us that ER predicts the same relativistic effects as SR. The rockets serve as an example. All other objects are orthogonally projected the same way. For an overview of orthogonal projections, the reader is referred to geometry textbooks [19,20].

We now transform the proper coordinates of observer R (unprimed) to the ones of B (primed). R cannot measure the proper coordinates of B, and vice versa, but we can always calculate them from ES diagrams. Figure 3 right tells us how to calculate the 4D motion of R in the proper coordinates of B. The transformation is a 4D rotation by the angle $\phi$.

$$d_{1,\mathrm{R}}^{\mathrm{\text{'}}}\left(\theta \right)=d_{4,\mathrm{R}}\left(\theta \right)\cos \phi =d_{4,\mathrm{R}}\left(\theta \right)v_{3\mathrm{D}}/c,$$

(13a)

$$d_{2,\mathrm{R}}^{\mathrm{\text{'}}}\left(\theta \right)=d_{2,\mathrm{R}}\left(\theta \right),d_{3,\mathrm{R}}^{\mathrm{\text{'}}}\left(\theta \right)=d_{3,\mathrm{R}}\left(\theta \right),$$

(13b)

$$d_{4,\mathrm{R}}^{\mathrm{\text{'}}}\left(\theta \right)=d_{4,\mathrm{R}}\left(\theta \right)\sin \phi =d_{4,\mathrm{R}}\left(\theta \right){\gamma }^{-1}.$$

(13c)

Up next, I show that not only the Lorentz factor is recovered in ER but also gravitational time dilation. We return to our two clocks. Clock “r” and Earth move in the $d_4$ axis of “r” at the speed $c$ (see Figure 4). Clock “b” accelerates in the 3D space of “r” toward Earth while maintaining the speed $c$. Because of Equation (7), all accelerations are transversal in ES. The speed $u_{1,\mathrm{b}}$ of “b” in $d_1$ increases at the expense of its speed $u_{4,\mathrm{b}}$ in $d_4$.

Initially, our two clocks shall be very far away from Earth. Eventually, clock “b” falls freely toward Earth. The kinetic energy of “b” (mass $m$) in the $d_1$ axis of “r” is

$${{\displaystyle \frac{1}{2}}mu}_{1,\mathrm{b}}^2=GMm/R,$$

(14)

where $G$ is the gravitational constant, $M$ is the mass of Earth, and $R=d_{1,\mathrm{E}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{h}}-d_{1,\mathrm{b}}$ is the distance of “b” to Earth in the 3D space of “r”. By applying Equation (7), we get

$$u_{4,\mathrm{b}}^2=c^2-u_{1,\mathrm{b}}^2=c^2-2GM/R.$$

(15)

With $u_{4,\mathrm{b}}={\mathrm{d}d}_{4,\mathrm{b}}/\mathrm{d}\theta$ (“b” moves in the $d_4$ axis at the speed $u_{4,\mathrm{b}}$) and $c={\mathrm{d}d}_{4,\mathrm{r}}/\mathrm{d}\theta$ (“r” moves in the $d_4$ axis at the speed $c$), we calculate

$$\mathrm{d}{d}_{4,\mathrm{b}}^2=(c^2-2GM/R)(\mathrm{d}{d}_{4,\mathrm{r}}/c{)}^2,$$

(16)

$$\mathrm{d}{d}_{4,\mathrm{r}}={\gamma }_{\mathrm{g}\mathrm{r}}\mathrm{d}{d}_{4,\mathrm{b}}(\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{v}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l} \mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e} \mathrm{d}\mathrm{i}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}),$$

(17)

where ${\gamma }_{\mathrm{g}\mathrm{r}}=(1-2GM/(R{c}^2{\left)\right)}^{-0.5}$ is the same dilation factor as in GR. Equation (17) tells us: ${\gamma }_{\mathrm{g}\mathrm{r}}$ is recovered in ER if we project ES to the $d_4$ axis of an observer. This result is significant: It tells us that ER predicts the same gravitational time dilation as GR. However, there is a big difference: In GR, curved spacetime replaces gravitational fields. In ER, gravitational fields celebrate a comeback. Acceleration rotates an object’s $\mathit{\tau }$ and curves its worldline in flat ES. “Action at a distance” is not an issue if any variation in field strength also spreads at the speed $c$. Gravitational waves [21] support the idea of GR that gravity is a feature of spacetime. I invite theorists to show two things: (1) Gravitational waves are also compatible with ER. (2) ER can also be derived from the variation of an action as it can be done for GR [22]. Here I showed that ER yields the same $\gamma$ and ${\gamma }_{\mathrm{g}\mathrm{r}}$ as SR/GR.

Summary of time dilation: In SR, a uniformly moving clock “b” is slow with respect to “r” in the time axis of “b”. In GR, an accelerating clock “b” or else a clock “b” in a more curved spacetime is slow with respect to “r” in the time axis of “b”. In ER, a clock “b” is slow with respect to “r” in the time axis of “r” (!) if the 4D vector ${\mathit{\tau }}^{\mathit{\text{'}}}$ of “b” differs from the 4D vector $\mathit{\tau }$ of “r”. Since both $\gamma$ and ${\gamma }_{\mathrm{g}\mathrm{r}}$ are recovered in ER, the Hafele–Keating experiment [23] supports ER too. GPS works in ER as well as in SR/GR.

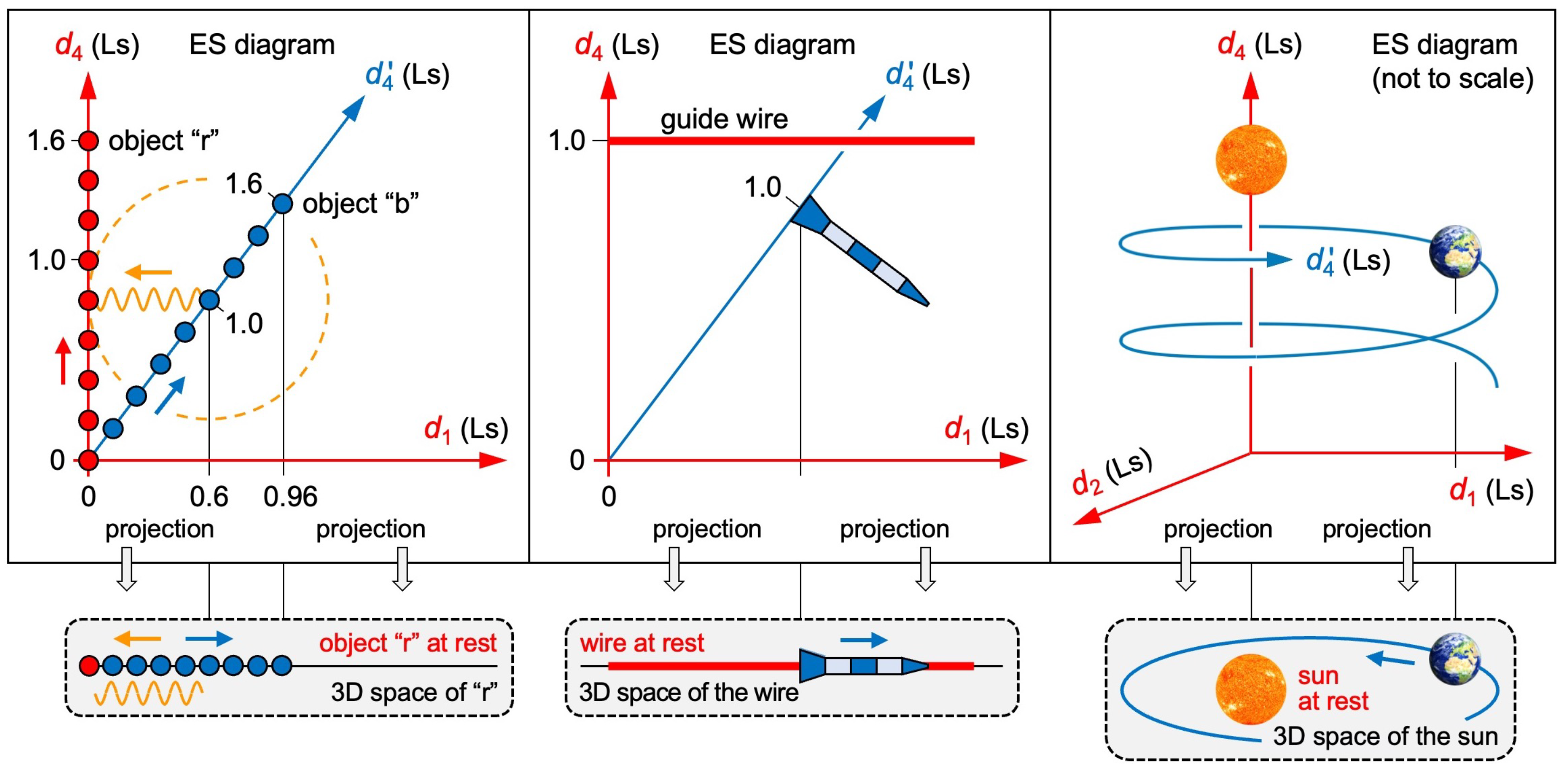
Three problems tell us how to read ES diagrams (see Figure 5). Problem 1: Two objects “r” and “b” move through ES at the speed $c$. “r” moves in $d_4$. “b” emits a radio signal at $d_4^{\text{'}}=1.0\mathrm{L}\mathrm{s}$. The signal recedes radially from “b” in all axes as a function of $\theta$, but it cannot catch up with “r” in the $d_4$ axis. Can the radio signal and “r” collide in the 3D space of “r” if they do not collide in ES? Problem 2: A rocket moves along a guide wire. In ES, both objects move at the speed $c$. The wire moves in $d_4$. As the rocket covers distance in $d_1$, its speed in $d_4$ is less than $c$. Doesn’t the wire escape from the rocket? Problem 3: Earth orbits the sun. In ES, both objects move at the speed $c$. The sun moves in $d_4$. As Earth covers distance in $d_1$ and $d_2$, its speed in $d_4$ is less than $c$. Doesn’t the sun escape from Earth’s orbit?

The questions in the last paragraph seem to disclose geometric paradoxes. The fallacy lies in the assumption that all four axes $d_{\mu }$ ($\mu =1,2,3,4$) would be spatial at once. This is not the case. Objects/observers experience only three axes as spatial and one as temporal. We solve all three problems by projecting ES to the 3D space of that object which moves in $d_4$ at the speed $c$. In its 3D space, it is always at rest. The radio signal collides with “r” in the 3D space of “r” if there is $d_{i,\mathrm{r}}=d_{i,\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}$ ($i=1,2,3$) at one instant in cosmic time $\theta$. Thus, a collision is possible even if there is $d_{4,\mathrm{r}}\ne d_{4,\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}$. In our example (see Figure 5 left), the signal collides with “r” once $\theta =1.6\mathrm{s}$ have elapsed since “r” started from the origin. Collisions in 3D space do not show up as collisions in ES. Here is why ES diagrams do not contract physics: ES diagrams do not show events but each object’s flow of proper time. The wire does not spatially escape from the rocket. The sun does not spatially escape from Earth’s orbit. In Figure 4, Earth does not spatially escape from clock “b”.

5. Outlining the Solutions to 15 Fundamental Mysteries

In Section 5.1–5.15, ER solves 15 mysteries and declares four concepts obsolete. We will focus on mysteries that do not involve gravitational fields (except for Section 5.5).

5.1. The Mystery of Time

Proper time $\tau$ is what a clock measures. Cosmic time $\theta$ is the total distance covered in ES divided by $c$. Any clock always displays both quantities: its $\tau$ and $\theta$. An observed clock’s 4D vector ${\mathit{\tau }}^{\mathit{\text{'}}}$ can differ from the observer’s 4D vector $\mathit{\tau }$. If it does, the observed clock is slow with respect to the observer’s clock in his time axis.

5.2. The Mystery of Time’s Arrow

“Time’s arrow” is a synonym of time moving only forward. Why does it move only forward? Here is the answer: Covered distance cannot decrease but only increase.

5.3. The Mystery of the Factor $c^2$

in the Energy Term $m{c}^2$

In SR, if forces are absent, the total energy $E$ of an object (mass $m$) is given by

$$E=\gamma m{c}^2=E_{\mathrm{k}\mathrm{i}\mathrm{n},3\mathrm{D}}+m{c}^2,$$

(18)

where $E_{\mathrm{k}\mathrm{i}\mathrm{n},3\mathrm{D}}$ is its kinetic energy in an observer’s coordinate space and $m{c}^2$ is its energy at rest. The term $m{c}^2$ can be derived from SR, but SR does not tell us why there is a factor $c^2$ in the energy of objects that move at a speed less than $c$. ER is eye-opening: An object is never “at rest”. From its perspective, $E_{\mathrm{k}\mathrm{i}\mathrm{n},3\mathrm{D}}$ is zero and $m{c}^2$ is its kinetic energy in $d_4^{\text{'}}$. The factor $c^2$ is a hint that it moves through ES at the speed $c$. In SR, there is also

$$E^2=p^2{c}^2=p_{3\mathrm{D}}^2{c}^2+m^2{c}^4,$$

(19)

where $p$ is the total momentum of an object and $p_{3\mathrm{D}}$ is its momentum in an observer’s coordinate space. Again, ER is eye-opening: From its perspective, $p_{3\mathrm{D}}$ is zero and $mc$ is its momentum in $d_4^{\text{'}}$. The factor $c$ is a hint that it moves through ES at the speed $c$.

5.4. The Mystery of Length Contraction and Time Dilation

In SR, length contraction and time dilation can be traced back to Einstein’s instruction for synchronizing clocks. ER gives us a non-empirical explanation. It discloses that these effects stem from projecting worldlines in ES to the axes $d_1$ and $d_4$ of an observer.

5.5. The Mystery of Gravitational Time Dilation

In GR, gravitational time dilation stems from curved spacetime. ER discloses that this effect stems from projecting curved worldlines in ES to the $d_4$ axis of an observer. Equation (7) tells us: If an object accelerates in his proper space, it automatically decelerates in his proper time. More studies are required to understand other gravitational effects in ER.

5.6. The Mystery of the Cosmic Microwave Background (CMB)

In the inflationary Lambda-CDM model, the Big Bang occurred “everywhere” (space inflated from a singularity). In Section 5.6–5.12, I outline an ER-based model of cosmology, in which the Big Bang is locatable: It injected a huge amount of energy into ES at an origin O. Cosmic time $\theta$ is the total time that has elapsed since the Big Bang. At $\theta =0$, all energy started moving radially away from O. The Big Bang was a singularity in providing energy and radial momentum. Shortly after $\theta =0$, energy was highly concentrated. While it became less concentrated, plasma particles were created in the projection to any 3D space. Recombination radiation was emitted that we still observe as CMB today [24].

The ER-based model must be able to answer these questions: (1) Why is the CMB so isotropic? (2) Why is the temperature of the CMB so low? (3) Why do we still observe the CMB today? Here are some possible answers: (1) The CMB is so isotropic because it has been scattered equally in the 3D space $d_1,d_2,d_3$ of Earth. (2) The temperature of the CMB is so low because the plasma particles had a very high recession speed $v_{3\mathrm{D}}$ (see Section 5.7) shortly after $\theta =0$. (3) We still observe the CMB today because it reaches Earth after having covered the same distance in $d_1,d_2,d_3$ (multiple scattering) as Earth in $d_4$.

5.7. The Mystery of the Hubble–Lemaître Law

Earth and a galaxy G recede from the origin O of ES at the speed $c$ (see Figure 6 left). While doing so, G recedes from the $d_4$ axis at the speed $v_{3\mathrm{D}}$. Because of the 4D Euclidean geometry, $v_{3\mathrm{D}}$ relates to $D$ as $c$ relates to the radius $r$ of an expanding 4D hypersphere. All energy is within this hypersphere. Some energy is within its 3D hypersurface. Energy can change the direction of its 4D motion either continuously by a transversal acceleration (scattering, gravitational field) or discontinuously (photon emission, pair production).

$$v_{3\mathrm{D}}=Dc/r=H_{\theta }D,$$

(20)

where $H_{\theta }=c/r=1/\theta$ is the Hubble parameter. If we observe G today at the cosmic time ${\theta }_0$, the recession speed $v_{3\mathrm{D}}$ and $c$ remain unchanged. Thus, Equation (20) turns into

$$v_{3\mathrm{D}}=D_{0}c/r_0=H_0{D}_0,$$

(21)

where $H_0=c/r_0=1/{\theta }_0$ is the Hubble constant, $D_0=D{r}_0/r$ is today’s 3D distance of G to Earth, and $r_0$ is today’s radius of the 4D hypersphere. Equation (21) is the improved Hubble–Lemaître law [25,26]. Cosmologists are aware of $\theta$ and $H_{\theta }$. They are not yet aware that the 4D geometry is Euclidean, that $\theta$ is absolute, and that $v_{3\mathrm{D}}$ is equal to $H_0{D}_0$ (not to $H_{0}D$). Out of two galaxies, the one farther away recedes faster, but each galaxy maintains its speed $v_{3\mathrm{D}}$. The $d_4$ values of Earth and an energy $\mathsf{\Delta }E$ (emitted by G at the time $\theta$) never match. Can $\mathsf{\Delta }E$ and Earth collide in the 3D space of Earth if they do not collide in ES? The answer is the same as for Figure 5 left: Collisions in 3D space do not show up as collisions in ES. $\mathsf{\Delta }E$ collides with Earth once $\mathsf{\Delta }E$ has covered the same distance in $d_1$ as Earth in $d_4$.

5.8. The Mystery of the Flat Universe

An observer’s view is created by orthogonally projecting ES to his proper space and to his proper time. Thus, he experiences two discrete structures: flat space and time.

5.9. The Mystery of Cosmic Inflation

Most cosmologists [27,28] believe that an inflation of space shortly after the Big Bang explains the isotropic CMB, the flat universe, and large-scale structures. The latter inflated from quantum fluctuations. I just showed that ER explains the first two effects. ER even explains large-scale structures if the impacts of quantum fluctuations have been expanding like the 3D hypersurface. In ER, cosmic inflation is an obsolete concept.

5.10. The Mystery of Cosmic Homogeneity (Horizon Problem)

How can the universe be so homogeneous if there are causally disconnected regions? In the Lambda-CDM model, region A at $x_1=+r_0$ and region B at $x_1=-r_0$ are causally disconnected unless we postulate a cosmic inflation. Without inflation, information could not have covered $2r_0$ since the Big Bang. In the ER-based model, we use natural concepts: Region A is at $d_1=+r_0$ (see Figure 6 left). Region B is at $d_1=-r_0$ (not shown in Figure 6 left). For A and for B, their $d_4^{\text{'}}$ axis (equal to Earth’s $d_1$ axis) disappears because of length contraction at the speed $c$. Since A and B overlap spatially in their 3D space, they are causally connected. Note that their opposite 4D vectors “flow of proper time” do not affect causal connectivity as long as A and B overlap spatially.

5.11. The Mystery of the Hubble Tension

Up next, I explain the 10 percent deviation in the published values of $H_0$ (known as the “Hubble tension” or the “$H_0$ tension”). Let us compare CMB measurements (Planck space telescope) with calibrated distance ladder measurements (Hubble space telescope). According to team A [29], there is $H_0=67.66\pm 0.42\mathrm{k}\mathrm{m}/\mathrm{s}/\mathrm{M}\mathrm{p}\mathrm{c}$. According to team B [30], there is $H_0=73.04\pm 1.04\mathrm{k}\mathrm{m}/\mathrm{s}/\mathrm{M}\mathrm{p}\mathrm{c}$. Team B made efforts to minimize the error margins in the distance measurements. However, there is a systematic error in team B’s calculation of $H_0$, which arises from assuming a wrong cause of the redshifts.

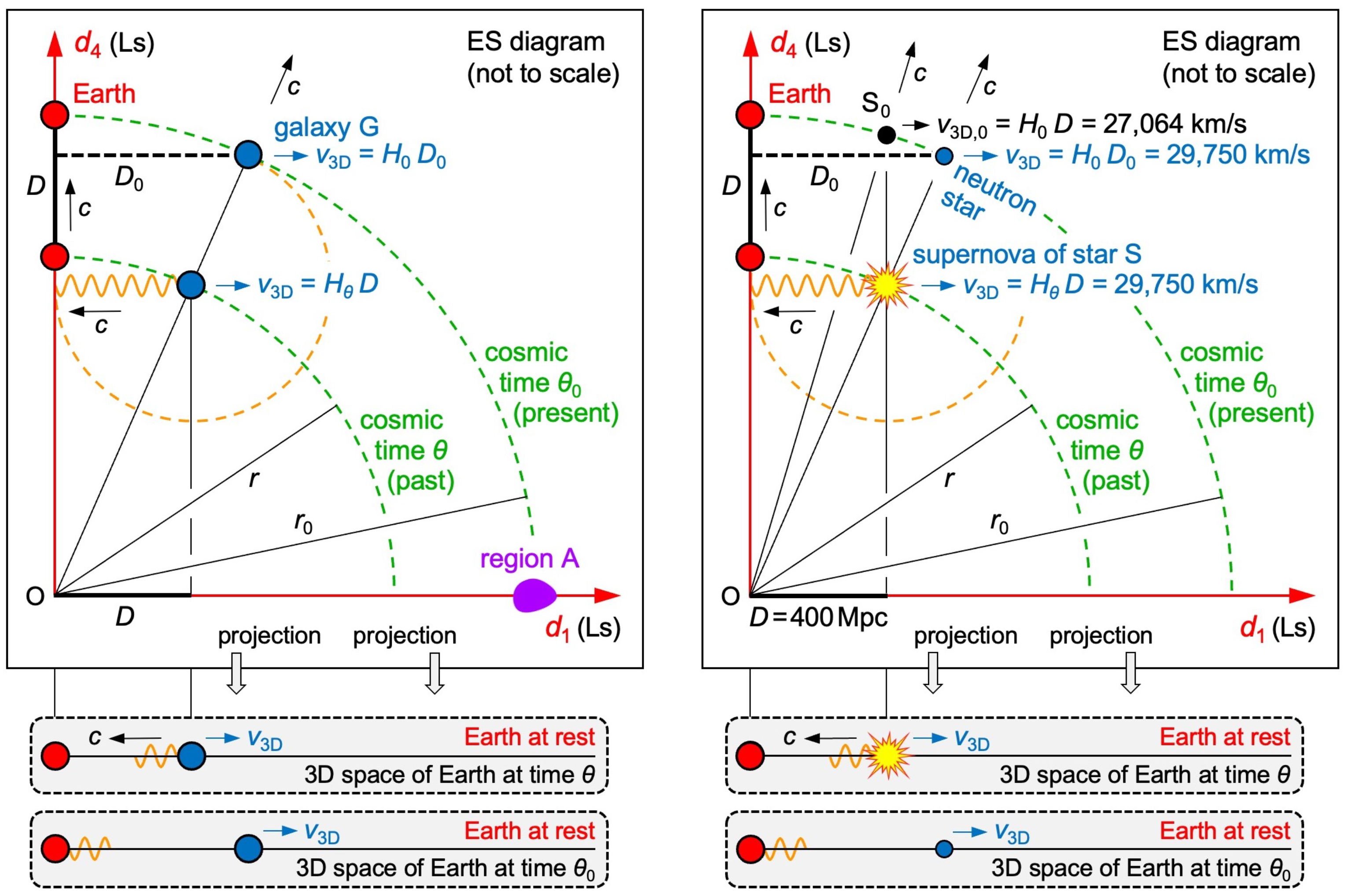
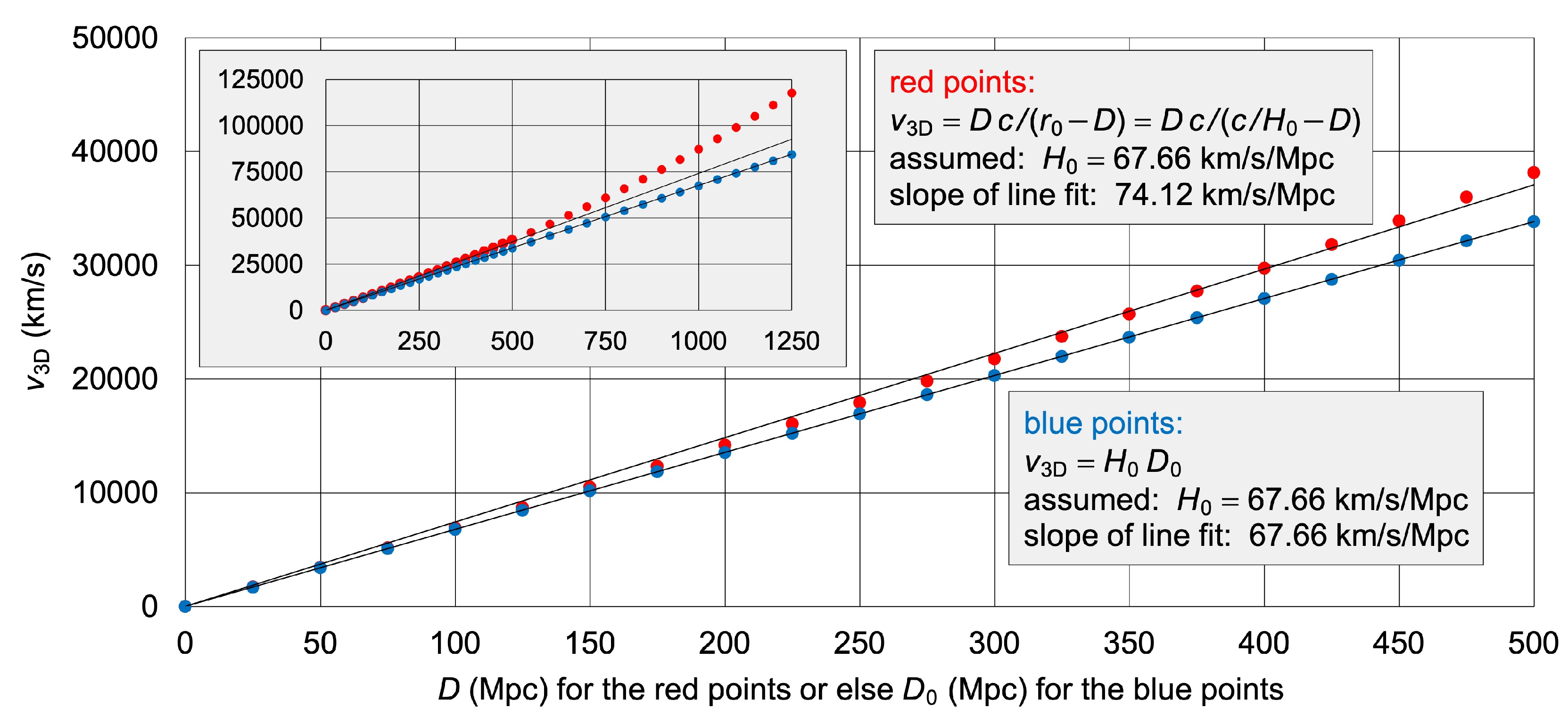
We assume that team A’s value of $H_0$ is correct. We simulate the supernova of a star S that occurred at a distance of $D=400\mathrm{M}\mathrm{p}\mathrm{c}$ from Earth (see Figure 6 right). The recession speed $v_{3\mathrm{D}}$ of S is calculated from measured redshifts. The redshift parameter $z=\mathsf{\Delta }\lambda /\lambda$ tells us how each wavelength $\lambda$ of the supernova’s light is either stretched by an expanding space (team B) or else Doppler-redshifted by receding objects (ER-based model). The supernova occurred at the cosmic time $\theta$ (arc called “past”), but we observe it at the cosmic time ${\theta }_0$ (arc called “present”). While the supernova’s light moved the distance $D$ in $d_1$, Earth moved the same distance $D$ but in $d_4$ (first postulate). There is

$$1/H_{\theta }=r/c={(r_0-D)/c=1/H}_0-D/c.$$

(22)

For a very short distance of $D=400\mathrm{k}\mathrm{p}\mathrm{c}$, Equation (22) tells us that $H_{\theta }$ deviates from $H_0$ by only 0.009 percent. When plotting $v_{3\mathrm{D}}$ versus $D$ for distances from 0 Mpc to 500 Mpc in steps of 25 Mpc (red points in Figure 7), the slope of a straight-line fit through the origin is roughly 10 percent greater than $H_0$. Since team B calculates $H_0$ from relating $z$ to magnitude, which is like plotting $v_{3\mathrm{D}}$ versus $D$, its value of $H_0$ is roughly 10 percent too high. Team B’s value is not correct because, according to Equation (21), we must plot $v_{3\mathrm{D}}$ versus $D_0$ (!) to get a straight line (blue points in Figure 7). Ignoring the 4D Euclidean geometry leads to an overestimation of the Hubble constant. This solves the Hubble tension.

Since we cannot measure $D_0$ (observable magnitudes relate to $D$ and not to $D_0$), the easiest way to fix the calculation of team B is to rewrite Equation (21) as

$$v_{3\mathrm{D},0}=Dc/r_0=H_{0}D,$$

(23)

where $v_{3\mathrm{D},0}$ is today’s 3D speed of a star ${\mathrm{S}}_0$ that happens to be at the same distance $D$ today at which the supernova of S occurred (see Figure 6 right). I kindly ask team B to recalculate $H_0$ after converting all $v_{3\mathrm{D}}$ to $v_{3\mathrm{D},0}$ by applying Equations (22), (23), and (20):

$$H_{\theta }=H_{0}c/(c-H_{0}D)=H_0/(1-v_{3\mathrm{D},0}/c),$$

(24)

$$v_{3\mathrm{D},0}=v_{3\mathrm{D}}/(1+v_{3\mathrm{D}}/c).$$

(25)

By applying Equation (25) and plotting $v_{3\mathrm{D},0}$ versus $D$, we also get a straight line according to Equation (23). In addition, Figure 7 tells us: The more high-redshift data are included in team B’s calculation, the more the $H_0$ tension increases. The moment of the supernova is irrelevant to team B’s calculation. In the Lambda-CDM model, all that counts is the duration of the light’s journey to Earth ($z$ increases during the journey). In the ER-based model, all that counts is the moment of the supernova. Wavelengths are redshifted by the Doppler effect ($z$ is constant during the journey). Space is not expanding. Energy recedes from the location of the Big Bang in ES. In ER, expanding space is an obsolete concept.

5.12. The Mystery of Dark Energy

Team B can fix the systematic error in its calculation of $H_0$ by converting all $v_{3\mathrm{D}}$ to $v_{3\mathrm{D},0}$ according to Equation (25). I now reveal another systematic error, but it is inherent in the Lambda-CDM model. It stems from assuming an accelerating expansion of space and can be fixed only by replacing this model with the ER-based model unless we postulate a dark energy. Most cosmologists [31,32] believe in an accelerating expansion because the calculated recession speeds $v_{3\mathrm{D}}$ deviate from a straight line in the Hubble diagram (if $v_{3\mathrm{D}}$ is plotted versus $D$) and because the deviations increase with $D$. An accelerating expansion would indeed stretch each wavelength even further and explain the deviations.

In ER, the cause of the deviations is far less speculative: The longer ago a supernova occurred, the more $H_{\theta }$ deviates from $H_0$, and thus the more $v_{3\mathrm{D}}$ deviates from $v_{3\mathrm{D},0}$. If a star ${\mathrm{S}}_0$ happens to be at the same distance of $D=400\mathrm{M}\mathrm{p}\mathrm{c}$ today at which the supernova of S occurred, Equation (25) tells us: ${\mathrm{S}}_0$ recedes more slowly (27,064 km/s, the shortest arrow in Figure 6 right) from $d_4$ than S (29,750 km/s). It does so because of the 4D Euclidean geometry: The 4D vector ${\mathit{\tau }}^{\mathit{\text{'}}}$ of ${\mathrm{S}}_0$ deviates less from $\mathit{\tau }$ of Earth than ${\mathit{\tau }}^{\mathit{\text{'}}\mathit{\text{'}}}$ of S deviates from $\mathit{\tau }$. As long as cosmologists are not aware of ER, they hold a “dark energy” [33] responsible for an accelerating expansion of space. Dark energy has not been confirmed. It is a stopgap for an effect that the Lambda-CDM model cannot explain. Older supernovae recede faster because of a larger $H_{\theta }$ in Equation (20) and not because of a dark energy.

The Hubble tension and dark energy are solved exactly the same way: In Equation (21), we must not confuse $D_0$ with $D$. Because of Equation (20) and because of $H_{\theta }=c/{(r}_0-D)$, the recession speed $v_{3\mathrm{D}}$ is not proportional to $D$ but to $D/(r_0-D)$. This is why the red points in Figure 7 run away from a straight line. Any expansion of space (uniform or else accelerating) is only virtual even if the Nobel Prize in Physics 2011 was given “for the discovery of the accelerating expansion of the Universe through observations of distant supernovae”. This particular prize was given for an illusion that stems from interpreting astronomical observations in the wrong concepts. Most galaxies recede from Earth, but they do so uniformly in a non-expanding spacetime. In ER, dark energy is an obsolete concept.

The Hubble tension and dark energy are solved by taking the 4D Euclidean geometry into account, and the 4D vector $\mathit{\tau }$ in particular. These results cast doubt on the Lambda-CDM model. GR itself is correct as long as $\mathit{\tau }$ is not crucial, but it is crucial for high-redshift supernovae. Space is not driven by dark energy. Galaxies are driven by their momentum and maintain their recession speed $v_{3\mathrm{D}}$ with respect to Earth. Because of various effects (scattering, gravitational field, photon emission, pair production), some energy deviates from a radial motion in ES while maintaining the speed $c$. Gravitational attraction enables near-by galaxies to move toward our galaxy. 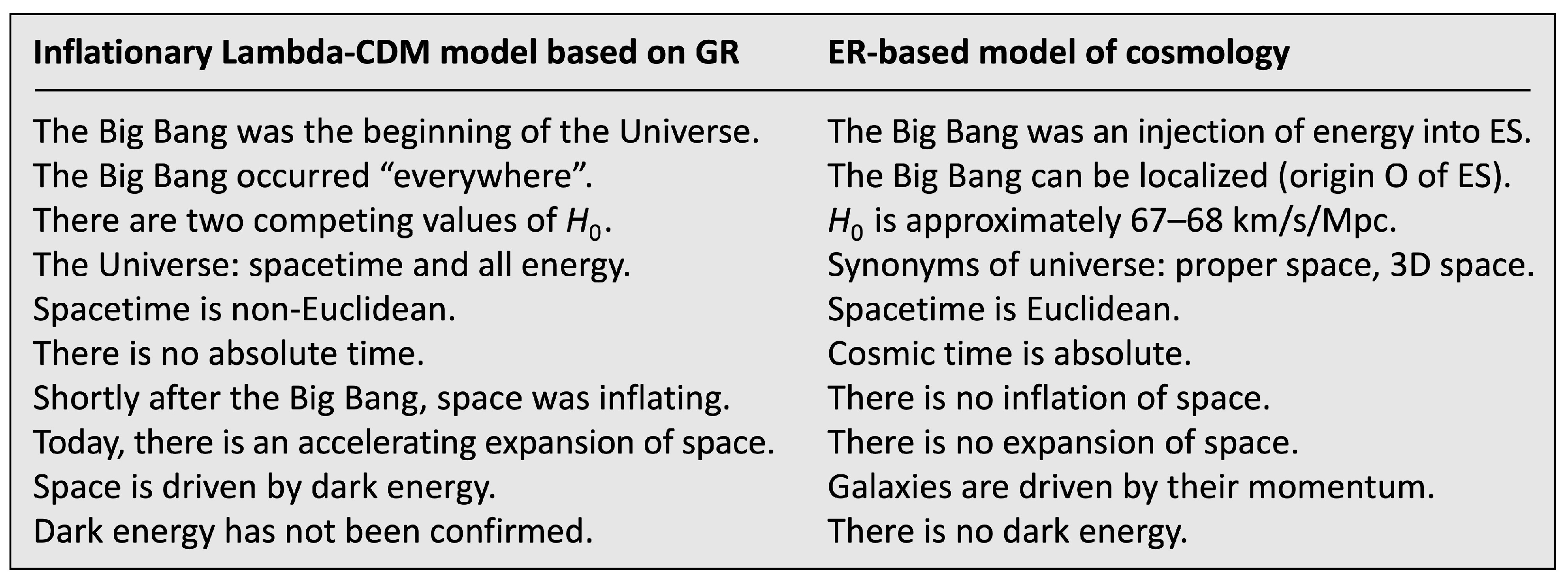Table 1 compares two models of cosmology. Note that “the Universe” (Lambda-CDM model) and “universe” (ER-based model) are not the same thing. Each observer experiences three axes of ES as his universe. Cosmology benefits from ER. In Sects. 5.13 and 5.14, I show that QM also benefits from ER.

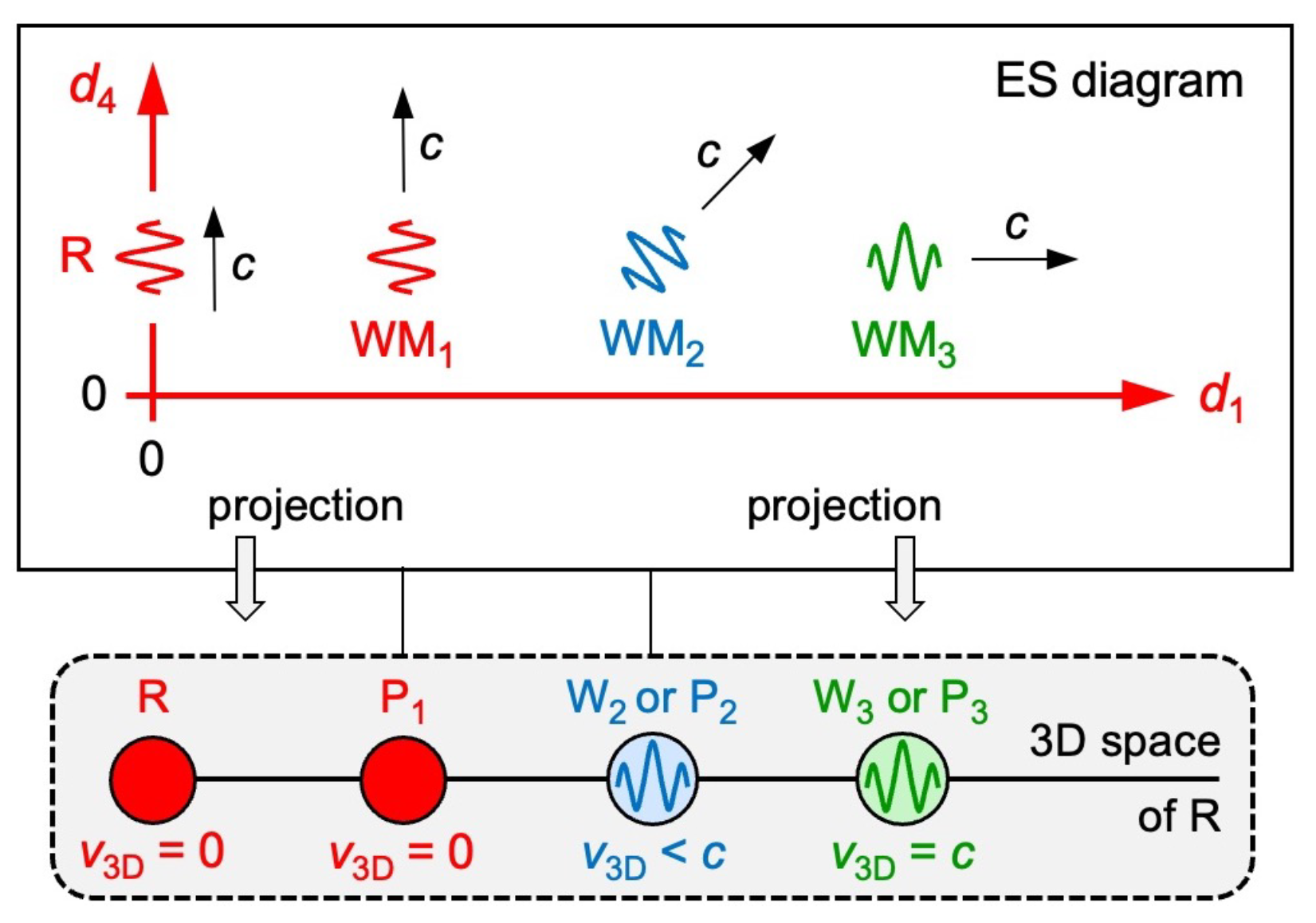
5.13. The Mystery of the Wave–Particle Duality

The wave–particle duality was first discussed by Niels Bohr and Werner Heisenberg [34]. It has bothered physicists ever since. In some experiments, objects behave like waves. In others, the same objects behave like particles (known as the “wave–particle duality”). One object cannot be both because a wave’s energy spreads out in space, whereas a particle’s energy is localized in space. We overcome the duality by introducing another natural concept: Pure energy moves as “wavematters” through ES at the speed $c$. As explained in Section 3, we interpret wavematters as waves propagating through and oscillating in ES as a function of $\theta$. In an observer’s view, wavematters reduce to wave packets if not tracked by the observer or else to particles if tracked by the observer.

In Figure 8, observer R moves in the $d_4$ axis at the speed $c$. Three wavematters ${\mathrm{W}\mathrm{M}}_1$, ${\mathrm{W}\mathrm{M}}_2$, and ${\mathrm{W}\mathrm{M}}_3$ move in different 4D directions at the speed $c$. To improve readability, a wavematter’s oscillation is drawn in the $d_1,d_4$ plane although it can oscillate in any axis that is orthogonal to its propagation axis. In the 3D space of R, ${\mathrm{W}\mathrm{M}}_2$ and ${\mathrm{W}\mathrm{M}}_3$ reduce to wave packets (${\mathrm{W}}_2,{\mathrm{W}}_3$) if not tracked by R or else to particles (${\mathrm{P}}_2,{\mathrm{P}}_3$) if tracked. ${\mathrm{W}\mathrm{M}}_1$ does not move relative to R. Thus, it is automatically tracked and reduces to a particle (${\mathrm{P}}_1$). For R, ${\mathrm{W}\mathrm{M}}_3$ is the only wavematter that reduces to an electromagnetic wave packet (${\mathrm{W}}_3$) or else to a photon (${\mathrm{P}}_3$). Light gives us a good idea of how all wavematters move through ES. In the 3D space of R, ${\mathrm{W}}_2$ moves at a speed less than $c$. Thus, ${\mathrm{W}}_2$ is not an electromagnetic wave packet but a “matter wave”, as termed by Louis de Broglie [35]. Erwin Schrödinger described matter waves by applying his Schrödinger equation [36].

Three important remarks regarding wavematters: (1) “Wavematter” is not just a different word for the wave–particle duality. Rather, this natural concept tells us where there the duality stems from and that the duality is experienced by observers only. (2) In today’s physics, there is no “photon’s view”. In ER, we can assign a 3D space and a proper time to each wavematter. In its view, its 4D motion disappears because of length contraction at the speed $c$. In its 3D space, it is always at rest and reduces to a particle. (3) In a particle, a wavematter’s energy “condenses” (concentrates) to what we call “mass”. Albert Einstein taught that energy and mass are equivalent [37]. The concept “wavematter” suggests that, likewise, a wave’s polarization and a particle’s spin are equivalent.

In double-slit experiments, a light beam passes through a double-slit and creates an interference pattern on a screen. As long as an observer does not track through which slit single portions of energy are passing, the light of this beam behaves like a wave. In experiments on the photoelectric effect, an electron is released from a metal surface if and only if the energy of an incoming photon exceeds the binding energy of that electron. To release that electron, the photon must interact with it. The interaction process reveals the position of the photon. Thus, the photon is tracked and behaves like a particle.

The duality also applies to objects that we usually classify as matter, such as electrons [38]. In double-slit experiments, electrons behave like waves as long as they are not tracked. Once they are tracked, they behave like particles. Since an observer automatically tracks objects that are slow in his 3D space, he classifies all slow objects and thus all macroscopic objects as matter. To improve readability, most of my ES diagrams do not show wavematters but how they appear to observers (clocks, rockets, galaxies, etc.).

5.14. The Mystery of Non-Locality

It was Erwin Schrödinger who coined the word “entanglement” in his comment [39] on the Einstein–Podolsky–Rosen paradox [40]. The three authors argued that QM would not provide a complete description of reality. Schrödinger’s neologism does not solve the paradox, but it demonstrates our difficulties in comprehending QM. John Bell [41] showed that QM is incompatible with local hidden-variable theories. Meanwhile, it has been confirmed in several experiments [42,43,44] that entanglement violates locality in an observer’s 3D space. Entanglement has been interpreted as a non-local effect ever since.

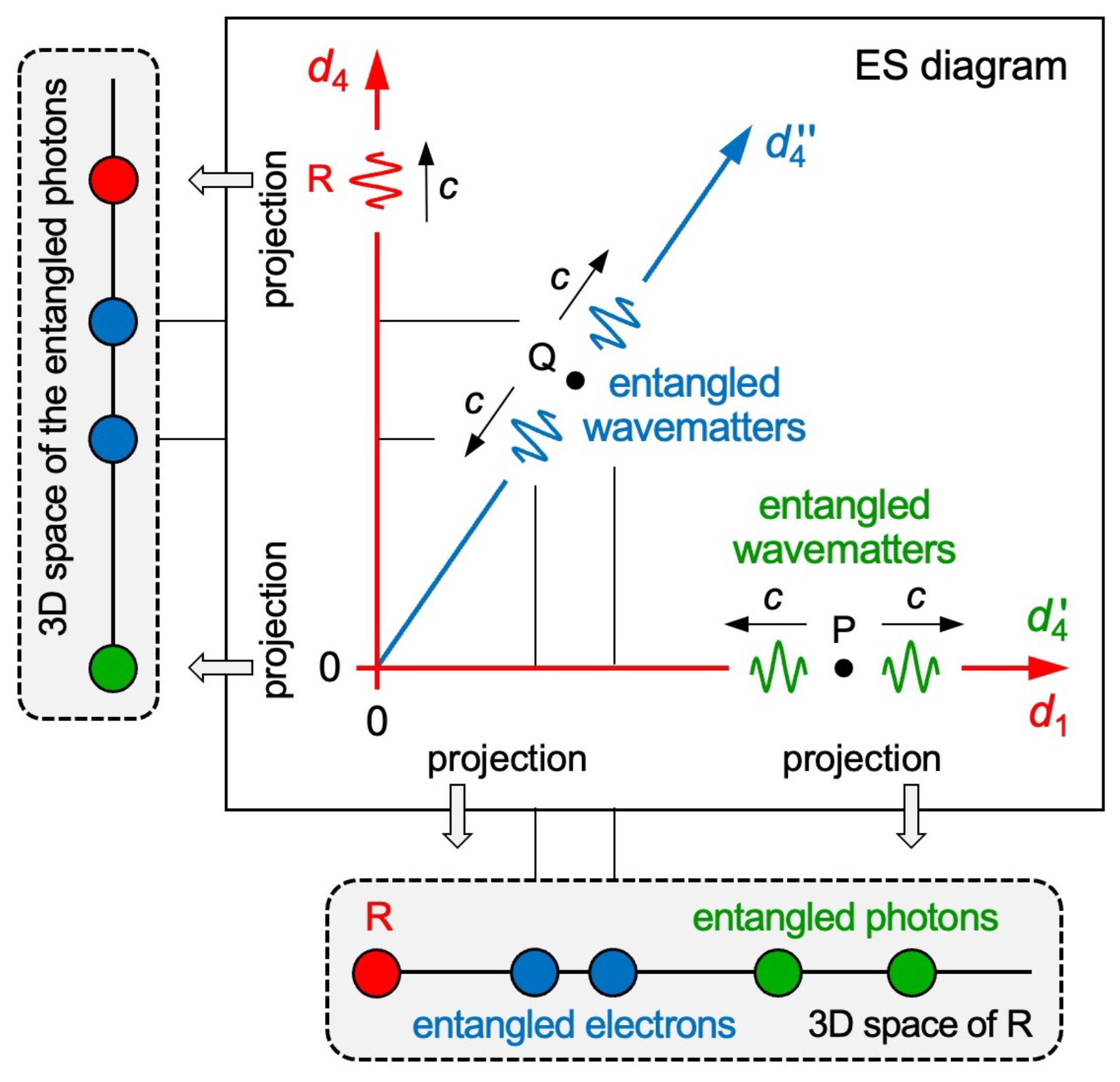
Up next, I show that ER “untangles” entanglement. There is no violation in four symmetric dimensions. Figure 9 shows two pairs of entangled wavematters. Observer R moves in the $d_4$ axis at the speed $c$. One pair was created at the point P and moves in opposite directions $\pm d_4^{\text{'}}$ (equal to R’s axes $\pm d_1$) at the speed $c$. The other pair was created at the point Q and moves in opposite directions $\pm d_4^{\text{'}\text{'}}$ at the speed $c$. In the 3D space of R, the pairs reduce to two entangled photons and to two entangled material objects (for instance, electrons), but R has no idea how one pair is able to “communicate” in no time.

In the photons’ view (or electrons’ view), the $d_4^{\text{'}}$ axis (or else the $d_4^{\text{'}\text{'}}$ axis) disappears because of length contraction at the speed $c$. Thus, each pair stays together in its respective 3D space. Entangled objects have never been spatially separated in their view, but their proper time flows in opposite 4D directions. This is how two entangled objects are able to communicate in no time. Note that their opposite 4D vectors “flow of proper time” do not affect local communication as long as the twins stay together spatially. There is a “spooky action at a distance” (attributed to Einstein) in an observer’s view only.

The horizon problem and entanglement are solved exactly the same way: An observed region’s (or an observed object’s) 4D vector ${\mathit{\tau }}^{\mathbf{\text{'}}}$ and its 3D space can differ from the observer’s 4D vector $\mathit{\tau }$ and his 3D space. This is possible only if all four $d_{\mu }$ ($\mu =1,2,3,4$) are interchangeable. The SO(4) symmetry of ES solves entanglement. Figure 9 tells us that ER also explains the entanglement of material objects, such as atoms or electrons [45]. Any physical measurement will tilt the axis of 4D motion of one entangled wavematter. Single-sided tilting destroys the entanglement. In ER, non-locality is an obsolete concept.

5.15. The Mystery of the Baryon Asymmetry

In the Lambda-CDM model, almost all matter was created shortly after $\theta =0$, when the temperature was high enough to enable pair production. But this process creates equal amounts of particles and antiparticles, and the process of annihilation annihilates equal amounts of particles and antiparticles. So, why do we observe more baryons than antibaryons (known as the “baryon asymmetry”)? In an observer’s view, wavematters reduce to wave packets or else to particles. Pair production creates particles and antiparticles, which annihilate each other very soon. Thus, there is one source of long-lived particles (reduction of wavematters), one source of short-lived particles (pair production), but only one source of short-lived antiparticles (pair production). This solves the baryon asymmetry.

ER also tells us why an antiparticle’s proper time seems “to flow backward”: Proper time flows in opposite 4D directions for any two wavematters created in pair production. The antiparticle’s 4D vector ${\mathit{\tau }}^{\mathit{\text{'}}\mathit{\text{'}}}$ is reversed with respect to the particle’s 4D vector ${\mathit{\tau }}^{\mathit{\text{'}}}$. In the antiparticle’s view, its proper time moves forward. Note that galaxies moving in $-d_4$ (not shown in Figure 6 left) are not made up of antimatter. Only their flow of proper time is reversed with respect to galaxies moving in $+d_4$. Their physical charges are not reversed. ER predicts that any two wavematters created in pair production are entangled. This gives us a chance to falsify ER. All scientific theories must be falsifiable [46].

6. Conclusions

ER solves many unsolved mysteries (time’s arrow, the Hubble tension, the wave–particle duality, the baryon asymmetry) and mysteries that are already solved but only by adding obsolete concepts (cosmic inflation, expanding space, dark energy, non-locality). This is a perfect example of where to apply Occam’s razor. It shaves off all obsolete concepts. Full stop. SR and GR rank among the greatest achievements of physics. I showed that they do not provide a holistic view. Physics got stuck in its own concepts.

It was a wise decision to award Albert Einstein the Nobel Prize for his theory of the photoelectric effect [47] and not for SR/GR. I showed that ER penetrates to a deeper level. Einstein—one of the most brilliant physicists ever—failed to realize that the fundamental metric chosen by Mother Nature is Euclidean. Einstein sacrificed absolute space and time. ER restores absolute, cosmic time, but it sacrifices the absolute nature of wave and particle. For the first time ever, mankind understands the nature of time: Cosmic time is the total distance covered in ES divided by $c$. The human brain is able to imagine that we move through ES at the speed $c$. With that said, conflicts of mankind become all so small.

Is ER a physical or a metaphysical theory? This is a very good question because only in proper coordinates can we access ES, but the proper coordinates of other objects cannot be measured. I now explain why this is fine: We can always calculate these proper coordinates from ES diagrams as I showed in Equations (13a–c). Measuring is an observer’s source of knowledge, but ER tells us not to interpret too much into whatever we measure. Measurements are wedded to observers, whose concepts can be obsolete. I was often told that physics is all about observing. I disagree. We cannot observe quarks, can we? Regrettably, physicists have applied empirical concepts—which work well in our everyday life—to the very far and to the very small. This is why cosmology and QM benefit the most from ER. ER is a physical theory because it solves fundamental mysteries of physics.

To sum it up: (1) Acceleration rotates an object’s $\mathit{\tau }$ and curves its worldline in flat ES. (2) Information hidden in $\mathit{\tau }$ solves many mysteries. It is extremely unlikely that 15 solutions in different (!) areas of physics are just 15 coincidences. (3) Different concepts disable a unification of SR/GR and ER. Either scope is limited. We must not apply SR/GR but ER whenever $\mathit{\tau }$ is crucial (high-redshift supernovae, entanglement). We must not apply ER but SR/GR whenever we use empirical concepts (waves, particles).

Final remarks: (1) I only touched on gravity. We must not reject ER because gravity is still an issue. GR seems to solve gravity, but GR is incompatible with QM unless we add another speculative concept (quantum gravity). More studies are required to understand gravitational effects in ER. (2) Mysteries often disappear once the symmetry is matched. The symmetry group of natural concepts is SO(4). (3) The new invariant $\theta$ finally puts an end to all discussions about time travel. Does any other theory solve the mystery of time’s arrow as beautifully as ER? (4) Physics does not ask: Why is my reality a projection? Nor does it ask: Why is it a wave function? Projections are far less speculative than postulating four obsolete concepts. (5) It seems that Plato anticipated ER in his Allegory of the Cave [48]: Mankind experiences projections and cannot observe any reality beyond.

The primary question behind my theory is: How does all our insight fit together without adding highly speculative concepts? I trust that this very question leads us to the truth. I laid the groundwork for ER and showed how powerful it is. Paradoxes are only virtual. The true pillars of physics are ER, SR/GR (for an observer’s view), and QM. Together they describe Mother Nature from the very far to the very small. Introducing a holistic view to physics is probably the most significant achievement of this paper. All observers’ views taken together do not make a holistic view because they still do not provide absolute time. Everyone is welcome to solve even more mysteries by applying ER.