Qluster: An Easy-to-Implement Generic Workflow for Robust Clustering of Health Data

1. Introduction

Health data is of great importance to public health, research and medical development. It is any data related to the health conditions, outcomes and quality of life of an individual or population. Health data may be collected during the course of ongoing patient care (e.g., claims data, medical records, administrative data) or as part of a formal clinical trial program.

In health data analysis, clustering methods are a primary tool, by finding pockets of homogeneity within a heterogeneous population, to uncover different disease phenotype, stages of a disease, or variation in disease outcomes (Franti¨ et al. 2022). A precise understanding of the clusters of patients suffering from a disease ultimately allows for the overall improvement of their care (Windgassen et al. 2018). In this respect, there is an extensive literature to discuss clustering tasks, be it for the choice of appropriate clustering methods (Obembe et al. 2019), for the clustering algorithms for large data (Herawan et al. 2014), for clustering methods for qualitative/mixed data (Hennig 2013), for methods to assess clustering quality, stability and number of clusters (Lange et al. 2004; Nietto et al. 2017), or for performing in-depth comparative statistical analysis of methods (Jain 2010; Nagpal et al. 2013).

The profusion of methods makes it difficult for most data scientists to choose and systematically apply a methodology that is complete, reasonably fast and satisfactory from a robustness point of view with respect to the clinical question they are trying to answer. The data scientist is indeed confronted with a very wide range of choices regarding both the algorithms and their implementations (including R, Python) in particular according to the nature of the data and their volume. Furthermore, on the contrary to the more “conventional” bio-statistical methods in clinical studies, the lack of clear guidelines on the data science approaches to be used leads to a greater subjectivity in the choice of approaches, and in particular, those of clustering in clinical data. This makes the statistical analysis plans for observational studies proposed by data scientists and the results obtained more variable.

The clustering process involves many decision steps, from the data preparation step to the evaluation of clusters’ stability and clusters’ description. To the authors’ knowledge, there is not yet a single, simplified workflow in the literature that is easy to implement for both expert and non-expert health data scientists (with off-the-shelf tools in R or Python), well-supported by the literature, generic (e.g., regardless of the nature -continuous/binary/categorical/mixed- or volume of data -small/large), which facilitates its routine application. Most of the articles that come close to this goal focus on process automation (autoML, e.g., Kamoshida et al. 2020) or clustering methods comparison (Wiwie et al. 2015). This work (obviously) does not pretend to impose a single solution to a clustering problem as experience and literature have both shown that there is no single solution to a clustering task (see in particular Kleinberg (2002)). However, this work aims to give the data scientist guidance through an easy framework that can be used in routine practice in a wide variety of cases. This article is thus intended to:

• health data scientists, companies, or institutions that need a general workflow for routine - possibly automated - clustering projects on data of various types and volumes (e.g. for preliminary data mining), or
• health data scientists with limited experience, who are looking for both an overview of the literature and an accessible and reusable workflow with concrete practical recommendations to quickly implement a complete unsupervised clustering approach adapted to various projects.

In this paper, we propose in section 2 a synthesis of the different methods related to unsupervised clustering in the literature and in relation to the implementations available in R or Python. In section 3, we propose Qluster, a generic workflow for clustering tabular data of any nature and size, while considering (1) the literature guidelines on how to perform robust clustering, and (2) the availability and ease of use of R or Python implementations for data scientist users. Then, in section 4, we detail this workflow through a step-by-step application on the open access Cardiovascular Disease ¹ practice dataset to help data scientists to reapply this workflow on their own project with concrete recommendations. We then provide a practical discussion in section 5 and conclude in section 6. Data scientists will also find in both section 2 and section 4 all the necessary literature (rationale) to support the use of this workflow, which greatly facilitates the tedious work of writing the statistical analysis plan with innovative approaches (data science) in clinical research.

2. Statistical rationale and literature review on data clustering

This section discusses the state-of-the-art of clustering methods in the general clustering process (see in Figure 1 the steps 2 to 4. Step 2 will be discussed both in this section and in Section 4 through an illustrative example).

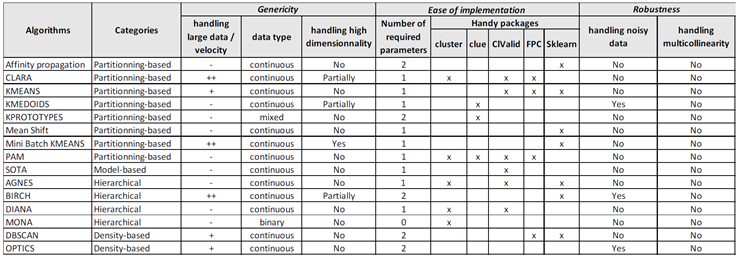
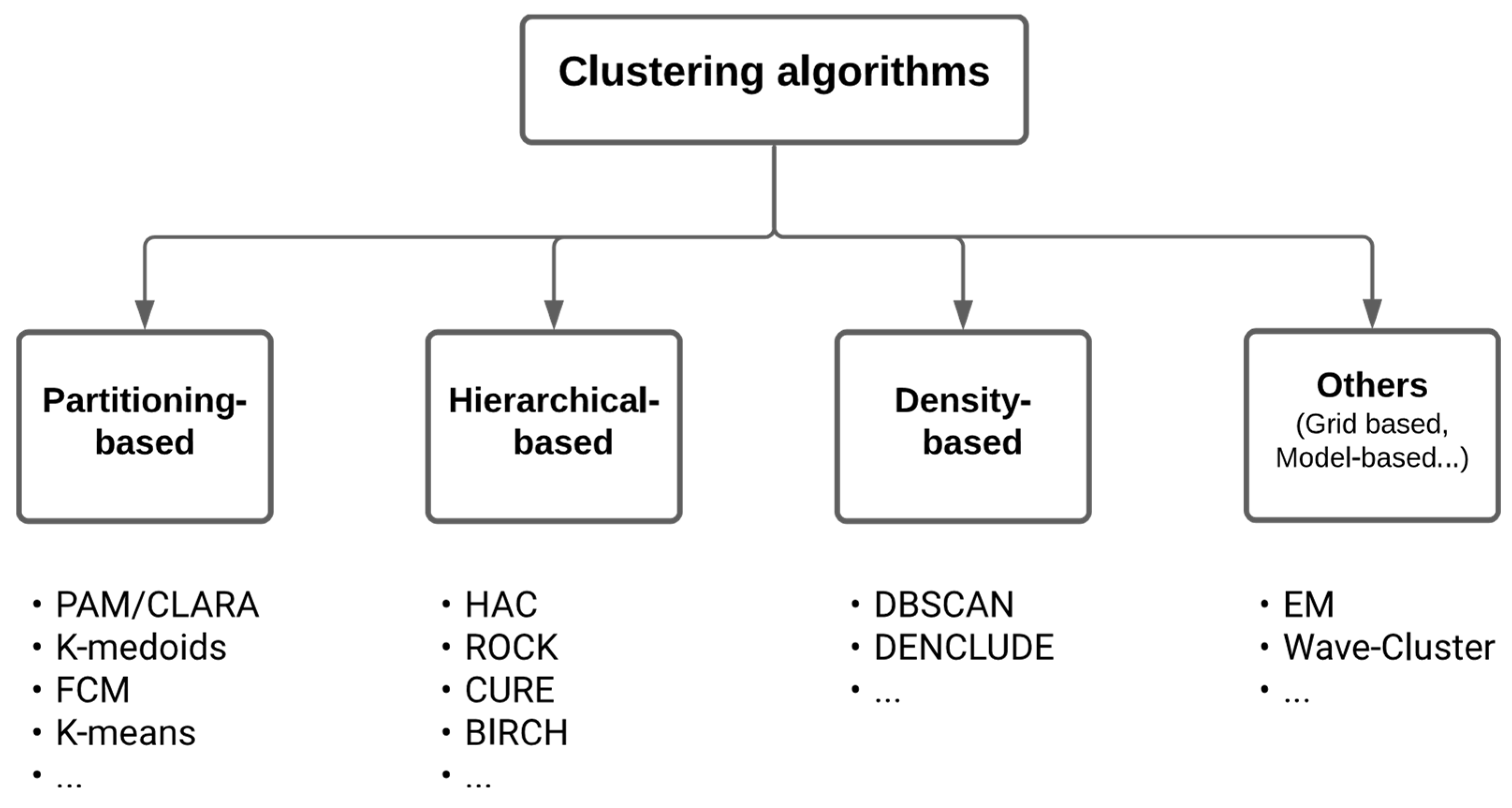
2.1. Overview of unsupervised clustering methods

As generally defined, clustering is “the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters)” (Altman et al. 2017; “Cluster analysis” 2021). Such a task is used to group homogeneous subsets of observations to better understand their global heterogeneity. This is particularly true in clinical data analysis to describe disease heterogeneity, stratify patients and obtain profiles of targeted populations. The result of a clustering task is in general an assignment of the input data into a fixed number of clusters. Two categories of clustering methods are usually distinguished according to the nature of such assignment: hard and soft clustering methods. Hard clustering provides a partition in which each object in the data set is assigned to one and only one cluster. Soft (or Fuzzy) clustering generates a fuzzy partition that provides a degree of membership of each object to a given cluster. This gives the possibility to express that objects belong to more than one cluster at the same time. It is of note that the definition of a cluster itself is not very precise which partly explains why there are so many clustering algorithms (Estivill-Castro 2002).

In the field of Machine Learning, clustering methods pertain to the so-called unsupervised learning methods. Clustering should not be confused with the field of Subgroup Discovery, which also aims at finding groups but in a supervised way, for example to identify prognostic factors of an outcome or predictive factors of the treatment effect on an outcome (Esnault et al. 2020; Zhou et al. 2019). The many clustering algorithms that exist in the literature (Fahad et al. 2014 ; Ahmad et al. 2019; Xu et al. 2010) can be classified according to the cluster models (centroid, connectivity, group, distribution, density, graph, etc.). Among the wide variety of methods, they are three main types, all producing a hard partition of the observations (Figure 2, which is adapted from Figure 1 in Fahad et al. (2014)):

• Partitioning-based methods (e.g. K-means (MacQueen 1967), K-medoid (Jin et al. 2010), PAM (Ng et al. 1994), K-modes (Huang 1997), K-prototype (Huang 1998), CLARA (Kaufman et al. 2009), FCM (Bezdek, Ehrlich, et al. 1984), etc ².),
• Hierarchical-based methods (e.g. BIRCH (Zhang et al. 1996), CURE (Guha et al. 1998), ROCK (Guha et al. 2000), etc.),
• Density-based methods (e.g. DBSCAN (Ester et al. 1996), DENCLUDE (Keim et al. 1998), etc.).

The first type of method is considered to be the most popular class of clustering algorithms for its ease-of-implementation, simplicity, efficiency, and empirical success (Jain 2010). It aims at directly obtaining a single data partition into K clusters. Partitioning-based methods require setting the number K of clusters which is rarely known a priori but can be estimated from the data using several known methods (Calinski´ et al. 1974; Gordon 1999; Halkidi et al. 2001; Hennig 2013; Hennig 2014; Meila˘ 2007; Milligan et al. 1985). These include the optimization of internal validity metrics that reflect the compactness and separation of the clusters (e.g. average Silhouette Width, Davies-Bouldin index, Calinski-Harabasz index, Dunn index, etc.). Equally, some of the partitioning-based methods rely on a random initialization of different K-centroids which can lead to different outputs (local optimum), non-reproducible clusters, or wrong or empty clustering. Some solutions exist, such as the K-means++ algorithm, which includes a smart centroid initialization method for the K-means algorithm (Arthur et al. 2007). The goal is to spread out the initial centroid by assigning the first centroid randomly then selecting the rest of the centroids based on the maximum squared distance. The idea is therefore to push the centroids as far as possible from one another. Similarly, the PAM algorithm is a deterministic K-medoid algorithm that directly integrates an initialization procedure called BUILD. During the BUILD phase the first medoid is selected to be the one that has the minimum cost, with cost being the sum over all distances to all other points.

The second type produces a hierarchy of clusters, called dendrogram, especially useful when one needs several hard partitions at different hierarchical levels (i.e., from a macro vision with a few groups, to a micro vision with many groups). These hierarchical methods have a major drawback though, that once a step (merge or split) is performed, it is not undone, potentially making erroneous decisions impossible to correct: they are often greedy algorithms that optimize a local criteria without backtracking while the clustering problem is by definition a global optimization problem. Moreover, hierarchical-based methods generally have higher time and space complexities than partitioning-based ones, and rely on more input parameters which leaves more room for subjectivity regarding the choice of settings, with a direct impact on the generated clusters (Fahad et al. 2014). Some studies have also shown that hierarchical-based algorithms lead to worse clustering results than partitioning algorithms, suggesting that the latter are well-suited for clustering large datasets due to not only their relatively low computational requirements, but also comparable or even better clustering performance (Kaushik et al. 2014; Zhao et al. 2002).

The third type of method does not either explicitly require a number of clusters nor does it mainly rely on a distance threshold from a “center” (like partitioning-based methods do). On the contrary, density-based methods rely on the estimated density of observations to perform the partitioning. Such a method is in this sense more local and allows to represent clusters whose topology are less induced by the sole distance used (like hyper-spheres when using the Euclidean distance in partitioning-based methods). This strategy may however be associated with a greater propensity to overfit data and greater difficulties to set up the hyper-parameters.

Beyond these three main types of methods there are many other alternative clustering approaches including grid-based methods (e.g. Wave-Cluster (Sheikholeslami et al. 1998), STING (Wang et al. 1997), ...). They perform the clustering on grids rather than on the whole dataset. There are also model-based methods that optimize the fit between the data and predefined models, assuming that the data is generated by a mixture of underlying probability distribution (e.g. mixture density model (EM (Do et al. 2008)), conceptual clustering (COBWEB (Fisher 1987)), neural networks model (SOMs (Ciampi et al. 2000))). More recently, a wide range of new approaches to clustering based on deep learning have emerged (Aljalbout et al. 2018); they are mainly used to cluster unstructured data. Deep neural networks (DNN) can be effective ways to map a high-dimensional data space to a lower dimensional feature space, and thus improving clustering results. Nevertheless, DNN often requires large datasets and a procedure for post-hoc interpretability of the clusters (the representation learned by DNN architectures is not easily understandable). Finally, recent methods for graph clustering focus more specifically on finding sets of nodes in networks or graphs that have more connections within the set than outside the set (Sieranoja et al. 2022). For more on the types of clustering algorithms and their suitability to the data types (categorical, text, multimedia, stream, time series, etc.), see Oyelade et al. (2019).

2.2. Choosing an appropriate clustering approach

The choice of the appropriate approach to be used rely on many aspects (Fahad et al. 2014; Ahmad et al. 2019) such as:

• its ability to handle the desired type of data (binary / nominal / ordinal / numerical),
• the dimensionality of the data (see e.g. Mittal et al. (2019)),
• the size of the data (small to large data),
• the availability of reliable implementations in software (e.g. R and Python - the 2 most used statistical software by data scientists).

Partitioning-based methods are known to be composed of many variants to directly handle continuous (K-means, PAM, CLARA, FCM, etc.), categorical (K-modes, K-medoid, etc.) and mixed variables (K-prototype, KAMILA (Foss et al. 2018), etc.). In addition, the ability of some of these algorithms to directly handle input dissimilarity matrices facilitates the pre-transformation of the original data into data of the desired type prior to clustering, using suited distance measure (e.g. McCane et al. 2008). This method is particularly used to convert categorical or mixed data into numerical data, as there is more literature and algorithms implemented in software for continuous data. (e.g. scikit-learn ³ in Python, or cluster ⁴ and fpc ⁵ R packages. The two latter packages both provide a large number of clustering and clusters stability assessments methods, as well as functions to compute dissimilarity matrices and describe the results). Another known alternative consists of one-hot-encoding categorical data into binary variables and treating the latter as continuous (e.g. in Li et al. 2017). It is however necessary to downweigh the obtained variables so that no more weight is given to the original variables with more modalities. Finally, dimensionality reduction methods, such as factor analysis (Principal Component Analysis (PCA) for continuous data, Multiple Correspondence Analysis (MCA) for qualitative data, Factor Analysis of Mixed Data (FAMD) for mixed data (Pages` and Husson 2017)), can be used before the clustering as a first step to transform the data into numerical components (i.e., the coordinates of the observations on each dimension).

Factor analysis has many other advantages for clustering tasks, such as reducing the dimensionality (making easier the clustering task), reducing noises (by removing the last components that only bear random noise, leading to a more robust unsupervised learning) and dealing with variables that bear similar information and/or are highly correlated (Pages` and Husson 2017). In the case of qualitative data, a convenient practice for accommodating cluster-level observation heterogeneity in MCA is to adopt a two-step sequential, tandem approach (Arabie et al. 1994): in the first step a low-dimensional representation of the categorical variables is obtained via MCA; in the second step some variety of cluster analysis is used to identify a set of relatively homogeneous observations groups on the basis of the low-dimensional data. In addition to the ease in which the two-step sequential approach can be implemented, there can be substantive reasons for adopting this approach as well (Green et al. 1995). Alternative methods consist of using simultaneously both MCA and a clustering approach in a single framework, so that the low-dimensional data can be chosen to facilitate the identification of clusters (Bock 1987; DeSarbo et al. 1991; De Soete et al. 1994). However, these methods lack implementations (both in R and Python), hindering their use within a clustering workflow. Finally, the selection of the number of components to be kept is then the key step. This can be based on several methods including permutation tests (Hwang and Takane 2010), cross-validation-based methods (Bro et al. 2008, Josse, Chavent, et al. 2012), or methods based on the amount of information carried by each of the dimensions generated by the analysis, either compared to an average value equivalent to the Kaiser’s rule in PCA (Lorenzo-Seva 2011) and/or represented by a scree plot (Clausen 1998; Drennan 2010). The latter method has been found to perform fairly well and is the most widely used to select the optimal number of dimensions (Zwick et al. 1986; Bandalos et al. 2009). It consists of looking at the bend in the falling curve (so called “elbow”) indicating an optimal dimensionality (if there is no obvious elbow, one can choose the number of components just before a flat appears). It has been adapted from PCA (Cattell 1966) and used in the context of correspondence analysis (Costa et al. 2013). All factor analysis methods can notably be found in R in the well-known FactoMineR ⁶ package, and in Python in the prince ⁷ GitHub library (although issues are still open for the latter). Methods for estimating the number of dimensions to be kept can be found in R in many packages such as the FactoMineR and missMDA ⁸packages, using cross-validation methods, or in the factoextra ⁹ package (e.g. scree plot). In Python and to the best of authors knowledge, one would need to code these methods to apply them as no specific functions were found.

Whether a factor analysis is performed as a first step or not, the need to choose a distance measure is critical, as some of them are only appropriate according to the type of data, or are preferred in some cases. Indeed, continuous data require appropriate distance measure to obtain the dissimilarity matrix (e.g. Euclidean and Manhattan distances), while categorical data are4 widely handled with simple matching methods (e.g. Hamming distance for symmetric measures, which is equivalent to Manhattan distance on binary variables, and Jaccard distance for asymmetric measures to favor positive co-occurrences over the negative ones). Methods to handle mixed data can consist of combining above-mentioned methods, such as the Gower distance (i.e. simple matching methods and Manhattan distance).

Finally, some aspects need careful attention when dealing with large data. This includes the size of the dataset, as the candidate algorithm must handle either or both high dimensionality and a massive number of observations (including outliers/noisy data), which makes difficult, and sometimes impossible, dissimilarity matrices to be computed. Equally, fast running time is essential with large data as the clustering needs to be performed several times, notably to assess cluster stability and optimize the clustering hyperparameters (e.g. in the use case in section 4, clustering was replicated 550 times). Few strategies exist to deal with massive data, such as relying on algorithms of lower complexity (e.g. K-modes and FCM that are O(n), (Fahad et al. 2014)). The latter however is quickly limited as computing time increases linearly with the size of data. Alternative methods consist of working on approximations (Sieranoja et al. 2019) or subsets of the whole dataset to cluster smaller datasets before generalizing them (e.g. Mini Batch K-means (Sculley 2010), CLARA (Kaufman et al. 2009), CLARANS (Ng et al. 2002)).

The CLARA algorithm is an extension to K-medoids methods (e.g. PAM), that is known to be more robust than K-means-based algorithms as they minimize a sum of dissimilarities instead of a sum of squared Euclidean distances (Jin et al. 2010). CLARA allows to deal with data containing a large number of observations (more than several thousand) using a sampling approach, in order to reduce computing time and RAM storage problems. Instead of finding medoids for the entire dataset, CLARA considers a small sample of the data and applies the PAM algorithm to generate an optimal set of medoids. CLARA repeats the sampling and clustering processes several times in order to minimize the sampling bias. In practice, its strength lies in the possibility to adjust the number of samples and the sample sizes, in order to both make calculation time acceptable and storage in RAM possible. This is indeed essential to enable the stability of clustering to be assessed and the best partitioning to be found by repeating the clustering process many times. Compared to CLARA, CLARANS presents a trade-off between the cost and the effectiveness of using samples to obtain clustering. Mini-batch K-means, CLARA and CLARANS can all be found both in R (e.g. respectively cluster, FPC, and QTCAT ¹⁰ packages) and in Python (e.g. respectively scikitlearn, pycluster ¹¹ and pyclustering ¹²). Please note though that both the quality and the maintenance of libraries on GitHub (QTCAT, pycluster and pyclustering) cannot be guaranteed by the present authors.

2.3. Methods for clusters description

The interpretability of clusters generated by clustering algorithms remains one of the most important challenges in clinical data analysis, as it is often the case with machine learning algorithms (Vellido 2020). Indeed, the best results will only make sense if they are interpretable by end users. Conventional methods do not provide consensus on how to characterize clusters and this is even more valid in the health sector, where the interpretation of clusters is a matter of medical knowledge of the data itself (Kiselev et al. 2019).

The simplest yet most efficient method remains to compute relevant intra- and inter-clusters descriptive statistics using the initial variables to identify a mapping of the generated clusters based on means or median values (resp. proportions) for continuous (resp. categorical) variables. This can be completed by performing clusterwise distributions comparison with overall distributions, as well as using hypothesis testing to identify input variables whose differences are statistically significant between clusters (Bousquet et al. 2015). Such implementations dedicated for clusters’ description may be found in R (e.g. the cluster.varstats() function in the FPC package that also provides tables and plots) and to the best of our knowledge no such function was found in Python.

Alternative for making the clusters’ description step easier may consist of learning an interpretable multiclass supervised classifier (e.g. decision tree) on clusters labels (outcome) to highlight characteristics and specificities associated with each group. Other methods propose to include the interpretability of clusters directly within the clustering algorithm, and not as a step done afterwards (Bertsimas et al. 2021), notably by adding tunable parameters related to interpretability (e.g. see Saisubramanian et al. (2020), with a Python implementation found on GitHub ¹³).

Finally, methods dedicated to the visualization of clusters make it easier their interpretation, such as PCA, multidimensional scaling (Torgerson, 1952), t-SNE (Maaten and Hinton, 2008) and uniform manifold approximation and projection (UMAP, McInnes et al., 2018).

2.4. Methods for clustering validity and stability assessment

Clustering assessment step is an important phase to increase confidence in results and consists of evaluating both the clustering validity and stability.

Regarding the validity of clustering, one can first distinguish the external validity metrics (Rezaei et al. 2016) that can be used to compare the clusters obtained with the ground truth, which is rarely known. Then, the internal validity metrics that assess the goodness of a data partition using quantities inherited from the data, such as compactness (e.g. the maximum pairwise intra-cluster distances), connectedness (e.g. Connectivity metric) or separation (Handl et al. 2005; Bezdek and Pal 1998). The Dunn Validity Index and the Silhouette coefficient are both commonly used metrics, notably to define the optimal number of clusters, as they both assess the separation (i.e. the inter-cluster distances) over the compactness (intra-cluster distances). Although previous works have shown that there is no single internal cluster validation index that outperforms the other indices, Arbelaitz et al. (2013) compare a set of internal cluster validation indices in many distinct scenarios, indicating that the Silhouette coefficient yielded the best results in most cases. Alternatives exist for estimating the number of clusters in a dataset regardless of the clustering methods, such as the “gap statistic” that compares the change in within-cluster dispersion with that expected under an appropriate reference null distribution (R. Tibshirani et al. 2001).

Regarding the stability of clustering, several methods are proposed in the literature, by repeating the clustering process several times under conditions that are different from those of origin. These include procedures used in bioinformatics that remove one column at a time (Datta et al. 2006; Handl et al. 2005). Several metrics can then be computed between the set of clusters (Brock et al. 2008), such as the average proportion of non-overlap (APN), the average distance (AD) and the figure of merit (FOM). These methods are notably proposed in the clValid ¹⁴ R package and its main function clValid(). The latter includes many clustering algorithms (hierarchical, K-means, diana, fanny, som, model, sota, pam, clara, and agnes) and allows for a direct assessment of clusters’ stability through the “validation” argument.

Other approaches consist in perturbing the original data, either using bootstrapping (Efron 1979; Efron and R. J. Tibshirani 1994), noising and/or sampling methods (Hennig 2008). The Jaccard similarity statistic is then often used as a metric for assessing stability, by computing the similarities of the original clusters to the most similar clusters in the resampled data. Such methods are implemented in the FPC R package, notably in the clusterboot() function. The latter is an all-inclusive package that also allows for clustering using a wide variety of algorithms. (e.g. K-means, hierarchical clustering, normal mixture models, PAM, CLARA, DBSCAN, spectral clustering, etc.), making it easy for a data scientist to generate, compare and assess stability of clusters.

As for Python, while there are packages to evaluate the internal validity of clusters (Silhouette coefficient, Rand Index, Calinski-Harabasz Index (Calinski´ et al. 1974), see in particular the sklearn.cluster library), no Python library was found to evaluate the stability of generated clusters. This reinforces the fact that Python does not cover as easily as R the whole clustering process, as there is no Python package that includes all the steps of interest (clusters generation, internal validity evaluation, clustering optimization, clusters stability evaluation and clusters description), as in the FPC R package.

Finally, methods for testing cluster stability on a hold-out dataset are barely mentioned in the literature. This would consist of pre-allocating the observations in the test set into the clusters obtained from the learning set, and by clustering the test dataset to check for good allocation. Though no implementation has been found either in R or Python. We can see a simplified application of clustering of 2 independent datasets in Saint Pierre et al. (2020).

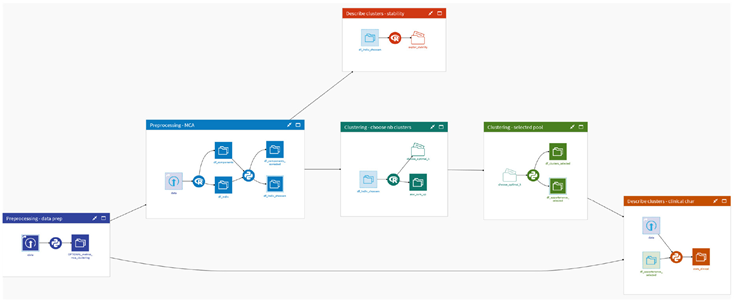
3. The Qluster workflow

3.1. Research objective

Many statisticians/data scientists are confronted with the great number of algorithms and implementations for data clustering. This can make it difficult to manage clustering studies, and is likely to generate analytical strategies that are insufficiently rigorous, not consensual or not adapted to the problem. This is particularly the case for any statistician/data scientist in contract research organizations that provide support to healthcare industries, who has the responsibility to conduct clustering analyses but is still little experienced in using them. Our goal is to propose a practical workflow for data scientists because of its genericity of application (e.g. usable on small or big data, on continuous, categorical or mixed variables, on database of high-dimensionality or not, with multicollinearity or not, etc.) while preserving the simplicity of implementation and use (need for few packages, algorithms, parameters, …) and the robustness and reliability of the methodology (e.g. evaluation of the stability of clusters, use of proven algorithms and robust packages, etc.). The objective of this workflow is therefore not to be the solution to all situations, but to propose a simple and robust basis that is as generic as possible. In a way, a choice that aims to be “globally optimal” for practice, but not optimal in every case. This generic workflow can be useful both for data scientists with little experience in the field to make data clustering easier and more robust, and for more experienced data scientists who are looking for a straightforward and reliable solution to routinely perform preliminary data mining.

3.2. Method

The criteria ¹⁵ defining the properties of the desired workflow are the following:

• Criteria for achieving genericity: applicability to small and big data, applicability to continuous or categorical or mixt data, and management of high dimensionality.
• Criteria for achieving ease of implementation and use: number of packages used, of algorithms used, of parameters to tune, use of “all-inclusive” packages covering at best the general clustering process
• Criteria for achieving robustness and reliability: management of noise data, of multicollinearity, methods considered for clusters’ stability assessment, reliability of packages used (e.g. hosting site, renown, …), reliability of algorithms used (e.g. renown, literature, …).

Facing the great diversity of packages ¹⁶ and algorithms, and considering our goal of preserving the simplicity of implementation and use of the desired generic workflow, we focused on handy ¹⁷ packages to cover main algorithms and steps in the general clustering process (see Figure 1). The latter can include functions e.g. for clustering, clusters optimization, clusters evaluation, clusters stability evaluation and clusters description (clustering algorithms suites). For Python, we considered the module sklearn.cluster from the scikit-learn library. For R, the following packages were selected: FPC, cluster, clue and ClValid. All these implementations, functions and algorithms that compose them are considered robust and therefore meet part of the criteria for achieving robustness and reliability.

3.3. Preliminary work

When relevant, we matched the selected implementations to the defined criteria (see Table 1 for R packages and skikit-learn library, and Appendix A for clustering algorithms that compose them).

Table 1 shows that neither the cluster R package nor the sklearn-cluster module in Python allow to evaluate the stability of clusters. As indicated in section 2, one should code this step oneself in python, or link (if possible) with other packages in R. Of the selected R packages, FPC was the most downloaded in 2021, and provides the most internal assessment metrics. Clue and FPC evaluate clusters stability by bootstrapping but only FPC include others methods such as noising, the complementarity of the two methods being recommended by Hennig (2008). ClValid on the other hand proposes simpler methods, mainly used in genomics, for evaluating the stability of clusters by removing one by one the variables.

The table in Appendix A was created based on Table 1 in Fahad et al. (2014), which we adapted for our purpose. Overall, Appendix A shows that none of the algorithms included in the selected packages satisfies all the properties sought in terms of genericity, simplicity of use and implementation, and robustness. For example, CLARA and Mini-batch K-means both allow very good handling of large data, are adapted to some extent to high dimensionality, and rely on few parameters to be optimized. However, they only apply to continuous data, and are not particularly suitable for noisy data. Also and unlike CLARA, Mini-batch K-means is only included in the scikit-learn module on Python.

This first synthesis work highlights the challenge to overcome.

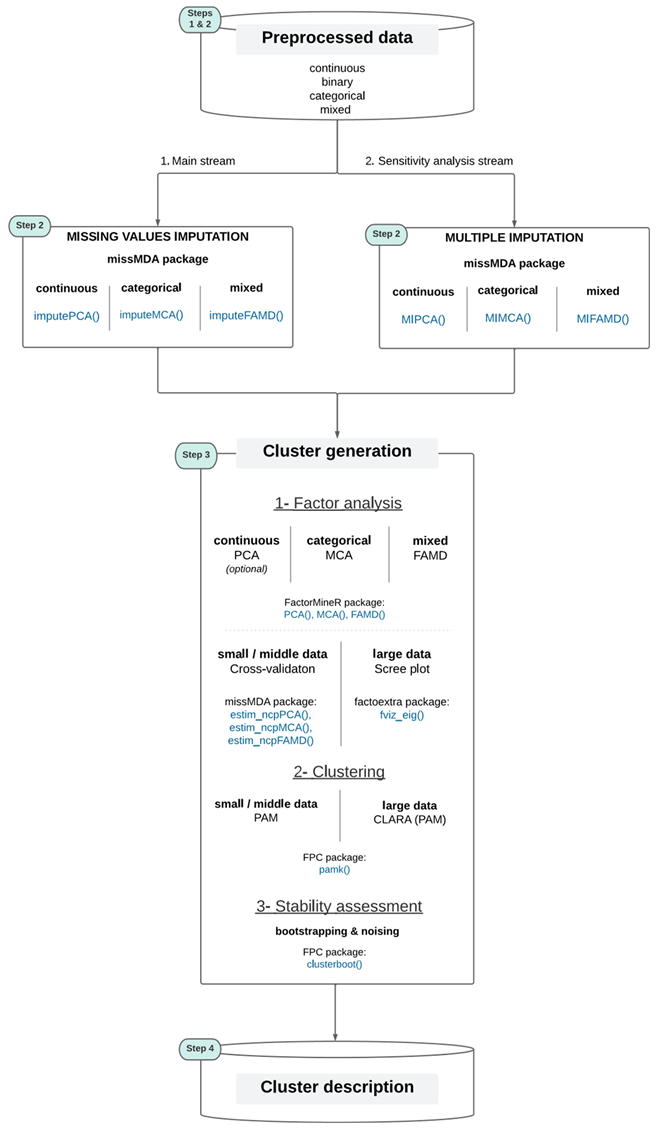
3.4. Qluster

Based on the literature review (section 2) and the preliminary work (section 3.3), we propose the Qluster workflow (see Figure 3), a set of methods that together represent a good balance for data scientists to make clustering on health data in a practical, efficient, robust and simple way. It covers the cluster generation step (step 3) through: 1- factor analysis, 2- data clustering and 3- stability evaluation. The output of the factor analysis (PCA, MCA, or FAMD) is the matrix of the coordinates of the individuals on the factorial dimensions, a table of continuous variables, allowing then the clustering by a PAM algorithm. For an in-depth discussion regarding the Qluster workflow, see section 5.

To summarize, Qluster tries to generalize clustering tasks through a generic framework that is:

• Adapted to variables of any nature, be it categorical only, continuous only, or a mix of both. This is made possible by transforming all data in the continuous setting (that is both more mature in the literature and simpler to process) using methods for factor analysis (MCA for categorical data only or FAMD for mixed data (Pages` 2004)). As mentioned in section 2.2, the latter also allows for dealing with collinearity, high-dimensionality and noise. It also makes the work for a clustering algorithm easier, as there are both fewer variables to deal with and greater clarity in information to cluster (factor analysis methods are themselves meant to uncover profiles into components of richer information).
• Adapted to datasets of any volume, be it small or large data. Indeed, the same partitioning-based algorithm is used (PAM), either applied entirely on a dataset of reasonable size, or on samples of a large ¹⁸ dataset (CLARA algorithm), using the same pamk() function from the FPC R package. In addition to this practical aspect, PAM was chosen over the (widely used) K-means algorithm based on its ability to be deterministic and to deal with Manhattan distance which is less sensitive to outliers than the Euclidean distance (Jin et al. 2010). Moreover, PAM is known for its simplicity of use (fewer parameters e.g. than with DBSCAN or BIRCH (Fahad et al. 2014)) and is also implemented in an easy-to-use all-inclusive package (not the case for e.g. CLARANS, KAMILA, Mini batch K-means, DENCLUE and STING that are suited for large datasets but where assessing clusters stability would require extensive code development by data scientists). More details on the choice of the clustering algorithm can be found in section 5.

In addition, the Qluster workflow relies solely on four state-of-the-art R packages, allowing data scientists to quickly manage data of different nature and volume and perform robust clustering:

• Both the tasks of clustering and clusters stability assessment are handled using the FPC R package (functions pamk() and clusterboot() respectively). R has been chosen over Python because the former offers all the clustering methods desired, and no package including all the steps of interest to clustering was found for the latter (one would have to code some steps by him/herself, see section 2 for more details). The clusterboot() function offers many ways to assess clusters’ stability, but one selects the two followings for routine practice and for their complementarity as mentioned in Hennig (2008): bootstrapping and noising.
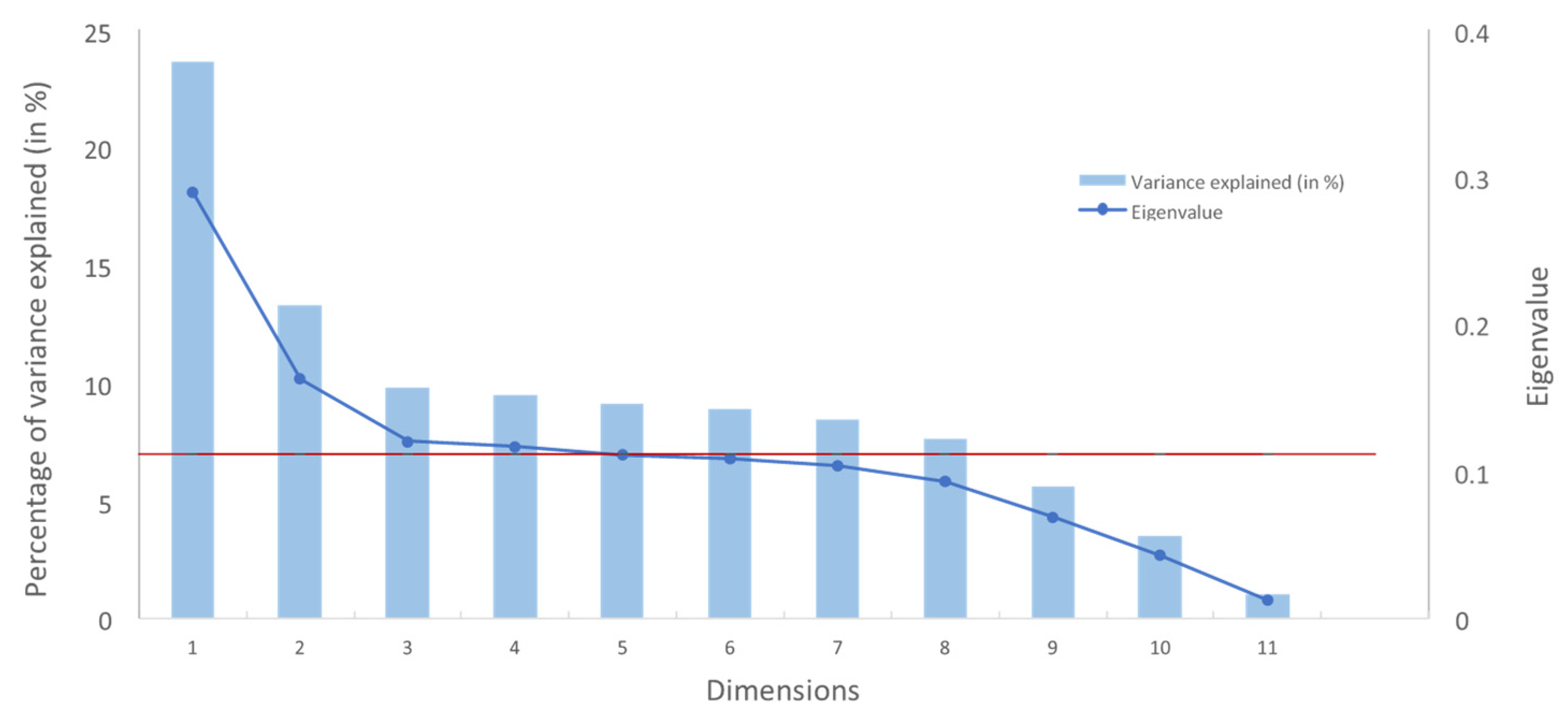
• The factor analysis part is handled using the FactoMineR R package (function PCA(), MCA(), FAMD(), for continuous, categorical, and mixed data respectively - the latter function generalizing the others). This step is optional in the case where only continuous variables are in input ¹⁹. To select the optimal number of components to keep, one recommends for small data to use the deterministic cross-validation technique implemented in the missMDA package (function estim ncpPCA(), estim ncpMCA(), estim ncpFAMD() (Josse, Chavent, et al. 2012)). As this method requires high computing time, the standard “elbow” method in a scree plot is recommended for large data, using the factoextra R package (function fviz eig()).

Finally, the Qluster workflow is operationalizable and implementable from end to end (see in Appendix in section B a picture of implementation in the Dataiku ²⁰ platform. Available upon request: contact@quinten-france.com).

This generic workflow, usable in most situations, can be described through the following pseudocode (Algorithm 1):

Algorithm 1: The Qluster pseudo-code

4. Detailed workflow methodology

4.1. The Cardiovascular Disease dataset and the objective

The Cardiovascular Disease ²¹ dataset includes 70,000 patients with or without a cardiovascular disease, and 12 variables (5 of them are continuous).

The following raw variables was used (raw variables name are in italic):

• Age (days, converted into years) - age
• Height (cm) - height
• Weight (kg) - weight
• Gender (M/F) - gender
• Systolic blood pressure (SBP) (mmHg) - ap hi
• Diastolic blood pressure (DBP) (mmHg) - ap lo
• Cholesterol (categories 1: normal, 2: above normal, 3: well above normal) - cholesterol
• Glucose (categories 1: normal, 2: above normal, 3: well above normal) - gluc
• Smoking (Y/N) - smoke
• Alcohol intake (Y/N) - alco
• Physical activity (Y/N) - active
• Presence or absence of cardiovascular disease (Y/N) - cardio

The objective of this section is to present in detail the application of the Qluster workflow proposed in section 3 on the following use case: to characterize the phenotypes of patients with a cardiovascular disease (subset of patients with cardio = Y). This represents 34,979 patients (about 50% of the whole population).

4.2. Step-by-step application of the Qluster workflow

The following section details the application of the Qluster workflow to the cardiovascular dataset to help scientists use it for their own project. Additional elements to the ones presented in section 2 supporting the present methodology are also provided when relevant. We first present the preprocessing of the dataset, in which notably the few continuous variables are converted into qualitative data, before applying a MCA, that is a data-reduction technique for exploring the associations among multiple categorical variables (Greenacre and Blasius 2006; Greenacre 1984; Warwick et al. 1989; Murtagh 2005; Nishisato 2019). Then, given the large size of the database, the CLARA algorithm is applied and optimized. Finally, clusters’ stability is assessed and a brief interpretation of clusters is provided.

4.2.1. Data preparation

Features derivation and selection First, the Body Mass Index (BMI) variable was created from both the height and weight (Ortega et al. 2016). Then, outliers were detected by defining for each quantitative variable thresholds above or below which values are more likely to be inaccurate. Acceptable values should be in the following ranges: 18 ≤ Age < 120, 10 ≤ BMI < 100, SBP ≤ 400, DBP ≤ 200 (Ortega et al. 2016, Mayo Clinic ²², French HTA (HAS) reccomandations ²³). For simplicity, patients with at least one outlier were removed from the analysis (sensitivity analyses could be performed). Quantitative variables were then discretized in order to both create variables with clinical sense and enable the use of the MCA algorithm (see Table 2).

Nota bene: the database has no missing values.

An additional binary hypertension variable were created based on both high sbp and high dbp variables that are used as a proxy for patients with hypertension (hypertension = 1 if high sbp = 1 and high dbp = 1 ; else hypertension = 0 (Desormais et al. 2021)).

Finally, the variables selected to discriminate the population must be chosen according to their medical relevance to the context of the study. To this end, the user must always consider the results he would obtain if a variable is included or not. In particular, the user has to ask himself whether active discrimination of the clusters by a variable is sought: considering the example of the two common variables age and race, if they are are actively included in the clustering step, it will tend to create groups of young versus old, Caucasian versus non-Caucasian patients. If not, such variables can be kept for a passive analysis of the generated clusters and assess a posteriori a possible heterogeneity on these variables. In this use case, we removed the height, weight, systolic and diastolic blood pressure features, as they are used to create the derived features listed above and are not useful alone for clustering.

At the end of these treatments, we obtained a database of 34,134 patients described with 11 variables.

Dealing with low prevalent features and modalities Clustering variables with low prevalence are known to be challenging in data analysis, especially for techniques that are very sensitive to data and/or anomalous cases (e.g. regression analysis and factor analysis (Fahrmeir et al. 2013)). Most common techniques consist of either gathering rare modalities in groups of higher frequency, or to discard the concerned modalities and/or variables. Additionally, binary clustering variables with low prevalence in the study population may be discarded from the analysis or grouped with other features when appropriate.

An arbitrary threshold of 10% was set to distinguish and eliminate features with rare modalities from the clustering features. This is consistent with recommendations before using Multiple Correspondence Analysis which over-weighs rare modalities and multi-modality variables (Di Franco 2016; Le Roux et al. 2010). When possible, modalities with less than 10% of prevalence were grouped with others based on medical relevance. As a result, both the Smoking (8.3% with smoke = Yes) and Alcohol intake (5.2% with alco = Yes) variables were ruled out to cluster data and were only used for a posteriori clusters description.

Moreover, some modalities were aggregated for the 2 following variables:

• Glucose (gluc): modalities 2 (above normal, 8.8%) and 3 (well above normal, 9.5%) were grouped into one modality 2 (above normal)
• BMI (BMI): modalities “underweight” (0.5%) and “normal” were grouped into one modality “underweight & normal”.

Finally, the dataset used to perform MCA contains a total number of 9 categorical variables (age, BMI, high sbp, high dbp, hypertension, gluc, gender, cholesterol, physical activity).

4.2.2. Perform Multiple Correspondence Analysis

As with other methods for factor analysis (e.g. PCA, CA, etc.), MCA was combined with cluster analysis to capture data heterogeneity, through clusters of observations in the population that show distinctive patterns (Testa et al. 2021; Mitsuhiro et al. 2015; Van de Velden et al. 2014; Hwang, Montreal´ , et al. 2006; Buuren et al. 1989).

The number of MCA components to be used was decided using the standard scree plot by identifying the “elbow” of the curve (method widely used with PCA (Cattell 1966)), while constraining eigenvalues to be strictly above a threshold of 0.11 equivalent of Kaiser’s rule in PCA (i.e. 1 / C with C the number of categorical variables).

Based on the scree plot (see Figure 4), 3 dimensions were chosen, the 3rd marking a clear elbow in the curve (related eigenvalue: 0.12; related percentage of variance explained: 9.8%).

Moreover and for interpretation purposes, eigenvalues were corrected using the Benzecri correction ²⁴ to consider that the binary coding scheme used in MCA creates artificial factors and therefore reduces the inertia explained (Greenacre 1984). The top 3 components gather 99.9% of inertia after correcting with Benzecri method (more details in Appendix in section D).

4.2.3. Clustering of the data

Parameters specification The CLARA algorithm was used through the pamk() function in the FPC R package (version 2.2-5), a reliable package for flexible procedures for clustering, and with the following main parameters:

• Distance measure: dissimilarity matrix was computed using the Manhattan distance. The latter is more robust and less sensitive to outliers than the standard Euclidean distance (Jin et al. 2010).
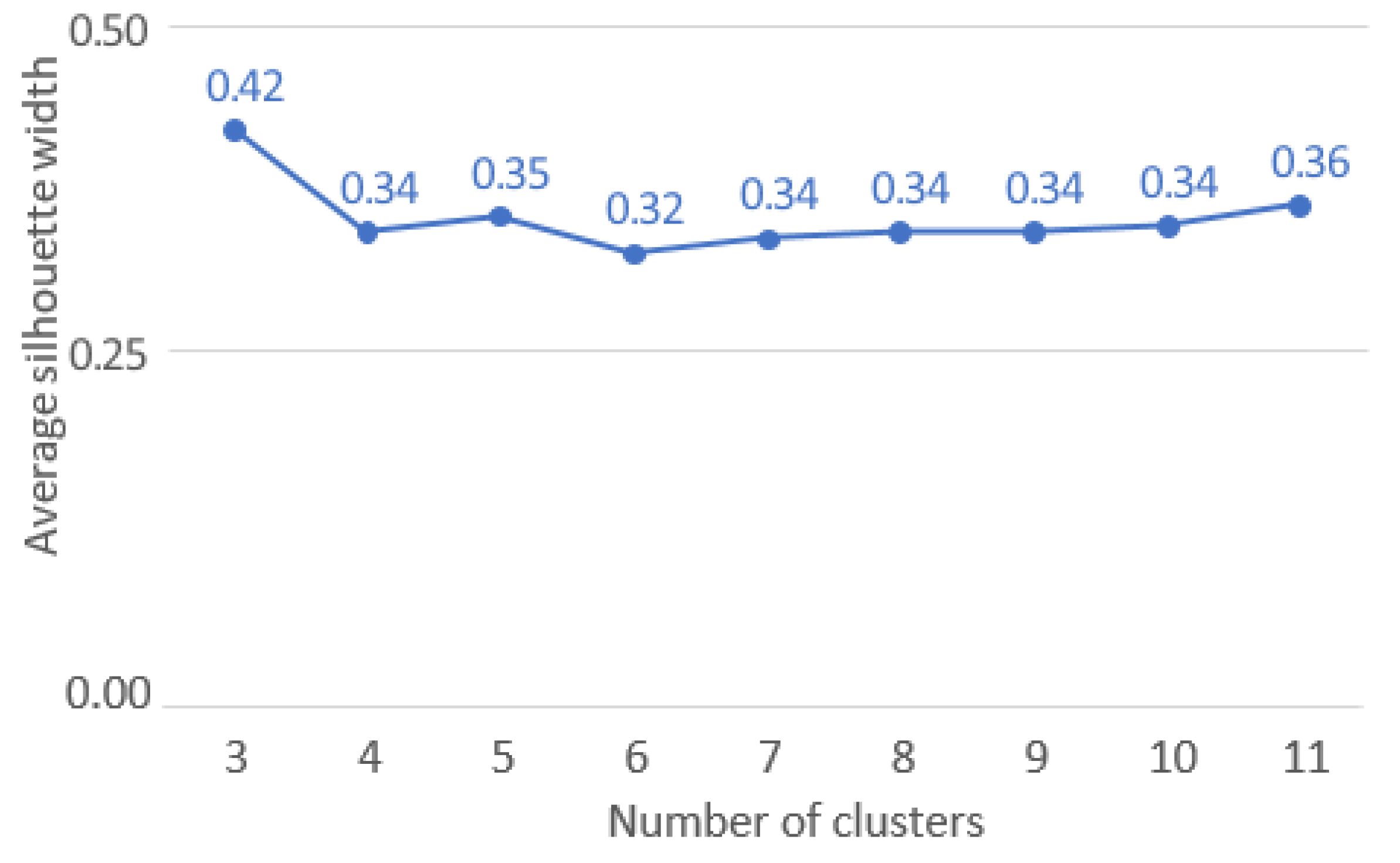
• Number K of clusters: From 3 to 11.

  -

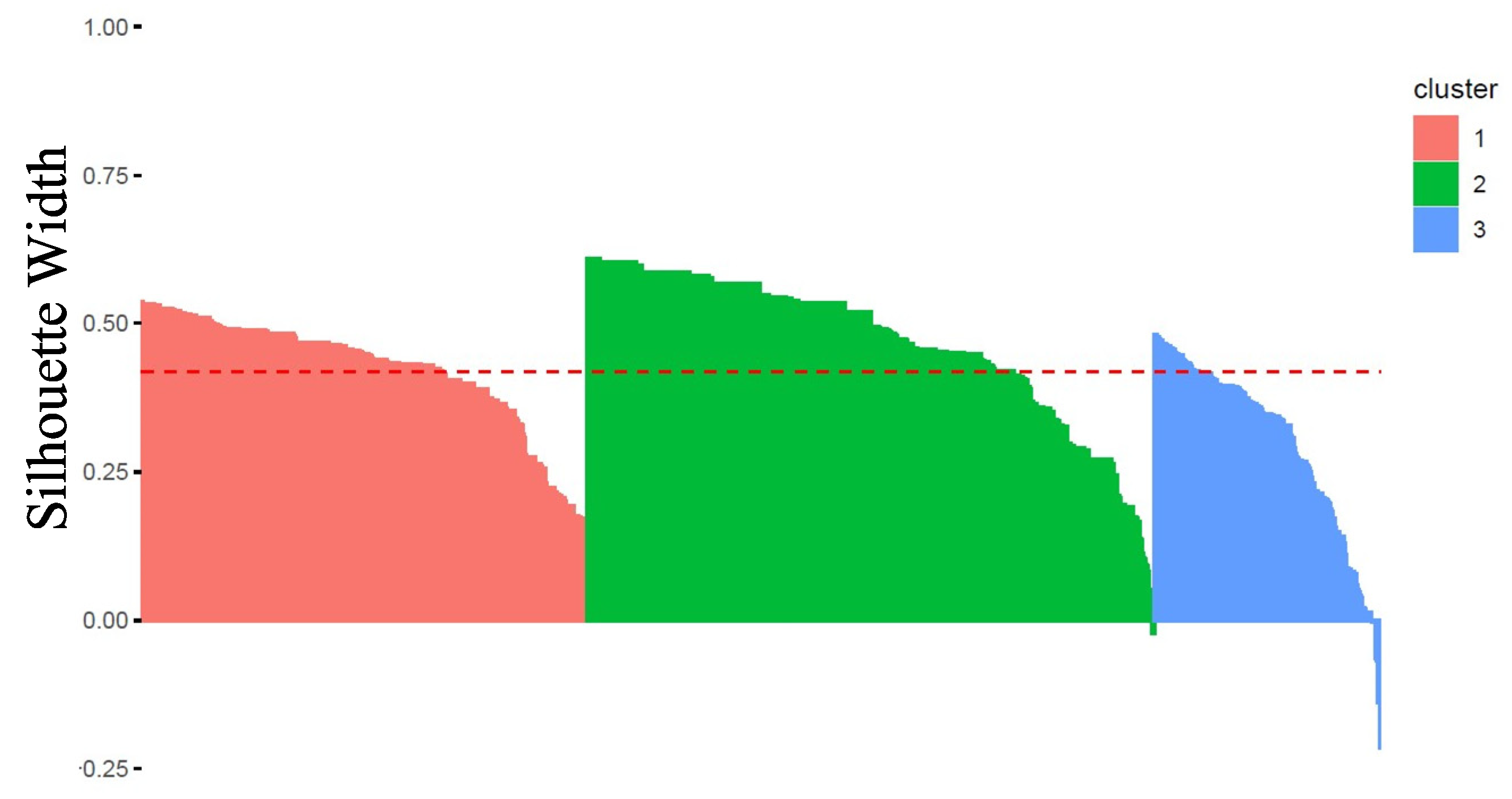
  The number of clusters was optimized on the Average Silhouette Width (ASW) quality measure, that is an internal validity metric reflecting the compactness and separation of the clusters. The ASW is based on Silhouettes Width that were calculated for all patients in the best sample, i.e., the one used to obtain cluster medoids and generate clusters (Rousseeuw 1987).

  -

  The range of clusters to be tested was determined to enable the identification of phenotypically similar subgroups while not generating an excessive number of subgroups for interpretation.

• Number of samples and sample size: 100 samples of 5% study population size (1,706 patients).

  -

  Experiments have shown that 5 samples of size 40+2C (with C the number of variables in input) give satisfactory results (Kaufman et al. 1990). However, increasing these numbers is recommended (if feasible), to limit sampling biases and favor converging toward the best solution. Equally, the higher the sample size is, the higher it is representative of the entire dataset. We therefore recommends to pretest on his own material up to what parameters values the computation times are acceptable considering the size of the input dataset and the other steps of the workflow (including the clusters stability evaluation step, the most time consuming).

Other parameters include the non-scaling of the input data to not modify the observation space obtained from MCA.

Results: The optimal ASW was obtained for a pool of 3 clusters (ASW: 0.42, see Figure 5).

Homogeneity and separability of clusters were further studied by analyzing Silhouettes Width of patients in the best sample used to generate the clusters’ medoids, using the fviz silhouette() function in the factoextra R package. As a reminder, the Silhouette Width characterizes both the cohesion of the cluster and its separation to the other clusters: a positive (respectively negative) Silhouette Width for a patient is in favor of a correct (respectively incorrect) affiliation to its own cluster.

The Figure 6 shows a high level of intra-cluster cohesion and inter-clusters separability as only few patients (in clusters 2 and 3) have negative Silhouettes. Clusterwise Silhouette Widths are also all positive (ASW of 0.42, 0.47, 0.30, for clusters 1, 2 and 3 respectively).

4.2.4. Clusters stability assessment

Parameters specification In order to evaluate clustering robustness, the clustering was performed several times on a cohort that was randomly modified. This allows to generate under perturbations new versions of the original clusters and thus to evaluate the stability of the clusters to them. The stability of the clusters is all the higher as the new versions of the clusters generated under perturbations are similar to the original clusters. The data perturbation step was performed using two approaches that may provide complementary information based on results in Hennig (2007): bootstrap and noise methods.

• Bootstrap approach:

  -

  This approach consists in performing the clustering as described in section 4.2.3 on B = 50 bootstrapped data (i.e. random sampling with replacement (Efron 1979; Efron and R. J. Tibshirani 1994)), using the clusterboot() function in the FPC R package (version 2.2-5).

  -

  The Jaccard similarity metric is used to compute, for each cluster, the proximity between the clusters of patients obtained on the modified population and the original clusters. It is given by the number of patients in common between the new cluster (modified population) and the original cluster divided by the total number of distinct patients considered (i.e. present in either the new or the original cluster).

  -

  For each cluster, the following results are provided:

  ■

  the mean of the Jaccard similarity statistic

  ■

  the number of times the cluster has been “dissolved”, defined as a Jaccard similarity value ≤ 0.5. This value indicates instability.

  ■

  the number of times the cluster has been “recovered”, defined as a Jaccard similarity value ≥ 0.75. This value indicates stability.

There is some theoretical justification to consider a Jaccard similarity value smaller or equal to 0.5 as an indication of a “dissolved cluster”, see Hennig (2008). Between 0.6 and 0.75, clusters may be considered as indicating patterns in the data, but which points exactly should belong to these clusters is highly doubtful.

• Noise approach:

  -

  This approach consists in performing the clustering as described in section 4.2.3 on B = 50 noisy data and for different values of noise, using the clusterboot() function in the FPC R package.

  ■

  Level of noise values: from 1% to 10%

  -

  The number of times each cluster was “dissolved” and “recovered” is provided, as well as the mean of the Jaccard similarity statistic, according to the noise values.

Results: Clusters are all the more stable as the Jaccard similarity statistics and the number of recovered clusters are high, and as the number of dissolved clusters are low.

The results of the data perturbation step are:

• For the bootstrap approach, clusters 1, 2 and 3 have all 100% of Jaccard similarity statistics over 50 iterations. The 3 clusters were recovered for 100% of bootstrapped iterations, which characterizes a very high stability to resampling with replacement.
• For the noise approach, clusters 1, 2 and 3 have at worst (for 2% of noise) 100%, 98%, 96% of Jaccard similarity statistics respectively over 50 iterations. The 3 clusters were recovered for 100% of iterations and regardless of the level of noise (from 1% to 10%), which characterizes a very high stability to noise.

Regardless of the method used, the results seem therefore to be very robust and can certainly be explained by the large database’s size and the small number of clusters retained in a context of synthetic data. Clusters’ stability can be more variable on real cases.

It is worth noting that although the clusterboot() function can also provide useful results and plots of clusters’ stability (histogram of Jaccard similarity statistics by cluster, summary information for each cluster, etc.) we did not provide them in this article since the obtained Jaccard similarity metrics were all around 100%.

4.2.5. Clusters interpretation

Descriptive statistics (proportions and lift values) were computed from variables included or not in the clustering step. Cluster 1 (n = 12,272 (36.0%)) groups patients who all have high values of diastolic and systolic blood pressure, and consequently hypertension. These patients are slightly more than the average with well above normal cholesterol values (18.5% versus 17.7%) and above normal glucose values (20.0% versus 18.3%). On the contrary, patients from clusters 2 and 3 (n = 15,477 (45.3%) and n = 6,385 (18.7%) respectively) are between 81% and 87% to have normal values of diastolic and systolic blood pressures, and none have hypertension. In contrast with cluster 2, patients from cluster 3 are many more with well above normal cholesterol values (26.6% versus 8.5%) and above normal glucose values (57.3% versus 0.8%).

Patients from clusters 1 and 2 are overall younger than cluster 3 (age ≤ 55: 54.7% and 51.8% versus 65.9%). Patients from clusters 1 and 3 are overall more obese than cluster 2 (41.4% and 44.5% versus 21.8%).

To summarize, among patients with a cardiovascular disease, cluster 1 gathers patients with hypertension, cluster 2 gathers patients healthier (although about the same age than cluster 1) and cluster 3 gathers slightly older patients with cholesterol and high levels of glucose (although no hypertension). Interestingly, description of cluster 1 is consistent with a poorer lifestyle (lift values of 1.21 and 1.28 for Smoke and Alcohol respectively) although this did not actively participate in partitioning. See Table 3 below for more details.

5.1. Limitations and proposition for enhancing this workflow

When large data is too large As often in data mining, one limit concerns the size of the data. It is clear that for massive data, where the number of rows is several million, specific algorithms such as grid-based methods or canopy pre-clustering algorithm (McCallum et al. 2000) are needed for the algorithms to scale up.

More specifically, in such case, factor analysis may be impossible to calculate, as it requires to make matrix calculations and to invert matrix of size n * p (n individuals, p binary variables). Please note though that in the case of categorical variables, one may prefer to use the anglo-saxon MCA method that applies the CA algorithm on a Burt table (p * p) instead of the complete disjunctive table (n * p), which is more efficient in computing time and thus more appropriate for large data (also implemented in the MCA() function in FactoMineR (Greenacre 2007)). Equally, in the case of very large data, CLARA algorithm may be too time-consuming to be calculated as we still need to maintain enough samples and observations per sample for representativeness. For all these reasons, one suggests simply analyzing a random sample of the original dataset that is likely to be very representative of the latter while allowing the use of the Qluster workflow. Please note that PCA() and FAMD() are known to take more time for computation than MCA(). As a consequence, the notion of “large” data may depend on the nature of data (continuous, categorical, mixed). One also suggests (when possible) in a data preparation step to converge into one type of data (continuous only or categorical only). This is especially true for mixed data where the upstream scaling of the data can be challenging, and where the computation times by FAMD are more important. Alternatives may consist in not using the proposed workflow but algorithms which go fast on (very) large data such as Mini Batch K-means used on continuous variables or on one-hot-encoded categorical variables. However, in addition to the fact that it relies on the Euclidean distance only, these strategies may not allow the beforehand use of factor analysis because of data’s size, as well as to easily and properly assess clusters’ stability, which hinders confidence and support in results. One therefore recommends the first option.

Conversely, when the number of columns is greater than the number of rows (p > n), the dimension reduction step via factor analysis methods makes very sense to easily manage the high dimensionality of the data. However, in the most extreme cases where p >> n, standard factor methods may fail to yield consistent estimators of the loading vectors. Also, the results may be difficult to interpret. In such situations, standardized methods may be a solution to improve the robustness, consistency, and interpretability of results (e.g., penalized PCA, Lee et al. 2012). It is also recommended that, when possible, a subset of the variables be selected strictly prior to analysis.

Generalizability of this workflow to missing data Missing values management is not covered in this workflow, and it is therefore assumed that no missing values are present in the dataset. Indeed, both factor methods (PCA, MCA, FAMD) and proposed clustering methods (PAM, CLARA, ...) require data without missing values. However, this workflow can be easily generalized to missing data, using the same missMDA package as for performing the selection of the optimal number of dimensions in factor analysis, in order to impute in a first step missing values using factor methods. The latter are state-of-the-art methods for handling missing values (e.g. function imputePCA(), imputeMCA() and imputeFAMD() for simple imputations (Audigier et al. 2013)) and can thus easily be integrated and/or used in an automated workflow to handle missing data. In addition, this R package makes it possible to perform multiple imputations (MIPCA(), MIMCA() and MIFAMD()) for assessing incertitudes from imputed values and increasing confidence in results (Josse, Pages` , et al. 2011). In this sense, the Qluster workflow is therefore adapted for handling missing data (see in Appendix in section E an example of the Qluster workflow adapted for handling missing values).

Discussion on using factor analysis as a first step As mentioned on several occasions, factor analysis allows the transformation of structured data of all kinds into continuous data, while dealing with large, collinear, noisy, high-dimensional data. It also facilitates clustering by aggregating groups of homogeneous information within dimensions. Nevertheless, it cannot always be guaranteed that the results will be “better” or “as good” with factor analysis in the clustering process. Similarly, the choice of factor analysis in this workflow comes with drawbacks that include the following items:

• The packages used cannot handle the ordinal nature of the variables. The latter must be treated as categorical or continuous.
• The observations x components matrix is continuous, although some raw variables could be categorical. This prevents the user from favoring (respectively, not favoring) positive cooccurrence over negative co-occurrence via the Jaccard (respectively, Hamming) distance

Alternatives can be to perform data dimension reduction using features selection methods, or manually, by grouping, transforming and/or deleting variables based on clinical expertise.

Discussion on using a single K-medoid algorithm In order to offer a simple, yet generic and robust workflow to make practical use of the same methodology in many applications, we performed an arbitrary (but well chosen) selection of both algorithms and software packages. In particular, the choice to use the PAM/CLARA algorithm is based on many aspects such as the fact that it is:

• one of the best known, studied and used algorithm by the community, for general purpose, - adapted to the continuous setting (i.e., the most mature in the literature).
• meant for the most frequent use case of clustering (i.e., hard partitioning),
• suitable to the Manhattan distance, a less sensitive to outliers distance, unlike its counterpart on the euclidean distance (K-means),
• deterministic, thanks to its internal medoid initialization procedure, unlike the basic K-means algorithm that may lead to inconsistent or non-reproducible clusters
• requiring few parameters to set up (e.g. conversely to BIRCH and DBSCAN, see Fahad et al.(2014)),
• very well implemented within a recognized reference R package (the FPC package) facilitating its use within a complete and robust clustering approach,
• usable within the same R function (pamk()) regardless of the volume of data.

Yet, it is clear that other algorithms than the ones chosen could be routinely used instead, including those present in the FPC R package to facilitate its integration within the workflow (e.g. DBSCAN and HAC). In particular, it is well known that with non-flat geometry and/or uneven cluster size, DBSCAN is more appropriate than K-means and PAM. Equally, if the final goal is to obtain a hierarchy rather than a unique hard partition, the user will be encouraged to prefer an algorithm such as HAC, which can easily be used with the proposed packages in this workflow. However, the presence of additional parameters to tune or the lack of compatibility with massive data would require the workflow to become more complex. Also, this workflow is not meant to replace more in-depth work by the data scientist to find what is optimal on a specific case study. More experienced data scientists can use the generic Qluster workflow for a first look at the data, but are encouraged to adapt the general principles of this workflow to their own case study (e.g., finding the most suitable algorithm, etc.). Such adaptations would be out-of-scope of this workflow in the sense of the initial objectives: genericity of applications while preserving the simplicity of implementation and reliability/robustness of metholodogy.

Equally, the user may want to benchmark several clustering algorithms as suggested in Hennig (2020). The comparison of methods solutions can be based on information measures (e.g. entropy, mutual information, etc.), internal validity measures (e.g. silhouette, see section 2.4.), set-matching (i.e., mapping each cluster from the first clustering to the most similar cluster in the second clustering and computing recall, precision or some other measure) and pair counting (including dedicated visualization tools, see Achtert et al. (2012)). Some of these strategies are directly implemented in the clusterbenchstats() function from the FPC R package or in the clValid() function of the clValid R package. However, as our goal is to propose a simple-to-use workflow, this complexification - which would also greatly impact computing times and memory capacities - is left to the user’s discretion. Moreover, multiplying the algorithms and combination of parameters forces one to rely more heavily on a purely statistical criterion (e.g. ASW) to select the “best” clustering of the data, although this may not reflect the best partitioning in the clinical sense. Indeed, ASW remains a criterion characterizing the average separability over all the clusters, and its optimum may miss (the set of) results that is clinically relevant and/or useful for the desired objective ²⁵. If the data scientist wishes to compare different algorithms, we would rather recommend to fully investigate the results from a well-chosen first algorithm (here PAM/Clara), before challenging it with others, in order to be less dependent on the sole selection criterion of the ASW. This paper thus takes the opposite view of the auto-ML literature by first advocating a full investigation of a parsimonious workflow made of well-chosen algorithms, rather than directly a broad coverage of algorithmic possibilities. Nevertheless, readers may be interested in recent areas of research around meta-clustering (Caruana et al. 2006) and ensemble clustering methods (Greene et al. 2004; Alqurashi et al. 2019). The first one aims to produce several partitioning results in order for the user to select those which are most useful. The second one is intended to combine the clustering of several methods with the aim of proposing a consensual result.

Discussion on the clusters’ stability assessment step Bootstrapping and noising methods were chosen in the workflow for both their availability in the same function clusterboot() from the same package as for pamk(), and for their complementarity as recommended by Hennig (2007). Nevertheless, other methods may also be used as sensitivity analyses, including those proposed in the same FPC package. Furthermore, although this step allows for the clusters to be assessed, data scientists should keep in mind that stability is not the only important validity criterion - clusters obtained by very inflexible clustering methods may be stable but not valid, as discussed in Hennig (2008). Finally, although several choices were made to try to manage outliers as best as possible, such as using a k-medoid algorithm and the Manhattan distance, the Qluster workflow does not fully address the issues related to outliers and extreme values. One solution may be to define threshold values to manually detect extreme values as a pre-processing step (as in the case study in section 4), or to use more sophisticated statistical methods such as Yang et al. (2021).

Discussion on the clusters’ interpretation Clusters’ description is not covered in the Qluster workflow. However, many methods exist to interpret clusters (see section 2.3). Data scientists can easily generalize Qluster to the description of clusters by using the functions already present in the FPC package in order not to make the workflow too complex, such as plotcluster() and cluster.varstats() following methodologies recommended by Hennig (2004).

Discussion on the types of data that are supported by the Qluster workflow Although general, the Qluster workflow does not cover all types of data and it is clear that for medical imaging data, omics data or data in the form of signals, dedicated approaches must be considered. Nevertheless, most tabular data can be processed using the Qluster workflow. In this respect, and although the Qluster workflow was specifically designed in the context of healthcare data analysis, it can easily be applied in other fields.

5.2. Discussion and recommendation on the practical use of the workflow

Use of clusters stability as a criterion to be optimized Cluster stability assessment could be considered as a criterion to be optimized, by iterating on this step in order to make this property an integral part of the clustering process itself. For example, stability measures could be used to select the optimal number of clusters, assuming that the clustering results are more stable with the correct number of clusters (Pasi Franti¨ 2020).

Attention should be paid, however, to the fact that the bootstrap and noise methods are more computationally and thus time-consuming than simple methods such as deleting variables one by one (methods used on biological measurements and proposed in the ClValid R package). Also, it may not be obvious to optimize the clustering on clusters’ stability if the 2 proposed methods do not give similar results. For example, relatively to the noising method, the bootstrap method is more likely to give stable results with the increase in the volume of the dataset in the case of PAM, and the increase in the % of representativeness of the samples in the case of CLARA.

What if results are not satisfying The question of the ultimate relevance of clusters has not been covered in this workflow. It is worth pointing out that an absence of results may be a result in itself, as it can characterize a population that cannot be described in several homogeneous subgroups (either because such subgroups do not exist, or because the variables used do not allow to find them). Nevertheless, it is clear that, as in the Data Mining process, we can consider looping back on this workflow by changing certain parameters if the results are not satisfactory or if an important criterion of the clustering was not taken into account at the beginning (for example the maximum number of clusters, etc.). More generally, the data scientist is encouraged to keep in mind that the final objective of clustering is often the clinical relevance and usefulness of the results generated. In this sense and as mentioned in 5.1, it is not forbidden to relax a purely statistical criterion, such as the ASW (whose optimum may miss some relevant subgroups as it is an indicator of the overall separability) to better represent the diversity of the population studied, or to favor the generation of hypotheses in the case where the statistical optimum only gives broad results not enough specific for the initial objective.

In the same spirit, negative Silhouette values are too pejoratively considered in the cluster’s validity analysis (interpreted as clustering failures). Indeed, negative Silhouettes characterize patients who are, on average, closer to patients from another cluster than to the patients of their own cluster. Therefore, patients with a negative Silhouette may be informative of potential relationships between clusters, and should therefore be considered as potential additional information about disease history and phenotypic complexity, such as one cluster that is the natural evolution of another. Hence, it is recommended that an analysis of patients with negative Silhouettes be included in the workflow to better assess whether they are a reflection of “bad” clustering or the key to better understanding the disease.

What if the optimum number of clusters is the minimum of range K? In the case where the optimal number of clusters is the minimum of the range of K (as in our example in section 4), we recommend (if appropriate) that data scientists be testing for lower values of K to challenge the obtained optimum. Equally, if the optimum is obtained for K = 2, data scientists should test whether the dataset should be split into two clusters, using the Duda-Hart test that tests the null hypothesis of homogeneity in the whole dataset. This can be done using the same pamk() function by setting up the minimum of K to 1, or directly using the dudahart2() function (also in FPC R package). In any case, if the primary objective is to provide fine-grained knowledge of the study population, it will still be possible to provide results with the optimal K that was initially obtained, keeping in mind that the levels of inter-cluster separability and intra-cluster homogeneity are not really higher than those that would be obtained with a smaller number of clusters.

Using this workflow routinely The Qluster workflow is highly subject to automation for data scientists and companies that need a routine way to cluster clinical data. Indeed, data scientists may create a main function for applying this workflow, including by setting the nature of data (categorical/continuous/mixed), the volume (normal/large), and parameters related to each called function. It is worth mentioning, however, that the quality of the input data or the structure of the groups to be found are factors that may not allow the present workflow to identify relevant results every time. In this case, the data scientist can refer to the indications given above or, if necessary, consider an approach more adapted to his data.

6. Conclusion

In this article, we propose Qluster, a practical workflow for data scientists because of its genericity of application (e.g. usable on small or big data, on continuous, categorical or mixed variables, on database of high-dimensionality or not, etc.) while preserving the simplicity of implementation and use (e.g. need for few packages and algorithms, few parameters to tune, …), and the robustness and reliability of the methodology (e.g. evaluation of the stability of clusters, use of proven algorithms and robust packages, management of noisy or multicollinear data, etc.). It therefore does not rely on any innovative approach per se, but rather on a careful selection and combination of state-of-the-art clustering methods for practical purposes and robustness.

One of the underlying motivations is the observation of research teams, including statisticians/data scientists in contract research organizations that provide support to healthcare industries, who have the responsibility to conduct clustering analyses but are still little experienced in using them. They are also confronted with a very large literature, and a very large number of algorithms and implementations, which makes the exercise difficult. We believe that Qluster can improve (1) the quality of analyses carried out as part of such studies (thanks to Qluster’s criteria for robustness and reliability), promote and ease clustering studies (thanks to Qluster’s genericity and simplicity of use), and increase the skills of some of the statisticians/data scientists involved (thanks to the literature review provided and the general principles of Qluster). This workflow can also be used by more experienced data scientists for initial explorations on the data before designing more in-depth analyses.

Finally, this workflow can be fully operationalized, using either scripted tools or a Data Science platform supporting the use of R packages. As an illustrative example, we made an implementation on the Dataiku platform of the Qluster workflow to process a kaggle dataset (see in Appendix in section B). This implementation is usable on the free edition and is made available on request (email: contact@quinten-france.com).