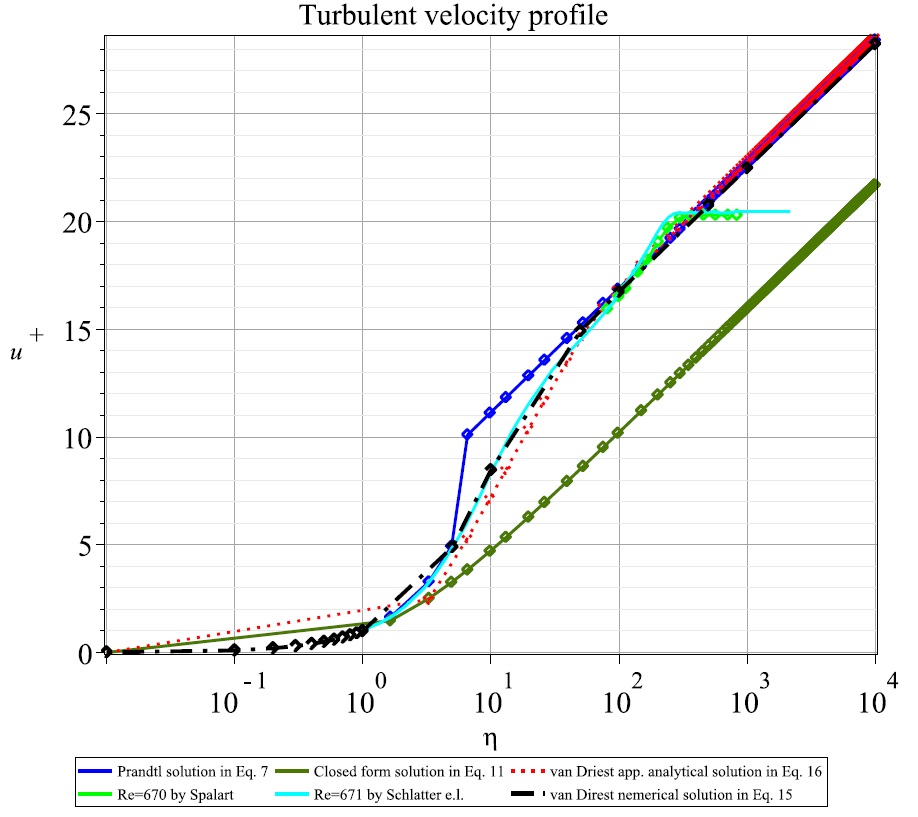
In this letter, a century-old problem is studied; namely, to find a unified analytic description of the non-uniform distribution of mean velocity across the entire domain of turbulent flow for all Reynolds numbers within the framework of the Prandtl mixing length theory. Considering the Prandtl mixing length model, a closed form solution of the mean velocity profile of plane turbulent flow is obtained, and approximate analytical solution of the van Driest mixing length theory is proposed. The profiles of several useful quantities are given, such as turbulent viscosity, Reynolds turbulent stress, Kolmogorov's scaling law, and energy dissipation density. It is shown that the energy dissipation density at the surface is finite, whereas Landau's energy dissipation density is infinite. The closed form solution reveals that the universality of the turbulent velocity logarithmic profile no longer holds, but the von K\'arm\'an constant is still universal. Furthermore, a new formulation of the resistance coefficient of turbulent flow in pipes is given in implicit form.