Version 1
: Received: 30 October 2021 / Approved: 1 November 2021 / Online: 1 November 2021 (11:28:02 CET)
Version 2
: Received: 15 November 2021 / Approved: 15 November 2021 / Online: 15 November 2021 (13:33:20 CET)
Version 3
: Received: 5 January 2022 / Approved: 6 January 2022 / Online: 6 January 2022 (11:26:17 CET)
Version 4
: Received: 7 June 2022 / Approved: 8 June 2022 / Online: 8 June 2022 (12:27:48 CEST)
How to cite:
Sun, B. Closed Form Solution of Plane-Parallel Turbulent Flow Along an Unbounded Plane Surface. Preprints2021, 2021110008. https://doi.org/10.20944/preprints202111.0008.v1
Sun, B. Closed Form Solution of Plane-Parallel Turbulent Flow Along an Unbounded Plane Surface. Preprints 2021, 2021110008. https://doi.org/10.20944/preprints202111.0008.v1
Sun, B. Closed Form Solution of Plane-Parallel Turbulent Flow Along an Unbounded Plane Surface. Preprints2021, 2021110008. https://doi.org/10.20944/preprints202111.0008.v1
APA Style
Sun, B. (2021). Closed Form Solution of Plane-Parallel Turbulent Flow Along an Unbounded Plane Surface. Preprints. https://doi.org/10.20944/preprints202111.0008.v1
Chicago/Turabian Style
Sun, B. 2021 "Closed Form Solution of Plane-Parallel Turbulent Flow Along an Unbounded Plane Surface" Preprints. https://doi.org/10.20944/preprints202111.0008.v1
Abstract
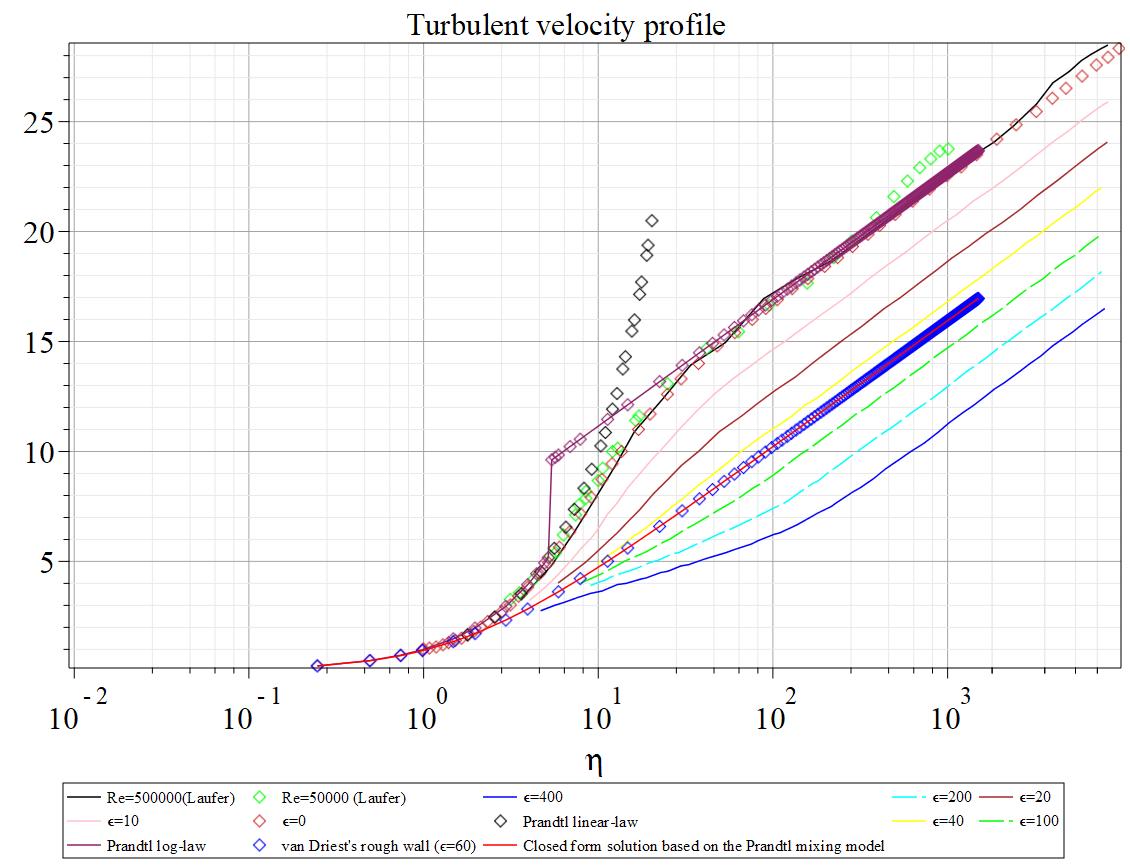
In this letter, a century-old problem is studied; namely, to find a unified analytic description of the non-uniform distribution of mean velocity across the entire domain of turbulent flow for all Reynolds numbers within the framework of the Prandtl mixing length theory. Considering the Prandtl mixing length model, a closed form solution of the mean velocity profile of plane turbulent flow is obtained. The profiles of several useful quantities are given, such as turbulent viscosity, Reynolds turbulent stress, Kolmogorov's scaling law, and energy dissipation density. It is shown that the energy dissipation density at the surface is finite, whereas Landau's energy dissipation density is infinite. The closed form solution reveals that the universality of the turbulent velocity logarithmic profile no longer holds, but the von K\'arm\'an constant is still universal. The closed form solution is validated by both direct numerical simulation and experiments. The studies confirm that the van Driest mixing length theory is suitable for smooth walls, and the Prandtl mixing length theory is suitable for rough walls. Furthermore, a new formulation of the resistance coefficient of turbulent flow in pipes is given in implicit form.
Copyright:
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
