Celestial and Quantum Propagation, Spinning, and Interaction as 4D Relativistic Cloud-Worlds Embedded in a 4D Conformal Bulk: From String to Cloud Theory

Preprint

Article

Celestial and Quantum Propagation, Spinning, and Interaction as 4D Relativistic Cloud-Worlds Embedded in a 4D Conformal Bulk: From String to Cloud Theory

Altmetrics

Downloads

2616

Views

3063

Comments

Mohammed B. Al-Fadhli^*

This version is not peer-reviewed

Submitted:

10 January 2023

Posted:

12 January 2023

Read the latest preprint version here

Alerts

Abstract

Considerable efforts have been devoted to modifying gravity, which aim to elucidate the possible existence or nature of dark matter and energy, describe observational data more effectively, and formulate quantum gravity. In addition, despite the immense success of the quantum field theory, the framework requires renormalization techniques and breaks down at high energies. Recently, the Planck legacy 2018 release has confirmed the existence of an enhanced lensing amplitude in the cosmic microwave background power spectra, which prefers a positively curved early Universe with a confidence level higher than 99%. This study considers the implied curvature of the early Universe as the curvature of “the background or 4D conformal bulk as a manifestation of vacuum energy” and distinguishes it from the localized curvature that is induced in the bulk by the presence of celestial objects that are regarded as ”4D relativistic cloud-worlds.” Analogously, because gravity appears to emerge owing to spacetime curvature and does not exhibit critical characteristics shared by other fields, it has been incorporated as the local curvature of the bulk affecting the embedded quantum fields that are regarded as propagating “4D relativistic quantum clouds.” To consider the effects of the bulk on embedded clouds, this paper presents interaction field equations in terms of brane-world modified gravity and the perspective of geometrization of the quantum mechanics wherein gravity is manifested by the curvature of 4D conformal bulk as an indicator of the field strength of vacuum energy on the embedded 4D relativistic clouds in addition to the boundary interactions, which could remove the singularities and satisfy a conformal invariance theory. A visualization of the evolution of the 4D relativistic cloud-worlds over the conformal spacetime of the 4D bulk is presented, whereas the standard said theories can be recovered from the interaction field equations.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

After the formulation of Einstein’s theory of General Relativity (GR) by utilizing 4D spacetime, Kaluza discovered in 1919 a potential unification of gravitational and electromagnetic fields in 5D spacetime. To handle the fifth dimension, Klein posited that it can be compactified. Nonetheless, these attempts and their expansions to higher dimensions have not culminated in testable predictions nor the competence to elucidate observations yet. As an alternative to compactification, Gogberashvili, Randall, and Sundrum demonstrated in 1999 that the weak force of gravity could be explained by using a model of 4D spacetime that is embedded in a negatively curved and large fifth dimension; nevertheless, the model demanded massive gravitons [1,2,3].

On the other hand, to achieve an effective action for the quantum corrections, several theories were formulated based on the modification of curvature terms and Lagrangian fields. Such alterations appear to be inevitable, which included high-order curvature terms and non-minimally coupled scalar fields [4,5,6]. Moreover, although quantum anomalies require a non-local Lagrangian, one of the major differences between GR and quantum field theory (QFT) is that GR is background independent; consequently, it requires fewer inputs whereas QFT involves a background metric that in turn impacts its predictions [7].

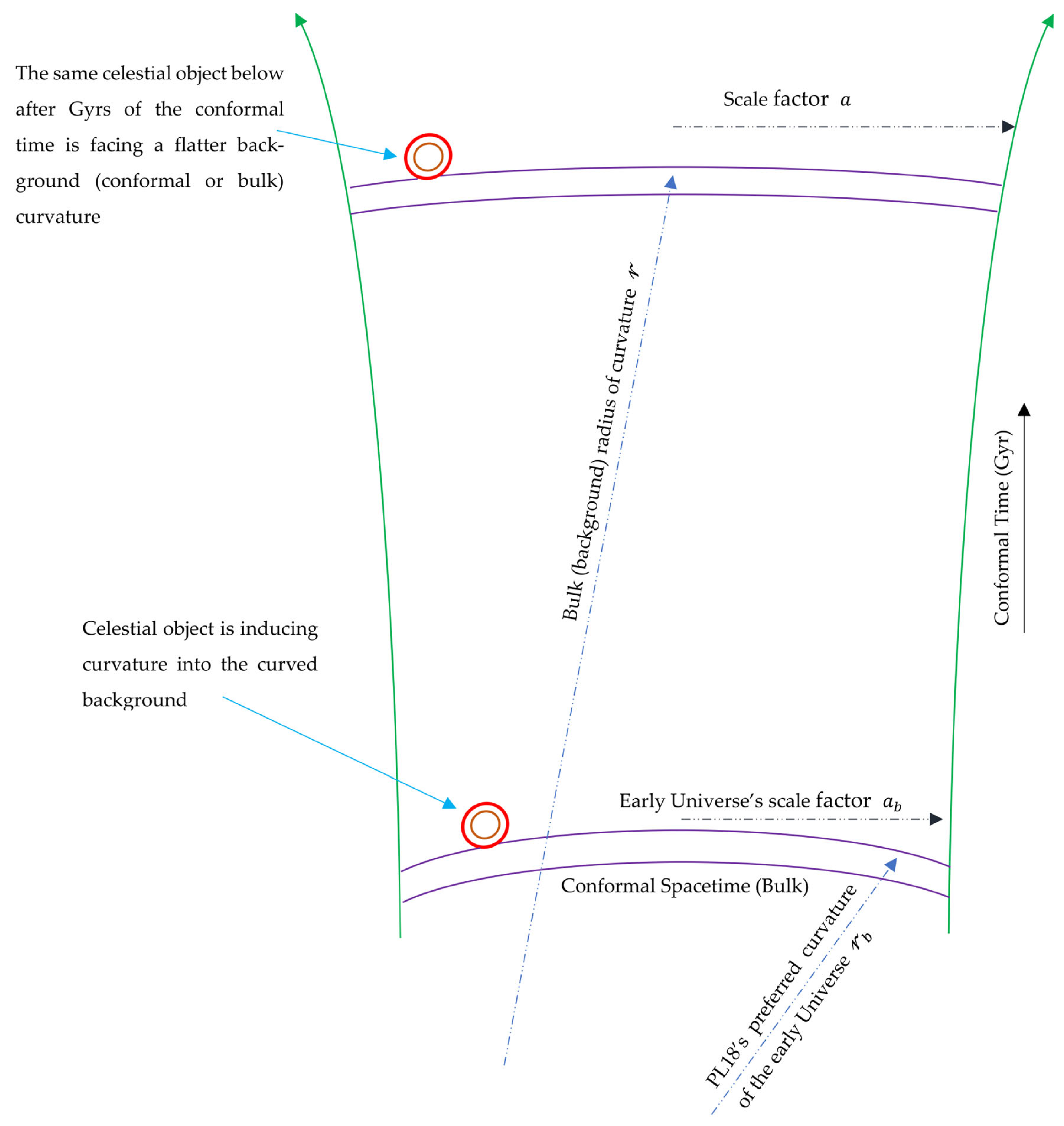
Recently, the Planck legacy 2018 (PL18) release has confirmed the existence of an enhanced lensing amplitude in the cosmic microwave background power spectra, which prefers a positively curved early Universe with a confidence level higher than 99% [8,9]. Based on this sign of early curved background and its feasible evolution over conformal time, it is obvious that background-independent theories, such as GR, do not consider the background curvature evolution and regard celestial objects in the early Universe with a preferred curvature on equal footing with their counterparts in the present Universe with a spatially flat background; this shortcoming can be the cause of the dark matter problem.

A desirable gravity theory should consider metrics of both the celestial object and the background, and reduce to GR in a flat spacetime background. Moreover, to incorporate gravity to quantum fields, the geometrization of quantum mechanics approach rather than quantizing gravity in favour of De Broglie and Penrose assessments is considered, which can maintain the equivalence principle and count for the impact of gravity on quantum fields while the latter lacks these features [10]. Besides, gravity appears to be an emergent field because it cancels out in a free-fall and cannot be shielded from its influence.

This study aims to formulate interaction field equations that consider the background curvature, signified as the 4D conformal bulk curvature, and its impact on celestial objects that are regarded as 4D relativistic cloud-worlds. In addition, it aims to incorporate the influence of the gravity, indicated by the local curvature of the 4D conformal bulk, on quantum fields that are regarded as propagating 4D relativistic quantum clouds. This paper is organized as follows. Sections 2 presents the mathematical derivations of the interaction field equations and Section 3 presents their visualizations while Section 4 incorporates the quantum interactions. Section 5 reproduces quantum electrodynamics. Finally, Section 6 summarizes the conclusions and suggests directions for future works.

2. Gravitational and Electromagnetic Interaction Field Equations

The PL18 release prefers a positively curved early Universe, that is, is a sign of a primordial background curvature or a curved conformal bulk where the evolution of the conformal curvature is associated with the Universe scalar factor expansion (Appendix B). To consider the bulk curvature and its evolution over the conformal time, a modulus of spacetime deformation,

E_{D}

in terms of energy density, is introduced based on the theory of elasticity [11]. The modulus can be expressed in terms of the resistance of the bulk to the localized curvature that is induced by celestial objects by using Einstein field equations or in terms of the field strength of the bulk by using the Lagrangian formulation of the energy density existing in the bulk as a manifestation of the vacuum energy density as

E_{D} = \frac{T_{μ ν} - \frac{1}{2} T g_{μ ν}}{R_{μ ν} / R} = \frac{{- F}_{λ ρ} F^{λ ρ}}{4 μ_{0}}

(1)

where the stress is signified by the stress-energy tensor

T_{μ ν}

of trace

T

while the strain is signified by the Ricci curvature tensor

R_{μ ν}

as the change in the curvature divided by the existing curvature

R

given as the scalar of the bulk curvature denoting the background or conformal curvature.

F_{λ ρ}

is the field strength tensor and

μ_{0}

is vacuum permeability. By incorporating the bulk influence, the Einstein–Hilbert action can be extended to

S = E_{D} \int_{C}^{} [\frac{R}{R} + \frac{L}{L}] {\sqrt{- g} d}^{4} σ

(2)

where

R

denotes the Ricci scalar curvature representing the localized curvature induced into the bulk by a celestial object that is regarded as a 4D relativistic cloud-world of metric

g_{u v}

and Lagrangian density

L

whereas

R

denotes the scalar curvature of the 4D bulk of metric

{\tilde{g}}_{μ ν}

and Lagrangian density

L

as its internal stresses and momenta reflecting its curvature.

As the bulk modulus,

E_{D}

, is constant with regards to the cloud-world action under the constant vacuum energy density condition, and by considering the expansion of the bulk over conformal time owing to the expansion of the Universe and its implication on the field strength of the bulk, a dual-action concerning the conservation of energy on global (bulk) and local (cloud-world) scales can be introduced as follows

S = \int_{B}^{} [\frac{- F_{λ ρ} {\tilde{g}}^{λ γ} F_{γ α} {\tilde{g}}^{ρ α}}{4 μ_{0}}] \sqrt{- \tilde{g}} \int_{C}^{} [\frac{R_{μ ν} g^{μ ν}}{R_{μ ν} {\tilde{g}}^{μ ν}} + \frac{L_{μ ν} g^{μ ν}}{L_{μ ν} {\tilde{g}}^{μ ν}}] \sqrt{- g} d^{4} ρ d^{4} σ

(3)

This action implies eight-dimensional degrees of freedom as

d^{4} ρ d^{4} σ = φ^{2} d^{8} σ

where

ϑ^{2}

is a dimensional-hierarchy factor. The conformal bulk metric,

{\tilde{g}}_{μ ν}

, and cloud-world metric,

g_{u v}

, are associated by Weyl’s conformal transformation as

{\tilde{g}}_{μ ν} = g_{μ ν} Ω^{2}

, where

Ω^{2}

is a conformal function [12]. The global-local action should hold for any variation as follows

δ S = \int_{B}^{} [\begin{matrix} \frac{- δ (F_{λ ρ} {\tilde{g}}^{λ γ} F_{γ α} {\tilde{g}}^{ρ α}) \sqrt{- \tilde{g}}}{4 μ_{0}} \\ - \frac{F_{λ ρ} {\tilde{g}}^{λ γ} F_{γ α} {\tilde{g}}^{ρ α} δ \sqrt{- \tilde{g}}}{4 μ_{0}} \end{matrix}] \int_{C}^{} [\begin{matrix} \frac{δ (R_{μ ν} g^{μ ν}) \sqrt{- g}}{R_{μ ν} {\tilde{g}}^{μ ν}} - \frac{δ (R_{μ ν} {\tilde{g}}^{μ ν}) R_{μ ν} g^{μ ν} \sqrt{- g}}{{(R_{μ ν} {\tilde{g}}^{μ ν})}^{2}} + \frac{R_{μ ν} g^{μ ν} δ \sqrt{- g}}{R_{μ ν} {\tilde{g}}^{μ ν}} \\ + \frac{δ (L_{μ ν} g^{μ ν}) \sqrt{- g}}{L_{μ ν} {\tilde{g}}^{μ ν}} - \frac{δ (L_{μ ν} {\tilde{g}}^{μ ν}) L_{μ ν} g^{μ ν} \sqrt{- g}}{{(L_{μ ν} {\tilde{g}}^{μ ν})}^{2}} + \frac{L_{μ ν} g^{μ ν} δ \sqrt{- g}}{L_{μ ν} {\tilde{g}}^{μ ν}} \end{matrix}] d^{4} ρ d^{4} σ

(4)

By utilizing Jacobi's formula,

δ \sqrt{- g} = - \sqrt{- g} g_{μ ν} δ g^{μ ν} / 2

[13], the variation is

δ S = \int_{B}^{} [\begin{matrix} \frac{{- F}_{λ ρ} F_{γ}^{ρ} δ {\tilde{g}}^{λ γ} - F_{λ ρ} {\tilde{g}}^{λ γ} δ F_{γ}^{ρ}}{2 μ_{0}} \\ + F_{λ ρ} {\tilde{g}}^{λ γ} F_{γ α} {\tilde{g}}^{ρ α} \frac{{\tilde{g}}_{μ ν} δ {\tilde{g}}^{μ ν}}{8 μ_{0}} \end{matrix}] \sqrt{- \tilde{g}} \int_{C}^{} [\begin{matrix} \frac{R_{μ ν} {δ g}^{μ ν} + g^{μ ν} δ R_{μ ν}}{R} - \frac{R_{μ ν} {δ \tilde{g}}^{μ ν} + {\tilde{g}}^{μ ν} δ R_{μ ν}}{R^{2}} R - \frac{g_{μ ν} δ g^{μ ν}}{2 R} R \\ + \frac{L_{μ ν} {δ g}^{μ ν} + g^{μ ν} δ L_{μ ν}}{L} - \frac{L_{μ ν} {δ \tilde{g}}^{μ ν} + {\tilde{g}}^{μ ν} δ L_{μ ν}}{L^{2}} L - \frac{g_{μ ν} δ g^{μ ν}}{2 L} L \end{matrix}] \sqrt{- g} d^{4} ρ d^{4} σ

(5)

By considering the boundary term of the cloud-world:

\int_{c}^{} g^{μ ν} δ R_{μ ν} \sqrt{- g} d^{4} ρ / R

, the variation in the Ricci curvature tensor,

δ R_{u v}

, can be expressed in terms of the covariant derivative of the difference between two Levi-Civita connections, the Palatini identity:

δ R_{μ ν} = \nabla_{ρ} (δ Γ_{ν μ}^{ρ}) - \nabla_{ν} (δ Γ_{ρ μ}^{ρ})

, where this variation with respect to the inverse metric,

g^{μ ν}

, can be obtained by using the metric compatibility of the covariant derivative:

\nabla_{ρ} g^{μ ν} = 0

[13], as

g^{μ ν} δ R_{μ ν} = \nabla_{ρ} (g^{μ ν} δ Γ_{ν μ}^{ρ} - g^{μ ρ} δ Γ_{σ μ}^{σ})

. Therefore, the cloud-world’s boundary term as a total derivative for any tensor density can be transformed based on Stokes’ theorem as follows

\int_{C}^{} [\frac{g^{μ ν} δ R_{μ ν}}{R}] \sqrt{- g} d^{4} ρ = \frac{1}{R} \int_{C}^{} [\nabla_{ρ} (g^{μ ν} δ Γ_{ν μ}^{ρ} - g^{μ ρ} δ Γ_{σ μ}^{σ})] \sqrt{- g} d^{4} ρ = \frac{1}{R} \int_{C}^{} [\nabla_{μ} H^{μ}] \sqrt{- g} d^{4} ρ = \frac{ϵ}{R} \int_{\partial C}^{} [K] \sqrt{|q|} d^{3} ϱ

(6)

where the bulk scalar curvature,

R

, is left outside the integral transformation as it only acts as a scalar. In addition, a second approach can be applied to the bulk boundary term:

\begin{array}{l} \int_{C}^{} [\frac{{\tilde{g}}^{μ ν} {δ R}_{μ ν}}{R^{2}} R] \sqrt{- g} d^{4} ρ = \int_{C}^{} [\frac{R}{R^{}} \frac{{{\tilde{g}}^{μ ν} δ R}_{μ ν}}{{δ \tilde{g}}^{μ ν} R_{μ ν}} {\tilde{g}}_{μ ν}] {δ \tilde{g}}^{μ ν} \sqrt{- g} d^{4} ρ = \int_{C}^{} [\frac{R}{R^{}} \frac{{δ l n R}_{μ ν}}{{δ l n \tilde{g}}^{μ ν}} {\tilde{g}}_{μ ν}] {δ \tilde{g}}^{μ ν} \sqrt{- g} d^{4} ρ \\ = \int_{C}^{} [\frac{R}{R^{}} \emptyset^{2} {\tilde{g}}_{μ ν}] {δ \tilde{g}}^{μ ν} \sqrt{- g} d^{4} ρ = \int_{C}^{} [\frac{R}{R^{}} \frac{\emptyset^{2}}{Ω^{2}} {\tilde{g}}_{μ ν}] {δ g}^{μ ν} \sqrt{- g} d^{4} ρ \\ = \int_{C}^{} [\frac{R}{R^{}} {\overset{̿}{g}}_{μ ν}] {δ g}^{μ ν} \sqrt{- g} d^{4} ρ \end{array}

(7)

where

\emptyset^{2} = {δ l n R}_{μ ν} / {δ l n \tilde{g}}^{μ ν}

resembles the Ricci flow in a normalized form reflecting the conformal evolution in the extrinsic curvature of the bulk that can be expressed as a function based on Weyl’s transformation as

{\overset{̿}{g}}_{μ ν} = {\tilde{g}}_{μ ν} \emptyset^{2} / Ω^{2} = g_{μ ν} \emptyset^{2}

By using the first approach of boundary terms’ transformations given in Equation (6), the transformed boundary action,

S_{b}

, is

S_{b} = \int_{\partial B}^{} [\frac{ϵ f_{λ}}{2}] \sqrt{- \tilde{q}} (\frac{ϵ}{R} \int_{\partial C}^{} [K] \sqrt{|q|} - \frac{R ϵ}{R^{2}} \int_{\partial C}^{} [K] \sqrt{|q|} + \frac{ϵ}{L} \int_{\partial C}^{} [l] \sqrt{|q|} - \frac{L ϵ}{L^{2}} \int_{\partial C}^{} [l] \sqrt{|q|}) d^{3} ϱ d^{3} ς

(8)

where

K

and

K

are the traces of the cloud-world and the bulk extrinsic curvatures,

l

and

l

are the extrinsic traces of the Lagrangian density on the cloud-world and the bulk boundaries,

q

and

q

are the determinants of their induced metrics respectively, and

ϵ

equals 1 when the normal

{\hat{n}}_{u}

is a spacelike entity and equals -1 when it is a timelike entity.

f_{λ} = F_{λ ρ} J^{ρ}

is the 4D Lorentz force density. The boundary action should hold for any variation and by considering the transformed cloud-world’s boundary term, the variation is

\frac{ϵ}{R} \int_{\partial C}^{} [K_{μ ν} δ q^{μ ν} + q^{μ ν} δ K_{μ ν} + K \frac{δ \sqrt{|q|}}{\sqrt{|q|}} - K \frac{δ R_{}}{R^{}}] \sqrt{|q|} d^{3} ϱ

(9)

where

{K = K}_{μ ν} q^{μ ν}

. By utilizing Jacobi's formula for the determinant differentiation; thus,

δ \sqrt{|q|} = - \sqrt{|q|} q_{μ ν} δ q^{μ ν} / 2

and by utilizing the variation in the metric times the inverse metric,

q^{μ ν} q_{μ ν} = D

q^{μ ν} = - q_{μ ν} δ q^{μ ν} / δ q_{μ ν}

, where

D

is the number of dimensions; thus, the boundary term is

\frac{ϵ}{R} \int_{\partial C}^{} [K_{μ ν} δ q^{μ ν} - \frac{1}{2} K (q_{μ ν} + 2 q_{μ ν} \frac{{δ K}_{μ ν}}{δ q_{μ ν} K_{}} + 2 ϑ^{2} (\frac{R_{μ ν}}{R} - {\tilde{g}}_{μ ν} \frac{{δ R}_{μ ν}}{δ {\tilde{g}}_{μ ν} R}))] δ q^{μ ν} \sqrt{|q|} d^{3} ϱ

(10)

here

{δ K}_{μ ν} / δ q_{μ ν} K = {(δ K}_{μ ν} / K_{μ ν}) (q_{μ ν} / δ q_{μ ν}) = δ l n K_{μ ν} / δ l n q_{μ ν} = \emptyset^{2}

resembles the Ricci flow in a normalized form reflecting the conformal distortion in the boundary over conformal time, which can be expressed as a function according to Weyl’s conformal transformation [14] while the term

R_{μ ν} / R = R_{μ ν} / R_{μ ν} {\tilde{g}}^{μ ν} = {\tilde{g}}_{μ ν} = q_{μ ν} ϑ^{2}

. Consequently, the boundary term is

ϵ \int_{\partial C}^{} [K_{μ ν} - K {\hat{q}}_{μ ν} / 2] δ q^{μ ν} \sqrt{|q|} d^{3} ϱ / R

, where

{\hat{q}}_{μ ν} = q_{μ ν} + 2 q_{μ ν} \emptyset^{2} + 2 q_{μ ν} φ^{2}

is the conformally transformed induced metric on the cloud-world boundary. The same is applied to bulk and Lagrangian boundary terms. The variation in the whole action with renaming the dummy indices is

δ S = (- \int_{B}^{} \begin{matrix} [\frac{1}{2 μ_{0}} (F_{μ λ} F_{ν}^{λ} - \frac{F_{λ ρ} F^{λ ρ}}{4} {\tilde{g}}_{μ ν})] δ {\tilde{g}}^{μ ν} \sqrt{- \tilde{g}} d^{4} σ - \int_{\partial B}^{} [\frac{ϵ}{2} δ f_{ν} / δ {\tilde{q}}^{μ ν}] δ {\tilde{q}}^{μ ν} \sqrt{|\tilde{q}|} d^{3} ς \end{matrix}) (\int_{C}^{} [\frac{R_{μ ν} δ g^{μ ν}}{R} - \frac{R_{μ ν} δ {\tilde{g}}^{μ ν}}{R^{2}} R - \frac{g_{μ ν} δ g^{μ ν}}{2 R} R + \frac{L_{μ ν} δ g^{μ ν}}{L} - \frac{L_{μ ν} δ {\tilde{g}}^{μ ν}}{L^{2}} L - \frac{g_{μ ν} δ g^{μ ν}}{2 L} L] \sqrt{- g} d^{4} ρ) + \int_{\partial C}^{} [\frac{ϵ}{R} (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν}) + \frac{ϵ}{L} (l_{μ ν} - \frac{1}{2} l {\hat{q}}_{μ ν})] {δ q^{μ ν} \sqrt{|q|} d}^{3} ϱ (- \int_{\partial C}^{} [\frac{R ϵ}{R^{2}} (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν}) + \frac{L ϵ}{L^{2}} (l_{μ ν} - \frac{1}{2} l {\hat{q}}_{μ ν})] δ q^{μ ν} \sqrt{|q|} d^{3} ϱ)

(11)

where the outcome of the global part of the action has resembled an extended electromagnetic stress-energy tensor as

T_{μ ν} ≔ (F_{μ λ} F_{ν}^{λ} - F_{λ ρ} F^{λ ρ} {\tilde{g}}_{μ ν} / 4) / μ_{0}) + δ f_{ν} / δ {\tilde{q}}^{μ ν}

denoting energy density exists in the bulk as the vacuum energy density in addition to the 4D Lorentz force density on the bulk boundary.

By applying the principle of stationary action for the Equation (11) while choosing 𝜖 as a time-like entity, the general form of the field equations can be obtained based on the first approach of boundary term transformations as follows

\frac{R_{μ ν}}{R} - \frac{1}{2} \frac{R}{R} g_{μ ν} - \frac{{R R}_{μ ν}}{R^{2}} + \frac{R (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν}) - R (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν})}{R^{2}} = \frac{{\hat{T}}_{μ ν}}{T_{μ ν}}

(12)

These interaction field equations can be interpreted as indicating that the induced curvature,

R

, of the cloud-world over the background (conformal) curvature,

R

, of the bulk equals the ratio of the imposed energy density of the cloud-world and its flux,

{\hat{T}}_{μ ν}

, to the vacuum energy density of the bulk and its flux,

T_{μ ν}

, throughout the expanding/contracting Universe. The field equations feature the following:

${\hat{T}}_{μ ν} = T_{μ ν} - t_{μ ν}$ is an extended conformal stress-energy tensor that is defined by including the energy density and flux of the cloud-world as $T_{μ ν} = ({2 L}_{μ ν} - {L \hat{g}}_{μ ν})$ and the electromagnetic energy flux from its boundary over conformal time as $t_{μ ν} = (2 l_{μ ν} - l {\hat{q}}_{μ ν})$ .
The background conformal curvature term $R R_{μ ν} / R = R {\tilde{g}}_{μ ν} = R g_{μ ν} Ω^{2} = Λ g_{μ ν}$ reflects the cosmological ‘constant’ (parameter). The form in Equation (14) is utilized.
The boundary term given by the extrinsic curvatures of the cloud-world, $K$ , and the bulk, $K$ , is only significant at high energies when the difference between the induced and background curvatures is significant.

The field equations include four contributions that come from the cloud-world’s intrinsic and extrinsic curvatures and the bulk’s intrinsic and extrinsic curvatures. The field equations can be expressed in different forms depending on which contribution is required to be implicit or explicit. By applying the second approach in Equation (7) on the bulk boundary terms, the variation in the action with renaming the dummy indices is

δ S = (- \int_{B}^{} \begin{matrix} [\frac{1}{2 μ_{0}} (F_{μ λ} F_{ν}^{λ} - \frac{F_{λ ρ} F^{λ ρ}}{4} {\tilde{g}}_{μ ν})] δ {\tilde{g}}^{μ ν} \sqrt{- \tilde{g}} d^{4} σ - \int_{\partial B}^{} [\frac{ϵ}{2} δ f_{ν} / δ {\tilde{q}}^{μ ν}] δ {\tilde{q}}^{μ ν} \sqrt{|\tilde{q}|} d^{3} ς \end{matrix}) (\int_{C}^{} [\frac{R_{μ ν}}{R} - \frac{R}{R} {\tilde{g}}_{μ ν} - \frac{R}{2 R} g_{μ ν} - \frac{R}{R} {\overset{̿}{g}}_{μ ν} + \frac{L_{μ ν}}{L} - \frac{L}{L^{}} {\tilde{g}}_{μ ν} - \frac{L}{2 L} g_{μ ν} - \frac{L}{L} {\overset{̿}{g}}_{μ ν}] δ g^{μ ν} \sqrt{- g} d^{4} ρ) (+ \int_{\partial C}^{} [\frac{ϵ}{R} (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν}) + \frac{ϵ}{L} (l_{μ ν} - \frac{1}{2} l {\hat{q}}_{μ ν})] {δ q^{μ ν} \sqrt{|q|} d}^{3} ϱ)

(13)

From Equations (1), (2) and (11),

T_{μ ν} ≔ E_{D} = L = R c^{4} / 8 π G_{R}

is proportional to the fourth power of the speed of light that in turn is directly proportional to the frequency, which can be in harmony with frequency cut-off predictions of vacuum energy density in QFT [15,16]. By applying the principle of stationary action as

R_{μ ν} - \frac{1}{2} R {\hat{g}}_{μ ν} - (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν}) = \frac{8 π G_{R}}{c^{4}} (T_{μ ν} - t_{μ ν})

(14)

where

{{\hat{g}}_{μ ν} = g}_{μ ν} + 2 R_{μ ν} / R + 2 {\overset{̿}{g}}_{μ ν}

or can be simplified to

{{\hat{g}}_{μ ν} = g}_{μ ν} + 2 {\tilde{g}}_{μ ν} + 2 {\overset{̿}{g}}_{μ ν}

is the the conformally transformed metric tensor counting for the contributions of the cloud-world metric,

g_{μ ν},

in addition to the contribution from intrinsic and extrinsic curvatures of the bulk, whereas Einstein spaces are a subclass of conformal spaces [12]. Similarly, the conformably transformed induced metric on the cloud-world’s boundary is

{\hat{q}}_{μ ν} = q_{μ ν} + 2 {\tilde{q}}_{μ ν} + 2 {\overset{̿}{q}}_{μ ν}

. The effective Newtonian gravitational parameter,

G_{R}

, depends on the bulk (background) curvature, which can accommodate the bulk curvature evolution against constant

G_{}

for a special flat spacetime case. The field equations could remove the singularities and satisfy a conformal invariance theory.

3. Evolution of the 4D Relativistic Cloud-World Travelling in the 4D Conformal Bulk

This section visualizes the evolution of the 4D relativistic cloud-words over the conformal space-time of the 4D bulk. Galaxy formation and evolution as a 4D relativistic cloud-world travelling in a curved 4D conformal bulk as preferred by the PL18 release is considered. The entire contribution comes from the boundary term when calculating the black hole entropy using the semiclassical approach [17,18]. By applying this concept on the field equations in Equation (13) and multiplying by the bulk curvature,

R

, as

R_{μ ν} - \frac{1}{2} R g_{μ ν} - \frac{R}{R} R_{μ ν} = \frac{8 π G_{R}}{c^{4}} {\hat{T}}_{μ ν} - \frac{R (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν}) - R (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν})}{R^{2}} = 0

(15)

From Equation (16), the field equations yield

R_{μ ν} = \frac{1}{2} R g_{μ ν} + \frac{R}{R} R_{μ ν} = \frac{1}{2} R (g_{μ ν} + 2 {\tilde{g}}_{μ ν}) = \frac{1}{2} R g_{μ ν} (1 + 2 Ω^{2}) = 0

(16)

where

{\tilde{g}}_{μ ν} = R_{μ ν} / R = R_{μ ν} / R_{μ ν} {\tilde{g}}^{μ ν}

representing the intrinsic curvature of the bulk. The conformally transformed metric,

{\hat{g}}_{μ ν} = g_{μ ν} + 2 {\tilde{g}}_{μ ν} = g_{μ ν} (1 + 2 Ω^{2})

, can be expressed as

d s^{2} = - A (r) (1 + 2 Ω^{2} (r, r)) c^{2} d t^{2} + S^{2} (B (r) (1 + 2 Ω^{2} (r, r)) d r^{2} + r^{2} d θ^{2} + r^{2} {s i n}^{2} θ d ϕ^{2})

(17)

where

A^{}

and

B

are functions of the cloud-world curvature radius

r

, while the conformal function

Ω^{2}

is a function of the bulk curvature radius

r

and it can be influenced by the cloud-world curvature radius.

S^{2}

is a dimensionless conformal scale factor. The derived functions in [19] are

Ω^{2} (r, r) = - \frac{G_{p} M_{p}}{r c^{2}} {(1 - \frac{2 G M}{r c^{2}})}^{- 1}, A (r) = 1 - \frac{2 G M}{r c^{2}}, B (r) = {(1 - \frac{2 G M}{r c^{2}})}^{- 1}

(18)

where the conformal function

Ω^{2}

relies on the gravitational potential of the bulk while its influence is inversely proportional to cloud-world potential. In the case of PI18’s preferred early Universe positive curvature, the gravitational potential of the bulk can be expressed in terms of the early Universe plasma of mass,

M_{p}

, and

r

denoting the radius of curvature of the bulk, where the bulk’s potential decreases with the Universe expansion and vanishes in the flat spacetime background (

r \to \infty)

. The minus sign of

Ω^{2}

reveals a spatial shrinking through evolving in the conformal time. Consequently, the conformally transformed metric

{\hat{g}}_{μ ν} = g_{μ ν} + 2 {\tilde{g}}_{μ ν} = g_{μ ν} (1 + 2 Ω^{2})

d s^{2} = (1 - \frac{r_{s}}{r} - \frac{r_{p}}{r}) (- c^{2} d t^{2} + S^{2} (\frac{d r^{2}}{1 + \frac{{r_{s}}^{2}}{r^{2}} - 2 \frac{r_{s}}{r}} + \frac{r^{2} d θ^{2} + r^{2} {s i n}^{2} θ d ϕ^{2}}{1 - \frac{r_{s}}{r} - \frac{r_{p}}{r}}))

(19)

This metric reduces to the Schwarzschild metric in a flat background (

r \to \infty)

. The metric can be visualized through evolving in the conformal time by using Flamm's approach as

W (r, r) = \mp \int \frac{\sqrt{(\frac{r_{s}}{r} - \frac{{r_{s}}^{2}}{r^{2}} - \frac{r_{p}}{r})}}{{(1 - \frac{r_{s}}{r})}^{}} d r = \mp \sqrt{r_{s} (r - {r_{s}}^{}) - r_{p} \frac{r^{2}}{r}} + O + C

(20)

where

C

is a constant and

O

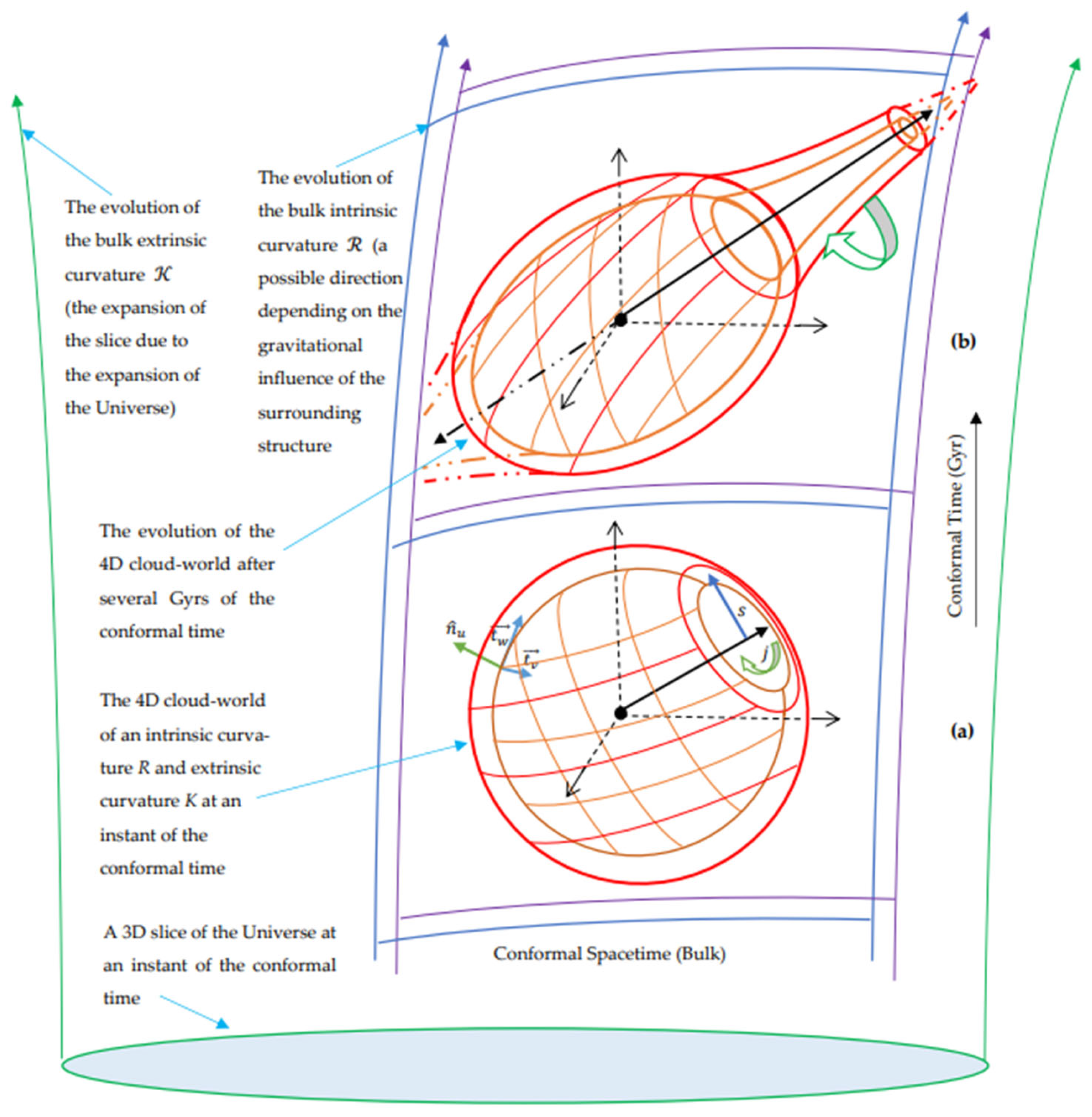
denotes less significant terms. Figure 1 shows this scenario, which reveals that a galaxy forms as a dual forced vortices due to the curved background.

The visualization of Equation (20) as the scenario of the galaxy formation as a dual forced vortices due to the curvature of the background is shown in Figure 1, the evolution of the 4D cloud-world of metric

g_{μ ν}

through its travel and spin in the conformal space-time of the 4D bulk of metric

{\tilde{g}}_{μ ν}

4. Gravitational, Electromagnetic and Quantum Interaction Field Equations

The action in Equation (3) is expanded to investigate the interaction of quantum fields under the influence of the field strength of vacuum energy that is reliant on the curvature of the cloud-world and bulk as follows

S = \int_{B}^{} [\frac{- F_{λ ρ} {\tilde{g}}^{λ γ} F_{γ α} {\tilde{g}}^{ρ α}}{4 μ_{0}}] \sqrt{- \tilde{g}} \int_{C}^{} [\frac{R_{μ ν} g^{μ ν}}{R_{μ ν} {\tilde{g}}^{μ ν}}] \sqrt{- g} \int_{Q}^{} [\frac{p_{μ} p_{v} q^{μ ν}}{π_{μ} π_{v} g^{μ ν}} + \frac{L_{α β} q^{α λ} L_{λ γ} q^{β γ}}{n L_{μ ν} g^{μ ν}}] \sqrt{- q} ϑ^{2} d^{12} σ

(21)

where

L_{α β} L^{α β}

are the Lagrangian densities of two entangled quantum fields of a metric

q_{μ ν}

and four-momentum

p_{μ} p^{ν}

while

π_{μ} π^{v}

are the four-momentum of vacuum energy density (the Lorentz invariant zero-point energy in QFT) of a Lagrangian density

L_{μ ν} g^{μ ν}

and

n

is a proportionality constant. The action should hold for any variation as

δ S = \int_{B}^{} [\begin{matrix} - \frac{F_{λ ρ} F_{γ}^{ρ} δ {\tilde{g}}^{λ γ}}{2 μ_{0}} \\ - \frac{F_{λ ρ} {\tilde{g}}^{λ γ} δ F_{γ}^{ρ}}{2 μ_{0}} + \\ \frac{{F_{λ ρ} F^{λ ρ} \tilde{g}}_{μ ν} δ {\tilde{g}}^{μ ν}}{8 μ_{0}} \end{matrix}] \sqrt{- \tilde{g}} \int_{C}^{} [\begin{matrix} \frac{R_{μ ν} {δ g}^{μ ν} + g^{μ ν} δ R_{μ ν}}{R} \\ - \frac{R_{μ ν} δ {\tilde{g}}^{μ ν} + {\tilde{g}}^{μ ν} δ R_{μ ν}}{R^{2}} \\ - \frac{g_{μ ν} δ g^{μ ν}}{2 R} R \end{matrix} R] \sqrt{- g} \int_{Q}^{} [\begin{matrix} \frac{p_{μ} p_{v} δ q^{μ ν} + q^{μ ν} δ (p_{μ} p_{v})}{π_{μ} π^{ν}} - p_{μ} p^{ν} \frac{(π_{μ} π_{v}) {δ g}^{μ ν} + g^{μ ν} δ (π_{μ} π_{v})}{{(π_{μ} π^{ν})}^{2}} - \frac{p_{μ} p^{ν}}{π_{μ} π^{ν}} \frac{q_{μ ν} δ q^{μ ν}}{2} + \\ 2 \frac{L_{α γ} L_{β}^{γ} δ q^{α λ} + q^{α λ} L_{α β} δ L_{β}^{γ}}{n L} - {2 L}_{α β} L^{α β} \frac{L_{μ ν} {δ g}^{μ ν} + g^{μ ν} δ L_{μ ν}}{n L^{2}} - L_{α β} L^{α β} \frac{q_{μ ν} δ q^{μ ν}}{2 n L} \end{matrix}] \sqrt{- q} ϑ^{2} d^{12} σ

(22)

By considering the boundary term of the quantum cloud:

\int_{Q} q^{μ ν} δ (p_{μ} p_{v}) \sqrt{- q} d^{4} α / π_{μ} π^{ν}

, the variation in the four-momentum

δ p_{μ}

, i.e., the change in the total energy of charged fields enclosed within the quantum cloud boundary

Q

can represent the flow of the four-current

J_{μ}

through the cloud boundary

\partial Q

, where multiplying this current by the four potential that is generated by the current itself,

A_{μ}

, and that externally applied,

B_{μ}

, gives a scalar as follows

δ p_{μ} \equiv δ \sqrt (E / c - p) \equiv (A_{μ} + B_{μ}) J^{μ}

. This deduction is based on the gauge theory. However, the cloud’s volume and its boundary surface should be taken into consideration. The boundary term signifies variation of two entangled quantum clouds

q^{μ ν} δ (p_{μ} p_{v})

; thus

\int_{Q}^{} [\frac{q^{μ ν} δ (p_{μ} p_{v})}{π_{μ} π^{ν}}] \sqrt{- q} d^{4} α = \int_{\partial Q}^{} [ϵ \frac{J_{λ} (A_{ρ} + B_{ρ}) e^{λ γ} J_{α} (A_{γ} + B_{γ}) e^{ρ α}}{π_{μ} π^{ν}}] \sqrt{- e} d^{3} ς

(23)

where

e_{μ ν}

is the induced metric tensor on the quantum cloud boundary. On the other hand, the cloud-world’s boundary term can be transformed as follows

\int_{Q}^{} [\frac{g^{μ ν} δ (π_{μ} π_{v})}{{(π_{μ} π^{ν})}^{2}} p_{μ} p^{ν}] \sqrt{- q} d^{4} α = \int_{Q}^{} [\frac{p_{μ} p^{ν}}{{π_{μ} π^{ν}}^{}} \frac{g^{μ ν} δ (π_{μ} π_{v})}{{δ g}^{μ ν} π_{μ} π_{v}} g_{μ ν}] {δ g}^{μ ν} \sqrt{- q} d^{4} α = \int_{Q}^{} [\frac{p_{μ} p^{ν}}{{π_{μ} π^{ν}}^{}} \frac{δ l n (π_{μ} π_{v})}{{δ l n g}^{μ ν}} g_{μ ν}] {δ g}^{μ ν} \sqrt{- q} d^{4} α = \int_{Q}^{} [\frac{p_{μ} p^{ν}}{{π_{μ} π^{ν}}^{}} {\bar{q}}_{μ ν}] {δ q}^{μ ν} \sqrt{- q} d^{4} α

(24)

where

\emptyset^{2} = δ l n (π_{μ} π_{v}) / {δ l n g}^{μ ν}

resembles the Ricci flow in a normalized form reflecting the conformal evolution of the extrinsic curvature of the cloud-world that can be expressed as a positive function

\emptyset^{2}

according to Weyl’s conformal transformation as

{\bar{q}}_{μ ν} = {\tilde{g}}_{μ ν} ϑ^{2}

;

ϑ^{2} = \emptyset^{2} / Ω^{2}

δ q^{μ ν} = Ω^{2} {δ g}^{μ ν}

The variation in the boundary term in Equation (23) with relabelling

A_{ρ} + B_{ρ}

A_{ρ}

yields

\frac{ϵ}{π_{μ} π^{ν}} \int_{\partial Q}^{} [J_{λ} A_{ρ} J^{ρ} A_{γ} {δ e}^{λ γ} - \frac{1}{2} J_{λ} A_{ρ} J^{ρ} A^{λ} (e_{μ ν} {δ e}^{μ ν} - 2 e^{λ γ} \frac{δ J_{λ} A_{ρ} J^{ρ} A_{γ}}{J_{λ} A_{ρ} J^{ρ} A^{λ}} + 2 \frac{δ π_{μ} π^{ν}}{π_{μ} π^{ν}})] \sqrt{- e} d^{3} ς

(25)

The last two terms resemble the Ricci flow in a normalized form reflecting the conformal distortion in the boundary, which can be expressed as a conformal function according to Weyl’s conformal transformation [14] with renaming the dummy indices as follows

\int_{\partial Q}^{} ϵ [\frac{e_{μ ν} δ (J_{μ} A_{ρ} J^{ρ} A_{ν}) e_{μ ν}}{π_{μ} π^{ν} δ e_{μ ν} (J_{μ} A_{ρ} J^{ρ} A_{ν})}] {δ e}^{μ ν} \sqrt{- e} d^{3} ς = \int_{\partial Q}^{} ϵ [\frac{e_{μ ν} δ l n (J_{μ} A_{ρ} J^{ρ} A_{ν})}{π_{μ} π^{ν} δ l n e_{μ ν}}] {δ e}^{μ ν} \sqrt{- e} d^{3} ς \int_{\partial Q}^{} ϵ [\frac{e_{μ ν} \emptyset^{2}}{π_{μ} π^{ν}}] {δ e}^{μ ν} \sqrt{- e} d^{3} ς

(26)

where

e^{λ γ} = - e_{λ γ} δ e^{λ γ} / δ e_{λ γ}

. Accordingly, the variation in the whole action is

δ S = (- \int_{B}^{} \begin{matrix} [\frac{1}{2 μ_{0}} (F_{μ λ} F_{ν}^{λ} - \frac{F_{λ ρ} F^{λ ρ}}{4} {\tilde{g}}_{μ ν})] δ {\tilde{g}}^{μ ν} \sqrt{- \tilde{g}} d^{4} σ - \int_{\partial B}^{} [\frac{ϵ}{2} δ f_{ν} / δ {\tilde{q}}^{μ ν}] δ {\tilde{q}}^{μ ν} \sqrt{|\tilde{q}|} d^{3} ς \end{matrix}) (\int_{C}^{} [\frac{R_{μ ν}}{R} - \frac{R_{μ ν}}{R^{2}} R - \frac{R {\overset{̿}{g}}_{μ ν}}{R} - \frac{R g_{μ ν}}{2 R}] δ g^{μ ν} \sqrt{- g} d^{4} ρ + \int_{\partial C}^{} [\frac{ϵ}{R} (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν})] {δ q^{μ ν} \sqrt{|q|} d}^{3} ϱ) (\int_{Q}^{} [\frac{p_{μ} p_{v}}{π_{μ} π^{ν}} - \frac{π_{μ} π_{v}}{{(π_{μ} π^{ν})}^{2}} p_{μ} p^{ν} - \frac{p_{μ} p^{ν}}{π_{μ} π^{ν}} \frac{q_{μ ν}}{2}] {δ q}^{μ ν} \sqrt{- q} d^{4} α) + \int_{Q}^{} [\frac{{2 L}_{μ γ} L_{ν}^{γ}}{n L} - \frac{L_{μ ν}}{n L^{2}} L_{α β} L^{α β} - \frac{L_{α β} L^{α β}}{{n L^{}}^{}} {\bar{q}}_{μ ν} - \frac{L_{α β} L^{α β}}{n L} \frac{q_{μ ν}}{2}] δ q^{μ ν} \sqrt{- q} d^{4} α - ϵ \int_{\partial Q}^{} [\frac{J_{μ} A_{ρ} J^{ρ} A_{ν}}{π_{μ} π^{ν}} - \frac{1}{2} \frac{J_{λ} A_{ρ} J^{λ} A^{ρ}}{π_{μ} π^{ν}} e_{μ ν} - \frac{J_{λ} A_{ρ} J^{λ} A^{ρ}}{π_{μ} π^{ν}} \emptyset^{2} e_{μ ν} - \frac{J_{λ} A_{ρ} J^{λ} A^{ρ}}{π_{μ} π^{ν}} ϑ^{2} e_{μ ν}] {δ e}^{μ ν} \sqrt{- e} d^{3} ς (+ ϵ \int_{\partial Q}^{} \frac{p_{μ} p_{v}}{π_{μ} π^{ν}} [\frac{J_{μ} A_{ρ} {J^{ρ} A}_{ν}}{π_{μ} π^{ν}} - \frac{1}{2} \frac{J_{λ} A_{ρ} J^{λ} A^{ρ}}{π_{μ} π^{ν}} e_{μ ν} - \frac{J_{λ} A_{ρ} J^{λ} A^{ρ}}{π_{μ} π^{ν}} \emptyset^{2} e_{μ ν} - \frac{J_{λ} A_{ρ} J^{λ} A^{ρ}}{π_{μ} π^{ν}} ϑ^{2} e_{μ ν}] {δ e}^{μ ν} \sqrt{- e} d^{3} ς)

(27)

By applying the principle of stationary action as

\frac{p_{μ} p_{v}}{π_{μ} π^{ν}} - \frac{1}{2} \frac{p_{μ} p^{ν}}{π_{μ} π^{ν}} ς_{μ ν} - (\frac{{J_{μ} A}_{ρ} {J^{ρ} A}_{ν}}{π_{μ} π^{ν}} - \frac{1}{2} \frac{J_{λ} A_{ρ} J^{λ} A^{ρ}}{π_{μ} π^{ν}} ζ_{μ ν}) + \frac{p_{μ} p^{ν}}{π_{μ} π^{ν}} (\frac{{J^{μ} A}_{μ} {J^{ρ} A}_{ν}}{π_{μ} π^{ν}} - \frac{1}{2} \frac{J^{μ} A^{ν} J^{λ} A^{ρ}}{π_{μ} π^{ν}} e_{μ ν}) = \frac{T_{μ} T_{ν}^{}}{{\bar{T}}_{μ ν}}

(28)

where

T_{μ} T_{ν}^{} = (2 L_{μ α} L_{ν}^{α} - L_{α β} L^{α β} ξ_{μ ν} / 2) / n

are Cauchy stress tensors, extended into four-dimensions as shown in Figure 1, of the deformed configuration of two entangled quantum fields whereas

{\bar{T}}_{μ ν}

is the overall stress-energy tensor of the cloud-world and the bulk.

By separating the two entangled quantum fields with renaming the dummy indices and utilizing the dimensional analysis,

p_{μ} - \frac{1}{2} p^{ν} ς_{μ ν} + \frac{p_{μ}}{π_{μ}} ({J^{μ} A}_{μ} - \frac{1}{2} J^{μ} A^{ν} e_{μ ν}) - (J^{μ} A_{μ} - \frac{1}{2} J^{μ} A^{ν} ζ_{μ ν}) = \frac{1}{2} \frac{ℏ G_{R}}{c^{2} g_{R}} T_{μ}

(29)

where

ς_{μ ν} = q_{μ ν} + 2 {\tilde{q}}_{μ ν}

is the conformally transformed metric tensor counting for the contribution of the quantum cloud’s metric,

q_{μ ν},

and from the intrinsic,

{\tilde{q}}^{μ ν}

, curvature of the cloud-world. Compatibly,

ζ_{μ ν} = e_{μ ν} + 2 {\tilde{e}}_{μ ν} + 2 {\overset{̿}{e}}_{μ ν}

is the conformally induced metric on the quantum cloud boundary.

By using the transformation approach of the cloud-world boundary term in Equation (24), the field equations can be further simplified to

p_{μ} - \frac{1}{2} p^{ν} ξ_{μ ν} - (J^{μ} A_{μ} - \frac{1}{2} J^{μ} A^{ν} ζ_{μ ν}) = \frac{1}{2} \frac{ℏ G_{R}}{c^{2} g_{R}} T_{μ}

(30)

where

ξ_{μ ν} = q_{μ ν} + 2 {\tilde{q}}_{μ ν} + 2 {\overset{̿}{q}}_{μ ν}

is the conformally transformed metric tensor counting for the contribution of the quantum cloud’s metric,

q_{μ ν},

in addition to the contribution from the intrinsic,

{\tilde{q}}^{μ ν}

, and extrinsic,

{\overset{̿}{q}}_{μ ν}

, curvatures of the cloud-world.

ℏ

is the Planck constant and

T_{μ}

denotes the energy density and its flux of the quantum cloud and

g_{R}

is the cloud-world gravitational field strength. The equations in terms of operators are

{\hat{p}}_{μ} ψ - \frac{1}{2} {\hat{p}}^{ν} ξ_{μ ν} ψ - (J^{μ} A_{μ} - \frac{1}{2} J^{μ} A^{ν} ζ_{μ ν}) ψ = \frac{1}{2} \frac{{ℏ G}_{R}}{c^{2} g_{R}} {\hat{T}}_{μ} ψ

(31)

where

{\hat{p}}_{μ}

is the momentum operator and

{\hat{T}}_{μ}

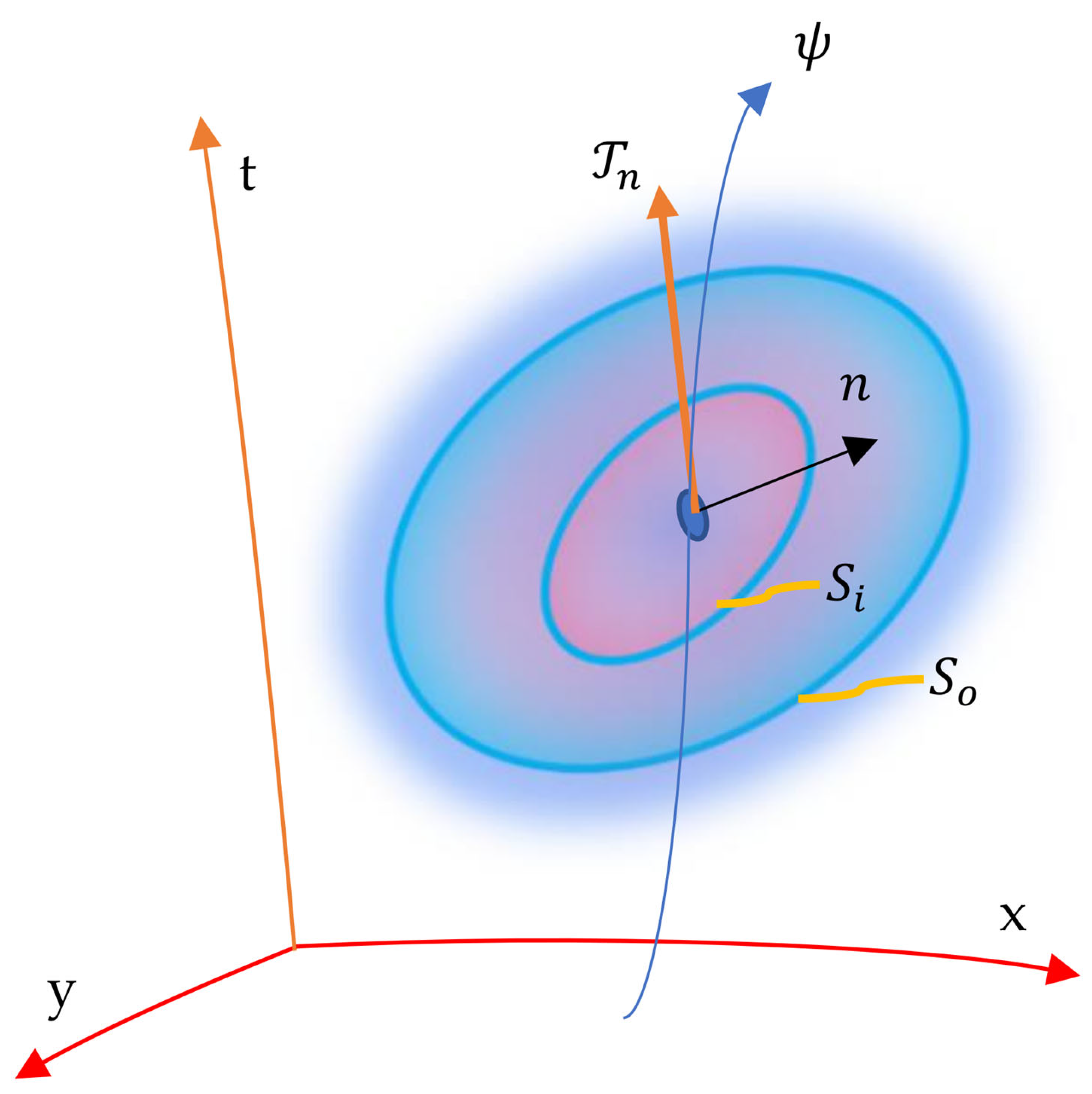
is the stress-energy (gravitational) operator. Figure 2 shows the quantum cloud where

T_{n}

is the traction vector on the inner surface

S_{i}

and

n

is the unit normal vector.

The configuration is given by,

S_{i}

, the inner surface of the quantum cloud that separates its continuum into two portions and encloses an arbitrary inner volume while

S_{o}

is the outer surface of the cloud’s boundary.

Because the gravitational field strength of the cloud-world of mass

M_{}

and at radius

R

g_{R} = M G_{R} / R^{2}

, a plane wavefunction,

ψ = A e^{- i (ω t - k x)}

, can be expressed by utilizing the Equation (31) as

ψ = A e^{- i (R^{2} / 2 M c^{2}) T_{μ} x^{μ}}

, consequently:

i ℏ γ^{μ} \partial_{μ} ψ - \frac{1}{2} i ℏ γ^{μ} \partial^{ν} ξ_{μ ν} ψ - (J^{μ} A_{μ} - \frac{1}{2} J^{μ} A^{ν} ζ_{μ ν}) ψ = \frac{1}{2} \frac{ℏ}{x^{μ}} R \partial_{R} ψ

(32)

where

γ^{μ}

are the Dirac matrices. On the other hand, by using the explicit boundary term of the bulk in Equation (29),

{J^{μ} A}_{μ}

, which could contribute towards the emergence of mass, the equations are

i ℏ γ^{μ} \partial_{μ} ψ - \frac{1}{2} i ℏ γ^{μ} \partial^{ν} ς_{μ ν} ψ - (J^{μ} A_{μ} - \frac{1}{2} J^{μ} A^{ν} ζ_{μ ν}) ψ + ({J^{μ} A}_{μ} - \frac{1}{2} J^{μ} A^{ν} e_{μ ν}) \frac{\partial_{μ} ψ}{\partial_{μ} ϕ} = \frac{1}{2} \frac{ℏ}{x^{μ}} R \partial_{R} ψ

(33)

where

\partial_{μ} ψ / \partial_{μ} ϕ

could represent conventional and vacuum energy spin-spin correlation.

5. Reproducing the Quantum Electrodynamics

The interaction field equations can be utilized to reproduce the quantum electrodynamics using an undeformed configuration of the quantum cloud and its boundary given by the Minkowski’s metric

η_{μ ν}

while disregarding the curvature of the background and its gravitational field strength and using

G

as the Newtonian present valve as

i ℏ γ^{μ} \partial_{μ} ψ - \frac{1}{2} i ℏ γ^{μ} \partial^{ν} η_{μ ν} ψ - (J^{μ} A_{μ} - \frac{1}{2} J^{μ} A^{ν} η_{μ ν}) ψ = \frac{1}{2} \frac{ℏ G}{c^{2} g_{}} T_{μ} ψ

(34)

From Equation (30), the expected value of the quantum cloud’s volume is

V = ℏ G / c g

. This reveals that the quantum cloud’s volume is quantized and is reliant on the gravitational strength. Consequently, for a single electron of mass

m

and by considering it has the same properties from all directions, the stress-energy tensor of the quantum cloud is then

T_{μ} = m c^{2} / V = m {g c}^{3} / ℏ G

. Accordingly, the field equations are

i ℏ γ^{μ} (\frac{\partial_{t}}{c} + \vec{\nabla}) ψ - \frac{1}{2} i ℏ γ^{μ} (\frac{\partial_{t}}{c} - \vec{\nabla}) η_{μ ν} ψ - (J^{μ} A_{μ} - \frac{1}{2} J^{μ} A^{ν} η_{μ ν}) ψ = \frac{1}{2} m c ψ

(35)

By applying the same approach for the boundary term and choosing the quantum metric signature as

(1, - 1, - 1, - 1)

where the four-current density is

J^{μ} = e \bar{ψ} γ^{μ} ψ

, then

\frac{1}{2} i ℏ γ^{μ} (\frac{\partial_{t}}{c} + \vec{\nabla}) ψ - \frac{1}{2} e {\bar{ψ} γ}^{μ} ψ A_{μ} ψ = \frac{1}{2} m c ψ

(36)

where

e

is the charge of a single electron, thus, Equation (36) can be reformatted as

i ℏ γ^{μ} \partial_{μ} ψ - m c ψ = {e γ}^{μ} A_{μ} ψ

(37)

This resembles the Dirac equation and the interaction with the electromagnetic field.

6. Conclusions and Future Works

This study presented interaction field equations in terms of brane-world modified gravity and the perspective of geometrization of the quantum mechanics that count for the curvature of the 4D conformal bulk as the induced gravity on the embedded 4D relativistic clouds in addition to the boundary interactions. The study considered the implied positive curvature of the early Universe y as the curvature of the background or 4D conformal bulk and distinguished it from the localized curvature that is induced into the bulk by the presence of celestial objects that are regarded as ‘relativistic 4D cloud-worlds’. Similarly, the quantum clouds are regarded as propagating ‘4D relativistic quantum clouds’ that are embedded in vacuum energy of a field strength that is reliant on the background curvature as the induced gravity. The interaction field equations were utilized to reproduce the quantum electrodynamics using an undeformed configuration of the quantum cloud. The new boundary term is only significant at high-energy limits such as within black holes. The field equations could remove the singularities and satisfy a conformal invariance theory. Finally, this theoretical work will be tested using observational data in future works.

Acknowledgments

I am grateful to the Preprints Editors Mila Marinkovic and Bojana Djokic for their rapid and excellent processing of a series of preprints during this work development.

Conflicts of Interest

The author declares no conflict of interest.

Appendix A

The conformal time

η_{}

is associated with the scale factor,

a

, as

d t = a d η

. As shown is Figure A.1, the radius of curvature increases through the conformal time as well as the scale factor where this curvature can be expressed as the background curvature or the curvature of the 4D conformal bulk. The preferred curved early Universe

Figure A1. The conformal curvature.

Appendix B

The action in Equation (3) could be possible to be expanded to the non-abelian group to investigate the interaction of quantum chromodynamics fields with the electromagnetic and other quantum fields as follows

S = \int_{B}^{} [\frac{- F_{λ ρ} {\tilde{g}}^{λ γ} F_{γ α} {\tilde{g}}^{ρ α}}{4 μ_{0}}] \sqrt{- \tilde{g}} \int_{C}^{} [\frac{R_{μ ν} g^{μ ν}}{R_{μ ν} {\tilde{g}}^{μ ν}}] \sqrt{- g} \int_{Q}^{} [\frac{p_{μ} p_{v} q^{μ ν}}{π_{μ} π_{v} g^{μ ν}} + \frac{L_{α β}^{σ} q^{α λ} L_{λ γ}^{σ} q^{β γ}}{n L_{μ ν} g^{μ ν}}] \sqrt{- q} {d^{4} α d}^{4} ρ d^{4} σ

(A.2)

where

L_{α β}^{σ} L_{σ}^{α β}

are non-abelian Lagrangian densities of two entangled quantum fields.

References

Randall L and Sundrum R 1999 An alternative to compactification Phys. Rev. Lett. 83 4690–3. [CrossRef]
Gogberashvili M 1999 Four Dimensionality in Non-compact Kaluza-Klein Model Mod. Phys. Lett. A 14 2025–31. [CrossRef]
Randall L and Sundrum R 1999 Large Mass Hierarchy from a Small Extra Dimension Phys. Rev. Lett. 83 3370. [CrossRef]
Vilkovisky G A 1992 Effective action in quantum gravity Class. Quantum Gravity 9 895–903. [CrossRef]
Capozziello S and Lambiase G 2000 Higher-order corrections to the effective gravitational action from Noether symmetry approach Gen. Relativ. Gravit. 32 295–311. [CrossRef]
Garattini R 2013 Distorting general relativity: Gravity’s rainbow and f(R) theories at work J. Cosmol. Astropart. Phys. 2013 017. [CrossRef]
Rickles D 2008 Chapter 7 Who’s Afraid of Background Independence? Philos. Found. Phys. 4 133–52. [CrossRef]
Di Valentino E, et al 2020 Planck evidence for a closed Universe and a possible crisis for cosmology Nat. Astron. 4 196–203. [CrossRef]
Handley W 2021 Curvature tension: Evidence for a closed universe Phys. Rev. D 103 L041301. [CrossRef]
Penrose R 2014 On the Gravitization of Quantum Mechanics 1: Quantum State Reduction Found Phys 44 557–75. [CrossRef]
Landau L D 1986 Theory of Elasticity (Elsevier).
Kozameh C, Newman E, gravitation K T-G relativity and and 1985 undefined 1985 Conformal Einstein spaces Springer. [CrossRef]
S. M. Carroll 2003 Spacetime and Geometry: An Introduction to General Relativity.
Straub W O 2006 Simple Derivation of the Weyl Conformal Tensor.
Rugh S E and Zinkernagel H 2000 The Quantum Vacuum and the Cosmological Constant Problem Stud. Hist. Philos. Sci. Part B - Stud. Hist. Philos. Mod. Phys. 33 663–705. [CrossRef]
Gómez-Valent A 2017 VACUUM ENERGY IN QUANTUM FIELD THEORY AND COSMOLOGY.
Dyer E and Hinterbichler K 2009 Boundary terms, variational principles, and higher derivative modified gravity Phys. Rev. D - Part. Fields, Gravit. Cosmol. 79. [CrossRef]
Brown J D and York J W 1993 Microcanonical functional integral for the gravitational field Phys. Rev. D 47 1420–31. [CrossRef]
Al-Fadhli M B 2021 Galaxy Formation, Evolution and Rotation as a 4D Relativistic Cloud-World Embedded in a 4D Conformal Bulk. Preprints.org.

Figure 1. The hypersphere of a compact core of a galaxy (the red-orange 4D cloud-world) along with its travel and spin through the conformal spacetime (the blue-purple 4D bulk representing the bulk of distinctive curvature evolving over the conformal time.

Figure 2. The deformed configuration of the 4D relativistic quantum cloud of metric

q_{μ ν}

along its travel and spin though the curved background of the cloud-world of metric

g_{μ ν}

Figure 2. The deformed configuration of the 4D relativistic quantum cloud of metric

q_{μ ν}

along its travel and spin though the curved background of the cloud-world of metric

g_{μ ν}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Celestial and Quantum Propagation, Spinning, and Interaction as 4D Relativistic Cloud-Worlds Embedded in a 4D Conformal Bulk: From String to Cloud Theory

Abstract

1. Introduction

2. Gravitational and Electromagnetic Interaction Field Equations

3. Evolution of the 4D Relativistic Cloud-World Travelling in the 4D Conformal Bulk

4. Gravitational, Electromagnetic and Quantum Interaction Field Equations

5. Reproducing the Quantum Electrodynamics

6. Conclusions and Future Works

Acknowledgments

Conflicts of Interest

Appendix A

Appendix B

References

MDPI Initiatives

Important Links

Subscribe