Electro-Optical Properties of Excitons in CdSe Nanoplatelets

1. Introduction

Beginning with the pioneering work by Miller et. al. [1], where the term ’Quantum Confined Stark Effect’ (QCSE) was introduced, the optical response of quantum semiconductor nanostructures (wells, dots, wires) subjected to an interaction with the external constant electric field, has attracted many interest over the past decades, (for a recent review see, for example, [2]). Besides the cognitive value, this attention is motivated by possible technological applications of QCSE, for example, Self-Electrooptic Effect Devices (SEEDs), fast optical switches and modulators, crucial for optical communications (for example, [3]). Recently many works have been done on so-called nanoplatelets (for example, [4,5] and references there in). They are cuboid shaped quantum dots where electrons and holes are confined in three dimensions. Such type of confinement causes differences in electro-optical properties, as compared with quantum wells.

The optical properties of NPLs, including electro-absorption, were subject of extensive experimental and theoretical studies (for example,[6]). However, it seems, that there are few theoretical articles on electro-optical effects. This makes an inspiration to the present work. We will discuss the effects of applied static electric field on NPL with dielectric confinement. The electron-hole Coulomb potential dielectrically screened with the static dielectric constant is adopted, and the valence band structure is considered in the cylindrical approximation, thus separating light- and heavy hole motions. In calculations we use the so-called Real Density Matrix Approach (RDMA) (see Ref. [7] for details about RDMA). This method enables to obtain analytic expressions for the NPLs electro-optical functions.

The paper is organized as follows. In Sect. Section 2 we present the calculation method, based on RDMA. In Section 3 and Section 4 we discuss the case of the electric field applied parallel to the NPL growth axis (z-axis). In the next section we analyze the case of the field applied parallel to the NPL plane, when the exciting electromagnetic wave energy is below the fundamental gap. The case with the field applied parallel to the NPL plane, when the exciting wave energy exceeds the fundamental gap, is discussed in Sect. Section 6. We close with conlusions in Sect. Section 7. Appendices A and B contain calculation details.

2. The Method

The real density matrix approach (RDMA) seems to be especially appropriate for computing the effects of external fields since it includes both the relative motion of the carriers and the center-of-mass motion, where the interaction with the radiation field takes place.

We analyze the weak field limit, where the set of basic RDMA equations (’constitutive equations’) reduces to a set of linearized equations which are the inter-band equations with only the linear source on the right-hand-side retained. The resulting linearized equations for the coherent amplitudes for the electron-hole pair of coordinates ${\mathbf{r}}_1={\mathbf{r}}_h$ and ${\mathbf{r}}_2={\mathbf{r}}_e$ between any pair of bands $\alpha$ (valence band) and b (conduction band) read:

$$-i(\hslash {\partial }_t+{\Gamma }_{\alpha ,b})Y_{12}^{\alpha b}+H_{eh\alpha b}{Y}_{12}^{\alpha b}={\mathbf{M}}_{\alpha ,b}\mathbf{E},$$

(1)

where ${\Gamma }_{\alpha b}=\hslash /T_2^{\alpha b}$ is a phenomenological damping coefficient, E is the electric vector of the impinging electromagnetic wave, and ${\mathbf{M}}_{\alpha b}$ is the inter-band transition dipole density. The notation $Y_{12}^{\alpha ,b}=Y^{\alpha ,b}({\mathbf{r}}_1,{\mathbf{r}}_2)$ is used. When external static fields F (electric field), and B (magnetic field), are applied, the effective-mass two-band Hamiltonian $H_{eh\alpha b}$ with gap $E_{g,\alpha ,b}$ for any pair of bands is

$$\begin{array}{ccc}\hfill & & H_{eh\alpha ,b}=E_{g\alpha }+{\displaystyle \frac{1}{2}}{\underline{\underline{m_e}}}^{-1}{\left({\mathbf{p}}_e-e{\displaystyle \frac{{\mathbf{r}}_e\times \mathbf{B}}{2}}\right)}^2\hfill \\ & & +{\displaystyle \frac{1}{2}}{\underline{\underline{m_h}}}^{-1}{\left({\mathbf{p}}_h+e{\displaystyle \frac{{\mathbf{r}}_h\times \mathbf{B}}{2}}\right)}^2+e\mathbf{F}·({\mathbf{r}}_e-{\mathbf{r}}_h)\hfill \\ & & +V_{\mathrm{conf}}({\mathbf{r}}_e,{\mathbf{r}}_h)-{\displaystyle \frac{e^2}{4\pi {ϵ}_0{ϵ}_1|{\mathbf{r}}_e-{\mathbf{r}}_h|}},\hfill \end{array}$$

(2)

choosing appropriate values of $E_{g,\alpha }$ and the effective mass tensors ${\underline{\underline{m}}}_{e,h}$, and $V_{\mathrm{conf}}$ are the surface potentials for electrons and holes. The coherent amplitudes $Y_{12}^{\alpha b}$ determine the total NPL polarization

$$\mathbf{P}\mathbf{R}=2\sum _{\alpha ,\dots ,b,\dots }\mathrm{Re}{\mathbf{M}}_{cv}\left(r\right)Y^{cw}(\mathbf{R},\mathbf{r}),$$

(3)

where the summation includes all allowed excitonic transitions between the valence $(w=\alpha ,\beta \dots )$ and conduction $(c=a,b,\dots )$ bands, R and r are the electron-hole pair center-of-mass and the relative coordinate, respectively. The equations (1)-(3) connect the polarization to the electric field. In addition, the electric field must obey the Maxwell equation

$$-c^2{ϵ}_0\nabla \times \nabla \times \mathbf{E}-{ϵ}_0{ϵ}_1\ddot{\mathbf{E}}=\ddot{\mathbf{P}},$$

(4)

where the polarization is given in Eq.(3), and ${ϵ}_1$ is the dielectric constant of the material contained inside the NPL.

The RDMA scheme, described by Eqs. (1)-(4), is solved in the following steps.

1.

We solve Eq. (1), with the Hamiltonian (2), to obtain the excitonic amplitudes $Y_{12}^{\alpha ,b}$.

2.

Having calculated the amplitudes, we use them in Eq. (3) and, in the long wave approximation, determine the NPL susceptiblity.

3.

The so obtained susceptibility enables to calculate the optical functions (electro-reflectivity, transmissivity, absorption).

We consider dipole-allowed transitions at the $\Gamma$ point of the Brillouin zone within a simple two-band model. Further, we assume that the electric field E is linearly polarized with a component $E_x$ and that the vector M has a non-vanishing component $M_x\left(\mathbf{r}\right)$ in the same direction. For the quantities $Y,\mathbf{E}\mathrm{and}\mathbf{P}$ the center-of-mass dependence is of the plane-wave form $exp(i{k}_{z}Z-i\omega t)$. As in previous works, in the NPL internal region we separate the exciton center-of-mass and relative motion, and consider the case $\mathbf{B},\mathbf{F}\Vert z$. This assumption forces the cylindrical symmetry, and the Hamiltonian (2) is transformed into the form

$$\begin{array}{ccc}\hfill H& =& E_g+{\displaystyle \frac{p_{hz}^2}{2m_{hz}}}+V_h\left(z_h\right)+{\displaystyle \frac{p_{ez}^2}{2m_{ez}}}+V_e\left(z_e\right)\hfill \\ & +& {\displaystyle \frac{1}{2{\mu }_{\Vert }}}({\mathbf{p}}_{e\rho }^2+{\mathbf{p}}_{e\rho }^2)+V_e\left({\rho }_e\right)+V_h\left({\rho }_h\right)\hfill \\ & +& {\displaystyle \frac{1}{8}}{\mu }_{\Vert }{\omega }_c^2{\rho }^2+{\displaystyle \frac{e}{2{\mu }_{\Vert }^{\prime }}}B{\mathcal{L}}_z+eF(z_e-z_h)\hfill \\ & -& {\displaystyle \frac{e}{M_{\Vert }}}{\mathbf{P}}_{\Vert }·(\mathbf{\rho }\times \mathbf{B})-{\displaystyle \frac{e^2}{\sqrt{{\rho }^2+{(z_e-z_h)}^2}}},\hfill \end{array}$$

(5)

where the cyclotron frequency is

$${\omega }_c={\displaystyle \frac{eB}{{\mu }_{\Vert }}},$$

(6)

and the reduced mass ${\mu }_{\Vert }^{\prime }$ is defined as

$${\displaystyle \frac{1}{{\mu }_{\Vert }^{\prime }}}={\displaystyle \frac{1}{m_{e\Vert }}}-{\displaystyle \frac{1}{m_{h\Vert }}}.$$

(7)

The operator ${\mathcal{L}}_z$ is the z-component of the angular-momentum operator. We must solve the constitutive equations with the above Hamiltonian to obtain the polarization and finally the optical functions. Since we aim to analyze the electro-optical effects, all terms in the Hamiltonian (5) related to the magnetic field will be put equal zero.

3. The Electric Field Parallel to the Z-Axis

We will discuss the changes of the NPL optical response when a constant external electric field F is applied in the z-direction. We consider a CdSe nanoplatelet of cuboid shape, located at the $z=0$ plane, and with the barriers located at $x=\pm L_x/2,y=\pm L_y/2,z=\pm L_z/2$. Typically, for NPLs the vertical dimension (’thickness’) $L_z$ is of the order of a few monolayers, which, for example, in the below considered CdSe NPLs, means 1-2 nm. The lateral extension is much larger, mostly several dozen nm. As was merely proved, the small vertical extension forces changes in electron and hole effective masses. They increase with decreasing thickness. This situation is illustrated in Table Section 3. We consider the response of the NPL to a normally incident electromagnetic wave, linearly polarized in the x-direction

$${\mathbf{E}}_i(z,t)={\mathbf{E}}_{i0}exp(i{k}_{0}z-i\omega t),k_0={\displaystyle \frac{\omega }{c}}.$$

(8)

Table 1. Masses , reduced masses, Rydberg energies, Luttinger parameters, and coherence radii, from Ref. [5]. Lengths in nm, masses in free electron mass $m_0$, energies in meV.

Parameter	3ML	4ML	5ML
$L_z$	1	1.33	1.67
$m_{ez}$	0.2567	0.2015	0.1635
$m_{e\Vert }$	0.3208	0.2519	0.2044
$a_{ez}^{*}$	1.236	1.575	1.94
$m_{hzH}$	1.1925	0.9754	0.8153
$m_{h\Vert H}$	0.4957	0.4337	0.3879
$m_{hzL}$	0.4149	0.3659	0.3302
$m_{h\Vert L}$	0.8121	0.6887	0.5963
${\mu }_{zH}$	0.2112	0.167	0.1362
${\mu }_{zL}$	0.1586	0.13	0.1094
$a_{ez}^{*}$	1.236	1.575	1.94
$a_{e\Vert }^{*}$	0.989	1.26	1.55
$a_{hzH}^{*}$	0.266	0.325	0.389
$a_{hzL}^{*}$	0.765	0.867	0.961
$E_{ez}$	918.13	686.81	530
$E_{hzH}$	221.13	162.1	130
$E_{hzL}$	579.53	352.26	277.58
$E_{zH}$	1139.4	816.8	636
$E_{zL}$	1497.4	1036.5	783.1
$R_{ez}^{*}$	96.98	76.12	61.77
$R_{\Vert H}^{*}$	73.58	60.20	51.28
$R_{hzH}^{*}$	450.5	368.5	308
$R_{hzL}^{*}$	156.74	138.23	124,66
$R_{\Vert L}^{*}$	86.88	69.67	57.49
${\gamma }_1$	1.6243	1.8789	2.1062
${\gamma }_2$	0.3929	0.4269	0.4488
${\rho }_{0H}$	0.20	0.18	0.17
${\rho }_{0L}$	0.22	0.19	0.18

Table 1. Masses , reduced masses, Rydberg energies, Luttinger parameters, and coherence radii, from Ref. [5]. Lengths in nm, masses in free electron mass $m_0$, energies in meV.

Parameter	3ML	4ML	5ML
$L_z$	1	1.33	1.67
$m_{ez}$	0.2567	0.2015	0.1635
$m_{e\Vert }$	0.3208	0.2519	0.2044
$a_{ez}^{*}$	1.236	1.575	1.94
$m_{hzH}$	1.1925	0.9754	0.8153
$m_{h\Vert H}$	0.4957	0.4337	0.3879
$m_{hzL}$	0.4149	0.3659	0.3302
$m_{h\Vert L}$	0.8121	0.6887	0.5963
${\mu }_{zH}$	0.2112	0.167	0.1362
${\mu }_{zL}$	0.1586	0.13	0.1094
$a_{ez}^{*}$	1.236	1.575	1.94
$a_{e\Vert }^{*}$	0.989	1.26	1.55
$a_{hzH}^{*}$	0.266	0.325	0.389
$a_{hzL}^{*}$	0.765	0.867	0.961
$E_{ez}$	918.13	686.81	530
$E_{hzH}$	221.13	162.1	130
$E_{hzL}$	579.53	352.26	277.58
$E_{zH}$	1139.4	816.8	636
$E_{zL}$	1497.4	1036.5	783.1
$R_{ez}^{*}$	96.98	76.12	61.77
$R_{\Vert H}^{*}$	73.58	60.20	51.28
$R_{hzH}^{*}$	450.5	368.5	308
$R_{hzL}^{*}$	156.74	138.23	124,66
$R_{\Vert L}^{*}$	86.88	69.67	57.49
${\gamma }_1$	1.6243	1.8789	2.1062
${\gamma }_2$	0.3929	0.4269	0.4488
${\rho }_{0H}$	0.20	0.18	0.17
${\rho }_{0L}$	0.22	0.19	0.18

The calculations of electro-optical properties become much simpler when we consider an NPL of thickness $L_z$, with parabolic confinement potentials in the form of an harmonic oscillator potential

$$V_{\mathrm{conf}}={\displaystyle \frac{1}{2}}{m}_{ez}{\omega }_{ez}^2{z}_e^2+{\displaystyle \frac{1}{2}}{m}_{hz}{\omega }_{hz}^2{z}_h^2,$$

(9)

where the energies $\hslash {\omega }_{ez},\hslash {\omega }_{hz}$ correspond to the electron and hole barriers. When concerning the in-plane electron and hole motion, we retain the assumptions presented in Ref. [5], where the cuboidal NPL is replaced by a cylinder of hight $L_z$, and a radius $r_{eff}=\sqrt{L_x{L}_y/\pi }.$ We neglect the motion of the hole, and the electron moves under the influence of the Coulomb attraction with the hole located at the point $\rho =0,z=0$, and the confinement potential

$$\begin{array}{ccc}\hfill & & V_e\left({\rho }_e\right)=\left\{\begin{array}{c}0for{\rho }_e\le R,\hfill \\ \infty for{\rho }_e>R.\hfill \end{array}\right.\hfill \end{array}$$

(10)

where we put $R=r_{eff}$. In this case, and with the applied constant electric field, the NPL Hamiltonian has the form

$$\begin{array}{ccc}\hfill H& =& E_g+H_{m_{ez},{\omega }_{ez}}^{\left(1D\right)}\left(z_e\right)+H_{m_{hz},{\omega }_{hz}}^{\left(1D\right)}\left(z_h\right)\hfill \\ & +& H_{\mathrm{Coul}}^{\left(2D\right)}\left(\mathbf{\rho }\right)+eF(z_e-z_h)\hfill \\ & +& {\displaystyle \frac{e^2}{4\pi {ϵ}_0{ϵ}_b{\rho }_e}}-{\displaystyle \frac{e^2}{\sqrt{{\rho }_e^2+{(z_e-z_h)}^2}}},\hfill \end{array}$$

(11)

containing the one-dimensional oscillator Hamiltonians

$$H_{m,\omega }^{\left(1D\right)}\left(z\right)={\displaystyle \frac{p_z^2}{2m}}+{\displaystyle \frac{1}{2}}{m}_z{\omega }^2{z}^2,$$

(12)

and the two-dimensional Coulomb Hamiltonian

$$H_{\mathrm{Coul}}^{\left(2D\right)}\left(\mathbf{\rho }\right)={\displaystyle \frac{{\mathbf{p}}_{\Vert }^2}{2m_{e\Vert }}}-{\displaystyle \frac{e^2}{4\pi {ϵ}_0{ϵ}_b{\rho }_e}}+V_e\left({\rho }_e\right).$$

(13)

Using the substitution

$$\begin{array}{ccc}\hfill & & {\zeta }_e=z_e+z_{0e},z_{0e}={\displaystyle \frac{eF}{m_{ez}{\omega }_{ez}^2}},\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& & {\zeta }_h=z_h-z_{0h},z_{0h}={\displaystyle \frac{eF}{m_{hz}{\omega }_{hz}^2}},\hfill \end{array}$$

(15)

we obtain the QW Hamiltonians in the form

$$\begin{array}{ccc}\hfill H& =& E_g+H_{m_{ez},{\omega }_{ez}}^{\left(1D\right)}\left({\zeta }_e\right)+H_{m_{hz},{\omega }_{hz}}^{\left(1D\right)}\left({\zeta }_h\right)\hfill \\ & -& {\displaystyle \frac{{\left(eF\right)}^2}{2m_{ez}{\omega }_{ez}^2}}-{\displaystyle \frac{{\left(eF\right)}^2}{2m_{hz}{\omega }_{hz}^2}}+H_{\mathrm{Coul}}^{\left(2D\right)}\left({\rho }_e\right)\hfill \\ & +& {\displaystyle \frac{e^2}{4\pi {ϵ}_0{ϵ}_b{\rho }_e}}-{\displaystyle \frac{e^2}{\sqrt{{\rho }_e^2+{(z_e-z_h)}^2}}}.\hfill \end{array}$$

(16)

With the above QW Hamiltonians we can solve the constitutive equations

$$(H-\hslash \omega -i\Gamma )Y=\mathbf{M}\mathbf{E}.$$

(17)

We use the long wave approximation, and seek solutions in the form

$$\begin{array}{ccc}\hfill Y({\rho }_e,{\zeta }_e,{\zeta }_h)& =& E\left(Z\right)\sum _{jm}{Y}_{0,jm}{\psi }_{jm}\left({\rho }_e\right)\hfill \\ & \times & {\psi }_{{\alpha }_{ez}}^{\left(1D\right)}\left({\zeta }_e\right){\psi }_{{\alpha }_{hz}}^{\left(1D\right)}\left({\zeta }_h\right),\hfill \end{array}$$

(18)

where ${\psi }_{jm}$ are the eigenfunctions of the Hamiltonian (13),

$$\begin{array}{ccc}\hfill {\psi }_{jm}(\xi ,\varphi )& =& C{\xi }^{\left|m\right|}{e}^{-\xi /2}\hfill \\ & \times & M\left(m+{\displaystyle \frac{1}{2}}-\eta ,2\left|m\right|+1;\xi \right){\displaystyle \frac{e^{im\varphi }}{\sqrt{2\pi }}}.\hfill \end{array}$$

(19)

Here j and m are the principal and magnetic quantum numbers of the 2-dimensional excitonic state, $M(a,b,z)$ is the confluent hypergeometric function (notation by Ref. [8]), $\rho ={\rho }_e/a_{e\Vert }^{*}$, and we used notation

$$\begin{array}{ccc}\hfill \eta & =& {\displaystyle \frac{2}{\kappa }},\xi =\kappa \rho ,a_{e\Vert }^{*}={\displaystyle \frac{m_0}{m_{e\Vert }}}{ϵ}_1{a}_B^{*},\hfill \\ \hfill {\kappa }^2& =& -4{\displaystyle \frac{2m_{e\Vert }}{{\hslash }^2}}{a}_{e\Vert }^{*2}E=4/ϵ,\hfill \end{array}$$

where $m_0$ is the free electron mass, and $a_B^{*}=0.0529\mathrm{nm}$ the hydrogen Bohr radius. The functions ${\psi }_{{\alpha }_z,N}^{\left(1D\right)}\left(z\right)$ (N=0,1,...) are the quantum oscillator eigenfunctions of the Hamiltonian (12),

$$\begin{array}{ccc}\hfill & & {\psi }_{{\alpha }_z,N}^{\left(1D\right)}\left(z\right)={\pi }^{-1/4}\sqrt{{\displaystyle \frac{{\alpha }_z}{2^{N}N!}}}{H}_N\left({\alpha }_{z}z\right)e^{-{\displaystyle \frac{{\alpha }_z^2}{2}}{z}^2},\hfill \\ & & {\alpha }_z=\sqrt{{\displaystyle \frac{m_z{\omega }_z}{\hslash }}},\hfill \end{array}$$

(20)

$H_N\left(x\right)$ being Hermite polynomials $(N=0,1,\dots )$. We consider in detail the lowest confinement state $N_e=N_h=0$.

For further calculations we must define the dipole density M. Having in mind the experiments from Refs. [6], and [4], where resonances due to 1SH and 1SL excitons were observed, we choose M in the form

$${\mathbf{M}}_{S,\alpha }\left(\mathbf{r}\right)={\mathbf{M}}_{0,S\alpha }{N}_{S\alpha }exp(-\rho /{\rho }_{0\alpha })\delta (z_e-z_h),$$

(21)

where ${\rho }_{0\alpha }$ are the so-called coherence radii

$$\begin{array}{ccc}\hfill {\rho }_{0H}& =& \sqrt{{\displaystyle \frac{R_{\Vert H}^{*}}{E_g}}},{\rho }_{0L}=\sqrt{{\displaystyle \frac{R_{\Vert L}^{*}}{E_g}}},\hfill \end{array}$$

(22)

and $N_{S,\alpha }$ are normalization constants

$$N_{S,\alpha }\underset{0}{\overset{\mathcal{R}}{\int }}\rho exp(-\rho /{\rho }_{0\alpha })d\rho =1.$$

(23)

The integrated dipole strengths ${\mathbf{M}}_{0,S\alpha }$ for CdSe NPLs od various sizes, are given in Ref. [5]

Inserting the series (18) into constitutive equation (17) we calculate the expansion coefficients $Y_{0,jm}$. The so obtained exciton amplitudes are used in Eq. (3), giving the NPL polarization and, by relation $\mathbf{P}={ϵ}_0\chi \mathbf{E}$, the susceptibility $\chi$

$$\begin{array}{ccc}\hfill \chi & =& {\displaystyle \frac{2}{{ϵ}_0}}\sum {\displaystyle \frac{|\langle M|{\psi }_{jm}\left({\rho }_e\right){\psi }_{{\alpha }_{ez}}^{\left(1D\right)}\left({\zeta }_e\right){\psi }_{{\alpha }_{hz}}^{\left(1D\right)}\left({\zeta }_h\right)\rangle {|}^2}{E_{res,jm}-\hslash \omega -i\Gamma }},\hfill \end{array}$$

(24)

where the summation runs over the excitonic transitions taken into account. The exciton resonance energies are defined by the relation

$$\begin{array}{ccc}\hfill E_{res,jm}& =& E_g+W_{0e}+W_{0h}+E_{jm}\hfill \\ & +& 〈{\displaystyle \frac{2}{\rho }}〉+\Delta E+E_{b,jm},\hfill \end{array}$$

(25)

where

$$\begin{array}{ccc}\hfill W_{0e,h}& =& {\displaystyle \frac{1}{2}}\hslash {\omega }_{e,hz},\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill 〈{\displaystyle \frac{2}{\rho }}〉& =& 2R_{e\Vert }^{*}\underset{0}{\overset{R}{\int }}d\rho {\psi }_{jm}^2\left(\rho \right),\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill \Delta E& =& -{\displaystyle \frac{{\left(eF\right)}^2}{2m_{ez}{\omega }_{e{z}^2}}}-{\displaystyle \frac{{\left(eF\right)}^2}{2m_{hz}{\omega }_{hz}^2}},\hfill \end{array}$$

(28)

and $E_{jm}$ are the eigenvalues of the operator (13), $\Delta E$ is the Stark shift. The excitonic binding energy $E_{b,jm}$ is defined as

$$\begin{array}{ccc}\hfill E_{b,jm}& =& -2R_{e\Vert }^{*}\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}d{z}_{e}d{z}_h{\left({\psi }_{{\alpha }_{ez}}^{\left(1D\right)}\right)}^2\left(z_e\right){\left({\psi }_{{\alpha }_{hz}}^{\left(1D\right)}\right)}^2\left(z_h\right)\hfill \\ & \times & \underset{0}{\overset{R}{\int }}{\displaystyle \frac{{\psi }_{jm}^2\left(\rho \right)\rho d\rho }{\sqrt{{\rho }^2+{(z_e-z_h)}^2}}}.\hfill \end{array}$$

(29)

4. Results of Specific Calculations for $F\Vert z$

We performed calculations for 3 CdSe nanoplatelets analyzed in Ref.[4], with sizes

• 3ML $1.0\times 56\times 41\mathrm{nm}$,,
• 4ML $1.33\times 17\times 15\mathrm{nm}$,
• 5 ML $1.67\times 30\times 11\mathrm{nm}$.

All the parameters used in the calculations are collected in Table 1. We have calculated the Stark shift, depending on the lateral dimension $L_z$, and the applied field strength F, obtaining the result

$$\Delta E_{H,L}=-C{\left({\displaystyle \frac{F}{F_{IB}}}\right)}^2{M}_{zH,L}{L}_z^4,$$

(30)

where

$$C={\displaystyle \frac{R_B^{*3}}{{\left(556\right)}^2}}=8.137\times {10}^6,$$

(31)

and $M_{zH,L}=m_{ez}+m_{hzH,L}$ is the total exciton mass in the z-direction. The quantity $F_{IB}$ represents the ionization field strength

$$F_{IB}=2.57\times {10}^6{\displaystyle \frac{\mathrm{kV}}{\mathrm{cm}}}.$$

(32)

The details of the calculations are given in Appendix A

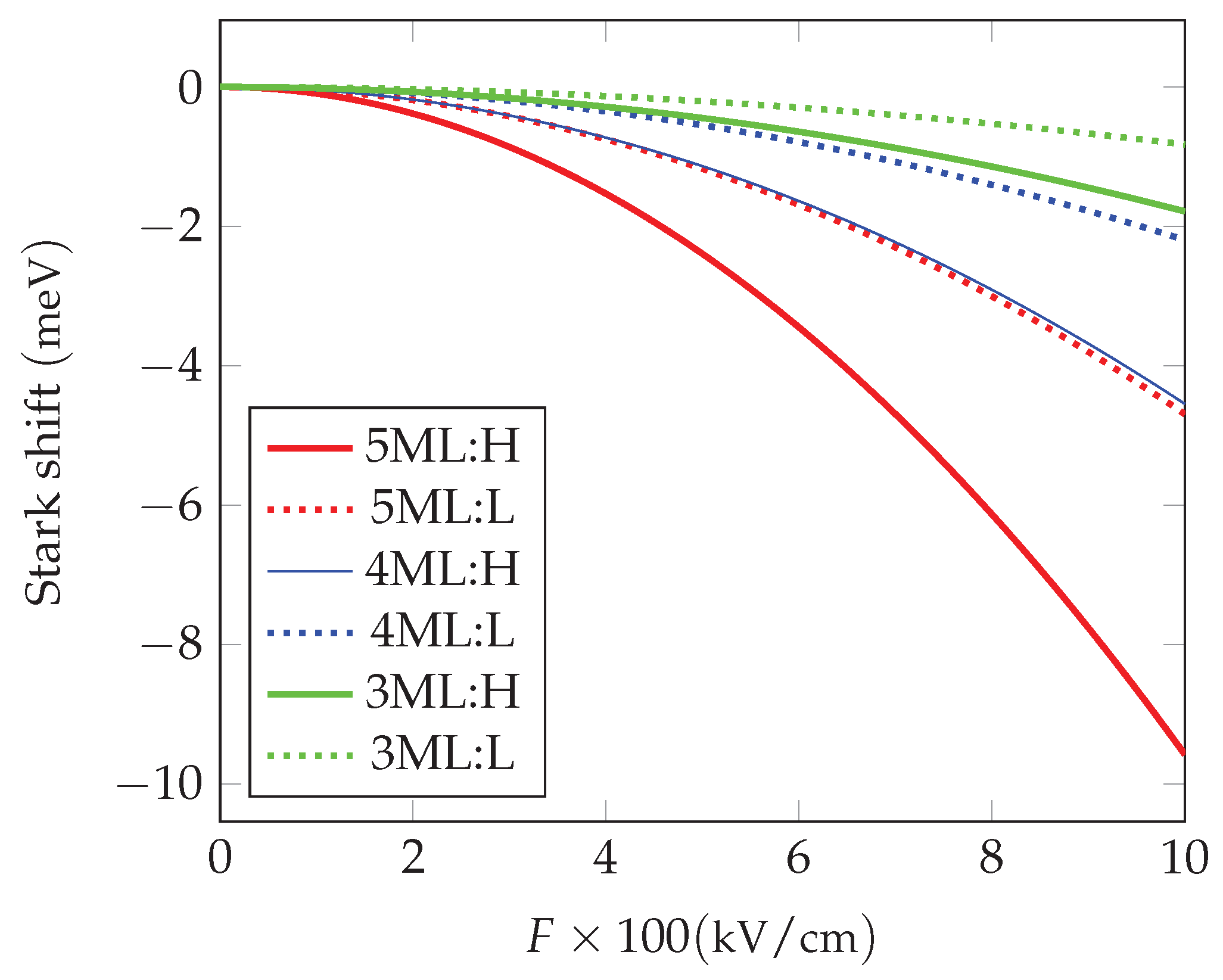
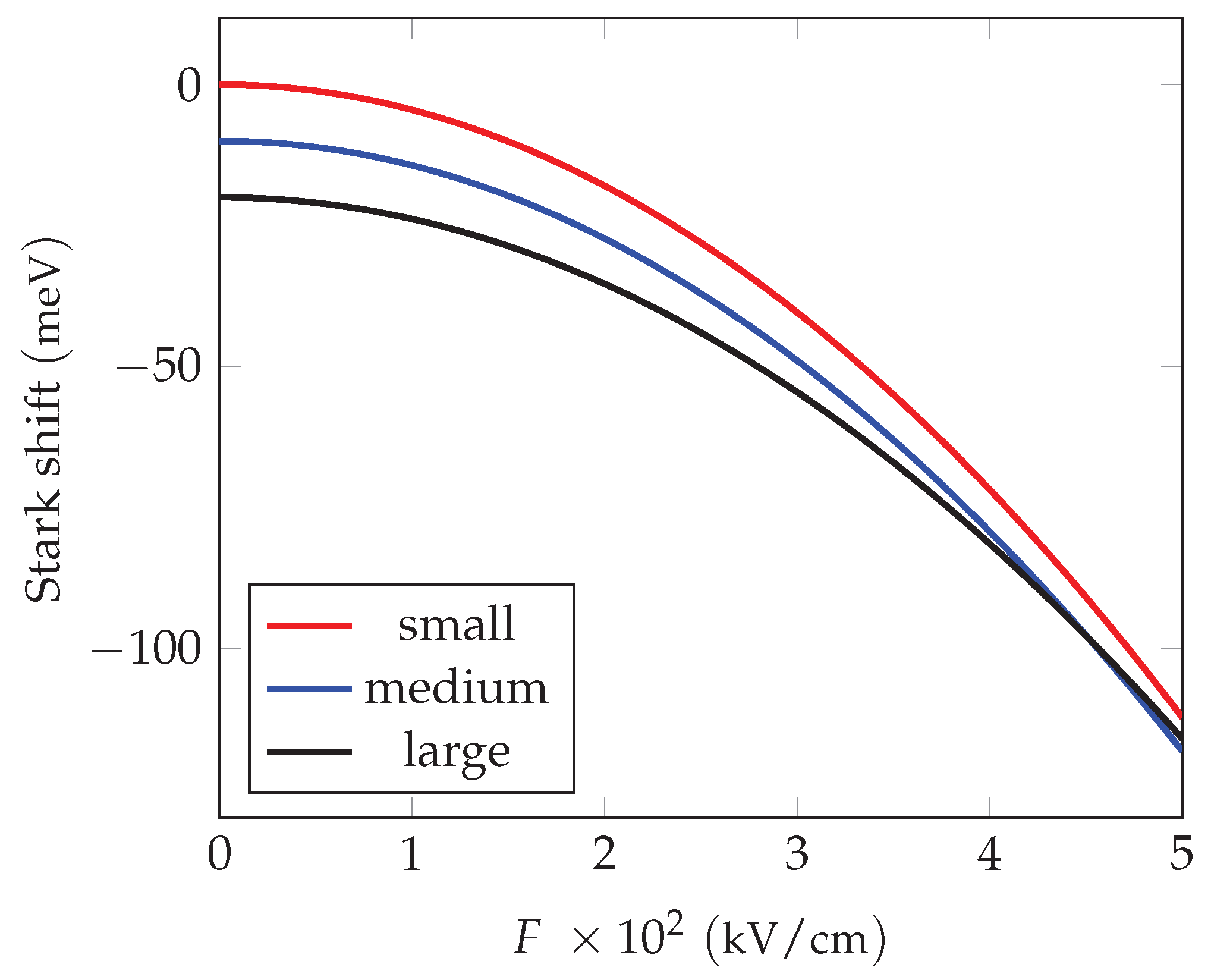
Figure 1. Stark shift for CdSe NPLs and heavy-hole excitons (solid lines), and light-hole excitons (dotted lines)

Figure 1. Stark shift for CdSe NPLs and heavy-hole excitons (solid lines), and light-hole excitons (dotted lines)

Using the eigenfunctions (20), and the dipole densities (21), we calculated the oscillator strengths (the part related to the vertical motion), obtaining the expression

$$f_{L_z,F}=exp\left(-1.15M_z{L}_z^2·{10}^{-4}{x}^2\right).$$

(33)

Table 2. Sizes and exciton states energies, transition matrix elements M, oscillator strengths, and damping parameters, for disks analyzed by Brumberg et al. [4], lengths in nm, matrix elements M in $e·\mathrm{nm}$, energies in meV, the energy gap at room temperature 1750 meV, notation: 1: $56\times 41,3\mathrm{ML}$, 2: $17\times 15,4\mathrm{ML}$ 3: $30\times 11,5\mathrm{ML}$, 4: $17\times 15,4\mathrm{ML}$, 5: $30\times 11,4\mathrm{ML}$, 6: $56\times 41,4\mathrm{ML}$

lat. extension	1	2	3	4	5	6
$a_{e\Vert }^{*}$	1	1.26	1.553	1.26	1.26	1.26
$r_{\mathrm{eff}}$	27	9	10.25	9	10.25	27
$\mathcal{R}$	27	7.15	6.6	7.15	8.134	21.455
1SH	2640.44	2382.2	2242.2	2540	2537.7	2531
$\lambda$	469.2	520.5	553	488.6	489	490.4
1SL	3178.4	2745.25	2498.4	2761	2758.7	2752
$\lambda$	390	451.68	496.31	449.5	449.8	450.9
$M_{0SH}$	0.625	0.22	0.19	0.22	0.19	0.625
$f_{SH}$	4.16	4.77	5.47	4.77	4.6	4.96
$f_{SL}$	3.72	3.75	4.77	3.75	4.44	4.41
${\Gamma }_{SH}$	4.63	2.53	2.86	2.53	2.86	2.86

Table 2. Sizes and exciton states energies, transition matrix elements M, oscillator strengths, and damping parameters, for disks analyzed by Brumberg et al. [4], lengths in nm, matrix elements M in $e·\mathrm{nm}$, energies in meV, the energy gap at room temperature 1750 meV, notation: 1: $56\times 41,3\mathrm{ML}$, 2: $17\times 15,4\mathrm{ML}$ 3: $30\times 11,5\mathrm{ML}$, 4: $17\times 15,4\mathrm{ML}$, 5: $30\times 11,4\mathrm{ML}$, 6: $56\times 41,4\mathrm{ML}$

lat. extension	1	2	3	4	5	6
$a_{e\Vert }^{*}$	1	1.26	1.553	1.26	1.26	1.26
$r_{\mathrm{eff}}$	27	9	10.25	9	10.25	27
$\mathcal{R}$	27	7.15	6.6	7.15	8.134	21.455
1SH	2640.44	2382.2	2242.2	2540	2537.7	2531
$\lambda$	469.2	520.5	553	488.6	489	490.4
1SL	3178.4	2745.25	2498.4	2761	2758.7	2752
$\lambda$	390	451.68	496.31	449.5	449.8	450.9
$M_{0SH}$	0.625	0.22	0.19	0.22	0.19	0.625
$f_{SH}$	4.16	4.77	5.47	4.77	4.6	4.96
$f_{SL}$	3.72	3.75	4.77	3.75	4.44	4.41
${\Gamma }_{SH}$	4.63	2.53	2.86	2.53	2.86	2.86

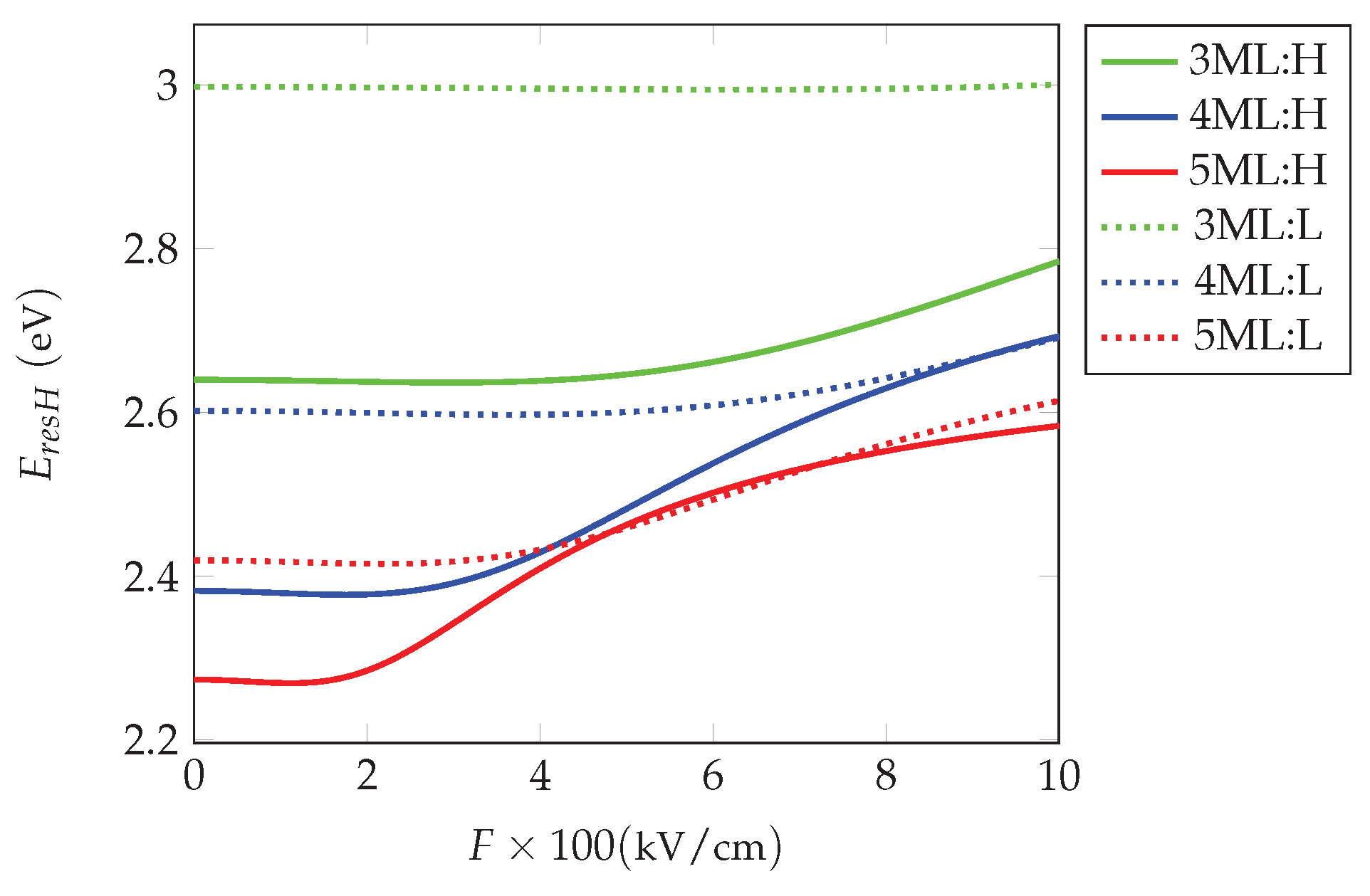
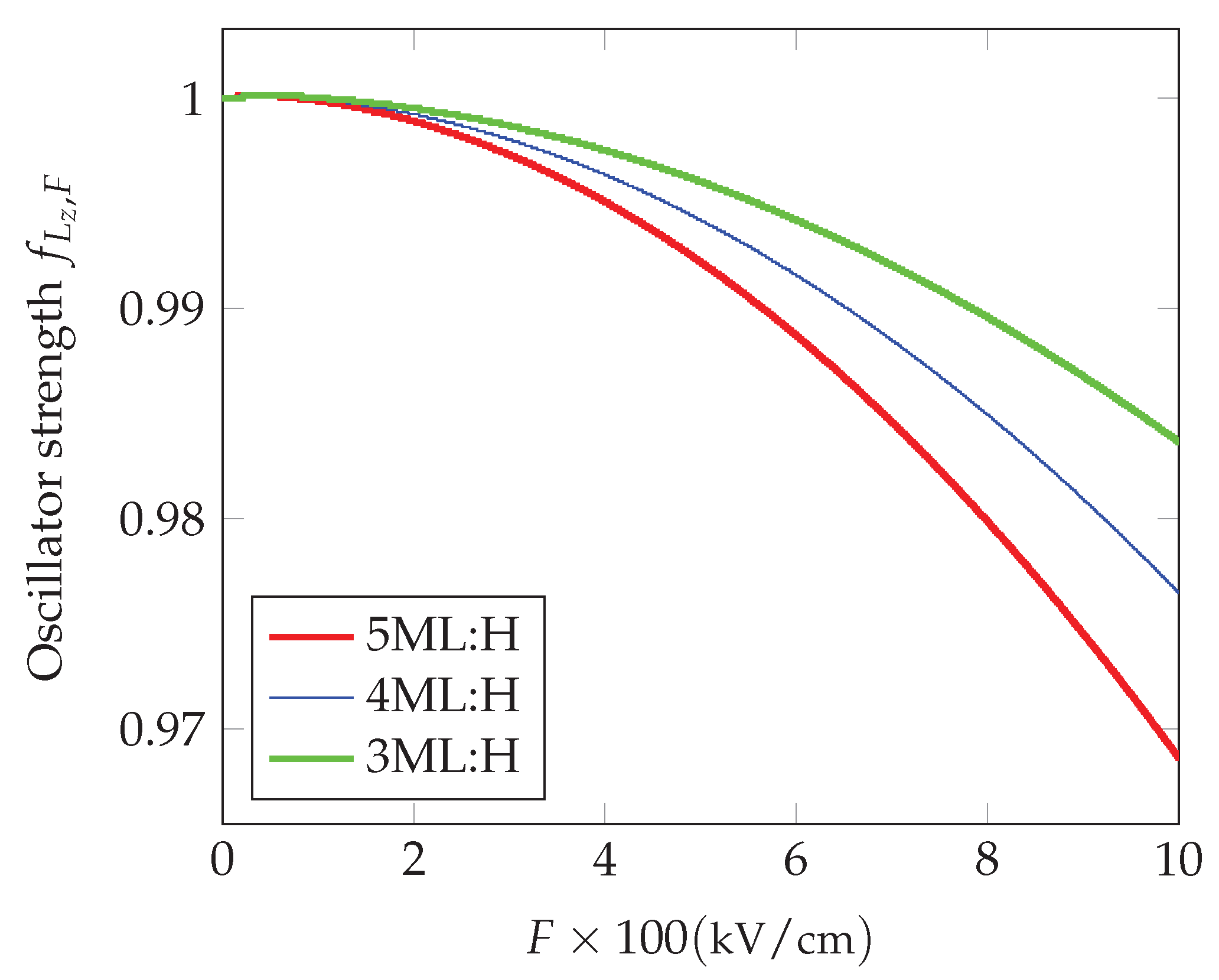
The dependence on the applied field strength is depicted in Figure 2. We observe the decreasing of oscillator strengths with the increasing field strength.

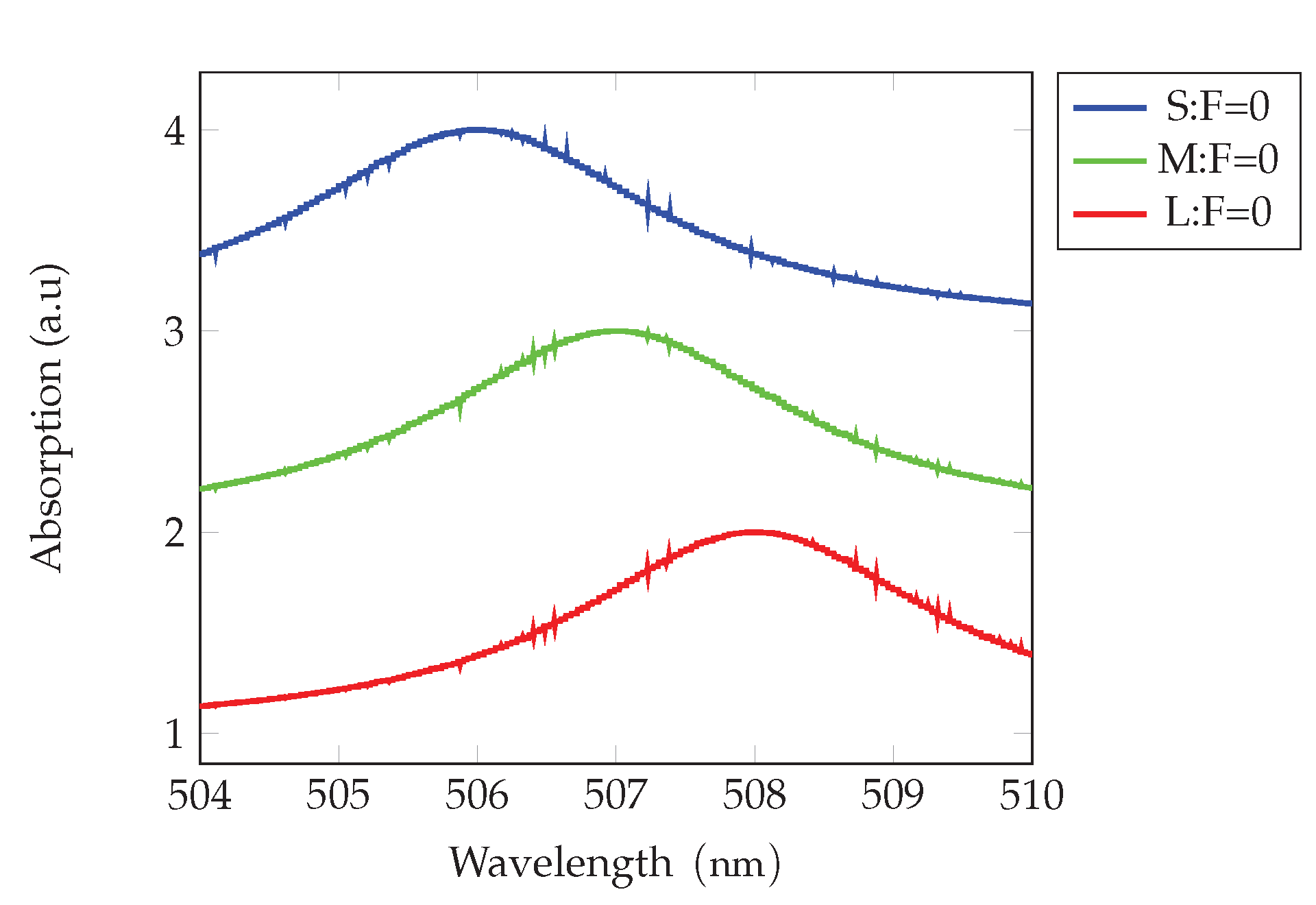
Finally, we have calculated the absorption coefficient, as the imaginary part of the susceptibility (24). In this equation the resonance energies $E_{res,jm}$ are needed. An important component of the resonance energy is the exciton binding energy, defined in Eq. (29). We observe that the binding energy decreases with the increasing field, as shown in Fig. In consequence, the resonance energies increase, despite of the Stark shift, acting in opposite direction. The absorption maxima are shifted versus higher energies (smaller wave lengths), in difference to the behavior in quantum wells. Such shift was observed in experiments by Baghdasaryan et al. [6]. Besides, the heavy- end light exciton absorption maxima are nearing and merge in the limit of high fields (Figure 4). The dependence of the binding and resonance energies, and the absorption coefficient, on the applied field strength, is shown in Figures –Figure 4.

Figure 3. Resonance energies for heavy (H) and light (L) hole exciton vs applied field strength.

Figure 3. Resonance energies for heavy (H) and light (L) hole exciton vs applied field strength.

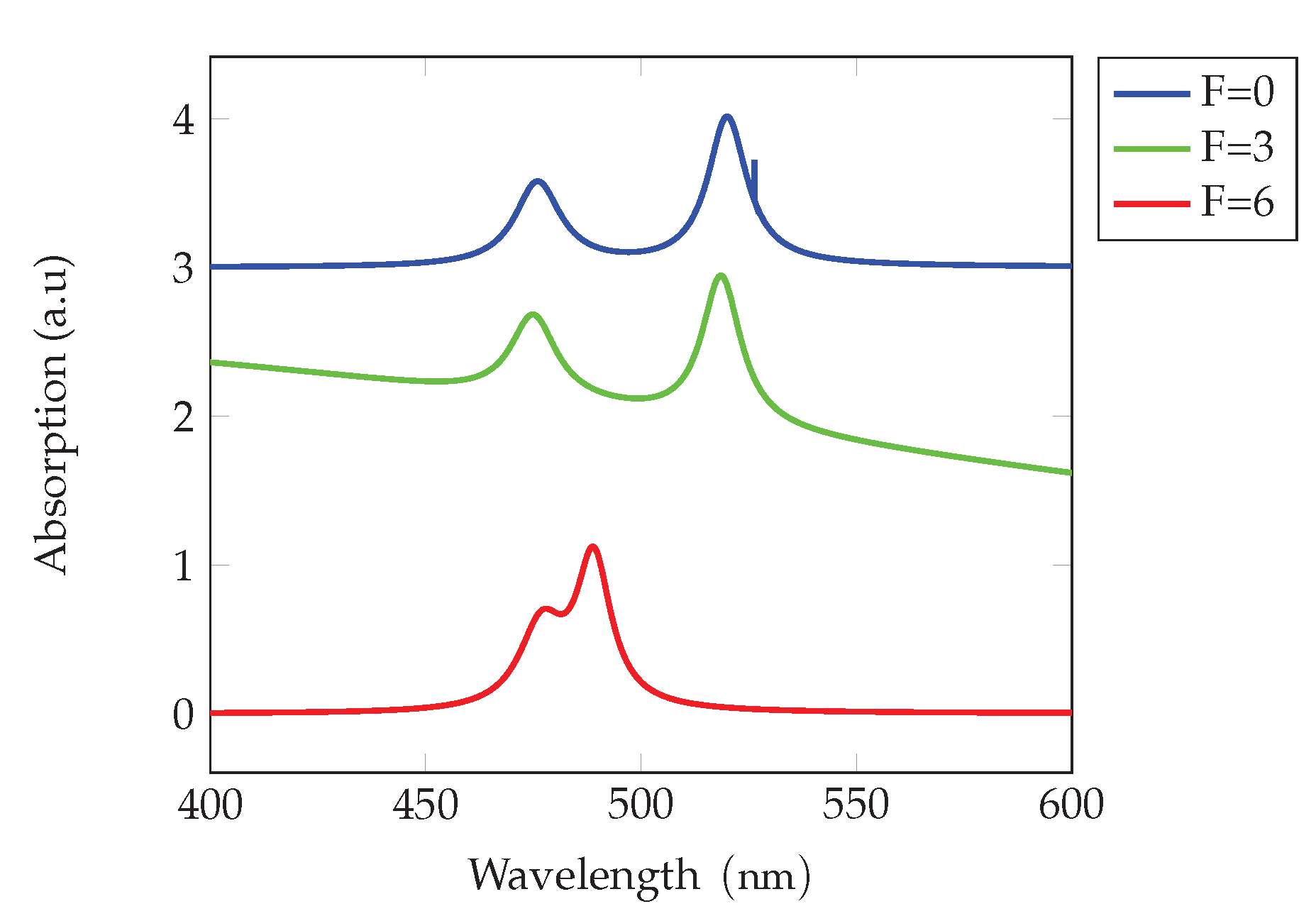
Figure 4. Normalized absorption for the case ’Thickness’ at 273 K, for three values of the applied field in the case 4ML thickness.

Figure 4. Normalized absorption for the case ’Thickness’ at 273 K, for three values of the applied field in the case 4ML thickness.

5. The Electric Field Parallel to the NPL Plane, Excitation Below Gap

In this section we analyze the electro-optical effects, when the external electric field F is applied parallel to the NPL-plane, choosing the axis $0x$. The considered case is more complicated than the case $F\Vert z$, where the electric field was decoupled from the 2-dimensional Coulomb potential, acting in the $x-y$ plane. Here the field, parallel to the x-axis, acts in the same plane as the cylindrically symmetric Coulomb potential, which makes impossible to find analytic solution of the relevant Schrödinger equation. To have an insight into the effects of the electric field, we have chosen a 2-dimensional model, where the electron is moving along the x axis in the interval $-L_x/2\le x\le L_x/2$, and we maintain the electron and hole movement in the z-direction, in the plane $x,y=0$. With this assumptions the relevant Hamiltonian has the form

$$\begin{array}{ccc}\hfill H& =& E_g+H_{m_{ez},{\omega }_{ez}}^{\left(1D\right)}\left(z_e\right)+H_{m_{hz},{\omega }_{hz}}^{\left(1D\right)}\left(z_h\right)\hfill \\ & +& V\left(x\right)+H_{\mathrm{Coul}}^{\left(1D\right)}\left(x\right)+eFx\hfill \\ & -& H_{\mathrm{Coul}}^{\left(1D\right)}\left(x\right)-{\displaystyle \frac{e^2}{\sqrt{x^2+{(z_e-z_h)}^2}}},\hfill \\ \hfill H_{\mathrm{Coul}}^{\left(1D\right)}\left(x\right)& =& -{\displaystyle \frac{{\hslash }^2}{2m}}{\displaystyle \frac{d^2}{d{x}^2}}-{\displaystyle \frac{e^2}{4\pi {ϵ}_0{ϵ}_b\left|x\right|}}+V\left(x\right),\hfill \end{array}$$

(34)

where

$$\begin{array}{ccc}\hfill & & V\left(x\right)=\left\{\begin{array}{c}0for\left|x\right|\le L_x/2,\hfill \\ \infty for\left|x\right|>L_x/2.\hfill \end{array}\right\}.\hfill \end{array}$$

(35)

The eigenfunctions of the operator $H_{\mathrm{Coul}}^{\left(1D\right)}\left(x\right)$ have the form

$$\begin{array}{ccc}\hfill \psi \left(\xi \right)& =& \left|\xi \right|e^{-\left|\xi \right|/2}M(1-\eta ;2;|\xi \left|\right),\hfill \\ \hfill \xi & =& \kappa {\displaystyle \frac{x}{a_{e\Vert }^{*}}},\kappa =2\sqrt{-\epsilon }={\displaystyle \frac{2}{\eta }},\hfill \end{array}$$

(36)

see Appendix B. Repeating the method used in the case $F\Vert z$, i.e. replacing the eigenfunction (36) by the function (20), with appropriate values for the coefficient $\alpha$, we obtain the Stark shift in the form

$$\Delta E=4.5\times {10}^{-4}{F}^2,$$

(37)

where the results is given in meV. The magnitude of $\Delta E$ depends, besides of the field strengths F, on the NPL size, represented here by $L_x/2=R$, see Eq. (10). The values of $\Delta E$, for NPLs with different sizes, are displayed in Fig. Figure 5. It should be noted, that the presented values are larger, in order of magnitude, than the Stark shift for the field applied in the z- direction (Figure 1). Interestingly, that despite of the large simplification, the obtained eigenvalues are in a good agreement with the experimental values for $F=0$ presented in Ref. [4], see Figure 6. Using the data presented in Tab. Section 5 we have calculated the normalized absorption, which shows the dependence on the NPL size, and on the applied field strength.

Table 3. Parameters for calculating the Stark shift, excitonic resonance energies vs applied field strength and lateral area, field strength in kV/cm, $X={10}^{2}F$, energies in meV, wavelengths in nm, oscillator strength to be multiplied by ${10}^{-3}$

Param.	$17\times 15$	$30\times 11$	$56\times 41$
${\alpha }^{-2}$	3.283	3.22	3.03
${\alpha }^{-4}$	10.78	10.375	9.22
${10}^5·{\xi }_0/F^2$	1.89	1.82	1.62
${10}^6·\Delta \epsilon /F^2$	4.72	4.55	4.04
${10}^4\Delta E/F^2$	4.5	4.33	3.85
	$X=0$
$|E_b|$	227.9	226.38	281.76
$E_{resH}$	2450.166	2448	2441
$\lambda$	506	506.54	508
$E_{resL}$	2670.166	2668	2661
$\lambda$	464.39	464.77	466
	$X=0.5$
$|E_b|$	243.52	243.04	241.67
$E_{resH}$	2408.3	2410.5	2417.36
$\lambda$	514.88	514.41	512.95
$E_{resL}$	2628.3	2630.5	2637.6
$\lambda$	471.8	471.4	470.12
	$X=1$
$|E_b|$	288.15	287.46	278.72
$E_{resH}$	2360.2	2362.84	2377.42
$\lambda$	525.36	524.79	521.57
$E_{resL}$	2580	2582.84	2597.42
$\lambda$	480.6	480.1	477.4
	$X=2$
$|E_b|$	478.49	481.63	477.2
$E_{resH}$	2174.45	2173	2177.42
$\lambda$	570.25	570.63	569.48
$E_{resL}$	2394.45	2393.0	2397.4
$\lambda$	517.86	518.18	517.22

Table 3. Parameters for calculating the Stark shift, excitonic resonance energies vs applied field strength and lateral area, field strength in kV/cm, $X={10}^{2}F$, energies in meV, wavelengths in nm, oscillator strength to be multiplied by ${10}^{-3}$

Param.	$17\times 15$	$30\times 11$	$56\times 41$
${\alpha }^{-2}$	3.283	3.22	3.03
${\alpha }^{-4}$	10.78	10.375	9.22
${10}^5·{\xi }_0/F^2$	1.89	1.82	1.62
${10}^6·\Delta \epsilon /F^2$	4.72	4.55	4.04
${10}^4\Delta E/F^2$	4.5	4.33	3.85
	$X=0$
$|E_b|$	227.9	226.38	281.76
$E_{resH}$	2450.166	2448	2441
$\lambda$	506	506.54	508
$E_{resL}$	2670.166	2668	2661
$\lambda$	464.39	464.77	466
	$X=0.5$
$|E_b|$	243.52	243.04	241.67
$E_{resH}$	2408.3	2410.5	2417.36
$\lambda$	514.88	514.41	512.95
$E_{resL}$	2628.3	2630.5	2637.6
$\lambda$	471.8	471.4	470.12
	$X=1$
$|E_b|$	288.15	287.46	278.72
$E_{resH}$	2360.2	2362.84	2377.42
$\lambda$	525.36	524.79	521.57
$E_{resL}$	2580	2582.84	2597.42
$\lambda$	480.6	480.1	477.4
	$X=2$
$|E_b|$	478.49	481.63	477.2
$E_{resH}$	2174.45	2173	2177.42
$\lambda$	570.25	570.63	569.48
$E_{resL}$	2394.45	2393.0	2397.4
$\lambda$	517.86	518.18	517.22

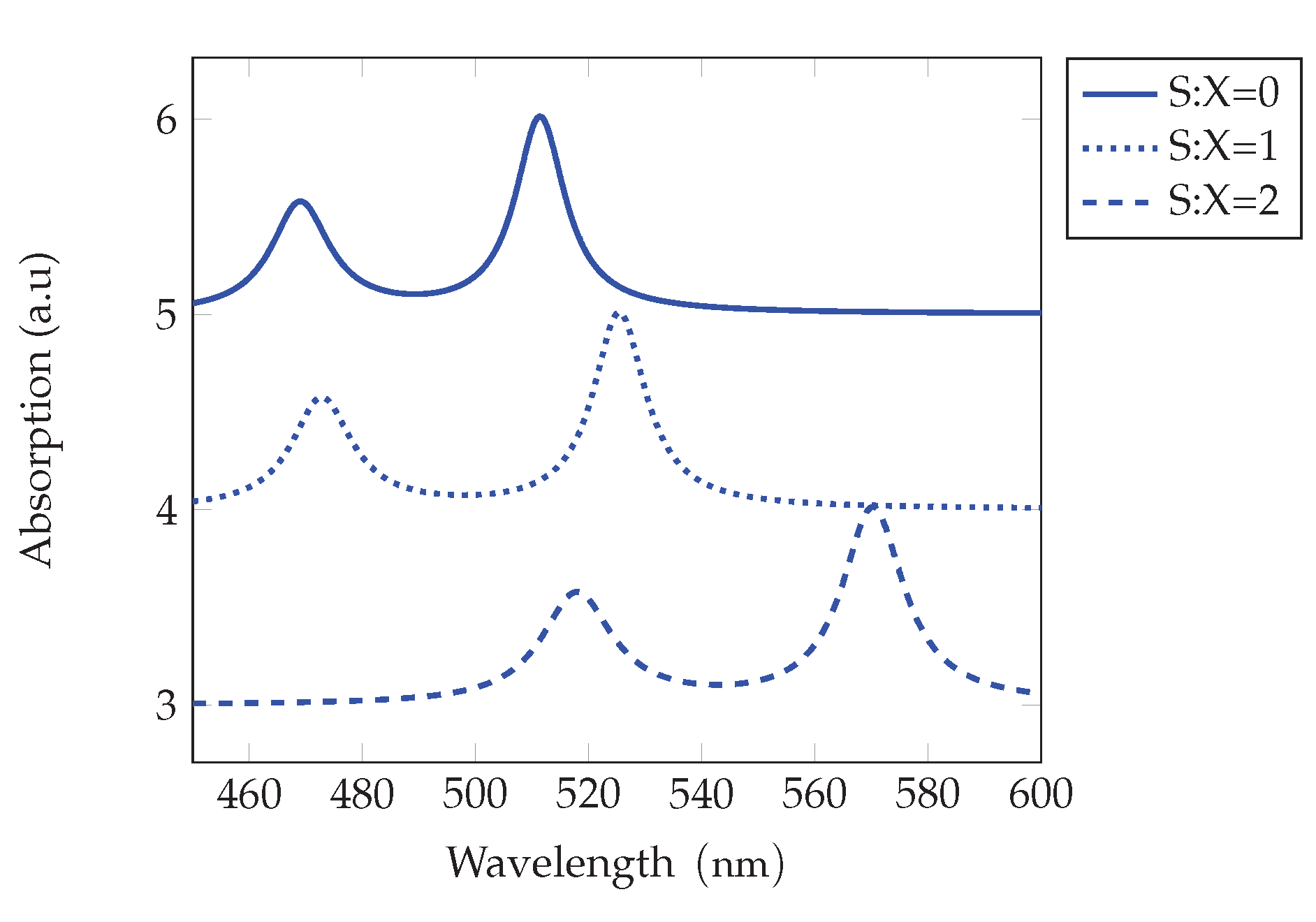
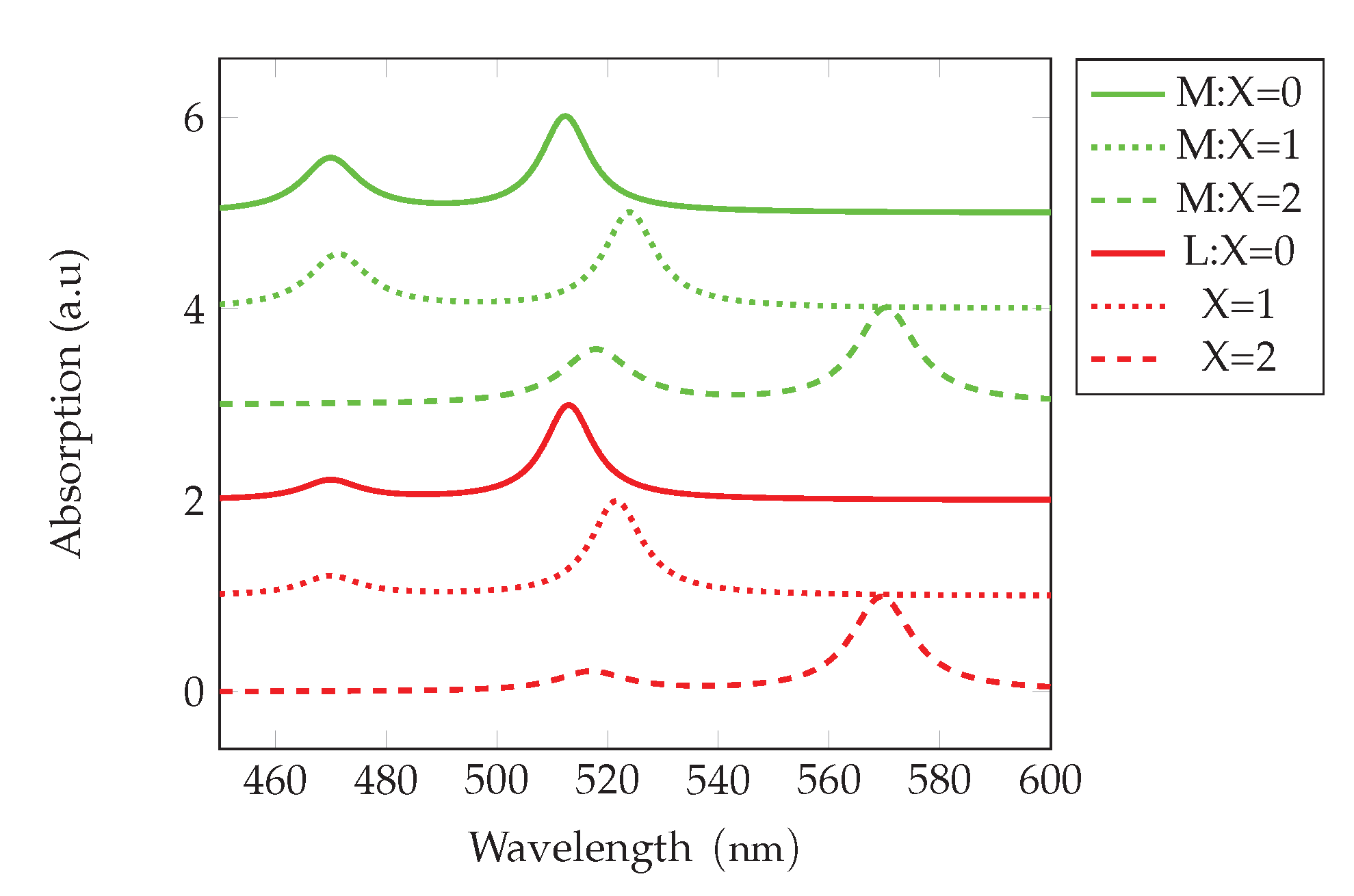
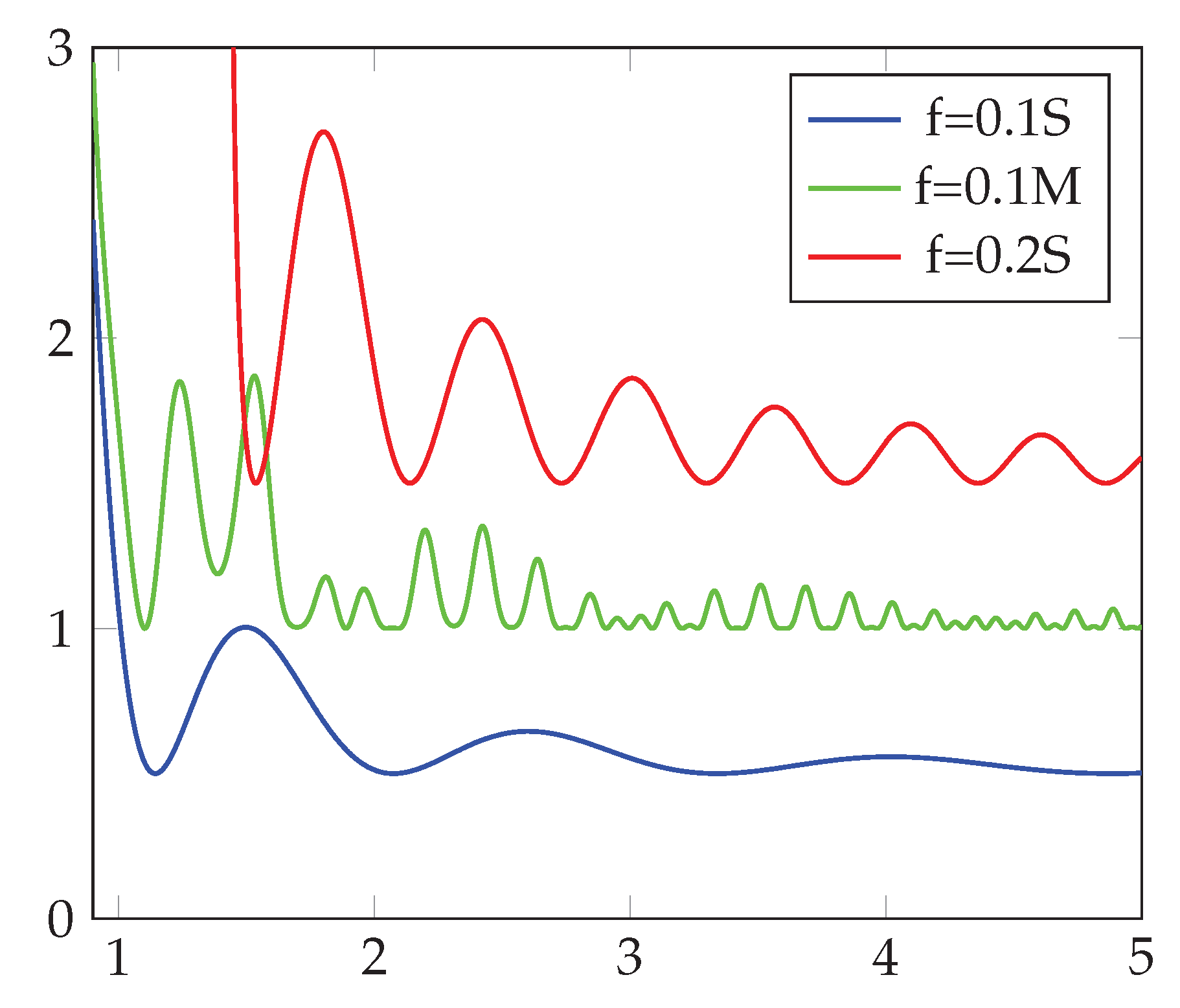
Figure 7. Normalized absorption for the case ’Lateral Area’ at 273 K, for three values of the applied field in the case 4ML thickness and area $17\times 15$ (S="small)", field strength in ${10}^2\times \mathrm{kV}/\mathrm{cm}$.

Figure 7. Normalized absorption for the case ’Lateral Area’ at 273 K, for three values of the applied field in the case 4ML thickness and area $17\times 15$ (S="small)", field strength in ${10}^2\times \mathrm{kV}/\mathrm{cm}$.

Figure 8. Normalized absorption for the case ’Lateral Area’ at 273 K, for three values of the applied field in the case 4ML thickness and area $30\times 11$ (M="medium"), $51\times 41$ (L="large"), field strength in ${10}^2\times \mathrm{kV}/\mathrm{cm}$.

Figure 8. Normalized absorption for the case ’Lateral Area’ at 273 K, for three values of the applied field in the case 4ML thickness and area $30\times 11$ (M="medium"), $51\times 41$ (L="large"), field strength in ${10}^2\times \mathrm{kV}/\mathrm{cm}$.

6. Quantum Confined Franz-Keldysh Effect

When the excitation energy exceeds the total confinement energy (including the energy gap), and an external electric field is applied parallel to the NPL plane, oscillations in the optical functions appear which, in the case of unbounded media, are known as the Franz-Keldysh effect (see, for example, [9]). For the unbounded media they have the form of outgoing waves, with variable periodicity and amplitudes (see, for example, [10,11]). The situation changes, when the medium, as considered here NPL, is finite. Instead of outgoing waves, standing waves appear, with periodicity and amplitude depending both on the applied field strength, and on the NPL size. This effect can be called Quantum Confined Franz-Keldysh effect (QCFKE). Such term appeared previously [12], but in the cited paper only a partial confinement was considered (QW), the field was applied in the z-direction, and the effect appears in the limits $L_z\to \infty$. The situation considered below is quite different, the confinement is applied in 3 direction, and the term Quantum Confined Franz-Keldysh effect seems to be justified. In the considered excitation region one can, in lowest approximation, neglect the e-h Coulomb interaction. Then the remaining terms in the Hamiltonian correspond to kinetic energies, and compose the total confinement. Therefore, to analyze the NPL’s QCFKE, we use the constitutive equation in the form

$$\begin{array}{ccc}\hfill & & \left(k^2-{\displaystyle \frac{d^2}{d{\xi }^2}}+f\xi \right)Y\left(\xi \right)={\displaystyle \frac{1}{a_{e\Vert }^{*}}}M\left(\xi \right)E,\hfill \\ & & k^2={\displaystyle \frac{E_{conf,tot}-\hslash \omega }{R_{e\Vert }^{*}}},\hfill \end{array}$$

(38)

where

$$\begin{array}{ccc}\hfill \xi & =& {\displaystyle \frac{x_e}{a_{e\Vert }^{*}}},f={\displaystyle \frac{F}{F_I}},F_I={\displaystyle \frac{R_{e\Vert }^{*}}{e·a_{e\Vert }^{*}}}.\hfill \end{array}$$

(39)

In the above equations the electric field F is parallel to the x-axis, and we retained the assumptions about the hole located in the NPL center. As in the case of unbounded media, the equation (38) can be solved by using appropriate Green’s function, which has the form

$$\begin{array}{ccc}\hfill G(\xi ,{\xi }^{\prime })& =& g^{<}·g^{>},\hfill \\ \hfill g^{<}& =& {\displaystyle \frac{\pi }{f^{1/3}}}\{\mathrm{Bi}\left[f^{1/3}\left({\xi }^{<}+{\displaystyle \frac{k^2}{f}}\right)\right]\hfill \\ & \times & \mathrm{Ai}\left[f^{1/3}\left({\displaystyle \frac{k^2}{f}}\right)\right]\hfill \\ & -& \mathrm{Bi}\left[f^{1/3}\left({\displaystyle \frac{k^2}{f}}\right)\right]\mathrm{Ai}\left[f^{1/3}\left({\xi }^{<}+{\displaystyle \frac{k^2}{f}}\right)\right]\},\hfill \\ \hfill g^{>}& =& \mathrm{Bi}\left[f^{1/3}\left({\xi }^{>}+{\displaystyle \frac{k^2}{f}}\right)\right]\hfill \\ & \times & \mathrm{Ai}\left[f^{1/3}\left(\mathcal{L}+{\displaystyle \frac{k^2}{f}}\right)\right]\hfill \\ & -& \mathrm{Bi}\left[f^{1/3}\left(\mathcal{L}+{\displaystyle \frac{k^2}{f}}\right)\right]\mathrm{Ai}\left[f^{1/3}\left({\xi }^{>}+{\displaystyle \frac{k^2}{f}}\right)\right].\hfill \end{array}$$

(40)

Here $\mathrm{Ai}\left(z\right),\mathrm{Bi}\left(z\right)$ are the Airy functions ([8]), and the notation ${\xi }^{<},{\xi }^{>}$ means ${\xi }^{<}=min(\xi ,{\xi }^{\prime }),{\xi }^{>}=max(\xi ,{\xi }^{\prime })$, and $\mathcal{L}=L_x/2a_{e\Vert }^{*}$. The confinement effect is included since

$$G(0,{\xi }^{\prime })=G(\xi ,\mathcal{L})=0.$$

(41)

When the dipole density $M\left(\xi \right)$ is defined, we obtain the NPL susceptibility in the form

$$\chi =MGM=\underset{0}{\overset{\mathcal{L}}{\int }}d\xi d{\xi }^{\prime }G(\xi ,{\xi }^{\prime })M\left(\xi \right)M\left({\xi }^{\prime }\right).$$

(42)

The absorption coefficient is proportional to the imaginary part of the susceptibility. Its shape, showing Franz-Keldysh oscillations, is presented in Figure 9, for two values of the applied fields, and two lateral NPL dimensions. We notice the large dependence on the NPL both on the field strength, and on the size.

7. Conclusions

In this paper we have studied the electro-optical properties of CdSe NPLs with excitons, for various orientations of the applied static electric field. This properties, compared with analogous for bulk materials and QWs, show strong modifications, which are due to the total confinement of electrons and holes, with a resulting dependence of the spectra on NPLs sizes. Besides of various orientations, we have separately analyzed the two possibilities of the exciting wave energy, below and above the gap. For the energy below the gap and for both orientations of the field, we observe exciton resonances, shifted red (electric field parallel to the NPL plane), and shifted blue (electric field parallel to the z-axis). The latter effect is due to the lowering of the exciton binding energy, which prevails over the, also observed, quadratic Stark shift. In the case of the excitation energy exceeding the gap (enlarged by the confinement energy), we observe the Franz-Keldysh oscillations, with periodicity depending both on the applied field strength, and NPLs sizes. Thus, NPLs add another degrees of freedom in controlling the absorption spectrum. It paves the way for construction of high sensitivity modulators, based on NPLs. The obtained results agree well with the available experimental results.