The Prevention Theorem: Time-Dependent Constraints on Post-Exposure Prophylaxis for HIV

1. Introduction

Despite the availability of antiretroviral agents with trial efficacies approaching or exceeding 99%, HIV prevention following exposure remains constrained by the biological dynamics of infection establishment [1,2]. Prevention is often discussed as a matter of coverage, adherence, or early treatment, implicitly assuming that post-exposure intervention remains feasible at all times following contact. A formal evaluation of this assumption requires specifying what prevention means in mathematical terms. Previous work has shown that HIV transmission and progression models are often highly sensitive to uncertain biological parameters, underscoring the difficulty of drawing robust conclusions from long-horizon simulations without strong constraints on initial conditions and system dynamics [3].

We define prevention for a specific viral exposure e as the condition R₀(e) = 0, corresponding to zero probability that the exposure establishes a productive, transmissible infection. Any state satisfying R₀(e) > 0 admits non-zero onward transmission and therefore cannot be considered complete prevention. Within this formulation, pre-exposure prophylaxis enforces R₀(e) = 0 by rendering the host non-susceptible prior to contact, whereas post-exposure prophylaxis (PEP) attempts to enforce R₀(e) = 0 after contact but before infection establishment becomes irreversible.

Crucially, PEP operates as a time-dependent operator acting on within-host establishment dynamics, racing against irreversible biological processes including proviral integration and latent reservoir seeding. Once these processes are complete, the system undergoes a phase transition to an irreducible infection state in which R₀(e) > 0 is permanently fixed, independent of subsequent therapeutic intervention [4,5,6]. This formulation applies to any pathogen in which irreversible genomic integration or long-lived latent reservoirs fix infection status beyond a critical temporal threshold.

In the sections that follow, we formalize this constraint through the Prevention Theorem and its corollaries, derive the finite temporal window during which PEP can enforce prevention, and illustrate the consequences of violating this boundary condition using the structural context of injection drug use as an applied example.

2. Methods

2.1. Theoretical Framework: The Prevention Theorem

We define the state of true prevention for a specific viral exposure e as the condition where the basic reproductive number for that exposure, R₀(e), is exactly zero.

Condition for Prevention: R₀(e) = 0

(1)

This condition implies that the probability of the exposure establishing a productive, transmissible infection is zero [7,8]. Interventions are classified by their ability to enforce this condition. Pre-exposure prophylaxis (PrEP) enforces R₀(e) = 0 by rendering the host non-susceptible prior to contact. Post-exposure prophylaxis (PEP) attempts to enforce R₀(e) = 0 by extinguishing the virus after contact but before the infection becomes self-sustaining.

2.2. Closed-Form Prevention Solution

Let R(t) denote the total number of infected cells resulting from a single exposure event at time t. The system admits exactly one closed-form prevention solution:

R(0) = 0 ⇒ R(t) = 0 ∀t.

(2)

If no infected cells exist at the initial condition, no infected cells can arise at any future time. For any initial condition satisfying R(0) > 0, no post-exposure or therapeutic intervention can mathematically guarantee R(t) = 0; all such interventions act only on the subsequent trajectory of R(t) and not on its initial condition [9].

2.3. Infection Establishment Dynamics

We model within-host establishment dynamics following a single exposure event using logistic formulations for reservoir seeding, Pseed(t), and proviral integration, Pint(t) [4]. These functions describe the cumulative probability that irreversible biological transitions have occurred by time t.

2.4. Master Equation for Time-Dependent Prevention

The efficacy of post-exposure intervention is time-dependent. We define the reproductive number as a function of intervention timing:

R₀(e, t) = 1 − EPEP(t)

(3)

with the efficacy function defined as:

EPEP(t) = (1 − Pseed(t)) εmax + (Pseed(t) − Pint(t)) εmid + Pint(t) εmin

(4)

Here, εmax represents efficacy prior to seeding, εmid represents efficacy during the seeding window, and εmin represents efficacy after integration is established (typically zero for prevention purposes).

Because EPEP(t) depends on cumulative probabilities of irreversible biological transitions, once integration is established, this operator, EPEP(t) → 0 and R₀(e, t), admits a hard temporal cutoff once established [10].

Corollary 1 (PEP Window Corollary): Post-exposure prophylaxis can enforce the prevention condition R₀(e) = 0 if and only if initiated within a finite biological window t < tcrit prior to irreversible proviral integration. Beyond this critical threshold, all reachable system states satisfy R₀(e) > 0 and are irreducible by post-exposure intervention or any therapeutic option currently available.

3. Results

3.1. Visualization of the Theorem

Figure 1 illustrates the four core components of the Prevention Theorem. Panel A shows the timeline of infection establishment, with reservoir seeding preceding proviral integration. Panel B demonstrates the time-dependent efficacy function EPEP(t), which decays monotonically toward zero as irreversible transitions accumulate. Panel C visualizes the phase transition into the irreducible infection state, where the probability of infection approaches certainty. Panel D summarizes the mathematical formalism.

3.2. Finite Prevention Window for Post-Exposure Prophylaxis

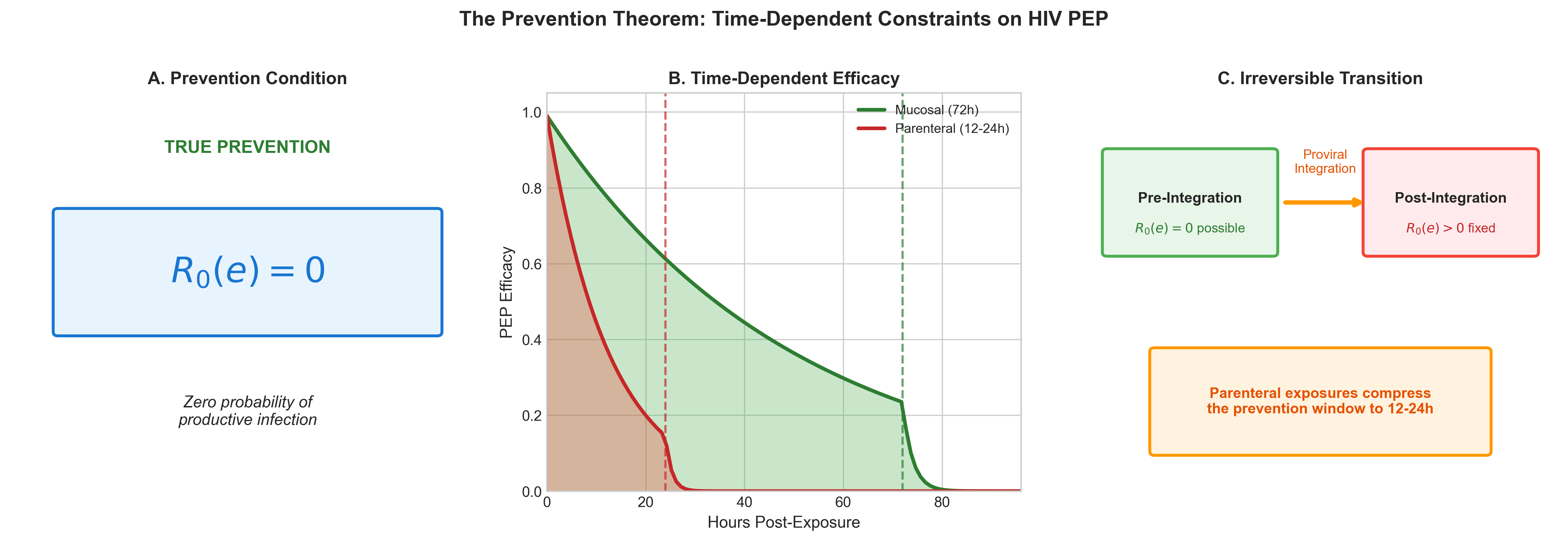
Model parameterization indicates that the window for enforcing R₀(e) = 0 extends to approximately 72 hours for mucosal exposures, constrained by local immune bottlenecks [10]. However, for parenteral exposures (e.g., injection), this window is compressed to roughly 12–24 hours due to the bypass of early mucosal barriers and rapid systemic dissemination [11]. This 'left-shift' of the critical window significantly reduces the timeframe for effective intervention.

Figure 2 demonstrates the quantitative compression of the prevention window between mucosal and parenteral exposures. The parenteral route (red dashed line) shows a precipitous decline in prevention efficacy within the first 24 hours, whereas the mucosal route (blue solid line) maintains higher efficacy through 72 hours. This differential is driven by the distinct immunological bottlenecks encountered in each tissue compartment.

3.3. Irreducible Infection State

Proviral integration represents a thermodynamically irreversible transformation of the host genome. Once integrated, viral DNA persists for the lifetime of the cell and is propagated to all daughter cells during division, producing clonal expansion independent of ongoing viral replication [5].

G(t + 1) = G(t) + HIVprovirus

(5)

No biologically realizable inverse transformation exists that restores the pre-integration genomic state. Consequently, once integration occurs, the condition R₀(e) = 0 is mathematically unattainable [12,13].

3.4. Reservoir Stratification

Long-lived viral reservoirs persist in specific cellular compartments, including naïve T-cells, central memory T-cells (TCM), stem cell-like memory T-cells (TSCM), and microglial cells [5,14]. These compartments are characterized by self-renewal capacity and longevity, allowing viral persistence independent of viral replication [15].

3.5. Applied Example: Structural Infeasibility Under Access Delays

Comparison of the derived biological windows against empirically observed access delays in high-risk populations (e.g., people who inject drugs) reveals a fundamental mismatch. Surveillance data indicates that while 85% of sexual exposure cases present to Emergency Departments within 72 hours, structural delays for injection-related exposures consistently exceed the compressed 24-hour parenteral window [16,17].

For this population, the cycle time required to navigate arrest, withdrawal, and housing instability (Tstruct) almost invariably exceeds the biological cycle time (Tbio). Consequently, the condition R₀(e) = 0 is biologically unreachable before access is even attempted. In these scenarios, failure is not a probabilistic outcome of drug efficacy or adherence, but a deterministic result of timing constraints.

4. Discussion

4.1. Theoretical Implications

Prevention is fundamentally an existence problem: does a state R₀(e) = 0 exist and is it reachable? Our analysis shows that PEP failure often represents a boundary violation rather than adherence failure; late intervention cannot alter the initial condition R(0) > 0 once it has been established [9].

4.2. Biological Proof of Concept: CCR5-Δ32

The only known 'cure' scenarios involve CCR5-Δ32 transplantation, which effectively eliminates the susceptibility term in the transmission equation [13]:

dR/dt = λSV · 0 = 0

(6)

This intervention functions as a system replacement rather than a reversal of the infection state, reinforcing the irreversibility of the integrated provirus in susceptible hosts.

4.3. Implications for Epidemic Control

Reactive interventions cannot achieve epidemic control when biological establishment precedes access. Prevention architectures must therefore be evaluated against biological feasibility constraints, not solely pharmacological efficacy [18].

5. Future Work

Future analyses will explore stochastic population dynamics and network-level avoidance collapse resulting from these constraints. The specific impact of architectural failure on population-level incidence is explicitly deferred to subsequent analysis.