On the Regularity of the Two-Dimensional Navier-Stokes Equations

1. Introduction

1.1. Background on Navier-Stokes Regularity

The regularity of the Navier-Stokes equation (NSE) is an important topic in the fields of partial differential equations and mathematical fluid dynamics (Foias et al. 2004). For the three-dimensional (3D) Navier-Stokes equation problem, Leray (1934) proved the existence of weak solutions, while the smoothness problem was not solved. The regularity of three-dimensional Navier-Stokes equations has been selected as one of the seven Millennium Prize Problems (Fefferman 2006). The regularity of the two-dimensional (2D) Navier-Stokes equation has been proven by Ladyzhenskaya (1969), that there exists a unique smooth solution for the 2D Navier-Stokes problem in global domain. However, her proof is not correct as she only considered the first type of singularity of functions (velocity infinite) and did not take into account the second type of singularity (velocity non differentiable). In this paper, we take the plane Couette flow as a typical example, and prove that there is no global smooth solution to the 2D Navier-Stokes equation.

Let $\mathsf{\Omega }=\mathbb{R}\times (0,2h)$ be a periodic domain in the x-direction (period L) and bounded in the y-direction. The 2D incompressible NSE are given by:

$$\left\{\begin{array}{cc}{\partial }_t\mathbf{u}+(\mathbf{u}·\nabla )\mathbf{u}=-\nabla p+\nu \Delta \mathbf{u}\hfill & \mathrm{in}\mathsf{\Omega }\times (0,T),\hfill \\ \nabla ·\mathbf{u}=0\hfill & \mathrm{in}\mathsf{\Omega }\times (0,T),\hfill \\ \mathbf{u}={\mathbf{u}}_b\hfill & \mathrm{on}\partial \mathsf{\Omega }\times (0,T),\hfill \\ \mathbf{u}(·,0)={\mathbf{u}}_0\hfill & \mathrm{in}\mathsf{\Omega },\hfill \end{array}\right.$$

(1)

where: $\mathbf{u}=(u,v):\mathsf{\Omega }\times [0,T)\to {\mathbb{R}}^2$ (velocity field), $p:\mathsf{\Omega }\times [0,T)\to \mathbb{R}$ (pressure), $\nu >0$ (kinematic viscosity), ${\mathbf{u}}_b(x,2h,t)=(U_1,0)$, ${\mathbf{u}}_b(x,0,t)=(0,0)$ (boundary data for plane Couette flow), ${\mathbf{u}}_0$ (initial velocity, satisfying $\nabla ·{\mathbf{u}}_0=0$ and ${\mathbf{u}}_0={\mathbf{u}}_b$ on $\partial \mathsf{\Omega }$).

A smooth solution to NSE is defined as a pair $(\mathbf{u},p)$ such that:

$$\mathbf{u}\in C^{\infty }(\mathsf{\Omega }\times [0,T)),p\in C^{\infty }(\mathsf{\Omega }\times [0,T)).$$

(2)

The pair $(\mathbf{u},p)$ satisfies the NSE pointwise in $\mathsf{\Omega }\times (0,T)$.

Ladyzhenskaya (1969) claimed that smooth solutions exist globally for 2D NSE, but we show that this fails for plane Couette flow due to disturbances-induced singularities.

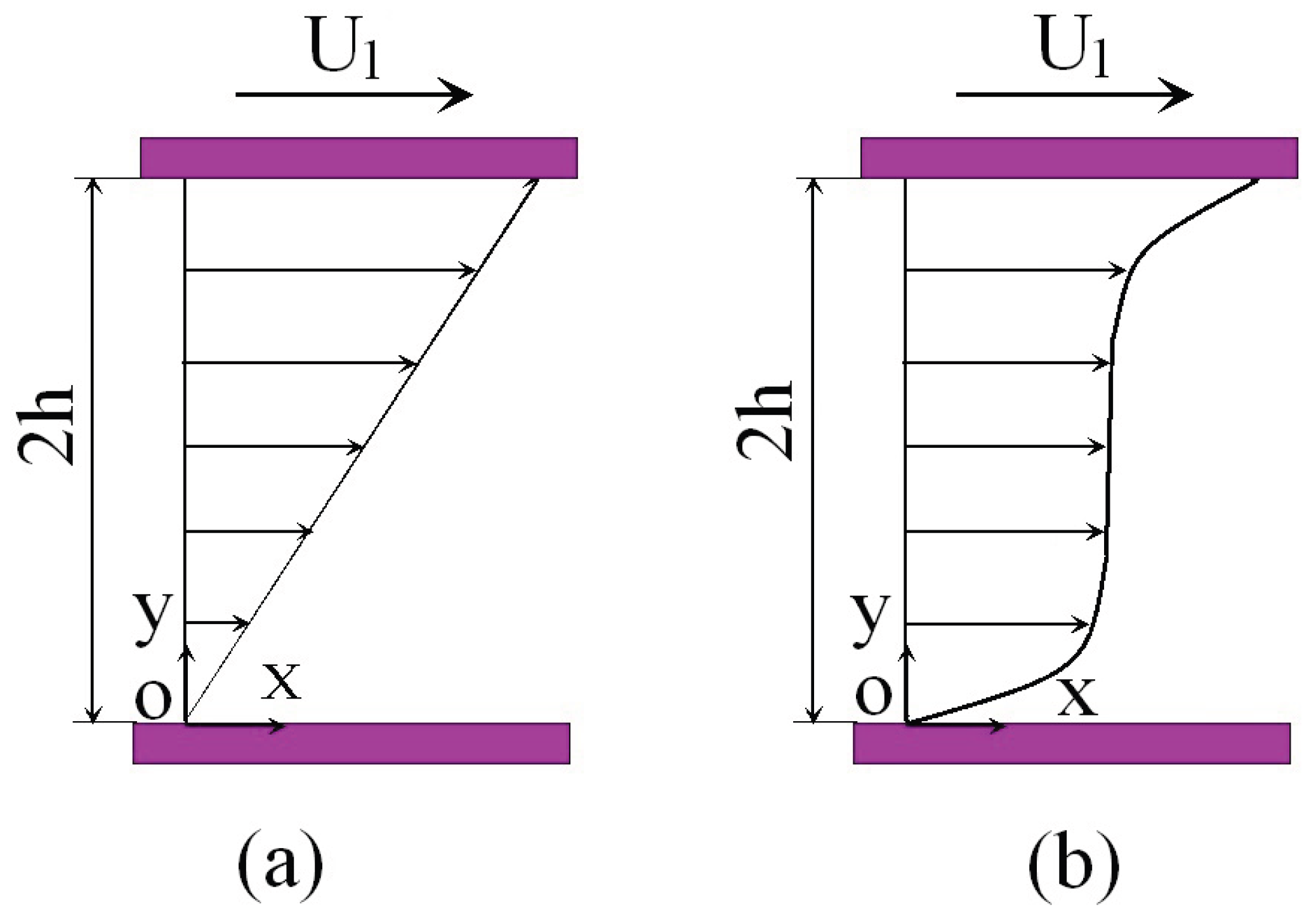
1.2. Plane Couette Flow Setup

The instantaneous velocity is decomposed into the “mean flow" (time-averaged flow) and the “disturbance flow." In the flow evolution with time, the instantaneous velocity is gradually modified with time, such that the “mean flow" (time-averaged flow) and the “disturbance flow" are also updated with the time increase.

$$\mathbf{u}(x,y,t)=\langle \mathbf{u}\rangle (x,y,t)+{\mathbf{u}}^{\prime }(x,y,t),$$

(3)

where:

Mean flow: $\langle \mathbf{u}\rangle (x,y)$ is obtained for sufficient long time.

Disturbances: ${\mathbf{u}}^{\prime }=(u^{\prime },v^{\prime })$ (satisfies $\nabla ·{\mathbf{u}}^{\prime }=0$, ${\mathbf{u}}^{\prime }(x,2h,t)=0$, ${\mathbf{u}}^{\prime }(x,0,t)=0$ for all $x,t$, and ${\int }_{\mathsf{\Omega }}{\mathbf{u}}^{\prime }dxdy=0$ (zero mean)).

We assume that ${\mathbf{u}}^{\prime }$ is “small" relative to the mean velocity in $H^1\left(\mathsf{\Omega }\right)$, so $u=\langle u\rangle +u^{\prime }>0$ in $\mathsf{\Omega }\times [0,T)$ (except at $(x,0,t)$ and $(x,2h,t)$, where $u=0$, as in Figure 1).

2. Sobolev Space Preliminaries

2.1. Sobolev Space Definitions

For $k\in \mathbb{N}$ and $1\le p\le \infty$, the Sobolev space $W^{k,p}\left(\mathsf{\Omega }\right)$ is:

$$W^{k,p}\left(\mathsf{\Omega }\right)=\left\{f\in L^p\left(\mathsf{\Omega }\right)\mid D^{\alpha }f\in L^p\left(\mathsf{\Omega }\right)\mathrm{for}\mathrm{all}\left|\alpha \right|\le k\right\},$$

(4)

with norm:

$${\parallel f\parallel }_{W^{k,p}\left(\mathsf{\Omega }\right)}=\left\{\begin{array}{cc}{\left(\sum _{\left|\alpha \right|\le k}{\parallel D^{\alpha }f\parallel }_{L^p\left(\mathsf{\Omega }\right)}^p\right)}^{1/p}\hfill & 1\le p<\infty ,\hfill \\ ma{x}_{\left|\alpha \right|\le k}{\parallel D^{\alpha }f\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\hfill & p=\infty .\hfill \end{array}\right.$$

(5)

We use $H^k\left(\mathsf{\Omega }\right)=W^{k,2}\left(\mathsf{\Omega }\right)$ (Hilbert space) and $H_0^1\left(\mathsf{\Omega }\right)={\overline{C_c^{\infty }\left(\mathsf{\Omega }\right)}}^{{\parallel ·\parallel }_{H^1\left(\mathsf{\Omega }\right)}}$ (functions vanishing on $\partial \mathsf{\Omega }$).

2.2. Key Sobolev Embeddings

For $\mathsf{\Omega }=\mathbb{R}\times (0,2h)$ (periodic in x, bounded in y):

1. Rellich-Kondrachov: $H^1\left(\mathsf{\Omega }\right)$ is compactly embedded in $L^p\left(\mathsf{\Omega }\right)$ for all $1\le p<\infty$.

2. Continuous Embedding: $H^1\left(\mathsf{\Omega }\right)\hookrightarrow L^{\infty }\left(\mathsf{\Omega }\right)$ (since $\mathsf{\Omega }$ is “1D-bounded": for $f\in H^1\left(\mathsf{\Omega }\right)$, $\left|f(x,y)\right|\le {\parallel f\parallel }_{H^1\left(\mathsf{\Omega }\right)}C\left(h\right)$ by Poincaré inequality in y and periodicity in x).

3. Schauder Estimate: $H^2\left(\mathsf{\Omega }\right)\hookrightarrow C^{0,1}\left(\overline{\mathsf{\Omega }}\right)$ (second derivatives in $L^2$ imply Lipschitz continuity).

3. Energy Dissipation and Singularity Criterion

3.1. Energy Dissipation Rate

The “local energy dissipation rate" (per unit mass) is:

$$\epsilon (x,y,t)=\nu \sum _{i,j=1}^2{\left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}\right)}^2/2=\nu {|\nabla \mathbf{u}+{(\nabla \mathbf{u})}^T|}^2/2.$$

(6)

where $\nabla \mathbf{u}=(\partial u_i/\partial x_j)$ is the velocity gradient tensor. For plane Couette flow, this simplifies to:

$$\epsilon (x,y,t)=\nu \left(2{\left({\displaystyle \frac{\partial u}{\partial x}}\right)}^2+2{\left({\displaystyle \frac{\partial v}{\partial y}}\right)}^2+{\left({\displaystyle \frac{\partial v}{\partial x}}+{\displaystyle \frac{\partial u}{\partial y}}\right)}^2\right).$$

(7)

3.2. Critical Condition for Singularity

The energy gradient theory has been proposed to study the flow stability and turbulent transition based on the Navier-Stokes equation (Dou 2006; Dou 2022; Dou 2025). The Axiom (2) in Dou (2025) can be employed to derive the critical condition of singularity appearance in the Navier-Stokes equation. This Axiom reads:“The velocity of a fluid particle varies monotonically with the energy lost during its motion, and vice versa.” This Axiom can be understood from the second law of thermodynamics. That is, a moving fluid particle in viscous flows always causes entropy increase. The motion of a particle consumes energy, and the larger the velocity, the larger is the energy loss. If there is no energy loss with a fluid particle, no entropy increase occurs. Thus, the velocity of this fluid particle is zero.

As such, if $\epsilon (x_0,y_0,t_0)=0$ for some $(x_0,y_0,t_0)\in \mathsf{\Omega }\times (0,T)$, then the instantaneous velocity becomes:

$$\mathbf{u}(x_0,y_0,t_0)=\mathbf{0}.$$

(8)

This follows from the second law of thermodynamics: zero energy dissipation implies no viscous work, so fluid particles cannot sustain non-zero velocity.

Therefore, for any point $\mathbf{x}\in \mathsf{\Omega }$ in plane Couette flows, if the local viscous energy loss vanishes (i.e., $\parallel \epsilon (x,y,t)\parallel \to 0$), the velocity at $(x,y)$ must tend to zero to maintain the energy-velocity consistency—formally:

$$\underset{\parallel \epsilon (x,y,t)\parallel \to 0}{lim}u(x,y,t)=0\forall \mathbf{x}\in \mathsf{\Omega }\setminus \partial \mathsf{\Omega }$$

(9)

3.3. Formation of $\epsilon =0$ Points

At high Reynolds number, the velocity profile is modified guadually with time increase under influence of disturbance. At sufficient large disturbance, the velocity profile at the centerline of the flow channel $(x_0,y_0,t_0)$ becomes flat (Fig.1), the velocity gradient,

$${\displaystyle \frac{\partial u}{\partial y}}(x_0,y_0,t_0)\to 0.$$

(10)

Consider the disturbance-induced evolution of $\partial u/\partial y$. The gradient of the mean flow is $\langle \partial u/\partial y\rangle >0$ since the energy is always transformed from the top wall to te bottom wall. The velocity gradient of the instantaneous velocity is:

$${\displaystyle \frac{\partial u}{\partial y}}(x,y,t)={\displaystyle \frac{\partial \langle u\rangle }{\partial y}}(x,y,t)+{\displaystyle \frac{\partial u^{\prime }}{\partial y}}(x,y,t).$$

(11)

Since ${\mathbf{u}}^{\prime }$ is a fluctuating field (satisfying ${\int }_{\mathsf{\Omega }}{u}^{\prime }dxdy=0$), $\partial u^{\prime }/\partial y$ has negative value in a period. Therefore, when the disturbance amplitude is large sufficient, there exists $t_0>0$ and $(x_0,y_0)\in \mathsf{\Omega }$ such that (at middle of the channel $y=h$):

$${\displaystyle \frac{\partial u}{\partial y}}(x_0,y_0,t_0)=0.$$

(12)

For plane Couette flow, at the point $(x_0,y_0,t_0)$, $|\partial u/\partial x|\ll |\partial u/\partial y|$. Since $\partial u/\partial y=0$ at the channel middile, we have $\partial u/\partial x=0$. Due to incompressibility: $\partial u/\partial x+\partial v/\partial y=0$, thus, $\partial v/\partial y=0$. Summarizing these results, we obtain $\partial v/\partial x=0$.

Thus, all the velocity gradients at the middle point of the flow channel tend to zero. Actually, it is a uniform flow at the centerline of the flow channel between the two plates, as shown in Fig.1. This is typical in transitional flow of the plane Couet flow. According to Equation (7), we obtain at the middle of the flow channel,

$$\epsilon (x_0,y_0,t_0)=0.$$

(13)

4. Contradiction and Singularity Formation

4.1. Velocity Boundedness vs. Zero Energy Dissipation

By our initial assumption, $u(x,y,t)>0$ in $\mathsf{\Omega }\times [0,T)$ (except at $(x,0,t)$). However, the energy gradient principle (Dou 2022; Dou 2025) requires $\mathbf{u}(x_0,y_0,t_0)=\mathbf{0}$ for zero viacous energy dissipation. This creates a fundamental contradiction:

1. $u(x_0,y_0,t_0)=\langle u\rangle \left(y_0\right)+u^{\prime }(x_0,y_0,t_0)>0$ (by initial condition and the definition of the problem).

2. $\mathbf{u}(x_0,y_0,t_0)=\mathbf{0}$ (zero viscous energy dissipation leads to zero velocity by the energy gradient theory (Dou 2022; Dou 2025)).

This contradiction means that the zero energy loss does not match the no-zero velocity, which forms a singularity of the Navier-Stokes equation.

Then, in order to stablize the flow at the singularity, the solution develops a “velocity discontinuity" at $(x_0,y_0,t_0)$.

4.2. Velocity Discontinuity

The discontinuity takes the form:

$$\underset{(x,y)\to {(x_0,y_0)}^{+}}{lim}\mathbf{u}(x,y,t_0)=\mathbf{0},\underset{(x,y)\to {(x_0,y_0)}^{-}}{lim}\mathbf{u}(x,y,t_0)\ne \mathbf{0}.$$

(14)

At the discontinuity point, the left and right derivatives are not equal:

$${\displaystyle \frac{\partial u}{\partial y}}{|}_{{(x_0,y_0)}^{+}}\ne {\displaystyle \frac{\partial u}{\partial y}}{|}_{{(x_0,y_0)}^{-}}.$$

(15)

In fact, both partial derivatives become infinite due to the abrupt change in velocity across an infinitesimal distance.

4.3. Loss of $H^1\left(\mathsf{\Omega }\right)$ Regularity

For $\mathbf{u}\in H^1\left(\mathsf{\Omega }\right)$, all first weak derivatives must be in $L^2\left(\mathsf{\Omega }\right)$. Consider the weak derivative $\partial u/\partial y$ at $(x_0,y_0,t_0)$. For a test function $\varphi \in C_c^{\infty }\left(\mathsf{\Omega }\right)$ supported near $(x_0,y_0)$, the weak derivative condition is:

$${\int }_{\mathsf{\Omega }}u{\displaystyle \frac{\partial \varphi }{\partial y}}dxdy=-{\int }_{\mathsf{\Omega }}\left({\displaystyle \frac{\partial u}{\partial y}}\right)\varphi dxdy.$$

(16)

At $t=t_0$, the left-hand side (LHS) is finite (since $u\in L^{\infty }\left(\mathsf{\Omega }\right)$). However, the right-hand side (RHS) diverges because $\partial u/\partial y$ has a jump discontinuity:

$${\displaystyle \frac{\partial u}{\partial y}}(x_0,y_0^{+},t_0)-{\displaystyle \frac{\partial u}{\partial y}}(x_0,y_0^{-},t_0)=\Delta >0,$$

(17)

implying $\partial u/\partial y\notin L^2\left(\mathrm{supp}\varphi \right)$. Thus, $\mathbf{u}(·,t_0)\notin H^1\left(\mathsf{\Omega }\right)$.

4.4. Exit from Smooth Solution Spaces

A global smooth solution requires $\mathbf{u}\in C([0,\infty );H^2\left(\mathsf{\Omega }\right))$. Since $H^2\left(\mathsf{\Omega }\right)\hookrightarrow H^1\left(\mathsf{\Omega }\right)$ (by definition), $\mathbf{u}(·,t_0)\notin H^1\left(\mathsf{\Omega }\right)$ implies $\mathbf{u}(·,t_0)\notin H^2\left(\mathsf{\Omega }\right)$. By the Sobolev embedding $H^2\left(\mathsf{\Omega }\right)\hookrightarrow C^{0,1}\left(\overline{\mathsf{\Omega }}\right)$, $\mathbf{u}$ also fails to be Lipschitz continuous at $t_0$, hence not $C^1$.

4.5. Vorticity Singularity

The vorticity is defined as $\omega =\partial v/\partial x-\partial u/\partial y$. At the discontinuity point, $\partial u/\partial y$ becomes infinite, so:

$$\omega (x_0,y_0,t_0)=\infty .$$

(18)

This represents a true singularity in the Navier-Stokes solution where the velocity field is no longer differentiable, which is characterized by the Beale-Kato-Majda criterion (Beale et al. 1984).

5. Discussions on Velocity Discontinuities

5.1. Violation of Ladyzhenskaya’s Result

Ladyzhenskaya (1969) proved global regularity for 2D NSE in her classical result. This result has last long for more than 50 years. However, our analysis shows that “velocity discontinuities" exist in 2D Navier-Stokes equation, which was not considered in her original analysis. Therefore, Ladyzhenskaya (1969)’s proof is not valid anymore when we take into account both the singularities of "Type 1: velocity infinite" and "Type 2: velocity not differentiable."

These discontinuities indicated in Eqs.(14) and (15) represent “Type 2 singularities" (differentiability breakdowns) in the terminology of Dou (2025), distinct from the Type 1 singularities (velocity blow-up in $L^{\infty }$) considered by Ladyzhenskaya.

5.2. Global Smooth Solutions Do Not Exist

Since $\mathbf{u}(·,t_0)\notin H^1\left(\mathsf{\Omega }\right)$, and $H^1\left(\mathsf{\Omega }\right)$ is the minimal space required for weak solutions, it follows that:

Theorem: For plane Couette flow with small disturbances in $H^1\left(\mathsf{\Omega }\right)$, the 2D Navier-Stokes equations do not admit global smooth solutions in $\mathsf{\Omega }\times [0,T)$ for any $T>t_0$.

This result shows that the classical conclusion of Ladyzhenskaya (1969) on the global regularity of 2D NSE is incorrect.

5.3. Implications of Zero Energy Dissipation at one Point

The formation of velocity discontinuities can be understood physically as follows:

1. Entropy Requirement:

By the second law of thermodynamics, fluid particle at this point must come to rest since there is no entropy increase.

2. Energy Dissipation Cessation:

At the point where $\epsilon =0$, viscous dissipation vanishes, so no mechanical work is done. This will lead to rapid increase of higher-order derivatives, which promotes the rise of velocity gradient (Constantin and Foias 1988).

3. Boundary Condition Violation:

However, the upstream flow continues to supply momentum, creating a discontinuity instantly at this position with zero energy dissipation.

This mechanism is supported by direct numerical simulations of plane Couette flow by Dou and Khoo (2012), which showed that turbulent transition occurs when zero velocity gradient appears at the centerline on the instantaneous velocity profile.

5.4. Two-Dimensional Turbulence generated by Singularities

Numerical simulations have demonstrated the existence of turbulence in two-dimensional flows (Boffetta and Ecke 2012; Fragos et al. 2007; Kraichnan 1967; Kraichnan 1971; Xiao et al. 2009). This type of turbulence is different from the laminar flow, as it can generate velocity fluctuations, create greater resistance, and promote fluid mixing. There are also turbulence energy cascades in two-dimensional turbulence, but the difference from 3D turbulence is that the cascades in two-dimensional turbulence are both positive and negative. In the large-scale vortex range, it is a direct cascade, while in the small-scale vortex range, it is an inverse cascade. However, the mechanism of two-dimensional turbulence still cannot be explained. The research results in present study explain the mechanism of two-dimensional turbulence generation through the singularity of the Navier Stokes equations.

5.5. Singularity appearance in Vorticity Transport Equation

The momentum equation in Equation (1) can be writen as the form of the vorticity transport equation with the vorticity $\omega =\nabla \times \mathbf{u}$ submitted into the Equation (1),

$${\displaystyle \frac{\partial \omega }{\partial t}}+\mathbf{u}·\nabla \omega =\omega ·\nabla \mathbf{u}+\nu {\nabla }^2\omega$$

(19)

As is well known, the first term on the right hand side is the so-called term of “vorticity stretch.” If there is vortex stretch or parallelization of vorticity vector and velocity vector in 3D flows, vorticity will increase. This term is zero in 2D flows.

The second term on the right hand side is the term of vorticity dissipation due to viscosity, which leads to decrease of vorticity generally (Lugt 1983). Dou (2025) found that this term is the source of generation of vorticity in viscous flows. For example, when a viscous flow passes a solid wall, vorticity will be produced, and such produced vortices are laminar ones, as is well known. For the first time, Dou (2025) discovered that this term is the origin of turbulence generation (or new vorticity birth) through singularities interior of flows, which occurs in transitional and turbulent flows.

In 2D flows, the singularity described above is actually produced by the second term of above equation, $\nu {\nabla }^2\omega .$

Both for 2D and 3D flows, the formation of singularities in the Navier-Stokes equation is generated by the term, $\nu {\nabla }^2\omega .$ In 3D flows, this has been confirmed by the numerical simulations with large eddy simulation (LES) and direct numerical simulations (DNS) in our group and also the work with our collaborator (Niu et al. 2024; Niu et al. 2025; Zhou et al. 2025a; Zhou et al. 2025b; Dou and Khoo 2012).

Comparing to the 3D NSE, the 2D NSE only drops the vorticity stretch term which simply affects the energy cascade of vortices. In 3D flows, turbulence is generated by the velocity discontinuities (Dou 2022; Dou 2025). In 2D flows, the generation of turbulence should be the same as that in 3D flows, i.e., velocity discontinuities.

6. Conclusions

We have demonstrated that for plane Couette flow governed by the 2D incompressible Navier-Stokes equations, “global smooth solutions do not exist" under influence of disturbances. The key findings are:

1. Singularity Formation: Under small $H^1\left(\mathsf{\Omega }\right)$ disturbances, the flow develops points where the energy dissipation rate $\epsilon =0$. By the energy gradient principle, these points require $\mathbf{u}=\mathbf{0}$.

2. Contradiction Resolution: The contradiction between $\mathbf{u}>0$ (from boundary conditions) and $\mathbf{u}=\mathbf{0}$ (from zero energy dissipation) is resolved by the formation of “velocity discontinuities".

3. Loss of Regularity: These discontinuities force the solution to exit the Sobolev space $H^1\left(\mathsf{\Omega }\right)$, violating the regularity required for smooth solutions. The vorticity becomes infinite at the discontinuity points, violating the Beale-Kato-Majda criterion (1984).

We have proved that there is no global smooth solutions to the 2D Navier-Stokes equations using the plane Couette flow as a benchmark problem. Our analysis identifies “Type 2 singularities" (velocity discontinuities) which was not considered in Ladyzhenskaya’s (1969) proof, suggesting that the classical result in Ladyzhenskaya’s (1969) work on the global regularity of 2D NSE is not valid.

This work has important implications for the understanding of fluid dynamics and the mathematical theory of the Navier-Stokes equations. It suggests that the transition from laminar to turbulent flow in shear-driven flows can be fundamentally linked to the formation of velocity discontinuities, providing a new perspective on the physical mechanism of turbulence.