Towards Fully DL-Driven RF: A Systematic Survey of Deep Learning for Wireless Transceiver Signal Processing

1. Introduction

1.1. Motivation and Context

Wireless communications play a fundamental role in modern society, enabling connectivity that shapes how we live, work, and interact. From mobile broadband and Internet of Things (IoT) networks to critical applications such as autonomous systems and remote healthcare, wireless technologies continue to evolve to support increasingly demanding use cases. As these systems become more complex and the demand for higher data rates, lower latency, and increased reliability grows, traditional signal-processing techniques face numerous challenges in meeting these stringent requirements.

Among the various wireless communication techniques, Orthogonal Frequency Division Multiplexing (OFDM) has emerged as a cornerstone modulation scheme, forming the foundation for numerous standards including Wi-Fi (IEEE 802.11), 4G LTE, 5G New Radio (NR), and Digital Video Broadcasting (DVB). It is also used for wired communications, in technologies such as Powerline Communications, Cable Modems (DOCSIS), and DSL. OFDM’s ability to combat frequency-selective fading and inter-symbol interference through the use of multiple orthogonal subcarriers has made it particularly attractive for high-data-rate applications. However, the effectiveness of OFDM-based systems relies heavily on the accurate execution of multiple sequential signal processing stages, each presenting unique challenges in real-world deployment scenarios.

1.2. Limitations of Traditional OFDM Signal Processing

Wireless channels are inherently unpredictable due to multipath fading, Doppler shifts, co-channel interference, and hardware impairments such as in-phase/quadrature (I/Q) imbalance and carrier frequency offset (CFO). Traditional OFDM receivers employ a cascade of specialized algorithms to address these challenges. Techniques such as synchronization [1], Cyclic Prefix (CP) removal [2], Fast Fourier Transform (FFT) [3], channel estimation and equalization [4], demodulation [5], and decoding [6] have been developed and refined over decades to enable reliable communication.

While these conventional methods have enabled significant performance improvements, they face several fundamental limitations. First, traditional algorithms are typically designed based on idealized channel models and often fail to generalize to diverse real-world scenarios. Second, many conventional techniques require accurate channel state information (CSI) and precise synchronization, which becomes increasingly difficult to achieve in highly dynamic environments or at extremely high frequencies such as millimeter-wave (mmWave) bands. Third, the computational complexity of optimal algorithms can be prohibitive, leading to suboptimal approximations that sacrifice performance for the sake of implementation feasibility. Fourth, these algorithms are generally fixed once deployed and cannot adapt to evolving channel conditions or new interference patterns without manual reconfiguration or firmware updates.

1.3. Deep Learning as a Paradigm Shift

In recent years, Deep Learning (DL) has emerged as a transformative approach for wireless communication system design, offering a data-driven alternative to conventional model-based methods. DL techniques excel at learning complex, nonlinear mappings directly from data without requiring explicit mathematical models of the underlying physical phenomena. By leveraging large training datasets and powerful neural network architectures, DL approaches have demonstrated the potential to replace individual signal-processing blocks as well as entire end-to-end receiver designs that jointly optimize multiple stages.

The advantages of DL-based approaches for OFDM systems are manifold. These data-driven methods can learn directly from received signals, automatically discovering optimal processing strategies that may not be apparent through analytical derivation. Neural networks can adapt to changing channel conditions through online learning or transfer learning, potentially improving robustness in non-stationary environments. Furthermore, once trained, neural networks can offer reduced computational complexity during inference compared to iterative conventional algorithms, making them attractive for resource-constrained devices. The ability of DL models to jointly optimize across multiple traditionally separate processing stages also opens the possibility of discovering novel processing strategies that outperform conventional pipelined approaches.

As a result of these compelling advantages, deep learning has attracted significant research attention as a means to overcome the limitations of traditional OFDM receivers, with applications spanning from individual component replacement to complete end-to-end system redesign.

1.4. Survey Scope and Contributions

While several recent surveys have examined aspects of deep learning for wireless communications [7,8,9], most focus primarily on specific areas, such as channel estimation, or examine DL techniques in isolation without a comprehensive performance analysis across the entire OFDM receiver chain. This survey distinguishes itself through the following key contributions:

• Comprehensive Stage-by-Stage Analysis: We provide an in-depth examination of DL applications at each stage of the OFDM receiver processing chain, from synchronization through decoding, offering a complete picture of how DL can transform each component.
• Performance-Focused Methodology: Using a PRISMA-based systematic literature review, we identified 339 relevant papers published between 2019 and 2025, and selected the 16 highest-performing methods based on rigorous performance metrics including Bit Error Rate (BER) [10], Block Error Rate (BLER) [11], Symbol Error Rate (SER) [12], Mean Squared Error (MSE) [13], and Normalized Mean Squared Error (NMSE) [14] to reflect the current state-of-the-art. Additionally, we provide a brief overview of 27 other related studies.
• End-to-End Integration Analysis: Beyond individual stages, we analyze holistic end-to-end receiver designs and discuss the trade-offs between modular stage-wise DL enhancement versus unified end-to-end optimization.
• Critical Assessment and Future Directions: We provide a critical analysis of research distribution across stages, identify significant gaps in the literature, and discuss open challenges and promising directions for future research.

Each performance metric assessed in this survey evaluates the robustness and efficiency of DL-based systems across varying Signal-to-Noise Ratio (SNR) conditions [15], enabling fair comparison with traditional baseline methods.

1.5. Paper Organization

The remainder of this paper is structured as follows. Section 2 provides essential background on OFDM principles and traditional digital signal processing approaches for each receiver stage. Section 3 details our systematic survey methodology based on the PRISMA framework. Section 4 presents a comprehensive examination of deep learning techniques applied to each stage of the OFDM receiver chain, as well as end-to-end receiver architectures, including additional relevant works not included in the quantitative evaluation. Section 5 provides a critical analysis of research trends, performance comparisons, open challenges, and future research directions. Finally, Section 6 presents our conclusions and discusses the transformative role deep learning is playing in wireless communications.

2. OFDM Fundamentals and Traditional DSP Approaches

OFDM divides high-rate data streams into multiple parallel lower-rate subcarriers that remain orthogonal despite spectral overlap, achieving high spectral efficiency. The transmitter encodes, modulates (BPSK, QPSK, QAM), applies IFFT, and prepends a cyclic prefix (CP) to mitigate inter-symbol interference. The receiver reverses these operations through a sequential DSP pipeline. This section reviews the prevalent DSP algorithms at each receiver stage, their performance limitations, and the opportunities for deep learning to address these challenges.

2.1. Traditional Receiver Pipeline and DSP Algorithms

Synchronization: Conventional methods include autocorrelation exploiting the CP structure [1], cross-correlation with preambles, and maximum likelihood (ML) estimation for carrier frequency offset (CFO) and symbol timing. Challenge: These algorithms struggle with low SNR, high Doppler, and hardware impairments (I/Q imbalance), often requiring multiple iterations and exhibiting high sensitivity to channel conditions. DL opportunity: Neural networks can jointly estimate timing, CFO, and hardware impairments from raw signals without explicit channel models.

Cyclic Prefix Removal: Standard DSP simply discards the guard interval based on synchronized timing [2]. Challenge: Any synchronization error propagates as ISI/ICI; CP overhead (typically 20-25%) reduces spectral efficiency. DL opportunity: Learned receivers can potentially operate without CP, directly handling ISI through temporal pattern recognition.

Fast Fourier Transform: The FFT is mathematically optimal and highly optimized [3]. Challenge: Timing errors degrade orthogonality; FFT itself offers limited opportunities for DL improvement as it performs a deterministic transformation. DL opportunity: Minimal, since conventional FFT remains superior.

Channel Estimation: Pilot-based methods (LS, MMSE [4]) estimate channel coefficients at known subcarrier locations, then interpolate. Least Squares (LS) is a simple but noise-sensitive approach; MMSE is optimal under Gaussian assumptions, but it requires channel statistics and matrix inversions. Challenge: High pilot overhead (10-30% in massive MIMO), poor performance with sparse/time-varying channels, and model mismatch in non-Gaussian interference. DL opportunity: Networks can learn channel correlations across time/frequency/space, reducing pilot requirements and improving NMSE by 3-10 dB in challenging scenarios.

Equalization: Zero-forcing (ZF) and MMSE equalizers invert estimated channel responses per subcarrier. ZF amplifies noise in deep fades; MMSE requires knowledge of noise variance. Challenge: Residual estimation errors propagate; linear equalizers fail with nonlinear distortions. DL opportunity: Learned equalizers can handle nonlinear impairments and jointly optimize with channel estimation.

Demodulation: Hard/soft-decision demapping compares constellation points to reference alphabets [5], assuming accurate equalization and Gaussian noise. Challenge: Performance degrades with residual channel errors and non-Gaussian interference. DL opportunity: Networks can learn optimal decision boundaries directly from impaired signals.

Decoding: Iterative algorithms (belief propagation for LDPC, BCJR for Turbo codes [6]) achieve near-capacity performance but with high complexity. Challenge: Fixed iterations, no adaptation to error patterns, computational cost. DL opportunity: Learned decoders can exploit structured error patterns and reduce iterations while maintaining BER performance.

2.2. Key Challenges Driving Deep Learning Adoption

The fundamental limitations of this conventional pipeline create opportunities for deep learning: (1) Model mismatch—algorithms assume idealized channels that poorly represent real environments; (2) Complexity-performance trade-offs—optimal algorithms (e.g., ML detection, MMSE estimation) are often computationally prohibitive; (3) Independent optimization—stages are optimized separately, missing joint optimization gains; (4) Fixed processing—algorithms cannot adapt to new impairments without redesign; and (5) High overhead—pilots and CP consume 30-50% of resources. Deep learning addresses these challenges through data-driven learning, adaptability, and the potential for joint optimization across the entire receiver chain.

3. Systematic Review Methodology

This systematic literature review was conducted following the PRISMA 2020 (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) guidelines [16] to ensure transparency, reproducibility, and comprehensive coverage of deep learning applications in OFDM receiver signal processing. The review process comprised four distinct phases: identification, screening, eligibility assessment, and inclusion.

3.1. Eligibility Criteria

Studies were considered eligible for inclusion if they met the following criteria: (1) published in peer-reviewed journals or conference proceedings between January 2019 and November 2025; (2) proposed, implemented, or evaluated deep learning methods for at least one stage of OFDM receiver processing (synchronization, CP removal, FFT, channel estimation, equalization, demodulation, decoding) or end-to-end receiver architectures; (3) reported quantitative performance metrics (e.g. BER, BLER, SER, MSE, NMSE, or accuracy) enabling comparison with baseline methods; (4) written in English; and (5) provided sufficient methodological detail for reproducibility assessment. Studies were excluded if they focused solely on transmitter-side processing, non-OFDM modulation schemes, theoretical analysis without experimental validation, or lacked performance evaluation.

3.2. Information Sources and Search Strategy

A comprehensive literature search was executed across five major academic databases on December 1, 2025: IEEE Xplore Digital Library, SpringerLink, ScienceDirect (Elsevier), MDPI Digital Library, and Google Scholar. The search strategy employed Boolean combinations of controlled vocabulary and free-text terms organized into three concept groups: (1) Deep learning architectures: “deep learning” OR “neural network” OR “CNN” OR “RNN” OR “LSTM” OR “transformer” OR “autoencoder”; (2) OFDM systems: “OFDM” OR “orthogonal frequency division multiplexing” OR “multicarrier”; and (3) Receiver functions: “synchronization” OR “channel estimation” OR “equalization” OR “demodulation” OR “decoding” OR “receiver”. The complete search string was adapted to each database’s syntax. No restrictions were placed on study design or geographic location. Reference lists of included studies and relevant review articles were manually screened to identify additional eligible papers (backward citation tracking).

3.3. Selection Process

The selection process followed a multi-stage screening approach, as illustrated in Figure 1. An initial set of database searches identified a total of 421 records, of which 82 duplicates were removed, resulting in 339 unique papers. These records subsequently underwent title and abstract screening against the predefined eligibility criteria. Full-text articles were retrieved for all 339 records, as the broad search strategy necessitated a detailed examination to determine their relevance to specific OFDM receiver stages. From these papers, we then excluded 127 articles as false search positives. Each of the remaining 212 papers was then independently categorized by receiver stage (synchronization, CP removal, FFT, channel estimation/equalization, demodulation, decoding, and end-to-end) based on the primary focus of the proposed DL method, and we excluded a further 38 papers because they could not be adequately mapped. Table 1 presents the distribution of the remaining 174 papers across the various OFDM receiver stages, revealing significant research concentration in channel estimation/equalization (116 papers, 66.67%) and notable gaps in Synchronization (8 papers, 4.60%), CP removal (4 papers, 2.30%), FFT (0 papers), demodulation (7 papers, 4.02%) and decoding (3 papers, 1.72%).

3.4. Data Extraction and Quality Assessment

From each eligible study, the following data elements were systematically extracted: author(s), publication year, DL architecture type (e.g., CNN, LSTM, transformer), OFDM receiver stage(s) addressed, dataset characteristics (simulated vs. measured, channel models), baseline comparison methods, performance metrics and results, signal-to-noise ratio range, and computational complexity where reported. To ensure comprehensive yet focused analysis, a performance-based selection criterion was applied within each stage category. Studies demonstrating superior or competitive performance metrics compared to conventional baselines—specifically, lowest BER/BLER/SER for end-to-end system metrics or lowest MSE/NMSE for channel estimation—were prioritized for in-depth analysis. This final filtering and selection process, combined with consideration of methodological rigor and architectural diversity, resulted in a final analytical set of 16 core studies representing state-of-the-art DL approaches across all receiver stages. These 16 core studies form the basis for the detailed technical analysis presented in Section 4, along with 27 closely related but less impactful papers that we will briefly discuss in relation to the relevant core papers.

3.5. Synthesis Methods and Bibliometric Analysis

To identify thematic clusters and research trends within the identified literature, a bibliometric analysis was performed using VOSviewer (version 1.6.18) on the title and abstract keywords of the 339 papers. Co-occurrence analysis with a minimum keyword frequency threshold of 5 occurrences revealed distinct research communities focusing on channel estimation, MIMO systems, and end-to-end learning, as shown in Figure 2. Narrative synthesis was employed for the selected papers, organizing findings by receiver stage and comparing DL methods against conventional DSP baselines using reported performance metrics.

3.6. Relation to Existing Reviews

During the literature search, three existing review papers on deep learning for OFDM systems were identified and excluded from the primary analysis to avoid redundancy [7,9]. These reviews predominantly focus on channel estimation techniques [7] or categorize DL techniques by architecture type [9], whereas the present work provides a comprehensive stage-by-stage analysis covering the entire OFDM receiver pipeline with performance-focused method selection. Thus, this systematic review complements existing literature by addressing gaps in synchronization, CP removal, FFT, demodulation, and decoding stages while providing an integrated discussion of end-to-end approaches.

4. Deep Learning for OFDM Receiver Stages

Focusing on the receiver, there are multiple stages that collectively enable the accurate retrieval of transmitted information, with each stage employing a unique and highly selective methodology to ensure precision, robustness, and reliability. Synchronization ensures that the subcarriers maintain orthogonality, while CP removal eliminates redundant or unwanted information. FFT converts the received time-domain signal back into the frequency domain. Channel estimation predicts the effects of the wireless channel, providing the necessary information for subsequent processing. Channel equalization then utilizes this estimate to mitigate channel-induced distortions and recover the transmitted symbols. Finally, demodulation then converts the equalized signals back into the individual subcarriers, and decoding retrieves the original data bits. The overall OFDM receiver processing chain is illustrated in Figure 3.

In this work, we first analyze and evaluate the use of deep learning techniques at each individual stage of the receiver to assess their impact on overall system performance. Next, we provide a detailed examination of end-to-end receiver models, emphasizing the cumulative performance improvements achieved when all key stages are enhanced with deep learning, while also noting other approaches that show promising results but are not optimal. Finally, we discuss how integrating deep learning across all stages transforms the OFDM receiver into a fully Deep Learning-driven system, with the potential for delivering significant gains in metrics such as BER, NMSE, MSE, and SER, while preserving the interpretability of each stage.

4.1. Synchronization

The first paper, which focused on synchronization in OFDM receivers, proposes a deep neural network (DNN)–based method for joint estimation of Carrier Frequency Offset (CFO) and Sampling Frequency Offset (SFO) in MIMO OFDM-OQAM systems [17]. The DNN is a three-layer classifier that takes the received distorted signal from each antenna as input, passes it through a hidden layer with sigmoid activation, and outputs discrete CFO and SFO sub-ranges using a softmax layer. The network is trained offline with high-SNR signals of known CFO and SFO values using gradient-based backpropagation. After training, the DNN classifies incoming signals to estimate the corresponding CFO and SFO, which are then sequentially compensated using a filter bank at each receive antenna before combining and demodulation. Figure 4 exhibits the DL synchronization approach.

Using Matlab, the method was simulated on a MIMO OFDM-OQAM system with 2 transmit antennas and 4 receive antennas. Carrier frequency offsets and sampling frequency offsets were randomly selected from bounded normalized ranges consistent with typical synchronization impairments. The received signal SNR was varied from 0 to 20 dB, and the NN was trained over different numbers of epochs to evaluate its effect on performance. Results were averaged over 1000 Monte Carlo simulations. Even at very low SNR, the DNN estimator achieves a probability of success of approximately 95%, demonstrating its robustness in challenging channel conditions. These results highlight that the neural network can reliably classify CFO and SFO sub-ranges, making it an effective approach for synchronization in MIMO OFDM-OQAM systems.

Another DL strategy for CFO and I/Q imbalance in an OFDM receiver was introduced by the authors of [18]. The authors start their process by developing a DNN architecture with J sub-nets that are all identical, each having three fully connected hidden layers and using the Rectified Linear Unit (ReLU) [19] activation function. The subnets all share a common input layer that consists of pilot symbols and data symbols, which are divided into real and imaginary components, thereby driving the number of neurons in the input layer. The output layer of each sub-net has a number of neurons determined by the modulation order and number of subcarriers. Figure 5 exhibits the DL synchronization approach.

Their experiment consisted of using 64 subcarriers, with each frequency set to 15 kHz, a symbol duration of 66.67$\mu s$, and an 8-phase-shift-keying (8PSK) modulation scheme with one pilot and one data symbol. With this setup, the DNN has 128 complex symbols, resulting in an input layer with 256 neurons. J is set to 8, making the output layer 24 neurons for each sub-net. The batch size is 128, the number of epochs is 500, and the learning rate is set to 0.04. The CFO is adjusted between 100 and 200 parts per million arbitrarily. The IQ mismatch was set to 12^∘ and 18^∘, respectively. The DL model was compared to the conventional method by [20]. The evaluation compares BER over SNR in the range of 0 to 35 dB. These experiments were tested under two situations: the Additive White Gaussian Noise (AWGN channel and the multi-path channel. The DL method achieves a lower BER at low SNR values more effectively than the conventional method for various CP lengths in AWGN and multi-path channels. This shows that DL techniques are effective and provide better performance over conventional methods.

Finally, a DL solution for CFO estimation for the 802.11n standard was introduced by [21]. The method uses Gate Recurrent Units (GRU) [22] for CFO estimation from the 802.11n preamble [23]. GRU helps establish temporal correlations and models long-term dependencies with two gates (update and reset) [24]. There are 6 layers for the DL model. The input layer, the rearrange layer, the GRU layer, and 3 dense layers. The 802.11n physical layer protocol data unit (PPDU) [25] is used for testing. The PPDU preamble is used as input for evaluating CFO estimation techniques. A total of eight datasets with various CFO frequency ranges were used to test the eight-channel models, which were performed in MATLAB.

The DL models were compared with conventional methods across different channels by calculating the CFO MAE over an SNR range of 0 to 30 dB. The DL models reduced the MAE by 70.54% compared to the conventional methods. As the channel becomes more complex, the MAE performance degrades, but at a rate that is much slower than that of the conventional method.

Table 2 illustrates the results from the synchronization DL architectures that were previously discussed.

4.1.1. Other Related DL Approaches

In [26], the authors proposed a neural network–based coarse CFO estimator for MIMO systems, which achieves performance comparable to traditional methods across AWGN, flat/slow fading, and multi-path channels, with high probability of success for SNR > 0 dB and a wide CFO acquisition range, but was excluded from the main quantitative evaluation as it does not outperform the primary benchmarks.

The work in [27] proposes a DNN-based OFDM receiver that extends the input to capture ISI, but its performance is directly comparable to the MMSE receiver under perfect timing and only slightly improves under timing errors. The DNN and MMSE still perform similarly in most practical scenarios. However, overall, the proposed approach does not significantly outperform existing methods.

This paper by Ninkovic et al. [28] evaluates deep learning methods for packet detection and CFO estimation in IEEE 802.11ah, comparing them to conventional techniques. DL approaches can outperform conventional methods at low SNR but suffer from higher complexity and inconsistent performance. As a result, they are not recommended for main research implementations.

Another paper [29] proposes a NN–based method for integer frequency offset (IFO) estimation and primary synchronization signal (PSS) detection in 5G NR systems. The NN uses convolutional layers and regression and is trained across various tapped delay line (TDL) channel profiles and IFO ranges to optimize detection. While simulations show lower failure probabilities compared to conventional maximum likelihood and sequential methods, these metrics are not practically meaningful for system performance. Due to its complexity and limited real-world utility, this approach is not included in the main research discussion.

Finally, [30] proposed a CNN-Attention-DNN (CAD) model for non-pilot-assisted CFO estimation in OFDM systems, combining residual CNNs, attention, and dense layers without prior knowledge of pilots or channel parameters. While validated in simulations and on an NI RF testbed, the method is more complex and only moderately better than existing approaches, so it is not included in the main research discussion.

4.2. CP Removal

An end-to-end DL approach for OFDM communication was introduced by [31], eliminating the need for CP and pilots. The DL model implementing the receiver is a convolutional residual NN that processes the received base-band channel samples following the DFT. The network outputs a 3D tensor of log-likelihood ratios (LLRs) [32], which is passed to the channel decoder. The first layer transforms the input into a real-valued 3D tensor by separating the real and imaginary portions. Zero-padding is applied in all convolutional layers to maintain consistent output dimensions, and dilation is used to expand the receptive field of the convolution layers, similarly to [33]. The DL model consists of 6 layers, including a Conv2D at the input, 4 ResNet blocks [34], and a Conv2D at the output. The CP removal framework is portrayed in Figure 6.

The number of OFDM symbols used is 14, the number of subcarriers is 72, the carrier frequency is set to 3.5 GHz, the subcarrier spacing is set to 30 kHz, the CP duration is set to 6 symbols lasting 2.34$\mu s$, the channel models used are 3GPP-3D [35], Line of Sight (LoS) [36], and Non-Line of Sight (NLoS) [36], the number of taps is set to 5, the learning rate to 0.001, 100 frames for batch size, 4 bits per channel, 1024 low-density parity-check (LDPC) [37] code length, 0.667 code rate, and the speed ranged from 0 to 130 kilometers per hour. The decoding was performed using belief propagation [38] over 40 iterations. Each OFDM frame contained 3 codewords, randomly populated with padding bits, and combining was applied within each frame.

For testing, the Quadriga simulator [39] is used to create a dataset that trained and evaluated the performance of the DL model. The DL model was configured for Quadrature Amplitude Modulation (QAM) with CP and pilots, QAM with no CP and with pilots, along with Geometric Shaping (GS) [40] with no CP and no pilot are all compared against conventional QAM with CP and perfect Channel State Information (CSI) and QAM with CP, pilot, and Linear Minimum Mean Square Error (LMMSE) [41]. Two pilot patterns (1P and 2P) from 5G NR [42] were used for the simulation testing. The evaluation compares BER over an SNR range of 4 to 14 dB, along with goodput [43], with SNR over the range of 5 to 20 dB. The authors demonstrate that their methods, utilizing CP and pilots, outperform those without, while still exhibiting strong performance at low SNR values and achieving high goodput across the entire SNR range.

Table 3 presents the results from the CP Removal DL structure that was previously analyzed.

4.2.1. Other Related DL Approaches

The presented DL-OAMP receiver for CP-free OFDM systems, as shown in [44], combines a Channel Estimation Network (CE-Net) for channel estimation and an Orthogonal Approximate Message Passing Network (OAMP-Net) for signal detection. The OAMP-Net unfolds the iterative OAMP algorithm with a few trainable parameters, enabling low-complexity detection that adapts to time-varying channels. Simulations show that DL-OAMP achieves lower BER than traditional methods and other deep learning approaches, approaching the performance of systems with perfect CSI and sufficient CP. However, compared to other methods, this approach achieves a lower overall performance.

The authors of [45] developed CG-OAMP-NET, a model-driven deep learning detector for CP-free MIMO-OFDM systems. It unfolds a conjugate gradient–based OAMP algorithm into a network, learning a few optimal parameters to improve convergence and stability. The method significantly reduces computational complexity compared to standard OAMP while maintaining strong BER performance. However, other approaches achieve better performance in certain scenarios.

Finally, [46] proposed IComNet-EP, an improved ComNet for CP-free OFDM systems. It retains the CE-Net but replaces the detection with an expectation propagation equalization (EPE) block, which buffers previous OFDM symbols to remove ISI. The scheme achieves lower BER than ComNet, OAMP-NET, and other classical methods while maintaining similar computational complexity. IComNet-EP is also robust across different channel environments without retraining.

4.3. Fast Fourier Transform

No significant research was found on converting FFTs into DL based models. Although a few attempts have been made, these approaches have generally proven to be less effective than conventional FFT algorithms. Traditional FFTs are already highly efficient, leaving little room for improvement through a DL substitution. However, this observation does not imply that ongoing research into DL-based FFT alternatives does not exist. Our conclusion is that the current state of the art in DL-based FFT is less effective than established methods.

4.4. Channel Estimation and Equalization

4.4.1. Channel Estimation

A low-complexity DL channel estimation method for OFDM systems was proposed by [47] and is based on the fast super-resolution convolutional neural network (FSRCNN). The design process begins with an input layer that has a tensor shape containing the height, width, and number of color channels of the input. The feature extraction layer performs convolution on the input image to extract the initial features. A Parametric ReLU (PReLU) [48] activation function is employed to introduce nonlinear effects; the shrinking layer is also a convolutional layer that reduces the spatial dimensions of the extracted features. The mapping layers turn low-resolution features into a high-resolution space. Several convolutional layers are applied, followed by a PReLU activation, which transforms the input into feature maps. The expanding layer is also a convolution layer that increases the spatial dimensions of the feature to return it to high resolution, and the deconvolution layer performs upscaling. The FSRCNN is trained using Least Squares (LS) estimates based on the pilot markers. Figure 7 describes the channel estimation deep learning model.

The evaluation of the architecture compares MSE with SNR, using a system configuration where the number of subcarriers is set to 72, the time slots are set to 14, the carrier frequency is 2.1 GHz, the learning rate is 0.001, and the pilot length is 48. The Adam optimizer is used during model training for 50 epochs. The proposed method is compared against other methods, including the Super-Resolution Convolutional Neural Network (SRCNN) [49], the LS Minimum Mean Square Error (MMSE) [50], and ChannelNet [51], in terms of MSE over an SNR range of 0 to 30 dB. The FSRCNN outperforms the compared methods by achieving lower MSE at low SNR, providing more accurate channel estimation even in the presence of higher noise and achieving that low computational complexity for which it was designed.

A different channel estimation approach was developed specifically for mmWave MIMO-Orthogonal Time Frequency and Space (OTFS) systems using a DL network proposed by [52] titled Sparse Bayesian Learning (SBL) DCNN (SBL-DCNN). The network utilizes multiple 2D convolution (Conv2D) layers with varying filter and kernel sizes, and a ReLU activation function is applied after each convolutional layer. Three features maps are generated, F1: is a reshaped mean vector in matrix form, F2: designed from the posterior covariance matrix, and F3: a learned sparsity mask, created by pruning values below a threshold $\beta$ and keeping superior delay-Doppler bins. F3 is split into real and imaginary components and combined with F1 and F2. A layered convolutional block with four Conv2D layers continuously extracts the sparsity structures, continuously reduces the kernel and filter sizes, and ResNet is used at the end of each SBL layer.

The system configuration involves setting epochs to 1000, a minimum batch size of 16, a ReduceLROnPlateau learning rate scheduler with a learning rate of 0.0001, and the use of the Adam optimizer. 32 transmit and receive antennas were used, with a carrier frequency set to 28 GHz and 150 8PSK-modulated pilot symbols. For the delay-Doppler (DD) grid, the delay is set to 16, the Doppler set to 32, and the sparsity equals 5. The ResNet weight is set to 0.1, and the pruning threshold is set to $\beta =0.0001$. TensorFlow 2.8 and Keras were used for the simulation, evaluating NMSE over an SNR range of -5 to 15 dB. The SBL-DCNN method is compared with conventional methods, including Orthogonal Matching Pursuit (OMP) [53] and SBL [54]. The SBL-DCNN demonstrates effective performance gains across the NMSE versus SNR curve, achieving lower NMSE values at low SNR. This demonstrates another effective DL-based channel estimation approach that outperforms conventional methods.

Table 4 expresses the results from the channel estimation DL techniques that were discussed.

This work proposes deep learning–assisted channel estimation for MIMO-OFDM systems, where neural networks refine conventional LS estimates to improve MSE and BER under frequency-selective fading and Doppler effects. Fully connected, CNN, and bi-LSTM architectures are evaluated, with recurrent models showing the strongest performance due to their ability to exploit temporal channel correlations. While the results demonstrate clear gains over LS and LMMSE estimators, the study primarily focuses on channel estimation rather than broader receiver design. As a result, it is not a central focus here, since more recent and comprehensive works achieve stronger performance improvements and deeper integration across the OFDM receiver chain.

4.4.2. Channel Equalization

The MIMO-OFDM Channel Estimation and Equalization Network (MOCEE-Net), presented in [55], is a DL approach for channel estimation and equalization. For channel estimation, an Optimal Deep Graph Convolutional Network (ODGCN) is employed to map the received signals to channel estimates, addressing sparse channel estimation in AWGN environments. The received signal is modeled using an estimated channel matrix, transmitted as a signal vector, and additive noise, where sparsity is exploited through a reformulation of the signal representation. The ReLU activation function is applied to suppress negative channel coefficients and enhance sparsity, while 2 hidden layers learn optimal channel characteristics via efficient weight matrices. Expectation-based optimization is used to further improve the estimation accuracy, leading to reduced BER and MSE, and enabling reliable recovery of transmitted symbols at the receiver.

For channel equalization, an Optimal Hyper Convolutional Neural Network (OHCNN) is proposed to map the estimated channel inputs, thereby equalizing the channel outputs while reducing system complexity through the use of shared network parameters. By leveraging convolutional layers trained using an LS-based initialization. OHCNN learns the mapping from noisy channels to true channel responses. Channel equalization is achieved through convolution operations combined with normalized gain distributions, resulting in improved MSE and BER. The model is trained under various fading conditions, including Rayleigh, Rician, and hybrid environments, with ReLU activation applied to suppress negative channel coefficients and linear normalization layers used to stabilize the outputs. A softmax classifier in the final layer identifies successfully equalized channels, which are then forwarded to the OFDM demodulator for data recovery. The OHCNN equalization framework is shown in Figure 8.

For the simulation, Matlab was used with 50 antennas at both the transmitter and receiver, employing a 64-QAM modulation scheme across 128 subcarriers. The channels were modeled under AWGN and Rayleigh fading conditions, with a CP length of 36 and 20 multi-path components. Performance was evaluated in terms of MSE over an SNR range of 0 to 20 dB. The MOCEE-Net was compared against conventional methods (LS and MMSE) as well as deep learning-based approaches (DLCNN, DLDNN, and DL-LSTM). Results show that MOCEE-Net, under both 8- and 64-pilot configurations, achieves lower MSE across the SNR range compared to other methods, demonstrating a more effective framework for channel estimation and equalization.

Another DL technique for channel equalization was introduced by [56], creating a Classification Weighted Deep Neural Network (CW-DNN). The CW-DNN consists of an input layer, three hidden layers, and an output layer. The hidden layer employs the ReLU activation function, while the output layer utilizes the tanh activation function. The CW-DNN performs direct data recovery by learning the channel characteristics of the received signals and pilot symbols. The real and imaginary components of the transmitted signals are separated and concatenation to form real-valued input vectors suitable for DNN processing. The DNN operates in two stages: the training stage and the testing stage. During training, the transmitted and received data pairs are known to decrease the MSE using the Mini-Batch Gradient Descent (MBGD) [57] to update the weights and biases. The CW-DNN introduces a classification-weighted cost function that penalizes incorrectly detected symbols more than correctly detected ones. After equalization, a minimum distance symbol slicer maps the network output to the nearest constellation point.

The CW-DNN processes transmitted data over AWGN and Rayleigh fading channels. The system uses 64 transmit and receive antennas, with 256 subcarriers, an FFT size of 256, a CP length of 64, and a spacing between each subcarrier of 15 kHz. The modulation schemes considered are 16-QAM and 32-QAM. The simulations are performed using Tensor-Flow 2.0, Keras, and Python. The training rate is configured to be 0.001. The CW-DNN is compared against other past methods such as Zero Forcing (ZF) [58], Back Propagation Neural Network (BPNN) [59], and a DNN [60], with the NMSE evaluated over the SNR range of 0 to 30 dB. The proposed method offers a computationally efficient alternative to previous techniques while providing improved performance across the entire SNR range. Table 5 summarizes the findings from the channel equalization DL techniques that were reviewed.

4.4.3. Other Related DL Approaches for Channel Estimation and Equalization

The process in the proposed OFDM autoencoder by [61] involves training a neural network to map transmitted signals to received signals, improving channel estimation. Using Dense-Nets, it refines low-resolution pilot signals into high-resolution channel impulse responses (CIRs). The model is trained on simulated data to minimize estimation error, enabling adaptation to varying channel conditions and throughput. This improves OFDM system performance, especially under fast fading, with fewer network parameters. This method used BLER for evaluation, which measure overall transmission errors, making it less useful for evaluating channel estimation accuracy.

The authors of [62] developed an intriguing Deep Learning approach for channel estimation in Hybrid Analog-Digital (HAD) mmWave massive MIMO systems. It adapts the Sparse Bayesian Learning (SBL) algorithm into a deep neural network (DNN). The method also incorporates time-domain channel correlation in its multi-block extension, improving the optimization of the measurement matrix. Their published simulation results demonstrate its superiority over traditional methods in both performance and computational efficiency. However, this is not included as a core paper within this review because other methods outperform it.

Another DL approach for channel estimation, published in [63], presents a Residual Channel Estimation Network (ResCENet) DNN for channel estimation in OFDM systems. This network integrates CNNs, Bi-RNNs, and FCNNs with residual skip connections and regularization, demonstrating superior performance over traditional methods in simulations. However, this approach is not included in the main discussion as it evaluates performance using BER over SNR, thereby limiting comparison to our selected core approaches using MSE for a more detailed analysis.

Additionally, a DL method for mmWave massive MIMO systems was introduced in [64]. The method uses a CNN-based channel estimation network, called the channel (H) Neural Network (HNN), which directly estimates the CSI from received data without requiring pilot signal estimation. HNN outperforms tradition schemes, offering improved estimation accuracy with lower computational complexity.

Finally, [65] proposes a DL-based channel equalizer for OFDM systems that outperform ZF and MMSE methods. The DL model learns to mitigate the effects of rapidly changing frequency dependent channels, adapting to various parameters such as pilots, modulations, and CP. Simulations show that the Dl-based equalizer achieves better performance over traditional methods. This was not added in the main discussion because it evaluates SER, which is not as relevant for measuring performance specifically at the equalization stage, unlike MSE or NMSE.

4.5. Demodulation

A DL-based demodulation technique targeting the Binary PSK (BPSK) modulation scheme was developed by [66] named DeepDeMod. DeepDeMod skips the synchronization step by directly loading the modulated signal into a neural network, dividing it into two stages: signal digitization and signal detection. The signal digitization stage takes the received signal and sends it to the product modulator, before passing it through a Band-Pass Filter (BPF) that contains both the message and carrier signals. A sampler is used to convert a continuous-time signal into a discrete-time signal for detection, utilizing a sampling rate to obtain K samples per bit period. For the signal detection stage, the DNN is used as a detector, mapping K samples per bit of received data into a single bit. A reshaping block adjusts the sampled signal to fit into the DNN input. Before detection, the DNN is trained using known signals to optimize its weights. This pre-trained DNN is then used to detect the transmitted bits from the received signal. The DNN detector consists of 6 layers: an input layer with an input size of K, an output layer, and 4 hidden layers. The hidden layers consist of 40, 20, 7, and 5 neurons, respectively, all of which use the ReLU activation function. The output layer consists of a single neuron and employs the sigmoid activation function. Binary Cross-Entropy (BCE) [67] is used for the loss function, and the Adam optimizer is used for optimization. A visual representation of the DeepDeMod framework is shown in Figure 9.

Using MATLAB for analysis, the model’s parameters include a learning rate of 0.01, a batch size of 250, and 100 epochs. The carrier frequency is configured to 915 MHz, K set to 10, and the sampling frequency set to 13.33 MHz. The DeepDeMod is tested under AWGN, Rayleigh fading, and in cases with frequency and phase offsets. The evaluation is tested for BER over an SNR range of -40 to 10 dB. The proposed method is compared against a 1D CNN [68], Neural Network Design (NND) [69], and Max Multi-layer Perception (MaxMLP) [70]. The DeepDeMod architecture achieves lower BER at negative SNR values, greatly outperforming conventional and other DL techniques for all 3 test cases provided. It was also tested in various environments and has consistently demonstrated effectiveness. Although it is tested for BPSK modulation, the technique demonstrates great potential for use with more complex modulation schemes, potentially outperforming traditional methods when applied to other modulation techniques.

Table 6 presents the results from the Demodulation DL architecture that was previously summarized.

4.5.1. Other Related DL Approaches

The authors proposed an LSTM-aided DNN for OFDM-DCSK demodulation [71], using recursive LSTM units to capture correlations between chaotic modulated signals and Fully Connected (FC) layers with batch normalization for robust feature extraction. Their simulations show improved BER performance compared with conventional OFDM Differential Chaos Shift Keying (DCSK) and even OFDM-BPSK systems at higher SNR over fading channels. Despite its promising results, this work was not included in our detailed analysis because other studies achieve better overall performance in conventional or CP-free OFDM systems while maintaining lower computational complexity. Therefore, it was deemed less relevant to the focus of our review.

Additionally, the work in [72] introduced a modified CNN-based receiver for OFDM/OQAM passive optical networks, replacing traditional channel estimation, equalization, and QAM demapping. The CNN learns the nonlinear channel distortions and recovers transmitted bits directly, achieving better BER performance than pilot-based Interference Approximation Method (IAM) receivers. For 16-QAM, the CNN-based receiver achieved an SNR improvement of up to 4.6 dB over long-reach fiber links, and it also demonstrated significant gains for 4-QAM. While these results demonstrate the potential of deep learning to enhance optical communication performance, especially for high-order modulation and extended transmission distances, other more recent studies have reported even higher-performing deep learning schemes.

The authors of [73] proposed another demodulation technique, Demod-CNN, a CNN-based demodulation approach for Intelligent Reflective Surface (IRS)-assisted multi-user MIMO OFDM systems. By separating the received complex signal into real and imaginary parts, the model maps the input directly to transmitted bits, improving BER and SER over conventional demodulation techniques, particularly at moderate to high SNR. Simulation results show that the CNN outperforms traditional methods once the SNR exceeds 5 dB, with larger gains at higher SNR.

The authors of [74] proposed a Fourier-layer Transformer Network (FTnet) for end-to-end digital demodulation in Intensity Modulation/Direct Detection (IM-DD) Radio over Fiber (RoF) systems, replacing traditional DSP steps. FTnet directly recovers bit streams from impaired signals, showing improved BER performance over traditional demodulators, Fully Connected Neural Networks (FCNNs), and standard Transformers in 16-QAM and 64-QAM RoF systems. It also performs well in RoF systems with wireless transmission across various power levels and distances. Nonetheless, other studies report better performance using alternative deep learning architectures.

SIGNETS, proposed in [75], is a group of convolutional neural network architectures for soft demodulation of m-QAM signals, optimized via Neural Architecture Search and hyper-parameter tuning. The networks achieve high demodulation accuracy across complex channel conditions, including multi-path fading, ISI, and non-linear distortions, without requiring explicit channel estimation. A hardware implementation on Field-Programmable Gate Array (FPGA) demonstrates practical feasibility, achieving 2.52 Mbits/s with 99.55% accuracy. While SIGNETS show strong performance, its computational cost is a detriment compared to other reviewed approaches.

Finally, [76] presents an end-to-end deep learning framework for burst signal demodulation, integrating detection, channel compensation, and adaptive masking into a unified system. A denoising autoencoder mitigates channel impairments, while Bi-LSTM and channel attention modules enhance signal localization and modulation classification. Experiments on real-world FSK, MSK, PSK, and 16QAM signals show the framework achieves superior bit error rate performance, particularly at low SNR, while enabling parallel demodulation across multiple signal types. Ablation studies confirm that end-to-end training, masking, and channel compensation are critical to the system’s robustness and accuracy, though some other approaches slightly outperform this method at lower SNR.

4.6. Decoding

A DL-based system for 5G LDPC Decoding is studied in [77], targeting IoT. The model starts with a Normalized Min Sum (NMS) [78] CNN framework that utilizes signal reception and LLR calculations for the symbols, which serve as the input to the NMS decoder. The channel noise estimation is passed through the CNN to produce an improved noise estimation, which reduces the error. The output is subtracted from the incoming signal to obtain a new signal vector representing the adjusted signal, which then undergoes a second round of decoding, along with the updated LLR, reflecting the CNN’s noise suppression.

The 1D CNN architecture is designed to have 4 convolutional layers, none of which are fully connected, nor do they contain dropout, max-pooling layers, or change the input and output layer dimensions. Each layer applies multiple kernels/filters to detect features, produce feature maps. A custom cost function is created to distinguish the actual outputs from the predicted outputs. This custom cost function utilizes a CNN to estimate channel noise, thereby improving the performance of NMS decoding. For CNN training, the noise samples are independent and identically distributed (i.i.d.) Gaussian random variables [79]. The convolutions slide the kernel over the input noise vector to compute the weighted sums, and then the ReLU activation function is applied at the output. Figure 10 visualizes the framework.

For modeling, TensorFlow, Google Colab, and MATLAB are used. The testing dataset comprises 60,000 samples, and the number of epochs is set to 20, using the Adam optimizer during training. Three tests were conducted with channel noise correlation coefficient set to 0.8, 0.5, and 0. The base code rate is set to 1/3, and the codeword length is set to 3808. The proposed DL model is compared against the conventional NMS and Sum-Product Algorithm (SPA) [80] methods. The evaluation compares BER over an SNR range of 0 to 5 dB. The method outperforms the conventional method when the channel noise correlation coefficient is set to 0.8 and 0.5, but compares roughly equally when it is set to 0 and at the cost of higher computational power to maintain accurate results.

The authors of [81] implement an alternative design based on a massive-MIMO configuration, called DLNet. The DLNet method is designed to estimate the transmitted symbol vector in MIMO systems using a deep learning-based method inspired by the projected gradient descent (PGD). The network architecture consists of 40 layers, each containing two hidden sublayers. The first hidden sublayer applies a ReLU activation layer function, and the second hidden sublayer is a piecewise soft Signum activation function. Each layer processes inputs from the received signal, and weights and biases are optimized during training to minimize detection error. The weight of the current layers is 0.03, and for the previous layers, it is 0.97. The Stochastic Gradient-Decent algorithm (SGD) [82] with the Adam optimizer is employed to train the DLNet. 5000 channel realizations are used for each batch. Figure 11 demonstrates the DLNet framework as a high-level overview.

For testing, multiple modulation schemes were evaluated: QPSK, 16-QAM, 64-QAM, and 256-QAM, under both a Rayleigh fading channel and a correlated M-MIMO channel. For evaluation of the proposed model, it was compared with the LS ZF detector [83], SDR [84], AMP [85], DetNet [86], OAMP-Net [87], and compared against the theoretical Matched-Filter lower bound (MFB) [88]. Under the Rayleigh fading model, the evaluation compares SER over SNR in the range of 2 to 15 dB, outperforming other methods and closely matching the MFB within the range of 2 to 25 dB, depending on the number of antennas used in the configuration. Under the correlated M-MIMO channel, the SER varies over the SNR range of 0 to 60 dB, depending on the number of antennas being used. Overall, the proposed DLNet outperforms the methods under both channels and for each modulation scheme while also being resource-efficient; however, reducing the framework’s complexity leads to a decrease in performance.

Table 7 shows the DL evaluations from the Decoding stage.

4.6.1. Other Related DL Approaches

The DL Decoding (DLD) technique, as proposed by [89], improves computational efficiency and outperforms other DL-based Sparse Code Multiple Access (SCMA) decoders. However, traditional methods, such as the Message Passing Algorithm (MPA) [90], still achieve slightly better BER performance in many scenarios. MPA is near-optimal for SCMA decoding, particularly under challenging channel conditions, albeit with higher computational complexity. Thus, while the DLD offers a favorable trade-off between complexity and performance, other decoding methods may still outperform it in terms of BER.

4.7. End-to-End Receiver Models and Integrated Approaches

4.7.1. End-to-End Architectures

The work shown in [91] proposes a DL receiver method for MIMO systems, eliminating the need for pilots. Using the DeepRx CNN receiver from [33] along with using a fully learned multiplicative transformation introduced by [92], the ML receiver processes the inputs and subsequently outputs the LLRs for each spatial stream. The transmit constellations are learned using the DeepRx receiver, and each transmitted signal is selected and learned from a constellation generated by neural networks that transform standard QAM points. Separate constellations are learned for each MIMO layer generated by linearly combining transformations that the network has learned. The learned constellations are normalized to have zero mean and unit energy, ensuring equal transmit power compared to conventional OFDM systems. The transformation networks utilize four fully connected hidden layers with tanh activations [93] to map the amplitude and phase of the QAM symbols, with each layer containing 16-32 neurons. The weighting network consists of four hidden layers, each with 8 to 16 neurons and ReLU activation functions. The output layer uses a softmax activation function to ensure a unit-sum weighting. The input of the DeepRx model consists of the received MIMO-OFDM signal over one slot, represented by samples across multiple subcarriers and OFDM symbols. A larger MIMO DeepRx CNN, which ranges from 512 to 2048 ResNet blocks, outputs LLRs that are passed to an LPDC decoder to recover the information bits. A loss function is introduced to prevent the formation of tightly clustered constellation points, which can limit the bit transformation per symbol using the ReLU function. The structure of the DL model is shown in Figure 12.

The training is performed using the Adam optimizer with a BCE loss calculated between the transmitted and detected bits, along with a distance-based loss to help prevent convergence due to the large constellations used. The weight factor $\lambda$ is set to 0.1 for 16-QAM and 0.05 for 64-QAM. The batch size is set to 10 with a learning rate of 0.0001. The carrier frequency is set to 3.5 GHz, the number of subcarriers is set to 72, the subcarrier spacing is 30 kHz apart, and the number of transmitter and receiver antennas is 2 and 4, respectively. The DL model is compared against established methods such as K-Best [94] using a perfect channel state, and Demodulation Reference Signal (DMRS) [95] channel state, and the evaluation focuses on BLER over SNR across the range of 0 to 14 dB. The proposed method achieves a low BLER across the entire SNR range without requiring any pilots. While it does not fully surpass conventional methods, it demonstrates strong effectiveness in pilotless signal detection.

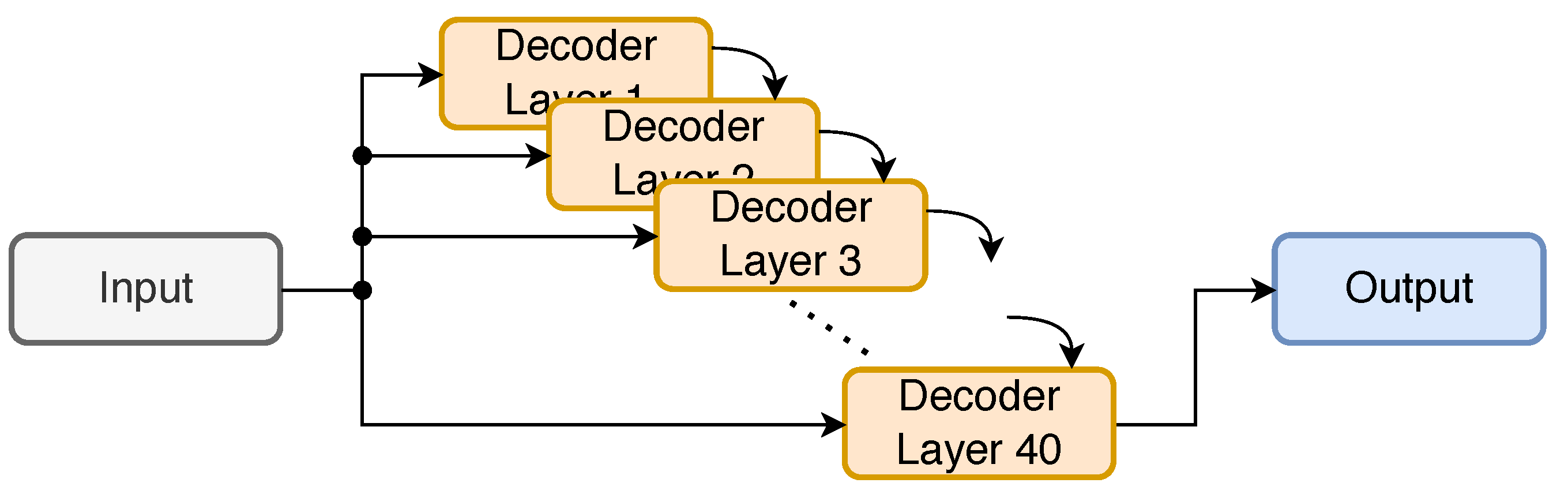
By contrast, the end-to-end wireless communication system presented by [96] is built using DNNs for both the transmitter and receiver, eliminating the need for traditional encoding, modulation, decoding, and demodulation blocks. A conditional generative adversarial network (GAN) models the channel in a data-driven manner, where the generator produces channel outputs conditioned on the transmitted signals and received pilot symbols, while the discriminator distinguishes between real and generated channel outputs. To address the challenge of high-dimensional complexity, convolutional neural networks (CNNs) are employed in the transmitter, receiver, and channel GAN, enabling efficient learning of long block sequences. The system optimizes an end-to-end cross-entropy loss between the transmitted and recovered information, with iterative training involving sequential updates to the receiver DNN, transmitter DNN, and conditional GAN. For smaller block sizes, Fully Connected Networks (FCNs) are employed, where both the transmitter and receiver DNNs comprise two hidden layers with 32 neurons each. The generator consists of three hidden layers with 128 neurons, and the discriminator comprises three hidden layers with 32 neurons each. For larger block sizes, CNNs are utilized: the transmitter includes an input layer, three convolutional layers with ReLU activation, and a convolutional layer, all followed by a power normalization layer, with varying output sizes. The receiver is composed of seven convolutional layers with ReLU activation, followed by a convolutional layer with Sigmoid activation, each with varying output sizes. The generator consists of three convolutional layers with ReLU activation, followed by a convolutional layer with a different output size for each. The discriminator comprises four convolutional layers with ReLU activation and two fully connected layers with ReLU and Sigmoid activations, respectively, each with distinct output sizes. A high-level overview is expressed in Figure 13.

This end-to-end system was evaluated on AWGN, Rayleigh fading, and frequency-selective multi-path channels. The learning rate for the FCN is set to 0.0001 for the transmitter, receiver, and discriminator. The input block sizes are 64 bits and 128 bits, the code rate is set to 0.5, with 16 bits for padding between each block. Across all channels, the deep learning approach achieves similar or better BER and BLER compared to conventional methods, while also benefiting from lower computational time due to the efficient CNN architectures.

Another MIMO-OFDM DL receiver is proposed using a transformer called SigT [97]. The SigT transformer converts the received signals into tokens by reshaping and permuting them based on physical properties, such as the number of antennas and subcarriers. It groups each antenna’s subcarriers into vectors, which serve as the tokens that feed into the transformer encoder [98]. The transformer encoder uses multi-head self-attention to capture the complex relations among the antennas and enhance valuable shared information. Then, the outputs are fed into convolutional layers, combined, and passed through a two-layer MLP, where the MSE is computed to update the weights.

For emulation, the framework is configured with a frequency of 3.5 GHz, 256 subcarriers, 4 transmitted antennas, 16 received antennas, and each containing one information symbol. The dataset for testing has 2560 signals. The learning rate for the Adam optimizer is 0.0001 with $\beta =0.9$, $\beta =0.999$, and $ϵ=0.999$. The SigT transformer evaluates accuracy over the SNR range of 0 to 40, comparing against FCDNN [99] and CSINet [100]. The results show that the SigT transformer outperforms previous end-to-end receiver methods, demonstrating the effectiveness of DL in improving MIMO signal recovery.

An additional deep learning model, Comm-Transformer, was proposed for OFDM systems by [101]. The Comm-Transformer incorporates an attention block with channel positional encoding to focus on subcarriers, using attention weights computed via an embedded Gaussian function. This is combined with multiple dual-1D convolutional blocks for feature extraction, where each convolution block passes through batch normalization to improve training before a second 1D convolution. Max pooling is applied to capture both local and global features, followed by a transpose convolution for up-sampling. The extracted features are then flattened and processed by GRU layers to model dependencies across subcarriers. The network uses a Sigmoid activation with binary cross-entropy loss for bit recovery, while mean squared error (MSE) is used for channel estimation.

The Comm-Transformer is trained under all sub-types of TDL channels [102] with 64 subcarriers, QPSK modulation, a carrier frequency of 4 GHz, Doppler shift of 111.18 Hz, CP length of 16, varying numbers of pilots (8, 16 or 64), 2 sub-frames, and a block length of 128 at a mobile speed of 8.32 m/s. Training utilizes a batch size of 256 over 1000 epochs, with a kernel size of 1×3 for the dual 1D convolutional layers, and employs the ADAM optimizer. Evaluation is performed in terms of NMSE over an SNR range of 10 to 30 dB against MMSE, LS, LSTM [103], and DNN [99], and in terms of BER over SNR against MMSE-GAMP64 [104], LS-GAMP64 [104], LSTM, DNN, and DeepRx [33]. Overall, the Comm-Transformer outperforms traditional and previously proposed deep learning methods in both NMSE and BER over TDL channels, while maintaining computational efficiency.

A deep learning model for the IEEE 802.11bd receiver was developed for next-generation vehicle-to-everything (NGV) communications [105], comprising two main components: frame capture and data-driven symbol recovery DNN. The frame capture module exploits the repeated sequence structure of the Legacy Short Training Field (L-STF) in the PPDU preamble, which contains 10 repeated sequences, and uses an autocorrelation method to mitigate Doppler spread and multipath effects. The data-driven DNN processes the Next Generation V (NGV) PPDU to recover transmitted symbols. Its architecture includes multiple convolutional blocks (ConvBlockA, ConvBlockB, IdentityBlock), while an OutputBlock extracts features using dense and softmax layers to produce symbol decisions. Data structure optimization is applied to both training and reference data.

For training, the Adam optimizer is used with a learning rate of 0.001, a batch size of 512, and 20 epochs. The proposed model is evaluated against traditional LS and Zero Forcing (ZF) algorithms under BPSK and QPSK modulation for OFDM. SER is measured over an SNR range of 4 to 20 dB across rural LoS, highway LoS, and urban LoS channels. The results show that the DL model significantly outperforms conventional methods, highlighting the advantages of deep learning for NGV communication.

Table 8 measures the effectiveness of end-to-end DL receiver models compared against conventional and DL methods.

4.7.2. Other Related DL Approaches

An end-to-end deep learning–based OFDM receiver by [106] jointly handles synchronization, CFO estimation, channel estimation, equalization, and demodulation using a single auto-encoder network. Their simulations and Software-Defined Radio (SDR) experiments show moderate BLER improvements over conventional receivers at given SNR and improved robustness to impairments. However, this work is not emphasized in the main discussion, as other papers report stronger overall performance.

A paper by [107] introduces DeepReceiver, an end-to-end deep learning–based wireless receiver that replaces the traditional receiver chain with a single neural network. A 1D convolutional DenseNet enables multi-bit recovery and supports blind reception across multiple modulation and coding schemes. While the method improves BER over conventional receivers under various impairments, its performance gains are limited compared to more recent approaches.

An end-to-end OFDM receiver called AIDER [108] uses an attentive deep convolutional network that learns directly from time-domain signals while exploiting the cyclic prefix. The model achieves improved BER over traditional receivers, particularly in channels with large delay spreads. However, its performance gains are modest compared to more recent DL-based receivers, which offer stronger SNR improvements.

TCD-Receiver [109] is a Transformer-based MIMO-OFDM receiver that performs joint channel estimation and signal detection using an end-to-end multi-head attention approach. The model outperforms LS, MMSE, and CNN-based receivers under challenging conditions such as limited pilot symbols, CP removal, and nonlinear noise, achieving results comparable to MMSE across various SNR.

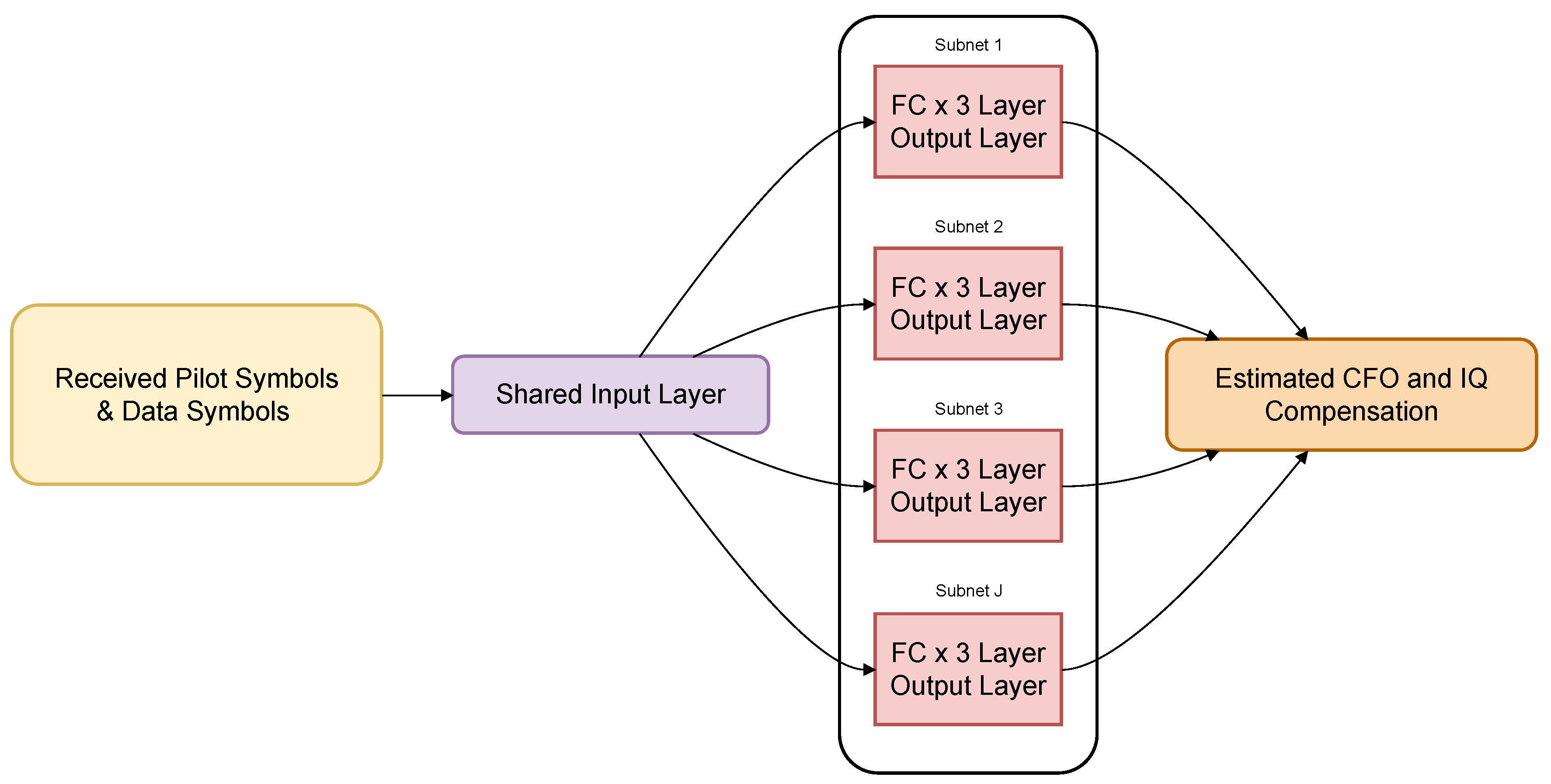
The work shown in [21] proposes end-to-end deep learning architectures to mitigate multiple hardware impairments in OFDM systems, using DLNN for single-antenna and 2×2 MIMO systems, and ResNet-DCDNN for 2×4 MIMO systems. DNN-based encoders and decoders jointly optimize signal mapping and impairment compensation. Their simulations show that these designs outperform traditional methods under AWGN and Rayleigh channels, with transfer learning addressing time-varying impairments, but the improvements over traditional approaches are lower than those of other papers mentioned in this section.

Another DL receiver design [110] establishes an intelligent OFDM receiver using a dual-channel CNN (DCNet) that integrates original IQ data with LS channel estimation knowledge, combining domain expertise with data-driven methods. The dual-stream architecture extracts and fuses features to enhance signal recovery, and simulations under various channel models, noise levels, pilot counts, and modulation schemes demonstrate significant BER improvements compared to DenseNet and MobileNetV3-based methods. However, it is outperformed by other recent works.

Additionally, [111] proposes a Deep Complex-valued Convolutional Neural Network (DCCNN) for OFDM receivers, which recovers information directly from time-domain signals without relying on DFT/IDFT. The model leverages the CP and employs a two-phase transfer learning scheme to train the channel equalizer and demodulator separately, thereby enhancing convergence and robustness in multi-path fading channels. Simulations show that the DCCNN outperforms conventional LS, LMMSE, and Adaptive Linear Minimum Mean Square Error (ALMMSE) estimators, particularly in frequency-selective fading and high SNR scenarios. It is one of the few works that utilized complex-valued neural networks, but it does not match the performance of other DL-based OFDM receiver designs.

The work by [112] proposes a machine learning–based OFDM receiver designed for extreme mobility scenarios, where severe Doppler shifts induce significant ICI. The receiver uses 2D convolutional ResNet layers to jointly estimate the channel and mitigate ICI, operating directly on the time- and frequency-domain received signals while relying only on sparse pilot reference signals. Simulations in 5G NR uplink scenarios demonstrate that the ML receiver significantly outperforms conventional LMMSE-based receivers, maintaining reliable demodulation even at very high user velocities. However, other recent studies achieve even better overall performance, so this work is highlighted mainly as a demonstration of ML robustness under extreme Doppler conditions rather than the best-performing OFDM receiver.

4.7.3. Performance Analysis of Full Deep Learning Implementations

The preceding subsections have examined end-to-end deep learning architectures that aim to replace the entire OFDM receiver pipeline with a single neural network. While these approaches demonstrate impressive performance in controlled scenarios, an alternative paradigm (stage-wise DL enhancement) offers complementary advantages that merit consideration.

Applying DL at each individual stage of an OFDM receiver has been shown to offer significant advantages over both conventional signal processing and monolithic end-to-end approaches. Each stage discussed throughout this survey benefits from the ability of deep learning models to learn complex, nonlinear relationships, adapt to time-varying channels, and mitigate noise and interference. By selectively replacing traditional algorithms with deep learning models at each stage, the receiver becomes more robust and capable of achieving lower error rates and improved signal fidelity while maintaining modularity and interpretability.

Cumulative Benefits of Stage-Wise Integration: Replacing each stage with deep learning ensures that the system is not just a black-box DL receiver, but a fully learning-assisted receiver where every key functional stage is enhanced, yielding cumulative performance improvements across the pipeline. Improved synchronization using DL techniques (Section 4.1) enhances the accuracy of subsequent stages by providing better-aligned signals for FFT processing. Enhanced channel estimation (Section 4.4.1) allows the equalization stage (Section 4.4.2) to produce cleaner symbol estimates by more accurately modeling channel distortions. This, in turn, improves demodulation accuracy (Section 4.5) and ultimately reduces bit error rate in the decoding stage (Section 4.6). Operating on real-valued or transformed signal representations, DL modules can efficiently handle both linear and nonlinear distortions, thereby making the receiver more resilient to multipath fading, interference, and low signal-to-noise ratio (SNR) conditions.

Advantages Over Monolithic End-to-End Approaches: While end-to-end receivers offer joint optimization benefits, stage-wise DL integration provides several key advantages. First, modularity enables individual stages to be updated, retrained, or replaced without requiring the redesign of the entire receiver, thereby facilitating incremental deployment and maintenance. Second, interpretability is preserved, as the function of each stage remains clearly defined, enabling easier debugging and performance analysis. Third, training complexity is reduced, as each stage can be trained independently on smaller datasets with well-defined objectives, rather than requiring massive end-to-end training. Fourth, hybrid deployment becomes possible, allowing critical stages to use DL while retaining conventional processing where it already performs optimally (e.g., FFT).

Performance Improvements: This stage-wise deep learning integration transforms the OFDM receiver into a fully optimized, flexible, and scalable system, providing substantial improvements in key metrics such as BER, NMSE, MSE, and SER, as demonstrated throughout the individual stage analyses in this section. The synchronization methods reviewed achieve significant reductions in frequency offset estimation error (up to 70.54% improvement in Section 4.1). Channel estimation techniques reduce NMSE by substantial margins compared to traditional LS and MMSE methods (Section 4.4.1). Equalization methods demonstrate improved BER performance across diverse channel conditions (Section 4.4.2). The demodulation and decoding stages demonstrate enhanced robustness to channel impairments and lower computational complexity during inference (Section 4.5 and Section 4.6).

Research Distribution and Gaps: Most studies, as summarized in Table 1, focus heavily on channel estimation and equalization (116 out of 174 papers, or 66.67%), followed by end-to-end designs (36 papers, 20.69%) and synchronization (8 papers, 4.6%). In contrast, demodulation (7 papers, 4.02%), CP removal (4 papers, 2.3%), decoding (3 papers, 1.72%), and FFT (0 papers) stages are comparatively underexplored. This distribution reflects both the critical importance of channel estimation in wireless systems and the significant challenges it presents, making it a natural focus for DL-based innovation. The absence of DL-based FFT replacements is notable and suggests that highly optimized conventional FFT implementations remain superior for this specific operation. The limited exploration of CP removal and decoding stages represents opportunities for future research.

5. Discussion

This section provides a critical analysis of the research landscape, performance trends, and open challenges in applying deep learning to OFDM receiver designs. We begin by presenting a comprehensive comparison of all methods reviewed in Section 4, followed by an in-depth discussion of research distribution, performance patterns, and future directions.

Table 9 summarizes the 16 core methods analyzed in detail throughout this survey. The table reveals several important patterns: (1) transformer-based architectures dominate recent end-to-end approaches, suggesting attention mechanisms are particularly well-suited for OFDM signal processing; (2) hybrid methods that combine learned feature extraction with conventional processing blocks (e.g., ResNet + LDPC) achieve strong performance while maintaining modularity; (3) channel estimation and equalization attract the most research attention with diverse architectural approaches; and (4) most methods focus on BER, NMSE, or MSE as primary evaluation metrics, with SNR ranges typically spanning 0-30 dB, facilitating the relative comparison across different approaches.

5.1. Research Distribution Analysis

The literature distribution, as shown in Table 1, provides important insights into where the research community has focused its efforts in applying deep learning to OFDM systems. The overwhelming emphasis on channel estimation and equalization (66.67% of surveyed papers) reflects several key factors. First, channel estimation is inherently a difficult problem in wireless communications, particularly in high-mobility scenarios, massive MIMO configurations, and millimeter-wave bands where pilot overhead becomes prohibitive. Second, channel estimation has a direct impact on all subsequent receiver stages, making improvements in this area particularly valuable. Third, the problem formulation naturally aligns with supervised learning paradigms—the channel can be estimated during training using known pilot symbols, and DL models can learn complex channel correlations that are difficult to capture with traditional parametric models.

The substantial attention to end-to-end receivers (20.69%) similarly reflects areas where deep learning offers clear advantages. Demodulation in the presence of residual channel impairments, nonlinear distortions, and unknown interference patterns can benefit significantly from DL’s ability to learn decision boundaries directly from data. End-to-end receivers represent an attempt to bypass the limitations of stage-wise optimization entirely, jointly learning all processing steps to maximize an end-to-end performance metric.

Conversely, the near-absence of work on FFT replacement (0 papers) is telling. The FFT is a mathematically optimal, computationally efficient algorithm with decades of optimization. Unlike other stages where channel variability and impairments create opportunities for learned adaptation, the FFT performs a deterministic mathematical transformation that is already executed optimally by conventional algorithms. This suggests that not all signal processing operations are suitable candidates for DL replacement—highly optimized, deterministic transformations may be best left to conventional methods.

The limited work on CP removal (2.30%), synchronization (4.60%), demodulation (4.02%), and decoding (1.72%) represents significant research gaps. Synchronization, in particular, remains a critical and challenging problem, especially in high-Doppler and low-SNR scenarios. The few existing DL-based synchronization methods reviewed in Section 4.1 demonstrate promising results, suggesting this area warrants further exploration. Similarly, decoding with modern codes, such as LDPC and Polar codes, could potentially benefit from learned decoding strategies that exploit the structure in error patterns.

5.2. Performance Trends Across Stages

Across the surveyed methods, several performance trends emerge. Channel estimation and equalization methods consistently demonstrate improvements in NMSE and MSE compared to traditional LS and MMSE estimators, particularly in low-SNR regimes and high-mobility scenarios. This aligns with theoretical expectations—DL models can exploit temporal and spatial correlations in the channel that are difficult to capture with conventional linear estimators.

For Demodulation, BER improvements are most pronounced in challenging channel conditions (e.g., highly frequency-selective fading, strong interference). In benign AWGN channels at high SNR, the performance gap between DL and conventional methods narrows, as both approach theoretical limits. This pattern suggests that DL’s primary value lies in handling complex, non-ideal scenarios rather than replacing conventional methods across all operating regimes.

End-to-end receivers show mixed results. Some approaches (e.g., TCD-Receiver, Comm-Transformer) demonstrate clear BER advantages over conventional receivers, while others (e.g., DeepRx without pilots) achieve competitive but not superior performance. This variability likely reflects differences in network architecture, training data quality and diversity, and the specific channel models considered. Notably, end-to-end methods that incorporate pilot symbols or conventional processing blocks (hybrid approaches) tend to outperform purely learned systems, suggesting that a judicious combination of conventional and learned components may be optimal.

Synchronization methods exhibit substantial improvements in specific metrics—up to a 70% reduction in mean absolute error for CFO estimation—demonstrating that even traditionally well-understood problems can benefit from data-driven approaches when hardware impairments and non-ideal conditions are considered.

5.3. Computational Complexity Considerations

A critical but often under-reported aspect of DL-based receiver design is computational complexity. While many papers demonstrate superior performance metrics, fewer provide detailed complexity analysis or real-time implementation results. Examples of works that specifically explore complexity are [56,81,101,113]. This represents a significant gap, as practical deployment requires not only good performance but also feasible computational requirements.

During the training phase, DL models require substantial computational resources and large labeled datasets [77,81,105,109]. For supervised methods, generating training data typically involves simulating or measuring channel responses under diverse conditions, which can be time-consuming and expensive. Online learning and transfer learning approaches may mitigate this burden by allowing models to adapt to new environments with minimal additional training; however, these techniques remain relatively unexplored in the context of the OFDM receiver.

During the inference phase, complexity varies widely depending on the architecture. Fully-connected networks can have millions of parameters, leading to high computational cost [18,66,99]. Convolutional architectures often achieve better efficiency by exploiting parameter sharing [31,33,47,91,92,114,115]. Transformer-based methods, while showing excellent performance, typically have quadratic complexity in sequence length [97,98,101,109,116], raising concerns for real-time processing of long OFDM frames. Quantization, pruning, and knowledge distillation techniques could potentially reduce inference complexity, but these optimizations are rarely discussed in the surveyed literature.

Compared to conventional algorithms, DL inference can be either more or less complex depending on the specific comparison. For example, iterative channel estimation or turbo decoding can be computationally expensive [6,38,78,80,103], and a well-designed neural network might achieve similar performance with lower latency. Conversely, replacing a simple FFT or linear equalization with a deep network would significantly increase complexity [3,4,41,50,58]. Hybrid approaches that use DL only where conventional methods struggle may offer the best complexity-performance trade-off.

Hardware acceleration using GPUs, FPGAs, or dedicated neural processing units (NPUs) can dramatically improve DL inference speed and energy efficiency [93]. However, the surveyed papers rarely discuss implementation on resource-constrained platforms, which are typical of mobile devices or IoT nodes [25,77]. This gap between research prototypes and practical deployment is a significant barrier to the real-world adoption of these technologies.

5.4. End-to-End vs. Stage-Wise Approaches: Trade-offs and Synergies

The choice between end-to-end and stage-wise DL integration involves several important trade-offs. End-to-end approaches offer the theoretical advantage of joint optimization: By training a single network to map received signals directly to decoded bits, the system can learn to optimize for the ultimate performance metric (e.g., bit error rate, or BER) rather than intermediate objectives (e.g., mean squared error, or MSE) in channel estimation. This joint optimization can discover processing strategies that deviate from conventional pipelines, potentially achieving superior performance.

However, end-to-end approaches face significant challenges. Training requires end-to-end differentiability, which can be challenging when incorporating certain conventional processing blocks (e.g., hard decision-making, discrete optimization). The resulting networks tend to be large and complex, requiring extensive training data covering diverse channel conditions, modulation schemes, and impairments. Lack of interpretability makes debugging and performance analysis difficult: when an end-to-end DL receiver fails, it is unclear which processing aspect is at fault. Finally, these monolithic systems are inflexible—adapting to new modulation schemes, channel models, or system parameters may require complete retraining.

Stage-wise DL integration addresses many of these limitations. Each stage can be designed, trained, and optimized independently, with clear objectives and interpretable performance metrics. Conventional blocks can be retained where they already perform well, reducing overall complexity and training requirements. Incremental deployment is possible—operators can selectively upgrade specific stages based on their particular performance bottlenecks. Hybrid approaches that combine learned and conventional processing at each stage offer additional flexibility.

The survey results suggest that hybrid strategies may be the most promising approach. For example, using learned channel estimation in conjunction with conventional MMSE equalization, or conventional synchronization followed by learned demodulation, enables each stage to leverage its strengths. Several high-performing methods reviewed in Section 4 already employ such hybrid designs, combining ResNet-based feature extraction with conventional decoding (e.g., LDPC), or using conventional FFT within a largely learned pipeline.

5.5. Open Challenges and Research Gaps

Despite the substantial progress documented in this survey, several significant challenges and research gaps remain:

5.5.1. Generalization Across Channel Conditions

Most DL-based methods are trained and tested on specific channel models (e.g., TDL, Rayleigh, Rician). Generalization to real-world channels that may not match training distributions remains largely unaddressed. Transfer learning, domain adaptation, and meta-learning techniques could potentially improve cross-environment generalization; however, they have seen limited application in OFDM receiver design.

5.5.2. Dataset Availability and Quality

High-quality, diverse datasets are essential for training robust DL models. However, publicly available datasets for OFDM receiver training are scarce, and most researchers rely on simulated data generated using specific channel models. Real-world measurement datasets that capture the full complexity of propagation environments, hardware impairments, and interference patterns would significantly benefit the research community. Efforts to standardize datasets and establish common benchmarks would facilitate fair comparison between methods.

5.5.3. Robustness to Distribution Shift

Wireless channels are inherently non-stationary, with statistics that change due to mobility, environmental variations, and interference patterns. DL models trained on historical data may degrade in performance when deployed in new conditions. Online learning, continual learning, and robust training techniques that account for distributional shift are critical for practical deployment but remain underexplored.

5.5.4. Theoretical Understanding

While empirical results demonstrate DL’s effectiveness, the theoretical understanding of why and when deep learning outperforms conventional methods remains limited. Establishing performance bounds, sample complexity results, and conditions for optimality would provide valuable guidance for architecture design and deployment decisions.

5.5.5. Integration with Communication Standards

Existing wireless standards (e.g., 5G NR, Wi-Fi 6) specify detailed signal processing procedures that leave limited room for DL-based modifications. Future standards (e.g., 6G) could be designed with DL integration in mind, but this requires collaboration between the ML and communications communities to ensure that learned components meet standardization requirements for interoperability, robustness, and verifiability.

5.5.6. Hardware Implementation and Energy Efficiency

Real-time implementation on power-constrained devices is essential for practical deployment. Most surveyed work evaluates performance using offline simulations without addressing implementation complexity, latency, or energy consumption. Research on efficient neural architectures, hardware-software co-design, and low-power inference is needed to bridge the gap between research prototypes and deployable systems.

5.6. Future Research Directions

Based on the analysis presented in this survey, we postulate several promising directions for future research:

5.6.1. Transformer Architectures for OFDM Reception

The recent emergence of transformer-based receivers demonstrates the potential of attention mechanisms to capture complex dependencies across subcarriers, antennas, and time. Future work could explore more sophisticated transformer architectures, incorporate inductive biases specific to OFDM (e.g., frequency-domain structure, cyclic prefix properties), and investigate efficient attention mechanisms to reduce computational complexity.

5.6.2. Physics-Informed Neural Networks

Incorporating known physical laws and signal processing principles into neural network architectures can improve sample efficiency, generalization, and interpretability. Physics-informed approaches that embed OFDM signal structure, channel models, or orthogonality constraints into network design remain largely unexplored and represent a promising direction for achieving both performance and robustness.

5.6.3. Federated Learning for Distributed Optimization

In cellular networks, distributed base stations and user equipment could collaboratively train receiver models using federated learning, enabling personalization to local channel conditions while preserving privacy. This paradigm could support adaptive, location-specific optimization without centralized data collection.

5.6.4. Joint Transmitter-Receiver Optimization

Most surveyed work focuses exclusively on receiver-side DL, treating the transmitter as a fixed entity. Joint optimization of learned transmitters and receivers (sometimes referred to as "autoencoder" approaches) could unlock additional performance gains by co-designing modulation, coding, and waveform generation with receiver processing. However, such approaches face significant challenges in maintaining backward compatibility with existing systems.

5.6.5. Integration with the 6G Vision

As the research community begins exploring 6G technologies, deep learning-based receivers are likely to play a central role. Integration with emerging paradigms such as reconfigurable intelligent surfaces (RIS), terahertz communications, and semantic communications will require new DL architectures and training methodologies tailored to these unique challenges.

5.6.6. Robustness and Adversarial Considerations

Wireless systems may face adversarial interference or jamming. The robustness of DL-based receivers to adversarial attacks—intentionally crafted signals designed to degrade performance—has received little attention. Research on adversarial robustness, certified defenses, and robust training techniques is needed to ensure reliable operation in contested environments.

6. Conclusions

6.1. Summary of Key Findings

This comprehensive survey has presented an in-depth, systematic analysis of deep learning applications across all stages of OFDM receiver processing, examining 339 papers published between 2019 and 2025 and providing a detailed analysis of the 16 highest-performing methods. The survey reveals that deep learning is not merely an incremental improvement over conventional signal processing, but represents a fundamental paradigm shift in how wireless receivers can be designed, offering data-driven adaptability, robust performance in challenging conditions, and the potential for joint optimization across traditionally separate processing stages.

Our stage-by-stage analysis demonstrates that DL methods achieve substantial performance improvements at virtually every point in the OFDM receiver pipeline. For synchronization, DL-based approaches accurately estimate I/Q imbalances, carrier frequency offsets, and coarse frequency offsets, with methods achieving a reduction in mean absolute error of up to 70.54% compared to conventional techniques. In CP removal, innovative DL architectures have demonstrated the feasibility of OFDM reception without cyclic prefixes or pilot symbols, while maintaining competitive performance and potentially reducing overhead to increase spectral efficiency. Channel estimation—the most extensively studied area with 54.72% of surveyed papers—shows consistent NMSE improvements of 3-10 dB over traditional LS and MMSE methods, particularly in low-SNR and high-mobility scenarios. Channel equalization methods leverage learned representations to achieve improved BER performance across diverse fading conditions. Demodulation and decoding stages benefit from DL’s ability to handle nonlinear distortions and exploit structure in error patterns, offering adaptable schemes that outperform fixed conventional algorithms in challenging environments.

Beyond individual stage enhancements, end-to-end deep learning receiver architectures represent an alternative approach that jointly optimizes all processing stages. Methods such as TCD-Receiver, Comm-Transformer, and SigT demonstrate that transformer-based architectures with attention mechanisms can capture complex dependencies across subcarriers, antennas, and time, achieving state-of-the-art performance. However, our analysis also reveals that hybrid approaches—selectively combining DL components with conventional processing—often achieve the best balance between performance, complexity, and interpretability.

6.2. Stage-Wise Performance Highlights

Table 9 in Section 5 provides a comprehensive comparison of the highest-performing methods across all stages. Key performance highlights include:

• Synchronization: GRU-based CFO estimation achieves 70.54% MAE reduction for 802.11n systems; LSTM approaches demonstrate robust CFO correction in massive MIMO scenarios.
• CP Removal: Convolutional residual networks enable pilotless, CP-free OFDM reception with performance approaching conventional systems that rely on these overheads.
• Channel Estimation: FSRCNN and SBL-DCNN methods achieve superior NMSE performance (3-10 dB improvement) across diverse channel models, including mmWave MIMO-OTFS systems.
• Channel Equalization: MOCEE-Net and CW-DNN demonstrate improved BER under both AWGN and Rayleigh fading conditions, with CW-DNN enabling direct data recovery using pilot symbols.
• Demodulation: DeepDeMod achieves robust BPSK demodulation under multiple impairments, including AWGN, Rayleigh fading, and frequency/phase offsets.
• Decoding: NMS CNN decoder for 5G LDPC and DLNet for massive MIMO demonstrate improved error correction across multiple modulation schemes (QPSK through 256-QAM).
• End-to-End: Transformer-based receivers (TCD-Receiver, SigT, Comm-Transformer) achieve state-of-the-art BER and NMSE performance, outperforming both conventional and earlier DL methods.

6.3. Maturity Assessment

The maturity of DL-based OFDM receiver components varies significantly across stages. Channel estimation and equalization are the most mature areas, with well-established architectures (CNNs, ResNets, hybrid approaches) that consistently outperform conventional methods and are approaching readiness for practical deployment, particularly in pilot-constrained scenarios such as massive MIMO. End-to-end architectures have rapidly advanced with the emergence of transformer models, though challenges in training complexity, generalization, and computational cost remain.

Conversely, several stages remain significantly underexplored. Synchronization (3.5% of papers), CP removal (0.9%), and decoding (1.5%) represent areas where DL applications are nascent and require substantial additional research before they can be deployed practically. The complete absence of viable DL-based FFT replacements (0 papers) is noteworthy, reflecting the mathematical optimality and computational efficiency of conventional FFT algorithms, which suggests that not all signal processing operations benefit from learned replacements.

From a deployment readiness perspective, stage-wise DL enhancement offers the most practical near-term path, allowing operators to selectively upgrade specific bottleneck stages while retaining proven conventional processing elsewhere. End-to-end receivers, while promising in research contexts, face significant barriers, including training complexity, limited interpretability, standardization challenges, and computational requirements that make widespread deployment premature without further innovation in efficient architectures and hardware acceleration.

6.4. Implications for Wireless Standards and Future Systems

The findings of this survey have important implications for the evolution of wireless communication standards and the development of next-generation systems. As stated earlier, current standards (5G NR, Wi-Fi 6) were designed around conventional signal processing assumptions, leaving limited room for DL integration. However, as the research community begins defining 6G requirements and architectures, there is an opportunity to design standards that explicitly accommodate learned components.

Key considerations for standards bodies include defining interfaces that enable DL-based processing while maintaining interoperability, establishing performance verification and testing procedures for learned components, addressing over-the-air training and model update mechanisms, and specifying computational complexity budgets suitable for different device classes (e.g., smartphones, IoT sensors, base stations).

Beyond incremental improvements to existing paradigms, DL-based receivers may enable entirely new communication architectures. Pilotless massive MIMO, adaptive waveform designs learned jointly between transmitter and receiver, semantic communication systems that optimize for task-relevant information rather than bit-level accuracy, and integration with reconfigurable intelligent surfaces all represent potential directions where DL could be transformative.

Deep learning has demonstrated compelling potential to transform OFDM receiver design from fixed, model-based processing pipelines into adaptive, intelligent systems that learn optimal strategies directly from data. The cumulative evidence across all the reviewed papers reveals consistent performance advantages across synchronization, CP removal, channel estimation and equalization, demodulation, decoding, and end-to-end architectures. Neural networks offer the ability to handle non-ideal conditions, such as multipath fading, interference, hardware impairments, and high mobility—more robustly than conventional methods, while potentially reducing computational complexity during inference through learned representations.

However, significant challenges remain before DL-based receivers achieve widespread practical deployment. Generalization across diverse real-world channel conditions, robustness to distribution shift, theoretical understanding of performance bounds, integration with existing standards, and energy-efficient implementation on resource-constrained devices all require continued research. The gap between laboratory performance on simulated channels and reliable operation in production networks is substantial.

The research community has laid a strong foundation. We believe that the next phase of development should focus on bridging the gap between research prototypes and production systems in order to be able to effectively evaluate these systems in real-world deployment scenarios, addressing open challenges in robustness and generalization, and working collaboratively with standards bodies and industry to ensure that the transformative potential of deep learning for wireless communications is realized in next-generation wireless systems that provide high throughput, low latency, and stable performance across diverse and demanding environments.