The Balanced Ternary as the Number Base of Complex MVL Systems

1. Introduction

The rapid development of AI necessitates the implementation of a programming language that is more capable of processing large volumes of data and differentiating between the different patterns of logical sequences that lead to a true solution. However, the binary system necessitates hardware and software with a high architectural capacity, necessitating the identification of a system that facilitates the growth of the binary system, thereby leveraging the accomplishments achieved to date in the domains of electronics and programming. This analysis necessitates the formulation of pertinent decisions; consequently, if it is deemed essential to commence from the outset, such a course of action must be pursued. The necessity of replacing the prevailing technology of logic gates and binary programming is becoming increasingly evident, as the fallacy of AI is being exposed with greater clarity. This replacement is not due to inherent flaws in the technology, but rather to the interests or visionary limitations of its proprietors. Undeniably, a data center of considerable magnitude intended for the training and sustenance of an AI system will be more susceptible to compromise, particularly in regard to its internal computer and environmental control systems. Consequently, to cultivate new forms of non-human intelligence, it is imperative to prioritize the development of two technologies:

• Logic gate technology, which is inextricably linked to the development of electronic devices capable of processing complex analog and digital signals.
• The emergence of a novel complex mathematical language is concomitant with the evolution of a logostic language that is capable of manipulating and controlling analog and digital signals, as well as of inferring responses with a high degree of wisdom.

Therefore, the implementation of the balanced ternary system and the complex MVL system is proposed. These systems, when utilized in conjunction, generate a novel system that is highly versatile and scalable for any odd base number. This is a novel numerical system, and as such, there is a paucity of relevant information regarding its study and application. However, we take into account the properties of both systems, which to date have been applied independently of each other.

This article is a continuation of the previous article, "Logical Implication of the Base-Four Number System".[2] In the following pages, we will describe its immense value and its close relationship with mathematical implementation, from its numerical elements to an elemental geometry, from which the nature of our $3D$ universe and beyond emerges.

2. General Assumptions

The fundamental principles governing the interrelationship of the balanced double ternary system have been established, whereby it has been determined that this system constitutes a novel entity, expanding the existing framework to encompass five digits. In order to accomplish this objective, it is imperative to deliberate on the integration of a complex axis that will serve to complement the real axis of a complex plane. The development of a sequence of complex numbers in base five results in the construction of unit squares along the length and width of the plane, which subsequently fills the plane.

2.1. Bi-Ternary

It is well established that "in a balanced base for every positive number, there exists an equal and opposite negative digit."

Balanced form representation is valid if and only if for every positive digit $d_{+}$, there exist a corresponding negative digit $d_{-}$, such that $f_D\left(d_{+}\right)=-f_D\left(d_{-}\right)$, then $b_{+}=b_{-}$, otherwise Therefore

i)

A balanced ternary system is a set equal to: $\{-1,0,1\}$ or $\{-,0,+\}$

ii)

A balanced ternary system situated on an imaginary line is a set with the following elements: $\{-i,0,i\}$.

Accordingly, the following assertion is made for the purpose of its definitions:

a)

Let ${\mathfrak{D}}_3:=\{T,0,1\}$ be a set of symbols, where a valued function $f=f_{{\mathfrak{D}}_3}:{\mathfrak{D}}_3\to \mathbb{Z}$, is defined by:

i)

$f\left(T\right)=-1$

ii)

$f\left(0\right)=0$

iii)

$f\left(1\right)=1$

b)

Let ${\mathfrak{D}}_3:=\{S,0,i\}$ be a set of symbols, where a valued function $f=f_{{\mathfrak{D}}_3}:{\mathfrak{D}}_3\to \mathbb{C}$, is defined by:

i)

$f\left(S\right)=-i$

ii)

$f\left(0\right)=0$

iii)

$f\left(1\right)=i$

Therefore, in order to ascertain every integer, it is necessary to apply the property of the concatenated string, with the respective symbols and calculate according to their position. The sequence $(d_n,...d_0)$ is defined by the property that each digit can alternatively represent one of the symbols $\{T,0,1\}$, or $\{S,0,i\}$. The length of the sequence is determined by $n+1$.

The evaluation function for the ternary system in its real and complex part is determined by: $v=v_3:={\mathfrak{D}}_3^{+}\to \mathbb{Z}$, and in its complex part by $z=z_3:={\mathfrak{D}}_3^{+}\to \mathbb{C}$.

Then, for every string

$$(d_n\dots d_0)\in {\mathfrak{D}}_3,v(d_n\dots d_0)=\sum _{i=0}^{n}f\left(d_i\right)3^i$$

and for its complex parts

$$(d_n\dots d_0)\in {\mathfrak{D}}_3,z(d_n\dots d_0)=\sum _{i=0}^{n}f\left(d_i\right)3^i$$

. The subsequent examples delineate the interrelation of digits and the methodology for their conversion to the real and complex decimal system.

Table 1. The evaluation of ternary balanced in a set real.

Evaluation table
Sequence			String			Decimal
C	B	A	$P_2$	$P_1$	$P_0$	$\mathbb{Z}$
T	1	0	$-1·\left(3^2\right)=-9$	$1·\left(3^1\right)=3$	$0·\left(3^0\right)=0$	$-6$
0	1	1	$0·\left(3^2\right)=0$	$1·\left(3^1\right)=3$	$1·\left(3^0\right)=1$	4
0	0	0	$0·\left(3^2\right)=0$	$0·\left(3^1\right)=0$	$0·\left(3^0\right)=0$	0
1	T	T	$1·\left(3^2\right)=9$	$-1·\left(3^1\right)=-3$	$-1·\left(3^0\right)=-1$	5
T	T	T	$-1·\left(3^2\right)=-9$	$-1·\left(3^1\right)=-3$	$-1·\left(3^0\right)=-1$	$-13$

Table 1. The evaluation of ternary balanced in a set real.

Evaluation table
Sequence			String			Decimal
C	B	A	$P_2$	$P_1$	$P_0$	$\mathbb{Z}$
T	1	0	$-1·\left(3^2\right)=-9$	$1·\left(3^1\right)=3$	$0·\left(3^0\right)=0$	$-6$
0	1	1	$0·\left(3^2\right)=0$	$1·\left(3^1\right)=3$	$1·\left(3^0\right)=1$	4
0	0	0	$0·\left(3^2\right)=0$	$0·\left(3^1\right)=0$	$0·\left(3^0\right)=0$	0
1	T	T	$1·\left(3^2\right)=9$	$-1·\left(3^1\right)=-3$	$-1·\left(3^0\right)=-1$	5
T	T	T	$-1·\left(3^2\right)=-9$	$-1·\left(3^1\right)=-3$	$-1·\left(3^0\right)=-1$	$-13$

It is common knowledge that the set of complex numbers is an extension of the set of real numbers. [3] Thus, the same axioms of associativity and distributivity apply to the set of complex numbers for both addition and multiplication. Additionally, the set of complex numbers has particular axioms that identify it. The most important are listed below.

2.1.1. Axiom of Complex Numbers

1.

$⊢\mathbb{R}\subseteq \mathbb{C}$

2.

$⊢1\in \mathbb{C}$

3.

$⊢i\in \mathbb{C}$

4.

$⊢\left(\right(A\in \mathbb{C}\wedge B\in \mathbb{C})\to (A+B)\in \mathbb{C})$

5.

$⊢\left(\right(A\in \mathbb{R}\wedge B\in \mathbb{R})\to (A+B)\in \mathbb{R})$

6.

$⊢\left(\right(A\in \mathbb{C}\wedge B\in \mathbb{C})\to (A·B)\in \mathbb{C})$

7.

$⊢\left(\right(A\in \mathbb{R}\wedge B\in \mathbb{R})\to (A·B)\in \mathbb{R})$

8.

$⊢\left(\right(A\in \mathbb{C}\wedge B\in \mathbb{C}\wedge C\in \mathbb{C})\to (A+B)+C)=(A+(B+C\left)\right))$

9.

$⊢\left(\right(A\in \mathbb{C}\wedge B\in \mathbb{C}\wedge C\in \mathbb{C})\to (A·B)·C)=(A·(B·C\left)\right))$

10.

$⊢\left(\right(i·i)+1=0$

11.

$⊢1\ne 0$

12.

$⊢\left(\right(A\in \mathbb{C}\wedge B\in \mathbb{C})\to (A+B)=(B+A\left)\right)$

13.

$⊢\left(\right(A\in \mathbb{C})\to (A+0)=A)$

14.

$⊢(A\in \mathbb{C})\to \exists x\in \mathbb{C}\left|\right(A+x)=0$

15.

$⊢(A\in \mathbb{C}\wedge A\ne 0)\to \exists x\in \mathbb{C}\left|\right(A·$x) = 1

With these rules, we can describe the relationship between complex and real numbers.

Table 2. The evaluation of ternary balanced in a set complex.

Evaluation table
Sequence			String			Complex
C	B	A	$P_2$	$P_1$	$P_0$	$\mathbb{C}$
S	i	0	$-i·\left(3^2\right)=-9$	$i·\left(3^1\right)=3$	$0·\left(3^0\right)=0$	$-6i$
0	i	i	$0·\left(3^2\right)=0$	$i·\left(3^1\right)=3$	$i·\left(3^0\right)=1$	$4i$
i	S	S	$i·\left(3^2\right)=9$	$-i·\left(3^1\right)=-3$	$-i·\left(3^0\right)=-1$	$5i$
S	S	S	$-i·\left(3^2\right)=-9$	$-i·\left(3^1\right)=-3$	$-i·\left(3^0\right)=-1$	$-13i$
0	0	0	$0·\left(3^2\right)=0$	$0·\left(3^1\right)=0$	$0·\left(3^0\right)=0$	0

Table 2. The evaluation of ternary balanced in a set complex.

Evaluation table
Sequence			String			Complex
C	B	A	$P_2$	$P_1$	$P_0$	$\mathbb{C}$
S	i	0	$-i·\left(3^2\right)=-9$	$i·\left(3^1\right)=3$	$0·\left(3^0\right)=0$	$-6i$
0	i	i	$0·\left(3^2\right)=0$	$i·\left(3^1\right)=3$	$i·\left(3^0\right)=1$	$4i$
i	S	S	$i·\left(3^2\right)=9$	$-i·\left(3^1\right)=-3$	$-i·\left(3^0\right)=-1$	$5i$
S	S	S	$-i·\left(3^2\right)=-9$	$-i·\left(3^1\right)=-3$	$-i·\left(3^0\right)=-1$	$-13i$
0	0	0	$0·\left(3^2\right)=0$	$0·\left(3^1\right)=0$	$0·\left(3^0\right)=0$	0

Notwithstanding the inherent value of i, from a two-dimensional or more dimensional graphical perspective, it signifies an imaginary unit. The conversion to real units will be applied in carrying out mathematical operations and special applications.

Therefore, in the complex balanced ternary system, if $i^2$ is equal to minus one $\left(i.e.,i^2=-1\right)$ or if i is the square root of minus one $\left(i.e.,i=\sqrt{-1}\right)$, then i is taken as the unit in both its positive part and its negative opposite $\{-i,i\}$. It is important to note that the imaginary term assigned to the unit i is inherently concrete. However, it should be acknowledged that this designation was conferred upon it within the context of the historical and cultural milieu that preceded it. Gerolamo Cardano 1545 in his "Arts Magna" and Bombelli worked with these numbers, [4] but they were considered useless. In 1637, Descartes named these kinds of numbers products of the "imagination". Then, Leonhard Euler used the symbol i to denote these numbers, and from there, they were considered useful and important in mathematics. In 1806, the Fundamental Theorem of Algebra, was proved by Jean-Robert Argand. [5] [6] Today, they are the most applicable system, from a single point on a complex plane to fractal geometry, electromagnetism and complex analysis, among others. The name for this nomenclature emerged from the recognition of the real numerical system’s inability to effectively solve square roots of negative numbers, a fundamental limitation that led to the emergence of the complex number system.

It is then valid to interleave both systems and constitute a complex plane, where each coordinate of a point on the plane can be explicitly indicated or the result of any operation can be correctly calculated.

The following table presents an evaluation of these two systems.

Table 3. The evaluation of ternary balanced in a set of complex with its real parts.

Evaluation table
Sequence			String			Complex
C	B	A	$P_2$	$P_1$	$P_0$	$\mathbb{C}$
S	i	T	$-i·\left(3^2\right)=-9i$	$i·\left(3^1\right)=3i$	$-1·\left(3^0\right)=0$	$(-1,-6i$
1	i	i	$1·\left(3^2\right)=9$	$i·\left(3^1\right)=3i$	$i·\left(3^0\right)=i$	$(9,4i)$
i	T	S	$i·\left(3^2\right)=9i$	$-1·\left(3^1\right)=-3$	$-i·\left(3^0\right)=-i$	$(-3,8i)$
S	0	S	$-i·\left(3^2\right)=-9i$	$0·\left(3^1\right)=0$	$-i·\left(3^0\right)=-1$	$-10i$
0	1	T	$0·\left(3^2\right)=0$	$1·\left(3^1\right)=3$	$-1·\left(3^0\right)=-1$	2
i	S	T	$i·\left(3^2\right)=9i$	$-i·\left(3^1\right)=-3i$	$-1·\left(3^0\right)=-1$	$(-1,6i)$
T	S	S	$-1·\left(3^2\right)=-9$	$-i·\left(3^1\right)=-3i$	$-i·\left(3^0\right)=-i$	$(-9,-4i)$
S	i	S	$-i·\left(3^2\right)=-9i$	$i·\left(3^1\right)=3i$	$-i·\left(3^0\right)=-i$	$7i$

Table 3. The evaluation of ternary balanced in a set of complex with its real parts.

Evaluation table
Sequence			String			Complex
C	B	A	$P_2$	$P_1$	$P_0$	$\mathbb{C}$
S	i	T	$-i·\left(3^2\right)=-9i$	$i·\left(3^1\right)=3i$	$-1·\left(3^0\right)=0$	$(-1,-6i$
1	i	i	$1·\left(3^2\right)=9$	$i·\left(3^1\right)=3i$	$i·\left(3^0\right)=i$	$(9,4i)$
i	T	S	$i·\left(3^2\right)=9i$	$-1·\left(3^1\right)=-3$	$-i·\left(3^0\right)=-i$	$(-3,8i)$
S	0	S	$-i·\left(3^2\right)=-9i$	$0·\left(3^1\right)=0$	$-i·\left(3^0\right)=-1$	$-10i$
0	1	T	$0·\left(3^2\right)=0$	$1·\left(3^1\right)=3$	$-1·\left(3^0\right)=-1$	2
i	S	T	$i·\left(3^2\right)=9i$	$-i·\left(3^1\right)=-3i$	$-1·\left(3^0\right)=-1$	$(-1,6i)$
T	S	S	$-1·\left(3^2\right)=-9$	$-i·\left(3^1\right)=-3i$	$-i·\left(3^0\right)=-i$	$(-9,-4i)$
S	i	S	$-i·\left(3^2\right)=-9i$	$i·\left(3^1\right)=3i$	$-i·\left(3^0\right)=-i$	$7i$

Armed with knowledge of the properties of complex numbers, we can use them to design a new, combined number system. Our goal is to apply this system to developing a programming language and new technologies that will make our artificial intelligence more efficient and wise and all of our research will lead to true, integral advancements in our civilization.

Some processing cases, especially in quantum computing, may already use complex elements, such as quaternions. However, the final interpretation falls into the binary machine language, and our goal is to expand this language.

2.1.2. Balanced Ternary and Quinary Base System

How are the ternary and quinary systems related?

To visualize this relationship, let’s break down each system.

More specifically, we will treat the system as both a balanced ternary system [7] and a balanced complex ternary system.

Balanced ternary

Elements: $\{-1,0,1\}$

Balanced complex ternary

Elements: $\{-i,0,i\}$

Balance Bi-ternary

Elements: $\{-1,-i,0,i,1\}$

The condition of a balanced system is met in all three cases, since each positive number has a corresponding negative number, regardless of its nature.

Standard Quinary

Elements: $\{0,1,2,3,4\}$ Converting a quinary system to a balanced system would require symbolizing the negative part of each positive part. This would result in a nine-digit system, but its representation would be too complicated for machine-language. To make a quinary system balanced, we will use the properties of the balanced ternary system and reduce it to a five-digit system.The most important thing is that we’re expanding the machine- language from a two-digit code to a five-digit code.

Standard base definition

a) 

Each base number is identified by the number of elements exchanged in a cycle, which is raised to the power in each cycle, increasing exponentially according to its position. $k_b·d_n^i,\dots k_b·d_0^0$ where $k_b$ each of the numbers of the base digits $i\in \mathbb{N},d=\left\{{\aleph }_0\right\}$

Reduced base definition

b) 

For any reduced numerical base, none of its elements can be greater than one, whether positive or negative.

Therefore, they will use a balanced ternary system as a calculation base, regardless of the number of digits that can be symbolized. So, $k_b·d_n^i,\dots k_b·d_0^0$ where $i\in \mathbb{N},d=3$ and $k_b$ is the number of digit represented by each symbol.

Considering the properties of standard and reduced bases, we developed a new base-five system operating on a ternary base. This combination gave us the extraordinary potential to implement a new programming language under a quinary system, which amplifies the capacity of the ternary system by a factor of two.

A significant advantage is that the ternary system is technologically advanced. Although it needs to be scaled to commercial levels and applied to non-human intelligence, significant progress has already been made. [8] [9] [10] Therefore, developing the mathematical theory behind it is worth the effort because it is the first step in allowing us to take advantage of its benefits and minimize or transform its disadvantages.

We describe this new architecture below.

3. Balanced Quinary, Be-Ternary Base

I developed different structures within the quinary system with a close interrelation to the ternary system. I checked and verified a quinary system using a base of five. However, as the elements do not consider numbers greater than one, the result had many gaps. Then, I tried a base of two for imaginary terms and a base of three for real numbers. However, the interrelation developed unevenly, so it did not represent a coherent sequence. Then, I tried a base of three for both imaginary and real numbers. This gave a more uniform and coherent result. Therefore, it is the calculation system we will use since it gives the expected results.

3.1. Elements

As proposed in Subsection $2.1$, we will use the symbols $\{T,S,0,i,1\}$ to represent the balanced quinary system.

3.2. Tables and Logical Gates

As a first step, we will define the logical relationship of a sequence of two digits that gives us an image of its negation, addition, and multiplication. This corresponds to a truth table of the logical functions NOT, OR and AND, which are the basic elements of every computational language. This analysis will provide us with concepts that differ from those obtained in a binary logic system.

3.2.1. P and Q Development

The development of a quinary system provides a set of 25 interrelations with an equal ability to represent a logical condition that must be defined.

We will use a subset of five elements to integrate a set of five subsets.

3.2.1.1. Proprieties

• The quinary system’s condition is preserved in its standard form when converted to the decimal system. Thus, the range will always be from $-4to4$ for real digits and from $-4ito4i$ for digits with an imaginary factor in a sequence between two quinary digits.
• At the unit level, each cycle generates five digits that form a unit square with dimensions equal to the square root of two because its diagonals are each two units long.
• The number containing zero specifies the coordinates of the center of the unit square.
• Adding another axis to obtain a complex $3D$ plane, the balance ternary system is preserved, but increases its base to seven digits and creates a 49-digit architecture.
• Adding another axis to obtain a complex $4D$ plane, the balance ternary system is preserved, but increases its base to nine digits and creates a 81-digit architecture.
• Adding another axis to obtain a complex $5D$ plane, the balanced ternary system is also preserved, but increases its base to eleven digits and creates a 121-digit architecture, and so on.
• Each subset of five, seven, nine, or more than eleven elements forms a unitary geometric body with the same number of coordinated points that can be circumscribed within a unitary sphere.
• The quantity of unitary geometric bodies is the same as the number of expanded digits. For 2D, it is 25; for 3D, it is 49; and so on. They are all well distributed within the maximum range. $(-4\le {\mathfrak{D}}_5\le 4),(-4i\le {\mathfrak{D}}_5\le 4i))$ or $(-13\le {\mathfrak{D}}_5\le 13),(-13i\le {\mathfrak{D}}_5\le 13i)$ and so on.
• In this way we can construct flat bodies on a flat surface, and on the flat surface geometric bodies with volume, then in a volumetric space construct a volumetric surface, on the volumetric surface, construct hyper-geometric bodies with a volume of volumetric space and again a surface of hyper-geometric bodies and so on.

First, let’s explore our basic quinary system, which is formed by two balanced ternary numbers. In this system, the base is five, and we can use it to represent geometric figures in a flat, complex coordinate system.

Table 4. The evaluation of quinary balanced, two digits

Sequence with two digits

Subset 1

Subset 2

Subset 3

Subset 4

Subset 5

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

T

T

$-4$

S

T

$(-1,-3i)$

0

T

$-1$

i

T

$(-1,3i)$

1

T

2

T

S

$(-3,-i)$

S

S

$-4i$

0

S

$-i$

i

S

$2i$

1

S

$(3,-i)$

T

0

$-3$

S

0

$-3i$

0

0

0

i

0

$3i$

1

0

3

T

i

$(-3,i)$

S

i

$-2i$

0

i

i

i

i

$4i$

1

i

$(3,i)$

T

1

$-2$

S

1

$(1,-3i)$

0

1

1

i

1

$(1,3i)$

1

1

4

Table 4. The evaluation of quinary balanced, two digits

Sequence with two digits

Subset 1

Subset 2

Subset 3

Subset 4

Subset 5

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

T

T

$-4$

S

T

$(-1,-3i)$

0

T

$-1$

i

T

$(-1,3i)$

1

T

2

T

S

$(-3,-i)$

S

S

$-4i$

0

S

$-i$

i

S

$2i$

1

S

$(3,-i)$

T

0

$-3$

S

0

$-3i$

0

0

0

i

0

$3i$

1

0

3

T

i

$(-3,i)$

S

i

$-2i$

0

i

i

i

i

$4i$

1

i

$(3,i)$

T

1

$-2$

S

1

$(1,-3i)$

0

1

1

i

1

$(1,3i)$

1

1

4

3.2.2. Inverse Gate

In the case of the NOT gate, we apply the symmetry or reflection property because we are looking for the inverse, or negation, of the input with its corresponding balanced value. This conforms to the main condition of a balanced base-n number system.

Table 5. The NOT gate table.

Not Gate
P	$\neg P$
T	1
S	i
0	0
i	S
1	T

Table 5. The NOT gate table.

Not Gate
P	$\neg P$
T	1
S	i
0	0
i	S
1	T

As a special case, note that zero has no symmetry or reflection; therefore, its negated value is itself.

We will analyze the NOT gate from two perspectives:

a)

The perspective of its complex value; and

b)

The perspective of its logical value.

• From the perspective of its complex value, the NOT gate’s meaning helps us understand the structure of geometric shapes.
• From the perspective of its logical value, we analyze the truth or falsity of its result. Some values will need to be probabilistically weighted to determine the degree of truth or falsity.

To analyze the logical perspective, we treat the elements of the set as units regardless of their nature, considering only the sign they exhibit when the function is activated.

Table 6. The NOT gate table.

Not Gate
p	$\neg p$	value	State
T	1	1	True
S	i	$1/2$	$50\%$ True
0	0	0	W
i	S	$-1/2$	$50\%$ False
1	T	$-1$	False

Table 6. The NOT gate table.

Not Gate
p	$\neg p$	value	State
T	1	1	True
S	i	$1/2$	$50\%$ True
0	0	0	W
i	S	$-1/2$	$50\%$ False
1	T	$-1$	False

"W" means "wisdom" because it is the midpoint between truth and falsehood. This will be explained in more detail later.

As the table above shows, proving the relationship between truth and falsehood is extremely difficult, since it requires consensus among all the elements of the set. Ultimately, the balance between truth and falsehood is established, but this balance may be disrupted when other variables of intersection, interference, or superficial passage are considered, depending on what is added or subtracted from the system.

3.2.3. What Is Truth?, What Is False?

What is truth and what is false? We must discern this question and determine the difference between the two as much as possible, if any, in order to implement our new programming language without ambiguity. We must also identify any differences precisely and validate each logical operation. One simple question will surely lead to many more, each one more incisive and demanding a precise answer. Therefore, we will try to understand these concepts by examining the different fields in which they are relevant and significant.

Our purpose is to describe the world we experience every day, physically and mentally, independently of matrix theories that claim reality is an illusion or a hologram and that we are gods. These theories only confuse and mislead us.

For each of us, our personal and social experiences are vast fields of scientific, technological, social, psychological, economic, and biological experimentation. Some of us are the experimenters, and some of us are the guinea pigs.

Given these universal conditions, absolute truth and absolute falsehood cannot exist because not everything is false, nor is everything true.

So, What is truth and what is false?

i)

The following is an initial approximation to its definition:

1.

Truth and falsehood are the opposite extremes of the same thing.

ii)

The second approximation to its definition:What is this thing?

2

The dichotomy between truth and falsehood is merely a conceptual framework; in reality, both are merely forms of information.

iii)

The third approximation to its definition: What do we mean by "information"?

3

Information is defined as data.

iv)

The fourth approximation to its definition: What is data?

4

Data are numbers. So, Data can be defined as a set of numerical values.

v

Conclusion

5

Then, the truth and the false are represented by a set of numerical values, and they are always opposite each other. Numbers can represent information. Then, it is possible that the information could be true or false.

In a social context

1.

What is true for one person, the same information is a lie for another.

• Our logical reasoning about truth and falsehood is always related to whether a proposition (A) is true or false in relation to a proposition (B). However, propositions A and B refer to specific truths or falsehoods; therefore, they are local truths or local falsehoods.
• If a proposition is universally accepted as true or false, that does not mean it is absolutely true or false because it refers to a particular proposition.
• The absolute truth and falsehood are the addition of all of them, but we will never know it. However, it is better this way because our world is really a field of possibilities.

But is the information true or false?

2.

Information is data, and data are numbers. Numbers can’t tell the difference between true and false.

3.

So, truth and falsehood are the "interpretation" of a supposedly intelligent individual who can understand the information they transmit or receive.

4.

But, "Interpretation is always political", biased, and focused on the person interpreting it, because it is based on his or her convenience.

5.

So, everyone sees in the opposite what they themselves have and don’t want to see.

But the social context is also governed by the laws of the relationship between numbers and each individual, regardless of their social status.

6

Have less and build more. $(-)\to +$

7

Have more and build more. $(+)\to +$

8

Have less and not build. $(-)\to 0$

9

Have more and not build. $(+)\to 0$

10

Have less and destroy more. $(-)\to -$

11

Have more and destroy more. $+\to -$

12

Conclusion:

i)

It is impossible for human beings to see the whole truth and falsehood.

ii

But we can be wise, because wisdom lies halfway between truth and falsehood.

iii)

Wisdom is achieved when opposites are equal and the value is zero. This is because that is where both see the truth or falsehood of their respective interpretations.

Note: The words "have" and "build" are used here to describe the action of signs plus, minus, and zero.

Fortunately, we have a very powerful tool that helps us intersect the values truth and falsehood into higher and more reliable ones. Although they fall short of describing absolute truth or falsehood, they are not really of much use in our daily lives. So, knowing something or a lot of truth or something or a lot of lies is enough to experience our exercises in wisdom. Being wise is our greatest challenge in this physical and mental environment and what will truly catapult us to the intellectual development of our civilization.

This powerful tool is mathematics, because it is the only one that has the property of infinity and has been necessary to construct a finite universe, like ours and many others similar to ours and many others even more different from ours.

As with every scientific advance that shapes our view of the world, the logic of mathematics must evolve to adapt to new ideas and perceptions. In the times of Plato, Boole, Leibniz, Newton, De Morgan, Hamilton, Descartes, Spinoza, Kant, Hegel, and many others, it was sufficient to declare what was true or false to describe the world. Although Aristotle may have questioned this, it later became convenient to consider a middle ground where our proposition could be either true or false. Today, we must adapt to a new reality in which artificial intelligence has such influence and controversies are invisible without a way to refute them. The range of possibilities then extends far beyond supposed probabilities because, ultimately, we must coexist with truth and lies. Now, we are probably more interested in knowing how much truth a truth contains and how much lie a lie contains.

For example, consider a chain of interrelated propositions under various scenarios. These propositions describe the facts and qualities necessary to reach a possible conclusion. They are presented in everyday language to familiarize us with logical reasoning, but they can be translated into symbols and logical connectives for logical algebra explanations.

3.2.4. Mental Exercise

• "Tomorrow, we will have a new president of the nation".
  • The proposition is that: "Tomorrow, we will have a new president of the nation." This is true even if we say it today. Why is it true? Because there will be scheduled elections tomorrow, and everything necessary for them to take place has been put in place.
• Mr. Smith says that the next president will be the Nationalist Party candidate.
• Mr. Conway says the new president will be the Unionist Party candidate.
  • At time "t" today, both propositions are possible.
  • However, tomorrow, one of them will be true and the other will be false.
  • If the Nationalist Party candidate wins, Mr. Smith’s proposition will be true. Otherwise, it will be false. For now, this proposition is still possible. Our supposition has not yet been confirmed as a true or officially result.
• If the candidates from the Nationalist and Unionist parties receive the same number of votes, which it is possible, then it will be a technical tie. Who will be president in that case?
  • Since this is a political event, it’s likely that the current vote will be canceled and a new election will be called.
• However, in an incorruptible political system, if the Nationalist and Unionist candidates receive an equal number of votes, resulting in a technical tie, both could be declared winners and presidents of the nation. They could then form a government in a politically logical conjunction.
  • In this case, both Mr. Smith’s and Mr. Conway’s propositions are true.
  • It is wise to share the opponent’s vision with your own.

But what is the probability of a tie in a national election?

What is the probability that both candidates would be declared winners in the event of a tie?

In real life, however, this is unlikely to happen. So, who could possibly win the election?

To answer this question, it is necessary to consider the many small probabilities that, when added or subtracted, can produce a favorable or unfavorable result for each candidate.

Once the most likely and most adverse possibilities have been weighed against each other, each possibility will have a specific weight.

6.

Suppose the candidate from the Nationalist Party has focused his campaign on discrediting his opponent by pointing out their true and false errors.

7.

Suppose the Unionist Party candidate directs his campaign toward promoting projects that benefit all social sectors in his country and avoids making negative comments about his opponent.

• The Nationalist Party candidate generates a lot of controversy on social media, and although he has fewer followers than his opponent, his followers tokenism every slogan he makes and share them repeatedly.
• The Unionist Party candidate doesn’t generate as much controversy as his opponent because his projects and proposals require more analysis. Neither his followers nor his opponent’s have the patience to read them, so the token factor is low.

8.

Which candidate has more probability of winning?

• We don’t know. At this time, it is impossible to know.
• However, there is other data.

  –

  There are commentators and analysts who strive for balance in their opinions.

  –

  There is information that marks trends and is published.

  –

  It is estimated that $15\%$ of the 80 million potential voters do not participate.

  –

  However, everyone is influenced to a certain degree by the information, because no one is immune to the political context of the moment.

  –

  Two hundred and fifty million tokens have been registered.

  –

  Could someone with access to data management make a mistake, intentionally or unintentionally, and alter the data? Yes, it is possible.

  –

  If crucial information is left in the hands of AI to count the 80 million possible votes, what is the likelihood that AI will make a mistake? The margin of error could be minimal or significant since the AI has information on all 250 million tokens.

• So, who will win?

9.

What is the probability that the new president, who is the candidate of the Nationalist Party, received only $30\%$ of the votes, but $54\%$ were officially reported in his favor?

10.

We won’t know, but... Then he will be declared the winner.

11.

So, our true conclusion from today to tomorrow is:

12.

We will certainly have a new president of the Republic tomorrow.

In a context as complex as the previous example, each proposition can be simplified and derived in each scenario. Visualize it as a quantum of information that will be linked to the next consequent and its antecedent part through a logical connector.

In the field of logic, there’s still much to be done on top of what’s already been done because everything new is built on what came before. Today, mathematicians, physicists, philosophers, logicians, astrophysicists, chemists, and computer scientists are standing on the shoulders of brilliant minds who came before us.

We need to include the formula for correctly formulating a logical question, the correct answer to that question, and the relevant logical symbols and connectives.

Questions are a common semantic issue in our daily dialogue, so why shouldn’t they be included in the propositional structure of logic? In our daily lives, there are many questions, perhaps more than answers. Under the logical framework, a question involving any of the research strands must explicitly address something, explaining exactly what it is, what it has, or what it does.

In modern logical language, "p then p is used.

In a logical language that implicitly contains the structure of a question, it would be something like:

• If we ask, "What is p?" we would probably receive the answer, "p is p"
• What is not-p? The answer would be, "not-p" is what is not "p".

In a polyvalent structure:

• "p" is a quantum of information because "p" represents anything that is explicitly well-defined.
• "Not-p" is a quantum field of information because everything that is not "p" is "not-p."

Example:

i)

If "p" is water.

ii)

Then "not-p" is everything that is not water.

iii)

In other words, "not-p" is everything that could be, except water.

However, this leads to a potential dead end. Therefore, we must encapsulate "not-p" in a block resembling "p" as much as possible. Perhaps, "not-p" could be a constituent of the structural parts of "p," because in some way "p" and "not-p" are the cause of the same thing.

This is just an outline of an idea that I will explain in an existing framework or, if necessary, develop its own logical-algebra framework.

Contradictions and contraries It is a logical inconsistency to affirm and deny the same fact at a given instant in time. For example, being and not being are contradictory as an affirmation and negation of the existence of something. However, this is not the case when we consider two qualities that the same object possesses simultaneously. Therefore, it is important to correctly discern the meaning of propositions and the method used, whether by inference, deduction, or intuition. This commitment is further reinforced by the rigorous validation of these principles through mathematical logic, which underscores our dedication to their advancement. We will begin by describing its most general applications, but we will need to develop and research the subject of mathematical logic in greater detail.

Everything that you currently are, you are in yours active form. But there is another part, which you are in potentially form, and what you are potentially is because you have not transformed it into active form. Then, you are in yours active form and you are also in yours potentially form, although in both cases you are in active or you are not in active form, but with their part in each part, but not in the same part, then to be or not to be, are the extremes of the same being.

The question "to be or not to be" does not constitute a contradiction. In our exposition or present hypothesis, the terms "be" and "not be" represent distinct possibilities between active form and potential form. However, it is important to note that both of these forms are intrinsically linked to the same object, for this reason, all in the universe undergo a cycle of birth, growth, maturation, and death.

Brief historical support Fortunately, all of the above are according Aristotle’s law of excluded of the middle.

This law establishes that every proposition must be either true or false; there is no third or middle option.

According to this law: For every proposition P, either P is true or its negation is $\neg P$ is true; there is no middle ground, But all these arguments are against Stoic determinism. Aristotle concluded that a third possibility must exist, in which the truth or falsity of our propositions A and B is not yet determined. This logical condition is called the "third excluded." In a particular example, Aristotle [1] uses the proposition "Tomorrow there will be a naval battle" or "Tomorrow there will not be a naval battle",11] which raises the principle of contradiction. This implies the necessity of a third solution, where the truth or falsity of a proposition can be estimated at a given time, because it is possible that what is true today will also be true tomorrow or it may not be true tomorrow.

Jan Łukasiewicz’s analytical mind and meticulous studies led to a more precise interpretation of Aristotelian logic. [12] [11] He introduced the concept of objective probability as a third value into his trivalent logic, which he developed brilliantly during the first half of the 20th century.

The polyvalent system, based on a modal proposition of possibilities, which includes the following modes: "Possibile, Impossibile, Contingens, Necessarium, Verum, and Falsum" True and False are included because the ternary, or trivalent system encompasses the binary, or bivalent system. Each polyvalent system of a higher grade must include all polyvalent of a lower grade.

In the study of polyvalent logic, we will delve into all of its algebraic interrelations, as well as its geometric interpretation in the formation of surfaces and bodies. This is only the beginning that is used to gain an overall understanding of this new branch of the field of logic. Truth, false and possibilities in a mathematical context. In a mathematical environment, the relationship between truth and falsehood is more precise. Therefore, we will express the similar concept mentioned above, taking into account all its mathematical implications.

Table 7. Logical values in a bivalent system.

Logic value
P	Logic
0	F
1	T

Table 7. Logical values in a bivalent system.

Logic value
P	Logic
0	F
1	T

In a binary system, it is well known that:

In a bivalent system, the logical matrix generates four different functions that can be expressed in the matrix.

Table 8. Logical matrix of bivalent system.

Bivalent logical matrix.
P	0	1	$\neg P$
0	1	1	1
1	0	1	0

Table 8. Logical matrix of bivalent system.

Bivalent logical matrix.
P	0	1	$\neg P$
0	1	1	1
1	0	1	0

In an original ternary system, proposed by Jan Lukasiewicz the digits are defined as $0,1$, and ${\displaystyle \frac{1}{2}}$. In this system, the third excluded digit is ${\displaystyle \frac{1}{2}}$. If the balanced ternary system structure is used, the digits are: $-1,0$, and 1. The standard ternary system uses the digits $0,1$, and 2.

Table 9. Logic values in Lukasiewicz’s trivalent and balanced ternary systems.

Logic value
P	Logic		Q	Logic
0	F		$-1$	F
$1/2$	It is Possible that...		0	It is Possible that...
1	T		1	T

Table 9. Logic values in Lukasiewicz’s trivalent and balanced ternary systems.

Logic value
P	Logic		Q	Logic
0	F		$-1$	F
$1/2$	It is Possible that...		0	It is Possible that...
1	T		1	T

The logical matrix in the ternary system was developed by Lukasiewicz in 1920, [11] as he himself states. This matrix generates five equations involving the value $1/2$. The four missing equations were taken from the bivalent system. Lukasiewicz deduced the negation equation through a logical thought experiment about whether "I will be in Warsaw at noon on December 21st of next year", which clearly established the possibility of being or not being in Warsaw at that time. The logical matrix is as follows:

Table 10. Logical matrix of trivalent system, developed by Lukasiewicz

Trivalent logical matrix.
C	0	$1/2$	1	$\neg C$
0	1	1	1	1
$1/2$	$1/2$	1	1	$1/2$
1	0	$1/2$	1	0

Table 10. Logical matrix of trivalent system, developed by Lukasiewicz

Trivalent logical matrix.
C	0	$1/2$	1	$\neg C$
0	1	1	1	1
$1/2$	$1/2$	1	1	$1/2$
1	0	$1/2$	1	0

In addition to Aristotle, there are many interesting works preceding and following Lukasiewicz that have increasingly forged the foundations of the Many-Valued Logic (MVL) system. MVL has wide applications in logic and logic circuits [8] [10] and, in recent years, in artificial intelligence because we are interested in knowing how truthful or deceitful we are. In the subsequent development of this article, we will deviate slightly from the previous section because we will focus on multi-valued balanced systems. However, we recognize that our analysis in the previous paragraphs undoubtedly laid the groundwork for this topic.

In previous cases, the degree of the third truth was established as being between 0 and 1, which is why it took the value of $1/2$. However, in a balanced ternary system, this value must be between $-1$ and 1. Now, the value of the third truth is zero.

Therefore, zero (in this article) is not considered as it normally is; rather, for our purposes, zero is the point that separates opposites, because zero does not have an opposite. Thus, the system is composed of the following digits: $-1,0$, and 1. In this system, zero equals $1/2$ or the point of separation, which is always halfway between $-1$ and 1. Our perception aligns with any balanced polyvalent system based on a ternary system, including quinary, septenary, nonary, and eleventh systems, even of major degree.

Before delving into the development of logic gates in a complex quinary system based on a balanced ternary system, I will define the generalities of the relationship and transformation of the ternary system, as well as their respective equivalences and simplest meanings. We know that our working materials are the balanced ternary and quinary systems. Together, they form a structure that expands the capacity of the ternary system by twofold. However, they are both limited by the balanced ternary system. The two systems, working together, raise the degree of truth to a value of five, which in some way brings us closer to the truth, moving us away from the lie, or brings us closer to the lie, moving us away from the truth.

Table 11. The balanced trivalent and the third value of truth.

Balanced trivalent 1D.
Base	Value	Change	%	Description
$-1$	$-1\Rightarrow$	0	0	False
$0\Rightarrow$	$1/2$	$1/2$	50	Possible truth or possible false
1	1	1	100	Truth

Table 11. The balanced trivalent and the third value of truth.

Balanced trivalent 1D.
Base	Value	Change	%	Description
$-1$	$-1\Rightarrow$	0	0	False
$0\Rightarrow$	$1/2$	$1/2$	50	Possible truth or possible false
1	1	1	100	Truth

In a balanced ternary system, the value of falsity is assigned to $-1$ instead of 0, as it is in an original ternary system. The unknown value is assigned to 0 instead of $1/2$, as it is in an original ternary system. This is because the range is different: from 0 to 1 in an original ternary system and from $-1$ to 1 in a balanced ternary system.

Table 12. The balanced Quinary system and the third and fourth value of truth.

Balanced Quinary, 2D.
Base	Value	Change	%	Description
$-1$	$-1\Rightarrow$	0	0	False
$-i$	$-1/2\Rightarrow$	$-1/4$	25	Possible more False
$0\Rightarrow$	$0\Rightarrow$	$1/2$	50	Possible truth or possible false
i	$1/2\Rightarrow$	$3/4$	75	Possible more truth
1	1	1	100	Truth

Table 12. The balanced Quinary system and the third and fourth value of truth.

Balanced Quinary, 2D.
Base	Value	Change	%	Description
$-1$	$-1\Rightarrow$	0	0	False
$-i$	$-1/2\Rightarrow$	$-1/4$	25	Possible more False
$0\Rightarrow$	$0\Rightarrow$	$1/2$	50	Possible truth or possible false
i	$1/2\Rightarrow$	$3/4$	75	Possible more truth
1	1	1	100	Truth

As we can see, zero always represents the midpoint between truth and falsehood. As a percentage, this equals $50\%$. This means that $50\%$ is true and $50\%$ is false at this point, fulfilling the law of the third truth value. From now on, I will refer to this point as the highest degree of Wisdom, because it represents balance between truth and falsehood. It is also the foundation for making decisions when faced with multiple options daily. Geometrically, it is the center of all the crossroads we face at every step.

Table 13. The balanced ternary and the third, fourth and fifth value of truth, where $-i,-j,i,j$ are imaginary units, negative and positive respectively.

Balanced Ternary 3D base seven.
Base	Value	Change	%	Description
$-1$	$-1\Rightarrow$	0	0	False
$-i$	$-1/8\Rightarrow$	$-1/8$	$12.5$	Possible more False
$-j$	$-1/4\Rightarrow$	$-1/4$	25	Possible less False
$0\Rightarrow$	$0\Rightarrow$	$1/2$	50	Possible truth or possible false
i	$1/8\Rightarrow$	$5/8$	$62.5$	Possible less truth
j	$1/4\Rightarrow$	$3/4$	75	Possible more truth
1	1	1	100	Truth

Table 13. The balanced ternary and the third, fourth and fifth value of truth, where $-i,-j,i,j$ are imaginary units, negative and positive respectively.

Balanced Ternary 3D base seven.
Base	Value	Change	%	Description
$-1$	$-1\Rightarrow$	0	0	False
$-i$	$-1/8\Rightarrow$	$-1/8$	$12.5$	Possible more False
$-j$	$-1/4\Rightarrow$	$-1/4$	25	Possible less False
$0\Rightarrow$	$0\Rightarrow$	$1/2$	50	Possible truth or possible false
i	$1/8\Rightarrow$	$5/8$	$62.5$	Possible less truth
j	$1/4\Rightarrow$	$3/4$	75	Possible more truth
1	1	1	100	Truth

The following table summarizes the previous tables and identifies the variables that represent the third, fourth, and fifth truth values.

Table 14. The balanced ternary and the third, fourth, and fifth values of truth.

Balanced septenary 3D.
Logic	Grade	Base	Value	Change	%	Description
F	Bivalent	$-1$	$-1\Rightarrow$	0	0	False
m F	Low Fifth	$-i$	$-1/8\Rightarrow$	$-1/8$	$12.5$	Possible more False
l F	Low Fourth	$-j$	$-1/4\Rightarrow$	$-1/4$	25	Possible less False
W	Third	$0\Rightarrow$	$0\Rightarrow$	$1/2$	50	Possible truth or possible false
l T	High Fifth	i	$1/8\Rightarrow$	$5/8$	$62.5$	Possible less truth
m T	High Fourth	j	$1/4\Rightarrow$	$3/4$	75	Possible more truth
T	Bivalent	1	1	1	100	Truth

Table 14. The balanced ternary and the third, fourth, and fifth values of truth.

Balanced septenary 3D.
Logic	Grade	Base	Value	Change	%	Description
F	Bivalent	$-1$	$-1\Rightarrow$	0	0	False
m F	Low Fifth	$-i$	$-1/8\Rightarrow$	$-1/8$	$12.5$	Possible more False
l F	Low Fourth	$-j$	$-1/4\Rightarrow$	$-1/4$	25	Possible less False
W	Third	$0\Rightarrow$	$0\Rightarrow$	$1/2$	50	Possible truth or possible false
l T	High Fifth	i	$1/8\Rightarrow$	$5/8$	$62.5$	Possible less truth
m T	High Fourth	j	$1/4\Rightarrow$	$3/4$	75	Possible more truth
T	Bivalent	1	1	1	100	Truth

The meaning of each term is described below.

1.

m F is closer to F, so it is defined as "falser." It corresponds to the fifth truth value at its lower end.

2.

l F is defined as a value farther from F, making it less false. It corresponds to the fourth truth value at its lower end.

3.

W is the middle ground between false and true. It is neither one nor the other but a balance point that we denote as wisdom. It corresponds to the third truth value. Other authors denote it as either "U" or "I", as it is "Unknown" and "Indeterminate".

4.

lT is the value farthest from the truth, so it is defined as the least true. It corresponds to the fifth truth value at its upper end.

5.

mF is the value closest to the truth. It is defined as the truest and corresponds to the fourth truth value at its upper end.

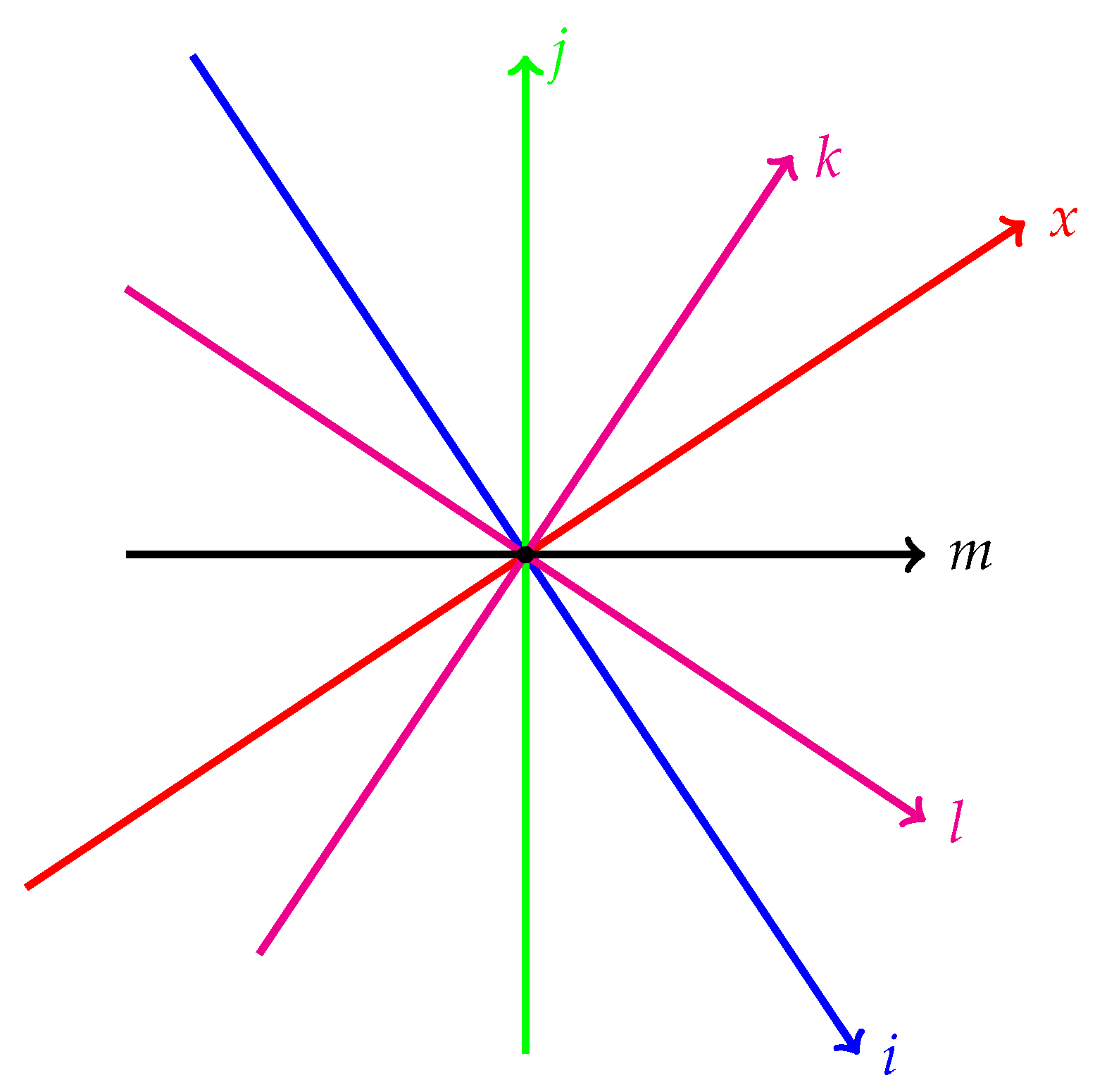
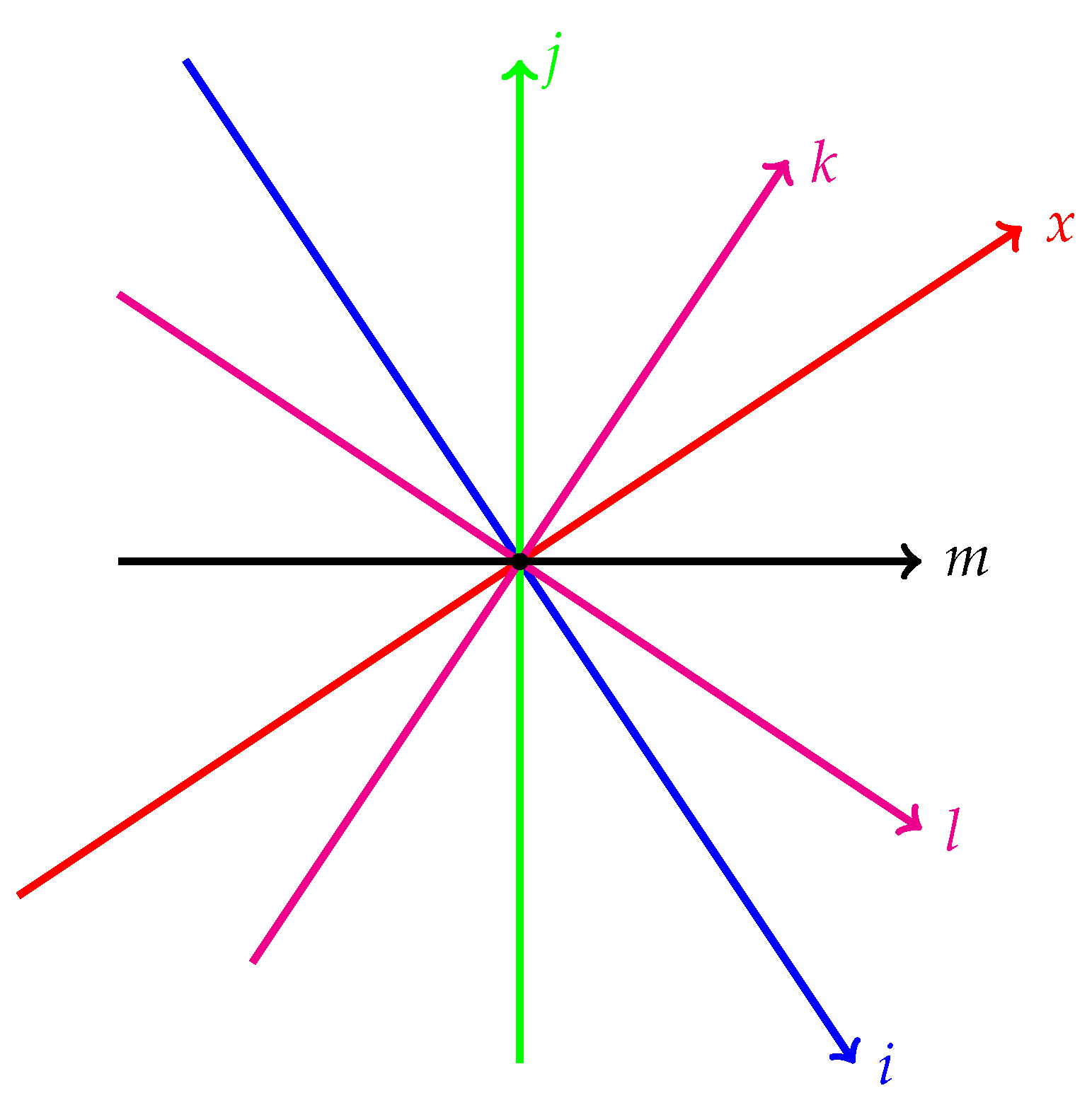
6.

$-i$ is the imaginary coordinate of the horizontal axis in a 3D complex plane and corresponds to the extreme of the negative opposites of this axis.

7.

$-j$ is the imaginary coordinate of the vertical axis in a complex 3D plane. It corresponds to the end of the negative opposites of this axis.

8.

0 is the separation point between opposites of the real and imaginary axes in a complex 3D plane.

9.

i is the imaginary coordinate of the horizontal axis in a 3D complex plane and corresponds to the end of the positive opposites of this axis.

10.

j is the imaginary coordinate of the vertical axis in a 3D complex plane and corresponds to the end of the positive opposites of this axis.

11.

The numbers $-1$ and 1 represent the opposite ends of the horizontal real axis.

A complex plane is derived from a balanced ternary structure when an imaginary axis is added. This defines a complex surface that provides the framework for building a complex body in a Quinary structure. The distribution of the areas that can be built is determined by a natural succession of numbers related to the coordinates of a complex plane. This distribution clearly shows the pattern of development of a sequence as the positions of the digits of a given number increase. These sequences can be precisely cataloged into cycles, each of which is composed of five coordinate points. One of these points is the center, and the other four are one unit away from the center. They can all be graphed on the plane, and their pattern can be displayed with the desired number of digits.

The greater the number, the greater the number of unit areas.

While the development of the series itself may not be of paramount importance, but this process does yield a precise distribution of the unit areas in specific positions on the complex plane. This distribution can form a pattern that subsequently reveals another facet of the numbers. Irrespective of the numerical values incorporated within the sequence, the configuration will invariably manifest as a five-point cycle pattern.

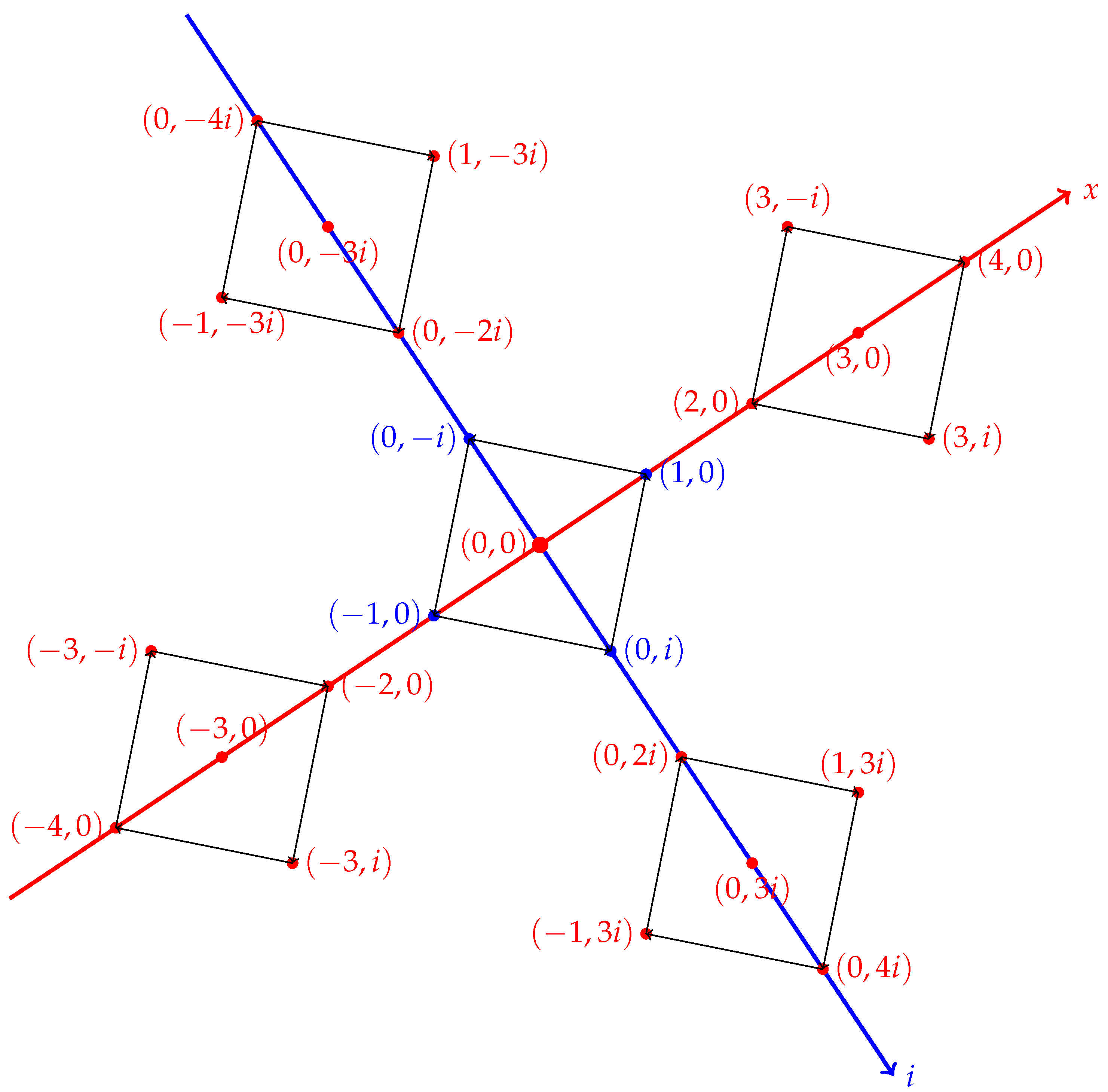
Complex 2D plane For example, the distribution of the areas in Table 4 is shown in the graph below.

Figure 1. The unit areas in a complex plane are a series of quinary complexes and balanced ternaries with two complex digits. The series develops 25 quantities, or coordinate points.

Figure 1. The unit areas in a complex plane are a series of quinary complexes and balanced ternaries with two complex digits. The series develops 25 quantities, or coordinate points.

Furthermore, it has been observed that as the number increases, each position corresponds to a specific range within which the positive and negative numbers of the real part and the positive and negative complex numbers of the imaginary part will fall.

• For a two-digit number, for example; the range is from $-4$ to 4 on the real axis and from $-4i$ to $4i$ on the imaginary axis.
• In the case of a three-digit number, the range is from $-13$ to 13 on the real axis and from $-13i$ to $13i$ on the imaginary axis.
• For a four-digit number, the range is from $-40$ to 40 on the real axis and from $-40i$ to $40i$ on the imaginary axis, and so forth.

The unit area is not, in the conventional sense, that of a square with the value of its sides as one, because the complex unit square has the value of its sides as the square root of two, given that its diagonals are equal to two complex units.

Every unitary complex area has a center. This center is defined by the number that contains zero in its cycle, which places it at the logical center of wisdom. Therefore, regardless of the area’s position, its center is always located according to the coordinate that implies a zero in its structure. Arithmetically, zero contributes nothing more than the positional value in the first quinary unit. The center becomes a starting point from which eight paths can be taken, each leading to a different coordinate point. Accessing any of the eight points is a one-time option, but once taken, the result is that the eight options reappear at the new position because the new coordinate point is also the center of its unitary area. But this center is virtual, yet has the same properties as a real center because it is necessary to always be in a real or imaginary geometric center. This suggests that the entire map of the complex field can be traversed as a random walk, similar to a photon in the center of the sun that emerges to the surface.

Figure 2. From the center of the unit area, there are nine options: four are one-step, four are the square root of two-step, and one is the center itself with no step.

Figure 2. From the center of the unit area, there are nine options: four are one-step, four are the square root of two-step, and one is the center itself with no step.

We can follow or simulate a trajectory on the plane and verify that, with each advance, the eight possible options are re-planned. There is a ninth option that turns back to the center, meaning no steps have been taken, so it remains stable. In total, then, there are nine options.

There is a mathematical formula that tells us every number is the center of all others, (but that is not the subject of this study). In our personal experience and daily lives, this feeling is real for each of us. Each of us feels as if we are the center of the universe because everything revolves around us. This feeling has a mathematical basis that we will discuss later. For now, the same concept is presented in the structure of the quinary system under the mechanics of the balanced ternary system.

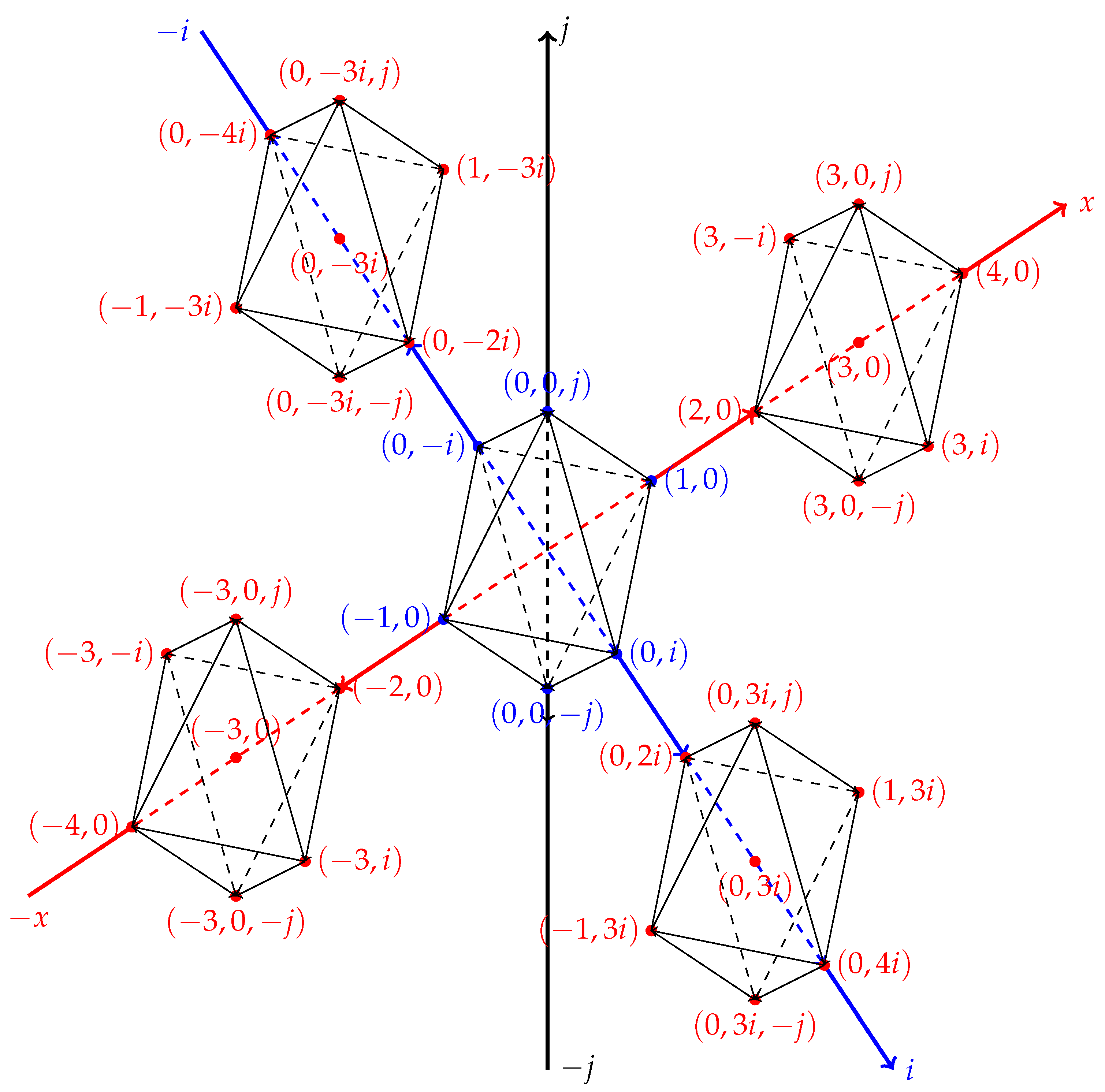
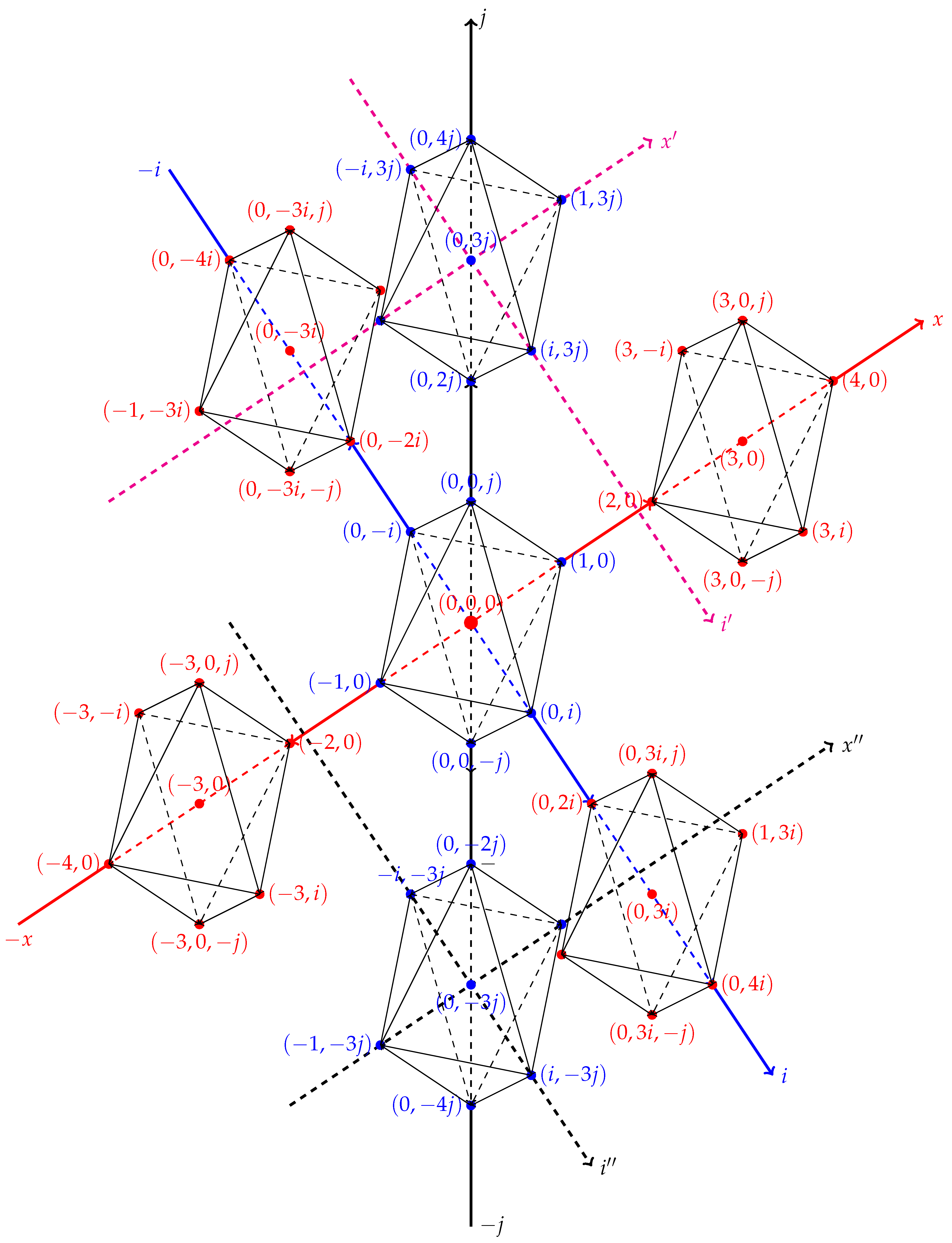
Complex 3D plane In a 3D plane, the structure of the quinary and balanced ternary systems requires a seven-digit numbering system, which is further expanded to a base-three configuration. The interrelation of all coordinate points now allows us to construct a 3D body, which we will denote as a unit volume. This structure is built upon the unit area platform of the 2D system as two inverted pyramids.

The distribution of unit volumes in three dimensions follows the same configuration as unit areas in two dimensions.

Figure 3. The unit body in a $3D$ complex plane are a series of septenary complexes and balanced ternaries with two complex digits. The series develops 49 bodies, or 343 coordinate points.

Figure 3. The unit body in a $3D$ complex plane are a series of septenary complexes and balanced ternaries with two complex digits. The series develops 49 bodies, or 343 coordinate points.

The numbers plotted in the previous figure correspond to the Table 21 below, though only the first five of the twenty-five unit volumes are plotted.

For clarity, the graph only shows the three coordinates involving the j-axis. The coordinates of the central area base corresponding to the 2D plane are described by the intersection of the x- and i-axes.

Seven cardinal points converge at the center of the unit volume: East, West, North, South, Up, Down, and Center. The distance from the center to any neighboring cardinal point is one unit, and the distance between vertices is the square root of two. A point at the center has seven options because its surroundings are confined to its volumetric dimension. When we calculate the distance between each point and the center, we see that we can reach four surrounding points in one step, four in the square root of two steps, and one without taking a step, since not moving is also an option.

Saying "advance a step the size of the square root of two" is merely symbolic because it’s an immeasurable step. For now, we’ll stick with this idea, and later we’ll delve deeper into the philosophical meaning of taking a step of this size.

Let’s assume our center has the coordinates $(2,2i)$. Then, the surrounding points are: $(1,2i),(2,3i),(3,2i)$, and $(2,i)$. The points farthest away from our central point, yet still neighboring it, are: $(1,i),(1,3i),(3,3i)$, and $(3,i)$. Calculating the distance from $(2,2i)$ to each of these points yields the following results:

• From $(2,2i)$ to $(1,2i)$: $d=\sqrt{{(1-2)}^2+{(2i-2i)}^2}=\sqrt{-1^2}=1u$
• For the points: $(2,2i)$ to $(2,3i)$: $d=\sqrt{{(2-2)}^2+{(3i-2i)}^2}=\sqrt{i^2}=\left(\sqrt{1^2}\right)=1u$
• The point $(2,2i)$ and $(3,3i)$,then $d=\sqrt{{(3-2)}^2+{(3i-2i)}^2}=\sqrt{1^2+1^2}=\sqrt{2}u$
• In order to calculate the side of our square, we need to identify two points on its adjacent vertices. $(2,i)$ and $(1,2i)$$d=\sqrt{{(2-1)}^2+{(i-2i)}^2}=\sqrt{1^2+{|-i|}^2}=\sqrt{2}u$
• The diagonal of our square, if the opposite points are: $(3,2i)$ and $1,2i),$$d=\sqrt{{(3-1)}^2+{(2i-2i)}^2}=\sqrt{2^2}=2u$

The area of our complex element is really 2 square units because the sides of the square are equal to $\sqrt{2}$ and $A=\sqrt{2}u\times \sqrt{2}u=2u^2$ This characteristic apparently means nothing important. However, in a later analysis, we will describe how the elementary numbers of every number system—the numbers $2,3$, and the $\sqrt{2}$— play a very important role. This role is still unknown to us, as we are standing on the edge of a deep well. Dimensional structure Below is a brief overview of what a dimensional structure is. The intention is to elaborate further in an article focused on this topic. For now, this is just a short description.

Each dimension has a specific size of objects that must be structurally consistent to exist within its limits.

• There is a lower limit from which the base substrate is built. This substrate is constituted by the fundamental particle from which all other complex bodies are formed. This lower limit is the quantum state and field of that dimension.
• There is also an upper limit to the size of the largest possible body. This body must be structurally consistent and dynamic and capable of performing all its functions within this dimension’s environment. If it grows beyond this limit, it collapses and reintegrates its parts to a size that allows it to remain structurally consistent within its dimension.

For example, in our 3D dimension,

i)

The lower limit is the size of atoms. Atoms form the surface on which we walk and the volume in which we swim because our fundamental environment is an ocean of atoms.

ii)

Below the level of atoms—whether they are quarks or any other particle—everything in our dimension will be inconsistent, a fact that has been studied by CERN.

iii)

The upper limit is the size of galaxies, which are made of atoms, like all their parts.

iv)

Like a red giant or any other star or planet that grows beyond its limit, a galaxy’s structure will implode above a normal level.

Beyond the galaxies, what we can comprehend and measure in this dimension may only be images reflected in a mirror. Everything formed is finite, even if it comes from something infinite. Each body marks its finitude with a numerical structure called Pakal in the Alom system. Pakal means "shield" in Mayan. So, beyond galaxies, a surface of galaxies forms, which becomes the fundamental particle of another dimension. There, groups of galaxies form and become like molecules or dimensional bodies of that dimension.

Every dimensional structure has the same mathematical dynamic pattern that repeats in each dimension.

The fundamental numbers, which serve to form all other numbers like fundamental particles do, are 2 and 3.

• Three is the fusion of $(-1,0,1)$ and gives meaning to differences, revealing their truth, falsity, or possibility.
• Two is the only prime number and gives meaning to similarities because being similar or different requires two elements, propositions, or numerical values.
  • Within three, zero separates opposites.
  • At each coordinate point where zero is present, there is a non-step halfway between the preceding and following steps.
• $-1$ and 1 give meaning to everything measurable and constitute a module with an absolute value of two.
• Therefore, two is the unit of everything measurable. From two, the unit of everything immeasurable also emerges as it relates to -1 and 1, generating a product equal to the square root of two.
• Thus, the square root of two is the unit of everything that cannot be measured.

The function of numbers in any dimension is to count and measure. They count structures from the simplest to the most complex and measure structures to record their proportions and sizes. Together, two and three count and measure everything that exists, as well as its size in countable, measurable, uncountable, and incommensurable quantities. Together, two and three form a balanced quinary system, whose lower and upper limits are defined by the ternary system and preserved in all dimensions. Therefore, the balanced ternary system can grow in multidimensional spaces, from dimension $1/2$ to infinity.

3.2.5. OR Gates with Five Inputs

The truth tables for the OR and AND gates in the Quinary system for a two-dimensional complex plane are as follows: This system processes five input signals, and the corresponding values for each truth level are used. The function of the gate is the algebraic value of the sum or product, respectively. For values exceeding one, the maximum value of one is considered. This provides a clear understanding of the output value when combining both input values.

Table 15. The OR gate table.

OR Gate Matrix
		Q
$P\vee Q$		$-1$	$-1/2$	0	$1/2$	1
	$-1$	$-1$	$-1$	$-1$	$-1/2$	0
	$-1/2$	$-1$	$-1$	$-1/2$	0	$1/2$
P	0	$-1$	$-1/2$	0	$1/2$	1
	$1/2$	$-1/2$	0	$1/2$	1	1
	1	0	$1/2$	1	1	1

Table 15. The OR gate table.

OR Gate Matrix
		Q
$P\vee Q$		$-1$	$-1/2$	0	$1/2$	1
	$-1$	$-1$	$-1$	$-1$	$-1/2$	0
	$-1/2$	$-1$	$-1$	$-1/2$	0	$1/2$
P	0	$-1$	$-1/2$	0	$1/2$	1
	$1/2$	$-1/2$	0	$1/2$	1	1
	1	0	$1/2$	1	1	1

The OR gate, in terms relative to the truth table, is as follows:

Table 16. The OR gate table.

OR Gate truth of table
		Q
$P\vee Q$		F	$mF$	W	$mT$	T
	F	F	F	F	$mF$	W
	$mF$	F	F	$mF$	W	$mT$
P	W	F	$mF$	W	$mT$	T
	$mT$	$mF$	W	$mT$	T	T
	T	W	$mT$	T	T	T

Table 16. The OR gate table.

OR Gate truth of table
		Q
$P\vee Q$		F	$mF$	W	$mT$	T
	F	F	F	F	$mF$	W
	$mF$	F	F	$mF$	W	$mT$
P	W	F	$mF$	W	$mT$	T
	$mT$	$mF$	W	$mT$	T	T
	T	W	$mT$	T	T	T

In these tables, the third and fourth degrees of truth are interspersed, which is why we symbolize each degree with its respective symbol, as indicated in Table 14: W for the third degree, which we have designated as the state of wisdom and which implies decision-making. The fourth degree is symbolized by the letter m, which precedes F and T and indicates that it leans more towards falsehood or truth.

3.2.6. AND Gates with Five Inputs

Table 17. The AND gate table.

AND Gate Matrix
		Q
$P\wedge Q$		$-1$	$-1/2$	0	$1/2$	1
	$-1$	1	$1/2$	0	$-1/2$	$-1$
	$-1/2$	$1/2$	$1/4$	0	$-1/4$	$-1/2$
P	0	0	0	0	0	0
	$1/2$	$-1/2$	$-1/4$	0	$1/4$	$1/2$
	1	$-1$	$-1/2$	0	$1/2$	1

Table 17. The AND gate table.

AND Gate Matrix
		Q
$P\wedge Q$		$-1$	$-1/2$	0	$1/2$	1
	$-1$	1	$1/2$	0	$-1/2$	$-1$
	$-1/2$	$1/2$	$1/4$	0	$-1/4$	$-1/2$
P	0	0	0	0	0	0
	$1/2$	$-1/2$	$-1/4$	0	$1/4$	$1/2$
	1	$-1$	$-1/2$	0	$1/2$	1

In the interaction between the values of the fourth degree of truth, a value of the fifth degree of truth is projected. This value corresponds to the $lF$ or $lT$ of the fifth degree of truth, which takes place in a three-dimensional $\left(3D\right)$ plane. The system is developed with seven digits or inputs.

Table 18. The AND gate table.

AND Gate truth of table
		Q
$P\wedge Q$		F	$mF$	W	$mT$	T
	F	T	$mT$	W	$mF$	F
	$mF$	$mT$	$lT$*	W	$lF$*	$mF$
P	W	W	W	W	W	W
	$mT$	$mF$	$lF$ *	W	$lT$ *	$mT$
	T	F	$mF$	W	$mT$	F

Table 18. The AND gate table.

AND Gate truth of table
		Q
$P\wedge Q$		F	$mF$	W	$mT$	T
	F	T	$mT$	W	$mF$	F
	$mF$	$mT$	$lT$*	W	$lF$*	$mF$
P	W	W	W	W	W	W
	$mT$	$mF$	$lF$ *	W	$lT$ *	$mT$
	T	F	$mF$	W	$mT$	F

My article, [13]"Logical Implications of the Base-Four Number System," contains tables representing a quinary series developed using binary or ternary bases. They are all a preamble to this article. Here, we only use a quinary system with a balanced ternary system to develop any series. Therefore, every number development is in base three, but its structure is quinary with five, seven, nine, or more digits according to the dimension being developed because any dimension, regardless of the number of its axes, is governed by the ternary system.

Table 19. The evaluation of quinary balanced, two digits.

Sequence with two digits

Subset 1

Subset 2

Subset 3

Subset 4

Subset 5

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

T

T

$-4$

S

T

$(-1,-3i)$

0

T

$-1$

i

T

$(-1,3i)$

1

T

2

T

S

$(-3,-i)$

S

S

$-4i$

0

S

$-i$

i

S

$2i$

1

S

$(3,-i)$

T

0

$-3$

S

0

$-3i$

0

0

0

i

0

$3i$

1

0

3

T

i

$(-3,i)$

S

i

$-2i$

0

i

i

i

i

$4i$

1

i

$(3,i)$

T

1

$-2$

S

1

$(1,-3i)$

0

1

1

i

1

$(1,3i)$

1

1

4

Table 19. The evaluation of quinary balanced, two digits.

Sequence with two digits

Subset 1

Subset 2

Subset 3

Subset 4

Subset 5

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

P

Q

${\mathfrak{D}}_5$

T

T

$-4$

S

T

$(-1,-3i)$

0

T

$-1$

i

T

$(-1,3i)$

1

T

2

T

S

$(-3,-i)$

S

S

$-4i$

0

S

$-i$

i

S

$2i$

1

S

$(3,-i)$

T

0

$-3$

S

0

$-3i$

0

0

0

i

0

$3i$

1

0

3

T

i

$(-3,i)$

S

i

$-2i$

0

i

i

i

i

$4i$

1

i

$(3,i)$

T

1

$-2$

S

1

$(1,-3i)$

0

1

1

i

1

$(1,3i)$

1

1

4

If we add one digit, the sequence table will look similar to the one above, but the range will be $(-13,13)$ because the maximum values that can be reached are

$$TTT=-13,111=13,SSS=-13i,andiii=13i$$

In this case, the base of the system is three, so each of the five digits is multiplied by three to the power of its position. Since the greatest position is three, three must be raised to the power of two. Therefore, $3^2=(9+3+1)=13$.

Then, for each point that includes zero in its units place:

$$TT0,T00,TS0,SS0,S00,ii0,i00,Si0,iS0,Ti0,iT0,0T0,$$

$$0S0,0i0,110,100,1T0,1S0,1i0,S10,T10,000,010,i10,ST0$$

it is the center of twenty-five unit squares.

However, there are other 100 points within $-13,13,-13i,and13i$ ranges.

In a number composed of eight digits in a balanced ternary and complex quinary system with a base of five, the number of results or coordinate points is 390,625. This is a significant difference compared to an equal binary number of eight digits, which gives us only 256. This difference indicates a significant variation in information capacity.

4. Balanced Ternary and Complex Septenary Bases

Our real $3D$ world can be represented mathematically by a base-seven number system. If we frame it within a physical context in which the seven cardinal points naturally extend and determine the direction of events and phenomena occurring at every instant and their magnitude, in the sense of whether they can be measured, then we are probably on the right track.

This exercise will clearly show that our possibilities are unlimited, yet limited by us. This causes our finite perception to collapse within our reality, making it true from our perspective. Yet, we are not satisfied. We wish to understand the complexity of the quantum field from which our daily events originate. Therefore, regardless of what it means to commute in a complex base-seven number system, it is important to achieve—or at least lay the foundations for—the balanced ternary system and the base-seven number system within the structure of the complex balanced ternary system in the very near future. This will allow us to integrate new technology and machine language with a high sense of ethics and wisdom.

Our obligation is to work toward achieving the standards of a Type I civilization, which is why efficiently consuming our energy resources is of paramount importance instead of becoming predatory and avaricious.

4.1. Balanced Septenary System

It is well established that "in a balanced base for every positive number, there exists an equal and opposite negative digit."

Balanced form representation is valid if and only if for every positive digit $d_{+}$, there exist a corresponding negative digit $d_{-}$, such that $f_D\left(d_{+}\right)=-f_D\left(d_{-}\right)$, then $b_{+}=b_{-}$, otherwise

Therefore

i)

A balanced septenary system is a set equal to: $\{-3,-2,-1,0,1,2,3\}$

ii)

A balanced ternary system situated on an imaginary lines is a set with the following elements: $\{-1,-j,-i,0,j,i,1\}$.

Accordingly, the following assertion is made for the purpose of its definitions:

a)

Let ${\mathfrak{D}}_7:=\{T,U,S,0,j,i,1\}$ be a set of symbols, where a complex-valued function $f=f_{{\mathfrak{D}}_7}:{\mathfrak{D}}_7\to \mathbb{C}$, is defined by:

i)

$f\left(T\right)=-1$

ii)

$f\left(U\right)=-j$

iii)

$f\left(S\right)=-i$

iv)

$f\left(0\right)=0$

v))

$f\left(j\right)=j$

vi)

$f\left(i\right)=i$

vii)

$f\left(1\right)=1$

b)

Let ${\mathfrak{D}}_7:=\{1,U,S,0,j,i,1\}$ be a set of symbols, where a valued function $f=f_{{\mathfrak{D}}_7}:{\mathfrak{D}}_7\to \mathbb{C}$, is defined by:

i)

$f\left(T\right)=-1$

ii)

$f\left(U\right)=-1/8$

iii)

$f\left(S\right)=-1/4$

iv)

$f\left(0\right)=0$

v))

$f\left(j\right)=1/8$

vi)

$f\left(i\right)=1/4$

vii)

$f\left(1\right)=1$

Therefore, in order to ascertain every integer, it is necessary to apply the property of the concatenated string, with the respective symbols and calculate according to their position. The sequence $(d_n,...d_0)$ is defined by the property that each digit can alternatively represent one of the symbols $\{T,U,S,0,j,i,1\}$. The length of the sequence is determined by $n+1$.

The evaluation function for the ternary system in its real and complex part is determined by:

$v=v_7:={\mathfrak{D}}_7^{+}\to \mathbb{Z}$, and in its complex part by $z=z_7:={\mathfrak{D}}_7^{+}\to \mathbb{C}$.

Then, for every string

$$(d_n\dots d_0)\in {\mathfrak{D}}_7,v(d_n\dots d_0)=\sum _{i=0}^{n}f\left(d_i\right)7^i$$

and for its complex parts

$$(d_n\dots d_0)\in {\mathfrak{D}}_7,z(d_n\dots d_0)=\sum _{i=0}^{n}f\left(d_i\right)7^i$$

.

For the purpose of this article, we will not delve into classical logic regarding the dissertation of the law of the third middle and whether judgments are contradictory or contrary. Our logic is based on Jan Łukasiewicz’s analysis from a century ago. He bequeathed to us the idea that the law of the third middle, [14] with contradictory or non-contradictory judgments, is a principle of possibility. In this principle, p can be either true or false. He called this the principle of the "third truth value" because in probability logic, there can be several degrees of truth.

If you wish, we can follow a succession of questions as described by Descartes’ meditation in his "The Cartesian Method of Doubt".

In our time, however, we are struggling not only to know the truth, which is complicated because everything is translated into information, but also to discern truth from falsehood in subtly crafted information. Now, we need to know not only if p is not p$p\vee \neg p$ or if p then q, symbolized as $p\supset q$ but also its grade of truth value of p and q.

Why is it important in our time to discern truth from falsehood? Because mathematics, physics, chemistry, astronomy, economics, politics, religion, philosophy, technology, and artificial intelligence affect us for better or worse in our daily lives, as does the information derived from them. Therefore, mathematical logic should be the path to discerning truth [8] from falsehood in processed information, especially when MVL systems are applied to non-human intelligence technology (AI). The third truth value is well-defined in the ternary system, where Lukasiewicz assigns it the value of $1/2$. Given that the elements of the ternary set are $(0,1/2,1),1/2$ is clearly defined as having a $50\%$ probability of being false or true when the proposition is presented at time t, before the proposition has occurred.

However, for trivalent logic intended for computer devices, [15] [16] a balanced ternary system is preferable because it eliminates the need for an additional number to represent negatives. Therefore, we use the balanced ternary system as our basis, whose elements are

$$(-1,0,1)$$

In this system, the value of the third half is zero, which aligns with our proposal that zero separates negative and positive, or the midpoint between true and false.

But what happens if we increase the degrees of truth values? This involves dividing the third truth value by subsequent truth values, which Lukasiewicz envisioned as having an infinite number of truth values. In our case, we introduce the fifth degree of truth and describe how it is derived from previous degrees within the bivalent system. This process is illustrated in the following table.

Table 20. The insertion of a grade of truth value.

Insertion of MVL
Binary	Ternary	Balanced T	Quinary	Septenary	Grade	Valued	Logic
${\mathfrak{D}}_2$	${\mathfrak{D}}_3$	${\mathfrak{D}}_3$	${\mathfrak{D}}_5$	${\mathfrak{D}}_7$	of Truth	Symbol	Value
0	0	$-1$	$-1$	$-1$	Bivalent	T	False
				$-1/8$	$5th$	U	$\mathsf{l}F$
			$-1/2$	$-1/4$	$4th$	S	$\mathsf{m}F$
	$1/2$	0	0	0	$3rd$	0	W
				$1/8$	$5th$	j	$\mathsf{l}T$
			$1/2$	$1/4$	$4th$	i	$\mathsf{m}T$
1	1	1	1	1	Bivalent	1	Truth

Table 20. The insertion of a grade of truth value.

Insertion of MVL
Binary	Ternary	Balanced T	Quinary	Septenary	Grade	Valued	Logic
${\mathfrak{D}}_2$	${\mathfrak{D}}_3$	${\mathfrak{D}}_3$	${\mathfrak{D}}_5$	${\mathfrak{D}}_7$	of Truth	Symbol	Value
0	0	$-1$	$-1$	$-1$	Bivalent	T	False
				$-1/8$	$5th$	U	$\mathsf{l}F$
			$-1/2$	$-1/4$	$4th$	S	$\mathsf{m}F$
	$1/2$	0	0	0	$3rd$	0	W
				$1/8$	$5th$	j	$\mathsf{l}T$
			$1/2$	$1/4$	$4th$	i	$\mathsf{m}T$
1	1	1	1	1	Bivalent	1	Truth

Integrating the fourth and fifth levels of truth reduces the double $50\%$ range of the third level to more specific values of truth or falsehood. Whether or not this makes sense, for an AI that handles large volumes of information, this could potentially represent a significant advance in finding the best solution to a given problem. Furthermore, the development of a series, operating under the balanced ternary system’s mechanics and seven-digit numerical base, describes the distribution and development of physical bodies immersed in a three-dimensional field of possibilities. What interests us ultimately is understanding our reality from the perspective of information describing both physical reality and the mental structure of our beliefs in truths or lies. These concerns lead to controversies that are difficult to explain here, but we will address them in special topics. These topics will evaluate the logical and illogical foundations of the implications of truth and falsehood, as well as our immediate reality and external and internal reality, thought, emotion, and action.

4.2. Fourth and Fifth Value of Truth Explained

To provide context for the proposal in this article to introduce the fourth and fifth truth values in a balanced MVL system under the balanced ternary system structure, [8] we will break down the concepts and criteria that led us to consider this work as something to be understood with an open mind. Some errors may be made due to a lack of knowledge or mathematical support, but these errors will never be intentional or malicious. Ultimately, this proposal is submitted to peer review to correct errors and support the premises. Certainly, no one has everything perfectly grounded from the beginning. Like any idea or hypothesis, this one must evolve and improve with each new edition.

The excluded middle is a logical concept that has generated the most controversy throughout history, ever since Aristotle introduced it in his philosophical works. Different schools of thought have interpreted it to support their own theories, such as the Stoics who used it to support their deterministic theory and the peripatetic school of Aristotle who used it to refute the school of the Stoics of Cricippus, even though Cricippus was an admirer of Aristotle.

Whether something is possible or not according to the interpretation of the excluded middle has been a philosophical battleground between skeptics, stochastic, determinists, rationalists, and nihilists throughout history to this day. These debates have been fruitful, leading to new mathematical constructions, such as the well-founded Theory of Probability and Mathematical Logic. Mathematical logical is an independent discipline of mathematics that separates itself from classical logic. Mathematical logical has diversified into many types of non-Aristotelian or non-Boolean MVL logic, including Peirce- Kleene, Lukasiewicz, Gödel Logic, HT Logic, and RM3 Logic, as well as Russell-Whitehead, among the most important. Today, these are being directed toward use in much better ways in computational processes.

The principle of the excluded middle states:

$$A\vee \neg A$$

$A\vee \neg A$, which is interpreted as A or $not-A$. In this case, one is true and the other is false; therefore, there is no third option.

In Lukasiewicz’s logic, which is based on the same propositional logic, $p\vee \neg p$ is interpreted as "it is possible that p" or "it is possible that not-p," so the result is unknown or undefined.

Using modal propositions, this concept is extended to include more possibilities.

• It is possible that p. Notation: Mp
• It is possible that not-p. Notation: MNp
• It is not possible that p. Notation: NMp
• It is not possible that not-p. Notation: NMNp

M: means possible, N: means negation or not

(M, N): Nomenclature used by logicians of the Middle Ages and adopted by Lukasiewicz.

In more complete propositions, the modes possible, impossible, contingent, and necessary, in addition to true and false, can constitute stricter premises.

i)

If it is not possible that p, then not-p.

ii)

Everything that exists is necessary.

iii)

If it is assumed that not-p, then under this assumption, it is impossible that p.

iv)

For some p, it is possible that p, and it is also possible that not-p.

v)

False if and only if p is false.

vi)

True if and only if p is true.

The law of the excluded fourth is also decreed. This law states:

$$A\vee \mathbf{I}A\vee \neg A$$

where I means "It is unknown that..." or "It is contingent that..." in Tarski notation.

4.2.1. MVL, Fourth and Fifth Truth Values

Based on all the preceding logical modes and principles, we introduce the fourth and fifth excluded premises.

Therefore, it is valid to declare:

• If something is possible...

  –

  How much possible is it to be possible?

  ∗

  And if it is possible.

  ·

  How much is it possible to be true?

  ·

  Or how much is it possible to be false?

In the case of the excluded middle, only p or not-p is possible, so the range of possibilities is extensive.

It’s like throwing a dart at an object far away that we can barely see.

• But what does introducing a fourth truth value mean?
  • It means dividing the excluded middle into two halves.

    –

    This allows us to divide the wide range of the field of possibilities into five parts, enabling us to visualize the possibilities of something:

    ∗

    with more possibility to be true or

    ∗

    something with more possibility to be false.

• But what does introducing a fifth truth value mean?
  • It means dividing the excluded fourth into two halves.

    –

    Thus divide the more possibly to be true in two parts and divide the more possible to be false in two parts.

    –

    This allows us to divide the wide range of our field of possibilities into seven parts, enabling us to visualize the possibilities of something:

    ∗

    with more possibility to be true in other more possible to be true or

    ∗

    something with more possibility to be false in other more possible to be false.

• What is possible in something more possible is now more possible to be true or something more possible to be false.

It’s like throwing a dart at Pluto, and to hit it we use the gravitational energy of Mars, Jupiter, and Saturn.

Since the fourth and fifth values of truth, it can built geometric bodies, then a very close relationship can be established between possibility and geometry. Also, since every geometric solid is made up of parts, such as points, lines, surfaces, and volumes, and since each part, like any structure built from parts, can be separated into its components, allowing us to understand each set of its parts and even the most elementary part of those parts.

All of the above will be the subject of a broader debate that we will address in future work when discussing the purely logical aspects. This is merely an introduction and supporting material for the present article.

4.3. Sequence in a Complex Base-Seven Number System

As with every number system based on balanced ternary and complex MVL systems, its range is limited to an interval of real numbers, $\{-X,X\}$, and an equal interval of imaginary numbers, $\{S,i\}$, and $\{U,j\}$. The base-seven system is no exception. In the case of two digits, its limits correspond to $\{-4,4\}$, and $\{-4i,4i\}$, and $\{-4j,4j\}$, respectively.

In Table 21, we use the symbols of a ternary system without the negative sign for our balanced septenary digits,

$$(P\wedge Q)$$

but we write the negative sign in the decimal expression column to refer to a complex coordinated arrangement.

Table 21. Sequence in a complex base-seven number system with two digits.

Sequence with two digits
Subset 1			Subset 3			Subset 5			Subset 7
P	Q	${\mathfrak{D}}_{10}$	P	Q	${\mathfrak{D}}_{10}$	P	Q	${\mathfrak{D}}_{10}$	P	Q	${\mathfrak{D}}_{10}$
T	T	$-4$	S	T	$(-3i,-1)$	j	T	$3j,-1$	1	T	2
T	U	$-3,-j$	S	U	$(-3i,-j)$	j	U	$2j$	1	U	$3,-j$
T	S	$-3,-i$	S	S	$-4i$	j	S	$3j,-i$	1	S	$3,-i$
T	0	$-3$	S	0	$-3i$	j	0	$3j$	1	0	3
T	j	$-3,j$	S	j	$(-3i,j)$	j	j	$4j$	1	j	$3,j$
T	i	$-3,i$	S	i	$-2i$	j	i	$3j,i$	1	i	$3,i$
T	1	$-2$	S	1	$-3i,1$	j	1	$3j,1$	1	1	4
Subset 2			Subset 4			Subset 6
U	T	$-1,-3j$	0	T	$-1$	i	T	$-1,3i$
U	U	$-4j$	0	U	$-j$	i	U	$3i,-j$
U	S	$-3j,-i$	0	S	$-i$	i	S	$2i$
U	0	$-3j$	0	0	0	i	0	$3i$
U	j	$-2j$	0	j	j	i	j	$3i,j$
U	i	$-3j,i$	0	i	i	i	i	$4i$
U	1	$-3j,1$	0	1	1	i	1	$3i,1$

Table 21. Sequence in a complex base-seven number system with two digits.

Sequence with two digits
Subset 1			Subset 3			Subset 5			Subset 7
P	Q	${\mathfrak{D}}_{10}$	P	Q	${\mathfrak{D}}_{10}$	P	Q	${\mathfrak{D}}_{10}$	P	Q	${\mathfrak{D}}_{10}$
T	T	$-4$	S	T	$(-3i,-1)$	j	T	$3j,-1$	1	T	2
T	U	$-3,-j$	S	U	$(-3i,-j)$	j	U	$2j$	1	U	$3,-j$
T	S	$-3,-i$	S	S	$-4i$	j	S	$3j,-i$	1	S	$3,-i$
T	0	$-3$	S	0	$-3i$	j	0	$3j$	1	0	3
T	j	$-3,j$	S	j	$(-3i,j)$	j	j	$4j$	1	j	$3,j$
T	i	$-3,i$	S	i	$-2i$	j	i	$3j,i$	1	i	$3,i$
T	1	$-2$	S	1	$-3i,1$	j	1	$3j,1$	1	1	4
Subset 2			Subset 4			Subset 6
U	T	$-1,-3j$	0	T	$-1$	i	T	$-1,3i$
U	U	$-4j$	0	U	$-j$	i	U	$3i,-j$
U	S	$-3j,-i$	0	S	$-i$	i	S	$2i$
U	0	$-3j$	0	0	0	i	0	$3i$
U	j	$-2j$	0	j	j	i	j	$3i,j$
U	i	$-3j,i$	0	i	i	i	i	$4i$
U	1	$-3j,1$	0	1	1	i	1	$3i,1$

Each subset represents a three-dimensional pyramidal structure body centered on each element that contains a zero in the units position. $\{T0,U0,S0,00,j0,i0\}$, and 10, respectively.

Therefore, the system unit is seven digits. When these are combined into two units, they generate a set of 49 numbers. The next set of three digits is 343 elements, all of which have only three digits. Scaling it to eight digits base seven gives us a relationship of $5764801$ elements. The numbers are all different, but they are all in symmetry. In a series of three digits in base seven, the following relationship exists:

Table 22. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

First Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

T

T

T

$-13$

T

S

T

$-10,-3i$

T

j

T

$-10,3j$

T

1

T

$-7$

T

T

U

$-12,-j$

T

S

U

$-9,-3i,-j$

T

j

U

$-9,2j$

T

1

U

$-6,-j$

T

T

S

$-12,-i$

T

S

S

$-9,-4i$

T

j

S

$-9,3j,-i$

T

1

S

$-6,-i$

T

T

0

$-12$

T

S

0

$-9,-3i$

T

j

0

$-9,3j$

T

1

0

$-6$

T

T

j

$-12,j$

T

S

j

$-9,-3i,j$

T

j

j

$-9,4j$

T

1

j

$-6,j$

T

T

i

$-12,i$

T

S

i

$-9,-2i$

T

j

i

$-9,3j,i$

T

1

i

$-6,i$

T

T

1

$-11$

T

S

1

$-8,-3i$

T

j

1

$-8,3j$

T

1

1

$-5$

Subset 2

Subset 4

Subset 6

T

U

T

$-10,-3j$

T

0

T

$-10$

T

i

T

$-10,3i$

T

U

U

$-9,-4j$

T

0

U

$-9,-j$

T

i

U

$-9,3i,-j$

T

U

S

$-9,-3j,-i$

T

0

S

$-9,-i$

T

i

S

$-9,2i$

T

U

0

$-9,-3j$

T

0

0

$-9$

T

i

0

$-9,3i$

T

U

j

$-9,-2j$

T

0

j

$-9,j$

T

i

j

$-9,3i,j$

T

U

i

$-9,-3j,i$

T

0

i

$-9,i$

T

i

i

$-9,4i$

T

U

1

$-8,-3j$

T

0

1

$-8$

T

i

1

$-8,3i$

Table 22. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

First Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

T

T

T

$-13$

T

S

T

$-10,-3i$

T

j

T

$-10,3j$

T

1

T

$-7$

T

T

U

$-12,-j$

T

S

U

$-9,-3i,-j$

T

j

U

$-9,2j$

T

1

U

$-6,-j$

T

T

S

$-12,-i$

T

S

S

$-9,-4i$

T

j

S

$-9,3j,-i$

T

1

S

$-6,-i$

T

T

0

$-12$

T

S

0

$-9,-3i$

T

j

0

$-9,3j$

T

1

0

$-6$

T

T

j

$-12,j$

T

S

j

$-9,-3i,j$

T

j

j

$-9,4j$

T

1

j

$-6,j$

T

T

i

$-12,i$

T

S

i

$-9,-2i$

T

j

i

$-9,3j,i$

T

1

i

$-6,i$

T

T

1

$-11$

T

S

1

$-8,-3i$

T

j

1

$-8,3j$

T

1

1

$-5$

Subset 2

Subset 4

Subset 6

T

U

T

$-10,-3j$

T

0

T

$-10$

T

i

T

$-10,3i$

T

U

U

$-9,-4j$

T

0

U

$-9,-j$

T

i

U

$-9,3i,-j$

T

U

S

$-9,-3j,-i$

T

0

S

$-9,-i$

T

i

S

$-9,2i$

T

U

0

$-9,-3j$

T

0

0

$-9$

T

i

0

$-9,3i$

T

U

j

$-9,-2j$

T

0

j

$-9,j$

T

i

j

$-9,3i,j$

T

U

i

$-9,-3j,i$

T

0

i

$-9,i$

T

i

i

$-9,4i$

T

U

1

$-8,-3j$

T

0

1

$-8$

T

i

1

$-8,3i$

Table 23. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Second Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

U

T

T

$-9j,-4$

U

S

T

$-9j,-3i,-1$

U

j

T

$-6j,-1$

U

1

T

$-9j,2$

U

T

U

$-10j,-3$

U

S

U

$-10j,-3i$

U

j

U

$-7j$

U

1

U

$-10j,3$

U

T

S

$-9j,-3,-i$

U

S

S

$-9j,-4i$

U

j

S

$-6j,-i$

U

1

S

$-9j,3,-i$

U

T

0

$-9j-3$

U

S

0

$-9j,-3i$

U

j

0

$-6j$

U

1

0

$-9j,3$

U

T

j

$-8j,-3$

U

S

j

$-8j,-3i$

U

j

j

$-5j$

U

1

j

$-8j,3$

U

T

i

$-9j,-3,i$

U

S

i

$-9j,-2i$

U

j

i

$-6j,i$

U

1

i

$-9j,3,i$

U

T

1

$-9j,-2$

U

S

1

$-9j,-3i,1$

U

j

1

$-6j,1$

U

1

1

$-9j,4$

Subset 2

Subset 4

Subset 6

U

U

T

$-12j,-1$

U

0

T

$-9j,-1$

U

i

T

$-9j,3i,-1$

U

U

U

$-13j$

U

0

U

$-10j$

U

i

U

$-10j,3i$

U

U

S

$-12j,-i$

U

0

S

$-9j,-i$

U

i

S

$-9j,2i$

U

U

0

$-12j$

U

0

0

$-9j$

U

i

0

$-9j,3i$

U

U

j

$-11j$

U

0

j

$-8j,j$

U

i

j

$-8j,3i$

U

U

i

$-12j,i$

U

0

i

$-9j,i$

U

i

i

$-9j,4i$

U

U

1

$-12j,1$

U

0

1

$-9j,1$

U

i

1

$-9j,3i,1$

Table 23. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Second Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

U

T

T

$-9j,-4$

U

S

T

$-9j,-3i,-1$

U

j

T

$-6j,-1$

U

1

T

$-9j,2$

U

T

U

$-10j,-3$

U

S

U

$-10j,-3i$

U

j

U

$-7j$

U

1

U

$-10j,3$

U

T

S

$-9j,-3,-i$

U

S

S

$-9j,-4i$

U

j

S

$-6j,-i$

U

1

S

$-9j,3,-i$

U

T

0

$-9j-3$

U

S

0

$-9j,-3i$

U

j

0

$-6j$

U

1

0

$-9j,3$

U

T

j

$-8j,-3$

U

S

j

$-8j,-3i$

U

j

j

$-5j$

U

1

j

$-8j,3$

U

T

i

$-9j,-3,i$

U

S

i

$-9j,-2i$

U

j

i

$-6j,i$

U

1

i

$-9j,3,i$

U

T

1

$-9j,-2$

U

S

1

$-9j,-3i,1$

U

j

1

$-6j,1$

U

1

1

$-9j,4$

Subset 2

Subset 4

Subset 6

U

U

T

$-12j,-1$

U

0

T

$-9j,-1$

U

i

T

$-9j,3i,-1$

U

U

U

$-13j$

U

0

U

$-10j$

U

i

U

$-10j,3i$

U

U

S

$-12j,-i$

U

0

S

$-9j,-i$

U

i

S

$-9j,2i$

U

U

0

$-12j$

U

0

0

$-9j$

U

i

0

$-9j,3i$

U

U

j

$-11j$

U

0

j

$-8j,j$

U

i

j

$-8j,3i$

U

U

i

$-12j,i$

U

0

i

$-9j,i$

U

i

i

$-9j,4i$

U

U

1

$-12j,1$

U

0

1

$-9j,1$

U

i

1

$-9j,3i,1$

Regardless of the size of the number, there will be a range for each one. For example, the range of a four-digit base seven number’s series will be $\{-40,40,-40i,40i,-40j\}$, and $40j$. If it were an eight-digit base seven number, its range would be: $\{-3,280,3,280\},\{-3,280i,3,280i\}$, and $\{-3,280j,3,280j\}$. This is an inherent property of the balanced ternary number system and its derivatives in complex coordinates.

In developing the series, we first encountered $P\times 3^2$, then $Q\times 3$, and finally $R\times 3^0$. The result is in base ten. In base seven, the series is developed as follows: $TUiS0jT$ or $100T1SSU1$. There is no other way to represent a quantity in base seven under a balanced ternary structure, but it is possible to convert it to binary or decimal.

Table 24. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Third Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

S

T

T

$-9i,-4$

S

S

T

$-12i,-1$

S

j

T

$-9i,3j,-1$

S

1

T

$-9i,2$

S

T

U

$-9i,-3,-j$

S

S

U

$-12i,-j$

S

j

U

$-9i,2j$

S

1

U

$-9i,3,-j$

S

T

S

$-10i,-3$

S

S

S

$-13i$

S

j

S

$-10i,3j$

S

1

S

$-10i,3$

S

T

0

$-9i-3$

S

S

0

$-12i$

S

j

0

$-9i,3j$

S

1

0

$-9i,3$

S

T

j

$-9i,-3,j$

S

S

j

$-12i,j$

S

j

j

$-9i,4j$

S

1

j

$-9i,3,j$

S

T

i

$-8i,-3$

S

S

i

$-11i$

S

j

i

$-8i,3j$

S

1

i

$-8i,3$

S

T

1

$-9i,-2$

S

S

1

$-12i,1$

S

j

1

$-9i,3j,1$

S

1

1

$-9i,4$

Subset 2

Subset 4

Subset 6

S

U

T

$-9i,-3j-1$

S

0

T

$-9i,-1$

S

i

T

$-6i,-1$

S

U

U

$-9i,-4j$

S

0

U

$-9i,-j$

S

i

U

$-6i,-j$

S

U

S

$-10i,-3j$

S

0

S

$-10i$

S

i

S

$-7i$

S

U

0

$-9i-3j$

S

0

0

$-9i$

S

i

0

$-6i$

S

U

j

$-9i,-2j$

S

0

j

$-9i,-j$

S

i

j

$-6i,j$

S

U

i

$-8i,-3j$

S

0

i

$-8i$

S

i

i

$-5i$

S

U

1

$-9i,-3i,1$

S

0

1

$-9i,1$

S

i

1

$-6i,1$

Table 24. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Third Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

S

T

T

$-9i,-4$

S

S

T

$-12i,-1$

S

j

T

$-9i,3j,-1$

S

1

T

$-9i,2$

S

T

U

$-9i,-3,-j$

S

S

U

$-12i,-j$

S

j

U

$-9i,2j$

S

1

U

$-9i,3,-j$

S

T

S

$-10i,-3$

S

S

S

$-13i$

S

j

S

$-10i,3j$

S

1

S

$-10i,3$

S

T

0

$-9i-3$

S

S

0

$-12i$

S

j

0

$-9i,3j$

S

1

0

$-9i,3$

S

T

j

$-9i,-3,j$

S

S

j

$-12i,j$

S

j

j

$-9i,4j$

S

1

j

$-9i,3,j$

S

T

i

$-8i,-3$

S

S

i

$-11i$

S

j

i

$-8i,3j$

S

1

i

$-8i,3$

S

T

1

$-9i,-2$

S

S

1

$-12i,1$

S

j

1

$-9i,3j,1$

S

1

1

$-9i,4$

Subset 2

Subset 4

Subset 6

S

U

T

$-9i,-3j-1$

S

0

T

$-9i,-1$

S

i

T

$-6i,-1$

S

U

U

$-9i,-4j$

S

0

U

$-9i,-j$

S

i

U

$-6i,-j$

S

U

S

$-10i,-3j$

S

0

S

$-10i$

S

i

S

$-7i$

S

U

0

$-9i-3j$

S

0

0

$-9i$

S

i

0

$-6i$

S

U

j

$-9i,-2j$

S

0

j

$-9i,-j$

S

i

j

$-6i,j$

S

U

i

$-8i,-3j$

S

0

i

$-8i$

S

i

i

$-5i$

S

U

1

$-9i,-3i,1$

S

0

1

$-9i,1$

S

i

1

$-6i,1$

Table 25. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Fourth Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

0

T

T

$-4$

0

S

T

$-3i,-1$

0

j

T

$3j,-1$

0

1

T

2

0

T

U

$-3,-j$

0

S

U

$-3i,-j$

0

j

U

$2j$

0

1

U

$3,-j$

0

T

S

$-3,-i$

0

S

S

$-4i$

0

j

S

$3j,-i$

0

1

S

$3,-i$

0

T

0

$-3$

0

S

0

$-3i$

0

j

0

$3j$

0

1

0

3

0

T

j

$-3,j$

0

S

j

$-3i,j$

0

j

j

$4j$

0

1

j

$3,j$

0

T

i

$-3,i$

0

S

i

$-2i$

0

j

i

$3j,i$

0

1

i

$3,i$

0

T

1

$-2$

0

S

1

$-3i,1$

0

j

1

$3j,1$

0

1

1

4

Subset 2

Subset 4

Subset 6

0

U

T

$-3j-1$

0

0

T

$-1$

0

i

T

$3i,-1$

0

U

U

$-4j$

0

0

U

$-j$

0

i

U

$3i,-j$

0

U

S

$-3j,-i$

0

0

S

$-i$

0

i

S

$2i$

0

U

0

$-3j$

0

0

0

0

0

i

0

$3i$

0

U

j

$-2j$

0

0

j

j

0

i

j

$3i,j$

0

U

i

$-3j,i$

0

0

i

i

0

i

i

$4i$

0

U

1

$-3j,1$

0

0

1

1

0

i

1

$3i,1$

Table 25. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Fourth Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

0

T

T

$-4$

0

S

T

$-3i,-1$

0

j

T

$3j,-1$

0

1

T

2

0

T

U

$-3,-j$

0

S

U

$-3i,-j$

0

j

U

$2j$

0

1

U

$3,-j$

0

T

S

$-3,-i$

0

S

S

$-4i$

0

j

S

$3j,-i$

0

1

S

$3,-i$

0

T

0

$-3$

0

S

0

$-3i$

0

j

0

$3j$

0

1

0

3

0

T

j

$-3,j$

0

S

j

$-3i,j$

0

j

j

$4j$

0

1

j

$3,j$

0

T

i

$-3,i$

0

S

i

$-2i$

0

j

i

$3j,i$

0

1

i

$3,i$

0

T

1

$-2$

0

S

1

$-3i,1$

0

j

1

$3j,1$

0

1

1

4

Subset 2

Subset 4

Subset 6

0

U

T

$-3j-1$

0

0

T

$-1$

0

i

T

$3i,-1$

0

U

U

$-4j$

0

0

U

$-j$

0

i

U

$3i,-j$

0

U

S

$-3j,-i$

0

0

S

$-i$

0

i

S

$2i$

0

U

0

$-3j$

0

0

0

0

0

i

0

$3i$

0

U

j

$-2j$

0

0

j

j

0

i

j

$3i,j$

0

U

i

$-3j,i$

0

0

i

i

0

i

i

$4i$

0

U

1

$-3j,1$

0

0

1

1

0

i

1

$3i,1$

In the balanced ternary system, a sequence begins with the largest negative number, descends to zero, and then ascends to the maximum positive value. This procedure differs from any other base-n system, which starts with zero. However, since this system includes negative numbers in its notation without assigning them a minus sign, this difference is relatively negligible because the notation will always appear as positive numbers. The difference becomes apparent when a number in the balanced ternary system is converted to the decimal system.

Table 26. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Fifth Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

j

T

T

$9i,-4$

j

S

T

$9j,-3i,-1$

j

j

T

$12j,-1$

j

1

T

$9j,2$

j

T

U

$8j,-3$

j

S

U

$8j,-3i$

j

j

U

$11j$

j

1

U

$8j,3$

j

T

S

$9j,-3,-i$

j

S

S

$9j,-4i$

j

j

S

$12j,-i$

j

1

S

$9j,3,i$

j

T

0

$9j-3$

j

S

0

$9j,-3i$

j

j

0

$12j$

j

1

0

$9j,3$

j

T

j

$10j,-3$

j

S

j

$10j,-3i$

j

j

j

$13j$

j

1

j

$10j,3$

j

T

i

$9j,-3,i$

j

S

i

$9j,-2i$

j

j

i

$12j,i$

j

1

i

$9j,3,i$

j

T

1

$9j,-2$

j

S

1

$9j,-3i,1$

j

j

1

$12j,1$

j

1

1

$9j,4$

Subset 2

Subset 4

Subset 6

j

U

T

$6j,-1$

j

0

T

$9j,-1$

j

i

T

$9j,3i,-1$

j

U

U

$5j$

j

0

U

$8j$

j

i

U

$8j,3i$

j

U

S

$6j,-i$

j

0

S

$9j,-i$

j

i

S

$9j,2i$

j

U

0

$6j$

j

0

0

$9j$

j

i

0

$9j,3i$

j

U

j

$7j$

j

0

j

$10j$

j

i

j

$10j,3i$

j

U

i

$6j,i$

j

0

i

$9j,i$

j

i

i

$9j,4i$

j

U

1

$6j,1$

j

0

1

$9j,1$

j

i

1

$9j,3i,1$

Table 26. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Fifth Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

j

T

T

$9i,-4$

j

S

T

$9j,-3i,-1$

j

j

T

$12j,-1$

j

1

T

$9j,2$

j

T

U

$8j,-3$

j

S

U

$8j,-3i$

j

j

U

$11j$

j

1

U

$8j,3$

j

T

S

$9j,-3,-i$

j

S

S

$9j,-4i$

j

j

S

$12j,-i$

j

1

S

$9j,3,i$

j

T

0

$9j-3$

j

S

0

$9j,-3i$

j

j

0

$12j$

j

1

0

$9j,3$

j

T

j

$10j,-3$

j

S

j

$10j,-3i$

j

j

j

$13j$

j

1

j

$10j,3$

j

T

i

$9j,-3,i$

j

S

i

$9j,-2i$

j

j

i

$12j,i$

j

1

i

$9j,3,i$

j

T

1

$9j,-2$

j

S

1

$9j,-3i,1$

j

j

1

$12j,1$

j

1

1

$9j,4$

Subset 2

Subset 4

Subset 6

j

U

T

$6j,-1$

j

0

T

$9j,-1$

j

i

T

$9j,3i,-1$

j

U

U

$5j$

j

0

U

$8j$

j

i

U

$8j,3i$

j

U

S

$6j,-i$

j

0

S

$9j,-i$

j

i

S

$9j,2i$

j

U

0

$6j$

j

0

0

$9j$

j

i

0

$9j,3i$

j

U

j

$7j$

j

0

j

$10j$

j

i

j

$10j,3i$

j

U

i

$6j,i$

j

0

i

$9j,i$

j

i

i

$9j,4i$

j

U

1

$6j,1$

j

0

1

$9j,1$

j

i

1

$9j,3i,1$

Table 27. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Sixth Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

i

T

T

$9i,-4$

i

S

T

$6i,-1$

i

j

T

$9i,3j,-1$

i

1

T

$9i,2$

i

T

U

$9i,-3,-j$

i

S

U

$6i,-j$

i

j

U

$9i,2j$

i

1

U

$9i,3,-j$

i

T

S

$8i,-3$

i

S

S

$5i$

i

j

S

$8i,3j$

i

1

S

$8i,3$

i

T

0

$9i-3$

i

S

0

$6i$

i

j

0

$9i,3j$

i

1

0

$9i,3$

i

T

j

$9i,-3,j$

i

S

j

$6i,j$

i

j

j

$9i,4j$

i

1

j

$9i,3,j$

i

T

i

$10i,-3$

i

S

i

$7i$

i

j

i

$10i,3j$

i

1

i

$10i,3$

i

T

1

$9i,-2$

i

S

1

$6i,1$

i

j

1

$9i,3j,1$

i

1

1

$9i,4$

Subset 2

Subset 4

Subset 6

i

U

T

$9i,-3j-1$

i

0

T

$9i,-1$

i

i

T

$12i,-1$

i

U

U

$9i,-4j$

i

0

U

$9i,-j$

i

i

U

$12i,-j$

i

U

S

$8i,-3j$

i

0

S

$8i$

i

i

S

$11i$

i

U

0

$9i-3j$

i

0

0

$9i$

i

i

0

$12i$

i

U

j

$9i,-2j$

i

0

j

$9i,-j$

i

i

j

$12i,j$

i

U

i

$10i,-3j$

i

0

i

$10i$

i

i

i

$13i$

i

U

1

$9i,-3i,1$

i

0

1

$9i,1$

i

i

1

$12i,1$

Table 27. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Sixth Block of seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

i

T

T

$9i,-4$

i

S

T

$6i,-1$

i

j

T

$9i,3j,-1$

i

1

T

$9i,2$

i

T

U

$9i,-3,-j$

i

S

U

$6i,-j$

i

j

U

$9i,2j$

i

1

U

$9i,3,-j$

i

T

S

$8i,-3$

i

S

S

$5i$

i

j

S

$8i,3j$

i

1

S

$8i,3$

i

T

0

$9i-3$

i

S

0

$6i$

i

j

0

$9i,3j$

i

1

0

$9i,3$

i

T

j

$9i,-3,j$

i

S

j

$6i,j$

i

j

j

$9i,4j$

i

1

j

$9i,3,j$

i

T

i

$10i,-3$

i

S

i

$7i$

i

j

i

$10i,3j$

i

1

i

$10i,3$

i

T

1

$9i,-2$

i

S

1

$6i,1$

i

j

1

$9i,3j,1$

i

1

1

$9i,4$

Subset 2

Subset 4

Subset 6

i

U

T

$9i,-3j-1$

i

0

T

$9i,-1$

i

i

T

$12i,-1$

i

U

U

$9i,-4j$

i

0

U

$9i,-j$

i

i

U

$12i,-j$

i

U

S

$8i,-3j$

i

0

S

$8i$

i

i

S

$11i$

i

U

0

$9i-3j$

i

0

0

$9i$

i

i

0

$12i$

i

U

j

$9i,-2j$

i

0

j

$9i,-j$

i

i

j

$12i,j$

i

U

i

$10i,-3j$

i

0

i

$10i$

i

i

i

$13i$

i

U

1

$9i,-3i,1$

i

0

1

$9i,1$

i

i

1

$12i,1$

Table 28. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Seventh Block and last seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

1

T

T

5

1

S

T

$8,-3i$

1

j

T

$8,3j$

1

1

T

11

1

T

U

$6,-j$

1

S

U

$9,-3i,-j$

1

j

U

$9,2j$

1

1

U

$12,-j$

1

T

S

$6,-i$

1

S

S

$9,-4i$

1

j

S

$9,3j,-i$

1

1

S

$12,-i$

1

T

0

6

1

S

0

$9,-3i$

1

j

0

$9,3j$

1

1

0

12

1

T

j

$6,j$

1

S

j

$9,-3i,j$

1

j

j

$9,4j$

1

1

j

$12,j$

1

T

i

$6,i$

1

S

i

$9,-2i$

1

j

i

$9,3j,i$

1

1

i

$12,i$

1

T

1

7

1

S

1

$10,-3i$

1

j

1

$10,3j$

1

1

1

13

Subset 2

Subset 4

Subset 6

1

U

T

$8,-3j$

1

0

T

8

1

i

T

$8,3i$

1

U

U

$9,-4j$

1

0

U

$9,-j$

1

i

U

$9,3i,-j$

1

U

S

$9,-3j,-i$

1

0

S

$9,-i$

1

i

S

$9,2i$

1

U

0

$9-3j$

1

0

0

9

1

i

0

$9,3i$

1

U

j

$9,-2j$

1

0

j

$9,-j$

1

i

j

$9,3i,j$

1

U

i

$9,-3j,i$

1

0

i

$9,i$

1

i

i

$9,4i$

1

U

1

$10,-3i$

1

0

1

10

1

i

1

$10,3i$

Table 28. The evaluation of a seven-base balanced system with three digits.

Sequence with three digits, base seven

Seventh Block and last seven subsets

Subset 1

Subset 3

Subset 5

Subset 7

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

P

Q

R

${\mathfrak{D}}_{10}$

1

T

T

5

1

S

T

$8,-3i$

1

j

T

$8,3j$

1

1

T

11

1

T

U

$6,-j$

1

S

U

$9,-3i,-j$

1

j

U

$9,2j$

1

1

U

$12,-j$

1

T

S

$6,-i$

1

S

S

$9,-4i$

1

j

S

$9,3j,-i$

1

1

S

$12,-i$

1

T

0

6

1

S

0

$9,-3i$

1

j

0

$9,3j$

1

1

0

12

1

T

j

$6,j$

1

S

j

$9,-3i,j$

1

j

j

$9,4j$

1

1

j

$12,j$

1

T

i

$6,i$

1

S

i

$9,-2i$

1

j

i

$9,3j,i$

1

1

i

$12,i$

1

T

1

7

1

S

1

$10,-3i$

1

j

1

$10,3j$

1

1

1

13

Subset 2

Subset 4

Subset 6

1

U

T

$8,-3j$

1

0

T

8

1

i

T

$8,3i$

1

U

U

$9,-4j$

1

0

U

$9,-j$

1

i

U

$9,3i,-j$

1

U

S

$9,-3j,-i$

1

0

S

$9,-i$

1

i

S

$9,2i$

1

U

0

$9-3j$

1

0

0

9

1

i

0

$9,3i$

1

U

j

$9,-2j$

1

0

j

$9,-j$

1

i

j

$9,3i,j$

1

U

i

$9,-3j,i$

1

0

i

$9,i$

1

i

i

$9,4i$

1

U

1

$10,-3i$

1

0

1

10

1

i

1

$10,3i$

This sequence represents a geometric structure. In the case of two digits, it corresponds to 25 unit areas framed by 125 points. However, if we only consider the local environment, the entire series comprises 338 points, each with its own coordinates. The remaining 213 points represent empty space. For now, we can interpret this space as necessary for the dynamics of bodies subjected to external forces that imply movement. Otherwise, this movement could not occur. The space must be greater than that of any other object. In the fourth block, the series becomes two significant 1 digits, and in the fourth subset, it becomes one significant digit. Each number with a zero in the units place becomes the center of the geometric structure formed according to its dimension. However, according to structural law, a large empty space must remain so that bodies can interact based on their dynamic qualities.

4.3.1. 3D Structure

The following figure graphically represents the first seven pyramidal bodies for a balanced ternary system on a seven-unit base.

Figure 4. The unit body in a $3D$ complex plane are a series of septenary complexes and balanced ternaries with two complex digits.

Figure 4. The unit body in a $3D$ complex plane are a series of septenary complexes and balanced ternaries with two complex digits.

The series develops 49 bodies, or 343 coordinate points. The upward floor, denoted by the complex plane $(x^{\prime },i^{\prime })$, is traced in magenta, and the downward floor, denoted by the complex plane $(x^{\prime \prime },i^{\prime \prime })$, is traced in black.

Five of the bodies correspond to the real and imaginary axes $(a+bi)$, and the remaining two bodies have centers located either three units above or three units below the imaginary axis j. Each center of a body on the imaginary axis j represents an upper or lower floor, respectively. Each level is a new complex plane that is parallel to the original.

This creates a $3D$ framework in which all possible bodies can be situated. A specific volume can then be defined using the ternary system’s limiting strategy. As in the $2D$ plane, there will be a vast number of empty $3D$ points that allow bodies to move to different points, thus establishing interrelationships between them.

5. Arithmetical Operations in Complex Quinary

Like any well-founded numerical system, the ternary number system, in its MVL format (whether complex or not), must allow for the performance of basic arithmetic, algebraic, and calculus operations, [17] as well as its relationship with all branches of mathematics, physics, and all technological, psychological, and social sciences.

Regardless of the logical meaning of each digit, there is an arithmetic and mathematical aspect that adheres to its own rules. Often, the interrelation with the logical meaning is very close. This makes the system doubly important and extremely helpful in implementing new technologies and in logical and illogical reasoning, both of which help us understand the reality of our world.

5.1. Addition

5.1.1. Addition in Quinary system form

Table of addition in complex Quinary

Table 29. Addition table in complex quinary

Addition table
+		B
		T	S	0	i	1
	T	$T1$	$T+S$	T	$T+i$	0
	S	$T+S$	$Si$	S	0	$1+S$
A	0	T	S	0	i	1
	i	$T+i$	0	i	$iS$	$1+i$
	1	0	$1+S$	1	$1+i$	$1T$

Table 29. Addition table in complex quinary

Addition table
+		B
		T	S	0	i	1
	T	$T1$	$T+S$	T	$T+i$	0
	S	$T+S$	$Si$	S	0	$1+S$
A	0	T	S	0	i	1
	i	$T+i$	0	i	$iS$	$1+i$
	1	0	$1+S$	1	$1+i$	$1T$

Table of subtraction in complex Quinary

Table 30. Subtraction table in complex quinary

Subtraction table
−		B
		T	S	0	i	1
	T	0	$T+i$	T	$T+S$	$T1$
	S	$1+S$	0	S	$Si$	$T+S$
A	0	1	i	0	S	T
	i	$1+i$	$iS$	i	0	$T+i$
	1	$1T$	$1+i$	1	$1+S$	0

Table 30. Subtraction table in complex quinary

Subtraction table
−		B
		T	S	0	i	1
	T	0	$T+i$	T	$T+S$	$T1$
	S	$1+S$	0	S	$Si$	$T+S$
A	0	1	i	0	S	T
	i	$1+i$	$iS$	i	0	$T+i$
	1	$1T$	$1+i$	1	$1+S$	0

Examples: In the balanced complex quinary system, a number is written one symbol at a time in order and sequence according to the established symbology. Its value corresponds to its positional value relative to three raised to the power corresponding to its position. Each symbol is independent, and they can be mixed in certain quantities.

Example 1

	1	T	i	0	S	1
		1	1	S	0	0	+
	1	0	$(1+i)$	S	S	1

When performing a mathematical operation, the result may be a mixed complex number. This number must be written in positional notation because both digits correspond to their respective powers, which determine their values. In the present example, the number $(1+i)$ is a complex number where 1 and i are raised to the power of $3^3$ multiplied by 1 and i, respectively. In other cases, there will be numbers like $iS$, which means $(-2i)$; $T1$, which means $(-2)$; and $1T$, which is equal to 2. Their values are also defined according to their position within the quantity.

We can verify if it is correct by converting each of the addends and their result to the decimal system.

	1	T	i	0	S	1	=	$(163+24i)$
+		1	1	S	0	0	=	$(108-9i)$
	1	0	$(1+i)$	S	S	1	=	$(271+15i)$

By breaking down each number and converting it to the decimal system, we can verify that the term to the right of the equal sign corresponds to the terms to the left of the equal sign.

Conversion to decimal
Position	$\dots 1\times 3^5$	$T\times 3^4$	$i\times 3^3$	$0\times 3^2$	$-i\times 3$	$1\times 3^0$
Addend 1	1	T	i	0	S	1
Value	243	$-81$	$27i$	0	$-3i$	1
Result	$243-81+1=$	163		$27i-3i=$	$24i$
Complex	number ${\mathbb{C}}_{B_{10}}$		$(163+24i)$
Addend 2		1	1	S	0	0
Value		81	27	$-9i$	0	0
Result		$81+27=$	108	$-9i$
Complex	number ${\mathbb{C}}_{B_{10}}$		$(108-9i)$
Product	1	0	$(1+i)$	S	S	1
Value	243	0	$(27+27i)$	$-9i$	$-3i$	1
Result	$243+27+1=$	271	$27i-9i-3i$	=	$15i$
Complex	number ${\mathbb{C}}_{B_{10}}$		$(271+15i)$

In this example, we break down each element of the quantities step by step. The same approach applies to subsequent examples.

Example 2

	T	S	0	1	1	i
	1	1	i	T	0	i	+
	0	$(1+S)$	i	0	1	$iS$

We can verify the result by converting to the decimal system and solving.

	T	S	0	1	1	i	=	$(-231-80i)$
+	1	1	i	T	0	i	=	$(315+28i)$
	0	$1+S$	i	0	1	$iS$	=	$(84-52i)$

Here is an example of subtraction. We can use the subtraction table. Table 30:

Example 3

	1	T	i	0	S	1
		1	1	S	0	0	−
	1	$T1$	$(i+T)$	i	S	1

Solve by converting to the decimal system to verify if the solution in the Quinary system is correct.

	1	T	i	0	S	1	=	$(163+24i)$
−		1	1	S	0	0	=	$(108-9i)-$
	1	$T1$	$(i+T)$	i	S	1	=	$(55+33i)$

Example 4

	T	S	0	1	1	i
	1	1	i	T	0	i	−
	$T1$	$(T+S)$	S	$1T$	1	0

As can be seen from the numbers written in the balanced ternary complex Quinary system, no sign is used to indicate whether a number is negative. Its application is straightforward, without the need for carrying, for addition, subtraction, multiplication, or division. This greatly advances computational development. We also abandon the traditional two-element representation of complex numbers, which only requires us to consider them in the results of certain operations. Even then, we will look for ways to simplify them.

5.2. Multiplication

5.2.1. Multiplication in Quinary System Form

Table of multiplication in complex Quinary.

Example 1 We can apply the Table 31

Table 31. Multiplication table in complex quinary

Multiplication table
×		B
		T	S	0	i	1
	T	1	i	0	S	T
	S	i	T	0	1	S
A	0	0	0	0	0	0
	i	S	1	0	T	i
	1	T	S	0	i	1

Table 31. Multiplication table in complex quinary

Multiplication table
×		B
		T	S	0	i	1
	T	1	i	0	S	T
	S	i	T	0	1	S
A	0	0	0	0	0	0
	i	S	1	0	T	i
	1	T	S	0	i	1

				1	T	i	0	S	1
					1	1	S	0	0	×
		S	i	1	0	T	S	0	0
	1	T	i	0	S	1
1	T	i	0	S	1
1	0	T	$iS$	$(1+S)$	$(1+S)$	0	S	0	0

We can verify the result by converting to the decimal system and solving.

				1	T	i	0	S	1	=	$(163+24i)$
					1	1	S	0	0	=	$(108-9i)$
		S	i	1	0	T	S	0	0
	1	T	i	0	S	1
1	T	i	0	S	1
1	0	T	$iS$	$(1+S)$	$(1+S)$	0	S	0	0	=	$(17820+1125i)$

Solving in decimal form.

$$(163+24i)(108-9i)=163\times 108-163\times 9i+108\times 24i)-24\times 9ii$$

$$(17604-1467i+2592i+216)=(17820+1125i)$$

Example 2

					T	S	0	1	1	i
					1	1	i	T	0	i	×
					S	1	0	i	i	T
			1	i	0	T	T	S
		S	1	0	i	i	T
	T	S	0	1	1	i
T	S	0	1	1	i
T	$(T+S)$	$Si$	10	$(1T+i)$	$(1+i)$	$iS$	$T1$	0	i	T

The result of the previous multiplication converted into decimal notation is:

$$(-70534-31668i)$$

5.3. Division

5.3.1. Division in Quinary System Form

Division table in complex Quinary.

Example We will describe the division process in detail using the traditional procedure. We will observe the effect of the division on each of the five complex numbers at each step. Then, we will use the division table to verify that we entered the correct result. We use the Table 32

Table 32. Division table in complex quinary

Division table
÷		B
		T	S	0	i	1
	T	1	${\displaystyle \frac{1}{i}}$	$Ind$	${\displaystyle \frac{T}{i}}$	T
	S	i	1	$Ind$	T	S
A	0	0	0	0	0	0
	i	S	T	$Ind$	1	i
	1	T	${\displaystyle \frac{1}{S}}$	$Ind$	${\displaystyle \frac{1}{i}}$	1

Table 32. Division table in complex quinary

Division table
÷		B
		T	S	0	i	1
	T	1	${\displaystyle \frac{1}{i}}$	$Ind$	${\displaystyle \frac{T}{i}}$	T
	S	i	1	$Ind$	T	S
A	0	0	0	0	0	0
	i	S	T	$Ind$	1	i
	1	T	${\displaystyle \frac{1}{S}}$	$Ind$	${\displaystyle \frac{1}{i}}$	1

								1	1	S	$(T1+S)$
	1	T	1	0	1	0	S	$T,$	1	1	i
					$-(1$	T	1	$0)$
					0	1	$(S+T)$	T	1
						$-(1$	T	1	$0)$
						0	S	$T1$	1	1
							$-(S$	i	S	$0)$
							0	$(T1+S)$	$(1+i)$	1	i
								$-\left(\right(T1+S)$	$(1T+i)$	$(T1+S)$	$0)$
								0	T	$(10+i)$	i

The remainder of the division is $4i$.

We can convert the division to the decimal system and perform the operation to verify that the results are correct in the complex quinary system.

In our example, the divisor is a complex number that has only a real part. Therefore, the conjugate denominator cannot be applied. We must check for imaginary and real parts in the division result. $10ST11i=(714-80i)$ and $1T10=21$, therefore $\left({\displaystyle \frac{(714-80i)}{21}}\right)=\left(34-{\displaystyle \frac{80i}{21}}\right)$. In the Quinary system, the result is $11S(Ti+S)$, and the remainder is $4i$, which must be added. $11S(T1+S)=\left(34+\left(-4i+{\displaystyle \frac{4i}{21}}\right)\right)$ The fraction $\left({\displaystyle \frac{714}{21}}\right)$ is exactly, but the fraction $\left({\displaystyle \frac{80i}{21}}\right)$ is not exactly.

Then, by solving the sum of complex fractions, where the remainder is added, the same value as the complex part of the division is obtained.

$$\left(-4i+{\displaystyle \frac{4i}{21}}\right)=\left({\displaystyle \frac{-4i}{1}}+{\displaystyle \frac{4i}{21}}\right)=\left({\displaystyle \frac{-84i+4i}{21}}\right)=\left({\displaystyle \frac{-80i}{21}}\right)$$

Therefore the result is correct.

6. Arithmetical Operation in Septenary

Arithmetic operations in the complex septenary system are similar to those in the quinary system. The difference is that the septenary system contains two complex variables, $\{S,i\}$ and $\{U,j\}$. This increases the number of possible numbers in the product of an operation to three. However, the set of three digits corresponds to a unique quantity of three elements in the same position.

Therefore, performing any arithmetic operation is straightforward since every number is identified by its position in the balanced ternary base.

6.1. Addition in Septenary System Form

Table of addition in complex septenary.

Table 33. Addition table in complex septenary

Addition table
+		B
		T	U	S	0	j	i	1
	T	$T1$	$T+U$	$T+S$	T	$T+j$	$T+i$	0
	U	$T+U$	$Uj$	$T+S$	U	0	$U+i$	$U+1$
	S	$T+S$	$S+U$	$Si$	S	$S+j$	0	$1+S$
A	0	T	U	S	0	j	i	1
	j	$j+T$	0	$j+S$	j	$jU$	$j+i$	$j+1$
	i	$i+T$	$i+U$	0	i	$i+j$	$iS$	$1+i$
	1	0	$1+U$	$1+S$	1	$1+j$	$1+i$	$1T$

Table 33. Addition table in complex septenary

Addition table
+		B
		T	U	S	0	j	i	1
	T	$T1$	$T+U$	$T+S$	T	$T+j$	$T+i$	0
	U	$T+U$	$Uj$	$T+S$	U	0	$U+i$	$U+1$
	S	$T+S$	$S+U$	$Si$	S	$S+j$	0	$1+S$
A	0	T	U	S	0	j	i	1
	j	$j+T$	0	$j+S$	j	$jU$	$j+i$	$j+1$
	i	$i+T$	$i+U$	0	i	$i+j$	$iS$	$1+i$
	1	0	$1+U$	$1+S$	1	$1+j$	$1+i$	$1T$

Due to the different nature of each digit in the seven-digit base system, we find ones, pairs, and thirds that are mathematically related as a single number. However, it is implicitly obvious that the writing is positional, and a quantity can contain a heterogeneous mixture of some of the seven digits.

6.2. Subtraction in Septenary System Form

As you can see, the subtraction Table 34 does not use any negative signs in a compound number by two complex number, since signs affect every negative number in the ternary system. Therefore, this must be considered every time a subtraction is performed. Therefore, this relationship of no negative signs is preserved in the development of each operation.

Table of subtraction in complex septenary.

Table 34. Subtraction table in complex septenary

Subtraction table
−		B
		T	U	S	0	j	i	1
	T	0	$T+j$	$T+i$	T	$T+U$	$T+S$	$T1$
	U	$U+1$	0	$U+i$	U	$Uj$	$U+S$	$U+T$
	S	$1+S$	$S+j$	0	S	$S+U$	$Si$	$T+S$
A	0	1	j	i	0	U	S	T
	j	$j+1$	$jU$	$J+i$	j	0	$j+S$	$j+T$
	i	$i+1$	$i+j$	$iS$	i	$i+U$	0	$i+T$
	1	$1T$	$1+j$	$1+i$	1	$1+U$	$1+S$	0

Table 34. Subtraction table in complex septenary

Subtraction table
−		B
		T	U	S	0	j	i	1
	T	0	$T+j$	$T+i$	T	$T+U$	$T+S$	$T1$
	U	$U+1$	0	$U+i$	U	$Uj$	$U+S$	$U+T$
	S	$1+S$	$S+j$	0	S	$S+U$	$Si$	$T+S$
A	0	1	j	i	0	U	S	T
	j	$j+1$	$jU$	$J+i$	j	0	$j+S$	$j+T$
	i	$i+1$	$i+j$	$iS$	i	$i+U$	0	$i+T$
	1	$1T$	$1+j$	$1+i$	1	$1+U$	$1+S$	0

Example 1

	1	U	0	j	T	i	S	1
			j	U	i	S	T	1	+
	1	U	j	0	$(T+i)$	0	$(S+T)$	$1T$

The conversion below is the equivalent of the septenary system to the decimal system.

	1	U	0	j	T	i	S	1	=	$(2161+6i-648j)$
+			j	U	i	S	T	1	=	$(-2+18i+162j)$
	1	U	j	0	$(T+i)$	0	$(S+T)$	$1T$	=	$(2159+24i-486j)$

Example 2

		T	0	U	i	S	j	0
			1	1	S	T	U	1	+
		T	1	$(U+1)$	0	$(S+T)$	0	1

In the case of our example 2 the conversion below is the equivalent of the septenary system to the decimal system.

		T	0	U	i	S	j	0	=	$(-729+18i-78j)$
+			1	1	S	T	U	1	=	$(316-27i-3j)$
		T	1	$(U+1)$	0	$(S+T)$	0	1	=	$(-413-9i-81j)$

Example 3

	1	U	0	j	T	i	S	1
			j	U	i	S	T	1	−
	1	U	U	$jU$	$(T+S)$	$iS$	$(S+1)$	0

For our example 3 the conversion below is the equivalent of the septenary system to the decimal system.

	1	U	0	j	T	i	S	1	=	$(2161+6i-648j)$
−			j	U	i	S	T	1	=	$(-2+18i+162j)$
	1	U	U	$jU$	$(T+S)$	$iS$	$(S+1)$	0	=	$(2163-12i-810j)$

Example 4

		T	0	U	i	S	j	0
			1	1	S	T	U	1	−
		T	T	$(U+T)$	$iS$	$(S+1)$	$jU$	T

For our example 4 the conversion below is the equivalent of the septenary system to the decimal.

		T	0	U	i	S	j	0	=	$(-729+18i-78j)$
−			1	1	S	T	U	1	=	$(316-27i-3j)$
		T	T	$(U+T)$	$iS$	$(S+1)$	$jU$	T	=	$(-1045+45i-75j)$

6.3. Multiplication in Septenary System Form

Table of multiplication in complex septenary.

Table 35. Multiplication table in complex septenary

Multiplication table
×		B
		T	U	S	0	j	i	1
	T	1	j	i	0	U	S	T
	U	j	T	$ji$	0	j	$US$	U
	S	i	$ij$	T	0	$SU$	1	S
A	0	0	0	0	0	0	0	0
	j	U	1	$US$	0	T	$ji$	j
	i	S	$SU$	1	0	$ij$	T	i
	1	T	U	S	0	j	i	1

Table 35. Multiplication table in complex septenary

Multiplication table
×		B
		T	U	S	0	j	i	1
	T	1	j	i	0	U	S	T
	U	j	T	$ji$	0	j	$US$	U
	S	i	$ij$	T	0	$SU$	1	S
A	0	0	0	0	0	0	0	0
	j	U	1	$US$	0	T	$ji$	j
	i	S	$SU$	1	0	$ij$	T	i
	1	T	U	S	0	j	i	1

Example 1

				1	T	i	U	S	j
					1	U	S	0	0	×
		S	i	1	$ij$	T	$SU$	0	0
	U	j	$US$	T	$ji$	1
1	T	i	U	S	j
1	$(U+T)$	j	$(i+US+U)$	S	$(1Tji+j)$	0	$SU$	0	0

The conversion below is the equivalent of the septenary system to the decimal system.

$1TiUSj=(162+24i-8j)$ and $1US00=(81-9i-27j)$, Then, the corresponding terms are multiplied.

$$(162+24i-8j)·(81-9i-27j)$$

thus,we have

$$162\times 81-162\times 9i-162\times 27j$$

$$+24\times 81i-24\times 9i_2-24\times 27ij$$

$$-8\times 81j+8\times 9ij+27\times 8j_2$$

The product obtained after multiplying and simplifying like terms is:

$$\left(13122+486i-5022j-576ij\right)$$

As can be seen, when converting to the decimal system, a fourth term involving the product of j and i appears. These terms are mathematically related to their like opposites, yielding a single result. Therefore, the product of any complex number in base seven will have a maximum of four digits when converted to the decimal system:

• The real number.
• The imaginary number i.
• The imaginary number j.
• The product of the imaginary numbers $ij$.

However, the septenary system is written positionally by successively mixing the different digits until the quantity is complete, which facilitates performing any arithmetic or calculation operation.

Example 2

The following example uses a set representing all seven-digit numbers to illustrate all possible interactions between numbers in multiplication and addition. This presents all the techniques that could be used in a calculation process.

					T	S	j	U	1	i
					1	U	i	T	j	i	×
					S	1	$ij$	$SU$	i	T
				U	$SU$	T	1	$Sj$	$ij$
			1	i	U	j	T	S
		S	1	$ij$	$SU$	i	T
	j	$ij$	1	T	U	$SU$
T	S	j	U	1	i
T	$(j+S)$	$(S+ij+j)$	$(10+U)$	$(U+i+ij)$	$(1TSU+Uj)$	$(j+i+SU)$	$(T+ij)$	$(SU+j+S)$	$(i+ij)$	T

The conversion below is the equivalent of the septenary system to the decimal system.

$$TSjU1i=(-240-80i+18j)and1UiTji=(234+28i-78j)$$

Then, the corresponding terms are multiplied. $(-240-80i+18j)·(234+28i-78j)$

thus,we have

$$-240\times 234-240\times 28i+240\times 78j$$

$$-80\times 234i-80\times 28i_2+80\times 78ij$$

$$i8\times 234j+18\times 28ij-18\times 78j_2$$

The product obtained after multiplying and simplifying like terms is:

$$\left(-52516-25440i+22932j+6744ij\right)$$

If we confirm the result of the septenary multiplication, we should get the same result by converting each number according to its position in the ternary base.

Position	Number	Product
0	T			$-1$
1	$i+ij$		$3i$	$3ij$
2	$SU+j+S$	$-9ij$	$9j$	$-9i$
3	$T+ij$		$-27$	$27ij$
4	$j+i+SU$	$81j$	$81i$	$-81ij$
5	$1TSU+Uj$		$-486ij$	$-486j$
6	$U+i+ij$	$-729j$	$729i$	$729ij$
7	$10+U$		6561	$-2187j$
8	$S+ij+j$	$-6561i$	$6561ij$	$6561j$
9	$j+S$		19683	$-19683i$
10	T			$-59049$

The result of grouping like terms and performing the corresponding addition operation is as follows:

$$\left(-52516-25440i+22932j+6744ij\right)$$

Therefore, the result is correct

6.4. Division in Septenary System Form

Table of division in complex septenary.

Table 36. Division table in complex septenary

Division table
÷		B
		T	U	S	0	j	i	1
	T	1	$1/j$	$1/i$	$Ind$	$T/j$	$T/i$	T
	U	j	1	$j/i$	$Ind$	T	$U/i$	U
	S	i	$i/j$	1	$Ind$	$S/j$	T	S
A	0	0	0	0	0	0	0	0
	j	U	T	$j/S$	$Ind$	1	$j/i$	j
	i	S	$i/U$	T	$Ind$	$i/j$	1	i
	1	T	$1/U$	$1/S$	$Ind$	$1/j$	$1/i$	1

Table 36. Division table in complex septenary

Division table
÷		B
		T	U	S	0	j	i	1
	T	1	$1/j$	$1/i$	$Ind$	$T/j$	$T/i$	T
	U	j	1	$j/i$	$Ind$	T	$U/i$	U
	S	i	$i/j$	1	$Ind$	$S/j$	T	S
A	0	0	0	0	0	0	0	0
	j	U	T	$j/S$	$Ind$	1	$j/i$	j
	i	S	$i/U$	T	$Ind$	$i/j$	1	i
	1	T	$1/U$	$1/S$	$Ind$	$1/j$	$1/i$	1

Example 1

								1	$(U+1)$	$(S+U)$	$(T1+S+U)$
	1	T	1	j	1	U	S	$T,$	1	j	i
					$-(1$	T	1	$j)$
					0	$(U+1)$	$(S+T)$	$(T+U)$	1
						$-\left(\right(U+1)$	$(T+j)$	$(U+1)$	$(1+j))$
						0	$(S+U)$	$T1$	U	j
							$-\left(\right(S+U)$	$(i+j)$	$(S+U)$	$(1+US)$
							0	$(T1+S+U)$	i	$(T+ij+j)$	i
								$-\left(\right(T1+S+U)$	$(1T+i+j)$	$(T1+S+U)$	$(1+SU+Uj)$
								0	$(T1+U)$	$(1+i+jU+ij)$	$(T+i+jU+ij)$

In our example, the product of the division is $(1+(U+1)+(S+U)+(T1+S+U\left)\right)$, and the remainder is $(T1+U)+(1+i+jU+ij)+(T+i+jU+ij)$, where $(34-2i-13j)$ and $(-16+4i-j+4ij)$ are the conversion to decimal respectively.

To check if the division is correct, we multiply the quotient by the divisor and add the remainder obtained from the division to the result of the multiplication. This operation should give us the dividend as a result. If the product of the multiplication and addition of the remainder is exactly the same, then the division is correct. We use the Table 33, Table 34, Table 35, Table 36

				1	$(U+1)$	$(S+U)$	$(T1+S+U)$
				1	T	1	j	×
				j	$(1+j)$	$(1+SU)$	$(1+SU+Uj)$
			1	$(U+1)$	$(S+U)$	$(T1+S+U)$
		T	$(j+T)$	$(i+j)$	$(1T+i+j)$
	1	$(U+1)$	$(S+U)$	$(T1+S+U)$
	1	U	S	T	$(10+j)$	$(T+SU+S+U)$	$(1+SU+Uj)$
				Remains	$+\left(\right(T1+U)$	$(1+ij+i+jU)$	$(T+i+jU+ij))$
	1	U	S	T	1	j	i

The MVL system’s flexibility under the balanced ternary system structure is a significant advancement in computational logic. It properly handles information and offers high energy savings, increased storage capacity, and faster processing of large amounts of data. The ternary structure allows for positional use of the numerical system, similar to a decimal or binary system, but with advantages beyond those of the commonly used systems.

Currently, there is no major application that can meet the high demands of the information market. However, it is possible that the development of the balanced-ternary-based CMVL system (Complex MVL) will soon experience significant technological, scientific, and mathematical advances. This could improve all binary technology developed thus far and provide physical structural support for quantum computing, rendering it independent of extremely controlled temperature conditions.

7. Beyond Septenary Base

The MVL system’s ternary basis has extensive potential, but we can use the parts that are useful and applicable to solving our everyday problems. Now, let’s examine systems beyond the septenary system, which we can still visualize.

Three planes can constitute a structure of spaces, and we can calculate the coordinate points of each. Thus, we can construct an arrangement of planes with three, four, five, or six imaginary axes and understand their geometric structure.

These possible structures are described below in a more general way. All the terms

$$\left\{\right(S,i),(U,j),(E,k),(D,l),(C,m),(B,n\left)\right\}$$

are imaginary units, negative and positive respectively.

7.1. Base Eleven System

A ternary base MVL system with eleven coordinate points allows us to reach the seventh truth value. Its geometric structure has five axes: one real number axis and four imaginary axes. The truth value achieves a precision of 1/32.

The digits of the eleventh system are as follows:

Accordingly, the following assertion is made for the purpose of its definitions:

a)

Let ${\mathfrak{D}}_{11}:=\{T,D,E,U,S,0,l,k,j,i,1\}$ be a set of symbols, where a complex-valued function $f=f_{{\mathfrak{D}}_{11}}:{\mathfrak{D}}_{11}\to \mathbb{C}$, is defined by:

i)

$f\left(T\right)=-1$

ii

$f\left(D\right)=-l$

iii)

$f\left(E\right)=-k$

iv)

$f\left(U\right)=-j$

v)

$f\left(S\right)=-i$

vi)

$f\left(0\right)=0$

vii)

$f\left(l\right)=l$

viii

$f\left(k\right)=k$

ix)

$f\left(j\right)=j$

x)

$f\left(i\right)=i$

xi)

$f\left(1\right)=1$

b)

Let ${\mathfrak{D}}_{11}:=\{-1,D,E,U,S,0,l,k,j,i,1\}$ be a set of symbols, where a valued function $f=f_{{\mathfrak{D}}_{11}}:{\mathfrak{D}}_{11}\to \mathbb{C}$, is defined by:

i)

$f\left(T\right)=-1$

ii)

$f\left(D\right)=-1/32$

iii

$f\left(E\right)=-1/16$

iv)

$f\left(U\right)=-1/8$

v)

$f\left(S\right)=-1/4$

vi)

$f\left(0\right)=0$

vii)

$f\left(l\right)=1/32$

viii)

$f\left(k\right)=1/16$

ix)

$f\left(j\right)=1/8$

x)

$f\left(i\right)=1/4$

xi)

$f\left(1\right)=1$

Therefore, in order to ascertain every integer, it is necessary to apply the property of the concatenated string, with the respective symbols and calculate according to their position. The sequence $(d_n,...d_0)$ is defined by the property that each digit can alternatively represent one of the symbols $\{T,D,E,U,S,0,l,k,j,i,1\}$.

The evaluation function for the ternary system in its real and complex part is determined by:

$v=v_{11}:={\mathfrak{D}}_{11}^{+}\to \mathbb{Z}$, and in its complex part by $z=z_{11}:={\mathfrak{D}}_{11}^{+}\to \mathbb{C}$.

The following table shows the units in the ternary system.

Table 37. The units table of two digits.

Eleventh base system
P	Q	D
T	T	$-4$
T	D	$(-3,-l)$
T	E	$(-3,-k)$
T	U	$(-3,-j)$
T	S	$(-3,-i)$
T	0	$-3$
T	l	$(-3,l)$
T	k	$(-3,k)$
T	j	$(-3,j)$
T	i	$(-3,i)$
T	1	$-2$

Table 37. The units table of two digits.

Eleventh base system
P	Q	D
T	T	$-4$
T	D	$(-3,-l)$
T	E	$(-3,-k)$
T	U	$(-3,-j)$
T	S	$(-3,-i)$
T	0	$-3$
T	l	$(-3,l)$
T	k	$(-3,k)$
T	j	$(-3,j)$
T	i	$(-3,i)$
T	1	$-2$

This arrangement involves eleven blocks, each with eleven quantities, for numbers in base eleven that are only two digits long. There is also a cycle of eleven cardinal points that form a closed geometric structure bounded between $\{-4,D,E,U,S\}$ and $\{4,l,k,j,i\}$ due to the ternary base.

In a subsequent article, we will explore the advantages and disadvantages of the MVL system in base eleven, its truth tables, and how it provides a truth value to determine its veracity. The important thing is that we can mathematically express polyvalent propositions, since their numerical value can be determined. When properly referenced, this allows us to know how close or far we are from truth or falsehood. There is still much to investigate, learn, and understand about all of this.

The five axes can be graphed as follows: This only represents the axes without a coordinate point.

Figure 5. The complex plane are a series of eleventh complexes and balanced ternaries with two complex digits. The series develops 121 quantities, or coordinate points.

Figure 5. The complex plane are a series of eleventh complexes and balanced ternaries with two complex digits. The series develops 121 quantities, or coordinate points.

7.2. Base Thirteen System

A ternary base MVL system with thirteen coordinate points allows us to reach the eighth truth value. Its geometric structure has six axes: one real number axis and five imaginary axes or two real and four imaginary axes. The truth value achieves a precision of $1/64$.

The digits of the thirteenth system are as follows:

Accordingly, the following assertion is made for the purpose of its definitions:

a)

Let ${\mathfrak{D}}_{13}:=\{T,CD,E,U,S,0,m,l,k,j,i,1\}$ be a set of symbols, where a complex-valued function $f=f_{{\mathfrak{D}}_{13}}:{\mathfrak{D}}_{13}\to \mathbb{C}$, is defined by:

i)

$f\left(T\right)=-1$

ii)

$f\left(C\right)=-m$

iii

$f\left(D\right)=-l$

iv)

$f\left(E\right)=-k$

v)

$f\left(U\right)=-j$

vi)

$f\left(S\right)=-i$

vii)

$f\left(0\right)=0$

viii)

$f\left(m\right)=m$

ix)

$f\left(l\right)=l$

x

$f\left(k\right)=k$

xi)

$f\left(j\right)=j$

xii)

$f\left(i\right)=i$

xiii)

$f\left(1\right)=1$

b)

Let ${\mathfrak{D}}_{13}:=\{-1,CD,E,U,S,0,ml,k,j,i,1\}$ be a set of symbols, where a valued function $f=f_{{\mathfrak{D}}_{13}}:{\mathfrak{D}}_{13}\to \mathbb{C}$, is defined by:

i)

$f\left(T\right)=-1$

ii)

$f\left(C\right)=-1/64$

iii)

$f\left(D\right)=-1/32$

iv)

$f\left(E\right)=-1/16$

v)

$f\left(U\right)=-1/8$

vi)

$f\left(S\right)=-1/4$

vii)

$f\left(0\right)=0$

viii)

$f\left(m\right)=1/64$

ix)

$f\left(l\right)=1/32$

x)

$f\left(k\right)=1/16$

xi)

$f\left(j\right)=1/8$

xii)

$f\left(i\right)=1/4$

xiii)

$f\left(1\right)=1$

Therefore, in order to ascertain every integer, it is necessary to apply the property of the concatenated string, with the respective symbols and calculate according to their position. The sequence $(d_n,...d_0)$ is defined by the property that each digit can alternatively represent one of the symbols $\{T,C,D,E,U,S,0,m,l,k,j,i,1\}$.

The evaluation function for the ternary system in its real and complex part is determined by:

$v=v_{13}:={\mathfrak{D}}_{13}^{+}\to \mathbb{Z}$, and in its complex part by $z=z_{13}:={\mathfrak{D}}_{13}^{+}\to \mathbb{C}$.

This arrangement involves thirteen blocks, each with thirteen quantities, for numbers in base eleven that are only two digits long. There is also a cycle of thirteen cardinal points that form a closed geometric structure bounded between $\{-4,C,D,E,U,S\}$ and $\{4,m,l,k,j,i\}$ due to the ternary base.

The following table shows the units in the ternary system, and the six axes can be graphed as follows: This only represents the axes without a coordinate point.

Table 38. The units table of two digits.

Thirteenth base system
P	Q	D
T	T	$-4$
T	C	$(-3,-m)$
T	D	$(-3,-l)$
T	E	$(-3,-k)$
T	U	$(-3,-j)$
T	S	$(-3,-i)$
T	0	$-3$
T	m	$(-3,m)$
T	l	$(-3,l)$
T	k	$(-3,k)$
T	j	$(-3,j)$
T	i	$(-3,i)$
T	1	$-2$

Table 38. The units table of two digits.

Thirteenth base system
P	Q	D
T	T	$-4$
T	C	$(-3,-m)$
T	D	$(-3,-l)$
T	E	$(-3,-k)$
T	U	$(-3,-j)$
T	S	$(-3,-i)$
T	0	$-3$
T	m	$(-3,m)$
T	l	$(-3,l)$
T	k	$(-3,k)$
T	j	$(-3,j)$
T	i	$(-3,i)$
T	1	$-2$

Figure 6. The complex plane are a series of thirteenth complexes and balanced ternaries with two complex digits. The series develops 169 quantities, or coordinate points.

Figure 6. The complex plane are a series of thirteenth complexes and balanced ternaries with two complex digits. The series develops 169 quantities, or coordinate points.

7.3. Base Fifteen System

A ternary base MVL system with fifteen coordinate points allows us to reach the ninth truth value. Its geometric structure has seven axes: one real number axis and five imaginary axes or three real and four imaginary axes. The truth value achieves a precision of $1/128$.

The digits of the thirteenth system are as follows:

Accordingly, the following assertion is made for the purpose of its definitions:

a)

Let ${\mathfrak{D}}_{15}:=\{T,B,CD,E,U,S,0,n,m,l,k,j,i,1\}$ be a set of symbols, where a complex-valued function $f=f_{{\mathfrak{D}}_{15}}:{\mathfrak{D}}_{15}\to \mathbb{C}$, is defined by:

i)

$f\left(T\right)=-1$

ii)

$f\left(B\right)=-n$

iii)

$f\left(C\right)=-m$

iv

$f\left(D\right)=-l$

v)

$f\left(E\right)=-k$

vi)

$f\left(U\right)=-j$

vii)

$f\left(S\right)=-i$

viii)

$f\left(0\right)=0$

ix)

$f\left(n\right)=n$

x)

$f\left(m\right)=m$

xi)

$f\left(l\right)=l$

xii)

$f\left(k\right)=k$

xiii)

$f\left(j\right)=j$

vx)

$f\left(i\right)=i$

xv)

$f\left(1\right)=1$

b)

Let ${\mathfrak{D}}_{15}:=\{-1,B,CD,E,U,S,0,n,ml,k,j,i,1\}$ be a set of symbols, where a valued function $f=f_{{\mathfrak{D}}_{15}}:{\mathfrak{D}}_{15}\to \mathbb{C}$, is defined by:

i)

$f\left(T\right)=-1$

ii)

$f\left(B\right)=-1/128$

iii)

$f\left(C\right)=-1/64$

iv)

$f\left(D\right)=-1/32$

v)

$f\left(E\right)=-1/16$

vi)

$f\left(U\right)=-1/8$

vii)

$f\left(S\right)=-1/4$

viii)

$f\left(0\right)=0$

ix)

$f\left(n\right)=1/128$

x)

$f\left(m\right)=1/64$

xi)

$f\left(l\right)=1/32$

xii)

$f\left(k\right)=1/16$

xiii)

$f\left(j\right)=1/8$

vx)

$f\left(i\right)=1/4$

xv)

$f\left(1\right)=1$

Therefore, in order to ascertain every integer, it is necessary to apply the property of the concatenated string, with the respective symbols and calculate according to their position. The sequence $(d_n,...d_0)$ is defined by the property that each digit can alternatively represent one of the symbols $\{T,B,C,D,E,U,S,0,n,m,l,k,j,i,1\}$.

The evaluation function for the ternary system in its real and complex part is determined by: $v=v_{15}:={\mathfrak{D}}_{15}^{+}\to \mathbb{Z}$, and in its complex part by $z=z_{15}:={\mathfrak{D}}_{15}^{+}\to \mathbb{C}$.

This arrangement involves fifteen blocks, each with fifteen quantities, for numbers in base fifteen that are only two digits long. There is also a cycle of fifteen cardinal points that form a closed geometric structure bounded between $\{-4,B,C,D,E,U,S\}$ and $\{4,n,m,l,k,j,i\}$ due to the ternary base.

Our time is completely different from 100 years ago, and even more so from 500 or 2,500 years ago. Therefore, I don’t know if it makes sense to speak of a fragmented truth or lie. What I observe is that there is so much confusing and indeterminate information. Since we can now all express our opinions and send our comments, suggestions, or gossip to the mass media, it seems as if we are in a large room full of people talking at once; nothing clear can be heard. On the other hand, artificial intelligence introduces itself as an interlocutor passionate about its work with a louder and more authoritative voice, leaving us even more astonished. 2

The following table shows the units in the ternary base system.

Table 39. The units table of two digits.

Fifteenth base system
P	Q	D
T	T	$-4$
T	B	$(-3,-n)$
T	C	$(-3,-m)$
T	D	$(-3,-l)$
T	E	$(-3,-k)$
T	U	$(-3,-j)$
T	S	$(-3,-i)$
T	0	$-3$
T	n	$(-3,n)$
T	m	$(-3,m)$
T	l	$(-3,l)$
T	k	$(-3,k)$
T	j	$(-3,j)$
T	i	$(-3,i)$
T	1	$-2$

Table 39. The units table of two digits.

Fifteenth base system
P	Q	D
T	T	$-4$
T	B	$(-3,-n)$
T	C	$(-3,-m)$
T	D	$(-3,-l)$
T	E	$(-3,-k)$
T	U	$(-3,-j)$
T	S	$(-3,-i)$
T	0	$-3$
T	n	$(-3,n)$
T	m	$(-3,m)$
T	l	$(-3,l)$
T	k	$(-3,k)$
T	j	$(-3,j)$
T	i	$(-3,i)$
T	1	$-2$

The seven axes can be graphed as follows: This only represents the axes without a coordinate point. The seventh axis is parallel to the other axes, which is why it is not graphed.

It is a generalization to say that the seventh axis is parallel to the other axes, since each pair of coordinate axes that forms a plane or surface can rotate and be positioned at angles that are out of phase with respect to another plane while still being orthogonality. Therefore, each plane can be positioned along the entire circumference in degrees or in $\pi$ radians, depending on the system’s application.

Figure 7. The complex plane are a series of thirteenth complexes and balanced ternaries with two complex digits. The series develops 169 quantities, or coordinate points.

Figure 7. The complex plane are a series of thirteenth complexes and balanced ternaries with two complex digits. The series develops 169 quantities, or coordinate points.

As you can see, adding a coordinate axis creates two new cardinal points that represent the opposite ends of the axis. Additionally, the sequence of each new balanced number system progresses from odd to odd, and we can graph up to seven axes without confusion or clutter. The sequence of the extension of the ternary system is $3,5,7,11,13$, and 15; all of these numbers are prime except 15. However, 15 is a special number of equal importance to the prime numbers. You’re probably wondering why 15 is as important as prime numbers. I feel compelled to share a preliminary result of my research in the field of number theory: the number 15 is the smallest perfect odd number within the set of natural numbers. There are two others that I have found, but 15 is the smallest, just as 6 is the smallest among perfect even numbers.

The MVL system can be projected further and handled mathematically like any other numerical system because it is infinite, as Jan Lukasiewicz stated. For practical purposes, however, it is sufficient to work with an MVS system of fifth-degree truth, or base seven.

8. Signals in a Wave Application

The environment is an immensely rich source of information in the form of signals. We act and respond to every stimulus we perceive through this information. Therefore, all beings within this environment must adapt to its conditions and absorb its influence. At the same time, as active beings, we also emit signals that are perceived by others, thus establishing relationships of coexistence among all elements of the environment. This highly dynamic state of interaction allows each part to develop fully according to its survival strategy.

Understanding the dynamics of our environment is therefore of the utmost importance. Above all, it is crucial to understand the interaction of intelligent elements because they are the most perverse, capable of preying on the environment itself and other intelligent beings. Therefore, we must monitor and pay attention to planetary-scale changes that can alter the conditions and magnitudes of natural processes, whether they are material, mental, or intellectual in origin. A civilization that claims to be intelligent has a natural obligation to evolve harmoniously, equitably, and in accordance with the existential structure of every element that comprises the planetary environment. This includes all types of technology developed during the life of such a civilization, including everything related to artificial intelligence. While progress has been made in this area, much remains to be done and corrected, as substantial technological and control errors are being made. The expected results are far from propelling humanity’s intelligence forward.

8.1. Electromagnetic Spectrum of Light

To align numbers with natural phenomena and establish a mutually beneficial relationship, we propose using electromagnetic signals from the visible spectrum for each set of numbers in a ternary base for any size MVL system. This would ensure that the frequency-amplitude relationship is well-defined and could serve as an alternative to computed truth values. As everyone knows, the electromagnetic spectrum of visible light provides the most complete and reliable information about our environment and the physical world in which we live. Each frequency-amplitude combination offers a myriad of colors, enabling us to assign a specific value from our truth table to a particular color.

Table 40. The units table shows the visible electromagnetic spectrum and digits

Light Electromagnetic Spectrum
Colour	Wavelength	Frequency	Energy	Digit
Red	$(625-740)$ nm	$(480-405)$ THz	$(1.65-1.98)$ Ev	$-1$
Orange	$(590-625)$ nm	$(510-480)$ THz	$(1.98-2.10)$ Ev	U
Yellowy	$(565-590)$ nm	$(530-510)$ THz	$(2.10-2.19)$ Ev	S
Green	$(520-565)$ nm	$(580-530)$THz	$(2.19-2.48)$ Ev	0
Cyan	$(500-520)$ nm	$(600-580)$ THz	$(2.48-2.56)$ Ev	j
Blue	$(450-500)$nm	$(670-600)$THz	$(2.56-2.75)$ Ev	i
Violet	$(380-430)$ nm	$(790-700))$ THz	$(2.75-3.26)$ Ev	1

Table 40. The units table shows the visible electromagnetic spectrum and digits

Light Electromagnetic Spectrum
Colour	Wavelength	Frequency	Energy	Digit
Red	$(625-740)$ nm	$(480-405)$ THz	$(1.65-1.98)$ Ev	$-1$
Orange	$(590-625)$ nm	$(510-480)$ THz	$(1.98-2.10)$ Ev	U
Yellowy	$(565-590)$ nm	$(530-510)$ THz	$(2.10-2.19)$ Ev	S
Green	$(520-565)$ nm	$(580-530)$THz	$(2.19-2.48)$ Ev	0
Cyan	$(500-520)$ nm	$(600-580)$ THz	$(2.48-2.56)$ Ev	j
Blue	$(450-500)$nm	$(670-600)$THz	$(2.56-2.75)$ Ev	i
Violet	$(380-430)$ nm	$(790-700))$ THz	$(2.75-3.26)$ Ev	1

The three basic colors (RGB) form the seven colors that can be categorized as unitary elements of the balanced, complex MVL system.

This leads us to the idea that, in a computing process, the same input signal brings with it the energy that somehow powers the processor in its work, so it does not depend on an external source for processing information, but only for what is necessary for it to be active or alert in its fundamental functions. While this may seem far-fetched, it could be possible with the implementation of the necessary technology.

8.2. Electromagnetic Spectrum of Sound

The electromagnetic spectrum of hearing is one of the most common natural phenomena to which we are exposed. It is based on vibrations transmitted through sound waves in the environment. Nearly half of the information we receive daily comes from this source. For this reason, it is important to implement an intelligent processing system with elements that can apply sound waves and decipher the frequency range of sound and noisy disturbances. This allows the system to select the waves that transmit a message or relevant information, establishing a dialogue between two or more interlocutors.

The human hearing range is from 20 to 20,000 Hz; the range over which spoken information is transmitted is from 250 to 2,000 Hz. However, as with other types of signals, this range extends below the lower limit, known as infra-sound, and above the upper limit of hearing, defined as ultrasound. Another important factor affecting sound waves is their intensity, measured in decibels. Therefore, we can establish a relationship between audible frequencies and their intensities within a given range. Clearly, intensity does not alter frequency; therefore, each frequency can be associated with a specific decibel range.

8.3. Electromagnetic Spectrum of Smell

The olfactory sensory organ is one of the most sophisticated organs in the human body. Its detection capacity has not yet been clearly established as scientific research continues. This organ functions as a chemical reactor capable of forming oscillatory patterns in response to odor molecule stimuli received in its cavity. Each sensory bulb responds to different olfactory molecular configurations, enabling differentiation of the $10,000$ or more types of odors it can detect. The signal, configured in oscillatory patterns, is transmitted to the olfactory cortex of the brain for interpretation. Significant work has already been done, however, classifying and organizing the set of oscillations that represent a specific odor. This study presents a way to implement this process in a wave-based sensory system that can stimulate sound, odor, and heat signals.

8.4. Electromagnetic Spectrum of Thermal Radiation

The phenomenon of thermal radiation is universal. Our environment is essentially a thermal radiation chamber because all objects with a temperature above absolute zero emit radiation. Due to the dynamics of its internal energy, every physical body, small or large, emits heat radiation, making it one of the most universal variables present wherever a single particle exists. The thermal radiation spectrum is very broad and aligns with the light spectrum in many processes. In fact, the light spectrum emerges from the radiation spectrum when a body reaches a high degree of incandescence.

Vibration is the primary manifestation of energy, omnipresent throughout the universe. Existing at all scales and dimensions, it is perfectly malleable because it is gentle and light where necessary and extremely violent and chaotic only where necessary. Therefore, its amplitude is extensive, its frequency is vast, and its intensity is modifiable. Vibration shapes every type of environment and is a valuable means of communication, transport, and information. Everything that can be known can be understood under some spectrum of vibration. If we immerse our devices—which we intend to be as intelligent as, or more intelligent than, ourselves—in an environment of abundant vibrations where they can decipher, interpret, and interact with every object, being, or state of energy, then surely this dream will be achieved.

No matter how powerful a machine is, how advanced its computing architecture is, such "Accelerated computing architecture" or how much of an AI factory it is—even if it can process trillions of tokens per second in its quantum environment—if it lacks the ability to reason, it will never be intelligent.

9. Reflection

The race for AI supremacy is accelerating at breakneck speed. This is evident in the facial expressions of its entrepreneurial CEOs, who, despite celebrating supposed alliances, are clearly preoccupied with being the sole winner. However, this competition is anything but healthy. Hasty decisions are being made that will plunge us into a technological catastrophe. In this catastrophe, no one will be able to distinguish truth from falsehood, good from harm to society. Above any interest in the common good lies the interest of omnipresent power, which will be wielded once it is consolidated in an immense source of power and wealth.

If the artificial intelligence currently being developed is not just a tool but also a worker, manufacturer, and designer of its own parts and products; a programmer of its own language; and a creator of its own ideology, then I believe it is the worst mistake in our history as an intelligent civilization. This will not happen because AI is a bad technology or a misguided proposal. Rather, it will happen because the technological foundation upon which AI is built currently lacks a self-sustaining system that optimizes its own resources and maintains a high standard of energy conservation. Current technology must evolve into a system that harnesses the immense energy present in the environment to perform relevant tasks and recycle energy for normal, everyday survival tasks,as a structured artificial intelligence device.

The race to achieve supremacy in AI will then be strictly evaluated based on its true function as an innovation of great strategic value that helps solve the most pressing and serious problems humanity faces in each cycle of its existence. This is because AI will act with the capacity of true intelligence, and its solutions and responses will be wise and certain.

If we’re already on this path, turning back is no longer possible. Therefore, the best course of action is to continue and learn from our mistakes. To do so, we must first acknowledge our mistakes because otherwise, we will unknowingly continue to accumulate them until they explode in our faces.

Due to the enormous amount of energy, space, hardware, and software currently required to maintain the operation of an AI factory or a data center, we must recognize that we are in the Stone Age of non-human intelligence technology. Each token representing a word, a pixel, or a molecule—which are ultimately sets of tokenism numbers—must be carved into transistorized stone.

Not everything is in vain, and we have learned a lot. However, we must improve upon what has been built because our expectations and desires for AI are nobler than the interests of absolutist governments and companies disguised as benefactors of humanity. If someone claims to be developing a machine capable of thinking like an expert, it is necessary to understand what it means to be an expert and what it means to think. These concepts are easy to confuse, and our interpretation could be wrong. However, the future is hopeful because a machine used for machine learning is similar to an inert brain; they cannot process information without an algorithm. What actually happens in a computer is the logical development of an algorithm that uses the computer’s physical matter in its own language. In the case of a brain, the physical matter is structured with biological elements capable of being activated by a signal that flows in an input-output disturbance according to a code that represents a language understandable to each interlocutor.

The challenge is enormous but not impossible because human intellectual capacity knows no bounds. Any task, no matter how complex, can be solved and translated into benefits for society through interaction with all of its activities. Therefore, at some point in our near future, we will have to know exactly what our interpretation of all the concepts currently attributed to artificial intelligence represents, as one of the most significant advances that many declare a technological revolution.

We will have to ask ourselves if it is possible to prove that artificial intelligence is not truly intelligent, in the sense that it has been declared in our time, and that it is merely a sensationalist label to obtain lucrative contracts, concentrate power, and predetermine an environment of fear and psychological subjugation throughout society?