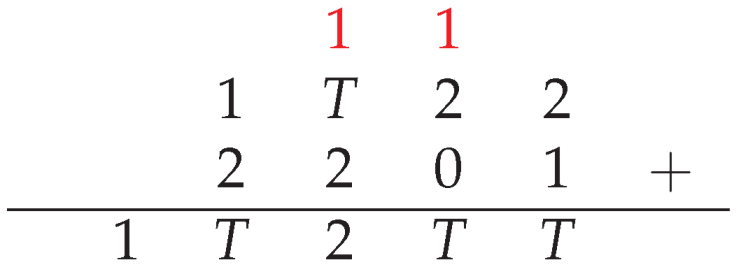
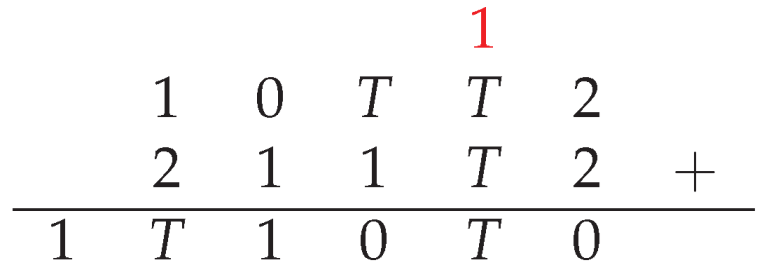
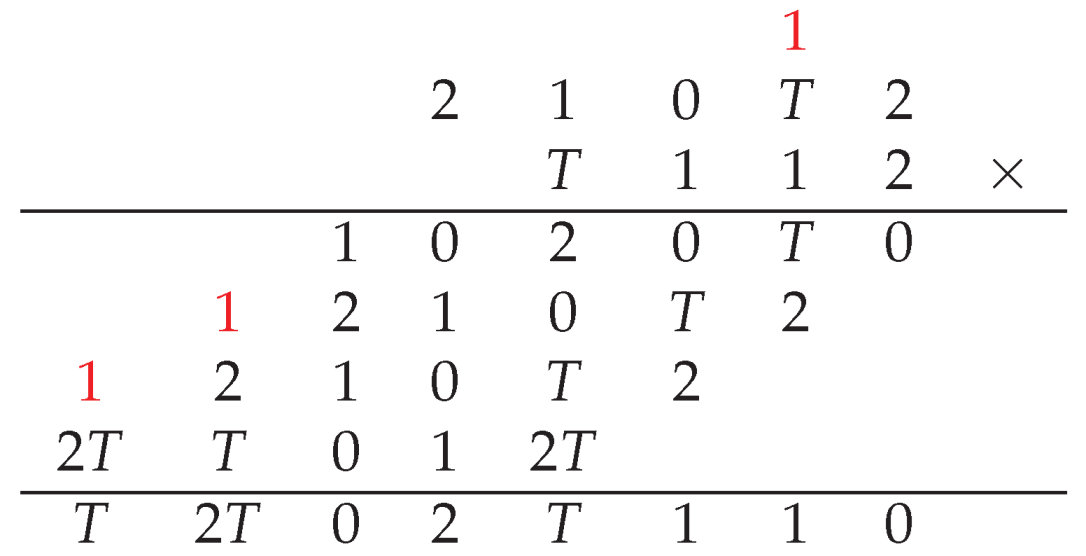
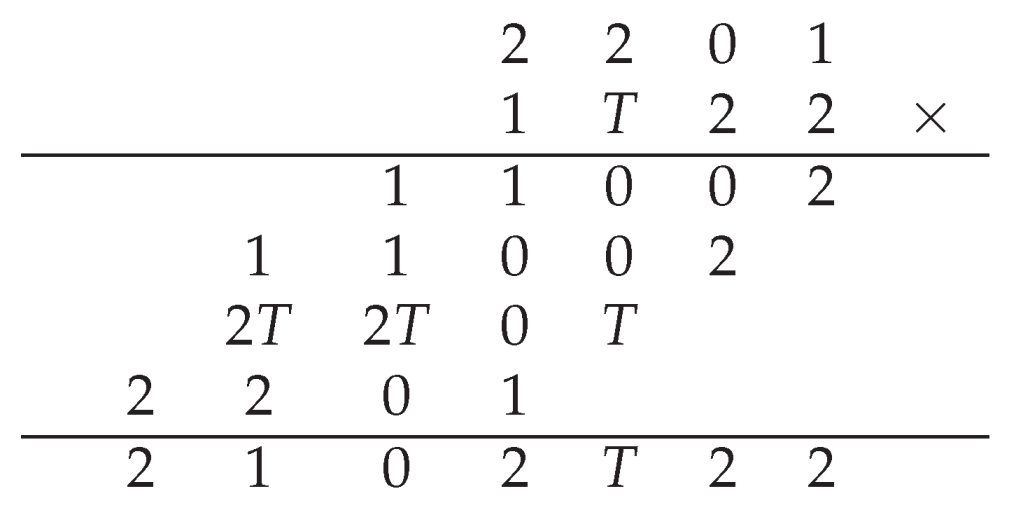
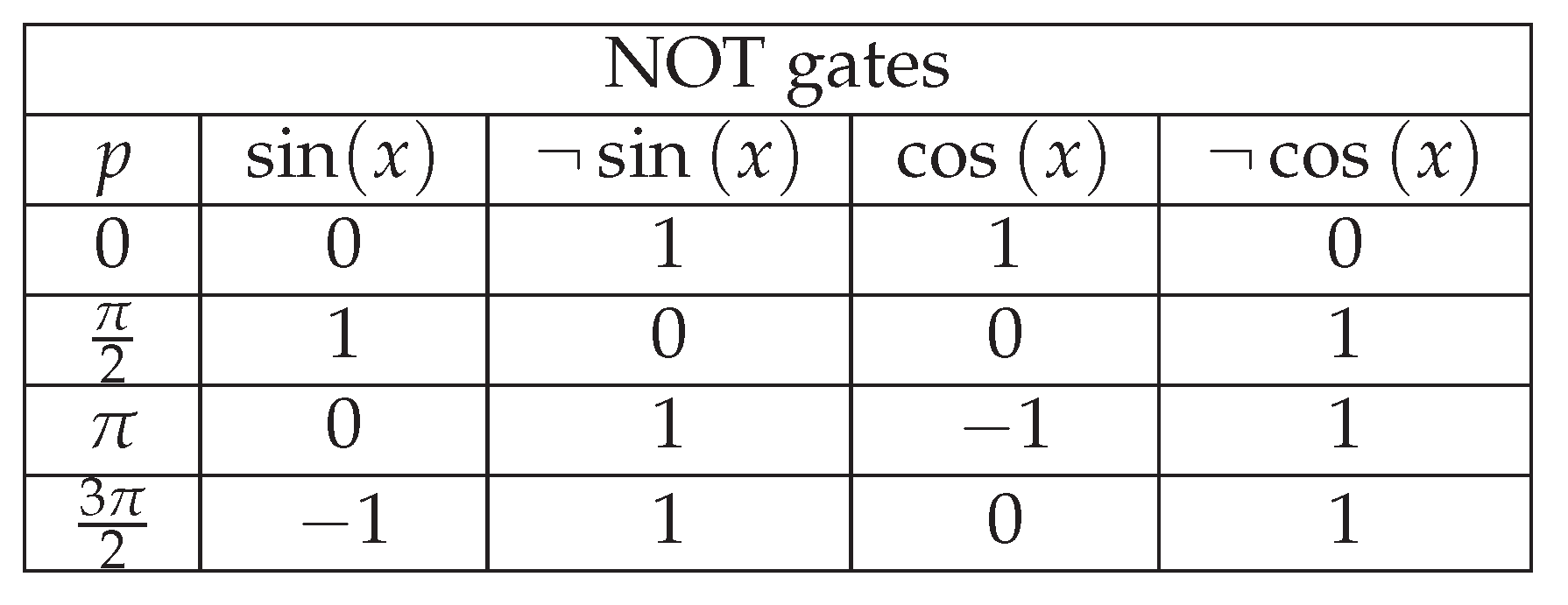The Logical Implications of the Base-Four Number System

Rafael Garcia-Sandoval

doi:10.20944/preprints202510.0835.v1

Submitted:

10 October 2025

Posted:

13 October 2025

You are already at the latest version

Abstract

In this article, the logical concepts that underpin the translation of logic circuits will be defined and presented. The intention is to apply these concepts directly to hardware and to the management of language codes in computer systems. The Quaternary System has a wide range of applications, including data transmission, for example the 2B1Q code utilized in ISDN devices, and the analysis of Hilbert curves. Notably, the quaternary system plays a crucial role in the digitization of the human genome due to its direct relationship with the binary system, which is analogous to the pairs of digits found in DNA. The pair [0, 3] corresponds to the paired nucleotides {AT}, and the pair [1, 2] corresponds to the paired nucleotides {CG}. The Base four System bears a certain relation to the Ternary System (0, 1, 2) , the balance ternary system had been taking more advanced, particularly with regard to the significant advancements made in NMAX, NMIN logic gates similar to binary NOR and NAND gates respectively. The Balanced Ternary System (-1, 0, +1) has played a substantial role in the development of computers. This claim is evidenced by its application in the Setun computer at Moscow State University in 1958 and 1970, and more recently at the Peking University, Beijing, China, where research was conducted on the application the Ternary System in digital gates CNT- SGTs transistors in MVL architecture and in TNN ternary neural network application. So, it is necessary to continue researching materials such as CNT carbon nanotube and new program languages. This article describes technical proposals for the base-four system and introduces a new approach to a mixed-balanced form quaternary system and its application to a new coding system based on the theory of Banach field functions. This approach complements intermediate values between true and false and has potential applications in quantum computing. The mixed-balanced Quaternary system is an appropriate tool for achieving this, as the collapse of a wave function can be any intermediate value, not just zero or one. As a result of the investigation of this topic, the development of this research has revealed the Quinary number system, which has great potential in this area. This system is introduced in the final pages of this study.

Keywords:

adaptive MOSFET

;

balance quinary

;

balanced ternary

;

bi-ternary

;

complete false

;

complete truth

;

complex binary

;

incomplete false

;

incomplete truth

;

mixed-balance quaternary

;

quaternary sphere

;

radians

Subject:

Computer Science and Mathematics - Computational Mathematics

1. Introduction

To understand the fundamental concepts of our physical world, we must first grasp the relationship between falsehood and truth within a logical mathematical framework. This vision is facilitated by the underlying structure of the Base-four Number System, which contrasts with the more prevalent Quaternary System despite both systems’ utilization of the same digits

{0, 1, 2,

and

3}

. For this reason, I do not refer to the Quaternary System and prefer to distinguish it from the Base-four System.

The evolution of this research endeavor is characterized by its dynamic nature, which renders it susceptible to potential inaccuracies. Consequently, with each advancement, novel strategies will be refined and implemented. Technological development exhibits a rapid pace, rendering what was previously deemed implausible yesterday as feasible today. This necessitates the rectification of the course to ensure its alignment with the evolving landscape. Moreover, theoretical research may necessitate a reorientation of developers of new technologies, thereby fostering a symbiotic relationship that will ultimately yield tangible outcomes.

This article is a continuation of the previous article [3], which provided a rudimentary introduction to the base four number system and the proposals for logic gates. These proposals were elementary and straightforward, as they encompassed only the foundational concept of representing the number system. However, we now confront a technological reality where electronic components have inherent limitations and advantages. Consequently, we are compelled to deliberate on both aspects to capitalize on the contributions of eminent scientists, engineers, technologists, and programmers. These individuals have been engaged in this field for over 90 years since the transistor’s inception and have been involved even before that, starting from the era of Boole, Venn, de Morgan, and Leibniz, who solidified and prepared the binary system for implementation in machines capable of counting, deciphering codes, and engaging in conversations, akin to those in existence today, with the aid of artificial intelligence.

As with any number system, the Base four System

{0, 1, 2, 3}

also has its secrets, which must be revealed and understood before its implementation in information processing or intelligent machines. The success of this implementation depends on the system being beneficial and useful to humanity; otherwise, humanity will be deceiving itself by adopting a technology that will not produce any benefit. In this article, the initial step will be to explore the interpretation of the system’s structural framework. Subsequently, an mixed-balanced base four number system will be developed, denoted by

{- 1, 0, + 1 + 2}

. There is also a direct balanced quaternary base system in a complex plane, denoted by

- 1, i, 1, - i

. I will discuss this system at the end of the article. This prompts an examination of the technological challenges associated with its implementation in computational processes and neural networks. Existing technologies can likely be applied, those in development can be utilized, or new technologies can be developed specifically for the system. The primary benefit of the base four number system is its close relationship with the binary system. The purpose of the base four system is to extend the capacity of the binary system, which is already at its physical hardware limit. The mixed-balanced base four system can also be configured to couple with emerging technologies in the ternary system. This allows for the implementation of both systems, taking advantage of the advantages of each. The mixed-balanced base four system itself will serve as a wild-card, perhaps, I don’t know yet.

2. This is How We Usually Understand the Nature of Our Physical and Mental World

The manner in which we comprehend the natural world and our environment is contingent upon our self-perception. This phenomenon can be likened to a state of dualism, in which the distinction between our self-perception and nature becomes indistinct. Therefore, the influence is reciprocal, yet the value of this relationship is disadvantageous for the individual. This is due to the fact that while the individual generates one signal, nature impacts the individual with billions of signals. However, the individual possesses the capacity to be susceptible to the influence of signals that align with their interests (conscious attention). This capacity can be readily disrupted, and it is within this interaction that one of the most intriguing struggles of our existence unfolds.

The fundamental question, therefore, is not merely what information is relevant, but rather, what is the nature of the information that is pertinent to this issue? A critical question to pose is the distinction between the information that individuals generate and the information that individuals receive from their immediate environment. Assuming the correct decoding of each unit of information, the subsequent step is to interpret it. It is imperative to ascertain whether decoding and interpreting are synonymous. If this were the case, then we would possess perfect knowledge of truth and falsehood. However, if the interpretation is affected by another signal of intelligent interference, the relationship between true code and false code becomes disturbed, resulting in a mutual ambiguity where, in many cases, the lie will prevail over the truth, and it will be very difficult for the truth to be more evident than the lie.

In the context of this controversy, philosophical logic has been employed since ancient times to resolve the issue. Notable philosophers such as Pythagoras, Aristotle, Plato, Socrates, and Parmenides have contributed to this field. Subsequently, mathematical logic emerged, leading to significant advancements in various branches of mathematics, including set theory, model theory, proof theory, and recursion theory. The mathematical logic serves to reinforce and validate the distinction between false and true postulates through the precise categorization of postulates under correct mathematical reasoning.

However, from a modest standpoint, the universe’s actuality is not wholly encapsulated by these algorithms. This phenomenon is further accentuated in the contemporary era, marked by significant advancements in artificial intelligence [4] and the expeditious management of voluminous informational data. It is evident that not all the information present on our websites is necessarily accurate, yet the most unfortunate aspect is the absence of the necessary algorithms and technological capabilities to ascertain the veracity of a particular piece of information.

2.1. Preliminaries

In this article, we will delineate the various methodologies by which the base-four system can be applied.

1.: General form.
2.: The mixed-balanced form encompasses negative numbers.
3.: The oscillatory form, which involves a $π$ -adic system and its relationship to the sine and cosine functions, with the objective of applying it to analog computation.
4.: The direct balance of quaternary system in a complex plane and its relationship with quaternion numbers.

It is probable that a considerable number of these systems are already in the research and development pipeline of other researchers and technology developers. The distinguishing factor may be that the systems proposed herein are closely related to the base-four number system. 1

Consequently, it is imperative that I delve into a more comprehensive analysis at the designated stage of our progression. 2

2.1.1. Generalizations

The following table presents a truth table for the sequential relationship of each and every digit in the system. As is commonly understood, the numbers in the base-four or quaternary number system are:

{0, 1, 2, 3}

The inclusion of the numbers 2 and 3 contributes their qualities to the strangest, yet most consistent, vision of the base-four system. These qualities are logically and mathematically significant, as they facilitate our ability to describe the world as it is, both mentally, materially, and energetically.

It is conceivable that many individuals, particularly those of the Orthodox mathematical persuasion, may perceive these attributes as mere imagination. However, through rigorous analysis and experimentation, it has been demonstrated that these qualities are indeed complementary to one of the fundamental properties of numbers. Consequently, since antiquity, these attributes have been methodically categorized into two distinct classes: Even and Odd numbers.

In my forthcoming article, "The Structure of Odd Perfect Numbers is Slightly Different from that of Even ones, but they Really do Exist!", which is scheduled for submission to the Preprints.org platform, a comprehensive analysis of the completeness property of the number two, in the sense of being a complete number, and the incompleteness property of the number three, in the sense of being an incomplete number, is presented. It is evident that the number two is the generator of all even numbers, according [5] Book VII Definition: 8 and the number three is the generator half of the odd numbers when multiplied by an odd numbers and half of the even numbers when multiplied by an even numbers, according Euclid’s Elements Book VII Definitions: 9 and 10, the other half of odd number are generated by

2 n + 1

relation, where

n \in N

.

Therefore, it can be concluded that all even numbers are complete numbers, and all odd numbers are incomplete numbers. This includes prime numbers, with the exception of two.

The property of completeness and incompleteness of the numbers two and three, as the originators of even and odd numbers, has led us to consider two categories of prime numbers:

1.: Authentic prime numbers. ${2, 3}$ . They are unique.
2.: Common prime numbers. $(p > 3)$ , $p : = p r i m e$ . They are infinite.

The property of authentic prime numbers serves to reinforce the base-four number system. Consequently, prime numbers two and three are not merely arbitrary prime numbers; rather, they are the fundamental elements that provide the foundation for the building bricks (Common primes) of any number system, irrespective of its base.

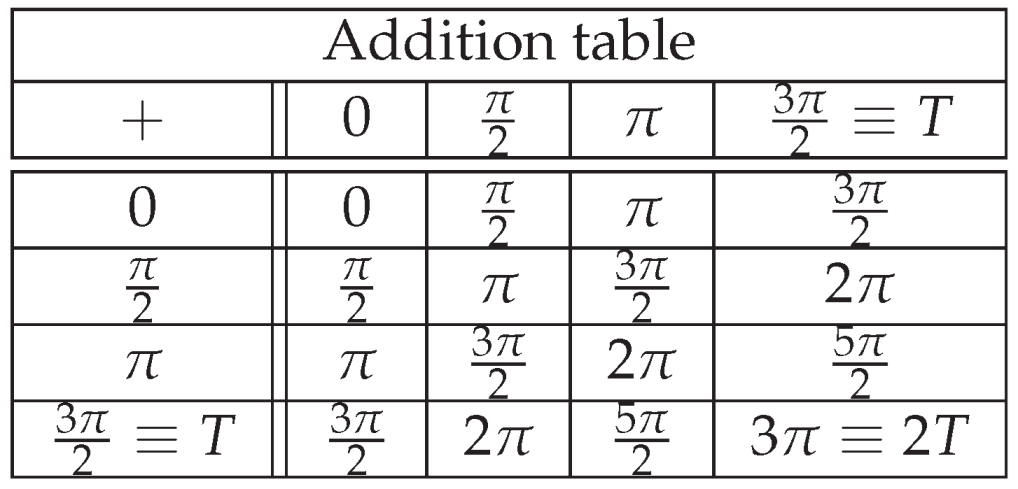
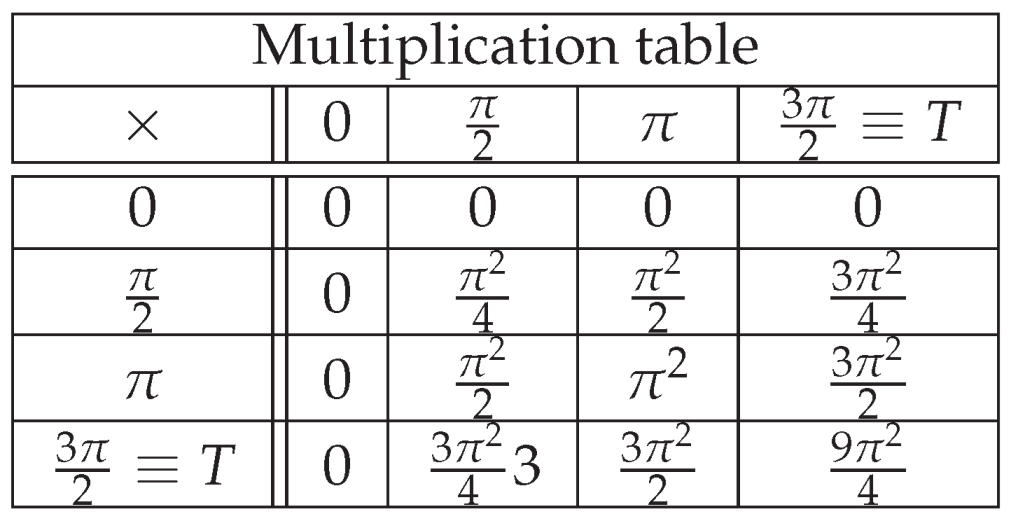
The following table provides a detailed description of the relationship between the set of numbers

{0, 1, 2, 3}

.

Table 1. Relation between { 0, 1, 2, 3} and its significance under the concepts of true and false.

Description Table
Description		Digits		Results
Value	Meaning	p	q	State	Concept 1	Concept 2
0	False - False	0	0	F	$100 %$ F	True
0	False - True	0	1	F - T	Contradiction	Negation
$< 25 %$	False - Complete	0	2	Fc	Affirmation	Hight: Probably false
$< 50 %$	False - Incomplete	0	3	Fi	Affirmation	Less likely to be false
0	Truth - False	1	0	T - F	Contradiction	Negation
1	Truth - Truth	1	1	T	100 % T	True
$> 99 %$	Truth - Complete	1	2	Tc	Affirmation	It is probably true.
$> 75 %$	Truth - Incomplete	1	3	Ti	Affirmation	Less likely to be true.
$< 25 %$	Complete - False	2	0	cF	Affirmation	Hight: Probably false.
$> 99 %$	Complete - Truth	2	1	cT	Affirmation	It is probably true.
0	Complete - Complete	2	2	cc	Indefinable	Without reference
0	Complete - Incomplete	2	3	ci	Indefinable	Without reference
$< 50 %$	Incomplete - False	3	0	iF	Affirmation	Hight: Probably false
$< 75 %$	Incomplete - Truth	3	1	iT	Affirmation	Less likely to be true.
0	Incomplete - Complete	3	2	ic	Indefinable	Without reference
0	Incomplete - Incomplete	3	3	ii	Indefinable	Without reference

There are five pairs on symmetric relation:

{F - T | T - F}

, where | is a mirror axis.

{F c | c F}

,

{F i | i F}

,

{T c | c T}

,

{T i | i T}

which can get a some value and the F, T pair, which has a

100 %

value respectively. The states

c c, c i, i c, i i

are indefinable.

But what does it mean for a proposition to be true—incomplete or complete? Or for a proposition to be false—incomplete or complete? If it’s incomplete, it means there’s a lack of evidence. The evidence will then be part of a series of interrogative and affirmative propositions that formalize the proof in each case.3

One of the most significant challenges for mathematicians throughout history has been to uncover the profound connection between nature and numbers, particularly in regard to the implications of the language we use to communicate with one another. Natural language is so diverse and versatile that it is incredibly difficult to classify it in a mathematical formula or equation. Nevertheless, significant efforts have been made to establish rules of logical thinking that unequivocally define every proposition as either true or false, depending on the implication.

Mathematical logic, even at the present moment, is no longer adequate to meet the expectations inherent in the most common sense of our current daily reality. The use of mass and social media complicates the discernment of factual information, necessitating the evaluation of such content through a parameter that fluctuates between truth and falsehood. The development of an algorithm capable of discerning truth from falsehood will facilitate the calculation of this parameter.

In light of the aforementioned points, it is imperative to explore the implementation of the base-four number system in the context of research and development initiatives concerning novel codes, software, and electronic devices. These devices encompass logic gates that facilitate the activation of truth and falsehood values, in addition to their intermediate values. The assessment of these values enables the determination of the proximity to truth or falsehood. The subsequent discussion will address the classification of information as either factual or fabricated, with the understanding that such classification is the intentional decree of governing bodies, whether they be governmental entities, individuals, corporations, political movements, religious congregations, or scientific collectives.

Some examples of how we can treat new logical concepts that are intermediate between true and false are as follows:

Proposition A: If I make mistakes but also have successes, then I am human.
Proposition B: If I only have successes, then I am not human.
Proposition C: If I only make mistakes, then I am not human.
Conclusion: Therefore, I am half human and half non-human.

We only have qualities because a defect is a quality that has been diminished, and a quality is a defect that has been overcome.

Recalling René Descartes’s thoughts.

Proposition A: I think, therefore I am. (cogito, ergo sum )
Proposition B: But, if I don’t think, then I don’t exist. (Non cogito, ergo non sum)
Proposition C: If I exist and don’t exist, then I don’t exist. Why?
Conclusion: Yes I am or I am not, but not both at the same time.

In some cases the conclusion will be logical, but in many other cases the conclusion will have an illogical answer.

This will be discussed in more detail in my book,Introduction to Logostics Thought,because we need to discuss what it means to be human or non-human, and whether or not to exist.

So this series of articles focuses more on the technological aspect.

However, the question remains: is there a demand for maintaining the truth in secrecy? I would like to know whether there is interest in maintaining the status quo. What if the lie is disguised as truth? There will certainly be many interests in keeping the information we receive camouflaged between truth and lies.

The development of the Discern of Information Algorithm (DIA) could represent a significant step forward for our civilization, potentially leading to a new era of evolution. If we can successfully implement this algorithm, it will contribute to a more gnostic, just, and truthful civilization. The truth has the potential to make us truly free, more intelligent, and wise, and it can help resolve conflicts through the use of good reason and true justice. However, humans face a significant challenge in this regard. At birth, the human being is said to possess

50 %

truth and

50 %

falsehood. Initially, the foundation of our perception of truth is generally a truth induced by those in our inner circle. The emergence of reason invariably gives rise to inquiries into the veracity of previously held beliefs, yet the influence of others remains an inescapable reality. Consequently, individuals adapt their perception of reality to align with the prevailing circumstances, thereby positioning themselves within the interplay of external influences, encompassing the inquiries and skepticism of others, and their own attempts to exert influence on others.

Consequently, individuals tend to assume that their personal truths are universally valid, yet the recognition that these truths may differ from those of others is crucial for avoiding conflicts that are multifaceted and intricate in nature. The implications of truth or falsehood extend to all aspects of an individual’s existence, making it difficult to categorize or simplify these disagreements.

It is imperative to acknowledge that the concepts of absolute truth and falsehood are illusory. The only method by which to ascertain a veritable truth is to aggregate the individual truths of all the inhabitants of our planet. Furthermore, it would be necessary to aggregate the cumulative falsehoods perpetrated by the entire global population. For all of the aforementioned points, a potential methodology has been identified that could serve as a means to assess the extent of veracity and falsehoods present within our society.

It is acknowledged that, under the initial approach of this theory, there will be a preponderance of questions over answers. However, as the algorithms that are not yet fully comprehended are investigated in greater depth, the theoretical foundation will be solidified. However, it is imperative to transcend the threshold of Type I civilization as delineated by Kardashev’s [7] classification system, even predicted by machine learning. The necessity arises from the imperative to evolve beyond the confines of our current state, thereby attaining the attributes of a universal civilization. This universal civilization must be characterized by the presence of a well-formed collective consciousness and a heightened level of wisdom. Consequently, the present moment necessitates the initiation of practices that will facilitate the realization of these objectives.

2.1.2. Basic Structure

In the event that the base-four number system is to be applied in its basic form, that is, with its natural digits, the possibility of logically representing the numbers 2 and 3 must be considered. To accomplish this objective, it is possible to consider a logic circuit with two outputs and four inputs, equipped with two normally closed resets.

Table 2. The table delineates the true for a elementary electrical control circuit see Figure 1, referenced as Figure 1 that can represent the numbers 2 and 3, among the 0 and 1.

States table
Sequence	Inputs					Outputs		Digits
I/Os	$P b_{0}$	$I n_{1}$	$I n_{2}$	$I n_{3}$	$P b_{4}$	$O_{2}$	$O_{1}$	$B_{4}$
Initial	1	0	0	0	1	0	0	0
Output 1	1	1	0	0	1	0	1	1
Reset 0/1	0	0	0	0	1	0	0	0
Output 2	1	0	1	0	1	1	0	2
Reset 0/2	0	0	0	0	1	0	0	0
Output 3	1	0	0	1	1	1	1	3
Reset 3	1	0	0	0	0	0	0	0
Initial again	1	0	0	0	1	0	0	0

This is just a very general representation, which can be expanded and strengthened through peer discussion with engineers and technicians specialized in the field. The important thing is to realize that there are other possible options, in addition to those already existing and strongly positioned in the field of electronics and software.

I’m not sure if there’s a logic gate other than a multiplexer or an adder that can generate this sequence. However, the configuration of an electrical control circuit is possible, and is presented above as an analogy to the development of a future logic gate. The salient point is that we are capable of configuring the digits of the base-four system as an independent output. The numerical values 0 and 1 do not present a problem, as the same procedure can be used as in a binary system.

In an electrical circuit, a signal is interlocked by a normally open contact that remains closed as long as an electromagnetic relay is energized. An entire sequence can be developed by establishing the initial conditions for activating a signal and acting on the final control element for the time that the signal remains active. The same process should occur in a logical circuit, where its versatility is leveraged to implement it in a more user-friendly language.

Figure 1. This is an elementary electrical circuit with three inputs and two normally closed push buttons. The buttons are used to reset sequences in the simulated process of digits in the basic four system.

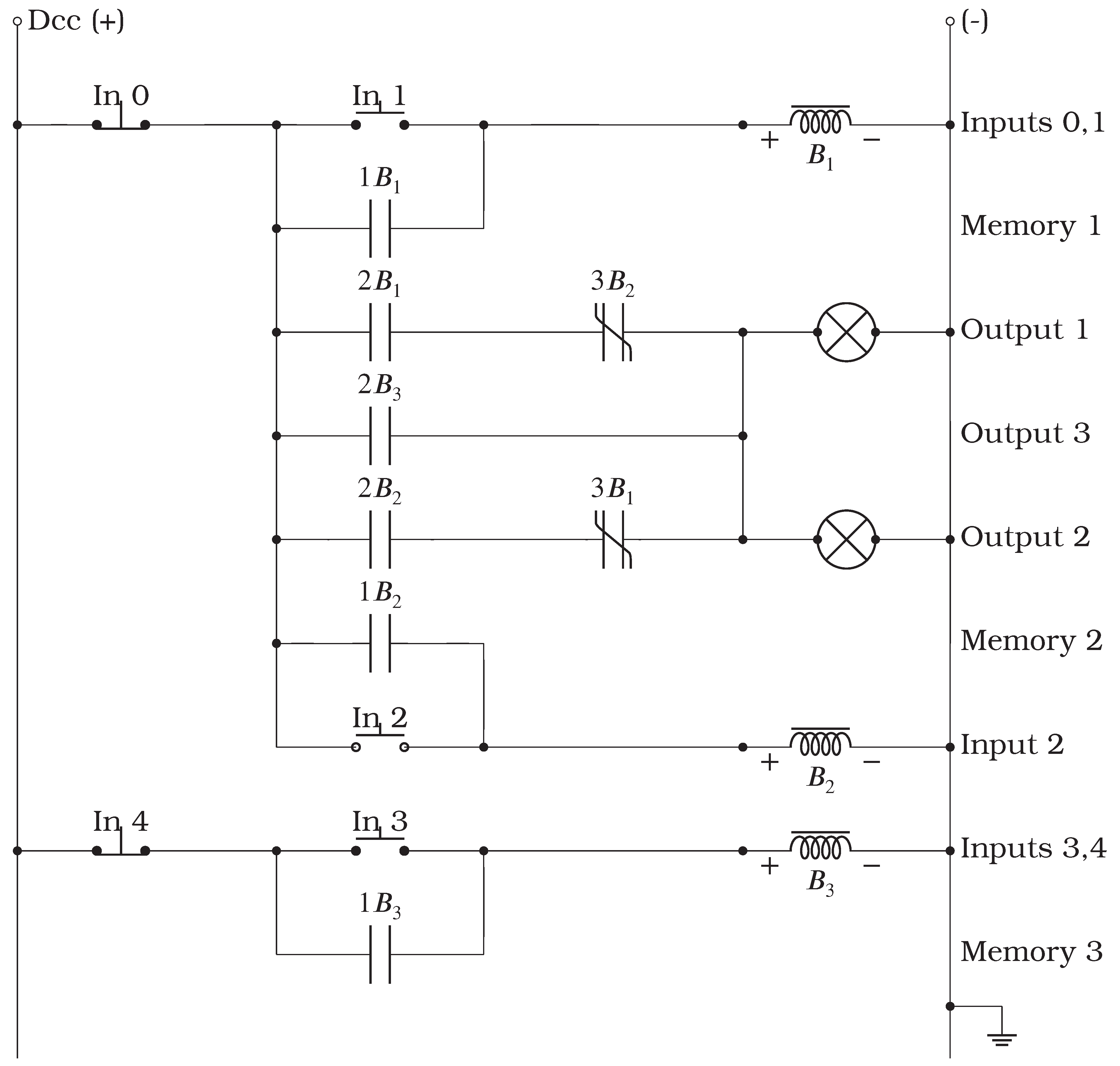
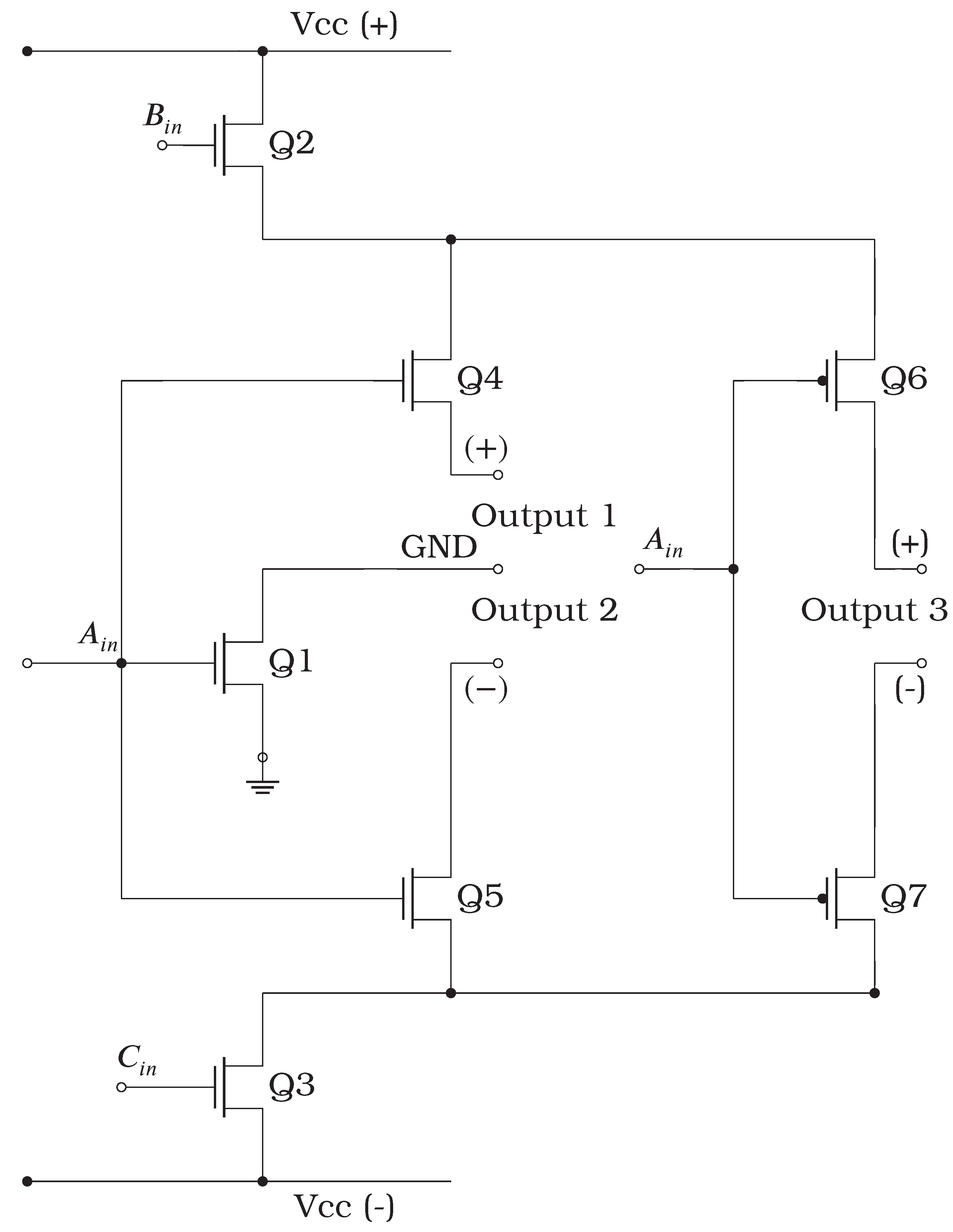
2.1.3. Adaptive MOSFETs (AMOS).

I’m not sure if it’s appropriate to consider an application other than the one commonly used for MOSFETs, particularly in regard to their use in logic gates through their complementary structural arrangement. This is why they are known as CMOS. In the following diagram, Figure 2 referenced as Figure 2, I propose a different architecture and present it to the strictest consensus of engineers and scientists who specialize in researching and developing such wonderful electronic devices. Therefore, this proposal should be taken as just that—a proposal that may or may not work. When tested, it will either prove successful or reveal the need for an alternative. It will, however, prompt the search for an alternative because I’m certain one exists, but we haven’t found it yet.

In a simulation table with three inputs and three outputs, the number system’s cycles are reduced to four states, see Table 3, referenced as Table 3.

In a circuit with MOSFET elements, it is possible to consider the interaction with a negative voltage. In this case, the first two outputs are activated between positive and ground, and the other input is separately activated between negative and ground.

The third output is activated by the sum of the two voltages with respect to ground, that is, between the positive and negative polarity voltages. For instance, if the system is activated with 1 volt, the third output would be activated with 2 volts.

For this application, CNT-SGT transistors in MVL architecture are a viable option [1]. These systems are currently being researched and developed at Peking University for application in balanced ternary systems. However, our primary objective is to identify the most effective way to express the base-four system. These proposals will be analyzed later in this article, but it is important to consider all possible options.

As outlined in Table 1, the general interpretation of the interrelationship of the digits in the base-four number system is clearly defined for all possible ranges of uncertainty that can arise between false and true. To provide a more meaningful summary of this relationship, we consider:

i): $0 =$ False.
ii): $1 =$ True

This values have been correctly established and are well understood by all relevant parties.

The following values are logical complements that define a certain value between 0 and 1. If desired, these values can be made more precise. This property suggests a new paradigm for quantum computing, as the collapse of a wave function does not have to be zero or one. Instead, it can collapse to any interval between 0 and 1, thanks to the base-four system, which allows for measurement. Generally speaking, we can enhance precision and reduce errors in the following ways:

i): $02 =$ complete false.
ii): $03 =$ incomplete false.
iii: $12 =$ complete true.
iv): $13 =$ incomplete true.

For the following circuit, we developed the following state table, considering the active elements in the circuit and the preliminary interpretation we are proposing. This is subject to the scrutiny of specialists in this technology and logic.

Figure 2. Circuit TiTo without R, C or any other electronic devices implemented in a real circuits, to simulate the base-four system.

2.1.4. Not gate.

To implement not gate logic, it is necessary to use two not gates in parallel. This method allows us to determine the four digits of the system, as well as their intermediate values with respect to the extremes of truth and falsehood. In this relationship, it is important to note that it pertains to the binary system. As long as an electronic logical device is designed, developed, and built to output the four numbers of the base four system, this relationship remains valid.

Table 4. Table states for a NOT gate.

The states table of a NOT gate.
Inputs	p		Inverse Outputs			Value
States	2nd. Place	1st. Place	$\neg p$		State	%	Description
F		0		1	T	$100 %$	True
T		1		0	F	$00 %$	False
cF	0	1	1	0	cT	$75 \leq T < 100 %$	complete True
cT	1	0	0	1	cF	$0 < F < 25 %$	complete False
iF	0	0	1	1	iT	$50 \leq T < 75 %$	incomplete True
iT	1	1	0	0	iF	$25 \leq F < 50 %$	incomplete False

According to the above table, a diagram is provided that illustrates the relationship between the two not gates. The table provides a clear explanation of the meaning and interrelationship of the intermediate values between 0 and 1. The diagram focuses exclusively on the inputs and outputs of the digital values.

Figure 3. The double NOT gate diagram, complete with inputs and output digits. This diagram illustrates the NOT gate’s operational functionality.

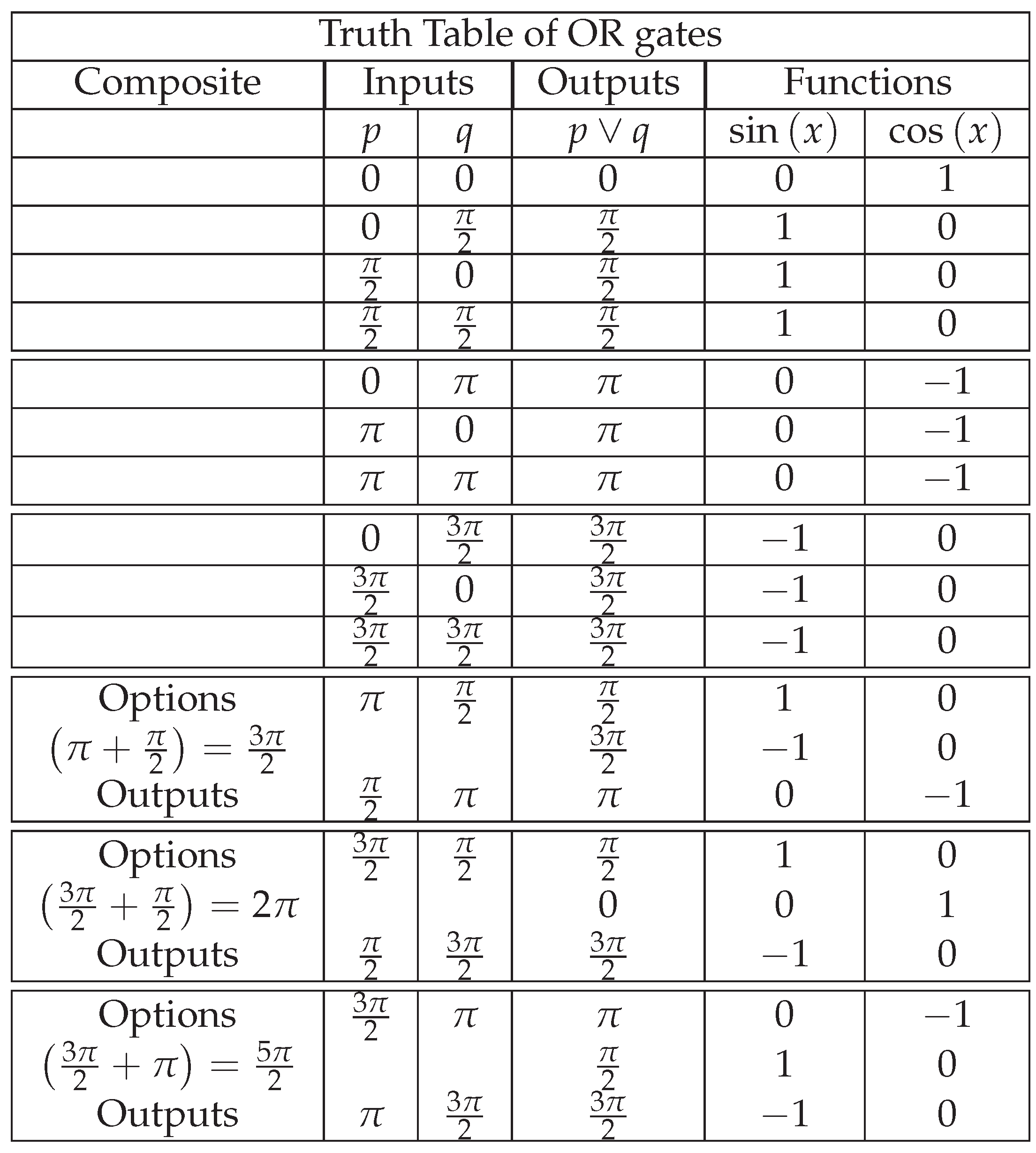
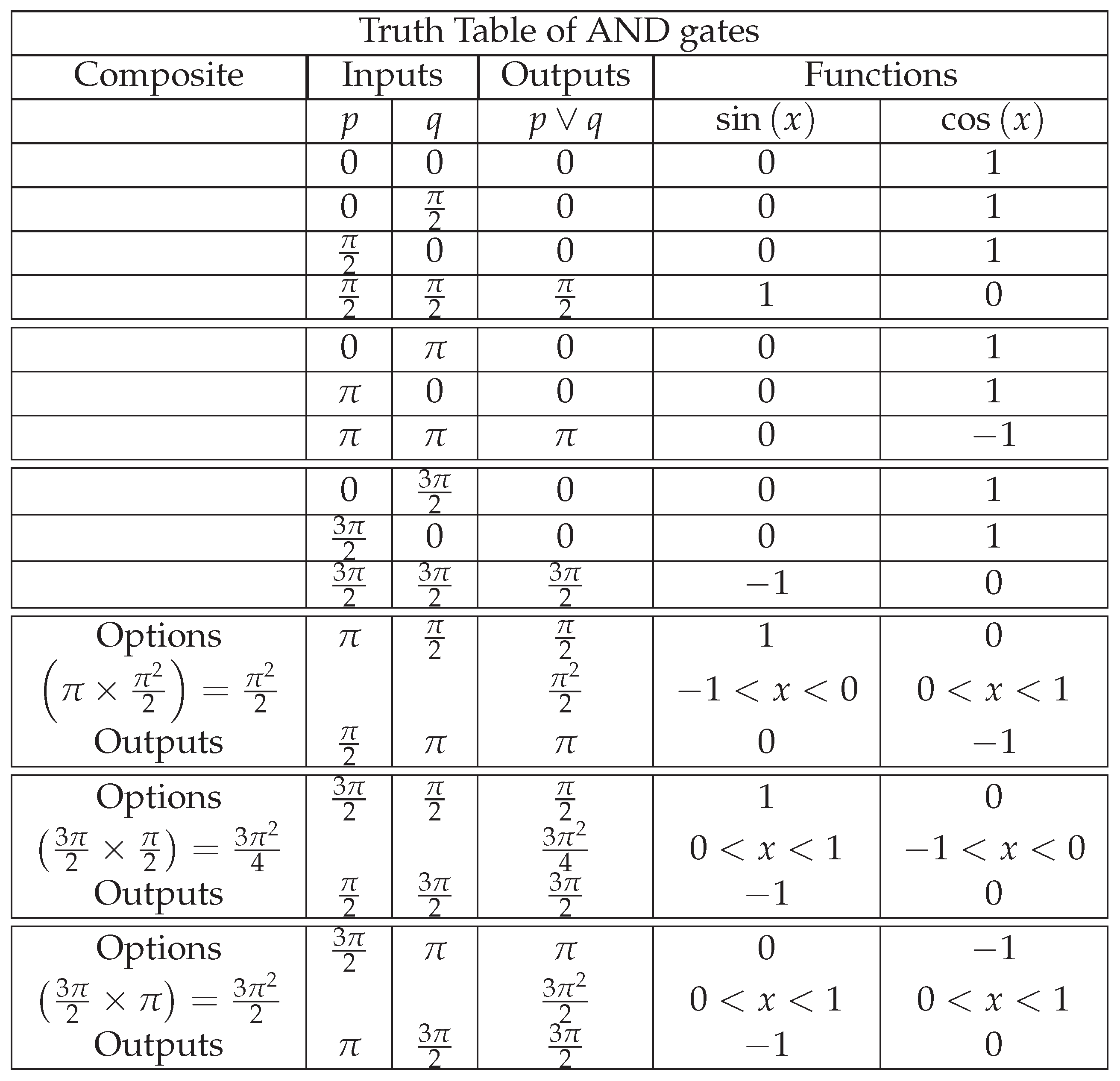
2.1.5. AND and OR Gates

The relationship between the AND and OR gates can be described in two ways. First, it can be described by its development with the complete sequence. Second, it can be summarized in the elementary cycles that are always repeated. These cycles simplify the operation of the gates. Let

P = {p_{1}, p_{2}}

be a set of P and

Q = {q_{1}, q_{2}}

the elements of the set Q. Therefore the table is the following:

Table 5. General Table for P and Q sets.

The states table P,Q.
Elements of P		Elements of Q		Quaternary	Decimal
$p_{1}$	$p_{2}$	$q_{1}$	$q_{2}$	$B_{4}$	$a_{10}$
0	0	0	0	0	0
0	0	0	1	1	1
0	0	1	0	2	2
0	0	1	1	3	3
0	1	0	0	10	4
0	1	0	1	11	5
0	1	1	0	12	6
0	1	1	1	13	7
1	0	0	0	20	8
1	0	0	1	21	9
1	0	1	0	22	10
1	0	1	1	23	11
1	1	0	0	30	12
1	1	0	1	31	13
1	1	1	0	32	14
1	1	1	1	33	15

After employing the logical operators of conjunction and disjunction to each set, we obtain the following results.

Table 6. General table for sets P and Q in conjunction and disjunction operations.

The states table P,Q.
P		Q		$p_{1} \land p_{2}$	$q_{1} \land q_{2}$	$p_{1} \lor p_{2}$	$q_{1} \lor q_{2}$	$p \land q, p \lor q$		$P \land Q$	$P \lor Q$
0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	1	0	0	0	1	0	1	0	1
0	0	1	0	0	0	0	1	0	1	0	1
0	0	1	1	0	1	0	1	0	1	0	1
0	1	0	0	0	0	1	0	0	1	0	1
0	1	0	1	0	0	1	1	0	1	0	1
0	1	1	0	0	0	1	1	0	1	0	1
0	1	1	1	0	1	1	1	0	1	0	1
1	0	0	0	0	0	1	0	0	1	0	1
1	0	0	1	0	0	1	1	0	1	0	1
1	0	1	0	0	0	1	1	0	1	0	1
1	0	1	1	0	1	1	1	0	1	0	1
1	1	0	0	1	0	1	0	0	1	0	1
1	1	0	1	1	0	1	1	0	1	0	1
1	1	1	0	1	0	1	1	0	1	0	1
1	1	1	1	1	1	1	1	1	1	1	1

As we can see from the table above, the term in the first position is repeated every four successions, so it can be considered a quadrupling pattern with the second term. The first term is identical to a binary system of two propositions.

Table 7. Reducing the inputs and outputs of AND and OR gates.

States table
Block q				Block p
$q_{2}$	$q_{1}$	$q_{2} \land q_{1}$	$q_{2} \lor q_{1}$	Factor	$p_{2}$	$p_{1}$	$p_{2} \land p_{1}$	$p_{2} \lor p_{1}$
0	0	0	0	$4 t$	0	0	0	0
0	1	0	1	$4 t$	0	1	0	1
1	0	0	1	$4 t$	1	0	0	1
1	1	1	1	$4 t$	1	1	1	1

The relationship between the quaternary and binary systems is very close, as demonstrated by the truth tables and application of each binary operator. We haven’t gone into much detail since this information is widely known.

The most important thing at this point is to take full advantage of the base-four system when developing electronic elements that can operate this logic directly using its digits

(0, 1, 2, 3)

. This would give us a significant advantage because we wouldn’t need to make major changes to programming, computer languages, codes, or special software.

However, the base-four system has much more interesting potential that we can explore in future computing developments. One of the most intriguing aspects is presented in the following section of this article.

3. Mixed-Balanced Base-Four Number System

One of the most difficult challenges the binary system has faced is including negative numbers in its standard form. This requires adding one more digit to the code to indicate whether a sign magnitude is included. Initially, this was not a problem because operations were limited to the digital representation capacity of computers. However, as the amount of information to be processed and stored increased, this problem became more serious. Therefore, at this level of development, it is necessary to find ways to optimize this disadvantage.

Alongside the development of computing, another ternary number system was developed that includes negative numbers without increasing the number of digits. However, the computing system that used the ternary system did not reach the level of technological development required for satisfactory application at great scale. Thus, our challenge is twofold: we must improve both systems, leveraging their strengths and redesigning the technological elements that limit them.

It is very important in computational processes that a number system includes negative numbers without having to sign them. The ternary system, whose digits are

(- 1, 0, 1)

, is one of the most studied systems, so I will refer to it only when necessary, to reinforce the structure of the unbalanced base-four system.

3.1. Digits of Mixed-Balanced Quaternary System

Technological and material advances at the atomic level make it possible to successfully implement the ternary system [1] in computational systems. Fortunately, the same advances that can be achieved in ternary computation can also be applied to quaternary computation because both systems integrate negative numbers. However, the quaternary system considers one more digit, in addition to the positive and negative ones. Furthermore, the quaternary system can be applied successfully in analog and quantum computing.

Regardless of its usefulness in specific branches of computing, it is important to first describe its arithmetic foundations and, therefore, its logical and physical implications.

3.1.1. Definition

The law of balanced ternary systems is well-established and universally known and applied. Therefore, it is unnecessary to mention it here. In general, it applies to odd-base systems. However, in the case of balanced systems for even bases, there is no law, definition, or postulate that validates them. This is why I propose it here to lend validity to our project. However, it is subject to acceptance and, if necessary, correction and validation by the mathematical community.

Definition 1.

For every even base to have a representation in balanced form, there must be at least one correspondence between a positive digit and a negative digit such that

F_{D} (d +) = - F_{D} (d -)

, fulfilling

b + = b -

, constituting an odd base system within an even base system and representing the entire set of negative numbers in the even base. This system is called: The mixed-balanced form for any even base.

Let

D_{4} : {T, 0, 1, 2}

be a set of symbols.

Therefore,

D_{4} = {{- 1, 0, 1} 2}

Then, we must define an integer using the valuator function described below.

f = f_{D_{4}} : D_{4} \to Z

by:

f (T) = - 1

f (0) = 0

f (1) = 1

f (2) = 2

The set

D_{4}

, in conjunction with the function f, constitutes a balanced signed -digit representation that is referred to as: "The mixed-balanced quaternary system". This system number can be used to represent both integers and real numbers.

The mixed-balance quaternary system differs from the Quaternary Signed Digit (QSD) system described in [8], but the purpose is the same.

In this study, the symbol

(T)

, utilized in the ternary system, has been adopted for the purpose of facilitating understanding, given its equivalent function.

3.1.2. Rules for Arithmetical Operations

The following are the established guidelines for performing arithmetic operations.

Table 8. Addition of units in a mixed-balanced quaternary system.

Addition table
+	0	1	2	T	2T
0	0	1	2	T	2T
1	1	2	$[1 + T]$	0	T
2	2	$[1 + T]$	10	1	0
T	T	0	1	$2 T$	T+1
$2 T$	$2 T$	T	0	$T + 1$	T+0

Addition table:

The terms

(1 + T \lor T + 1 \lor T + 0)

is not the same as

1 T

or

2 T

because

(1 + T)

has two digits with different positional values:

(1 \times 4^{1} + (- 1) \times 4^{0})

, whilst

1 T

or

2 T

are digits in the same position,

(1 \times (- 1) \times 4^{0})

. In addition processes, the 1 in

1 + T

is usually a carried number, and the T in

T + 1

is a term that is carried.

The great value that can be added is the term

2 T + 2 T

, which, in the decimal notation, is a product of

4 T

. However,

4 T

does not exist, so it must be

T + 0

. This is why T is carried.

Multiplication table:

Table 9. Multiplication of units in a mixed-balanced quaternary system.

Multiplication table
×	0	1	2	T	$2 T$
0	0	0	0	0	0
1	0	1	2	T	$2 T$
2	0	2	10	$2 T$	$T + 0$
T	0	T	$2 T$	1	2
$2 T$	0	$2 T$	$T + 0$	2	$1 + 0$

In multiplication,

(T T = T^{2})

means 1 because

(- 1) \times (- 1) = 1

. Its position doesn’t matter, and

2 T = - 2

. If another T is added, the negative value increases. The T value is reduced by only 1 or 2, the same amount of

(T s)

.

3.1.3. Sequence

The mixed-balanced quaternary system’s sequence has an interesting arrangement: every fourth number shifts four spaces. This would imply that the series could not be completed, as the sequence generates negative numbers. However, by making the sequence long enough, no number is excluded.

Below, I describe the first 170 numbers in the sequence to demonstrate this property of the mixed-balanced quaternary system.

Reading the table to understand its sequence goes from the table on the top left to the table, then descend to the bottom right and continues in the table on the top right and descends to the table on the bottom right. Every sixteen numbers there is a change in the last digit on the left for a three-digit quantity. For a four-digit quantity, the change of the last digit on the left occurs every sixty-four numbers.

Please consider that the following three tables have the same configuration to avoid any confusion.

As the Table 10 above referenced as Table 10 shows, the sequence in the mixed-balanced quaternary system is strictly ordered. However, when converting to the decimal system, a phase shift of four units is observed between each set of four. For the purposes of integrating the base-four system into computer codes, however, the codes must respond to this sequence or the organization and architecture of the mixed-balanced quaternary system and not to decimal system. On the decimal system, the conversion will be directly expressed.

Table 10. Sequencing of numbers in a mixed-balanced quaternary system.

Series of $D_{4}$ Mixed-balanced Quaternary System
Table 1					Table 3
$a \cdot 4^{3}$	$a \cdot 4^{2}$	$a \cdot 4$	$a \cdot 4^{0}$	$b_{10}$	$a \cdot 4^{3}$	$a \cdot 4^{2}$	$a \cdot 4$	$a \cdot 4^{0}$	$b_{10}$
0	0	0	0	0	0	2	0	0	32
0	0	0	1	1	0	2	0	1	33
0	0	0	2	2	0	2	0	2	34
0	0	0	T	$- 1$	0	2	0	T	31
0	0	1	0	4	0	2	1	0	36
0	0	1	1	5	0	2	1	1	37
0	0	1	2	6	0	2	1	2	38
0	0	1	T	3	0	2	1	T	35
0	0	2	0	8	0	2	2	0	40
0	0	2	1	9	0	2	2	1	41
0	0	2	2	10	0	2	2	2	42
0	0	2	T	7	0	2	2	T	39
0	0	T	0	$- 4$	0	2	T	0	28
0	0	T	1	$- 3$	0	2	T	1	29
0	0	T	2	$- 2$	0	2	T	2	30
0	0	T	T	$- 5$	0	2	T	T	27
Table 2					Table 4
0	1	0	0	16	0	T	0	0	$- 16$
0	1	0	1	17	0	T	0	1	$- 15$
0	1	0	2	18	0	T	0	2	$- 14$
0	1	0	T	15	0	T	0	T	$- 17$
0	1	1	0	20	0	T	1	0	$- 12$
0	1	1	1	21	0	T	1	1	$- 11$
0	1	1	2	22	0	T	1	2	$- 10$
0	1	1	T	19	0	T	1	T	$- 13$
0	1	2	0	24	0	T	2	0	$- 8$
0	1	2	1	25	0	T	2	1	$- 7$
0	1	2	2	26	0	T	2	2	$- 6$
0	1	2	T	23	0	T	2	T	$- 9$
0	1	T	0	12	0	T	T	0	$- 20$
0	1	T	1	13	0	T	T	1	$- 19$
0	1	T	2	14	0	T	T	2	$- 18$
0	1	T	T	11	0	T	T	T	$- 21$

Table 11. Sequencing of numbers in a mixed-balanced quaternary system.

Series of $D_{4}$ Mixed-balanced Quaternary System
Table 5					Table 7
$a \cdot 4^{3}$	$a \cdot 4^{2}$	$a \cdot 4$	$a \cdot 4^{0}$	$b_{10}$	$a \cdot 4^{3}$	$a \cdot 4^{2}$	$a \cdot 4$	$a \cdot 4^{0}$	$b_{10}$
1	0	0	0	64	1	2	0	0	96
1	0	0	1	65	1	2	0	1	97
1	0	0	2	66	1	2	0	2	98
1	0	0	T	63	1	2	0	T	95
1	0	1	0	68	1	2	1	0	100
1	0	1	1	69	1	2	1	1	101
1	0	1	2	70	1	2	1	2	102
1	0	1	T	67	1	2	1	T	99
1	0	2	0	72	1	2	2	0	104
1	0	2	1	74	1	2	2	1	105
1	0	2	2	75	1	2	2	2	106
1	0	2	T	71	1	2	2	T	103
1	0	T	0	60	1	2	T	0	92
1	0	T	1	61	1	2	T	1	93
1	0	T	2	62	1	2	T	2	94
1	0	T	T	59	1	2	T	T	91
Table 6					Table 8
1	1	0	0	80	1	T	0	0	48
1	1	0	1	81	1	T	0	1	49
1	1	0	2	82	1	T	0	2	50
1	1	0	T	79	1	T	0	T	47
1	1	1	0	84	1	T	1	0	52
1	1	1	1	85	1	T	1	1	53
1	1	1	2	86	1	T	1	2	54
1	1	1	T	83	1	T	1	T	51
1	1	2	0	88	1	T	2	0	56
1	1	2	1	89	1	T	2	1	57
1	1	2	2	90	1	T	2	2	58
1	1	2	T	87	1	T	2	T	55
1	1	T	0	76	1	T	T	0	44
1	1	T	1	77	1	T	T	1	45
1	1	T	2	78	1	T	T	2	46
1	1	T	T	75	1	T	T	T	43

This is the second group of 64 numbers. As you can see, no negative numbers were generated because the T term has a number to its left. Whatever is subtracted from it leaves a positive remainder. Negative numbers will appear when the T term is on the far left of the quantity. Since the T term is the largest value, adding all the numbers to its right together would barely decrease it. However, it would never produce a positive result.

The above Table 12 is the last group of sequences that generates positive numbers because the highest digit in the quaternary mixed-balanced system is in the last position on the left. The next group, Table 13 will have the number T in this position, and all the numbers in the sequence will be negative. Amazingly, this sequence behaves the same as the sequence of positive numbers, but in the opposite direction. That is, the sequence will be descending until it reaches its maximum negative value. This value will be reflected in the last digit when all the positions are occupied by the number T.

If we add another digit to the sequence, creating a five-digit number, the last number on the left will change every 192 digits. The largest positive number will be 22222; the largest negative number will be

T T T T T

; and the smallest negative number will be

T 2222

.

Although the conversion to decimal does not follow the correct sequence, it establishes a pattern that repeats every four numbers. A detailed examination of the sixteen tables reveals that all positive numbers from 0 to 170 and all negative numbers from −1 to −85 are present, because at first glance it would seem there are gaps.

3.2. Arithmetical Operation

3.2.1. Addition

Now, we are going to apply the rules of addition, Table 8 described in 8 to some examples to understand the procedure.

Example 1

Example 2

Example 3

The red digits are those carried forward when adding, whose sum is greater than the largest unit in the number system. The carried digit enters as the addend of the term on the left because it has acquired the value of that position’s power.

3.2.2. Multiplication

Now, we are going to apply the rules of multiplication, Table 9 described in Table 9

Example 4

As one of the factor is negative, the product is also negative. The top carry digit is the product of the multiplication. The red numbers inside the products of the multiplication by each term are the digits carried by the addition of each product.

Example 5

Example 6

Up to this point, the fundamental operations that can be performed using computational logic have been presented. Next, a book will be published that describes the operations of division, exponentiation, logarithms, and functions, as well as their applications to calculus, numerical analysis, and number theory using the mixed-balanced quaternary system. Thus, much research and study remains on this wonderful system.

4. Some Applications of Mixed-Balanced Quaternary

The mixed-balanced quaternary system is closely related to the way all natural processes occur, from the simplest to the most complex and from the weakest to the strongest. It reflects the most intricate organizational structure between numbers and nature. This leads us to consider the possibility that nature can only be described mathematically. Therefore, all information can be coded and handled by a non-human intelligence developed by humans. Here, "non-human intelligence" refers to an intelligent process created by machines that can manage large amounts of information. These machines have been designed and built by humans. However, it does not refer to alien beings because any extraterrestrial beings are also a species of human, only more advanced scientifically, technologically, socially, intellectually, and emotionally than us.

4.1. Phenomenon Sequences

Every physical phenomenon, whether mechanical, energetic, or mental, invariably has four stages. Each stage represents the necessary and sufficient conditions for the sequence of stages to occur. This means that one stage will not occur if the previous stage has not occurred, even if they meet again in endless cycles. However, no cycle is the same as another, so each cycle is unique and cannot be repeated, as experiencing one cycle always implies experiencing the previous one.

4.1.1. Step by Step

Over 20 years ago, I developed a process to determine the sequence of every physical or metaphysical phenomenon. In doing so, I established the distinctions between steps, events, and cycles. This generated a series of definitions and theorems that are off-topic for this article. I will only consider the concept of steps because it applies to the present case and is related to the development of the quaternary system’s structure.

The Properties of Steps

Definition 2.

Every step must be quantifiable, regardless of whether it is measurable. Therefore, its essence is mathematical, and its appearance is possibly physical or philosophical.

Definition 3.

Every step is unique and different from other steps, but it is dependent on and valued by the experience of its predecessor.

Definition 4.

Every step is unique and different from other steps, but it is the former of its successor.

Definition 5.

A step is not a step if and only if it is not a step.

Definition 6.

Every step has a unique direction, which establishes an unequivocal relationship between the preceding step and the subsequent step.

Definition 7.

A step is always the consequence of a precedent, meaning there is no turning back energetically.

Definition 8.

No step between a precedent and a consequence is a step.

Definition 9.

Every step between a precedent and a consequence has a relative value of at most

\frac{1}{2}

, so it does not exist.

Definition 10.

A step is a step regardless of its magnitude or the number of events, with its number of cycles.

Theorem 1.

Every step is indivisible, such that it is always equal to the unit, even if between the preceding step and the subsequent one there exists an infinity of events with an infinity of cycles.

Theorem 2.

Every step has its own time. Like it, its value is unity when the finite number of events and their finite number of cycles have been fulfilled.

Theorem 3.

If a step has not fulfilled its finite events or completed its finite cycles, it will remain motionless. At every moment, it will appear halfway between the preceding and subsequent steps.

Theorem 4.

Any step is, if and only if the sum of all its possible cycles or intrinsic frequency is equal to one.

Theorem 5.

A step is not a step if and only if the sum of the cycles of all its possible events is less than one.

Theorem 6.

If a step has not completed its cycle, then it is not a step. It remains that way for all the necessary cycles until the events are completed. However, at the consummation of each event, its energy will strengthen until it reaches sufficient strength to overcome the relative inertia. Then, it will happen.

Theorem 7.

Every step has inertia that is released and loaded, between events and cycles, as it happens.

Theorem 8.

The release of energy is instantaneous in every step, but only if the step has occurred.

Theorem 9.

In every step the energy charge occurs during the succession of events with its finite of cycles, if and only if the sum of all possible events, with its finite of cycles is equal to one.

These definitions and theorems complement the definitions and theorems of events and cycles because adding any of them gives a product value of one. Here, I only state them without proof.

Symbols of steps. The symbols are in the form of hieroglyphics.

The following hieroglyph is the step on the others direction, but it means the same of the previous figure.

The following hieroglyph represents a stationary state, but in reality, it is merely an instant. Physically, energetically, and mentally, nothing is still, either relatively or absolutely. There is no way to describe this because everything is in a constant state of movement, change, or vibration. Therefore, saying that something is still or in repose is an illusion that can only be represented mathematically.

Every phenomenon occurs in one step with four stages. Every active step must be considered as a unit vector, and this is true for all steps in the process.

1.: In the first stage, the necessary and sufficient conditions that give rise to the phenomenon’s dynamics under a physical process involving mass, energy, and intelligence are conceived. This gestation phase amplifies until all its conditions detonate simultaneously and it emerges significantly in the next stage.
2.: The second stage contains all of the phenomenon’s energy and increases to shape its final form. This is one of the most flourishing stages, where all the successes that will be achieved in the next stage are consolidated to the maximum degree. Once all of its highly productive reactions have been described and deciphered, it moves on to the next stage.
3.: The third stage is the phenomenon’s culmination in its most extreme, wild, and unstoppable form. However, it does not stray from the initial objective, which will culminate sooner or later. Therefore, it diversifies in all its qualities to generate the greatest works for which it was designed.
4.: In the fourth and final stage, most reactions have fully evolved and matured. It’s time to reap the rewards and reorganize the potential consequences that have arisen. Most reactions are on the verge of consuming their energy sources and neutralizing their effects. Yet, this is one of the most creative stages within a less violent realm. It allows us to rethink and evaluate what has been built, left unbuild, or destroyed without arrogance. This is the stage of greatest wisdom because the climax of what was achieved has been reached but not possessed because it has passed. It is the point where the end is visualized, and the ashes of extermination are relished. At the same time, an extraordinary force of hope is generated because it is known that the next step will emerge from these ashes. Ashes are the most valuable product because they are essentially the preserved energy from all the experiences obtained in this step. This energy transcends to the next step, making it possible for subsequent steps to maintain their sequence. It is like a hereditary information code that will define the necessary and desirable changes in its evolution.

4.1.2. Mathematical expression of a step

The four stage of any step can be substitute by the units number of the mixed-balanced quaternary system.

4.1.3. The units of the mixed-balanced quaternary system are extended to the step concept

According to the units and functions of the mixed-balanced quaternary system, it can be extended to a trigonometric function. In this function, it is possible to evaluate the step as a sine or cosine wave.

Let

D_{4} : {T, 0, 1, 2}

be a set of symbols.

Then, we must define an integer using the valuator function described below.

f = f_{D_{4}} : D_{4} \to Z

by:

f (T) = \{- 1 \lor \frac{3}{2} π\}

f (0) = \{0 \lor 2 π\}

f (1) = \{1 \lor \frac{π}{2}\}

f (2) = \{2 \lor π\}

The set

D_{4}

, in conjunction with the function f, constitutes a balanced signed -digit representation that is referred to as: "The mixed-balanced quaternary system". This system number can be used to represent both sine end cosine functions.

1.: Let $\vec{S}$ be a step.
2.: Let $\neg S$ be a non-step.

One of the most important conditioning of the steps is the following rules:

1.: Let ${\vec{S}}_{n}$ be a nth-step, so every ${\vec{S}}_{n} = 1$ when is completed, but if ${\neg S_{n - 1}, \neg S_{n}, \neg S_{n + 1}}$ then the position of $\neg S_{n} = \frac{1}{2}$ respect to $\neg S_{n - 1}$ and $\neg S_{n + 1}$ , but when ${\vec{S}}_{n}$ go ahead one step the value of ${\vec{S}}_{n}$ is ${\vec{S}}_{n} = 1$ , then ${\vec{S}}_{n}$ displace ${\vec{S}}_{n + 1}$ one place ahead and ${\vec{S}}_{n}$ is preserved, taken again the value $\neg S_{n} = \frac{1}{2}$ respect the position between $S_{n - 1}$ and $S_{n + 1}$ . The $S_{n - 1}$ now is in previous place of $S_{n}$ , but conserve its original value, because it continue to the left of $S_{n}$ .
2.: Let ${\vec{S}}_{n}$ be a nth-step, and if ${\vec{S}}_{n}$ is a cycle of four stage, then ${\vec{S}}_{n} = a_{k} cos θ \land b_{k} sin θ$ , where $0 \leq θ \leq 2 π, k \in N$
3.: Let ${\vec{S}}_{n}$ be a nth-step. The process is the same in any direction because, mathematically, there is only one way: From nothingness to totality $- 1 \to 0 \to + 1$ . So, if we choose the starting point, we will know where the ending point will be.

The relationship between the quaternary number system and trigonometric functions implies that the number system can be applied to functional analysis [2] and many other branches of mathematical physics. Above all, it can be used to implement a more direct programming language. In the binary system, the computation of sine and cosine functions is not performed directly but through mathematical approximations, such as the Taylor series expansion method. and many other application, see [9,10]

sin (x) = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} \dots

Where the sine function is an odd function.

cos (x) = 1 - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} - \frac{x^{6}}{6!} \dots

Where, the cosine function is an even function.

Below, we will explain how we can interpret the structure of the mixed-balanced quaternary system applied to trigonometric functions in the simplest and most accessible way. From there, we can visualize the practical implications for different fields of science and mathematics, as well as the theoretical implications, which may lead to new discoveries.

We know that the mixed-balanced system its digits are:

D_{4} = \{{- 1 0 1} 2\} \Rightarrow \{{T 0 1} 2\}

To identify each digit of a mixed-balanced quaternary system in a unitary circle, we can trace a circumference centered at

0, 1

. The figure is in the

1 : 2

scale.

Figure 4. The relationship between the trigonometric functions of sine and cosine and the unitary circle.

The most effective way to use trigonometric functions is to measure angles in radians. Therefore, let’s convert the mixed-balanced base-four system into radian units.

\{0 = 0 \lor 2 π r a d, 1 = \frac{π}{2} r a d, 2 = π r a d, T = \frac{3 π}{2} r a d\}

Let’s look at the addition and multiplication tables below.

Table 14. Addition of π rad in a mixed-balanced quaternary system.

If we substitute

π

radians for T, then T must equal

(4.7124)

rad, so that its ratio is equal to the sine and/or cosine of

3 π / 2

. Taking the value of

{(- 1)}_{4}

of the mixed-balanced quaternary system will establish a direct relationship with the aforementioned trigonometric functions. Similarly, if

π

rad has a direct relationship with the mixed-balanced quaternary system, it corresponds to the number two in the system and to the radians value of

(3.1416)

rad for the sine and cosine functions. For

π / 2

radians, the corresponding value of

1.5708

rad will be used, along with the respective sine and cosine results.

Table 15. Multiplication of

π

in a mixed-balanced quaternary system.

Table 15. Multiplication of

π

in a mixed-balanced quaternary system.

The following is the truth table for an OR gate when the mixed-balanced quaternary conversion system is applied to trigonometric functions in radian base.

Table 16. The inputs and outputs of an OR gate and its sine and cosine functions.

If there is a relationship between two different inputs. If they are different from zero and by themselves, we can reduce them to one input. To do so, the terms must be added.

(π + \frac{π}{2}) = \frac{3 π}{2}

Therefore, the outputs of the sine and cosine functions are:

{- 1, 0}

, respectively.

In the next case:

(\frac{3 π}{2} + \frac{π}{2}) = 2 π

Therefore, the outputs of the sine and cosine functions are:

{0, 1}

, respectively.

In the last case:

\{\frac{π}{2} + π) = \frac{5 π}{2} = 2 π + \frac{π}{2}

As

\frac{5 π}{2}

is a cycle plus

\frac{1}{4}

of cycle, we take

\frac{π}{2}

as the active part of the cycle. Therefore, the outputs of the sine and cosine functions are:

{1, 0}

, respectively.

The following is the truth table for an AND gate when the mixed-balanced quaternary conversion system is applied to trigonometric functions in radian base.

Table 17. The inputs and outputs of an AND gate and its sine and cosine functions.

For a negation relation or NOT gate, the traditional concept used in the binary system would have to be deviated from, and it would have to refer only to the opposite poles of a circle or sphere. This relation has been submitted to the mathematical community for analysis and/or replacement with more appropriate terms. For now, it is merely a proposal.

Table 18. NOT gates as opposite poles.

The truth table for applying the NOT gate to the sine and cosine would be as follows:

Table 19. Addition of

π

rad in a mixed-balanced quaternary system.

Table 19. Addition of

π

rad in a mixed-balanced quaternary system.

4.1.4. Quaternary Sequence in Radians

Developing a sequence of the mixed-balanced quaternary system with its equivalent digits in

π

radians shows that the number line increases by

π / 2

times the number of cycles considered. This provides a direct conversion from the base-four system to the set of trigonometric functions, along with all its implications, given the wide range of applications of trigonometric functions. In this article, we will describe this relationship. We plan to study each area in which it can be applied in detail, building on what is known about functions.

Table 20. Cycle of the first sequence.

If we expand the first cycle and develop the sequence for three positions of the mixed-balanced quaternary number system in radians, we get the following:

Table 21. Cycles of sequence.

By drawing a line using

π / 2

radians as a unit and plotting the sine and cosine functions, we can stretch or shrink the line according to the frequency of the functions. All mathematicians are familiar with this property of the function, but the reason it is mentioned here is to try to find a set of algorithms and software that can be used with a mixed-balanced base four in an analog computer. Analog and digital computers must work together. The conversion from an analog signal to a digital signal is easier with the mixed-balance quaternary system. The analog computer will process the information, and the digital computer will provide the answers.

Figure 5. Sine and cosine function

Increasing the frequency decreases the amplitude, causing the points on the line to contract while maintaining the same values.

Figure 6. The sine and cosine functions shrink the line as the frequency increases.

4.2. The Mixed-Balance Quaternary System Sphere

A circle has an infinite number of positions around to the same center; together, they form a sphere. Therefore, if we consider this scenario, the mixed-balanced quaternary system can also have an infinite number of paths. This amplifies our understanding of how the various inputs can be commuted in a computational processor. Then, the interpretation of the intermediates between true and false can be scaled to a sphere similar to the Bloch sphere [11]. In the Bloch sphere, each point represents a different state of the qubit, and each pair of diametrically opposite points represents [2] two orthonormal states of Hilbert space. Given that the distance between the two points is equal to two, one point or a single-qubit state on the Bloch sphere can be expressed as follows:

| ψ 〉 = e^{i ϕ_{0}} (c o s (θ / 2) | 0 〉 + e^{i ϕ} (s i n (θ / 2)) | 1 〉)

Where

0 \leq θ \leq π

and

0 \leq ϕ \leq 2 π

In the quaternary sphere, these points will be where two circles intersect. These circles are the vertical and horizontal circles. Each intersection forms a virtual pole. However, the only precise values of the poles that we will know are those of the pair of circles that we select before our calculation. The position of the selected pair of circles is the probability that we hope will represent our estimate of the degree of truth or falsehood. Our greatest advantage in our perception of the results or reality is the probability of our hope, but the definitive answer or the most precise value is the processing of information.

One pair of circles has six precise values where every wave function can collapse. These form six poles or three pair of poles, two of which are repeated because we must analyze two paths. One path goes around the vertical and horizontal axes from north to south and west to east, respectively, or from northwest to southeast and northeast to southwest if the axes are inclined.

This scenario is presented as a quantum field. However, we will not consider the solution regarding the spin of a quantum particle. Instead, it will resemble a field of functions forming an elementary mathematical structure similar to a quantum field, but of a mathematical nature. From this perspective, there will, of course, also be a certain degree of uncertainty. However, we can reduce or increase it a priori knowing that there are six possible answers and that the best answer will represent the smallest distance from our original perception or initial variable. This means that our perception influences the outcome in some way, but not completely, so we must process the information to obtain the correct result.

Figure 7. The relationship between the trigonometric functions of sine and cosine and the unitary sphere.

In a Cartesian coordinate system, the location of each point on the surface of a sphere is determined by the following well-known relationship:

P (r, θ, ϕ), \leq r < \infty, - π \leq θ \leq π, 0 \leq ϕ \leq 2 π

Where

r \geq 0

is the radial distance.

θ

is the azimuthal angle, and

ϕ

is the polar or inclination angle.

x = r c o s (θ) s i n (ϕ)

y = r s i n (θ) s i n (ϕ)

z = r c o s (ϕ)

Figure 8. The trigonometric functions of sine and cosine and the unitary sphere with six poles with a rotation on x axis.

Alternatively, if the

3 D

plane were rotated

90^{\circ}

in the same direction as clockwise rotation around the x axis, the result would be the same. The sphere would also rotate, but the four poles would be conserved in their corresponding pairs.

So, as the sphere can rotate in any direction due to its high degree of freedom [12], it causes a random and diverse projection of waves. This randomness best represents our nearest and farthest universe because it is composed of signals that carry a large amount of information. Therefore, the quaternary sphere can represent the essence of any object immersed within an environment full of signals and the environment as a whole.

Figure 9. The trigonometric functions of sine and cosine, as well as the unitary sphere with six poles, which are produced by rotation around the vertical and horizontal axes.

However, this rotation transforms a fixed point on the surface into a point with a changed position. Therefore, a force has been applied to it, and it must now be treated as a vector. Since this condition is normal for a sphere with a high degree of freedom, we must establish base coordinates. In our case, these must correspond to a spherical coordinate system.

Figure 10. The circles rotate around the new axis as if it were a precession movement.

Now, our point on the surface is a vector field, which is equally valid as the points of a three-dimensional Cartesian plane. The only difference is that they implicitly include the possible variables of force, velocity, and acceleration, as well as other states of energy [13], matter, and the probability of a logical state of truth or falsehood. The concept of the probability of a state relative to its degree of truth or falsehood is new and will be developed in more depth. However, its foundations are cemented in the physical and mathematical concepts of the spherical coordinate system, where we subscribe to the balanced base-four system. For this reason, we start here, and will address it in more depth in future articles because it requires more space for analysis.

Figure 11. Coordinates spherical system in convention mathematics format.

The notation for a point on the surface of a sphere is the base system.

P (\hat{r}, \hat{θ}, \hat{ϕ}) Here, the hat symbol means unitary coordinates .

If

\hat{r} = \frac{\vec{r}}{| \vec{r} |}

Then

\vec{r} = \frac{r c o s (θ) s i n (Φ) \hat{x} + r s i n (θ) s i n (Φ) \hat{y} + r c o s (Φ) \hat{z}}{r}

\hat{r} = c o s (θ) s i n (Φ) \hat{x} + s i n (θ) s i n (Φ) \hat{y} + c o s (Φ) \hat{z}

The bases vector are tangent to the coordinate lines, then form an orthonormal bases

({\hat{e}}_{r}, {\hat{e}}_{θ}, {\hat{e}}_{ϕ})

and represent the current position as follows.

{\hat{e}}_{r} = c o s (θ) s i n (ϕ) \hat{i} + s i n (θ) s i n (ϕ) \hat{j} + c o s (ϕ) \hat{k}

{\hat{e}}_{θ} = - s i n (θ) \hat{i} + c o s (θ) \hat{j}

{\hat{e}}_{ϕ} = c o s (θ) c o s (ϕ) \hat{i} + s i n (θ) c o s (ϕ) \hat{j} - s i n (ϕ) \hat{k}

The notation

(\hat{i}, \hat{j}, \hat{k})

is equivalent to the notation of

(\hat{x}, \hat{y}, \hat{z})

which are the component vectors of the unitary vector

\hat{r}

Thus, we can denote them in an indistinguishable way.

\hat{i} = c o s (θ) s i n (ϕ) \hat{e_{r}} - s i n (θ) \hat{e_{θ}} + c o s (θ) c o s (ϕ) \hat{e_{ϕ}}

\hat{j} = s i n (θ) s i n (ϕ) \hat{e_{r}} + c o s (θ) \hat{e_{θ}} + s i n (θ) c o s (ϕ) \hat{e_{ϕ}}

\hat{k} = c o s (ϕ) \hat{e_{r}} - s i n (ϕ) \hat{e_{ϕ}}

Knowing the corresponding functions for each coordinate, we can determine the value of any point on the sphere’s surface, whether we treat it as a scalar or vector field. We can express the azimuthal angle, inclination, or polar angle in radians. Thus, a point can be specified in radians as in the following examples.

Point

A) = (1, π / 4, π / 6)

point

B) = (1, 5 π / 4, π / 2)

If our coordinate system is a unitary sphere, then the radial distance is always one, and we only need to consider the azimuthal and polar angles.

In order to apply the balanced base four system, we must consider all points not defined by the values:

{- 1, 0, 1, 2}

Therefore, we assign values other than these to the sine and cosine functions.

θ \neq \{0, \frac{π}{2}, π, \frac{3 π}{2}, 2 π\}

ϕ \neq \{\frac{π}{2}, π, \frac{3 π}{2}, 0\}

Where

0 = 2 π

,

π = 2

,

\frac{3 π}{2} = (- 1)

and

\frac{π}{2} = 1

.

Each point on the surface of a sphere can be defined by azimuthal and polar angles. For our purposes, however, we can consider the intersection of two circles, with the axes perpendicular or inclined at certain degrees across the vertical axis, ranging from Π/2 to −Π or Π. This means that when you travel halfway around the sphere, the other half is automatically projected.

5. The Mixed-Balanced Quaternary System in a Complex Plane

When we insert the balanced base four system into a complex plane, several systems are derived. We can then choose the most interesting one for our intended purpose, which, in our case, is computational processing.

In the mixed-balanced quaternary system, we replace the four digits with four digits that can be represented in the complex plane. These digits are:

\{{- 1, 0, 1,} 2\} \to {- i, - 1, 1, i}

However, zero is not included in the conversion. If we include it, then the system becomes a base-five system.

5.1. Quinary System

A normal quinary system uses the digits

{0, 1, 2, 3

, and

4}

. [14] We can convert the standard quinary system into a balanced system by extending the quaternary system to the complex plane and including the digit zero.

In this case, the origin of the complex coordinate system will be the center of our circle.

Figure 12. Unitary circle.

In a balanced quinary system, the real and imaginary parts of a complex number are combined to create a single number.

The standard quinary system

(0, 1, 2, 3

, and

4)

is not employed in this project due to its challenges in implementation in electronic devices or logic gates. However, a particularly noteworthy and valuable transformation exists that allows us to more precisely implement the potential of the quinary system with the possible simplicity of the electronic devices that can be built.

To circumvent any potential confusion with the conventional quinary system, which is held in high esteem for its aesthetic appeal and inherent simplicity, it is imperative to refer to the "Complex Computational Quinary Balanced System" (CCQBS). This nomenclature is employed to distinguish between the system under discussion and the traditional quinary system, which is widely regarded for its elegance and straightforwardness. Furthermore, it is crucial to acknowledge the continued utilization of the quinary system by Aboriginal Australian, African, and American communities, a practice that underscores its enduring relevance and significance.

The system is base five, a development that emerged from the base four system when applied to a set of complex numbers and graphing the trigonometric functions sine and cosine on a complex plane. Conversely, the implementation of a spherical surface facilitates the determination of any point on its surface under a complex area structure. Consequently, the sphere under consideration will be a unitary sphere of a set of complex elements.

The CCQBS system comprises two complex structures, which are presented in this project with the aim of technologically determining which of the two is more versatile and provides the simplest and most versatile way to construct a logic gate system that can take advantage of the full capacity and power of the quinary system.

a)

The CCQBS system is comprised of two distinct components: a balanced ternary system and a complex binary system. The combination of both systems exhibits a substantial advantage in reducing the complexity of electronic devices capable of performing the logical functions of computational processes when compared to the utilization of a standard system. The digits of the system are as follows:

i): The balance ternary system: ${- 1, 0, 1}$ .
ii): Complex binary system: ${i, - i}$

b)

In the second case, the CCQBS system is composed of a balanced double ternary system, which is referred to as a balanced bi-ternary. Given the observation that both systems possess an equal number of digits in common, it can be posited that the base three can be applied to each of the five digits in the system. The digits of the system are as follows:

i): Balanced ternary system ${- 1, 0, 1}$
ii): Complex balanced ternary system: ${- i, 0, i}$

Within the framework of complex numbers, the zero is representative of the real part of the set and is also a common element to the set of real numbers in the balanced ternary system.

In both scenarios, a sequence of complex numbers is generated by the balanced ternary system, in conjunction with the complex binary system, or by the balanced bi-ternary system. The sequence is mathematically satisfied in both cases. The complex binary system has other applications in neural networks. Its digits differ from our complex binary digits, but all of these topics are important. [15].

5.1.1. Formal Definition

Let

D_{5} : {- 1, - i, 0, 1, i}

be a set of symbols.

Then, we must define an integer using the valuator function described below:

f = f_{D_{5}} : D_{5} \to C

by:

1.: $f (- 1) = (- 1) \to T$
2.: $f (- i) = (- i) \to S$
3.: $f (0) = 0$
4.: $f (1) = 1$
5.: $f (i) = i$

The set

D_{5}

, in conjunction with the function f, constitutes a balanced signed -digit representation that is referred to as: "The complex computational balanced quinary system". This system number can be used to represent both integers real numbers and imaginary numbers.

The ensuing tables present the sequence of base-five numbers in both proposals. The objective of this study is to assess which of the two structures is most conducive to the development of logic gate technology, capable of processing information under a range of conditions, thereby enabling the scaling of processors for the implementation of intelligent, truly intelligent processes.

5.1.2. Sequence in Balance Ternary and Complex Binary

The tables are presented using natural nomenclature with the number sign, so it should not be confused with the operation sign. The complex number system comprises three distinct structures that must be distinctly delineated.

i): A pure real number that can be expressed with a positive or negative sign.
ii): A pure imaginary number that can be expressed as a positive or negative real number.
iii): A composite complex number is defined as the combination of its real and imaginary parts, with their respective positive and negative signs, according to their value, irrespective of the operation’s sign, whether it is an addition or a subtraction.

The amalgamation of both number systems (balance ternary and complex binary) is not a common occurrence, as each is typically regarded in isolation. However, in the context of our investigation, its implementation is facilitated by the inherent nature of the set of complex numbers. In general, a binary complex system continues to use the digits 0 and 1 and integrates

- 1

and the imaginary number i [15]. However, the structure of the balanced quinary system forces us to consider only the positive and negative imaginary numbers, leaving the set of real numbers for the balance ternary system. Consequently, the complex system is perfectly complementary in both its real and imaginary parts.

In the context of code or programming languages, to circumvent the use of the negative sign, we will employ the equivalent symbols that have been previously defined: the symbol T for the negative part of the real numbers and the symbol S for the negative part of the imaginary numbers. In the tables that follow, these symbols are not employed to illustrate the interrelationship between the positive and negative numbers of both sets, as they are not indicative of any arithmetic operation, such as addition or subtraction.

The utilization of the symbols T and S enhances their utility in arithmetic, algebraic, polynomial operations, or in the functions calculation.

As illustrated in Table 22 and Table 23, referenced as 22 and 23 respectively, the balance ternary base and the complex binary base are employed to develop the sequence. In the context of real numbers, the base is three, while for complex numbers, the base is two.

A combination of the balance ternary and complex binary systems results in a five-digit system, irrespective of the balance or imbalance of these systems.

In the context of a conventional quinary number system, each position is expressed as a base five raised to the power corresponding to its position. However, in the case of a balanced quinary system, which is composed of a balanced ternary system and a complex binary system, the calculation of each position is determined by base three or two, contingent on whether the position is an element of the balance ternary or complex binary system.

As illustrated in Table 24 and Table 25, referenced as 24 and 25 respectively, the base of the set of real and complex numbers is three, irrespective of whether it is considered real or imaginary. Therefore, to calculate the position of either of them, the exponentiation of three corresponding to the position of the digit will be used.

The two sets of numbers are unified under a shared base, as they are considered to share the number zero as a real part of the imaginary set. From a technological standpoint, this is analogous to the development of a single balanced ternary system that is capable of handling both systems. This could be considered an advantage over the balance ternary and complex binary systems of the previous examples; however, it is also likely to be a disadvantage, given that the binary system is one of the most technologically developed and advanced coding systems. It is imperative to consider all pertinent advantages and disadvantages, particularly those associated with technology and coding, when assessing the efficacy of systems in managing and processing substantial volumes of information.

This evaluation necessitates a thorough analysis to determine the relative merits of each system in handling such large amounts of data.

As demonstrated in the tables, irrespective of the configuration of the bases, a set of two digits generates an output of twenty five numbers. Furthermore, increasing the number of digits by occupying additional positions to the left results in a growth rate of five raised exponentially. Consequently, a three-digit number will generate, through all its combinations, a number of numbers equal to five raised to the power of three, and so on.

Example

Let

10 i T 10 S 10

be a quinary number. Therefore, in the event that the initial case is employed, wherein the real numbers are situated beneath the balance ternary form and the imaginary numbers are situated beneath the complex binary form, the resultant quantity is equivalent to:

As illustrated in the Table 26 and Table 27, the results in base five are equivalent in both arrangements. However, the discrepancy emerges when these values are converted to decimal or any other number system.

The application of the second case for the same quinary number yields the following result.

The resultant quantity is expressed as a set of two elements, wherein one element corresponds to the real part and the other element corresponds to the imaginary part. This number can then be represented as a sum or subtraction of complex numbers; however, in this case, the relevance of the arithmetic operation is negligible.

The quinary system proposed here as an arrangement of two systems (balance ternary, and complex binary or complex balance bi-ternary) that collectively comprise the five digits. While these digits do not correspond precisely to the natural digits of the quinary system, they do adhere to the elementary rule of being five digits. However, there are several aspects that necessitate further analysis. This present work is merely an introduction to the quinary system, pending the comprehensive development of its laws, operations, and mathematical functions. Most notably, its application to computational data processing remains to be explored, a subject that will be addressed in subsequent articles.

6. Comments

This article is the third topic[3] on the search for extending the binary system to facilitate the management and computational processing of large amounts of information. This approach improves codes and programming for developing non-human intelligence that is truly intelligent and useful to our civilization. However, we must continue to spare technological efforts to achieve a level beyond mere intelligence because true intelligence requires wisdom [4].

This analysis has led us to a series of numerical systems with great potential. In any case, this project aims to consider all possible options, no matter how far-fetched they may seem, because one of them will produce the desired result and propel us toward real progress, not only scientifically and technologically, but also as a civilization. We are obligated to progress and resolve our controversies wisely.

The implementation of either the balanced quaternary system or the quinary system in both versions, applied to a complex field with trigonometric functions, will establish the foundations for a perspective of truth and falsehood. It must be recognized that in contemporary society, the truth that is preached is not aligned with reality. Lies have effectively masked themselves, becoming indistinguishable to the majority. It is posited that if we possess the capacity to transform a falsehood into a veracity within the framework of the category of true statements, then it follows that we can also genuinely place truth within the category of true truth and falsehood within the category of a true lie.

The aforementioned challenges collectively pose a formidable obstacle, necessitating a substantial enhancement in our logical reasoning capabilities. Such logic must be a pure logic of fundamental mathematics, and within the mathematical language, each degree of truth and falsehood must be qualified, because only the language of mathematics is simpler and more straightforward than the language of any people, even the most logical and polished on planet Earth. The text is characterized by the presence of words and concepts that bear dual meanings, which, by their very nature, engender confusion. This linguistic complexity is employed strategically to obfuscate the distinction between truth and falsehood. However, even the language of mathematics must advance and simplify its symbolism, becoming a universal language that transcends our current, limited planetary context and becomes a cosmological language.

Consequently, there is still much to be done, much to be researched and developed, in what was apparently believed to be the pinnacle of knowledge, but not yet. It is evident that there is still a considerable amount of knowledge to be acquired. We need to learn a lot, but above all, we must interpret it correctly. Significant advancements must be made, and a multitude of tasks must be completed.

References

Wang, X.Y.; Dong, C.T.; Wu, Z.R.; Cheng, Z.Q. A review on the design of Ternary Logic Circuits. Chinese Physics B 2021, 30. [CrossRef]
Banach, S. Theory of linear operations; Vol. 38, Elsevier, 1987.
Garcia-Sandoval, R. Extending the Digital Structure of the Binary Base Number System. Preprints 2025. [CrossRef]
Garcia-Sandoval, R. Challenges Necessary for the Development of Truly Intelligent AI. Preprints 2025. [CrossRef]
Euclid, Sr T. L. Heath, J.L.H. The Thirteen Books of Euclid’s Elements; Vol. II, University Press, 1908.
Hamilton, E.; Cairns, H.; et al. The collected dialogues of Plato; Princeton University Press, 1961.
Zhang, A.; Yang, J.; Luo, Y.; Fan, S. Forecasting the progression of human civilization on the Kardashev Scale through 2060 with a machine learning approach. Scientific Reports 2023, 13, 11305.
Rani, R.; Singh, L.K.; Sharma, N. FPGA implementation of fast adders using Quaternary Signed Digit number system. In Proceedings of the 2009 International Conference on Emerging Trends in Electronic and Photonic Devices & Systems. IEEE, 2009, pp. 132–135.
Jacquemin, T.; Tomar, S.; Agathos, K.; Mohseni-Mofidi, S.; Bordas, S. Taylor-series expansion based numerical methods: a primer, performance benchmarking and new approaches for problems with non-smooth solutions. arXiv preprint arXiv:2009.11953 2020.
Wright, E.M. The asymptotic expansion of integral functions defined by Taylor series. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 1940, 238, 423–451.
Glendinning, I. The bloch sphere. In Proceedings of the QIA meeting. Vienna, 2005.
Lu, T.; Miao, X.; Metcalf, H. Bloch theorem on the Bloch sphere. Physical Review A—Atomic, Molecular, and Optical Physics 2005, 71, 061405.
Ekert, A.; Hosgood, T.; Kay, A.; Macchiavello, C. Introduction to Quantum Information Science. https://qubit.guide.
Eels, W. Number systems of the North American Indians. The American Mathematical Monthly 1913, 20, 293–299.
Li, Y.; Geng, T.; Li, A.; Yu, H. BCNN: Binary complex neural network. Microprocessors and Microsystems 2021, 87, 104359.

1	I’m also proposing this in the simplest and most straightforward way possible.
2	It is also pertinent to note that the present author is undertaking this proposal independently, lacking the support of a research team or laboratory that could expedite the project’s progression. Consequently, I am willing to present this research to any research team, university, or company that wishes to implement it.
3	Extensive study is required to delve deeper into this type of logic, so it will be the subject of another topic, not presented in these article formats, but rather a book of logical and illogical analysis, which will allow us to step outside Plato’s cave [6]. Indeed, we only observe our universe through one window, when in reality there are three: the logical window, the illogical window, about which we know nothing, and the logostic window, a product of the vision of the first two windows.

Table 3. Of the eight possible interactions, those that represent a digit of the base four system are extracted.

States table
Sequence			Outputs			Decimal
C	B	A	$O_{3}$	$O_{2}$	$O_{1}$	D
0	0	0	0	0	0	0
0	1	1	0	0	1	1
1	0	1	0	1	0	2
1	1	0	1	0	0	3

Table 12. Sequencing of numbers in a mixed-balanced quaternary system.

Series of $D_{4}$ Mixed-balanced Quaternary System
Table 9					Table 11
$a \cdot 4^{3}$	$a \cdot 4^{2}$	$a \cdot 4$	$a \cdot 4^{0}$	$b_{10}$	$a \cdot 4^{3}$	$a \cdot 4^{2}$	$a \cdot 4$	$a \cdot 4^{0}$	$b_{10}$
2	0	0	0	128	2	2	0	0	160
2	0	0	1	129	2	2	0	1	161
2	0	0	2	130	2	2	0	2	162
2	0	0	T	127	2	2	0	T	159
2	0	1	0	132	2	2	1	0	164
2	0	1	1	133	2	2	1	1	165
2	0	1	2	134	2	2	1	2	166
2	0	1	T	131	2	2	1	T	163
2	0	2	0	136	2	2	2	0	168
2	0	2	1	137	2	2	2	1	169
2	0	2	2	138	2	2	2	2	170
2	0	2	T	135	2	2	2	T	167
2	0	T	0	124	2	2	T	0	156
2	0	T	1	125	2	2	T	1	157
2	0	T	2	126	2	2	T	2	158
2	0	T	T	123	2	2	T	T	155
Table 10					Table 12
2	1	0	0	144	2	T	0	0	112
2	1	0	1	145	2	T	0	1	113
2	1	0	2	146	2	T	0	2	114
2	1	0	T	143	2	T	0	T	111
2	1	1	0	148	2	T	1	0	116
2	1	1	1	149	2	T	1	1	117
2	1	1	2	150	2	T	1	2	118
2	1	1	T	147	2	T	1	T	115
2	1	2	0	152	2	T	2	0	120
2	1	2	1	153	2	T	2	1	121
2	1	2	2	154	2	T	2	2	122
2	1	2	T	151	2	T	2	T	119
2	1	T	0	140	2	T	T	0	108
2	1	T	1	141	2	T	T	1	109
2	1	T	2	142	2	T	T	2	110
2	1	T	T	139	2	T	T	T	107

Table 13. Sequencing of numbers in a mixed-balanced quaternary system.

Series of $D_{4}$ Mixed-balanced Quaternary System
Table 13					Table 15
$a \cdot 4^{3}$	$a \cdot 4^{2}$	$a \cdot 4$	$a \cdot 4^{0}$	$b_{10}$	$a \cdot 4^{3}$	$a \cdot 4^{2}$	$a \cdot 4$	$a \cdot 4^{0}$	$b_{10}$
T	0	0	0	$- 64$	T	2	0	0	$- 32$
T	0	0	1	$- 63$	T	2	0	1	$- 31$
T	0	0	2	$- 62$	T	2	0	2	$- 30$
T	0	0	T	$- 65$	T	2	0	T	$- 33$
T	0	1	0	$- 60$	T	2	1	0	$- 28$
T	0	1	1	$- 59$	T	2	1	1	$- 27$
T	0	1	2	$- 58$	T	2	1	2	$- 26$
T	0	1	T	$- 61$	T	2	1	T	$- 29$
T	0	2	0	$- 56$	T	2	2	0	$- 24$
T	0	2	1	$- 55$	T	2	2	1	$- 23$
T	0	2	2	$- 54$	T	2	2	2	$- 22$
T	0	2	T	$- 57$	T	2	2	T	$- 25$
T	0	T	0	$- 68$	T	2	T	0	$- 36$
T	0	T	1	$- 67$	T	2	T	1	$- 35$
T	0	T	2	$- 66$	T	2	T	2	$- 34$
T	0	T	T	$- 69$	T	2	T	T	$- 37$
Table 14					Table 16
T	1	0	0	$- 48$	T	T	0	0	$- 80$
T	1	0	1	$- 47$	T	T	0	1	$- 79$
T	1	0	2	$- 46$	T	T	0	2	$- 78$
T	1	0	T	$- 49$	T	T	0	T	$- 81$
T	1	1	0	$- 44$	T	T	1	0	$- 76$
T	1	1	1	$- 43$	T	T	1	1	$- 75$
T	1	1	2	$- 42$	T	T	1	2	$- 74$
T	1	1	T	$- 45$	T	T	1	T	$- 77$
T	1	2	0	$- 40$	T	T	2	0	$- 72$
T	1	2	1	$- 39$	T	T	2	1	$- 71$
T	1	2	2	$- 38$	T	T	2	2	$- 70$
T	1	2	T	$- 41$	T	T	2	T	$- 73$
T	1	T	0	$- 52$	T	T	T	0	$- 84$
T	1	T	1	$- 51$	T	T	T	1	$- 83$
T	1	T	2	$- 50$	T	T	T	2	$- 82$
T	1	T	T	$- 53$	T	T	T	T	$- 85$

Table 22. The series under consideration is part of a balanced quinary system, which itself is comprised of a balanced ternary and binary structure. The device under consideration is a three-digit generator.

Table 23. The series under consideration is part of a balanced quinary system, which itself is comprised of a balanced ternary and complex binary structure. The device under consideration is a three-digit generator for Tables 4 and 5, but a four-digit generator for Column 6.

Table 24. The series is presented in a balanced quinary system on the complex plane and is structured in a bi-ternary manner.

Table 25. Series balanced quinary system in a complex plane, bi-ternary structure. Column 6 with four digits.

Table 26. Breakdown of a quinary number into its parts according to its position.

Table 27. Breakdown of a quinary number into its parts according to its position.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

The Logical Implications of the Base-Four Number System

Abstract

Keywords:

Subject:

1. Introduction

2. This is How We Usually Understand the Nature of Our Physical and Mental World

2.1. Preliminaries

2.1.1. Generalizations

2.1.2. Basic Structure

2.1.3. Adaptive MOSFETs (AMOS).

2.1.4. Not gate.

2.1.5. AND and OR Gates

3. Mixed-Balanced Base-Four Number System

3.1. Digits of Mixed-Balanced Quaternary System

3.1.1. Definition

3.1.2. Rules for Arithmetical Operations

3.1.3. Sequence

3.2. Arithmetical Operation

3.2.1. Addition

3.2.2. Multiplication

4. Some Applications of Mixed-Balanced Quaternary

4.1. Phenomenon Sequences

4.1.1. Step by Step

The Properties of Steps

4.1.2. Mathematical expression of a step

4.1.3. The units of the mixed-balanced quaternary system are extended to the step concept

4.1.4. Quaternary Sequence in Radians

4.2. The Mixed-Balance Quaternary System Sphere

5. The Mixed-Balanced Quaternary System in a Complex Plane

5.1. Quinary System

5.1.1. Formal Definition

5.1.2. Sequence in Balance Ternary and Complex Binary

6. Comments

References

MDPI Initiatives

Important Links

Subscribe