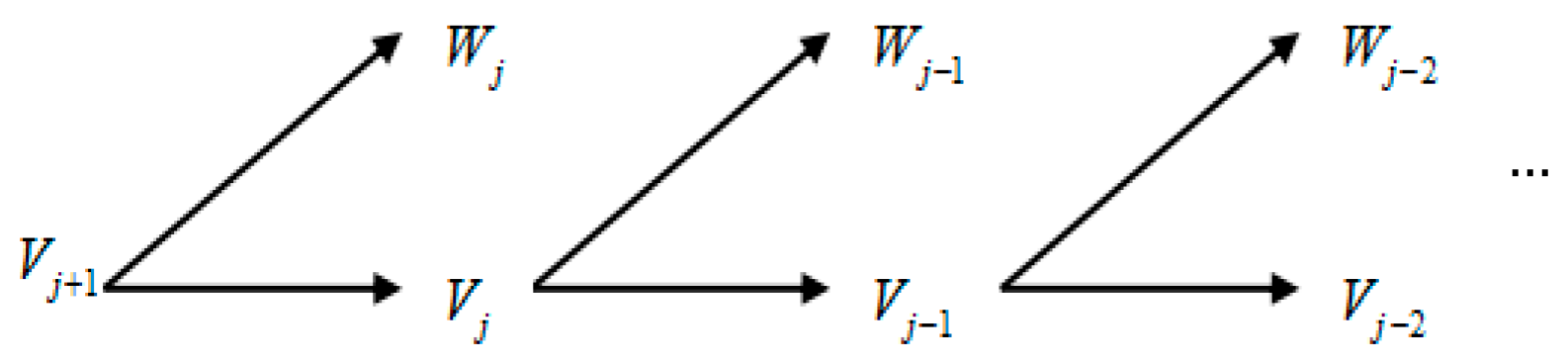1. Introduction
In recent years, with the advancement of large-scale artificial intelligence (AI) models such as ChatGPT and Sora, the security, confidentiality, and privacy of diverse information types (including text, images, audio, and video) have become increasingly urgent and critical [1]. These forms of information are more prone to theft, modification, or misuse by attackers, potentially resulting in data breaches, privacy violations, and other related problems. A multitude of technologies have been developed to safeguard this information, including encryption algorithms and steganographic techniques. Steganography is a technology that guarantees the confidentiality of information (text, images, audio, video) between the sender and the recipient. It also serves as a means of covert communication. Some notable technologies include the least significant bit (LSB) [2], the generative adversarial network (GAN) [3,4,5], and the discrete wavelet transform (DWT), among others. In the context of cloud data protection, a steganography method for audio encryption based on the least significant bit (LSB) has been proposed. This method employs the LSB of a byte to represent a message and replaces each LSB with a binary message to encrypt a substantial amount of data. Compared with other approaches, this technique has improved performance by an average of 1.732125% [2].
In the field of secure communication, scholars have explored various methods for concealing text. However, these methods often encounter limitations such as high embedding distortion or low capacity. To address these issues, a coverless information-hiding method has been introduced using generative adversarial networks (GANs)[3]. This approach transforms secret data into attribute labels for animated characters and directly generates the characters from these labels. The super-resolution GAN model has enhanced the quality.
Furthermore, wavelet analysis [7,8,9,22] is a crucial methodology for information hiding and encryption. It is well-suited for embedding diverse data types into a given signal. In recent years, scholars have conducted extensive research in this domain. For instance, Sanivarapu (2020) [10] concealed patient information in electrocardiogram (ECG) signals using a wavelet-based watermarking approach. Digital watermarking is a significant topic in information security, helping to prevent the misuse of images on the Internet. Haghighi (2020) [11] proposed a novel watermarking approach for tamper detection and recovery based on a feed-forward neural network and the LWT (lifting wavelet transform). To enhance robustness and security, Raju (2021) [12] presented a method for hiding multiple images using a combination of the DCT (discrete cosine transform) and LWT. Through this reversible data hiding (RDH) process, secret data can be safeguarded. The LWT can divide the color-space-converted image into four sub-bands. Khan (2021) [13] proposed a novel image watermarking approach for color images to address the imperceptibility and robustness issues of previous methods. Moreover, based on the discrete wavelet transform (DWT), a wavelet representation is provided for each patch with entropy less than the threshold. To achieve high invisibility, rather than hiding secret information in the pixel domain, Jing (2021) [14] suggested hiding it in the wavelet domain. Given that the wavelet domain provides a robust and valuable platform for concealing audio data, Zhao (2022) investigated the security issues of audio data compression for transmitting private data over the Internet or via micro-electro-mechanical systems (MEMS) audio sensors with digital microphones [15]. It utilized multiple coefficients of DWT.
In addition to audio and images, wavelet watermarking is also applied to text hiding and restoration. Based on a wavelet digital watermarking approach, the wavelet text-hiding algorithm (WTHA) was proposed to embed text data into a signal using random numbers, and a corresponding recovery method was also discussed to obtain the original text data from a synthesized signal [16]. Wen D., Jiao W., et al. (2024) [17] discussed the application of BCI (brain-computer interface) technology in online medical treatment and the risks of leakage of electroencephalogram (EEG) signals and private information during transmission. To address this, they proposed a hiding algorithm based on the wavelet packet transform, singular value decomposition, and logistic regression. This approach effectively concealed private information within EEG signals while minimally degrading signal quality. The results indicated that it was superior in terms of robustness and signal-to-noise ratio compared to similar techniques. In the case of color images, Wu T, Hu X, Liu C, et al. (2024) [18] emphasized the significance of high-quality side information in enhancing the security of steganography in JPEG images. They introduced WTSNet, a steganographic network that employed the wavelet transform to estimate side-channel information via iterative optimization. Simulation results demonstrated that the proposed method enhanced the security of JPEG image hiding and significantly outperformed existing methods in terms of computational efficiency.
Most of the work above involved hiding and restoring common data types, such as text, images, and audio. In fact, there are numerous types of data in our standard documents, such as web pages and PowerPoint presentations. These documents may contain various types of data, such as text, images, audio, tables, etc. However, wavelet analysis can simultaneously hide and restore different types of data. To address this issue, a color image and text steganography scheme based on the multi-wavelet transform is presented in this paper, along with its recovery. Multi-wavelets are more abundant, and the methods for their construction are more flexible. Thus, it may provide better security.
The content of this paper is briefly stated as follows: In
Section 2, we introduce the multi-wavelet transform, the wavelet text hiding algorithm (WTHA), and the wavelet text recovery algorithm (WTRA); in
Section 3, we present text and image examples. A multi-wavelet scheme is proposed to hide image and text information in a one-dimensional signal simultaneously. The method is called the multi-wavelet figure-and-text hiding algorithm (MWFTHA). An example is shown to demonstrate the hiding steps. In
Section 4, the corresponding multiwavelet figure and text-restoring algorithm (MWFTRA) is proposed to recover the original image and text from the synthetic signal in
Section 3. It demonstrates the restoration steps by continuing Example 1 in
Section 3. In
Section 5, the running time of the steganography technology is estimated using 1000 simulation groups. The security of this system is briefly discussed, including the private-key space, data-tampering scenarios, and performance metrics. Finally, the prospects of its application are discussed in light of this new steganography technology.
2. Preliminary
2.1. Multi-Wavelet Transform [7,19,20]
Assume that a closed subspace sequence in space satisfies the following properties:
- (1)
,
- (2)
,
- (3)
- (4)
There exists a function vector
, such that the set
constitutes an orthogonal basis of space
. Then, an orthogonal multiple multi-resolution analysis is generated by the sequence
, where
. For a given integer
,
is an orthogonal complementary space of
in the subspace
, that means,
. So,
. If the set
, generated by integer translation of functions
, constitutes an orthogonal basis of
, where
then the function vector
is a multi-scale function, and
is the multi-wavelet corresponding to the multi-scaling function
. The two-scale matrix equation can be obtained as follows:
where
r×r matrix sequences
and
are called the low-pass filter and the high-pass filter, respectively. The decomposition and reconstruction formula of the multi-wavelet transform are given in the following equations: for a continuous signal
, the decomposition formula is
where
and
are low-frequency coefficients and high-frequency coefficients of coefficients
Cj+1,k, respectively.
Its corresponding reconstruction formula is
where
and
are the conjugate transpositions of the matrix
and
, respectively. These can also be explained by a decomposition figure of the wavelet closed subspace, as shown in Figure 1.
The inverse of the process in
Figure 1 is called multi-wavelet reconstruction (for more details, see Refs. [7,8,9,19,20,21]). In addition, the front and post prefilters are required for practical applications of multi-wavelet transforms (see Refs. [20,21] for details).
2.2. Wavelet Text Hiding Algorithm (WTHA) and Wavelet Text Recovery Algorithm(WTRA)[16]
As outlined in
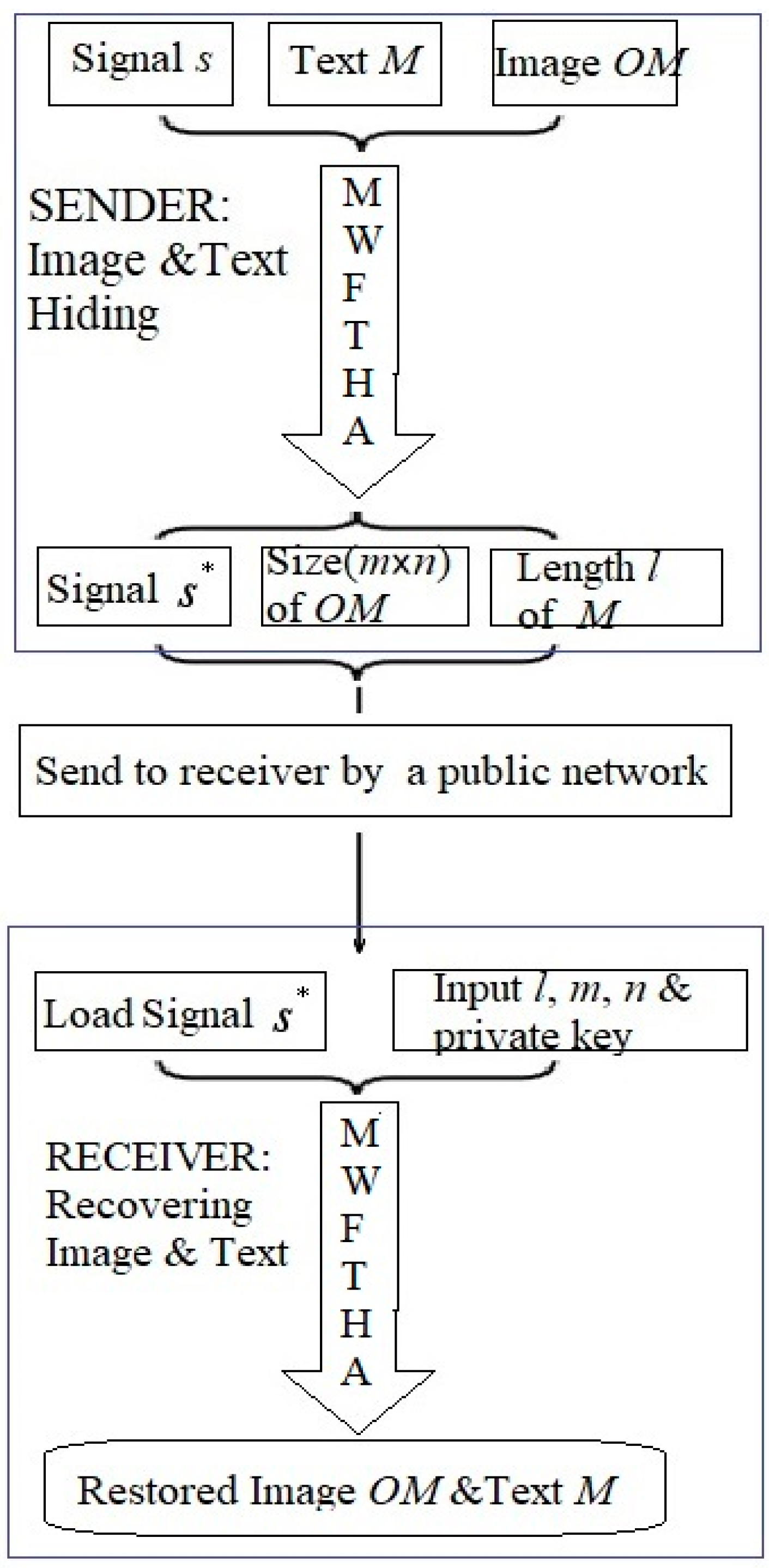
Section 1, the wavelet digital watermarking scheme is instrumental in ensuring information security. The primary goal of this scheme is to protect digital content, including images, video, audio, and other media, from copyright infringement, integrity breaches, unauthorized replication, and tracking. Moreover, a novel method has been proposed to enhance the security of text information transmission by employing a one-dimensional wavelet digital watermarking scheme. In the Ref.[16], A text information transmission system is introduced that integrates WTHA and WTRA via a public-key mechanism.
For a sender, the wavelet text-hiding algorithm (WTHA) can be used to effectively conceal an essential text M within a random signal. We will provide a concise overview of this algorithm. Initially, the text M is encoded using a private data set, allowing us to determine its length. Subsequently, a random signal s is decomposed k times using the DWT. High-frequency data d1, d2, ..., dk can be captured in this step. Next, the code of the M is seamlessly integrated into the i-th high-frequency data di by using a watermarking technique. Finally, the wavelet reconstruction formula is utilized to obtain a synthetic signal , indicating that the text M has been successfully concealed in this signal.
For the corresponding receiver, the text M needs to be recovered from the received data (signal and text length) using the wavelet text recovery algorithm (WTRA). We also briefly state this algorithm. First, based on information extracted from the private key (e.g., wavelet function, embedding position, decomposition level k, and related parameters), the received signal can be analyzed to obtain k high-frequency data samples d1, d2, ..., dk via wavelet decomposition. Secondly, the raw text data can be obtained from the i-th high-frequency data di using the watermarking method. Finally, given the text’s length, the original text can be reconstructed from the code. This means the original text has been recovered from the received signal .
For the corresponding receiver, the text M can be restored from the received data by the wavelet text recovery algorithm (WTRA). We will outline this algorithm below. Initially, based on information obtained from the private key (e.g., the wavelet function, embedded position, decomposition time k), the received signal is decomposed to yield k high-frequency data samples d1, d2, ..., dk. Subsequently, the data of the original text is extracted from the i-th high-frequency data di. Finally, the raw text is extracted from the recovered code, along with its length. This signifies that the original text has been recovered from the received signal.
This text-secret transmission system for the WTHA and WTRA is similar to the public-key mechanism. Thus, it has a critical characteristic. If some data without critical information were tampered with during signal transmission, the original text could still be restored. If key data were tampered with by others, some of the original text could be restored. It implies that the system can resist data tampering.
3. An Approach for Hiding Different Types of Data via Multi-Wavelet Transform
In many studies, data-hiding algorithms are designed primarily for a single data type, such as text, audio, or images. However, with the development of large-scale AI models such as ChatGPT and SORA, algorithms capable of embedding multiple types of data simultaneously have become a focus of research. Nevertheless, by using multi-wavelet space decomposition, it is feasible to conceal various types of data within a noisy signal. In this section, we describe a method for embedding diverse data types, such as text and color images, into a loud signal. Using the multi-wavelet transform, we present a simple example of simultaneously concealing text and an image. We first introduce the multi-wavelet figure and text-hiding algorithm as follows.
Multi-Wavelet Figure and Text Hiding Algorithm (MWFTHA):
All English characters, including common punctuation marks, numbers, etc., are contained in a data set, and these can be encoded as
where
n is the number of all chosen characters. The original text can be encoded as a one-dimensional array(data)
M:
where the integer
l is the length of the raw text content.
Construct an image dimension reduction projection, and the two-dimensional digital image can be projected into a one-dimensional digital signal(data) TN.
The formula can generate a random signal s
where
ε is a (normal) random number. The data
s can be decomposed
k times by the decomposition formula Equation (2) to obtain an approximate data
ck and
k detail data
d1,
d2,...
dk.
Take an invertible linear transform on the one-dimensional digital signal corresponding to the digital image and take another invertible linear transform on the one-dimensional array corresponding to text data; Then embed the transformed digital signals into the high-frequency data di and dj to obtain di*and dj*, respectively.
By the multi-wavelet reconstruction formula, ck and k new detail data d1,..,di*,..,dj*,..dk are mixed to construct a synthetic signal s* by Equation (3).
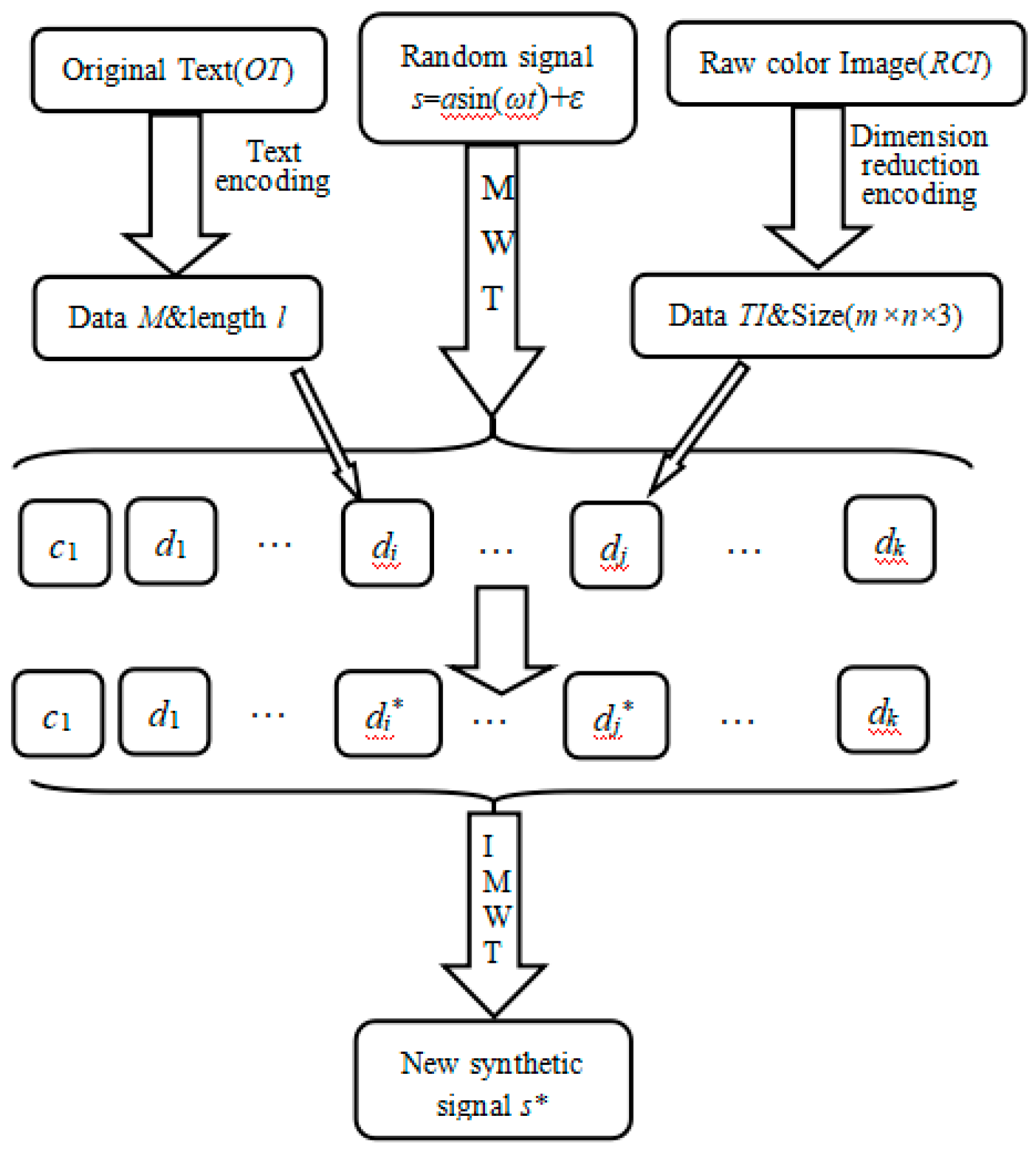
The five steps above are used to hide the text and image within a single noisy signal. It is referred to as the multi-wavelet figure and text hiding algorithm (MWFTHA). This diagrammatic sketch of the scheme is also evident in
Figure 2.
Notes 1:
- 1)
In the above algorithm, the text and the color image can be hidden in a random signal simultaneously. The random number ε can be generated by ‘randn’ or the wavelet random number algorithm in Ref.[21].
- 2)
The set T (denoted as Equation (4)) can be built with an alphabet and a character table (This is the simplest way, but it has little impact on its security). Alternatively, it can be constructed in complex ways to increase the difficulty of decipherment.
- 3)
The dimension reduction projection for a digital image needs to have the following characteristics. The critical information in the image (such as eigenvalues, pixels, color, texture, and shape) can be used to restore the original image as closely as possible (similar to the method of intelligent recognition).
- 4)
It is arbitrary to choose the key elements, such as wavelet base, embedded position, embedded high-frequency space, and so on. These guarantee the security of the information. In addition, the design of the private key is not discussed in this paper at this time.
Example 1: To introduce the algorithm, we consider the following text and original image.
Text: ‘The picture shows a sea of zinnia flowers in various colors, such as red, pink, and white, blooming vibrantly. The flowers are arranged to create a stunning visual effect, immediately drawing the viewer’s attention. The picture’s composition highlights the beauty of nature, emphasizing the colors and patterns of the flowers.’
Image:
According to the Multi-Wavelet Figure and Text Hidden Algorithm (WIMHA), two different kinds of data (Text and original image) can be hidden in a random signal. The specific process is as follows:
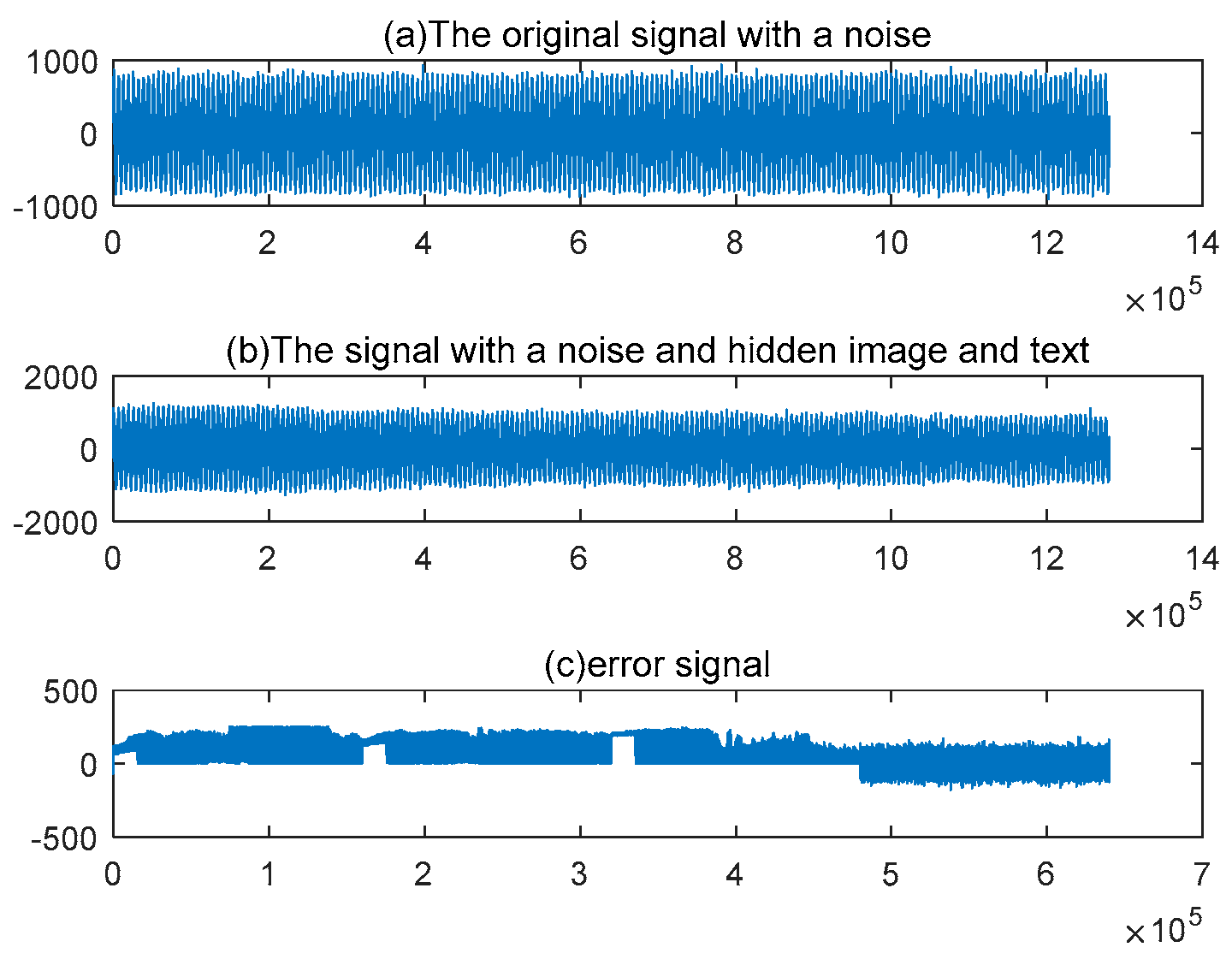
According to Example 1, the original text and image are hidden in a one-dimensional signal
s*, which is shown in the middle graph (b) of
Figure 4. The error between the signal
s* and the original signal
s. This error in the graph (c) of
Figure 4 suggests that the text and image have been successfully hidden. But it is almost useless for restoring the raw text and images. In fact, this
s* is publicly transmitted and can be seen by others. But the original
s does not need to be sent to the receiver publicly. Therefore, it cannot be seen by others.
4. Restoring Different Types of Data from a Synthetic Signal
In
Section 3, we introduce the hiding approach for various data types. The specific steps of the algorithm for simultaneously hiding text and image data are given. In this section, we will investigate how to recover raw text and images from the synthetic signal
s*. The main tools include the multiwavelet method and the private key. First, the multi-wavelet figure and text-restoring algorithm are introduced in the following section. For ease of understanding, we continue the notation from
Section 3.
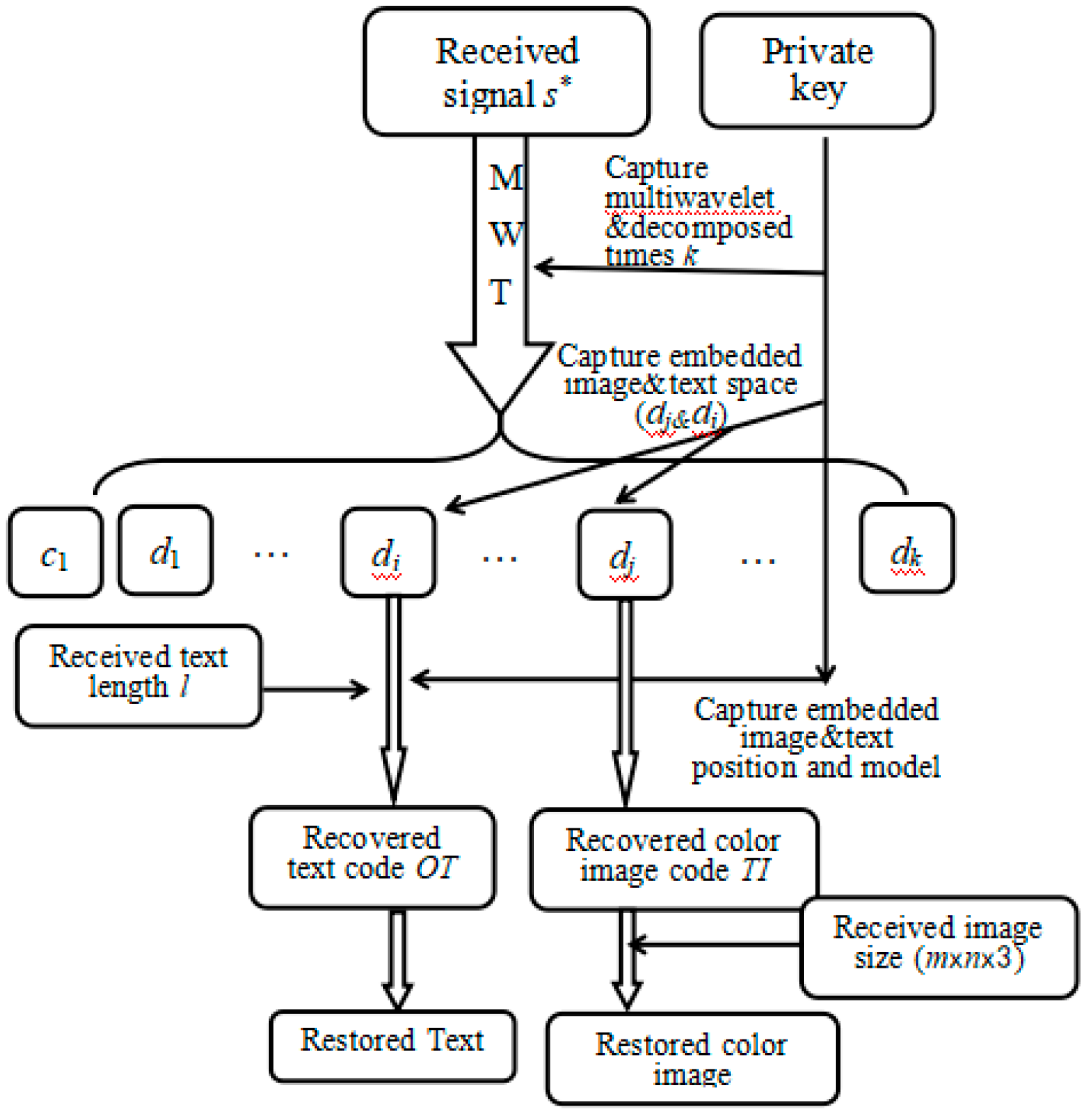
Multi-Wavelet Figure and Text Restoring Algorithm (MWFTRA):
The sender simultaneously transmits a synthetic signal s*, the text length l, and the image size (m×n×3) to the receiver over the public network. Assume that the receiver successfully accepts the data and that no data is lost.
- 2.
Capture the encoded information of the Figure and Text
After extracting relevant information from the private key, several parameters must be determined, including the wavelet decomposition levels, the text and image locations, the embedded positions in the space, the wavelet basis, and other key parameters. The synthesis signal s* is decomposed k times to obtain ck and k high-frequency data d1, ..., di,..., dj, ..., dk. The encoded data for text and image can be extracted from the high-frequency data di and dj, respectively, using the key elements obtained above.
- 3.
Recovery of the original image
Recover the characteristic data of the original image from the high-frequency data dj (or di) obtained in Step 2. The original image can be restored by the inverse mapping for the dimension-reduction projection and the image information obtained from the private key.
- 4.
Restoration of original text
Recover the encoded data of the original text from the high-frequency data di (or dj) obtained in Step 2. The original text can then be restored using the initial dataset T (defined in Equation (7)) and the inverse linear transform in Step 4 of the Multi-Wavelet Figure and Text Hidden Algorithm (MWFIHA).
The above four steps indicate that the original text and image can be successfully restored using the multi-wavelet method, known as the Multi-Wavelet Figure and Text Restoring Algorithm (MWFTRA). The diagrammatic sketch of this scheme is also shown in
Figure 5.
Notes 2:
- 1)
The multi-wavelet figure and text restoration algorithm (MWFTRA) can reconstruct the original text and image from a one-dimensional random signal s*, given the text length and image size.
- 2)
Key elements for decrypting information from the private key include the times of multi-wavelet decomposition, the locations of the text and image, the positions embedded in the space, the multi-wavelet basis, and other relevant parameters.
- 3)
In steps 3 and 4, there is an interference from the noise ε. In the process of restoring text and images, multi-wavelet denoising is required. The key information of noise ε can be captured from the private key.
Next, the following example illustrates the Multi-Wavelet Figure and Text Restoring Algorithm.
Continuation of Example 1
A synthetic signal
s* in subgraph (b) of
Figure 4, the length (328) of the text and the size (400×400×3) of the image are sent to the receiver from the public network simultaneously. Assume that the receiver accepts the data successfully and no data is lost.
According to the private key (saved by the receiver himself), some key elements need to be determined such as the times(5) of wavelet decomposition, the spaces (W1 and W2) where the image and text are located respectively, position(200) embedded in the space, multi-wavelet(CL)[15] and other key elements. The signal s* is decomposed for 5 times to obtain c5 and 5 high-frequency data d1, d2, d3, d4, d5. The M and TN data for text and image, respectively, can be extracted from the high-frequency data d2 and d1 using the key elements obtained above.
Recovery of the original image
Based on the data
TN obtained in Step 2, the original image can be restored via the inverse mapping of the dimension-reduction projection and the image information obtained from the private key. The restored result is shown in
Figure 6. The original image is shown in the bottom graph (Restored image) of
Figure 6.
- 4.
Restoration of original text
Based on the data
M obtained in Step 2, the original text can be restored from the initial dataset. The restored result can also be seen in
Figure 6. The original text is shown in the top axes(restored Text) of
Figure 6.
In fact, according to Example 1 and Continuation of Example 1, the union of the multi-wavelet figure and text hiding algorithm (MWFTHA) and the multi-wavelet figure and text recovery algorithm (MWFTRA) can be recognized as a public key principle (or cryptography) for figure and text information transmission. They form a complete system. Next, we introduce this system architecture.
5. Some Performances
5.1. System Architecture and Running Time for MWFIHA and MWFIRA
The union system architecture of MWFTHA and MWFTRA will be elaborated in this section. Compared to the system architecture in Ref.[11], Both the private and public keys are more complex. Take Example 1 and its Continuation for an example:
Public key: data s*, size(400×400×3) of image, length l(328) of raw text content.
Private key: the elements of a private key include multi-wavelet basis (CL), the number of multi-wavelet decompositions (5), noise ε, embedding way & position (d1, continuous way in d1; d2, continuous way in d2), and other details.
Obtain the plain content:
‘The picture shows a sea of zinnia flowers in various colors, such as red, pink, and white, blooming vibrantly. The flowers are arranged to create a stunning visual effect, immediately drawing the viewer’s attention. The picture’s composition highlights the beauty of nature, emphasizing the colors and patterns of the flowers, as shown in the original image in
Figure 7.
The architecture sketch for the MWFTHA and MWFTRA is shown in
Figure 7. It includes a sender and a receiver. To a sender, an enciphered data
s* can be obtained from a random data
s, raw text
M, and image (
OM) by MWFTHA. Then, the length
l of the text content and the image size (
m×
n×3) can be directly obtained. The encrypted data
s*, its length
l, and the size (
m×
n×3) can be sent to a receiver over the Internet or in communication networks. According to the MWFTRA and the private key, the receiver can recover the raw text
M and the image (
OM) from the received data
s*, the length
l, and the size (
m×
n×3).
In the MWFTHA and MWFTRA, the codes of image and text content are hidden by a random number ε. And the codes of image and text content can protect each other. This means the hidden codes for image and text content cannot be readily obtained using a multi-wavelet transform, since the codes for image (OM) and raw text (M) are mixed with a random variable ε. The random number ε ensures the security of the image (OM) and text (M) codes. To a certain extent, the mix of image (OM) and text (M) can also ensure security for each other.
In the MWFTHA and MWFTRA, the multi-wavelet transform (MWT) accounts for the majority of the computational complexity. Assume that
L is the length of a data
s, satisfying
L=
n02
J0, where
n0∈
Z+ and
Z+ denotes the set of positive integers, the MWT can be accomplished by computing O(
L*l0) multiplications,
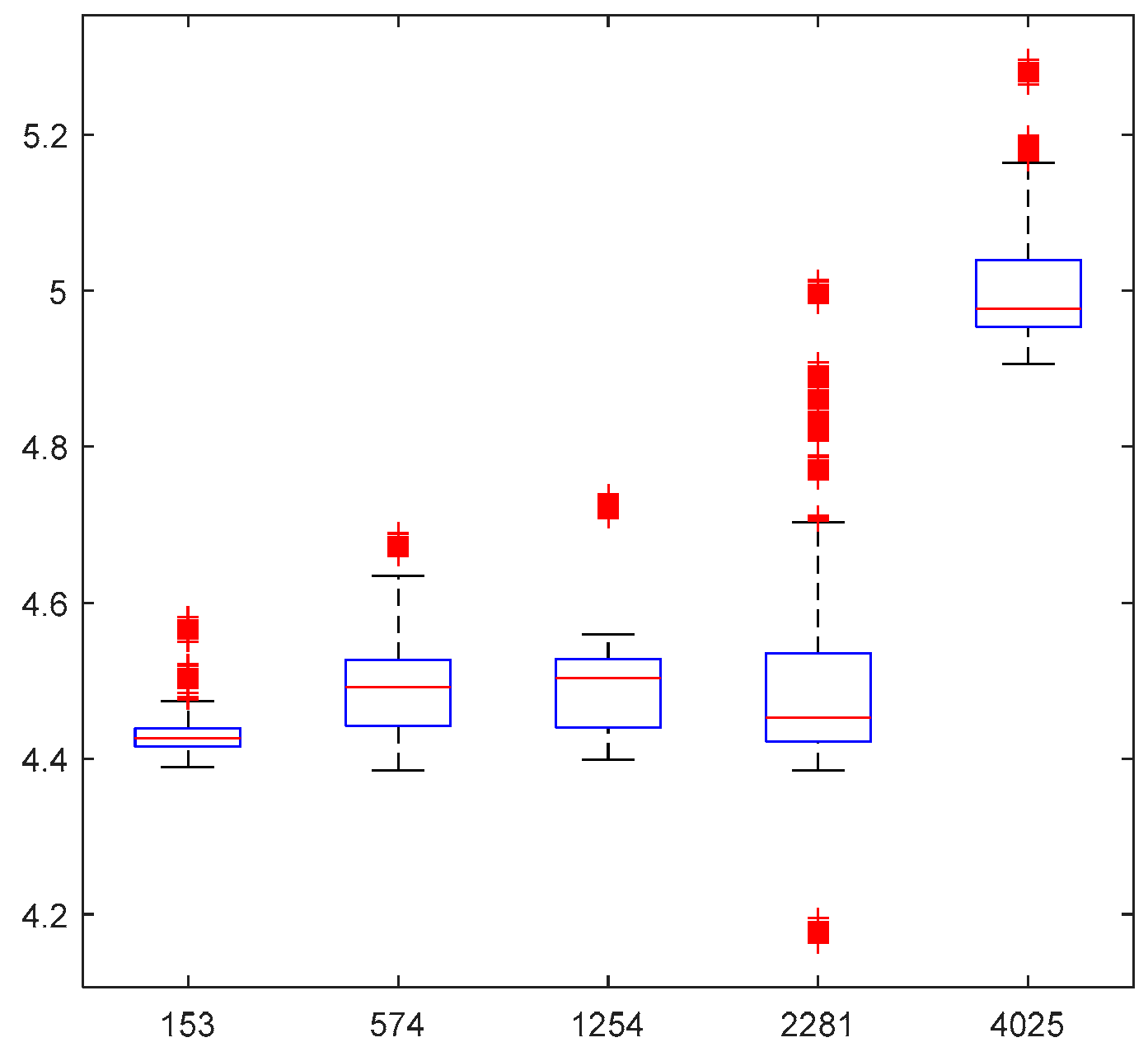
where l0 is the length of the multi-wavelet filters. So text content and images can be quickly hidden by MWFTHA and rapidly restored by MWFTRA. To estimate the running time of the MWFTHA, 1000 groups of texts and figures with varying lengths and fixed sizes are used. In
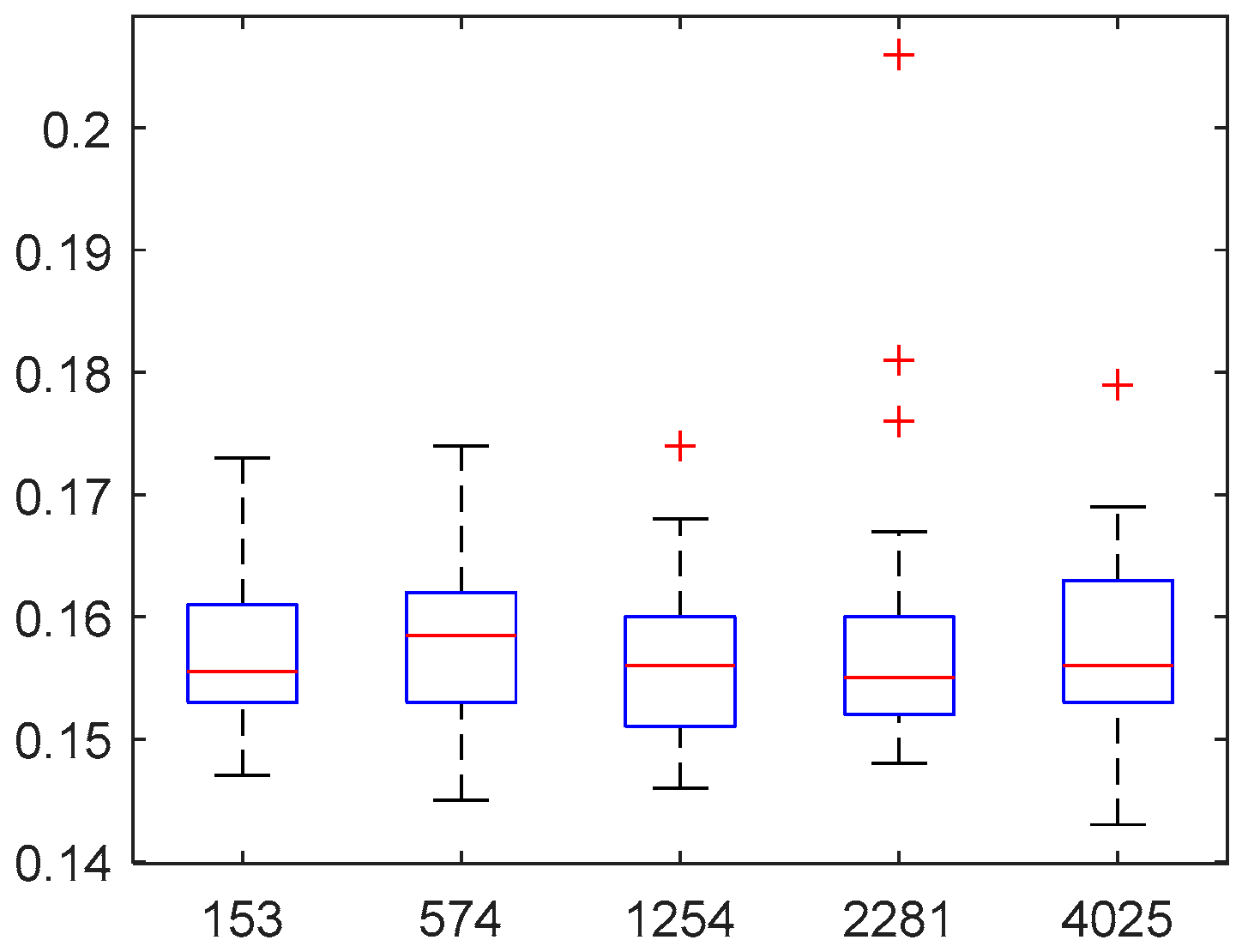
Figure 8, fixing the image size (400×400×3), the distribution of running time is shown to illustrate the influence on running time with varying text length. The X-axis (horizontal axis) shows the length of text, and the Y-axis(vertical axis) represents the running time (Unit: seconds). As shown in
Figure 8, the running time of the hidden image (400×400×3) and text is mostly between 4 and 5 seconds. More precisely,
Table 1 lists the estimated mean running time. For example, the mean running time is 4.4902s when a text has 1254 characters (Fixed an image (400×400×3)). The corresponding estimated standard deviation(S.D.) is 0.0561s in
Table 1.
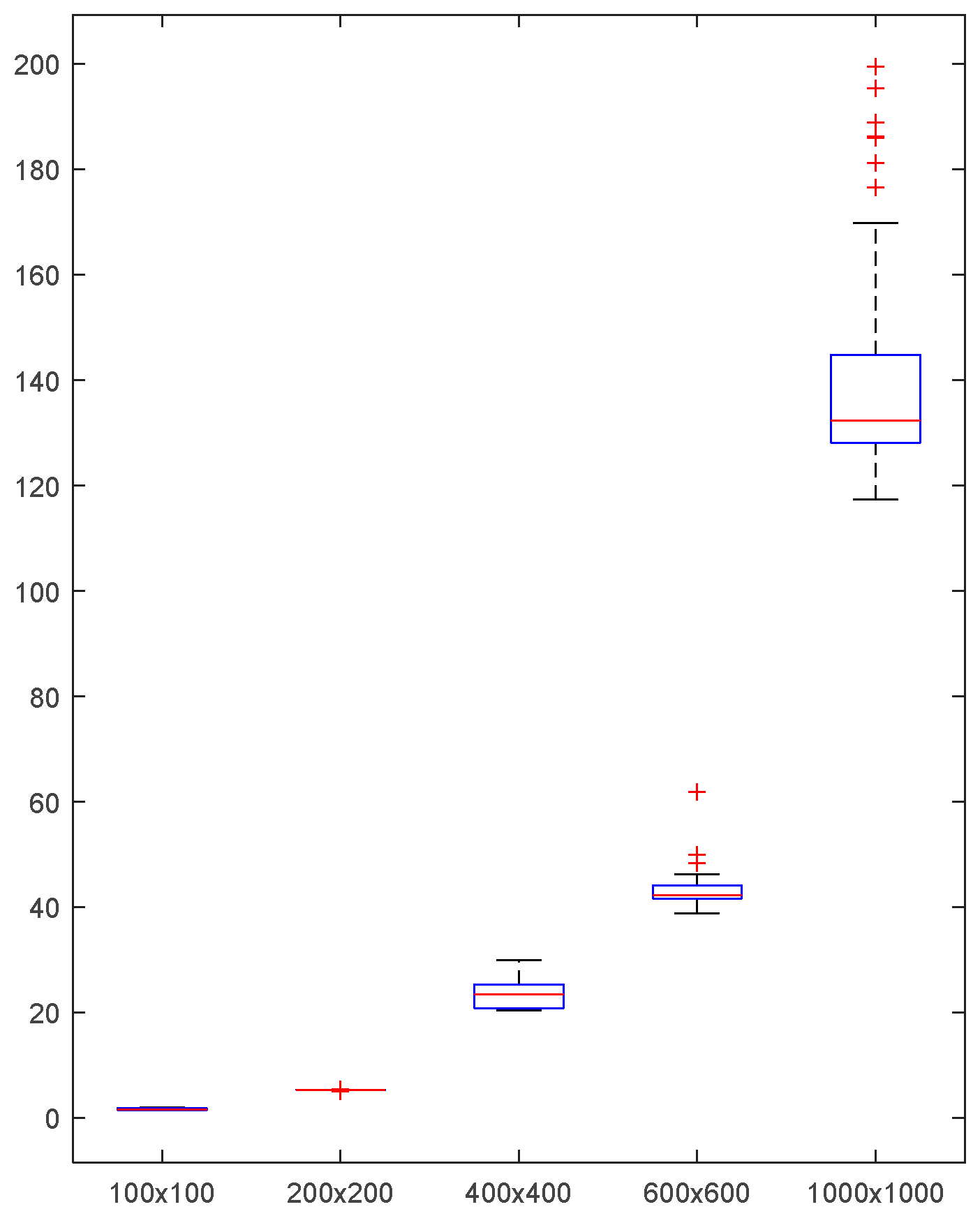
In
Figure 9, a 1000-group of text and images with fixed length(328) and different sizes are considered for estimating the distribution of the MWFTHA’s running time. Fixed the text’s length (328). The distribution of running time illustrates the effect of image size on running time. The X-axis (horizontal axis) shows the size of an image, and the Y-axis(vertical axis) shows the running time (Unit: seconds). As shown in
Figure 9, the running time of the recovered text (328) and image increases significantly with image size. More precisely,
Table 2 lists the estimated mean running time. For example, the mean running time is 142.4761s for an image size of 1000×1000×3. (Fixed a text(328)). The corresponding estimated standard deviation(S.D.) is 21.0665s in
Table 2.
To estimate the running time of the MWFTRA, 1000 groups of texts and images of varying lengths and fixed size are used to characterize the distribution of running time. In
Figure 10, fixing the image size (400×400×3), the distribution of running time is shown to illustrate the influence on running time as text length varies. The X-axis(horizontal axis) shows the length of text, and the Y-axis( vertical axis) shows the running time (Unit: seconds). As shown in
Figure 10, the running time for recovering the image (400×400×3) and text is mostly between 0.14 and 0.16 seconds. More precisely,
Table 3 lists the estimated mean running time. For example, the estimated mean value of running time is 0.1559s if a text has 1254 characters (Fixed an image(400×400×3)). The corresponding estimated standard deviation(S.D.) is 0.0067s in
Table 3.
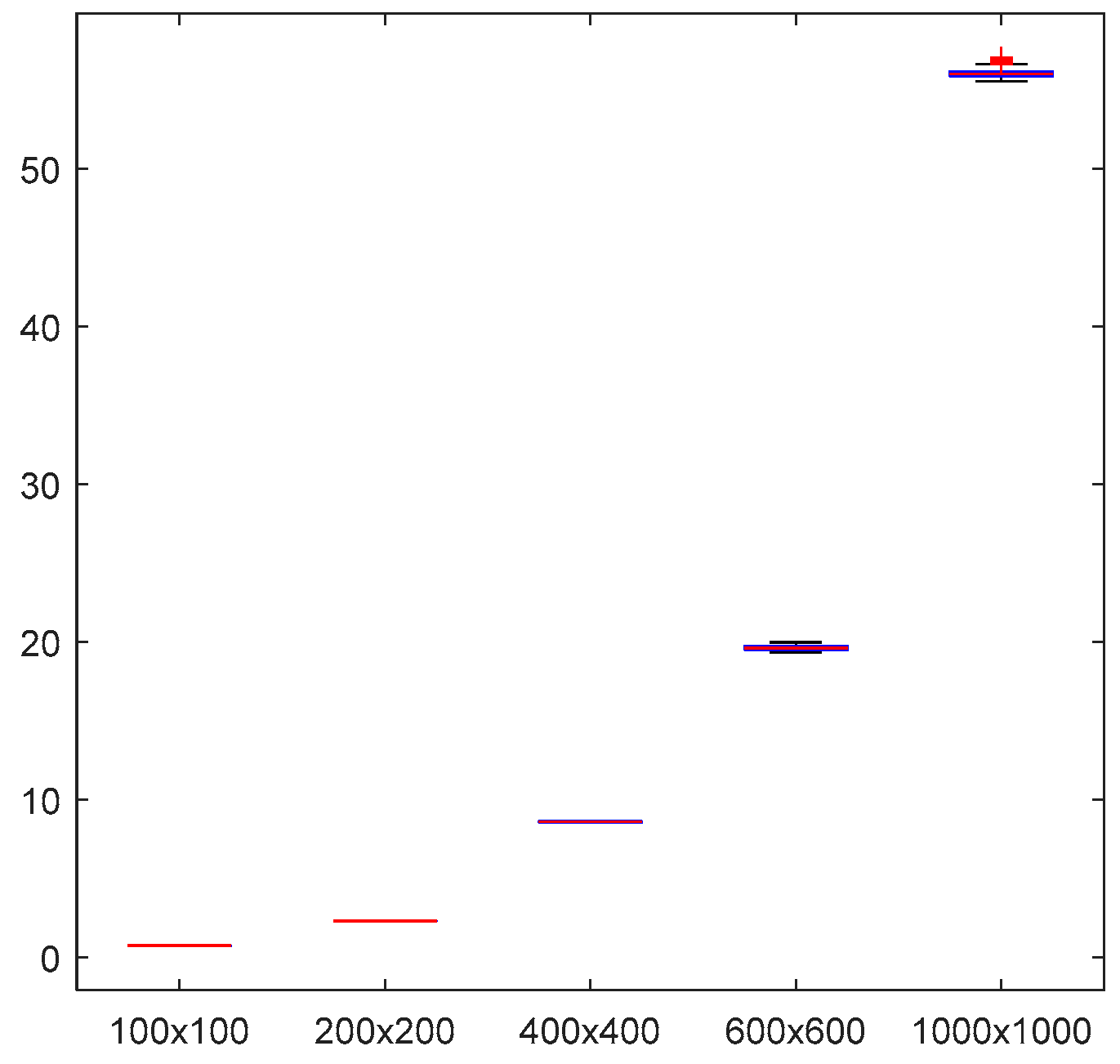
Moreover, a 1000-image dataset comprising fixed-length texts of varying sizes is used to estimate the distribution of MWFTRA’s running time. Fixed a text’s length(328), the distribution of running time is shown to illustrate the influence on running time with the variation of image size. The X-axis(horizontal axis) shows the size of an image, and the Y-axis( vertical axis) shows the running time (Unit: seconds). As shown in
Figure 11, the running time of the recovering text (328) and image increases significantly with increasing image size. More precisely,
Table 4 lists the estimated mean running time. For example, the mean value of running time is 56.1528s if the size of an image is 1000×1000 (Fixed a text(328)). The corresponding estimated standard deviation(S.D.) is 3.6168s in
Table 4.
Based on the above estimation results, the running times of the MWFTHA and MWFTRA algorithms increase slightly with increasing text length but increase significantly as the number of image pixels increases. Based on the estimated mean and standard deviation of running time, the image and text can be hidden and recovered quickly by MWFTHA and MWFTRA, respectively. Moreover, the time spent hiding and recovering the image accounts for a significant portion of the running time in MWFTHA and MWFTRA. In this system, MWFTRA is a little faster than MWFTHA.
5.2. Private Key Space Ω
In the algorithms MWFTHA and MWFTRA, the multi-wavelet basis can be chosen arbitrarily to hide and recover the image and text, and this choice is critical. In the text-hiding and recovery process, wavelets must be consistent [10]. Of course, in the system of MWFTHA and MWFTRA, wavelets need to be consistent, too. Similar to the conclusion in Ref.[16], If the embedding spaces of the image and text are inconsistent in MWFTHA and MWFTRA, the original image and text cannot be restored either. The discussion of the text’s recovery is similar to that in the Reference.[16], It is not elaborated here. Next, some results are given to introduce the failure of the recovered image.
If the embedding space of the image is unknown or mistaken in the continuation of Example 1, the restored results are shown in
Figure 11. The recovery of the image fails. If other information of the private key is captured, the restored text information is correct.
If the embedding space of the image is correct in the continuation of Example 1, but the embedding position and information of noise
ε are unknown. In the MWFTHA, the embedding position of the image is the sampling point (200) of the data d1 with noise. However, the capturing position from data d1 is the sampling point (400), and it is not denoised by the noise captured from the private key in the MWFTRA. The results of the recovery are shown in
Figure 12. The image recovery also failed. If additional information about the private key is obtained, the restored text is also correct.
The data can be embedded in either an intermittent or a continuous manner. Suppose the embedding mode is sporadic in the MWFTHA. In that case, one data point of image information is embedded at five intervals in the continuation of Example 1, but the MWFTRA captures continuously. The recovery results are shown in
Figure 13. Image recovery also failed. If additional information about the private key is available, the restored text is also correct.
According to the above discussion, perfectly restoring images and text requires knowing all the detailed information captured from the private key, such as the wavelet basis, embedding position, decomposition level, and so on. These also ensure the security of the hidden image and text. Take the embedding point as an example. If the above 328 characters in Example 1 are embedded in the data with 1000 sampling points, then there are about 4.42136×10
957 kinds of different embedding cases, which can be estimated by Equation (9)
With an estimated mean time of 0.0078s in
Table 4, we will need approximately 1.2064×10
954 years to compute all results.
Definition (Private Key Space)
According to the elements in the private key, the private key space Ω can be defined in an easy way as follows:
where a set
MWF consists of many kinds of multi-wavelet functions as
The set
W consists of multi-wavelet spaces as
The set
EP is a positive integer set as
and
Ls is the length of signal generated by Equation (2). The set EM denotes as
The set
RN is defined as
Indeed, the key space Ω may be more complex. Multi-wavelet functions can be constructed by a lot of algorithms, such as parametric multi-wavelet functions, balanced multi-wavelet functions, and so on. So, according to the definition of private key space in Equation (10), if the private key can be denoted as the following character string:
In this key, CL denotes the CL multiwavelet filter, and ap denotes the prefilters of the CL multiwavelet. W1 is the subspace of embedding an image. 200 indicates that the embedding position is after the 200th data point in W1. W2 is the subspace of embedding a text. 400 suggests that the embedding position is after the 400th data point in W2. I5 denotes the embedding mode with five intervals. Number 967 is an initial random number. In fact, the key may be more complex, including renamed multi-wavelet filters, newly constructed multi-wavelet filters, and more complex embedding modes.
5.3. Cases of Data Tampering
In this subsection, only brief statements are discussed regarding data tampering. Simply speaking, the security of this method comprises two main aspects: the data transmission and decryption processes, and the data set (character set) used in encoding and decoding. The dataset (a character set) is stored locally without being transmitted publicly. However, it is one of the key pieces of information for accurately recovering the plain information, which is also largely unaffected. This means that even if the digital code of the original text is completely deciphered, the plain text cannot be recovered without an accurate data set (a character set) (It is designed by the order of characters complexly and randomly, increasing or decreasing the other characters, etc.). Therefore, the primary discussion of data security concerns known or stolen data sets. This is a public transmission, and the part is under attack.
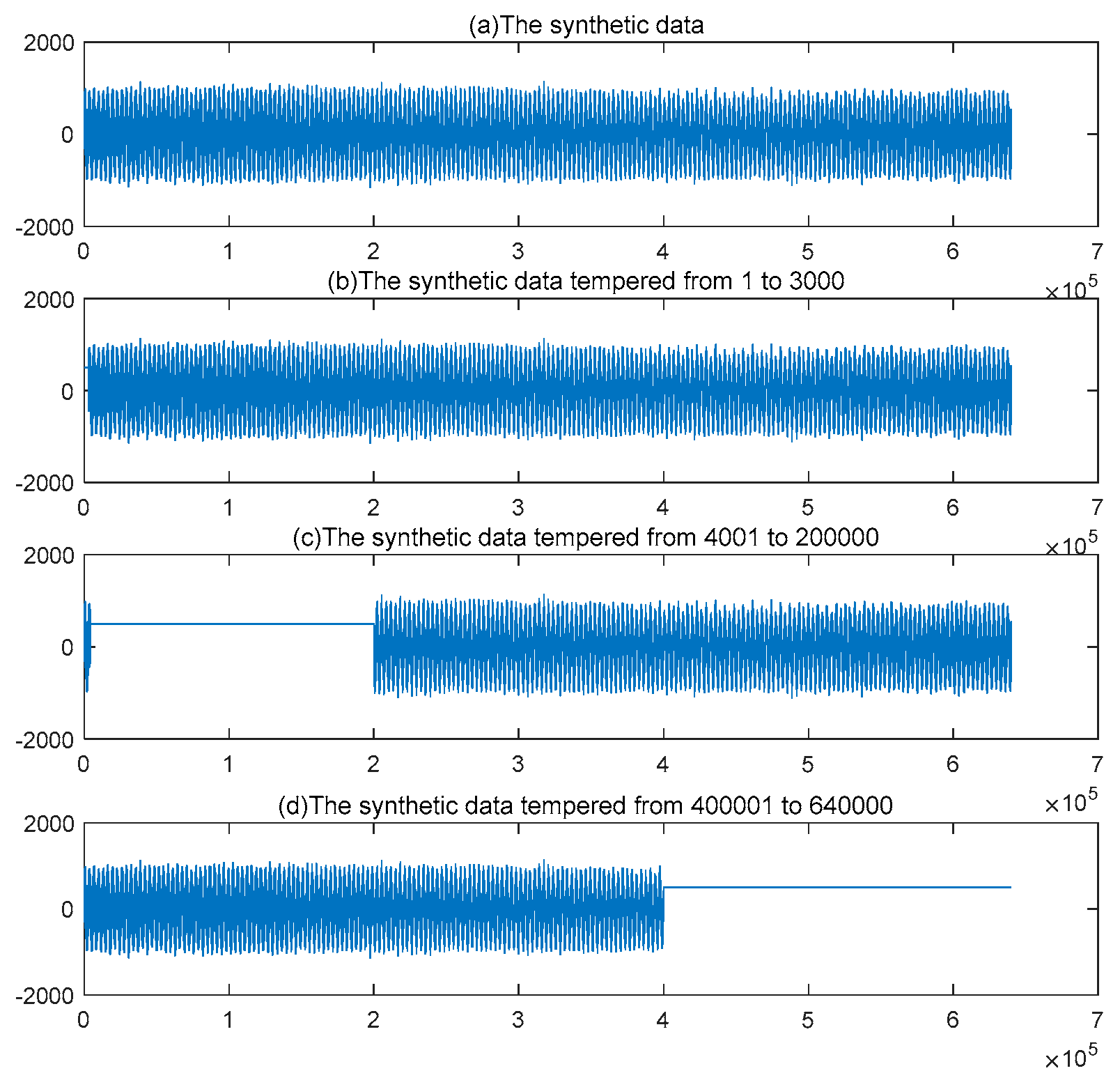
The synthetic signal with 640000 sample points is transmitted to the receiver publicly, as given in the graph(a) of
Figure 15. Some brief discussions are provided for data tampering in three cases, considering the data in the graph(a) of
Figure 14. In the graph(b) of
Figure 15, the value of data is tampered to 500 from sample point 1 to 3000. The value changes from 500 at sample point 4001 to 200000 in graph (c). The graph (d) shows the value is tampered with to 500 from sample point 400000 to 640000.
Figure 14.
tampered data of the synthetic signal.
Figure 14.
tampered data of the synthetic signal.
In
Figure 14, there are three cases of tampered data. In the first case, the raw data from sample points 1 to 3000 contain less information in the text and image (especially the image). The recovered results is shown in the
Figure 15. It implies that restored text and image reflects the most information of the original text and image intuitively and less information is missing, where * denotes the failure of the character recovery in
Figure 15,
Figure 16 and
Figure 17. If the raw data from sample point 1 to 3000 is tampered to 500, the recovered results are the same with that in
Figure 6. Because these data don’t contain the information about text and image.
In the second case, the original data from sample points 4001 to 200000 contain substantial information in the text and images (text in particular). The restored results are shown in
Figure 16. It is evident that the three rows of characters are not restored, and some regions of the image are not restored.
Figure 15.
Restored text and image in the first tampered case.
Figure 15.
Restored text and image in the first tampered case.
Figure 16.
Restored text and image in the second case.
Figure 16.
Restored text and image in the second case.
Figure 17.
Restored text and image in the third case.
Figure 17.
Restored text and image in the third case.
In the third case, the original data from sample points 400001 to 640000 contains substantial information in the image but none in the text. The restored results are shown in
Figure 17. It is evident that the characters of the original text are fully restored. Three parts of the raw image cannot be restored.
Based on simulation results across three tampered-data cases, the novel steganography demonstrates some resistance to data tampering. This means that if a data point in the novel steganography does not contain the hidden information and is tampered with by an attacker, the raw text and image can still be fully restored. If some data points in the novel steganography contain hidden information and are tampered with by an attacker, the corresponding portions of the raw text and image can also be restored. However, if all key data points are tampered with by an attacker, the text and image cannot be recovered. In short, the novel steganography technique has local performance for resisting data tampering.
5.4. Evaluation Metrics for Hiding Text and Image
For evaluating the performance of the hiding text and image method, the four objective evaluation metrics are computed in
Table 5, which are MAE (mean absolute error), RMSE (root mean square error), SSIM (structural similarity index measure), and PSNR (peak signal to noise ratio). In addition, the results are compared with the chaotic dynamical system using DOMT (discrete orthogonal moment transforms)[5], WT (wavelet transforms)[12], LWT (lifting wavelet transform)[26,27], and IWT (integer wavelet transform)[9]. The MAE (mean absolute error), RMSE(root mean square error), SSIM (structural similarity index measure), and PSNR(peak signal to noise ratio) are defined by the following equations.
The MAE is the average absolute error between the data and
s*. The MAE is calculated by
where
n is the number of data points.
The RMSE is a metric that quantifies the average magnitude of discrepancies between corresponding data points in two signals. So, a lower RMSE indicates a greater similarity between data
s and
s*. The RMSE is computed by
where
n is the number of data points.
The SSIM is a metric for evaluating the similarity between two images. It is widely used in image quality assessment. The SSIM quantifies the perceived change in structural information and accounts for luminance, contrast, and structure. It can also be adapted to one-dimensional signals. It can evaluate the similarity between data
s and
s*. It can be calculated by the following formula.
and
are the means of the data
s and
s*, respectively.
and
are the variances of the data
s and
s*, respectively.
is the covariance between the data
s and
s*. The constants
C1 and
C2 are small to stabilize the division, especially when the means or variances are close to zero.
The PSNR is an objective measure of signal quality that quantifies distortion by computing the mean squared error between the data s and its reconstruction s*. A higher PSNR indicates a higher quality of the hidden signal. It is calculated by the following formula.
where MSE denotes the mean square error between the data
s and
s*, and
is the maximum value of the signal
s.
According to
Table 5, the PSNR of MWFTHA in this paper indicates a slightly higher quality of the hidden signal than that of DOMT, WT, and IWT. Moreover, the SSIM of MWFTHA implicates the slightly better structural similarity of the hidden signal. The PSNR and SSIM of MWFTRA in this paper are slightly smaller than those of MWFTHA. This is evident from the simulation results presented in
Section 3 and
Section 4. The PSNR and SSIM between the recovered and original text data are also computed, yielding Inf and 1, respectively. This demonstrates that the text has been fully and accurately recovered. This result is consistent with the simulation in
Section 4.
6. Conclusions
According to the above discussion, a novel steganographic method can hide both text and a color image within a one-dimensional signal. This technology involves the MWFTHA and MWFTRA. Based on the estimated mean and standard deviation of the running times for MWFTHA and MWFTRA, a color image and text can be hidden and recovered stably and quickly by MWFTHA and MWFTRA, respectively. Moreover, MWFTRA is a little faster than MWFTHA. Based on simulation results across three tampered-data cases, the novel steganography demonstrates some resistance to data tampering. According to the SSIM and PSNR metrics for MWFTHA, the hidden signal is slightly higher in quality than for DOMT, WT, and IWT. Indeed, multi-wavelets have superior properties compared with wavelets, such as balance, high-order vanishing moments, and high approximation order. Whether these beneficial properties can improve the quality of the hidden information is an interesting question worth discussing. In addition, this paper simultaneously hides two types of data (color images and text) within a single signal. Can this novel steganographic method hide multiple types of data in a single signal? What is the quality of the hidden information? Furthermore, can this novel steganographic method hide static web pages containing various types of data and restore them in full? Based on the multi-wavelet function, whether lifting the multi-wavelet transform and the integer multi-wavelet transform will improve the quality of data hiding better? In combination with the work presented in this paper, these problems may be solved in the near future.
References
- A review of steganography techniques[J].AIP Conference Proceedings, 2024, 3051(1).
- Ullah A , Haque M I , Hossain M M ,et al.A Novel LSB Steganography Technique for Enhancing Cloud Security[J]. Journal of Information Security, 2024, 15(3):23.
- Rehman H A , Bajwa U I , Raza R H ,et al.Leveraging coverless image steganography to hide secret information by generating anime characters using GAN[J].Expert Systems With Applications, 2024, 248. [CrossRef]
- Kang Y.A. Computerized Information Security Communication Method Based on Deep Learning Theory[J].Applied Mathematics and Nonlinear Sciences, 2024, 9(1). [CrossRef]
- Yamni M, Daoui A, El-Latif A A A. Efficient color image steganography based on a new adapted chaotic dynamical system with discrete orthogonal moment transforms[J]. Mathematics and Computers in Simulation, 2024, 225:1170-1198. [CrossRef]
- Wang T , Cheng H , Liu X ,et al.Lossless image steganography: Regard steganography as super-resolution[J]. Information Processing and Management, 2024, 61(4). [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets (Society for Industrial and Applied Mathematics, 1993).
- Zhou, X. Wavelet transform on regression trend curve and its application in financial data. Int. J. Wavelets Multiresolut. Inf. Process. 18(05), 2050040 (2020).
- Mandal P C , Mukherjee I , Chatterji B N . An integer wavelet transform-based high-performance secure steganography scheme QVD-LSB[J]. Multimedia Tools and Applications, 2024, 83(23):62651-62675.
- Prasanth Vaidya Sanivarapu; Kandala N. V. P. S. Rajesh; N. V. Rajasekhar Reddy; N. Chandra Sekhar Reddy; “Patient Data Hiding Into ECG Signal Using Watermarking in Transform Domain”, PHYSICAL AND ENGINEERING SCIENCES IN MEDICINE, 2020.
- Behrouz Bolourian Haghighi; Amir Hossein Taherinia; Reza Monsefi; “An Effective Semi-fragile Watermarking Method for Image Authentication Based on Lifting Wavelet Transform and Feed-Forward Neural Network”, COGNITIVE COMPUTATION, 2020.
- K. Upendra Raju; N. Amutha Prabha; “Dual Images in Reversible Data Hiding with Adaptive Color Space Variation Using Wavelet Transforms”, INTERNATIONAL JOURNAL OF INTELLIGENT UNMANNED SYSTEMS, 2021.
- Ahmed Khan; “2DOTS-multi-bit-encoding for Robust and Imperceptible Image Watermarking”, MULTIMEDIA TOOLS AND APPLICATIONS, 2021.
- Junpeng Jing; Xin Deng; Mai Xu; Jianyi Wang; Zhenyu Guan; “HiNet: Deep Image Hiding By Invertible Network”, ICCV, 2021.
- Ming Zhao; Shuo-Tsung Chen; Shu-Yi Tu; “Wavelet-Domain Information-Hiding Technology with High-Quality Audio Signals on MEMS Sensors”, SENSORS (BASEL, SWITZERLAND), 2022.
- Zhou Xiaohui; “Text Information Hiding and Recovery Via Wavelet Digital Watermarking Method”, SCIENTIFIC REPORTS, 2023.
- Keinert F Wavelets and multiwavelets[M].Chapman & Hall/CRC Press, 2004.
- Xia X G, Geronimo J S . Design of prefilters for discrete multiwavelet transforms[J].IEEE Trans Signal Process, 1996, 44(1):25-35. [CrossRef]
- Xiaohui, Z., Guiding, G. An algorithm of generating random number by wavelet denoising method and its application. Comput Stat 37, 107–124 (2022).
- Cui C K, Lian J A. A study on orthonormal multiwavelets[J] J.Appl, Numer, Math, 1996,20273-298.
- Khedr, O.S., Wahed, M.E., Al-Attar, AS.R. et al. The classification of the bladder cancer based on Vision Transformers (ViT). Sci Rep 13, 20639 (2023).
- Alwan, Iman M.G. (2014) Image Steganography by Using Multiwavelet Transform[J]. Baghdad Science Journal: Vol. 11: Iss. 2, Article 11. [CrossRef]
Figure 1.
decomposition of closed subspace {Vj}.
Figure 1.
decomposition of closed subspace {Vj}.
Figure 2.
diagrammatic sketch of MWFTHA.
Figure 2.
diagrammatic sketch of MWFTHA.
Figure 3.
Original image(OM).
Figure 3.
Original image(OM).
Figure 4.
Original signal s and synthetic signal s*.
Figure 4.
Original signal s and synthetic signal s*.
Figure 5.
diagrammatic sketch of MWFTRA.
Figure 5.
diagrammatic sketch of MWFTRA.
Figure 6.
Restored results.
Figure 6.
Restored results.
Figure 7.
system architecture figure for the MWFTHA and MWFTRA.
Figure 7.
system architecture figure for the MWFTHA and MWFTRA.
Figure 8.
Distribution of running time for the MWFTHA (Fixed an image(400×400×3)).
Figure 8.
Distribution of running time for the MWFTHA (Fixed an image(400×400×3)).
Figure 9.
Distribution of running time for the MWFTHA (Fixed a text(328)).
Figure 9.
Distribution of running time for the MWFTHA (Fixed a text(328)).
Figure 10.
Distribution of running time for the MWFTRA (Fixed an image(400×400×3)).
Figure 10.
Distribution of running time for the MWFTRA (Fixed an image(400×400×3)).
Figure 11.
Distribution of running time for the MWFTRA (Fixed a text(328)).
Figure 11.
Distribution of running time for the MWFTRA (Fixed a text(328)).
Figure 11.
Restored results in the case of unknown or mistaken embedding space.
Figure 11.
Restored results in the case of unknown or mistaken embedding space.
Figure 12.
Restored results in the case of unknown or mistaken embedding position.
Figure 12.
Restored results in the case of unknown or mistaken embedding position.
Figure 13.
Restored results in the case of unknown or mistaken embedding mode.
Figure 13.
Restored results in the case of unknown or mistaken embedding mode.
Table 1.
Estimated mean and standard deviation(S.D.) of running time for the MWFTHA (Fixed an image(400×400×3)).
Table 1.
Estimated mean and standard deviation(S.D.) of running time for the MWFTHA (Fixed an image(400×400×3)).
| Length |
328 |
574 |
1254 |
2281 |
4025 |
| mean |
4.4310 |
4.4895 |
4.4902 |
4.5114 |
5.0072 |
| S.D. |
0.0279 |
0.0563 |
0.0561 |
0.1508 |
0.0792 |
Table 2.
Estimated mean and variance of running time for the MWFTHA (Fixed a text(328)).
Table 2.
Estimated mean and variance of running time for the MWFTHA (Fixed a text(328)).
| Size |
100x100×3 |
200x200×3 |
400x400×3 |
600x600×3 |
1000x1000×3 |
| mean |
1.6879 |
5.3005 |
23.7041 |
43.3394 |
142.4761 |
| S.D. |
0.1691 |
0.0505 |
2.8806 |
3.4524 |
21.0665 |
Table 3.
Estimated mean and standard deviation(S.D.) of running time for the MWFTRA (Fixed an image(400×400×3)).
Table 3.
Estimated mean and standard deviation(S.D.) of running time for the MWFTRA (Fixed an image(400×400×3)).
| Length |
328 |
574 |
1254 |
4025 |
| mean |
0.1568 |
0.1579 |
0.1559 |
0.1577 |
| S.D. |
0.0062 |
0.0066 |
0.0067 |
0.0075 |
Table 4.
Estimated mean and standard deviation(S.D.) of running time for the MWFTRA (Fixed a text(328)).
Table 4.
Estimated mean and standard deviation(S.D.) of running time for the MWFTRA (Fixed a text(328)).
| Size |
100x100×3 |
200x200×3 |
400x400×3 |
600x600×3 |
1000x1000×3 |
| mean |
0.7375 |
2.2604 |
8.6050 |
19.7920 |
56.1528 |
| S.D. |
0.2318 |
0.1736 |
0.4419 |
1.2965 |
3.6168 |
Table 5.
Comparison of four objective evaluation metrics.
Table 5.
Comparison of four objective evaluation metrics.
| Method |
MAE |
RMSE |
SSIM |
PSNR |
| DOMT[5] |
133.7350 |
169.69 |
0.9435 |
39.8363 |
| WT[12] |
141.3224 |
179.5542 |
0.9169 |
37.3686 |
| IWT[9] |
138.8251 |
174.11 |
0.9241 |
39.5859 |
| MWFTHA |
132.6976 |
168.9371 |
0.9614 |
41.4560 |
| MWFTRA |
134.5143(0) |
169.5871(0) |
0.9403(1) |
40.2015(Inf) |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).