Submitted:
05 January 2026
Posted:
07 January 2026
You are already at the latest version
Abstract
Multivariable optimization is an essential mathematical exercise in daily engineering design and troubleshooting. To this end, simplex multivariable optimization method is a powerful optimization approach that has served many engineering disciplines well over the years. One such simplex algorithm is the Nelder Mead algorithm. But, the reflection step of the Nelder Mead algorithm may increase the number of iterations needed to arrive at the optimal point, as it reflects the starting point to the opposite side of the function. This work proposes an automated two-stage adjustable ratio simplex optimization method that first search within and around the optimization surface for a good starting point, followed by a narrow and more refined search for the optimal point. For both stages of the new simplex algorithm, only contraction and extension steps are used, and this helps to remove possible oscillatory effects common to other simplex algorithms as the iterations progress. Demonstrative use of the new simplex algorithm on optimizing the coefficients of a quadratic function reveals good accuracy and speed as compared to the Nelder Mead algorithm which uses significantly more iterations. Future testing should be conducted with other optimization functions as well as objective functions. Interested readers are invited to explore and expand on the work reported herein.
Keywords:
Nelder Mead algorithm
; simplex optimization
; reflection step
; number of iterations
; contraction and extension steps
Introduction
Simplex is a powerful multivariable optimization method in use in many engineering disciplines to find optimal values for a variety of functions and problems. While there are many variants and implementations of simplex algorithms, the most common remains the Nelder Mead algorithm. [1]
In the Nelder Mead algorithm, the reflection step and shrinkage steps are prominent vertices movement steps to explore the other side of the optimization surface and to shrink the simplex to a good point, respectively.[2,3] This preprint describes an attempt to use an alternative approach to explore the optimization surface from an initial guess.
Specifically, my two-stage adjustable ratio simplex algorithm primarily uses an initial search for a good starting point for the second stage narrow (refined) search for the optimal point. In the first stage, a series of contraction of different percentages, and a series of extension of different multiplier are used to search the optimization surface for a better starting point than the initial guess. This step does suffer from high computational expense, especially if the objective function is to minimize the mean of sum of error.
Following the first stage, an iterative second stage uses a series of contraction and extension steps to further refine the initial good point selected by the first stage to finally narrow down to the optimal point. At the end of each iteration, a simplex is defined around the good point, and function evaluations are made to ascertain if the good point is still some distance away from the optimal point. Finally, a simplex reordering exercise rearranges the vertices such that the point with the smallest function evaluation is made the good point for the start of the next iteration of the narrow search.
Computational Implementation of the Algorithm
The new simplex optimization is coded in Python using the Spyder 6 editor with Python 3.12.11 as computational engine. Laptop used for this research is a Lenovo Ideapad Slim 3 Windows 11 Home (64 bit) with AMD Ryzen 5 (7520U) processor running at 2.80 GHz, with AMD Radeon graphics (2 GB video RAM), 16 GB of RAM, and 512 GB of SSD storage.
Results and Discussion of Demonstrative Use of Algorithm
The two stage adjustable ratio simplex algorithm was tasked to optimize the coefficients of a quadratic function of 3x2 + 6x + 10 with h as the optimization parameter of x2 and g as optimization parameter of x. The comparative algorithm for this exercise is Nelder Nead simplex algorithm from the Scipy optimize library of Python.
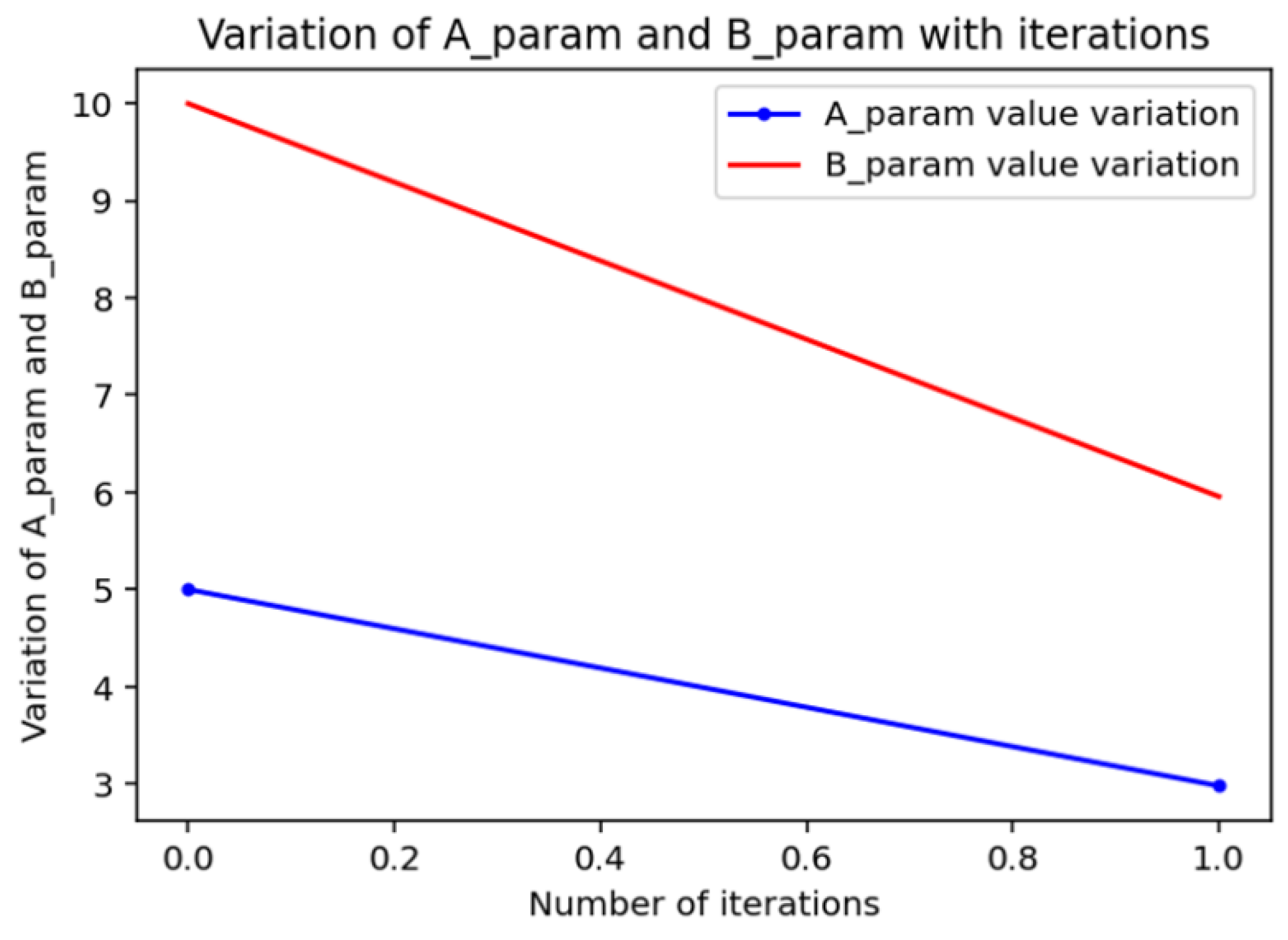
Figure 1.
Variation of A parameter (h) and B parameter (g) during the narrow search phase of the two stage adjustable ratio simplex algorithm developed in this work.
Figure 1.
Variation of A parameter (h) and B parameter (g) during the narrow search phase of the two stage adjustable ratio simplex algorithm developed in this work.
Demonstrative use of the two stage adjustable ratio simplex algorithm with initial guess of h = 5 and g = 10, reveals a 2 iteration narrow search after a 10 iteration search for a good starting point. Final optimal value obtained is h = 2.97, and g = 5.96, which is comparable to the h = 2.99, and g = 6.00 values obtained by the Nelder Mead algorithm after 64 iterations.
Conclusion
This work attempts to develop a two-stage adjustable ratio simplex algorithm different from the Nelder Mead algorithm to help reduce the number of iterations incurred due to the reflection steps in the Nelder Mead algorithm. The new simplex algorithm works by first using a series of contraction and extension steps to find a good starting point for a second stage more refined and narrower search for the optimal point. Such an approach allows the simplex algorithm to at least search a significant portion of the optimization surface before settling on a good starting point for a narrow search for the optimal point. Demonstrative use of the two stage adjustable ratio simplex method on optimizing the coefficients of a quadratic function demonstrates good performance in comparison to the robust Nelder Mead algorithm. But, more test cases and optimization functions are needed to further examine the functional properties of the new simplex algorithm. Interested readers are invited to explore and expand on the work reported herein.
Funding
No funding was used in this work.
Conflicts of interest
The author declares no conflicts of interest.
References
- Galántai. The Nelder–Mead Simplex Algorithm Is Sixty Years Old: New Convergence Results and Open Questions. Algorithms 2024, 17, 523. [Google Scholar] [CrossRef]
- Gao, F.; Han, L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 2012, 51, 259–277. [Google Scholar] [CrossRef]
- Wang, P. C.; Shoup, T. E. Parameter sensitivity study of the Nelder–Mead Simplex Method. Adv. Eng. Softw. 2011, 42, 529–533. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
