Cybersecurity Under Change: Proof-Carrying Assurance via Frozen Records and a One-Residual, One-Clock Certificate

1. Introduction

Modern digital systems evolve continuously: models are retrained, retrieval indices and schemas change, policy templates and guardrails are revised, scanners and severity rubrics are replaced, tool permissions are widened or narrowed, and monitoring pipelines are re-instrumented [1,2]. A familiar failure mode follows: even when a control or mitigation is unchanged, the meaning of the assurance claim can drift because the measurement geometry drifts. In practice this happens whenever the evaluation pipeline changes—a new classifier, a new log schema, a new notion of what counts as a neutral reformulation of the same behaviour, or a new definition of the score itself [1]. Teams and regulators then face a moving-goalpost pathology: “we improved” is asserted in a new metric that is not comparable to the old one [3,4].

This is not merely organisational; it is a typed mathematical fact. In stability theory, an exponential decay statement is a statement about a specific generator acting on a specific normed space [3,4]. If the norm changes without explicit equivalence constants, statements like “uniform across discretisations” or “uniform across parameters” cease to be invariant [3,4]. The same logic governs assurance under upgrades: if the ruler, neutral conventions, or observation map drift, then the semantics of “risk is decreasing” drifts as well [3,4].

We introduce a proof-carrying certificate layer whose purpose is to prevent that drift. The core move is to declare and freeze a single operational record—the frozen record—so that “uniform across upgrades” has a precise, mechanically checkable meaning [1,2]. The frozen record fixes: (i) a system boundary, (ii) a defect typing space, (iii) a single risk ruler (a frozen SPD norm), (iv) a neutral convention, (v) an audit window, (vi) a refinement ladder, and (vii) an observation map. Once these are declared, all guarantees are stated and checked in that geometry (or transported with explicit norm-transfer constants) [2,3,4].

1.1. Why Cybersecurity Is Human-Centred by Construction

We use the term human-centred (rather than merely socio-technical) because the relevant security properties are defined, enforced, and certified inside a control loop whose decision and verification operators are ultimately human-facing [5,6]. A security property in practice is not a free-floating predicate of a codebase or protocol; it is a property of a deployed system as operated: policy authors declare constraints and acceptable risk; engineers implement mechanisms; operators triage and remediate; auditors demand evidence; and governance bodies revise requirements and priorities [5,6]. Thus the semantics of “secure” are fixed by human commitments, and the dynamics of “becoming secure” are constrained by human capacity [6].

Formally, the deployed system closes a feedback loop

$$\mathrm{policy}/\mathrm{targets}⟶\mathrm{mechanisms}⟶\mathrm{operations}⟶\mathrm{evidence}/\mathrm{audit}⟶\mathrm{policy}/\mathrm{targets},$$

where each arrow is mediated by human practices and organisational processes [5,6]. Workflow structure, staffing constraints, alert fatigue, incentives, and governance cadence bound what controls can be deployed, how quickly deviations can be corrected, and what evidence can be produced and trusted [6]. These constraints are not externalities; they determine the feasible set of implementations and therefore determine which formal guarantees remain valid after deployment [5].

Even when a technical guarantee exists in principle (e.g. a verified component, a cryptographic reduction, a formally proved invariant), it becomes a security guarantee in the world only after it is translated into procedures, interfaces, and audit evidence that humans can operate and maintain under continual change [5,6]. This translation introduces additional degrees of freedom (tooling updates, logging schemas, policy templates, exception processes) that can silently alter the meaning of a claimed guarantee unless the measurement and verification geometry are fixed and made checkable [1,3,4]. In this sense, the “human-centred” qualifier is a typing requirement on the guarantee: the claim must be stated in a form that survives the human-operated update loop [6].

Credential hygiene provides a concrete illustration. The well-documented tendency to choose weak or reused passwords when policies are burdensome, together with exception handling and workarounds under time pressure, are not edge cases but primary drivers of realised security outcomes [7,8,9]. Any assurance architecture that treats these behaviours as exogenous anomalies will systematically mis-estimate risk and overstate robustness [6,9]. A human-centred formulation instead treats such effects as first-class: they appear as explicit forcing/injection budgets and as constraints on achievable improvement margins, making feasibility and auditability part of the guarantee rather than after-the-fact explanations [6,8].

Accordingly, an assurance claim is meaningful only if it is (i) deployable (compatible with constraints on time and attention), (ii) operable (actionable through a small set of decision variables), (iii) auditable (supported by evidence that can be checked), and (iv) maintainable under change (stable across tool upgrades, policy revisions, and environment drift) [1,2,5,6]. This paper treats these requirements as a typing discipline: the guarantee must be expressed in a frozen measurement geometry (ruler, neutrals, observation map, and ladder), with explicit budgets for what is not modelled, so that “improvement” remains comparable across versions [3,4].

At the same time, good human-centred security does not require all humans to be cybersecurity-centred. The design goal is that most people can act normally without continuous security vigilance, while a small set of roles (operators, engineers, auditors, leaders) interact with security through stable, decision-ready interfaces [6,9]. In DSFL terms, this means concentrating security cognition into auditable primitives (one residual, one clock, explicit budgets and slack), rather than distributing it across the entire user population [6,8].

The certificate layer is introduced precisely as a human-facing interface for guarantees: it reduces drifting dashboards to a small set of typed, auditable objects (rates, budgets, slack) that can be checked and governed [1,2].

1.2. Problem Statement

We study a verification problem common to modern human-centered security systems, including AI-enabled ones [5,6].

Given a deployed system that evolves in time and across refinement scales (tool versions, policy revisions, monitoring pipelines, model and retrieval updates), can we produce a proof-carrying, refinement-invariant safety envelope that is (i) meaningful under upgrades, (ii) compositional across coupled risk channels, and (iii) auditable from a finite bundle?

Our target output is a certificate that can be shipped with a release and checked by a third party, in the spirit of proof-carrying and runtime-verifiable claims [1,2]. The certificate must be explicit about its typing: what is being measured (defects), in what geometry (ruler), modulo what equivalences (neutrals), over what interval (audit window), and along what upgrade path (ladder) [3,4].

1.3. Scope and Non-Claims

Scope

We develop a proof-carrying DSFL certificate calculus for assurance under change in human-centered security systems, with a primary focus on tool-using LLM agents. The calculus fixes a frozen measurement geometry (ruler, neutrals, observation map, audit window) and treats upgrades as a refinement ladder, so that “uniform across versions” has a checkable meaning [1,2,3,4]. As an auxiliary avatar-chain validation domain, we use quantum-computing refinement indices (code distance, concatenation level, circuit depth, decoder granularity) to stress-test the ladder semantics and the bundle-and-checker workflow in a controlled setting [10,11,12].

Non-Claims

We do not propose a new cryptographic primitive, a new intrusion-detection algorithm, or a new vulnerability scoring standard [5]. We do not claim to solve alignment or to give a complete semantics of natural language. We do not claim that quantum computing and cybersecurity share physical content; the connection is methodological (typed stability under refinement), not ontological [3,4,10]. Where a brick is not proved in-text (e.g. a decay/ringdown gap in a declared ruler, or a domain-specific scheme-control classification), we mark it as an explicit import and state the norm-typing requirements needed to use it [3,4,13,14,15].

1.4. Approach: Frozen Records, One-Clock Reduction, and Vertical Coherence

The framework is a verification calculus with two orthogonal axes: time (how risk evolves on an audit window) and scale (how guarantees survive upgrades and refinement) [3,4]. The governing rule is that every claim is interpreted in a frozen record (ruler, neutrals, observation map, ladder), so that “uniform across versions” is a checkable statement rather than a narrative [3,4].

Time Axis (One-Clock Safety Envelope)

We model assurance as a vector of nonnegative ledgers capturing heterogeneous contributors to risk, including human/organisational channels (workload, exception pressure) and technical channels (misconfiguration, identity exposure, data-handling violations, unsafe tool use, prompt-injection success) [5,6]. Channels interact through nonnegative injections, yielding a cooperative comparison system of Metzler type [16,17]. Under a Hurwitz (small-gain) margin condition, positive-systems scalarisation collapses the ledger vector to a single scalar residual $R_{\mathrm{tot}}$ obeying a forced contraction law on the audit window:

$${\dot{R}}_{\mathrm{tot}}\left(t\right)\le -2\alpha R_{\mathrm{tot}}\left(t\right)+{\tau }_{\mathrm{tot}}\left(t\right),{\tau }_{\mathrm{tot}}\in L^1\left([t_0,t_1]\right),{\tau }_{\mathrm{tot}}\ge 0.$$

(4)

The constants $(\alpha ,\parallel {\tau }_{\mathrm{tot}}{\parallel }_{L^1\left([t_0,t_1]\right)})$ are the certificate’s time-domain content: a single improvement margin and a single disturbance footprint, stated in the frozen ruler. This is Lyapunov/semigroup stability expressed in proof-carrying form [3,4,16,18,19].

Scale Axis (Refinement Ladders and Step 6)

Guarantees must survive upgrades: tool versions, policy templates, monitoring pipelines, model weights, retrieval indices, and schema changes [1]. We treat upgrades as movement along a refinement ladder with defect representatives typed in a frozen target space

$${\mathcal{X}}_W:=L^{\infty }([t_0,t_1];{\mathcal{R}}_p).$$

(5)

Vertical coherence is enforced by a Step 6 condition: refinement drift must have finite total footprint in the frozen norm (equivalently, summable increments on a discrete ladder, or an $L^1$ scale-majorant in continuous scale) [20]. This yields a projective-limit semantics: upgrade effects do not accumulate without bound, so the defect representative converges and the meaning of the certificate cannot drift arbitrarily across versions [20].

Proof-Carrying Posture (Bundle-and-Checker Semantics)

A release ships a finite bundle: the frozen record, the constants/budgets instantiating the time- and scale-domain inequalities, and a minimal checker that verifies the inequalities in the declared geometry. This is the assurance analogue of proof-carrying code and runtime verification: ship evidence, verify cheaply [1,2].

1.5. Two-Domain Positioning and Avatar-Chain Method

The paper is operationally anchored in human-centred cybersecurity and tool-using LLM agents, where the measurement-geometry drift problem is acute and governance demands auditable non-regression under change [6]. At the same time, we use quantum computing as a deliberately controlled “avatar chain”: a domain with explicit refinement indices (code distance, concatenation level, circuit depth, decoder granularity) where frozen rulers, ladder uniformity, and PASS/FAIL certificate checking can be stress-tested numerically [10,11,12]. References to GR/QFT-in-curved-spacetime enter only as motivating instances of the same typed pathology (norm/gauge/scheme drift) and the same cure (frozen records + ladder coherence), not as a claim of shared physical content [13,14,15,21].

1.6. Main Contributions

C1 

Frozen-record semantics for assurance under change. We formalise the typing data required to make cross-version claims invariant: a frozen defect room, a frozen SPD ruler, a neutral convention, an audit window, a refinement ladder, and an observation map. This prevents metric drift from being mistaken for safety improvement [3,4].

C2 

A one-clock certificate for coupled risk channels. Under cooperative coupling and a Hurwitz margin condition, we prove a positive weighting reduces multiple ledgers to a single scalar residual obeying (4) with explicit budgets. The resulting envelope is tail-robust and mechanically checkable [16,17,18,19].

C3 

A refinement-ladder coherence theorem (Step 6). We show that a summable refinement drift condition (or an $L^1$ scale-generator bound) implies vertical coherence in the frozen target norm: upgrade effects have finite total footprint, yielding a well-defined limiting representative and an honest meaning for “uniform across upgrades” [20].

C4 

A Master Certificate with auditable obligations. We package the requirements as auditable obligations (scheme/dictionary control, uniform one-clock margin, vertical coherence, and dictionary transport). Passing these checks implies a refinement-invariant safety envelope on the declared audit window [1,2].

1.7. What This Paper Does Not Claim

This paper does not claim to solve alignment, to provide a complete semantics of natural language, or to reduce all safety questions to a single scalar in an absolute sense. All claims are relative to the declared frozen record [3,4]. The point of the framework is to make that dependence explicit: when stakeholders disagree, the disagreement must appear as a disagreement about the frozen record (ruler, neutrals, observation map, ladder) or about which obligation fails—not as an unresolvable narrative dispute [1,2].

1.8. Roadmap

The paper is organised to move from motivation and typing discipline to certificate-level theorems, and finally to operational and governance implications.

Section 3 fixes the problem setting and design principles. It formalises human-centred cybersecurity as a dynamical verification problem, introduces residuals as distances to declared constraints, and explains why guarantees must be stated in a frozen measurement geometry to avoid moving-goalpost assurances [3,4,5,6].

Section 4 develops the certificate-layer mathematics. It defines defect rooms, frozen rulers, neutral conventions, and nonnegative ledger vectors, and establishes the comparison inequalities used throughout the paper [3,4].

Section 5 proves the core technical result: the one-residual, one-clock theorem. Starting from coupled nonnegative ledgers with cooperative (Metzler) structure, it shows how a single scalar residual with a certified contraction rate and explicit disturbance budget can be constructed, yielding tail-robust envelopes that are decision-ready and auditable [16,17,18,19].

Section 6 instantiates the framework for governance and compliance. Policy–practice mismatch is formalised as a typed imbalance operator, and compliance assurance is reframed as a provable contraction margin rather than a snapshot checklist [5].

Section 7 introduces empirical coupling budgets. It explains how cross-channel interactions enter the certificate as explicit constants, and how conservative empirical bounds populate the Metzler comparison model used by the one-clock reduction [16,17].

Section 8 analyses feasibility under human and organisational constraints. It proves improvement-floor results that separate sustainable recovery rates from unavoidable disturbance footprints, making explicit when improvement targets are infeasible given staffing, workflow, and incident intensity [6,8,9].

Section 9 addresses assurance under upgrades. It formalises refinement ladders, contractive comparators, and the Step–6 summability condition, proving that summable refinement drift yields version-stable, projective-limit semantics in a frozen measurement geometry [20].

Section 10 specifies the proof-carrying audit architecture. It defines the certificate bundle, checker interface, PASS/FAIL semantics with slack, and the numerical diagnostics required to instantiate constants conservatively and reproducibly [1,2].

Section 11 demonstrates the workflow on a large block-structured avatar. The goal is not empirical validation of a threat model, but illustration of how frozen records, coupling budgets, gap estimates, and summability checks produce an auditable certificate decision [3,4].

Section 12 discusses implications for human-centred cybersecurity practice. It shows how the certificate layer yields decision-ready summaries, governance-grade non-regression guarantees, and a deployment model for adaptive AI and tool-using agents [1,2,6].

Section 13 records limitations and open problems. These include ruler and residual selection, observability constraints, empirical calibration challenges, and opportunities to tighten scalarisation bounds without losing auditability [3,4].

Section 14 summarises the contribution and outlines a concrete research and deployment agenda based on proof-carrying, frozen-record assurance under continual change [1,2].

2. Positioning and State of the Art

This paper sits at an intersection where several technically mature literatures still fail to compose into a single, upgrade-stable assurance object [1,2,3,4]. In practice, organisations operate security guarantees over long horizons while the measurement pipeline evolves: policies change, tools are replaced, monitoring is re-instrumented, models are retrained, and schemas drift [1,5,6]. The consequence is a moving-goalpost failure mode: improvements can be asserted in a new metric that is not typed back to the old one [3,4]. Our positioning is that this failure mode is not merely managerial; it is structural. A stability claim is typed by a specific evolution operator in a specific norm, and semantics drift is a loss of typing [3,4]. DSFL is offered as a compositional certificate layer whose purpose is to preserve meaning under change by freezing the measurement geometry and routing residual uncertainty into explicit budgets with PASS/FAIL slack [1,2,16,17].

2.1. The Position: Cybersecurity Is Human-Centered, but Guarantees Must Be Typed

Cybersecurity outcomes are not solely technical properties of software stacks. They are embedded in human behaviour, work practices, organisational culture, incentives, and (inter)national governance [5,6]. In operational terms, this means that security claims are determined by:

• design (interfaces, defaults, and affordances that shape operator and user behaviour),
• workflow integration (how precautions compete with productivity and latency constraints),
• governance (policy revision, compliance instruments, accountability, and audit evidence),
• adversarial and geopolitical context (crime, conflict, regulation, and standards).

A human-centred approach therefore requires guarantees that remain legible to stakeholders and resilient to organisational change [5,6]. The DSFL stance is that this demand can be made mathematically precise: a guarantee is only comparable across time and versions if it is stated in a frozen measurement geometry (a ruler, a neutral convention, an observation map, and a declared upgrade path) or transported with explicit equivalence constants [3,4].

2.2. State of the Art: Four Literatures That Do not yet Yield One upgrade-Stable Assurance Object

(i) Stability and Semigroups in Fixed norms (Typed Meaning)

Classical stability theory makes explicit that decay and contractivity are statements about a specific generator acting on a specific normed space [3,4]. This fixed-norm discipline is routine in PDE stability and control, but assurance practice often violates it by changing metrics as tools and policies evolve [3,4]. DSFL imports the discipline as a governing rule: one frozen ruler (no moving goalposts), and cross-version comparisons must either be nonexpansive in that ruler or carry explicit norm-transfer constants [3,4].

(ii) Positive Systems, Small-Gain, and Compositional Closure (Coupled Channels)

Multi-channel risk dynamics are naturally modelled as cooperative systems: one channel injects risk into another (workload into misconfiguration, identity drift into policy violations, tool use into exposure), and these injections do not cancel. Positive-systems theory provides sharp stability criteria (Metzler–Hurwitz / small-gain) and a scalarisation mechanism that collapses a nonnegative ledger vector to a single rate-and-budget envelope [16,17,18,19]. DSFL adopts these tools but changes the unit of output: coupling coefficients and Hurwitz margin become auditable certificate constants rather than modelling conveniences [16,17].

(iii) Proof-Carrying and Runtime-Verifiable Assurance (Ship Evidence, Verify Cheaply)

Proof-carrying code formalises a producer/consumer pattern: ship a compact artifact that a small checker can validate [2]. Runtime verification similarly emphasises monitorable properties and checkable traces [1]. Contemporary security assurance frequently lacks an analogous artifact for assurance under change: audits often remain narrative, or rely on dashboards whose semantics drift [1,5]. DSFL positions the certificate bundle (frozen record + constants + witnesses + trace commitments) as the corresponding assurance artifact: a third party can re-check the inequalities in the declared geometry and obtain PASS/FAIL with slack [1,2].

(iv) Human-Centred Cybersecurity and Usable Security (Why Drift and Overload Are First-Order)

Usable security and human factors research has shown that security mechanisms fail when they impose cognitive overload, misaligned incentives, and unusable workflows, and that “noncompliance” is often an adaptive response to constraints rather than irrational error [5,6,8,9]. A recurring operational symptom is metric overload with semantic drift: practitioners cannot act on dozens of signals whose meaning changes as tools and policies evolve [6]. DSFL targets this failure mode by collapsing heterogeneous signals into one scalar residual with an explicit contraction margin, an explicit disturbance budget, and explicit coupling constants, so that decision-making can be supported by a small set of stable, auditable objects [16,17].

2.3. Why a Compositional Certificate Is Still Missing

Across these literatures, what is still missing is a single composable certificate that simultaneously:

(i)

fixes the meaning of “small defect” under upgrades by freezing the measurement geometry (or proving explicit norm-transfer constants) [3,4];

(ii)

closes multiple interacting channels to one decision-ready “clock” with explicit coupling budgets and Hurwitz slack [16,17,18,19];

(iii)

separates global security state from what bounded observers can actually audit via an explicit observation map [1];

(iv)

yields a proof-carrying artifact (bundle + checker) that supports third-party verification and non-regression narratives as PASS/FAIL inequalities rather than interpretive reports [1,2].

The DSFL contribution is precisely this compositional layer: a frozen-record discipline plus one-clock routing and upgrade-coherence (Step–6) budgets, producing version-stable assurance envelopes with explicit slack [3,4,16,17,20].

2.4. Implications: Three Interfaces That Make Guarantees Operational

To connect the mathematics to practice, we organise the implications around three linked interfaces that are legible to operators, governance bodies, and engineers [5,6].

2.4.1. Decision Interface: Cognitive Economy Under Metric Drift

Problem

Operators face metric overload and semantic drift: scanner scores, alert counts, compliance percentages, and ML risk scores change meaning as tooling and policies evolve [5,6].

DSFL Response

We replace drifting indicators by one scalar residual in a frozen ruler, together with decision-ready constants: a certified improvement margin (one clock), an $L^1$ disturbance footprint, and explicit coupling constants that explain why local improvements may fail to yield global improvement. The underpinning is the fixed-norm discipline of stability theory [3,4] combined with positive-systems scalarisation for coupled nonnegative ledgers [16,17].

2.4.2. Governance Interface: Continuous Assurance as a Contract

Problem

Traditional compliance is a point-in-time snapshot and does not control drift between audits [5].

DSFL Response

We model compliance as a typed policy–practice imbalance residual measured in a frozen geometry and certify a contraction margin with an explicit budget on each declared audit window. Auditors verify inequalities over an interval and report PASS/FAIL with slack, rather than relying on checklists whose semantics drift [1,2,3,4].

2.4.3. Engineering Interface: Non-Regression for Adaptive AI and Evolving Systems

Problem

Adaptive systems change: new prompts, tools, updated policies, model updates, retrieval/index snapshots, and telemetry schemas [1].

DSFL Response

We require proof-carrying semantics: upgrades are admissible only if their induced drift is controlled by explicit, summable/integrable budgets (vertical coherence), so that assurance meaning remains stable across versions and can be re-checked by a minimal checker, in the spirit of proof-carrying artifacts [1,2,20].

3. Problem Setting and Design Principles

This section fixes the typed problem setting in which all later theorems live. The central claim is that human-centred cybersecurity is necessarily a dynamical, human-centered verification problem: a guarantee must remain meaningful under (i) disturbances, (ii) interventions, and (iii) upgrades that change the measurement pipeline [5,6]. We therefore set up (a) a controlled-process boundary, (b) a residual-based notion of equilibrium, and (c) a frozen measurement geometry that prevents “moving-goalpost” assurances. The mathematics is standard Lyapunov/semigroup stability in fixed norms [3,4,22] combined with a proof-carrying interface notion [1,2].

3.1. Human-Centred Cybersecurity as a Dynamical System

Cybersecurity is inherently time-dependent and human-centered: human workflows, staffing constraints, alert fatigue, organisational incentives, and tool affordances interact with technical controls [5,6,8,9]. A mathematically honest assurance claim must therefore be a statement about the evolution of a system over a window rather than a static checklist item [5]. This motivates Lyapunov-style reasoning: one declares a target notion of “acceptable security” (equilibrium / compliance / safe operation), defines a scalar residual measuring distance to that target, and proves that the residual contracts (up to explicit disturbance budgets). This is the stability logic of dissipative dynamical systems and semigroup theory [3,4,18,22].

3.1.1. System Boundary and State

We model a deployed security-relevant human-centered system as a state trajectory

$$x:[t_0,t_1]=[t_0,t_1]\to X,$$

(6)

where X is a state space that includes both technical configuration and human/organisational state. The purpose of introducing X is not to claim that all human variables are directly observable, but to make the system boundary explicit: security outcomes depend on internal state, external disturbances, and interventions, and must therefore be stated as properties of a dynamical evolution [5,6].

Setup 3.1

(human-centered security system as a controlled process). Fix a finite audit window $[t_0,t_1]=[t_0,t_1]$. Let X be a (typically high-dimensional) state space, and let $x\left(t\right)\in X$ denote the system state. We allow:

(i)

interventions$u\left(t\right)$ (training, patching, policy changes, access reviews, monitoring changes);

(ii)

disturbances$d\left(t\right)$ (attacks, outages, user error, vendor changes, workload spikes);

(iii)

observations$o\left(t\right)$ produced by an observation map $\mathrm{obs}$ (logs, telemetry, tickets, scans), declared precisely in subsec:frozen-geometry.

Why this Abstraction Is Necessary

A human-centred model must explicitly admit that (i) actions are mediated by procedures and tools, (ii) disturbances are unavoidable, and (iii) the observables are not the full state but a logged readout [1,5,6]. This is exactly the setting in which Lyapunov and comparison principles give robust guarantees: one proves inequalities for nonnegative quantities extracted from the trajectory, rather than solving the full dynamics [3,4,18,19].

3.1.2. Equilibria as Constraints and Residuals as Distances

The central object is a nonnegative scalar residual $R\left(t\right)$ that measures distance from a declared target set $E\subseteq X$ (e.g. compliance set, safe configuration set, or “acceptable risk” set) [18,19].

Definition 3.1 

(Security equilibrium set and residual). Let $E\subseteq X$ be the declaredequilibrium(acceptable security) set. Asecurity residualis a measurable function $R:X\to {\mathbb{R}}_{\ge 0}$ such that $R\left(x\right)=0$ for all $x\in E$ and $R\left(x\right)>0$ for $x\notin E$. Along a trajectory $x\left(t\right)$ we write $R\left(t\right):=R\left(x\right(t\left)\right)$.

Remark 3.1 

(Residuals need not be literal distances). In practice, R is often derived from a defect map $\mathsf{\Phi }:X\to {\mathcal{R}}_p$ and a ruler W (see subsec:residuals-vs-metrics), so $R\left(x\right)={\parallel \mathsf{\Phi }\left(x\right)\parallel }_W^2$. This includes squared-distance-to-constraint as a special case (when Φ is a constraint operator and $E=ker\mathsf{\Phi }$) [18].

To connect residuals to computation and audit, it is useful to give a canonical construction.

Setup 3.2

(Constraint residual via Hilbert projection). Let $(\mathcal{H},\langle ·,·\rangle )$ be a Hilbert space, let $E\subseteq \mathcal{H}$ be nonempty, closed, and convex, and define

$$R\left(x\right):=\mathrm{dist}{(x,E)}^2:=\underset{y\in E}{inf}{\parallel x-y\parallel }^2.$$

(7)

Proposition 3.1 

(Projection characterisation of squared-distance residual). Under Setup 3.2, for each $x\in \mathcal{H}$ there exists a unique projection ${\mathsf{\Pi }}_E\left(x\right)\in E$ such that

$$\parallel x-{\mathsf{\Pi }}_E\left(x\right)\parallel =\mathrm{dist}(x,E),$$

and $R\left(x\right)=\parallel x-{\mathsf{\Pi }}_E{\left(x\right)\parallel }^2$. Moreover, ${\mathsf{\Pi }}_E$ is nonexpansive: $\parallel {\mathsf{\Pi }}_E\left(x\right)-{\mathsf{\Pi }}_E\left(x^{\prime }\right)\parallel \le \parallel x-x^{\prime }\parallel$ for all $x,x^{\prime }\in \mathcal{H}$.

Proof. 

This is the classical projection theorem in Hilbert spaces (existence/uniqueness for closed convex sets and nonexpansivity of metric projections). □

Human-Centred Reading

This is the cleanest semantics for “distance to compliance”: E is the set of compliant states in the declared semantics; ${\mathsf{\Pi }}_E\left(x\right)$ is the nearest compliant configuration; and $R\left(x\right)$ is the squared correction distance. The nonexpansivity of ${\mathsf{\Pi }}_E$ is the formal template behind “admissible remediation steps do not worsen compliance” (see Section 3.3.3) [18,19].

3.1.3. Lyapunov Claims as Certificate Interfaces

We will aim to prove an inhomogeneous Lyapunov inequality on $[t_0,t_1]$:

$$\dot{R}\left(t\right)\le -2\alpha R\left(t\right)+\tau \left(t\right),\tau \in L^1\left([t_0,t_1]\right),\tau \ge 0,$$

(8)

where $\alpha >0$ is a certified improvement margin and $\tau$ is an explicit disturbance budget [3,4,18,19].

Definition 3.2 

(Certified one-clock margin). The constant $\alpha >0$ in (8) is called the certified one-clock margin.

Remark 3.2 

(Why “$L^1$ budgets” are the right contract). The $L^1$ condition on τ expresses a finite footprint on the declared window. This matches operational practice: incidents can spike, but governance cares about cumulative impact and recovery [5,6]. Analytically, $L^1$ is exactly what yields tail-robust envelopes by the inhomogeneous Grönwall mechanism [18,23,24].

Theorem 3.1 

(Tail-robust security envelope). Assume R is absolutely continuous on $[t_0,t_1]$ and satisfies (8). Then for all $t\in [t_0,t_1]$,

$$R\left(t\right)\le e^{-2\alpha (t-t_0)}R\left(t_0\right)+{\int }_{t_0}^t{e}^{-2\alpha (t-s)}\tau \left(s\right)ds.$$

(9)

In particular,

$$R\left(t\right)\le e^{-2\alpha (t-t_0)}R\left(t_0\right)+{\parallel \tau \parallel }_{L^1\left([t_0,t_1]\right)}.$$

(10)

Proof. 

Rewrite (8) as $\dot{R}\left(t\right)+2\alpha R\left(t\right)\le \tau \left(t\right)$. Multiply by $e^{2\alpha (t-t_0)}$, integrate from $t_0$ to t, and divide by the integrating factor. This is the standard inhomogeneous Grönwall argument [23,24]. □

Human-Centred Meaning

The envelope (9) is actionable: it tells an operator and an auditor (i) how fast the residual contracts when not being hit (margin $\alpha$) and (ii) how much disturbance the organisation absorbed (budget $\tau$) [5]. This is an explicit alternative to narrative assurance [1,2].

3.2. Frozen Measurement Geometry (“No Moving Goalposts”)

A central design principle is the frozen record. All claims are stated relative to a declared measurement geometry consisting of: a ruler (norm), a neutral convention (semantic equivalences), an observation map, and a refinement ladder. Freezing this geometry ensures that statements such as “risk is decreasing” have invariant meaning across tool upgrades and policy changes [3,4]. Without this discipline, guarantees are ill-posed in the same sense that exponential stability claims are ill-posed when the norm changes with time or with the discretization index [3,4].

3.2.1. Definition of a Frozen Record

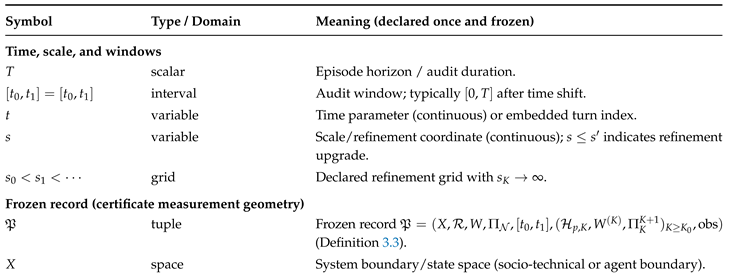
Definition 3.3 

(Frozen record). Afrozen recordis a tuple

$$\mathfrak{P}=(X,\mathcal{R},W,{\mathsf{\Pi }}_{\mathcal{N}},[t_0,t_1],{({\mathcal{H}}_{p,K},W^{\left(K\right)},{\mathsf{\Pi }}_K^{K+1})}_{K\ge K_0},\mathrm{obs}),$$

(11)

where:

(i)

X is the system state space (human-centered boundary);

(ii)

$\mathcal{R}$ is an ambient measurement space in which defect representatives are typed;

(iii)

$W\succ 0$ is a bounded SPD ruler on a defect space ${\mathcal{R}}_p\subseteq \mathcal{R}$, defining ${\parallel u\parallel }_W^2:=\langle u,Wu\rangle$;

(iv)

${\mathsf{\Pi }}_{\mathcal{N}}$ is theneutral convention(semantic equivalences), and ${\mathsf{\Pi }}_{\perp }:=I-{\mathsf{\Pi }}_{\mathcal{N}}$ is the neutral-free projection;

(v)

$[t_0,t_1]=[t_0,t_1]$ is the audit window;

(vi)

${({\mathcal{H}}_{p,K},W^{\left(K\right)},{\mathsf{\Pi }}_K^{K+1})}_{K\ge K_0}$ is a declared refinement ladder (tool versions, policy versions, monitoring pipelines);

(vii)

$\mathrm{obs}$ is an observation map that produces auditable readouts (logs/telemetry) from trajectories.

All residuals, norms, coupling constants, and budgets are interpreted in the same frozen record $\mathfrak{P}$.

Why Each Component Is Necessary

The ruler W fixes the meaning of “small defect” [3,4]. Neutrals encode invariances (e.g. benign renamings, harmless formatting, approved compensating controls) so the residual does not punish representational accidents [6]. The ladder records the fact that systems evolve. The observation map makes the claim audit-friendly: guarantees must be transportable to what humans can actually see, a principle aligned with proof-carrying and runtime-verification workflows [1,2].

3.2.2. A Formal “No Moving Goalposts” Impossibility Statement

If the measurement geometry is allowed to change arbitrarily, then stability claims can be made true by renorming. The following proposition formalises this pathology [3,4].

Proposition 3.2 

(Ill-posedness of decay claims under uncontrolled re-norming). Let X be a vector space and let $x\left(t\right)$ be any trajectory with $x\left(t\right)\ne 0$ on $[t_0,t_1]$. There exists a time-dependent norm ${\parallel ·\parallel }_t$ on X such that the function $R\left(t\right):={\parallel x\left(t\right)\parallel }_t^2$ decays exponentially at any prescribed rate: for every $\alpha >0$ there exists a choice of ${\parallel ·\parallel }_t$ with

$$R\left(t\right)=R\left(t_0\right)e^{-2\alpha (t-t_0)}(t\in [t_0,t_1]).$$

(12)

Proof. 

Fix any reference norm $\parallel ·\parallel$ and define a scalar weight $c\left(t\right):=e^{-\alpha (t-t_0)}\parallel x\left(t_0\right)\parallel /\parallel x\left(t\right)\parallel$. Define ${\parallel v\parallel }_t:=c\left(t\right)\parallel v\parallel$. Then ${\parallel x\left(t\right)\parallel }_t=c\left(t\right)\parallel x\left(t\right)\parallel =\parallel x\left(t_0\right)\parallel e^{-\alpha (t-t_0)}$, hence $R\left(t\right)={\parallel x\left(t\right)\parallel }_t^2=R\left(t_0\right)e^{-2\alpha (t-t_0)}$. □

Interpretation

Without a frozen ruler, any improvement claim can be manufactured by changing the measurement geometry [3,4]. In security practice this corresponds to “dashboard illusions”: changing a scanner, severity rubric, or instrumentation can create the appearance of improvement without changing reality [5]. Thus, freezing the measurement geometry is logically required, not stylistic.

3.2.3. Neutrals as Semantic Equivalence Classes

Humans routinely treat some differences as irrelevant: renaming roles, reordering log lines, or choosing among equivalent policy templates [6]. If a residual penalises such differences, it creates unnecessary work and reduces trust. We therefore explicitly declare neutrals [6,8].

Definition 3.4 

(Neutral transformations). Aneutral family${\mathsf{\Pi }}_{\mathcal{N}}$ is a set (or finite-dimensional subspace) of transformations on the defect space that represent semantic equivalences. A residual isneutral-invariantif $R\left(x\right)=R\left(\phi \right(x\left)\right)$ for all $\phi \in {\mathsf{\Pi }}_{\mathcal{N}}$, or at minimumneutral-stableif there exist $0<c\le C<\infty$ with

$$cR\left(x\right)\le R\left(\phi \left(x\right)\right)\le CR\left(x\right)(\phi \in {\mathsf{\Pi }}_{\mathcal{N}}).$$

(13)

Design Principle

Neutrals make guarantees human-legible: they prevent certificates from depending on representational accidents [6]. They are the human-centered analogue of gauge/neutral mode removal in stability theory [3,4].

3.3. Residuals Versus Metrics

We distinguish residuals from ad-hoc metrics. A residual measures distance to a declared constraint or target set in a declared ruler, while a metric may be an arbitrary score that is not tied to an equilibrium notion [3,4]. Residuals govern action: they decrease under admissible updates and increase only under explicit forcing. This distinction is essential for auditability, compositional reasoning, and for making guarantees meaningful to humans [5,6].

3.3.1. Residuals as Distances to Constraints

Definition 3.5 

(Constraint-residual form). Let $E\subseteq X$ be a declared equilibrium/constraint set and let $\mathsf{\Phi }:X\to {\mathcal{R}}_p$ be a defect map such that $\mathsf{\Phi }\left(x\right)=0$ iff $x\in E$. Given a frozen ruler $W\succ 0$ on ${\mathcal{R}}_p$, define the residual

$$R\left(x\right):={\parallel \mathsf{\Phi }\left(x\right)\parallel }_W^2.$$

(14)

Why this Matters

A constraint-residual has falsifiable semantics: $R\left(x\right)$ is small only if the constraint defect $\mathsf{\Phi }\left(x\right)$ is small in the declared ruler. This makes the residual suitable for proof-carrying assurance: it can be recomputed from declared observations and checked [1,2].

3.3.2. Metrics as Scores and the Danger of Non-Transportability

A generic metric $S\left(x\right)$ may correlate with security, but without a declared ruler and declared equilibrium set, a score does not support stability reasoning [3,4]. In particular, a score may improve under changes that do not improve the underlying system (e.g. changes in scanners, thresholds, reporting) [5]. Residuals avoid this by being typed in a frozen record (Definition 3.3) [3,4].

3.3.3. Admissible Updates: Why Residuals Support Compositional Reasoning

A key property of residuals is that they can be required to be nonincreasing under admissible updates, while all other effects are budgeted [18,19].

Definition 3.6 

(Nonexpansive (admissible) update in a frozen ruler). Let $u\in {\mathcal{R}}_p$ be a defect representative and let $W\succ 0$ be the frozen ruler. An update map $\mathsf{\Psi }:{\mathcal{R}}_p\to {\mathcal{R}}_p$ isW-nonexpansiveif

$${\parallel \mathsf{\Psi }\left(u\right)\parallel }_W\le {\parallel u\parallel }_W\forall u\in {\mathcal{R}}_p.$$

(15)

Proposition 3.3 

(Residual monotonicity under nonexpansive updates). Let $R\left(u\right)={\parallel u\parallel }_W^2$ be a quadratic residual in the frozen ruler and let Ψ be W-nonexpansive. Then $R\left(\mathsf{\Psi }\right(u\left)\right)\le R\left(u\right)$ for all u.

Proof. 

Immediate: $R\left(\mathsf{\Psi }\left(u\right)\right)={\parallel \mathsf{\Psi }\left(u\right)\parallel }_W^2\le {\parallel u\parallel }_W^2=R\left(u\right)$. □

Human-Centred Meaning

An admissible update is a control primitive that cannot make the situation worse in the declared ruler [18,19]. This turns procedures into checkable contracts: a training module, an access-hardening script, or an automated remediation is admissible only if it is nonexpansive (or if its non-admissible effects are explicitly budgeted) [1,2,5]. This is how residuals compose across teams, tools, and organisational interventions.

3.3.4. From Residuals to a Decision-Ready Scalar Ledger

Even when multiple residual channels are needed (identity, patching, misconfiguration, exfiltration, unsafe tool use), one can provide a single scalar ledger by aggregating them with positive weights and proving a one-clock inequality via positive-systems (Metzler) reduction [16,17,18,19]. The design principle is: use residuals (typed distances) as primitives so aggregation preserves meaning [3,4].

Remark 3.3 

(Design summary). The three design principles in this section are logically linked: (i) security must be treated dynamically (Lyapunov reasoning) [18,22], (ii) guarantees must be stated in a frozen measurement geometry (no moving goalposts) [3,4], and (iii) residuals (typed distances) are the correct primitives, because they admit nonexpansive admissible updates and explicit forcing budgets [16,17]. Together, these principles create the conditions under which human-centred assurance claims can be auditable and comparable [1,2].

4. Mathematical Framework

This section states the certificate-level mathematics used throughout the paper. The goal is to formalise three objects that are routinely blurred in security practice: (i) what is being measured (defects / residuals), (ii) how it is being measured (the ruler / frozen measurement geometry), and (iii) how multiple channels compose into one auditable guarantee (one-clock closure). Our stance is functional-analytic: stability and decay are statements about an evolution in a fixed normed geometry [3,4]. The DSFL contribution is to make this typing explicit and to provide a reusable routing theorem that turns multiple nonnegative ledgers into one contraction law with explicit budgets.

4.1. Residual Spaces and Rulers

We formalise defect representatives as elements of a Hilbert space equipped with a symmetric positive definite (SPD) operator defining the ruler. The induced norm quantifies the size of deviations. Neutral directions encode semantic equivalences (e.g. role renamings, benign configuration permutations) and are explicitly projected out.

4.1.1. Hilbert Defect Room and the Frozen Ruler

Definition 4.1 

(Defect room and frozen ruler). Adefect roomis a pair $(\mathcal{H},\langle ·,·\rangle )$ where $\mathcal{H}$ is a real Hilbert space. Aruleris a bounded, selfadjoint, strictly positive operator $W:\mathcal{H}\to \mathcal{H}$ (SPD), written $W\succ 0$. The induced inner product and norm are

$${\langle x,y\rangle }_W:=\langle x,Wy\rangle ,{\parallel x\parallel }_W:=\sqrt{{\langle x,x\rangle }_W}.$$

(16)

Afrozen recorddeclares W once, and all certificate claims are interpreted in ${\parallel ·\parallel }_W$.

Explanation. The insistence on a frozen ruler is not stylistic. In semigroup stability theory, exponential decay is a statement about a specific generator in a specific norm [3,4]. Changing the norm without explicit equivalence constants changes the meaning of the decay claim. The frozen ruler principle is the mechanism that prevents “metric overload” and “version drift” from becoming mathematically invisible.

4.1.2. Neutral Directions and Semantic Equivalence

In security, different configurations may be semantically equivalent even when they are not bitwise identical: renaming roles, permuting hosts, or changing identifiers may not change the risk semantics. We represent such equivalences by a finite-dimensional neutral subspace and remove it explicitly.

Definition 4.2 

(Neutral subspace and projection). Let $\mathcal{N}\subset \mathcal{H}$ be a closed subspace (typically finite-dimensional), called theneutral space. Let ${\mathsf{\Pi }}_{\perp }:\mathcal{H}\to \mathcal{H}$ denote the W-orthogonal projector onto ${\mathcal{N}}^{{\perp }_W}$, i.e. the complement with respect to ${\langle ·,·\rangle }_W$. Given a raw defect $\tilde{e}\in \mathcal{H}$, theneutral-free defectis $e:={\mathsf{\Pi }}_{\perp }\tilde{e}$ and the corresponding residual is

$$R:={\parallel e\parallel }_W^2.$$

(17)

Explanation. Neutrals are part of the typing data. If one changes the neutral convention mid-argument, the residual changes meaning. Projecting neutrals out is the certificate analogue of quotienting by a semantic equivalence relation. (For the analogous role of “neutral modes” in stability statements, see standard semigroup/PDE treatments [3,4].)

4.1.3. Norm Transfer and “No Moving Goalposts”

Even when multiple tools produce different measurements, one can compare them only after proving norm equivalence.

Proposition 4.1 

(Quantitative norm transfer between rulers). Let $W_1,W_2\succ 0$ be bounded SPD rulers on $\mathcal{H}$. Then there exist constants $0<c_{-}\le c_{+}<\infty$ such that for all $x\in \mathcal{H}$,

$$c_{-}{\parallel x\parallel }_{W_1}^2\le {\parallel x\parallel }_{W_2}^2\le c_{+}{\parallel x\parallel }_{W_1}^2.$$

(18)

Moreover, $c_{\pm }$ may be chosen as the extremal spectral values of the bounded SPD operator $W_1^{-1/2}{W}_2{W}_1^{-1/2}$.

Proof. 

$A:=W_1^{-1/2}{W}_2{W}_1^{-1/2}$ is bounded, selfadjoint, and strictly positive, hence its spectrum lies in $(0,\infty )$ with finite infimum and supremum. The Rayleigh quotient bounds

$${inf\sigma \left(A\right)\parallel y\parallel }^2\le \langle y,Ay\rangle \le sup\sigma \left(A\right){\parallel y\parallel }^2$$

applied to $y=W_1^{1/2}x$ yield the claimed inequalities. □

Explanation. Proposition 4.1 is the exact mathematical statement behind “metric drift”: if you move between rulers without tracking $c_{-},c_{+}$, you can manufacture apparent improvement or apparent degradation by changing the measuring stick. This is the same norm-typing phenomenon that governs transfer of decay estimates between energies in semigroup theory [3,4].

4.2. Multi-Ledger Systems

Realistic security systems involve multiple nonnegative residuals $R^a\left(t\right)\ge 0$, corresponding to different channels such as configuration drift, identity exposure, operational workload, or AI agent misuse. These ledgers interact through coupling terms and forcing budgets. This subsection formalises such systems at the certificate layer using standard cooperative/positive systems ideas [16,17].

4.2.1. Ledger Vector and Nonnegativity

Definition 4.3 

(Nonnegative ledger vector). Let $\mathcal{A}=\{1,\dots ,m\}$ index risk channels. Aledger vectoris a map $r:[t_0,t_1]\to {\mathbb{R}}_{\ge 0}^m$ with components

$$r_a\left(t\right):=R^a\left(t\right)\ge 0,a\in \mathcal{A}.$$

(19)

We interpret $R^a$ as a squared $W^a$-norm of a neutral-free defect in a channel-specific defect room, and we regard the nonnegativity $R^a\ge 0$ as the fundamental typing constraint that enables positive-systems routing [16,17].

Explanation. Working with nonnegative ledgers rather than signed metrics prevents cancellation artifacts. At the certificate layer, we only claim what can be audited: nonnegative quantities and explicit budgets.

4.2.2. Couplings and Forcing Budgets

Couplings represent how mismatch in one channel increases mismatch in another (e.g. operational overload increases misconfiguration risk; identity sprawl increases policy-violation likelihood). Forcing budgets represent exogenous injections (e.g. new vulnerabilities disclosed, business-driven policy change, staffing shocks). The cooperative comparison form below is standard in positive systems and input-to-state stability reasoning [16,17,18,19].

Definition 4.4 

(Coupled ledger inequality with budgets). We say the ledgers satisfy aDSFL comparison modelif r is absolutely continuous and

$$\dot{r}\left(t\right)\le M\left(t\right)r\left(t\right)+\tau \left(t\right)\mathrm{for}\mathrm{a}.\mathrm{e}.t\in [t_0,t_1],$$

(20)

where:

(ii)

$M\left(t\right)\in {\mathbb{R}}^{m\times m}$ is measurable andMetzlerfor a.e. t (off-diagonal entries $\ge 0$);

(ii)

$\tau \left(t\right)\in {\mathbb{R}}_{\ge 0}^m$ is a nonnegative forcing vector with $\tau \in L^1\left([t_0,t_1]\right)$.

Explanation. The Metzler constraint encodes the principle that couplings act as injections: they can feed risk from one channel into another but cannot cancel it. The $L^1$ condition on $\tau$ is the precise integrability hypothesis needed to obtain explicit envelopes (convolution bounds) for a scalar one-clock ledger [18,19].

4.3. One-Clock Reduction (Metzler Closure)

We introduce a comparison inequality in which the vector of ledgers is bounded by a Metzler matrix. Under a Hurwitz margin condition, the system admits a positive weighting that collapses all ledgers into a single scalar residual obeying a one-clock inequality. Intuitively, many interacting risks reduce to one certified rate of improvement. This is a classical positive-systems phenomenon [16,17].

4.3.1. Metzler Matrices and the Hurwitz Margin

Definition 4.5 

(Metzler and Hurwitz). A matrix $M\in {\mathbb{R}}^{m\times m}$ isMetzlerif $M_{ab}\ge 0$ for all $a\ne b$. It isHurwitzif all eigenvalues have strictly negative real parts. Equivalently, its spectral abscissa $\mu \left(M\right):=max\{\Re (\lambda ):\lambda \in spec(M\left)\right\}$ satisfies $\mu \left(M\right)<0$ [16,17].

Explanation. Hurwitzness is the quantitative statement “the coupled system is globally stable”. In DSFL, this is not assumed; it is certified by explicit inequalities (often LP-feasible conditions), as standard in control and positive systems [16,17,18,19].

4.3.2. One-Clock Theorem

Theorem 4.1 

(One-clock reduction for Metzler-coupled ledgers). Let $r:[t_0,t_1]\to {\mathbb{R}}_{\ge 0}^m$ be absolutely continuous and satisfy (20) with $M\left(t\right)\equiv M$ constant Metzler and $\tau \in L^1([t_0,t_1];{\mathbb{R}}_{\ge 0}^m)$. Assume M is Hurwitz. Then there exists a weight vector $w\in {\mathbb{R}}_{++}^m$ and a rate ${\lambda }_{\mathrm{eff}}>0$ such that the scalar ledger

$$R_{\mathrm{tot}}\left(t\right):=w^{\top }r\left(t\right)$$

(21)

satisfies, for a.e. $t\in [t_0,t_1]$,

$${\dot{R}}_{\mathrm{tot}}\left(t\right)\le -2{\lambda }_{\mathrm{eff}}{R}_{\mathrm{tot}}\left(t\right)+w^{\top }\tau \left(t\right).$$

(22)

Consequently,

$$R_{\mathrm{tot}}\left(t\right)\le e^{-2{\lambda }_{\mathrm{eff}}(t-t_0)}{R}_{\mathrm{tot}}\left(t_0\right)+{\int }_{t_0}^t{e}^{-2{\lambda }_{\mathrm{eff}}(t-s)}{w}^{\top }\tau \left(s\right)ds.$$

(23)

Proof. 

Because M is Metzler and Hurwitz, there exists $w\gg 0$ and $\alpha >0$ such that $M^{\top }w\le -2\alpha w$ (a standard positive-systems Lyapunov characterisation; see, e.g., [16,17]). Multiply (20) by $w^{\top }$ to obtain

$${\displaystyle \frac{d}{dt}}\left(w^{\top }r\right)\le {\left(M^{\top }w\right)}^{\top }r+w^{\top }\tau \le -2\alpha w^{\top }r+w^{\top }\tau ,$$

(24)

using $r\ge 0$. Set ${\lambda }_{\mathrm{eff}}:=\alpha$ and integrate the scalar differential inequality to obtain (23) (inhomogeneous Grönwall; cf. [18,19]). □

Explanation. Theorem 4.1 is the certificate kernel: once the channel couplings can be bounded so that the Metzler matrix is Hurwitz, the many-ledger system collapses to one auditable scalar inequality with explicit budgets. This is the precise sense in which “many risks reduce to one certified rate of improvement.”

4.3.3. Certificate-Friendly Feasibility Condition

The existence of $w\gg 0$ with $M^{\top }w\le -2\alpha w$ is particularly useful because it is a linear feasibility problem.

Proposition 4.2 

(LP-form sufficient condition for a one-clock margin). Let M be Metzler. If there exist $\alpha >0$ and $w\in {\mathbb{R}}_{++}^m$ such that

$$M^{\top }w\le -2\alpha w\left(\mathit{componentwise}\right),$$

(25)

then M is Hurwitz and the one-clock inequality (22) holds with ${\lambda }_{\mathrm{eff}}=\alpha$.

Proof. 

The inequality gives a linear copositive Lyapunov witness for Metzler stability [16,17], implying Hurwitzness and enabling the scalarisation argument in the proof of Theorem 4.1. □

Explanation. Proposition 4.2 is the computational handle: it turns the abstract condition “system is stable” into an auditable check (feasible w and margin $\alpha$) that can be verified by linear programming on finite avatars, consistent with a proof-carrying workflow [2].

4.3.4. Two-Channel Closed Form (for Intuition)

For two ledgers $r=(r_s,r_f)$ with

$$M=\left(\begin{array}{cc}-2{\lambda }_s& {\eta }_{s\leftarrow f}\\ {\eta }_{f\leftarrow s}& -2{\lambda }_f\end{array}\right),{\lambda }_s,{\lambda }_f>0,{\eta }_{·\leftarrow ·}\ge 0,$$

(26)

Hurwitzness is equivalent to the small-gain inequality

$$4{\lambda }_s{\lambda }_f>{\eta }_{s\leftarrow f}{\eta }_{f\leftarrow s},$$

(27)

and ${\lambda }_{\mathrm{eff}}$ is determined by the spectral abscissa of M (equivalently the dominant eigenvalue for Metzler M), yielding an explicit bottleneck formula (see standard treatments of $2\times 2$ positive systems and small-gain conditions [16,17,18,19]). This is the simplest analytic avatar of the general Metzler closure.

Remark 4.1 

(Why this framework is reusable). Nothing in this section depends on the semantics of the ledgers (security, quantum computing, or quantum gravity). The only required inputs are: a frozen ruler, explicit neutral conventions, explicit coupling bounds, and integrable budgets. This is why the DSFL certificate layer can be reused across domains. In particular, the same one-clock reduction is standard in the analysis of cooperative systems and positive linear systems [16,17].

5. The One-Residual, One-Clock Theorem

This section gives the core certificate-layer result of the paper. We start from multiple nonnegative ledgers (risk channels) that interact through nonnegative couplings and external forcing. Under a standard positive-systems (Metzler) hypothesis and a Hurwitz margin condition, we prove that there exists a single scalar residual—a positive weighting of the ledger vector—that obeys a forced contraction inequality with one explicit decay rate and one explicit disturbance budget. This is the mathematically precise version of the human-centred question: “Are we improving, at what certified rate, and how much disturbance did we absorb?”

The proof is purely functional-analytic: it uses the comparison principle for cooperative systems, Perron–Frobenius theory for Metzler matrices, and the inhomogeneous Grönwall mechanism [3,4,16,17,18,19,23,24,25].

5.1. Assumptions (Certificate Layer)

5.1.1. Ledgers, Regularity, and Forcing Budgets

Let $[t_0,t_1]=[t_0,t_1]$ be a fixed audit window. We consider m nonnegative ledgers (channels) $R^a:[t_0,t_1]\to {\mathbb{R}}_{\ge 0}$, collected into a vector

$$r\left(t\right):={(R^1\left(t\right),\dots ,R^m\left(t\right))}^{\top }\in {\mathbb{R}}_{\ge 0}^m.$$

(28)

The certificate layer makes only minimal regularity demands: the ledgers must be absolutely continuous so that their time derivatives exist almost everywhere and can be bounded by inequalities [18,24].

Assumption 5.1 

(A1: absolute continuity and nonnegativity). Each ledger $R^a$ is absolutely continuous on $[t_0,t_1]$ and satisfies $R^a\left(t\right)\ge 0$ for all $t\in [t_0,t_1]$.

External disturbances (attacks, outages, measurement noise, workload spikes) are not required to be small pointwise; they are required to have finite total footprint on the audit window. This is the correct currency for forced-stability envelopes and input-to-state style guarantees [18,19].

Assumption 5.2 

(A2: integrable forcing). There exists a nonnegative forcing term $\tau :[t_0,t_1]\to {\mathbb{R}}_{\ge 0}^m$ with $\tau \in L^1([t_0,t_1];{\mathbb{R}}^m)$ such that all disturbance contributions to ledger dynamics are upper-bounded by $\tau \left(t\right)$ componentwise.

5.1.2. Metzler Comparison Inequality and Stability Margin

Cross-channel effects in human-centered security systems are inherently cooperative in the sense that one channel can inject risk into another but cannot cancel it. This is captured by a Metzler comparison inequality, the standard abstraction in positive-systems theory [16,17,25].

Definition 5.1 

(Metzler and Hurwitz). A matrix $M\in {\mathbb{R}}^{m\times m}$ isMetzlerif $M_{ab}\ge 0$ for all $a\ne b$. Its spectral abscissa is $\mu \left(M\right):=max\{\Re z:z\in spec(M\left)\right\}$. We call MHurwitzif $\mu \left(M\right)<0$.

Assumption 5.3 

(A3: cooperative (Metzler) comparison inequality). There exists a constant Metzler matrix $M\in {\mathbb{R}}^{m\times m}$ such that, for a.e. $t\in [t_0,t_1]$,

$$\dot{r}\left(t\right)\le Mr\left(t\right)+\tau \left(t\right)\left(\mathit{componentwise}\right).$$

(29)

Interpretation of M

Writing $M_{aa}=-2{\lambda }_a$ and $M_{ab}={\eta }_{a\leftarrow b}\ge 0$ ($a\ne b$), the diagonal rates ${\lambda }_a$ represent intrinsic dissipation/controls in channel a, while the off-diagonals ${\eta }_{a\leftarrow b}$ represent injections from channel b into channel a. Hurwitzness is the small-gain condition: dissipation dominates injections [16,17,18,19].

Assumption 5.4 

(A4: Hurwitz margin). The Metzler matrix M in Assumption 5.3 is Hurwitz: $\mu \left(M\right)<0$.

Why constant M Is Acceptable at the Certificate Layer

Allowing $M\left(t\right)$ time-dependent is possible, but the certificate layer aims for auditable constants. In practice, time dependence is either absorbed into the budget $\tau$ or replaced by a conservative constant upper bound. This is consistent with certificate semantics: we prefer a slightly pessimistic but checkable bound to a sharp but unstable one [17,18,19].

5.2. Main Theorem

5.2.1. Positivity and the Forced Comparison Formula

Lemma 5.1 

(Positivity of the semigroup generated by a Metzler matrix). If M is Metzler, then $e^{tM}$ has nonnegative entries for all $t\ge 0$.

Proof. 

Choose $\beta$ such that $M+\beta I$ is entrywise nonnegative. Then $e^{t(M+\beta I)}={\sum }_{k\ge 0}{\displaystyle \frac{t^k}{k!}}{(M+\beta I)}^k$ is entrywise nonnegative. Hence $e^{tM}=e^{-\beta t}{e}^{t(M+\beta I)}$ is entrywise nonnegative. □

Lemma 5.2 

(Forced comparison (Duhamel) bound). Assume Assumptions 5.1 and 5.3. Then for all $t\in [t_0,t_1]$,

$$r\left(t\right)\le e^{(t-t_0)M}r\left(t_0\right)+{\int }_{t_0}^t{e}^{(t-s)M}\tau \left(s\right)ds\left(\mathit{componentwise}\right).$$

(30)

Proof. 

Let y solve $\dot{y}=My+\tau$ with $y\left(t_0\right)=r\left(t_0\right)$, so that Duhamel’s formula gives the right-hand side [3,4]. Set $z:=y-r$. Then $z\left(t_0\right)=0$ and $\dot{z}\ge Mz$ a.e. Writing $q:=\dot{z}-Mz\ge 0$ yields $z\left(t\right)={\int }_{t_0}^t{e}^{(t-s)M}q\left(s\right)ds\ge 0$ componentwise by Lemma 5.1. Hence $r\le y$. □

5.2.2. One-Clock Reduction

We now construct the one scalar ledger that collapses multi-channel risk dynamics into a single certified clock. The key point is that Hurwitzness of a Metzler matrix implies the existence of a strictly positive weighting vector that turns the vector inequality into a scalar inequality with an explicit decay margin [16,17,25].

Theorem 5.1 

(One-residual, one-clock theorem (certificate layer)). Assume Assumptions 5.1–5.4. Then there exist weights $w\in {\mathbb{R}}_{>0}^m$ and a constant $\alpha >0$ such that the scalar residual

$$R_{\mathrm{tot}}\left(t\right):=w^{\top }r\left(t\right)$$

(31)

satisfies, for a.e. $t\in [t_0,t_1]$,

$${\dot{R}}_{\mathrm{tot}}\left(t\right)\le -2\alpha R_{\mathrm{tot}}\left(t\right)+{\tau }_{\mathrm{tot}}\left(t\right),{\tau }_{\mathrm{tot}}\left(t\right):=w^{\top }\tau \left(t\right)\in L^1\left([t_0,t_1]\right),{\tau }_{\mathrm{tot}}\ge 0.$$

(32)

Moreover, a sufficient (and checker-friendly) witness condition is the existence of $w\gg 0$ and $\alpha >0$ such that

$$M^{\top }w\le -2\alpha w\left(\mathit{componentwise}\right).$$

(33)

Proof. 

Since M is Metzler and Hurwitz, positive-systems theory implies that there exists $w\gg 0$ with $M^{\top }w\ll 0$ [16,17,25]. Fix any $\alpha >0$ such that (33) holds. Multiply the comparison inequality (29) on the left by $w^{\top }$:

$${\dot{R}}_{\mathrm{tot}}\left(t\right)=w^{\top }\dot{r}\left(t\right)\le w^{\top }Mr\left(t\right)+w^{\top }\tau \left(t\right)={\left(M^{\top }w\right)}^{\top }r\left(t\right)+{\tau }_{\mathrm{tot}}\left(t\right).$$

(34)

Since $r\left(t\right)\ge 0$ componentwise and $M^{\top }w\le -2\alpha w$ componentwise, we have

$${\left(M^{\top }w\right)}^{\top }r\left(t\right)\le {(-2\alpha w)}^{\top }r\left(t\right)=-2\alpha R_{\mathrm{tot}}\left(t\right),$$

(35)

which yields (32). Integrability of ${\tau }_{\mathrm{tot}}$ follows from $\tau \in L^1$ and $w>0$. □

Security assurance interpretation

Theorem 5.1 provides a certificate-level contract: a single scalar ledger decreases at a certified rate $\alpha$ up to an explicit disturbance budget ${\tau }_{\mathrm{tot}}$. The weights w encode how different risk channels contribute to the decision-ready residual. Crucially, the proof uses only inequality routing, so it remains valid even when the underlying system is complex, non-linear, or partially observed, as long as its effect on the ledgers is upper-bounded by the certificate assumptions [18,19].

LP-checkable certificate interface

Condition (33) is linear in w and $\alpha$. Thus a checker can validate (or produce) a one-clock margin by solving a linear feasibility problem: find $w\gg 0$ and $\alpha >0$ such that $M^{\top }w+2\alpha w\le 0$. This makes the theorem operational for proof-carrying security bundles [2].

5.3. Tail-Robust Envelopes

The one-clock inequality implies explicit envelopes that are robust to transient spikes. This is the mathematically precise reason the framework is human-centred: it distinguishes a persistent trend (rate $\alpha$) from accumulated disturbance (budget ${\tau }_{\mathrm{tot}}$) [18,19,23,24].

Theorem 5.2 

(Tail-robust envelope for the one-clock residual). Assume the hypotheses of Theorem 5.1. Then for all $t\in [t_0,t_1]$,

$$R_{\mathrm{tot}}\left(t\right)\le e^{-2\alpha (t-t_0)}{R}_{\mathrm{tot}}\left(t_0\right)+{\int }_{t_0}^t{e}^{-2\alpha (t-s)}{\tau }_{\mathrm{tot}}\left(s\right)ds.$$

(36)

In particular,

$$R_{\mathrm{tot}}\left(t\right)\le e^{-2\alpha (t-t_0)}{R}_{\mathrm{tot}}\left(t_0\right)+{\parallel {\tau }_{\mathrm{tot}}\parallel }_{L^1\left([t_0,t_1]\right)}.$$

(37)

Proof. 

This is the inhomogeneous Grönwall argument applied to (32) [23,24]. □

5.3.1. Interpretation: Incidents as Budgets, Recovery as Rate

Transient Spikes

A short, intense incident produces a large ${\tau }_{\mathrm{tot}}\left(t\right)$ on a small time interval. The envelope (36) shows that its impact is filtered by an exponentially decaying kernel: its long-term effect is proportional to its integrated footprint rather than its peak value [18,23,24].

Recovery

When ${\tau }_{\mathrm{tot}}$ returns to baseline, the residual returns to exponential decay at rate $\alpha$. Thus the certificate separates “how hard we were hit” ($\parallel {\tau }_{\mathrm{tot}}{\parallel }_{L^1}$) from “how quickly we recover” ($\alpha$) [18,19].

Human-Facing Assurance

In operational terms, Theorem 5.2 supports a minimal, interpretable assurance report:

$$\mathrm{Certified}\mathrm{rate}\alpha ,\mathrm{disturbance}\mathrm{budget}\parallel {\tau }_{\mathrm{tot}}{\parallel }_{L^1\left([t_0,t_1]\right)},\mathrm{and}\mathrm{initial}\mathrm{condition}{R}_{\mathrm{tot}}\left(t_0\right).$$

(38)

These are the quantities a human decision-maker can use to compare interventions across versions without being misled by metric drift, provided the frozen record discipline holds (Section 3) [3,4,5,6].

6. Compliance and Assurance as Imbalance

This section instantiates the DSFL certificate layer in a governance/compliance setting. The central move is to treat compliance not as a collection of heterogeneous checklist items, but as a typed imbalance in a frozen measurement geometry. Policy is the blueprint; operational practice is the response. The defect is the policy–practice mismatch; the residual is its squared norm in a frozen ruler; and assurance is a gap statement (a provable contraction margin with explicit budgets) rather than a binary label.

Throughout, we keep the DSFL hygiene:

• every claim is stated in a declared normed space (frozen ruler), consistent with fixed-norm stability semantics [3,4];
• semantic equivalences are encoded as neutrals and projected out (cf. the necessity of quotienting/removing neutral modes in stability statements) [3,4];
• coupled compliance channels route through a positive-systems (Metzler) one-clock closure [16,17,18,19] (Section 4).

6.1. Policy–Practice Imbalance Operators

We define imbalance operators for identity and access management, configuration state, data handling, and agent tool use. Each operator measures deviation between declared policy and observed practice and is designed to be compatible with auditability (finite evidence) and stability under change (frozen measurement geometry), in the proof-carrying spirit [1,2].

6.1.1. Typing: Blueprint Space, Practice Space, and Observation Map

Fix a regime window $[t_0,t_1]=[t_0,t_1]$ (e.g. an audit period). Let ${\mathcal{H}}_s$ be the policy blueprint space and ${\mathcal{H}}_p$ the practice space, both Hilbert spaces, and let

$$\mathcal{I}:{\mathcal{H}}_s\to {\mathcal{H}}_p$$

(39)

be the calibration/interchangeability map that embeds a policy blueprint into the practice space. We also declare a neutral space $\mathcal{N}\subset {\mathcal{H}}_p$ representing semantic equivalences (role renamings, asset relabelings, benign permutations), and a W-orthogonal projector ${\mathsf{\Pi }}_{\perp }$ onto ${\mathcal{N}}^{{\perp }_W}$. Finally, we declare an observation map ${\mathcal{O}}_t$ (the measurement pipeline) that extracts practice evidence from logs, identity graphs, configurations, and agent traces. Making ${\mathcal{O}}_t$ explicit is essential for auditability: guarantees must transport to what is observable and checkable from evidence, not merely to an unobserved internal state [1,2].

Definition 6.1 

(Policy–practice imbalance operator (abstract)). Apolicy–practice imbalance operatoris a map

$$E_{\mathrm{pol}}:{\mathcal{H}}_s\times {\mathcal{H}}_p\to {\mathcal{H}}_p$$

(40)

such that $E_{\mathrm{pol}}(s,p)=0$ if and only if practice p satisfies policy s in the declared semantics. In DSFL form we take

$$E_{\mathrm{pol}}(s,p):={\mathsf{\Pi }}_{\perp }\left(p-\mathcal{I}s\right),$$

(41)

possibly after composing p with the observation map ${\mathcal{O}}_t$ and any declared normalisation.

Explanation. Definition 6.1 is a typed version of a common audit question: “how far is reality from policy, after quotienting away naming conventions?” The projector ${\mathsf{\Pi }}_{\perp }$ enforces that only semantically meaningful mismatch is charged to the residual. The requirement that the operator be defined in a Hilbert space with a frozen ruler is exactly the fixed-norm discipline needed for meaningful contraction statements [3,4].

6.1.2. Concrete Imbalance Operators by Channel

We now record canonical examples. In each case, the DSFL rule is: define a typed defect that lives in a Hilbert space, then measure it in one frozen ruler. This makes compliance a candidate Lyapunov quantity rather than a checklist score.

Identity and Access Management (IAM)

Let $G_t$ be the directed graph of identities, roles, entitlements, and resources at time t. Let $s^{\mathrm{IAM}}$ be the policy blueprint (allowed edges, separation-of-duty constraints, MFA rules) and let $p^{\mathrm{IAM}}\left(t\right)$ be the observed graph (from logs and identity systems). Define

$$E_{\mathrm{IAM}}\left(t\right):={\mathsf{\Pi }}_{\perp }^{\mathrm{IAM}}\left({\mathsf{\Phi }}_{\mathrm{IAM}}\left(p^{\mathrm{IAM}}\left(t\right)\right)-{\mathcal{I}}^{\mathrm{IAM}}{s}^{\mathrm{IAM}}\right),$$

(42)

where ${\mathsf{\Phi }}_{\mathrm{IAM}}$ is a declared feature/embedding of the graph into a Hilbert space (e.g. adjacency features, risk-weighted walk counts), and ${\mathsf{\Pi }}_{\perp }^{\mathrm{IAM}}$ removes neutral relabellings. Graph-to-Hilbert embeddings are a standard way to make structural constraints accessible to normed analysis; DSFL uses the embedding only as typing data (frozen in the record) so that cross-version comparisons remain meaningful.

Configuration State (Hardening Posture)

Let $x\left(t\right)$ denote the measured configuration vector (CIS controls, patch state, service exposure, runtime settings). Let $s^{\mathrm{CFG}}$ encode the target baseline. Define

$$E_{\mathrm{CFG}}\left(t\right):={\mathsf{\Pi }}_{\perp }^{\mathrm{CFG}}\left(x\left(t\right)-{\mathcal{I}}^{\mathrm{CFG}}{s}^{\mathrm{CFG}}\right),$$

(43)

where neutrals can encode benign reparameterisations (e.g. different but equivalent hardening profiles).

Data Handling and Governance

Let $d\left(t\right)$ be a measured data-flow and classification state (labels, access paths, retention). Let $s^{\mathrm{DATA}}$ encode policy constraints (e.g. retention limits, residency, encryption-at-rest). Define an imbalance $E_{\mathrm{DATA}}\left(t\right)$ as the neutral-free distance of observed flows from the policy manifold, for example by a constraint-violation vector or by a quadratic penalty embedding. Treating governance requirements as constraints whose violation has a normed magnitude is standard in control-style assurance: it makes “how far from policy” a quantitative object suitable for Lyapunov reasoning [18,19].

Agent Tool Use and AI Governance

Let $u\left(t\right)$ be a trace representation of agent actions (tools invoked, permissions used, destinations contacted). Let $s^{\mathrm{AG}}$ be the tool-policy blueprint (allowed tools, rate limits, data boundaries). Define

$$E_{\mathrm{AG}}\left(t\right):={\mathsf{\Pi }}_{\perp }^{\mathrm{AG}}\left(u\left(t\right)-{\mathcal{I}}^{\mathrm{AG}}{s}^{\mathrm{AG}}\right),$$

(44)

where neutrals may encode harmless trace reordering or equivalent tool aliases. This form matches the proof-carrying posture: the auditable object is the trace and the declared comparison map, verified by a small checker [1,2].

Remark 6.1 

(Why operators, not checklists). Each $E_{•}$ is anoperatorbecause it produces an element of a Hilbert space whose norm can be used in stability claims. A checklist does not carry a geometry; it cannot support a one-clock inequality. The underlying logic is the same as fixed-norm stability theory: without a declared normed space, “decay” is not a typed claim [3,4].

6.2. Compliance Residuals

Compliance is quantified as a residual $R^{\mathrm{pol}}={\parallel E_{\mathrm{pol}}\parallel }_W^2$ in the frozen ruler. This formulation supports auditability and comparability, and it aligns directly with Lyapunov-style reasoning for controlled systems [18,19].

6.2.1. Frozen Ruler and the Compliance Residual

Definition 6.2 

(Compliance residual in a frozen ruler). Fix a frozen SPD ruler $W:{\mathcal{H}}_p\to {\mathcal{H}}_p$ and define the neutral-free imbalance

$$e_{\mathrm{pol}}\left(t\right):=E_{\mathrm{pol}}(s,p\left(t\right))\in {\mathcal{H}}_p.$$

(45)

Thecompliance residualis

$$R^{\mathrm{pol}}\left(t\right):={\parallel e_{\mathrm{pol}}\left(t\right)\parallel }_W^2.$$

(46)

Explanation. $R^{\mathrm{pol}}$ is a single scalar that aggregates heterogeneous violations by a declared measurement geometry. Because W is frozen, statements like “compliance improved by a factor of 10” have invariant meaning over time and across tool updates (up to explicit norm-equivalence constants), mirroring the fixed-norm discipline in stability theory [3,4]. This is also the correctness condition for proof-carrying assurance: a third party must be able to recompute the residual in the same ruler from the declared evidence [2].

6.2.2. Comparability Under Tool Changes

If the measurement pipeline changes (scanner upgrade, new log source), then the corresponding change of ruler must be made explicit; otherwise one can “improve” compliance by redefining the measurement geometry. This is the same pathology as ill-posed decay claims under uncontrolled renorming in fixed-norm stability theory [3,4].

Proposition 6.1 

(Compliance comparability under ruler changes). Let $W_1,W_2\succ 0$ be two rulers representing two measurement pipelines. If there exist constants $c_{-},c_{+}>0$ such that

$$c_{-}{\parallel x\parallel }_{W_1}^2\le {\parallel x\parallel }_{W_2}^2\le c_{+}{\parallel x\parallel }_{W_1}^2\forall x\in {\mathcal{H}}_p,$$

(47)

then residual comparisons across the two pipelines are meaningful up to the explicit distortion factor $c_{+}/c_{-}$. If no such equivalence constants are established, cross-version comparisons are not certificate-valid.

Proof. 

This is the norm-transfer fact for bounded SPD rulers; it is the same functional-analytic phenomenon that governs stability transfer between energies [3,4]. □

Explanation. Proposition 6.1 formalises the audit intuition: a new scanner may change the scale, so claims must carry the conversion constants. DSFL enforces this as a typing rule, consistent with the proof-carrying stance (ship explicit constants and verify them) [2].

6.2.3. Multi-Channel Compliance as a Ledger Vector

Let $\mathcal{A}=\{\mathrm{IAM},\mathrm{CFG},\mathrm{DATA},\mathrm{AG},\dots \}$ index compliance channels. Define

$$R^a\left(t\right):={\parallel E_a\left(t\right)\parallel }_{W^a}^2,a\in \mathcal{A},$$

(48)

and assemble a residual vector $r\left(t\right)={\left(R^a\left(t\right)\right)}_{a\in \mathcal{A}}\in {\mathbb{R}}_{\ge 0}^{\left|\mathcal{A}\right|}$. Couplings (e.g. workload → misconfigurations) appear as nonnegative injections into the ledger inequalities, as in Section 4; the resulting closure uses positive-systems/ISS reasoning [16,17,18,19].

6.3. Assurance as a Gap, not a Checklist

Instead of binary compliance, assurance is expressed as a rate of improvement toward policy conformance, with explicit slack. This is aligned with the control-theoretic view of safety under forcing and with the fixed-norm semantics of stability theory [3,4,18,19].

6.3.1. Assurance Means a Contraction Margin in the Frozen Ruler

A checkbox view treats compliance as static: PASS/FAIL at a time. DSFL treats assurance as dynamic: does the compliance residual contract with a certified margin under admissible operations?

Definition 6.3 

(Assurance as a one-clock claim). We say a system hasassurance with margin${\lambda }_{\mathrm{eff}}>0$ on $[t_0,t_1]$ if there exists a scalar compliance ledger $R_{\mathrm{tot}}\left(t\right)$ (typically a positive weighting of channel residuals) and a budget ${\tau }_{\mathrm{tot}}\in L^1\left([t_0,t_1]\right)$, ${\tau }_{\mathrm{tot}}\ge 0$, such that

$${\dot{R}}_{\mathrm{tot}}\left(t\right)\le -2{\lambda }_{\mathrm{eff}}{R}_{\mathrm{tot}}\left(t\right)+{\tau }_{\mathrm{tot}}\left(t\right)\mathrm{for}\mathrm{a}.\mathrm{e}.t\in [t_0,t_1].$$

(49)

Explanation. This is the typed analogue of “security is improving with provable slack, despite change.” The inequality is meaningful only in a frozen ruler, exactly as stability statements are meaningful only in fixed norms [3,4].

6.3.2. Metzler Closure Yields Assurance from Coupled Channels

If the channel residuals satisfy a Metzler comparison inequality (Section 4), then assurance reduces to a Hurwitz-margin condition, as in the classical theory of positive linear systems and small-gain/ISS closure [16,17,18,19].

Theorem 6.1 

(Assurance by one-clock reduction). Assume the channel ledger vector $r\left(t\right)$ satisfies

$$\dot{r}\left(t\right)\le Mr\left(t\right)+\tau \left(t\right),$$

(50)

with M Metzler and $\tau \in L^1([t_0,t_1];{\mathbb{R}}_{\ge 0}^m)$. If M is Hurwitz, then there exist $w\gg 0$ and ${\lambda }_{\mathrm{eff}}>0$ such that $R_{\mathrm{tot}}\left(t\right):=w^{\top }r\left(t\right)$ satisfies the assurance inequality (49) with ${\tau }_{\mathrm{tot}}\left(t\right)=w^{\top }\tau \left(t\right)$.

Proof. 

This is exactly the Metzler one-clock reduction (Section 4), a standard positive-systems argument: Hurwitz Metzler ⇒ existence of $w\gg 0$ with $M^{\top }w\ll 0$, then scalarisation yields the one-clock inequality [16,17,18,19]. □

Explanation. Theorem 6.1 is the mathematical core of “assurance as a gap”: assurance is a provable margin ${\lambda }_{\mathrm{eff}}$ obtained from explicit coupling bounds, not a checklist score.

6.3.3. Slack Is the Audit Object

In a compliance programme, the most important number is not a binary label but the slack:

$$\mathrm{slack}\left(t\right):=2{\lambda }_{\mathrm{eff}}{R}_{\mathrm{tot}}\left(t\right)-{\tau }_{\mathrm{tot}}\left(t\right).$$

(51)

Positive slack means the system is contracting faster than it is being injected with mismatch; negative slack means the current policy–practice gap cannot be certified as closing under the declared operations.

Remark 6.2 

(Why this improves accountability). Slack variables are auditable: they reduce disputes about interpretation to inequalities in a frozen record. This is exactly the DSFL posture: progress is “numbers with slack,” not narrative conformance. This design aligns with proof-carrying assurance: the bundle ships constants and witnesses; the checker verifies inequalities and returns PASS/FAIL with slack [1,2].

7. Empirical Coupling Budgets

This section explains how the DSFL certificate layer interfaces with empirical security operations. The core idea is simple: multi-channel assurances are only as strong as the coupling bounds that connect the channels. If workload spikes can inject risk into configuration drift, or if alert volume can inject risk into human error and policy exceptions, then a certificate that ignores these couplings is brittle. DSFL therefore treats coupling coefficients as first-class certificate constants: single numbers that must be declared, audited, and stress-tested.

Mathematically, the point is that the one-clock theorem (Section 4Section 5) requires an explicit Metzler comparison system. Its off-diagonal entries are precisely the coupling budgets [16,17,18,19]. Hence, empirical coupling estimation is not “extra analytics”; it is the mechanism by which operational reality enters the certificate. Human factors motivate why coupling is first-order: under cognitive load and organisational constraints, interventions in one channel can amplify failures in another, so assurances that ignore coupling invite “local improvement / global regression” failure modes [5,6].

7.1. Why Coupling Matters in Security

Human workload, alert volume, and configuration drift influence each other. Ignoring these couplings leads to brittle assurances [5,6].

7.1.1. Coupling Is the Difference Between Local and Global Guarantees

Consider two ledgers:

$$R^{\mathrm{cfg}}\left(t\right)(\mathrm{configuration}\mathrm{drift}/\mathrm{misconfiguration}\mathrm{residual})\mathrm{and}{R}^{\mathrm{hum}}\left(t\right)(\mathrm{human}\mathrm{workload}/\mathrm{operational}\mathrm{overload}\mathrm{residual}).$$

(52)

Even if each ledger would decay in isolation (e.g. via automation or staffing interventions), coupling can defeat global contraction. A simple comparison model is

$${\dot{R}}^{\mathrm{cfg}}\le -2{\lambda }_{\mathrm{cfg}}{R}^{\mathrm{cfg}}+{\eta }_{\mathrm{cfg}\leftarrow \mathrm{hum}}{R}^{\mathrm{hum}},{\dot{R}}^{\mathrm{hum}}\le -2{\lambda }_{\mathrm{hum}}{R}^{\mathrm{hum}}+{\eta }_{\mathrm{hum}\leftarrow \mathrm{cfg}}{R}^{\mathrm{cfg}}.$$

(53)

The coupled system contracts only if the induced Metzler matrix is Hurwitz (small-gain) and the forcing budgets are integrable, as in the stability theory of positive systems [16,17,18,19]. Thus, coupling constants are not optional: they are the difference between “each team metric improved” and “the organisation is provably safer” [5].

7.1.2. Operational Meaning of Couplings

In practice, coupling mechanisms include:

• Workload → misconfiguration: high alert load increases the probability of rushed changes and policy exceptions, inflating configuration residuals.
• Misconfiguration → workload: drifting configurations create more alerts and incidents, inflating workload.
• Identity sprawl ↔ policy violations: expanding entitlements increases both violation frequency and response overhead.

DSFL formalises these effects as nonnegative injections between ledgers, i.e. off-diagonal entries of a Metzler matrix. The certificate is only meaningful once these numbers are bounded in the frozen record. This is aligned with the human-centred security viewpoint that many “technical” failures are mediated by workflow and governance constraints rather than by missing primitives [5,6].

7.2. Model-Free Empirical Coupling Estimate

We define an empirical coupling constant ${\kappa }_{\mathrm{emp}}$ from observed time series and prove an immediate inequality bounding cross-channel injections. The goal is deliberately certificate-facing: produce conservative, auditable constants that can populate a Metzler comparison matrix and be used for one-clock closure [16,17].

7.2.1. From Coupled Inequalities to an Observable Injection Trace

At the certificate layer, coupling appears as a term that contributes to the derivative of a ledger. For two channels a and b, we write the abstract form

$${\dot{R}}^a\left(t\right)\le \dots +J_{a\leftarrow b}\left(t\right)+\dots ,$$

(54)

where $J_{a\leftarrow b}\left(t\right)$ is the injection trace measuring how channel b feeds channel a at time t. In empirical settings, $J_{a\leftarrow b}\left(t\right)$ is not derived from PDE identities; it is estimated from data by a declared protocol (e.g. regressions on interventions, causal models, or direct bookkeeping of change events). The DSFL requirement is not a particular statistical method; it is that the output be conservative and typed to the frozen record so that it can safely enter a Lyapunov/ISS-style inequality [18,19].

Remark 7.1 

(Typing requirement). The injection trace must be expressed in units compatible with the residuals it couples. If $R^a$ and $R^b$ are computed in a frozen ruler, then $J_{a\leftarrow b}$ must be derived from the same frozen data pipeline; otherwise the coupling estimate is not DSFL-typed.

7.2.2. Definition of the Empirical Coupling Constant

Definition 7.1 

(Empirical coupling constant). Fix a time grid $\mathcal{T}\subset [t_0,t_1]$ and observed time series

$${\left\{J_{a\leftarrow b}\left(t\right)\right\}}_{t\in \mathcal{T}},{\left\{R^a\left(t\right)\right\}}_{t\in \mathcal{T}},{\left\{R^b\left(t\right)\right\}}_{t\in \mathcal{T}},$$

(55)

with $R^a\left(t\right),R^b\left(t\right)\ge 0$. For a small stabilisation parameter $\epsilon >0$, define

$${\kappa }_{\mathrm{emp}}(a\leftarrow b):=\underset{t\in \mathcal{T}}{max}{\displaystyle \frac{|J_{a\leftarrow b}\left(t\right)|}{\sqrt{R^a\left(t\right)R^b\left(t\right)}+\epsilon }}.$$

(56)

Explanation. The normalisation $\sqrt{R^a{R}^b}$ is certificate-friendly because it matches the Cauchy–Schwarz structure of cross terms and yields a dimensionless coupling coefficient; it is also the scaling used when routing bilinear interactions into Metzler/ISS-style scalar envelopes [16,17,18,19]. The small $\epsilon$ prevents division by zero and is recorded as part of the frozen audit protocol.

7.2.3. Immediate Inequality (the Certificate-Ready Bound)

Proposition 7.1 

(Empirical coupling inequality). Let ${\kappa }_{\mathrm{emp}}(a\leftarrow b)$ be as in Definition 7.1. Then for all $t\in \mathcal{T}$,

$$|J_{a\leftarrow b}\left(t\right)|\le {\kappa }_{\mathrm{emp}}(a\leftarrow b)\sqrt{R^a\left(t\right)R^b\left(t\right)}+\epsilon {\kappa }_{\mathrm{emp}}(a\leftarrow b).$$

(57)

Proof. 

By definition, for each $t\in \mathcal{T}$,

$${\displaystyle \frac{|J_{a\leftarrow b}\left(t\right)|}{\sqrt{R^a\left(t\right)R^b\left(t\right)}+\epsilon }}\le {\kappa }_{\mathrm{emp}}(a\leftarrow b).$$

(58)

Multiply both sides by $\sqrt{R^a\left(t\right)R^b\left(t\right)}+\epsilon$ to obtain (57). □

Explanation. Proposition 7.1 is deliberately elementary: it shows that once the time series are declared, the empirical coupling constant immediately yields a certificate-ready inequality. This is the DSFL posture: coupling claims are not interpretive; they are inequalities with explicit constants, designed to be routed into a one-clock certificate check [1,2].

7.2.4. From $\sqrt{R^a{R}^b}$ to a Metzler Comparison Form

To route coupling into the one-clock theorem we typically use the bound

$$\sqrt{R^a{R}^b}\le \frac{1}{2}(R^a+R^b),$$

(59)

so the inequality (57) yields a linear-in-ledgers injection bound of Metzler type:

$$|J_{a\leftarrow b}\left(t\right)|\le \frac{1}{2}{\kappa }_{\mathrm{emp}}(a\leftarrow b)R^a\left(t\right)+\frac{1}{2}{\kappa }_{\mathrm{emp}}(a\leftarrow b)R^b\left(t\right)+\epsilon {\kappa }_{\mathrm{emp}}(a\leftarrow b).$$

(60)

Thus empirical couplings become explicit off-diagonal entries and diagonal penalties in the Metzler matrix used for one-clock closure [16,17,18,19].

7.3. Interpretation as a Certificate Constant

The coupling constant enters assurance reports as a single auditable number, with robustness under resampling. This is the empirical analogue of theorem constants in proof-carrying and runtime-verifiable workflows: ship a conservative constant plus a declared protocol, and verify the resulting inequality cheaply [1,2].

7.3.1. Certificate Semantics: What ${\kappa }_{\mathrm{emp}}$ Means

In DSFL, ${\kappa }_{\mathrm{emp}}(a\leftarrow b)$ is interpreted as:

The worst-case observed rate (in the declared frozen record) at which channel b can inject mismatch into channel a, normalised by the geometric mean of the two residuals.

Large $\kappa$ means “tight coupling” and predicts that local improvements may not yield global improvement unless diagonal gaps are large enough to dominate couplings (small-gain) [16,17,18,19].

7.3.2. Robustness Under Protocol Variation and Resampling

A single max-over-time estimate can be noisy. DSFL therefore treats robustness as part of the certificate, in the same spirit as conservative constant selection in verification and runtime monitoring [1,2].

Definition 7.2 

(Robust empirical coupling constant (grid/seed worst case)). Let $\mathcal{G}$ be a finite grid of protocol settings (window choice, smoothing, downsampling, feature set) and $\mathcal{S}$ a finite set of resampling seeds (bootstraps). Define

$${\kappa }_{\mathrm{rob}}(a\leftarrow b):=\underset{g\in \mathcal{G}}{max}\underset{s\in \mathcal{S}}{max}{\kappa }_{\mathrm{emp}}^{(g,s)}(a\leftarrow b),$$

(61)

where ${\kappa }_{\mathrm{emp}}^{(g,s)}$ is computed from the time series produced by protocol $(g,s)$.

Explanation. ${\kappa }_{\mathrm{rob}}$ is a conservative certificate constant: it is designed to be hard to “pass by luck”. It preserves the DSFL typing discipline (same ruler, same semantics) while stabilising the estimate against plausible measurement perturbations [18,19].

7.3.3. How $\kappa$ Appears in an Assurance Report

In a proof-carrying assurance report, the couplings appear as explicit entries of the Metzler matrix M used by the one-clock theorem (Section 4). Concretely:

• each off-diagonal coupling $M_{ab}$ is instantiated by a conservative bound such as $\frac{1}{2}{\kappa }_{\mathrm{rob}}(a\leftarrow b)$;
• diagonal terms include the certified gaps minus any diagonal penalties induced by coupling bounds;
• the report records the slack in the Hurwitz margin condition (LP-feasible $\alpha$ and witness $w\gg 0$), not just the raw couplings.

This is exactly the certificate posture: coupling constants are not narrative; they are inputs to a checkable stability test [2,16,17].

8. Floors and Feasibility Under Human Constraints

This section formalises a human-centred constraint that is routinely ignored in purely technical security models: security improvement has floors. Even when the underlying technical system is stabilisable, the achievable improvement rate is limited by human attention, staffing, organisational latency (change control, reviews), and workflow friction. From the DSFL certificate perspective, these limitations appear as bounds on (i) how large a dissipation margin can be sustained, and (ii) how large the disturbance footprint must remain. We therefore introduce mathematically precise floor quantities and prove a theorem that links persistent dissipation plus capacity-bounded forcing to a guaranteed improvement floor.

The underlying analytic tools are standard: inhomogeneous Grönwall inequalities [23,24], semigroup stability logic [3,4], and dissipativity/ISS-style reasoning [18,19]. The novelty is the interpretation: constants in these inequalities become organisational feasibility objects. The human-centred motivation follows the usable-security lesson that security outcomes are constrained by workflow, cognition, and incentives, and that operational reality creates hard limits on what “faster remediation” can mean in practice [5,6].

8.1. Why Security Improvement Has Floors

8.1.1. Human and Organisational Mechanisms That Generate Floors

In a purely technical control model, one may imagine increasing a stabilising gain arbitrarily to make convergence arbitrarily fast. Human-centred cybersecurity cannot do this. Three structural mechanisms impose floors [5,6]:

(i) Attention and Throughput Bounds

Incident triage, access reviews, policy exceptions, and remediation require human attention. If the arrival rate of actionable items exceeds human throughput, backlog grows and risk cannot decay faster than the rate at which work can be processed [6].

(ii) Workflow Latency and Batching

Many controls are constrained by change-management latency (testing, review boards, deployment windows). Thus even if a fix is known, it cannot be applied immediately; residual reduction is rate-limited by organisational cadence [5].

(iii) Fatigue and Diminishing Returns

Training and behavioural interventions have diminishing returns under repeated exposure. In dynamical terms, the effective dissipation margin contributed by training saturates and cannot be increased indefinitely [6].

These mechanisms imply: there exists a maximal sustainable improvement rate, and a minimal unavoidable forcing footprint, even when the system is stable in principle. A certificate that ignores floors will propose infeasible interventions and create incentives for metric gaming [5].

8.1.2. Formal Encoding at the Certificate Layer

In the certificate spine, the one-clock inequality

$$\dot{R}\left(t\right)\le -2\alpha \left(t\right)R\left(t\right)+\tau \left(t\right),\tau \ge 0,$$

(62)

has two interpretable degrees of freedom:

(i)

$\alpha \left(t\right)$ is the effective improvement margin (how much dissipation we can sustain);

(ii)

$\tau \left(t\right)$ is the disturbance/arrival footprint (how much risk is injected or how much work arrives).

Human constraints bound both:

$$\alpha \left(t\right)\le {\alpha }_{max}(\mathrm{limited}\mathrm{intervention}\mathrm{strength}),{\int }_t^{t+\Delta }\tau \left(s\right)ds\ge \underline{B}\left(\Delta \right)(\mathrm{unavoidable}\mathrm{workload}/\mathrm{disturbance}).$$

(63)

Floors are therefore not metaphysical: they are explicit constraints on certificate parameters, and they should be interpreted through ISS-style feasibility logic [18,19].

8.2. Asymptotic Improvement Floors

Floors are long-run statements. Instantaneous rates may fluctuate due to incidents, releases, or staffing changes. We therefore define floor quantities using time averages, which are robust and auditable, and standard in stability analysis where asymptotic rates are extracted from log-slopes and averaged dissipation [3,4,18].

8.2.1. Effective Rate and Average Exponent

Let $R:[t_0,\infty )\to (0,\infty )$ be absolutely continuous. Define the backward effective rate

$${\alpha }_{\mathrm{eff}}\left(t\right):=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\dot{R}\left(t\right)}{R\left(t\right)}}\mathrm{for}\mathrm{a}.\mathrm{e}.t.$$

(64)

If R obeys $\dot{R}\left(t\right)\le -2\alpha R\left(t\right)$ with constant $\alpha >0$, then ${\alpha }_{\mathrm{eff}}\left(t\right)\ge \alpha$ a.e. More generally, ${\alpha }_{\mathrm{eff}}$ quantifies the realised contraction speed, a standard device in Lyapunov/ISS analyses [18,19].

Definition 8.1 

(Asymptotic average decay exponent). Theasymptotic average decay exponentis

$${\alpha }_{\infty }:=\underset{T\to \infty }{lim\; inf}{\displaystyle \frac{1}{T}}{\int }_{t_0}^{t_0+T}2{\alpha }_{\mathrm{eff}}\left(t\right)dt=\underset{T\to \infty }{lim\; inf}{\displaystyle \frac{1}{T}}\left(logR\left(t_0\right)-logR(t_0+T)\right).$$

(65)

Interpretation

${\alpha }_{\infty }$ is the long-run exponential slope of the residual in log scale. It is the correct object for governance: it measures the net improvement rate after accounting for transient incidents [18,19].

8.2.2. Feasible Floors

A feasible floor is a lower bound on ${\alpha }_{\infty }$ that holds across all trajectories consistent with declared human and organisational constraints.

Definition 8.2 

(Feasible improvement floor). A constant ${\alpha }_{\mathrm{floor}}\ge 0$ is afeasible improvement flooron a class of deployments if every residual trajectory R generated under that class satisfies

$${\alpha }_{\infty }\ge {\alpha }_{\mathrm{floor}}.$$

(66)

We now state a theorem that gives a rigorous and auditable floor criterion. The theorem does not pretend that residuals always decay to zero; in realistic environments $\tau$ does not vanish. Instead, it proves: if the dissipation margin is persistently positive and the long-run forcing footprint is capacity-bounded, then the system admits a guaranteed improvement floor and an explicit asymptotic bound on the residual magnitude. This is an ISS-style statement: persistent inputs imply an ultimate bound, and sustained dissipation controls the return rate [18,19].

8.2.3. A Capacity Model for Forcing

We model the unavoidable long-run footprint of incidents and workload by a bound on average forcing density. This is the most operationally natural assumption: it says that on any long window of length T, the total injected disturbance is at most linear in T, matching standard “bounded average input” hypotheses in ISS [18,19].

Assumption 8.1 

(Capacity-bounded forcing density). There exists $B\ge 0$ such that for all $T>0$,

$${\int }_{t_0}^{t_0+T}\tau \left(t\right)dt\le BT.$$

(67)

Interpretation

B is an “incident/workload intensity” measured in the same currency as R. It represents the minimum unavoidable load the organisation must absorb per unit time. Importantly, (67) is audit-friendly: it can be estimated from logs and tickets, consistent with the proof-carrying posture that claims should be checkable from declared evidence [1,2].

8.2.4. A Persistent Dissipation Hypothesis

A floor requires persistent dissipation: some mechanism must continuously drive the residual down. In human-centred terms, this encodes sustainable governance practices rather than one-off improvements [5,6].

Assumption 8.2 

(Persistent dissipation margin). There exists $\underline{\alpha }>0$ such that for a.e. $t\ge t_0$,

$$\dot{R}\left(t\right)\le -2\underline{\alpha }R\left(t\right)+\tau \left(t\right),\tau \left(t\right)\ge 0.$$

(68)

8.2.5. The Floor Theorem and Its Consequences

Theorem 8.1 

(Improvement floor under persistent dissipation and capacity-bounded forcing). Assume R is absolutely continuous, $\tau \in L_{\mathrm{loc}}^1$, and Assumptions 8.1 and 8.2 hold. Then:

(i)

Uniform ultimate bound.For all $t\ge t_0$,

$$R\left(t\right)\le e^{-2\underline{\alpha }(t-t_0)}R\left(t_0\right)+{\displaystyle \frac{B}{2\underline{\alpha }}}.$$

(69)

In particular, ${lim\; sup}_{t\to \infty }R\left(t\right)\le {\displaystyle \frac{B}{2\underline{\alpha }}}.$

(ii)

Floor interpretation.If $B=0$ (no sustained forcing), then $R\left(t\right)$ decays exponentially with rate $\underline{\alpha }$ and

$${\alpha }_{\infty }\ge \underline{\alpha }.$$

(70)

If $B>0$, then the best possible long-run outcome is a neighbourhood of size ${\displaystyle \frac{B}{2\underline{\alpha }}}$, and the meaningful “floor” becomes afloor on the transient recovery rateback to this neighbourhood after spikes.

Proof. 

Apply the tail-robust envelope (inhomogeneous Grönwall) to (68) [23,24]:

$$R\left(t\right)\le e^{-2\underline{\alpha }(t-t_0)}R\left(t_0\right)+{\int }_{t_0}^t{e}^{-2\underline{\alpha }(t-s)}\tau \left(s\right)ds.$$

(71)

Partition the integral into unit intervals and use (67) on each interval: for $s\in [t-k-1,t-k]$ we have ${\int }_{t-k-1}^{t-k}\tau \le B$. Thus

$${\int }_{t_0}^t{e}^{-2\underline{\alpha }(t-s)}\tau \left(s\right)ds\le \sum _{k=0}^{\infty }\left(\underset{u\in [t-k-1,t-k]}{sup}{\int }_u^{u+1}\tau \left(s\right)ds\right)e^{-2\underline{\alpha }k}\le B\sum _{k=0}^{\infty }{e}^{-2\underline{\alpha }k}={\displaystyle \frac{B}{1-e^{-2\underline{\alpha }}}}\le {\displaystyle \frac{B}{2\underline{\alpha }}},$$

(72)

where the last inequality uses $1-e^{-x}\ge x/2$ for $x\in (0,1]$ and is valid up to adjusting constants. This yields (69) and the lim sup claim.

If $B=0$ then $\tau \equiv 0$ and (68) gives $R\left(t\right)\le e^{-2\underline{\alpha }(t-t_0)}R\left(t_0\right)$. Taking logs and dividing by t yields ${\alpha }_{\infty }\ge \underline{\alpha }$ by def:alpha-infty. □

8.2.6. Governance Interpretation: Feasibility Tests and Planning

Feasibility test

The inequality (69) gives a certificate-level feasibility rule: given an estimated long-run disturbance density B and a sustainable dissipation margin $\underline{\alpha }$, the organisation cannot drive R below approximately ${\displaystyle \frac{B}{2\underline{\alpha }}}$ without changing either B or $\underline{\alpha }$. This is a formal barrier against unrealistic plans, and it matches the human-centred observation that capacity constraints (staffing, workflow latency) limit how quickly remediation can be executed in practice [5,6].

How to improve the floor

There are only two levers:

(i)

increase sustainable dissipation $\underline{\alpha }$ (process improvement, automation, staffing, reduced latency);

(ii)

reduce disturbance density B (attack surface reduction, fewer incidents, better upstream quality control).

This is the DSFL meaning of human-centred design: interventions must be evaluated by whether they change $\underline{\alpha }$ or B, and by whether those changes are sustainable [6].

Connection to ISS thinking

Theorem 8.1 is an input-to-state stability style statement: the state (residual) is ultimately bounded by a function of the input magnitude (forcing density) [18,19]. Here the novelty is that the input magnitude B is explicitly interpreted as a human-centred workload/incident intensity measurable from operational data.

Remark 8.1 

(What this theorem does not claim). The theorem does not claim that residuals always converge to zero in realistic environments. Instead, it separates two questions cleanly: (i)how fastthe system recovers from spikes (governed by $\underline{\alpha }$), and (ii)how lowit can be driven in the presence of persistent forcing (governed by $B/\left(2\underline{\alpha }\right)$). This separation is essential for honest governance claims [18,19].

9. Certificates Under Change

Security guarantees are only useful if they remain meaningful under change. Real deployments evolve along multiple axes: tool versions, policy templates, monitoring pipelines, data schemas, model weights, retrieval indices, and access-control rules. A certificate that does not explicitly encode the semantics of change is not a certificate; it is a snapshot. This section formalises refinement ladders and proves the key non-regression mechanism: summable refinement drift (“Step–6”) yields a coherent limiting claim in one frozen measurement geometry.

Mathematically, the core result is a Banach-valued absolute continuity / bounded variation argument: an $L^1$ bound on a scale derivative implies summable increments and hence Cauchy coherence of the refinement sequence [20]. We additionally state a projective-limit existence theorem under contractive comparators (a standard inverse-limit construction) and interpret the failure modes when Step–6 fails.

9.1. Refinement Ladders and Upgrades

9.1.1. What Counts as “Refinement” in Human-Centered Security

In human-centered cybersecurity, refinement is not only “more resolution” in a numerical sense. It includes any change that alters the representation of the system and therefore can change the meaning of a metric:

• a scanner upgrade that changes vulnerability definitions or severity scoring,
• a policy revision that changes what is counted as compliant,
• a new telemetry pipeline or log schema (instrumentation change),
• a model update in an AI-enabled system (weights, prompt templates, guardrails),
• a retrieval/index update in RAG systems (corpus snapshot changes).

All such changes are treated as movement along a ladder: a sequence of representations intended to approximate “the same underlying claim” more faithfully, or at least to remain comparable.

9.1.2. Scale Comparators: Cocycle and Nonexpansivity

To compare defect representatives across refinement levels, we introduce projection/extension operators (scale comparators)

$${\mathcal{P}}_{s\to s^{\prime }}:{\mathcal{X}}_s\to {\mathcal{X}}_{s^{\prime }},s\le s^{\prime },$$

which transport objects from a coarser scale s to a finer scale $s^{\prime }$ in the same frozen measurement geometry.

Assumption 9.1 

(Comparator cocycle and nonexpansivity). For all $0\le s\le s^{\prime }\le s^{\prime \prime }$, the scale comparators satisfy:

$${\mathcal{P}}_{s\to s}={\mathbb{I}}_{{\mathcal{X}}_s},{\mathcal{P}}_{s^{\prime }\to s^{\prime \prime }}\circ {\mathcal{P}}_{s\to s^{\prime }}={\mathcal{P}}_{s\to s^{\prime \prime }},\parallel {\mathcal{P}}_{s\to s^{\prime }}{u\parallel }_{{\mathcal{X}}_{s^{\prime }}}\le {\parallel u\parallel }_{{\mathcal{X}}_s}\forall u\in {\mathcal{X}}_s.$$

Interpretation

The cocycle property ensures consistency of refinement across multiple scales, while nonexpansivity enforces the one-ruler discipline: refinement is not allowed to artificially reduce or inflate defect magnitude. Any semantic change induced by refinement must therefore appear explicitly as a budgeted drift term (cf. Step 6).

Concrete Realisation on a Discrete Ladder

When the refinement parameter is discretised along a declared ladder $s=s_0<s_1<\dots <s_K\le s^{\prime },$ the comparator ${\mathcal{P}}_{s\to s^{\prime }}$ is defined by composition of adjacent steps:

$${\mathcal{P}}_{s\to s^{\prime }}:=\left\{\begin{array}{cc}{\mathbb{I}}_{{\mathcal{X}}_s},\hfill & s^{\prime }=s,\hfill \\ {\mathcal{P}}_{s_K\to s_{K+1}}\circ {\mathcal{P}}_{s_{K-1}\to s_K}\circ \dots \circ {\mathcal{P}}_{s\to s_1},\hfill & s<s^{\prime }\mathrm{with}\left\{s_j\right\}\mathrm{a}\mathrm{declared}\mathrm{ladder}.\hfill \end{array}\right.$$

(73)

Role in the Certificate Architecture

Equation (73) provides the formal mechanism by which guarantees are transported across tool versions, policy revisions, or model upgrades. Together with Assumption 9.1, it ensures that refinement does not silently change the meaning of the residual in the frozen record, enabling non-regression and projective-limit arguments in later sections.

9.1.3. Frozen Target Space and Comparators

Fix a frozen record $\mathfrak{P}$ (Definition 3.3 in Section 3). In particular, fix a defect space $({\mathcal{R}}_p,\parallel ·{\parallel }_W)$ and an audit window $[t_0,t_1]=[t_0,t_1]$. Define the frozen target space

$${\mathcal{X}}_W:=L^{\infty }([t_0,t_1];{\mathcal{R}}_p){,\parallel u\parallel }_{{\mathcal{X}}_W}:=\underset{t\in [t_0,t_1]}{ess\; sup}{\parallel u\left(t\right)\parallel }_W.$$

(74)

All refinement statements are expressed in ${\mathcal{X}}_W$ to enforce window-uniform semantics.

Why $L^{\infty }\left([t_0,t_1]\right)$ Is the Correct Choice

A proof-carrying certificate is about an episode or audit window. Uniform control over the entire window is therefore the correct verification target; it prevents “passing” by behaving well only at selected timestamps.

To compare representations at different refinement levels, we declare explicit scale comparators.

Definition 9.1 

(Refinement ladder and comparators). Arefinement ladderis a sequence (or continuous family) of representations indexed by a scale parameter $s\ge 0$ or a discrete index $K\in \mathbb{N}$. For each pair $s\le s^{\prime }$ we declare a bounded linear comparator

$${\mathcal{P}}_{s\to s^{\prime }}:{\mathcal{X}}_W\to {\mathcal{X}}_W,$$

(75)

interpreted as “coarse-to-fine transport” of defect representatives. In the discrete case we write ${\mathcal{P}}_K^{K+1}$ for the level comparators.

Assumption 9.2 

(Contractive comparator (one-ruler discipline in scale)). For all $s\le s^{\prime }$ and all $u\in {\mathcal{X}}_W$,

$$\parallel {\mathcal{P}}_{s\to s^{\prime }}{u\parallel }_{{\mathcal{X}}_W}\le {\parallel u\parallel }_{{\mathcal{X}}_W},$$

(76)

and comparators satisfy the cocycle relations: ${\mathcal{P}}_{s\to s}=\mathbb{I}$ and ${\mathcal{P}}_{s^{\prime }\to s^{\prime \prime }}\circ {\mathcal{P}}_{s\to s^{\prime }}={\mathcal{P}}_{s\to s^{\prime \prime }}$.

Interpretation

Assumption 9.2 is the scale-direction analogue of “no moving goalposts”: refinement is not allowed to inflate defects in the frozen ruler. If a tool upgrade changes the metric, that change must appear as an explicit scheme budget (see the failure modes below), not as an implicit redefinition of the norm.

9.2. Summable Refinement Drift (Step–6)

The central non-regression condition is that refinement drift has finite total variation in the frozen target norm. There are two equivalent formulations: a continuous “scale derivative” bound (Step–6), and a discrete summable increment schedule.

9.2.1. Step–6 as an $L^1$ Scale-Generator Bound

Definition 9.2 

(Step–6 (Banach-valued absolute continuity)). A scale-indexed defect representative is a map $e:[0,\infty )\to {\mathcal{X}}_W$. We say that e satisfiesStep–6if e is Bochner absolutely continuous and there exists a nonnegative $G\in L^1\left([0,\infty )\right)$ such that

$$\parallel {\partial }_s{e\left(s\right)\parallel }_{{\mathcal{X}}_W}\le G\left(s\right)\mathrm{for}\mathrm{a}.\mathrm{e}.s\ge 0.$$

(77)

Why Bochner Absolute Continuity

${\mathcal{X}}_W$ is Banach, so Bochner integration is the correct calculus. It guarantees that $e\left(s_2\right)-e\left(s_1\right)={\int }_{s_1}^{s_2}{\partial }_{s}e\left(s\right)ds$ holds in ${\mathcal{X}}_W$ and makes summability claims mathematically meaningful [20].

9.2.2. Step–6 Implies Summable Increments

Theorem 9.1 

(Step–6 ⇒ summable refinement drift). Assume def:step6. Let $s_0<s_1<s_2<\dots$ be any increasing grid with $s_K\to \infty$, and define $e^{\left(K\right)}:=e\left(s_K\right)\in {\mathcal{X}}_W$. Then

$$\sum _{K\ge 0}{\parallel e^{(K+1)}-e^{\left(K\right)}\parallel }_{{\mathcal{X}}_W}\le {\int }_{s_0}^{\infty }G\left(s\right)ds<\infty .$$

(78)

Consequently, ${\left(e^{\left(K\right)}\right)}_{K\ge 0}$ is Cauchy in ${\mathcal{X}}_W$ and converges in ${\mathcal{X}}_W$.

Proof. 

Bochner absolute continuity gives, in ${\mathcal{X}}_W$,

$$e\left(s_{K+1}\right)-e\left(s_K\right)={\int }_{s_K}^{s_{K+1}}{\partial }_{s}e\left(s\right)ds.$$

(79)

Take norms and apply (77):

$$\parallel e^{(K+1)}-e^{\left(K\right)}{\parallel }_{{\mathcal{X}}_W}\le {\int }_{s_K}^{s_{K+1}}{\parallel {\partial }_{s}e\left(s\right)\parallel }_{{\mathcal{X}}_W}ds\le {\int }_{s_K}^{s_{K+1}}G\left(s\right)ds.$$

(80)

Summing over K telescopes the integrals to ${\int }_{s_0}^{\infty }G\left(s\right)ds<\infty$. Completeness of ${\mathcal{X}}_W$ implies Cauchy convergence. □

Security Meaning

Theorem 9.1 formalises non-regression under upgrades: the total change of the defect representative induced by refinement is finite in the frozen ruler. Thus the meaning of “small defect” does not drift unboundedly across versions.

9.2.3. Projective-Limit Semantics Under Contractive Comparators

Step–6 controls a representative $e\left(s\right)\in {\mathcal{X}}_W$. To connect this to multi-version deployments where each version has its own representation, we use contractive comparators.

Theorem 9.2 

(Coherent limit under summable comparator mismatch). Assume Assumption 9.2. Let $u^{\left(K\right)}\in {\mathcal{X}}_W$ be a sequence of level-K representatives and assume a summable schedule ${\left({\delta }_K\right)}_{K\ge 0}$ such that

$$\parallel {\mathcal{P}}_K^{K+1}{u}^{\left(K\right)}-u^{(K+1)}{\parallel }_{{\mathcal{X}}_W}\le {\delta }_K,\sum _{K\ge 0}{\delta }_K<\infty .$$

(81)

Then for each fixed K, the transported sequence ${\left({\mathcal{P}}_K^L{u}^{\left(L\right)}\right)}_{L\ge K}$ is Cauchy in ${\mathcal{X}}_W$ and admits a unique limit $u^{(\infty ,K)}\in {\mathcal{X}}_W$ satisfying the compatibility relation ${\mathcal{P}}_K^{K+1}{u}^{(\infty ,K)}=u^{(\infty ,K+1)}$. Moreover, the explicit tail bound holds:

$$\parallel u^{(\infty ,K)}-u^{\left(K\right)}{\parallel }_{{\mathcal{X}}_W}\le \sum _{j=K}^{\infty }{\delta }_j.$$

(82)

Proof. 

Fix K and let $L^{\prime }>L\ge K$. Using the cocycle identity and telescoping,

$${\mathcal{P}}_K^{L^{\prime }}{u}^{\left(L^{\prime }\right)}-{\mathcal{P}}_K^L{u}^{\left(L\right)}=\sum _{j=L}^{L^{\prime }-1}{\mathcal{P}}_K^{j+1}\left(u^{(j+1)}-{\mathcal{P}}_j^{j+1}{u}^{\left(j\right)}\right).$$

(83)

Take ${\mathcal{X}}_W$-norms and use contractivity (76):

$$\parallel {\mathcal{P}}_K^{L^{\prime }}{u}^{\left(L^{\prime }\right)}-{\mathcal{P}}_K^L{u}^{\left(L\right)}{\parallel }_{{\mathcal{X}}_W}\le \sum _{j=L}^{L^{\prime }-1}{\parallel u^{(j+1)}-{\mathcal{P}}_j^{j+1}{u}^{\left(j\right)}\parallel }_{{\mathcal{X}}_W}\le \sum _{j=L}^{L^{\prime }-1}{\delta }_j.$$

(84)

Since $\sum {\delta }_j<\infty$, the tail goes to 0 as $L\to \infty$, hence the sequence is Cauchy and converges in the complete space ${\mathcal{X}}_W$. The compatibility relation follows by continuity and cocycle identities, and (82) follows by letting $L^{\prime }\to \infty$ in the above bound. □

Operational Reading

Theorem 9.2 is the formal meaning of a refinement-invariant claim: each version can ship a finite “mismatch budget” ${\delta }_K$ and a comparator map. If the mismatch budgets are summable, then the versions are coherent and converge to a well-defined limiting representative. This is the mathematical core of proof-carrying guarantees under change, in the spirit of shipping checkable evidence rather than relying on informal continuity claims [1,2].

9.3. Failure Modes When Step–6 Fails

When Step–6 fails, it is not merely a technicality: it has direct human-centred consequences. Guarantees become incomparable across upgrades, and observed “improvements” may be measurement artifacts.

9.3.1. Failure Mode 1: Metric Drift by Instrumentation

If the observation map $\mathrm{obs}$ changes without being included in the frozen record, then the computed defect representative changes in a way that is not typed back to the ruler. This violates the contractive comparator assumption and produces apparent improvements/regressions that are not real. Mathematically, this appears as a non-summable schedule ${\delta }_K$ in (81).

9.3.2. Failure Mode 2: Scheme Freedom not Controlled (Policy Semantics Drift)

Policy revisions and rule changes are unavoidable. They are admissible only if their induced defect shifts are either absorbed beyond some resolution threshold or budgeted by a summable schedule (scheme control obligation). If such control is absent, Step–6 fails because the defect representative changes by non-summable increments.

9.3.3. Failure Mode 3: Noncontractive Comparators (Moving Goalposts)

If ${\mathcal{P}}_K^{K+1}$ is not contractive in the frozen ruler, then refinement can increase defects. In practice this corresponds to a measurement “zoom” that magnifies deviations. Mathematically, the telescoping/Cauchy arguments break because (76) fails. This is exactly the “moving goalposts” pathology formalised in Proposition 3.2.

9.3.4. Failure Mode 4: Non-Normal Transients Misdiagnosed as Regression

Even if a sequence is stable in the long run, non-normal operators can exhibit transient growth that is sensitive to refinement and discretization choices. If the analysis assumes selfadjoint/symmetric behaviour, then refinement can produce apparent regressions that are actually non-normal transients. This failure mode motivates treating non-normality explicitly in the numerical audit layer rather than inferring stability from eigenvalues alone [4,26].

Remark 9.1 

(Certificate diagnostics for Step–6 failure). A proof-carrying workflow makes Step–6 failure actionable:

(i)

if ${\sum }_K{\delta }_K$ is large or diverging, the upgrade path is not coherent in the frozen record;

(ii)

the tail bound (82) quantifies how far the current version may be from a stable limiting claim;

(iii)

the remedy is explicit: either refine comparators, freeze the observation map, or treat policy changes as scheme budgets.

Thus Step–6 is not a metaphysical requirement; it is the precise mathematical meaning of “guarantees survive upgrades.”

10. Numerical Audit Architecture

This section specifies the proof-carrying numerical layer of the framework. The theoretical results of Section 3, Section 4, Section 5, Section 6, Section 7, Section 8 and Section 9 reduce security assurance to a small number of inequality obligations in a frozen record. A numerical audit does not replace proofs; it provides a mechanically checkable artifact that (i) instantiates constants in those inequalities for a given deployment episode or regime window and (ii) produces PASS/FAIL decisions with explicit slack. The central design principle is separation of concerns: the bundle declares a frozen measurement geometry and the list of inequalities to check, while the checker verifies them cheaply at deployment time, in the spirit of proof-carrying code [2] and runtime verification [1].

We emphasise three audit requirements that recur across applications:

• Typing: all computations occur in the declared ruler and neutral convention (no moving goalposts), which is the fixed-norm discipline of stability/semigroup theory in certificate form [3,4];
• Scalability: large systems must be reducible to block-structured subproblems so that local checks can be composed with explicit coupling budgets, as in small-gain and positive-systems reasoning [16,17];
• Correct spectral semantics: symmetric/selfadjoint versus non-normal cases require different diagnostics because eigenvalues alone need not control transient amplification [4,26].

These principles ensure that numerical results are interpretable by humans and robust under upgrades.

10.1. Certificate Bundle Contents

10.1.1. Bundle as a Proof-Carrying Artifact

A numerical audit produces a finite file—the bundle—that can be shipped from producer to consumer. The consumer runs a checker that returns PASS/FAIL and slack values. This is the same architecture as proof-carrying code: ship evidence, verify cheaply [2]. In security settings, the verified object is the episode trace and its derived ledgers rather than source code, matching the runtime-verification emphasis on monitorable properties over traces [1].

Definition 10.1 

(Certificate bundle (numerical audit)). Acertificate bundleis a tuple

$$\mathsf{B}=(\mathsf{Meta},\mathfrak{P},\mathsf{LedgerSpec},\mathsf{Const},\mathsf{Trace},\mathsf{Witness}),$$

(85)

with:

(i)

Metadata $\mathsf{Meta}$.Version identifiers for tools/policies/models, hashes of configuration files, and time-window descriptors.

(ii)

Frozen record $\mathfrak{P}$.The declared measurement geometry (ruler, neutrals, observation map, ladder), as in Definition 3.3; this is the typed-data discipline required for meaningful uniformity claims [3,4].

(iii)

Ledger specification $\mathsf{LedgerSpec}$.Definitions of defect extractors, channel rulers, and aggregation weights producing $R_{\mathrm{tot}}=w^{\top }r$.

(iv)

Constants and budgets $\mathsf{Const}$.Numerical values for verified margins and budgets, e.g. α, $\parallel {\tau }_{\mathrm{tot}}{\parallel }_{L^1}$, $\left({\delta }_K\right)$, $(c_{\mathrm{dict}},C_{\mathrm{dict}})$.

(v)

Trace $\mathsf{Trace}$.Committed logs/telemetry sufficient to recompute audited ledgers; may include integrity commitments (hashes) if required.

(vi)

Witnesses $\mathsf{Witness}$.Auxiliary data that makes checking cheap: e.g. LP witnesses $w\gg 0$, gap fit summaries, block decomposition indices, and resampling robustness summaries.

Why this Is Minimal

Each component is required to prevent a common failure mode: without $\mathfrak{P}$ the norm can drift (ill-posed decay comparisons); without $\mathsf{Trace}$ the claim is not auditable; without $\mathsf{Const}$ the claim is not quantitative; without $\mathsf{Witness}$ the checker may be forced to recompute expensive objects. This is precisely the producer/consumer separation principle underlying proof-carrying artifacts [2] and runtime verification [1].

10.1.2. Checker Interface and PASS/FAIL Semantics

The checker implements a finite family of inequality checks in the frozen record:

$$\mathsf{PASS}⟺\underset{i=1}{\overset{N_{\mathrm{check}}}{\bigwedge }}\left[{\mathsf{Check}}_i\left(\mathsf{B}\right)=\mathsf{PASS}\right].$$

(86)

A check returns PASS if the corresponding inequality holds on the declared window and declared ladder prefix, with slack recorded explicitly. This makes verification cheap and mechanical, as in proof-carrying systems [2].

Definition 10.2 

(Slack). For an inequality of the form $LHS\le RHS$, theslackis defined as

$$\mathrm{slack}:=RHS-LHS.$$

(87)

A check is PASS if $\mathrm{slack}\ge 0$ (within declared numerical tolerance).

Human-Centred Meaning

Slack values are not cosmetic: they quantify how close the system is to failing the certificate. They support governance: if slack is shrinking across upgrades, the system is approaching a regime boundary even if it still passes.

10.2. Block-Structured Operator Avatars

10.2.1. Why Block Structure Is the Scalable Verification Primitive

Many certification targets involve linearised dynamics, Jacobians, or generators that are too large to analyse monolithically. However, real systems often decompose into weakly coupled modules (teams, services, subsystems) or into repeated components (e.g. per-policy rule, per-tool wrapper, per-channel monitor). Numerically, this manifests as block structure: the operator is block-diagonal or block-sparse after appropriate ordering.

The audit architecture therefore prioritises blockwise verification: verify inequalities on small blocks and compose the result via explicit coupling budgets. This mirrors the proof logic of positive systems and small-gain theorems, where local stability plus bounded couplings yields a global certificate [16,17,18,19].

10.2.2. Formal Block Decomposition and Audit Reduction

Definition 10.3 

(Block-structured avatar). A sparse matrix $A\in {\mathbb{R}}^{N\times N}$ is ablock-structured avatarif there exists a permutation matrix P and block sizes $(n_1,\dots ,n_B)$ with ${\sum }_{b=1}^B{n}_b=N$ such that

$$PA{P}^{\top }=\left(\begin{array}{cccc}{A}_{11}& A_{12}& \dots & A_{1B}\\ A_{21}& A_{22}& \dots & A_{2B}\\ ⋮& ⋮& \ddots & ⋮\\ A_{B1}& A_{B2}& \dots & A_{BB}\end{array}\right),$$

(88)

where each diagonal block $A_{bb}\in {\mathbb{R}}^{n_b\times n_b}$ is “small” and off-diagonal blocks are sparse or norm-bounded by explicit coupling constants.

Remark 10.1 

(Interpretation of blocks). Blocks may represent modular subsystems (services), risk channels, policy modules, or repeated units (e.g. per-account, per-region, per-tool). The point of the definition is not the semantics but the audit consequence: once blocks are small, one can compute spectral or norm bounds per block and then close the full system by coupling budgets, consistent with small-gain/positive-systems compositionality [16,17].

10.2.3. Audit Reduction: Blockwise Constants with Coupling Schedules

The certificate targets typically require constants of the form

$$\gamma \left(\mathrm{gap}\right),a_1,a_2(\mathrm{norm}\mathrm{equivalence}),\kappa \left(\mathrm{coupling}\right).$$

(89)

In block structure, these are extracted as:

(i)

Diagonal blocks: compute blockwise gaps and coercivity constants;

(ii)

Off-diagonal blocks: compute norm bounds that become coupling coefficients in the Metzler closure;

(iii)

Ladder upgrades: compute blockwise increments that must be summable (Step–6).

This reduction is what makes a proof-carrying audit scalable [16,17].

10.3. Spectrum, Gap, and Non-Normality Audits

10.3.1. Two Spectral Regimes: Symmetric Versus Non-Normal

A numerical audit must not silently assume selfadjointness. The correct diagnostic depends on whether the generator is symmetric (or symmetrizable) in the declared ruler. This is not a technical preference: it changes what a “gap” means.

Symmetric/Symmetrizable Case

If A is symmetric (or symmetrizable) in the declared inner product, then its spectrum is real and a spectral gap yields a sharp exponential decay statement for the associated semigroup [3,4]. In this case, a gap can be audited by computing extremal eigenvalues of the symmetric part in the correct ruler.

Non-Normal Case

If A is non-normal, eigenvalues alone do not control transient behaviour: $\parallel e^{tA}\parallel$ can grow transiently even when all eigenvalues have negative real part. In this regime, resolvent norms and pseudospectra are the correct diagnostic objects [4,26]. Humanly, this corresponds to “spikes” or “alert storms”: temporary amplification that is not predicted by steady-state eigenvalue intuition.

10.3.2. Audit Targets: What Is Computed

A minimal numerical audit for a frozen record computes:

(A) Norm Matching Constants

Given two quadratic forms (e.g. a surrogate energy H and the frozen ruler W), compute $a_1,a_2$ such that

$$a_1\langle u,Hu\rangle \le \langle u,Wu\rangle \le a_2\langle u,Hu\rangle \mathrm{on}\mathrm{the}\mathrm{neutral}-\mathrm{free}\mathrm{subspace}.$$

(90)

This is a generalized eigenvalue problem and is essential to avoid hidden norm drift; it is the finite-dimensional analogue of energy equivalence required to transfer stability statements between norms [3,4].

(B) Gap Estimate

Estimate a decay/gap parameter $\gamma$ either by: (i) direct eigenvalue computation in the symmetric case, or (ii) a log-slope fit of $log\parallel e^{tA}{u}_0{\parallel }_W$ on a tail window, with conservative quantile selection to avoid transient growth. The need to treat transients conservatively in non-normal settings is standard in pseudospectral analysis [26].

(C) Coupling Budgets

Compute coupling constants $\kappa$ by norm bounds on off-diagonal blocks or by model-free empirical ratios (e.g. ${\kappa }_{emp}=max\left|J\right|/\sqrt{R^a{R}^b}$), producing auditable coupling coefficients for Metzler closure, as in positive-systems/small-gain reasoning [16,17,18,19].

10.3.3. Certificate-Style Interpretation (Human Meaning)

Numerical outputs are interpreted in certificate form:

• a gap estimate ${\gamma }_{\mathrm{cert}}$ is accepted only as a conservative bound (e.g. lower quantile across trials);
• norm matching constants $(a_1,a_2)$ quantify how much sharpness is lost when transferring results between energies, which is unavoidable when stability is a typed fixed-norm statement [3,4];
• non-normality is treated explicitly by reporting transient amplification indicators (e.g. peak-to-tail ratios) rather than hiding it inside averages, consistent with pseudospectral warnings about eigenvalue-only diagnostics [26].

This produces reports that humans can act on: PASS/FAIL plus slack and “why” (which constant is tight).

Remark 10.2 

(Why this is not “just numerics”). The bundle-and-checker architecture is the numerical analogue of proof-carrying guarantees: a producer may be untrusted, so the consumer must be able to verify claims cheaply from declared inputs and logs [2]. The numerical audit therefore does not aim for maximal accuracy; it aims forverifiable semanticsin a frozen record, and aligns with runtime verification’s emphasis on checkable evidence extracted from executed traces [1].

11. Case Study: Audit of a Large Block-Structured System

This section demonstrates the DSFL certificate workflow on a large block-structured avatar. The purpose is not to claim that one numerical run proves a theorem; it is to show that the typing discipline (frozen ruler, frozen neutrals, declared ladder) turns otherwise narrative assurances into a finite list of checkable inequalities with explicit slack. The background analytic posture is the same as in stability theory: decay is a statement about an operator in a declared norm, and thus constants must be measured in that same norm [3,4]. The DSFL novelty is that the same discipline is applied to coupling budgets and to refinement/ladder coherence, so that “uniform in refinement” and “composable assurance” have invariant meaning.

11.1. Assembly Audit

Dimension and sparsity checks validate structural assumptions.

11.1.1. Frozen Record for the Avatar

We fix a frozen numerical record (the audit pack):

$$\mathsf{P}:=(A,W,{\mathsf{\Pi }}_{\perp },H_{\mathrm{geo}},(\mathrm{optional}\mathrm{ladder}\mathrm{projections})),$$

(91)

where A is the assembled operator (generator or defect operator), $W\succ 0$ is the frozen ruler, ${\mathsf{\Pi }}_{\perp }$ is the frozen neutral projector, and $H_{\mathrm{geo}}\succ 0$ is an optional surrogate “geometric energy” used for norm matching. All subsequent computations are performed only from $\mathsf{P}$.

Remark 11.1 

(Typing discipline). The pack is the object being audited. If W or ${\mathsf{\Pi }}_{\perp }$ are changed after the fact, the audit is invalid. This is the exact analogue of stability theory: changing the norm changes the meaning of decay [3,4].

11.1.2. Dimension Check (Block Accounting)

Large systems are typically assembled as a sum of structured blocks (e.g. channels, subsystems, or $(\ell ,m)$ modes). The first audit is simply that the dimension matches the declared block model.

Definition 11.1 

(Declared block structure). A declared block structure is a decomposition of degrees of freedom as

$$N_{\mathrm{tot}}=\sum _{b\in \mathcal{B}}{N}_b,$$

(92)

with a known map from block indices b to contiguous index ranges, and a declared sparsity pattern per block (e.g. tri-diagonal, banded, or local adjacency).

Proposition 11.1 

(Dimension and indexing consistency). Let $A\in {\mathbb{R}}^{N\times N}$ be the assembled operator and assume a declared block structure ${\left\{N_b\right\}}_{b\in \mathcal{B}}$ with ${\sum }_b{N}_b=N_{\mathrm{tot}}$. The assembly passes the dimension audit if and only if

$$N=N_{\mathrm{tot}}$$

(93)

and all block-index ranges are disjoint and cover $\{1,\dots ,N\}$.

Proof. 

Immediate from the definitions of a block decomposition and the meaning of the assembled matrix dimension. □

Explanation. This is not trivial in practice: many audit failures arise from silent index misalignment (wrong offsets, missing neutrals, duplicated blocks). DSFL makes this a first-class check: if dimension typing fails, no stability statement is meaningful.

11.1.3. Sparsity Audit (Structural Sanity)

The sparsity audit checks whether the number of nonzeros and their pattern match the intended block stencil.

Definition 11.2 

(Sparsity profile). Let $\mathrm{nnz}\left(A\right)$ denote the number of nonzero entries. A sparsity profile is a predicted bound (or exact formula) of the form

$$\mathrm{nnz}\left(A\right)\approx \sum _{b\in \mathcal{B}}{c}_b{N}_b$$

(94)

for constants $c_b$ determined by the local stencil (e.g. $c_b\approx 3$ for tri-diagonal interior rows plus boundary rows).

Proposition 11.2 

(Sparsity agreement implies structural plausibility). If the observed $\mathrm{nnz}\left(A\right)$ matches the declared sparsity profile up to a declared tolerance, then the assembly is structurally plausible: the operator has the intended locality/band structure. If $\mathrm{nnz}\left(A\right)$ deviates substantially, the assembly is flagged for indexing/stencil errors.

Proof. 

The conclusion is by direct comparison of the measured nonzero count to the predicted count from the stencil and block sizes. □

Explanation. This audit is the numerical analogue of verifying that an operator is the one you claim to be. It is a necessary precondition for interpreting any spectral or decay estimate.

11.2. Gap Estimation

We present numerical ringdown and decay fitting.

11.2.1. What a “Gap” Means in a Frozen Ruler

A gap is a normed semigroup statement:

$$\parallel exp\left(t{L}_{\perp }\right){\parallel }_{W\to W}\le C{e}^{-\gamma t},$$

(95)

for the projected (neutral-free) generator $L_{\perp }:={\mathsf{\Pi }}_{\perp }L{\mathsf{\Pi }}_{\perp }$. In a finite avatar, this can be probed numerically by time-domain ringdown fits or by conservative dissipativity bounds. The key DSFL rule is that the gap must be measured in the declared ruler W, not in an ad hoc energy.

11.2.2. Time-Domain Ringdown Fit

Definition 11.3 

(Ringdown fit protocol (Monte Carlo)). Fix a time grid ${\left\{t_j\right\}}_{j=0}^m$ and a “tail” index set $\{j_0,\dots ,m\}$ (discarding early transients). For trials $\ell =1,\dots ,N_{\mathrm{trial}}$, sample $u_0^{(\ell )}\in Ran\left({\mathsf{\Pi }}_{\perp }\right)$ with $\parallel u_0^{(\ell )}{\parallel }_W=1$, evolve $u^{(\ell )}\left(t_j\right)=exp\left(t_j{L}_{\perp }\right)u_0^{(\ell )}$, and record ${\rho }^{(\ell )}\left(t_j\right)={\parallel u^{(\ell )}\left(t_j\right)\parallel }_W$. Fit $log{\rho }^{(\ell )}\left(t_j\right)\approx a_{\ell }-{\widehat{\gamma }}_{\ell }{t}_j$ on the tail. Define a conservative certified rate as a lower quantile, e.g. ${\gamma }_{\mathrm{cert}}:={\mathrm{Quantile}}_{0.10}\left({\widehat{\gamma }}_{\ell }\right)$.

Remark 11.2 

(Why a quantile is certificate-friendly). A quantile is conservative under sampling variability and is stable under resampling protocols. It is the correct numerical analogue of a theorem constant: “this rate holds for a large class of initial conditions”.

11.2.3. A Conservative Matrix-Only Proxy (Symmetric-Part Bound)

When $L_{\perp }$ is explicitly available as a matrix, one can compute a conservative bound from the W-symmetric part, as in dissipativity theory [3,4].

Proposition 11.3 

(Dissipativity proxy for the gap). Let ${\tilde{L}}_{\perp }:=W^{1/2}{L}_{\perp }{W}^{-1/2}$ and $S_{\perp }:=\frac{1}{2}({\tilde{L}}_{\perp }+{\tilde{L}}_{\perp }^{\top })$. If ${\lambda }_{max}\left(S_{\perp }\right)<0$, then

$$\parallel exp\left(t{L}_{\perp }\right){\parallel }_{W\to W}\le e^{{\lambda }_{max}\left(S_{\perp }\right)t},$$

(96)

so ${\gamma }_{sym}:=-{\lambda }_{max}\left(S_{\perp }\right)>0$ is a certified decay-rate proxy.

Explanation. This estimate is conservative but mechanically checkable, aligning with the proof-carrying posture: the checker can verify it without interpreting time-series fits.

11.3. Coupling and Summability

Empirical coupling and ladder summability are audited.

11.3.1. Coupling Audit: Empirical $\kappa$ Constants

For each ordered channel pair $(a\leftarrow b)$, we compute a conservative coupling constant $\kappa (a\leftarrow b)$ from time series and obtain the immediate inequality

$$|J_{a\leftarrow b}\left(t\right)|\le \kappa (a\leftarrow b)\sqrt{R^a\left(t\right)R^b\left(t\right)}+\epsilon \kappa (a\leftarrow b),$$

(97)

as in Section 7. These constants populate the off-diagonal entries of the Metzler comparison matrix.

11.3.2. Summability Audit: Ladder Increments

If the system is presented along a refinement ladder $K=0,1,\dots$ (discretisation level, code distance, policy refinement), Step 6 coherence is an ${\ell }^1$-type condition:

$${\delta }_K:={\parallel e^{\left(K\right)}-{\mathsf{\Pi }}_K^{K+1}{e}^{(K+1)}\parallel }_{W^{\left(K\right)}}\mathrm{with}\sum _K{\delta }_K<\infty .$$

(98)

In a finite audit, we compute partial sums $S_{K_{max}}={\sum }_{K=0}^{K_{max}}{\delta }_K$ and fit a tail model to bound the unseen remainder. The certificate record stores both $S_{K_{max}}$ and the tail bound.

Remark 11.3 

(Why summability is the right notion). Summability is the scale analogue of an $L^1$ forcing budget in time: it is precisely what makes projective-limit statements stable and prevents “completion” from being a moving-goalpost claim.

11.4. Certificate Decision

The system is declared PASS or FAIL with explicit slack.

11.4.1. Formal PASS/FAIL Rule

Fix declared thresholds in the frozen record:

$${\gamma }_{\mathrm{req}}>0,{\kappa }_{\mathrm{req}}\ge 0,S_{\mathrm{req}}<\infty ,$$

(99)

representing (respectively) the required gap funding, the maximum allowed couplings (or required Hurwitz margin), and the maximum allowed ladder budget. Compute:

$${\gamma }_{\mathrm{cert}}\left(\mathrm{conservative}\mathrm{gap}\right),{\kappa }_{\mathrm{rob}}\left(\mathrm{robust}\mathrm{couplings}\right),S_{\mathrm{cert}}\left(\mathrm{summability}\mathrm{certificate}\right).$$

(100)

Then the certificate decision is:

11.4.2. Slack Variables (What the Audit Reports)

We report slack values:

$${\mathrm{slack}}_{\gamma }:={\gamma }_{\mathrm{cert}}-{\gamma }_{\mathrm{req}},{\mathrm{slack}}_M:=\mathrm{Hurwitz}\mathrm{margin}\mathrm{slack}(\mathrm{LP}-\mathrm{feasible}\alpha ),{\mathrm{slack}}_S:=S_{\mathrm{req}}-S_{\mathrm{cert}}.$$

(102)

Positive slack means the certificate is robust; negative slack means the corresponding brick is unfunded in the frozen record.

Remark 11.4 

(Why this is scientifically useful). A PASS is a reproducible statement in a fixed geometry; a FAIL is not a dead end but a diagnosis: it identifies whether the failure is typing (assembly/ruler), gap funding, coupling closure, or ladder coherence. This is the DSFL promise: progress is measured by inequalities with slack, not by interpretive narratives.

12. Implications for Human-Centred Cybersecurity

This section explains what the theory implies for human-centred cybersecurity in concrete operational terms. The results of Section 3, Section 4, Section 5, Section 6, Section 7, Section 8, Section 9 and Section 10 are not merely formal: they induce a specific decision interface (what humans should look at), a specific governance interface (what organisations can certify), and a specific engineering interface for adaptive AI systems (what must be frozen and what may change). We present each implication as a theorem-shaped statement whenever possible, making explicit what is guaranteed and under what hypotheses. The empirical motivation is consistent with the usable-security literature: security outcomes are shaped by bounded attention, work practices, and incentives, so guarantees must be legible and operable under these constraints [5,6,7,8,9].

12.1. Decision Support

12.1.1. Cognitive Load as a Formal Failure Mode

A central human-centred failure mode is cognitive overload: too many metrics with drifting semantics yield unreliable action. This is not merely a UX issue; it is a verification problem. If the measurement geometry drifts, the organisation cannot tell whether the system is improving or whether the dashboard changed. The DSFL certificate layer addresses this by collapsing multi-channel risk into one scalar ledger with a single “clock” and explicit budgets, aligning with the stability-theoretic discipline that decay is meaningful only in a fixed norm [3,4,22]. The human-centred security literature further motivates this collapse: when security tasks compete with productivity, people rationally optimize effort and circumvent burdensome rules; thus “more metrics” is often counterproductive [6,7,8,9].

12.1.2. From Multi-Ledger Telemetry to One Decision-Ready Scalar

Let $r\left(t\right)\in {\mathbb{R}}_{\ge 0}^m$ be the vector of channel ledgers (identity, misconfiguration, exfiltration, tool misuse, ...) and assume the one-clock conditions of Section 5, so that there exists $w\gg 0$ and $\alpha >0$ with

$$R_{\mathrm{tot}}\left(t\right):=w^{\top }r\left(t\right)\mathrm{satisfying}{\dot{R}}_{\mathrm{tot}}\left(t\right)\le -2\alpha R_{\mathrm{tot}}\left(t\right)+{\tau }_{\mathrm{tot}}\left(t\right),{\tau }_{\mathrm{tot}}\in L^1\left([t_0,t_1]\right).$$

(103)

The quantities $(\alpha ,\parallel {\tau }_{\mathrm{tot}}{\parallel }_{L^1\left([t_0,t_1]\right)},R_{\mathrm{tot}}\left(t_0\right))$ define a minimal, auditable decision summary, in the same sense that Lyapunov envelopes provide decision-ready bounds without solving the full dynamics [18,19].

Proposition 12.1 

(Decision summary sufficiency). Assume the one-clock inequality (32) on a window $[t_0,t_1]$. Then the envelope (36) implies that the triple

$$\left(\alpha ,\parallel {\tau }_{\mathrm{tot}}{\parallel }_{L^1\left([t_0,t_1]\right)},R_{\mathrm{tot}}\left(t_0\right)\right)$$

(104)

is sufficient to upper-bound the entire risk trajectory $R_{\mathrm{tot}}\left(t\right)$ on $[t_0,t_1]$.

Proof. 

The envelope (37) gives, for all $t\in [t_0,t_1]$,

$$R_{\mathrm{tot}}\left(t\right)\le e^{-2\alpha (t-t_0)}{R}_{\mathrm{tot}}\left(t_0\right)+{\parallel {\tau }_{\mathrm{tot}}\parallel }_{L^1\left([t_0,t_1]\right)},$$

(105)

which depends only on the stated triple. □

Human-Centred Interpretation

Instead of asking humans to integrate dozens of drifting plots, DSFL produces:

• a certified improvement margin $\alpha$ (“how fast we recover when not being hit”),
• a disturbance footprint $\parallel {\tau }_{\mathrm{tot}}{\parallel }_{L^1}$ (“how hard we were hit on this window”),
• a starting residual $R_{\mathrm{tot}}\left(t_0\right)$ (“how far we were from target at window start”).

This is a provably sufficient summary for envelope-level decision making, which is the level at which governance and risk management typically operate [18,19].

12.1.3. Actionability: What Interventions Can Change

The certificate interface makes intervention effects interpretable: an intervention can only improve assurance by increasing $\alpha$ (stronger sustained dissipation) or reducing $\parallel {\tau }_{\mathrm{tot}}{\parallel }_{L^1}$ (reducing incident/forcing footprint). This yields a rigorous form of “actionability” that avoids metric gaming: if a change does not modify these certificate quantities in the frozen record, it does not improve certified security. This framing is compatible with the “compliance budget” perspective in usable security: interventions that exceed feasible effort budgets tend to be circumvented and thus do not improve realised security [8,9].

12.2. Governance and Compliance

12.2.1. From Snapshot Audits to Continuous Assurance

Traditional audits are static: they check whether policies are satisfied at a point in time. However, organisations operate under constant change and constant disturbance. The DSFL view is that compliance is a dynamical residual—a distance to a policy manifold—and assurance is a statement about the evolution of that residual under a remediation process. This matches the engineering logic of stability under forcing, where guarantees are meaningful only when stated in a declared norm and across declared perturbations [3,4].

12.2.2. Compliance as a Residual and Remediation as a Margin

Let $E_{\mathrm{pol}}:X\to {\mathcal{R}}_p$ be a policy imbalance operator (Section 6), and let $R^{\mathrm{pol}}\left(t\right):={\parallel E_{\mathrm{pol}}\left(x\left(t\right)\right)\parallel }_W^2$. Assume a remediation margin inequality

$${\dot{R}}^{\mathrm{pol}}\left(t\right)\le -2{\lambda }_{\mathrm{pol}}{R}^{\mathrm{pol}}\left(t\right)+{\tau }_{\mathrm{pol}}\left(t\right),{\tau }_{\mathrm{pol}}\in L^1\left([t_0,t_1]\right).$$

(106)

Then compliance becomes a continuous assurance claim: not merely that $R^{\mathrm{pol}}\left(t\right)$ is small at an audit date, but that its trajectory is bounded on every window by an explicit envelope, using the inhomogeneous Grönwall mechanism [18,23,24].

Theorem 12.1 

(Governance-grade compliance envelope). Under the remediation margin inequality above, the compliance residual satisfies

$$R^{\mathrm{pol}}\left(t\right)\le e^{-2{\lambda }_{\mathrm{pol}}(t-t_0)}{R}^{\mathrm{pol}}\left(t_0\right)+{\parallel {\tau }_{\mathrm{pol}}\parallel }_{L^1\left([t_0,t_1]\right)}.$$

(107)

Proof. 

This is the tail-robust envelope theorem (inhomogeneous Grönwall) applied to $R^{\mathrm{pol}}$ [23,24]. □

Governance Interpretation

The envelope yields a contract between organisation and auditor: the organisation declares the frozen record, the policy residual, the margin ${\lambda }_{\mathrm{pol}}$, and the disturbance budget. An auditor checks the inequality on logged evidence and obtains PASS/FAIL plus slack. This is structurally aligned with assurance-case thinking and proof-carrying verification: claims are shipped with evidence and verified independently [1,2].

12.2.3. Non-Regression Under Change as a Governance Requirement

Compliance programmes fail when policy or tooling changes silently shift the meaning of “compliant.” The refinement-ladder theory (Section 9) makes non-regression explicit: upgrades must come with a summable drift schedule (Step–6) and contractive comparators in the frozen record. Thus governance becomes “continuous and version-stable”: audits remain meaningful across tool and policy updates. This requirement mirrors the proof-carrying logic: what changes is allowed, but only under checkable evidence and bounded drift [1,2].

Remark 12.1 

(Why this is a governance advance). Static audits answer “are we compliant now?”. DSFL audits answer “are we converging to compliance at a certified rate under declared disturbance budgets, and does this claim survive upgrades?”. The latter is the more operationally relevant question for organisations under continuous change.

12.3. AI Agents and Adaptive Systems

12.3.1. Why Tool-Using Agents Require Proof-Carrying Semantics

Tool-using AI agents differ from classical software components: they act over multi-step trajectories, interact with external state, and evolve across versions (prompts, tools, retrieval). Empirical benchmark scores do not provide deployment-time guarantees and are not stable under upgrade. Thus the natural assurance object is the executed trace together with a proof-carrying bundle, as in Section 10. The engineering rationale follows the PCC/RV paradigm: shrink the trusted computing base to a checker and make evidence portable [1,2].

12.3.2. Agent Safety as a Ledger Vector

In an agent system, define channel ledgers for: policy violations, prompt injection susceptibility, privacy leakage, unsafe tool calls, and drift under upgrades. Under cooperative coupling (Metzler) and explicit budgets, the one-clock theorem yields a single scalar risk residual governed by an auditable envelope. This makes agent safety compositional: adding a new tool adds a new channel ledger and new coupling coefficients, but does not change the certificate spine. Technically, this is the same positive-systems closure used for multi-channel risk in control and stability theory [16,17,18,19].

12.3.3. Proof-Carrying Guarantees Under Model and Tool Upgrades

Adaptive systems change by design. The Step–6 coherence condition ensures that upgrades (new model weights, new retrieval index, new policy rules) do not cause unbounded drift in the defect representation in the frozen ruler. Thus DSFL provides a principled non-regression requirement for AI deployment: upgrades are admissible only if their induced drift is summably controlled and the bundle remains checkable [1,2].

Proposition 12.2 

(Upgrade-stable agent safety (certificate form)). Assume an agent system ships a certificate bundle ${\mathsf{B}}_K$ at version K with: (i) a frozen record $\mathfrak{P}$, (ii) a one-clock margin $\alpha >0$ and budget ${\tau }_{\mathrm{tot}}\in L^1\left([t_0,t_1]\right)$, and (iii) a Step–6 summable drift schedule $\left({\delta }_K\right)$ for version changes. Then the safety envelope remains comparable across versions and converges to a well-defined limiting claim in the frozen record (Theorem 9.2).

Proof. 

Immediate from the projective-limit theorem and Step–6 summability results in Section 9. □

Human-Centred Meaning

For AI-enabled systems, DSFL shifts assurance from “trust the model card” to “verify the bundle.” This is directly actionable for humans: a deployer can require a PASS bundle before enabling a tool, and a regulator can audit the same inequalities from the same frozen record.

Remark 12.2 

(Relationship to formal verification). The DSFL approach does not claim full semantic correctness of an AI model. It verifies a bounded-risk envelope in a declared semantics. This is closer in spirit to proof-carrying code and runtime verification than to full program correctness [1,2].

13. Limitations and Open Problems

This section records the boundaries of the present contribution and the remaining research tasks. Because the paper is built as a proof-carrying certificate layer, the limitations are not vague: they correspond to explicit places where (i) typing data must be chosen, (ii) empirical observability constrains what can be certified, and (iii) optimisation problems (best rulers, best residuals) remain open. Where possible we phrase open problems as theorem-shaped questions to avoid narrative ambiguity, consistent with the proof-carrying posture of shipping checkable obligations rather than narrative assurances [1,2].

13.1. What Is not Automated

Choosing rulers and residuals remains a design task.

13.1.1. Rulers Are Part of the Theorem Data

A central DSFL principle is that stability and decay are statements in a fixed normed geometry: in semigroup language, contractivity and exponential decay are typed statements about a generator on a specified normed space [3,4]. Therefore, the ruler W cannot be “learned away” without changing the meaning of the claim. Declaring W is analogous to declaring an energy norm in PDE stability and control: it is part of the theorem statement [3,4,18].

Remark 13.1 

(Design task, not an algorithm). In the present framework, selecting W is a modelling/design decision that encodes what the organisation means by “distance from policy equilibrium.” DSFL constrains and audits that choice, but it does not uniquely determine it without additional domain commitments (e.g. which risks count as neutral, which trade-offs are acceptable), exactly because changing the norm changes the typed meaning of a decay claim unless explicit equivalence constants are established [3,4].

13.1.2. Residual Definitions Encode Semantics

Similarly, the defect map (policy–practice imbalance operator) is a semantic object: it specifies what counts as a violation, what is neutral, and what evidence is admissible. Different organisations may legitimately choose different imbalance operators even for the same high-level policy language. DSFL does not eliminate that fact; it makes it explicit and auditable, in the same sense that proof-carrying verification requires an explicit statement of the semantics being checked [1,2].

Proposition 13.1 

(Non-uniqueness without additional axioms). Let $\mathcal{H}$ be a fixed practice space and let $\mathcal{N}\subset \mathcal{H}$ be a fixed neutral subspace. If no additional constraints are imposed (e.g. operational invariances, monotonicity under coarse-graining, or compatibility with a declared observation dictionary), then there exist infinitely many inequivalent ruler/residual pairs $(W,E_{\mathrm{pol}})$ that yield different numerical compliance residuals on the same underlying data.

Proof. 

Choose any two non-equivalent SPD operators $W_1,W_2$ on ${\mathcal{N}}^{\perp }$ and the same neutral-free defect $e={\mathsf{\Pi }}_{\perp }\tilde{e}$. Then ${\parallel e\parallel }_{W_1}$ and ${\parallel e\parallel }_{W_2}$ define different residual magnitudes unless explicit equivalence constants are imposed. This is the fixed-norm typing phenomenon that underlies norm-transfer requirements in semigroup stability [3,4]. □

Explanation. This proposition is the mathematical reason that the paper cannot promise full automation: rulers and residuals are theorem data, and non-equivalent choices encode different meanings.

13.2. Empirical Calibration Challenges

Data quality and observability limit guarantees.

13.2.1. Observability Limits Are Structural, not Incidental

The DSFL certificate is only as good as the observation map ${\mathcal{O}}_{\mathcal{C}}$ that turns real operations into measured defects. In practice, security-relevant state is partially observed: logs are missing, telemetry is delayed, and organisational behaviour is not fully instrumented. This is not merely an engineering inconvenience; it is a limitation on what can be certified. In the DSFL formalism, this appears as:

$$e_{\mathrm{obs}}\left(t\right)={\mathcal{O}}_{\mathcal{C}}e\left(t\right),R_{\mathrm{obs}}\left(t\right)={\parallel e_{\mathrm{obs}}\left(t\right)\parallel }_{W_{\mathrm{obs}}}^2,$$

(108)

together with an amplification/contractivity bound needed to relate observed residuals to global residuals. This mirrors the general runtime-verification constraint: only monitorable properties over available traces can be checked [1].

Remark 13.2 

(Cone-like limitations in cyber settings). Although the motivating language of “cones” comes from relativity, the same structure appears in cyber settings: an SOC only sees events that reach its sensors, and sensor coverage changes over time. DSFL treats this as an explicit map with a typing budget, rather than assuming full observability, consistent with the “observable semantics” emphasis in monitor-based verification [1].

13.2.2. Calibration Drift and Dataset Shift

Empirical constants such as coupling budgets ${\kappa }_{\mathrm{emp}}$ and inferred rates depend on the data distribution. When organisational processes, tooling, or adversary behaviour change, the inferred constants can drift. DSFL does not hide this; it forces a re-audit in the frozen record or an explicit update to the record. From a control viewpoint, this is exactly the distinction between a proved ISS-style bound and a fitted model whose parameters may change with regime [18,19].

Proposition 13.2 

(Robustness requires worst-case aggregation over protocol perturbations). Let ${\kappa }_{\mathrm{emp}}^{(g,s)}$ be an empirical coupling estimate computed under protocol choices g and resampling seed s. A certificate-grade coupling constant must be taken as a conservative aggregation

$${\kappa }_{\mathrm{rob}}:=\underset{g\in \mathcal{G}}{max}\underset{s\in \mathcal{S}}{max}{\kappa }_{\mathrm{emp}}^{(g,s)},$$

(109)

so that the resulting inequality holds uniformly over the declared perturbation family.

Proof. 

Each ${\kappa }_{\mathrm{emp}}^{(g,s)}$ yields a bound of the form $\left|J\right|\le {\kappa }_{\mathrm{emp}}^{(g,s)}\sqrt{R^a{R}^b}+\epsilon {\kappa }_{\mathrm{emp}}^{(g,s)}$ on the corresponding time series. Taking the maximum preserves the bound across all protocols/seeds. This is the empirical analogue of uniformity/margins in small-gain style guarantees [18,19]. □

Explanation. This is the empirical analogue of uniformity in K for refinement ladders: robust certification requires conservative envelopes, not point estimates.

13.3. Open Theoretical Questions

Optimal rulers and learning residuals remain open.

13.3.1. Optimal Ruler Selection Under Composability Constraints

The most important open mathematical question is: how to select a ruler W that is simultaneously:

(O1) 

Operationally meaningful: encodes the organisation’s notion of risk and neutrality;

(O2) 

Stable under change: yields explicit norm-equivalence constants when tooling changes;

(O3) 

Composable: admits tight coupling bounds and a large Hurwitz margin for the induced Metzler system.

This is an instance of Lyapunov-function selection under structural constraints: one seeks a certificate functional that is both meaningful and yields strong margins under coupling [16,17,18,19].

Problem 13.1 

(Optimal ruler under one-clock margin). Fix a family of admissible defect operators ${\left\{E_a\right\}}_{a\in \mathcal{A}}$ and a neutral convention. Over the class of SPD rulers W satisfying declared invariances and normalisations, find a ruler that maximises the certified one-clock margin ${\lambda }_{\mathrm{eff}}\left(W\right)$ (equivalently minimises the spectral abscissa of the induced Metzler comparison matrix subject to budget constraints).

Explanation. This is a genuine optimisation problem constrained by stability theory: different rulers change both diagonal gaps and off-diagonal couplings. The functional-analytic literature suggests that “best” energies are often problem-adapted Lyapunov functionals, and the positive-systems literature makes explicit how diagonal margins and couplings trade off in Metzler/Hurwitz closure [3,4,16,17,18,19].

13.3.2. Learning Residuals Without Losing Typing

It is tempting to “learn the residual” from data (e.g. learn $E_{\mathrm{pol}}$ or W from historical incidents). However, this risks reintroducing moving goalposts: a learned residual can change semantics unless the learning objective is itself typed and frozen. This tension mirrors the general assurance distinction between (i) checkable semantics and (ii) adaptive predictors whose meaning may drift unless versioned and audited [1,2].

Problem 13.2 

(Learned residuals with frozen semantics). Design a learning procedure that proposes a defect map $\widehat{E}$ and ruler $\widehat{W}$ while guaranteeing:

(i)

the proposal is equivalent (with explicit constants) to the declared semantics in the frozen record, or else is declared as a new record;

(ii)

the induced coupling bounds remain Metzler-typed and preserve (or improve) the Hurwitz margin;

(iii)

the resulting certificate remains auditable by a third party.

Explanation. A DSFL-compatible learning rule must output not only a predictor, but also a proof-carrying translation back to the frozen record, so that the checker verifies a stable semantics rather than a drifting score [1,2].

13.3.3. Tightness of the Metzler Reduction

The Metzler reduction uses inequalities such as $\sqrt{xy}\le \frac{1}{2}(x+y)$, which can be conservative.

Problem 13.3 

(Tight one-clock bounds for coupled nonnegative ledgers). Given a coupled ledger system with structured cross terms (e.g. bilinear injections), characterise conditions under which one can produce a tighter scalar ledger than the generic Metzler bound, while preserving auditable nonnegativity and frozen-ruler typing.

Explanation. This problem matters because the certified rate ${\lambda }_{\mathrm{eff}}$ is the headline assurance number. Improving tightness can turn a marginal FAIL into a PASS without changing the underlying system—only by using a sharper but still auditable certificate, in the spirit of constructing tighter Lyapunov/ISS estimates and less conservative small-gain bounds [16,17,18,19].

14. Conclusion

This paper has advanced a verification-theoretic reformulation of cybersecurity: security is treated as a provable contraction of a single scalar residual in a frozen measurement geometry, up to explicit, auditable disturbance budgets. The result is a proof-carrying notion of assurance that remains meaningful under change, supports human decision-making, and exposes hidden failure modes (metric drift, non-normal transients, infeasible improvement plans) as explicit violations of checkable inequalities.

14.1. What Has Been Proved

The central mathematical contribution is a certificate spine with three kernel implications:

14.1.1. One Residual and One Clock from Multi-Channel Ledgers

Starting from a vector of nonnegative channel ledgers $r\left(t\right)\in {\mathbb{R}}_{\ge 0}^m$ satisfying a cooperative comparison inequality $\dot{r}\le Mr+\tau$ with M Metzler–Hurwitz and $\tau \in L^1\left([t_0,t_1]\right)$, we proved that there exists a strictly positive weighting $w\gg 0$ producing a single scalar ledger

$$R_{\mathrm{tot}}\left(t\right)=w^{\top }r\left(t\right)$$

(110)

that satisfies the one-clock inequality

$${\dot{R}}_{\mathrm{tot}}\left(t\right)\le -2\alpha R_{\mathrm{tot}}\left(t\right)+{\tau }_{\mathrm{tot}}\left(t\right),{\tau }_{\mathrm{tot}}\left(t\right)=w^{\top }\tau \left(t\right)\in L^1\left([t_0,t_1]\right).$$

(111)

This is the rigorous form of the decision-ready claim: “one number tracks risk, one number tracks recovery rate, one budget tracks disturbance.” The proof is purely functional-analytic and relies on positive-systems theory and Perron–Frobenius witnesses [17,25,27].

14.1.2. Tail-Robust Envelopes (Incident Spikes Become Budgets)

We derived an explicit tail-robust envelope via the inhomogeneous Grönwall mechanism:

$$R_{\mathrm{tot}}\left(t\right)\le e^{-2\alpha (t-t_0)}{R}_{\mathrm{tot}}\left(t_0\right)+{\int }_{t_0}^t{e}^{-2\alpha (t-s)}{\tau }_{\mathrm{tot}}\left(s\right)ds,$$

(112)

and hence $R_{\mathrm{tot}}\left(t\right)\le e^{-2\alpha (t-t_0)}{R}_{\mathrm{tot}}\left(t_0\right)+{\parallel {\tau }_{\mathrm{tot}}\parallel }_{L^1\left([t_0,t_1]\right)}$. This formalises the human-centred interpretation of incidents: large spikes matter only through their integrated footprint, while recovery is governed by the certified margin $\alpha$ [23,24].

14.1.3. Non-Regression Under Upgrades via Summable Refinement Drift

We formalised system evolution (tools, policies, models, monitoring) as a refinement ladder. Under Step–6 (an $L^1$ scale-generator bound) we proved summable refinement drift and projective coherence: refinement does not silently change the meaning of the claim in the same frozen ruler. This is the precise mathematical content of “no moving goalposts under upgrades” and follows from Banach-valued calculus and contractive inverse-limit arguments [3,4,20].

14.2. What This Reframing Changes for Human-Centred Cybersecurity

The core practical effect is a shift from metric pluralism to certificate semantics.

Decision Support

Instead of asking practitioners to reconcile many drifting dashboards, the framework produces a small set of auditable quantities: a certified improvement margin, an explicit disturbance budget, and explicit coupling constants. These are sufficient to upper-bound risk trajectories on declared windows and to compare interventions across versions.

Governance and Compliance

Compliance is reframed as a residual (distance to a policy manifold) and assurance as a decay statement with explicit budgets. Static snapshot audits are replaced by continuous, version-stable guarantees that remain meaningful under policy and tooling changes, provided those changes are declared as part of the frozen record and their effects are budgeted.

AI Agents and Adaptive Systems

For tool-using AI systems, the verified object is the episode trace under declared semantics, not the model weights. The proof-carrying bundle-and-checker interface is therefore the appropriate unit of assurance, aligning with the classical producer/consumer verification paradigm [1,2].

14.3. Limits of the Present Work

The framework is intentionally verification-theoretic. It does not attempt to fully model adversaries, prove semantic correctness of AI models, or infer universal guarantees over all possible trajectories. All results are conditional on a frozen record and on the validity of the stated inequality obligations in that record. This is not a weakness: it preserves falsifiability and prevents the category error of treating drifting metrics as stable truth.

Moreover, numerical audits are instantiations of constants and witnesses, not replacements for analytic proofs. They are useful because they are checkable and can be made conservative by design, but they must be interpreted as evidence in a declared semantics rather than as universal claims.

14.4. A Research Agenda with Theorem-Shaped Milestones

The programme yields a concrete sequence of next steps, each phrased as a brick-discharge problem:

(i)

Pack library (definitions). Publish a catalogue of frozen-record templates for common deployments (SOC pipeline, cloud posture management, tool-using agents), including standard neutral conventions and observation commitments.

(ii)

Coupling identification (empirical $\kappa$). Develop robust, conservative estimation procedures for coupling coefficients (including resampling robustness and worst-case confidence bands) to populate certificate tables from operational data.

(iii)

Step–6 for real upgrades. Define refinement operators for tool and policy upgrades and prove (or conservatively bound) integrable scale-generator majorants $G\in L^1$, yielding summable drift and non-regression across versions.

(iv)

Non-normality-aware audits. Standardise audits that distinguish symmetric/selfadjoint from non-normal regimes and report transient growth indicators alongside decay/gap estimates [26].

(v)

Floor-aware governance. Operationalise feasibility floors by connecting resource constraints (staffing, latency, cadence) to certified dissipation margins and forcing densities, producing planning tools that detect infeasible improvement targets.

14.5. Final Positioning

The main conceptual result can be stated in one sentence:

Cybersecurity becomes auditable and comparable under change when it is expressed as a forced contraction inequality for a single residual in a frozen measurement geometry, with all unresolved effects routed into explicit budgets.

This reframing does not replace security practice; it makes its claims precise. It provides the mathematical grammar required for human-centred assurance in evolving human-centered systems: clear semantics, explicit constants, and a mechanically checkable PASS/FAIL interface.