Oscillation Detection in Difference Equations with Several Non-Monotone Advanced Arguments via a New Approach

1. Introduction

Consider the first-order difference equations with several advanced arguments

$$\nabla z\left(n\right)+\sum _{r=1}^m{c}_r\left(n\right)z\left({\theta }_r\left(n\right)\right)=0,n\in \mathbb{N},$$

(1)

where $\mathbb{N}$ denotes the set of positive integers and $\nabla z\left(n\right)=z\left(n\right)-z(n-1)$ is the backward difference operator. Throughout the paper, the coefficient sequences $c_r\left(n\right)$, $r=1,2,\dots ,m$, are assumed to be nonnegative real-valued for all sufficiently large n. Moreover, the integer-valued sequences ${\theta }_r\left(n\right)$ represent advanced arguments and satisfy

$${\theta }_r\left(n\right)\ge n+1,n\in \mathbb{N},r=1,2,\dots ,m.$$

A sequence ${\left(z\left(n\right)\right)}_{n\ge n_0}$, for some $n_0\in \mathbb{N}$, is said to be a solution of equation (1) if it satisfies the equation for all $n\ge n_0$.

The oscillation theory of differential and difference equations provides fundamental insights into the qualitative behavior of dynamical systems across diverse domains, including population dynamics, control systems, biological feedback or feedforward mechanisms [24,31], neural modeling [30,33], and economics, see [2,23,28,29]. The analysis of oscillatory behavior enables researchers to determine whether solutions fluctuate around equilibrium states or converge monotonically, thereby revealing underlying stability properties, periodic tendencies, or chaotic dynamics in physical and biological processes. In discrete systems, oscillation analysis assumes particular significance, as many real-world models evolve through discrete time steps and incorporate delay or advance arguments to capture memory effects or anticipation mechanisms, see [2,23].

The study of oscillation in difference equations plays an essential role in discrete mathematics, and its development has been addressed in a wide range of contributions; see [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,18,19,20,22,23,25,26,27,32,34,35,36,37]. While classical results typically assume single monotone arguments, realistic systems often involve several advanced arguments that may vary non-monotonically over time. Such complex structures arise naturally in predictive control systems, biological population models with anticipation mechanisms, and signal propagation through feedback networks [10,20,31].

Ladas [27] investigated the oscillatory behavior of the first-order differential equation with non-decreasing delay

$$y^{\prime }\left(t\right)+a\left(t\right)y\left(g\left(t\right)\right)=0,a\in C([t_0,\infty ),[0,\infty )),t\ge t_0,$$

and established the well-known lim sup-type oscillation criterion

$$\underset{t\to \infty }{lim\; sup}{\int }_{g\left(t\right)}^{t}a\left(s\right)ds>1.$$

(2)

Motivated by the continuous case, Chatzarakis and Stavroulakis [21] extended Ladas’ condition to the discrete setting. In particular, they obtained the following discrete analogue of (2):

$$\underset{n\to \infty }{lim\; sup}\sum _{r=n}^{h\left(n\right)}c\left(r\right)>1,$$

(3)

for the advanced difference equation

$$\nabla z\left(n\right)-c\left(n\right)z\left(h\left(n\right)\right)=0,n\in \mathbb{N},$$

(4)

where ${\left\{c\left(n\right)\right\}}_{n\ge 1}$ is a sequence of nonnegative real numbers and ${\left\{h\left(n\right)\right\}}_{n\ge 1}$ is an integer-valued non-decreasing sequence satisfying

$$h\left(n\right)\ge n+1.$$

Subsequently, Chatzarakis, Pinelas, and Stavroulakis [14] extended condition (3) to Eq. (1) and obtained

$$\underset{n\to \infty }{lim\; sup}\sum _{r=1}^m\sum _{r_1=n}^{{\theta }_{min}\left(n\right)}{c}_r\left(r_1\right)>1.$$

(5)

where ${\theta }_{min}\left(n\right)={min}_{1\le r\le m}{\theta }_r\left(n\right)$ and each ${\theta }_r\left(n\right)$ represents a non-decreasing sequence.

Braverman and Karpuz [9] demonstrated that condition (2) is not valid for both the continuous and the corresponding discrete cases when the assumption of monotonicity is relaxed to allow for general, not necessarily monotone, delay arguments. This finding highlights the limitations of directly extending results from monotone to non-monotone delays and shows that more specific methods are required for equations with non-monotone arguments [25,26].

Despite notable progress in the oscillation theory of delay difference equations, the case involving several advanced arguments remains insufficiently explored. Existing studies [1,9] present only sufficient conditions for the oscillation of all solutions; however, they do not reveal the qualitative differences between equations with one or with several advanced arguments. Following the approach in [9], we construct a counterexample showing that some extensions of condition (3) cannot hold for Eq. (1), even when the advanced arguments are non-decreasing and satisfy ${\theta }_r\left(n\right)\ge n+1$. In this work, we show that there is no constant $B>0$ such that any of the following conditions guarantees the oscillation of all solutions of Eq. (1):

$$\underset{n\to \infty }{lim\; inf}\sum _{r=1}^m\sum _{r_1=n+1}^{{\theta }_{max}\left(n\right)}{c}_r\left(r_1\right)>B,{\theta }_{max}\left(n\right)=\underset{1\le i\le m}{max}{\theta }_i\left(n\right),$$

or

$$\underset{n\to \infty }{lim\; inf}\sum _{r=n+1}^{{\theta }_k\left(n\right)}{c}_l\left(r\right)>B,k\ne l,k,l=1,2,\dots ,m.$$

This paper has two additional goals. First, we develop a new framework for studying oscillatory behavior and obtain new sufficient conditions that extend and unify earlier results (see Table 1 on page 7). Second, we show that, for a certain class of equations of the form (1), some of our criteria guarantee oscillation, while all previously known conditions, whether iterative or not, fail for this class. Finally, we introduced a new concept for difference equations with advanced arguments, namely, the distance between generalized successive zeros of solutions, illustrated through numerical simulations.

2. Main Results

Theorem 1. 

None of the following conditions, for any constant $B>0$, guarantees the oscillation of Eq. (1) when ${\theta }_r\left(n\right)$ is non-decreasing for all $r=1,2,\dots ,m$ and $m\ge 2$:

(i)

$$\underset{n\to \infty }{lim\; inf}\sum _{r=1}^m\sum _{r_1=n+1}^{{\theta }_{max}\left(n\right)}{c}_r\left(r_1\right)>B,{\theta }_{max}\left(n\right)=\underset{1\le r\le m}{max}{\theta }_r\left(n\right),$$

(ii)

$$\underset{n\to \infty }{lim\; inf}\sum _{r=n+1}^{{\theta }_k\left(n\right)}{c}_l\left(r\right)>B,k\ne l,k,l=1,2,\dots ,m.$$

Proof. 

Consider the first–order difference equation with several advanced arguments

$$\nabla z\left(n\right)-{\displaystyle \frac{1-e^{-1}}{2e}}z(n+1)-{\displaystyle \frac{1-e^{-1}}{2e^M}}z(n+M)=0,M>2,n\in \mathbb{N}.$$

(6)

It is evident that this equation is a particular case of (1), with

$${\theta }_1\left(n\right)=n+1,{\theta }_2\left(n\right)=n+M,c_1\left(n\right)={\displaystyle \frac{1-e^{-1}}{2e}},c_2\left(n\right)={\displaystyle \frac{1-e^{-1}}{2e^M}}.$$

The above equation possesses a non-oscillatory solution

$$z\left(n\right)=e^n,n\in \mathbb{N}.$$

Furthermore, we obtain

$$\sum _{r=1}^2\sum _{r_1=n+1}^{{\theta }_{max}\left(n\right)}{c}_r\left(r_1\right)=\sum _{r=1}^2\sum _{r_1=n+1}^{n+M}{c}_r\left(r_1\right)=M(1-e^{-1})\left({\displaystyle \frac{1}{2e}}+{\displaystyle \frac{1}{2e^M}}\right)>{\displaystyle \frac{M(1-e^{-1})}{2e}},$$

and similarly,

$$\sum _{r=n+1}^{{\theta }_2\left(n\right)}{c}_1\left(r\right)={\displaystyle \frac{M(1-e^{-1})}{2e}}.$$

As the integer M may be taken arbitrarily large, the proof of the theorem is complete. □

In what follows, and throughout the remainder of this work, we assume that ${\left({\theta }_r\left(n\right)\right)}_{n\ge 1}$, for $r=1,2,\dots ,m$, are integer-valued (it is not necessarily assumed to be non-decreasing). Accordingly, we introduce the non-decreasing sequences

$${\varphi }_r\left(n\right)=\underset{r_1\ge n}{min}{\theta }_r\left(r_1\right)r=1,2,\dots ,m.$$

Furthermore, for integers $p\ge q$, we define

$$\begin{array}{cc}\hfill C_1(p,q)& =\prod _{r_1=q+1}^p\left(1-\sum _{r=1}^m{c}_r\left(r_1\right)\right),\hfill \\ \hfill C_k(p,q)& =\prod _{r_1=q+1}^p\left(1-\sum _{r=1}^m{c}_r\left(r_1\right)C_{k-1}^{-1}\left({\theta }_r\left(r_1\right),r_1\right)\right),k=2,3,\dots .\hfill \end{array}$$

The following lemma provides an iterative sequence of lower bounds for the ratio ${\displaystyle \frac{z\left(p\right)}{z\left(q\right)}}$, which progressively increases as k increases. The proof of this Lemma, for difference equation with several delays, can be found in [10].

Lemma 1. 

Assume that $\left(z\right(n\left)\right)$ is a positive solution of Eq. (1). Then for all $p\ge q$, $k\in \mathbb{N}$, we have

$$z\left(p\right)\ge z\left(q\right)C_k^{-1}(p,q).$$

(7)

Proof. 

Dividing Eq. (1) by $z\left(n\right)$ and taking the product from $q+1$ to p, we obtain

$$0<{\displaystyle \frac{z\left(q\right)}{z\left(p\right)}}=\prod _{r_1=q+1}^p\left(1-\sum _{r=1}^m{c}_r\left(r_1\right){\displaystyle \frac{z\left({\theta }_r\left(r_1\right)\right)}{z\left(r_1\right)}}\right).$$

(8)

Since the sequence $\left(z\right(n\left)\right)$ is positive, it follows from Eq. (1) that $z\left(n\right)$ is eventually non-decreasing. Consequently,

$${\displaystyle \frac{z\left({\theta }_r\left(r_1\right)\right)}{z\left(r_1\right)}}\ge 1.$$

Hence, from (8) we have

$$0<{\displaystyle \frac{z\left(q\right)}{z\left(p\right)}}=\prod _{r_1=q+1}^p\left(1-\sum _{r=1}^m{c}_r\left(r_1\right){\displaystyle \frac{z\left({\theta }_r\left(r_1\right)\right)}{z\left(r_1\right)}}\right)\le \prod _{r_1=q+1}^p\left(1-\sum _{r=1}^m{c}_r\left(r_1\right)\right).$$

That is,

$${\displaystyle \frac{z\left(p\right)}{z\left(q\right)}}\ge \prod _{r_1=q+1}^p{\left(1-\sum _{r=1}^m{c}_r\left(r_1\right)\right)}^{-1}=C_1^{-1}(p,q).$$

Moreover, since ${\theta }_r\left(r_1\right)\ge r_1$, it follows that

$${\displaystyle \frac{z\left({\theta }_r\left(r_1\right)\right)}{z\left(r_1\right)}}\ge C_1^{-1}({\theta }_r\left(r_1\right),r_1).$$

Substituting this estimate into (8) and rearranging the terms yields

$${\displaystyle \frac{z\left(p\right)}{z\left(q\right)}}\ge \prod _{r_1=q+1}^p{\left(1-\sum _{r=1}^m{c}_r\left(r_1\right)C_1^{-1}({\theta }_r\left(r_1\right),r_1)\right)}^{-1}=C_2^{-1}(p,q).$$

Proceeding inductively in this manner, we finally arrive at inequality (7). □

Theorem 2. 

(Main oscillation criterion for several non-monotone advanced arguments)

Let $k\in \mathbb{N}$. Suppose that there exists an unbounded sequence ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ such that

$$\underset{i\to \infty }{lim}\left(\sum _{r=1}^m\sum _{r_1={\alpha }_i}^{{\varphi }_r\left({\alpha }_i\right)}{C}_k^{-1}\left({\theta }_{j^{*}}\left(r_1\right),{\varphi }_{j^{*}}\left({\alpha }_i\right)\right)c_{j^{*}}\left(r_1\right)\right)>1\mathit{for}\mathit{every}{j}^{*}\in \{1,2,\dots ,m\}.$$

(9)

Then Eq. (1) is oscillatory.

Proof. 

Assume, for the sake of contradiction, that Eq. (1) possesses a non-oscillatory solution $\left(z\right(n\left)\right)$. Without loss of generality, we may suppose that $z\left(n\right)>0$ for all sufficiently large values of n. Hence, $z\left(n\right)$ is eventually non-increasing for all sufficiently large n.

Summing Eq. (1) from n to ${\varphi }_r\left(n\right)$, $r=1,2,\dots ,m$, yields

$$\begin{array}{c}\hfill z\left({\varphi }_r\left(n\right)\right)-z(n-1)-\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{c}_1\left(r_1\right)z\left({\theta }_1\left(r_1\right)\right)-\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{c}_2\left(r_1\right)z\left({\theta }_2\left(r_1\right)\right)\\ \hfill -\dots -\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{c}_m\left(r_1\right)z\left({\theta }_m\left(r_1\right)\right)=0.\end{array}$$

(10)

By virtue of inequality (7) and the fact that ${\theta }_j\left(r_1\right)\ge {\varphi }_j\left(n\right)$ for all $r_1\in \{n,n+1,\dots ,{\varphi }_r\left(n\right)\}$, it follows that

$$z\left({\theta }_j\left(r_1\right)\right)\ge z\left({\varphi }_j\left(n\right)\right)C_k^{-1}({\theta }_j\left(r_1\right),{\varphi }_j\left(n\right)).$$

Substituting this estimate into the previous equality gives

$$\begin{array}{ccc}& & z\left({\varphi }_r\left(n\right)\right)-z(n-1)-z\left({\varphi }_1\left(n\right)\right)\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{C}_k^{-1}({\theta }_1\left(r_1\right),{\varphi }_1\left(n\right))c_1\left(r_1\right)\hfill \\ & & -z\left({\varphi }_2\left(n\right)\right)\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{C}_k^{-1}({\theta }_2\left(r_1\right),{\varphi }_2\left(n\right))c_2\left(r_1\right)-\dots \hfill \\ & & -z\left({\varphi }_m\left(n\right)\right)\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{C}_k^{-1}({\theta }_m\left(r_1\right),{\varphi }_m\left(n\right))c_m\left(r_1\right)\ge 0.\hfill \end{array}$$

Summing this inequality for $r=1,2,\dots ,m$, we obtain

$$\begin{array}{ccc}\hfill & & -mz(n-1)-z\left({\varphi }_1\left(n\right)\right)\left(\sum _{r=1}^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{C}_k^{-1}({\theta }_1\left(r_1\right),{\varphi }_1\left(n\right))c_1\left(r_1\right)-1\right)\hfill \\ & & -z\left({\varphi }_2\left(n\right)\right)\left(\sum _{r=1}^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{C}_k^{-1}({\theta }_2\left(r_1\right),{\varphi }_2\left(n\right))c_2\left(r_1\right)-1\right)\hfill \\ & & -\dots -z\left({\varphi }_m\left(n\right)\right)\left(\sum _{r=1}^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{C}_k^{-1}({\theta }_m\left(r_1\right),{\varphi }_m\left(n\right))c_m\left(r_1\right)-1\right)\ge 0.\hfill \end{array}$$

(11)

Now, according to condition (9), there exists a sufficiently large i such that

$$\sum _{r=1}^m\sum _{r_1={\alpha }_i}^{{\varphi }_r\left({\alpha }_i\right)}{C}_k^{-1}({\theta }_{j^{*}}\left(r_1\right),{\varphi }_{j^{*}}\left({\alpha }_i\right))c_{j^{*}}\left(r_1\right)>1\mathrm{for}\mathrm{every}{j}^{*}\in \{1,2,\dots ,m\}.$$

Combining this fact with inequality (11) yields a contradiction that completes the proof. □

Theorem 3. 

Assume that $c_i\left(n\right)\ge c\left(n\right)$ for $n\ge n_0$, $n_0\in \mathbb{N}$, $i\in \{1,2,\dots ,m\}$. If

$$\underset{n\to \infty }{lim\; sup}\left(\sum _{r=1}^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}c\left(r_1\right)\right)>1,$$

(12)

then, Eq. (1) is oscillatory.

Proof. 

By applying the same approach employed in the proof of Theorem 2, we deduce that

$$\begin{array}{ccc}& & z\left({\varphi }_r\left(n\right)\right)-z(n-1)-z\left({\varphi }_1\left(n\right)\right)\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{c}_1\left(r_1\right)-z\left({\varphi }_2\left(n\right)\right)\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{c}_2\left(r_1\right)-\dots \hfill \\ & & -z\left({\varphi }_m\left(n\right)\right)\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{c}_m\left(r_1\right)\ge 0,\hfill \end{array}$$

where $r=1,2,\dots ,m$ and $\left(z\right(n\left)\right)$ is a positive solution of Eq. (1). Using the inequality $c_i\left(n\right)\ge c\left(n\right)$ for all $i\in \{1,2,\dots ,m\}$, and summing over $r=1,2,\dots ,m$, we get

$$\sum _{r=1}^{m}z\left({\varphi }_r\left(n\right)\right)-mz(n-1)-\left(z({\varphi }_1\left(n\right)+z\left({\varphi }_2\left(n\right)\right)+\dots +z\left({\varphi }_m\left(n\right)\right))\right)\sum _{r=1}^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}c\left(r_1\right)\ge 0,$$

that is,

$$-mz(n-1)-\left(\sum _{r=1}^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}c\left(r_1\right)-1\right)\sum _{r=1}^{m}z\left({\varphi }_r\left(n\right)\right)\ge 0.$$

Consequently,

$$\sum _{r=1}^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}c\left(r_1\right)\le 1.$$

Therefore,

$$\underset{n\to \infty }{lim\; sup}\left(\sum _{r=1}^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}c\left(r_1\right)\right)\le 1,$$

contradicts (12). □

It is straightforward to reorder the sequences $\left\{c_r\left(n\right)\right\}$ and $\left\{{\theta }_r\left(n\right)\right\}$, for $r=1,2,\dots ,m$, associated with Eq. (1), so that the following inequality is eventually satisfied:

$$\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{c}_{j^{*}}\left(r_1\right)\ge \sum _{r_1=n}^{{\varphi }_r\left(n\right)}{c}_{i^{*}}\left(r_1\right),j^{*}\ge i^{*},1\le i^{*},j^{*}\ge m.$$

(13)

Theorem 4. 

Let $k\in \mathbb{N}$ and $\ell \in \{1,2,\dots ,m\}$. Assume that there exists an unbounded sequence ${\left\{{\alpha }_i\right\}}_{i\ge 0}$ such that

$$\underset{i\to \infty }{lim}\left(\sum _{r=\ell }^m\sum _{r_1={\alpha }_i}^{{\varphi }_r\left({\alpha }_i\right)}{C}_k^{-1}\left({\theta }_{j^{*}}\left(r_1\right),{\varphi }_{j^{*}}\left({\alpha }_i\right)\right)c_{j^{*}}\left(r_1\right)\right)>1\mathit{for}\mathit{every}{j}^{*}\in \{\ell ,\ell +1,\dots ,m\}.$$

(14)

Then Eq. (1) is oscillatory.

Proof. 

As before, let $z\left(n\right)$ denote a positive solution of Eq. (1). From Eq. (1), it immediately follows that

$$\nabla z\left(n\right)-\sum _{r=\ell }^m{c}_r\left(n\right)z\left({\theta }_r\left(n\right)\right)\ge 0.$$

(15)

Following the same arguments as in the proof of Theorem 2, and using (7) with ${\theta }_j\left(r_1\right)\ge {\varphi }_j\left(n\right)$ for all $r_1\in \{n,n+1,\dots ,{\theta }_j\left(r\right)\}$, summing from ℓ to m yields

$$\begin{array}{ccc}\hfill & & -(m-\ell )z(n-1)-z\left({\varphi }_{\ell }\left(n\right)\right)\left(\sum _{r=\ell }^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{C}_k^{-1}({\theta }_{\ell }\left(r_1\right),{\varphi }_{\ell }\left(n\right))c_{\ell }\left(r_1\right)-1\right)\hfill \\ & & -z\left({\varphi }_{\ell +1}\left(n\right)\right)\left(\sum _{r=\ell }^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{C}_k^{-1}({\theta }_{\ell +1}\left(r_1\right),{\varphi }_{\ell +1}\left(n\right))c_{\ell +1}\left(r_1\right)-1\right)\hfill \\ & & -\dots -z\left({\varphi }_m\left(n\right)\right)\left(\sum _{r=\ell }^m\sum _{r_1=n}^{{\varphi }_r\left(n\right)}{C}_k^{-1}({\theta }_m\left(r_1\right),{\varphi }_m\left(n\right))c_m\left(r_1\right)-1\right)\ge 0.\hfill \end{array}$$

(16)

From this and condition (14), we arrive at a contradiction, which completes the proof of the theorem. □

Remark 1. 

It is worth noting that one of the significant consequences of Theorem 1 is that none of the conditions

$$\sum _{r=1}^m\sum _{r_1=n}^{{\theta }_{max}\left(n\right)}{c}_r\left(r_1\right)<A<+\infty ,\mathbf{where}A>0\mathbf{and}{\theta }_{max}\left(n\right)=\underset{1\le r\le m}{max}{\theta }_r\left(n\right),$$

or

$$\sum _{r=n+1}^{{\theta }_k\left(n\right)}{c}_l\left(r\right)<A<+\infty ,\mathbf{where}A>0,k\ne l,k,l=1,2,\dots ,m,$$

where each ${\theta }_r\left(n\right)$ denotes a non-decreasing sequence of positive integers, is a necessary condition for the non-oscillation of Eq. (1).

3. Numerical Results and Simulations

In this section, we provide a comparative analysis between our results and those reported in previous studies, as summarized in Table 1. It is clear that all existing works establish only sufficient conditions for the oscillation of Eq. (1). In contrast, our results not only yield new and sharper oscillation criteria but also reveal that certain formulates are not sufficient to ensure the oscillatory behavior of all solutions of Eq. (1).

We also present two numerical examples to demonstrate the validity and sharpness of the obtained results. The first example applies one of the main theorems to show that a class of difference equations of the form (1) is oscillatory, while previously known criteria fail to detect this behavior; several solution simulations and graphical representations further illustrate the oscillatory nature and identify regions where earlier conditions are ineffective. The second example addresses a qualitative property that, to the best of the authors’ knowledge, has not been previously studied for difference equations advanced arguments, namely the distance between generalized zeros, and the simulations indicate that this distance decreases as the sequence of coefficients increases, highlighting the relevance of this property for a deeper understanding of the solution dynamics.

Example 1. 

Consider the first-order difference equation with several advanced arguments

$$\nabla z\left(n\right)-c_1\left(n\right)z\left({\theta }_1\left(n\right)\right)-c_2\left(n\right)z\left({\theta }_2\left(n\right)\right)-c_3\left(n\right)z\left({\theta }_3\left(n\right)\right)=0,n\in \mathbb{N},$$

(17)

where

$${\theta }_1\left(n\right)=\left\{\begin{array}{cc}n+1,\hfill & \mathrm{if}n=2k,\hfill \\ n+3,\hfill & \mathrm{if}n=2k+1,\hfill \end{array}\right.k\in \mathbb{N},$$

and

$${\theta }_2\left(n\right)=n+⌊\frac{1}{2\delta }⌋,{\theta }_3\left(n\right)=n+⌊\frac{1}{\delta }⌋,$$

where $0<\delta <\frac{1}{3}$, and $⌊\frac{1}{\delta }⌋$ denotes the greatest integer less than or equal to $\frac{1}{\delta }$.

Furthermore, $c_1\left(n\right)={\delta }^2$, and

$$c_2\left(n\right)=c_3\left(n\right)=\left\{\begin{array}{cc}a,\hfill & ifn={\alpha }_k,{\alpha }_k+1,{\alpha }_k+2,\dots ,{\alpha }_{k+⌊{\displaystyle \frac{1}{\delta }}⌋},\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.k\in \mathbb{N},$$

where $a=\frac{2}{3}(\delta +ϵ)$, $ϵ>0$, and the sequence $\left\{{\alpha }_k\right\}$ satisfies

$${\alpha }_{k+1}>{\alpha }_{k+⌊{\displaystyle \frac{1}{\delta }}⌋+1}+⌊{\displaystyle \frac{1}{\delta }}⌋\mathrm{for\; all}\in \mathbb{N}.$$

It follows directly that condition (13) holds, and

$${\varphi }_2\left(n\right)=\underset{r_1\ge n}{min}{\theta }_2\left(r_1\right)={\theta }_2\left(n\right),{\varphi }_3\left(n\right)=\underset{r_1\ge n}{min}{\theta }_3\left(r_1\right)={\theta }_3\left(n\right).$$

Consequently, for $j^{*}=2,3$, we obtain

$$\begin{array}{cc}\hfill \sum _{r=2}^3\sum _{r_1={\alpha }_k}^{{\varphi }_r\left({\alpha }_k\right)}{c}_{j^{*}}\left(r_1\right)& =\sum _{r_1={\alpha }_k}^{{\varphi }_2\left({\alpha }_k\right)}{c}_{j^{*}}\left(r_1\right)+\sum _{r_1={\alpha }_k}^{{\varphi }_3\left({\alpha }_k\right)}{c}_{j^{*}}\left(r_1\right)\hfill \\ \hfill & \ge a\left({\displaystyle \frac{1}{2\delta }}+{\displaystyle \frac{1}{\delta }}\right)={\displaystyle \frac{2}{3}}(\delta +ϵ)·{\displaystyle \frac{3}{2\delta }}=1+{\displaystyle \frac{ϵ}{\delta }}\mathrm{for}\mathrm{all}k\in \mathbb{N}.\hfill \end{array}$$

Therefore, condition (14) is satisfied with $\ell =2$, and hence Eq. (17) is oscillatory.

However, as will be demonstrated below, all known iterative and non-iterative oscillation criteria fail to establish the oscillatory behavior of Eq. (17). For example,

$$\begin{array}{cc}\hfill \sum _{r=1}^3\sum _{r_1={\alpha }_{k+⌊{\displaystyle \frac{1}{\delta }}⌋+1}}^{{\theta }_r\left({\alpha }_{k+⌊{\displaystyle \frac{1}{\delta }}⌋+1}\right)}{c}_r\left(r_1\right)& \le \sum _{r=1}^3\sum _{r_1={\alpha }_{k+⌊{\displaystyle \frac{1}{\delta }}⌋+1}}^{{\theta }_{min}\left({\alpha }_{k+⌊{\displaystyle \frac{1}{\delta }}⌋+1}\right)}{c}_r\left(r_1\right)\hfill \\ \hfill & \le \sum _{r=1}^3\sum _{r_1={\alpha }_{k+⌊{\displaystyle \frac{1}{\delta }}⌋+1}}^{{\alpha }_{k+⌊{\displaystyle \frac{1}{\delta }}⌋+1}+⌊{\displaystyle \frac{1}{\delta }}⌋}{c}_r\left(r_1\right)=0\mathrm{for}\mathrm{all}k\in \mathbb{N}.\hfill \end{array}$$

where ${\theta }_{min}\left(n\right)={min}_{1\le r\le m}{\theta }_r\left(n\right)={\theta }_3\left(n\right)$. Therefore,

$$\underset{n\to \infty }{lim\; inf}\sum _{r=1}^3\sum _{r_1=n+1}^{{\theta }_r\left(n\right)}{c}_r\left(r_1\right)\le \underset{n\to \infty }{lim\; inf}\sum _{r=1}^3\sum _{r_1=n+1}^{{\theta }_{min}\left(n\right)}{c}_r\left(r_1\right)=0.$$

Consequently, ([14] Theorem 3.2) cannot be applied to Eq. (17). Furthermore, we observe that

$$\theta \left(n\right)=\underset{1\le r\le m}{min}{\theta }_r\left(n\right)={\theta }_1\left(n\right)\le n+3,$$

and

$$\varphi \left(n\right)=\underset{1\le r\le n}{min}{\varphi }_r\left(n\right)\le \theta \left(n\right)\le n+3.$$

Moreover, define

$$\begin{array}{cc}\hfill G\left(n\right)& =G_0\left(n\right)=\sum _{r=1}^3{c}_r\left(n\right),\hfill \\ \hfill G_k\left(n\right)& =G\left(n\right)\left[1+\sum _{r=n+1}^{\theta \left(n\right)}G\left(r\right)exp\left(\sum _{r_1=r+1}^{\theta \left(r\right)}G\left(r_1\right)\prod _{r_2=r_1+1}^{\theta \left(r_1\right)}{\displaystyle \frac{1}{1-G_{k-1}\left(r_2\right)}}\right)\right],k=1,2,\dots .\hfill \end{array}$$

Therefore,

$$G\left(n\right)=G_0\left(n\right)=\sum _{r=1}^3{c}_r\left(n\right)\le {\delta }^2+\frac{4}{3}(\delta +ϵ)=W(\delta ,ϵ),$$

and

$$\begin{array}{cc}\hfill G_1\left(n\right)& =G\left(n\right)\left[1+\sum _{r=n+1}^{\theta \left(n\right)}G\left(r\right)exp\left(\sum _{r_1=r+1}^{\theta \left(r\right)}G\left(r_1\right)\prod _{r_2=r_1+1}^{\theta \left(r_1\right)}{\displaystyle \frac{1}{1-G_0\left(r_2\right)}}\right)\right]\hfill \\ \hfill & \le W(\delta ,ϵ)\left[1+3W(\delta ,ϵ)exp\left(3W(\delta ,ϵ){\left({\displaystyle \frac{1}{1-W(\delta ,ϵ)}}\right)}^3\right)\right]<R_1(\delta ,ϵ)<+\infty .\hfill \end{array}$$

Similarly,

$$G_k\left(n\right)\le R_k(\delta ,ϵ)<+\infty ,k=1,2,\dots .$$

Consequently,

$$\sum _{r=n}^{\theta \left(n\right)}G\left(r\right)\prod _{r_1=\varphi \left(n\right)+1}^{\varphi \left(r\right)}{\displaystyle \frac{1}{1-G_k\left(r_1\right)}}\le 4W(\delta ,ϵ){\left({\displaystyle \frac{1}{1-R_k(\delta ,ϵ)}}\right)}^3<1$$

for sufficiently small $\delta$ and $ϵ$. Hence, [17] (Theorem 2.7) is not satisfied.

Likewise, it can be shown that the remaining oscillation conditions are not satisfied for Eq. (17).

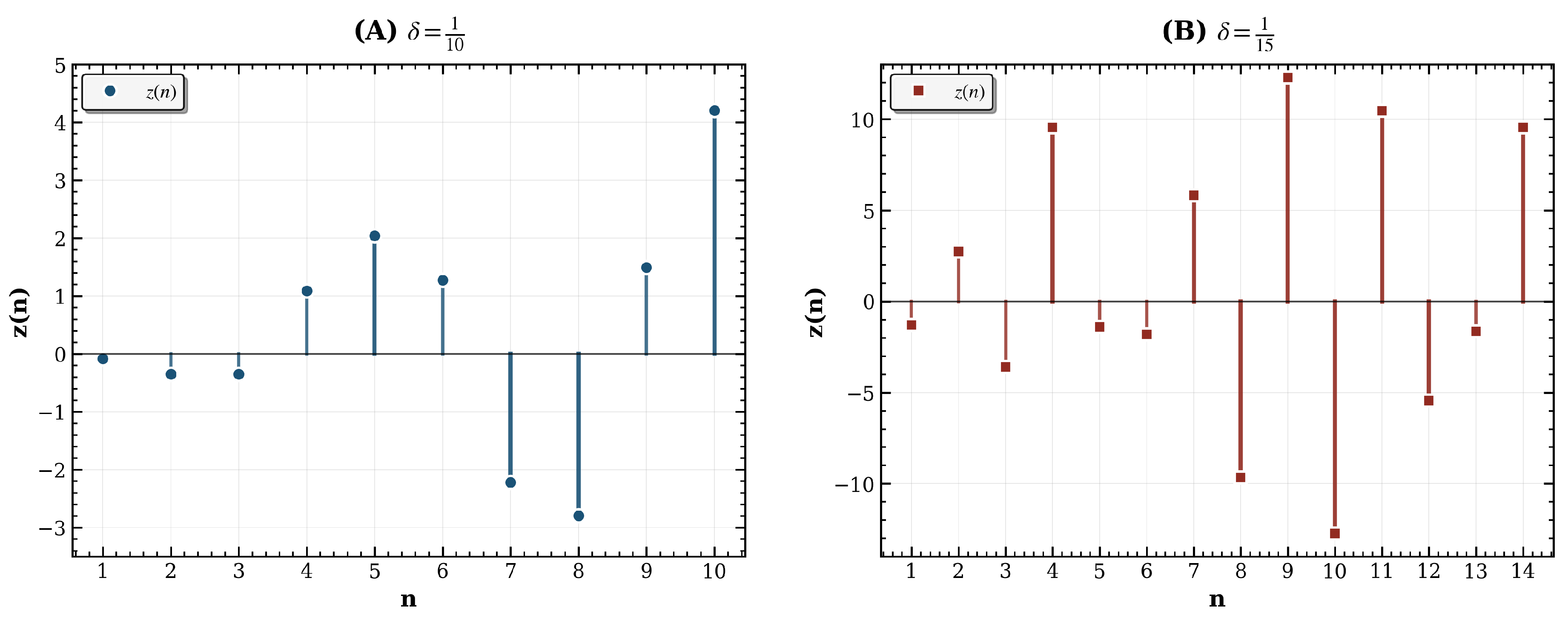
This example demonstrates that condition (14) yields sharper results than existing ones. The numerical results confirm the oscillatory behavior of Eq. (17). As seen in Figure 1, the solution $z\left(n\right)$ oscillates for $\delta =\frac{1}{10}$ and $\delta =\frac{1}{15}$ with $ϵ={10}^{-4}$, while smaller $\delta$ leads to more sign changes, motivating further study of the distance between generalized zeros (see Example 2).

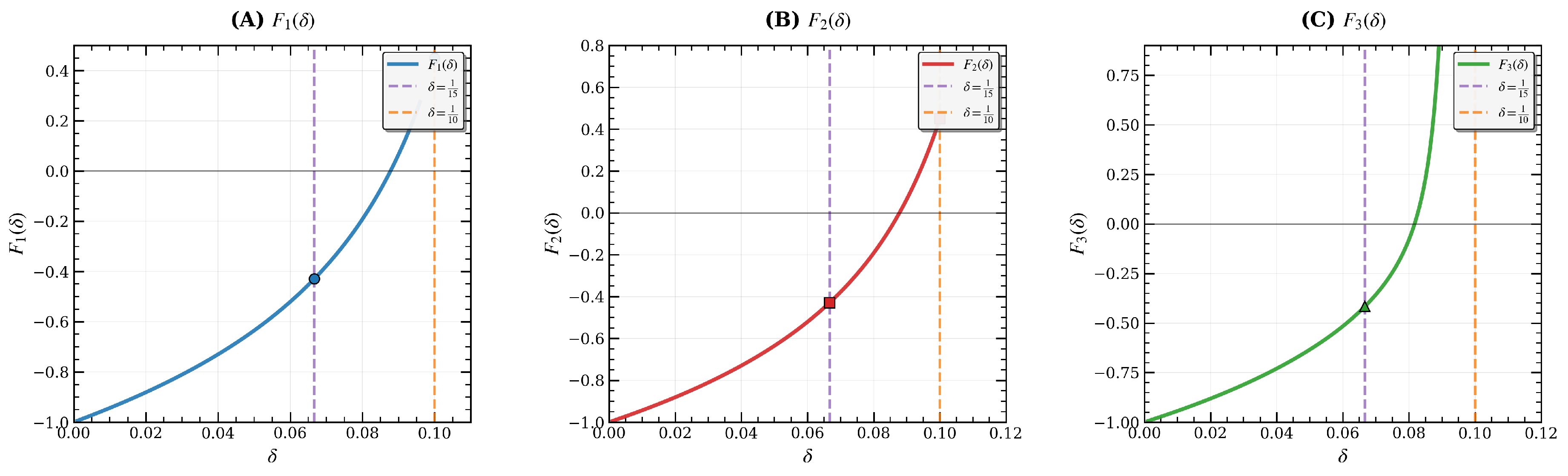
In addition, we illustrate, through several graphical representations, a comparison between condition (14) and [17] (Theorem 2.7). Specifically, we define the function

$$F_k\left(\delta \right)\ge \sum _{r=n}^{\theta \left(n\right)}G\left(r\right)\prod _{r_1=\varphi \left(n\right)+1}^{\varphi \left(r\right)}{\displaystyle \frac{1}{1-G_k\left(r_1\right)}}-1,$$

where $ϵ={10}^{-4}$. We plot the relationship between $F_k\left(\delta \right)$ and the parameter $\delta$. As illustrated in Figure 2 and Table 2, the oscillation condition of [17] (Theorem 2.7), for $k=1,2,$ and 3, is not satisfied on the intervals

$$[0,0.08776083032],[0,0.08584232790],[0,0.08545505006],$$

respectively. However, as shown above, Eq. (17) is oscillatory for all $0<\delta <\frac{1}{3}$ and $ϵ>0$.

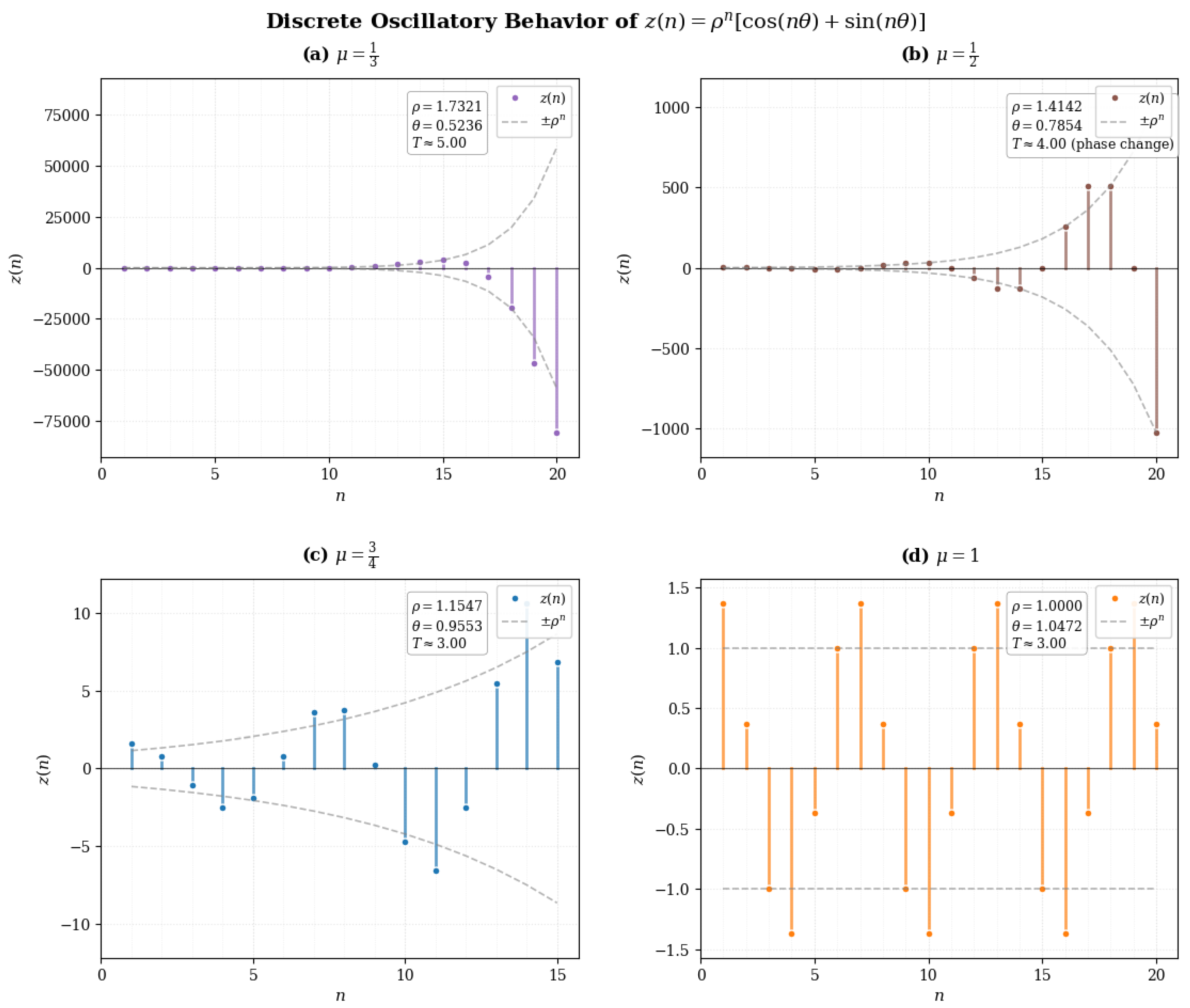
Example 2. 

Consider the difference equation with advanced argument

$$\nabla z\left(n\right)-\mu z(n+1)=0,n\in \mathbb{N}.$$

(18)

This equation represents a particular case of Eq. (4) with $h\left(n\right)=n+1$ and $c\left(n\right)=\mu$. Numerical simulations of Eq. (18) reveal a clear dependence between the parameter $\mu$ and the distance between consecutive generalized zeros of the solutions. Here, a generalized zero is a positive integer at which the solution is zero or has a different sign than at the preceding integer. The numerical results show that the maximum interval length T, over which the solution remains positive (or negative), decreases as $\mu$ increases. Specifically, for $\mu =\frac{1}{3},\frac{1}{2},\frac{3}{4},and1$, the corresponding lengths are $T\simeq 5,4,3,$ and 3, respectively (see Figure 3). These findings highlight the importance of examining the spacing between successive generalized zeros in advanced-type difference equations, as such an analysis provides deeper insight into the qualitative oscillatory dynamics of these equations.