Oscillation Criteria for Delay Difference Equations with Continuous Time, Piecewise Linear Delay Functions, and Oscillatory Coefficients

1. Introduction

The application and importance of delay difference equations with continuous time can be found in mechanical and electrical systems, as it is stated in [1], also in modeling of distributed chaos, as it is pointed out in [2,3]. Analysis of oscillatory properties of solutions of delay difference equations with continuous time have been the subject of papers [4,5,6,7,8,9,10,11,12,13]. Literature concerned with oscillatory properties of solutions of differential and discrete difference equations can be divided into two groups: one with nonnegative or positive coefficients and the other with oscillatory coefficients. Studies on oscillatory properties of solutions of differential equations with nonnegative coefficients can be found, for example, in papers [14,15,16], while with oscillating coefficients in [17,18]. For example, papers [15,19,20,21] and [22,23,24] are devoted to discrete difference equations with positive coefficients and oscillatory coefficients, respectively. Since many papers dealing with difference equations with continuous time analyze equations with positive or nonnegative coefficients (all mentioned above), but only (to the best of our knowledge) paper [25] considers oscillatory coefficients, our aim is to expand the set of known oscillatory conditions of solutions of delay difference equations with continuous time and oscillatory coefficients.

In this paper, we analyze the oscillatory property of the solutions of the delay difference equation

$$\Delta x\left(t\right)+\sum _{i=1}^m{p}_i\left(t\right)x\left({\tau }_i\left(t\right)\right)=0,t\ge t_0,$$

(1)

where $\Delta x\left(t\right)=x(t+1)-x\left(t\right)$, $m\in \mathbb{N}$ and $t_0\in \mathbb{R}$. For $i=1,2,\dots ,m$, $p_i:[t_0,\infty )\to \mathbb{R}$ is a piecewise continuous and oscillatory function, but the delay argument ${\tau }_i$ is in the form

$${\tau }_i\left(t\right)=t-k_i\left(t\right),$$

(2)

where the function $k_i:[t_0,\infty )\to \mathbb{N}$ is piecewise constant. Also, the delay arguments have the following properties:

$${\tau }_i\left(t\right)<t\mathrm{for}\mathrm{all}t\ge t_0\mathrm{and}i=1,2,\dots ,m,$$

(3)

and

$$\underset{t\to \infty }{lim}{\tau }_i\left(t\right)=\infty ,i=1,2,\dots ,m.$$

(4)

We present two oscillatory criteria and compare them to oscillatory conditions in [25]. The comparison shows that there is a set of difference equations such that our new oscillatory criteria prove that their solutions oscillate, while the known criteria are not applicable to them.

A solution of the delay difference equation (1) is a real-valued function x defined on the interval $[t_{-1},\infty )$, with

$$t_{-1}=\underset{1\le i\le m}{min}\left\{inf\{{\tau }_i\left(s\right):s\ge t_0\}\right\},$$

(5)

that satisfies Eq. (1). If a solution of (1) changes sign on the interval $(s,\infty )$ for any s, it is oscillatory. Otherwise, it is nonoscillatory. As in [8,26], for any bounded real-valued function $\phi$ defined on the interval $[t_{-1},t_0+1)$ there exists a unique solution x of (1) that satisfies the initial condition $x\left(t\right)=\phi \left(t\right)$, $t\in [t_{-1},t_0+1)$, since it can be represented by

$$\begin{array}{cc}\hfill x\left(t\right)& =\phi \left(t\right),t_{-1}\le t<t_0+1,\hfill \\ \hfill x\left(t\right)& =x(t-1)-\sum _{i=1}^m{p}_i(t-1)x\left({\tau }_i(t-1)\right),t\ge t_0+1.\hfill \end{array}$$

Standardly, for any $a\in \mathbb{R}$, $n\in {\mathbb{N}}_0$, and a real-valued function f,

$$\sum _{q=a}^{a-1}f\left(q\right)=0\mathrm{and}\sum _{q=a}^{a+n}f\left(q\right)=f\left(a\right)+f(a+1)+\dots +f(a+n)$$

and

$$f^n\left(t\right)=f\left(f^{n-1}\left(t\right)\right),\mathrm{with}{f}^0\left(t\right)=t.$$

2. The New Oscillation Criteria

We define a real-valued functions

$$\tau \left(t\right)=t-\underset{t_0\le s\le t}{inf}\left(\underset{1\le i\le m}{min}{k}_i\left(s\right)\right)$$

(6)

and

$$\underline{\tau }\left(t\right)=\underset{s\ge t}{inf}\left(\underset{1\le i\le m}{min}{\tau }_i\left(s\right)\right).$$

(7)

These functions have the following properties:

• $$t-\tau \left(t\right)\in \mathbb{N}\mathrm{for}\forall t\ge t_0,i=1,2,\dots ,m,$$

  (8)
• $$\tau \left(t\right)-{\tau }_i\left(t\right)\in {\mathbb{N}}_0\mathrm{for}\forall t\ge t_0,i=1,2,\dots ,m,$$

  (9)
• $$\tau (t+n)-\tau \left(t\right)\in \mathbb{N}\mathrm{for}\forall t\ge t_0\mathrm{and}\mathrm{any}n\in \mathbb{N},$$

  (10)
• $$\mathrm{if}t\in [a,b]\subset [t_0,\infty ),\mathrm{then}t,\tau \left(t\right),{\tau }_1\left(t\right),\dots ,{\tau }_m\left(t\right)\in [\underline{\tau }\left(a\right),b],$$

  (11)
• $$\tau \left(t\right)\ge \underline{\tau }\left(t\right)\mathrm{for}\forall t\in [t_0,\infty ).$$

  (12)

For more details and illustrations by example see [25].

First we give the following lemma.

Lemma 1.

If there exists a sequence of disjoint intervals ${\left\{[a_j,b_j]\right\}}_{j\in \mathbb{N}}$ with properties: $b_j-a_j\in \mathbb{N}$ for every $j\in \mathbb{N}$,

$$p_i\left(t\right)\ge 0fort\in \bigcup _{j\in \mathbb{N}}[a_j,b_j],i=1,2,\dots ,m,$$

(13)

and, for some $c>0$,

$$\sum _{q=a_j}^{b_j}\sum _{i=1}^m{p}_i\left(q\right)\ge c\mathit{for}\forall j\in \mathbb{N},$$

(14)

then there exists a sequence ${\left\{{\eta }_j\right\}}_{j\in \mathbb{N}}$ such that ${\eta }_j\in \{a_j,a_j+1,\dots ,b_j\}$ and

$$\sum _{q=a_j}^{{\eta }_j-1}\sum _{i=1}^m{p}_i\left(q\right)<{\displaystyle \frac{c}{2}}$$

(15)

but

$$\sum _{q=a_j}^{{\eta }_j}\sum _{i=1}^m{p}_i\left(q\right)\ge {\displaystyle \frac{c}{2}}.$$

(16)

Proof. 

For any $j\in \mathbb{N}$, if

$$\sum _{i=1}^m{p}_i\left(a_j\right)\ge {\displaystyle \frac{c}{2}},$$

then

$$\sum _{q=a_j}^{a_j-1}\sum _{i=1}^m{p}_i\left(q\right)=0<{\displaystyle \frac{c}{2}}\mathrm{and}\sum _{q=a_j}^{a_j}\sum _{i=1}^m{p}_i\left(q\right)=\sum _{i=1}^m{p}_i\left(a_j\right)\ge {\displaystyle \frac{c}{2}},$$

so (15) and (16) hold for ${\eta }_j=a_j$.

For $a_j=b_j$, (14) gives that

$$\sum _{q=a_j}^{b_j}\sum _{i=1}^m{p}_i\left(q\right)=\sum _{i=1}^m{p}_i\left(a_j\right)\ge c\ge {\displaystyle \frac{c}{2}},$$

that is, (15) and (16) hold for ${\eta }_j=a_j$. Besides that, if

$$\sum _{i=1}^m{p}_i\left(a_j\right)<{\displaystyle \frac{c}{2}},$$

then $a_j<b_j$ and there exists ${\eta }_j\in \{a_j+1,a_j+2,\dots ,b_j\}$ such that (15) and (16) hold.

Consequently, for every $j\in \mathbb{N}$, there exists ${\eta }_j\in \{a_j,a_j+1,\dots ,b_j\}$ such that (15) and (16) hold. □

Now we prove an auxiliary lemma.

Lemma 2.

Let $t_{-1}$, τ, and $\underline{\tau }$ be defined by (5), (6), and (7), respectively. Assume that the function $x:[t_{-1},\infty )\to \mathbb{R}$ is a nonoscillatory solution of (1). If there exists a sequence of real numbers ${\left\{{\xi }_j\right\}}_{j\in \mathbb{N}}$ such that

$$\underset{j\to \infty }{lim}{\xi }_j=\infty ,$$

(17)

$$\left[\underline{\tau }\left(\tau (\tau \left({\xi }_j\right)-1)\right),{\xi }_j-1\right]\subset [t_0,\infty )\mathit{are}\mathit{nonempty}\mathit{and}\mathit{disjoint}\mathit{for}j\in \mathbb{N},$$

(18)

$$p_i\left(t\right)\ge 0fort\in \bigcup _{j\in \mathbb{N}}\left[\underline{\tau }\left(\tau (\tau \left({\xi }_j\right)-1)\right),{\xi }_j-1\right],i=1,2,\dots ,m,$$

(19)

and

$$\alpha =\underset{j\to \infty }{lim\; inf}\underset{s\in \{\tau \left({\xi }_j\right),\dots ,{\xi }_j\}}{min}\sum _{q=\tau \left(s\right)}^{s-1}\sum _{i=1}^m{p}_i\left(q\right)\mathit{such}\mathit{that}0<\alpha <2,$$

(20)

then

$$\underset{j\to \infty }{lim\; inf}{\displaystyle \frac{x\left(\tau \left({\xi }_j\right)\right)}{x\left(\tau (\tau \left({\xi }_j\right)-1)\right)}}\ge {\displaystyle \frac{{\alpha }^2}{2(2-\alpha )}}.$$

(21)

Proof. 

Let $I_j$ and ${\underline{I}}_j$, for $j\in \mathbb{N}$, denote the $\left[\tau (\tau \left({\xi }_j\right)-1),{\xi }_j-1\right]$ and $\left[\underline{\tau }\left(\tau (\tau \left({\xi }_j\right)-1)\right),{\xi }_j-1\right]$, respectively. Note that properties (10) and (8) give that

$$\tau (\tau \left({\xi }_j\right)-1)<\tau \left(\tau \left({\xi }_j\right)\right)<\tau \left({\xi }_j\right)\le {\xi }_j-1,$$

so $\{\tau \left(\tau \left({\xi }_j\right)\right),\dots ,\tau \left({\xi }_j\right),\tau \left({\xi }_j\right)+1,\dots ,{\xi }_j-1\}\subset I_j\subset {\underline{I}}_j$.

Due to the definition of limit inferior and (20), for arbitrary $\epsilon >0$, so for $0<\epsilon <\alpha$,

$$\underset{s\in \{\tau \left({\xi }_j\right),\dots ,{\xi }_j\}}{min}\sum _{q=\tau \left(s\right)}^{s-1}\sum _{i=1}^m{p}_i\left(q\right)\ge \alpha -\epsilon \mathrm{for}\forall j\in \mathbb{N}.$$

Hence,

$$\sum _{q=\tau \left(s\right)}^{s-1}\sum _{i=1}^m{p}_i\left(q\right)\ge \alpha -\epsilon \mathrm{for}\forall s\in \{\tau \left({\xi }_j\right),\dots ,{\xi }_j\},\forall j\in \mathbb{N}$$

(22)

and consequently,

$$\sum _{q=\tau \left({\xi }_j\right)}^{{\xi }_j-1}\sum _{i=1}^m{p}_i\left(q\right)\ge \alpha -\epsilon \mathrm{for}\forall j\in \mathbb{N}.$$

(23)

Since $\{\tau \left({\xi }_j\right),\tau \left({\xi }_j\right)+1,\dots ,{\xi }_j-1\}\subset {\underline{I}}_j$, condition (19) ensures that $p_i\left(q\right)\ge 0$ for every $q\in \{\tau \left({\xi }_j\right),\tau \left({\xi }_j\right)+1,\dots ,{\xi }_j-1\}$ and $i=1,2,\dots ,m$. Besides that, (18), (19), and (23) ensure that the sequence of intervals ${\left\{[\tau \left({\xi }_j\right),{\xi }_j-1]\right\}}_{j\in \mathbb{N}}$ satisfies the conditions of Lemma 1 with $c=\alpha -\epsilon$. Therefore, there exists a sequence ${\left\{{\eta }_j\right\}}_{j\in \mathbb{N}}$ such that ${\eta }_j\in \{\tau \left({\xi }_j\right),\tau \left({\xi }_j\right)+1,\dots ,{\xi }_j-1\}$,

$$\sum _{q=\tau \left({\xi }_j\right)}^{{\eta }_j-1}\sum _{i=1}^m{p}_i\left(q\right)<{\displaystyle \frac{\alpha -\epsilon }{2}},$$

(24)

$$\sum _{q=\tau \left({\xi }_j\right)}^{{\eta }_j}\sum _{i=1}^m{p}_i\left(q\right)\ge {\displaystyle \frac{\alpha -\epsilon }{2}}.$$

(25)

By (22),

$$\sum _{q=\tau \left({\eta }_j\right)}^{{\eta }_j-1}\sum _{i=1}^m{p}_i\left(q\right)\ge \alpha -\epsilon \mathrm{for}\forall j\in \mathbb{N},$$

so, using (24), we obtain

$$\sum _{q=\tau \left({\eta }_j\right)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right)=\sum _{q=\tau \left({\eta }_j\right)}^{{\eta }_j-1}\sum _{i=1}^m{p}_i\left(q\right)-\sum _{q=\tau \left({\xi }_j\right)}^{{\eta }_j-1}\sum _{i=1}^m{p}_i\left(q\right)>{\displaystyle \frac{\alpha -\epsilon }{2}}.$$

(26)

Property (10) secures that $\tau \left({\eta }_j\right)\le \tau \left({\xi }_j\right)-1$.

Since x is a nonoscillatory solution of (1), without loss of generality, we can assume that

$$x\left(t\right)>0\mathrm{for}\mathrm{every}t\ge t_1,\mathrm{where}{t}_0\le t_1\le {\underline{\tau }}^2\left(\tau (\tau \left({\xi }_1\right)-1)\right).$$

(27)

For every $t\in {\underline{I}}_j$, property (11) ensures that, for every $i=1,2,\dots ,m$, ${\tau }_i\left(t\right)\in \left[{\underline{\tau }}^2\left(\tau (\tau \left({\xi }_j\right)-1)\right),{\xi }_j-1\right]$, thus ${\tau }_i\left(t\right)\ge t_1$, so (1), (19), and (27) provide

$$x(t+1)-x\left(t\right)=-\sum _{i=1}^m{p}_i\left(t\right)x\left({\tau }_i\left(t\right)\right)\le 0\mathrm{for}\forall t\in {\underline{I}}_j,$$

i.e.,

$$x(t+1)\le x\left(t\right)\mathrm{for}\forall t\in {\underline{I}}_j.$$

Consequently,

$$\mathrm{if}t,t+n\in {\underline{I}}_j\mathrm{for}\mathrm{some}n\in \mathbb{N},\mathrm{then}x\left(t\right)\ge x(t+n).$$

(28)

Also, (11) ensures that ${\tau }_1\left(t\right),{\tau }_2\left(t\right),\dots ,{\tau }_m\left(t\right),\tau \left(t\right)\in {\underline{I}}_j$ for every $t\in I_j$. Therefore, (9) and (28) provide that

$$x\left({\tau }_i\left(t\right)\right)\ge x\left(\tau \left(t\right)\right)\mathrm{for}\mathrm{every}t\in I_j.$$

(29)

Summing up (1) from $t=\tau \left({\xi }_j\right)$ to $t={\eta }_j$, we obtain

$$\begin{array}{cc}\hfill x\left(\tau \left({\xi }_j\right)\right)& =x({\eta }_j+1)+\sum _{q=\tau \left({\xi }_j\right)}^{{\eta }_j}\sum _{i=1}^m{p}_i\left(q\right)x\left({\tau }_i\left(q\right)\right)\hfill \\ \hfill & \left(q\in [\tau \left({\xi }_j\right),{\eta }_j]\subset [\tau \left({\xi }_j\right),{\xi }_j-1]\subset I_j,\mathrm{so}\mathrm{by}\left(29\right)\mathrm{and}\left(19\right)\right)\hfill \\ \hfill & \ge x({\eta }_j+1)+\sum _{q=\tau \left({\xi }_j\right)}^{{\eta }_j}\sum _{i=1}^m{p}_i\left(q\right)x\left(\tau \left(q\right)\right)\hfill \\ \hfill & (\tau \left({\eta }_j\right)-\tau \left(q\right)\in {\mathbb{N}}_0\mathrm{by}\left(10\right)\mathrm{and}\tau \left(q\right)\in {\underline{I}}_j\mathrm{by}\left(11\right),\hfill \\ \hfill & \mathrm{thus}\left(28\right)\mathrm{gives}\mathrm{that}x\left(\tau \left(q\right)\right)\ge x\left(\tau \left({\eta }_j\right)\right),\mathrm{so}\mathrm{by}\left(19\right))\hfill \\ \hfill & \ge x({\eta }_j+1)+x\left(\tau \left({\eta }_j\right)\right)\sum _{q=\tau \left({\xi }_j\right)}^{{\eta }_j}\sum _{i=1}^m{p}_i\left(q\right).\hfill \end{array}$$

Hence, by (25),

$$x\left(\tau \left({\xi }_j\right)\right)\ge x({\eta }_j+1)+x\left(\tau \left({\eta }_j\right)\right){\displaystyle \frac{\alpha -\epsilon }{2}}.$$

(30)

Similarly, summing up (1) from $t=\tau \left({\eta }_j\right)$ to $t=\tau \left({\xi }_j\right)-1$, we obtain

$$\begin{array}{cc}\hfill x\left(\tau \left({\eta }_j\right)\right)& =x\left(\tau \left({\xi }_j\right)\right)+\sum _{q=\tau \left({\eta }_j\right)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right)x\left({\tau }_i\left(q\right)\right)\hfill \\ \hfill & \left(q\in [\tau \left({\eta }_j\right),\tau \left({\xi }_j\right)-1]\subset [\tau \left(\tau \left({\xi }_j\right)\right),\tau \left({\xi }_j\right)-1]\subset I_j\right)\hfill \\ \hfill & \ge x\left(\tau \left({\xi }_j\right)\right)+\sum _{q=\tau \left({\eta }_j\right)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right)x\left(\tau \left(q\right)\right)\hfill \\ \hfill & \left(\tau (\tau \left({\xi }_j\right)-1)-\tau \left(q\right)\in {\mathbb{N}}_0\mathrm{and}\tau \left(q\right)\in {\underline{I}}_j\right)\hfill \\ \hfill & \ge x\left(\tau \left({\xi }_j\right)\right)+x\left(\tau (\tau \left({\xi }_j\right)-1)\right)\sum _{q=\tau \left({\eta }_j\right)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right).\hfill \end{array}$$

Therefore, (26) implies

$$x\left(\tau \left({\eta }_j\right)\right)\ge x\left(\tau \left({\xi }_j\right)\right)+x\left(\tau (\tau \left({\xi }_j\right)-1)\right){\displaystyle \frac{\alpha -\epsilon }{2}}.$$

(31)

Combining inequalities (30) and (31), we get

$$x\left(\tau \left({\xi }_j\right)\right)\ge x({\eta }_j+1)+x\left(\tau \left({\xi }_j\right)\right){\displaystyle \frac{\alpha -\epsilon }{2}}+x\left(\tau (\tau \left({\xi }_j\right)-1)\right){\left({\displaystyle \frac{\alpha -\epsilon }{2}}\right)}^2,$$

i.e.,

$$x\left(\tau \left({\xi }_j\right)\right)\left(1-{\displaystyle \frac{\alpha -\epsilon }{2}}\right)\ge x({\eta }_j+1)+x\left(\tau (\tau \left({\xi }_j\right)-1)\right){\displaystyle \frac{{\left(\alpha -\epsilon \right)}^2}{4}}.$$

Since $x({\eta }_j+1)>0$,

$$x\left(\tau \left({\xi }_j\right)\right){\displaystyle \frac{2-\left(\alpha -\epsilon \right)}{2}}\ge x\left(\tau (\tau \left({\xi }_j\right)-1)\right){\displaystyle \frac{{\left(\alpha -\epsilon \right)}^2}{4}}.$$

Using that $\alpha <2$ and $\epsilon >0$, we have

$${\displaystyle \frac{x\left(\tau \left({\xi }_j\right)\right)}{x\left(\tau (\tau \left({\xi }_j\right)-1)\right)}}\ge {\displaystyle \frac{{\left(\alpha -\epsilon \right)}^2}{2\left(2-\left(\alpha -\epsilon \right)\right)}}.$$

Consequently,

$$\underset{j\to \infty }{lim\; inf}{\displaystyle \frac{x\left(\tau \left({\xi }_j\right)\right)}{x\left(\tau (\tau \left({\xi }_j\right)-1)\right)}}\ge {\displaystyle \frac{{\left(\alpha -\epsilon \right)}^2}{2\left(2-\left(\alpha -\epsilon \right)\right)}}.$$

(32)

Since (32) holds for arbitrarily small $\epsilon$, it implies (21). The proof of the lemma is complete. □

Now we are ready to formulate and prove a new criterion that provides that all solutions of the observed difference equation are oscillatory.

Theorem 1.

For $t_{-1}$, τ and $\underline{\tau }$ defined by (5), (6), and (7) respectively, assume that there exists a sequence of real numbers ${\left\{{\xi }_j\right\}}_{j\in \mathbb{N}}$ such that conditions (17)-(20) are satisfied. If

$$\underset{j\to \infty }{lim\; sup}\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right)>1-{\displaystyle \frac{{\alpha }^2}{2\left(2-\alpha \right)}},$$

(33)

then all solutions of (1) are oscillatory.

Proof. 

As in the proof of the previous lemma, for $j\in \mathbb{N}$, $I_j$ and ${\underline{I}}_j$ denote the intervals $\left[\tau (\tau \left({\xi }_j\right)-1),{\xi }_j-1\right]$ and $\left[\underline{\tau }\left(\tau (\tau \left({\xi }_j\right)-1)\right),{\xi }_j-1\right]$, respectively.

Supposing the opposite, let the function $x:[t_{-1},\infty )\to \mathbb{R}$ be a nonoscillatory solution of (1). Without loss of generality, we can assume that

$$x\left(t\right)>0\mathrm{for}\mathrm{every}t\ge t_1,\mathrm{where}{t}_0\le t_1\le {\underline{\tau }}^2\left(\tau (\tau \left({\xi }_1\right)-1)\right).$$

(34)

Therefore (11), (1), (19), and (34) imply

$$x(t+1)-x\left(t\right)=-\sum _{i=1}^m{p}_i\left(t\right)x\left({\tau }_i\left(t\right)\right)\le 0\mathrm{for}\forall t\in {\underline{I}}_j.$$

Consequently, for every $j\in \mathbb{N}$,

$$\mathrm{if}t,t+n\in {\underline{I}}_j\mathrm{for}\mathrm{some}n\in \mathbb{N},\mathrm{then}x\left(t\right)\ge x(t+n).$$

(35)

Since (11) ensures that ${\tau }_1\left(t\right),{\tau }_2\left(t\right),\dots ,{\tau }_m\left(t\right),\tau \left(t\right)\in {\underline{I}}_j$ for every $t\in I_j$, (9) and (35) provide that

$$x\left({\tau }_i\left(t\right)\right)\ge x\left(\tau \left(t\right)\right)\mathrm{for}\forall t\in I_j.$$

(36)

For any $j\in \mathbb{N}$, summing up (1) from $t=\tau (\tau \left({\xi }_j\right)-1)$ to $t=\tau \left({\xi }_j\right)-1$, then using that $\left\{\tau (\tau \left({\xi }_j\right)-1),\dots ,\tau \left({\xi }_j\right)-1\right\}\subset I_j$ and applying (19), (36), afterwards by (19), (10), and (35), we have

$$\begin{array}{cc}\hfill x\left(\tau (\tau \left({\xi }_j\right)-1)\right)& =x\left(\tau \left({\xi }_j\right)\right)+\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right)x\left({\tau }_i\left(q\right)\right)\hfill \\ \hfill & \ge x\left(\tau \left({\xi }_j\right)\right)+\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right)x\left(\tau \left(q\right)\right)\hfill \\ \hfill & \ge x\left(\tau \left({\xi }_j\right)\right)+x\left(\tau (\tau \left({\xi }_j\right)-1)\right)\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right).\hfill \end{array}$$

Dividing the obtained inequality by $x\left(\tau (\tau \left({\xi }_j\right)-1)\right)$, that is positive, we obtain

$$1\ge {\displaystyle \frac{x\left(\tau \left({\xi }_j\right)\right)}{x\left(\tau (\tau \left({\xi }_j\right)-1)\right)}}+\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right),$$

i.e.,

$$\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right)\le 1-{\displaystyle \frac{x\left(\tau \left({\xi }_j\right)\right)}{x\left(\tau (\tau \left({\xi }_j\right)-1)\right)}}.$$

Hence,

$$\underset{j\to \infty }{lim\; sup}\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right)\le 1-\underset{j\to \infty }{lim\; inf}{\displaystyle \frac{x\left(\tau \left({\xi }_j\right)\right)}{x\left(\tau (\tau \left({\xi }_j\right)-1)\right)}}.$$

Applying (21) from Lemma 2, we have

$$\underset{j\to \infty }{lim\; sup}\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right)\le 1-{\displaystyle \frac{{\alpha }^2}{2(2-\alpha )}},$$

(37)

which is a contradiction to condition (33). The proof of the theorem is complete. □

Due to the following corollary, the nonnegativity of the coefficients in the definition of $\alpha$ and coefficients in condition (33) combined with property (10) yield to conclusion that for $\alpha >3-\sqrt{5}$ there is no need to check the condition (33).

Corollary 1.

For $t_{-1}$, τ and $\underline{\tau }$ defined by (5), (6), and (7) respectively, assume that there exists a sequence of real numbers ${\left\{{\xi }_j\right\}}_{j\in \mathbb{N}}$ such that conditions (17)-(20) are satisfied. If $\alpha >3-\sqrt{5}$, then all solutions of (1) are oscillatory.

Proof. 

Since $\tau (\tau \left({\xi }_j\right)-1)\le \tau \left(\tau \left({\xi }_j\right)\right)$, condition (19) and definition (20) give

$$\alpha \le \underset{j\to \infty }{lim\; inf}\sum _{q=\tau \left(\tau \left({\xi }_j\right)\right)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right)\le \underset{j\to \infty }{lim\; sup}\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^m{p}_i\left(q\right).$$

(38)

For $2>\alpha >3-\sqrt{5}$, the inequality

$$\alpha >1-{\displaystyle \frac{{\alpha }^2}{2(2-\alpha )}}$$

holds, so (38) ensures that condition (33) is satisfied and, based on Theorem 1, it implies that all solutions of (1) are oscillatory. □

Notice that the oscillatory conditions in Theorem 1 and Corollary 1 require the nonnegativity of coefficients in the disjoint intervals and do not use the intervals where the coefficients are negative. Therefore, the presented oscillatory conditions can be applied to establishing the oscillatory property of solutions of difference equations in form (1) but with positive coefficients.

3. Examples and Comparisons

The following examples illustrate the presented conditions for oscillatory solutions of the observed difference equation. For first two examples, the oscillatory conditions from Theorem 1 are satisfied, but the oscillatory conditions from Corollary 1 and oscillatory conditions from [25] are not fulfilled. The last example shows the application of oscillatory conditions from Corollary 1 on delay difference equation with unbounded delays. Moreover, oscillatory conditions from [25] are not satisfied for that example either.

Theorem 2

([25, Theorem 2.2]). For the functions τ and $\underline{\tau }$ defined by (6) and (7) respectively, assume that there exists a sequence of real numbers ${\left\{{\xi }_j\right\}}_{j\in \mathbb{N}}$ such that condition (17) holds and the intervals of the sequence ${\left\{\left[\underline{\tau }\left(\tau \left({\xi }_j\right)\right),{\xi }_j\right]\right\}}_{j\in \mathbb{N}}$ are nonempty, disjoint, and contained in $[t_0,\infty )$. If, in addition,

$$p_i\left(t\right)\ge 0\mathrm{for}t\in \bigcup _{j\in \mathbb{N}}\left[\underline{\tau }\left(\tau \left({\xi }_j\right)\right),{\xi }_j\right],i=1,2,\dots ,m,$$

(39)

and

$$\underset{j\to \infty }{lim\; sup}\sum _{q=\tau \left({\xi }_j\right)}^{{\xi }_j}\sum _{i=1}^m{p}_i\left(q\right)>1,$$

(40)

then all solutions of (1) are oscillatory.

Theorem 3

([25, , Theorem 2.3]). For the functions τ and $\underline{\tau }$ defined by (6) and (7) respectively, assume that there exists a sequence of real numbers ${\left\{{\xi }_j\right\}}_{j\in \mathbb{N}}$ such that condition (17) holds and the intervals of the sequence ${\left\{\left[\underline{\tau }\left({\tau }^j\left({\xi }_j\right)\right),{\xi }_j\right]\right\}}_{j\in \mathbb{N}}$ are nonempty, disjoint, and contained in $[t_0,\infty )$. If, moreover,

$$p_i\left(t\right)\ge 0fort\in \bigcup _{j\in \mathbb{N}}\left[\underline{\tau }\left({\tau }^j\left({\xi }_j\right)\right),{\xi }_j\right],i=1,2,\dots ,m,$$

(41)

and there exists a real number $c>1/e$ such that

$$\underset{j\to \infty }{lim}\underset{t\in I_j^{j-1}}{inf}\sum _{q=\tau \left(t\right)}^{t-1}\sum _{i=1}^m{p}_i\left(q\right)>c,\mathrm{where}{I}_j^{j-1}=[{\tau }^{j-1}\left({\xi }_j\right),{\xi }_j],$$

(42)

then all solutions of (1) are oscillatory.

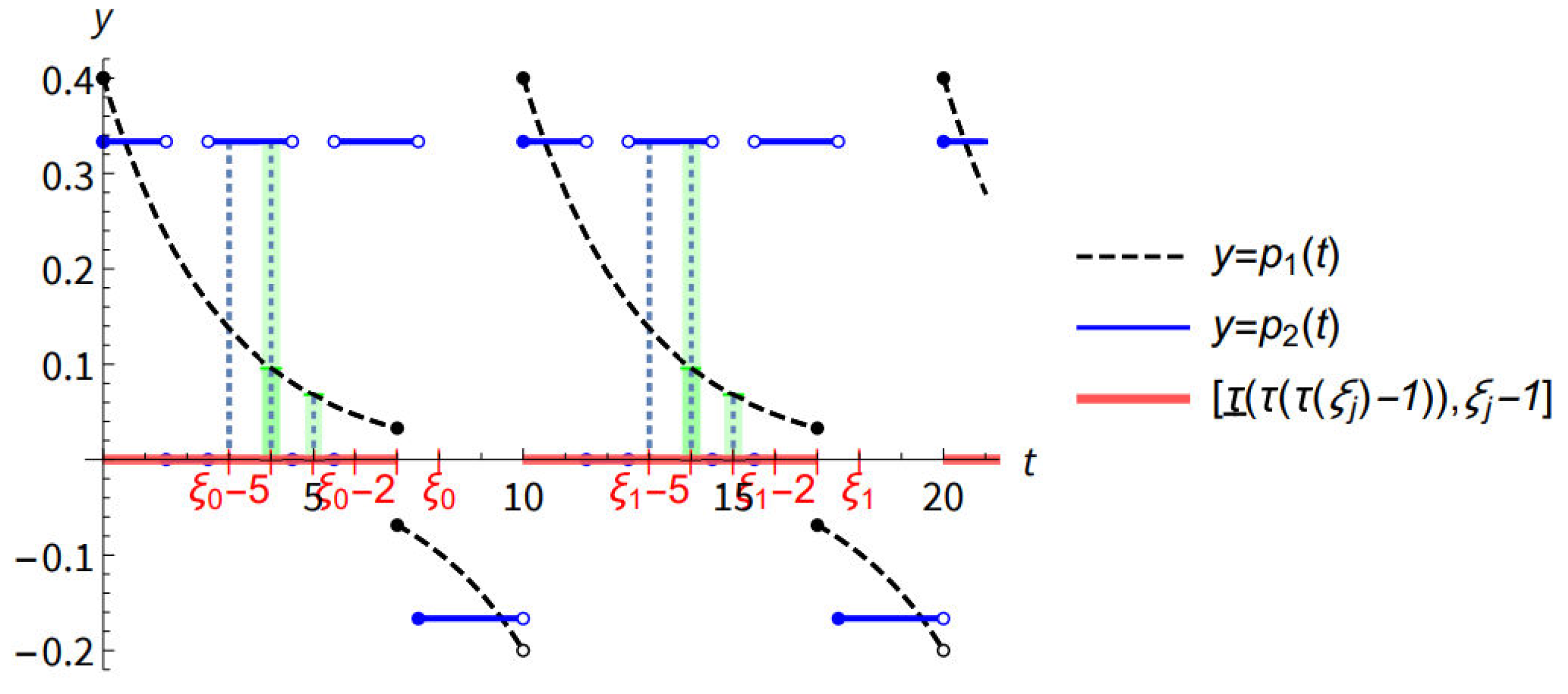
Example 1.

Consider the difference equation

$$\Delta x\left(t\right)+p_1\left(t\right)x(t-2)+p_2\left(t\right)x(t-3)=0,t\ge 0,$$

(43)

where functions $p_1$ and $p_2$ are periodic, with the basic period 10, such that

$$\begin{array}{c}\hfill p_1\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{2}{5}}·{\left({\displaystyle \frac{7}{10}}\right)}^t,\hfill & t\in [0,7],\hfill \\ -{\displaystyle \frac{1}{5}}·{\left({\displaystyle \frac{7}{10}}\right)}^{10-t},\hfill & t\in (7,10),\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill p_2\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{3}},\hfill & t\in [0,1.5)\cup (2.5,4.5)\cup (5.5,7.5),\hfill \\ 0,\hfill & t\in [1.5,2.5]\cup [4.5,5.5],\hfill \\ -{\displaystyle \frac{1}{6}},\hfill & t\in [7.5,10).\hfill \end{array}\right.\end{array}$$

Here, ${\tau }_1\left(t\right)=t-2$ and ${\tau }_2\left(t\right)=t-3$, thus $\tau \left(t\right)=t-2$ and $\underline{\tau }\left(t\right)=t-3$. Therefore, $\tau \left(\tau \right(t)-1)=t-5$ and $\underline{\tau }\left(\tau (\tau \left(t\right)-1)\right)=t-8$. For the sequence of real numbers ${\left\{{\xi }_j\right\}}_{j\in {\mathbb{N}}_0}$ such that ${\xi }_j=10j+8$,

$$\tau \left({\xi }_j\right)=10j+6,\tau (\tau \left({\xi }_j\right)-1)=10j+3,\underline{\tau }\left(\tau (\tau \left({\xi }_j\right)-1)\right)=10j,j\in {\mathbb{N}}_0,$$

so, for every $j\in {\mathbb{N}}_0$,

$$\begin{array}{cc}\hfill I_j& =\left[\tau (\tau \left({\xi }_j\right)-1),{\xi }_j-1\right]=[10j+3,10j+7],\hfill \\ \hfill {\underline{I}}_j& =\left[\underline{\tau }\left(\tau (\tau \left({\xi }_j\right)-1)\right),{\xi }_j-1\right]=[10j,10j+7].\hfill \end{array}$$

It means that conditions (17), (18), and (19) are satisfied with

$$\begin{array}{cc}\hfill \alpha & =\underset{j\to \infty }{lim\; inf}\underset{s\in \{\tau \left({\xi }_j\right),\dots ,{\xi }_j\}}{min}\sum _{q=\tau \left(s\right)}^{s-1}\sum _{i=1}^2{p}_i\left(q\right)=\underset{j\to \infty }{lim\; inf}\underset{s\in \{10j+6,\dots ,10j+8\}}{min}\sum _{q=\tau \left(s\right)}^{s-1}\sum _{i=1}^2{p}_i\left(q\right)\hfill \\ \hfill & =\underset{j\to \infty }{lim\; inf}min\left\{\sum _{q=10j+4}^{10j+5}\sum _{i=1}^2{p}_i\left(q\right),\sum _{q=10j+5}^{10j+6}\sum _{i=1}^2{p}_i\left(q\right),\sum _{q=10j+6}^{10j+7}\sum _{i=1}^2{p}_i\left(q\right)\right\}\hfill \\ \hfill & \approx min\left\{0.496601,0.447621,0.746668\right\}=0.447621.\hfill \end{array}$$

Due to $1-{\displaystyle \frac{{\alpha }^2}{2(2-\alpha )}}\approx 0.935465$ and

$$\begin{array}{cc}\hfill \underset{j\to \infty }{lim\; sup}\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^2{p}_i\left(q\right)& =\underset{j\to \infty }{lim\; sup}\sum _{q=10j+3}^{10j+5}\sum _{i=1}^2{p}_i\left(q\right)\approx 0.967135,\hfill \end{array}$$

condition (33) is also fulfilled, thus all conditions of Theorem 1 are satisfied, and therefore all solutions of equation (43) are oscillatory.

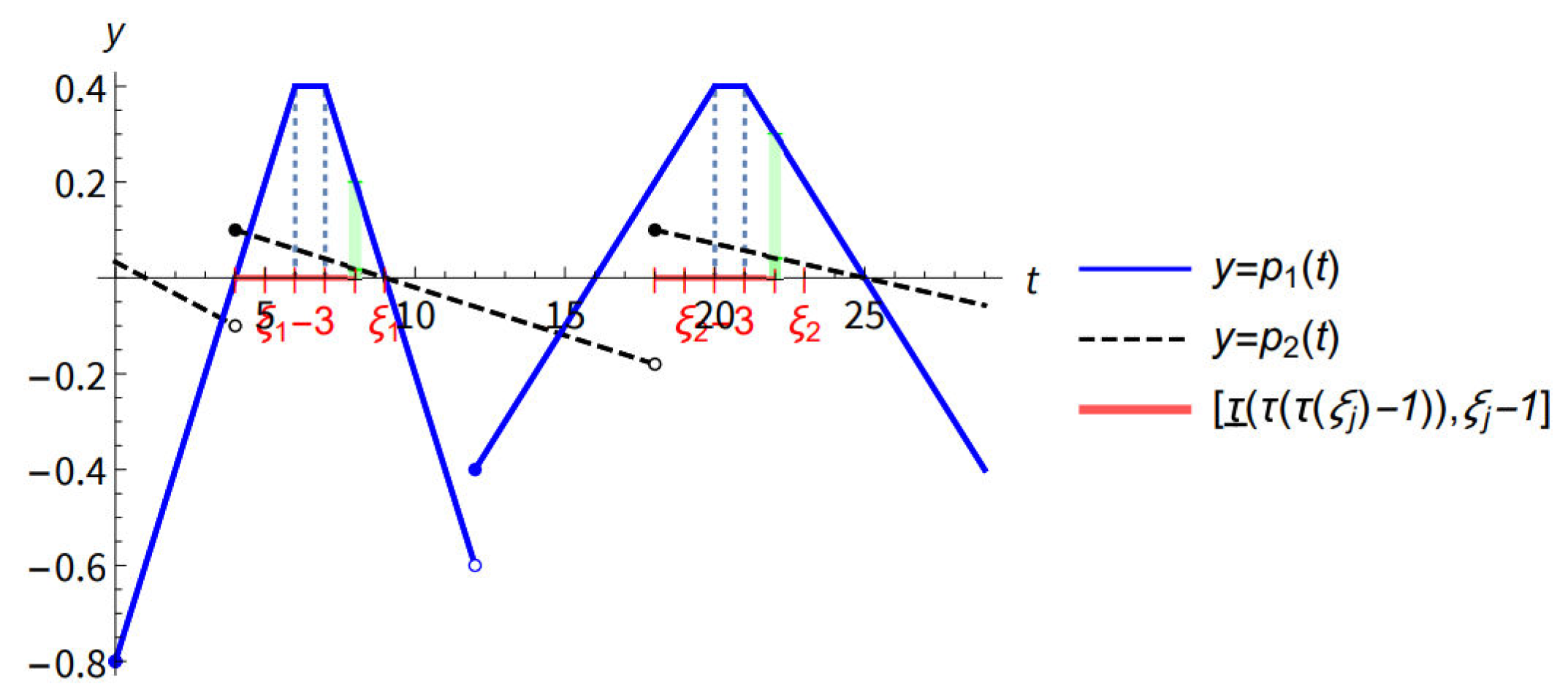
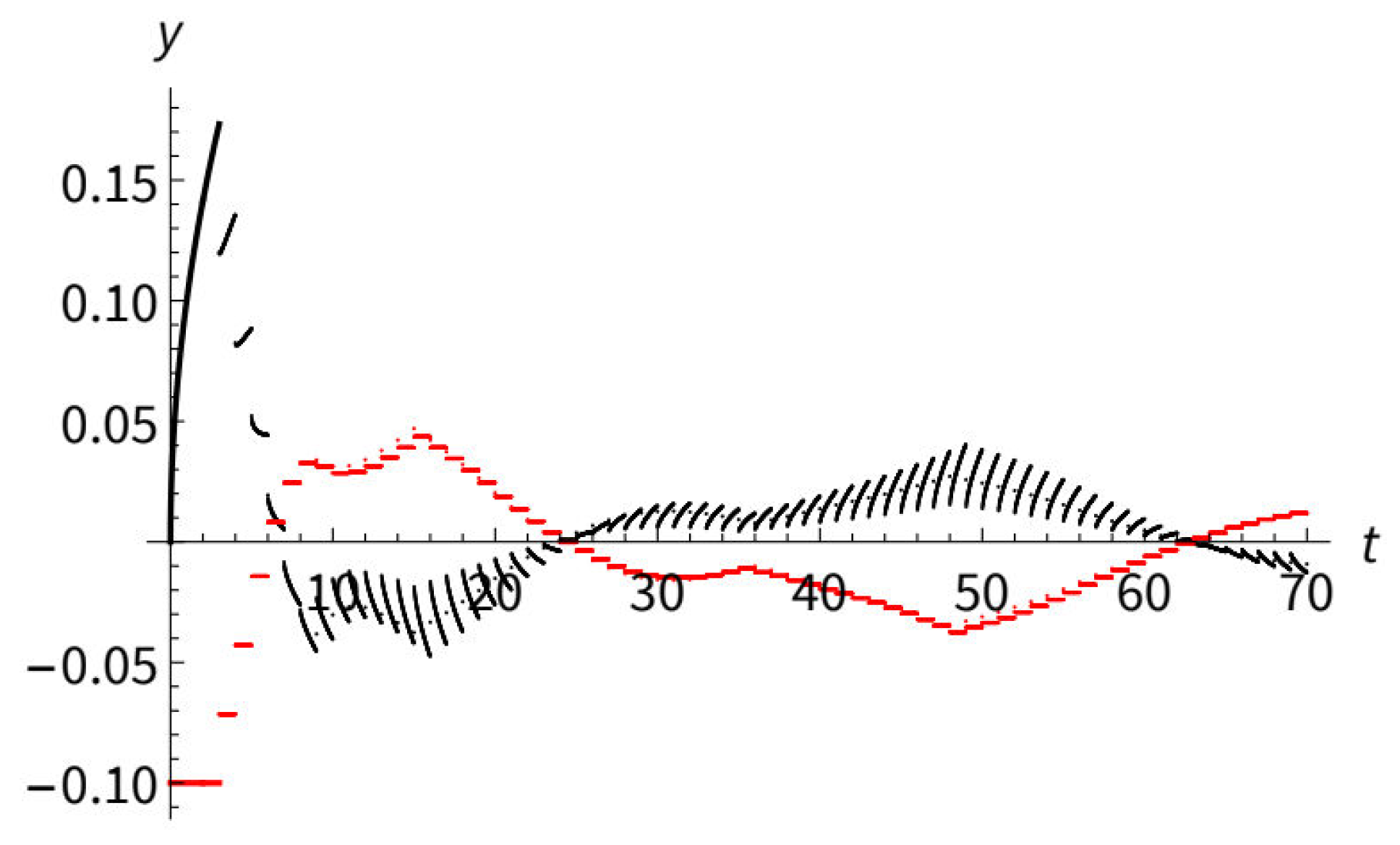
The graphs of the functions $p_1$ and $p_2$, the intervals ${\underline{I}}_j$, and relevant points from conditions (20) and (33) are presented at Figure 1. Figure 2 shows the graphs of some solutions of Eq. (43).

Conditions of Theorem 3 cannot be fulfilled since the length of intervals of condition (41) are expanding as j increases, but the functions $p_1$ and $p_2$ are nonnegative only on the interval with length 7. Therefore, the oscillatory conditions of Theorem 3 cannot be satisfied.

The oscillatory conditions of Theorem 2 also cannot be satisfied. Namely, for any sequence of real numbers ${\left\{{\zeta }_j\right\}}_{j\in {\mathbb{N}}_0}$ such that condition (39) is fulfilled,

$$\left[\underline{\tau }\left(\tau \left({\zeta }_j\right)\right),{\zeta }_j\right]=\left[{\zeta }_j-5,{\zeta }_j\right].$$

Besides that, $p_1\left(t\right)\ge 0$ and $p_2\left(t\right)\ge 0$ are for $t\in [10j,10j+7]$ with $j\in {\mathbb{N}}_0$, so ${\zeta }_j\in [10j+5,10j+7]$. Therefore,

$$\begin{array}{cc}\hfill \underset{j\to \infty }{lim\; sup}\sum _{q=\tau \left({\zeta }_j\right)}^{{\zeta }_j}\sum _{i=1}^2{p}_i\left(q\right)& =\underset{j\to \infty }{lim\; sup}\sum _{q={\zeta }_j-2}^{{\zeta }_j}\sum _{i=1}^2{p}_i\left(q\right)\hfill \\ \hfill & \le \underset{j\to \infty }{lim\; sup}\underset{{\zeta }_j\in [10j+5,10j+7]}{max}\sum _{q={\zeta }_j-2}^{{\zeta }_j}\left(p_1\left(q\right)+p_2\left(q\right)\right)\hfill \\ \hfill & =\sum _{q=10j+3}^{10j+5}\left(p_1\left(q\right)+p_2\left(q\right)\right)\approx 0.967135<1.\hfill \end{array}$$

Consequently, condition (40) cannot be fulfilled.

Example 2.

Conditions of Theorem 1 are satisfied for equation

$$\Delta x\left(t\right)+p_1\left(t\right)x(t-1)+p_2\left(t\right)x(t-2)=0,t\ge 1,$$

(44)

with

$$p_1\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{5j}}t-{\displaystyle \frac{4j}{5}},\hfill & t\in \left[4j^2-4,4j^2+2j\right]\hfill \\ {\displaystyle \frac{2}{5}},\hfill & t\in \left[4j^2+2j,4j^2+2j+1\right]\hfill \\ {\displaystyle \frac{{(2j+1)}^2}{5j}}-{\displaystyle \frac{1}{5j}}t,\hfill & t\in \left[4j^2+2j+1,4{(j+1)}^2-4\right)\hfill \end{array}\right.\mathrm{for}j\in \mathbb{N},$$

and

$$p_2\left(t\right)={\displaystyle \frac{{(2j+1)}^2}{20j+30}}-{\displaystyle \frac{1}{20j+30}}t\mathrm{for}t\in \left[4j^2+2j-2,4{(j+1)}^2+2j\right),j\in \mathbb{N},$$

so all solutions of equation (44) are oscillatory.

Namely, ${\tau }_1\left(t\right)=t-1$ and ${\tau }_2\left(t\right)=t-2$, thus $\tau \left(t\right)=t-1$ and $\underline{\tau }\left(t\right)=t-2$. Therefore, $\tau \left(\tau \right(t)-1)=t-3$ and $\underline{\tau }\left(\tau (\tau \left(t\right)-1)\right)=t-5$. For every $j\in \mathbb{N}$,

$$p_1\left(t\right)\ge 0,p_2\left(t\right)\ge 0\mathrm{for}\forall t\in \left[4j^2+2j-2,{(2j+1)}^2\right].$$

For the sequence of real numbers ${\left\{{\xi }_j\right\}}_{j\in \mathbb{N}}$ such that ${\xi }_j=4j^2+2j+3$,

$$\tau \left({\xi }_j\right)=4j^2+2j+2,\tau (\tau \left({\xi }_j\right)-1)=4j^2+2j,\underline{\tau }\left(\tau (\tau \left({\xi }_j\right)-1)\right)=4j^2+2j-2,$$

so, for $j\in \mathbb{N}$,

$$\begin{array}{cc}\hfill I_j& =\left[\tau (\tau \left({\xi }_j\right)-1),{\xi }_j-1\right]=[4j^2+2j,4j^2+2j+2],\hfill \\ \hfill {\underline{I}}_j& =\left[\underline{\tau }\left(\tau (\tau \left({\xi }_j\right)-1)\right),{\xi }_j-1\right]=[4j^2+2j-2,4j^2+2j+2].\hfill \end{array}$$

Hence, conditions (17), (18), and (19) are satisfied and

$$\begin{array}{cc}\hfill \alpha & =\underset{j\to \infty }{lim\; inf}\underset{s\in \{\tau \left({\xi }_j\right),\dots ,{\xi }_j\}}{min}\sum _{q=\tau \left(s\right)}^{s-1}\sum _{i=1}^2{p}_i\left(q\right)=\underset{j\to \infty }{lim\; inf}\underset{s\in \{{\xi }_j-1,{\xi }_j\}}{min}\sum _{i=1}^2{p}_i(s-1)\hfill \\ \hfill & =\underset{j\to \infty }{lim\; inf}min\left\{\sum _{i=1}^2{p}_i(4j^2+2j+1),\sum _{i=1}^2{p}_i(4j^2+2j+2)\right\}\hfill \\ \hfill & =\underset{j\to \infty }{lim\; inf}min\left\{{\displaystyle \frac{2}{5}}+{\displaystyle \frac{j}{10j+15}},{\displaystyle \frac{2}{5}}-{\displaystyle \frac{1}{5j}}+{\displaystyle \frac{2j-1}{20j+30}}\right\}={\displaystyle \frac{2}{5}}+{\displaystyle \frac{1}{10}}={\displaystyle \frac{1}{2}}.\hfill \end{array}$$

Since $1-{\displaystyle \frac{{\alpha }^2}{2(2-\alpha )}}={\displaystyle \frac{11}{12}}\approx 0.916667$ and

$$\begin{array}{cc}\hfill \underset{j\to \infty }{lim\; sup}\sum _{q=\tau (\tau \left({\xi }_j\right)-1)}^{\tau \left({\xi }_j\right)-1}\sum _{i=1}^2{p}_i\left(q\right)& =\underset{j\to \infty }{lim\; sup}\sum _{q={\xi }_j-3}^{{\xi }_j-2}\sum _{i=1}^2{p}_i\left(q\right)\hfill \\ \hfill & =\underset{j\to \infty }{lim\; sup}\left(\sum _{i=1}^2{p}_i(4j^2+2j)+\sum _{i=1}^2{p}_i(4j^2+2j+1)\right)\hfill \\ \hfill & =\underset{j\to \infty }{lim\; sup}\left({\displaystyle \frac{2}{5}}+{\displaystyle \frac{2j+1}{20j+30}}+{\displaystyle \frac{2}{5}}+{\displaystyle \frac{j}{10j+15}}\right)=1,\hfill \end{array}$$

also condition (33) holds, so all conditions of Theorem 1 are fulfilled.

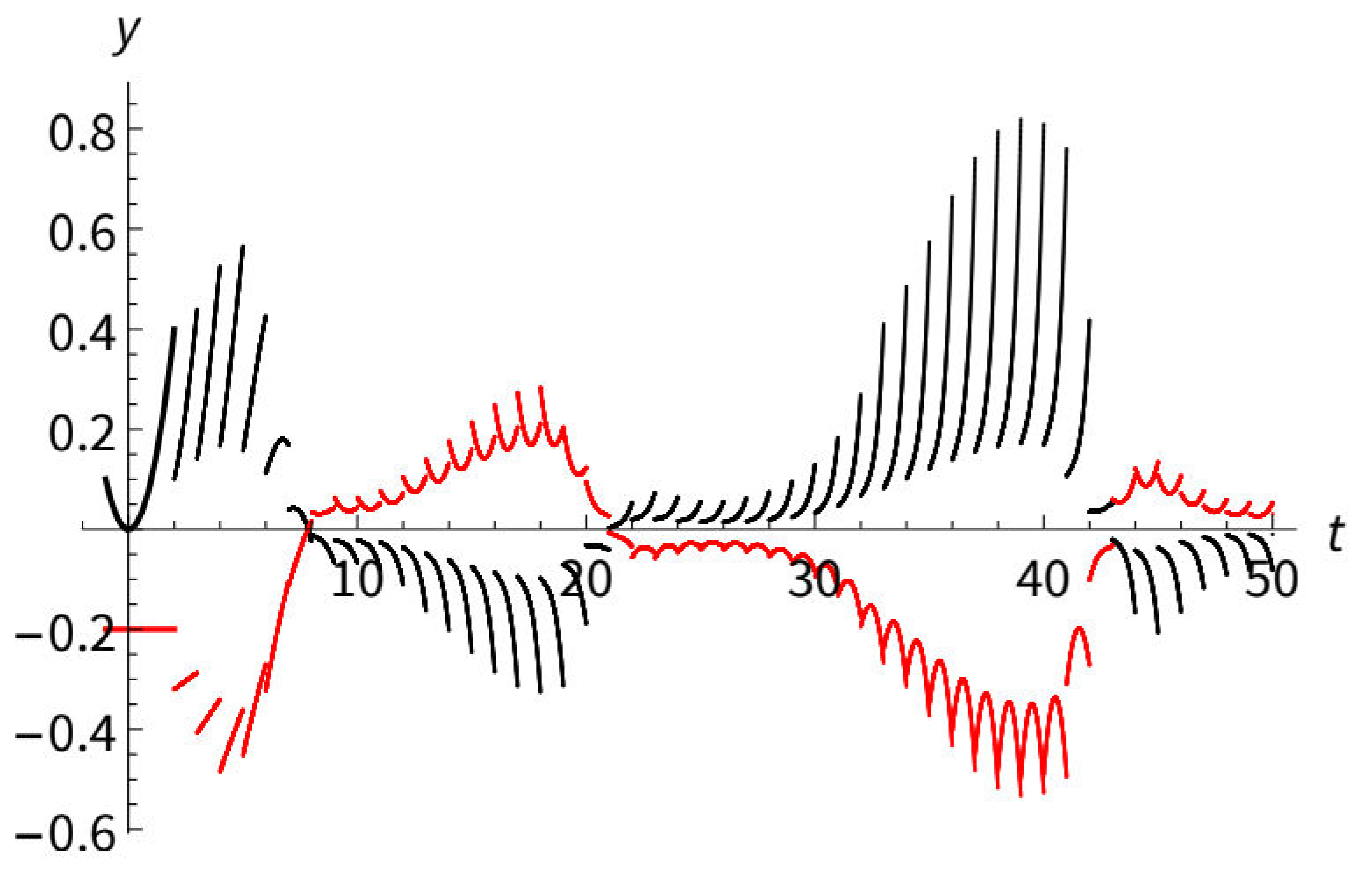
The graphs of the functions $p_1$ and $p_2$, the intervals ${\underline{I}}_j$, and relevant points from conditions (20) and (33) are presented at Figure 3. Figure 4 shows the graphs of some solutions of Eq. (44).

Now, we show that the oscillatory conditions of Theorem 2 cannot be fulfilled. For any sequence of real numbers ${\left\{{\zeta }_j\right\}}_{j\in \mathbb{N}}$ such that condition (39) holds,

$$\left[\underline{\tau }\left(\tau \left({\zeta }_j\right)\right),{\zeta }_j\right]=\left[{\zeta }_j-3,{\zeta }_j\right]\subset \left[4j^2+2j-2,{(2j+1)}^2\right],$$

so ${\zeta }_j\in \left[4j^2+2j+1,{(2j+1)}^2\right]$. Therefore, using that the functions $p_1$ and $p_2$ are nonincreasing on $\left[4j^2+2j,{(2j+1)}^2\right]$,

$$\begin{array}{cc}\hfill \underset{j\to \infty }{lim\; sup}\sum _{q=\tau \left({\zeta }_j\right)}^{{\zeta }_j}\sum _{i=1}^2{p}_i\left(q\right)& =\underset{j\to \infty }{lim\; sup}\sum _{q={\zeta }_j-1}^{{\zeta }_j}\sum _{i=1}^2{p}_i\left(q\right)\hfill \\ \hfill & \le \underset{j\to \infty }{lim\; sup}\underset{{\zeta }_j\in \left[4j^2+2j+1,{(2j+1)}^2\right]}{max}\sum _{q={\zeta }_j-1}^{{\zeta }_j}\sum _{i=1}^2{p}_i\left(q\right)\hfill \\ \hfill & \le \underset{j\to \infty }{lim\; sup}\left(\sum _{i=1}^2{p}_i(4j^2+2j)+\sum _{i=1}^2{p}_i(4j^2+2j+1)\right)=1.\hfill \end{array}$$

Consequently, condition (40) cannot be satisfied.

At the end, we show that the oscillatory conditions of Theorem 3 cannot be fulfilled. For any sequence of real numbers ${\left\{{\zeta }_j\right\}}_{j\in \mathbb{N}}$ such that condition (41) holds,

$$\left[\underline{\tau }\left({\tau }^j\left({\zeta }_j\right)\right),{\zeta }_j\right]=\left[{\zeta }_j-j-2,{\zeta }_j\right]\subset \left[4j^2+2j-2,{(2j+1)}^2\right],$$

so ${\zeta }_j\in \left[4j^2+3j,{(2j+1)}^2\right]$. Hence,

$$I_j^{j-1}=\left[{\tau }^{j-1}\left({\zeta }_j\right),{\zeta }_j\right]=\left[{\zeta }_j-j+1,{\zeta }_j\right]\subset \left[4j^2+2j+1,{(2j+1)}^2\right].$$

Using that the functions $p_1$ and $p_2$ are nonincreasing on $\left[4j^2+2j,{(2j+1)}^2\right]$ and the fact that $4j^2+3j-1\ge 4j^2+2j+1$ for $j>2$,

$$\begin{array}{cc}\hfill \underset{j\to \infty }{lim}\underset{t\in I_j^{j-1}}{inf}\sum _{q=\tau \left(t\right)}^{t-1}\sum _{i=1}^2{p}_i\left(q\right)& =\underset{j\to \infty }{lim}\underset{t\in I_j^{j-1}}{inf}\sum _{i=1}^2{p}_i(t-1)\hfill \\ \hfill & \le \underset{j\to \infty }{lim}\underset{t\in \left[4j^2+2j+1,4j^2+3j\right]}{inf}\sum _{i=1}^2{p}_i(t-1)\hfill \\ \hfill & =\underset{j\to \infty }{lim}\sum _{i=1}^2{p}_i(4j^2+3j-1)\hfill \\ \hfill & =\underset{j\to \infty }{lim}\left({\displaystyle \frac{j+2}{5j}}+{\displaystyle \frac{j+2}{20j+30}}\right)={\displaystyle \frac{1}{4}}<{\displaystyle \frac{1}{e}}.\hfill \end{array}$$

Consequently, condition (42) cannot be fulfilled.

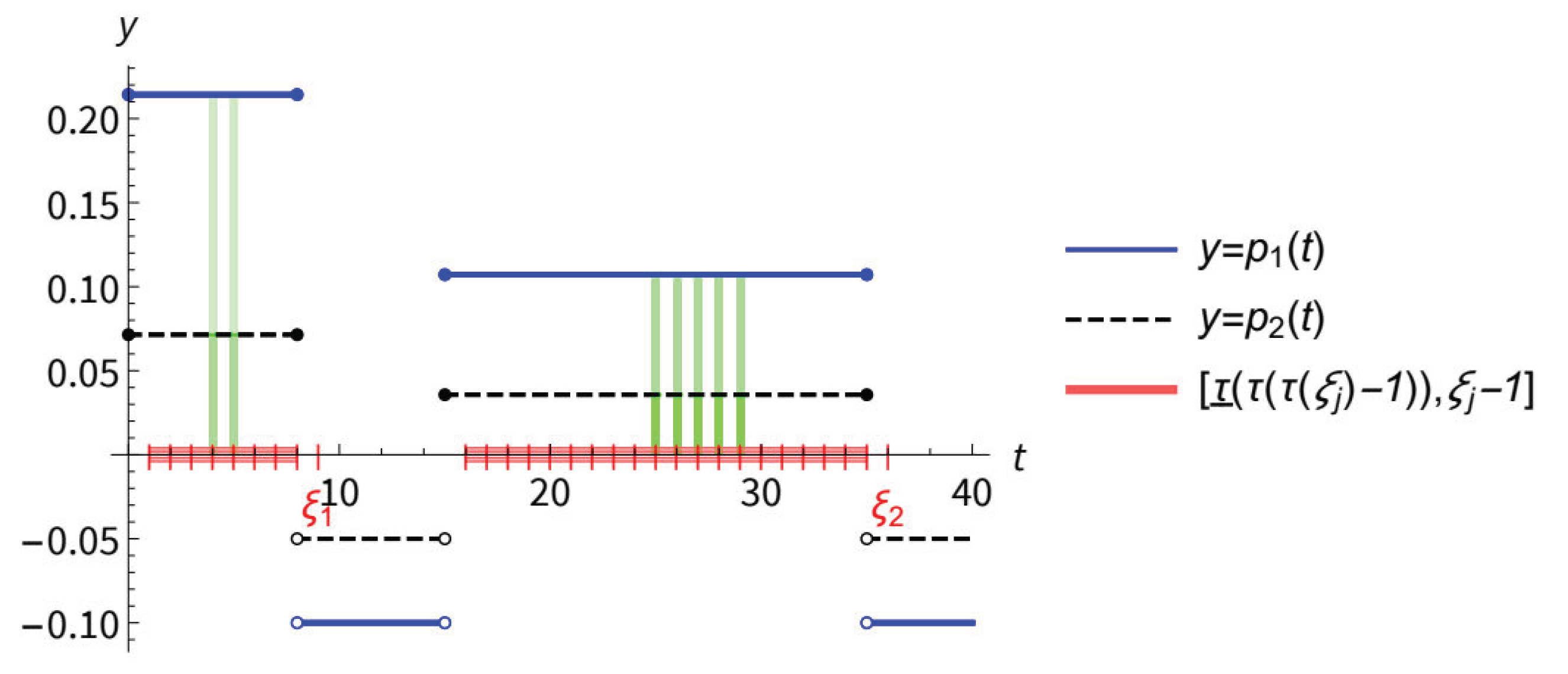
Example 3.

Consider the difference equation

$$\Delta x\left(t\right)+p_1\left(t\right)x\left(t-\left[\sqrt{t}\right]\right)+p_2\left(t\right)x\left(t-2\left[\sqrt{t}\right]\right)=0,t\ge 2,$$

(45)

with

$$p_1\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{3}{14j}},\hfill & t\in \left[{(3j-2)}^2-1,{\left(3j\right)}^2-1\right]\hfill \\ -0.1,\hfill & t\in \left({\left(3j\right)}^2-1,{(3j+1)}^2-1\right)\hfill \end{array}\right.\mathrm{for}j\in \mathbb{N},$$

and

$$p_2\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{14j}},\hfill & t\in \left[{(3j-2)}^2-1,{\left(3j\right)}^2-1\right]\hfill \\ -0.05,\hfill & t\in \left({\left(3j\right)}^2-1,{(3j+1)}^2-1\right)\hfill \end{array}\right.\mathrm{for}j\in \mathbb{N},$$

where $[·]$ denotes the integer part.

Delay functions, ${\tau }_1\left(t\right)=t-\left[\sqrt{t}\right]$ and ${\tau }_2\left(t\right)=t-2\left[\sqrt{t}\right]$, are unbounded, but satisfy conditions (3) and (4). $\tau \left(t\right)=t-\left[\sqrt{t}\right]$ and $\underline{\tau }\left(t\right)=t-2\left[\sqrt{t}\right]$, thus, for the sequence of real numbers ${\left\{{\xi }_j\right\}}_{j\in \mathbb{N}}$ such that ${\xi }_j={\left(3j\right)}^2$,

$$\begin{array}{cc}\hfill \tau \left({\xi }_j\right)& ={\left(3j\right)}^2-3j,\hfill \\ \hfill \tau \left(\tau \left({\xi }_j\right)\right)& ={\left(3j\right)}^2-3j-(3j-1)={\left(3j\right)}^2-6j+1={(3j-1)}^2,\hfill \\ \hfill \tau (\tau \left({\xi }_j\right)-1)& ={\left(3j\right)}^2-3j-1-(3j-1)={\left(3j\right)}^2-6j,\hfill \\ \hfill \underline{\tau }\left(\tau (\tau \left({\xi }_j\right)-1)\right)& ={\left(3j\right)}^2-6j-2(3j-2)={\left(3j\right)}^2-12j+4={(3j-2)}^2.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill {\underline{I}}_j& =\left[\underline{\tau }\left(\tau (\tau \left({\xi }_j\right)-1)\right),{\xi }_j-1\right]=[{(3j-2)}^2,{\left(3j\right)}^2-1],\hfill \end{array}$$

so conditions (17), (18), and (19) are satisfied. Besides,

$$[\tau \left(\tau \left({\xi }_j\right)\right),{\xi }_j-1]\subset {\underline{I}}_j\mathit{for}j\in \mathbb{N},$$

implying that

$$p_1\left(t\right)+p_2\left(t\right)={\displaystyle \frac{2}{7j}}\mathit{for}t\in [\tau \left(\tau \left({\xi }_j\right)\right),{\xi }_j-1].$$

Hence,

$$\begin{array}{cc}\hfill \alpha & =\underset{j\to \infty }{lim\; inf}\underset{s\in \{\tau \left({\xi }_j\right),\dots ,{\xi }_j\}}{min}\sum _{q=\tau \left(s\right)}^{s-1}\sum _{i=1}^2{p}_i\left(q\right)=\underset{j\to \infty }{lim\; inf}\underset{s\in \{\tau \left({\xi }_j\right),\dots ,{\xi }_j\}}{min}\sum _{q=\tau \left(s\right)}^{s-1}{\displaystyle \frac{2}{7j}}\hfill \\ \hfill & =\underset{j\to \infty }{lim\; inf}\left({\displaystyle \frac{2}{7j}}·\underset{s\in \{\tau \left({\xi }_j\right),\dots ,{\xi }_j\}}{min}\left(s-\tau \left(s\right)\right)\right)=\underset{j\to \infty }{lim\; inf}\left({\displaystyle \frac{2}{7j}}·\underset{s\in \{\tau \left({\xi }_j\right),\dots ,{\xi }_j\}}{min}\left[\sqrt{s}\right]\right)\hfill \\ \hfill & =\underset{j\to \infty }{lim\; inf}\left({\displaystyle \frac{2}{7j}}·\left[\sqrt{\tau \left({\xi }_j\right)}\right]\right)=\underset{j\to \infty }{lim\; inf}\left({\displaystyle \frac{2}{7j}}·\left(3j-1\right)\right)={\displaystyle \frac{6}{7}}>3-\sqrt{5}.\hfill \end{array}$$

Consequently, conditions of Corollary 1 are satisfied, so all solutions of Eq. (45) are oscillatory.

The graphs of the functions $p_1$ and $p_2$, the intervals ${\underline{I}}_j$, and relevant points from condition (20) are presented at Figure 5. Figure 6 shows the graphs of some solutions of Eq. (45).

The oscillatory conditions of Theorem 2 cannot be satisfied since for any sequence of real numbers ${\left\{{\zeta }_n\right\}}_{n\in \mathbb{N}}$ such that condition (39) is fulfilled, $\left[\underline{\tau }\left(\tau \left({\zeta }_n\right)\right),{\zeta }_n\right]\subset \left[{(3j-2)}^2-1,{\left(3j\right)}^2-1\right]$ for some $j\in \mathbb{N}$, so

$$p_1\left(t\right)+p_2\left(t\right)={\displaystyle \frac{2}{7j}}\mathrm{for}t\in \left[\underline{\tau }\left(\tau \left({\zeta }_n\right)\right),{\zeta }_n\right].$$

Hence,

$$\sum _{q=\tau \left({\zeta }_n\right)}^{{\zeta }_n}\sum _{i=1}^2{p}_i\left(q\right)={\displaystyle \frac{2}{7j}}\left({\zeta }_n-\tau \left({\zeta }_n\right)+1\right)={\displaystyle \frac{2}{7j}}\left(\left[\sqrt{{\zeta }_n}\right]+1\right).$$

Using that ${\zeta }_n\subset \left[{(3j-2)}^2-1,{\left(3j\right)}^2-1\right]$,

$$3j-3<\left[\sqrt{{\zeta }_n}\right]<3j$$

and therefore

$${\displaystyle \frac{2(3j-2)}{7j}}<\sum _{q=\tau \left({\zeta }_n\right)}^{{\zeta }_n}\sum _{i=1}^2{p}_i\left(q\right)<{\displaystyle \frac{2(3j+1)}{7j}}.$$

(46)

Since the intervals of sequence $\left\{\left[\underline{\tau }\left(\tau \left({\zeta }_n\right)\right),{\zeta }_n\right]\right\}$ are disjoint, $n\to \infty$ implies that $j\to \infty$, so inequality (46) gives

$$\underset{n\to \infty }{lim\; sup}\sum _{q=\tau \left({\zeta }_n\right)}^{{\zeta }_n}\sum _{i=1}^2{p}_i\left(q\right)={\displaystyle \frac{6}{7}}<1.$$

Consequently, condition (40) cannot be fulfilled.

Conditions of Theorem 3 also cannot be fulfilled since there is no sequence of real numbers ${\left\{{\zeta }_n\right\}}_{n\in \mathbb{N}}$ such that condition (41) is satisfied. Namely, by condition (41), there is a sequence of real numbers ${\left\{{\zeta }_n\right\}}_{n\in \mathbb{N}}$ such that

$$\left[\underline{\tau }\left({\tau }^n\left({\zeta }_n\right)\right),{\zeta }_n\right]\subset \left[{(3j-2)}^2-1,{\left(3j\right)}^2-1\right],$$

(47)

for some $j\in \mathbb{N}$. The length of interval $\left[\underline{\tau }\left({\tau }^n\left({\zeta }_n\right)\right),{\zeta }_n\right]$ are expanding as n increases and the length of interval $\left[{(3j-2)}^2-1,{\left(3j\right)}^2-1\right]$ is $12j-4$. Even for ${\zeta }_3={\left(3j\right)}^2-1$,

$$\begin{array}{cc}\hfill \tau \left({\zeta }_3\right)={\left(3j\right)}^2-3j,{\tau }^2\left({\zeta }_3\right)& ={(3j-1)}^2,{\tau }^3\left({\zeta }_3\right)=(3j-1)(3j-2),\hfill \\ \hfill \underline{\tau }\left({\tau }^3\left({\zeta }_3\right)\right)& =(3j-2)(3j-3),\hfill \end{array}$$

so the length of interval $\left[\underline{\tau }\left({\tau }^3\left({\zeta }_3\right)\right),{\zeta }_3\right]$ is $15j-7$. Since $12j-4<15j-7$ for every $j>1$, the condition (47) cannot be fulfilled for any integer $j>1$ and $n\ge 3$. Hence, the oscillatory conditions of Theorem 3 cannot be satisfied.

4. Conclusions

Our study of the oscillatory properties of the solutions of the first-order difference equations with continuous time, piecewise linear delay functions, and oscillatory coefficients has led us to the new condition that ensures the oscillatory solutions. By the proposed results, the oscillatory property of all solutions of the considered difference equation is ensured by sufficiently positive coefficients of the equation in the sense that the sum of the values of the coefficients defined by $\alpha$ in (20) is in the interval $(3-\sqrt{5},2)$. For $\alpha \in \left(0,3-\sqrt{5}\right]$, the oscillatory property of all solutions is ensured when condition (33) is fulfilled.

We have shown, through examples, that there are difference equations for which the previously known oscillatory conditions for the same type of difference equations are not applicable, but the proposed criteria are satisfied. Therefore, we have extended the set of difference equations with oscillatory coefficients for which conditions verifying their oscillatory properties exist.