Visualising Earthquakes: Plate Interfaces and Seismic Decay

1. Introduction

Through the application of modern statistical methods, seismic data can be effectively organised, revealing the parameters necessary for meaningful analysis [1,2,3,4]. As a result, it has become possible to predict earthquakes of a certain magnitude to some extent. However, the intrinsic characteristics of seismic data have long been fundamentally misunderstood. For example, the Gutenberg–Richter law concerning earthquaearthquake prediction; calculation method; exploratory data analysis; programming; contact surface; attenuation; Omori equation

ke magnitude [5] is entirely incorrect; the distribution is in fact normalized [1]. This error not only misrepresents the distribution pattern itself but also leads to a mistaken understanding of why such a distribution arises. Consequently, the widely accepted view of earthquake formation is likely flawed, as it rests upon the Gutenberg–Richter law [6].

What occurs between the onset of an earthquake and its resolution also appears to be a field where modern statistical approaches have not been applied. Visualising epicentres in three dimensions has enabled clearer representation of plate arrangements. Earthquakes tend to increase in frequency in these regions prior to a major event, yet communicating such 3D phenomena remains challenging. Beyond the practical difficulties of printing, the absence of suitable vocabulary to describe three-dimensional structures contributes to this limitation. It is therefore necessary to translate these observations into two dimensions. To this end, we experimented with a method based on principal component analysis (PCA), which enabled plate boundaries to be expressed using simple equations.

Whether seismic activity will subside is a major concern for affected regions. Research by Omori in the 19th century examined how aftershocks diminish following an earthquake [7], later refined by Utsu and widely adopted [8,9]. Yet these approaches may warrant reconsideration. Here, I report results from exploratory data analysis (EDA) [10], examining the distributional characteristics of several earthquakes.

2. Materials and Methods

2.1. Data

Earthquake data, comprising extensive catalogue data, was obtained from the Japan Meteorological Agency (JMA) and utilized [11]. Earthquakes were measured within a grid of one degree latitude and longitude, with the number of occurrences and magnitude examined [4]. For the grid with the highest count in the year of interest, its properties were investigated. The sole exception was 2011, where we examined the grid containing the epicentre of the Tohoku earthquake. All calculations were performed using R [12]. The necessary code is provided in the supplement. Counts of earthquake occurrences, etc., utilised content from the preceding paper [4]. The data utilises all available information and has not been filtered by any criteria whatsoever. The spatial relationships of earthquakes were plotted whilst verifying JMA materials [13], employing Leaflet [14] Latitude and longitude verification utilised the Latitude and longitude map [15]. Maps employed were sourced from the Geospatial Information Authority of Japan [16]. As these are rendered in Mercator projection, they were appropriately transformed to align with the square-based latitude-longitude diagram [4] used herein.

2.2. Three-Dimensional Presentation

For the 3D display, the rgl package for R [17] was employed. Furthermore, the rglwidget function from this package was used to generate the HTML file. Previous studies often relied on oversimplified assumptions regarding plate boundaries. Here, we apply modern statistical methods to re-examine epicentre distributions and correct these inaccuracies.

The plate interface is estimated from the epicentre location. In this process, principal component analysis (PCA) [18,19] is applied in two distinct phases (Appendix A). PCA is a technique that shifts and rotates data along recognisable axes. Centring is performed at the desired rotation centre, here the centre of mass was used, followed by singular value decomposition (SVD). The resulting unitary matrix is then used to rotate the data. The first application here was during 3D-to-2D dimensionality reduction. In this case, each dimension of the 3D data (latitude, longitude, depth) was centred per item, then scaled before application of SVD. The second instance occurs when observing epicentres concentrated on a specific interface, projecting the epicentre position data onto that surface. Here, data unrelated to the interface was removed as much as possible (the trick is to be generous in discarding it, as discarded data can be recovered later; furthermore, as PCA is vulnerable to noise, it is preferable to remove unnecessary data where possible). After centring this data, SDV was applied; the data was not scaled. This approach allows PC1 to be fixed at the largest scale, depth data, and ensures the scale of the PCA results matches that of the actual data. Since the plate position does not change significantly from year to year, the obtained centre of gravity and unitary matrix were also applied to data from other years. All R code and the parametrs for the plate interfaces is presented in the supplement.

3. Results

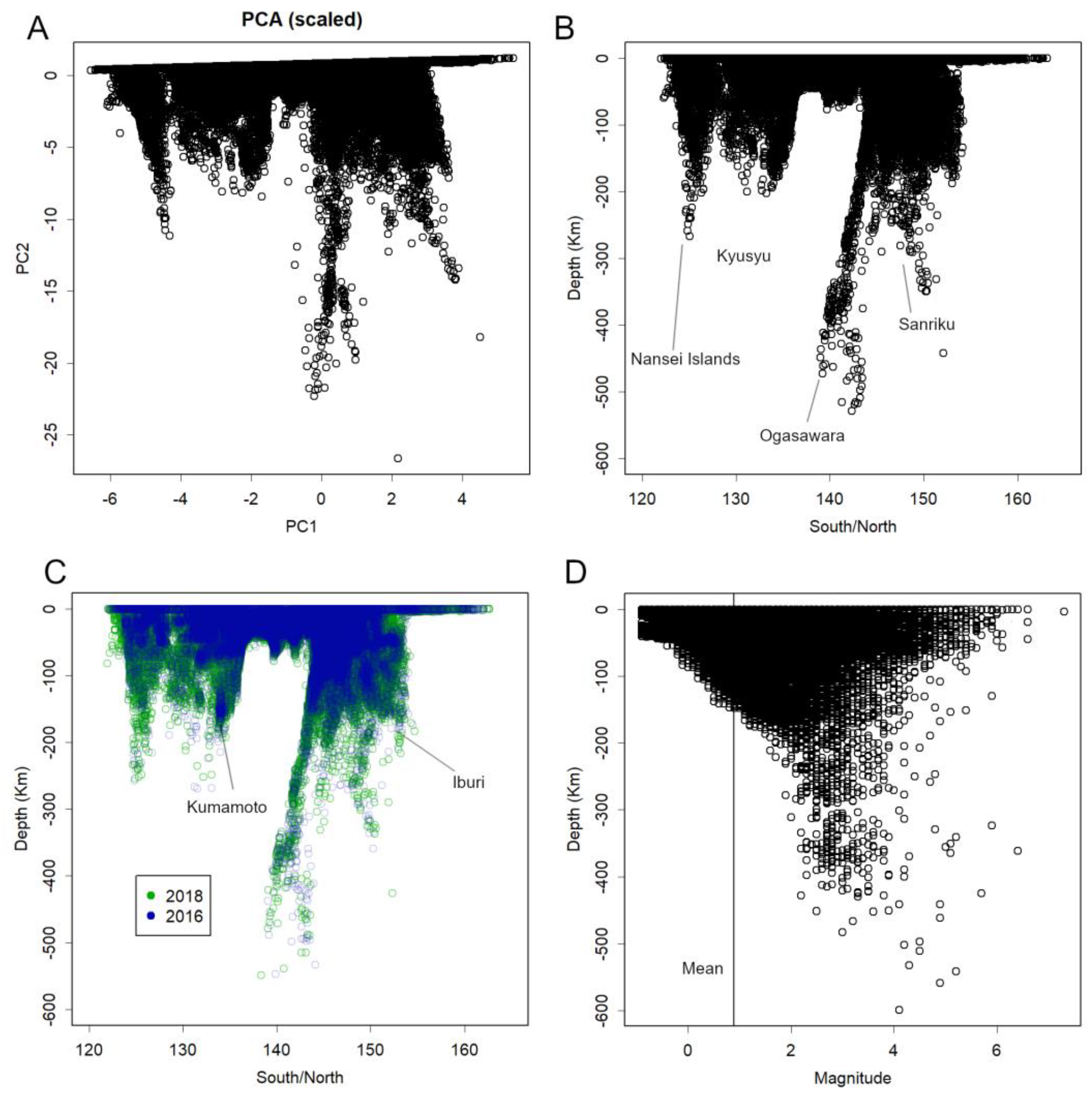
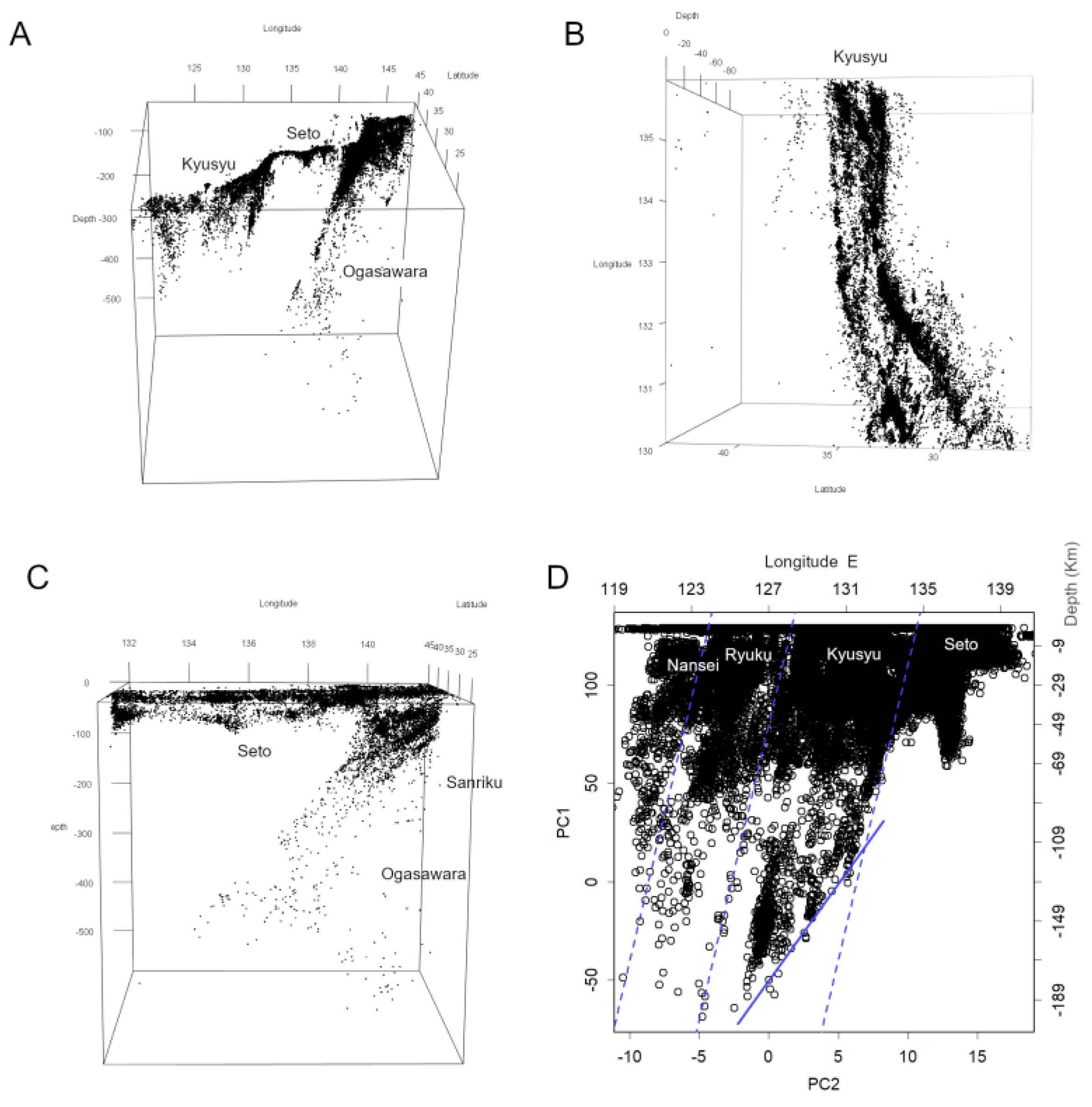
3.1. Three-Dimensional Visualisation Considering the Epicentre Depth

Japan is a country prone to frequent earthquakes, many of which are caused by plate tectonics [20,21,22]. When two plates rub against each other, friction or locking at their interface creates conflict, which becomes the energy for earthquakes. The Japanese archipelago lies at the collision zone between the North American Plate and the Eurasian Plate, with the Pacific Plate and the Philippine Sea Plate subducting beneath each of these plates, creating a rather complex structure [23]

Measurement and recording of deep earthquakes in Japan likely became feasible around 1985 [11]. (data from 1983 did not yield depths greater than 100 km). Earthquake depths roughly follow a log-normal distribution (Figure 1AB, with a normal qqplot superimposed), and are generally shallower. Observing deep epicentres reveals they lie on a single solid surface (Figure 1CD; these 3D visualisations are available as interactive HTML files in Figure S1 of the Supporting Information). This likely indicates a plate boundary, the interface between plates. Energy required to generate earthquakes should readily accumulate there. Consequently, epicentre locations are likely observed at this interface.

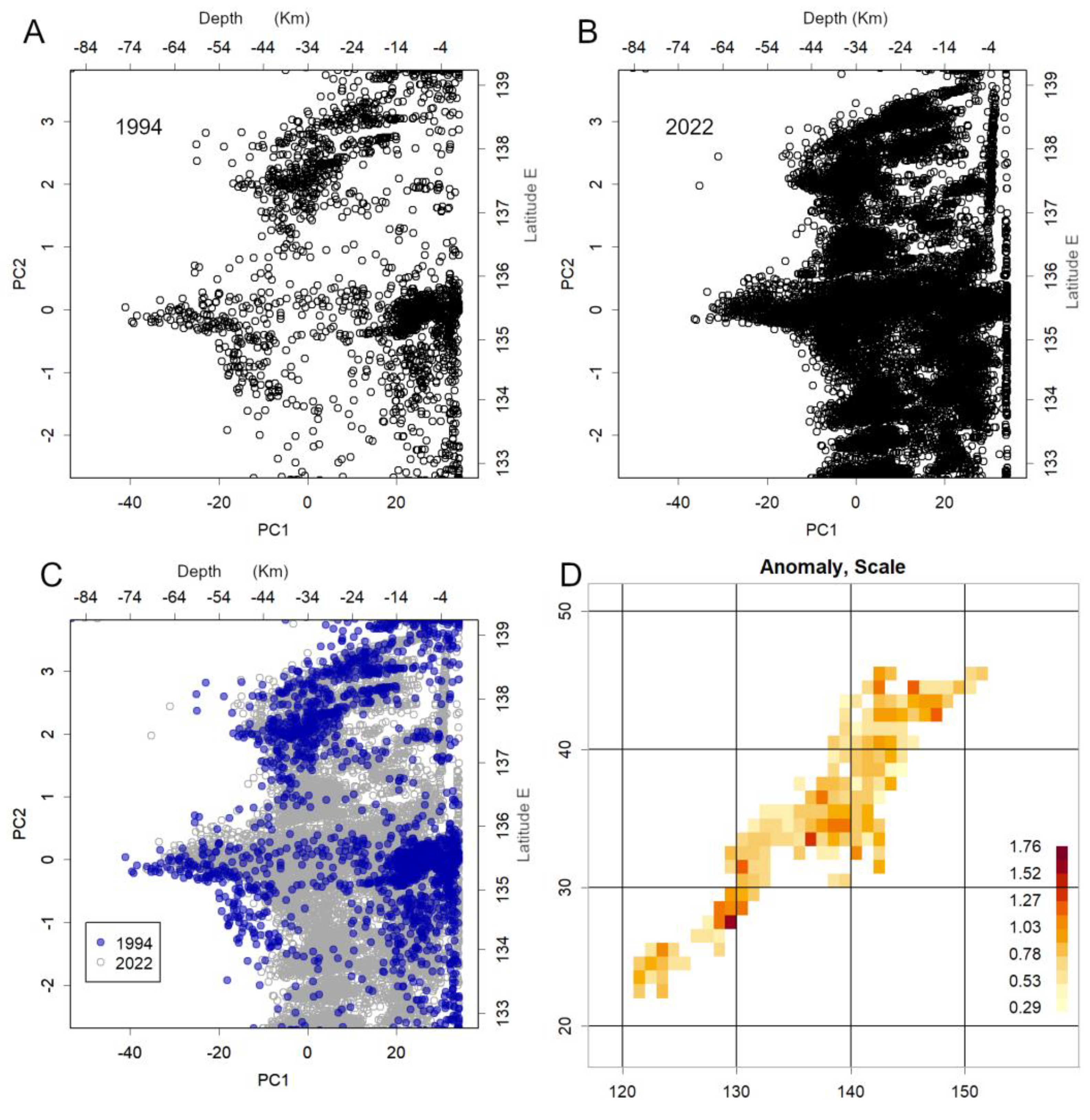
3.2. Convert to Two-Dimensional Data for More Convenient Visualisation

Observing in 3D reveals that prior to major earthquakes, the number of epicentres on these interfaces increases, allowing active seismic activity to be detected. As the supplementary material contains a highly robust, interactive output, please rotate it with your mouse or move it forwards and backwards to view it from various angles. While these movements become clear in 3D, translating such results into 2D requires some ingenuity. Figure 2A-C shows the entire projection. First, we attempted Principal Component Analysis (PCA) as a dimensionality reduction method (Figure 2A). Applying PCA to scaled 3D latitude-longitude-intensity data revealed Japan's width along PC1 and depth along PC2. However, this method suffers from poor reproducibility, making comparisons between different years difficult (indeed, the baseline in this figure is slightly tilted upwards, likely to straighten the vertical line representing the central contact surface). Therefore, we plotted the Euclidean distance between latitude and longitude from the point at longitude 0, latitude 0 on the first dimension, and depth on the second dimension (Figure 2B). This yielded a plot nearly identical to PCA, with good reproducibility. However, even after this two-dimensional representation, the differences between years do not appear particularly large (Figure 2C). This comparison covers the years of the Eastern Iburi Earthquake and the Kumamoto Earthquake, where numerous epicentres cluster near the main shocks' locations, yet distinctions remain elusive. This occurs because the plates themselves existed before the earthquakes and persist afterwards, and the positions of their interfaces show little movement.

Incidentally, deeper earthquakes tend to have larger magnitudes (Figure 2D). While greater depth may reduce seismic intensity, the impact area becomes more extensive. Furthermore, compared to the period before 2000, deep earthquakes have increased significantly recently (Figure 1). This would be primarily due to the results of deploying the latest equipment [24].

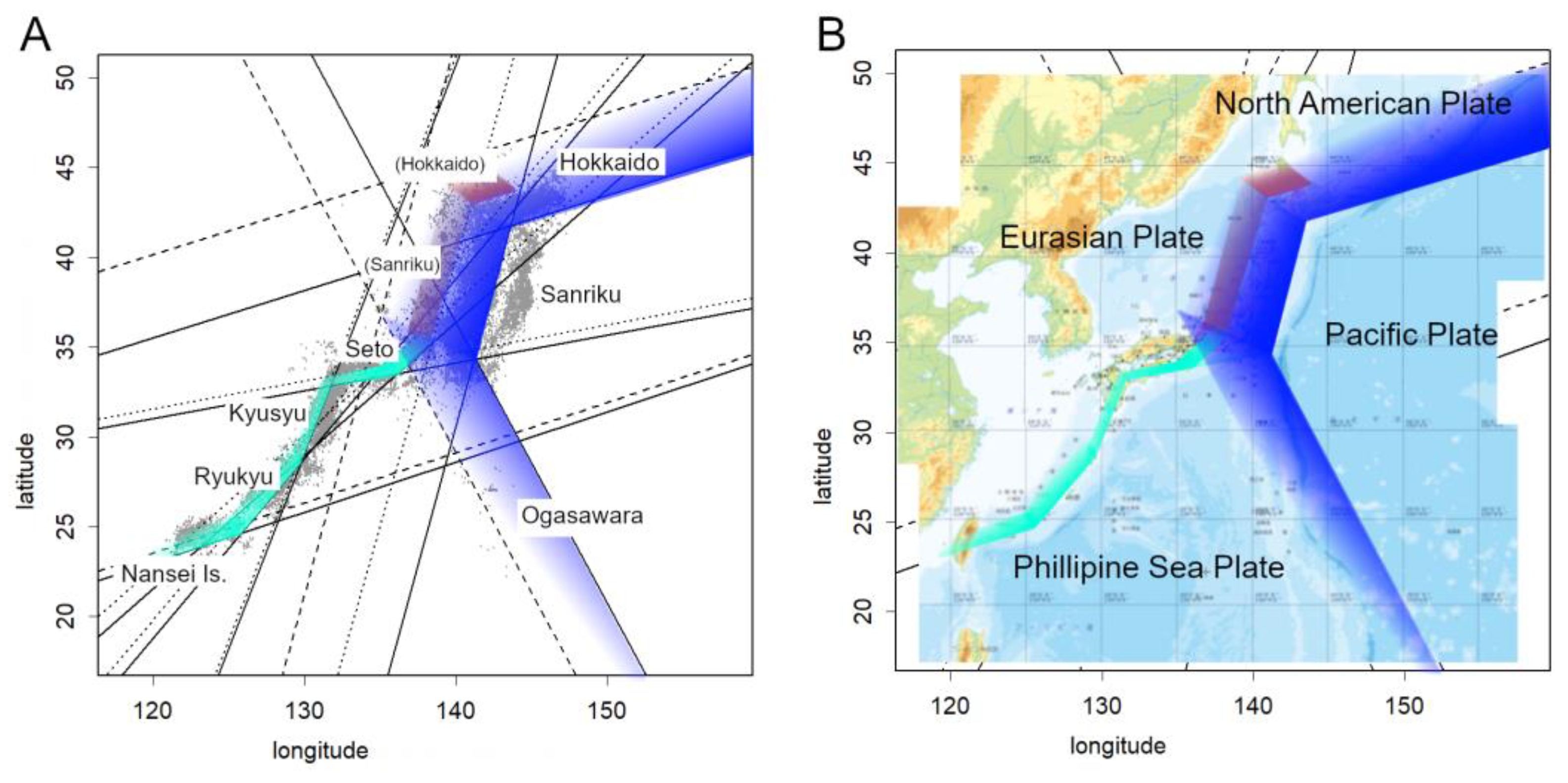
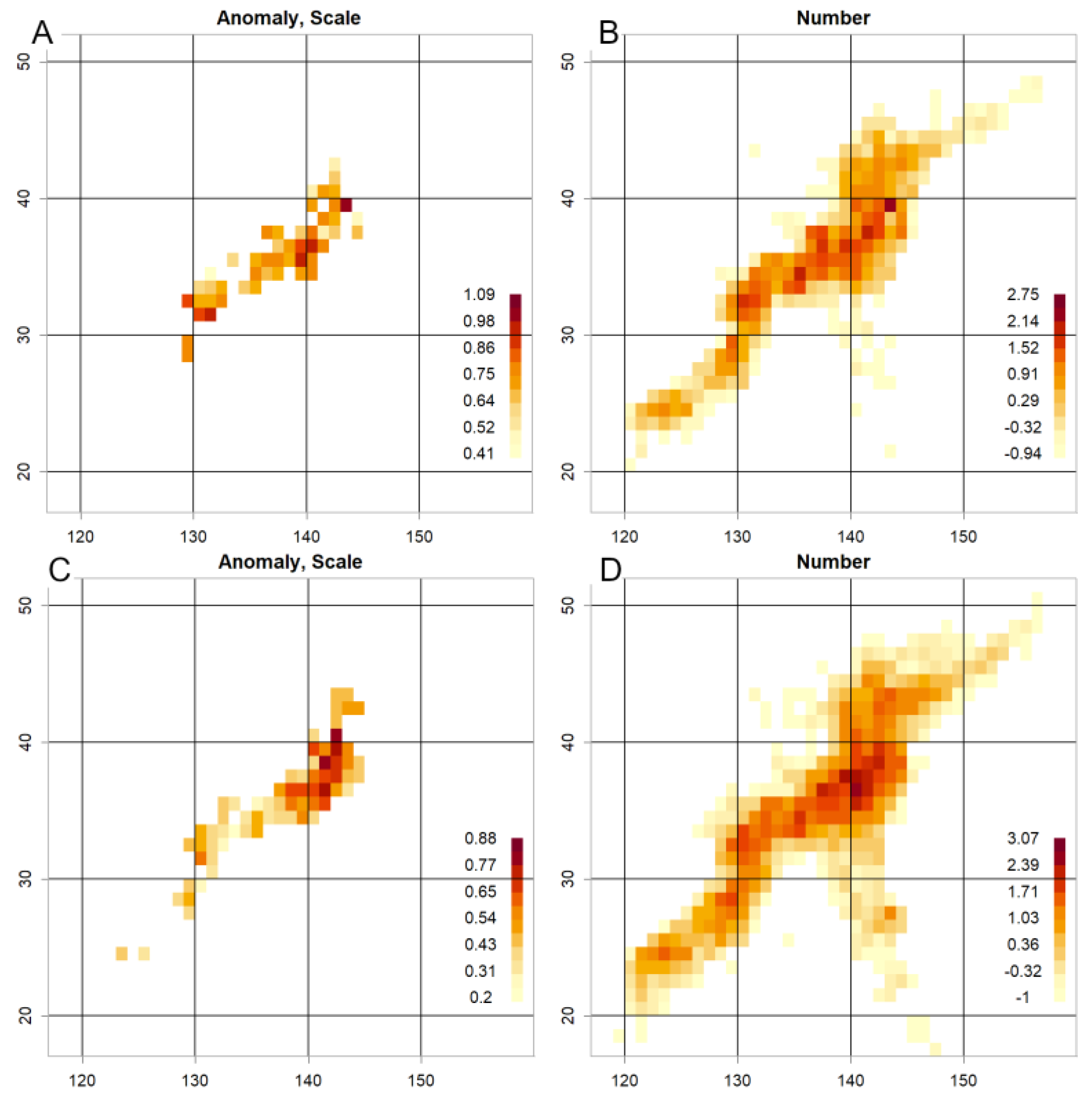
3.3. Isolation of Plate Boundaries

Because no clear differences emerge when examining the entire dataset, it is more informative to narrow the scope and isolate specific plate boundaries. Analysis of epicentre locations at depths greater than 50 km reveals two major boundaries in Japan: one in East Japan and another in Southwest (Figure 3A; an interactive 3D display is provided in Supplement 2A). Rather than appearing as a single, vast, flat slab, as often depicted in simplified explanatory models [20], these boundaries are divided into several segments and exhibit bending. Importantly, the interfaces forming these segments bend without overlapping. They are not independent but interconnected, suggesting that both boundaries are generated by the movement of a single plate.

To extract a specific plane from such a tilted structure, principal component analysis (PCA; Appendix A) can be applied [18]. PCA is a multivariate technique that translates and rotates data without altering its overall geometry. For example, if the direction of greatest variance passing through the centre of gravity of the plane is designated PC1, and the next greatest variance, perpendicular to PC1 and also passing through the centre of gravity, is designated PC2, then these two axes define a single plane. This plane represents the plate of interest. A third principal component (PC3), orthogonal to PC1 and PC2, captures information relating to plate thickness and undulation. Without scaling the data, depth (in kilometres) represents the largest scale, and thus the direction of increasing depth corresponds to PC1. PC2, orthogonal to PC1, represents the cardinal directions on a map, corresponding to latitude and longitude.

The procedure involves first extracting the approximate plane (Figure 3B), then calculating the average to determine the centre of gravity, which serves as the rotation centre. Singular value decomposition (SVD) is applied to identify the axes most representative of the data’s variation, namely PC1 and PC2. PCA then provides the unitary matrix required to rotate the data along these axes (Appendix A). Using this centre and matrix, the data are rotated around the centre of gravity. Figure 3C and 3D show rotated versions of Figure 3A. The data around the Sanriku region cluster on a plane near PC3 = 0, whereas plates from other regions exhibit large deviations along PC3. By selecting data where PC3 is close to zero (allowing for some thickness due to noise in epicentre estimation and slight plate curvature), the plate of interest can be isolated in two dimensions.

3.4. Structural Configuration of Japan’s Plate Interfaces

The Southwest interface comprises three segments: Kyushu, the Ryukyu Islands, and the Nansei Islands. These surfaces converge at a slight angle, producing an overall geometry that traces a broad arc. The East interface is primarily divided into three sections. The southernmost extends from the vicinity of the Ogasawara Islands, with the Fossa Magna lying along this extension [25]. The location of the Fossa Magna has been the subject of considerable scholarly debate [26], yet this boundary is notably planar and stable. Figure 3A shows it from a direct side view, appearing as a straight line running diagonally from top right to bottom left. This is the deepest section, reaching approximately 600 kilometres.

The northernmost segment of the East interface lies between Honshu and Hokkaido. The 2017 Eastern Iburi Earthquake may have occurred along this interface, which is also flat in structure. Collectively, these surfaces resemble the geometry that might result if Japan were diagonally cleaved with a sword. Connecting the southern and northern segments is the Sanriku interface, which spans nearly 1000 km and exhibits a slightly curved structure.

The convergence of these three interfaces forms a single, large-scale structure resembling the folds created when reinforcing paper with mountain folds, tracing a broad arc (Figure S2). The arcs of the East and Southwest interfaces are convex in opposite directions, creating a substantial gap between them. The Nankai Trough, a region of considerable seismic concern [27,28], lies within this gap, although here the epicentres are aligned at shallower depths.

3.5. Epicentres on the Sanriku Plate

Figure 4 shows the epicentres on the Sanriku plate after projecting PC3 onto PC1 and PC2. The number of epicentres gradually increases towards 2010, the year preceding the earthquake, with a particularly noticeable rise at greater depths. As expected, the number peaks in 2011, the year of the earthquake itself, and is especially high near the sea, at shallow Moho discontinuities.

3.6. The Seto Interface

The Southwest and East interfaces, each convex in opposite directions, are joined by a shallow transitional interface (Fig. 5A). As this interface spans the Hanshin, Chugoku, and Shikoku regions, it is hereafter referred to as the Seto interface. The term is inspired by the train service linking Tokyo to Shikoku. The junction between the Kyushu and Seto interfaces forms a pronounced curvature, which connects tangentially to the Sanriku and Ogasawara interfaces at the Seto interface (Fig. 5A, S3A).

The Southwest interface differs markedly from that of the East. Firstly, its dip angle is considerably steeper. Whereas the East interface subducts at 30–50°from the surface, the Southwest interface subducts at 60–80° (Appendix A). The Southwest interface is also notably thick, reaching approximately 50 km in places, with multiple discernible layers (Figure 5B, Figure S4A). This contrasts sharply with the sharp, fault-like interface of the East. It likely subducts while undergoing fracturing and delamination. The Seto interface is comparatively shallow, reaching only a maximum depth of 70 km. Epicentres at greater depths in this region originate from the Ogasawara or Sanriku interfaces (Figure 5C, S3C–F). The configuration of the Seto interface, positioned between the deep Chugoku and Ogasawara interfaces, is clearly visible in S3F.

A PCA analysis of the entire Southwest interface reveals fine-scale structures (Figure 5D). These were not observed, for example, in the Sanriku region (Figure 4). Moreover, all of these structures exhibit a consistent dip. In the deep sections of the Kyushu region, the interface is uplifted at its north-eastern edge, rapidly shallowing towards the north-east to connect with the Seto interface (Figure 5D). Viewed in three dimensions, this appears as if the interface is being uplifted from below by the Ogasawara interface and raised parallel to it (Figure S4B). These findings highlight the complex, multi-layered nature of the Southwest interface, underscoring the inadequacy of simplified slab models in capturing Japan’s tectonic reality.

Part of the Seto interface coincides with the 1995 Hanshin-Awaji Earthquake [29]. We compared the epicentres on this interface for 1994 and 2022 (Figure 6). As time progressed [24], the number of recorded epicentres increased by an order, making direct comparison difficult (Figure 6AB). By 2022, measurements are available in sufficient detail to reveal the fine structure of the region (Figure 6B). However, overlaying these shows that the 1994 epicentres were more deeply inclined (Figure 6C), particularly within the Hanshin area. With current measurement technology, one might expect to see even finer details. Furthermore, at this location in the Hanshin area, the magnitude scale observed via the mesh was exceptionally high in 1994 (Figure 6D). This, of course, constitutes a precursor to a major earthquake [1,4].

3.7. Estimation of Plate Positions in Japan

The sample position is represented by PCsample, with PCitem output as a complementary value. This indicates the rotation angle or the axes of PCA (Appendix A). PC1 represents the vertical angle of the interface, while PC2 denotes the angular position on the map. These two determine a plane. PC3 is perpendicular to these and passes through the centre of gravity, thus serving as the norm vector to that plane. Using this norm vector and the centre of gravity, the equation defining the surface can be derived (Appendix A).

Figure 7A depicts this surface on a map, and the concept diagram in Figure 7B is based on this depiction. It should be clear which plate's contact surface each corresponds to. The three East interfaces roughly corresponded, from north to south, to the Kuril-Kamchatka Trench, the Japan Trench, and the Izu-Ogasawara Trench. The deep sections of the Sanriku interfaces extend across the Japanese archipelago into the Sea of Japan, indicating the Pacific Plate reaches that far. The Southwest interface extends from Kyushu, and the Pacific side of the Ryukyu and Nansei Islands, towards the interior of the Japanese archipelago. The shallow Seto interface extends considerably further east than the Seto Inland Sea, stretching from the coast of the Kii Peninsula to the Enshu-nada, connecting to the Ogasawara interface. In this manner, the Eurasian Plate likely contacts other plates. This configuration likely reflects the contact between the Eurasian Plate and multiple other plates, giving rise to a unified interface.

Incidentally, these interfaces themselves exhibit little movement from year to year. Estimates based on 2022 data, when compared with similarly derived estimates for 2011, revealed almost no difference. Minor variation in the analysis arises because PCA is used to account for slight scatter in the measurement locations, and the choice of which dataset to apply also introduces small discrepancies. Even when these factors are considered, however, the differences are too subtle to be discerned in the graphic presentations. Such shifts are more likely to occur only over much longer timescales.

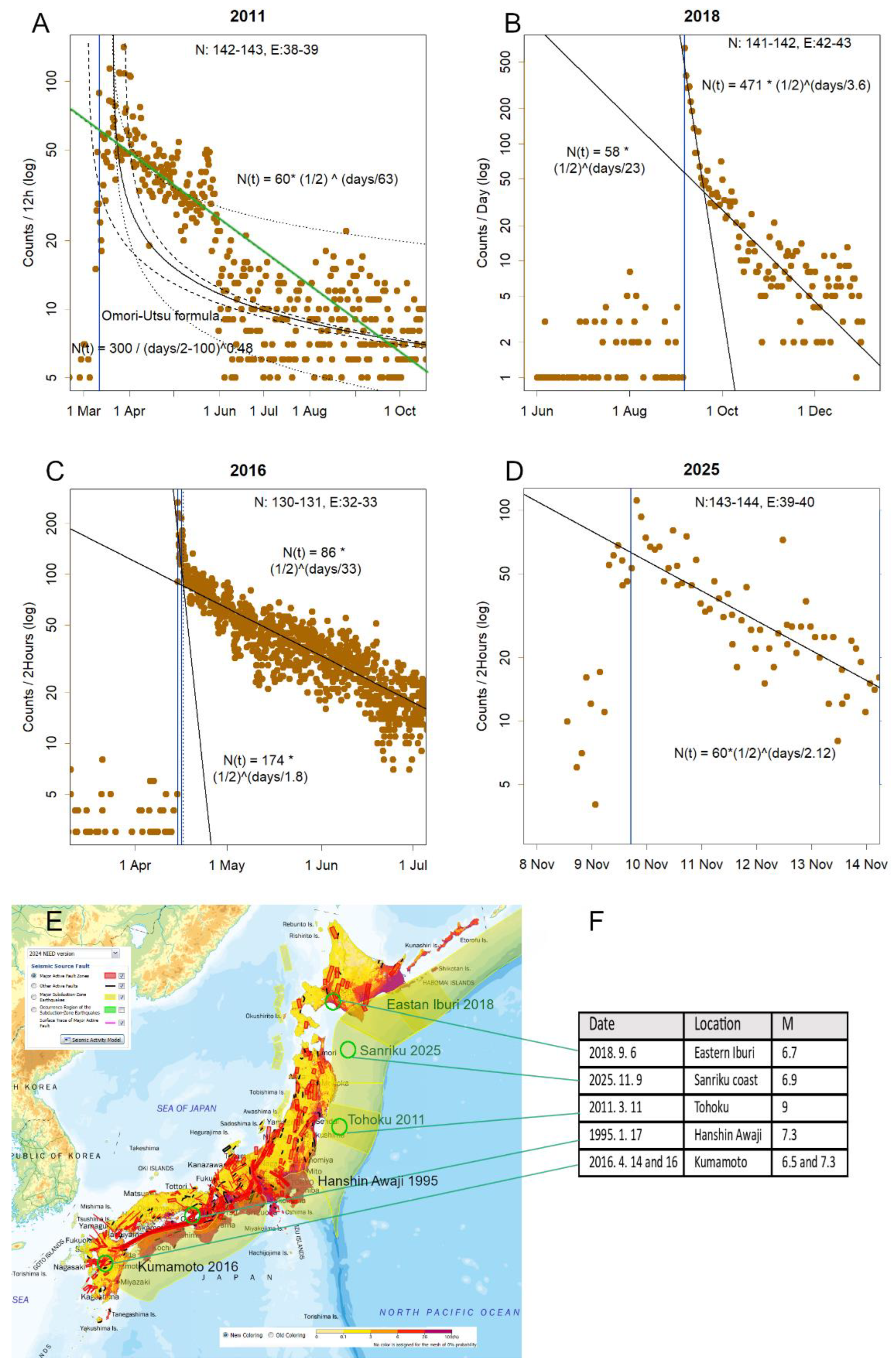
3.8. Decline of Aftershocks

The question of when earthquakes subside and how dangerous aftershocks diminish is a major concern for affected populations. Figure 8A examines the long-established Omori formula for the decline of aftershocks, using data from the 2011 Tohoku earthquake [30]. The original Omori formula expressed the number of aftershocks per unit time, N(t), as inversely proportional to elapsed time [7]. Utsu later modified this by introducing an additional parameter p, and this improved version is now widely used [8,9]:

N(t) = K/(t+c)^p

In Figure 8A, the time unit t is set to 12 hours, consistent with the original formulation. The equation contains three free parameters, each adjusted to achieve the best possible fit. Altering p shifts the curve vertically; the dotted lines from top to bottom represent p= 0.35 and p = 0.55. Changing c affects the initial position horizontally; the dashed lines from left to right represent c = +100 and -200. Modifying K shifts the entire curve vertically. No further improvement in data fit was achievable by adjusting any parameter.

A simpler linear relationship (green line) provides a closer fit to the observed data. Consequently, the Omori formula is not employed thereafter. Given the semi-logarithmic display, the linear relationship implies a decay characterised by a half-life.

Figure 8B presents data for the 2018 Eastern Iburi Earthquake (M6.7) [31]. Within the relevant grid, little precursory swarming was observed prior to the event [3,4]. Seismicity declined according to two linear relationships: a rapid decrease with a half-life of 3.6 days, followed by a slower decline over 23 days. Figure 8C, showing the 2016 Kumamoto earthquakes (M6.5 and M7), also exhibited two distinct decay patterns [32]. Well before this earthquake, a swarm of shallow, small-scale events—possibly linked to volcanic activity—had been occurring in the region [2,3,4]. On this occasion, a precursor earthquake of M6.4 occurred shortly before the M7 mainshock. This precursor decayed with a very short half-life, followed by a long, slow decline after the mainshock. Seismic activity eventually stabilised, but did not return to pre-earthquake levels for several years [3].

Figure 8D shows the recent Sanriku-oki earthquake (M6.7), where a precursor swarm occurred the day before, rapidly decaying with a half-life of approximately two days. In both cases, the behaviour demonstrates half-life phenomena, with smaller earthquakes tending towards shorter half-lives.

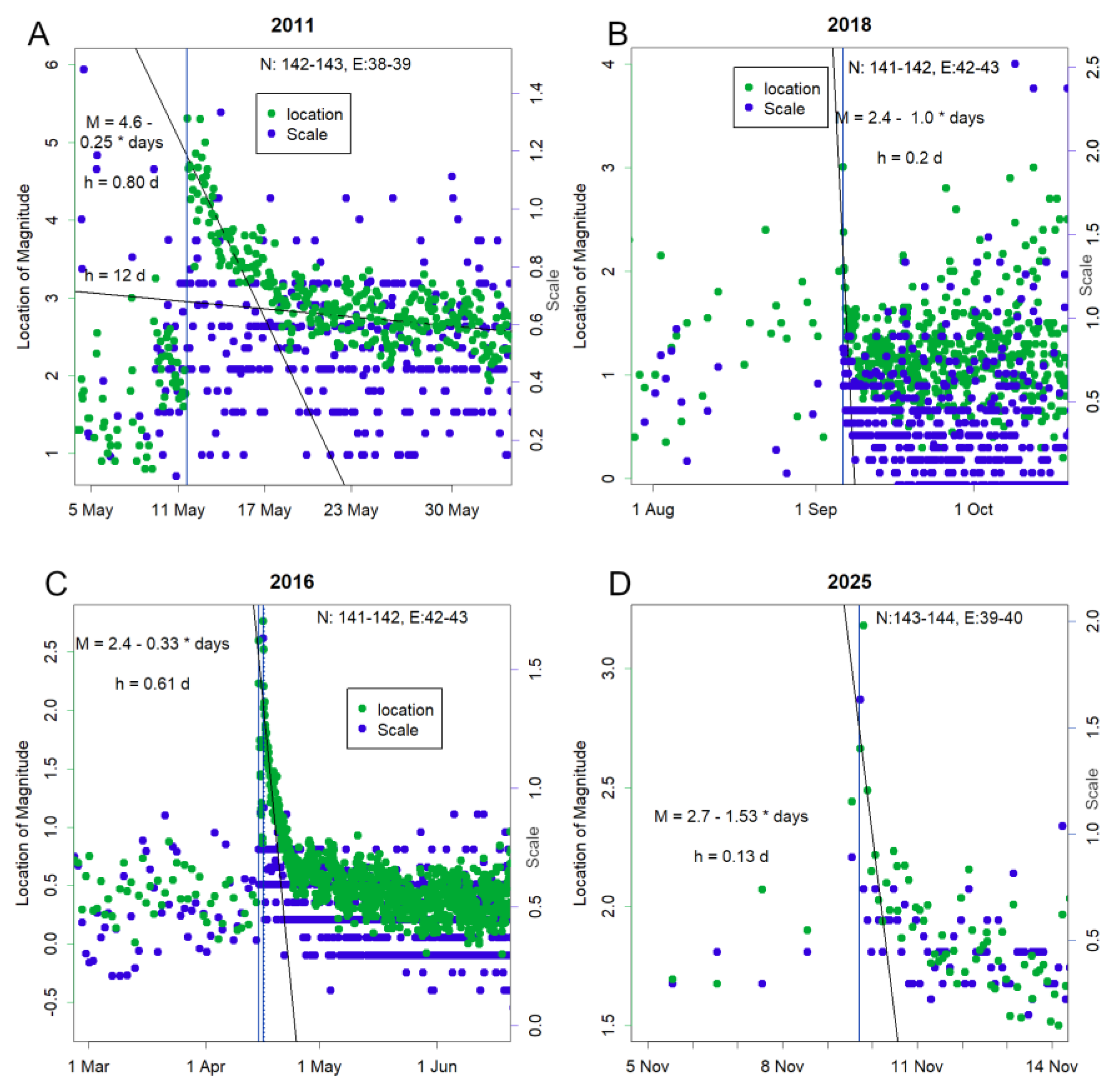
3.9. Aftershock Magnitude Parameters

During earthquakes, the two parameters of magnitude—location and scale—also exhibit properties of a normal distribution [1,3], but their values change significantly immediately after the event. In particular, the location parameter increased by about 2–3 units and then declined linearly (Figure 9). This increase was especially pronounced during the magnitude 9.0 Tohoku earthquake, though the rise had already commenced the day before (Figure 9A) [1].

Although these parameters decline linearly, magnitude is fundamentally a logarithmic measure with base 1000^0.5, representing seismic energy [33]. Thus, a linear decline in magnitude indicates that seismic energy itself exhibits a half-life. A decrease of approximately Log10(2)*2/3=0.2

corresponds to a halving of energy. The indicated h represents this half-life. The decline in energy occurs with a much shorter half-life than frequency, and smaller earthquakes appear to exhibit even shorter values.

Fundamentally, the scale remained largely unchanged; however, the two earthquakes in panel CD exhibited an increase only during the two hours surrounding the main shock. This likely allowed the location parameter of magnitude to increase.

3.10. Abrupt Onset of Earthquakes and Spatial Distribution of Energy Release

Some earthquakes commence abruptly, with a sudden rise in magnitude coinciding with a sharp increase in event counts. Panels C and D in Figure 8 and Figure 9 illustrate such behaviour. During the Tohoku earthquake [30], the rise in magnitude preceded the mainshock by several days, whereas in the recent Sanriku earthquake (Figure 8D) the increase in counts occurred first. It is conceivable that the occurrence of numerous earthquakes naturally heightened the probability of a high-magnitude event. The triggering of such a large earthquake may then release accumulated energy near the epicentre.

Indeed, the scale was large only in areas with high event counts (Figure 10A and 10B). However, during the Tohoku earthquake, regions with large scales (Figure 10C) did not coincide with areas of high epicentre density (Figure 10D). The highest counts were observed in Akita Prefecture, across the Japanese archipelago, which did not experience particularly severe damage. This suggests that the number of earthquakes and the energy released are not necessarily closely related.

Alternatively, the earthquakes in Akita may have originated from epicentres located deep within the Sanriku Plate (Figure 7B) beneath the region. While magnitudes tend to be larger for deep plate epicentres (Figure 2D), the resulting seismic intensity at the surface is not expected to be particularly high.

4. Discussion

4.1. Three-Dimentional Visualisation and the Interfaces

While most earthquakes occurred in the very shallow crust, observing this depth as well provided clear insight into the planes likely formed by plate slip within the mantle (Figure 1CD, Supplement). Japan harbours two large contiguous interfaces, each possessing a curved structure composed of several planes (Figure 3A, Supplement S2A). Determining their positions via PCA clarified the location of plates near Japan (Figure 3D). Although slightly different from previously accepted G, this estimation from epicentre locations would be more reliable. The interfaces are unambiguously represented by equations derived from PCA (Appendix A).

Many deep epicentres lie directly on these interfaces. The interfaces existed long before the earthquakes and persist after the mainshock. However, sharing results observed in three dimensions presents technical challenges (Figure 2C). Interactive 3D presentations, such as those provided in the Supplement, fundamentally require a computer to manipulate viewing angles and cannot be reproduced in print. Moreover, given cognitive limitations, the relationship between dynamic visual acuity and task performance is strong [34]. The ability to detect anomalies differs significantly between scenarios where one can manually manipulate and verify the data versus those where this is not possible.

Describing events in three dimensions using language is also difficult, largely due to the lack of appropriate vocabulary. We attempted to convert the 3D data into 2D using PCA (Figure 2A) and also tested a method with higher reproducibility (Figure 2B). Nevertheless, verification remains difficult unless anomalies are further narrowed down (Figure 2C), because interfaces persist independently of the mainshock. The method described in Figure 3, which involves selecting a single surface and plotting it in 2D, appears effective (Figure 4 and Figure 6). This approach uses PCA to identify two orthogonal axes representing the plane. The automatically determined third axis becomes the normal vector defining the plane (Appendix A).

Since plate positions appear relatively stable, the identified axes can be reused in subsequent years. Specifically, the centre of gravity and the unitary matrix for rotating the data can be applied repeatedly, ensuring consistency across temporal analyses. This reproducible PCA-based approach demonstrates that plate interfaces are stable over short timescales, providing a more reliable framework than earlier models for interpreting seismicity in Japan.

4.2. Subduction Zones and Plate Interactions

Near the subduction zone [21,22], observed here as the interface, major earthquakes are thought to occur because this is the location most susceptible to the accumulation of energy. As seismic activity increases along the interface prior to a mainshock, monitoring these changes could potentially aid prediction (Figure 4 and Figure 6). Given the limited number of interfaces, continuous observation is advisable. Since the interface location appears relatively stable, such monitoring should not require significant effort.

The Pacific Plate appears to be subducting beneath the other three plates, with interfaces inclined at angles of approximately 30–50° relative to the horizontal plane (Appendix A). This configuration is readily apparent in three-dimensional views (Figure 3A, Supplement S1). As the Pacific Plate pushes against the others to form the interfaces, each surface remains aligned without protrusion, likely creating a structure resembling a single folded plate.

Beneath the Philippine Sea Plate, the Pacific Plate is subducting with considerable force. However, despite bearing this underlying plate, the Philippine Sea Plate itself is subducting beneath the Eurasian Plate (Figure 7A; Supplementary Figures S3C–D), presenting a geodynamic contradiction.

4.3. Subduction Dynamics of the Philippine Plate and Seismicity in Seto

As it pushes upwards from below (Figure 5C), the Philippine Plate interface does not subduct vertically; rather, it appears to descend with some lateral drift (Figure 5D). In particular, the north-eastern end of the Kyushu interface seems to be uplifted by the Ogasawara interface. Owing to the motion of the Pacific Plate, subduction of the Philippine Plate beneath the Eurasian Plate appears impeded in this vicinity. This likely explains the absence of very deep earthquakes beneath the Seto interface (Figure 5B). Given that the interface controlled by the Pacific Plate is clearly observed in Figure 5B, the lack of deep epicentres here is probably not attributable to insufficient monitoring, but instead reflects their actual absence.

At the Seto interface, the Philippine Plate has not been able to subduct. Nevertheless, this region experiences frequent earthquakes almost continuously [4]. It is thought that seismicity here arises through a mechanism distinct from ordinary plate-induced earthquakes. Typically, stress accumulates at the frictional interface between plates, which then becomes the energy source for earthquakes. However, such a frictional interface does not exist at the Seto interface. Instead, the force exerted by the movement of the Philippine Plate is likely to be continuously applied, albeit more weakly, as compressive stress on the overlying plate. The elasticity of the plate may conserve this energy, allowing it to accumulate over shorter timescales.

Direct measurement of this process would be ideal, but at present, observations such as those shown in Figure 6 are crucial. The anomaly observed in the Hanshin region may reflect the fact that this westernmost area is subject to stronger forces.

4.4. Plate Positions and Implications for Seismic Interpretation

With the interface now defined, the positions of the plates appear clearer than before (Figure 7B). The Eurasian Plate is largely assumed [23], but the fact that the Seto interface is broken into several segments may suggest the presence of microplates, such as the Amur Plate [35]. Regarding plate positions near Japan, the diagram by Barnes (2003) [23], which synthesised much prior research, remains widely accepted. However, several aspects of plate positioning should now be reconsidered. This is particularly significant when evaluating earthquakes around Japan. For example, estimations for the Nankai Trough [27,28] are based on the older framework [23] and should be revised.

With regard to the interface between the Eurasian Plate and the Philippine Sea Plate, it currently appears reasonable to consider a configuration that encompasses both the Southwest interface and the shallow Seto interface. If this is the case, the Nankai Trough earthquake—long believed not to have occurred—may, in fact, have taken place in 1995 [36]. It is likely that the Nankai Trough, as presently defined by JMA, corresponds to this Seto interface. Notably, even in regions further south—where the JMA has traditionally located the Nankai Trough—no corresponding interface has yet been identified.

The interface between the North American Plate and the Eurasian Plate remains unclear. This is likely because their relative positions have ceased to shift significantly, thereby suppressing seismic activity. It is probable that this interface extends northwards from the tangent line connecting the Hokkaido and Sanriku interfaces (Figure 3D).

Finally, the fragmentation of the Philippine Sea Plate along the Southwestern boundary (Figure 5B) and the increasing angle of subduction (Appendix A) may suggest that this plate is ageing and will eventually become attached to the Eurasian Plate, though this process is likely to take considerable time. These findings underscore the need to revise conventional plate diagrams and re-evaluate historical seismic events in light of updated interface definitions.

4.5. Seismic Hotspots and Implications for Nuclear Power Plants

Earthquakes are naturally frequent near subduction zones. For instance, the Ogasawara subduction zone likely marks the precise location of the Fossa Magna, which connects with the Sanriku subduction zone in the Sea of Japan. The nearby Noto Peninsula is well known for its high seismic activity [37]. This represents a deeper zone, and the subduction line itself is a particularly earthquake-prone location [4]. Furthermore, on the shallower part of the fault line lies the Daiichi–Kashima Seamount [38], which may be considered a seismic hotspot.

Now that the locations of the interfaces are clearly defined, a major problem becomes apparent. Numerous nuclear power plants are situated directly above such faults, and many are currently operating beyond their original design service life. One such plant exploded during the 2011 earthquake, displacing approximately 200,000 evacuees, with vast areas still restricted today [39]. To date, no solution has been found for handling the wreckage, and no substantive action has been taken. Leaving the site untouched will likely result in secondary disasters.

At the very least, now that the positions of these interfaces are known, nuclear plants located on them should be decommissioned immediately and dismantled while conditions remain manageable. In practice, however, Japan has little experience in decommissioning, and this will inevitably be a difficult undertaking. In truth, much of Japan’s territory lies atop these interfaces, making it difficult to identify any location where nuclear plants could be constructed safely (Figure S1F). Considering the risk of catastrophic accidents [39], it is difficult to argue that any potential benefit outweighs this risk.These observations highlight the urgent need to integrate updated tectonic models into national energy policy and disaster preparedness planning.

4.6. Limitations of the Omori Formula and Alternative Modelling

Although the long-established Omori formula [7,8,9] has been widely used for many years, it should not be adopted going forward. It is unsuitable for the nature of the data (Figure 8A). Selecting an inappropriate mathematical model inevitably leads to erroneous analysis. Fundamentally, employing multiple arbitrary parameters when constructing a model is inadvisable, as it complicates verification of its validity [10] A model that fails to fit the data, despite using three parameters, as shown in Figure 8A, is simply unacceptable. Moreover, the Omori model was originally derived from extremely limited data, and its inverse proportionality framework was likely inappropriate from the outset [7].

In contrast, the linear model requires only two parameters: the maximum number of events and the half-life. The former is directly determined from the data, leaving only the half-life as adjustable—and even this becomes evident from the observed decay.

The fact that the number of earthquakes, including aftershocks, follows a log-normal distribution [1,3,4] suggests that seismicity is governed by the synergistic effects of multiple factors. A sudden increase is likely triggered by one of these factors rising abruptly. The subsequent decay with a half-life (Figure 8) indicates that this factor diminishes in a manner consistent with first-order kinetics. Such behaviour is characteristic of processes where the concentration or magnitude of a phenomenon determines its rate of decay.

This invites consideration of a damped oscillation model: a large earthquake generates new stress at its epicentre, which then decays at a rate proportional to the magnitude of that stress, analogous to the oscillation of a spring.

4.7. Energy Distribution, Frequency, and Predictive Potential

Since magnitude is a logarithmic measure of energy, its normal distribution implies that seismic energy itself follows a log-normal distribution, suggesting that it is governed by the synergistic effects of multiple factors [1] (Figure 9). The location parameter was exceptionally large during the mainshock, likely enabled by the amplification of these factors. This may occur simultaneously with an increase in event counts, but the factors driving frequency and those influencing magnitude are likely distinct. Their timing can differ, and their half-lives are markedly dissimilar. While dependent on earthquake magnitude, the decline in magnitude appears to occur with a considerably shorter half-life.

It is probable that the factors responsible for these increases are singular and isolated, abruptly intensifying and then dissipating. In the case of the Tohoku earthquake, it is likely that the energy was present first, and the subsequent earthquake triggered the conflict (Figure 9). Thus, even with a high number of earthquakes, the resulting damage was not necessarily severe (Figure 10). Conversely, in the recent example off the coast of Iwate, where the increase in frequency preceded the event, the frequent earthquakes may have released energy that had been accumulating nearby.

In either case, it is likely that this factor—whether expressed through frequency or magnitude—is consumed during the process. Consequently, seismic activity rarely returns to pre-earthquake conditions, sometimes requiring several years to stabilise. If we could identify and measure this factor directly, it might become possible to predict with greater accuracy the timing, location, and scale of future earthquakes.

4.8. Re-Examining Earthquake Mechanisms Through Modern Statistics

Understanding statistical properties should also deepen our knowledge of earthquake mechanisms. Revealing the processes hidden within the data is precisely the purpose of exploratory data analysis (EDA) [10]. Although earthquake mechanisms have long been studied, they have too often been inferred from misinterpreted data, such as the Gutenberg–Richter law [5]. The Omori formula was proposed more than a century ago [6] and refined some seventy years ago [8,9], yet it was derived from only five days of observations.

The continued reverence for such flawed concepts, together with the unquestioned perpetuation of outdated plate tectonic models, demonstrates how the field has neglected modern statistical approaches—a matter that warrants serious reflection. I recommend re-examining the mechanisms that have been inferred, employing contemporary analytical methods and ensuring that the data are correctly interpreted [6,20,24,40,41].

5. Conclusions

By employing modern statistical approaches, we investigated the visualisation of interfaces between plates and the decay of aftershocks. Both analyses challenge long-held conventional wisdom and provide new conceptual frameworks. These findings demonstrate that contemporary analytical methods enable the extraction of more accurate insights from seismic data. Such approaches are likely to be critically important for elucidating earthquake mechanisms and, ultimately, for advancing predictive capability.

Appendix A.1 Fundamentals of Principal Component Analysis [18]

Principal Component Analysis (PCA) is a commonly employed technique for compressing multidimensional data. Its simplicity and clarity make it particularly suitable for scientific applications. Due to the minimal assumptions required for its computation, it consistently yields the same results regardless of the analyst, ensuring high reproducibility and objectivity.

Here, the data is presented in five dimensions. It is often structured as Sample x Item.

Sample	Time	Latitude	Longitude	Depth	Magnitude
Sample1	2025111400:0041.3	34°11.7'N	135°14.1'E	5	0.4
Sample2	2025111400:045.2	36°36.4'N	141°1.5'E	16	1.3
Sample3	2025111400:0424.1	39°45.2'N	143°26.3'E	14	2.7
Sample4	2025111400:0438.1	37°56.9'N	138°9.7'E	13	0.6

Only the three dimensions Longitude, Depth, and Magnitude are used, so these are extracted.

Taking the mean value for each item gives the centre of gravity for the data. Here, we decide to rotate around this centre of gravity. Subtracting this value from all data achieves centring. This is equivalent to translating the data parallel to the rotation origin. The shape of the data remains unchanged; it remains a matrix of the same form.

$$\overline{\mathrm{item}}=\sum \mathrm{data}/\mathrm{n}, \mathrm{centered}= \mathrm{data}-\overline{\mathrm{item}}$$

Now, any matrix can be singular value decomposed. This is the act of decomposing the matrix into two complementary directions and their magnitudes.

$$\mathrm{centered}= \mathrm{U}·\mathrm{D}·{\mathrm{V}}^{*}$$

Here, U and V are unitary matrices, and V^* denotes the adjoint matrix of V. Since centred is a rational number here, the adjoint matrix may be considered as the transpose matrix. The U∙D denotes the matrix inner product. A unitary matrix is one that records the angle of rotation; each row and column is orthogonal, and all elements have magnitude 1. Consequently, it possesses the following property:

U∙U^* = U^*∙U = I

Here, I is the identity matrix. This holds because the sum of its own multiplications, i.e., its square, is 1, and its inner product with any other vector is zero. The inner product being zero with any other vector indicates that each angle is a right angle. Consequently, each vector is independent.

The magnitudes are recorded in D, which is a diagonal matrix with mostly zeros, containing the magnitudes in descending order along the diagonal. PCA involves calculating the principal components (PC) for both the sample and the item from these matrices [19].

PC_sample =U∙D∙V*∙V=U∙D=centered∙V

PC_item =V∙D∙U*∙U=V∙D=centered*∙U

U·D signifies assigning magnitude to a unitary matrix. Since the unitary matrix U represents orthogonal axes, it indicates the values a sample takes along those axes. This explains why PCA is described as a method for finding orthogonal axes representing the data. Alternatively, it can be viewed as rotating centred data using the unitary matrix V. This explains why PCA is described as a method for rotating data. Mathematically, both interpretations are equivalent. The PCsample represented by centred V is the rotated value of the item for each sample, while the PCitem represented by the transpose of centred V * U is the rotated value from the sample for each item. The former represents the sample's value under the new axes, while the latter represents how the item has been rotated; here, it becomes a 3x3 matrix.

Each is the result of a single inner product. Using R, this can be computed almost instantaneously with just a few lines of code. By now, it should be clear that there are scarcely any alternatives. If pressed, one might mention that data may sometimes be scaled as well as centred, or that the centre might be placed somewhere other than the centre of gravity [19]. Fig. 2A shows the result of a PCsample that was also scaled; all others are results from centring alone.

PCsample represents the principal component for each sample. PCs appear as vertical vectors. PC1 is the leftmost vertical vector, with subsequent ones progressively smaller in scale as they move further to the right.

PCitem [[,3]

This is R notation. [,3] denotes the third vertical vector from the left within the matrix, i.e., PC3. Incidentally, [1,] represents the first sample.

One point requires attention. In this calculation, the sign is determined randomly (the rotation direction may change by 180 degrees; it is indeterminate which direction the rotation terminates in). When displaying PC results, if inversion is preferable, multiply the corresponding PC values in both PCsample and PCitem by -1 simultaneously. Here, signs are adjusted as appropriate to avoid unnatural appearances when mapped.

PCsample [[,1] <- -1*PCsample [[,1]

PCitem [[,1] <- -1*PCitem [[,1]

PCsample represents the principal components of the sample. For instance, the values displayed in Fig. 3C are these. Here, due to rotation via PCA, the Sanriku data unfolds onto the plane where PC3 = 0. Other data points move away from this plane.

The corresponding PCitem records the rotation angle. PC1 records the depth axis. For instance, at the Sanriku interface, PCitem was:

	PC1	PC2	PC3
Longitude	44	51	-27
Latitude	-27	150	9.1
Depth	3093	0.59	0.46

PC1 is the depth axis. Since 1 unit of Longitude and Latitude roughly equals 100 km, and Depth is measured in km, the distance on the map is (44² + (-27²))⁰.⁵ * 100 = 3470. Thus, when moving this distance on the map, it appears to be diving 3093 km. Therefore, the angle from sea level would be approximately atan(3093/3470)/π*180 = 30°. Similarly, PC2 indicates the azimuth on the map.

Furthermore, PC3 is perpendicular to the plane specified by PC1 and PC2. This is the norm vector of the plane. Here, the centre of gravity was

Longitude	Latitude	Depth
140.6	37.8	98.7

Therefore, the equation of this tangent plane is specified by the norm vector and a point on the plane, giving:

-27(x-140.6) + 9.1(y-37.8) + 0.46(z-98.7) = 0

Simplifying this yields:

y = 3.1x - 0.054*z - 402

Plotting this graph at z=0 and z=-400 yields Fig. 5D. Specifically, after plotting each epiocentre, draw a straight line with an intercept of -402 and a slope of 3.1. The intercept at -400 km is 380. The position of the interfacde in Fig. 3D was constructed in this manner. In reality, the length of a meridian varies with latitude, so there is some error; however, at latitudes like those in Japan, this error is likely negligible.

The distance d between two parallel lines, ax + by + c = 0 and ax + by + d = 0, can be calculated as d = |c - d| / (a² + b²)⁰.⁵. Assuming a unit of latitude is 100 km, a depth of 400 km corresponds to 100*d km, yielding a slope of 31°. This is almost identical to the value observed from PC1 (though PC1 may be affected when the surface does not submerge straight, as in Southwest interface. Hence, this estimation is likely more accurate). The equations for each interface were as follows:

Location	equation	angle
Hokkaido interface:	y= 0.26*x -0.012 *z +3.8	42
Sanriku interface:	y= 3.1x -0.054* z -402	31
Ogasawara interface:	y= -1.6x+0.018z +255	46
Seto interface:	y=0.16x-0.011z+12	43
Southwest interface total:	y= 1.5x -0.0090z - 171	69
Kyushu interface:	y=2.2x -0.010z- 257	80
Ryukyu Is. interface:	y= 1.0x-+0.010z-102	64
Southwestern Is. interface:	y= 0.28x-0.0054z - 11	63

However, the Seto interface is shallow and the data sparse, so the angle is likely not very accurate.