Numerical Modeling of Stress-Field Formation in a Coal–Rock Mass During Excavation near a Geological Fault

1. Introduction

The aim of the study is to determine the mechanisms of formation of the stress–strain state of the coal–rock mass in the zone between a geological fault and a mine working, in order to identify areas of structural discontinuity and predict the probability of gas-dynamic phenomena. Previous research. Studies focused on the prediction and prevention of gas-dynamic phenomena (GDP) have remained a central topic for leading researchers in the field of mining science for many years [1,2,3]. Despite significant progress, such phenomena continue to occur, indicating the complex nature of these processes, the multiplicity of influencing factors, and the necessity for further improvement of predictive methods and preventive technologies. A number of fundamental studies have established that the main factors determining the development of GDP are: (I) gas pressure within methane-saturated coal seams, (II) the physico-mechanical properties of coal and the surrounding rocks, and (III) mining-induced stress that governs the stress–strain state of the rock mass. These findings have served as the scientific and methodological basis for the development of modern methods for predicting and preventing GDP.

However, the role of tectonic faults in the mechanism of gas-dynamic phenomena remains debatable. It has been reliably established that sudden outbursts are often associated with zones of disjunctive geological faults, which are characterized by weakened strength properties of coal and increased gas release.

In the Karaganda coal basin, all recorded cases of coal and gas outbursts have occurred within fault zones [4]. This underscores the importance of a detailed study of the structural and tectonic features of the rock mass using modern methods [5,6,7]. The Karaganda coal basin is characterized by a complex structure. The presence of geological heterogeneities, such as tectonic faults, washouts, and variable seam topography, complicates underground mining operations. The most accurate and reliable picture of the tectonic structure of the coal mass can be obtained by applying mine seismic survey methods to study the geological structure, the condition of the coal seam and surrounding rocks, and to identify tectonic faults.

Between 2009 and 2025, 14 sudden outbursts were recorded in the basin’s mines on seams d6, K7-8, and K10. The geological faults in these zones are generally characterized by reduced strength of the surrounding rocks, crushing of coal layers, or abrupt changes in seam topography — with or without visible displacements.

Previous studies have shown that progress in addressing this problem is possible through an integrated approach, which includes [8]:

• forecasting the distribution and characteristics of fault zones in areas of planned mining operations;
• investigating physical processes capable of initiating sudden outbursts;
• developing engineering measures to prevent gas‐dynamic phenomena (GDP) that are applicable under mine conditions.

Although the physics of GDP initiation has been described in detail in fundamental studies [2,3], a key practical problem remains unsolved — modeling the processes of initiation and development of gas-dynamic foci in fault zones to enable their early prediction and prevention. The present study aims to address this problem by analyzing the stress–strain state of the rock mass between a tectonic fault and the advancing excavation.

2. Materials and Methods

The research methodology is based on numerical modeling of the stress–strain state of the rock mass between a disjunctive geological fault and a mine working using the finite element method (FEM). In the FEM computational model, the disjunctive geological fault is represented as a thin slot — a section of the displacement plane between the edges of shifted rock blocks, as proposed by the authors of [6].

Problems related to determining the stress state of the rock mass can be solved using the framework and terminology of the finite element method [7]. In the present study, the stress parameters of the rock mass are computed in a two-dimensional formulation. The applied elastic medium model is considered as a first approximation that provides sufficient accuracy for analyzing the influence of geological factors and for making engineering-based decisions.

It is assumed that gas-dynamic phenomena may be initiated by the destruction of the near-contour rock mass in the zone ahead of the working face, in the roof, or in the sidewalls of the excavation.

To describe the limiting state and failure conditions of rocks, the Coulomb–Mohr criterion [9,10] is used, which allows t=he assessment of the probability of rock mass integrity disturbance under various stress levels.

$${\sigma }_1=\vartheta ·{\sigma }_2+{\sigma }_c$$

(1)

where ${\sigma }_c$is the uniaxial compressive strength of the rock (considering structural weakening of the rock mass), MPa; ${\sigma }_1$and ${\sigma }_2$are the acting maximum and minimum principal stresses, MPa; and $\vartheta$is the volumetric strength parameter of the rock, determined from the internal friction angle. [11]

$$\vartheta ={\displaystyle \frac{1+\sin \left(\phi \right)}{1-\sin \left(\phi \right)}}$$

(2)

.

To study the formation of failure zones in the rock mass under the influence of principal stresses and the possibility of creating conditions for sudden outbursts, the strength criterion (1) is expressed in the form of a difference [14].

$$\Delta \mathsf{\sigma }={\sigma }_1-\left(\vartheta ·{\sigma }_2+{\sigma }_c\right)$$

(3)

If the value of $\Delta \mathit{\sigma }>\mathbf{0}$, i.e., the acting maximum principal stress ${\mathit{\sigma }}_1$ exceeds the strength resistance of the rock to failure, then this region of the rock mass represents, following the terminology of N.V. Cherdantsev [10], a zone of structural discontinuity of the rock mass and, in the terminology of the present study, a potential zone for the initiation of a gas-dynamic event.

3. Results

In accordance with the proposed methodology, a detailed numerical simulation was conducted for a historically documented sudden coal and gas outburst that occurred in 1971 at the Saranskaya mine of the Coal Department of ArcelorMittal Temirtau JSC. This event, registered as Case No. 34 in the official Catalog [4], was selected as a reference case due to the distinct geological and structural conditions under which the outburst occurred. The disturbance zone is associated with a reverse fault exhibiting an amplitude of approximately 0.5 m and a shear displacement. Such structural features create favorable conditions for stress concentration and for the degradation of the mechanical integrity of the coal–rock mass. These characteristics make the Saranskaya mine outburst a representative and informative case for validating the proposed modeling approach.

The outburst took place during the development of the 4th Western transportation drift along seam K12. The mining, geological, and operational conditions in the outburst zone are summarized as follows:

• Mining depth: H = 382 m
• Seam thickness: m = 5.5 m

Immediate roof composition:

• fractured argillite — 6 m,
• siltstone — 7.5 m,
• sandstone — 3 m
• Seam dip angle: 14°
• Natural gas content: X = 12.8 m³/t
• Volatile matter: V = 26.3%
• Moisture content: W = 2.73%

The lithological succession of the roof, consisting of alternating layers of relatively weak argillite and stronger but brittle siltstone and sandstone, results in a heterogeneous stress response. This composite structure influences load transfer from the roof to the coal seam and contributes to the redistribution of stresses during excavation. The coal seam itself, characterized by notable gas content and moderate volatile matter, falls into a category of coals with an increased predisposition to sudden gas release when subjected to stress perturbations.

According to field observations conducted prior to excavation, no zones of elevated gas-dynamic hazard were identified in the area [12]. This absence of diagnostic indicators underscores the limitations of traditional hazard assessment methods and highlights the need for predictive models based on stress–strain analysis.

To construct an accurate numerical representation of the rock mass, weighted-average physical and mechanical properties were calculated considering the proportional thickness of each lithological layer. These parameters include uniaxial compressive strength, tensile strength, bulk density, elastic modulus, internal friction angle, and cohesion. The incorporation of these averaged properties into the finite-element model enabled the simulation of the stress–strain state of the coal–rock mass under the combined influence of in-situ stresses, the presence of a fault, and excavation-induced unloading.

The simulation results reveal distinct zones where the strength criteria of the coal–rock mass are exceeded, indicating areas of potential loss of structural integrity. These zones correspond to locations where gas-dynamic phenomena are most likely to be initiated. The modeled stress distribution demonstrates that the interaction between the tectonic disturbance and the advancing excavation front creates localized concentrations of compressive and shear stresses. These stress concentrations align with the geological observations recorded at the Saranskaya mine and provide a physical explanation for the mechanisms leading to the 1971 outburst.

Overall, the results confirm that the proposed numerical approach effectively captures the patterns of stress redistribution in the vicinity of a geological disturbance and can serve as a reliable tool for predicting the onset of sudden coal and gas outbursts during mine development in structurally complex zones [12].

The weighted average values of the physical and mechanical properties of the rock mass, calculated by the thickness of individual layers, are as follows:

uniaxial compressive strength ${\sigma }_c^{\left(w.a.\right)}=30$MPa;

tensile strength ${\sigma }_t^{\left(w.a.\right)}=4.7$MPa;

bulk density ${\gamma }^{\left(w.a.\right)}=2072$m³;

elastic modulus $E^{\left(w.a.\right)}=0.78\times {10}^4$MPa;

internal friction angle ${\phi }^{\left(w.a.\right)}=34°$;

cohesion $K^{\left(w.a.\right)}=57$MPa.

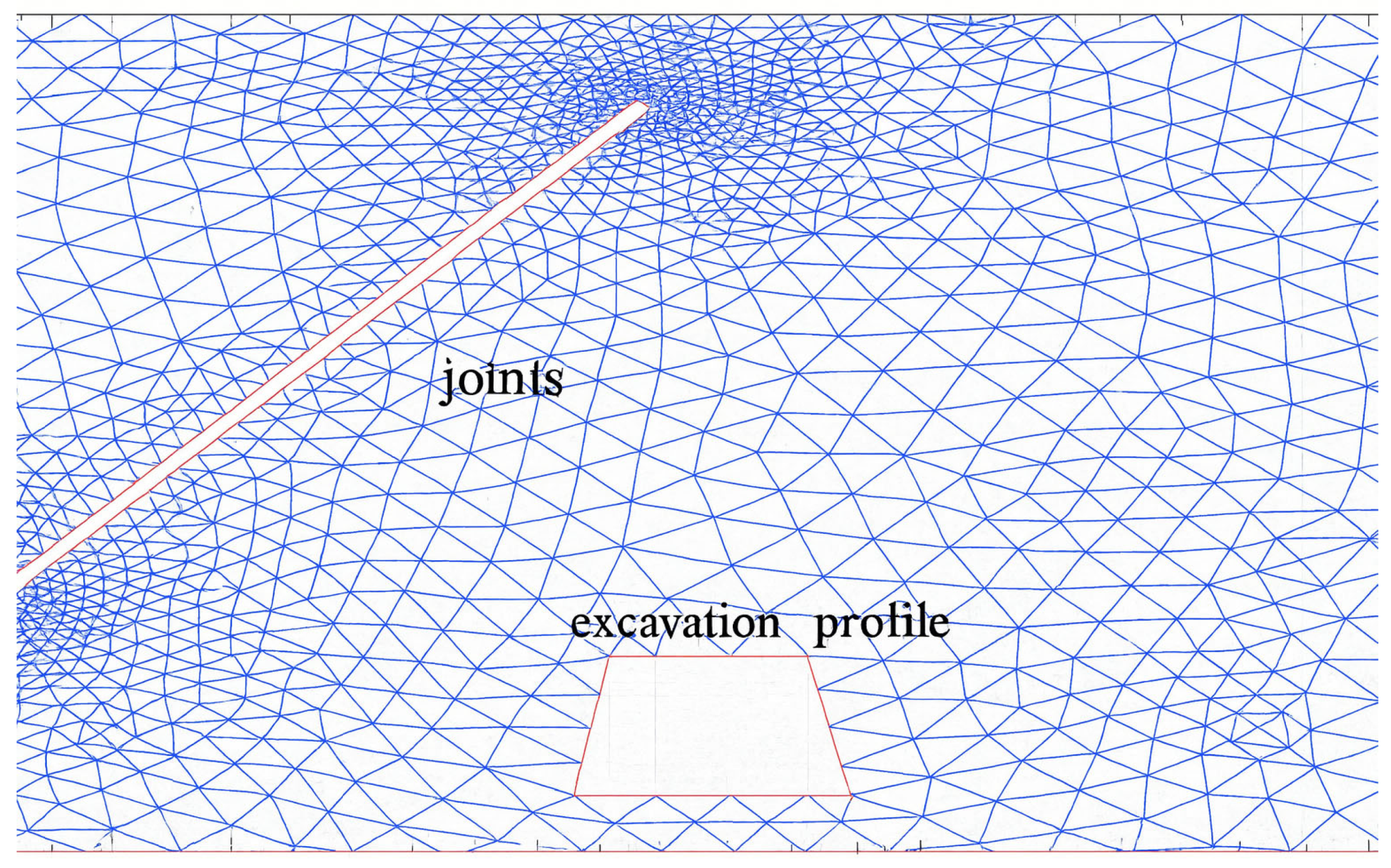
The cross section of the fault dislocation plane was modeled as a rectangular slit approximately 0.05 m thick and 20 m long (Figure 1).

• Numerical Simulation Setup

The excavation was carried out along the outburst-prone seam K₁₂; its cross-section had a trapezoidal shape with the following dimensions: height — 4 m, roof width — 3 m, and floor width — 5 m. The normal distance from the left upper corner of the excavation to the “bottom” of the slot (representing the displacement plane in the model) was 12 m.

Stress modeling and calculations were performed by numerically solving an elliptic partial differential equation using the MATLAB software package [13,14]. The rock mass, including the fault and the excavation, was subjected to gravitational loading γH on the upper and lower boundaries, and to lateral pressure λγH along the sides, where γ is the average unit weight of the overlying rocks and H is the depth of the excavation. For the conditions of the Karaganda coal basin, the lateral pressure coefficient was taken as λ = 1.56.

The implementation of the numerical stress–strain model made it possible to determine the fields of numerical values of the principal stresses ${\sigma }_1$, ${\sigma }_2$, and the horizontal stresses ${\sigma }_x$acting within the rock mass.

Based on the numerical stress values obtained from the graphical stress field maps, analytical expressions of approximating polynomials were derived to calculate stresses at arbitrary points within the near-contour rock mass and the “floor” of the fault slot (Table 1).

Using the derived analytical expressions of the acting stresses (Table 1), the graphs of the variation of the critical value of the parameter $\mathsf{\Delta }\sigma$according to criterion (3) were plotted, as shown in Figure 2, Figure 3 and Figure 4.

The results obtained from the numerical simulation of the 1971 Saranskaya mine outburst provide important insights into the mechanisms of stress redistribution and coal–rock mass destabilization in the vicinity of geological disturbances. Although traditional field indicators did not identify zones of elevated gas-dynamic hazard prior to excavation, the modeling outcomes clearly demonstrate that the interaction of a reverse fault with the advancing drift leads to the formation of stress concentrations that can trigger sudden coal and gas outbursts. This finding highlights a significant limitation of observational and empirical hazard assessment methods, which may fail to detect latent structural instabilities within the coal–rock mass.

One of the key observations is that even a relatively small-amplitude fault—approximately 0.5 m in this case—can significantly alter the stress–strain fields within the surrounding strata. The modeled stress patterns show that both compressive and shear stresses are enhanced near the fault plane and the excavation contour, forming localized zones of strength degradation. These observations align with prior studies reporting that faulted and sheared coal seams exhibit reduced cohesion, increased permeability, and heightened susceptibility to gas-dynamic events. Therefore, the Saranskaya case demonstrates that fault-related structural irregularities must be treated as critical factors when assessing outburst risk.

Another important aspect of the findings is the strong influence of lithological heterogeneity on stress transfer within the rock mass. The immediate roof, composed of alternating layers of argillite, siltstone, and sandstone, exhibits variable mechanical behavior that affects how loads are redistributed as excavation progresses. The modeling results suggest that zones of intense stress accumulation tend to form at interfaces between weak and strong lithological units, where mechanical contrasts cause strain localization. This supports previous research indicating that stratified roof structures can amplify local instabilities in coal seams, particularly in the presence of tectonic discontinuities.

The results also demonstrate that the coal seam’s natural gas content—12.8 m³/t—is sufficient to contribute to dynamic failure when combined with destabilizing stresses. Although gas pressure was not explicitly included in the finite-element model, the identification of structural zones where the strength criteria are exceeded provides a reasonable approximation of where gas-driven fracture propagation and sudden desorption could occur. These observations confirm that stress analysis is a valuable first step in identifying regions where gas-dynamic effects may subsequently develop.

Overall, the modeling approach proved effective in reconstructing the conditions that led to the historical outburst. The correspondence between simulated stress concentrations and the actual location of the outburst indicates that the method has strong diagnostic potential for application in modern mine planning. Unlike empirical indicators, which may overlook hidden structural hazards, numerical simulations can predict instability zones based on geological geometry and mechanical parameters alone.

However, several limitations should be acknowledged. The model assumes linear-elastic behavior of the rock mass, which simplifies the complex deformation mechanisms that may occur near faults, especially under high gas pressure. Additionally, gas-flow processes and coupled hydro-mechanical interactions were not included. Incorporating these factors into future models could further refine predictions and improve understanding of the critical conditions leading to outbursts.

Despite these limitations, the findings highlight the practical value of integrating numerical modeling into routine hazard assessment. By identifying zones of potential instability before excavation reaches them, mine operators can implement targeted preventive measures, such as intensified degasification, controlled drilling, or modified support systems. Thus, the presented methodology provides a scientific and practical basis for enhancing safety in underground coal mining, particularly in structurally complex areas affected by geological disturbances.

Results and Analysis of Stress Distribution

Analysis of the position of the plotted lines relative to the zero line, which represents the stability boundary of the rock mass, makes it possible to formulate predictive assessments regarding the localization of zones of disturbed rock integrity — that is, areas potentially hazardous in terms of gas-dynamic phenomena [15].

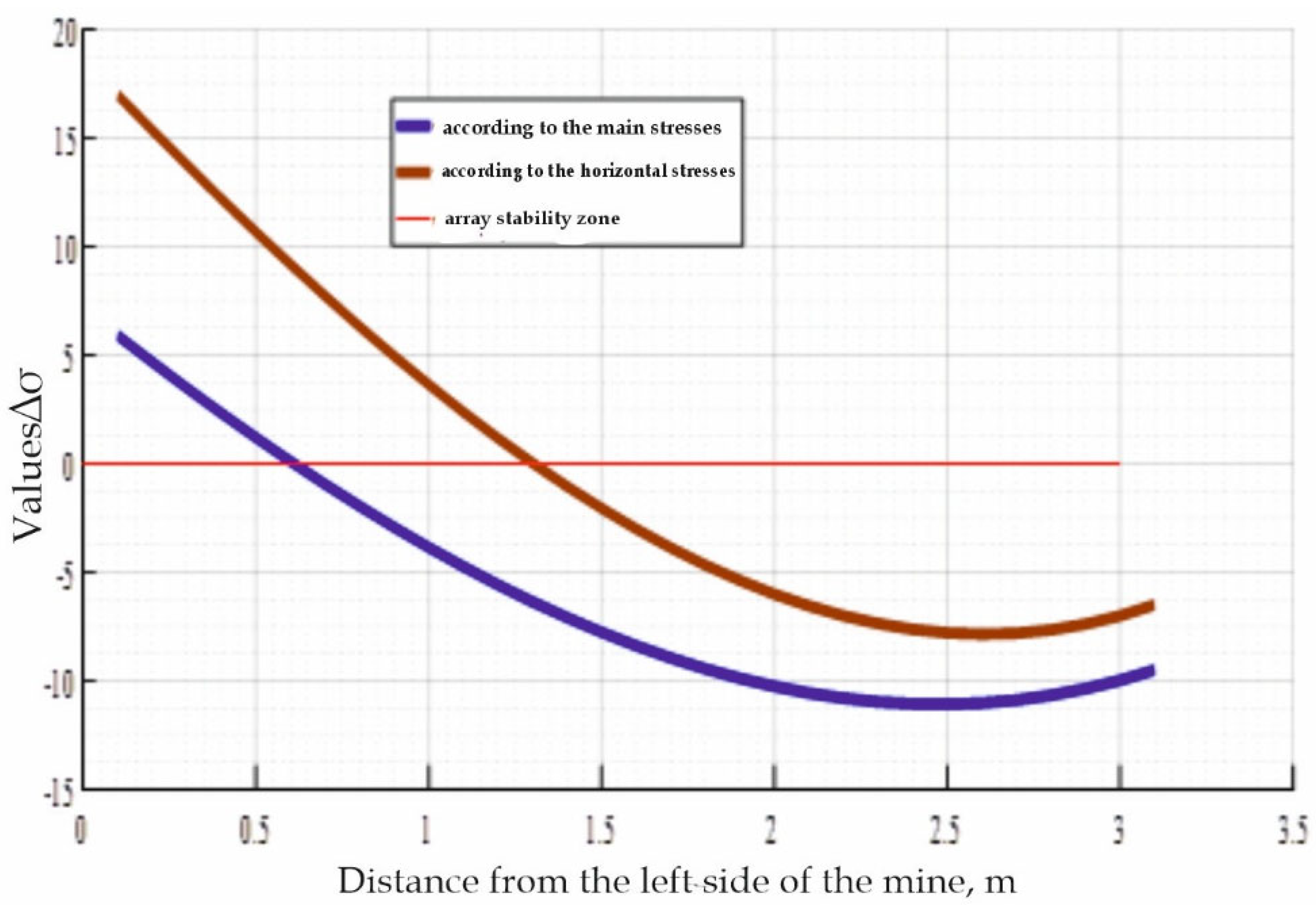
In the roof of the excavation (Figure 2), such zones are predicted:

• according to the principal stresses — up to 0.6 m from the left sidewall,
• and according to the horizontal stress component — at a distance of approximately 1.3 m.

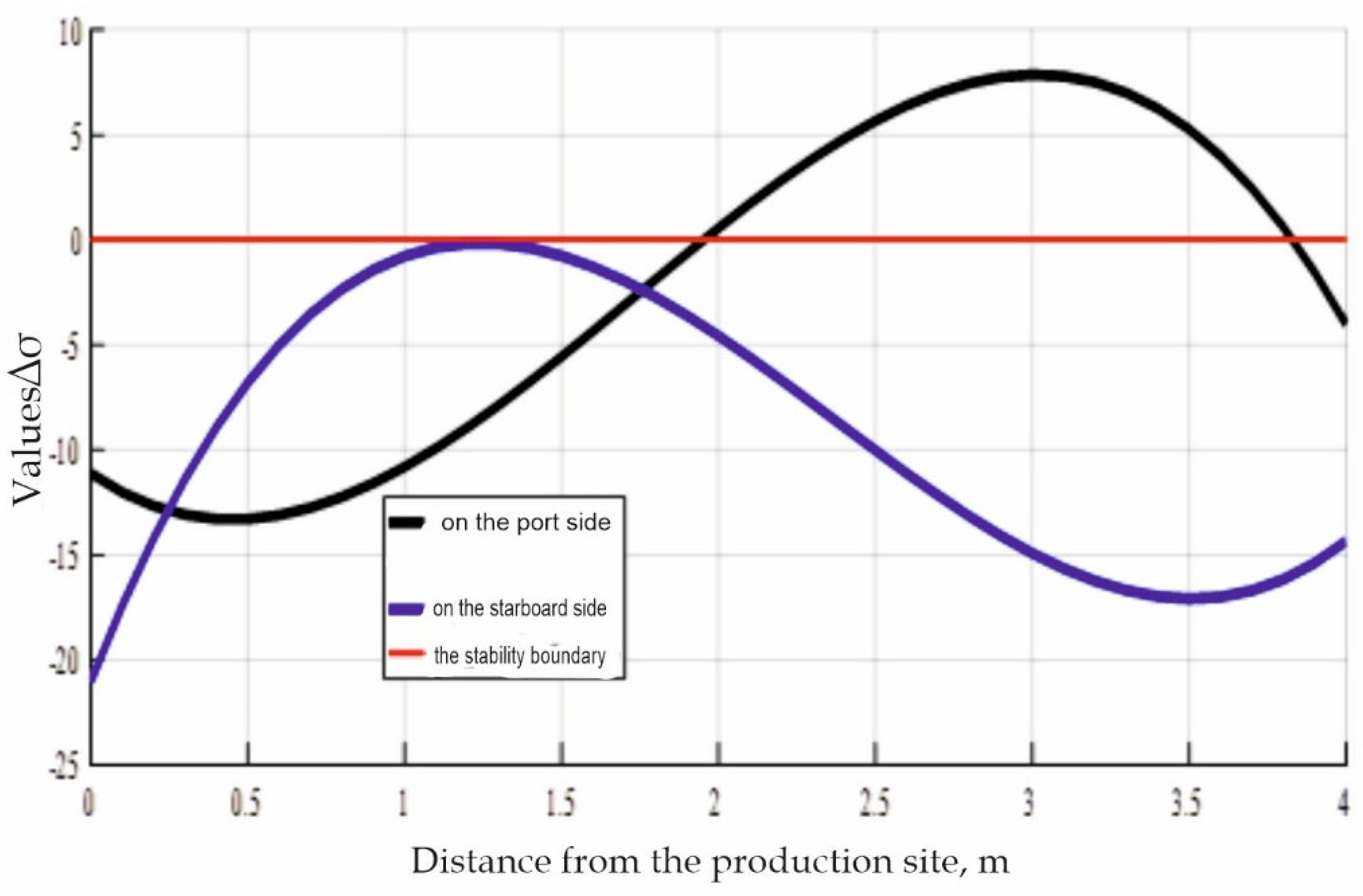
Along the left sidewall of the excavation (Figure 3), the zone of disturbed integrity is formed at a height of about 2 m from the floor, i.e., beginning roughly from half the excavation height. Along the right sidewall, a critical zone may occur at a distance of 1.2–1.5 m from the floor, where the near-contour rock mass is in a state of limiting equilibrium.

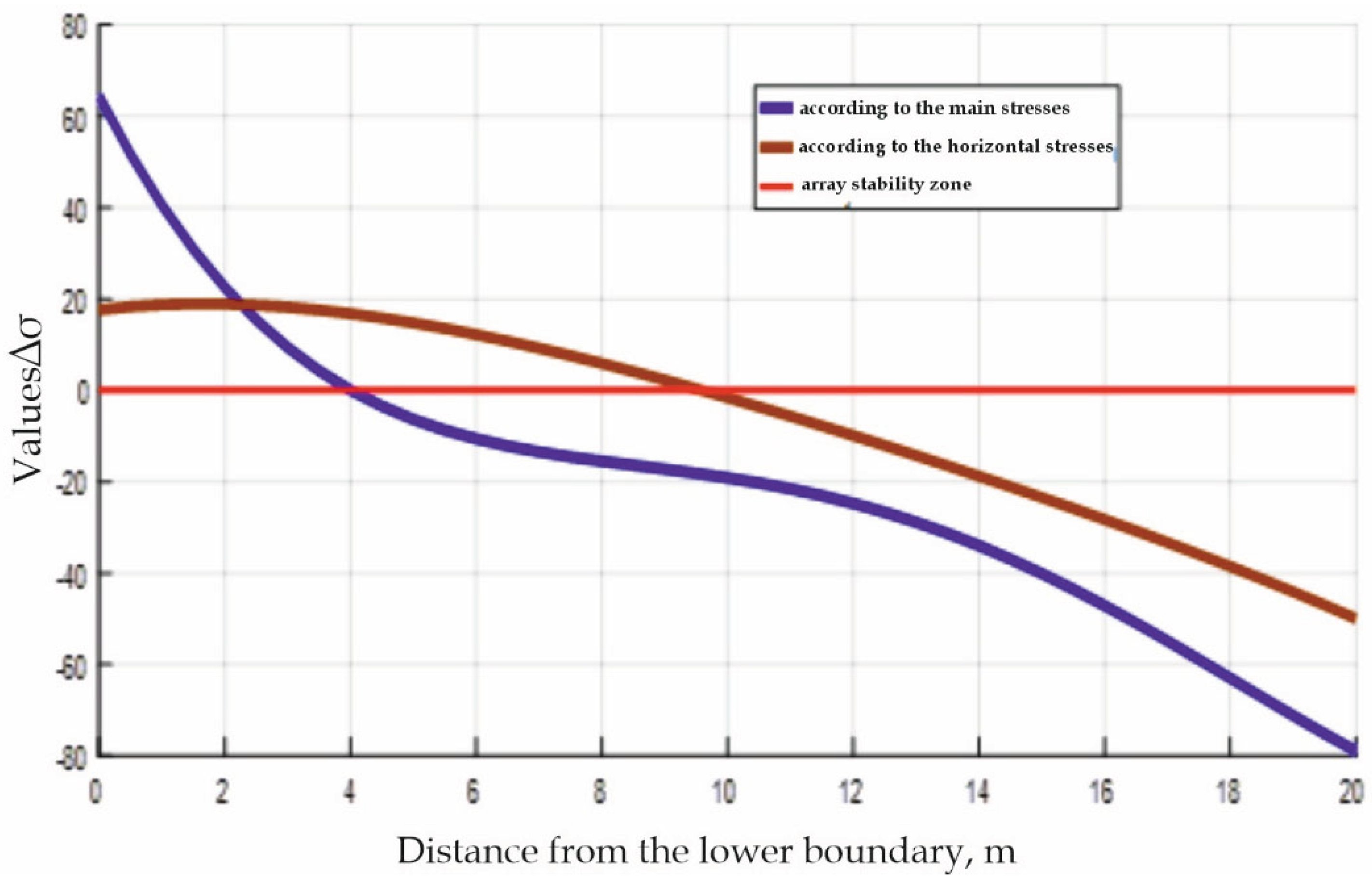
In the rocks located in the “floor” of the fault slot (Figure 4), the zone of integrity loss under the influence of both principal and horizontal stresses is formed at a depth of 4 to 10 m below the fault boundary. As shown in the schematic diagram (Figure 1), this area is spatially associated with the left sidewall of the excavation, within which the occurrence of dynamic processes in the form of a sudden outburst is predicted [16,17].

As intended by the research objective and methodology, the identification of zones of disturbed rock integrity — that is, potential foci of dynamic phenomena — was carried out based on the analysis of the stress–strain state and the limiting equilibrium conditions of the rock mass surrounding the excavation contour located near the geological fault. In this stage of the study, only principal stresses were considered [18]. The influence of gas pressure was not included in the current calculation, as its effect is assessed separately, based on the parameters of the internal surface of a potential outburst cavity.