Hopf Bifurcation Analysis in a Reaction-Diffusion-Advection Model with Strong Allee Effect and Delay

1. Introduction

In ecosystems, the logistic growth rate is commonly used to describe population growth, effectively capturing the effect of intraspecific competition. The logistic growth rate describes the fact that when population density increases, the growth rate declines. In 1931, the ecologist Allee observed that in social populations, the intrinsic growth rate decreases below a critical population threshold [1]. This phenomenon, known as the Allee effect, has since been extensively studied in subsequent ecological models [2,3,4].

The Allee effect describes the phenomenon of individual animals benefiting from the presence of conspecifics. The Allee effect is categorized into two types: strong and weak [5,6]. In comparison, models with strong Allee effect exhbit richer properties. The classic strong Allee effect model is as follows:

$$\dot{u}=ru(u-b)(1-{\displaystyle \frac{u}{K}}),$$

where $0<b<K$ is the Allee threshold, K is the carrying capacity of the population. A model incorporating strong Allee effect exhibits a growth rate influenced by cooperative and competitive interactions among individuals. Reference [7] provides numerical evidence that the strong Allee effect is characterized by a critical density threshold, below which population density is insufficient for long-term persistence.

Time delays are ubiquitous in the study of population dynamics [8,9,10]. For example, the birth of new individuals involves a gestation delay, the predation is followed by a digestion delay. Notably, the current population growth rate is determined by environmental pressure, which is governed by the population density $\tau$ times ago. This is a common and widespread phenomenon among social animals.

We should emphasize that in the study of population dynamics within bounded domains, it has been observed that population density varies with spatial location. Individuals undergo both random dispersal and directed movement [12,13]. The diffusion and advection enables the investigation of the spatiotemporal population distribution [11]. Based on these considerations, this paper investigates the following model subject to bounded region and the following boundary conditions:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial u(x,t)}{\partial t}}=d{\displaystyle \frac{{\partial }^{2}u(x,t)}{\partial x^2}}-\alpha {\displaystyle \frac{\partial u(x,t)}{\partial x}}+ru(x,t)[u(x,t)-1][1-u(x,t-\tau )/K],x\in (0,L),t\ge 0,\hfill \\ d{u}_x(0,t)-\alpha u(0,t)=-\alpha K,u(L,t)=K,t\ge 0,\hfill \end{array}\right.$$

(1)

where $u(x,t)$ denotes the density of the population at the location x and the time t, d ($\mathrm{units}\text{:}{\mathrm{km}}^2/\mathrm{day}$) denotes the diffusion rate, $\alpha$ ($\mathrm{units}\text{:}{\mathrm{km}}^2/\mathrm{day}$) denotes the advection rate, the parameter $K>1$ ($\mathrm{units}\text{:}\mathrm{individuals}$) represents the carrying capacity, the Allee threshold is rescaled to 1, L ($\mathrm{units}\text{:}\mathrm{km}$) denotes the region range and $\tau$ ($\mathrm{units}\text{:}\mathrm{days}$) represents the time-delayed effect of intraspecific competition on population growth. The boundary conditions are the modified No-flux/Hostile (NF/H) boundary conditions [14], these boundary conditions are commonly used in studying the distribution and migration of species in rivers.

In ecological systems, the stability and periodic oscillation of population sizes are crucial for the long-term persistence of populations. Bifurcation analysis is one of the classical methods for studying population oscillations, and numerous scholars have conducted relevant research in this field [15,16,17,18]. However, studies on the bifurcation theory of population models with advection and diffusion are relatively scarce. Most existing studies focus on abstract theoretical frameworks, and few have performed specific calculations of normal forms.

Recently, several studies have focused on the dynamics of advection-diffusion models [19,20]. Numerical evidence is provided for the occurrence of Hopf bifurcation in a competition model with diffusion and advection [19]. A rigorous analysis of spatially nonhomogeneous equilibrium solutions for a reaction-diffusion-advection model that evolves with nonlocal delay and nonlinear boundary conditions is presented in [20]. Unlike existing studies, this paper aims to theoretically investigate the Hopf bifurcation in the advection-diffusion model (1) and derive the normal form that determines the characteristics of the bifurcation.

Various analytical approaches are available for the study of advection-diffusion models. In our work, we draw support from the operator theory, observe that the eigenfunctions of the linear operator under consideration fail to form an orthogonal basis under the $L^2$ inner product. However, these eigenfunctions become orthogonal by introducing a suitably defined weighted inner product. We emphasize two points of this work: for one thing, we compute the normal forms in a delayed advection-diffusion model with a weighted inner product; for the other, Hopf bifurcation is proved both theoretically and numerically. Besides, the derivation of the normal form here can be extended to other advection-diffusion models with Robin boundary conditions.

The structure of this paper is as follows. Section 2 examines the stability of the positive steady state and the existence of Hopf bifurcations. The properties of the resulting periodic solutions are analyzed in Section 3. Finally, numerical simulations in Section 4 validate the theoretical findings.

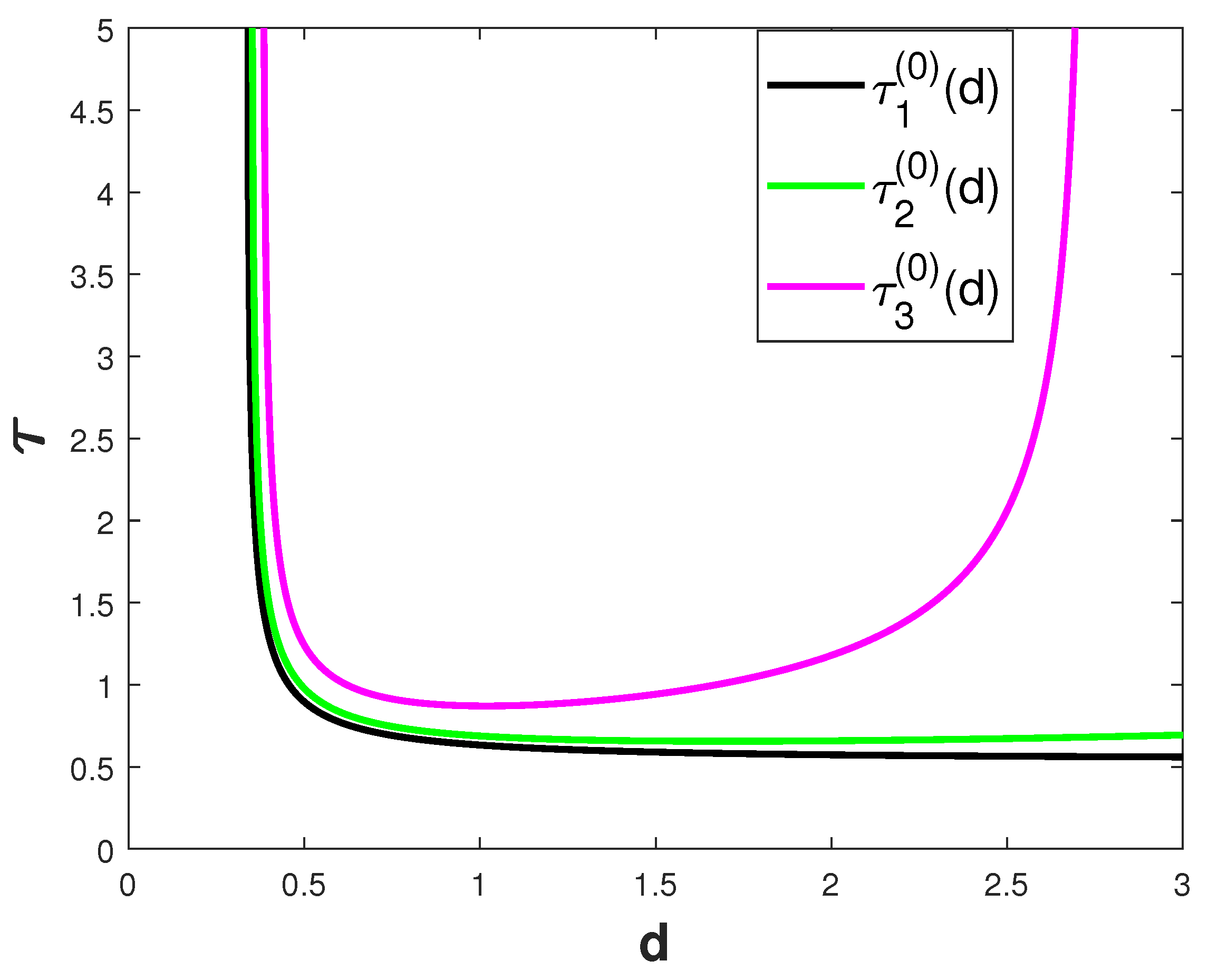
2. Stability and Bifurcations Analysis

To simplify notation, we define the following spaces:

$$X:=\left\{\varphi \in H^2(0,L)|d{\varphi }^{\prime }\left(0\right)-\alpha \varphi \left(0\right)=0,\varphi \left(L\right)=0\right\},$$

$Y=L^2(0,L)$, $C=C\left(\right[-\tau ,0],Y)$ and $\mathcal{C}=C\left(\right[-1,0],Y)$. Define the complexification of S be $S_{\mathbb{C}}:=S\oplus \mathrm{i}S=\{s_1+\mathrm{i}{s}_2\mid s_1,s_2\in S\}$.

By direct calculation, model (1) admits a constant steady state $u_{*}=K$. For convenience in calculations, let $\tilde{u}=u-K$, then (1) becomes

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial \tilde{u}(x,t)}{\partial t}}=d{\displaystyle \frac{{\partial }^2\tilde{u}(x,t)}{\partial x^2}}-\alpha {\displaystyle \frac{\partial \tilde{u}(x,t)}{\partial x}}-{\displaystyle \frac{r}{K}}[\tilde{u}(x,t)+K][\tilde{u}(x,t)+K-1]\tilde{u}(x,t-\tau ),x\in (0,L),t\ge 0,\hfill \\ d{\tilde{u}}_x(0,t)-\alpha \tilde{u}(0,t)=0,\tilde{u}(L,t)=0,t\ge 0.\hfill \end{array}\right.$$

(2)

Obviously, the dynamical properties of $u_{*}=K$ in (1) are equivalent to those of $\tilde{u}=0$ in (2). As to the stability of $\tilde{u}=0$ in (2), we will first analyze the distribution of eigenvalues in the linearized equation corresponding to the model (2) at the origin. In the rest, we remove the tilde on $\tilde{u}$ in (2) to simplify the symbols. For clarity, we rewrite Equation (2) as follows.

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial u(x,t)}{\partial t}}=d{\displaystyle \frac{{\partial }^{2}u(x,t)}{\partial x^2}}-\alpha {\displaystyle \frac{\partial u(x,t)}{\partial x}}-{\displaystyle \frac{r}{K}}[u(x,t)+K][u(x,t)+K-1]u(x,t-\tau ),x\in (0,L),t\ge 0,\hfill \\ d{u}_x(0,t)-\alpha u(0,t)=0,u(L,t)=0,t\ge 0.\hfill \end{array}\right.$$

(3)

For the well-posses of the solutions in system (3), we have the following theorem.

Theorem 1.  

For any initial function $u_0(x,\theta )\in X$ with $x\in [0,L]$ and $\theta \in [-\tau ,0]$, a unique solution $u(x,t)$ exists in system (3) for $x\in [0,L]$ and $t>0$.

Proof. 

First of all, we will prove that $T>0$ exists such that (3) has a unique solution $u(x,t)\in C^1([0,L]\times [0,T];Y)$. Define the linear operator $\tilde{A}:\mathcal{D}\left(\tilde{A}\right)\subset Y\to Y$ by $\tilde{A}v=d{v}^{″}-\alpha v^{\prime },$$\mathcal{D}\left(\tilde{A}\right)\subset X,$ then

$$\begin{array}{cc}\hfill \langle \tilde{A}v,v\rangle & ={\int }_0^L\tilde{A}v·v\mathrm{d}x\hfill \\ & ={\int }_0^L(d{v}^{″}-a{v}^{\prime })v\mathrm{d}x\hfill \\ & =-d{\int }_0^L{v}^{\prime 2}\mathrm{d}x-{\displaystyle \frac{1}{2}}a{v}^2\left(0\right)<0,\hfill \end{array}$$

which indicates that $\tilde{A}$ is dissipative. For $\tilde{\lambda }>0$ and $\tilde{f}\in Y$, the equation $\tilde{\lambda }v-\tilde{A}v=\tilde{f}$ has a unique solution $v\in \mathcal{D}\left(\tilde{A}\right)$ under the NF/H boundary condition. What’s more, $\tilde{A}$ is a densely defined closed operator, then $\tilde{A}$ generates a $C_0$-contraction semigroup $T\left(t\right)$ on Y.

Let $\eta \in Y$ with $\parallel \eta \parallel ={max}_{\theta \in [-\tau ,0]}\left|\eta \right(\theta \left)\right|$, and define

$$\tilde{F}\left(\eta \right)=-{\displaystyle \frac{r}{K}}[\eta (0,x)+K][\eta (0,x)+K-1]\eta (-\tau ,x).$$

For any $\tilde{M}>0$, ${\eta }_1,{\eta }_2\in Y$ with $\parallel {\eta }_i\parallel \le \tilde{M}$, we can prove that

$$|\tilde{F}\left({\eta }_1\right)-\tilde{F}\left({\eta }_2\right)|\le L\left(\tilde{M}\right)\parallel {\eta }_1-{\eta }_2\parallel ,$$

where $L\left(\tilde{M}\right)={\displaystyle \frac{r}{K}}[2{\tilde{M}}^2+2(2K-1)\tilde{M}+K(K-1)]$. Thus, $\tilde{F}$ is locally Lipschitz continuous on Y.

Now, system (3) is equivalent to the following abstract ODE:

$$\left\{\begin{array}{c}{\displaystyle \frac{d}{dt}}{\eta }_t=\tilde{A}{\eta }_t\left(\theta \right)+\tilde{F}\left({\eta }_t\right),\hfill \\ {\eta }_0\left(\theta \right)=u_0(x,\theta ).\hfill \end{array}\right.$$

(4)

Define a sequence $\{{\eta }_t^{\left(n\right)}$} as

$$\left\{\begin{array}{c}{\eta }_t^{\left(0\right)}={\eta }_0,\hfill \\ {\eta }_t^{\left(n\right)}=T\left(t\right){\eta }_0\left(0\right)+{\int }_0^{t}T(t-s)\tilde{F}\left({\eta }_s^{(n-1)}\right)ds,t\in [0,T].\hfill \end{array}\right.$$

For $T<{\displaystyle \frac{1}{L\left(\tilde{M}\right)}}$, the sequence $\{{\eta }_t^{\left(n\right)}$} converges uniformly in $C\left(\right[0,T];Y)$. Suppose that ${\eta }_t^{\left(a\right)}$ and ${\eta }_t^{\left(b\right)}$ are two solutions of (4), then

$$\parallel {\eta }_t^{\left(a\right)}-{\eta }_t^{\left(b\right)}\parallel \le L\left(\tilde{M}\right){\int }_0^t\parallel {\eta }_s^{\left(a\right)}-{\eta }_s^{\left(b\right)}\parallel ds.$$

By Gronwall’s Inequality, it follows that ${\eta }_t^{\left(a\right)}={\eta }_t^{\left(b\right)}$.

Therefore, Eq.(4) has a unique solution $\eta \in Y$, and thus system (3) has a unique solution $u(x,t)\in C^1([0,L]\times [0,T];Y)$. By expanding the local solution to $[0,\infty )$, We can finally conclude that the solution to system (3) with initial data compatible with the boundary conditions exists and is unique. □

In the following, we shall investigate the stability of constant steady state and the existence of Hopf bifurcation in system (3). The linearization of (3) around the origin reads

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial u(x,t)}{\partial t}}=d{\displaystyle \frac{{\partial }^{2}u(x,t)}{\partial x^2}}-\alpha {\displaystyle \frac{\partial u(x,t)}{\partial x}}-r(K-1)u(x,t-\tau ),x\in (0,L),t\ge 0,\hfill \\ d{u}_x(0,t)-\alpha u(0,t)=0,u(L,t)=0,t\ge 0.\hfill \end{array}\right.$$

(5)

By direct calculation, the eigenvalues of following problem

$$\left\{\begin{array}{c}d{\displaystyle \frac{{\partial }^2\phi \left(x\right)}{\partial x^2}}-\alpha {\displaystyle \frac{\partial \phi \left(x\right)}{\partial x}}=-\mu \phi \left(x\right),\hfill \\ d{\phi }^{\prime }\left(0\right)-\alpha \phi \left(0\right)=0,\phi \left(L\right)=0,\hfill \end{array}\right.$$

(6)

are given by ${\left\{{\mu }_n\right\}}_{n\ge 1}$ with ${\displaystyle \frac{{\alpha }^2}{4d}}<{\mu }_n<{\mu }_{n+1}$ and

$$tan{\displaystyle \frac{\sqrt{4d{\mu }_n-{\alpha }^2}}{2d}}L+{\displaystyle \frac{\sqrt{4d{\mu }_n-{\alpha }^2}}{\alpha }}=0,$$

(7)

The associated eigenfunction of ${\mu }_n$ is

$${\phi }_n=e^{{\displaystyle \frac{\alpha }{2d}}x}(\sqrt{4d{\mu }_n-{\alpha }^2}cos{\displaystyle \frac{\sqrt{4d{\mu }_n-{\alpha }^2}}{2d}}x+\alpha sin{\displaystyle \frac{\sqrt{4d{\mu }_n-{\alpha }^2}}{2d}}x),n=1,2,3,\dots$$

Then the characteristic equations of (5) are given by

$$\lambda +{\mu }_n+r(K-1)e^{-\lambda \tau }=0,n=1,2,\dots$$

(8)

When $\tau =0$, the roots of (8) take the form

$${\lambda }_n=-{\mu }_n-r(K-1),n=1,2,\dots$$

(9)

apparently, all roots of (8) are negative. Therefore, $u_{*}=K$ in system (1) is stable for $\tau =0$.

In the following, we will choose $\tau$ as the varying parameter to study the existence of Hopf bifurcation, that is, the conditions under which the system (1) can generate periodic solutions.

Let $\tau >0$ such that the characteristic Eq.(8) have a purely imaginary eigenvalue $\pm \mathrm{i}\omega (\omega >0)$, since $\mathrm{i}\omega$ is the root of Eq.(8), it follows that

$$\mathrm{i}\omega +{\mu }_n+r(K-1)(cos\omega \tau -\mathrm{i}sin\omega \tau )=0.$$

Decomposing the above equation into its real and imaginary components, we have

$$\left\{\begin{array}{c}r(K-1)cos\omega \tau =-{\mu }_n,\hfill \\ r(K-1)sin\omega \tau =\omega .\hfill \end{array}\right.$$

(10)

It follows from (10) that

$${\omega }^2+{\mu }_n^2=r^2{(K-1)}^2.$$

(11)

thus the roots of Eq.(11) are given by

$$\omega =\sqrt{r^2{(K-1)}^2-{\mu }_n^2}:={\omega }_n.$$

(12)

Clearly, (12) does not make sense when ${\mu }_n\ge r(K-1)$, which means that (8) has no purely imaginary roots if

$${\mu }_1\ge r(K-1).$$

(13)

Therefore, once if ${min}_{n\ge 1}\left\{{\mu }_n\right\}={\mu }_1<r(K-1)$, then there exists an integer $n_0>1$ such that (12) is well-defined for $1\le n<n_0$ and undefined for $n\ge n_0$. Since all roots of (8) with $\tau =0$ have negative real parts, and zero is not a root of Eq.(8), we can draw the following conclusion.

Theorem 2.  

For system (1), we can deduce that

(i) 

if ${\mu }_1\ge r(K-1)$, then the spectrum of Eq.(8) is confined to the left half of the complex plane for any any $\tau >0$;

(ii) 

if ${\mu }_1<r(K-1)$, an integer $n_0>1$ exists such that (12) is well-defined for $1\le n<n_0$ and undefined for $n\ge n_0$.

Now, we make the following assumption:

$$\left(H_1\right){\mu }_1<r(K-1).$$

Under hypothesis $\left(H_1\right)$, we define an integer $n_0>1$ with the following property: Eq.(12) is well-defined for all n satisfying $1\le n<n_0$, however, it is ill-defined for all $n\ge n_0$. From Eq.(10), we have

$${\tau }_n^{\left(j\right)}={\displaystyle \frac{1}{{\omega }_n}}arccos{\displaystyle \frac{-{\mu }_n}{r(K-1)}}+{\displaystyle \frac{2j\pi }{{\omega }_n}},n=1,2,\dots ,n_0-1,j=0,1,\dots$$

(14)

Indeed, since $cos({\omega }_n{\tau }_n^{(j)})<0$ and $sin({\omega }_n{\tau }_n^{\left(j\right)})>0$, it indicates that ${\omega }_n{\tau }_n^{\left(j\right)}\in ({\displaystyle \frac{\pi }{2}},\pi )$.

Lemma 1.  

Suppose $\left(H_1\right)$ holds. Then for all ${\tau }_n^{\left(j\right)}$ such that Eq.(12) is well-defined, we have

$$\underset{1\le n<n_0}{min}{\tau }_n^{\left(j\right)}={\tau }_1^{\left(0\right)}.$$

This lemma can be deduced from the monotone property of the arccosine function. For simplicity, we denote ${\tau }_{*}:={\tau }_1^{\left(0\right)}$ in the rest of this paper.

Through the analysis of the linearized system, we derived the characteristic equations (8). These equations clearly reveal the structural relationship among parameters in model (1): the diffusion coefficient d acts linearly on the eigenvalue through the additive term ${\mu }_n$, while the time delay $\tau$ is introduced nonlinearly via the multiplicative exponential term $e^{-\lambda \tau }$. These two terms are mathematically separated in structure, which fundamentally leads to the "decoupled" behavior between the diffusion coefficient d and the delay $\tau$ in triggering Hopf bifurcations.

Besides, since the expression for the Hopf bifurcation threshold ${\tau }_n^{\left(j\right)}$ includes ${\omega }_n$ and ${\mu }_n$, both of which are functions of the diffusion coefficient d, the Hopf bifurcation threshold ${\tau }_n^{\left(j\right)}$ is indeed dependent on d. The numerical results in the following Fig.Figure 1 in this paper directly reflect the relationship between d and ${\tau }_n^{\left(j\right)}$.

From Lemma 1, we can draw the following assertion.

Lemma 2.  

When considering the simultaneous variation of τ and d, system (1) exhbits no Hopf-Hopf or Turing-Hopf bifurcations.

By treating d as a variable and $\tau$ as a function, we consider the bifurcation curves ${\tau }_n^{\left(j\right)}\left(d\right)$. According to Lemma 1, it is impossible for two Hopf bifurcation curves to intersect on the boundary of the stable region in the $\tau -d$ plane. Bedides, zero is not a root of Eq.(8). Therefore, system (1) cannot undergo either Hopf-Hopf or Turing-Hopf bifurcations. This is illustrated in Figure 1.

It has been established that for $\tau ={\tau }_n^{\left(j\right)}$ (for $n=1,2,\dots ,n_0-1$, $j=0,1,\dots$), the values of $\pm \mathrm{i}{\omega }_n$ constitute two roots of Eq.(8). Define $\lambda \left(\tau \right)$ be a root of Eq.(8) that meets the conditions $Re\lambda \left({\tau }_n^{\left(j\right)}\right)=0$ and $Im\lambda \left({\tau }_n^{\left(j\right)}\right)={\omega }_n$, we can deduce the following lemma.

Lemma 3.  

Suppose $\left(H_1\right)$ holds. Then $Re{\lambda }^{\prime }\left({\tau }_n^{\left(j\right)}\right)>0$.

Proof. 

The substitution of $\lambda \left(\tau \right)$ into Eq.(8) is followed by performing the derivative with respect to $\tau$ on both sides, thereby obtaining

$${\lambda }^{\prime }+r(K-1)e^{-\lambda \tau }(-{\lambda }^{\prime }\tau -\lambda )=0,$$

thus

$${\left({\displaystyle \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }}\right)}^{-1}={\displaystyle \frac{1}{\lambda r(K-1)e^{-\lambda \tau }}}-{\displaystyle \frac{\tau }{\lambda }}.$$

When $\tau ={\tau }_n^{\left(j\right)}$, we know that $\lambda =\mathrm{i}{\omega }_n$, then

$$\begin{array}{cc}\hfill {\left.Re{\left({\displaystyle \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }}\right)}^{-1}\right|}_{\tau ={\tau }_{n,j}}& ={\left.Re\left[{\displaystyle \frac{1}{\lambda r(K-1)e^{-\lambda \tau }}}-{\displaystyle \frac{\tau }{\lambda }}\right]\right|}_{\tau ={\tau }_{n,j}}\hfill \\ & =Re{\left[{\displaystyle \frac{1}{-{\lambda }^2-\lambda {\mu }_n}}-{\displaystyle \frac{\tau }{\lambda }}]\right|}_{\lambda =\mathrm{i}{\omega }_{\mathrm{n}}}\hfill \\ & =Re{\left[{\displaystyle \frac{1}{{\omega }^2-\mathrm{i}\omega {\mu }_n}}]\right|}_{\lambda =\mathrm{i}{\omega }_{\mathrm{n}}}\hfill \\ & ={\displaystyle \frac{1}{{\omega }^2+{\mu }_n^2}}>0.\hfill \end{array}$$

Since

$$\mathrm{Sign}\left[{\left.Re\left({\displaystyle \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }}\right)\right|}_{\tau ={\tau }_{n,j}}\right]=\mathrm{Sign}\left[{\left.Re{\left({\displaystyle \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }}\right)}^{-1}\right|}_{\tau ={\tau }_{n,j}}\right]>0.$$

This completes the proof. □

The distribution of the roots of Eq.(8) is summarized as follows.

Lemma 4.  

Under assumption $\left(H_1\right)$, the roots of Eq.(8) all possess negative real parts for $\tau <{\tau }_{*}$. When $\tau ={\tau }_{*}$, a pair of purely imaginary roots $\pm i{\omega }_n$ emerges, while all others retain negative real parts. Once τ exceeds ${\tau }_{*}$, at least two roots acquire positive real parts.

Applying Lemmas 1-4, we have the following theorem on the dynamics of model (1).

Theorem 3.  

The stability of the $u_{*}=K$ depends on the parameters in system (1).

(i) 

If ${\mu }_1\ge r(K-1)$, $u_{*}=K$ possesses unconditional stability for all $\tau \ge 0$;

(ii) 

If ${\mu }_1<r(K-1)$, $u_{*}=K$ is stable for $\tau \in [0,{\tau }_{*})$ and unstable for $\tau >{\tau }_{*}$; Meanwhile, system (1) undergoes the Hopf bifurcation at $u_{*}=K$ when $\tau ={\tau }_n^{\left(j\right)},n=1,2,\dots ,n_0-1,j=0,1,2,\dots$

3. Property of Bifurcating Periodic Solutions

This section focuses on determining the Hopf bifurcation direction and the stability of the periodic solutions at ${\tau }_{*}$, employing the following variable transformation: $U\left(t\right)=u(·,t)-u_{*},s=\tau t,\tau ={\tau }_{*}+\mu$, Eq.(3) can be written as

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}U\left(t\right)}{\mathrm{d}s}}=& d{\tau }_{*}\Delta U\left(s\right)-\alpha {\tau }_{*}\nabla U\left(s\right)+L_1{U}_s+F(U_s,\mu ),\hfill \end{array}$$

(15)

with $U_s\in \mathcal{C}$,

$$\begin{array}{cc}\hfill L_1{U}_s=& -{\tau }_{*}r(K-1)U(s-1),\hfill \\ \hfill F(U_s,\mu )& =\mu \left[d\Delta U\left(s\right)-\alpha \nabla U\left(s\right)-r(K-1)U(s-1)\right]\hfill \\ & -({\tau }_{*}+\mu )\left[{\displaystyle \frac{r(2K-1)}{K}}U\left(s\right)U(s-1)+{\displaystyle \frac{r}{K}}{U}^2\left(s\right)U(s-1)\right].\hfill \end{array}$$

For better understanding, we will denote s as t from now on. As established in the previous section, a Hopf bifurcation occurs at the origin in system (3) when $\mu =0$. Furthermore, in this critical case, the characteristic equations admit a simple conjugate pair of purely imaginary roots, $\pm \mathrm{i}{\omega }_1{\tau }_{*}$. Specifically, aside from this conjugate pair, all other characteristic roots have negative real parts. The linearized equation of Eq.(15) for $\mu =0$ is

$${\displaystyle \frac{\mathrm{d}U\left(t\right)}{\mathrm{d}t}}=d{\tau }_{*}\Delta U\left(t\right)-\alpha {\tau }_{*}\nabla U\left(t\right)+L_1{U}_t.$$

(16)

Let ${\mathcal{A}}_0$ represents the infinitesimal generator corresponding to the solution semigroup of Eq.(16). Then we have

$${\mathcal{A}}_0\mathsf{\Psi }=\dot{\mathsf{\Psi }},$$

$$\mathcal{D}\left({\mathcal{A}}_0\right)=\left\{\mathsf{\Psi }\in {\mathcal{C}}_{\mathbb{C}}\cap {\mathcal{C}}_{\mathbb{C}}^1:\mathsf{\Psi }\left(0\right)\in X_{\mathbb{C}},\dot{\mathsf{\Psi }}\left(0\right)=d{\tau }_{*}\Delta \mathsf{\Psi }\left(0\right)-\alpha {\tau }_{*}\nabla \mathsf{\Psi }\left(0\right)-{\tau }_{*}r(K-1)\mathsf{\Psi }(-1)\right\},$$

where ${\mathcal{C}}_{\mathbb{C}}^1=C^1([-1,0],Y_{\mathbb{C}})$. Consequently, Eq.(15) can be expressed as:

$${\displaystyle \frac{\mathrm{d}{U}_t}{\mathrm{d}t}}={\mathcal{A}}_0{U}_t+X_{0}F(U_t,\mu ),$$

while $X_0\left(\theta \right)$ is the product of the Dirac function and the 2nd-order identity matrix, i.e. $X_0\left(\theta \right)=\delta \left(\theta \right)I_2$, $\theta \in [-1,0].$

The computation of normal forms requires the definition of a weighted inner product for the space $Y_{\mathbb{C}}$:

$${\langle u,v\rangle }_1={\int }_0^L{e}^{-{\displaystyle \frac{\alpha }{d}}x}\overline{u}\left(x\right)v\left(x\right)dx\mathrm{for}u,v\in Y_{\mathbb{C}}.$$

Here, the weight function is associated with the ratio of advective rate to diffusive rate. For $\alpha \ge 0$,

$$e^{-{\displaystyle \frac{\alpha }{d}}L}\langle u,v\rangle \le {\langle u,v\rangle }_1\le \langle u,v\rangle ,$$

and for $\alpha \le 0$,

$$\langle u,v\rangle \le {\langle u,v\rangle }_1\le e^{-{\displaystyle \frac{\alpha }{d}}L}\langle u,v\rangle .$$

Adopting the approach of [13], the formal duality $\langle \langle ·,·\rangle \rangle$ is established in $\mathcal{C}$ with

$$\langle \langle \psi ,\varphi \rangle \rangle ={\langle \psi \left(0\right),\varphi \left(0\right)\rangle }_1-{\tau }_{*}r(K-1){\int }_{-1}^0{\langle \psi (s+1),\varphi \left(s\right)\rangle }_1\mathrm{d}s.$$

(17)

for $\varphi \in {\mathcal{C}}_{\mathbb{C}}$ and $\psi \in {\mathcal{C}}_{\mathbb{C}}^{*}:=C([0,1],Y_{\mathbb{C}})$. We remark that ${\mathcal{A}}^{*}$ the formal adjoint operator of ${\mathcal{A}}_0$, if

$$\langle \langle {\mathcal{A}}^{*}\tilde{\mathsf{\Psi }},\mathsf{\Psi }\rangle \rangle =\langle \langle \tilde{\mathsf{\Psi }},{\mathcal{A}}_0\mathsf{\Psi }\rangle \rangle ,$$

for any $\mathsf{\Psi }\in \mathcal{D}\left({\mathcal{A}}_0\right)$ and $\tilde{\mathsf{\Psi }}\in \mathcal{D}\left({\mathcal{A}}^{*}\right)$.

Lemma 5.  

We define the formal adjoint operator ${\mathcal{A}}^{*}$ as

$${\mathcal{A}}^{*}\tilde{\mathsf{\Psi }}\left(s\right)=-\dot{\tilde{\mathsf{\Psi }}}\left(s\right),$$

with the domain

$$\mathcal{D}\left({\mathcal{A}}^{*}\right)=\left\{\tilde{\mathsf{\Psi }}\in {\mathcal{C}}_{\mathbb{C}}^{*}\cap {\left({\mathcal{C}}_{\mathbb{C}}^{*}\right)}^1:\tilde{\mathsf{\Psi }}\left(0\right)\in X_{\mathbb{C}},-\dot{\tilde{\mathsf{\Psi }}}\left(0\right)=d{\tau }_{*}\Delta \tilde{\mathsf{\Psi }}\left(0\right)-\alpha {\tau }_{*}\nabla \tilde{\mathsf{\Psi }}\left(0\right)-{\tau }_{*}r(K-1)\tilde{\mathsf{\Psi }}\left(1\right)\right\},$$

where ${\left({\mathcal{C}}_{\mathbb{C}}^{*}\right)}^1=C^1([0,1],Y_{\mathbb{C}})$.

Proof. 

For any $\tilde{\mathsf{\Psi }}$ in $\mathcal{D}\left({\mathcal{A}}^{*}\right)$ and $\mathsf{\Psi }$ in $\mathcal{D}\left({\mathcal{A}}_0\right)$, we have

$$\begin{array}{cc}\hfill \langle \langle \tilde{\mathsf{\Psi }},{\mathcal{A}}_0\mathsf{\Psi }\rangle \rangle & ={\langle \tilde{\mathsf{\Psi }}\left(0\right),\left({\mathcal{A}}_0\mathsf{\Psi }\right)\left(0\right)\rangle }_1-{\tau }_{*}r(K-1){\int }_{-1}^0{\langle \tilde{\mathsf{\Psi }}(s+1),\left({\mathcal{A}}_0\mathsf{\Psi }\right)\left(s\right)\rangle }_{1}ds\hfill \\ & ={\langle \tilde{\mathsf{\Psi }}\left(0\right),\dot{\mathsf{\Psi }}\left(0\right)\rangle }_1-{\tau }_{*}r(K-1){\int }_{-1}^0{\langle \tilde{\mathsf{\Psi }}(s+1),\dot{\mathsf{\Psi }}\left(s\right)\rangle }_{1}ds\hfill \\ & ={\langle \tilde{\mathsf{\Psi }}\left(0\right),d{\tau }_{*}\Delta \mathsf{\Psi }\left(0\right)-\alpha {\tau }_{*}\nabla \mathsf{\Psi }\left(0\right)-{\tau }_{*}r(K-1)\mathsf{\Psi }(-1)\rangle }_1\hfill \\ & -{\tau }_{*}r(K-1){\int }_{-1}^0{\langle \tilde{\mathsf{\Psi }}(s+1),\dot{\mathsf{\Psi }}\left(s\right)\rangle }_{1}ds\hfill \\ & ={\langle \tilde{\mathsf{\Psi }}\left(0\right),d{\tau }_{*}\Delta \mathsf{\Psi }\left(0\right)-\alpha {\tau }_{*}\nabla \mathsf{\Psi }\left(0\right)\rangle }_1-{\tau }_{*}r(K-1){\langle \tilde{\mathsf{\Psi }}\left(0\right),\mathsf{\Psi }(-1)\rangle }_1\hfill \\ & -{\tau }_{*}r(K-1){\int }_{-1}^0{\langle \tilde{\mathsf{\Psi }}(s+1),\dot{\mathsf{\Psi }}\left(s\right)\rangle }_{1}ds\hfill \\ & ={\langle \tilde{\mathsf{\Psi }}\left(0\right),d{\tau }_{*}\Delta \mathsf{\Psi }\left(0\right)-\alpha {\tau }_{*}\nabla \mathsf{\Psi }\left(0\right)\rangle }_1-{\tau }_{*}r(K-1){\langle \tilde{\mathsf{\Psi }}\left(0\right),\mathsf{\Psi }(-1)\rangle }_1\hfill \\ & -{\tau }_{*}r(K-1)\left[{\langle \tilde{\mathsf{\Psi }}(s+1),\mathsf{\Psi }\left(s\right)\rangle }_1\right]{|}_{-1}^0+{\tau }_{*}r(K-1){\int }_{-1}^0{\langle \dot{\tilde{\mathsf{\Psi }}}(s+1),\mathsf{\Psi }\left(s\right)\rangle }_{1}ds\hfill \\ & ={\langle d{\tau }_{*}\Delta \tilde{\mathsf{\Psi }}\left(0\right)-\alpha {\tau }_{*}\nabla \tilde{\mathsf{\Psi }}\left(0\right),\mathsf{\Psi }\left(0\right)\rangle }_1-{\tau }_{*}r(K-1){\langle \tilde{\mathsf{\Psi }}\left(1\right),\mathsf{\Psi }\left(0\right)\rangle }_1\hfill \\ & +{\tau }_{*}r(K-1){\int }_{-1}^0{\langle \dot{\tilde{\mathsf{\Psi }}}(s+1),\mathsf{\Psi }\left(s\right)\rangle }_{1}ds\hfill \\ & ={\langle -\dot{\tilde{\mathsf{\Psi }}}\left(0\right),\mathsf{\Psi }\left(0\right)\rangle }_1-{\tau }_{*}r(K-1){\int }_{-1}^0{\langle {\mathcal{A}}^{*}\tilde{\mathsf{\Psi }}(s+1),\mathsf{\Psi }\left(s\right)\rangle }_{1}ds\hfill \\ & =\langle \langle {\mathcal{A}}^{*}\tilde{\mathsf{\Psi }},\mathsf{\Psi }\rangle \rangle .\hfill \end{array}$$

This completes the proof. □

According to Lemma 4, the operator ${\mathcal{A}}_0$ posseses a unique pair of simple purely imaginary eigenvalues $\pm \mathrm{i}{\omega }_1{\tau }_{*}$, their corresponding eigenfunctions are ${\phi }_1{e}^{\mathrm{i}{\omega }_1{\tau }_{*}\theta }$ and ${\phi }_1{e}^{-\mathrm{i}{\omega }_1{\tau }_{*}\theta }$ for $\theta \in [-1,0]$. Similarly, ${\mathcal{A}}^{*}$ has a pair of eigenvalues $\pm \mathrm{i}{\omega }_1{\tau }_{*}$, the eigenfunctions are ${\phi }_1{e}^{\mathrm{i}{\omega }_1{\tau }_{*}s}$ and ${\phi }_1{e}^{\mathrm{i}{\omega }_1{\tau }_{*}s}$ for $s\in [0,1]$. Thus, $P_c=span\{p\left(\theta \right),\overline{p\left(\theta \right)}\}$ forms the center subspace of Eq.(15), with $p\left(\theta \right)$ defined as ${\phi }_1{e}^{\mathrm{i}{\omega }_1{\tau }_{*}\theta }$. Correspondly, $P^{*}$ forms the formal adjoint subspace of $P_c$ under the bilinear form (17), with $q\left(s\right)={\phi }_1{e}^{-\mathrm{i}{\omega }_1{\tau }_{*}s}$. Denote $\mathsf{\Phi }=(p\left(\theta \right),\overline{p(\theta }))$, $\mathsf{\Psi }={\displaystyle \frac{1}{M}}{(q\left(s\right),\overline{q\left(s\right)})}^T,$ where

$$M={\displaystyle \frac{L}{2}}\left[1-\tau r(K-1)e^{-\mathrm{i}{\omega }_1{\tau }_{*}}\right],$$

such that $\langle \langle \mathsf{\Psi },\mathsf{\Phi }\rangle \rangle =I_{2\times 2}$. Since the formulas for the properties of Hopf bifurcation are derived for $\mu =0$, we set $\mu =0$ in Eq.(15) to obtain the following center manifold:

$$c(z,\overline{z})=c_{20}\left(\theta \right){\displaystyle \frac{z^2}{2}}+c_{11}\left(\theta \right)z\overline{z}+c_{02}\left(\theta \right){\displaystyle \frac{{\overline{z}}^2}{2}}+{O\left(\right|z|}^3).$$

(18)

The solution semi-flow of Eq.(15), when restricted to the center manifold, is characterized by the following ODE:

$$U_t=\mathsf{\Phi }{(z\left(t\right),\overline{z}\left(t\right))}^T+c(z\left(t\right),\overline{z}\left(t\right)),$$

where $z\left(t\right)$ satisfies

$$\begin{array}{cc}\hfill \dot{z}\left(t\right)& ={\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\langle \langle q\left(s\right),U_t\rangle \rangle \hfill \\ & =\mathrm{i}{\omega }_1{\tau }_{*}z\left(t\right)+\frac{1}{M}{〈q\left(0\right),F\left(\mathsf{\Phi }{(z\left(t\right),\overline{z}\left(t\right))}^T+c(z\left(t\right),\overline{z}\left(t\right)),0\right)〉}_1.\hfill \end{array}$$

Denote $G(z,\overline{z})=\frac{1}{M}{〈q\left(0\right),F\left(\mathsf{\Phi }{(z\left(t\right),\overline{z}\left(t\right))}^T+c(z\left(t\right),\overline{z}\left(t\right)),0\right)〉}_1$, by direct calculation, we can obtain that

$$g(z,\overline{z})=G_{20}{\displaystyle \frac{z^2}{2}}+G_{11}z\overline{z}+G_{02}{\displaystyle \frac{{\overline{z}}^2}{2}}+G_{21}{\displaystyle \frac{z^2\overline{z}}{2}},$$

with

$$\begin{array}{cc}\hfill G_{20}=& -{\displaystyle \frac{2}{M}}·{\displaystyle \frac{r(2K-1){\tau }_{*}{e}^{-\mathrm{i}{\omega }_1{\tau }_{*}}}{K}}·{\int }_0^L{e}^{-{\displaystyle \frac{\alpha }{d}}x}{\phi }_1^3\left(x\right)dx,\hfill \\ \hfill G_{11}=& -{\displaystyle \frac{1}{M}}·{\displaystyle \frac{r(2K-1){\tau }_{*}(e^{-\mathrm{i}{\omega }_1{\tau }_{*}}+e^{\mathrm{i}{\omega }_1{\tau }_{*}})}{K}}{\int }_0^L{e}^{-{\displaystyle \frac{\alpha }{d}}x}{\phi }_1^3\left(x\right)dx,\hfill \\ \hfill G_{02}=& -{\displaystyle \frac{2}{M}}·{\displaystyle \frac{r(2K-1){\tau }_{*}{e}^{\mathrm{i}{\omega }_1{\tau }_{*}}}{K}}{\int }_0^L{e}^{-{\displaystyle \frac{\alpha }{d}}x}{\phi }_1^3\left(x\right)dx,\hfill \\ \hfill G_{21}=& -{\displaystyle \frac{2}{M}}·{\displaystyle \frac{r{\tau }_{*}}{K}}(2e^{-\mathrm{i}{\omega }_1{\tau }_{*}}+e^{\mathrm{i}{\omega }_1{\tau }_{*}}){\int }_0^L{e}^{-{\displaystyle \frac{\alpha }{d}}x}{\phi }_1^4\left(x\right)dx-{\displaystyle \frac{2}{M}}·{\displaystyle \frac{r(2K-1){\tau }_{*}}{K}}\times \hfill \\ \hfill & {\int }_0^L[{\displaystyle \frac{c_{20}(-1)}{2}}+c_{11}(-1)+{\displaystyle \frac{c_{20}\left(0\right)}{2}}{e}^{\mathrm{i}{\omega }_1{\tau }_{*}}+c_{11}\left(0\right)e^{-\mathrm{i}{\omega }_1{\tau }_{*}}]·e^{-{\displaystyle \frac{\alpha }{d}}x}{\phi }_1^3\left(x\right)dx,\hfill \end{array}$$

(19)

where $c_{20}\left(\theta \right)$ and $c_{11}\left(\theta \right)$ are to be determined. It should be noted that $c(z\left(t\right),\overline{z}\left(t\right))$ is governed by the equation:

$$\begin{array}{cc}\hfill \dot{c}& ={\mathcal{A}}_{0}c+X_{0}F(\mathsf{\Phi }{(z,\overline{z})}^T+c(z,\overline{z}),0)\hfill \\ & -\mathsf{\Phi }\langle \langle \mathsf{\Psi },X_{0}F({\mathsf{\Phi }}_I{(z,\overline{z})}^T+c(z,\overline{z}),0)\rangle \rangle \hfill \\ & ={\mathcal{A}}_{0}c+h_{20}{\displaystyle \frac{z^2}{2}}+h_{11}z\overline{z}+h_{02}{\displaystyle \frac{{\overline{z}}^2}{2}}+{O\left(\right|z|}^3),\hfill \end{array}$$

(20)

where the coefficients $h_{20},h_{11}$ and $h_{02}$ are determined from:

$$\begin{array}{cc}& X_{0}F(\mathsf{\Phi }{(z,\overline{z})}^T+c(z,\overline{z}),0)-\mathsf{\Phi }\langle \langle \mathsf{\Psi },X_{0}F(\mathsf{\Phi }{(z,\overline{z})}^T+c(z,\overline{z}),0)\rangle \rangle \hfill \\ & =h_{20}{\displaystyle \frac{z^2}{2}}+h_{11}z\overline{z}+h_{02}{\displaystyle \frac{{\overline{z}}^2}{2}}+{O\left(\right|z|}^3).\hfill \end{array}$$

The application of the chain rule shows that c also satisfies

$$\dot{c}={\displaystyle \frac{\partial c(z,\overline{z})}{\partial z}}\dot{z}+{\displaystyle \frac{\partial c(z,\overline{z})}{\partial \overline{z}}}\dot{\overline{z}}.$$

Thus,

$$\left\{\begin{array}{c}(2\mathrm{i}{\omega }_1{\tau }_{*}-{\mathcal{A}}_0)c_{20}=h_{20},\hfill \\ -{\mathcal{A}}_0{c}_{11}=h_{11}.\hfill \end{array}\right.$$

(21)

For $\theta \in [-1,0)$, the expressions for $h_{20}$ and $h_{21}$ are given by

$$\begin{array}{cc}\hfill & h_{20}\left(\theta \right)=-(G_{20}p\left(\theta \right)+{\overline{G}}_{02}\overline{p}\left(\theta \right)),\hfill \\ \hfill & h_{11}\left(\theta \right)=-(G_{11}p\left(\theta \right)+{\overline{G}}_{11}\overline{p}\left(\theta \right)).\hfill \end{array}$$

(22)

On the basis of Eqs.(21) and (22), $c_{20}$ and $c_{11}$ are given by the following forms:

$$c_{11}\left(\theta \right)={\displaystyle \frac{\mathrm{i}{\overline{G}}_{11}}{{\omega }_1{\tau }_{*}}}\overline{p}\left(\theta \right)-{\displaystyle \frac{\mathrm{i}{G}_{11}}{{\omega }_1{\tau }_{*}}}p\left(\theta \right)+F.$$

(23)

$$c_{20}\left(\theta \right)={\displaystyle \frac{\mathrm{i}{\overline{G}}_{02}}{3{\omega }_1{\tau }_{*}}}\overline{p}\left(\theta \right)+{\displaystyle \frac{\mathrm{i}{G}_{20}}{{\omega }_1{\tau }_{*}}}p\left(\theta \right)+E{e}^{2\mathrm{i}{\omega }_1{\tau }_{*}\theta },$$

(24)

Since

$$h_{20}\left(0\right)=-\left[{\overline{G}}_{02}\overline{p}\left(0\right)+G_{20}p\left(0\right)\right]-2{\tau }_{*}{e}^{-\mathrm{i}{\omega }_1{\tau }_{*}}r(K-1){\phi }_1\left(x\right),$$

from Eq.(20) and (21) with $\theta =0$, we know that

$$(2\mathrm{i}{\omega }_1{\tau }_{*}-{\mathcal{A}}_0)E{e}^{2\mathrm{i}{\omega }_1{\tau }_{*}\theta }{|}_{\theta =0}=-2{\tau }_{*}{e}^{-\mathrm{i}{\omega }_1{\tau }_{*}}r(K-1){\phi }_1\left(x\right),$$

that is,

$$\Delta (2\mathrm{i}{\omega }_1,{\tau }_{*})E=2{\tau }_{*}{e}^{-\mathrm{i}{\omega }_1{\tau }_{*}}r(K-1){\phi }_1\left(x\right).$$

Then we can obtain

$$E=2r(K-1)e^{-\mathrm{i}{\omega }_1{\tau }_{*}}\Delta {(2\mathrm{i}{\omega }_1,{\tau }_{*})}^{-1}{\phi }_1\left(x\right).$$

(25)

Similarly, we can get

$$F=r(K-1)\left(e^{-\mathrm{i}{\omega }_1{\tau }_{*}}+e^{\mathrm{i}{\omega }_1{\tau }_{*}}\right)\Delta {(0,{\tau }_{*})}^{-1}{\phi }_1\left(x\right).$$

(26)

In Eq.(25) and (26), the linear operator $\Delta (\mu ,\tau )$ is defined as follows:

$$\Delta (\mu ,\tau )\phi :=d\Delta \phi -\alpha {\phi }_x-r(k-1)\phi e^{\mu \tau }-\mu \phi .$$

Then two key values ${\mu }_2$ and ${\beta }_2$ are calculated as follows.

$$\begin{array}{cc}\hfill & c_2\left(0\right)={\displaystyle \frac{G_{21}}{2}}+{\displaystyle \frac{1}{2{\omega }_1{\tau }_{*}}}\left(\mathrm{i}{G}_{11}{g}_{20}-2\mathrm{i}{\left|G_{11}\right|}^2-\mathrm{i}{\displaystyle \frac{|G_{02}{|}^2}{3}}\right),\hfill \\ \hfill & {\nu }_2=-{\displaystyle \frac{\mathrm{Re}\left(c_2\left(0\right)\right)}{\mathrm{Re}\left({\lambda }^{\prime }\left({\tau }_{*}\right)\right)}},\hfill \\ \hfill & {\beta }_2=2\mathrm{Re}\left(c_2\left(0\right)\right).\hfill \end{array}$$

(27)

It is well-established that the sign of ${\nu }_2$ determines the bifurcation direction: ${\nu }_2>0(<0)$ corresponds to a forward (backward) bifurcation. The resulting periodic solutions are orbitally stable if ${\beta }_2<0$, and unstable if ${\beta }_2>0$. These solutions emerge when $\tau >{\tau }_{*}$ for the forward case and $\tau <{\tau }_{*}$ for the backward case.

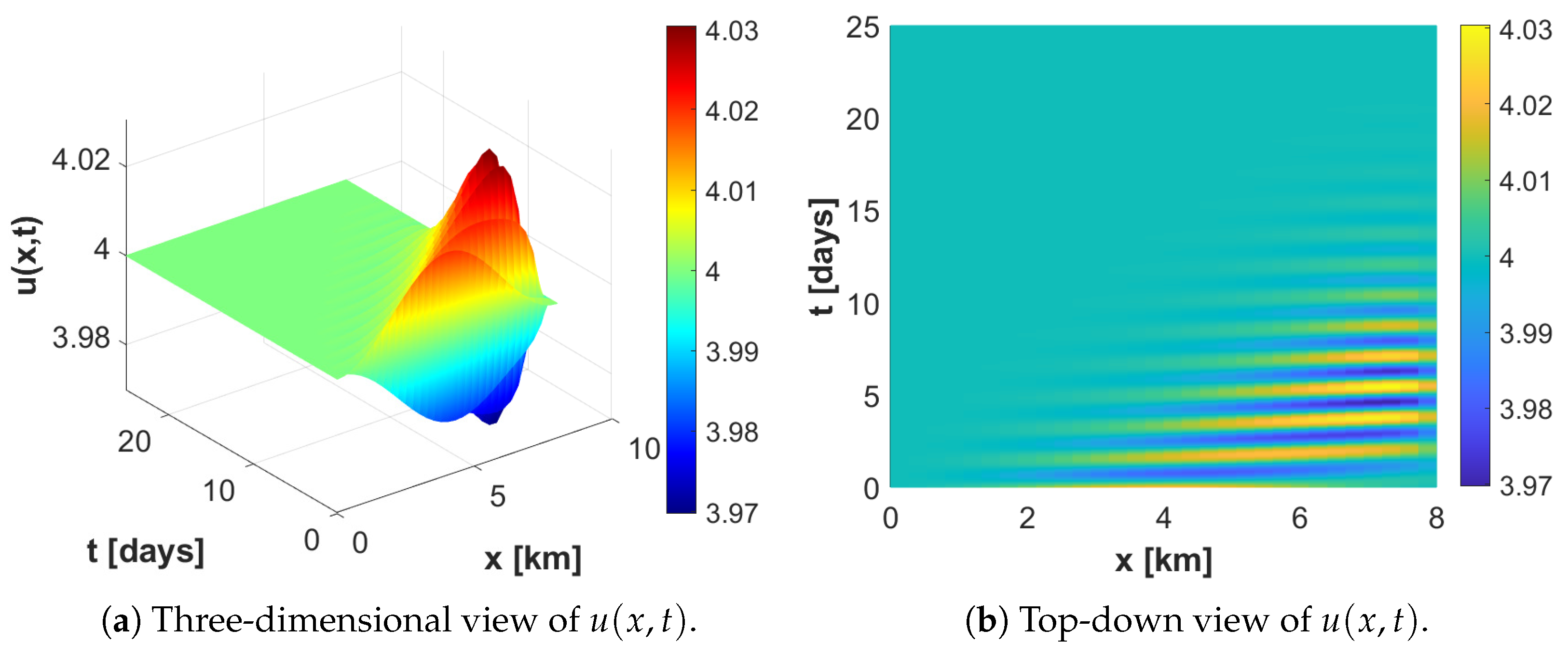
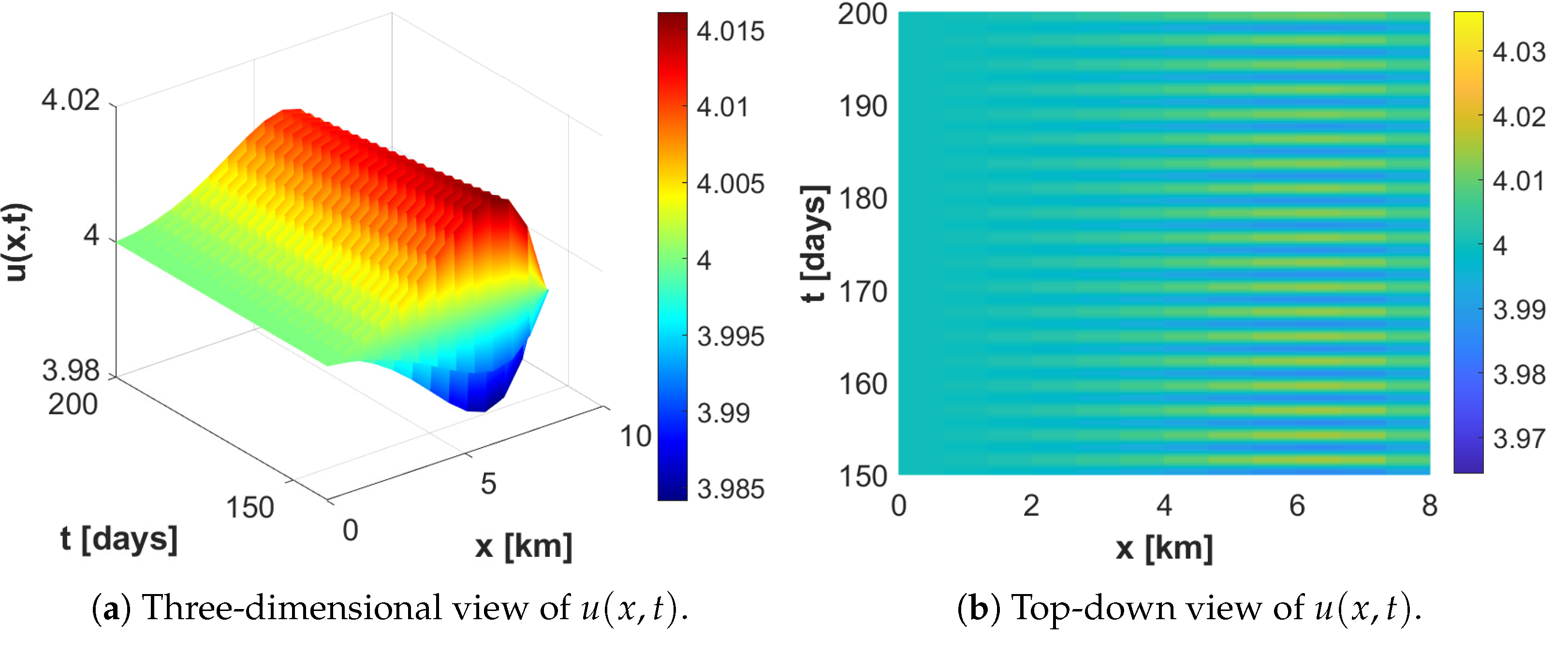
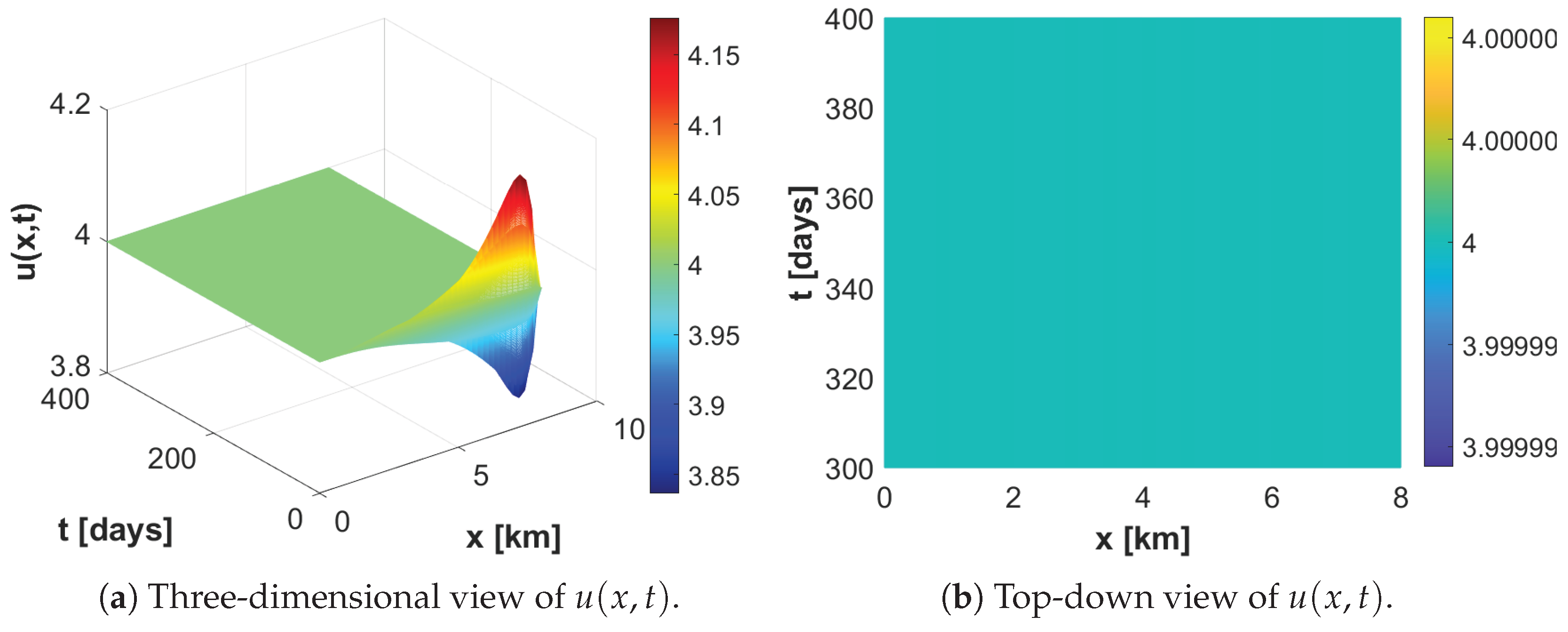
4. Numerical Simulations

To validate the theoretical results, numerical computations are carried out in this section. The parameters in model (1) are assigned as follows:

$$\left(\mathbf{P}\mathbf{1}\right)r=1,K=4,d=0.5,\alpha =2,L=8.$$

According to (7) we can get that

$${\mu }_1\approx 2.0684,{\mu }_2\approx 2.2748,{\mu }_3\approx 2.6211,{\mu }_4\approx 3.1117,\dots$$

In addition, we obtain ${\mu }_1<r(K-1)$, then $\left(H_1\right)$ holds, and $n_0=4$ from Theorem 2. Thus we have

$$\begin{array}{cc}& {\omega }_1\approx 2.1792,{\omega }_2\approx 1.9559,{\omega }_3\approx 1.4594,\hfill \\ & {\tau }_1^{\left(0\right)}\approx 1.0729,{\tau }_2^{\left(0\right)}\approx 1.2431,{\tau }_3^{\left(0\right)}\approx 1.8045.\hfill \end{array}$$

Clearly, ${\tau }_{*}={\tau }_1^{\left(0\right)}\approx 1.0729.$ Furthermore, by using the formula deduced in (27), we compute

$$\begin{array}{c}\hfill c_2\left(0\right)=(-1.2150+4.3080\mathrm{i})\times {10}^{14},{\nu }_2=2.0687\times {10}^{13},{\beta }_2=-2.4299\times {10}^{14}.\end{array}$$

By Theorem 3, we have the following conclusion: under the parameters chosen in (P1), the positive constant steady state $u_{*}=K$ is asymptotically stable for $\tau \in [0,1.0729)$, see Figure 2. Meanwhile, the model (1) undergoes a Hopf bifurcation at $u=K$ when $\tau ={\tau }_{*}\approx 1.0729$. Since ${\nu }_2>0$ and ${\beta }_2<0$, the direction of the Hopf bifurcation is forward, that is, the periodic solutions exist for $\tau >{\tau }_{*}$, and the bifurcating periodic solutions are orbitally asymptotically stable when $\tau$ is greater than ${\tau }_{*}$ and sufficiently close to ${\tau }_{*}$, see Figure 3.

When parameters in model (1) are chosen as:

$$\left(\mathbf{P}\mathbf{2}\right)r=1,K=4,d=0.5,\alpha =4,L=8.$$

we can get that ${\mu }_1\approx 8.0684<r(K-1)$, according to Theorem 2, $u=K$ is asymptotically stable for $\tau >0$, see Figure 4.

5. Conclusion

This paper studies a delayed diffusion-advection model for population dynamics, which incorporates the strong Allee effect. The model considers a bounded spatial region $(0,L)$ and the constant boundary values. This study examines the effect of the advection rate on the stability of constant steady state within the model. The results indicate that the constant steady state remains locally stable at larger advection rates, whereas it becomes unstable when the advection rate is sufficiently small. Under the condition of a smaller advection rate, the existence of Hopf bifurcations is examined by adopting delay as the bifurcation parameter.

To investigate the dynamical properties of the model near the Hopf singularity, we calculate the normal form on the center manifold near the Hopf singularity and provide the detailed calculation formulas. During the derivation of the normal form, a weighted inner product is crucial for constructing the orthonormal basis in the space. Furthermore, a defined formal duality is also important for constructing the formal adjoint operator.

The normal form theory for bifurcation analysis developed in this work can be extended to advection-diffusion models with other types of boundary conditions. The strong Allee effect model usually exhibits rich dynamical behavior. In our model, constant boundary conditions are adopted, which can be interpreted as a human intervention strategy for population management: when the population density at the boundary is low, it is replenished; when it becomes excessively high, it is reduced. Finally, numerical simulations are conducted to validate the theoretical results.

This work also suggests several promising directions for future research. By introducing environmental noise terms into the advection-diffusion equations under study, the properties of stochastic equation can be investigated. When considering interactions such as interspecific competition, predation, or mutualism would extend the research from a one-dimensional advection-diffusion model to a higher-dimensional framework. What’s more, replacing simple discrete delays with non-local or distributed delays in the model would more realistically capture the feedback effects in biological processes, which is expected to reveal richer bifurcation structures and spatiotemporal dynamics in the system.