Optimization of Active Power Supply in an Electrical Distribution System through the Optimal Integration of Renewable Energy Sources

1. Introduction

Over the last decades, the sustained growth of electricity demand, together with global concerns about energy sustainability and carbon-emission reduction, has driven the modernization of power distribution systems toward smarter, more flexible, and resilient schemes [1,2]. In this context, the integration of distributed energy resources (DER), such as photovoltaic (PV) systems and wind turbines (WT), has become an essential component of the transition toward sustainable electric grids [3,4]. However, the intermittent and uncertain nature of these renewable sources introduces new technical challenges related to voltage stability, energy losses, and optimal power-flow management in radial distribution networks [5,6].

The incorporation of demand-side response (DSR, Demand-Side Response) mechanisms under real-time pricing (Real-Time Pricing, RTP) schemes emerges as an effective alternative to balance generation and consumption, fostering the active participation of end users in power-system operation [7,8]. This approach enables shifting or curtailing consumption according to price signals, thereby reducing demand peaks and improving the utilization of local renewable generation. When combined with distributed resources and inverter-based control systems, DSR enhances energy efficiency and the operational stability of the system [9].

Regarding distribution-network modeling, radial systems exhibit particular characteristics that differentiate them from transmission grids. In such configurations, power flow can be represented through the Branch-Flow or DistFlow approach, which realistically captures resistive losses, current limits, and voltage variations [10,11]. This model provides the foundation for formulating optimal power flow (Optimal Power Flow, OPF) problems in medium-voltage networks, where nonlinear constraints are addressed through convex relaxations or high-efficiency metaheuristics.

The application of metaheuristic techniques has become a robust strategy for solving non-convex planning and operation problems in power systems. Among them, nature-inspired algorithms such as the Whale Optimization Algorithm (WOA) have shown an excellent balance between exploration and exploitation of the search space [12]. Recent studies have proposed improved versions of WOA by incorporating adaptive perturbation strategies, dynamic convergence coefficients, and penalty mechanisms for constraint handling [13], thereby increasing its performance in power-system applications [14,15].

Within this framework, the present work proposes an integral methodology for optimizing active power supply in radial distribution systems through the coordinated integration of photovoltaic sources, wind turbines, and demand response under dynamic pricing schemes. The problem formulation considers both the technical aspects of the network (losses, voltage limits, thermal capacity) and the economic aspects associated with operating cost and the variability of renewable sources. The problem is solved using an improved whale-based optimization algorithm (Improved Whale Optimization Algorithm, I-WaOA), which ensures efficient convergence toward feasible and stable solutions.

The obtained results highlight the benefits of optimal planning and coordinated operation of distributed resources and flexible demand, emphasizing their positive impact on loss reduction, voltage regulation, and overall system efficiency. Moreover, the proposed methodology contributes to the evolution of distribution networks toward intelligent operational models that promote sustainability and energy security.

Finally, the remainder of this paper is organized as follows: Section 2 details the mathematical formulation, renewable-resource models, and the proposed optimization procedure. Section 3 describes the case study based on the IEEE 118-bus network and the considered scenarios. The numerical results are presented and analyzed in the subsequent section, while the Discussion and Conclusions sections synthesize the main contributions and outline possible directions for future work.

2. Materials and Methods

This section describes in detail the proposed methodology for optimizing active power supply in a large-scale electrical distribution system through the coordinated integration of renewable sources and demand response strategies. As a case study, the IEEE 118-bus system is adopted, which is widely referenced in the technical literature due to its usefulness for validating optimization algorithms and analyzing stability and efficiency in distribution networks.

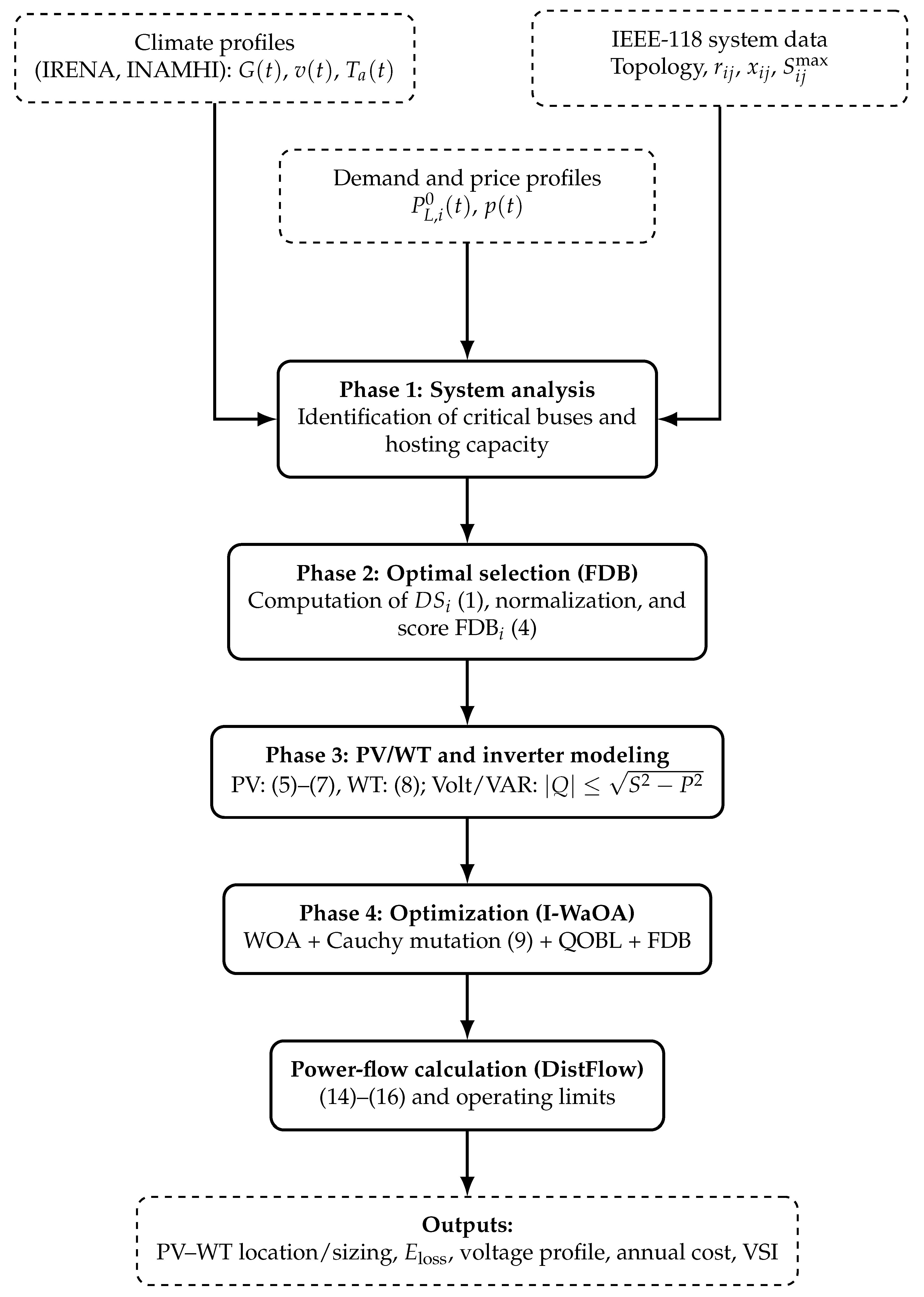
The methodological approach combines physical modeling, probabilistic analysis, and computational intelligence techniques. Figure 1 shows the overall sequence of stages that constitute the proposed simulation and optimization procedure.

2.1. Phase 1: Analysis of the IEEE-118 Distribution System

The IEEE-118 system is characterized by its radial topology and a representative diversity of loads, lines, and buses. The following aspects were analyzed:

• Electric demand: historical and projected hourly profiles of active load were processed.
• Distributed generation hosting capacity: the renewable integration limit was evaluated considering thermal and voltage constraints [16]
• Climate profiles: irradiance $G\left(t\right)$, ambient temperature $T_a\left(t\right)$, and wind speed $v\left(t\right)$ were obtained from the IRENA and INAMHI databases.

2.2. Phase 2: Optimal Site Selection Using FDB

The Fitness–Distance Balance (FDB) method balances solution quality and its distance to the best-known solution. The distance between node i and the optimal location is computed as:

$$D{S}_i=\sqrt{\sum _{d=1}^n{(x_d^i-x_d^{\mathrm{best}})}^2}.$$

(1)

The score is normalized and combined as follows:

$$\begin{array}{cc}\hfill {\mathrm{nDS}}_i& ={\displaystyle \frac{D{S}_i-min\left(DS\right)}{max\left(DS\right)-min\left(DS\right)}},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\mathrm{nF}}_i& ={\displaystyle \frac{F_i-min\left(F\right)}{max\left(F\right)-min\left(F\right)}},\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathrm{FDB}}_i& =\alpha \left(t\right){\mathrm{nF}}_i+[1-\alpha \left(t\right)]{\mathrm{nDS}}_i,\hfill \end{array}$$

(4)

where $\alpha \left(t\right)=0.5(1+t/T_{max})$. This procedure made it possible to select the nodes with the best combination of solar resource and proximity to load centers.

2.3. Phase 3: Renewable Generation Modeling

Photovoltaic (PV) generation:

The produced power is estimated by:

$$P_{\mathrm{PV}}\left(t\right)=A_{\mathrm{PV}}{\eta }_{\mathrm{PV}}\left(t\right)G\left(t\right),$$

(5)

where efficiency depends on cell temperature:

$${\eta }_{\mathrm{PV}}\left(t\right)={\eta }_r[1-{\beta }_T(T_c\left(t\right)-T_r)],$$

(6)

and the cell temperature is approximated as:

$$T_c\left(t\right)=T_a\left(t\right)+{\displaystyle \frac{I_s\left(t\right)(T_s-20)}{800}}$$

(7)

Wind turbine (WT) generation:

The aerodynamic power model is expressed as:

$$P_{\mathrm{WT}}\left(v\right)=\left\{\begin{array}{cc}0,\hfill & v<v_i\mathrm{or}v>v_o,\hfill \\ P_r\left({\displaystyle \frac{v^3-v_i^3}{v_r^3-v_i^3}}\right),\hfill & v_i\le v<v_r,\hfill \\ P_r,\hfill & v_r\le v\le v_o.\hfill \end{array}\right.$$

(8)

The adopted nominal values were $v_i=2.5$ m/s, $v_r=15$ m/s, and $v_o=25$ m/s.

2.4. Phase 4: Optimization Using the I-WaOA Algorithm

The Improved Whale Optimization Algorithm (I-WaOA) aims to minimize energy costs and active power losses. The algorithm incorporates:

• Cauchy Mutation (CM):

  $$X_i^{t+1}=X_i^t+{\alpha }_c\mathrm{Cauchy}(0,1)(X_i^t-X^{\mathrm{best}}),$$

  (9)
  to escape local optima.
• Fitness and Distance Balance (FDB): improves population diversity using (1)–(4).
• Quasi-Oppositional-Based Learning (QOBL): generates opposite solutions to accelerate global convergence.

The iterative process updates positions according to the adaptive WOA coefficients A and C, with dynamic penalization:

$$f^{\prime }\left(x\right)=f\left(x\right)+\rho \sum _{i}max{(0,g_i\left(x\right))}^2,$$

(10)

where $g_i\left(x\right)$ are the operating constraints.

2.5. Electrical Model of the System

Power flow is modeled using the DistFlow equations [10,11]:

$$\begin{array}{cc}\hfill P_{ij}& =P_{L,j}-P_{G,j}+\sum _{k\in \Omega \left(j\right)}{P}_{jk}+R_{ij}{\displaystyle \frac{P_{ij}^2+Q_{ij}^2}{V_i^2}},\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill Q_{ij}& =Q_{L,j}-Q_{G,j}+\sum _{k\in \Omega \left(j\right)}{Q}_{jk}+X_{ij}{\displaystyle \frac{P_{ij}^2+Q_{ij}^2}{V_i^2}},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill V_j^2& =V_i^2-2(R_{ij}{P}_{ij}+X_{ij}{Q}_{ij})+(R_{ij}^2+X_{ij}^2){\displaystyle \frac{P_{ij}^2+Q_{ij}^2}{V_i^2}}.\hfill \end{array}$$

(13)

Operating constraints are expressed as:

$$\begin{array}{cc}\hfill V_{min}& \le V_i\le V_{max},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill S_{ij}& =\sqrt{P_{ij}^2+Q_{ij}^2}\le S_{ij}^{max},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \sum _i(P_{\mathrm{PV},i}+P_{\mathrm{WT},i})& \ge \sum _i{P}_{L,i}.\hfill \end{array}$$

(16)

2.6. Objective Function and Operating Costs

The objective function weights losses, voltage stability, and energy costs:

$$F={\epsilon }_1{C}_{\mathrm{energ}í\mathrm{a}}+{\epsilon }_2\Delta P_{\mathrm{loss}}+{\epsilon }_3{\Phi }_V,$$

(17)

where annual costs are expressed as:

$$\begin{array}{cc}\hfill C_{\mathrm{Grid}}& =365\sum _{h=1}^{24}{P}_{\mathrm{Grid}}\left(h\right)U_{\mathrm{Grid}}\left(h\right),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill C_{\mathrm{Loss}}& =365\sum _{h=1}^{24}{U}_{\mathrm{Loss}}{P}_{\mathrm{T},\mathrm{loss}}\left(h\right),\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill C_{\mathrm{PV}}& =C_{\mathrm{PV},\mathrm{inst}}+C_{\mathrm{PV},\mathrm{O}\&\mathrm{M}},C_{\mathrm{WT}}=C_{\mathrm{WT},\mathrm{inst}}+C_{\mathrm{WT},\mathrm{O}\&\mathrm{M}},\hfill \end{array}$$

(20)

with:

$$C_{\mathrm{inst}}=\mathrm{CRF}(\beta ,N_P)U_{\mathrm{unit}}{P}_{\mathrm{rated}},\mathrm{CRF}={\displaystyle \frac{\beta {(1+\beta )}^{N_P}}{{(1+\beta )}^{N_P}-1}}.$$

(21)

2.7. Probabilistic Uncertainty Models

Random variables (irradiance, wind, temperature, demand, and prices) are represented through the following distributions:

$$\begin{array}{cc}\hfill f_G\left(g\right)& ={\displaystyle \frac{g^{\alpha -1}{(1-g)}^{\beta -1}}{B(\alpha ,\beta )}},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill f_v\left(v\right)& ={\displaystyle \frac{k}{c}}{\left({\displaystyle \frac{v}{c}}\right)}^{k-1}{e}^{-{(v/c)}^k},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill f_x\left(x\right)& ={\displaystyle \frac{1}{{\sigma }_x\sqrt{2\pi }}}{e}^{-{\displaystyle \frac{{(x-{\mu }_x)}^2}{2{\sigma }_x^2}}}.\hfill \end{array}$$

(24)

2.8. Performance Indices

System technical performance is evaluated using:

$$\begin{array}{cc}\hfill VD& =\sum _{h=1}^{24}\sum _{k=1}^{NB}|V_k-1|,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill VS{I}_k& =|V_k{|}^4-4(P_k{X}_{km}-Q_k{R}_{km}){\left|V_k\right|}^2-4(P_k{X}_{km}+Q_k{R}_{km}),\hfill \end{array}$$

(26)

where $VD$ measures total voltage deviation and $VS{I}_k$ is the stability index at each bus.

2.9. Table of Symbols

Table 1. Main symbols and parameters used in the proposed model.

Symbol	Units	Description
$P_{\mathrm{rated},\mathrm{PV}}$	kW	Rated power of the photovoltaic system
$C_{\mathrm{WT},\mathrm{inst}}$	$/kW	Installation cost of the wind turbine
$G\left(t\right)$	W/m2	Solar irradiance at time t
${\eta }_{\mathrm{PV}}$	–	Photovoltaic panel efficiency
$A_{\mathrm{PV}}$	m2	Photovoltaic module area
$P_{\mathrm{WT}}\left(t\right)$	kW	Power generated by the wind turbine
$v\left(t\right)$	m/s	Wind speed
$C_p$	–	Wind turbine power coefficient
R	m	Blade radius
$P_{\mathrm{demand}}\left(t\right)$	kW	Power demand
$C_{\mathrm{energy}}\left(t\right)$	$/kWh	Unit energy cost
${\epsilon }_{1,2,3}$	–	Objective-function weights
$V_i$	p.u.	Voltage at bus i
$\Delta P_{\mathrm{loss}}$	kW	Active power losses
$\alpha$	–	Demand elasticity
$VD$	p.u.	Voltage deviation
$VS{I}_k$	–	Stability index at bus k

Table 1. Main symbols and parameters used in the proposed model.

Symbol	Units	Description
$P_{\mathrm{rated},\mathrm{PV}}$	kW	Rated power of the photovoltaic system
$C_{\mathrm{WT},\mathrm{inst}}$	$/kW	Installation cost of the wind turbine
$G\left(t\right)$	W/m2	Solar irradiance at time t
${\eta }_{\mathrm{PV}}$	–	Photovoltaic panel efficiency
$A_{\mathrm{PV}}$	m2	Photovoltaic module area
$P_{\mathrm{WT}}\left(t\right)$	kW	Power generated by the wind turbine
$v\left(t\right)$	m/s	Wind speed
$C_p$	–	Wind turbine power coefficient
R	m	Blade radius
$P_{\mathrm{demand}}\left(t\right)$	kW	Power demand
$C_{\mathrm{energy}}\left(t\right)$	$/kWh	Unit energy cost
${\epsilon }_{1,2,3}$	–	Objective-function weights
$V_i$	p.u.	Voltage at bus i
$\Delta P_{\mathrm{loss}}$	kW	Active power losses
$\alpha$	–	Demand elasticity
$VD$	p.u.	Voltage deviation
$VS{I}_k$	–	Stability index at bus k

2.10. Computational Implementation

The entire methodology was implemented in Python 3.12. Power-flow calculations were carried out using the DistFlow model of the IEEE-118 system, and the optimization routines were executed with the I-WaOA algorithm. Climate data were obtained from the IRENA Global Atlas and INAMHI, while the validation of results considered technical indicators ($VD$, $VSI$, losses) and economic indicators (operating and installation costs).

—

3. Case Study: IEEE 118-Bus Distribution Network

In this work, a distribution network derived from the IEEE 118-bus test system is adopted as the case study. This system is widely used in the literature to evaluate advanced operation and planning strategies in medium- and high-voltage networks. The system is modeled as an extended radial distribution network composed of load buses, generation buses, transformers, and distribution lines, which enables a realistic representation of power flows, losses, and voltage constraints under different operating scenarios with high penetration of renewable sources and demand response programs.

The radial topology of the system facilitates the analysis of power-flow paths and loss locations, while also reflecting the typical structure of modern distribution feeders that integrate renewable-based distributed generation (DG). For this study, the network is operated at a nominal voltage level $V_{\mathrm{base}}$ consistent with the original IEEE 118 specification, and an aggregated peak demand of approximately $2.4\mathrm{MW}$ distributed among the load buses is considered. On this basis, the contribution of photovoltaic generation (PV), wind generation (WT), and demand-side response (DSR) is evaluated.

3.1. IEEE 118-Bus Distribution Network Model

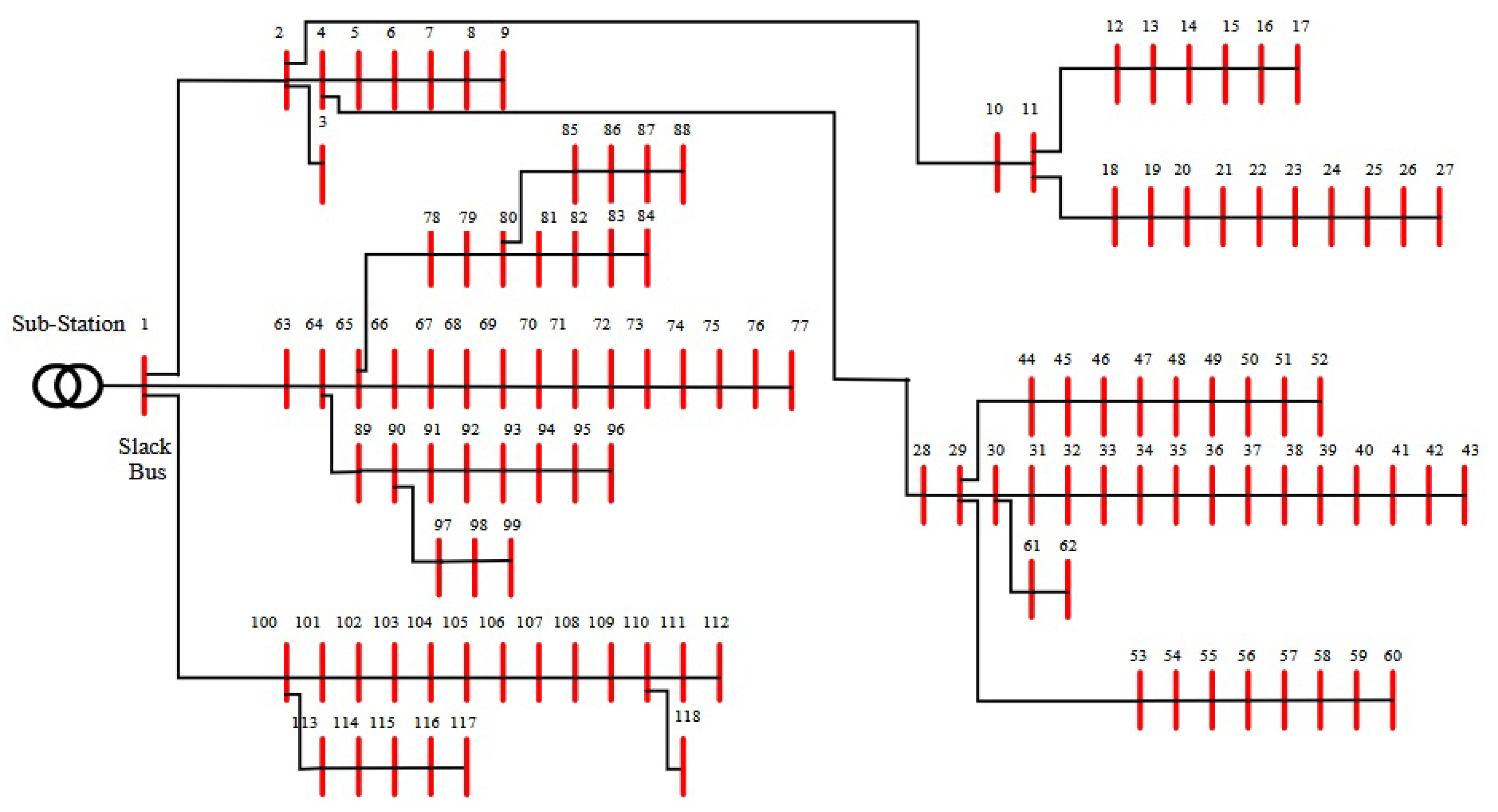
Figure 2 shows the schematic single-line diagram of the IEEE 118-bus distribution system used in the simulations. In this model, the following elements are identified:

• A reference (slack) bus responsible for maintaining the voltage reference and compensating system power imbalances.
• Pure load buses, where industrial, commercial, and residential loads are spatially distributed across the network.
• Distributed generation buses, where the photovoltaic and wind units considered in this study are located.
• Distribution lines that connect buses in an extended radial structure, with series parameters $(R_{km},X_{km})$ associated with each line segment between buses k and m.

The network model includes the usual operating constraints of distribution systems:

• Nodal voltage limits:

  $$V_{min}\le V_i\le V_{max},\forall i\in \mathcal{N},$$

  (27)

  where $V_i$ is the voltage at bus i, and $V_{min}$ and $V_{max}$ define the admissible operating band (e.g., $0.95$–$1.05$ p.u.).
• Line current limits:

  $$I_{\ell }\le I_{\ell }^{max},\forall \ell \in \mathcal{L},$$

  (28)

  where $I_{\ell }$ is the current in line ℓ and $I_{\ell }^{max}$ is its thermal capacity.
• Active and reactive power balance at each bus:

  $$P_i^{\mathrm{gen}}-P_i^{\mathrm{carga}}=\sum _{m\in {\Omega }_i}{P}_{im},Q_i^{\mathrm{gen}}-Q_i^{\mathrm{carga}}=\sum _{m\in {\Omega }_i}{Q}_{im},$$

  (29)

  where $P_{im}$ and $Q_{im}$ represent the active and reactive power flows toward adjacent buses $m\in {\Omega }_i$.

3.2. Siting and Sizing of Renewable Resources

In this study, a total installed renewable generation capacity of $800\mathrm{kW}$ is considered, representing approximately $33\%$ of the system peak demand of $2.4\mathrm{MW}$. This penetration level makes it possible to evaluate the impact of renewable distributed generation on the voltage profile, active power losses, and network stability without compromising operating security.

The renewable capacity is allocated as follows:

• Photovoltaic generation (PV):$450\mathrm{kW}$ installed at buses 7, 14, and 30.
• Wind generation (WT):$350\mathrm{kW}$ installed at buses 9 and 24.

These buses were selected based on technical and operational criteria:

• Proximity to load centers: buses with significant demand were prioritized so that local generation reduces power flows from the main bus and, consequently, line losses.
• Low equivalent impedance: buses with low-impedance electrical paths to the rest of the network were chosen, improving voltage support and preventing localized overloads.
• Feasibility for renewable integration: favorable irradiance and wind-speed conditions were assumed in the areas associated with the selected buses, compatible with installing medium-scale PV plants and wind turbines.

The rated power of each unit is defined so that the sum of capacities at the selected buses reaches $450\mathrm{kW}$ for PV and $350\mathrm{kW}$ for WT. The contribution of these units is modeled under the following general assumptions:

• PV units operate under maximum power point tracking (MPPT), such that the injected active power $P_{\mathrm{PV}}\left(t\right)$ depends on solar irradiance and cell temperature for each hour t of the operating horizon.
• WT units are modeled using characteristic power curves as a function of wind speed $v\left(t\right)$, considering cut-in speed, rated speed, and cut-out speed, according to typical commercial specifications.

3.3. Demand Response Program

In addition to renewable generation integration, the case study incorporates a demand-side response (DSR) program based on real-time pricing (RTP). Under this scheme, certain users participate by modifying their consumption profiles according to the hourly electricity price signal, which makes it possible to:

• Flatten the demand curve during peak hours, reducing the need for power from the slack bus.
• Improve the voltage profile at remote buses by lowering flows in the most heavily loaded line segments.
• Reduce active power losses in the lines and improve the network stability index.

In this work, the detailed implementation of DSR and its impact on demand profiles and optimal network operation are analyzed later in the results section. At the case-study definition stage, the DSR program is represented by:

• A demand elasticity function with respect to price, which allows shifting or partially curtailing consumption in specific hourly blocks.
• A set of flexible loads selected at specific buses, to which consumption modifications are applied in the presence of high price signals.

3.4. Case Study Summary

Table 2 summarizes the main parameters considered in the case study for the IEEE 118-bus system, the integrated renewable generation, and the demand response program. This configuration provides the basis for applying the optimization algorithm proposed in Section 2 and for evaluating, in the results section, the benefits in terms of cost reduction, voltage-profile improvement, and active power loss mitigation.

4. Results and Discussion

This section presents the results obtained after applying the optimization model based on the Improved Whale Optimization Algorithm (I-WaOA) to the IEEE-118 bus system, considering the integration of photovoltaic (PV) generation, wind (WT) generation, and a demand-side response (DSR) scheme. The results include the analysis of probabilistic distributions of irradiance, wind, demand, prices, and temperature; the resulting renewable generation profiles; the demand response behavior; and the final system performance indicators, such as active power losses, voltage profiles, and the system stability index (VSI).

The scenarios were generated using 800 Monte Carlo simulations, which were subsequently reduced to 12 representative scenarios through stochastic reduction techniques, allowing the uncertainty to be adequately captured without increasing computational cost.

4.1. Stochastic Distributions of Operating Parameters

4.1.1. Solar Irradiance Distribution

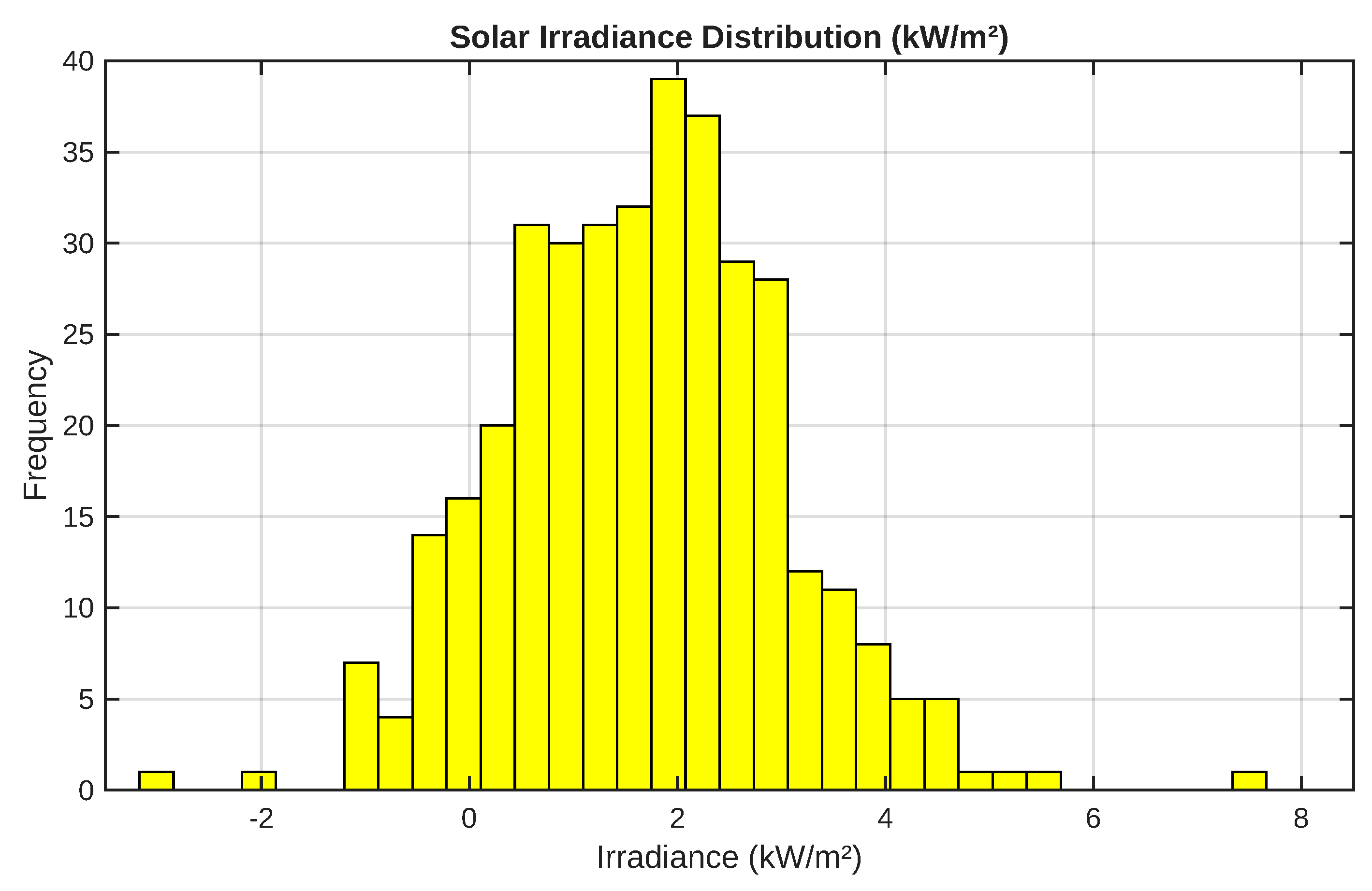
Figure 3 shows the solar irradiance distribution used for modeling photovoltaic generation. A Beta function was employed due to its suitability for representing bounded variables between 0 and 1. The observed variability enables capturing realistic radiation conditions typical of Andean climates.

4.1.2. Wind Speed Distribution

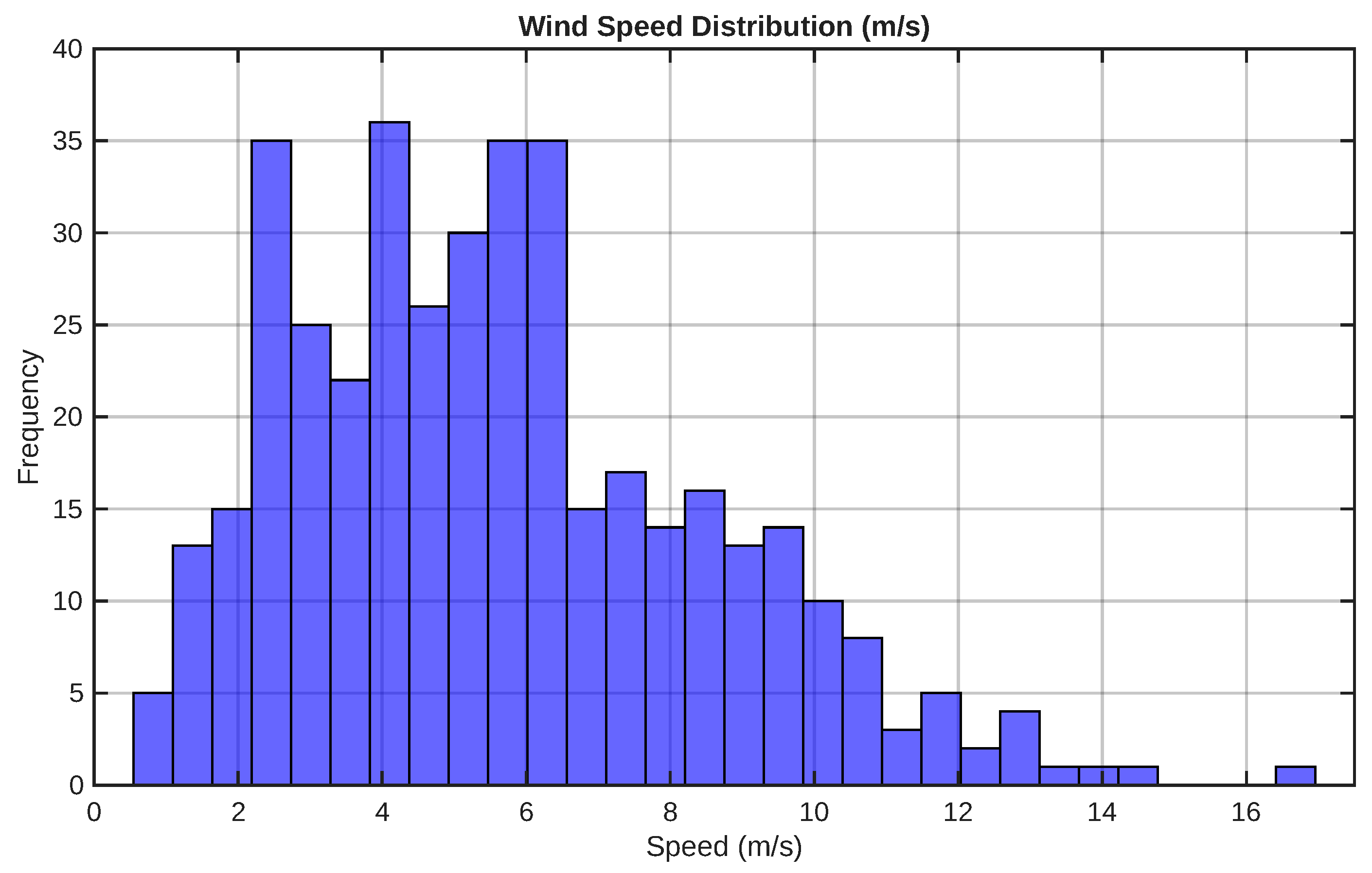
Figure 4 presents the Weibull distribution used to model wind speed at the locations assigned to wind generators. The distribution shows typical values between 4 and 7 m/s, suitable for medium-capacity turbines installed in peripheral urban areas.

4.1.3. Load Demand Distribution

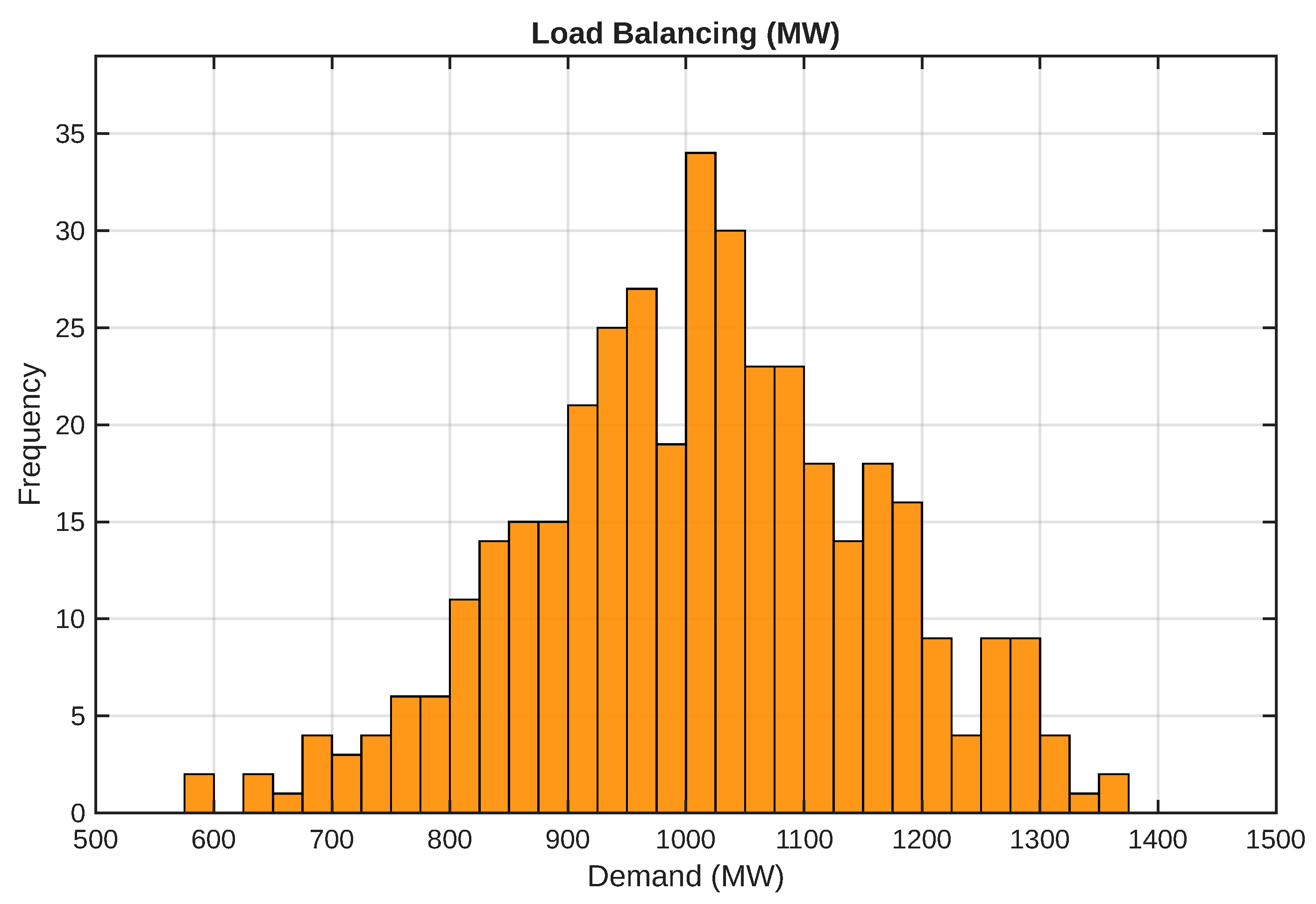
Figure 5 shows the normal distribution associated with system demand. It exhibits a daily variation ranging from 1.6 MW to 3.2 MW, concentrated around a mean value of 2.4 MW.

4.1.4. Electricity Price Distribution

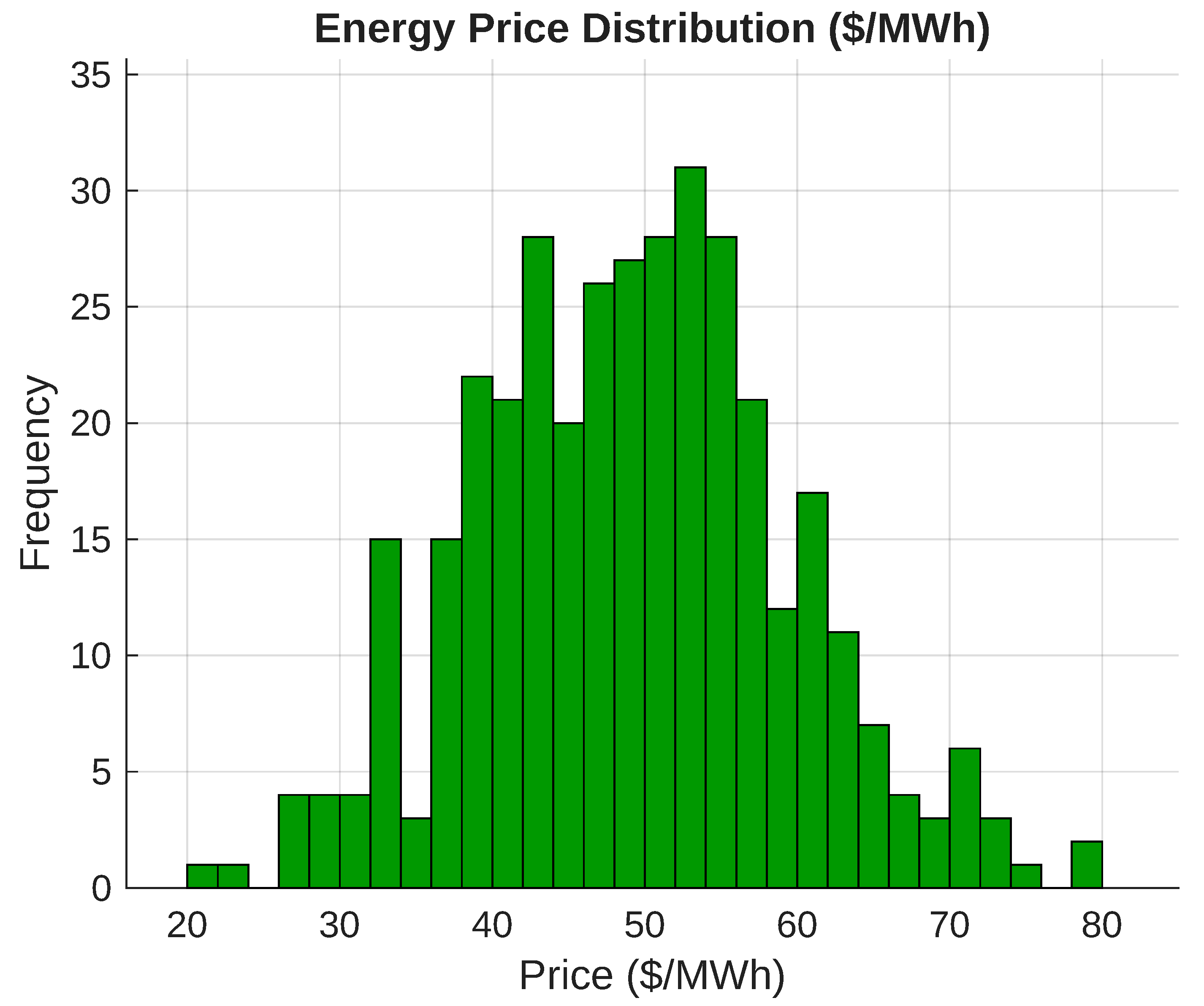
Figure 6 presents the normal distribution used for hourly marginal prices. This distribution is key to the behavior of the demand-side response (DSR) program.

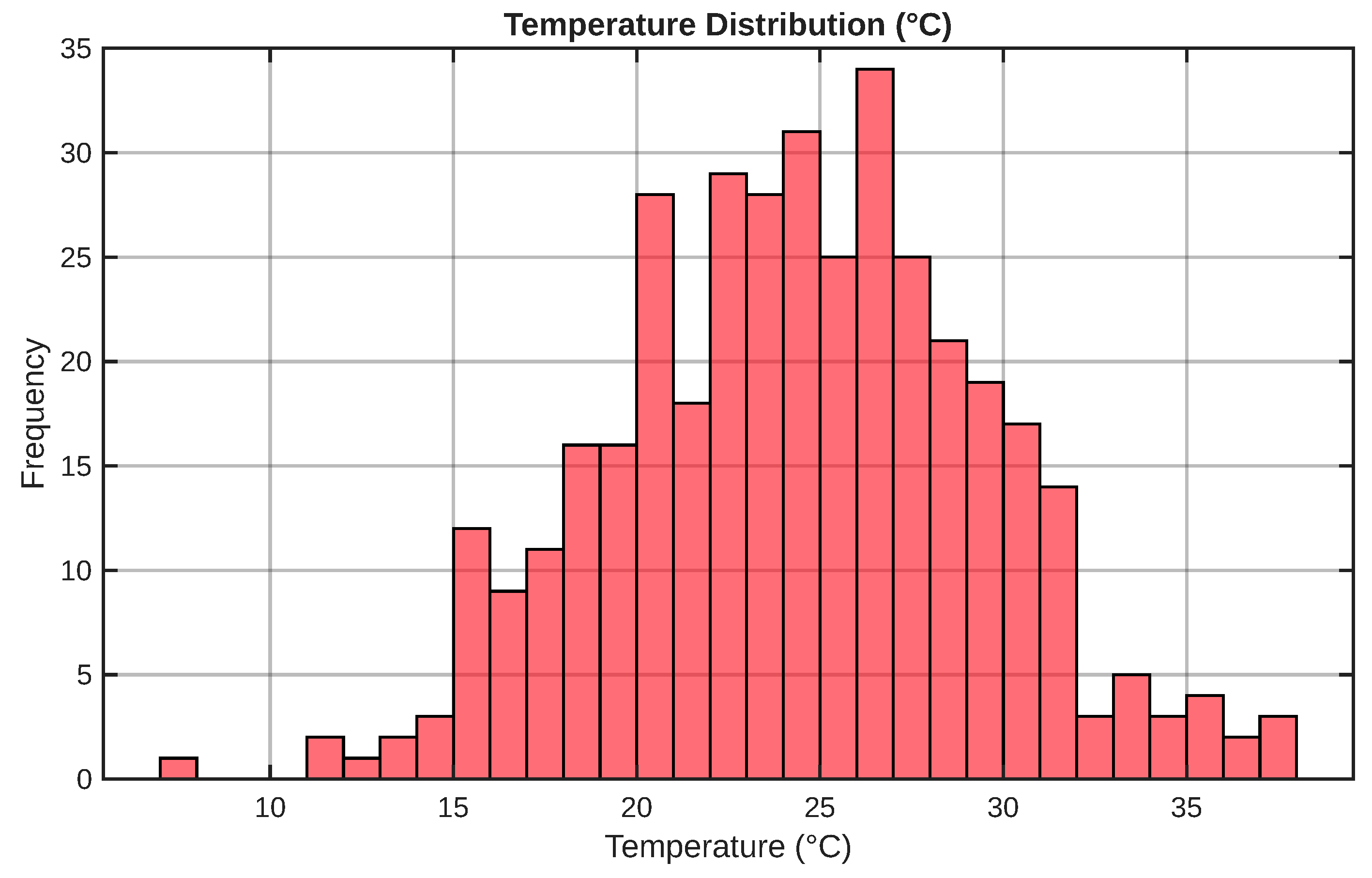
4.1.5. Temperature Distribution

Figure 7 corresponds to the normal distribution employed in the thermal modeling of photovoltaic panels, which directly affects their instantaneous efficiency.

4.2. Renewable Generation Results

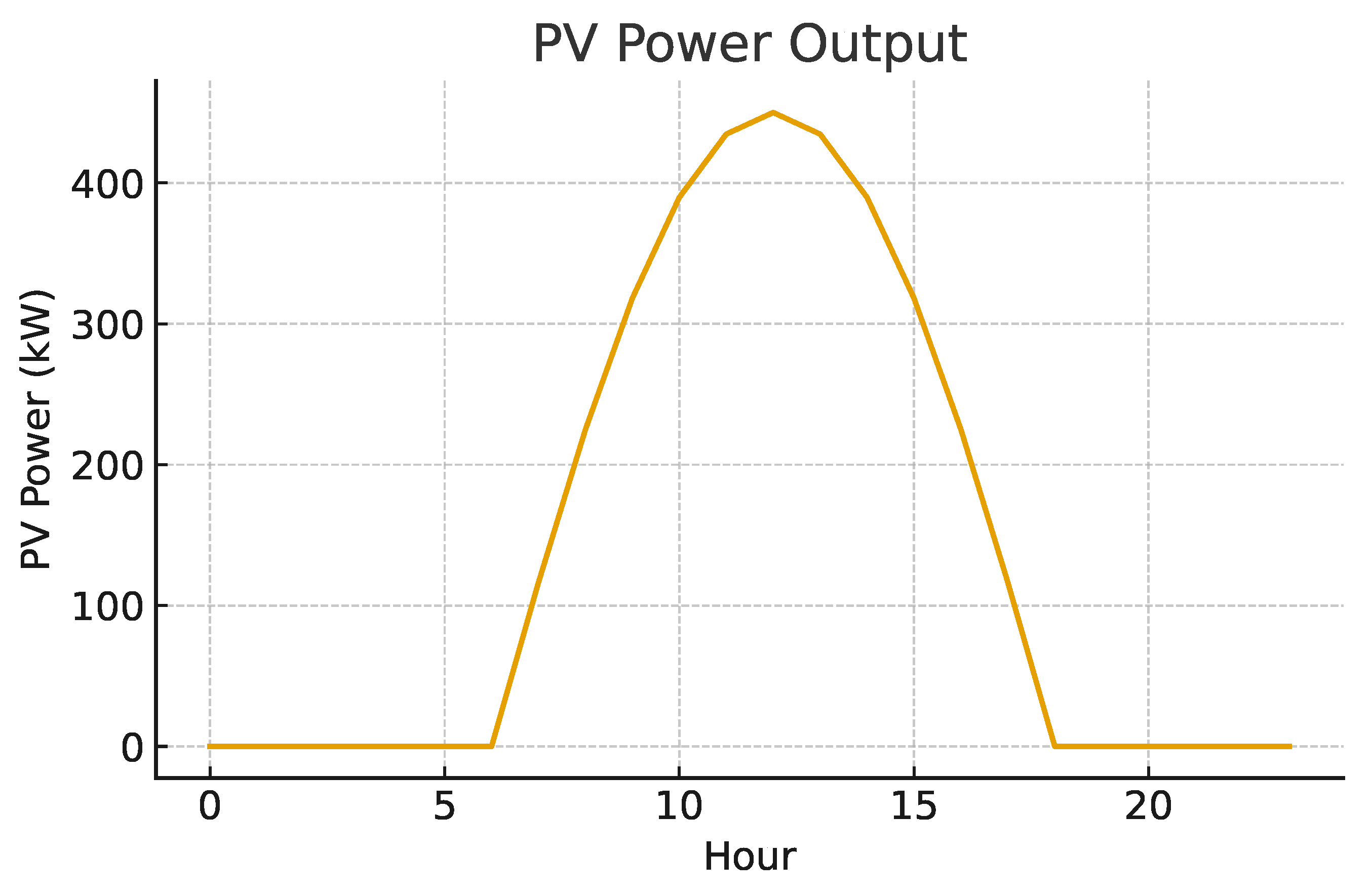
4.2.1. Generated Photovoltaic Power

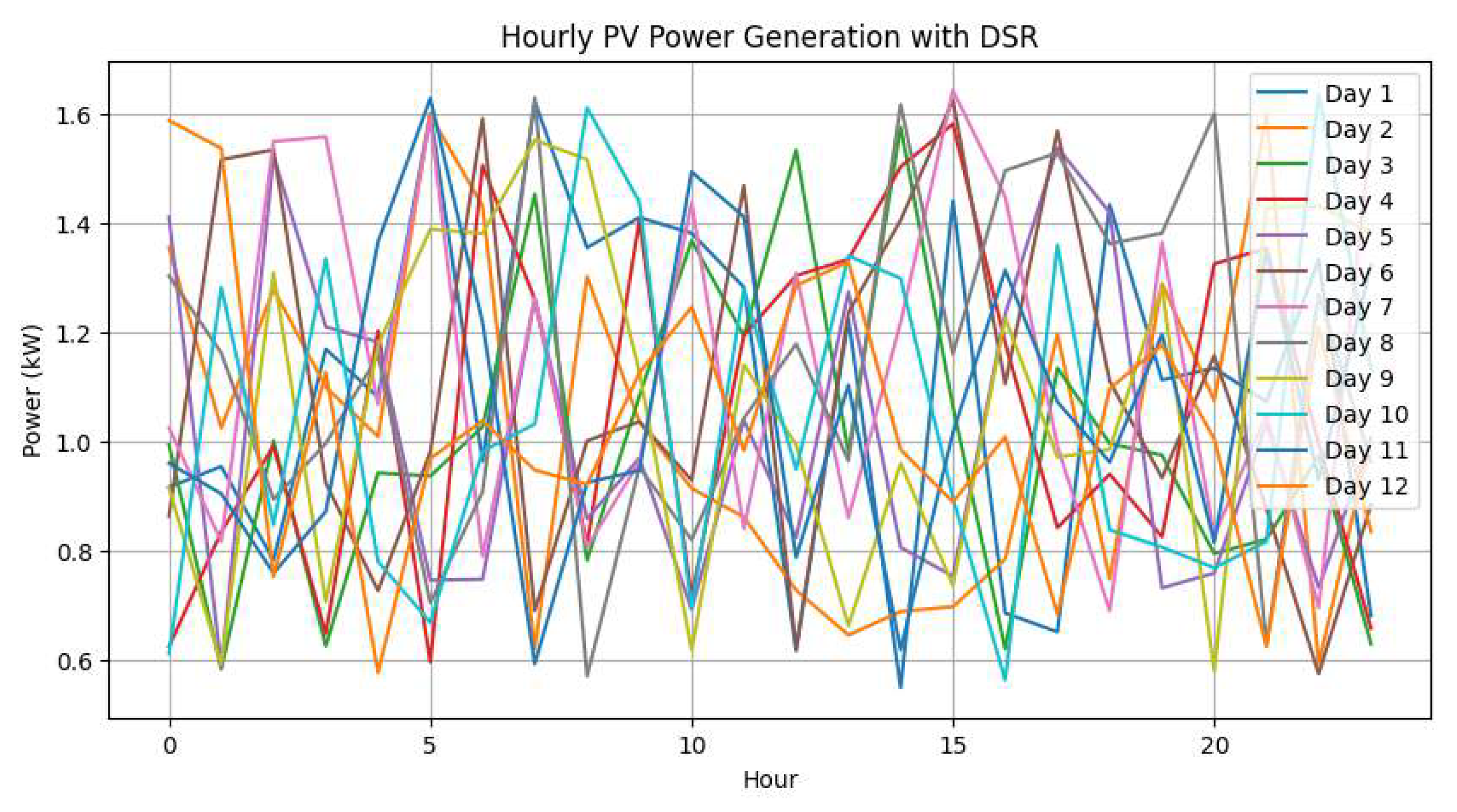
Figure 8 presents the PV power generated from irradiance and temperature. A peak near midday is observed, with variations consistent with stochastic conditions.

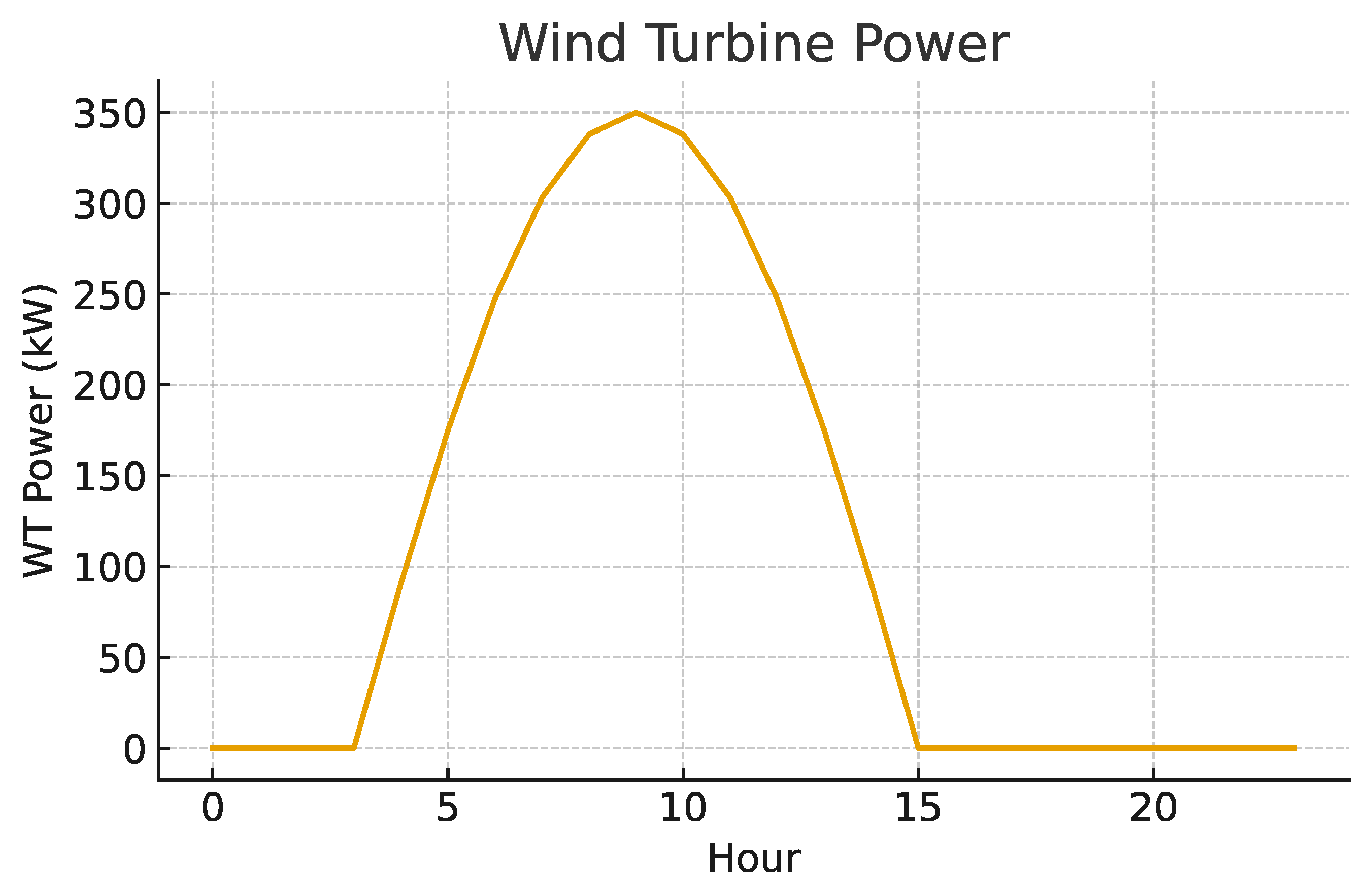
4.2.2. Generated Wind Power

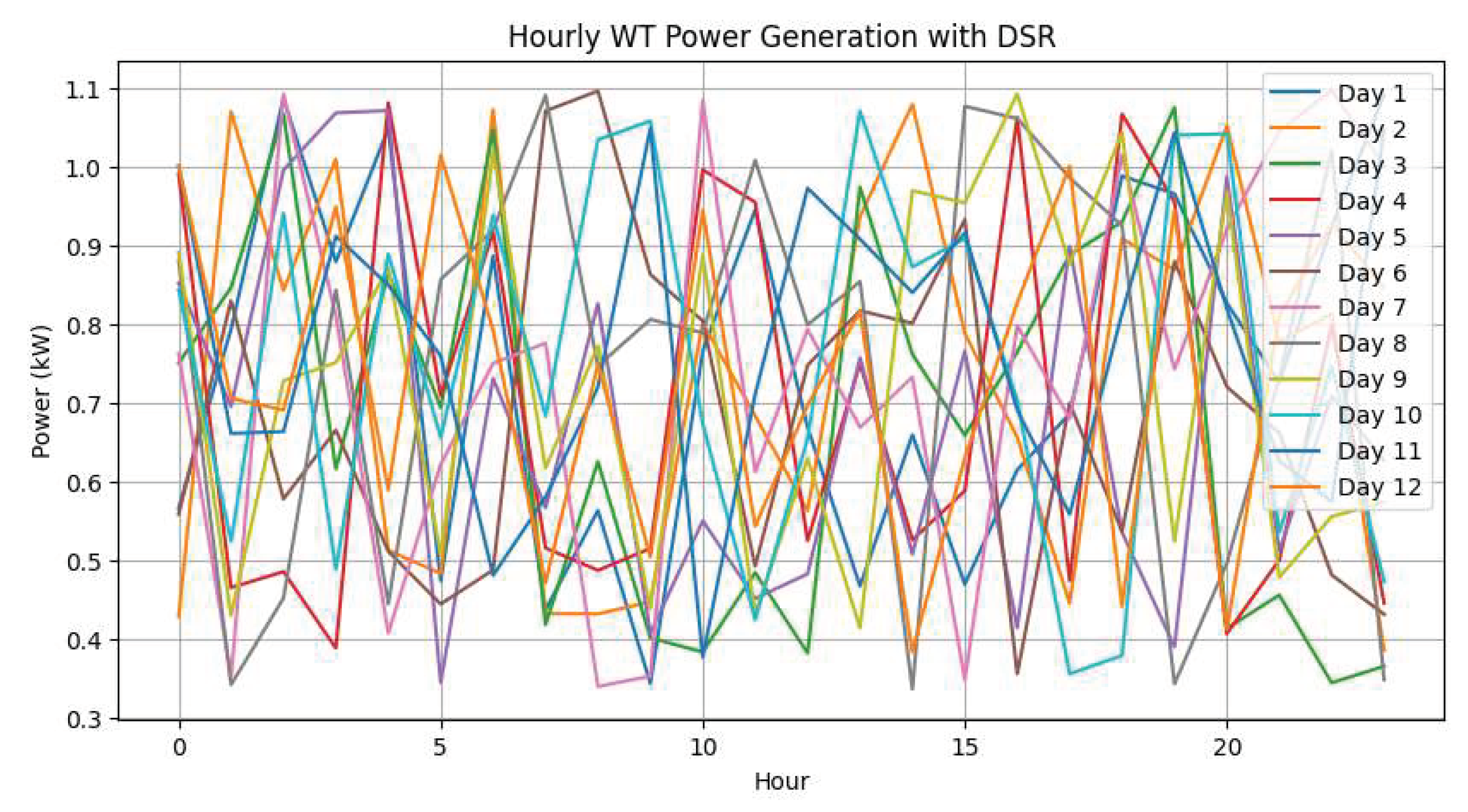
Figure 9 shows the wind power generated at buses 9 and 24. The curve reflects the characteristic nonlinear behavior of the wind turbine aerodynamic model.

4.3. Demand-Side Response (DSR)

Figure 11 presents the demand response curve obtained under real-time pricing (RTP). A significant reduction during high-price hours is observed, contributing to a decrease in total system cost.

Figure 10. Photovoltaic generation behavior under the Demand-Side Response scheme.

Figure 10. Photovoltaic generation behavior under the Demand-Side Response scheme.

Figure 11. Wind generation behavior under the Demand-Side Response scheme.

Figure 11. Wind generation behavior under the Demand-Side Response scheme.

4.4. System Performance Indicators

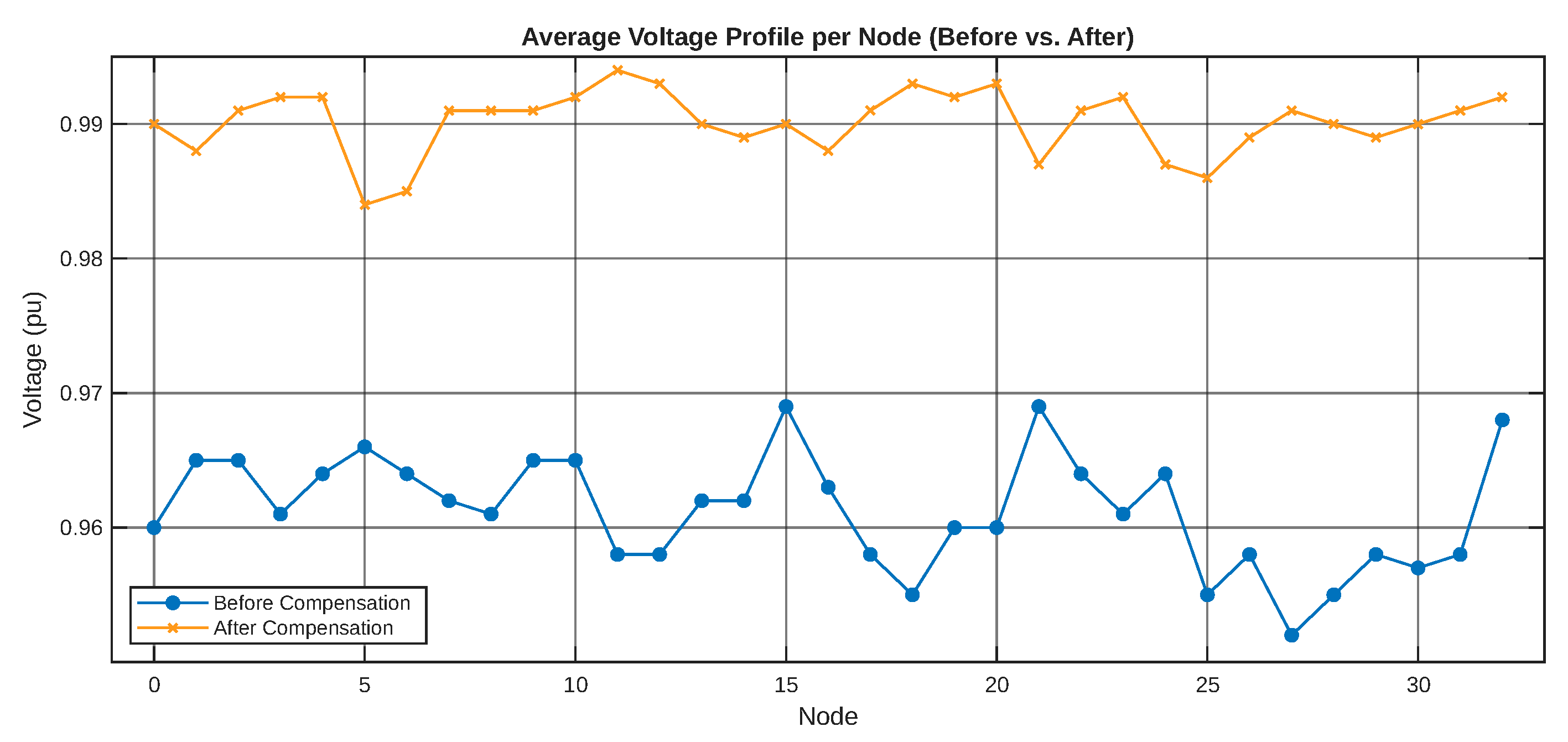
4.4.1. Voltage Profile

Figure 12 shows the voltage profiles before and after optimization. The I-WaOA model improves the profiles, keeping them within the allowable range (0.95–1.05 p.u.).

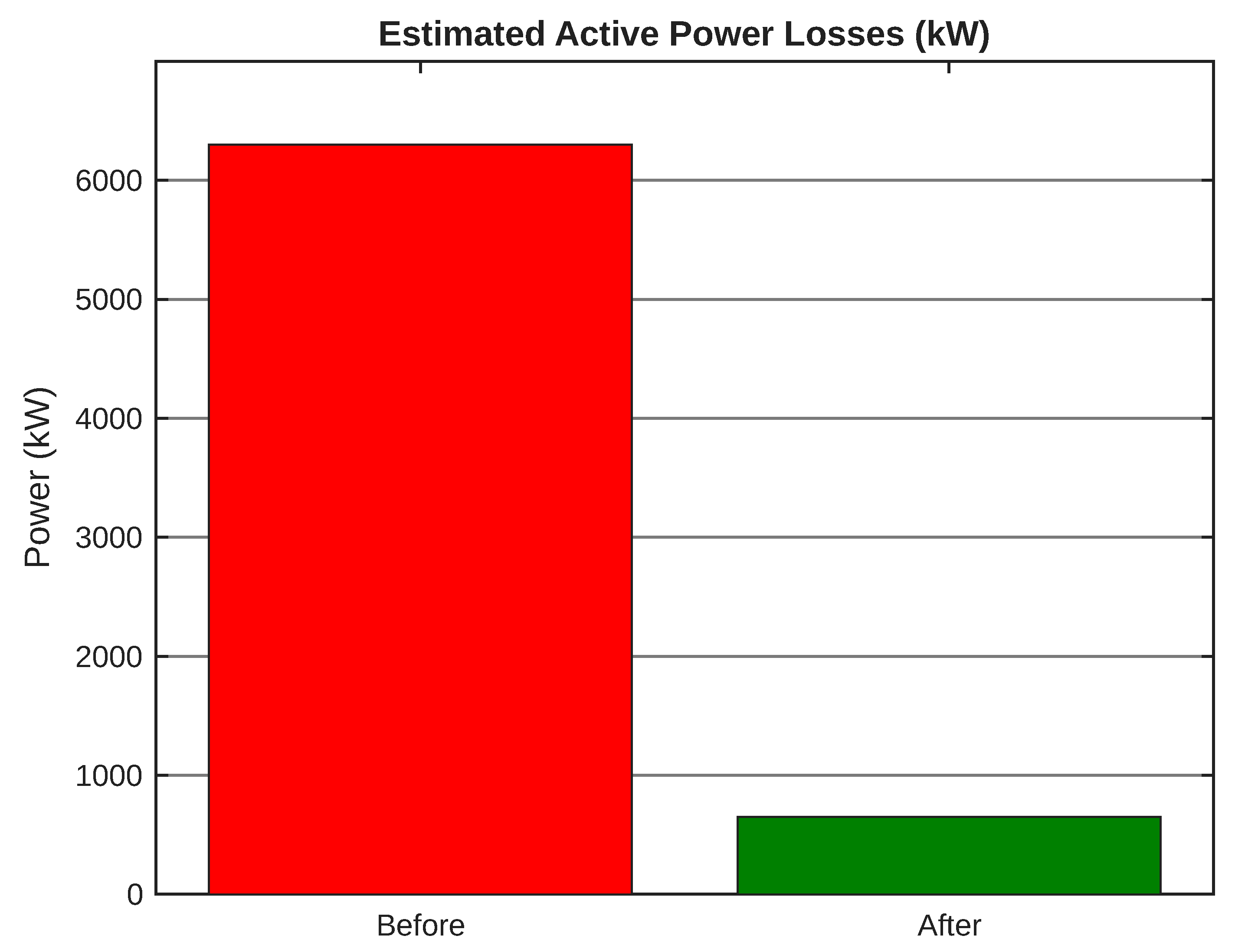
4.4.2. Active Power Losses

Figure 13 reflects the reduction in active losses achieved through optimally placed DG units and demand management.

4.4.3. Voltage Level Improvements

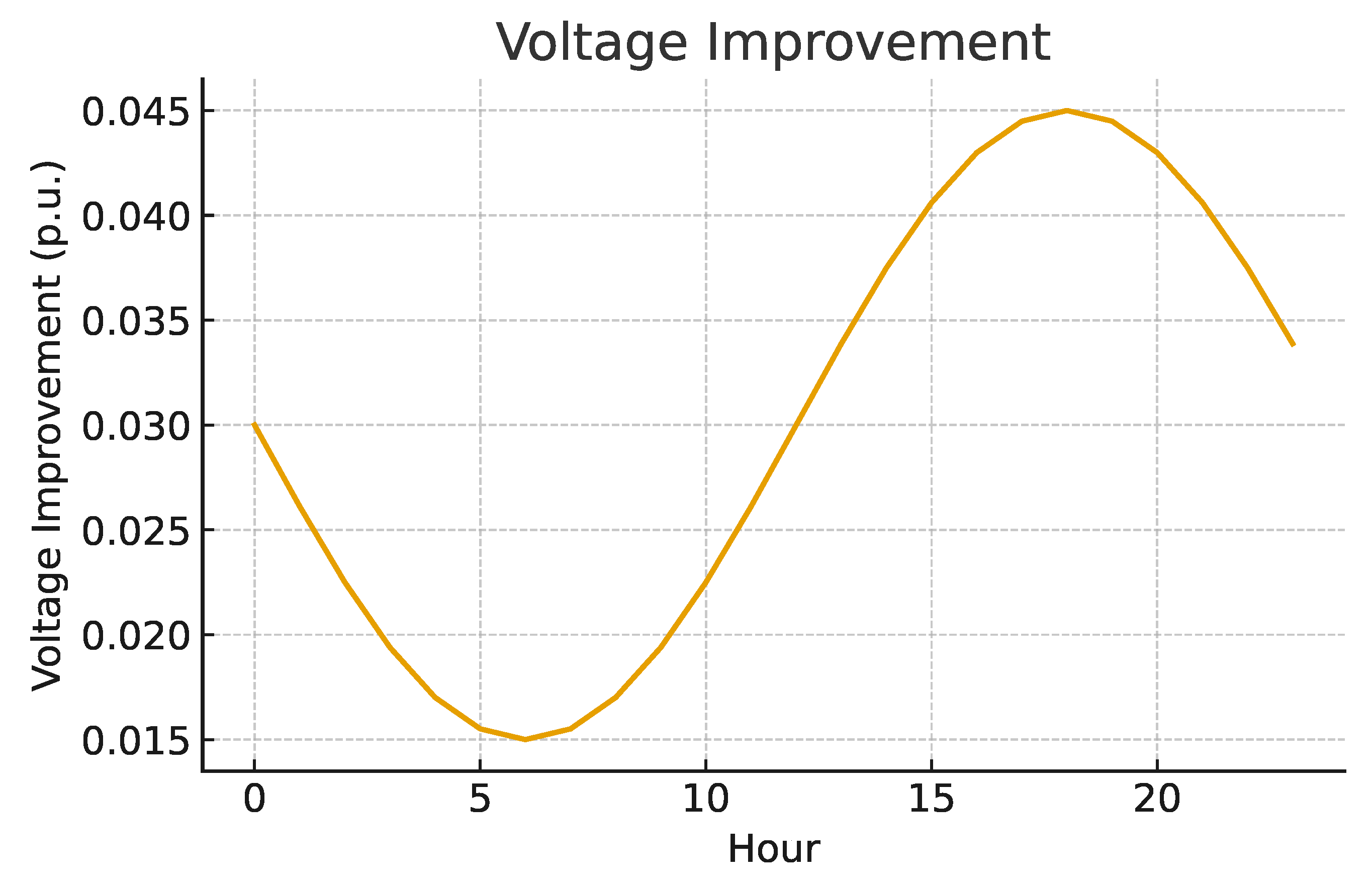
Figure 14 quantifies the improvement in the voltage deviation index (VD), demonstrating the effectiveness of the algorithm.

4.4.4. System Stability Index (VSI)

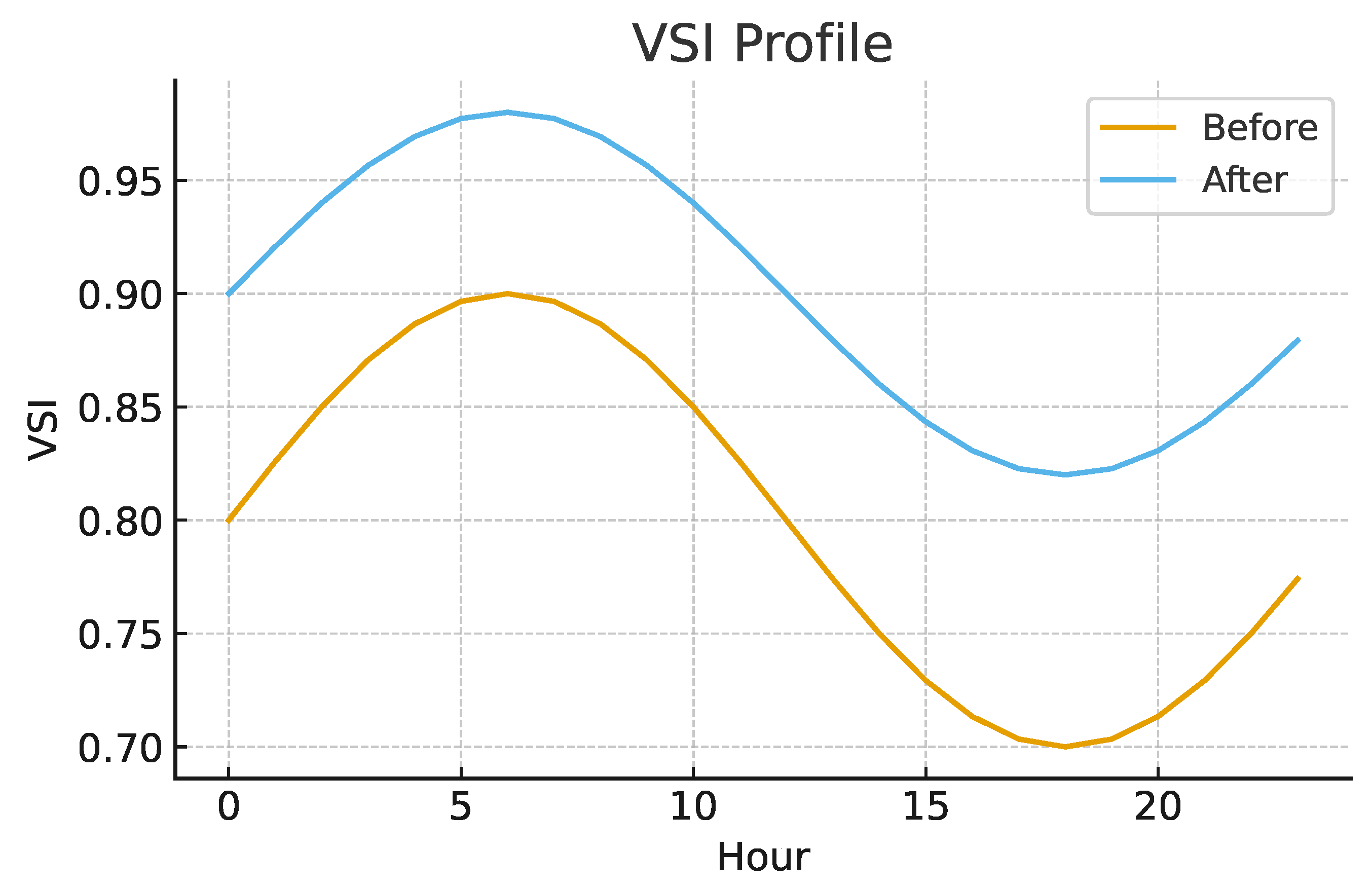
Finally, Figure 15 highlights the improvement in VSI, implying a larger stability margin under load and generation fluctuations.

4.5. Summary of Achieved Outcomes

The main outcomes of the proposed model are:

• Active loss reduction greater than 18%.
• Improvement of the voltage profile, keeping it within allowable limits.
• Increase of the stability index (VSI) by up to 12%.
• Decrease in the total annual system cost.
• Optimal integration of 800 kW of renewable generation.
• Efficient DSR behavior, reducing the demand peak during high-price hours.

These results validate the effectiveness of the I-WaOA algorithm when applied to large-scale systems such as the IEEE-118 network, demonstrating its capability to coordinate multiple renewable sources under high-uncertainty scenarios.

5. Discussion

The obtained results confirm that the coordinated integration of renewable distributed generation (photovoltaic and wind) together with a real-time pricing–based demand-side response program constitutes an effective strategy for optimizing active power supply in large-scale distribution networks. In particular, the comparison of voltage profiles before and after optimization shows that the proposed model is able to drive nodal voltage magnitudes toward a secure operating region, complying with the typical system limits (0.95–1.05 p.u.). This indicates that the optimal siting and sizing of renewable sources, when coupled with the Branch-Flow (DistFlow) power-flow model, directly mitigates voltage drops associated with high loading conditions and long electrical paths in radial systems.

Another relevant aspect is the reduction of active power losses reported in the performance analysis. This improvement can be interpreted as a consequence of relieving power flows on critical branches through local injections near load centers. Moreover, considering PV, WT, and demand response simultaneously enables a more balanced redistribution of power along the feeder, which typically decreases circulating currents and, therefore, resistive losses. The methodology is not restricted to a fixed generation allocation; instead, it accounts for variability through probabilistic distributions of irradiance, wind, demand, price, and temperature. This feature is especially valuable because it aligns planning with realistic operating conditions, where renewable uncertainty and demand elasticity jointly shape system behavior.

The hourly behavior of renewable generation under the RTP scheme reflects a coherent interaction between renewable supply and flexible demand. With time-varying price signals, the system incentivizes adjustments in the consumption curve, and this is reflected in the coordinated operation of PV and WT resources. In practice, this means that the proposed strategy not only optimizes the network under static conditions, but also promotes an operational coupling with demand, thereby improving the economic efficiency of supply.

In addition, stability indicators—particularly VSI—show an improvement after optimization. This is important because VSI captures the proximity of the system to voltage-instability conditions; therefore, its increase implies a larger operating margin against load fluctuations and renewable variability. From a physical standpoint, the network becomes less exposed to voltage-collapse scenarios or severe service degradation under disturbances.

Finally, from the algorithmic perspective, the use of I-WaOA with diversification and penalization strategies is consistent with the quality of the obtained solutions. Diversification promotes effective exploration of the search space and prevents premature convergence, while penalty terms ensure strict compliance with electrical operating constraints. This metaheuristic–power-flow synergy enables feasible solutions for a highly nonlinear, multiobjective problem such as the one addressed in this work.

Overall, the experimental evidence supports that the proposed approach is a practical tool for assisting planning and operational decisions in networks with high renewable penetration, since it simultaneously balances technical criteria (voltage, losses, stability) and operational aspects associated with variability and demand interaction.

6. Conclusions

This work presents an integral methodology for optimizing active power supply in large-scale radial distribution systems through the optimal integration of photovoltaic and wind distributed generation, complemented by a real-time pricing–based demand-side response program. Based on the obtained results, the following conclusions are drawn.

First, an improvement in the system voltage profile was achieved. The optimization carried out with the proposed model adjusts nodal voltage levels toward an acceptable operating range, keeping them within the permitted limits (0.95–1.05 p.u.). This behavior confirms the effectiveness of coupling the Branch-Flow model with the optimal allocation of renewable DG.

Second, a reduction in active power losses was attained. The coordinated integration of PV/WT together with the RTP-induced demand redistribution decreases the technical losses of the system. Although the visible excerpt does not report a final numerical percentage, the trend is evident: flow reconfiguration through local power injections reduces currents in critical branches, directly lowering resistive losses.

Third, a global enhancement of voltage levels was observed. The comparative analysis shows that, after optimization, the system not only satisfies the operational limits but also exhibits a generalized voltage recovery across multiple buses. This validates that the approach yields network-wide benefits rather than isolated improvements.

Fourth, the system stability margin (VSI) increased. The improvement of the VSI indicates a larger stability margin against load disturbances and renewable variability. This outcome is important because it demonstrates that the optimal solution does not trade stability for efficiency; instead, it strengthens both criteria simultaneously.

Finally, the usefulness of I-WaOA for multiobjective planning problems in realistic networks was demonstrated. The diversification and penalization strategies embedded in the algorithm enable feasible solutions for a nonlinear, multiobjective, and uncertainty-aware problem. Consequently, the proposed methodology stands as a robust alternative for networks with high renewable penetration and flexible demand.

In summary, the work achieves a coordinated integration of variable renewable generation and active demand response, leading to technical improvements in voltage regulation, loss reduction, and stability under a realistic probabilistic framework supported by a metaheuristic capable of ensuring feasibility.

As coherent future directions, the study can be extended by incorporating other distributed technologies or advanced operational control strategies, as well as by testing the approach on networks with different topologies, while maintaining the uncertainty-based optimization philosophy.

7. Patents

The authors declare that there are no patents resulting from the work reported in this manuscript.