Submitted:
18 November 2025
Posted:
20 November 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Hubble’s Law and Red Shift Law
3. Average Mass, Size and Brightness of Planets in the Universe
| Type | Temperature | Seen Color | Mass (M⊙) | Radius (R⊙) |
brightness (L⊙) |
Main sequence star proportion % |
Mass subtotal (M⊙) | Mass proportion | M%*L |
| O | 30,000-60,000K | blue | 64 | 16 | 1400000 | 0.00003 | 0.00192 | 3.31083E-05 | 46.352 |
| B | 10,000-30,000K | blue white | 18 | 7 | 20000 | 0.13 | 2.34 | 0.040350746 | 807.015 |
| A | 7,500-10,000K | White | 3.1 | 2.1 | 40 | 0.6 | 1.86 | 0.03207367 | 1.283 |
| F | 6000-7500K | White | 1.7 | 1.4 | 6 | 3 | 5.1 | 0.087943934 | 0.528 |
| G | 5000-6000K | Light yellowish white |
1.1 | 1.1 | 1.2 | 7.6 | 8.36 | 0.144159077 | 0.173 |
| K | 3500-5000K | yellow-orange | 0.8 | 0.9 | 0.4 | 12.1 | 9.68 | 0.166921036 | 0.067 |
| M | 2000-3500K | orange red | 0.4 | 0.5 | 0.04 | 76.45 | 30.58 | 0.527318728 | 0.021 |
| total | 99.88003 | 57.92192 | 0.9988003 |
4. Stefan-Boltzmann Law
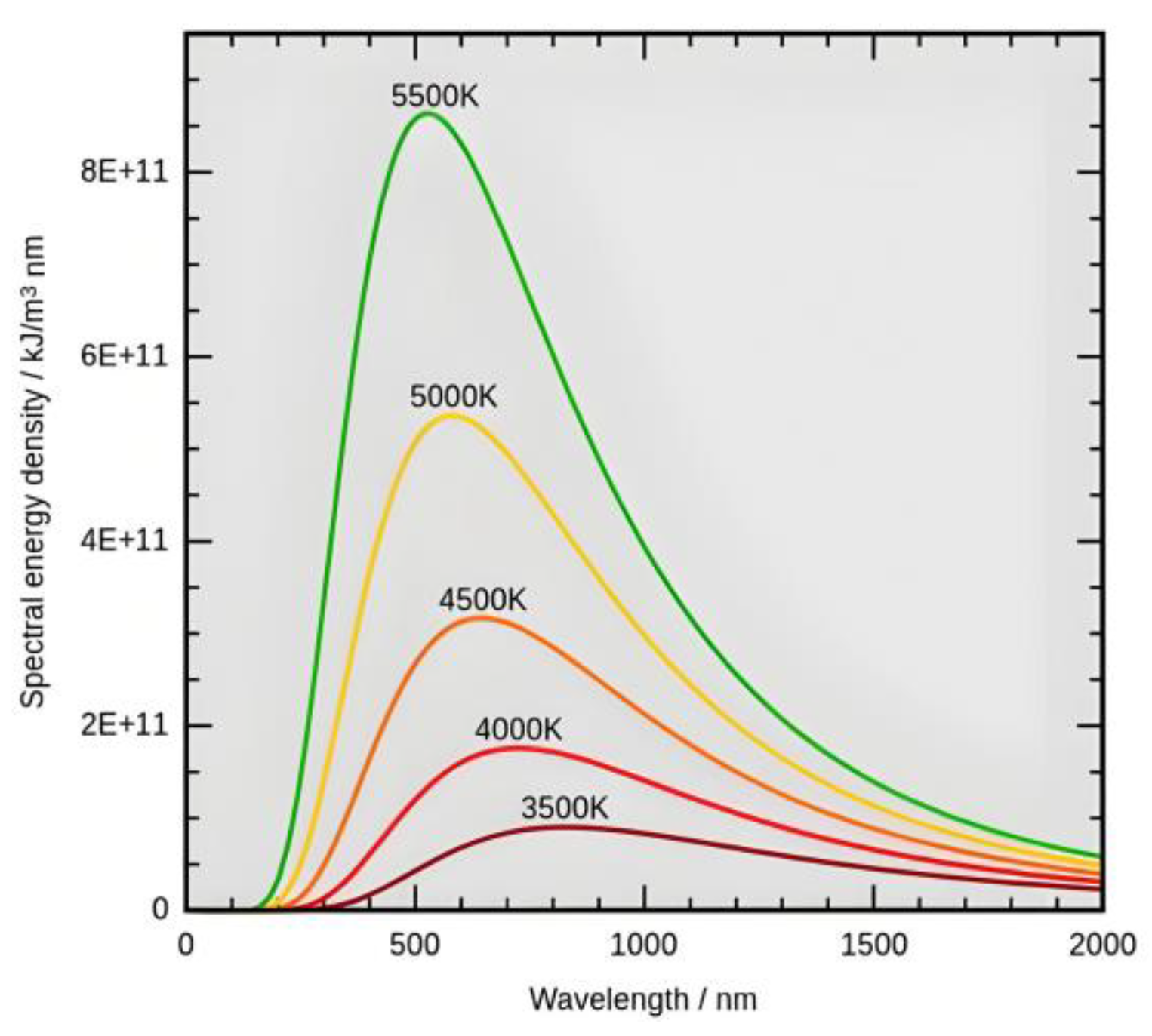
5. Planck’s Black Body Radiation Law
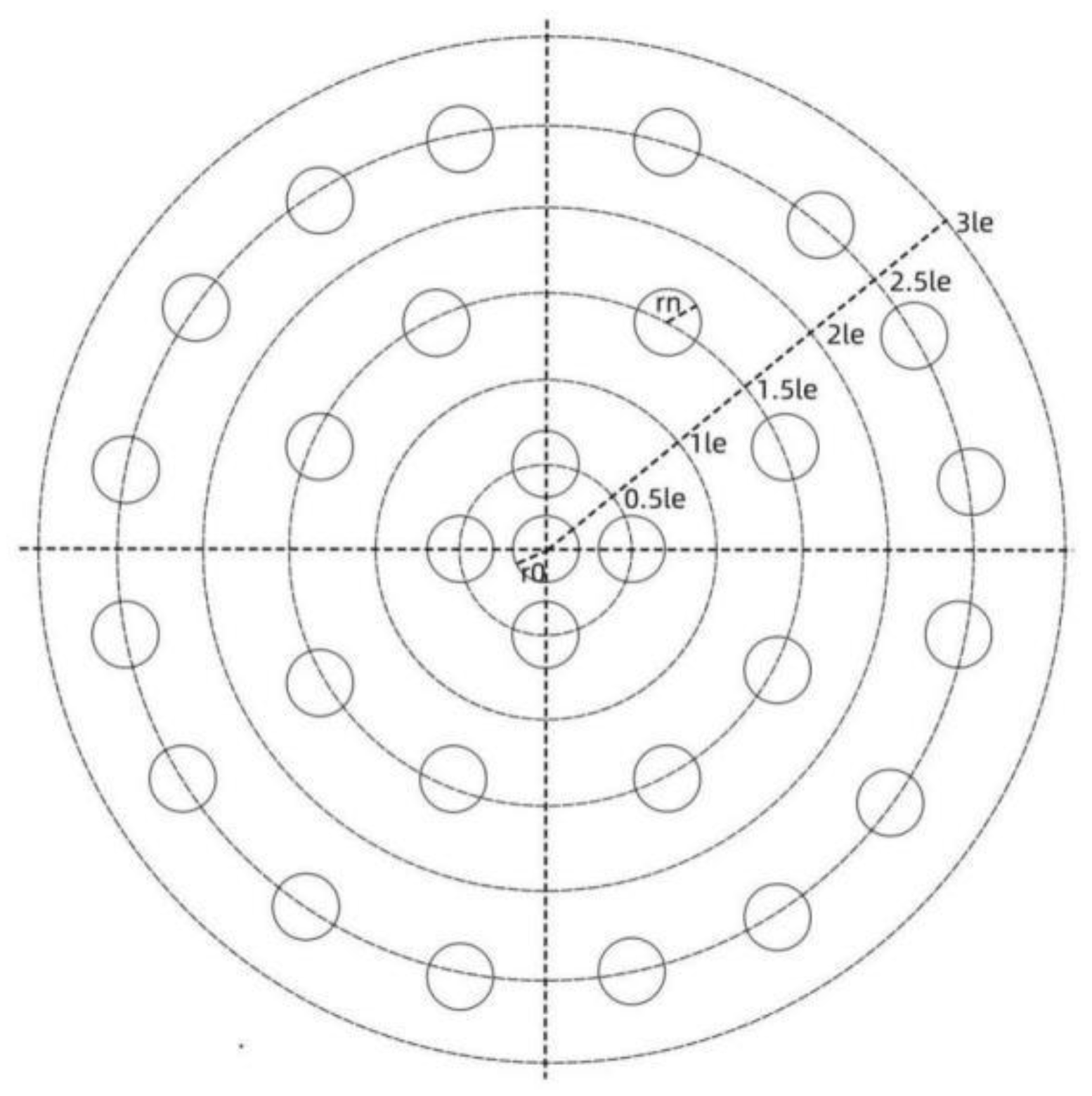
6. Distribution and Temperature Calculation of Equivalent Planets in the Universe
7. Wien’s Displacement Law
| λ0(m) | 0.0006 | 0.0007 | 0.0008 | 0.0009 | 0.001 | 0.0011 | 0.0012 | 0.0013 | dmax |
| O | 2.065E-27 | 1.879E-27 | 1.639E-27 | 1.395E-27 | 1.172E-27 | 9.784E-28 | 8.155E-28 | 6.805E-28 | 1.880E+30 |
| B | 2.734E-25 | 3.105E-25 | 3.379E-25 | 3.539E-25 | 3.588E-25 | 3.541E-25 | 3.422E-25 | 3.252E-25 | b(mk) |
| A | 4.233E-27 | 4.939E-27 | 5.644E-27 | 6.350E-27 | 7.055E-27 | 7.759E-27 | 8.459E-27 | 9.151E-27 | 0.002897 |
| F | 4.150E-27 | 4.842E-27 | 5.534E-27 | 6.225E-27 | 6.917E-27 | 7.609E-27 | 8.300E-27 | 8.991E-27 | T(k) |
| G | 1.939E-27 | 2.262E-27 | 2.585E-27 | 2.908E-27 | 3.231E-27 | 3.554E-27 | 3.877E-27 | 4.200E-27 | 2.897 |
| K | 1.085E-27 | 1.265E-27 | 1.446E-27 | 1.627E-27 | 1.808E-27 | 1.988E-27 | 2.169E-27 | 2.350E-27 | |
| M | 1.264E-27 | 1.474E-27 | 1.685E-27 | 1.896E-27 | 2.106E-27 | 2.317E-27 | 2.527E-27 | 2.738E-27 | |
| total | 2.881E-25 | 3.272E-25 | 3.565E-25 | 3.743E-25 | 3.811E-25 | 3.783E-25 | 3.683E-25 | 3.533E-25 |
8. Influencing Factors
8.1. Simulate Maximum Distance dmax
8.2. Minimum Detection Range of Observation Points
9. Conclusion
References
- She Xuechang. Doppler effect and its applications [J]. Physics Teaching, 2004, (1): 45-45.
- Baidu Encyclopedia. Hubble's Law [EB/OL]. [2025-11-13], https://baike.baidu.com/item/%E5%93%88%E5%8B%83%E5%AE%9A%E5%BE%8B/2390703.
- Baidu Encyclopedia. Redshift Law [EB/OL]. [2025-11-13], https://baike.baidu.com/item/%E7%BA%A2%E7%A7%BB%E5%AE%9A%E5%BE%8B/2348273.
- Zou Zhenlong, Qin Bo. Measuring the Hubble constant [J]. Physics, 2013, 42(10)733-734.
- Baidu Encyclopedia. Sun [EB/OL]. [2025-11-13], https://baike.baidu.com/item/%E5%A4%AA%E9%98%B3/24010.
- Baidu Encyclopedia. Spectral Type. [EB/OL]. [2025-11-13], https://baike.baidu.com/item/%E5%85%89%E8%B0%B1%E5%9E%8B/6728499?fr=aladdin.
- Cao Dinghan. Stefan-Boltzmann radiation law and its application [J]. Infrared Technology, 1994, 16(3):3.DOI:CNKI:SUN:HWJS.0.1994-03-014.
- Wang Mingmei. Planck’s blackbody radiation formula and classical expressions [J]. Journal of Hefei Normal University, 2003, 21(006)17-18.DOI10.3969j.issn.1674-2273.2003.06.007.
- Albert Smith. If all the matter in the universe were evenly distributed, what would be the density of the universe? [EB/OL].[2025-11-13], https://baijiahao.baidu.com/s?id=1617920513954940178&wfr=spider&for=pc.
- Cao Dinghan. Wien's displacement law and its application [J]. Infrared Technology, 1994, 16(2):3.DOI:CNKI:SUN:HWJS.0.1994-02-016.
- PS Wesson, He Chang. Obers' Paradox in Astronomy [J]. World Science, 1992(8)4.DOICNKISUNSJKE.0.1992-08-005.
- Chen Junli. Naive analysis of Olbers' paradox [J]. Chinese Science and Technology Journal Database (Full-text version) Natural Science, 2022(4):5.
- Lu Gengyuan, Lu Haimin. Cosmic expansion model--Discussion on the universe model [J]. Science and Technology Outlook, 2016, 26(028)294-294.DOI10.3969j.issn.1672-8289.2016.28.260.
- Junli Chen.Doubts About the Expansion of the Universe Derived from Einstein's Field Equations. [CrossRef]
- Marmet L.On the Interpretation of Spectral Red-Shift in Astrophysics: A Survey of Red-Shift Mechanisms - II[J]. 2018. [CrossRef]
- Chen Junli, Kang Yaohui. Observational results of Hubble’s law, universe expansion and pulsar time stability are inconsistent [J]. Science and Life, Issue 30, October 2021. https://zhuanlan.zhihu.com/p/454024406.
- Junli Chen.Why Can’t Large Galaxies Centered on Neutron Stars be Observed? [CrossRef]
- The leisurely water-controlling Dayu. 280 million years after the birth of the universe, the Webb Telescope actually photographed galaxies that should not exist [EB/OL]. [2025-11-13], https://baijiahao.baidu.com/s?id=1845014193499369815&wfr=spider&for=pc.
- Zhao Xiaoran Fuel. The Webb Telescope discovered the surprising similarity between early quasars in the universe and recent quasars [EB/OL]. [2025-11-13], https://baijiahao.baidu.com/s?id=1834713834177657118&wfr=spider&for=pc.


| Physical Quantity | Meaning | SI Units |
| I | Radiation rate, from unit surface in unit time product and unit solid angle at unit frequency The energy radiated at intervals or unit wavelength intervals |
Joule · second · meter · steradian · Hertz,Or joules·second·meter· steradian·meter |
| frequency | Hz | |
| λ | wavelength | m |
| T | blackbody temperature | K |
| h | Planck's constant | J·s |
| c | speed of light | m/s |
| e | The base of natural logarithms | 1 |
| k | Boltzmann constant | J/K |
| Type B | λ(m) | ||||||||||
| ms(kg) | d(m) | de(m) | n | 0.0006 | 0.0007 | 0.0008 | 0.0009 | 0.001 | 0.0011 | 0.0012 | 0.0013 |
| 1.989E+30 | 1.880E+26 | 1.492E+26 | 3.574E+14 | 2.140E-41 | 1.155E-41 | 6.773E-42 | 4.229E-42 | 2.775E-42 | 1.895E-42 | 1.338E-42 | 9.717E-43 |
| rs(m) | 3.760E+26 | 3.104E+26 | 2.502E+15 | 2.072E-40 | 1.118E-40 | 6.557E-41 | 4.094E-41 | 2.687E-41 | 1.835E-41 | 1.296E-41 | 9.408E-42 |
| 6.955E+08 | 5.640E+26 | 4.881E+26 | 6.790E+15 | 8.673E-40 | 4.683E-40 | 2.746E-40 | 1.714E-40 | 1.125E-40 | 7.685E-41 | 5.427E-41 | 3.940E-41 |
| Ls(J/s) | 7.520E+26 | 6.712E+26 | 1.322E+16 | 2.496E-39 | 1.348E-39 | 7.904E-40 | 4.935E-40 | 3.239E-40 | 2.212E-40 | 1.562E-40 | 1.134E-40 |
| 3.827E+26 | 9.400E+26 | 8.563E+26 | 2.180E+16 | 5.769E-39 | 3.115E-39 | 1.827E-39 | 1.141E-39 | 7.487E-40 | 5.114E-40 | 3.612E-40 | 2.623E-40 |
| km | 1.128E+27 | 1.042E+27 | 3.252E+16 | 1.154E-38 | 6.233E-39 | 3.655E-39 | 2.283E-39 | 1.498E-39 | 1.023E-39 | 7.227E-40 | 5.248E-40 |
| 18 | 1.316E+27 | 1.229E+27 | 4.539E+16 | 2.085E-38 | 1.126E-38 | 6.603E-39 | 4.124E-39 | 2.707E-39 | 1.849E-39 | 1.306E-39 | 9.483E-40 |
| kr | 1.504E+27 | 1.416E+27 | 6.040E+16 | 3.490E-38 | 1.885E-38 | 1.106E-38 | 6.905E-39 | 4.532E-39 | 3.096E-39 | 2.187E-39 | 1.588E-39 |
| 7 | 1.692E+27 | 1.604E+27 | 7.755E+16 | 5.508E-38 | 2.976E-38 | 1.745E-38 | 1.090E-38 | 7.156E-39 | 4.889E-39 | 3.453E-39 | 2.508E-39 |
| kL | 1.880E+27 | 1.791E+27 | 9.685E+16 | 8.298E-38 | 4.483E-38 | 2.630E-38 | 1.643E-38 | 1.078E-38 | 7.367E-39 | 5.203E-39 | 3.779E-39 |
| 20000 | 2.068E+27 | 1.978E+27 | 1.183E+17 | 1.203E-37 | 6.501E-38 | 3.814E-38 | 2.382E-38 | 1.564E-38 | 1.069E-38 | 7.547E-39 | 5.481E-39 |
| mu(kg) | 2.256E+27 | 2.166E+27 | 1.419E+17 | 1.690E-37 | 9.135E-38 | 5.359E-38 | 3.348E-38 | 2.198E-38 | 1.502E-38 | 1.061E-38 | 7.703E-39 |
| 3.580E+31 | 2.444E+27 | 2.354E+27 | 1.676E+17 | 2.312E-37 | 1.250E-37 | 7.332E-38 | 4.580E-38 | 3.007E-38 | 2.055E-38 | 1.451E-38 | 1.054E-38 |
| rus(m) | 2.632E+27 | 2.541E+27 | 1.955E+17 | 3.092E-37 | 1.671E-37 | 9.804E-38 | 6.125E-38 | 4.021E-38 | 2.748E-38 | 1.941E-38 | 1.410E-38 |
| 4.869E+09 | 2.820E+27 | 2.729E+27 | 2.255E+17 | 4.053E-37 | 2.191E-37 | 1.285E-37 | 8.032E-38 | 5.273E-38 | 3.603E-38 | 2.545E-38 | 1.849E-38 |
| Lus(J/s) | 3.008E+27 | 2.917E+27 | 2.577E+17 | 5.222E-37 | 2.823E-37 | 1.657E-37 | 1.035E-37 | 6.796E-38 | 4.645E-38 | 3.281E-38 | 2.383E-38 |
| 7.654E+30 | 3.196E+27 | 3.105E+27 | 2.920E+17 | 6.628E-37 | 3.583E-37 | 2.103E-37 | 1.314E-37 | 8.627E-38 | 5.896E-38 | 4.165E-38 | 3.025E-38 |
| j*(J/s·m^2) | 3.384E+27 | 3.293E+27 | 3.284E+17 | 8.299E-37 | 4.487E-37 | 2.634E-37 | 1.646E-37 | 1.081E-37 | 7.385E-38 | 5.217E-38 | 3.789E-38 |
| 2.570E+10 | 3.572E+27 | 3.481E+27 | 3.670E+17 | 1.027E-36 | 5.552E-37 | 3.259E-37 | 2.036E-37 | 1.337E-37 | 9.139E-38 | 6.457E-38 | 4.690E-38 |
| σ(W/m^2 T^4) |
3.760E+27 | 3.668E+27 | 4.078E+17 | 1.257E-36 | 6.795E-37 | 3.989E-37 | 2.493E-37 | 1.637E-37 | 1.119E-37 | 7.905E-38 | 5.742E-38 |
| 5.670E-08 | 3.948E+27 | 3.856E+27 | 4.507E+17 | 1.523E-36 | 8.237E-37 | 4.835E-37 | 3.022E-37 | 1.985E-37 | 1.356E-37 | 9.584E-38 | 6.962E-38 |
| T(k) | 4.136E+27 | 4.044E+27 | 4.957E+17 | 1.830E-36 | 9.896E-37 | 5.809E-37 | 3.631E-37 | 2.385E-37 | 1.630E-37 | 1.152E-37 | 8.366E-38 |
| 25946 | 4.324E+27 | 4.232E+27 | 5.429E+17 | 2.180E-36 | 1.179E-36 | 6.924E-37 | 4.328E-37 | 2.842E-37 | 1.943E-37 | 1.373E-37 | 9.972E-38 |
| ρu(kg/m^3) | 4.512E+27 | 4.420E+27 | 5.922E+17 | 2.579E-36 | 1.395E-36 | 8.191E-37 | 5.120E-37 | 3.363E-37 | 2.299E-37 | 1.624E-37 | 1.180E-37 |
| 4.7E-28 | 4.700E+27 | 4.608E+27 | 6.436E+17 | 3.029E-36 | 1.639E-36 | 9.624E-37 | 6.016E-37 | 3.951E-37 | 2.701E-37 | 1.909E-37 | 1.387E-37 |
| kρ | 4.888E+27 | 4.796E+27 | 6.972E+17 | 3.537E-36 | 1.913E-36 | 1.124E-36 | 7.025E-37 | 4.614E-37 | 3.154E-37 | 2.229E-37 | 1.619E-37 |
| 0.04035 | 5.076E+27 | 4.984E+27 | 7.530E+17 | 4.105E-36 | 2.221E-36 | 1.304E-36 | 8.155E-37 | 5.357E-37 | 3.662E-37 | 2.588E-37 | 1.880E-37 |
| ρui (kg/m^3) | 5.264E+27 | 5.172E+27 | 8.109E+17 | 4.738E-36 | 2.564E-36 | 1.506E-36 | 9.416E-37 | 6.186E-37 | 4.229E-37 | 2.988E-37 | 2.171E-37 |
| 1.896E-29 | 5.452E+27 | 5.360E+27 | 8.709E+17 | 5.443E-36 | 2.946E-36 | 1.730E-36 | 1.082E-36 | 7.107E-37 | 4.859E-37 | 3.434E-37 | 2.495E-37 |
| lue(m) | 5.640E+27 | 5.548E+27 | 9.331E+17 | 6.223E-36 | 3.368E-36 | 1.978E-36 | 1.237E-36 | 8.127E-37 | 5.557E-37 | 3.927E-37 | 2.853E-37 |
| 1.236E+20 | 5.828E+27 | 5.736E+27 | 9.974E+17 | 7.083E-36 | 3.834E-36 | 2.252E-36 | 1.408E-36 | 9.253E-37 | 6.327E-37 | 4.471E-37 | 3.249E-37 |
| Δθ | 6.016E+27 | 5.923E+27 | 1.064E+18 | 8.029E-36 | 4.347E-36 | 2.554E-36 | 1.597E-36 | 1.049E-36 | 7.174E-37 | 5.070E-37 | 3.684E-37 |
| 0.01745 | 6.204E+27 | 6.111E+27 | 1.133E+18 | 9.067E-36 | 4.909E-36 | 2.884E-36 | 1.804E-36 | 1.185E-36 | 8.104E-37 | 5.728E-37 | 4.162E-37 |
| dmax(m) | 6.392E+27 | 6.299E+27 | 1.203E+18 | 1.020E-35 | 5.524E-36 | 3.246E-36 | 2.030E-36 | 1.334E-36 | 9.121E-37 | 6.447E-37 | 4.684E-37 |
| 1.880E+30 | 6.580E+27 | 6.487E+27 | 1.276E+18 | 1.144E-35 | 6.195E-36 | 3.640E-36 | 2.277E-36 | 1.496E-36 | 1.023E-36 | 7.231E-37 | 5.255E-37 |
| N | 6.768E+27 | 6.675E+27 | 1.351E+18 | 1.279E-35 | 6.925E-36 | 4.069E-36 | 2.545E-36 | 1.673E-36 | 1.144E-36 | 8.085E-37 | 5.875E-37 |
| 10000 | 6.956E+27 | 6.863E+27 | 1.428E+18 | 1.425E-35 | 7.718E-36 | 4.535E-36 | 2.837E-36 | 1.864E-36 | 1.275E-36 | 9.013E-37 | 6.549E-37 |
| Δd(m) | 7.144E+27 | 7.051E+27 | 1.508E+18 | 1.583E-35 | 8.576E-36 | 5.040E-36 | 3.153E-36 | 2.072E-36 | 1.417E-36 | 1.002E-36 | 7.280E-37 |
| 1.880E+26 | 7.332E+27 | 7.239E+27 | 1.589E+18 | 1.754E-35 | 9.504E-36 | 5.586E-36 | 3.495E-36 | 2.297E-36 | 1.571E-36 | 1.110E-36 | 8.069E-37 |
| h(J·s) | 7.520E+27 | 7.427E+27 | 1.673E+18 | 1.939E-35 | 1.050E-35 | 6.175E-36 | 3.863E-36 | 2.539E-36 | 1.737E-36 | 1.228E-36 | 8.921E-37 |
| 6.626E-34 | 7.708E+27 | 7.615E+27 | 1.759E+18 | 2.138E-35 | 1.158E-35 | 6.809E-36 | 4.260E-36 | 2.800E-36 | 1.915E-36 | 1.354E-36 | 9.839E-37 |
| c(m/s) | 7.896E+27 | 7.803E+27 | 1.847E+18 | 2.351E-35 | 1.274E-35 | 7.490E-36 | 4.686E-36 | 3.080E-36 | 2.107E-36 | 1.490E-36 | 1.083E-36 |
| 2.998E+08 | 8.084E+27 | 7.991E+27 | 1.937E+18 | 2.580E-35 | 1.398E-35 | 8.221E-36 | 5.144E-36 | 3.381E-36 | 2.313E-36 | 1.635E-36 | 1.188E-36 |
| H0(/s) | 8.272E+27 | 8.179E+27 | 2.029E+18 | 2.826E-35 | 1.531E-35 | 9.004E-36 | 5.634E-36 | 3.704E-36 | 2.534E-36 | 1.791E-36 | 1.302E-36 |
| 2.197E-18 | 8.460E+27 | 8.367E+27 | 2.123E+18 | 3.088E-35 | 1.674E-35 | 9.842E-36 | 6.159E-36 | 4.049E-36 | 2.770E-36 | 1.958E-36 | 1.423E-36 |
| e | 8.648E+27 | 8.555E+27 | 2.220E+18 | 3.368E-35 | 1.826E-35 | 1.074E-35 | 6.719E-36 | 4.417E-36 | 3.022E-36 | 2.136E-36 | 1.553E-36 |
| 2.718 | 8.836E+27 | 8.743E+27 | 2.318E+18 | 3.667E-35 | 1.988E-35 | 1.169E-35 | 7.316E-36 | 4.810E-36 | 3.291E-36 | 2.327E-36 | 1.691E-36 |
| k(J/K) | 9.024E+27 | 8.931E+27 | 2.419E+18 | 3.985E-35 | 2.160E-35 | 1.271E-35 | 7.953E-36 | 5.228E-36 | 3.577E-36 | 2.529E-36 | 1.838E-36 |
| 1.381E-23 | 9.212E+27 | 9.119E+27 | 2.522E+18 | 4.323E-35 | 2.344E-35 | 1.379E-35 | 8.629E-36 | 5.674E-36 | 3.882E-36 | 2.745E-36 | 1.995E-36 |
| total | 2.734E-25 | 3.105E-25 | 3.379E-25 | 3.539E-25 | 3.588E-25 | 3.541E-25 | 3.422E-25 | 3.252E-25 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





