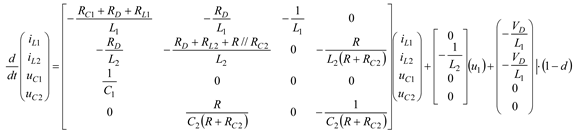1. Introduction
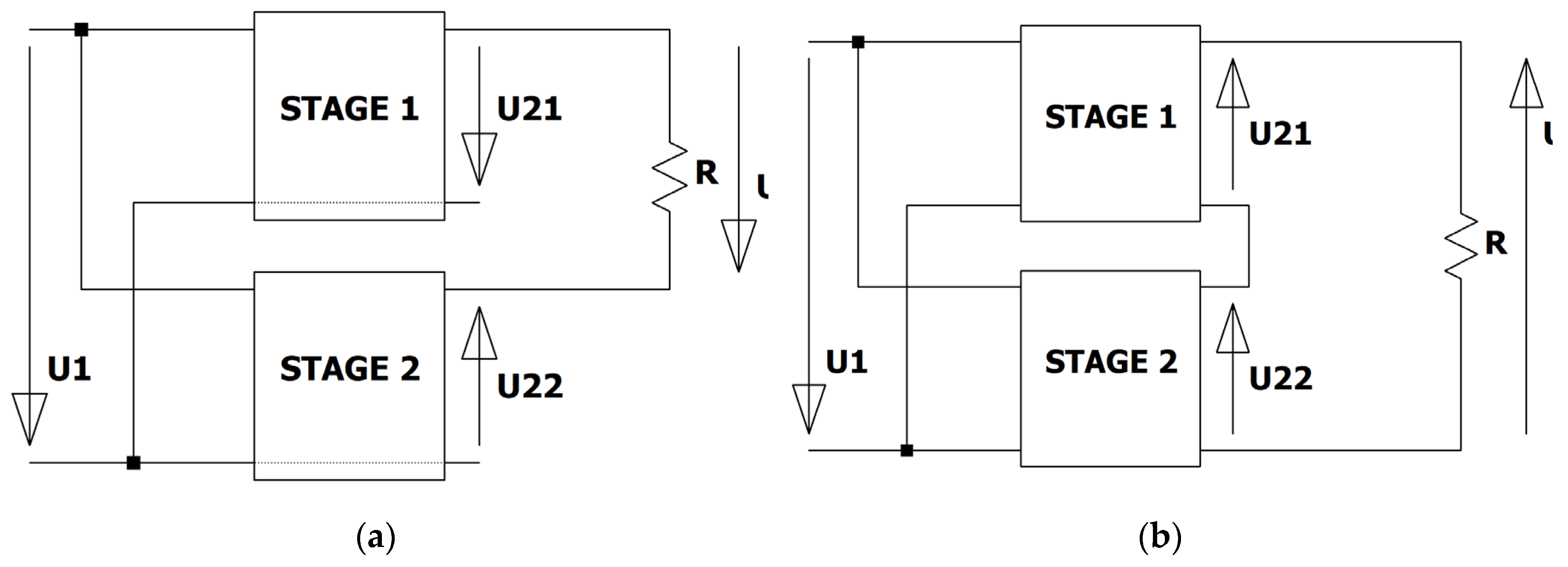
To increase the output power of a converter one can combine two converter stages. A common concept is to connect the converters in parallel as is displayed in
Figure 1a. The voltage transformation ratio of the complete converter is equal to the one of the stages. The second concept is to connect the inputs of the stages in parallel and the outputs of the stages in series and including the input voltage. This is shown in
Figure 1.b. The pointed line between one input terminal and one output terminal of the converter stages shows that they are directly connected. In this second concept the voltage transformation ratio is changed. The output voltage is now the sum of the two output voltages of the two stages and the input voltage
This concept leads to a large output voltage. It can be used when a stable input voltage is available. A sudden change at the input leads directly to a sudden change at the output. If one uses a diode in series to the input source and a capacitor behind the diode at the input of the two-stage converter, the direct influence can be avoided. The additional diode serves also as a reverse polarity protection.
Small letters in this paper symbolize the time variables. For the steady state one can write capital letters.
A third concept to combine two converters again is to connect the inputs in parallel and the outputs directly in series. This is depicted in
Figure 2a. Now it is not possible to use the same converter type, instead one must use an inverting and a noninverting converter stage. The output voltage is given by
This concept can also be used by input voltages which are not stiff and can change fast. The control of the converter stages has to correct the output voltage. In the method according to
Figure 1.b a change of the input voltage directly influences the output voltage.
A fourth concept is shown in
Figure 2b. The inputs of the converters are connected in parallel. The converter stages have no direct connection between the input and the output sides (which is shown by the pointed line in the other concepts). So one has to combine the outputs in series. Here converters with isolation between input and output can be used.
Using two inverting DC/DC converters leads to a high voltage transformation ratio. In this paper inverting limited duty cycle step-up-down converters are used to produce a floating two-stage converter with high voltage transformation ratio. They are taken from [
1], where 8 converters with reduced duty cycle range which are grounded to the positive input terminal are presented. Two of them are step-down, two of them are step-up and four of them are inverting step-up-down converters. These converters can be combined with stages, where the ground is connected to the negative input terminal.
The aim of this paper is to show four new floating two-stage converter topologies according to
Figure 1b with a high voltage transformation ratio. Two different voltage transformation ratios are achieved. The new floating converters are studied in detail.
In the Chinese patent application [
2] a converter according to
Figure 1.b consisting of two Boost converters is presented and the modes are described in detail. A more complicated converter with the same connection at the inputs and the outputs of the stages can be found in [
3]. Each stage consists of n bidirectional Boost converters which are connected in parallel. So a large output power can be produced. Another Chinese patent application [
4] shows a floating converter consisting of Boost converters with an additional capacitor, a diode and a winding, which is magnetically coupled with the winding used in the Boost converter. [
5] shows a modification of the Boost converter which is used for the stages of a converter according type
Figure 1.b. The advantage of this circuit is that compared to the normal Boost converter no inrush current occurs when connected to the input voltage. A publication concerning the concept according
Figure 2.b is [
6]. A complex converter is shown, where the active switches are working against ground and the capacitors are connected in series. Instead of the coils used in a Boost converter, here they are replaced by transformers. The secondary sides of the transformers are used to make an additional step-up of the output voltage. [
7] shows a two-stage converter, where the stages are constructed by tristate Boost converters. The tristate concept applied to a step-up converter makes it possible that it becomes a phase-minimum system, when the converter is controlled in a special way (c.f. [
8].) A converter consisting of two step-up stages, each built of one active switch, two diodes, two capacitors and two coupled coils is treated in [
9]. [
10] shows several bidirectional floating and interleaved converters which are built from bidirectional Boost converters. A quadratic Boost with two stages is treated in [
11]. The circuit is very complex. The design and the analyzes of a floating converter (type 1.b) is done in [
12]. The stages need one active switch, four diodes, two coils, and three capacitors. The extension of a floating two-stage Boost converter by resonance circuits is explained in [
13]. The main inductor of the Boost converter is here split into two magnetically coupled windings which form a resonance circuit with an additional capacitor.
Figure 1.
Possibilities to combine two DC/DC converters connected in parallel at the input sides: a. interleaved; b. floating with serial outputs and input voltage included.
Figure 1.
Possibilities to combine two DC/DC converters connected in parallel at the input sides: a. interleaved; b. floating with serial outputs and input voltage included.
Figure 2.
Possibilities to combine two DC/DC converters connected in parallel at the input sides: a. floating with series output; b. combination with serial output.
Figure 2.
Possibilities to combine two DC/DC converters connected in parallel at the input sides: a. floating with series output; b. combination with serial output.
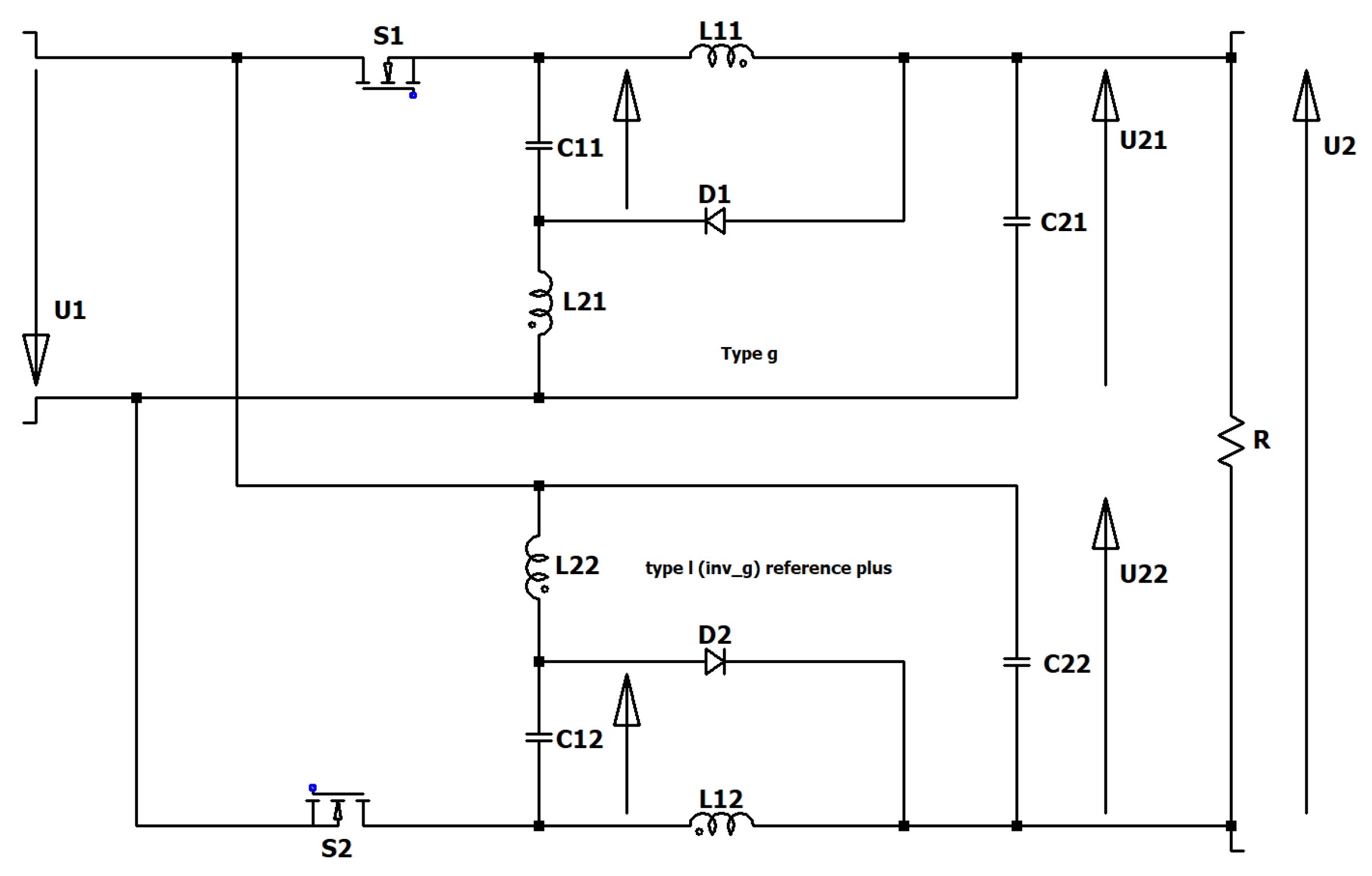
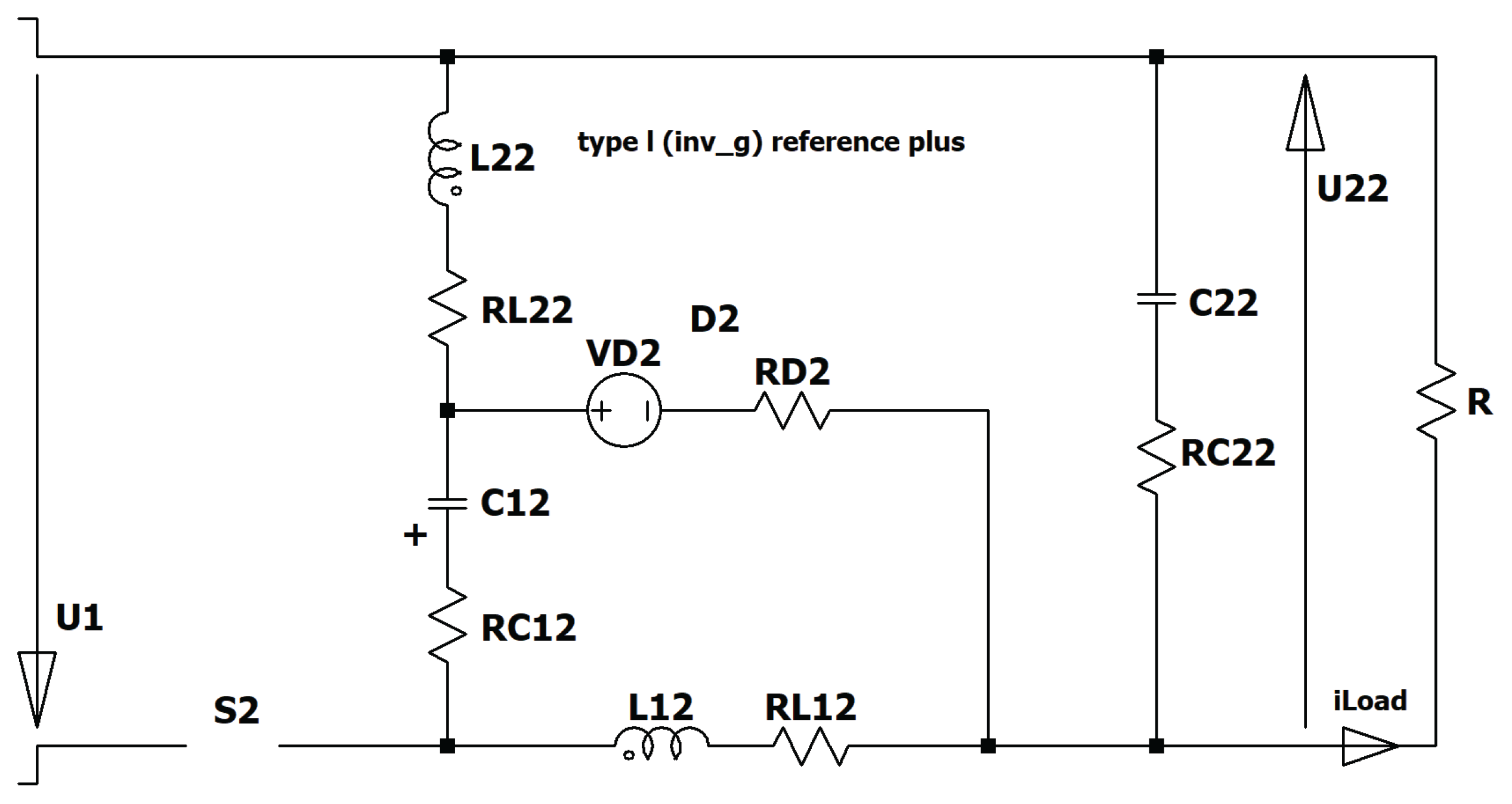
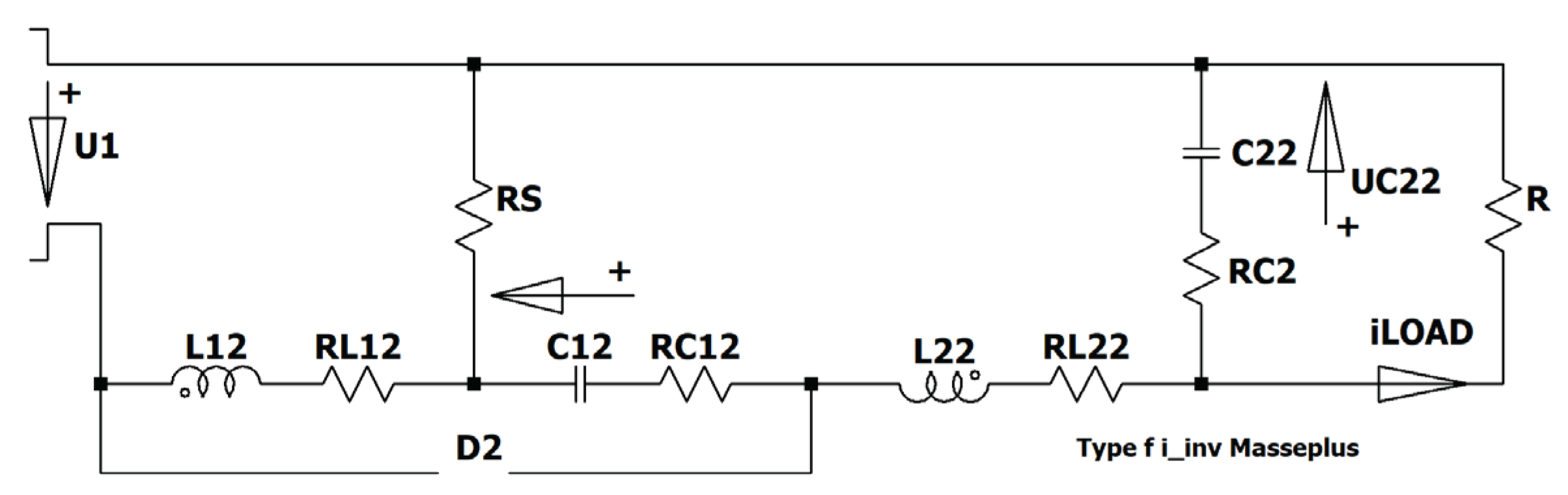
Figure 3.
Circuit diagram of the floating two-stage inverting Boost converter type I.
Figure 3.
Circuit diagram of the floating two-stage inverting Boost converter type I.
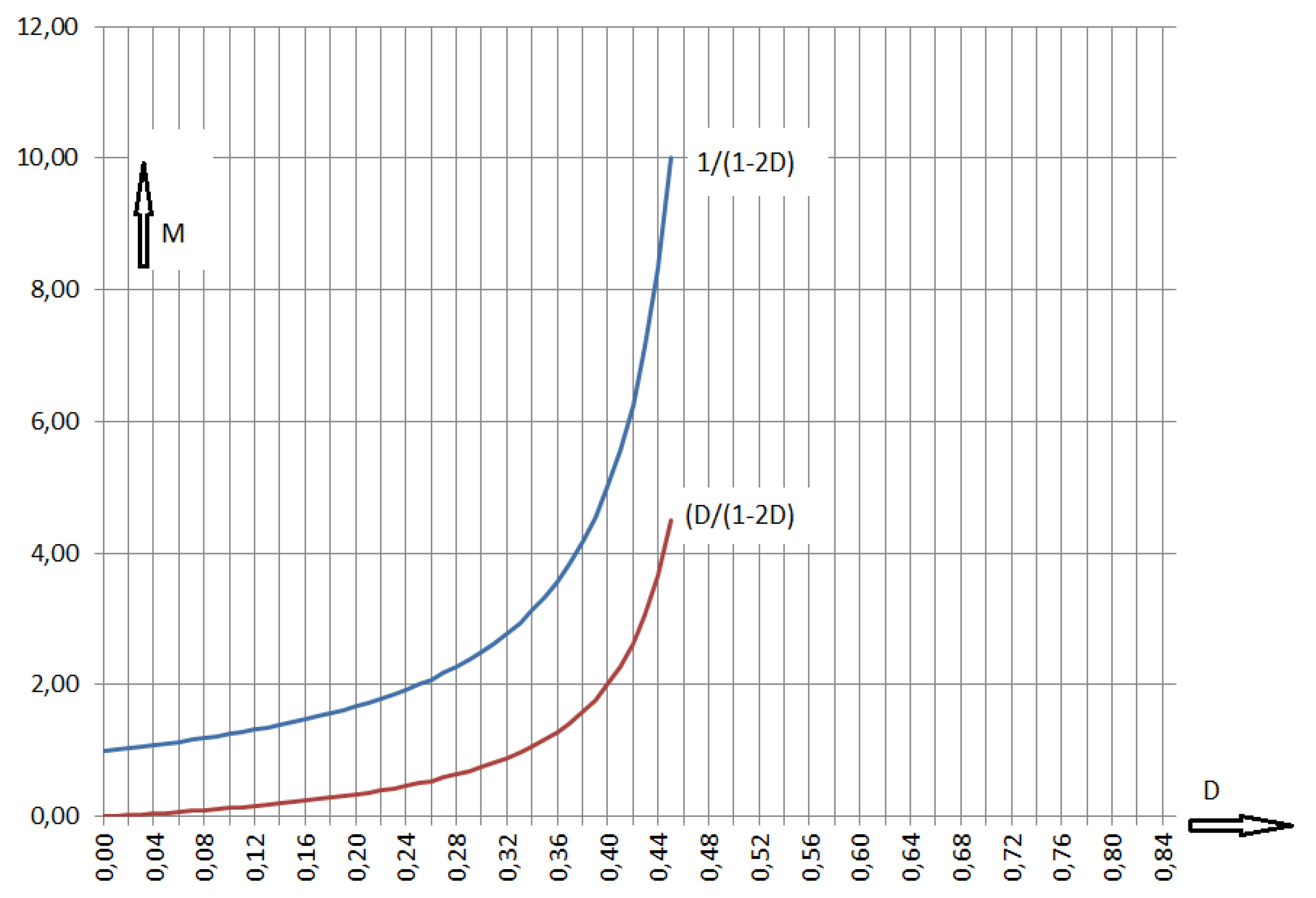
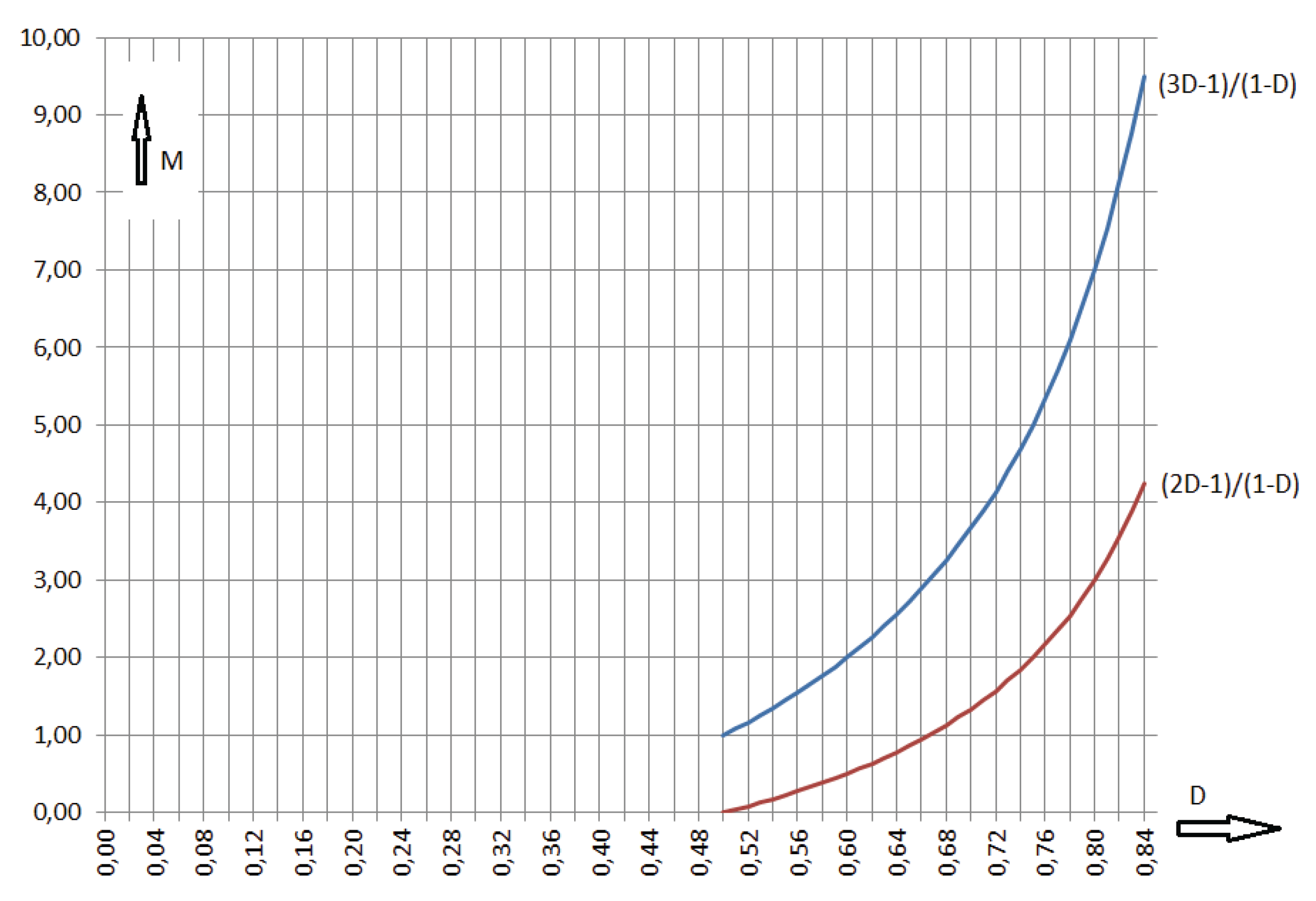
Figure 4.
Voltage transformation ratio M in dependence on the duty cycle; lower line: M of one stage and the higher line: M of the complete converter.
Figure 4.
Voltage transformation ratio M in dependence on the duty cycle; lower line: M of one stage and the higher line: M of the complete converter.
Figure 5.
Type I: Model with equivalent resistor, mode M1.
Figure 5.
Type I: Model with equivalent resistor, mode M1.
Figure 6.
Type I: model with equivalent resistor, mode M2.
Figure 6.
Type I: model with equivalent resistor, mode M2.
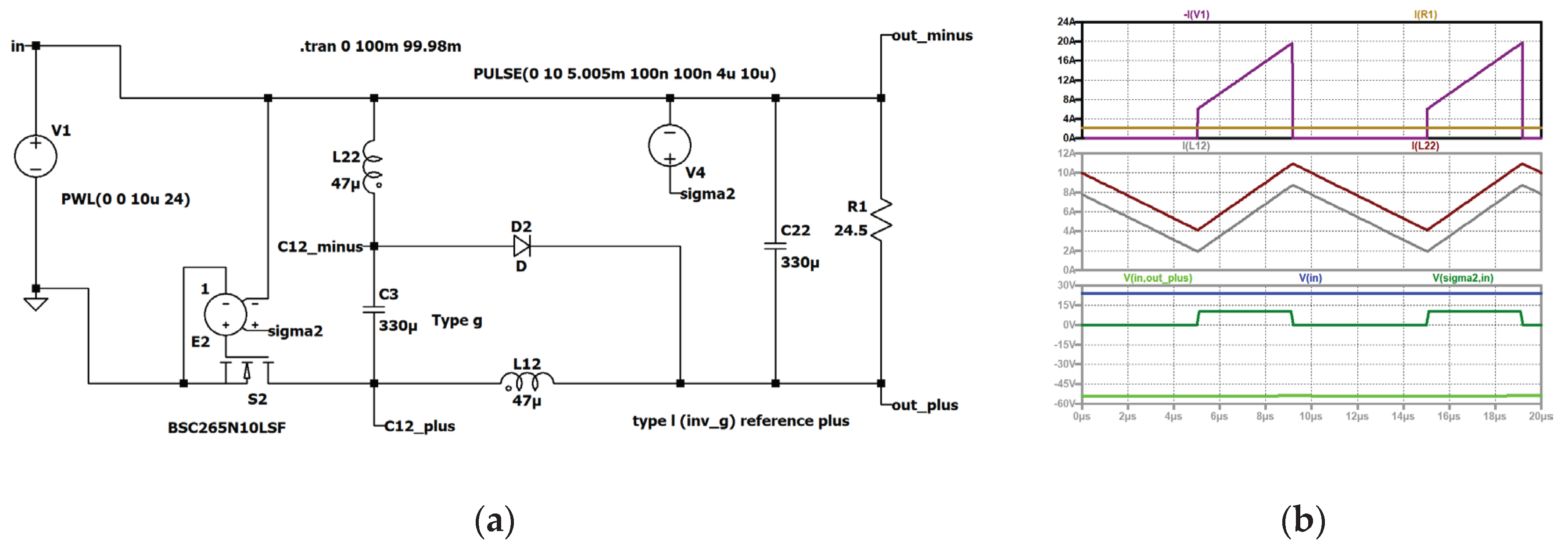
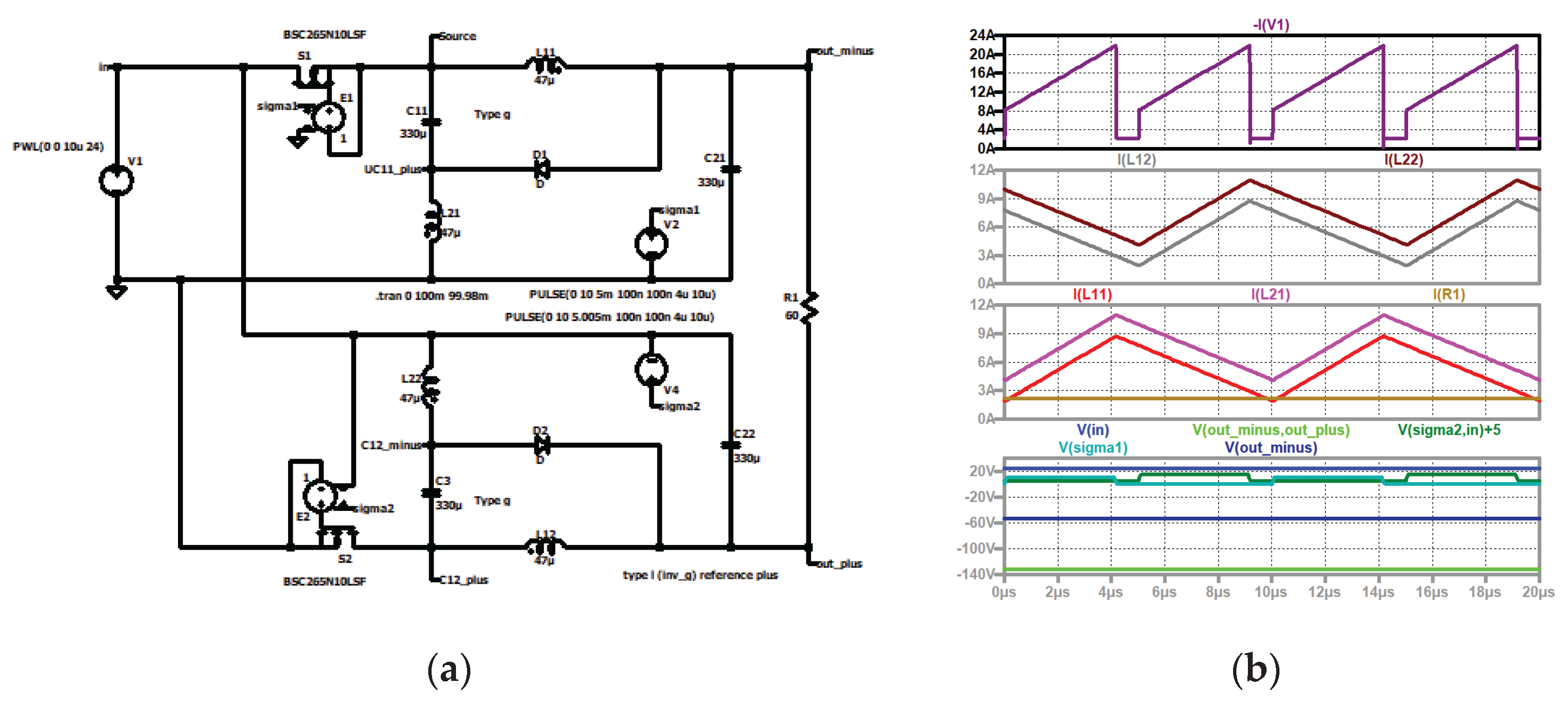
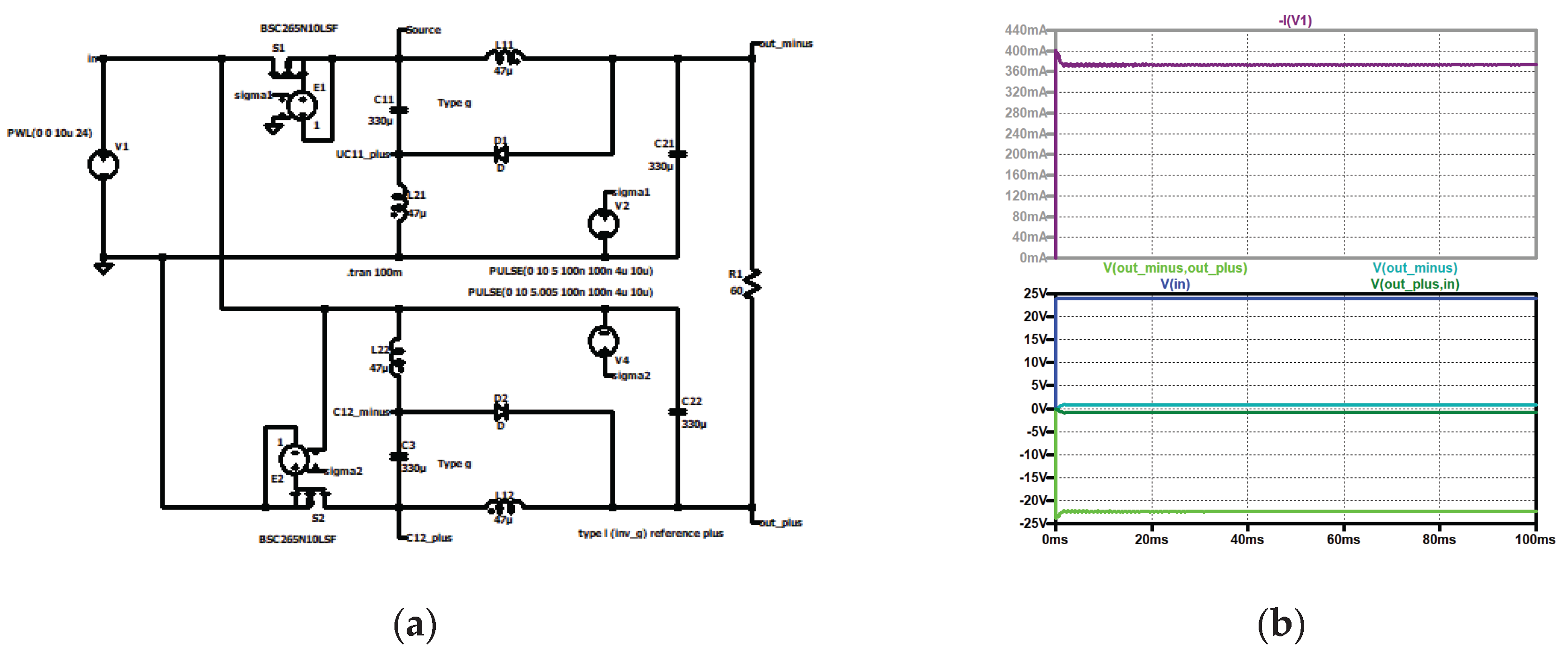
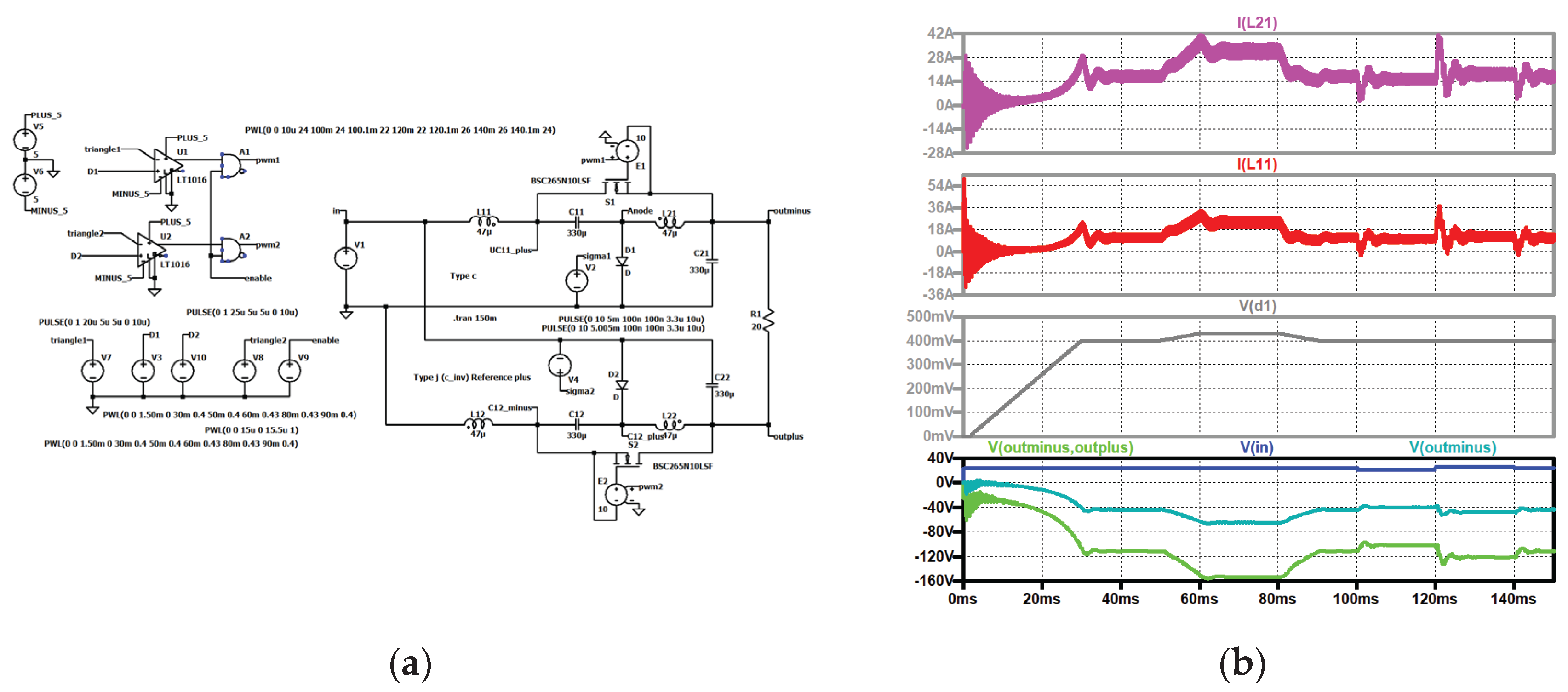
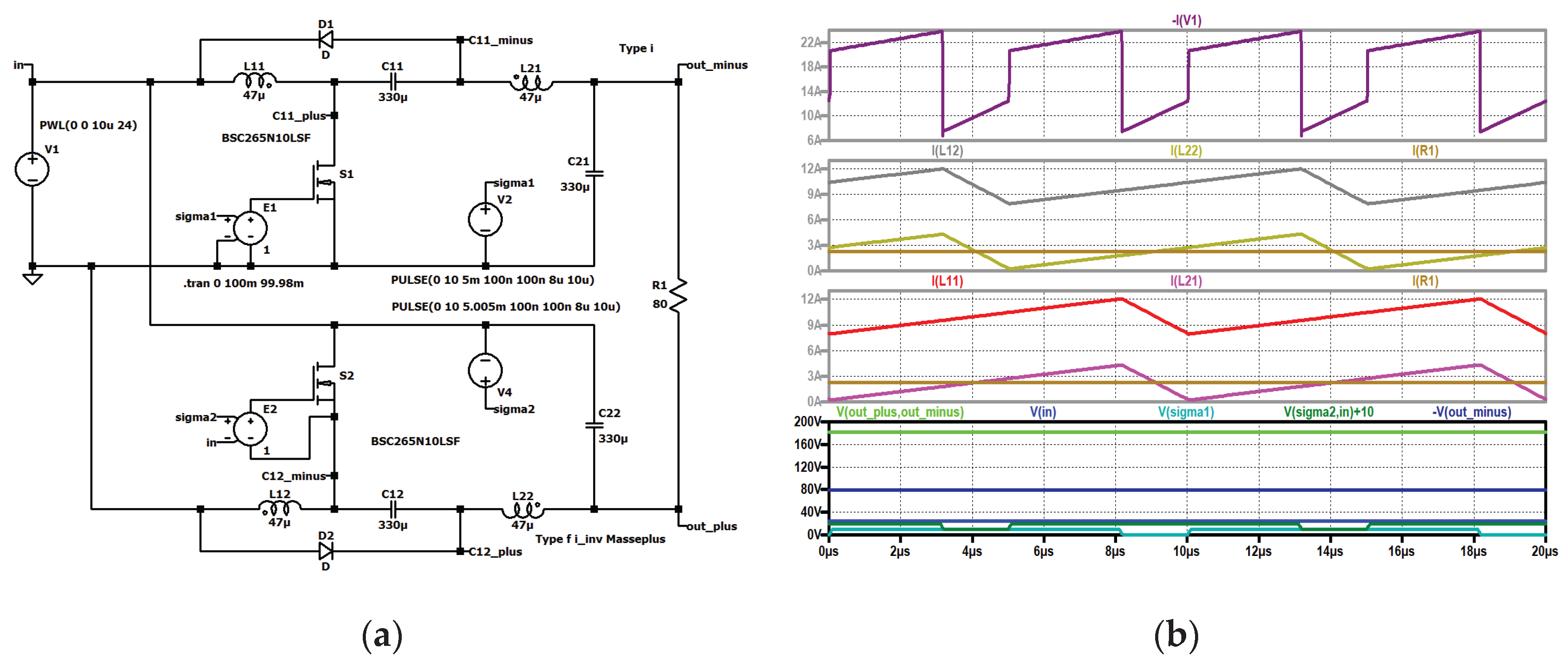
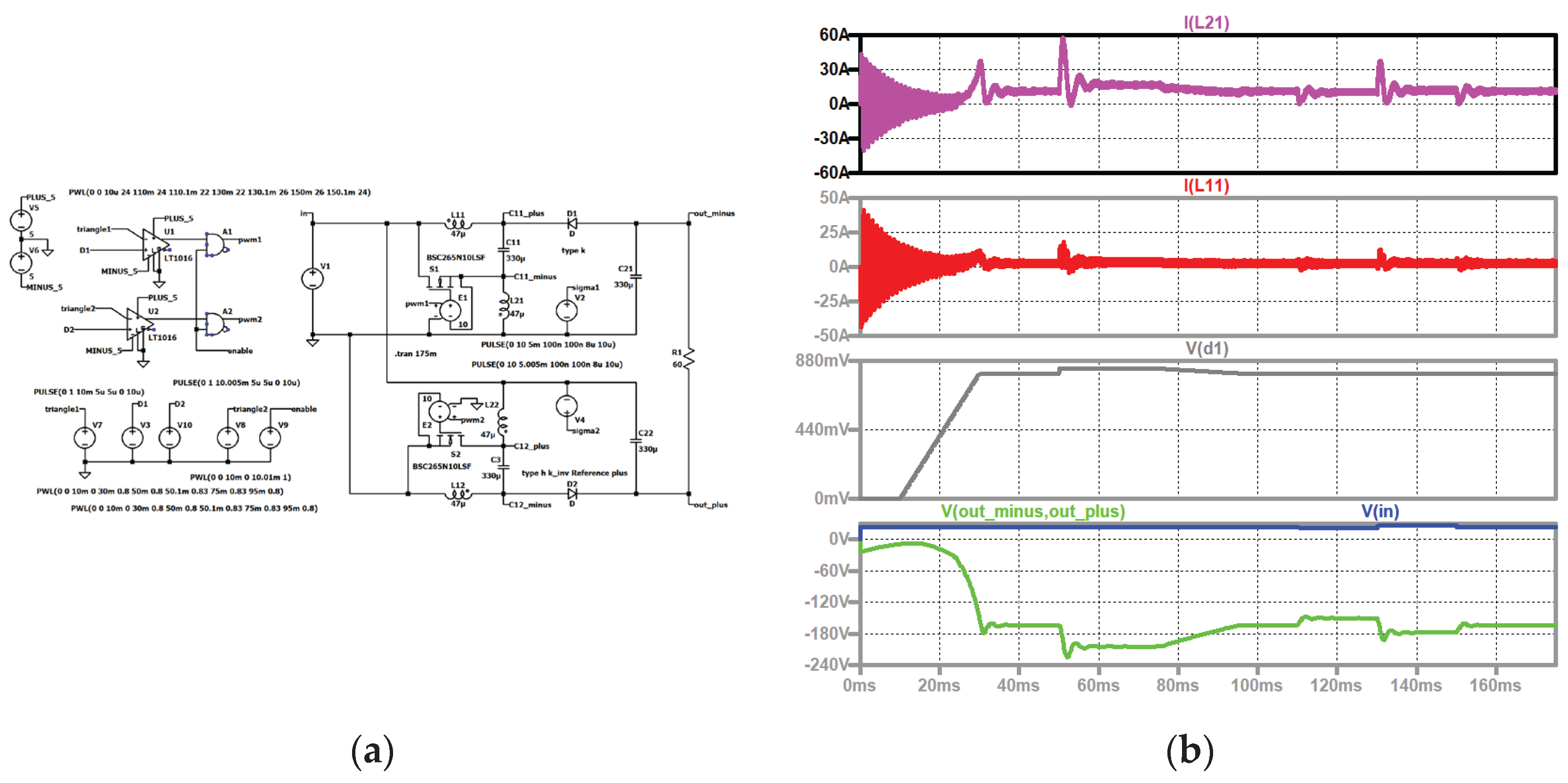
Figure 7.
Type I: (a) simulation circuit, (b) top to bottom: input current (dark violet); current through second coil of the second stage (black), current through the first coil of the second stage (grey); current through the second coil of the first stage (violet), current through the first coil of the first stage (red); input voltage (blue), control signal of the second stage (dark green, shifted), control signal of the first stage (turquoise), output voltage (green).
Figure 7.
Type I: (a) simulation circuit, (b) top to bottom: input current (dark violet); current through second coil of the second stage (black), current through the first coil of the second stage (grey); current through the second coil of the first stage (violet), current through the first coil of the first stage (red); input voltage (blue), control signal of the second stage (dark green, shifted), control signal of the first stage (turquoise), output voltage (green).
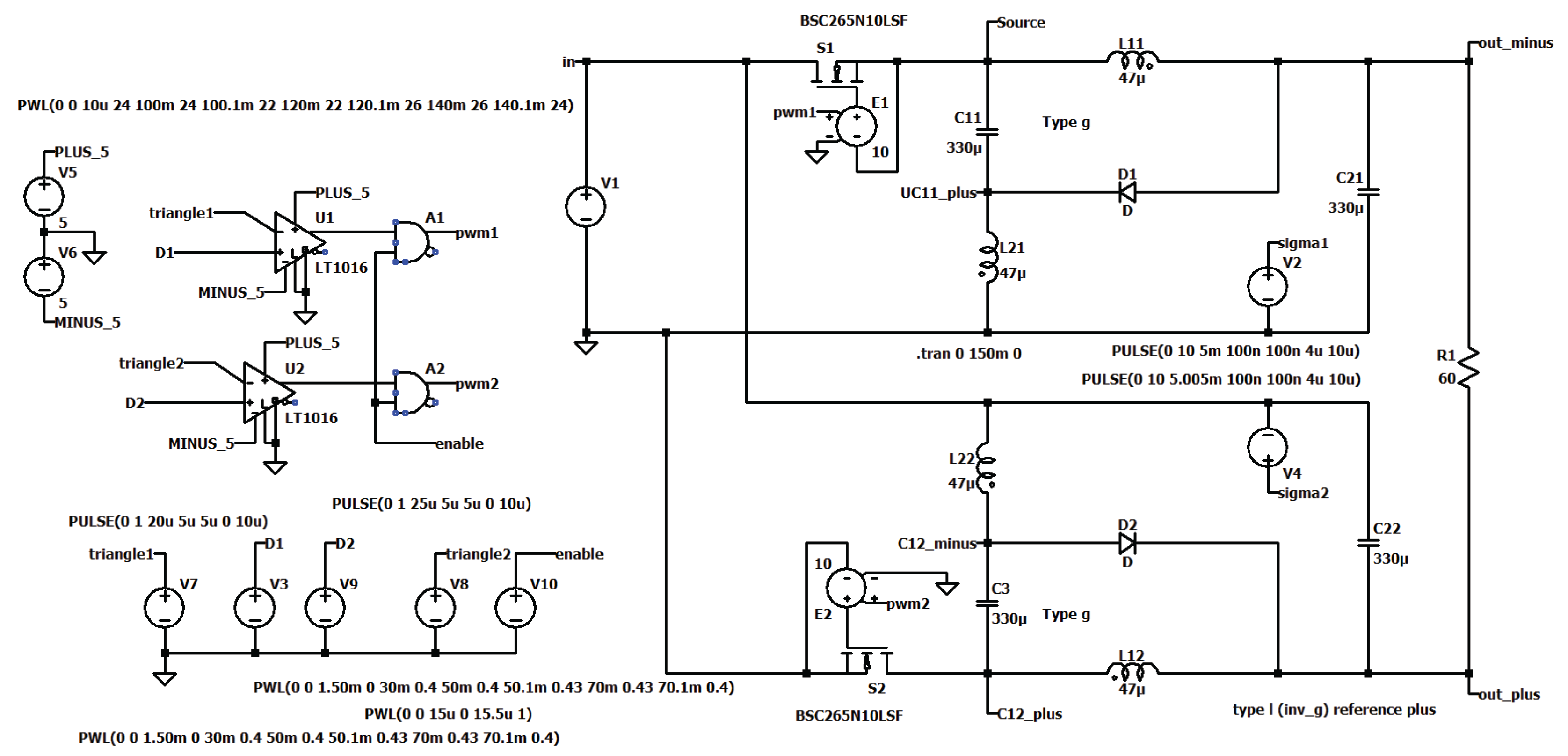
Figure 9.
Type I: simulation circuit.
Figure 9.
Type I: simulation circuit.
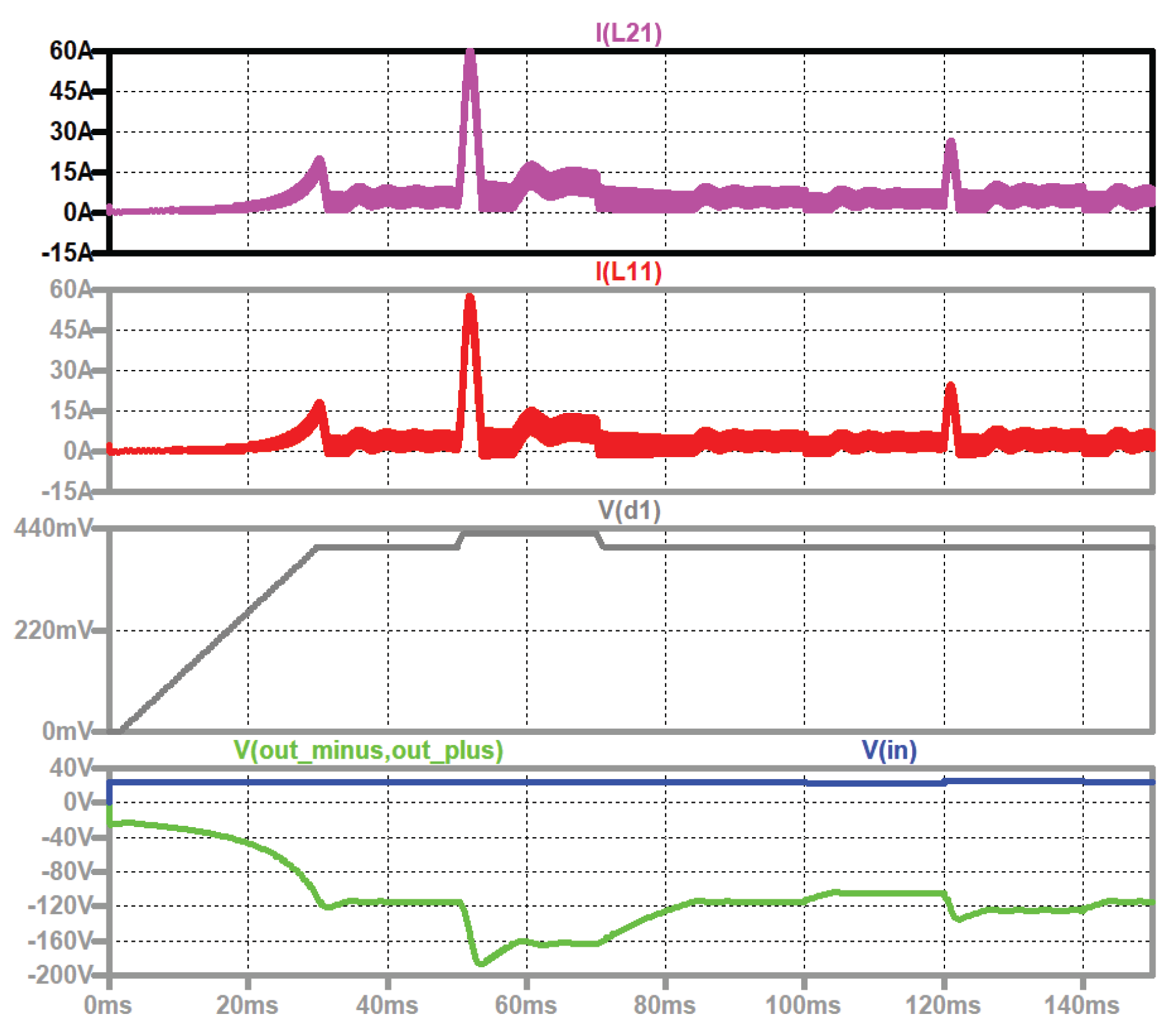
Figure 10.
Type I: start-up, duty cycle steps, input voltage steps: simulation circuit see
Figure 9, top to bottom: current through the second coil of stage one (violet); current through the first coil of stage one (red); duty cycle (grey); input voltage (blue), output voltage (green).
Figure 10.
Type I: start-up, duty cycle steps, input voltage steps: simulation circuit see
Figure 9, top to bottom: current through the second coil of stage one (violet); current through the first coil of stage one (red); duty cycle (grey); input voltage (blue), output voltage (green).
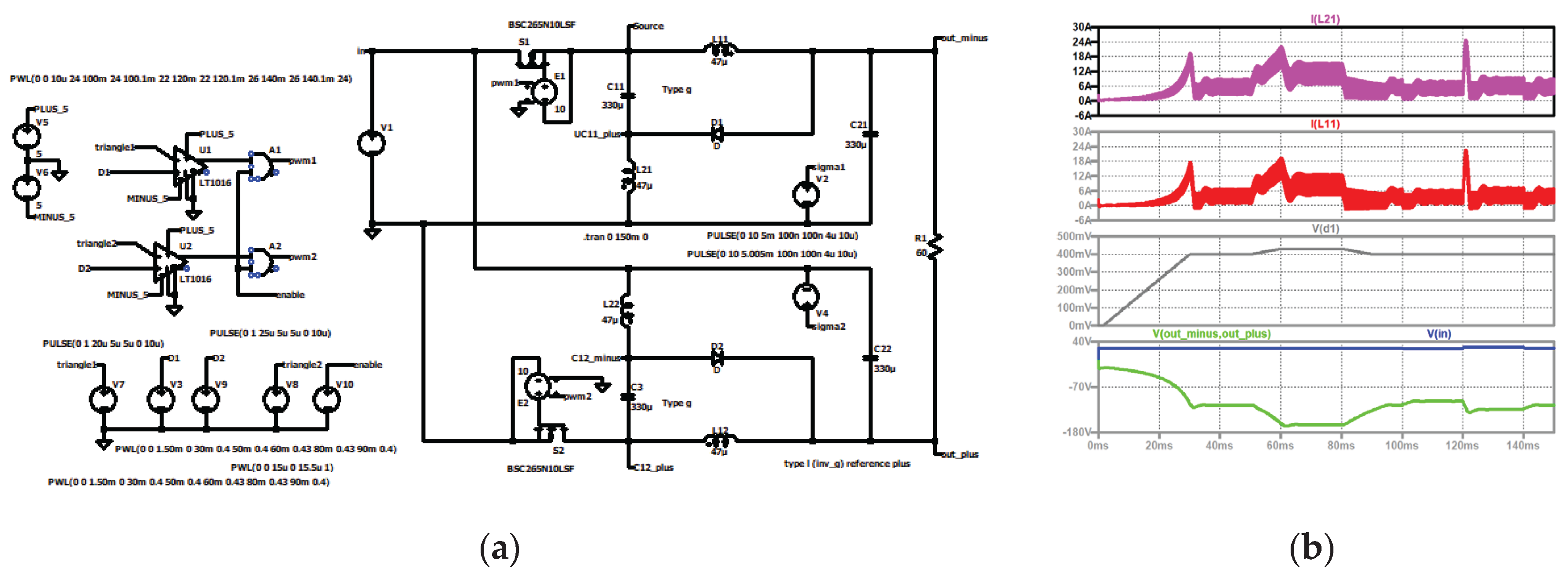
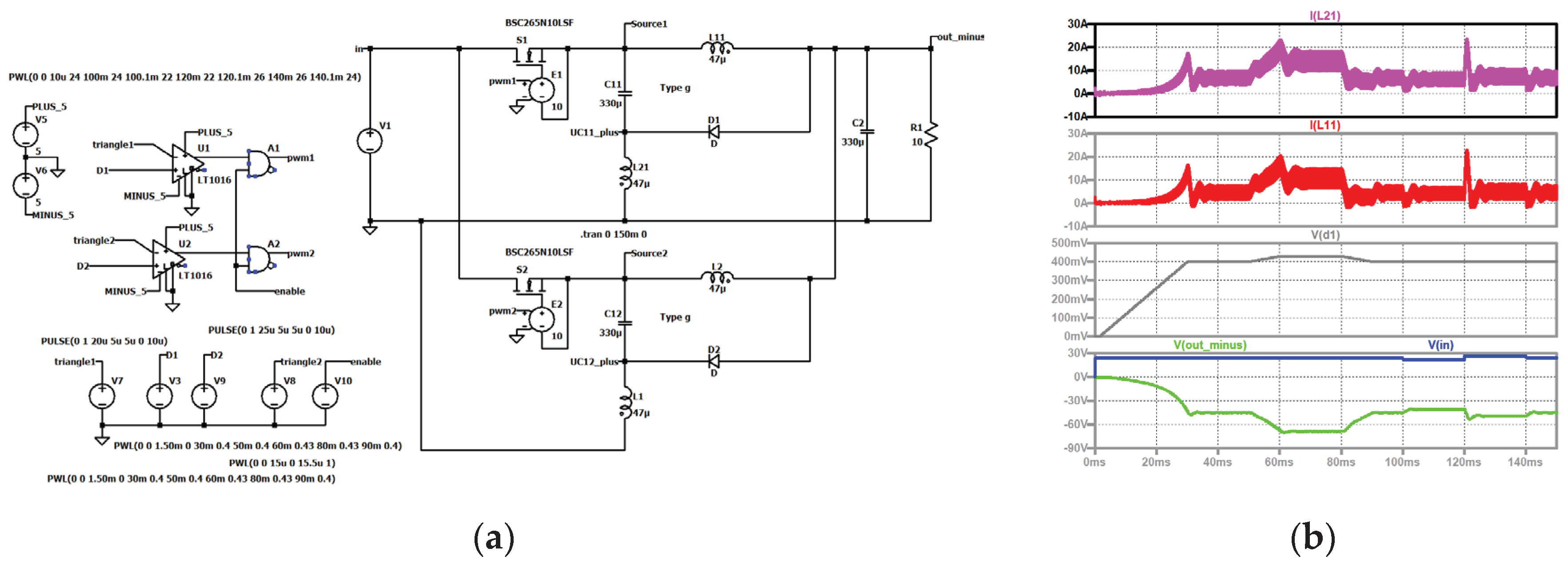
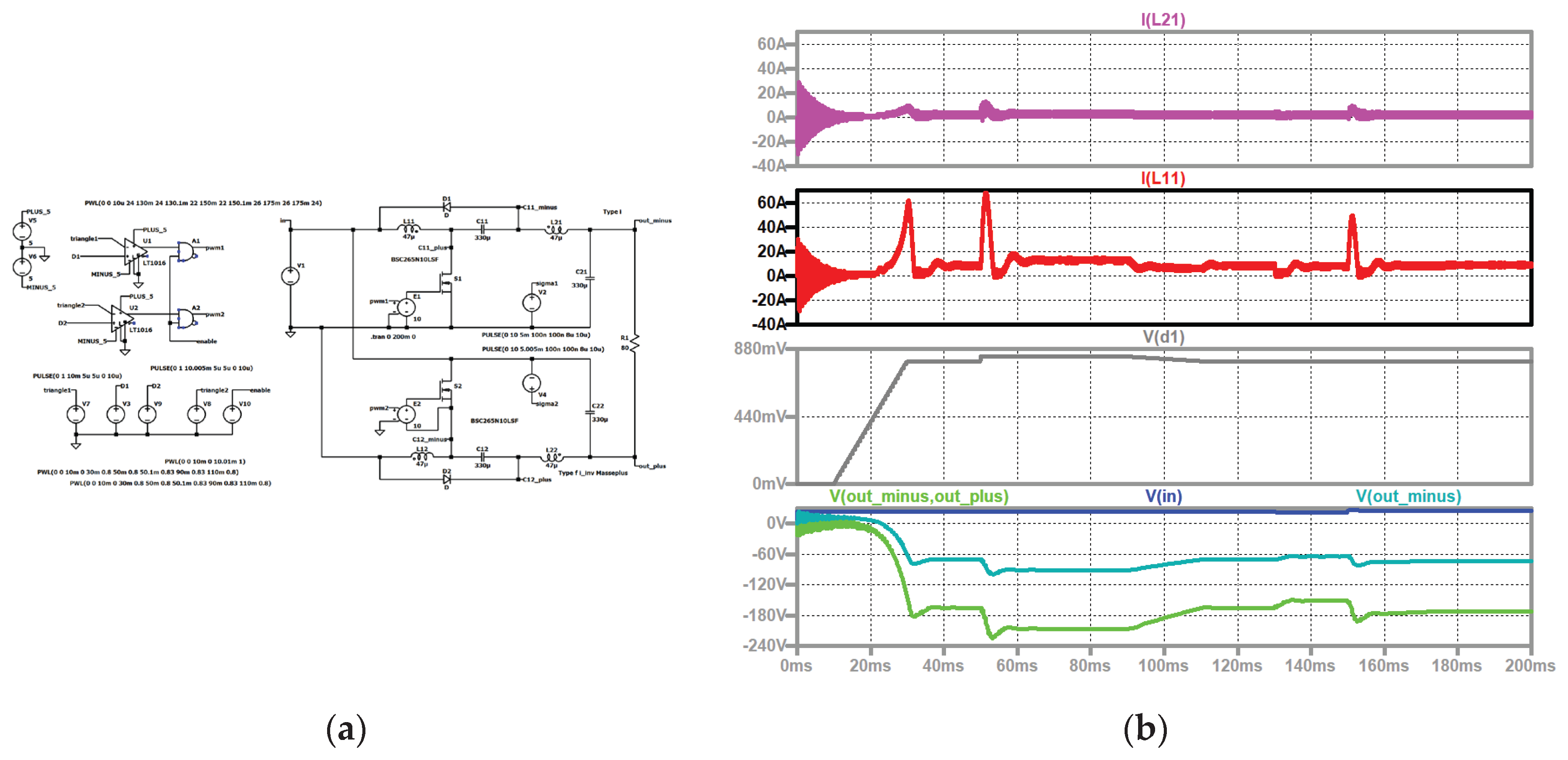
Figure 11.
Type I, start-up, duty cycle changes, input voltage steps: (a) simulation circuit; (b) top to bottom: current through the second coil of stage one (violet); current through the first coil of stage one (red); duty cycle (grey); input voltage (blue), output voltage (green).
Figure 11.
Type I, start-up, duty cycle changes, input voltage steps: (a) simulation circuit; (b) top to bottom: current through the second coil of stage one (violet); current through the first coil of stage one (red); duty cycle (grey); input voltage (blue), output voltage (green).
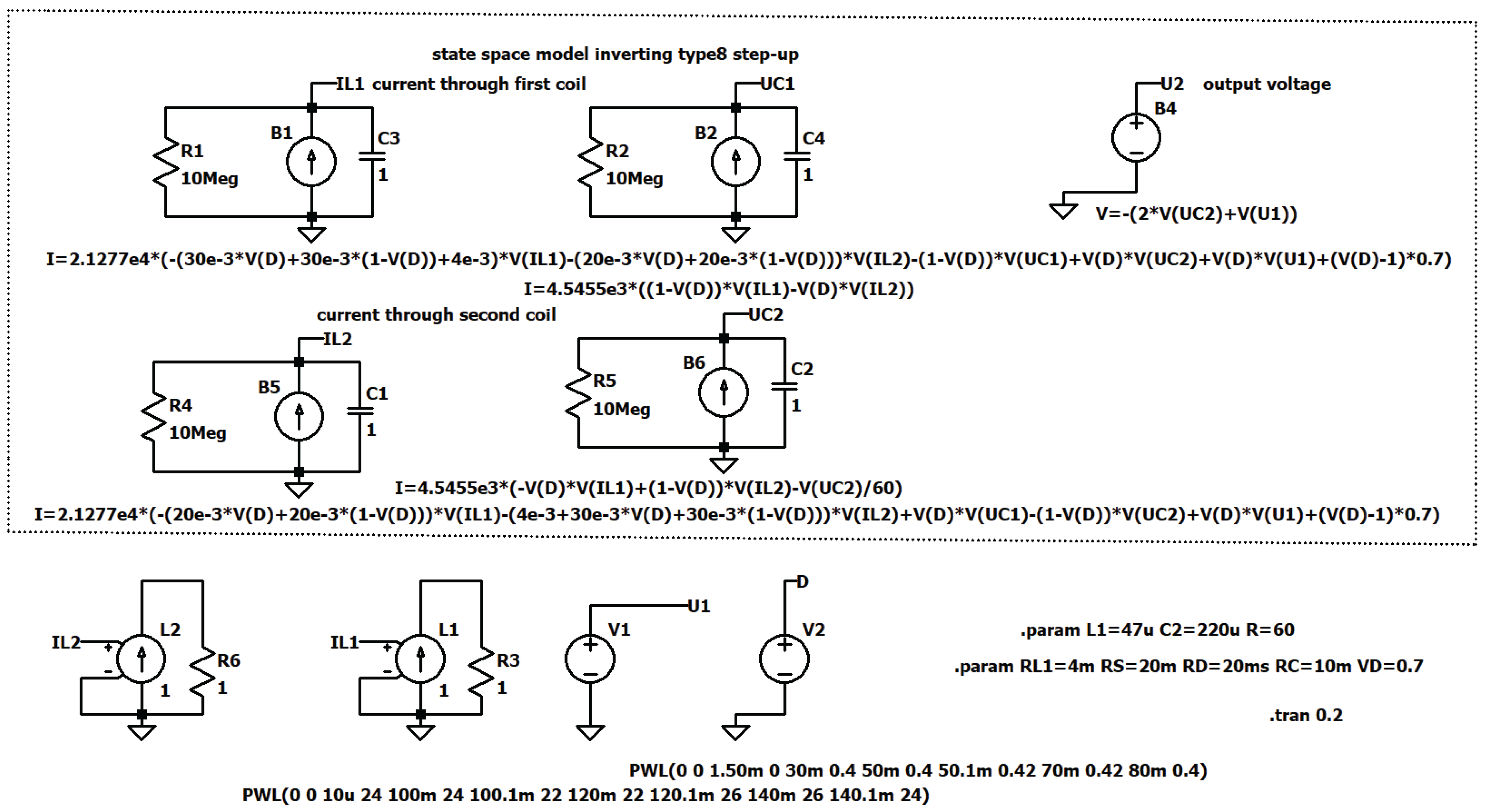
Figure 12.
Type I, simulation circuit to solve the differential matrix equation (18).
Figure 12.
Type I, simulation circuit to solve the differential matrix equation (18).
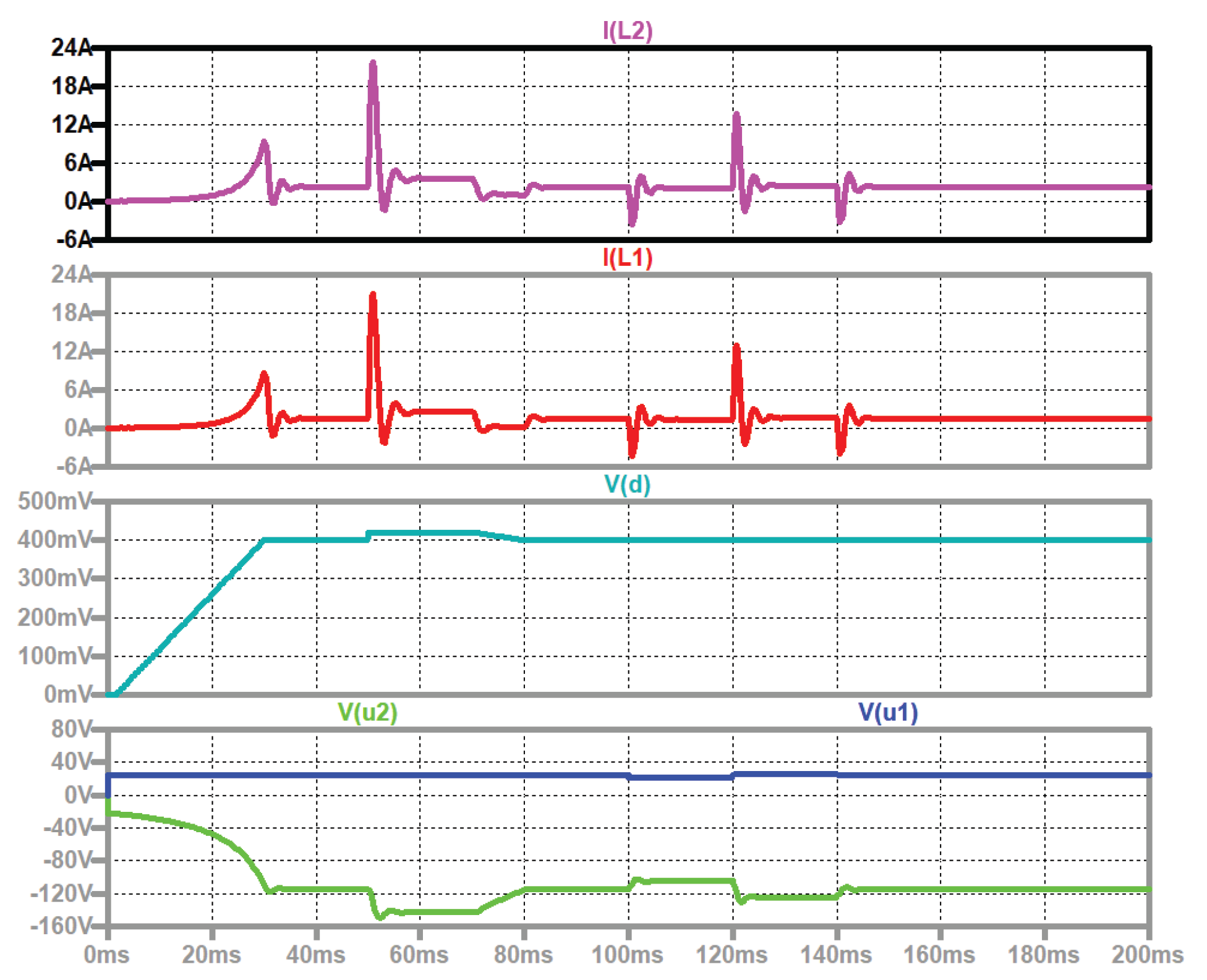
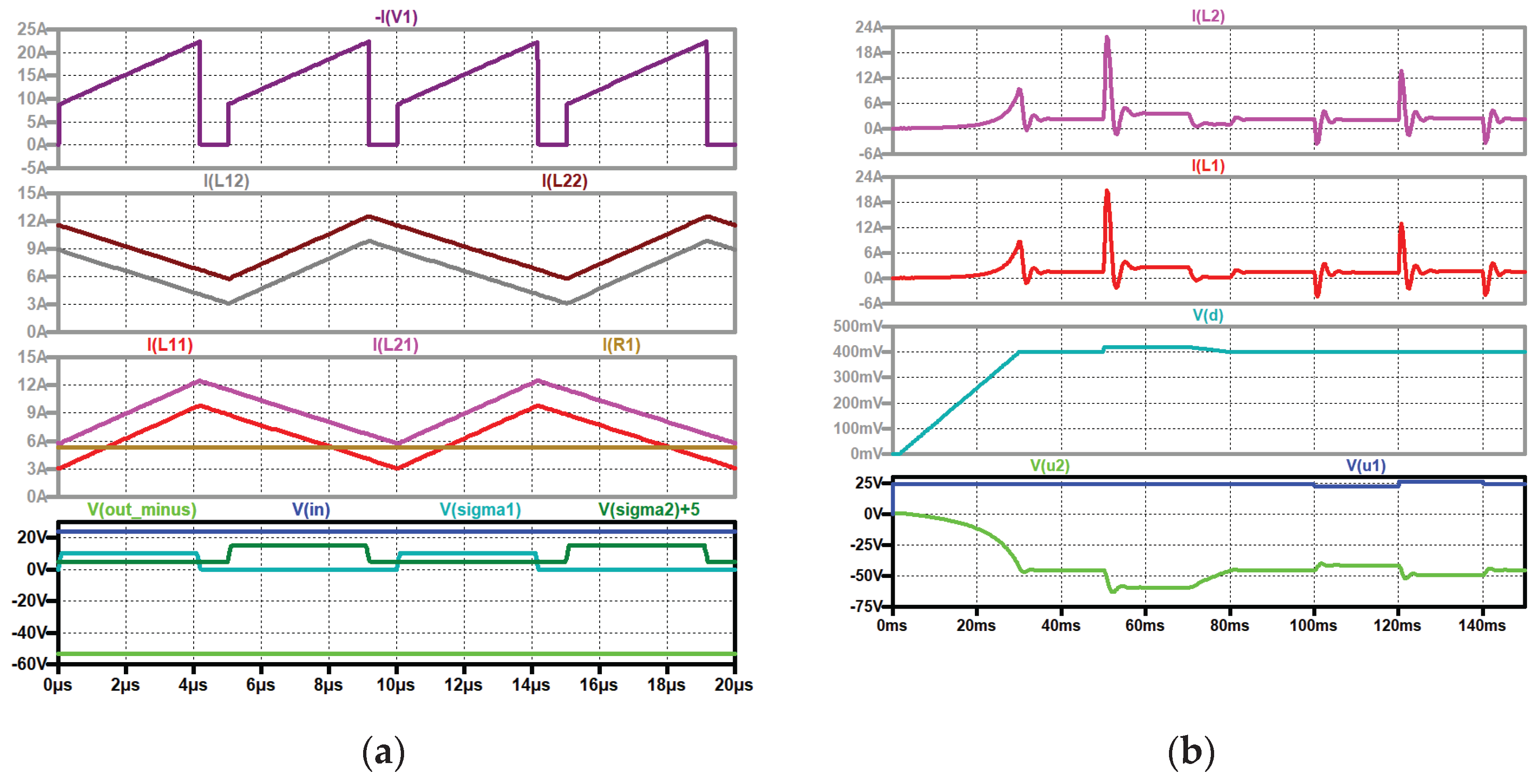
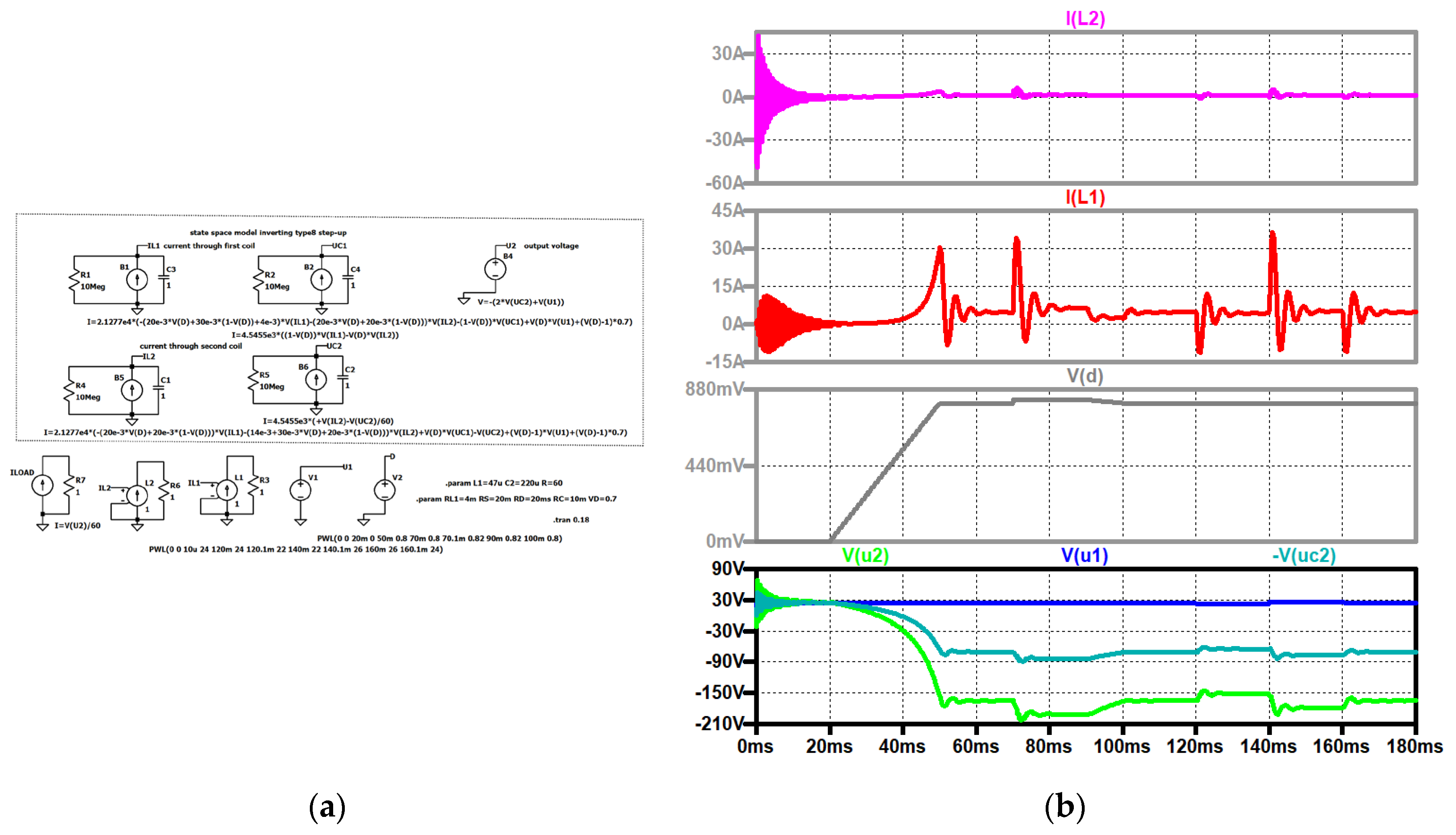
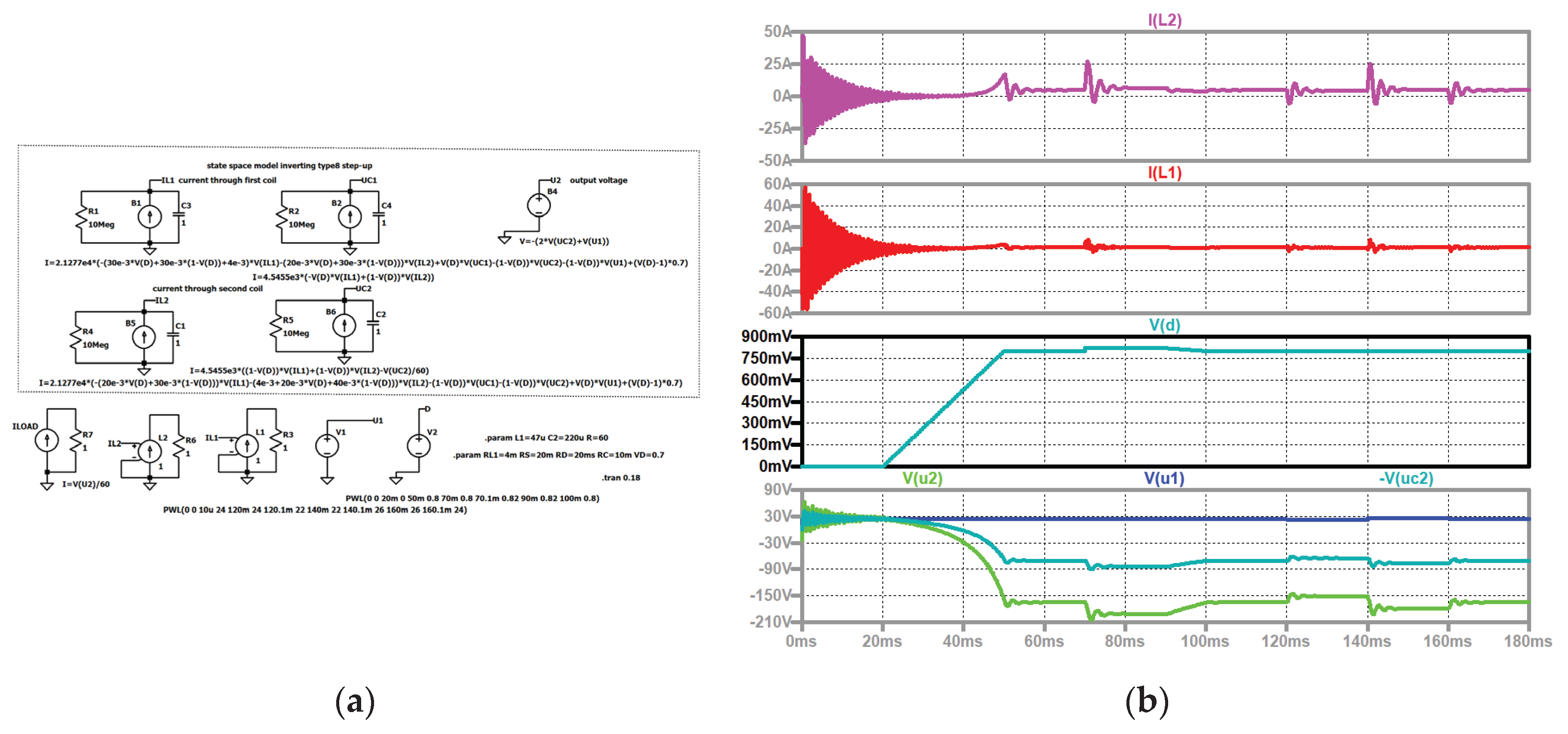
Figure 13.
Type I, simulation circuit see
Figure 12, start-up, duty cycle changes, input voltage steps, top to bottom: current through the second coil of the first stage (violet), current through the first coil of the first stage (red); duty cycle (grey); input voltage (blue), output voltage (green).
Figure 13.
Type I, simulation circuit see
Figure 12, start-up, duty cycle changes, input voltage steps, top to bottom: current through the second coil of the first stage (violet), current through the first coil of the first stage (red); duty cycle (grey); input voltage (blue), output voltage (green).
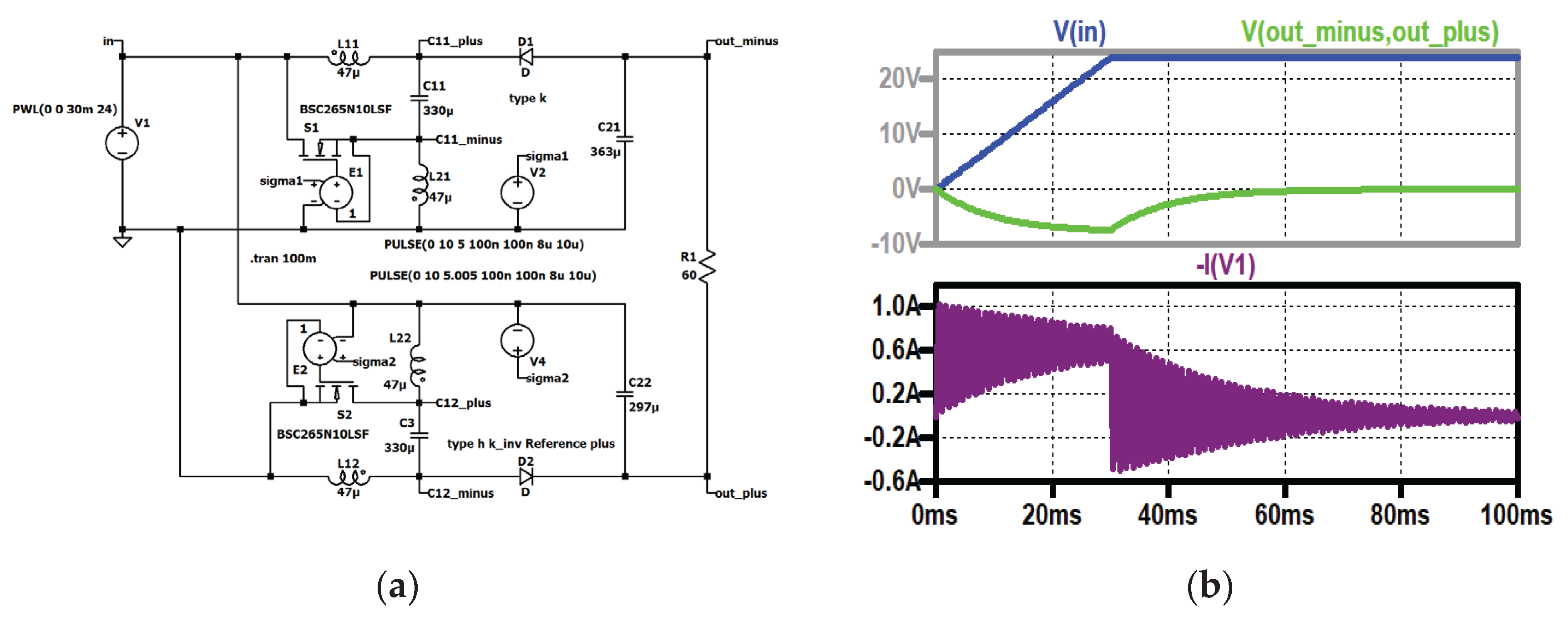
Figure 14.
Type I: (a) simulation circuit; (b) up to down: input current (dark violet); input voltage (blue), voltage across output capacitor of stage 1 (turquoise), voltage across output capacitor of stage 2 (dark green), output voltage (turquoise).
Figure 14.
Type I: (a) simulation circuit; (b) up to down: input current (dark violet); input voltage (blue), voltage across output capacitor of stage 1 (turquoise), voltage across output capacitor of stage 2 (dark green), output voltage (turquoise).
Figure 15.
Type I interleaved: (a) simulation circuit; (b) top to bottom: current through second coil of the first stage (violet), current through first coil of the first stage (red); duty cycle (grey); input voltage (blue), output voltage (green).
Figure 15.
Type I interleaved: (a) simulation circuit; (b) top to bottom: current through second coil of the first stage (violet), current through first coil of the first stage (red); duty cycle (grey); input voltage (blue), output voltage (green).
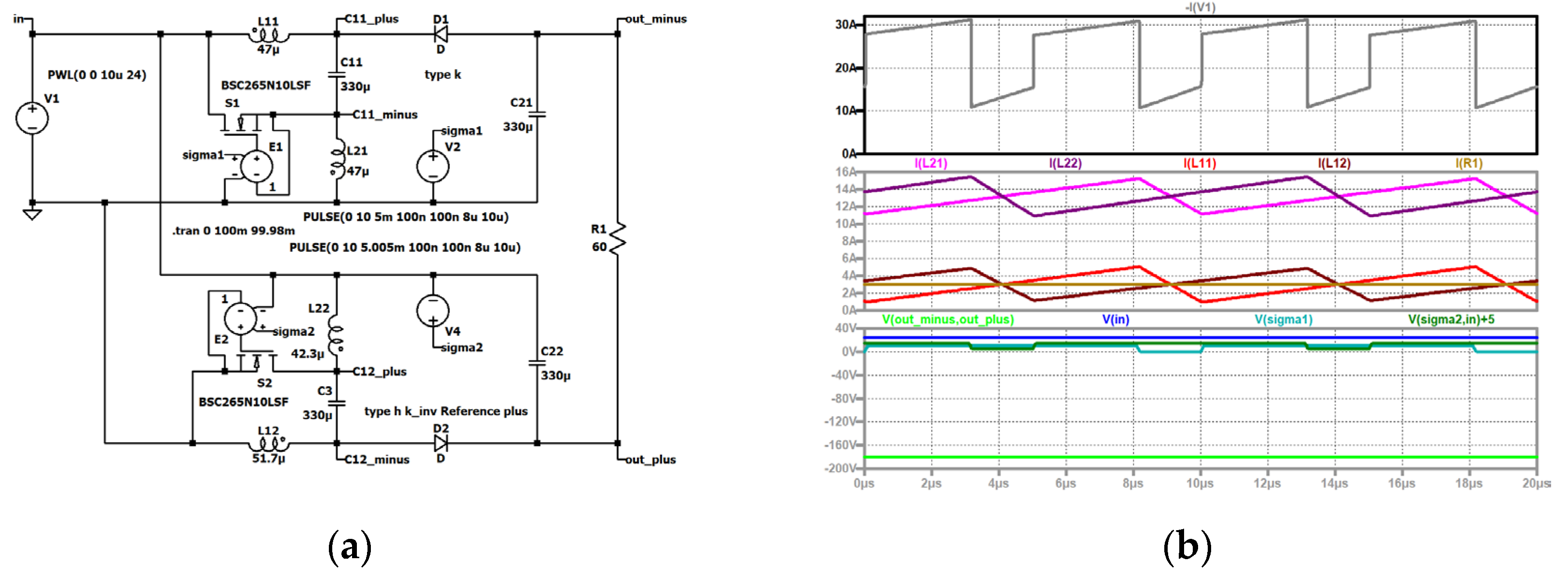
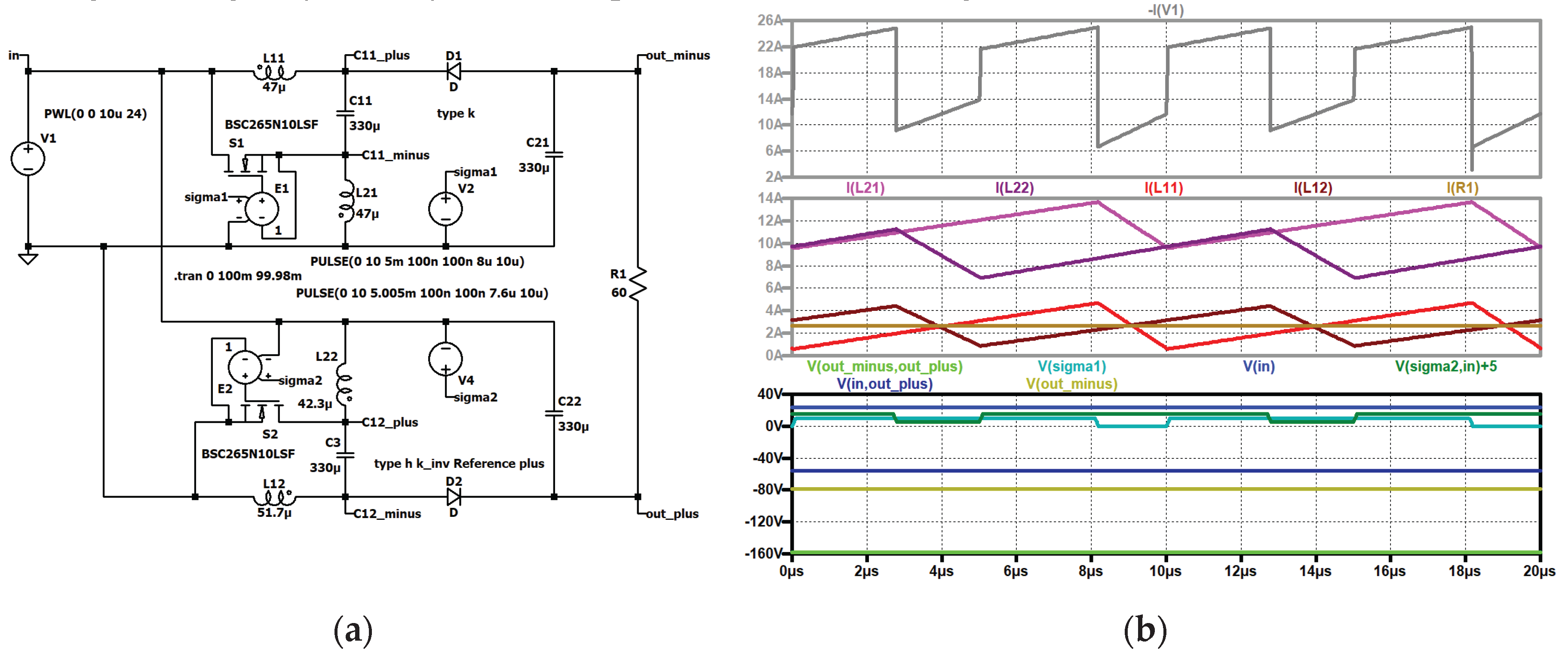
Figure 16.
type 8 interleaved: (a) in the steady state, simulation circuit, top to bottom: input current (dark violet); current through the second coil of the second stage (black), current through the first coil of the second stage (grey); current through second coil of the first stage (violet), current through the first coil of the first stage (red); input voltage (blue), control signal of the switch of the second stage (dark green, shifted), control signal of the switch of the first stage (turquoise), output voltage (green); (b) . top to bottom: current through the second coil of the first stage (violet), current through the first coil of the first stage (red); duty cycle (grey); input voltage (blue), output voltage (green).
Figure 16.
type 8 interleaved: (a) in the steady state, simulation circuit, top to bottom: input current (dark violet); current through the second coil of the second stage (black), current through the first coil of the second stage (grey); current through second coil of the first stage (violet), current through the first coil of the first stage (red); input voltage (blue), control signal of the switch of the second stage (dark green, shifted), control signal of the switch of the first stage (turquoise), output voltage (green); (b) . top to bottom: current through the second coil of the first stage (violet), current through the first coil of the first stage (red); duty cycle (grey); input voltage (blue), output voltage (green).
Figure 17.
Type II: circuit diagram.
Figure 17.
Type II: circuit diagram.
Figure 18.
Type II duty cycle 1/3: (a) simulation circuit; (b) top to bottom: current through the second coil of stage one (violet), current through the second coil of stage two (dark violet), current through the first coil of stage one (red), current through the first coil of stage two (black), load current (brown); input voltage (blue), control signal of the second switch (dark green, shifted), control signal of the first switch (turquoise), output voltage (green).
Figure 18.
Type II duty cycle 1/3: (a) simulation circuit; (b) top to bottom: current through the second coil of stage one (violet), current through the second coil of stage two (dark violet), current through the first coil of stage one (red), current through the first coil of stage two (black), load current (brown); input voltage (blue), control signal of the second switch (dark green, shifted), control signal of the first switch (turquoise), output voltage (green).
Figure 19.
Type II, dynamic simulation: (a) simulation circuit; (b) top to bottom: current through the second coil of stage one (violet); current through the first coil of the first stage (red); duty cycle (grey); input voltage (blue), output voltage of stage one, and output voltage of the complete converter.
Figure 19.
Type II, dynamic simulation: (a) simulation circuit; (b) top to bottom: current through the second coil of stage one (violet); current through the first coil of the first stage (red); duty cycle (grey); input voltage (blue), output voltage of stage one, and output voltage of the complete converter.
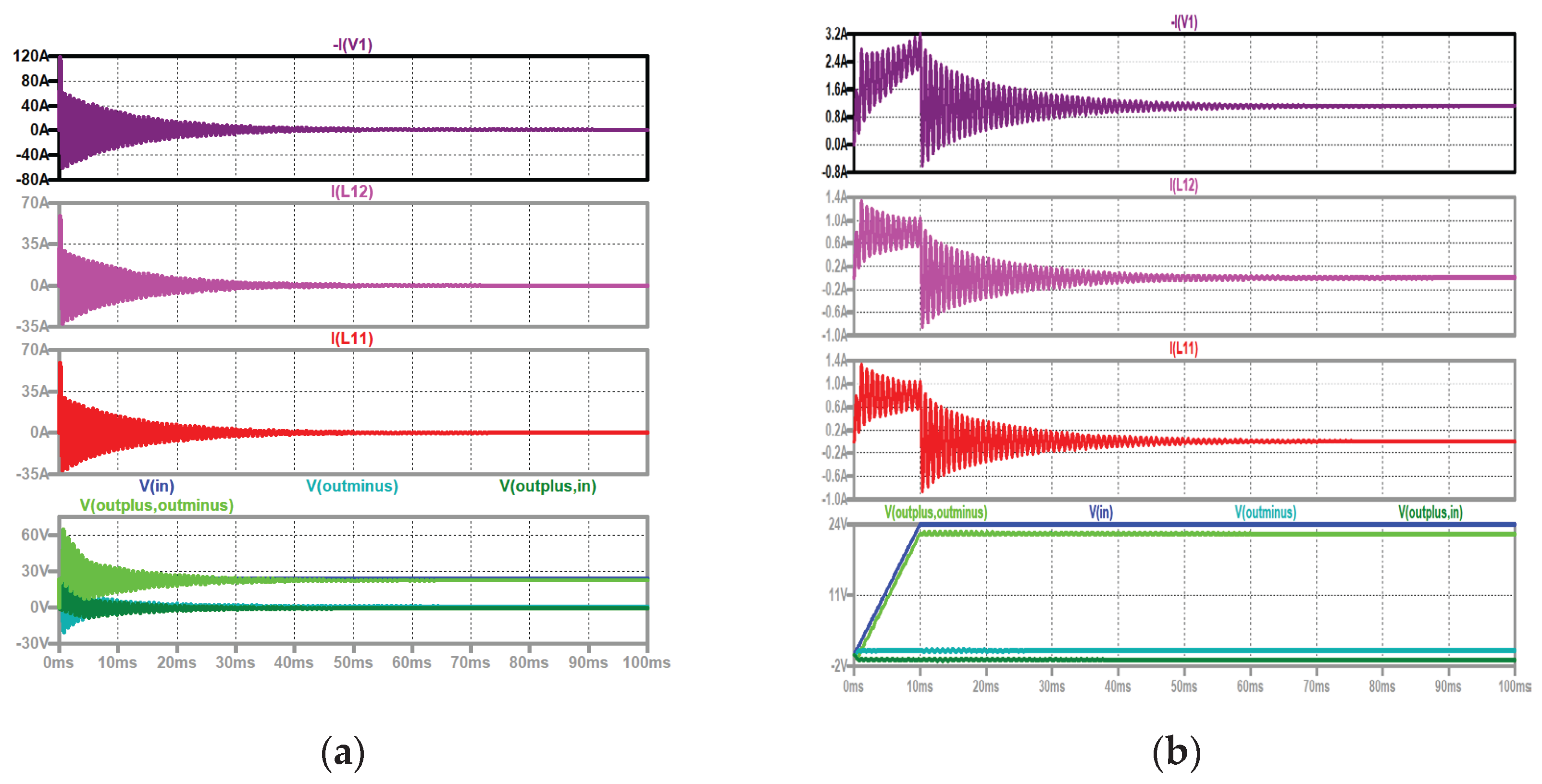
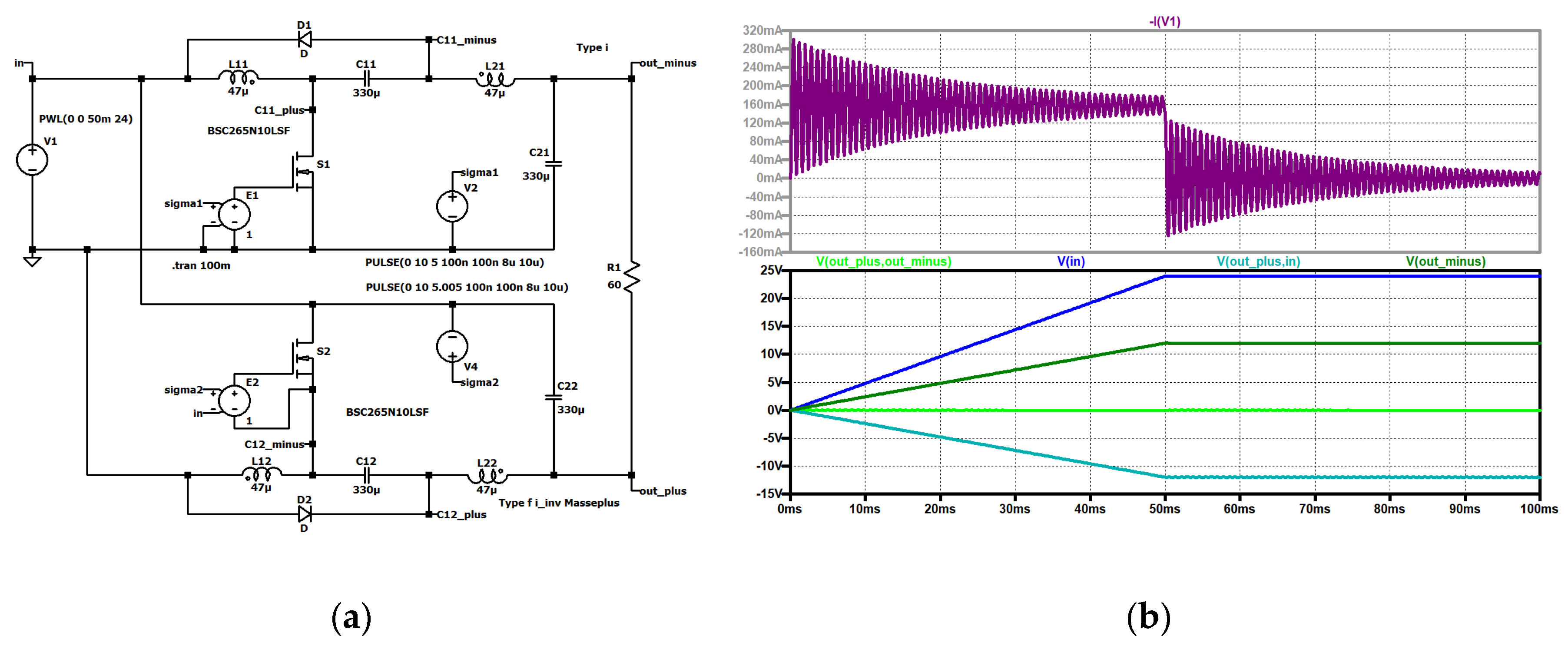
Figure 20.
Type II, inrush: (a) up to down: input current (dark violet); current through the first coil of stage 2 (violet); current through the first coil of stage 1 (red); output voltage of stage 1 (turquoise), output voltage (green), output voltage of stage 2 (dark green); (b) up to down: input current (dark violet); current through the first coil of stage 2 (violet); current through the first coil of stage 1 (red); input voltage (blue), output voltage (green), output voltage of stage 1 (turquoise), output voltage of stage 2 (dark green).
Figure 20.
Type II, inrush: (a) up to down: input current (dark violet); current through the first coil of stage 2 (violet); current through the first coil of stage 1 (red); output voltage of stage 1 (turquoise), output voltage (green), output voltage of stage 2 (dark green); (b) up to down: input current (dark violet); current through the first coil of stage 2 (violet); current through the first coil of stage 1 (red); input voltage (blue), output voltage (green), output voltage of stage 1 (turquoise), output voltage of stage 2 (dark green).
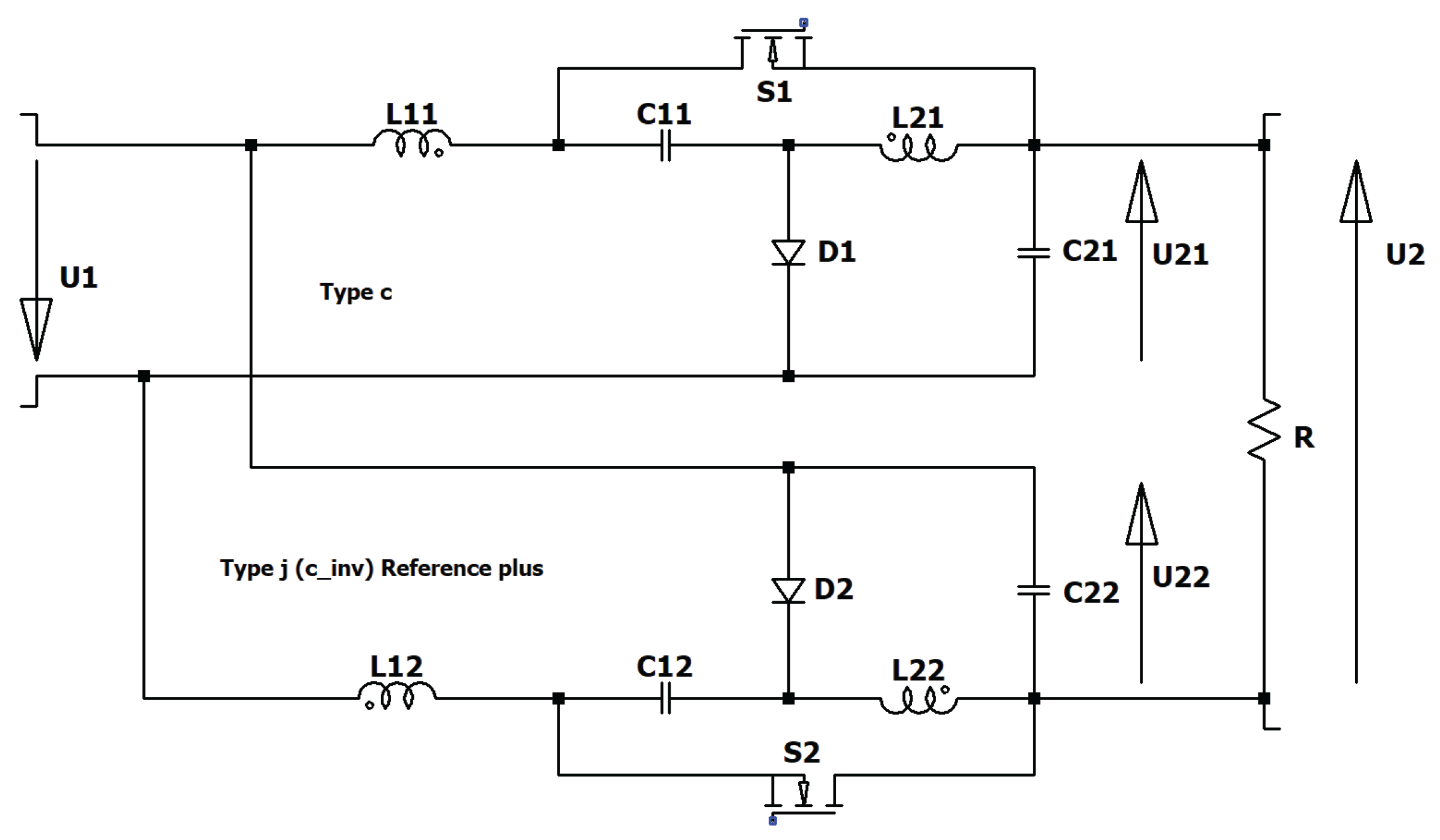
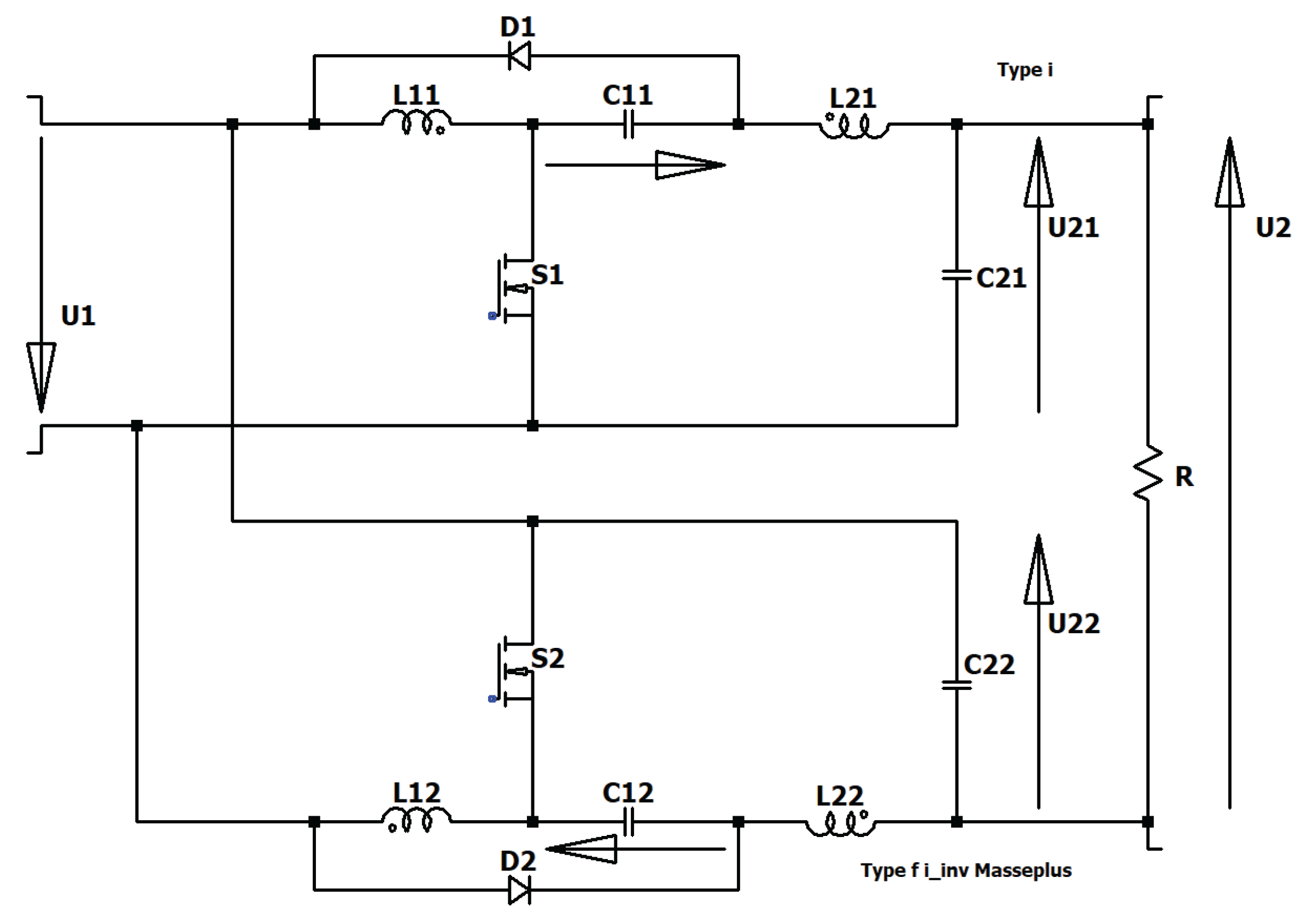
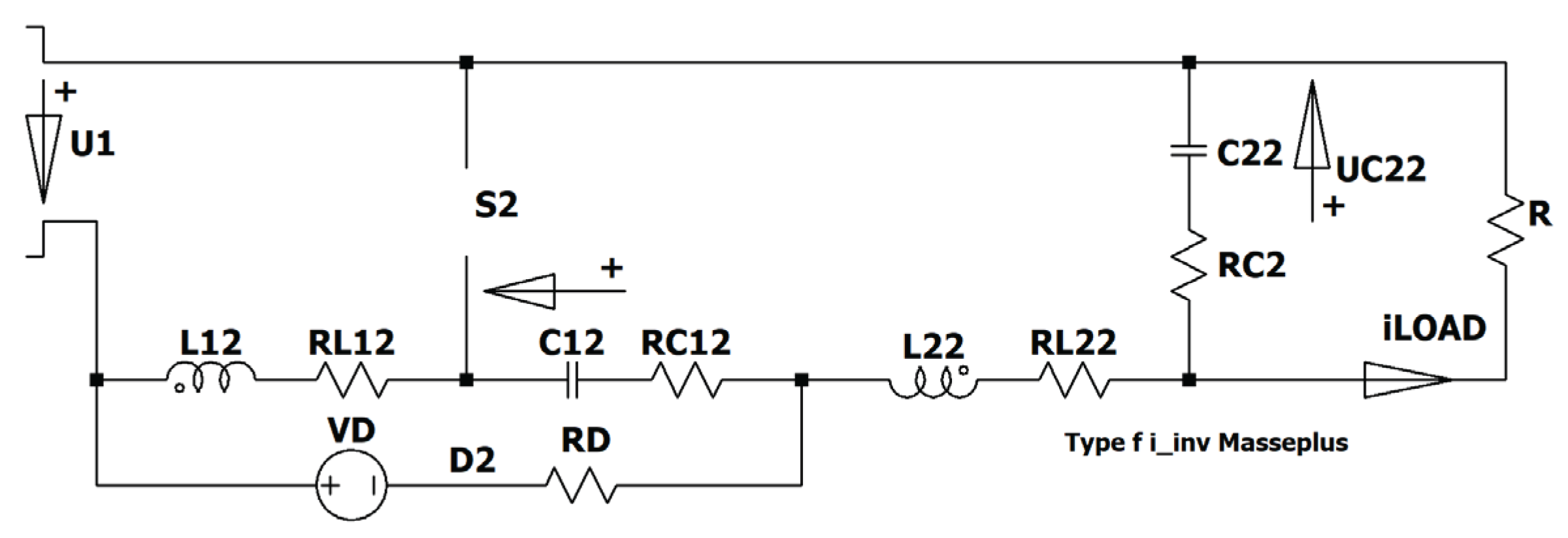
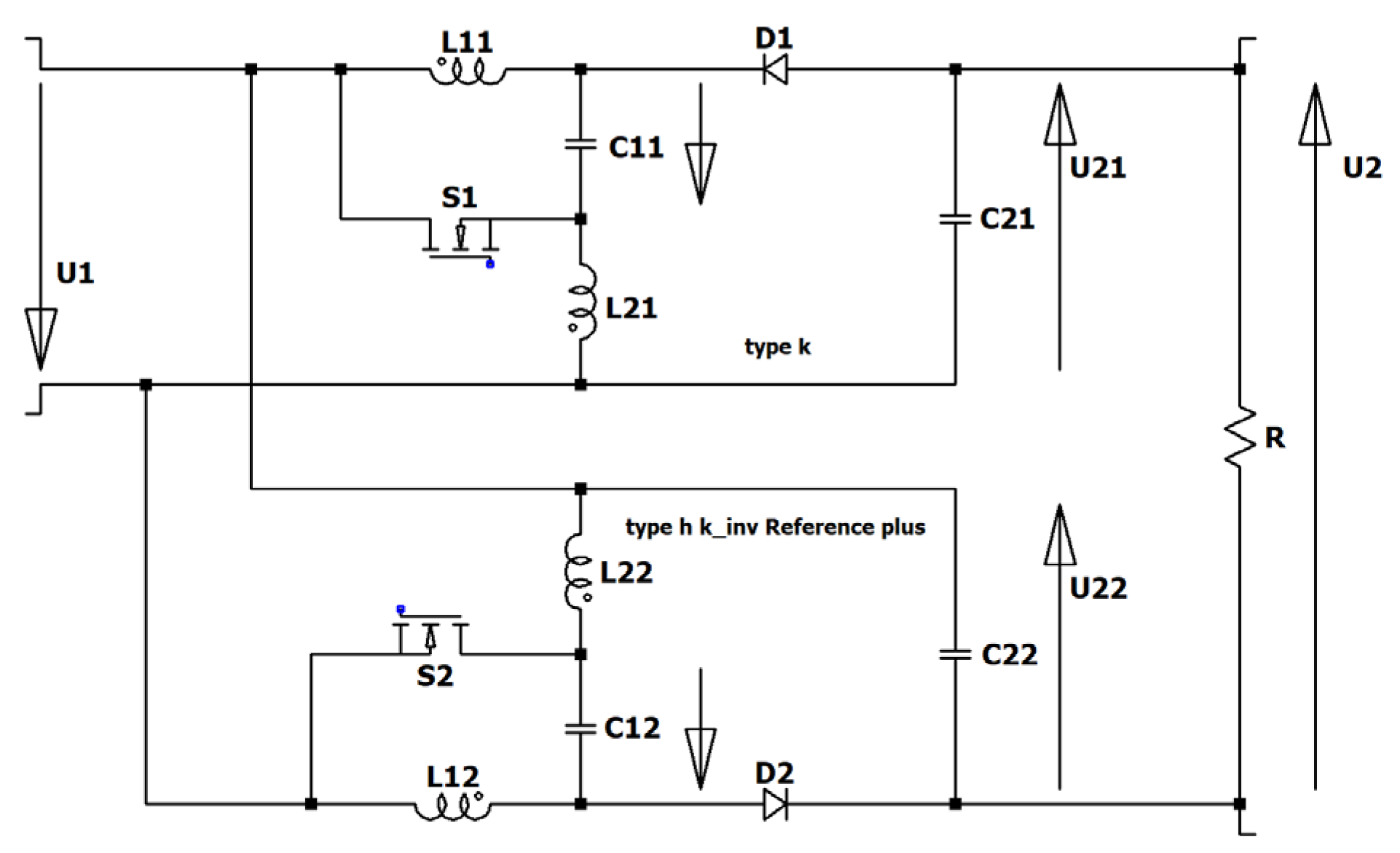
Figure 21.
Circuit diagram of the floating two-stage converter type III.
Figure 21.
Circuit diagram of the floating two-stage converter type III.
Figure 22.
type III: voltage transformation ratio of the two-stage converter (blue) and of a single stage (brown).
Figure 22.
type III: voltage transformation ratio of the two-stage converter (blue) and of a single stage (brown).
Figure 22.
type 5: equivalent circuit during M1.
Figure 22.
type 5: equivalent circuit during M1.
Figure 23.
Type III equivalent circuit during M2.
Figure 23.
Type III equivalent circuit during M2.
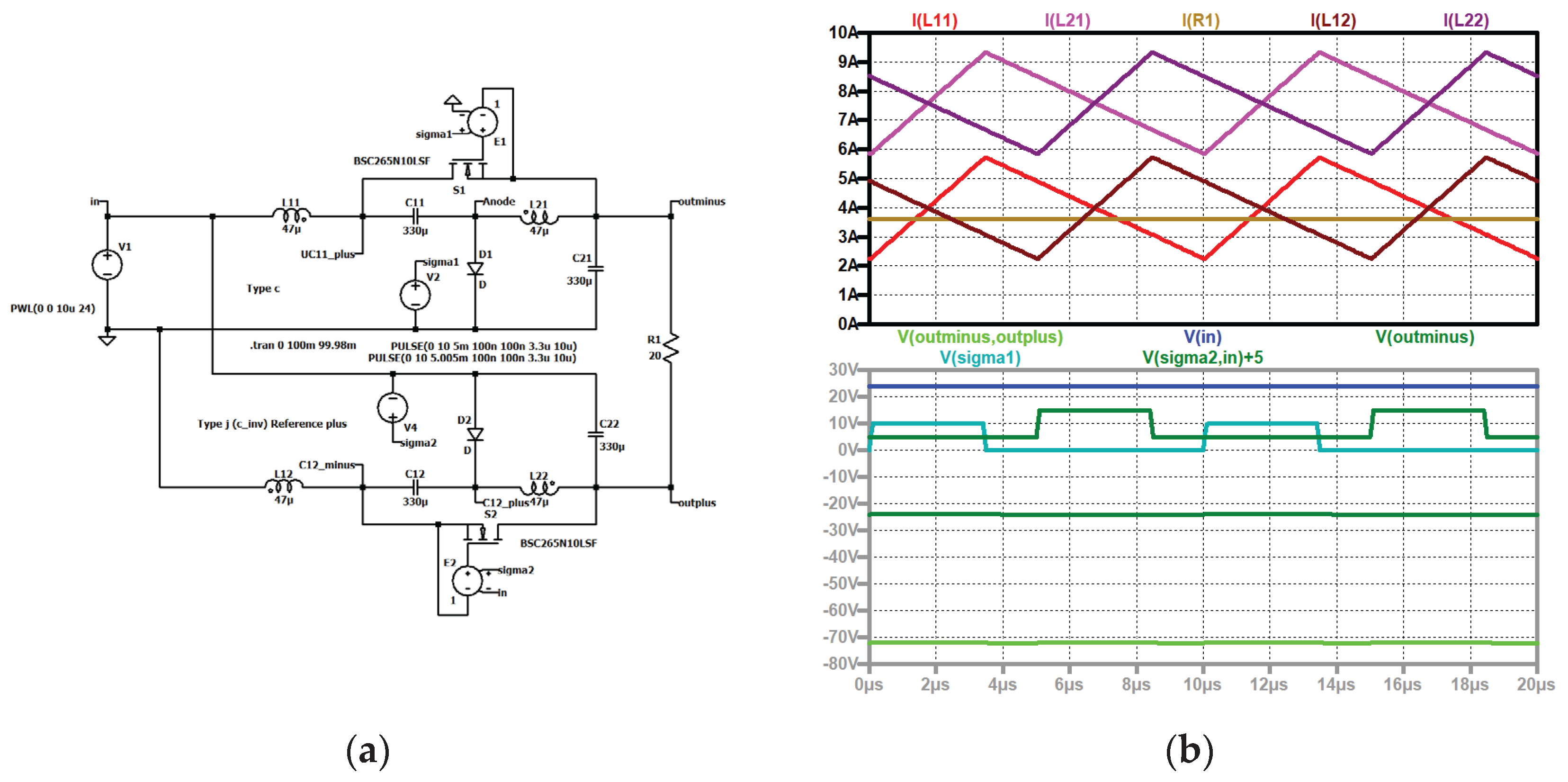
Figure 24.
Type III: (a) simulation circuit; (b), up to down: input current (dark violet); currents through the coils of stage 2 L12 (grey), L22 (light brown), load current (brown); currents through the coils of stage 1 L11 (red), L21 (violet), load current (brown); output voltage (absolute value, green), voltage across output capacitor of stage 1 (dark blue), input voltage (blue), control signal of S2 (dark green, shifted), control signal of S1 (turquoise).
Figure 24.
Type III: (a) simulation circuit; (b), up to down: input current (dark violet); currents through the coils of stage 2 L12 (grey), L22 (light brown), load current (brown); currents through the coils of stage 1 L11 (red), L21 (violet), load current (brown); output voltage (absolute value, green), voltage across output capacitor of stage 1 (dark blue), input voltage (blue), control signal of S2 (dark green, shifted), control signal of S1 (turquoise).
Figure 25.
Type III: (a) simulation circuit; (b) top to bottom: current through the second coil (violet); current through the first coil (red); duty cycle (grey); input voltage (blue), output voltage of stage 1 (turquoise), output voltage (green).
Figure 25.
Type III: (a) simulation circuit; (b) top to bottom: current through the second coil (violet); current through the first coil (red); duty cycle (grey); input voltage (blue), output voltage of stage 1 (turquoise), output voltage (green).
Figure 26.
Type III: (a) simulation circuit; (b) top to bottom: current through the second coil (violet); current through the first coil (red); duty cycle (grey); input voltage (blue), output voltage of stage 1 (turquoise), output voltage (green).
Figure 26.
Type III: (a) simulation circuit; (b) top to bottom: current through the second coil (violet); current through the first coil (red); duty cycle (grey); input voltage (blue), output voltage of stage 1 (turquoise), output voltage (green).
Figure 27.
Type III, with input voltage-ramp: (a) simulation circuit; (b) up to down: input current (dark violet); input voltage (blue), output voltage (green), voltages across the output of the stages stage 1 (turquoise), stage 2(dark green).
Figure 27.
Type III, with input voltage-ramp: (a) simulation circuit; (b) up to down: input current (dark violet); input voltage (blue), output voltage (green), voltages across the output of the stages stage 1 (turquoise), stage 2(dark green).
Figure 28.
Circuit diagram type IV.
Figure 28.
Circuit diagram type IV.
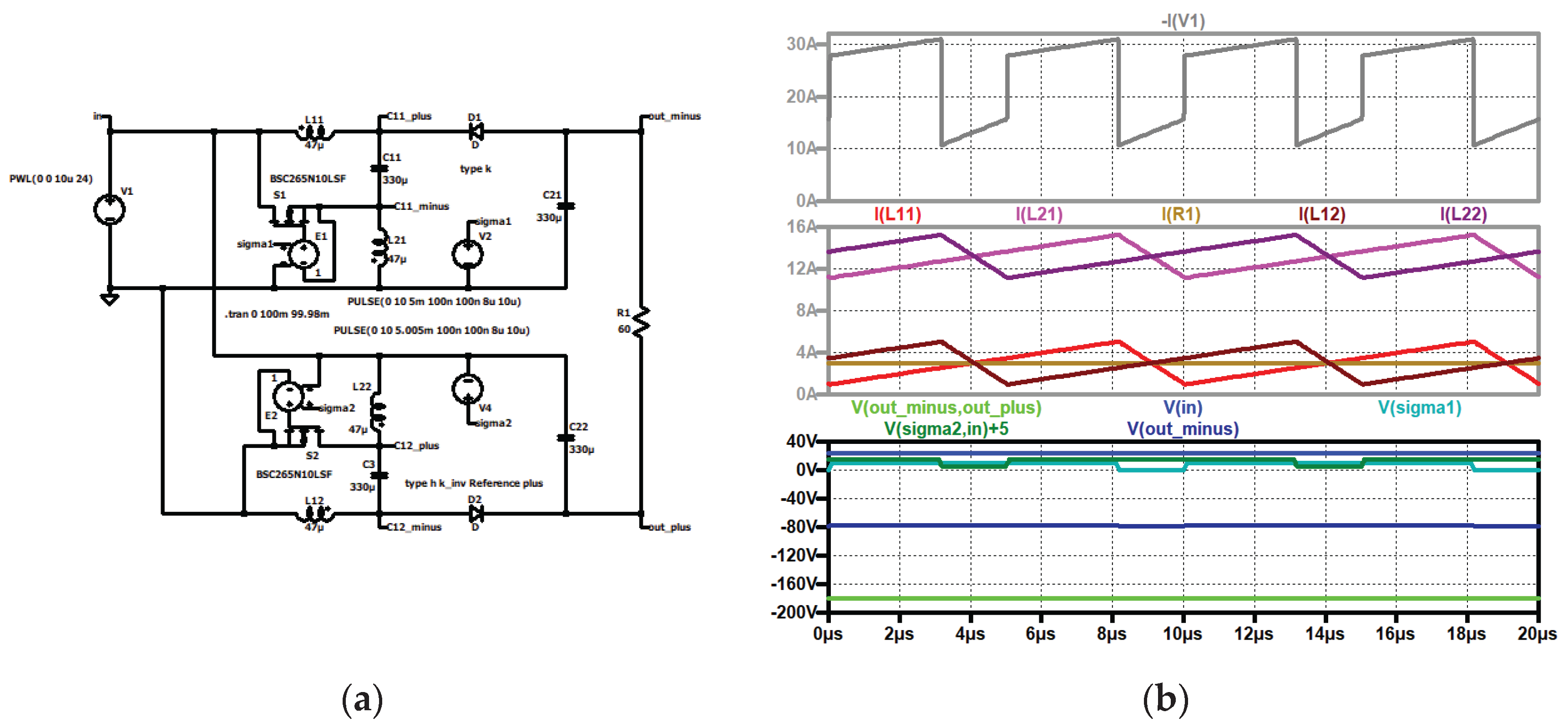
Figure 29.
Type IV steady state: (a) simulation circuit, (b) top to bottom: input current (grey); current through the second coil of stage one (violet), current through the second coil of stage two (dark violet), current through the first coil of stage one (red), current through the first coil of stage two (black), load current (brown); input voltage (blue), control signal of the second switch (dark green, shifted), control signal of the first switch (turquoise), output voltage (green).
Figure 29.
Type IV steady state: (a) simulation circuit, (b) top to bottom: input current (grey); current through the second coil of stage one (violet), current through the second coil of stage two (dark violet), current through the first coil of stage one (red), current through the first coil of stage two (black), load current (brown); input voltage (blue), control signal of the second switch (dark green, shifted), control signal of the first switch (turquoise), output voltage (green).
Figure 30.
Type IV: (a) simulation circuit; (b) top to bottom: current through the second coil (violet); current through the first coil (red); duty cycle (grey); input voltage (blue), output voltage (green).
Figure 30.
Type IV: (a) simulation circuit; (b) top to bottom: current through the second coil (violet); current through the first coil (red); duty cycle (grey); input voltage (blue), output voltage (green).
Figure 31.
Type IV: (a) simulation circuit; (b) top to bottom: current through the second coil (violet); current through the first coil (red); duty cycle (grey); input voltage (blue), output voltage of one stage (turquoise), output voltage (green).
Figure 31.
Type IV: (a) simulation circuit; (b) top to bottom: current through the second coil (violet); current through the first coil (red); duty cycle (grey); input voltage (blue), output voltage of one stage (turquoise), output voltage (green).
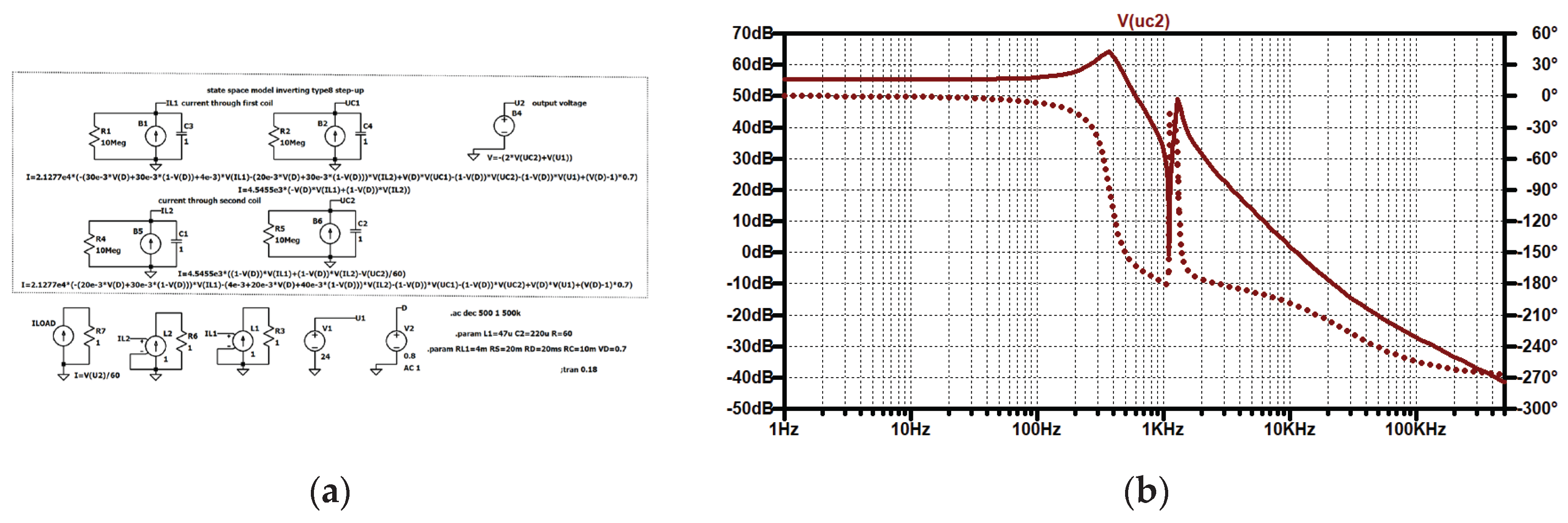
Figure 32.
Type IV, Bode diagram: (a) simulation circuit; (b) connection between the output voltage of one stage in dependence on the duty cycle.
Figure 32.
Type IV, Bode diagram: (a) simulation circuit; (b) connection between the output voltage of one stage in dependence on the duty cycle.
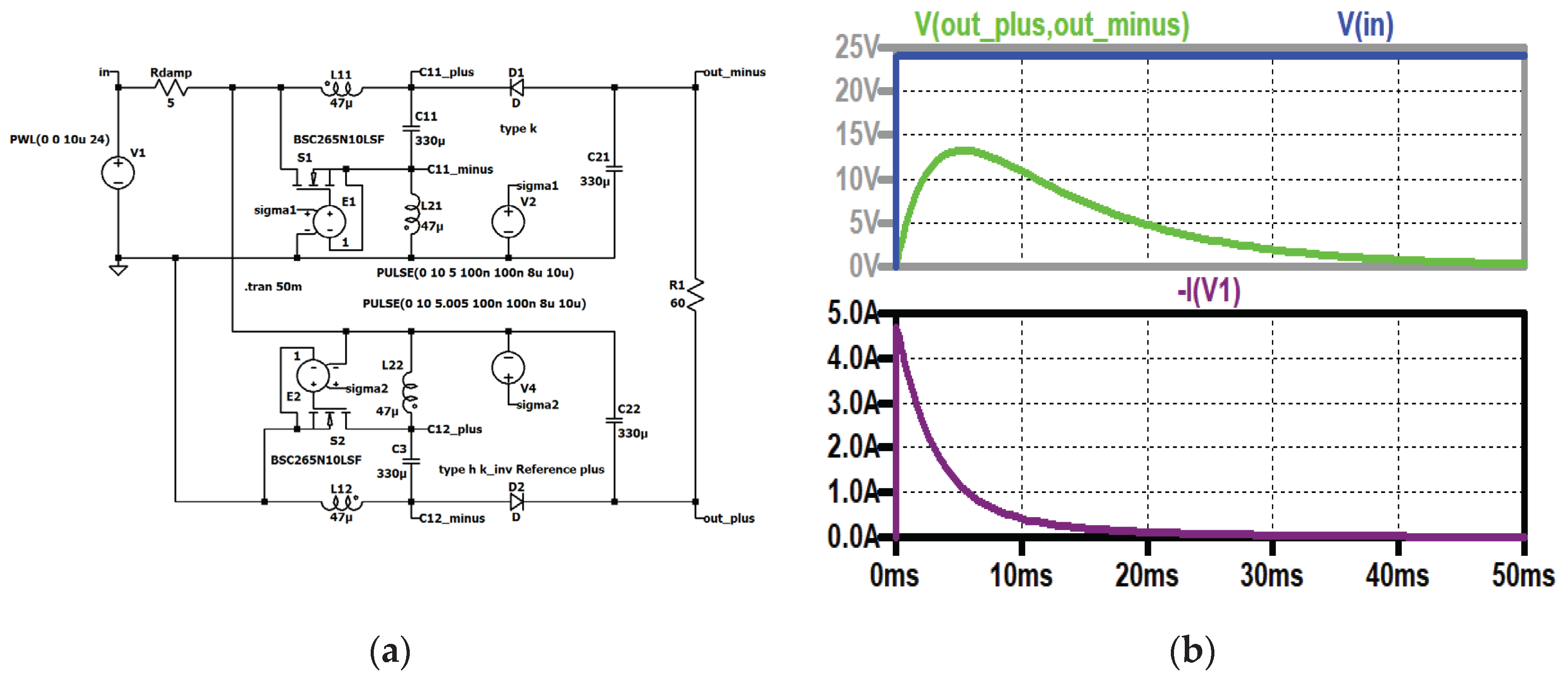
Figure 33.
Avoiding the inrush with a damping resistor, type IV: (a) simulation circuit; (b) top to bottom: input voltage (blue), output voltage (green); input current (dark violet).
Figure 33.
Avoiding the inrush with a damping resistor, type IV: (a) simulation circuit; (b) top to bottom: input voltage (blue), output voltage (green); input current (dark violet).
Figure 34.
Avoiding the inrush with a ramp, type IV: (a) simulation circuit; (b) top to bottom: input voltage (blue), output voltage (green); input current (dark violet).
Figure 34.
Avoiding the inrush with a ramp, type IV: (a) simulation circuit; (b) top to bottom: input voltage (blue), output voltage (green); input current (dark violet).
Figure 35.
Type IV steady state with tolerances of the coils, (a) simulation circuit, (b) top to bottom: input current (grey); current through the second coil of stage one (violet), current through the second coil of stage two (dark violet), current through the first coil of stage one (red), current through the first coil of stage two (black), load current (brown); input voltage (blue), control signal of the second switch (dark green, shifted), control signal of the first switch (turquoise), output voltage (green).
Figure 35.
Type IV steady state with tolerances of the coils, (a) simulation circuit, (b) top to bottom: input current (grey); current through the second coil of stage one (violet), current through the second coil of stage two (dark violet), current through the first coil of stage one (red), current through the first coil of stage two (black), load current (brown); input voltage (blue), control signal of the second switch (dark green, shifted), control signal of the first switch (turquoise), output voltage (green).
Figure 36.
Type IV steady state with tolerances of the coils by plus/minus 10 % and the duty cycles of the two stages differ by 5 %, (a) simulation circuit, (b) top to bottom: input current (grey); current through the second coil of stage one (violet), current through the second coil of stage two (dark violet), current through the first coil of stage one (red), current through the first coil of stage two (black), load current (brown); input voltage (blue), control signal of the second switch (dark green, shifted), control signal of the first switch (turquoise), output voltage of stage two (dark blue), output voltage of stage one (light brown), output voltage (green).
Figure 36.
Type IV steady state with tolerances of the coils by plus/minus 10 % and the duty cycles of the two stages differ by 5 %, (a) simulation circuit, (b) top to bottom: input current (grey); current through the second coil of stage one (violet), current through the second coil of stage two (dark violet), current through the first coil of stage one (red), current through the first coil of stage two (black), load current (brown); input voltage (blue), control signal of the second switch (dark green, shifted), control signal of the first switch (turquoise), output voltage of stage two (dark blue), output voltage of stage one (light brown), output voltage (green).