1. Introduction
The success and good name of any university solely lies on the effective management of the leadership on ground (
Ogunode & Sarkinfada, 2023). There’s no university that can perform well and maintain its reputation without strong and reliable leaders to occupy key offices such as the Vice Chancellor, the Deputy Vice Chancellors, Registrar, Bursar, Dean of Faculties, Heads of Departments and other important stakeholders. They are the key makers of policies, managers of resources and promoters of research, adequately ensuring that the University runs effectively. Therefore, selection of right personnel for these positions should be done with fairness and transparency. Nevertheless, in this our contemporary age, in many Nigerian Universities this selection process has been paralyzed by favouritism, political influence and nepotism rather than being based on merit. These problems destroy public trust in the selection procedures and reduces meritocracy (
Oparinde & Bamire, 2021;
Oladimeji & Oladejo, 2023).
As noted in recent studies, modern university leaders need variety of skills such as emotional intelligence, problem-solving skills, innovation, good communication and time management to fight present-day challenges (
Oparinde & Bamire, 2021;
Mbangula, 2025). However the conventional ways of selecting leaders usually neglect these qualities because it depends solely on seniority, personal and political influence or recommendations. When the process is being controlled or influenced by external forces, it invokes a sense of unfairness and damages accountability in leadership appointment (
Agboluaje, 2020). To solve the problem of unfair administrative personnel selection in Nigerian Universities, this study proposes a multi-criteria computational model called fuzzy-TOPSIS (fuzzy Technique for Order Preference by Similarity to Ideal Solution). This model is a mathematical algorithm that enables committee to assess and rank candidates fairly by using both numbers (quantitative) and opinions (qualitative). It is robust enough to accommodate uncertainty in human judgement and differences in opinions.
This computational approach improves fairness and transparency, minimize personal and political influence, rebuilds the society’s trust in the system and provides a reproducible structure for documenting the rationale behind each selection decision. Many multi-criteria decision-making (MCDM) tools such as AHP, ELECTRE, PROMETHEE, and TOPSIS have been applied extensively in various other sectors such as engineering, supply chain, and managerial contexts, but has very few application in academic personnel selection especially in Nigerian universities (
Baharin et al., 2021;
Gottwald et al., 2022). Existing literature on university leadership in Nigeria are qualitative, mostly focusing on policy or governance analysis rather than computational modeling (
Ogunode & Sarkinfada, 2023). After reviewing a considerable number of literature on personnel selection, it was discovered that no major study had demonstrated the application of fuzzy-TOPSIS for transparent administrative selection in Nigerian higher education. By proposing a mathematically sound, reproducible and evidence-based model for selecting university management personnel, this study closes that gap.
This study’s primary goal is to propose a fuzzy-TOPSIS decision support structure for the transparent and merit-based recruitment of key administrative personnel in Nigerian universities. Specific objectives include creating a fuzzy-TOPSIS model that combines qualitative and quantitative selection criteria, testing the model on a simulated dataset, and evaluating the model’s robustness by conducting a sensitivity analysis to prove how it can enhance transparency, accountability and fairness in Nigerian university leadership personnel selection.
2. Literature Review
2.1. Administrative Positions and the Need for Transparent Personnel Selection
Administrative positions in Universities require a strong blend of academic excellence, great leadership qualities, and ethical integrity. Positions such as Vice-Chancellor, Registrar, Deputy Vice Chancellors, Bursar, Dean of Faculties and Head of various departments and units has a great impact on all major institutional operations, including finances, academic research, staff and student welfare as well as health and safety (
Ogunode & Sarkinfada, 2023). In Nigeria, however, the appointment procedures has often been influenced by personal and political considerations, nepotism and favoritism (
Oladimeji & Oladejo, 2023;
Oparinde & Bamire, 2021). Many of these practices has weakened public confidence and trust in the process and create leadership instability, which negatively affect academic performance of staffs, students and institutional harmony. In opposing political and personal influence, improving accountability, structured, data-based evaluation frameworks are highly recommended for Nigerian University leadership recruitment. Computational and analytical models like MCDM give a structured pathway for quantifying subjective judgments and ensuring reproducibility in the decision-making processes.
2.2. Multi-Criteria Decision-Making (MCDM) in Personnel Selection
Personnel selection is generally a multi-criteria problem because it involves comparing alternatives across various quantitative and qualitative attributes. MCDM techniques are designed to aid experts in ranking alternatives/candidates where compromise exist among competing criteria (
Nabeeh et al., 2019;
Tuğrul, 2022). The most commonly used tools for Multi-Criteria Decision Making (MCDM) are quite varied. These methods typically include the Analytic Hierarchy Process (AHP), ELECTRE, and PROMETHEE. Researchers also frequently apply techniques like Simple Additive Weighting (SAW), ARAS, EDAS, MULTIMOORA, and CODAS. TOPSIS is another very popular method on this list. These specific techniques are widely recognized and utilized in the current literature (
Dhurkari, 2022;
Ismail et al., 2024;
Villalba et al., 2024). AHP give ordered pairwise comparisons but can be incoherent and computationally heavy when it involves many criteria or alternatives (
Saaty, 1980). ELECTRE and PROMETHEE use outranking processes useful for complex decision environments, but their mathematical details limits their accessibility to novice in the field of study. Ordinary TOPSIS, though spontaneous, relies on crisp numerical data that does not have the ability to capture the uncertainty embedded in human judgment in vague situations. Fuzzy extensions of various MCDM techniques have been developed to overcome this limitations. This has enhanced the use of linguistic variables (such as “low,” “medium,” “high”) which are being mapped to different fuzzy numbers as the case may be. These fuzzy number include triangular, trapezoidal, and Gaussian fuzzy numbers. The more complex ones include pentagonal, hexagonal, and heptagonal fuzzy numbers. This improvement better reflects the ambiguity of subjective assessments (
Sang et al., 2015). Fuzzy-TOPSIS has therefore been successfully applied in various personnel selection contexts (
Tuğrul, 2022;
Nabeeh et al., 2019).
2.3. Fuzzy Sets Theory, Linguistic Variables and TFN Mapping
Evaluators and experts find it quite difficult to express decision-making problems in personnel selection as crisp numerical figures because it often involve ambiguity, vagueness, and subjective judgments.
Zadeh (
1965) introduced fuzzy set theory, which has been widely used to evaluate uncertainty, vagueness and imprecise information. Fuzzy sets can accommodates degrees of membership between 0 and 1, thereby capturing the uncertainty and linguistic nature embedded in human opinion for various elements (
Lad & Joglekar, 2016). Formally, a fuzzy set A in a universal set X is expressed as:
where
(
)
: X → [0,1] denotes the membership function. It assigns each element
x a degree of membership. This reflects the extent to which it satisfies the concept represented by set
A (
Lad & Joglekar, 2016). Linguistic terms such as High, Medium, or Low are often use in fuzzy MCDM. They help in assiging importance to criteria and rate the performance of alternatives/candidates. These linguistic terms are then mapped to Triangular Fuzzy Numbers. They help to facilitate computational analysis while preserving linguistic uncertainty (
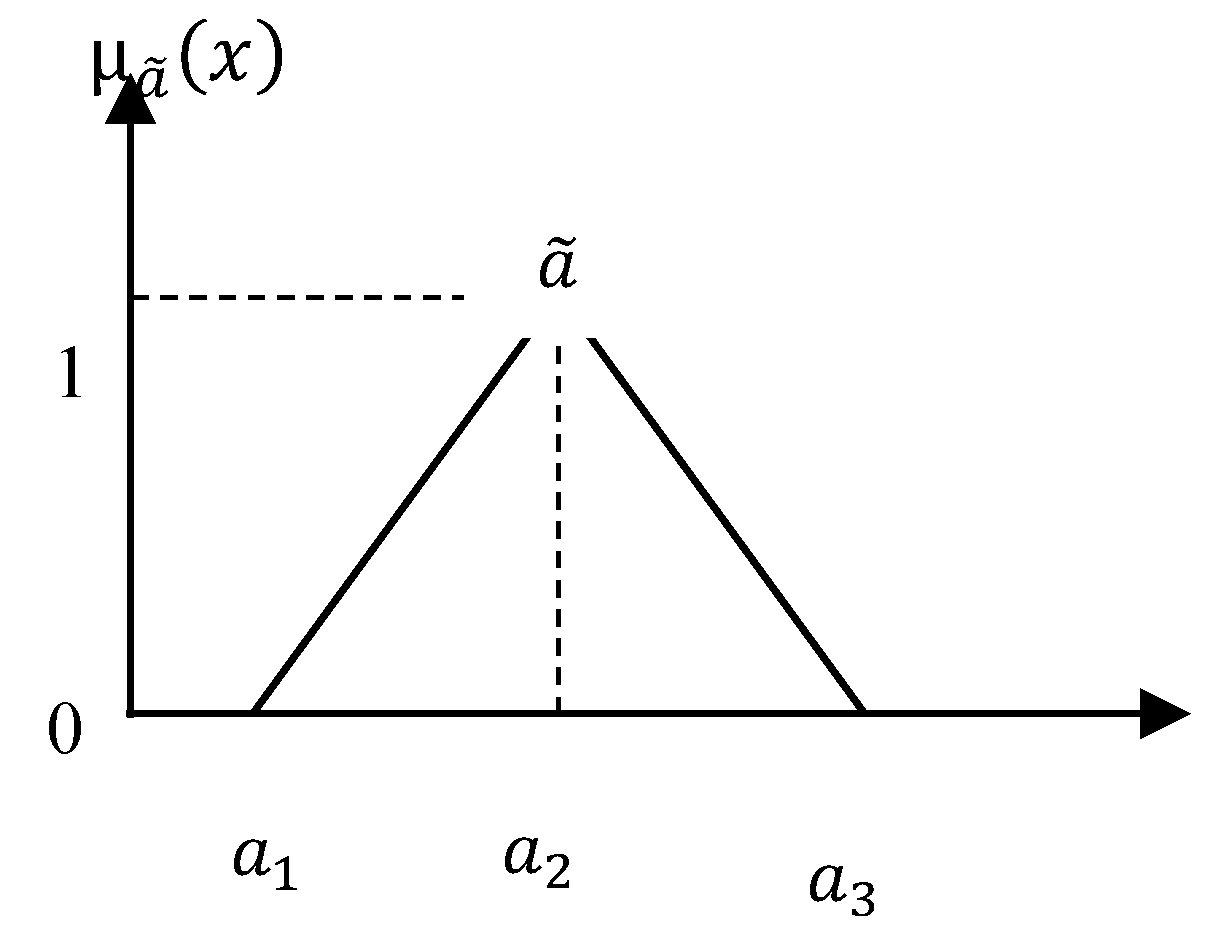
Kumar et al., 2018). TFNs, are characterized by three parameters;
= (
,
,
), a
1: the lower bound (smallest possible value), a
2: the modal value (most probable value), and a
3: the upper bound (largest possible value). The corresponding membership function
of a TFN defined in equation (2.2) below. It produces a triangular shape (
Figure 1) that reflects gradual transitions between membership degrees, rather than crisp limits. TFNs are widely used because they are simple and computational efficient. They are inherently interpretable in linguistic assessments (
Awasthi et al., 2011).
This study employs three experts (DMs) to assess each criterion weight and candidates performance evaluations using a seven point scale linguistic variables adapted from previous studies (
Sang et al., 2015;
Rahi et al., 2022), mapped into TFNs to provide finer resolution in judgment and accommodates varying levels of performance or importance.
Table 1.
Linguistic Scale and Corresponding Triangular Fuzzy Numbers (TFNs).
Table 1.
Linguistic Scale and Corresponding Triangular Fuzzy Numbers (TFNs).
| Codes |
Linguistic Term |
Triangular Fuzzy Number (a, b, c) |
|
1
|
Very Low (VL) |
(0, 0, 1) |
|
2
|
Low (L) |
(0, 1, 3) |
|
3
|
Moderately Low (ML) |
(1, 3, 5) |
|
4
|
Moderate (M) |
(3, 5, 7) |
|
5
|
Moderately High (MH) |
(5, 7, 9) |
|
6
|
High (H) |
(7, 9, 10) |
|
7
|
Very High (VH) |
(9, 10, 10) |
DMs used these linguistic variables to rate both the relative importance of each criterion and the performance of each candidate under each criterion. The use of a predefined mapping table ensures consistency across all evaluations while allowing the model to retain the qualitative nuance of human judgment.
2.4. Why Fuzzy-TOPSIS Is Suitable for University Personnel Selection
Fuzzy-TOPSIS is an extension of the ordinary TOPSIS method by integrating fuzzy logic into the procedure for handling subjectivity of linguistic judgments. This positions the technique as one of the best for evaluating candidates/alternatives for administrative leadership positions, where criteria such as integrity, and leadership qualities are qualitative and subjective (
Sang et al., 2015). The method translates experts’ linguistic assessments into TFNs, and the alternatives are ranked based on their closeness to the ideal solution. It can also accommodates a number of DMs, and aggregate their assessments into a unified fuzzy decision matrix. This aggregation dilutes each of the DMs biases and ensures that outcomes reflect collective judgment (
Nabeeh et al., 2019). In addition, fuzzy-TOPSIS finds application in an academic environment where interpretability is important because of its transparency and simpler computations when compared with other method such as AHP or outranking methods. (
Rahi et al., 2022). Thus, promotion of fairness and evidence based decision making in university personnel selection can be achieved by adopting fuzzy-TOPSIS which proposes a balanced, traceable, and linguistically sensitive framework that aligns with the goal of promoting fairness.
2.5. Criteria Selection and Use of Simulated Data
This study adopts ten criteria depicted in
Table 2 below which were derived from existing literature on academic and administrative personnel selection and Nigerian university statutes (
Baharin et al., 2021;
Fathi et al., 2011;
Gottwald et al., 2022;
Tuğrul, 2022). All the ten criteria were modeled as benefit-type, since higher values of these attributes are invaluably advantageous in administrative leadership selection. Cost-type criteria (such as administrative cost, disciplinary record) were excluded because they are less relevant in evaluating professional merit. Each criterion are chosen based on attribute relevancy to effective university administration. Due to confidentiality restrictions and limited access to real evaluation data from Nigerian universities, this study uses a simulated dataset comprising twelve candidates, ten criteria, and three experts (DMs). This technique is consistent with existing literature on MCDM studies that employ hypothetical data for methodological demonstration (
Tuğrul, 2022;
Nabeeh et al., 2019). Selection committee should maintain validity and replicability in the selection process and the simulated data used in this study reflects the same.
2.6. Bias Control, Robustness, and Sensitivity Analysis
In reality, fuzzy-TOPSIS cannot fully eliminate human bias since all assessments of both criteria and candidates originate from human judgment, but it provide a way to mitigates the DMs influence if any by applying structured aggregation and normalization rules (
Rahi et al., 2022). Also incorporating multiple DMs and fuzzy averaging ensures that the effect of any single biased DM is minimized. Sensitivity analysis further tests the robustness of rankings by dropping each criterion one after the other and computing the result after each drop or excluding DMs to assess result stability. Consistent rankings across these tests indicate a reliable model, DMs’ biases has been neutralized and enhance confidence in the decision outcomes (
Gottwald et al., 2022).
3. Methodology
3.1. Research Framework
This study adopts an MCDM technique based on the Technique for Order Preference by Similarity to Ideal Solution (fuzzy TOPSIS). This study research process follows a structured path: Simulated Data, Linguistic ratings by experts, TFN mapping, Aggregation, Fuzzy TOPSIS computation, Sensitivity analysis. This method integrates subjective human judgment (expressed linguistically) with mathematical rigor, ensuring that decision outcomes are both transparent and analytically defensible. Three experts were assumed, to reflect the typical size and diversity of Nigerian university selection committees. These DMs represent academic, administrative, and financial expertise to ensure balanced perspectives in evaluation. Each DM provided linguistic assessments of both the criteria weights and the candidate performance levels. The use of multiple DMs enhances objectivity and minimizes the influence of individual bias.
Due to confidentiality restrictions and limited access to actual university recruitment data, a simulated dataset was developed to illustrate the fuzzy-TOPSIS model. The dataset comprises evaluations of 12 candidates vying for the position of a Registrar in a Nigerian university against 10 criteria by 3 experts. This simulated approach follows similar methodological precedents (
Nabeeh et al., 2019;
Tuğrul, 2022) and ensures replicability while reflecting realistic decision-making dynamics within Nigerian universities. The following steps are fuzzy TOPSIS computational procedures adapted from
Baharin et al. (
2021) in evaluating the criteria weights and the ranking of candidates to determine the best fit to occupy the vacant Registrar position.
Step 1: Determination of Criterion Weights. The relative importance (weights) of the twelve criteria was elicited directly from the three experts using the same 7-point linguistic scale. This participatory weighting approach ensures that the prioritization of criteria reflects expert judgment rather than researcher assumptions. The linguistic weights were converted into TFNs and aggregated across
kth experts using the following rule:
where
This aggregation process captures both the diversity and consensus of committee evaluations. In decision situations such as personnel selection and appointments, experts may hold divergent views due to the inherently subjective and imprecise nature of the evaluation criteria. The min–mean–max aggregation method effectively accommodates this variability; it is inclusive and captures the full spectrum of expert uncertainty without suppressing individual perspectives. It yields a balanced aggregation by combining conservative boundary estimates with a consensus-based central tendency.
Step 2: Construct the aggregated fuzzy decision matrix,
by combining ratings from all DMs.
Let be the aggregated fuzzy ratings of each candidates with respect to each criterion in a group of K experts. It can can calculated as follows:
; i = 1, 2, …,
m (candidates),
j = 1, 2, …,
n (criteria)
and
Step 3: Normalize the decision matrix,
to ensure comparability across criteria.
Step 4: Multiply fuzzy weight,
by the normalized fuzzy decision matrix
to obtain the weighted normalized fuzzy decision matrix,
.
Step 5: Determine the Fuzzy Positive Ideal Solution (FPIS) and Fuzzy Negative Ideal Solution (FNIS).
Step 6: Compute the distance of each candidate’s performance from FPIS and FNIS using fuzzy Euclidean distance.
Step 7: Calculate the Closeness Coefficient (
CCi) for each candidate:
Step 8: Ranking and Decision Process: The closeness coefficients (CCi), which range between 0 and 1, serve as crisp indicators of overall candidate performance. A higher CCi value indicates greater proximity to the ideal solution and, thus, a higher ranking position. This stage yields a transparent and traceable ranking list of candidates, providing a defensible basis for final selection decisions by university committees. Candidates are then ranked in descending order of their crisp scores the higher the value, the better the candidate’s suitability for the Registrar appointment.
3.2. The Implementation of Fuzzy TOPSIS Model
In this study, a simulated dataset was constructed due to the unavailability of real recruitment data from Nigerian universities to illustrate the application of the fuzzy-TOPSIS model in the selection of university administrative personnel. The simulated scenario assumes 12 candidates (A1 – A12) competing for the position of Registrar, a key administrative post in a typical Nigerian university. The candidates were evaluated by three experts (DM1 – DM3), representing the diverse expertise of university selection committees (academic, administrative, and financial).
Each candidate was assessed across ten criteria (C1 – C10) derived from statutory university requirements and relevant literature. The criteria are as follows: Academic Qualification (C1), Years of Experience in Academia (C2), Leadership Ability (C3), Integrity and Ethical Standards (C4), Administrative/Managerial Skills (C5), Strategic Alignment and Institutional Impact (C6), Communication Skills (C7), Decision-Making and Problem-Solving Skills (C8), ICT and Digital Literacy (C9), Vision and Strategic Thinking (C10). All criteria were modeled as benefit criteria, meaning that higher values indicate more desirable qualities for the position.
The evaluation process began with each experts expressing the importance weights of the criteria and performance ratings of the candidates using linguistic variables, which were then converted into Triangular Fuzzy Numbers (TFNs) using the seven-point scale defined earlier. The individual fuzzy assessments were subsequently aggregated to form a group fuzzy decision matrix,
and a set of aggregated fuzzy weights for the criteria.
Table 3 presents the linguistic assessments of the experts on the importance of the criteria.
Table 4 displays the corresponding conversion of these linguistic variables into TFNs and the aggregated fuzzy weights (
) for each criterion.
Table 5 shows the linguistic ratings of the candidates across the ten criteria, while
Table 6 provides the aggregated fuzzy decision matrix
, representing the combined evaluations of all the three DMs. Detailed results of all the 8 steps discussed above are attached in
Appendix A below for review.
3.3. Sensitivity Analysis
The fuzzy TOPSIS model must stay stable when inputs change. Sensitivity analysis checks this stability. It helps to see if small changes in criteria or experts affect the final ranking. When results remain similar, the model is said to be robust. Adapting the style from previous studies (
Syamsuddin, 2013;
Hatami-Marbini & Kangi, 2017;
Baharin et al., 2021), two simple tests were used. The first test removed one criterion at a time while keeping others fixed. This shows which criteria strongly influence the result. Each model run was compared with the baseline ranking to see if the top candidates changed. The second test removed one expert at a time. This checks if any single expert had too much influence on the outcome.
The process began with the full model that used all ten criteria and three experts. The baseline closeness coefficients of each candidate were recorded. Then, each criterion was dropped in turn, and the model was recalculated. After that, each expert’s ratings were removed one after another, and the results were compared. The new rankings were placed beside the original list to measure changes in position. When the same candidates stayed near the top, the model proved stable.
This step also exposed how bias or unequal weights can affect the decision. If one expert or one criterion shifts the ranking sharply, it signals where review is needed. A steady pattern means the fuzzy TOPSIS process distributes influence fairly across evaluators and criteria. In the end, sensitivity analysis builds trust in the model. It shows that the ranking is not random or biased but grounded in balanced evaluation. A robust model gives reliable results even when small inputs vary, which is vital for transparent personnel selection in universities.
4. Results and Discussion
This section presents the outcomes obtained from the implementation of the fuzzy TOPSIS model and the subsequent sensitivity analyses carried out to assess the robustness and consistency of the proposed approach.
4.1. Candidates Result
This study demonstrated the practical application of the fuzzy TOPSIS method with a simulated dataset representing the recruitment of a qualified candidates for the office of a Registrar in a Nigerian university. This technique determines candidates’ ranking based on their closeness coefficient (
CCᵢ), which indicate the relative proximity of each candidates to the Fuzzy Positive Ideal Solution (FPIS) and the Fuzzy Negative Ideal Solution (FNIS). Only one qualified candidate can occupy the office of the Registrar at a time, therefore the computed
CCᵢ values and rankings of all the candidates are summarized in
Table 7.
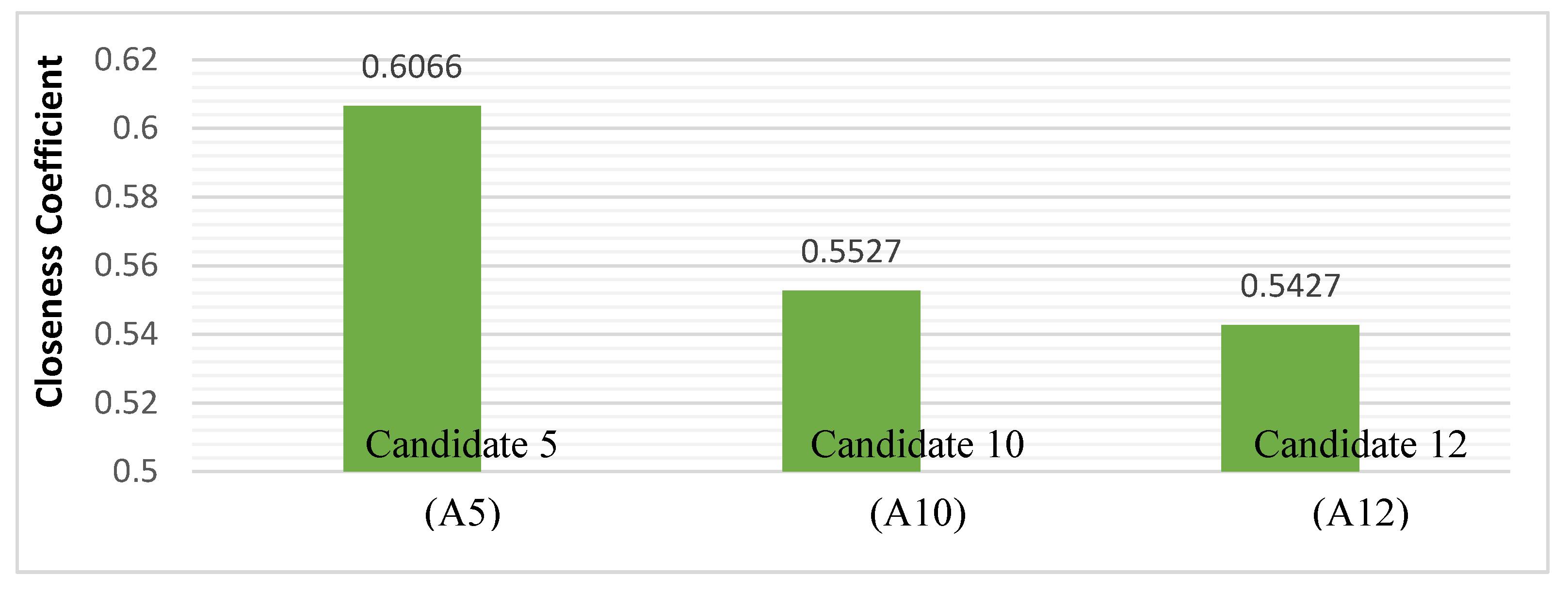
Figure 3 demonstrates the ranking distribution, emphasizing the best three candidates for the Registrar position.
The outcome of the model revealed that A5 has the highest
CCi score, suggesting it as the most suitable candidate to fill the role, because the higher the
CCᵢ value, the closer the candidate is to the FPIS and the farther from the FNIS, indicating superior performance across all evaluation criteria (
Amiri-Aref et al., 2012;
Collan et al., 2015). The outcome of the computations demonstrate that fuzzy TOPSIS provides a transparent, consistent, and justifiable approach to personnel selection, and also aligns with the findings of
Nabeeh et al. (
2019) and
Gottwald et al. (
2022), studies on MCDM techniques ability in handling uncertainty. This outcome supports the model’s applicability to academic personnel selection in an ideal Nigerian university settings.
4.2. Sensitivity Analysis
4.2.1. Results of Criteria-Based Sensitivity Test
The first test checked how each criterion affected the final ranking. One criterion was removed at a time, and the fuzzy TOPSIS model was recalculated. The new rankings were then compared with the original baseline. This method allows for evaluating how sensitive the entire decision is to the absence of any single criterion.
Table 8 contains the results of the first phase where Candidate 5 (A5) from the baseline ranking remains consistent across all the twelve scenarios carried out. This stability indicates that the model is robust and not majorly dependent on any specific criterion.
The
CCi value of each candidate at ten different states was show in the table above. The outcome which is the
CCi value of the candidates changed when the weight of each criterion was shifted to zero. The findings revealed that out of the ten states, A5 had the maximum scores in eight states (state 1, 2, 3, 4, 5, 6, 9, and 10). However, A10 was ranked first for one state (state 8), second for four states (state 2, 4, 6, and 10) and third for other one state (state 9). In addition, A12 obtained second for two states (state 1 and 5), and third for five out of ten states (state 3, 4, 6, 7, and 10) as depicted in
Table 8. Hence, it can be validated that A5 was the most preferred candidate to occupy the position while others were the least preferred. The results showed that small changes in the criteria had little effect on the overall order. The top three candidates stayed the same in all runs. Only minor shifts appeared in the middle positions. This means no single criterion dominated the result.
When the most weighted criteria, such as academic qualification (C1) and years of experience in academia (C2) were removed, the ranking still held steady. That stability confirms that the fuzzy TOPSIS structure balanced all inputs fairly. It also shows that the criteria weights assigned earlier were consistent with the model’s logic. This test proved that the model is not sensitive to any single criterion. A change in one factor does not distort the overall judgment, which is key for fair and repeatable personnel selection.
4.2.2. Results of Decision-Maker-Based Sensitivity Test
The second test focused on the influence of each expert. One expert’s ratings were removed in turn, and the fuzzy TOPSIS model was recalculated. The purpose was to check if any single expert’s opinion had too much weight in the final ranking. This approach was used in previous studies by
Hatami-Marbini & Kangi (
2017) and
Nabeeh et al. (
2019), to seek insight into the model’s adaptability to potential bias or inconsistencies among DMs.
Table 9.
Ranking variations under DM-drop sensitivity analysis.
Table 9.
Ranking variations under DM-drop sensitivity analysis.
| Candidates |
experts being dropped |
| |
State 1 (DM1) |
State 2 (DM2) |
State 3 (DM3) |
| |
CCi |
Ranking |
CCi |
Ranking |
CCi |
Ranking |
| A1 |
0.4646 |
10 |
0.3492 |
12 |
0.3184 |
12 |
| A2 |
0.5132 |
6 |
0.5233 |
6 |
0.4048 |
9 |
| A3 |
0.5743 |
3 |
0.4685 |
9 |
0.4698 |
7 |
| A4 |
0.5250 |
5 |
0.4470 |
11 |
0.5051 |
2 |
| A5 |
0.6152 |
1 |
0.6951 |
1 |
0.5010 |
4 |
| A6 |
0.5358 |
4 |
0.5324 |
5 |
0.4542 |
8 |
| A7 |
0.5039 |
7 |
0.4651 |
10 |
0.3837 |
10 |
| A8 |
0.4613 |
12 |
0.5205 |
8 |
0.4982 |
5 |
| A9 |
0.4636 |
11 |
0.5552 |
3 |
0.5020 |
3 |
| A10 |
0.6082 |
2 |
0.5210 |
7 |
0.4981 |
6 |
| A11 |
0.4976 |
8 |
0.5549 |
4 |
0.3250 |
11 |
| A12 |
0.4719 |
9 |
0.5851 |
2 |
0.5609 |
1 |
The results stayed stable across all runs. The same top candidates appeared even when one evaluator’s inputs were excluded. As observed from the table above, A5 was ranked first in two states (states 1 and 2), and fourth in state 3. Only slight ranking shifts occurred in lower positions, which did not affect the final choice. This shows that no expert dominated the process. The finding also means that the group decision was consistent and balanced. Each evaluator’s input added value, but none could change the outcome alone. This balance supports the fairness and transparency of the proposed method. The sensitivity analysis confirmed that the fuzzy TOPSIS model produced reliable and steady results. The model stayed firm when criteria or expert inputs changed, proving it is robust enough for real-world personnel decisions. In conclusion, the model demonstrates strong predictive consistency and provides a transparent, reproducible framework for university personnel selection.
4.3. Discussion
The results underscore the practical application of the fuzzy TOPSIS model to university personnel selection processes in Nigeria. By integrating linguistic assessments and fuzzy logic, the model accommodates the inherent subjectivity of human judgments while ensuring mathematical consistency. Compared to conventional ranking or scoring methods, the fuzzy TOPSIS approach enhances transparency and objectivity by providing a quantifiable rationale for each decision outcome. The consistent top ranking of Candidate A5 across multiple sensitivity analyses shows that the model’s decision outcome is not easily influenced by individual bias or the exclusion of specific criteria. This demonstrates the reliability and stability of the method in real decision environments where subjective assessments play a significant role.
From a practical standpoint, these results imply that university selection committees can rely on the fuzzy TOPSIS model to make fair and evidence-based choices rather than decisions driven by personal or political interests. The model also provides a traceable record of how final rankings were derived, improving accountability and transparency in leadership appointments. Additionally, by capturing the range of expert opinions through fuzzy aggregation, it ensures inclusiveness and minimizes conflict among experts.
More broadly, the findings suggest that implementing fuzzy TOPSIS in university recruitment could help restore public trust in academic governance by demonstrating that appointments are guided by measurable merit and structured evaluation. Therefore, beyond its computational strength, the model serves as a socially valuable decision-support tool for promoting fairness, credibility, and accountability within the Nigerian higher education system. Finally, these findings align with prior studies emphasizing the utility of fuzzy MCDM models in complex decision-making contexts (
Nabeeh et al., 2019;
Gottwald et al., 2022;
Tuğrul, 2022) and extend their application to the Nigerian higher education environment, where structured selection systems remain limited.
5. Conclusion and Recommendations
This study proposed and demonstrated a fuzzy TOPSIS-based decision support model for selecting management personnel in Nigerian universities, using a Registrar’s position as a case study. The model successfully incorporated qualitative and quantitative criteria, handled linguistic uncertainty via fuzzy logic, and aggregated multiple evaluators’ judgments to ensure fairness. The results identified Candidate 5 as the most suitable, achieving the highest closeness coefficient. Subsequent sensitivity analyses confirmed the model’s stability and reliability, as the ranking of top candidates remained largely consistent even when criteria or experts were modified. This outcome demonstrates that fuzzy TOPSIS provides a structured, transparent, and defensible framework for personnel selection, which can minimize subjectivity, promote merit-based selection, and enhance institutional accountability. Based on the findings, it is recommended that Nigerian universities should consider adopting fuzzy-based MCDM techniques like fuzzy TOPSIS for leadership selection. This would help reduce bias, improve transparency, and counter the negative influences of favouritism and nepotism identified in the literature (
Oladimeji & Oladejo, 2023;
Ogunode & Sarkinfada, 2023).
For future research, this model should be applied to real-world recruitment data from Nigerian universities to further validate its effectiveness and practical applicability. To promote consistent, data-driven, and auditable selection processes, it is recommended that fuzzy TOPSIS framework should be embedded within institutional e-recruitment platforms and digital decision-support systems. Also, the proposed framework is adaptable and can be extended to other key administrative and academic positions, such as Vice-Chancellor, Dean, Bursar, or for academic staff selection (
Paraskevas & Madas, 2024). Furthermore, the fuzzy TOPSIS model offers a reliable and innovative approach to enhancing fairness and accountability in university personnel selection. Its integration can significantly strengthen governance and institutional credibility within the Nigerian higher education system.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org. The supplementary file “Fuzzy-TOPSIS-Data File.xlsx” contains the input data and computational results supporting this study.
Author Contributions
Conceptualization, S.O. Ajeleye and A.D. Adeyeye; Methodology, S. O. Ajeleye; Data Curation, S. O. Ajeleye; Formal Analysis, S. O. Ajeleye and A. D. Adeyeye; Original Draft Preparation, S. O. Ajeleye and A. D. Adeyeye; Review and Editing, S. O. Ajeleye and A. D. Adeyeye. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The author expresses their sincere appreciation to colleagues and mentors who provided constructive comments during the development of this paper. Their valuable insights contributed to refining the clarity and quality of the study.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Ethics Statement
This study did not involve experiments on humans, animals, or plants. All data used in the analysis were simulated solely for research demonstration purposes. Therefore, institutional ethical approval was not required.
Data Availability
The dataset and analysis files supporting the findings of this study are available as
supplementary material in an Excel file titled Fuzzy-TOPSIS-Data File.xlsx. The file contains the simulated dataset, fuzzy-TOPSIS model computations, sensitivity analysis, and all related charts and results. It can be accessed in the Zenodo public repository at
https://doi.org/10.5281/zenodo.17592533.
Appendix A
The following tables contain results of the Fuzzy TOPSIS steps discussed in the methodology section
| |
ASSIGNATION OF IMPORTANCE TO CRITERIA BY THE EXPERTS |
| |
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
C9 |
C10 |
| DM1 |
High |
Very High |
High |
High |
Moderately High |
Very High |
High |
Very High |
High |
Moderately High |
| DM2 |
Very High |
Very High |
High |
High |
Very High |
Very High |
High |
High |
Very High |
Very High |
| DM3 |
Very High |
Very High |
Very High |
High |
High |
Moderately High |
Very High |
High |
High |
Moderately High |
| THE AGGREGATED FUZZY WEIGHT OF EACH CRITERION |
| DM1 |
7 |
9 |
10 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
5 |
7 |
9 |
9 |
10 |
10 |
7 |
9 |
10 |
9 |
10 |
10 |
7 |
9 |
10 |
5 |
7 |
9 |
| DM2 |
9 |
10 |
10 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
9 |
10 |
10 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
9 |
10 |
10 |
9 |
10 |
10 |
| DM3 |
9 |
10 |
10 |
9 |
10 |
10 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
5 |
7 |
9 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
5 |
7 |
9 |
| Wj |
7 |
9.666666667 |
10 |
9 |
10 |
10 |
7 |
9.333333333 |
10 |
7 |
9 |
10 |
5 |
8.666666667 |
10 |
5 |
9 |
10 |
7 |
9.333333333 |
10 |
7 |
9.333333333 |
10 |
7 |
9.333333333 |
10 |
5 |
8 |
10 |
| |
|
THE RATING OF THE CANDIDATES |
| |
|
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
C9 |
C10 |
| DM1 |
Candidate-1 |
VL |
VL |
VL |
VH |
L |
VL |
L |
M |
H |
M |
| Candidate-2 |
L |
VH |
VL |
L |
M |
M |
L |
VH |
L |
H |
| Candidate-3 |
L |
L |
M |
VL |
VL |
H |
M |
M |
M |
VH |
| Candidate-4 |
H |
VL |
L |
VH |
M |
MH |
MH |
VL |
VH |
VH |
| Candidate-5 |
VH |
VH |
M |
VL |
M |
VL |
H |
M |
VH |
M |
| Candidate-6 |
L |
L |
M |
M |
VL |
ML |
VH |
H |
H |
H |
| Candidate-7 |
VL |
M |
L |
L |
ML |
M |
H |
VH |
M |
L |
| Candidate-8 |
M |
H |
VH |
VL |
H |
H |
M |
VH |
VL |
H |
| Candidate-9 |
ML |
H |
H |
VL |
MH |
VH |
ML |
M |
H |
VL |
| Candidate-10 |
MH |
M |
M |
M |
VH |
L |
M |
ML |
M |
M |
| Candidate-11 |
H |
M |
M |
L |
VL |
VL |
H |
MH |
VL |
VH |
| Candidate-12 |
H |
MH |
VH |
H |
M |
L |
VH |
H |
H |
VH |
| DM2 |
Candidate-1 |
H |
M |
M |
M |
VL |
VL |
VL |
M |
VH |
H |
| Candidate-2 |
M |
H |
H |
VH |
VL |
M |
VL |
M |
VL |
M |
| Candidate-3 |
VH |
VH |
M |
VH |
VH |
M |
VH |
L |
VH |
VH |
| Candidate-4 |
VH |
VH |
ML |
M |
VH |
MH |
VL |
VH |
H |
L |
| Candidate-5 |
VL |
M |
MH |
ML |
H |
VL |
VH |
H |
H |
VH |
| Candidate-6 |
VH |
H |
VH |
MH |
VL |
L |
VH |
M |
L |
L |
| Candidate-7 |
VH |
L |
VH |
M |
VL |
VL |
VH |
M |
M |
VH |
| Candidate-8 |
M |
H |
VL |
M |
L |
VL |
H |
VH |
M |
L |
| Candidate-9 |
M |
VL |
VH |
H |
VL |
H |
M |
L |
VH |
VH |
| Candidate-10 |
H |
ML |
VH |
VH |
VH |
H |
H |
VL |
H |
VH |
| Candidate-11 |
M |
VH |
M |
H |
VL |
VL |
M |
VL |
VL |
ML |
| Candidate-12 |
VL |
VH |
H |
H |
VL |
H |
VL |
M |
VH |
MH |
| DM3 |
Candidate-1 |
L |
VL |
H |
H |
L |
M |
L |
L |
H |
H |
| Candidate-2 |
M |
VH |
M |
M |
VH |
M |
L |
VH |
ML |
VH |
| Candidate-3 |
ML |
H |
VH |
H |
VL |
MH |
VL |
M |
MH |
VH |
| Candidate-4 |
MH |
L |
L |
VH |
M |
M |
M |
M |
M |
H |
| Candidate-5 |
H |
VH |
VH |
VL |
VL |
ML |
H |
H |
H |
VL |
| Candidate-6 |
MH |
M |
VL |
M |
VH |
H |
MH |
VH |
L |
MH |
| Candidate-7 |
L |
MH |
VH |
VL |
M |
H |
ML |
L |
VH |
MH |
| Candidate-8 |
M |
ML |
MH |
VH |
VL |
H |
M |
M |
ML |
ML |
| Candidate-9 |
M |
M |
ML |
L |
VH |
ML |
H |
VL |
MH |
M |
| Candidate-10 |
VH |
M |
M |
M |
M |
MH |
VH |
M |
M |
VL |
| Candidate-11 |
H |
MH |
M |
VH |
MH |
VH |
H |
M |
M |
L |
| Candidate-12 |
VL |
MH |
L |
H |
ML |
VH |
VH |
M |
L |
L |
| |
|
REPLACING LINGUISTIC TERMS WITH TRIANGULAR FUZZY NUMBERS (TFNs) |
| |
|
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
C9 |
C10 |
| DM1 |
Candidate-1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
9 |
10 |
10 |
0 |
1 |
3 |
0 |
0 |
1 |
0 |
1 |
3 |
3 |
5 |
7 |
7 |
9 |
10 |
3 |
5 |
7 |
| Candidate-2 |
0 |
1 |
3 |
9 |
10 |
10 |
0 |
0 |
1 |
0 |
1 |
3 |
3 |
5 |
7 |
3 |
5 |
7 |
0 |
1 |
3 |
9 |
10 |
10 |
0 |
1 |
3 |
7 |
9 |
10 |
| Candidate-3 |
0 |
1 |
3 |
0 |
1 |
3 |
3 |
5 |
7 |
0 |
0 |
1 |
0 |
0 |
1 |
7 |
9 |
10 |
3 |
5 |
7 |
3 |
5 |
7 |
3 |
5 |
7 |
9 |
10 |
10 |
| Candidate-4 |
7 |
9 |
10 |
0 |
0 |
1 |
0 |
1 |
3 |
9 |
10 |
10 |
3 |
5 |
7 |
5 |
7 |
9 |
5 |
7 |
9 |
0 |
0 |
1 |
9 |
10 |
10 |
9 |
10 |
10 |
| Candidate-5 |
9 |
10 |
10 |
9 |
10 |
10 |
3 |
5 |
7 |
0 |
0 |
1 |
3 |
5 |
7 |
0 |
0 |
1 |
7 |
9 |
10 |
3 |
5 |
7 |
9 |
10 |
10 |
3 |
5 |
7 |
| Candidate-6 |
0 |
1 |
3 |
0 |
1 |
3 |
3 |
5 |
7 |
3 |
5 |
7 |
0 |
0 |
1 |
1 |
3 |
5 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
| Candidate-7 |
0 |
0 |
1 |
3 |
5 |
7 |
0 |
1 |
3 |
0 |
1 |
3 |
1 |
3 |
5 |
3 |
5 |
7 |
3 |
9 |
9 |
9 |
10 |
10 |
3 |
5 |
7 |
0 |
1 |
3 |
| Candidate-8 |
3 |
5 |
7 |
7 |
9 |
10 |
9 |
10 |
10 |
0 |
0 |
1 |
7 |
9 |
10 |
7 |
9 |
10 |
3 |
5 |
7 |
9 |
10 |
10 |
0 |
0 |
1 |
7 |
9 |
10 |
| Candidate-9 |
1 |
3 |
5 |
7 |
9 |
10 |
7 |
9 |
10 |
0 |
0 |
1 |
5 |
7 |
9 |
9 |
10 |
10 |
1 |
3 |
5 |
3 |
5 |
7 |
7 |
9 |
10 |
9 |
10 |
10 |
| Candidate-10 |
5 |
7 |
9 |
3 |
5 |
7 |
3 |
5 |
7 |
3 |
5 |
7 |
9 |
10 |
10 |
0 |
1 |
3 |
3 |
5 |
7 |
1 |
3 |
5 |
3 |
5 |
7 |
3 |
5 |
7 |
| Candidate-11 |
7 |
9 |
10 |
3 |
5 |
7 |
3 |
5 |
7 |
0 |
1 |
3 |
0 |
0 |
1 |
0 |
0 |
1 |
7 |
9 |
10 |
5 |
7 |
9 |
0 |
0 |
1 |
9 |
10 |
10 |
| Candidate-12 |
7 |
9 |
10 |
5 |
7 |
9 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
0 |
1 |
3 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
9 |
10 |
10 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| DM2 |
Candidate-1 |
7 |
9 |
10 |
3 |
5 |
7 |
3 |
5 |
7 |
3 |
5 |
7 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
3 |
5 |
7 |
9 |
10 |
10 |
7 |
9 |
10 |
| Candidate-2 |
3 |
5 |
7 |
7 |
9 |
10 |
7 |
9 |
10 |
9 |
10 |
10 |
0 |
0 |
1 |
3 |
5 |
7 |
0 |
0 |
1 |
3 |
5 |
7 |
0 |
0 |
1 |
3 |
5 |
7 |
| Candidate-3 |
9 |
10 |
10 |
9 |
10 |
10 |
3 |
5 |
7 |
9 |
10 |
10 |
9 |
10 |
10 |
3 |
5 |
7 |
9 |
10 |
10 |
0 |
1 |
3 |
9 |
10 |
10 |
9 |
10 |
10 |
| Candidate-4 |
9 |
10 |
10 |
9 |
10 |
10 |
1 |
3 |
5 |
3 |
5 |
7 |
9 |
10 |
10 |
5 |
7 |
9 |
0 |
0 |
1 |
9 |
10 |
10 |
7 |
9 |
10 |
0 |
1 |
3 |
| Candidate-5 |
0 |
0 |
1 |
3 |
5 |
7 |
5 |
7 |
9 |
1 |
3 |
5 |
7 |
9 |
10 |
0 |
0 |
1 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
9 |
10 |
10 |
| Candidate-6 |
9 |
10 |
10 |
7 |
9 |
10 |
9 |
10 |
10 |
5 |
7 |
9 |
0 |
0 |
1 |
0 |
1 |
3 |
9 |
10 |
10 |
3 |
5 |
7 |
0 |
1 |
3 |
0 |
1 |
3 |
| Candidate-7 |
9 |
10 |
10 |
0 |
1 |
3 |
9 |
10 |
10 |
3 |
5 |
7 |
0 |
0 |
1 |
0 |
0 |
1 |
9 |
10 |
10 |
3 |
5 |
7 |
3 |
5 |
7 |
9 |
10 |
10 |
| Candidate-8 |
3 |
5 |
7 |
7 |
9 |
10 |
0 |
0 |
1 |
3 |
5 |
7 |
0 |
1 |
3 |
0 |
0 |
1 |
7 |
9 |
10 |
9 |
10 |
10 |
3 |
5 |
7 |
0 |
1 |
3 |
| Candidate-9 |
3 |
5 |
7 |
0 |
0 |
1 |
9 |
10 |
10 |
7 |
9 |
10 |
0 |
0 |
1 |
7 |
9 |
10 |
3 |
5 |
7 |
0 |
1 |
3 |
9 |
10 |
10 |
9 |
10 |
10 |
| Candidate-10 |
7 |
9 |
10 |
1 |
3 |
5 |
9 |
10 |
10 |
9 |
10 |
10 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
0 |
0 |
1 |
7 |
9 |
10 |
9 |
10 |
10 |
| Candidate-11 |
3 |
5 |
7 |
9 |
10 |
10 |
3 |
5 |
7 |
7 |
9 |
10 |
0 |
0 |
1 |
0 |
0 |
1 |
3 |
5 |
7 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
3 |
5 |
| Candidate-12 |
0 |
0 |
1 |
9 |
10 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
0 |
0 |
1 |
7 |
9 |
10 |
0 |
0 |
1 |
3 |
5 |
7 |
9 |
10 |
10 |
5 |
7 |
9 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| DM3 |
Candidate-1 |
0 |
1 |
3 |
0 |
0 |
1 |
7 |
9 |
10 |
7 |
9 |
10 |
0 |
1 |
3 |
3 |
5 |
7 |
0 |
1 |
3 |
0 |
1 |
3 |
7 |
9 |
10 |
7 |
9 |
10 |
| Candidate-2 |
3 |
5 |
7 |
9 |
10 |
10 |
3 |
5 |
7 |
3 |
5 |
7 |
9 |
10 |
10 |
3 |
5 |
7 |
0 |
1 |
3 |
9 |
10 |
10 |
1 |
3 |
5 |
9 |
10 |
10 |
| Candidate-3 |
1 |
3 |
5 |
7 |
9 |
10 |
9 |
10 |
10 |
7 |
9 |
10 |
0 |
0 |
1 |
5 |
7 |
9 |
0 |
0 |
1 |
3 |
5 |
7 |
5 |
7 |
9 |
9 |
10 |
10 |
| Candidate-4 |
5 |
7 |
9 |
0 |
1 |
3 |
0 |
1 |
3 |
9 |
10 |
10 |
3 |
5 |
7 |
3 |
5 |
7 |
3 |
5 |
7 |
3 |
5 |
7 |
3 |
5 |
7 |
7 |
9 |
10 |
| Candidate-5 |
7 |
9 |
10 |
9 |
10 |
10 |
9 |
10 |
10 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
3 |
5 |
7 |
9 |
10 |
7 |
9 |
10 |
7 |
9 |
10 |
0 |
0 |
1 |
| Candidate-6 |
5 |
7 |
9 |
3 |
5 |
7 |
0 |
0 |
1 |
3 |
5 |
7 |
9 |
10 |
10 |
7 |
9 |
10 |
5 |
7 |
9 |
9 |
10 |
10 |
0 |
1 |
3 |
5 |
7 |
9 |
| Candidate-7 |
0 |
1 |
3 |
5 |
7 |
9 |
9 |
10 |
10 |
0 |
0 |
1 |
3 |
5 |
7 |
7 |
9 |
10 |
1 |
3 |
5 |
0 |
1 |
3 |
9 |
10 |
10 |
5 |
7 |
9 |
| Candidate-8 |
3 |
5 |
7 |
1 |
3 |
5 |
5 |
7 |
9 |
9 |
10 |
10 |
0 |
0 |
1 |
7 |
9 |
10 |
3 |
5 |
7 |
3 |
5 |
7 |
1 |
3 |
5 |
1 |
3 |
5 |
| Candidate-9 |
3 |
5 |
7 |
3 |
5 |
7 |
1 |
3 |
5 |
0 |
1 |
3 |
9 |
10 |
10 |
1 |
3 |
5 |
7 |
9 |
10 |
0 |
0 |
1 |
5 |
7 |
9 |
3 |
5 |
7 |
| Candidate-10 |
9 |
10 |
10 |
3 |
5 |
7 |
3 |
5 |
7 |
3 |
5 |
7 |
3 |
5 |
7 |
5 |
7 |
9 |
9 |
10 |
10 |
3 |
5 |
7 |
3 |
5 |
7 |
0 |
0 |
1 |
| Candidate-11 |
7 |
9 |
10 |
5 |
7 |
9 |
3 |
5 |
7 |
9 |
10 |
10 |
5 |
7 |
9 |
9 |
10 |
10 |
7 |
9 |
10 |
3 |
5 |
7 |
3 |
5 |
7 |
0 |
1 |
3 |
| Candidate-12 |
0 |
0 |
1 |
5 |
7 |
9 |
0 |
1 |
3 |
7 |
9 |
10 |
1 |
3 |
5 |
9 |
10 |
10 |
9 |
10 |
10 |
3 |
5 |
7 |
0 |
1 |
3 |
0 |
1 |
3 |
| |
AGGREGATED FUZZY DECISION MATRIX |
| |
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
C9 |
C10 |
| Candidate-1 |
0 |
3.333333333 |
10 |
0 |
1.666666667 |
7 |
0 |
4.666666667 |
10 |
3 |
8 |
10 |
0 |
0.666666667 |
3 |
0 |
1.666666667 |
7 |
0 |
0.666666667 |
3 |
0 |
3.666666667 |
7 |
7 |
9.333333333 |
10 |
3 |
7.666666667 |
10 |
| Candidate-2 |
0 |
3.666666667 |
7 |
7 |
9.666666667 |
10 |
0 |
4.666666667 |
10 |
0 |
5.333333333 |
10 |
0 |
5 |
10 |
3 |
5 |
7 |
0 |
0.666666667 |
3 |
3 |
8.333333333 |
10 |
0 |
1.333333333 |
5 |
3 |
8 |
10 |
| Candidate-3 |
0 |
4.666666667 |
10 |
0 |
6.666666667 |
10 |
3 |
6.666666667 |
10 |
0 |
6.333333333 |
10 |
0 |
3.333333333 |
10 |
3 |
7 |
10 |
0 |
5 |
10 |
0 |
3.666666667 |
7 |
3 |
7.333333333 |
10 |
9 |
10 |
10 |
| Candidate-4 |
5 |
8.666666667 |
10 |
0 |
3.666666667 |
10 |
0 |
1.666666667 |
5 |
3 |
8.333333333 |
10 |
3 |
6.666666667 |
10 |
3 |
6.333333333 |
9 |
0 |
4 |
9 |
0 |
5 |
10 |
3 |
8 |
10 |
0 |
6.666666667 |
10 |
| Candidate-5 |
0 |
6.333333333 |
10 |
3 |
8.333333333 |
10 |
3 |
7.333333333 |
10 |
0 |
1 |
5 |
0 |
4.666666667 |
10 |
0 |
1 |
5 |
7 |
9.333333333 |
10 |
3 |
7.666666667 |
10 |
7 |
9.333333333 |
10 |
0 |
5 |
10 |
| Candidate-6 |
0 |
6 |
10 |
0 |
5 |
10 |
0 |
5 |
10 |
3 |
5.666666667 |
9 |
0 |
3.333333333 |
10 |
0 |
4.333333333 |
10 |
5 |
9 |
10 |
3 |
8 |
10 |
0 |
3.666666667 |
10 |
0 |
5.666666667 |
10 |
| Candidate-7 |
0 |
3.666666667 |
10 |
0 |
4.333333333 |
9 |
0 |
7 |
10 |
0 |
2 |
7 |
0 |
2.666666667 |
7 |
0 |
4.666666667 |
10 |
1 |
7.333333333 |
10 |
0 |
5.333333333 |
10 |
3 |
6.666666667 |
10 |
0 |
6 |
10 |
| Candidate-8 |
3 |
5 |
7 |
1 |
7 |
10 |
0 |
5.666666667 |
10 |
0 |
2 |
10 |
0 |
3.333333333 |
10 |
0 |
6 |
10 |
3 |
6.333333333 |
10 |
3 |
8.333333333 |
10 |
0 |
2.666666667 |
7 |
0 |
4.333333333 |
10 |
| Candidate-9 |
1 |
4.333333333 |
7 |
0 |
4.666666667 |
10 |
1 |
7.333333333 |
10 |
0 |
3.333333333 |
10 |
0 |
5.666666667 |
10 |
1 |
7.333333333 |
10 |
1 |
5.666666667 |
10 |
0 |
2 |
7 |
5 |
8.666666667 |
10 |
3 |
8.333333333 |
10 |
| Candidate-10 |
5 |
8.666666667 |
10 |
1 |
4.333333333 |
7 |
3 |
6.666666667 |
10 |
3 |
6.666666667 |
10 |
3 |
8.333333333 |
10 |
0 |
5.666666667 |
10 |
3 |
8 |
10 |
0 |
2.666666667 |
7 |
3 |
6.333333333 |
10 |
0 |
5 |
10 |
| Candidate-11 |
3 |
7.666666667 |
10 |
3 |
7.333333333 |
10 |
3 |
5 |
7 |
0 |
6.666666667 |
10 |
0 |
2.333333333 |
9 |
0 |
3.333333333 |
10 |
3 |
7.666666667 |
10 |
0 |
4 |
9 |
0 |
1.666666667 |
7 |
0 |
4.666666667 |
10 |
| Candidate-12 |
0 |
3 |
10 |
5 |
8 |
10 |
0 |
6.666666667 |
10 |
7 |
9 |
10 |
0 |
4 |
10 |
0 |
6.666666667 |
10 |
0 |
6.666666667 |
10 |
3 |
6.333333333 |
10 |
0 |
6.666666667 |
10 |
0 |
6 |
10 |
| |
NORMALIZED FUZZY DECISION MATRIX |
| |
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
C9 |
C10 |
| Candidate-1 |
0 |
0.333333333 |
1 |
0 |
0.166666667 |
0.7 |
0 |
0.466666667 |
1 |
0.3 |
0.8 |
1 |
0 |
0.066666667 |
0.3 |
0 |
0.166666667 |
0.7 |
0 |
0.066666667 |
0.3 |
0 |
0.366666667 |
0.7 |
0.7 |
0.933333333 |
1 |
0.3 |
0.766666667 |
1 |
| Candidate-2 |
0 |
0.366666667 |
0.7 |
0.7 |
0.966666667 |
1 |
0 |
0.466666667 |
1 |
0 |
0.533333333 |
1 |
0 |
0.5 |
1 |
0.3 |
0.5 |
0.7 |
0 |
0.066666667 |
0.3 |
0.3 |
0.833333333 |
1 |
0 |
0.133333333 |
0.5 |
0.3 |
0.8 |
1 |
| Candidate-3 |
0 |
0.466666667 |
1 |
0 |
0.666666667 |
1 |
0.3 |
0.666666667 |
1 |
0 |
0.633333333 |
1 |
0 |
0.333333333 |
1 |
0.3 |
0.7 |
1 |
0 |
0.5 |
1 |
0 |
0.366666667 |
0.7 |
0.3 |
0.733333333 |
1 |
0.9 |
1 |
1 |
| Candidate-4 |
0.5 |
0.866666667 |
1 |
0 |
0.366666667 |
1 |
0 |
0.166666667 |
0.5 |
0.3 |
0.833333333 |
1 |
0.3 |
0.666666667 |
1 |
0.3 |
0.633333333 |
0.9 |
0 |
0.4 |
0.9 |
0 |
0.5 |
1 |
0.3 |
0.8 |
1 |
0 |
0.666666667 |
1 |
| Candidate-5 |
0 |
0.633333333 |
1 |
0.3 |
0.833333333 |
1 |
0.3 |
0.733333333 |
1 |
0 |
0.1 |
0.5 |
0 |
0.466666667 |
1 |
0 |
0.1 |
0.5 |
0.7 |
0.933333333 |
1 |
0.3 |
0.766666667 |
1 |
0.7 |
0.933333333 |
1 |
0 |
0.5 |
1 |
| Candidate-6 |
0 |
0.6 |
1 |
0 |
0.5 |
1 |
0 |
0.5 |
1 |
0.3 |
0.566666667 |
0.9 |
0 |
0.333333333 |
1 |
0 |
0.433333333 |
1 |
0.5 |
0.9 |
1 |
0.3 |
0.8 |
1 |
0 |
0.366666667 |
1 |
0 |
0.566666667 |
1 |
| Candidate-7 |
0 |
0.366666667 |
1 |
0 |
0.433333333 |
0.9 |
0 |
0.7 |
1 |
0 |
0.2 |
0.7 |
0 |
0.266666667 |
0.7 |
0 |
0.466666667 |
1 |
0.1 |
0.733333333 |
1 |
0 |
0.533333333 |
1 |
0.3 |
0.666666667 |
1 |
0 |
0.6 |
1 |
| Candidate-8 |
0.3 |
0.5 |
0.7 |
0.1 |
0.7 |
1 |
0 |
0.566666667 |
1 |
0 |
0.2 |
1 |
0 |
0.333333333 |
1 |
0 |
0.6 |
1 |
0.3 |
0.633333333 |
1 |
0.3 |
0.833333333 |
1 |
0 |
0.266666667 |
0.7 |
0 |
0.433333333 |
1 |
| Candidate-9 |
0.1 |
0.433333333 |
0.7 |
0 |
0.466666667 |
1 |
0.1 |
0.733333333 |
1 |
0 |
0.333333333 |
1 |
0 |
0.566666667 |
1 |
0.1 |
0.733333333 |
1 |
0.1 |
0.566666667 |
1 |
0 |
0.2 |
0.7 |
0.5 |
0.866666667 |
1 |
0.3 |
0.833333333 |
1 |
| Candidate-10 |
0.5 |
0.866666667 |
1 |
0.1 |
0.433333333 |
0.7 |
0.3 |
0.666666667 |
1 |
0.3 |
0.666666667 |
1 |
0.3 |
0.833333333 |
1 |
0 |
0.566666667 |
1 |
0.3 |
0.8 |
1 |
0 |
0.266666667 |
0.7 |
0.3 |
0.633333333 |
1 |
0 |
0.5 |
1 |
| Candidate-11 |
0.3 |
0.766666667 |
1 |
0.3 |
0.733333333 |
1 |
0.3 |
0.5 |
0.7 |
0 |
0.666666667 |
1 |
0 |
0.233333333 |
0.9 |
0 |
0.333333333 |
1 |
0.3 |
0.766666667 |
1 |
0 |
0.4 |
0.9 |
0 |
0.166666667 |
0.7 |
0 |
0.466666667 |
1 |
| Candidate-12 |
0 |
0.3 |
1 |
0.5 |
0.8 |
1 |
0 |
0.666666667 |
1 |
0.7 |
0.9 |
1 |
0 |
0.4 |
1 |
0 |
0.666666667 |
1 |
0 |
0.666666667 |
1 |
0.3 |
0.633333333 |
1 |
0 |
0.666666667 |
1 |
0 |
0.6 |
1 |
| |
WEIGHTED NORMALIZED FUZZY DECISION MATRIC |
| Wj |
7 |
9.666666667 |
10 |
9 |
10 |
10 |
7 |
9.333333333 |
10 |
7 |
9 |
10 |
5 |
8.666666667 |
10 |
5 |
9 |
10 |
7 |
9.333333333 |
10 |
7 |
9.333333333 |
10 |
7 |
9.333333333 |
10 |
5 |
8 |
10 |
| |
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
C9 |
C10 |
| Candidate-1 |
0 |
3.222222222 |
10 |
0 |
1.666666667 |
7 |
0 |
4.355555556 |
10 |
2.1 |
7.2 |
10 |
0 |
0.577777778 |
9 |
0 |
1.5 |
7 |
0 |
0.622222222 |
3 |
0 |
3.422222222 |
7 |
4.9 |
8.711111111 |
10 |
1.5 |
6.133333333 |
10 |
| Candidate-2 |
0 |
3.544444444 |
7 |
6.3 |
9.666666667 |
10 |
0 |
4.355555556 |
10 |
0 |
4.8 |
10 |
0 |
4.333333333 |
9 |
1.5 |
4.5 |
7 |
0 |
0.622222222 |
3 |
2.1 |
7.777777778 |
10 |
0 |
1.244444444 |
5 |
1.5 |
6.4 |
10 |
| Candidate-3 |
0 |
4.511111111 |
10 |
0 |
6.666666667 |
10 |
2.1 |
6.222222222 |
10 |
0 |
5.7 |
10 |
0 |
2.888888889 |
7 |
1.5 |
6.3 |
10 |
0 |
4.666666667 |
10 |
0 |
3.422222222 |
7 |
2.1 |
6.844444444 |
10 |
4.5 |
8 |
10 |
| Candidate-4 |
3.5 |
8.377777778 |
10 |
0 |
3.666666667 |
10 |
0 |
1.555555556 |
5 |
2.1 |
7.5 |
10 |
1.5 |
5.777777778 |
9 |
1.5 |
5.7 |
9 |
0 |
3.733333333 |
9 |
0 |
4.666666667 |
10 |
2.1 |
7.466666667 |
10 |
0 |
5.333333333 |
10 |
| Candidate-5 |
0 |
6.122222222 |
10 |
2.7 |
8.333333333 |
10 |
2.1 |
6.844444444 |
10 |
0 |
0.9 |
5 |
0 |
4.044444444 |
9 |
0 |
0.9 |
5 |
4.9 |
8.711111111 |
10 |
2.1 |
7.155555556 |
10 |
4.9 |
8.711111111 |
10 |
0 |
4 |
10 |
| Candidate-6 |
0 |
5.8 |
10 |
0 |
5 |
10 |
0 |
4.666666667 |
10 |
2.1 |
5.1 |
9 |
0 |
2.888888889 |
9 |
0 |
3.9 |
10 |
3.5 |
8.4 |
10 |
2.1 |
7.466666667 |
10 |
0 |
3.422222222 |
10 |
0 |
4.533333333 |
10 |
| Candidate-7 |
0 |
3.544444444 |
10 |
0 |
4.333333333 |
9 |
0 |
6.533333333 |
10 |
0 |
1.8 |
7 |
0 |
2.311111111 |
9 |
0 |
4.2 |
10 |
0.7 |
6.844444444 |
10 |
0 |
4.977777778 |
10 |
2.1 |
6.222222222 |
10 |
0 |
4.8 |
10 |
| Candidate-8 |
2.1 |
4.833333333 |
7 |
0.9 |
7 |
10 |
0 |
5.288888889 |
10 |
0 |
1.8 |
10 |
0 |
2.888888889 |
9 |
0 |
5.4 |
10 |
2.1 |
5.911111111 |
10 |
2.1 |
7.777777778 |
10 |
0 |
2.488888889 |
7 |
0 |
3.466666667 |
10 |
| Candidate-9 |
0.7 |
4.188888889 |
7 |
0 |
4.666666667 |
10 |
0.7 |
6.844444444 |
10 |
0 |
3 |
10 |
0 |
4.911111111 |
9 |
0.5 |
6.6 |
10 |
0.7 |
5.288888889 |
10 |
0 |
1.866666667 |
7 |
3.5 |
8.088888889 |
10 |
1.5 |
6.666666667 |
10 |
| Candidate-10 |
3.5 |
8.377777778 |
10 |
0.9 |
4.333333333 |
7 |
2.1 |
6.222222222 |
10 |
2.1 |
6 |
10 |
1.5 |
7.222222222 |
9 |
0 |
5.1 |
10 |
2.1 |
7.466666667 |
10 |
0 |
2.488888889 |
7 |
2.1 |
5.911111111 |
10 |
0 |
4 |
10 |
| Candidate-11 |
2.1 |
7.411111111 |
10 |
2.7 |
7.333333333 |
10 |
2.1 |
4.666666667 |
7 |
0 |
6 |
10 |
0 |
2.022222222 |
9 |
0 |
3 |
10 |
2.1 |
7.155555556 |
10 |
0 |
3.733333333 |
9 |
0 |
1.555555556 |
7 |
0 |
3.733333333 |
10 |
| Candidate-12 |
0 |
2.9 |
10 |
4.5 |
8 |
10 |
0 |
6.222222222 |
10 |
4.9 |
8.1 |
10 |
0 |
3.466666667 |
9 |
0 |
6 |
10 |
0 |
6.222222222 |
10 |
2.1 |
5.911111111 |
10 |
0 |
6.222222222 |
10 |
0 |
4.8 |
10 |
| A* |
3.500 |
8.378 |
10.000 |
6.300 |
9.667 |
10.000 |
2.100 |
6.844 |
10.000 |
4.900 |
8.100 |
10.000 |
1.500 |
7.222 |
9.000 |
1.500 |
6.600 |
10.000 |
4.900 |
8.711 |
10.000 |
2.100 |
7.778 |
10.000 |
4.900 |
8.711 |
10.000 |
4.500 |
8.000 |
10.000 |
| A- |
0.000 |
2.900 |
7.000 |
0.000 |
1.667 |
7.000 |
0.000 |
1.556 |
5.000 |
0.000 |
0.900 |
5.000 |
0.000 |
0.578 |
7.000 |
0.000 |
0.900 |
5.000 |
0.000 |
0.622 |
3.000 |
0.000 |
1.867 |
7.000 |
0.000 |
1.244 |
5.000 |
0.000 |
3.467 |
10.000 |
| |
DISTANCE FROM FPIS |
|
| |
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
C9 |
C10 |
D* |
| Candidate-1 |
3.597673002 |
6.12889332 |
1.880121264 |
1.698038084 |
3.932710769 |
3.524202037 |
6.793136817 |
3.285364728 |
0 |
2.039970951 |
32.88011097 |
| Candidate-2 |
3.85621192 |
0 |
1.880121264 |
3.661056314 |
1.879333127 |
2.114237451 |
6.793136817 |
0 |
5.909346019 |
1.902143041 |
27.99558595 |
| Candidate-3 |
3.011152111 |
4.028647416 |
0.359240167 |
6.645549889 |
2.888354651 |
0.173205081 |
3.668220771 |
3.285364728 |
1.942888266 |
7.83687863 |
33.83950171 |
| Candidate-4 |
0 |
5.022947342 |
4.373493862 |
7.318014303 |
0.833950389 |
0.776745347 |
4.073829959 |
2.16710347 |
1.769052663 |
6.543303051 |
32.87844038 |
| Candidate-5 |
2.403991879 |
2.216436914 |
0 |
3.092643601 |
2.028815057 |
4.462435807 |
0 |
0.359240167 |
0 |
6.3288093 |
20.89237273 |
| Candidate-6 |
2.50964395 |
4.526506297 |
1.746684101 |
6.040057859 |
2.647500568 |
1.78325545 |
0.828007674 |
0.179620084 |
4.1626252 |
6.433486853 |
30.85738804 |
| Candidate-7 |
3.445340385 |
4.800501517 |
1.225668542 |
5.668725116 |
2.964737894 |
1.634013464 |
2.653578995 |
2.020725942 |
2.162912227 |
7.841272572 |
34.41747665 |
| Candidate-8 |
2.800183709 |
3.477120989 |
1.508835432 |
7.229415221 |
2.647500568 |
1.109053651 |
2.286190427 |
0 |
4.889650614 |
7.184070169 |
33.13202078 |
| Candidate-9 |
3.385596458 |
4.643633635 |
0.808290377 |
6.286611288 |
1.590726728 |
0.577350269 |
3.127917568 |
4.014608099 |
0.884526332 |
7.47800873 |
32.79726948 |
| Candidate-10 |
0 |
4.711844807 |
0.359240167 |
7.106899369 |
0 |
1.224744871 |
1.769052663 |
3.714042976 |
2.286190427 |
7.243152009 |
28.41516729 |
| Candidate-11 |
0.982249874 |
2.476855832 |
2.140304967 |
7.48630849 |
3.124633312 |
2.25166605 |
1.849301948 |
2.693667318 |
5.29817501 |
7.646858469 |
35.95002127 |
| Candidate-12 |
3.753045403 |
1.416307144 |
1.264536871 |
7.550632982 |
2.334823158 |
0.932737905 |
3.173041018 |
1.077720502 |
3.173041018 |
7.630003587 |
32.30588959 |
| |
DISTANCE FROM FNIS |
D-
|
| Candidate-1 |
1.742012931 |
0 |
3.308574718 |
4.799305505 |
1.154700538 |
1.205542755 |
0 |
0.898100419 |
5.909346019 |
1.766457011 |
20.7840399 |
| Candidate-2 |
0.372070173 |
6.12889332 |
3.308574718 |
3.661056314 |
2.456569256 |
2.53048085 |
0 |
4.014608099 |
2.974818873 |
1.902143041 |
27.34921465 |
| Candidate-3 |
1.966017888 |
3.366501646 |
4.130689118 |
4.00166632 |
1.334320622 |
4.336281049 |
4.667530784 |
0.898100419 |
7.100620155 |
3.687867998 |
35.489596 |
| Candidate-4 |
4.13344285 |
2.081665999 |
0 |
4.931869152 |
3.216623488 |
3.709896674 |
3.902093983 |
2.369247419 |
7.30664335 |
1.077720502 |
32.72920342 |
| Candidate-5 |
2.541831102 |
4.499423831 |
4.373493862 |
0 |
2.310683721 |
0 |
6.793136817 |
3.714042976 |
7.679024161 |
0.307920144 |
32.21955661 |
| Candidate-6 |
2.409010862 |
2.589151155 |
3.399951585 |
3.561366779 |
1.764580646 |
3.366501646 |
6.370343454 |
3.863073043 |
6.204472036 |
0.615840287 |
34.14429149 |
| Candidate-7 |
1.771563212 |
1.924500897 |
4.073420823 |
1.266227994 |
1.528010083 |
3.458805189 |
5.422362627 |
2.495263002 |
6.802587143 |
0.769800359 |
29.51254133 |
| Candidate-8 |
1.648006652 |
3.570921657 |
3.602673904 |
2.933143933 |
1.764580646 |
3.883726733 |
5.208401728 |
4.014608099 |
4.289311052 |
0 |
30.9153744 |
| Candidate-9 |
0.846804694 |
2.449489743 |
4.221466794 |
3.13102752 |
2.755465948 |
4.387102309 |
4.874005122 |
0 |
7.435706548 |
2.040424792 |
32.14149347 |
| Candidate-10 |
4.13344285 |
1.624921651 |
4.130689118 |
4.298061579 |
4.006188628 |
3.770057471 |
5.780900153 |
0.359240167 |
6.706842091 |
0.307920144 |
35.11826385 |
| Candidate-11 |
3.354604967 |
4.016678193 |
2.455538797 |
4.123509832 |
1.424361817 |
3.13102752 |
5.659636162 |
1.579498279 |
5.010935914 |
0.153960072 |
30.90975155 |
| Candidate-12 |
1.732050808 |
4.808364625 |
3.948745699 |
5.797988157 |
2.028602065 |
4.123509832 |
5.175583703 |
3.150001633 |
6.819052628 |
0.769800359 |
38.35369951 |
| CCi |
Rank |
|
| 0.387298402 |
12 |
Candidate-1 |
| 0.494160506 |
8 |
Candidate-2 |
| 0.511900445 |
5 |
Candidate-3 |
| 0.498862656 |
6 |
Candidate-4 |
| 0.606635026 |
1 |
Candidate-5 |
| 0.525283219 |
4 |
Candidate-6 |
| 0.461638245 |
11 |
Candidate-7 |
| 0.482695265 |
9 |
Candidate-8 |
| 0.494950812 |
7 |
Candidate-9 |
| 0.552752515 |
2 |
Candidate-10 |
| 0.462307158 |
10 |
Candidate-11 |
| 0.542795394 |
3 |
Candidate-12 |
References
- Amiri-Aref, M., N. Javadian, and M. Kazemi. 2012. A new fuzzy positive and negative ideal solution for fuzzy TOPSIS. WSEAS Transactions on Circuits and Systems 11: 92–103. [Google Scholar]
- Baharin, N., N. Rashidi, and N. Mahad. 2021. Manager selection using fuzzy TOPSIS method. Journal of Physics: Conference Series 1988: 012057. [Google Scholar] [CrossRef]
- Collan, M., M. Fedrizzi, and P. Luukka. 2015. New closeness coefficients for fuzzy similarity-based fuzzy TOPSIS: An approach combining fuzzy entropy and multidistance. Advances in Fuzzy Systems 2015: 1–12. [Google Scholar] [CrossRef]
- Hatami-Marbini, A., and F. Kangi. 2017. An extension of fuzzy TOPSIS for group decision making with an application to Tehran Stock Exchange. Applied Soft Computing Journal 52: 1084–1097. [Google Scholar] [CrossRef]
- Kumar, S., S. Kumar, and A.G. Barman. 2018. Supplier selection using fuzzy TOPSIS multi-criteria model for a small-scale steel manufacturing unit. Procedia Computer Science 133: 905–912. [Google Scholar] [CrossRef]
- Nabeeh, N., M. Abdel-Basset, H. El-Ghareeb, A. Aboelfetouh, and F. Smarandache. 2019. An integrated neutrosophic-TOPSIS approach and its application to personnel selection: A new trend in brain processing and analysis. IEEE Access. 7: 29734–29744. [Google Scholar] [CrossRef]
- Syamsuddin, I. 2013. Multicriteria evaluation and sensitivity analysis on information security. International Journal of Computer Applications 69, 22: 22–25. [Google Scholar] [CrossRef]
- Tuğrul, E. 2022. Personnel selection utilizing the decision-making mechanism created with the intuitionistic fuzzy TOPSIS method. International Journal of Organizational Leadership 11, 1: 87–102. [Google Scholar] [CrossRef]
- Paraskevas, Antonios, and Michael Madas. 2024. Selection of Academic Staff Based on a Hybrid Multi-criteria Decision Method Under Neutrosophic Environment. Operations Research Forum 5. [Google Scholar] [CrossRef]
- Ogunode, N., and H. Sarkinfada. 2023. Appointment and selection of leaders in university system in Nigeria. Best Journal of Innovation in Science, Research and Development 2, 6: 311–322. [Google Scholar]
- Sang, X., X. Liu, and J. Qin. 2015. An analytical solution to fuzzy TOPSIS and its application in personnel selection for knowledge-intensive enterprise. Applied Soft Computing 30: 190–204. [Google Scholar] [CrossRef]
- Awasthi, A., S. Chauhan, and H. Omrani. 2011. Application of fuzzy TOPSIS in evaluating sustainable transportation systems. Expert System Application 38: 12270–12280. [Google Scholar] [CrossRef]
- Rahi, M., A. Ullah, and M. Alam. 2022. A Decision Support System (DSS) for interview-based personnel selection using fuzzy TOPSIS method. In Proceedings of International Conference on Fourth Industrial Revolution and Beyond 2021. Springer Nature Singapore: pp. 645-657,978-981. [Google Scholar]
- Fathi, M., H. Matin, M. Zarchi, and S. Azizollahi. 2011. The Application of Fuzzy TOPSIS Approach to Personnel Selection for Padir Company, Iran. Journal of Management Research 3, 2: 1–14. [Google Scholar] [CrossRef]
- Oladimeji, R. M., and M. A. Oladejo. 2023. Vice-chancellors’ appointment procedures and administrative effectiveness in Kwara State universities. Sapientia Foundation Journal of Education, Sciences and Gender Studies 5, 1: 429–437. [Google Scholar]
- Oparinde, O. R., and F. B. Bamire. 2021. Managing recruitment, selection and induction processes for tertiary institutions’ staff positions in Nigeria. International Journal of Educational Management 19, 1. Available online: https://www.ijem.org.ng/index.php/ijem/article/view/18.
- Mbangula, D. K. 2025. Examining the intersections between emotional intelligence and leadership practices in higher education institutions to improve institutional success. Innovare Journal of Education 13, 1: 1–6. [Google Scholar] [CrossRef]
- Agboluaje, R. 2020. Unending crisis in premier varsity over appointment of new VC. The Guardian (Nigeria). November 5. Available online: https://guardian.ng/features/unending-crisis-in-premier-varsity-over-appointment-of-new-vc/.
- Gottwald, D., S. Jovčić, and P. Lejsková. 2022. Multi-criteria decision-making approach in personnel selection problem — A case study at the University of Pardubice. Economic Computation and Economic Cybernetics Studies and Research 56, 2: 149–164. [Google Scholar]
- Dhurkari, R. K. 2022. MCDM methods: Practical difficulties and future directions for improvement. RAIRO-Operations Research 56, 4: 2221–2233. [Google Scholar] [CrossRef]
- Ismail, M. M., H. R. Abdelhady, and M. Emad. 2024. Multi-Criteria Decision-Making Techniques: A Comprehensive Review of Methodologies and Applications. International Journal of Computers and Informatics (Zagazig University) 2: 27–38. Available online: https://www.ijci.zu.edu.eg/index.php/ijci/article/view/70.
- Villalba, P., A. J. Sánchez-Garrido, and V. Yepes. 2024. A review of multi-criteria decision-making methods for building assessment, selection, and retrofit. Journal of Civil Engineering and Management 30, 5: 465–480. [Google Scholar] [CrossRef]
- Saaty, T. L. 1980. The analytic hierarchy process: Planning, priority setting, resource allocation. McGraw-Hill. [Google Scholar]
- Zadeh, L. A. 1965. Fuzzy sets. Information and Control 8, 3: 338–353. [Google Scholar] [CrossRef]
- Lad, S. V., and P. N. Joglekar. 2016. Decision making using fuzzy logic: A review. International Journal of Computer Applications 144, 5: 28–33. [Google Scholar] [CrossRef]
- Kumar, R., R. K. Singh, and R. Shankar. 2018. Evaluation of sustainable supply chain management practices using fuzzy TOPSIS in Indian automobile industry. Clean Technologies and Environmental Policy 20, 2: 313–329. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).