The Effect of Cognitively Guided Instruction on Students’ Mathematical Achievements and Conceptual Understanding in a US Curriculum-Based School in the UAE

1. Introduction

Improving the educational system in the United Arab Emirates (UAE) has been a national priority since the launch of the UAE 2021 Vision by H.H. Sheikh Mohammed bin Rashid Al Maktoum (Abdallah & Musah, 2021; The United Arab Emirates’ Government portal, 2018). To turn this vision into reality, the Ministry of Education has developed a strategic plan for 2017-2021 to enhance the educational system. The goal of this proposed programme is to improve models of academic excellence and foster students’ critical thinking, problem solving and application of knowledge in mathematics, science (Gokulan, 2018). This includes comparing the educational system with best performance countries through international assessments, to identify students’ requirements and improve academic results (The United Arab Emirates’ Government portal, 2018).

As a result of these improvements, leaders and teachers in UAE schools have started using teaching methods and practices that encourage students to think, communicate, conceptualize, and solve problems (Abdallah & Musah, 2021; Gokulan, 2018). There is a particular emphasis on implementing innovative approaches to teaching mathematics, as it is a challenging subject that requires a relational and cumulative understanding and is best taught through exploration rather than observation (Leon, 2019).

Achieving high results in international assessments has become a national priority in the UAE. Therefore, all schools in the UAE are working towards exceeding the average international benchmarks (Ministry of Education, 2019). However, some schools still perform lower than others due to various factors, such as having a large majority of English language learners (Jadeja, 2019).

The school where the study took place was one of these schools. The students in the school were performing below the average benchmark scores in mathematics, prompting school leaders to seek new ways of teaching mathematics to help students build their mathematical knowledge and improve their understanding of numbers and procedures.

The foregoing discussion is linked to learning environments by emphasizing the UAE’s national efforts to reform and enhance its educational systems in alignment with the UAE 2021 Vision (Abdallah & Musah, 2021; The United Arab Emirates’ Government portal, 2018). The Ministry of Education’s 2017–2021 strategic plan also targets the promotion of a learning environment where critical thinking, problem-solving and experiential application is emphasized in mathematics and science (Gokulan, 2018). This policy makes accountable education performance by international assessments which then serves to aid the school in diagnosing student needs and correcting achievement gaps (The United Arab Emirates’ Government portal, 2018). These are policies that create a product environment for teaching and learning in a way where everything can be put on the table and even compared to international benchmark.

The discussion also highlights how innovative teaching practices enhance the learning environment in UAE schools. By implementing strategies that promote critical thinking, communication, and problem-solving, educators can address challenges in mathematics that require relational and cumulative understanding (Leon, 2019). Cognitively guided instruction CGI enhances learning by focusing on students’ conceptual understanding and academic performance (Bognar et al., 2025; Empson, 2015; Machaba & Mangwiro, 2024; Wang et al., 2025). Additionally, adapting teaching methods for diverse student populations, particularly in underperforming schools with many English language learners (Jadeja, 2019, fosters inclusive learning environments in multicultural settings, such as the UAE. Through these strategies, the UAE aims to equip students with the skills and knowledge necessary for national and international educational success.

Therefore, this study was designed to investigate the effects of a specific mathematical teaching practice that could be implemented in schools to enhance students’ conceptual understanding of mathematics and improve their academic performance. This teaching practice, known as CGI, has been recommended for use in previous studies and research (Empson, 2015; Machaba & Mangwiro, 2024). This study examined the impact of CGI practices on fourth-grade students in a US curriculum-based school in Dubai, UAE. Grade four was chosen for this study because it is one of the grade levels that needs to be assessed and benchmarked in mathematics and science in the UAE by the Trends in International Mathematics and Science Study (TIMSS) Assessments (Knowledge and Human Development Authority, 2017).

2. Literature Review

2.1. Cognitively Guided Instruction

CGI is an approach to teaching mathematics developed by Thomas Carpenter and Elizabeth Fennema in the late 1980s. They argued that elementary students are naturally curious and that teachers should guide them in using their curiosity to find solutions to complex story problems without relying on traditional mathematical algorithms and procedures (Carpenter et al., 1996; Wang et al., 2025).

(Carpenter et al., 1996) stated that CGI depends on the students’ developmental stage. It utilizes problem-solving and rigorous questioning to develop students’ conceptual understanding of essential mathematical concepts and operations. Hence, CGI does not use a prespecified set of problems in a given sequence to teach the curriculum (Bognar et al., 2025; Empson, 2015; Machaba & Mangwiro, 2024; Ramaila, 2025), and it doesn’t provide teachers with a prescription of how to teach mathematics; instead it notifies teachers that they need to plan instruction based on the students’ thinking, knowledge and understanding of Mathematics (Wilson & Berne, 1999).

(Carpenter et al. 2014) found that when CGI is practiced, students are not instructed to use traditional procedures, algorithms, and formulas for math concepts. Instead, they will be guided to find as many solutions as possible to story problems. That is to say, when practicing CGI, students will use their spontaneous knowledge of mathematical concepts to solve the issues and they will also get the guidance which directs them to realize the big ideas, discover the links and the properties of mathematics, learn how to model, think, reason, reflect and dialogue mathematically, and develop the conceptual understandings without the need for the procedural instruction (Carpenter et al., 2003).

2.2. Theoretical Basis of Cognitively Guided Instruction

CGI is a research-based instructional approach designed to enhance students’ mathematical achievement and conceptual understanding by aligning teaching practices with their natural cognitive development. CGI draws from constructivist theories of learning, particularly those of Piaget and Vygotsky, emphasizing the active role of students in constructing their knowledge and the social context of learning (Piaget, 1970; Vygotsky, 1978).

At its core, CGI posits that students come to the classroom with intuitive mathematical ideas, which can be developed through guided exploration and problem-solving. Carpenter et al. (1996), Fennema et al. (1999), and Carpenter et al. (1989) identify that CGI teachers focus on understanding students’ thinking and leveraging it to guide instruction. This process involves listening to students, interpreting their strategies, and providing tasks that challenge their current level of understanding, thereby fostering deeper conceptual learning and improving problem-solving skills.

Given the diversity of student backgrounds, the application of CGI within a US curriculum-based school in the UAE is particularly significant. Research highlights the effectiveness of CGI in multicultural and multilingual settings by adapting instruction to students’ unique cognitive and cultural perspectives (Fennema et al., 1999; Carpenter et al., 2014; Fennema et al., 1996). Furthermore, the approach aligns with the Common Core State Standards for Mathematics (CCSSM) principles, which emphasize conceptual understanding, procedural fluency, and application (National Governors Association Center for Best Practices, 2010).

CGI has been shown to improve mathematical achievement and understanding by focusing on student-centered instruction and conceptual development. Studies suggest that students in CGI classrooms outperform their peers in problem-solving and conceptual knowledge (Fennema et al., 1999; Clements & Sarama, 2011), making it a powerful approach for fostering mathematical success in diverse educational contexts.

2.3. CGI Classroom

A typical CGI classroom requires the teacher to pose a story problem, then to request students to read it aloud, retell it, solve it independently using any strategy they select, and then to share these strategies and engage in rich discourse about the problem and the used strategies (Carpenter et al., 1996). Story problems are essential to CGI as they help students apply their existing understandings to these problems and make meaning of the mathematical concepts (Machaba & Mangwiro, 2024; Munday, 2016).

The CGI process can be practiced with large groups, small groups, or by using centers. Students can use any tool they want to solve the problems in any way that makes sense to them, their peers, and teachers (Empson, 2015; Machaba & Mangwiro, 2024).

2.4. CGI and Teachers

A study by Carpenter et al. (1996) indicated that students reason about mathematics in ways that do not align with the mathematical procedures taught in schools. Hence, the researchers continued to study children’s thinking of mathematical concepts and found that, as teachers get the required professional development to understand how children’s mathematical thinking develops, their teaching fundamentally changes in ways that reflect students’ learning (Carpenter et al., 2014).

Therefore, for CGI to be implemented successfully, teachers need to develop a strong understanding of how students reason mathematically and how they tend to solve problems (Carpenter et al., 1996; Illa et al., 2019; Machaba & Mangwiro, 2024). Once that is accomplished, their instruction shifts from a teaching perspective to understanding how students learn (Franke et al., 2009). When you discuss with those teachers what they will teach, along with their learning objectives and goals, you hear them discussing the strategies their students are using or explaining, as well as how they understand mathematics (Carpenter et al., 2014).

2.5. Conceptual Understanding

Conceptual understanding in mathematics refers to the development of a solid framework that illustrates the various interconnected relationships between mathematical concepts, patterns, and procedures (Hayati et al., 2024; Jamil et al., 2024; Okanda et al., 2023; Saparbayeva et al., 2024). This framework enables students to expand their knowledge and effectively solve unfamiliar problems (Niemi, 2010). In simple terms, conceptual understanding refers to the ability to comprehend and explain the rationale behind the workings of an algorithm, as well as the underlying processes involved in manipulating numbers (Funa et al., 2024; Kanive et al., 2014; Mahmud & Mustafa Bakri, 2024).

Many teachers often focus solely on instructing students on using a procedure, without explaining the underlying reasons. This teaching approach yields proficient students who follow procedures (Hayati et al., 2024; Jamil et al., 2024; Kanive et al., 2014; Munday, 2016). However, procedural fluency alone does not lead to true proficiency or the capacity to solve new and unknown problems. Consequently, conceptual understanding is crucial in attaining genuine mathematical proficiency (Carpenter et al., 2003; Funa et al., 2024; Mahmud & Mustafa Bakri, 2024; Saparbayeva et al., 2024).

Furthermore, the development of conceptual understanding lays the foundation for future mathematical learning. For instance, early math instruction emphasizes the conceptual understanding of numbers and their relationships, thus preparing students for more advanced mathematical concepts in the future (Baroody, 2001; Bognar et al., 2025; Hayati et al., 2024; Jamil et al., 2024; Okanda et al., 2023). This preparation includes recognizing the relationships between numbers within expressions and equations and utilizing these relationships to solve problems (Jacobs et al., 2001). Therefore, conceptual understanding of mathematics is essential for students to grasp more complex mathematical concepts later (Funa et al., 2024; Jacobs et al., 2001; Mahmud & Mustafa Bakri, 2024; Okanda et al., 2023; Ramaila, 2025).

2.6. Mathematical Achievements

Mathematical achievement refers to the competency demonstrated by students in mathematics (Li et al., 2024; Pandey, 2017; Shone et al., 2024; Zhu et al., 2024). It is an indication of their mathematical abilities, specifically their procedural fluency and conceptual understanding of mathematics (Egara & Mosimege, 2024; Jamil et al., 2024; Mahmud & Mustafa Bakri, 2024; Munday, 2016; Okanda et al., 2023).

Mathematical achievement can be measured through internal assessments and external international assessments. In the UAE, one of the international assessments used to evaluate students’ performance in mathematics is TIMSS. TIMSS is a large-scale international assessment of mathematics and science for students in the fourth and eighth grades. It is conducted every four years by the International Association for the Evaluation of Educational Achievement (IEA) (Knowledge and Human Development Authority, 2017; Wijaya et al., 2024). TIMSS has garnered significant attention in the UAE and has become one of the country’s national priorities. The UAE aims to be among the top 15 highest-performing countries in TIMSS by 2021 (Knowledge and Human Development Authority, 2017).

The most recent results announced for TIMSS were from 2015, which revealed that Dubai had the highest overall mathematical results in the region (Knowledge and Human Development Authority, 2017). However, a further analysis of student scores revealed significant differences in math scores across Dubai schools, as illustrated in Figure 1 and Figure 2.

With a TIMSS average score of 500, Figure 1 demonstrates that fourth-grade students in United Kingdom (UK) curriculum schools achieved the highest mathematical scores. Their average scores were approximately 50 points above the international average. Fourth-grade students in International Baccalaureate (IB) and Indian curriculum schools scored 30 points above the international average. These are the only curricula with average scale scores above the global average. In contrast, fourth-grade students in US curriculum-based schools did not meet the international benchmark, scoring an average of 467. However, they outperformed students in both the Private Ministry of Education (MoE) and Public Ministry of Education (MoE) curriculum schools. Private-MoE students outperformed their Public-MoE counterparts by nearly 30 points (Knowledge and Human Development Authority, 2017).

Figure 2 illustrates that eighth-grade students in UK curriculum schools achieved the highest mathematical scores. Their average scores were approximately 50 points above the international average. Eighth-grade students in IB and Indian curriculum schools scored 47 and 33 points above the international average, respectively. These are the only curricula with average scale scores above the global average. In contrast, eighth-grade students in US curriculum-based schools did not meet the international benchmark, scoring an average of 479. However, they outperformed students in Private-MoE and Public-MoE curriculum schools. Private-MoE school students fared better than Public-MoE school students by nearly 58 points (Knowledge and Human Development Authority, 2017).

Based on the data above, it is evident that students in US curriculum-based schools in Dubai are not performing as well as those in British, Indian, and International Baccalaureate-based schools. Therefore, these schools need to identify the reasons behind their students’ underperformance and work towards improving their mathematical achievements in the UAE.

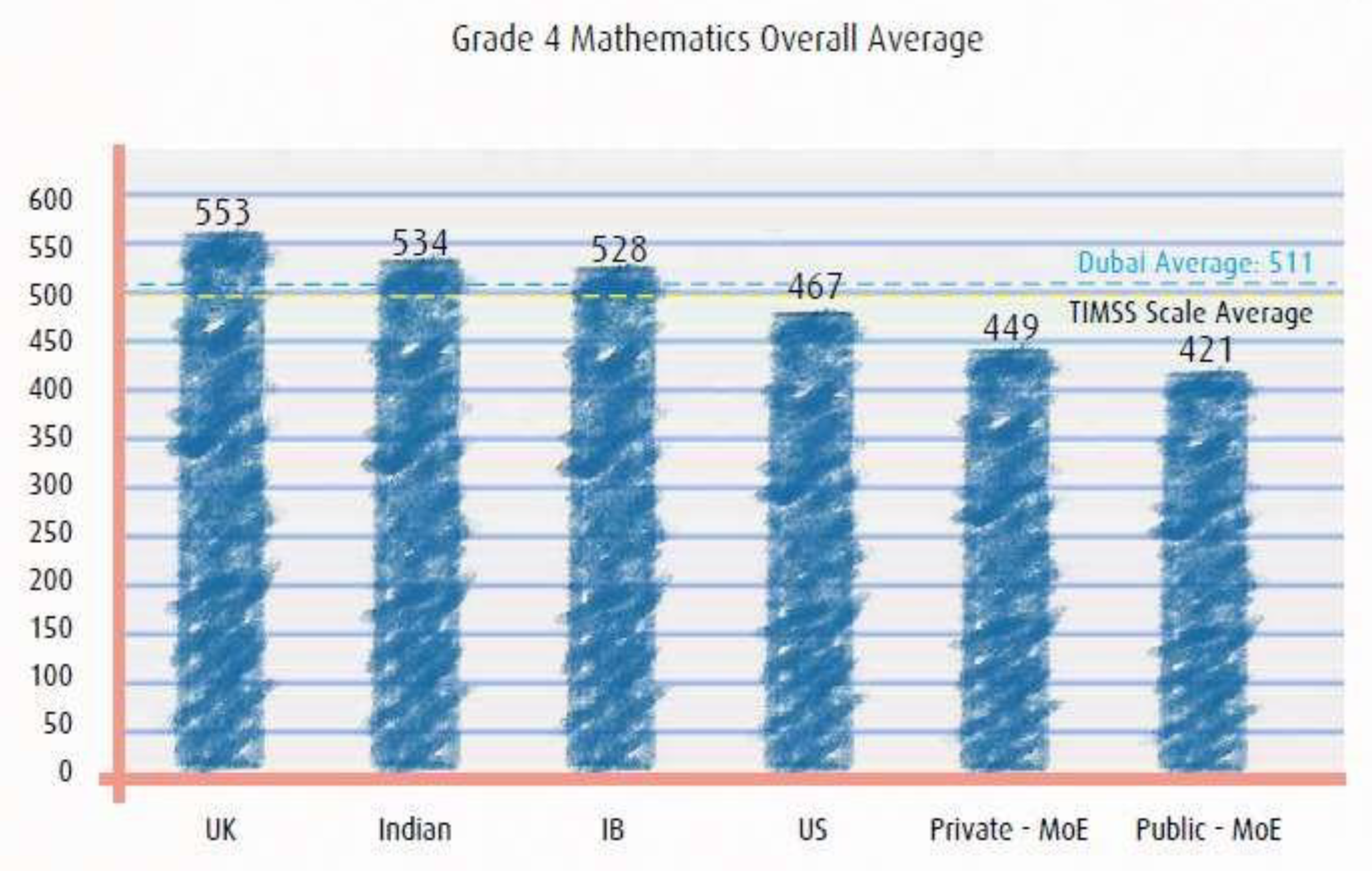
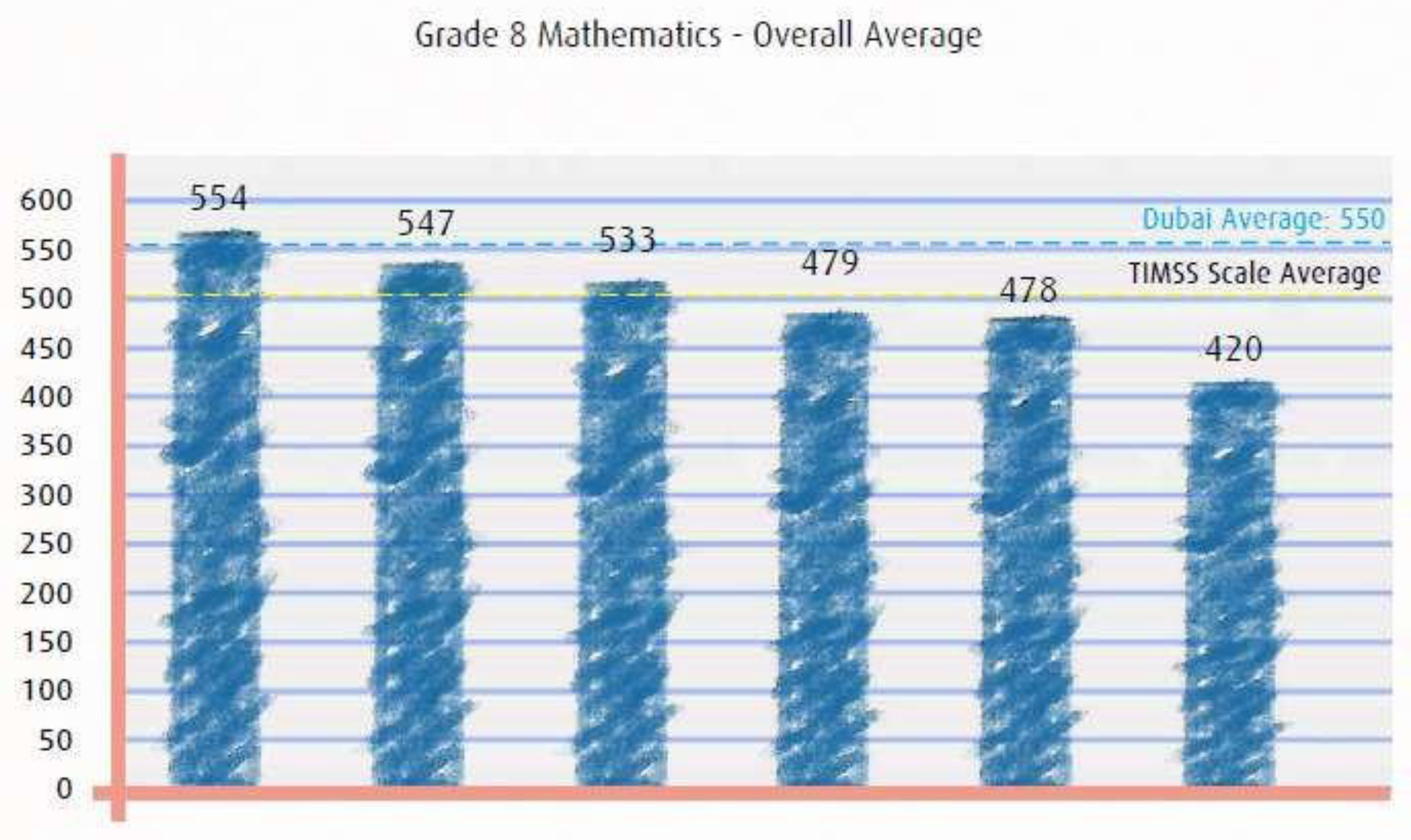
2.7. Potential Reasons for Low Achievements

Research indicates that there may be several reasons why students struggle with mathematics. Researchers, for instance, discovered that reading comprehension skills impact students’ mathematical performance (Cheung et al., 2024; Hidayatullah & Csíkos, 2023; Vista, 2013; Wijaya et al., 2024). In other words, students who can understand word problems tend to perform better in math. Another factor that influences mathematical achievement is students’ weak conceptual understanding of math, particularly regarding number sense. Findings of various research work concluded that a significant number of first-grade students lacked a solid grasp of fundamental number concepts, which are crucial for their future success in math (Cheung et al., 2024; Hidayatullah & Csíkos, 2023; Ibrahim et al., 2024; Kamii & Rummelsburg, 2008; Ramaila, 2025; Whalen et al., 2024).

2.8. The Effects of CGI on Students’ Conceptual Understanding

Research has shown that using CGI practices enhances students’ conceptual understanding. For instance, Berger (2017), Carpenter et al. (2014), Decristan et al. (2015), Illa et al. (2019), and Munday (2016) discovered that CGI practices contributed to students’ of addition and subtraction. Rather than relying solely on memorization of procedural knowledge, students were able to devise innovative methods for performing these operations. Their findings are consistent with the recommendations made by Fyfe et al. (2014), who suggested that “when instructional approaches encompass procedural techniques, it may be beneficial to postpone instruction to provide learners with an opportunity to generate their own procedures” (p. 503). Additionally, Carpenter et al.’s (1996) findings suggest that allowing students to create their own procedures enhances their problem-solving ability and fosters a deeper conceptual understanding.

2.9. The Effects of Using CGI on Students’ Mathematical Achievements

As mentioned earlier, students’ low mathematical achievements may be attributed to their limited comprehension skills and/or absence of fundamental skills and conceptual knowledge (Hu et al., 2024; Kamii & Rummelsburg, 2008; Siller & Ahmad, 2024; Vista, 2013). Numerous research studies have demonstrated the benefits of using CGI to enhance mathematical achievement (Hu et al., 2024; Schoen et al., 2022, 2024; Siller & Ahmad, 2024; Zhang et al., 2024). Research has shown that CGI plays a crucial role in improving instruction, leading to positive effects on student learning, the school environment, and national understanding of mathematics (Berger, 2017; Schoen et al., 2022; Schukajlow et al., 2023; Siller & Ahmad, 2024).

2.10. CGI as a Strategy to Overcome Comprehension Problems to Improve Mathematical Achievements

Munday (2016) and other researchers indicated that CGI can help low-attaining students, especially English language learners, because CGI problems are presented as stories with elaboration, discussion, and questioning (Berger, 2017; Moore & Cuevas, 2022; Schoen et al., 2022; Schukajlow et al., 2023; Siller & Ahmad, 2024). This technique helps students in the long run to improve their math performance, even if they have limited language proficiency.

2.11. CGI as a Strategy to Provide Students with Foundational Skills and Conceptual Knowledge to Improve Achievements

CGI emphasizes the importance of students engaging in discussions and sharing their strategies and solutions. This collaborative approach has been found to positively impact students’ mathematical achievement (Egara & Mosimege, 2024; Li et al., 2024; Shone et al., 2024; Webb et al., 2008). When students explain their strategies and thinking collaboratively, they can develop new understandings and clarify any misconceptions about foundational knowledge (Webb et al., 2008). Furthermore, CGI encourages students to draw upon their prior knowledge and make connections between mathematical relationships. By conceptualizing mathematics in this way, students can build a stronger understanding and ultimately achieve higher academic success (Carpenter et al., 1996).

3. Materials and Methods

3.1. Design

The study employed a mixed-methods paradigm, utilizing both quantitative and qualitative designs (Creswell & Clark, 2019; Creswell & Creswell, 2018; Edmonds & Kennedy, 2017; Gunasekare, 2015). Qualitative design was employed through classroom observations, while quantitative design utilized quasi-experimental pre-test and post-test assessments. Quasi-experimental design employed an experimental group and a non-equivalent control group, as the researcher was unable to randomize the selection of students (Campbell & Stanley, 1963; Creswell & Clark, 2019; Creswell & Creswell, 2018).

As discussed earlier, the study was conducted in a US curriculum-based school in Dubai. It aimed to investigate the effects of using CGI practices on the conceptual thinking and mathematical achievements of fourth-grade students. Therefore, two sections of grade four were selected for the study. The first section consisted of a non-equivalent control group, while the second comprised an experimental group.

The teacher of the experimental group was trained to use and apply CGI practices. The teacher of the control group was never trained to use CGI practices. She employed the traditional method of teaching mathematics, which involves using symbolic computation first and then expecting students to apply the concepts to problem-solving situations (Wistrom, 2011).

The study began by administering a pre-test to the students. Then, the experimental group started solving problems using CGI practices twice a week. Then, the experimental group was observed twice while solving story problems. Finally, a post-test was administered to evaluate the students’ progress in both the experimental and control groups.

3.2. The Population and Sample of the Study

The population of this study consists of fourth-grade students from a US curriculum-based school in Dubai, UAE. Fourth grade was chosen because their grade level is assessed by TIMSS every four years. The fourth-grade class had only two sections at that school. Thus, the study sample consisted of only these two sections. One of the sections was designated as the experimental group, while the other served as the control group.

The experimental group consisted of 18 students, and the control group consisted of 17 students. Hence, the total number of students representing the sample was 35, which is scientifically approved for use as a sample in quasi-experimental designs (Sekaran & Bougie, 2016).

The students’ ages range between 8 and 9 years old. According to their results in the Northwest Evaluation Association Measures of Academic Progress (NWEA MAP), they had different academic abilities. They also had varying English language proficiency. The students’ demographics are described in Table 1.

3.3. Instrumentation

The nature of the study required the researchers to use two instruments to collect qualitative and quantitative primary data. These instruments were 1) pre-test and post-test assessments and 2) direct observations.

3.4. Pre-Test and Post-Test Assessment

A test was designed to serve as a pre-test and a post-test assessment. The assessment was designed to evaluate the impact of using CGI practices on students’ mathematical achievement and conceptual thinking. As discussed earlier, mathematical achievements assess students’ mathematical abilities—focusing on examining procedural fluency and mathematical conceptual thinking (Munday, 2016). Therefore, the test design consisted of three parts, as described below.

The first part focused on checking the students’ fluency in solving direct multiplication number sentences. The multiplication sentences used were 1) sentences that can be solved using existing knowledge, 2) sentences that can be solved using the strategies that will be taught during the period of the study, and 3) multiplication sentences that will not be taught during the period of the study. Table 2 describes the frequency of these multiplication sentences.

The third type of multiplication sentence was purposely used to check if CGI practices can help students solve unknown multiplication sentences by inventing their own strategies. The second part of the test focused on the students’ ability to solve multiplication story problems and the students’ ability to explain their thinking and approach. The third part of the test focused on checking the students’ ability to solve a multistep multiplication word problem and their ability to connect and link different ideas while solving.

Multiplication was the topic examined because the test questions needed to be aligned with the Mathematical Common Core State Standards (CCSS) taught during that time (Common Core State Standards Ini, 2019). The three parts of the assessment helped evaluate the effect of CGI practices on students’ mathematical achievements. Parts two and three helped specifically determine the impact of CGI practices on students’ conceptual thinking and understanding. Therefore, the evaluation of parts two and three depended on using the following criteria:

1)

Students’ ability to solve problems without being able to explain their work.

2)

Students’ ability to solve problems and explain their thinking using any strategy, such as direct modeling, direct methods, or even invented strategies.

The final aspect considered while designing the pre-test and post-test is the correlation between the test and TIMSS questions. Therefore, the researchers used story problems similar to those used in the TIMSS assessments.

3.5. Direct Observations

The researchers also employed direct observation as a data collection instrument. This method involves collecting evaluative information, where researchers observe the class without altering the environment and record their findings (Drury, 1995). The researchers followed the environment twice to monitor the students’ thinking while they solved problems. The first observation took place at the beginning of the program, and the second observation occurred towards the end of the study. Thus, this instrument helped observe the effects of CGI practices on students’ conceptual understanding and whether CGI is assisting students to overcome the obstacles that may lower their achievements. The observation was recorded using a tablet, and notes were filled in an observation form.

3.6. Validity and Reliability

The validity and reliability of the research instruments are fundamental aspects to be considered for any study to be objective and accurate. Reliability refers to the degree to which a research method produces stable and consistent results. Validity refers to the extent to which a research method accurately measures what it is purported to measure (Phelan & Wren, 2007). The researchers observed and examined the same sample to ensure the reliability of the instruments. That is, none of the participants were absent during the pre-test and post-test assessments, as well as during the observations.

The researchers also considered the reliability of parallel forms while designing the pre-test and the post-test. According to Phelan & Wren (2007), parallel forms reliability is obtained by creating different versions of an assessment tool to ensure that memory effects do not occur. Hence, the researchers designed the same pre-test and post-test but changed the numbers and quantities used in both tests.

With reference to validity, the researchers applied face validity by 1) choosing the questions that align with the Common Core State Standards, 2) using the school’s scheme of work to identify the standards, and 3) approving the pre-tests and post-tests’ content by the class teachers, the head of department, and the head of section.

3.7. Data Collection Procedure

The data collection procedure was done over six weeks, during the 2019-2020 academic year. The process started by addressing the research questions:

1)

What is the effect of CGI practices on students’ mathematical achievements?

2)

What is the effect of CGI practices on students’ conceptual understanding?

3)

Can CGI practices help students overcome the challenges they face while solving mathematical problems?

To address the above questions, a data collection procedure was planned and conducted, as outlined in Table 3. Furthermore, as seen in Table 3, the researchers separated the pre-test and post-test by six weeks. This was done based on the recommendations of Brown et al. (2013), which indicated that any intervention requires a minimum period of six weeks to start showing effects.

3.8. Data Analysis Procedure

As discussed, the data were gathered using quantitative (quasi-experimental pretest and post-test assessment) and qualitative (direct observation) instruments. Therefore, qualitative and quantitative analyses were conducted to inform the sub-questions and the study’s central question, as described below.

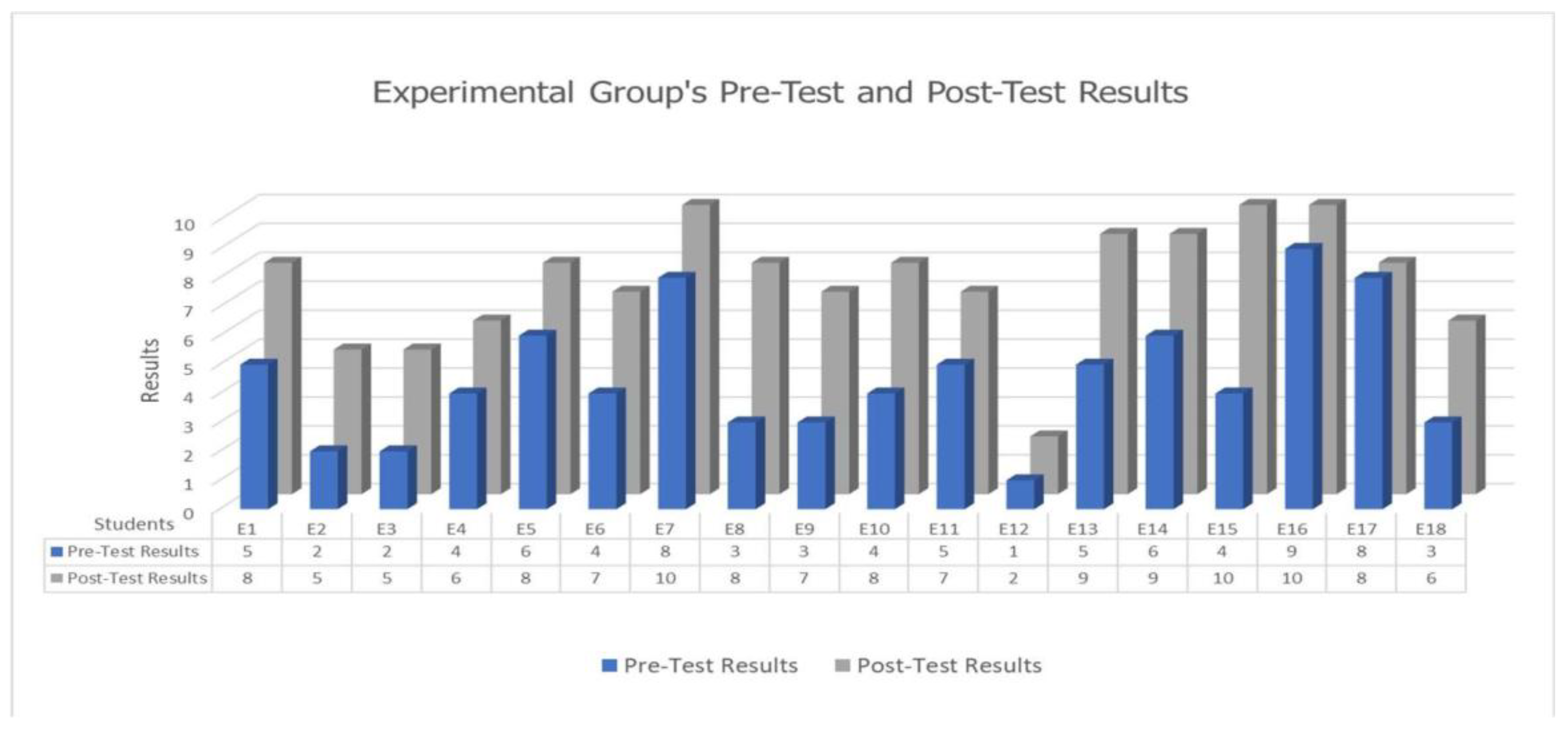
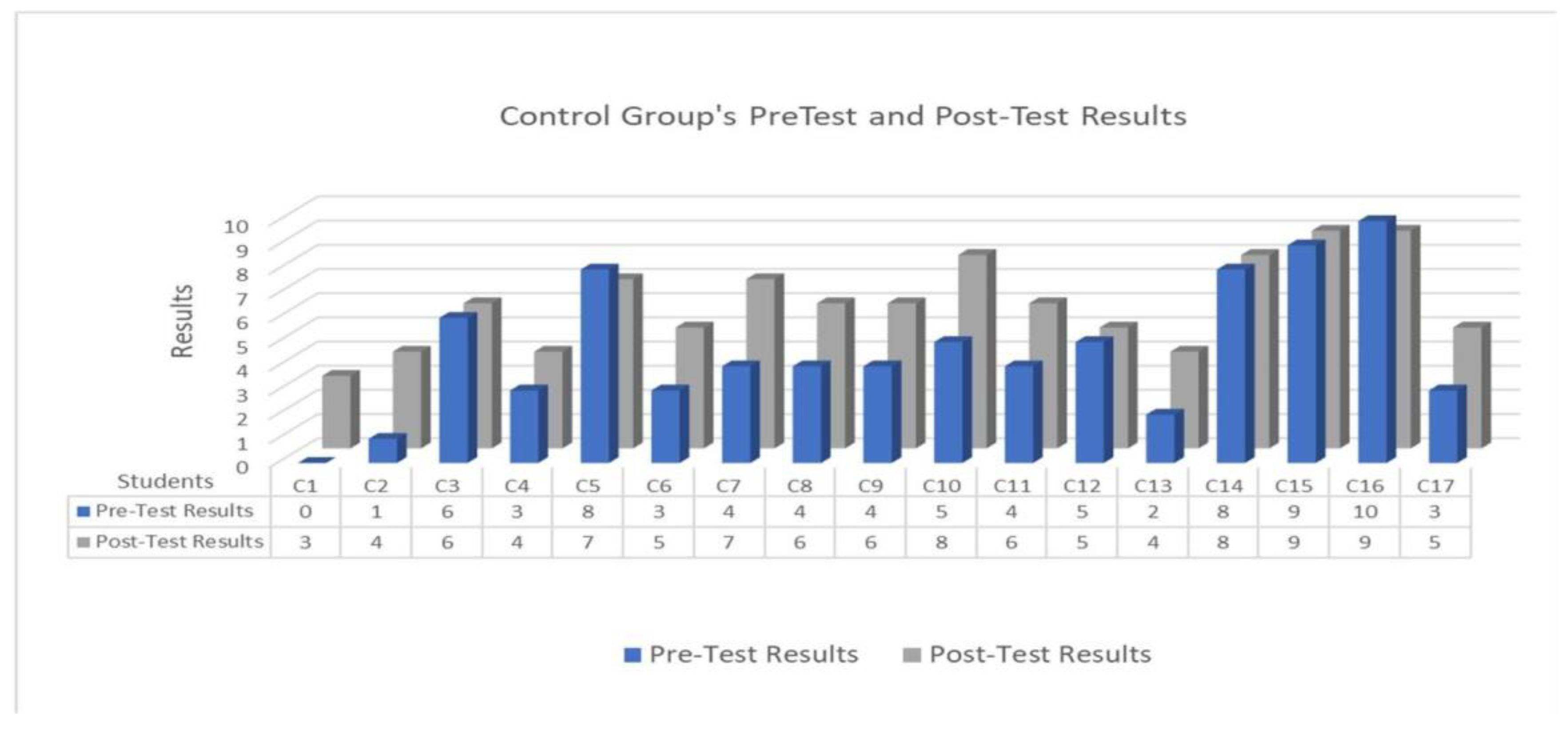
3.9. Analysis of the Pre-Test and Post-Test

The pre-test and post-test analysis helped determine the study’s validity and find the effects of CGI practices on students’ mathematical achievements. The analysis relied on comparing the arithmetic means of the tests and utilizing a t-test, a statistical process that assesses the probability of two samples being statistically different based on calculations involving means, standard deviations, and sample variations (Lavrakas, 2008).

The analysis for the pre-test and post-test was performed as follows:

1)

The arithmetic means of the pre-tests for both the control and experimental groups were compared to validate the analysis. A significant difference between the pre-test means has the potential to influence the post-test results(Campbell & Stanley, 1963). This comparison was performed utilizing the two-sample t-test available in the Data Analysis add-ins of Microsoft Excel.

2)

Analyzing the difference between the arithmetic means of the pre-test and post-test for the experimental group using the paired t-test tool, which is built into Microsoft Excel Data Analysis add-ins. This was done to check the significance of the change in the arithmetic mean after using CGI practices.

3)

Comparing the arithmetic means of the post-tests between the experimental and control groups to check whether there is a significant difference between their means. This was performed using the two-sample t-test tool built into the Microsoft Excel Data Analysis add-ins.

Analysis of parts 2 and 3 of the pre-test and post-test for the experimental group:

The analysis of parts two and three of the tests aimed to determine if CGI can enhance students’ ability to explain their strategies and whether they can devise their own strategy while solving assigned problems. The analysis compared the number of students who could solve and explain their thinking using any strategy in parts 2 and 3 before and after applying the CGI practice.

3.10. Analysis of Direct Observation

The data from the direct observations were analyzed and reviewed to draw inferences about the effect of CGI practices on students’ thinking and to determine if using story problems in a CGI classroom can help students overcome the difficulties that may hinder their mathematical achievements.

4. Results

4.1. Analysis and Results for the First Research Question

What is the effect of CGI practices on students’ mathematical achievements?

To address this question, the researchers calculated and presented the results of the pretest and post-test for the experimental and control groups. These results are presented in Figure 3 and Figure 4.

4.2. Comparing the Arithmetic Means of the Pre-Tests for the Control and Experimental Groups

The arithmetic mean of the pre-test for the experimental group was 4.56, while the control group’s pre-test had an arithmetic mean of 4.65. These findings suggest that the mean scores of the pre-tests for both groups were very similar, adding credibility to the subsequent analysis. Additionally, the researchers conducted a two-sample t-test to examine whether there was a significant difference between the two means, under the null hypothesis that the means are significantly close. The results of the t-test are presented in Table 4.

The results indicate that the p-values exceed 0.05, thereby supporting the acceptance of the null hypothesis. This finding suggests that there is no statistically significant difference between the pre-test means of the experimental and control groups. Subsequently, we will evaluate the difference in means between the pre-test and post-test for the experimental group.

This step aimed to evaluate whether the arithmetic mean of the experimental group’s scores exhibited a statistically significant change following the implementation of the CGI practices. A paired t-test was conducted, with the null hypothesis positing that the means are not significantly different from each other. The test results are presented in Table 5.

The results indicate that the p-values are less than 0.05, leading to rejection of the null hypothesis. This suggests a significant difference in the arithmetic means between the pre-test and post-test conducted by the experimental group. To determine if there is a substantial difference between the means, the arithmetic means of the post-tests for both the experimental and control groups were compared.

The experimental group’s post-test had an arithmetic mean of 7.39, while the control group’s had an arithmetic mean of 6.00. These findings demonstrate that the arithmetic mean of the experimental group is higher. Additionally, the researchers conducted a two-sample t-test to examine the significant difference between the two arithmetic means of the post-tests. The null hypothesis assumed that the means are significantly similar. The results of the t-test were then compiled and presented in Table 6.

The results indicate that the p-values are less than 0.05, which leads to the rejection of the null hypothesis. This suggests a significant difference between the arithmetic means of the experimental and control groups’ post-tests.

4.3. Analysis and Results for the Second Question

What is the effect of CGI practices on students’ conceptual understanding?

To assess students’ ability to explain their thinking and develop their own problem-solving strategies, the researchers analyzed data from Part 2 (story problems), Part 3 (multi-step story problems), and unfamiliar multiplication sentences (sentences not taught to the students). The results of direct observations are discussed below.

4.4. Results of Part 2, Part 3, and the Unfamiliar Multiplication Sentences

Table 7 presents the results of the experimental group. It reveals that the number of students who could solve and explain their thinking in part 2 (story problems) increased by seven, while in part 3 (multi-step problems), it increased by 3. Additionally, three more students were able to solve unfamiliar multiplication problems after implementing CGI.

The results for the control group are presented in Table 8. It is observed that the number of students who could only solve story problems without explaining has increased by three, which is a higher increase than the number of students who could solve story problems using CGI (1 student). There was no statistically significant increase in the number of students in the control group who were able to solve and explain Part 2 following traditional instructions. In contrast, the experimental group demonstrated an enhanced ability to solve and explain Part 3, as summarized in Table 9. Additionally, the control group had one fewer student who showed the ability to solve unfamiliar multiplication sentences.

4.5. Results of Direct Observations

As previously mentioned, two observations were conducted to evaluate the impact of CGI on students’ conceptual thinking. In these observations, the observers closely monitored the students’ thought processes as they solved problems and provided explanations for their findings. The results obtained from these two observations can be summarized as follows.

4.6. Results of the First Observation

The students’ skills were still in the process of developing. Some solved problems and shared their answers and strategies verbally without documenting them. Additionally, a few students were still seeking clarification from the teachers regarding the definition of “strategy”. Although the students recognized multiple ways to solve the question, they could only generate a solution using one specific strategy. Furthermore, not all students were actively involved when sharing their strategies.

4.7. Results of the Second Observation

The students were enthusiastic when the teachers announced they would solve the question using CGI. After the teachers read and hid the question, the students began standing up and retelling it. Each student solved the problem individually, using various methods, including direct modeling, skip counting, or direct procedures. One student even separated the numbers into smaller groups before conducting the multiplication. The students were fully engaged, sharing their answers to earn more points and utilizing math talk to agree or disagree with one another.

4.8. Analysis and Results for the Final Research Question

Can CGI practices help students overcome the challenges they face while solving mathematical problems?

Researchers collected primary data from a secondary observation. The findings indicated that educators read the questions aloud and encouraged students to read them multiple times. They prompted students to restate the questions to enhance comprehension. Furthermore, educators provided individualized support to ensure understanding.

The observation also revealed that students participated in mathematical discourse to articulate their thoughts and discuss solutions. Some students rectified misunderstandings among their peers, suggesting an improvement resulting from the implementation of CGI (Wang et al., 2025).

5. Discussion

The study’s findings suggest that implementing CGI practices has a positive impact on students’ mathematical achievements. The experimental group, which was taught using CGI-based methodologies, demonstrated a statistically significant improvement in their average scores following the intervention. The post-test average of the experimental group exceeded that of the control group, underscoring the efficacy of CGI practices in enhancing both mathematical understanding and performance.

This finding is consistent with prior research conducted by Carpenter et al. (1999), Hu et al. (2024), Schoen et al. (2022, 2024), Siller & Ahmad (2024), and Zhang et al. (2024). These studies have established that the CGI method facilitates the utilization and enhancement of students’ prior knowledge through conceptual thinking. By promoting active problem-solving, CGI fosters a deeper understanding of mathematical concepts and contributes to enhanced academic performance. Furthermore, CGI practices endorse differentiated instruction, effectively addressing diverse learning needs and enabling all students to progress at their individual cognitive levels.

This study demonstrates the potential of CGI to improve student performance in international assessments, such as the Trends in International Mathematics and Science Study (TIMSS) and the Programme for International Student Assessment (PISA), which emphasize problem-solving, critical thinking, and conceptual understanding—core components of CGI methodologies. By facilitating the integration of new information with preexisting knowledge and fostering active engagement in the learning process, CGI establishes a robust foundation for mathematical proficiency and prepares students for global competitiveness.

CGI’s focus on relational understanding, which encourages students to investigate the interconnections among mathematical concepts, effectively addresses prevalent challenges in mathematics instruction. In contrast to traditional pedagogical approaches, CGI emphasizes exploration, reasoning, and communication, thereby enabling students to cultivate transferable skills in mathematics. This pedagogical strategy not only enhances test scores but also equips students to tackle real-world problems, underscoring its significance in contemporary educational contexts.

By reinforcing the importance of conceptual thinking and active engagement, CGI offers a pathway for educators to enhance their teaching practices and improve student outcomes. The study’s results confirm CGI as a highly effective pedagogical strategy for enhancing mathematical achievement and achieving sustainable improvements in educational quality.

The study’s data also indicates that CGI practices have a significant influence on students’ conceptual understanding of mathematics. Although both the experimental and control groups demonstrated improvement in solving story problems, the experimental group exhibited superior performance relative to the control group in articulating their reasoning and establishing connections when addressing multi-step word problems that involved unfamiliar multiplication sentences. These findings are consistent with prior research (Berger, 2017; Carpenter et al., 2014; Decristan et al., 2015; Fyfe et al., 2014; Illa et al., 2019; Munday, 2016), suggesting that CGI practices, which prioritize procedural knowledge and conceptual depth, enhance students’ capabilities in solving unfamiliar mathematical problems.

The experimental group’s capacity to articulate their cognitive processes and implement strategies for resolving complex problems underscores the significance of CGI in promoting a profound comprehension of mathematical concepts. CGI fosters active engagement, encourages the exploration of multiple solution pathways, and facilitates connections between ideas. This aligns with the findings of Carpenter et al. (2003), Illa et al. (2019), and Munday (2016), who demonstrated that CGI practices substantially enhance students’ understanding and internalization of mathematical concepts, transcending mere rote application of procedures.

Students in the experimental group demonstrated significant problem-solving abilities, particularly in devising strategies to simplify multiplication. This finding is consistent with research conducted by Carpenter et al. (1996), Fyfe et al. (2014), and Munday (2016), which underscores the importance of CGI in fostering independent procedural generation and conceptual understanding. Such skills are essential for tackling unfamiliar problems, thereby promoting flexible thinking and diverse methodologies.

The study reveals that while both groups made progress, the experimental group outperformed the control group in critical areas of conceptual learning, including explaining reasoning and employing creative strategies. The emphasis on CGI procedures prepared students to tackle unfamiliar problems and develop a strong understanding of underlying mathematical concepts. CGI fosters deep engagement with mathematical ideas, promoting higher order thinking skills essential for academic success and real-world problem-solving.

The study’s findings highlight the transformative potential of CGI in mathematics education. CGI equips learners to approach mathematics as a coherent discipline by prioritizing conceptual understanding and procedural fluency. This holistic approach ensures that students are proficient in performing calculations and adept at reasoning, strategizing, and making meaning of mathematical ideas. As such, CGI represents a critical innovation in fostering a learning environment that values deep comprehension and intellectual independence.

The study’s findings underscore the significance of CGI practices in helping students navigate the challenges encountered in solving mathematical problems. Observational data indicate that these practices effectively mitigate comprehension difficulties by promoting activities such as reading, retelling, and engaging in discussions with instructors to address questions. This interactive pedagogical approach not only clarifies misunderstandings but also fosters a deeper understanding of the mathematical problem at hand. The results are consistent with the extant literature (Egara & Mosimege, 2024; Li et al., 2024; Shone et al., 2024; Webb et al., 2008), which suggests that CGI is particularly beneficial for struggling learners, including English Language Learners (ELLs), by presenting mathematical problems in narrative formats. This strategy, combined with elaboration, discourse, and inquiry, facilitates a deeper engagement with mathematical concepts and ultimately contributes to improved academic performance.

The observations highlighted the importance of peer interaction in the CGI approach. Students engaged in discussions, shared strategies, and expressed agreements or disagreements while solving problems. This collaborative environment enhanced their problem-solving abilities and helped address gaps in foundational knowledge. This finding aligns with Carpenter et al. (1996; Webb et al., 2008), who emphasize CGI practices in identifying and rectifying misconceptions in students’ mathematical thinking. Collaborative learning in CGI classrooms enables students to articulate their reasoning, test hypotheses, and refine their understanding through feedback.

CGI practices effectively support diverse student populations, including those with language barriers or limited prior knowledge. By integrating storytelling, questioning, and dialogue, CGI makes abstract mathematical concepts more relatable and accessible. For example, English language learners often struggle with understanding mathematical problems due to language barriers. CGI’s focus on contextualized, story-based problem-solving helps bridge this gap, allowing students to connect mathematical concepts with real-life scenarios.

The study highlights the role of teachers as facilitators in the CGI approach. Teachers guide discussions, pose questions, and encourage students to articulate their thought processes. This strategy helps identify areas of difficulty and empowers students to take ownership of their learning, fostering critical thinking and self-regulation skills necessary for tackling complex mathematical challenges.

In addition, CGI practices address cognitive and linguistic challenges, providing a framework for supporting students in their mathematical learning journey. By promoting comprehension, collaboration, and clarity, CGI equips students with the tools to overcome obstacles and achieve progress in mathematics. This approach demonstrates the potential of innovative teaching strategies to transform learning environments and empower students to achieve academic excellence.

6. Conclusion

The findings of the study culminated in the following conclusions regarding the influence of CGI practices on fourth-grade students:

6.1. Conceptual Understanding and Mathematical Achievement

CGI practices significantly enhance students’ comprehension of mathematical concepts and contribute to improved academic achievement. By leveraging students’ prior knowledge and promoting individualized problem-solving strategies, these practices facilitate a deeper understanding of mathematical principles and enhance procedural fluency. This approach enables students to execute operations accurately while grasping the foundational concepts that underpin them. By prioritizing both conceptual understanding and procedural precision, CGI practices offer a comprehensive mathematical education that equips students with critical skills necessary for success in academic settings and effective problem-solving in real-world contexts.

6.2. Integration of Mathematical Ideas and Problem-Solving

Through the implementation of CGI practices, students can connect and integrate various mathematical concepts, thereby enhancing their problem-solving skills and capacity to articulate reasoning. This pedagogical approach facilitates the identification of relationships among disparate ideas, promoting a more profound comprehension of mathematical principles. Students develop the confidence to engage with novel problems and apply their knowledge flexibly across various contexts (Dogbey, 2025). Moreover, the process of explaining their thought processes reinforces conceptual understanding and supports mathematical growth, effectively preparing students for both assessments and real-world applications.

6.3. Addressing Challenges in Learning Mathematics

The CGI practices facilitate students’ ability to navigate challenges in mathematics. Traditional pedagogical approaches frequently fail to accommodate learners with limited comprehension or insufficient foundational knowledge (Dogbey, 2025). CGI emphasizes the importance of understanding students’ cognitive processes and delivering tailored support. By fostering a deeper understanding of mathematical concepts and personalized problem-solving strategies, CGI effectively addresses learning gaps and establishes a solid foundation for future academic success. This methodology enables all students to achieve mathematical competence and confidence, regardless of their initial proficiency levels.

6.4. Enhancing Engagement and Collaboration

A significant advantage of Cognitively Guided Instruction (CGI) practices is their capacity to enhance student engagement and collaboration. By fostering an interactive learning environment, CGI enables students to assume ownership of their educational experiences and facilitates connections with their peers (Wang et al., 2025). Through collaborative problem-solving and discussions, students exchange perspectives, refine their strategies, and acquire insights. This social interaction not only deepens their mathematical understanding but also cultivates essential skills such as communication and teamwork, thereby transforming the classroom into a dynamic space for exploration and intellectual growth.

6.5. Broader Implications for Educational Practice

The implementation of CGI practices significantly transforms educational paradigms by transitioning from rote memorization to a student-centered, inquiry-driven approach. CGI facilitates the development of critical thinking, adaptability, and problem-solving skills that are essential for success in an increasingly dynamic world. Furthermore, it addresses individual learning needs, promotes equity, and fosters a collaborative community that supports all learners. These insights underscore the substantial impact of CGI on mathematical education and the broader context of teaching and learning.

7. Recommendations

The recommendations of the study can be summarized and expanded as follows:

7.1. Expanding CGI Research Across Mathematical Operations

Research should examine the impact of CGI practices on students’ conceptual understanding and mathematical achievements across a range of operations, including addition, subtraction, division, fractions, and decimals. Future studies will contribute to a deeper understanding of how students integrate various procedures when addressing story problems and will elucidate how CGI facilitates the application of knowledge in diverse mathematical contexts, ultimately enhancing skill development and problem-solving capabilities.

7.2. Exploring CGI’s Influence on Mathematical Beliefs and Attitudes

Future research should investigate the impact of CGI practices on students’ mathematical beliefs and attitudes, with a particular focus on whether CGI enhances students’ confidence, interest, and enjoyment in mathematics. By examining the psychological and emotional effects of CGI, researchers can elucidate how these instructional practices contribute to the development of a motivating learning environment (Dogbey, 2025). The findings could inform educators in designing targeted interventions to improve mathematical performance and foster a sustained appreciation for the subject.

7.3. Investigating CGI Across All Elementary Grades

To comprehend the long-term impact of CGI, future research should encompass students across all elementary grade levels. Analyzing its effects on both younger and upper elementary students will yield a comprehensive understanding of its influence on mathematical development. This investigation will facilitate the identification of how CGI practices can be tailored to various developmental stages, thereby optimizing benefits for students across all grade levels.

7.4. Increasing Sample Size and Diversity

Future research should encompass a larger and more diverse sample of students from various US curriculum-based schools in Dubai and other international contexts. Incorporating participants from a range of cultural and socio-economic backgrounds will enhance the validity and reliability of the findings, thereby facilitating stronger conclusions regarding the effectiveness of CGI. This diversity will yield valuable insights into how to adapt CGI practices to meet the distinct needs of different student populations.

7.5. Extending the Duration of CGI Implementation

Future research should extend the duration between the pre-test and post-test to improve the implementation of CGI practices. An extended timeframe will enable educators to more effectively incorporate CGI methodologies into their instructional routines, while also allowing students to acclimate to these practices. This adjustment is expected to yield a more precise evaluation of CGI’s impact on students’ comprehension, problem-solving abilities, and overall mathematical performance.

7.6. Addressing Educator Perspectives and Professional Development

Research should investigate educators’ perspectives on the implementation of Cognitively Guided Instruction (CGI) practices. Analyzing their experiences and challenges may yield valuable insights into enhancing support for teachers. Additionally, evaluating professional development programs centered on CGI training can identify effective methodologies for equipping educators with the requisite skills.

7.7. Informing Educational Practices and Policies

Future research has the potential to yield actionable insights that can enhance educational practices and policies by concentrating on critical areas. Examining the influence of CGI on students’ mathematical thinking, achievement, attitudes, and confidence will contribute to the development of more inclusive and effective mathematics curricula. This knowledge will help educators, administrators, and policymakers create an environment that promotes comprehensive mathematical development for all students.