Parameterized Kolmogorov-Smirnov Test for Normality

1. Introduction

Numerous goodness-of-fit tests (GoFTs) have been considered and applied in many scientific fields. GoFTs for normality are very popular in economics and finance. GoFTs are used to analyze market behavior (distribution of rates of return, trading volume or asset prices), assess market efficiency and identify deviations from ideal market conditions, analyze stochastic processes (asset prices or changes in commodity prices). In demography, the fertility curve is almost normally distributed. In econometrics, normality tests are used to check whether regression errors are normally distributed. This is important for the proper evaluation of regression models because violating the assumption of normality can lead to erroneous statistical conclusions.

One of the most common normality testing procedures available in statistical software is the Kolmogorov-Smirnov (KS) test [1,2], which belongs to the empirical distribution function (EDF) tests. Other popular EDF tests include the Cramer-von Mises (CM) test [3,4], Lilliefors (LF) test [5], Kuiper (K) test [6], Watson (W) test [7] and Anderson-Darling (AD) test [8].

Let $x_{\left(1\right)},x_{\left(2\right)},\dots ,x_{\left(n\right)}$ be independent, sorted, and identically distributed observations from an unknown continuous cumulative distribution function (CDF) $F\left(x\right)$. We wish to determine whether $F\left(x\right)$ coincides with the cumulative distribution function (CDF) of the normal distribution $\Phi \left(x\right)$. Then, we are interested in testing the following hypothesis $H_0:F\left(x\right)=\Phi \left(x\right)$ against $H_1:F\left(x\right)\ne \Phi \left(x\right)$. The EDF is given by $F_n\left(x\right)={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\theta \left(x-x_i\right)$, where $\theta \left(x\right)=1$ for $x\ge 0$ and $\theta \left(x\right)=0$ for $x<0$.

The $\delta$-corrected KS test [9], investigated further by Khamis [10,11,12], redefines the value of the EDF at the data points and compares the redefined EDF to the CDF at the data points. Let the EDF at the i-th data point be given by

$$F_{\delta }\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-\delta }{n-2\delta +1}},0\le \delta \le 1.$$

(1)

Harter [9] selected $\delta =0,0.5,1$ for study.

Bloom [13] proposed the $\alpha ,\beta$ transformation

$$F_{\alpha ,\beta }\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-\alpha }{n-\alpha -\beta +1}},0\le \alpha ,\beta \le 1$$

(2)

to decrease the mean square error (MSE) of certain statistics. Note that $F_{\delta ,\delta }\left(x\right)=F_{\delta }\left(x\right)$. The transformation (2) was used to create the GoFTs.

Sulewski [14] used the Bloom’s formula to create the one-component LF GoFT with statistic

$$LF\left(\alpha ,\beta \right)=\underset{1\le i\le n}{\underbrace{max}}\left\{\left|F_{\alpha ,\beta }\left(x_{\left(i\right)}\right)-\Phi \left(x_{\left(i\right)}\right)\right|\right\}.$$

(3)

We know perfectly well that the greatest discrepancy between the theoretical and empirical distribution functions may occur at different positions in the series. The probability of this discrepancy occurring for a given positional statistic $\mathrm{r}$ is smaller the more extreme $\mathrm{r}$ is. Hence, the idea of a two-component test statistic described in [15]. The first component is, as in the original LF test, absolute value of the greatest discrepancy between sample and population distributions. The second component is a position in an ordered sample at which this discrepancy is located.

Sulewski and Stoltmann [16] used the Bloom’s formula to create the modified CM (MCM) GoFT with statistic

$$MCM\left(\alpha ,\beta \right)={\displaystyle \frac{1}{12n}}+\sum _{i=1}^n{\left[F_{\alpha ,\beta }\left(x_{\left(i\right)}\right)-\Phi \left(x_{\left(i\right)}\right)\right]}^2.$$

(4)

Simulation studies for the MCM test and for the one- and two-component LF tests were carried out for the following methods of calculating $F_{\alpha ,\beta }\left(x_{\left(i\right)}\right)\left(0\le \alpha ,\beta \le 1\right)$:

• $F_{0,1}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i}{n}}$ – occurs in the KS statistic,
• $F_{1,0}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-1}{n}}$ – occurs in the KS statistic,
• $F_{0.5,0.5}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-0.5}{n}}$ – occurs in the CM statistic,
• $F_{0,0}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i}{n+1}}$ – the mean value of i-th order statistics of the beta distribution,
• $F_{0.3,0.3}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-0.3}{n+0.4}}$ – the median of i-th order statistics of the beta distribution,
• $F_{0.375,0.375}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-0.375}{n+0.25}}$ – the mean value of i-th order statistic of the normal distribution,
• $F_{0.3175,0.3175}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-0.3175}{n+0.365}}$ – founded by Filliben [17],
• $F_{1,1}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-1}{n-1}}$ – founded by Harter [9].

Six of the EDF definitions listed above (except $F_{0,1}$and $F_{1,0}$) have $\alpha =\beta$.

Recently, many articles have been devoted to the goodness-of-fit tests (GoFTs) for normality. Table 1 shows the authors of works created in the 21st century and analyzed sample sizes. Sample sizes $n\le 50$ are in bold.

The small samples that dominate in Table 1, can be used in experimental economics, where papers were published with samples of a dozen or so people in a group. This is where strong tests can be put to great use. It may happen that the results will be: in the original paper, the hypothesis was accepted, and when a stronger test is applied, the hypothesis is rejected.

The first (main) aim of the article is to define and practically apply the parameterized KS test for normality. The second aim is to expand the EDF family with four new proposals. The third aim is to create a family of alternative distributions (alternatives), consisting of both older and newer distributions that, thanks to their flexibility, belongs to various groups of skewness and excess kurtosis signs. The fourth aim is to calculate the power of the analyzed tests for alternatives based on ${10}^5$ values of test statistics, with parameters selected so, that alternatives are similar to the Gaussian distribution in various ways.

The rest of this article is structured as follows. In Section 2, we define the parameterized KS GoFT test for normality. Section 3 is devoted to the similarity measure of the alternative to the normal distribution. In Section 4, we present the alternatives divided into nine groups according to their skewness and excess kurtosis signs (values). Power study is presented in Section 5 and real data examples are provided in Section 6. Finally, concluding remarks are presented in Section 7. Additional material can be found in Appendix.

2. Parameterized Kolmogorov-Smirnov Test for Normality

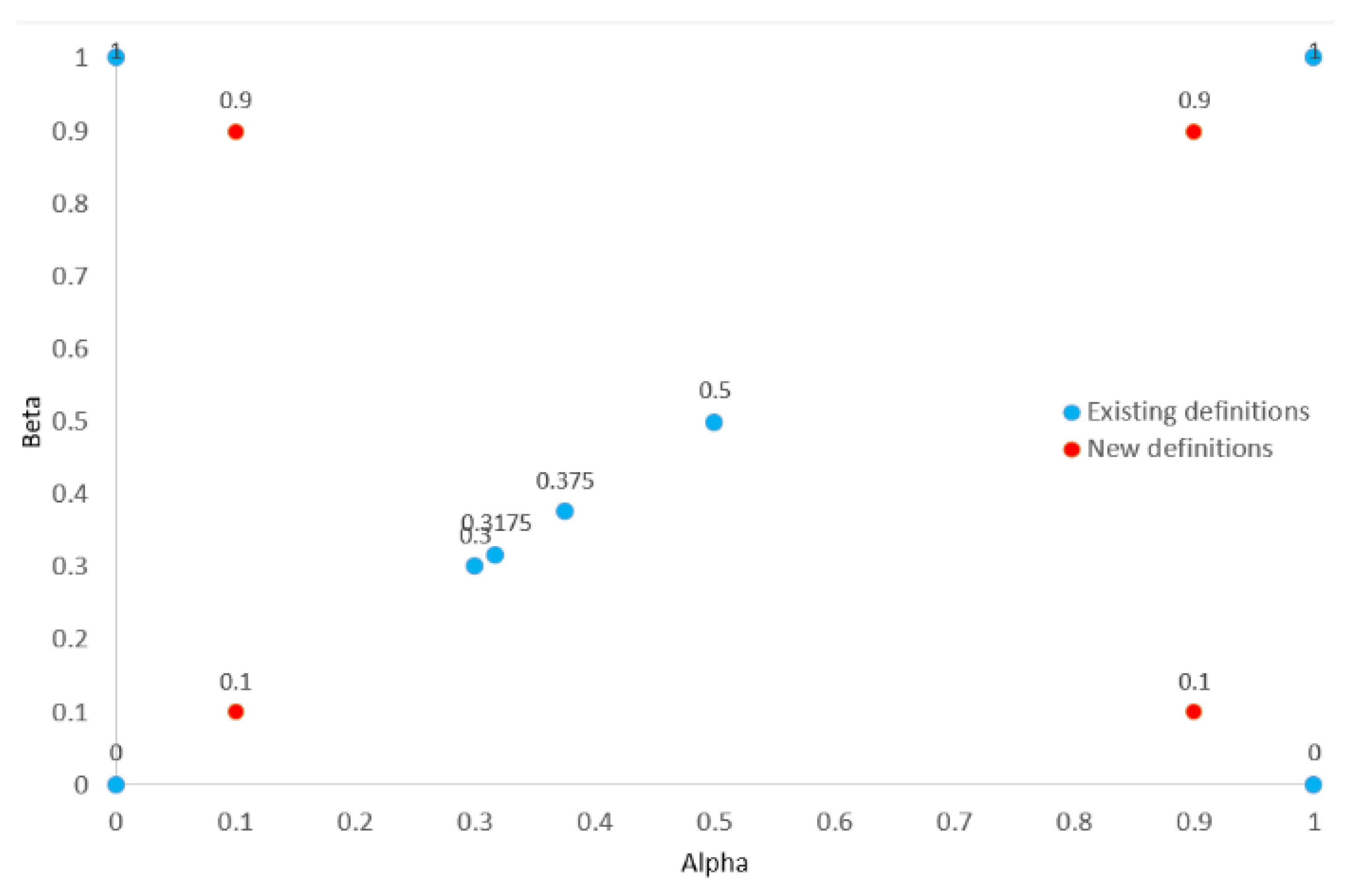
Before we present the parameterized KS test (the first contribution of the paper), we would like to expand the EDF family (the second contribution of the paper) with four new proposals $F_{0.1,0.1},F_{0.9,0.1},F_{0.9,0.9}$ and $F_{0.1,0.9}$ given by

$$F_{{\displaystyle \frac{1}{10}},{\displaystyle \frac{1}{10}}}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-0.1}{n+0.8}},$$

$${F_{{\displaystyle \frac{9}{10}},{\displaystyle \frac{1}{10}}}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-0.9}{n}},F}_{{\displaystyle \frac{9}{10}},{\displaystyle \frac{9}{10}}}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-0.9}{n-0.8}},F_{{\displaystyle \frac{1}{10}},{\displaystyle \frac{9}{10}}}\left(x_{\left(i\right)}\right)={\displaystyle \frac{i-0.1}{n}},$$

thus, eight of the EDF definitions listed earlier are on the line $\beta =\alpha$ and five of them are on the line $\beta =-\alpha +1$ (see Figure 1). The previously analyzed values unevenly fill the $\beta =\alpha$ line on the interval $\left[0,1\right]$. Four values belong to the interval $\left[0.3,0.5\right]$. The value $0.1$ represents the interval $\left(0,0.3\right)$ and the values 0.9 represent the interval $\left(0.5,1\right)$. The new representatives of $\beta =-\alpha +1$ line, also located at the corners of the square, are EDFs with $\alpha =0.9,\beta =0.1$ and $\alpha =0.1,\beta =0.9$.

Let $\widehat{x}=\left({\sum }_{i=1}^n{x}_i\right)/n,s^2=\left({\sum }_{i=1}^n{\left(x_i-\widehat{x}\right)}^2\right)/\left(n-1\right),z_{\left(i\right)}=\left(x_{\left(i\right)}-\overline{x}\right)/s$. Let’s remember that the KS test statistic is given by the formula

$$KS=\underset{1\le i\le n}{\underbrace{max}}\left\{\underset{1\le i\le n}{\underbrace{max}}\left[{\displaystyle \frac{i}{n}}-\Phi \left(z_{\left(i\right)}\right)\right],\underset{1\le i\le n}{\underbrace{max}}\left[\Phi \left(z_{\left(i\right)}\right)-{\displaystyle \frac{i-1}{n}}\right]\right\}.$$

(5)

Our idea is to parametrize the EDF in (5) using the Bloom’s formula (2). Parametrized KS (PKS) test statistic is defined as

$$PKS\left(\alpha ,\beta \right)=\underset{1\le i\le n}{\underbrace{max}}\left\{\underset{1\le i\le n}{\underbrace{max}}\left[{\displaystyle \frac{i-\alpha }{n-\alpha -\beta +1}}-\Phi \left(z_{\left(i\right)}\right)\right],\underset{1\le i\le n}{\underbrace{max}}\left[\Phi \left(z_{\left(i\right)}\right)-{\displaystyle \frac{i-\alpha -1}{n-\alpha -\beta +1}}\right]\right\}.$$

(6)

Note that $PKS\left(0,1\right)=KS$.

Sulewski and Stoltmann [16] as well as Sulewski [14,44] showed that noteworthy parameterized tests are defined using $F_{\alpha ,\beta }\left(x_{\left(i\right)}\right)\left(\alpha ,\beta \in \left\{0,1\right\}\right)$, so the values of $\left(\alpha ,\beta \right)$ chosen for the simulation study, except for new proposals, are: $\left(0,0\right),\left(1,0\right),\left(1,1\right),\left(0,1\right)$.

3. Similarity Measure

Let’s assume that $m_k={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(x_{\left(i\right)}-\overline{x}\right)}^k$ and ${\gamma }_1={\displaystyle \frac{m_3}{s^3}}$, ${\overline{\gamma }}_2={\displaystyle \frac{m_4}{s^4}}-3$. The Malachov inequality is defined as ${\overline{\gamma }}_2\ge {{\gamma }_1}^2-2$ [57].

A review of recent statistical literature shows that cases with small skewness ${\gamma }_1$ and excess kurtosis ${\overline{\gamma }}_2$ values do not dominate in testing for normality. It is very interesting to see how the GoFTs responds to samples coming from alternatives close to the normal distribution.

Let $f\left(x;\theta \right)$ be a PDF of the alternative distribution with the vector of parameters $\theta$. The similarity measure M of the alternative distribution (A) to the normal distribution is defined as [14]

$$M_A\left(\theta ;\mu ,\sigma \right)={\int }_{-\infty }^{\infty }min\left[f\left(x;\theta \right),\varphi \left(x;\mu ,\sigma \right)\right]dx,$$

(7)

where $\varphi \left(x;\mu ,\sigma \right)$ is the PDF of the normal distribution. The $M_A\left(\theta ;\mu ,\sigma \right)$ takes values on $\left[0,1\right]$. The $M_A\left(\theta ;\mu ,\sigma \right)=1$ when PDFs are identical.

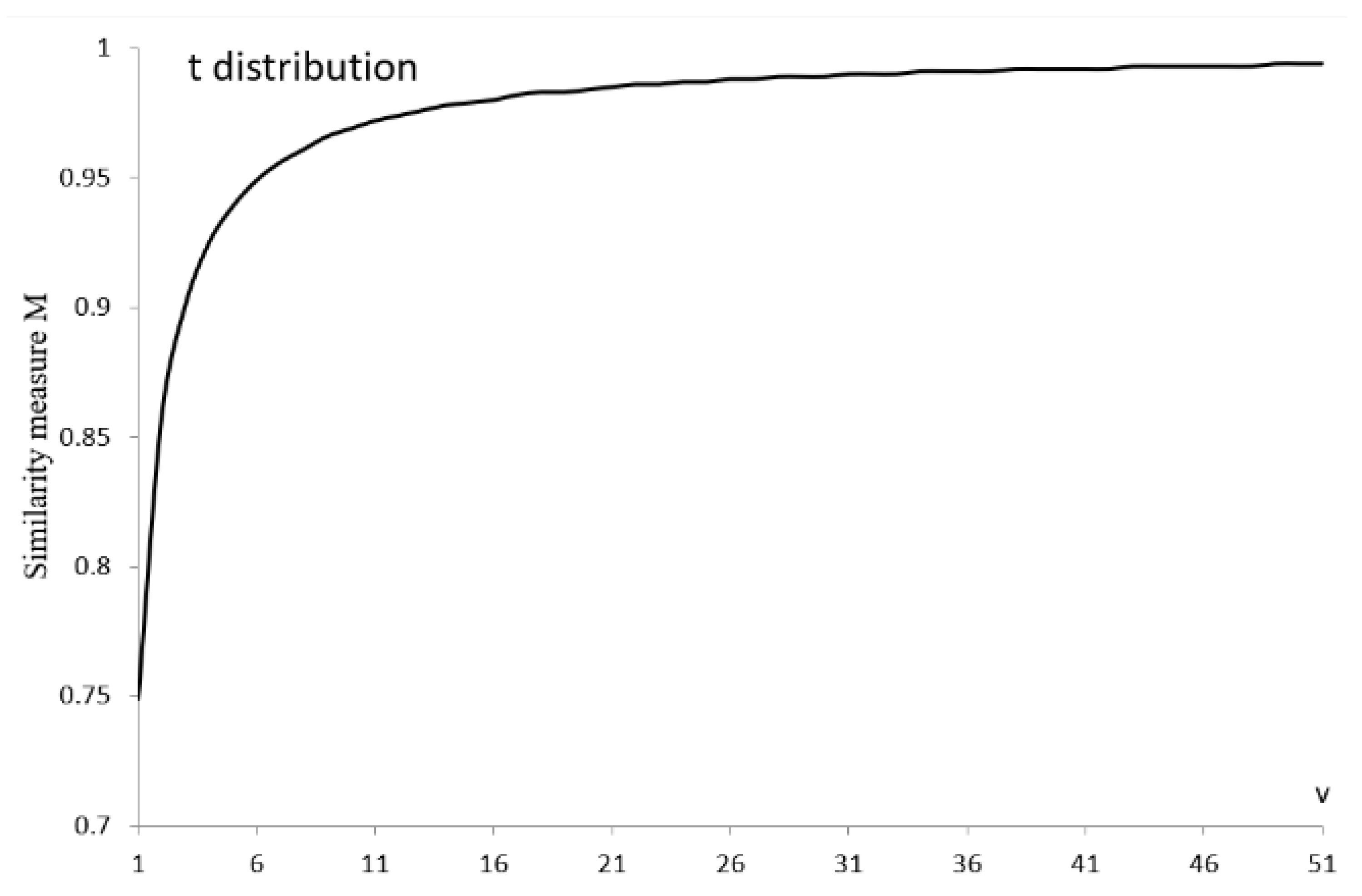
Figure 2 shows values of the similarity measure $M_A\left(\theta ;\mu ,\sigma \right)$, when an alternative distribution is the Student t distribution with v degrees of freedom. Note that if $v\to +\infty$ then obviously $M_t\left(v;0,1\right)\to 1$.

4. Alternative Distributions

As mentioned earlier, there are many articles devoted to testing for normality. In these articles, many alternative distributions (alternatives) have been used, among them asymmetric and symmetric ones. Recall that symmetric distributions with undefined ${\gamma }_1$ and ${\overline{\gamma }}_2$ are Cauchy and slash distributions.

The alternatives can be divided into four groups, depending on the support and shape of their densities (see e.g. [49,58]. These groups include symmetric alternatives with support $\left(-\infty ,\infty \right)$, asymmetric alternatives with support $\left(-\infty ,\infty \right)$, alternatives with support $\left(0,\infty \right)$ and alternatives with support $\left(0,1\right)$. Gan and Koehler [59], Krauczi [60] and Torabi et al. [49] divided alternatives into five groups, namely: asymmetric short-tailed, asymmetric long-tailed, symmetric short-tailed, symmetric close to normal and symmetric long-tailed alternatives. Sulewski [14,15] divided alternatives into twelve groups A1-F2 due to their ${\gamma }_1$ and ${\overline{\gamma }}_2$ signs as well as bimodality.

Our idea is to divide the alternatives into nine groups according to their ${\gamma }_1$ and ${\overline{\gamma }}_2$ signs [16]. Groups 0, A-H are defined in Table 2.

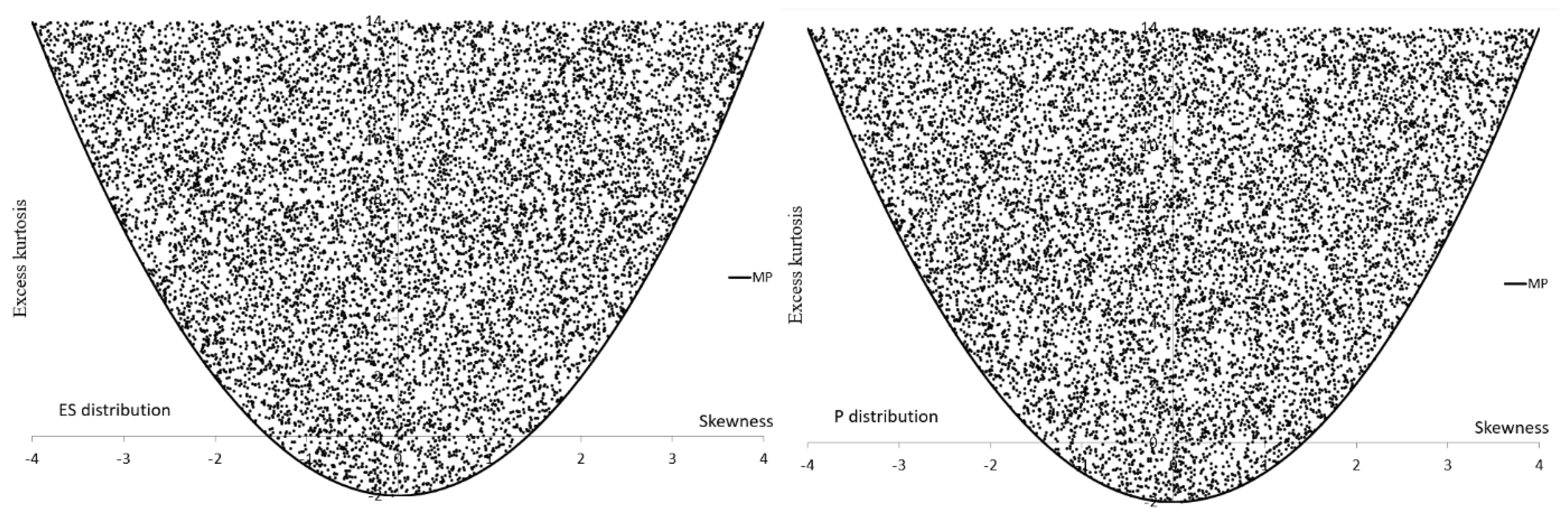
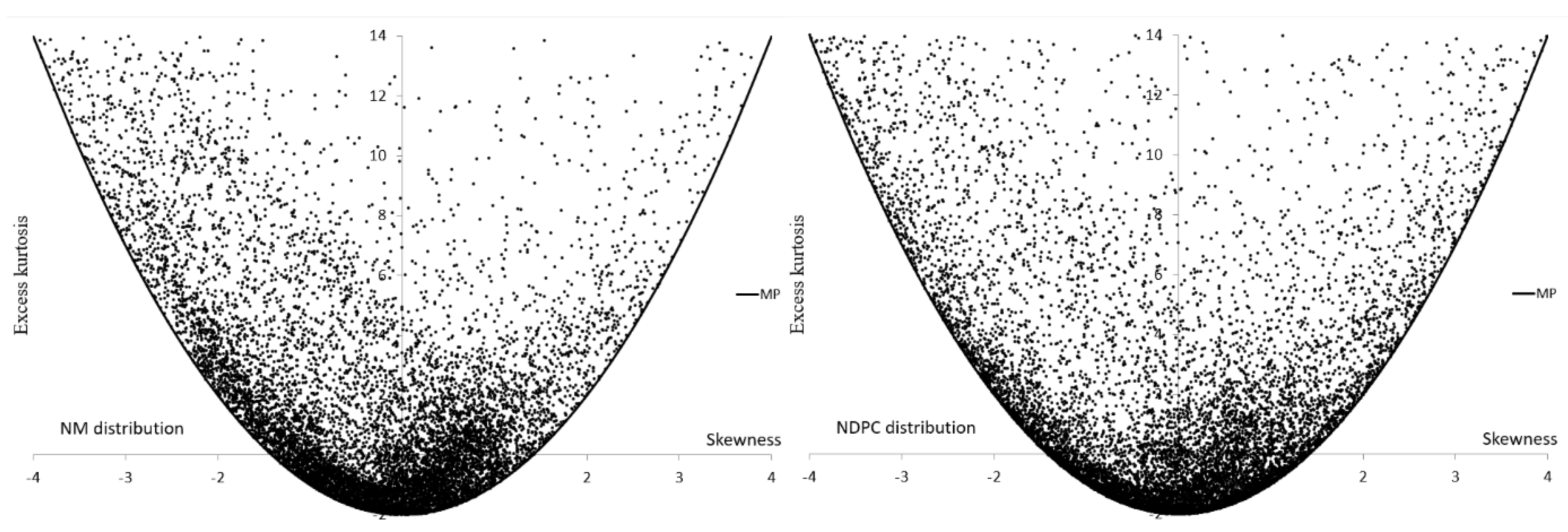
The first (main) criterion for selecting an alternative for Monte Carlo simulation is that ${\gamma }_1$ and ${\overline{\gamma }}_2$ calculated for the alternative parameters belong to all analyzed groups. This criterion is fulfilled by five distributions defined in an infinite domain, such as: the Edgeworth series (ES) and Pearson (P) as monolithic distributions with parameters ${\gamma }_1$ and ${\overline{\gamma }}_2$, the normal mixture (NM) as a mixture of two normal distributions, the normal distribution with plasticizing component (NDPC) as a mixture of normal and non-normal distributions and the plasticizing component mixture (PCM) as a mixture of two identical non-normal distributions.

The second criterion for selecting an alternative distribution for Monte Carlo simulation is that ${\gamma }_1$ and ${\overline{\gamma }}_2$ calculated for the alternative parameters belong to all analyzed groups except one (group 0). This criterion is fulfilled by the Laplace mixture (LM) distribution belonging to the groups A – H and defined in an infinite domain.

The third criterion for selecting an alternative for Monte Carlo simulation is that ${\gamma }_1$ and ${\overline{\gamma }}_2$ calculated for the alternative parameters belong to all analyzed groups except two groups. These alternatives can be very similar to the normal distribution. This criterion is fulfilled by the SB Johnson distribution (except groups 0, C) and SU Johnson distribution (except groups 0, D).

The fourth criterion for selecting an alternative for Monte Carlo simulation is that ${\gamma }_1$ and ${\overline{\gamma }}_2$ calculated for the alternative parameters belong to the C-D groups. These symmetric alternatives can be very similar to the normal distribution. This criterion is fulfilled by the extended easily changeable kurtosis (EECK) distribution defined in finite domain and the exponential power (EP) distribution defined in an infinite domain.

PDFs of selected alternatives and their special cases are presented in Appendix.

Let $\left({\gamma }_1,{\overline{\gamma }}_2\right)$ be coordinate of a point described by skewness and excess kurtosis, respectively. For every alternative, values of $\left({\gamma }_1,{\overline{\gamma }}_2\right)$ are calculated for ${10}^4$ randomly determined values of parameters influencing ${\gamma }_1$ and ${\overline{\gamma }}_2$ in the Malakhov area (MA) ${\overline{\gamma }}_2\ge {\gamma }_1^2-2$[57]. If ${\overline{\gamma }}_2\in \left[-2,14\right]$, then ${\gamma }_1\in \left[-4,4\right]$. The parameter ranges of the alternatives are selected to maximize MA filling (see Table 3). 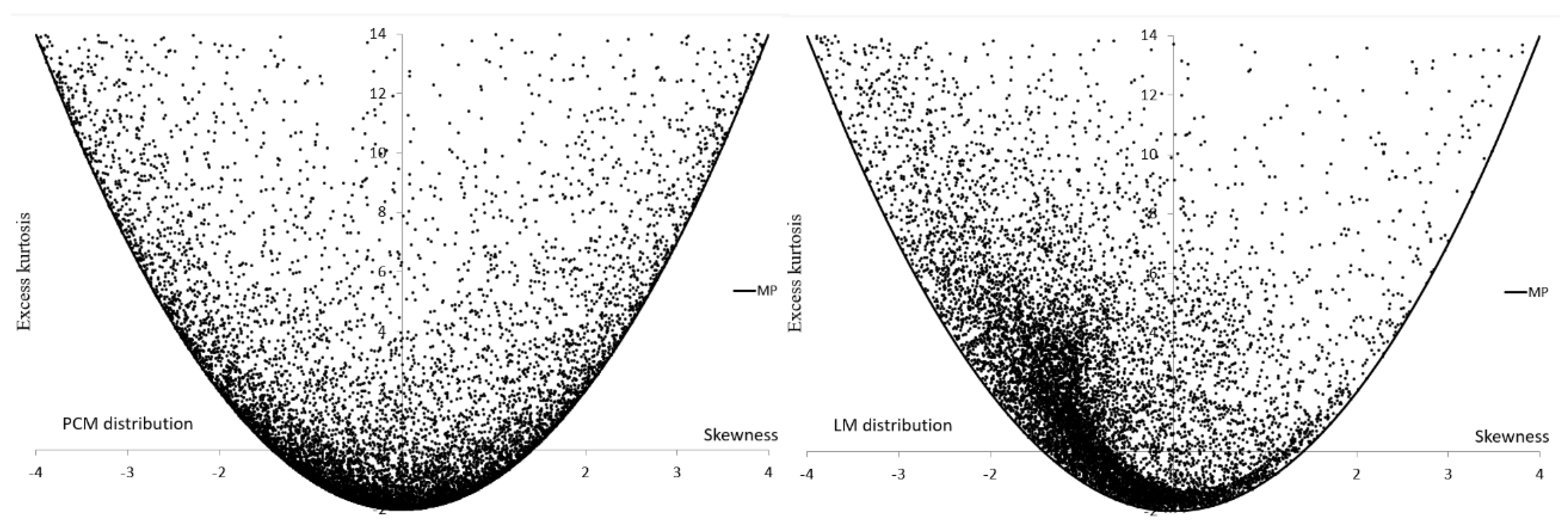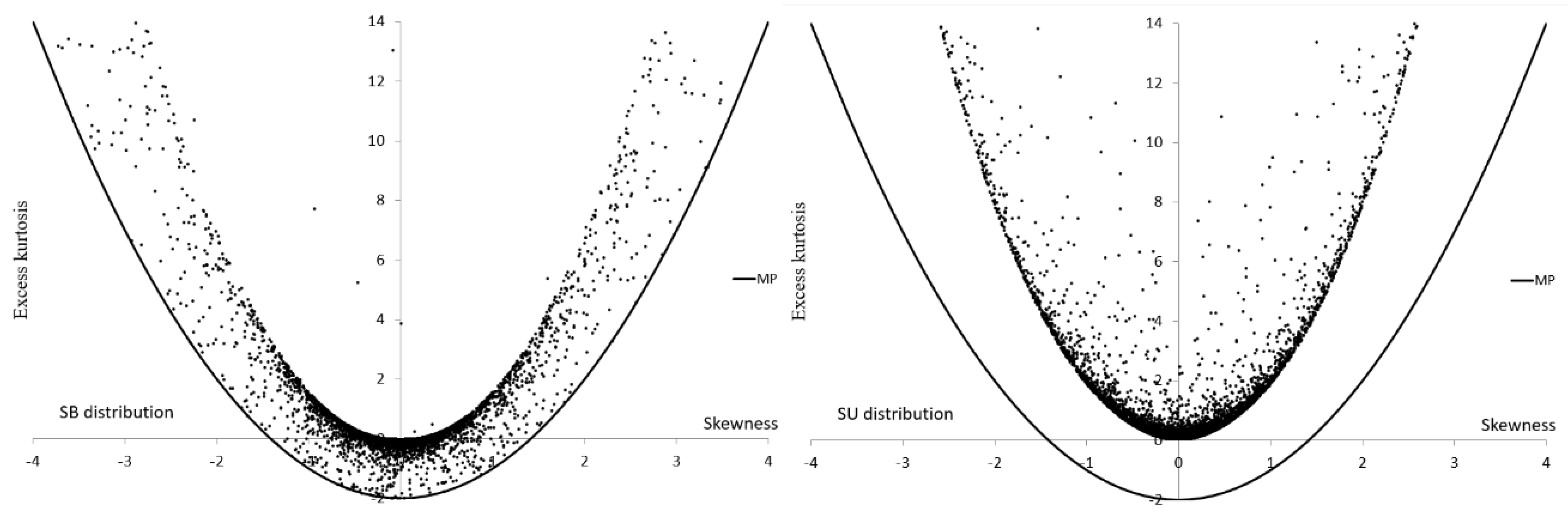Figure 2, Figure 3, Figure 4 and Figure 5 present sets of points $\left({\gamma }_1,{\overline{\gamma }}_2\right)$ located in the MA for non-symmetric alternatives. It is interesting that the MA for SB and SU are separate, they complement each other.

We also calculate the skewness-kurtosis-square (SKS) measure necessary to compare the flexibility of alternatives. Circles of diameter $\delta$ and coordinates of their centers determined by ${\gamma }_1$ and ${\overline{\gamma }}_2$ are placed within the MA. Then colored area fraction is calculated. Square sides equal to $\delta$ seem a reasonable alternative to circles since they simplify calculation of the total-colored area. Obviously, when some squares overlap, only one is taken into account. The SKS measure is given by [15]

$${SKS}_{\delta }=SS/TT,$$

where $TT$denotes a total number of squares within the MA, $SS$ – a number of squares to which the point $\left({\gamma }_1,{\overline{\gamma }}_2\right)$ has fallen. The ${SKS}_{\delta }$ measure takes values in $\left[0,1\right]$. The maximum value denotes a perfect dispersal of points $\left({\gamma }_1,{\overline{\gamma }}_2\right)$ in the MA.

Table 3 shows that the numerical ranges of ${\gamma }_1$ and ${\overline{\gamma }}_2$ for asymmetric alternatives in the MA $14\ge {\overline{\gamma }}_2\ge {\gamma }_1^2-2$, due to the appropriately randomly selected parameter of the alternatives, except the SU, are similar. The range is not the most important. The interior is also important and therefore we also present values of SKS measures obtained for square side $\delta =0.5,0.1,0.075,0.05$ (see Table 4). Figure 3 and Table 4 confirm what could be expected, that the most flexible distributions are P and ES.

Figure 5. A graphical range of ${\gamma }_1$ and ${\overline{\gamma }}_2$. The PCM and LM distributions.

Figure 5. A graphical range of ${\gamma }_1$ and ${\overline{\gamma }}_2$. The PCM and LM distributions.

Figure 6. A graphical range of ${\gamma }_1$ and ${\overline{\gamma }}_2$. The SB and SU distributions.

Figure 6. A graphical range of ${\gamma }_1$ and ${\overline{\gamma }}_2$. The SB and SU distributions.

We choose values of alternative parameters to obtain the appropriate similarity measure M. Dominant values of this measure are $M=0.5,0.75,0.9$.

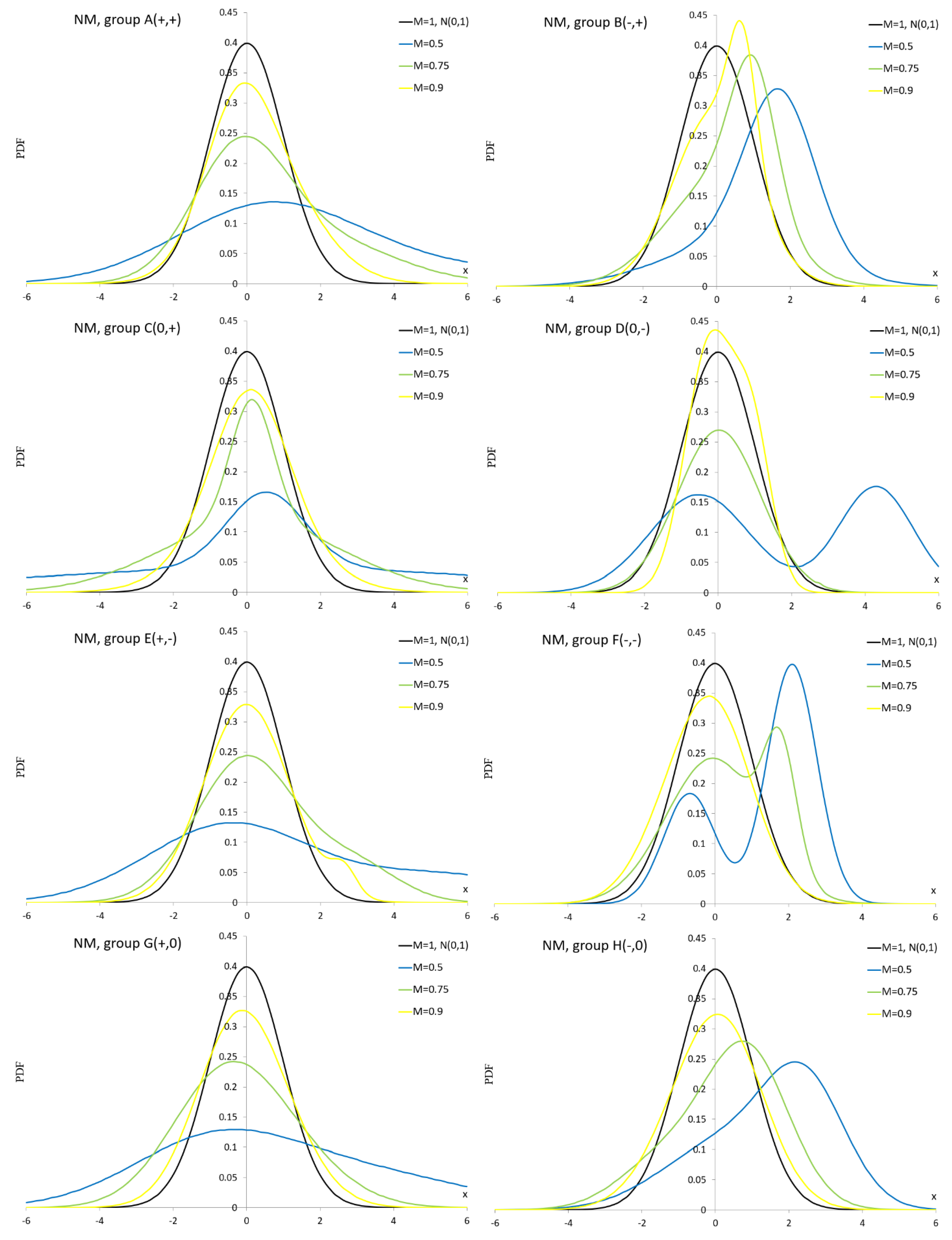
Appendix presents Table A1–Table A10 with vectors of the alternative parameter $\theta$, mean ${\mu }_a$,standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and the similarity measure M for the analyzed alternatives. The skewness and excess kurtosis tend to zero, while the similarity measure tends to unity. Often, the mean tends to zero, and the standard deviation tends to unity, while the similarity measure tends to unity. PDF formulas and PDF curves (see Figure A1–Figure A10) for the alternative $\theta$ values are also provided in Appendix.

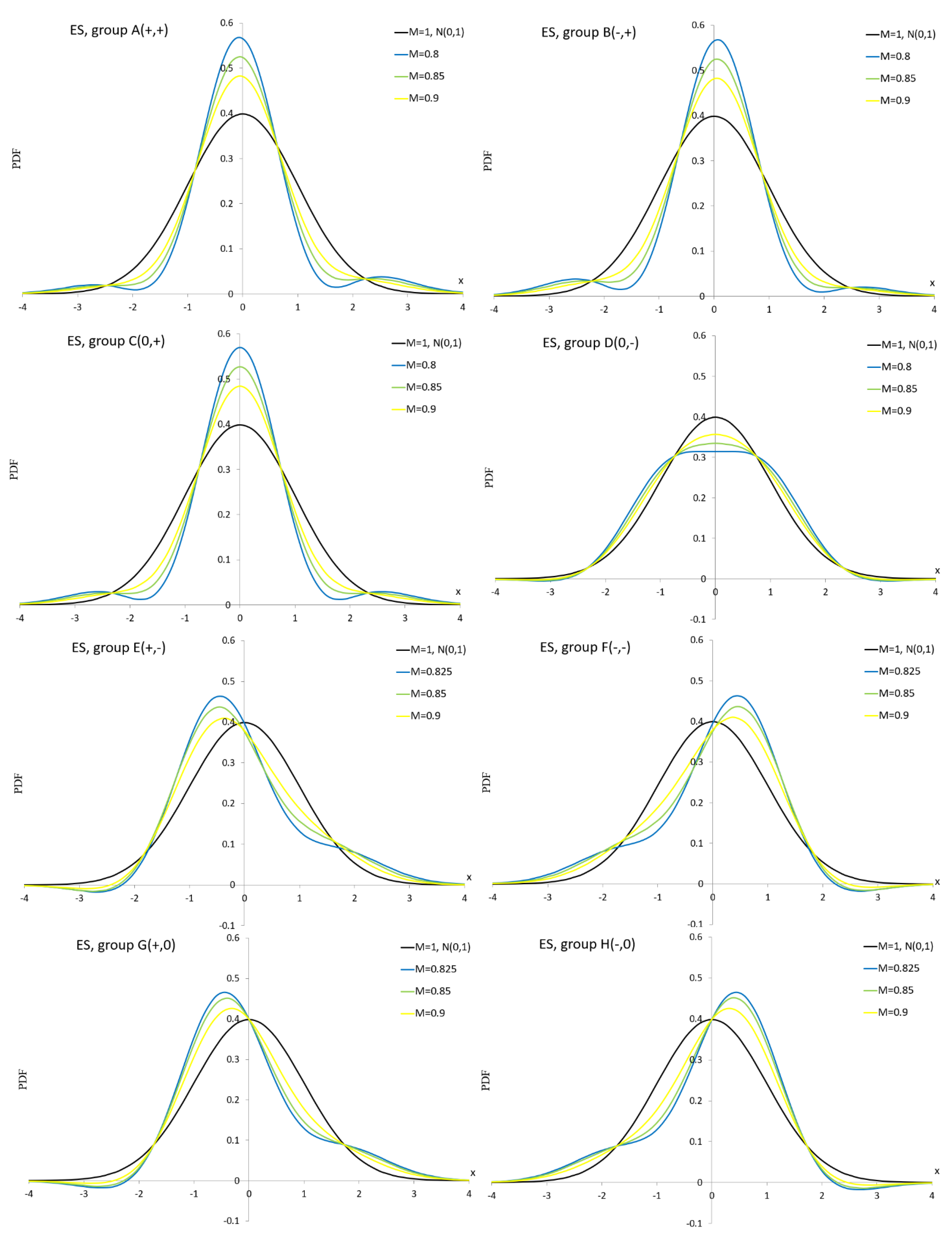
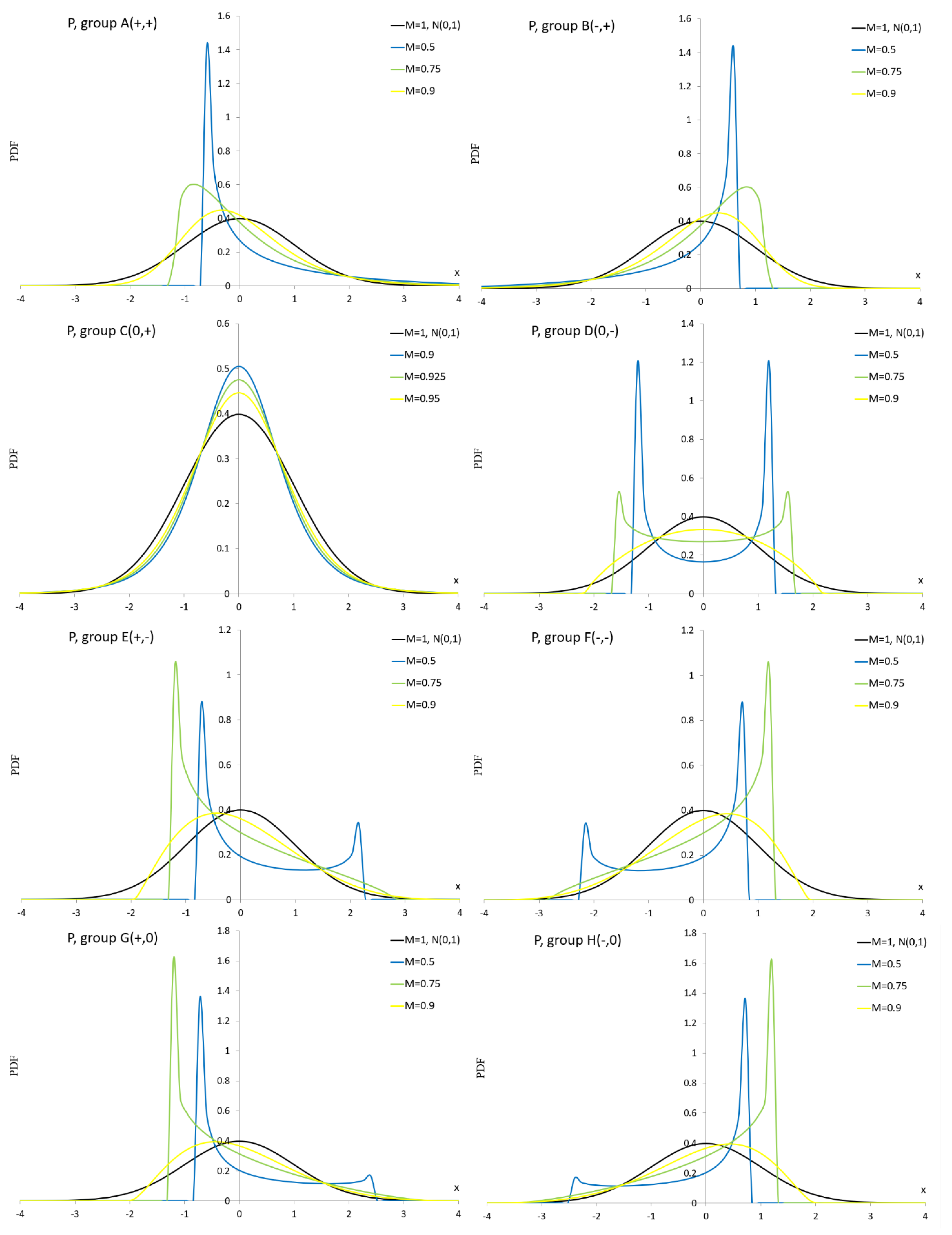
As can be seen in Figure A1, the ES distribution is not suitable for simulation studies for groups D–H because we observe negative PDF values even though the normalization condition is met. Figure A2 shows bathtub shapes. Figure A3, Figure A4 and Figure A6 show unimodal and bimodal shapes. In Figure A5 we can see very interesting multimodal shapes. In Figure A7 dominate unimodal shapes and Figure A8 shows only unimodal shapes. In Figure A9, we observe flat modes and in Figure A10, very flat modes with table shapes.

5. Power Study

In [34], a sample of the most recent comparisons (since 1990) has been used to rank 55 different normality tests. The overall winner of this analysis is the regression-based Shapiro-Wilk (SW) test of normality.

The parametrized KS (PKS) test with the statistic (6) was compared with the one-component LF test with the statistic (3), Shapiro–Wilk (SW) [61], Shapiro-Francia (SF) [62], AD and CM tests. To study the power of tests, critical values ${cv}_{0.05}$ (the type I error equals $\alpha =0.05$) were calculated using ${m=10}^6$ order statistics. The power of tests (PoTs) was calculated based on ${rep=10}^5$ values of test statistics. Table 5 shows critical values (CVs) and test sizes (TSs) for sample sizes $n=10,20$. The TS values are close to 0.05, so the simulation procedures are correct.

Complete simulation results with power values fill a table with 20 columns (20 tests) and 60 rows (10 alternatives, 2 sample sizes, 3 similarity measures). Presenting such large tables is difficult due to the size of the article. Therefore, the conclusions are applied to the full results, and only the most interesting results (tests with the highest power) will be shown in Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13. Alternatives are indexed, i.e. the larger the index, the more the distribution resembles a normal distribution (e.g. index three denotes the similarity measure 0.9). The highest values are in bold.

Of course, it is expected that the power of the GoFTs increases as the sample size increases. This basic assumption is not met for the SB (groups C and D) and SU (groups D and E) alternatives. In these cases, the power is close to the significance level. It is expected that the power of the GoFTs decreases as the value of the similarity measure (7) increases. This basic assumption is not met for the P (groups A - H), PCM (groups C, D and H), LM (groups D and H), SB (groups C, D and H), SU (groups C, D, E, F and H) and EECK (group C) alternatives.

The average PoTs is the highest for group B alternatives, followed by groups E and F. This means that the GoFTs best detect samples from asymmetric distributions with positive excess kurtosis. The worst thing, as you might expect, is detecting samples from symmetric distributions. The GoFTs best detect samples from the Pearson distribution and the worst from the EECK distribution.

Based on the results from Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13, we can conclude that $LF\left(0,1\right)$ and SF tests are the most powerful for the group A of alternatives; $PKS\left(0.9,0.1\right)$ and SF tests are the most powerful for the group B of alternatives; SF test is the most powerful for the group C of alternatives; $PKS\left(0,0\right)$ and $LF\left(0,0\right)$ tests are the most powerful for the group D of alternatives; $LF\left(0,1\right)$ test is the most powerful for the group E of alternatives; $PKS\left(0,0\right)$ and SW tests are the most powerful for the group F of alternatives; $LF\left(0,1\right)$ test is the most powerful for the group G of alternatives and $PKS\left(0,0\right)$ test is the most powerful for the group H of alternatives.

6. Real Data Examples

In this section, we present an application of the analyzed GoFT in real datasets to illustrate its potentiality. Details related to examples I – XXX are presented in Table 14.

When fitting the normal distribution to the data, we calculate p-values for the analyzed GoFTs based on ${10}^5$ statistic values (see Table 15, Table 16 and Table 17). The lowest p-value for the analyzed tests is in bold. The non-normality is the most pronounced by parameterized GoFTs, namely $LF\left(0,0\right)$ (example V), $LF\left(0,1\right)$ (examples I – III, V – VIII, XII, XIV, XV, XVII, XVIII, XXIV – XXVI, XXVIII and XXIX), $LF\left(0.1,0.1\right)$ (example V), $LF\left(0.1,0.9\right)$ (example V), $PKS\left(0,0\right)$ (examples IV, XIII, XVI and XX), $PKS\left(1,0\right)$ (examples IX, X, XI, XXII, XXIII, XXVII and XXX), $PKS\left(1,1\right)$ (examples XIX and XXIII) and $PKS\left(0.9,0.1\right)$ (examples X, XI and XXI).

7. Conclusions

The analyzed GoFTs detect samples from asymmetric distributions with positive excess kurtosis best and samples from symmetric distributions with positive excess kurtosis worst. The mentioned tests detect samples from a Pearson distribution best and those from the EP distribution worst.

The parameterized GoFT, called $LF\left(0,1\right)$, stands out in the alternative groups A, E and G. The new parameterized KS GoFT stands out among the alternatives B $\left(\alpha =0.9,\beta =0.1\right)$, D$\left(\alpha =0,\beta =0\right)$, F $\left(\alpha =0,\beta =0\right)$, and H $\left(\alpha =0,\beta =0\right)$.

The good performance of the parameterized GoFTs, including the new proposal, was demonstrated by analyzing thirty real datasets.

Appendix A.1. Edgeworth Series Distribution

PDF of the Edgeworth series (ES) with parameters ${\gamma }_1$ and ${\overline{\gamma }}_2$ is given by [63]

$$f_{ES}\left(x;{\gamma }_{1,},{\overline{\gamma }}_2\right)=\varphi \left(x;0,1\right)\left(1+{\displaystyle \frac{1}{3!}}{\gamma }_{1,}\left(x^3-3x\right)+{\displaystyle \frac{1}{4!}}{\overline{\gamma }}_2\left(x^4-6x^2+3\right)\right)\left(x\in R\right),$$

where${\gamma }_{1,}\in R,{\overline{\gamma }}_2\ge -2$. We have $\varphi \left(x;0,1\right)=f_{ES}\left(x;0,0\right)$, obviously.

Table A1. Vectors of ES parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups 0, A-H.

Group	$\mathit{\theta }=\left({\mathit{\gamma }}_{1,},{\overline{\mathit{\gamma }}}_2\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
0	$\left(0,0\right)$	0	1	0	0	$M\left(\theta ;0,1\right)=1$
A	(0.4,3.33)	0	1	0.4	3.33	$M\left(\theta ;0,1\right)=0.8$
	(0.3,2.499)	0	1	0.3	2.499	$M\left(\theta ;0,1\right)=0.85$
	(0.2,1.666)	0	1	0.2	1.666	$M\left(\theta ;0,1\right)=0.9$
B	(-0.4,3.33)	0	1	-0.4	3.33	$M\left(\theta ;0,1\right)=0.8$
	(-0.3,2.499)	0	1	-0.3	2.499	$M\left(\theta ;0,1\right)=0.85$
	(-0.2,1.666)	0	1	-0.2	1.666	$M\left(\theta ;0,1\right)=0.9$
C	(0,3.428)	0	1	0	3.428	$M\left(\theta ;0,1\right)=0.8$
	(0,2.571)	0	1	0	2.571	$M\left(\theta ;0,1\right)=0.85$
	(0,1.71)	0	1	0	1.71	$M\left(\theta ;0,1\right)=0.9$
D	(0,-3.428)	0	1	0	-3.428	$M\left(\theta ;0,1\right)=0.8$
	(0,-2.571)	0	1	0	-2.571	$M\left(\theta ;0,1\right)=0.85$
	(0,-1.71)	0	1	0	-1.71	$M\left(\theta ;0,1\right)=0.9$
E	(1.39,-0.067)	0	1	1.39	-0.067	$M\left(\theta ;0,1\right)=0.825$
	(1.175,-0.46)	0	1	1.175	-0.46	$M\left(\theta ;0,1\right)=0.85$
	(0.775,-0.408)	0	1	0.775	-0.408	$M\left(\theta ;0,1\right)=0.9$
F	(-1.39,-0.067)	0	1	-1.39	-0.067	$M\left(\theta ;0,1\right)=0.825$
	(-1.175,-0.46)	0	1	-1.175	-0.46	$M\left(\theta ;0,1\right)=0.85$
	(-0.775,-0.408)	0	1	-0.775	-0.408	$M\left(\theta ;0,1\right)=0.9$
G	(1.391,0)	0	1	1.391	0	$M\left(\theta ;0,1\right)=0.825$
	(1.19,0)	0	1	1.19	0	$M\left(\theta ;0,1\right)=0.85$
	(0.795,0)	0	1	0.795	0	$M\left(\theta ;0,1\right)=0.9$
H	(-1.391,0)	0	1	-1.391	0	$M\left(\theta ;0,1\right)=0.825$
	(-1.19,0)	0	1	-1.19	0	$M\left(\theta ;0,1\right)=0.85$
	(-0.795,0)	0	1	-0.795	0	$M\left(\theta ;0,1\right)=0.9$

Table A1. Vectors of ES parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups 0, A-H.

Group	$\mathit{\theta }=\left({\mathit{\gamma }}_{1,},{\overline{\mathit{\gamma }}}_2\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
0	$\left(0,0\right)$	0	1	0	0	$M\left(\theta ;0,1\right)=1$
A	(0.4,3.33)	0	1	0.4	3.33	$M\left(\theta ;0,1\right)=0.8$
	(0.3,2.499)	0	1	0.3	2.499	$M\left(\theta ;0,1\right)=0.85$
	(0.2,1.666)	0	1	0.2	1.666	$M\left(\theta ;0,1\right)=0.9$
B	(-0.4,3.33)	0	1	-0.4	3.33	$M\left(\theta ;0,1\right)=0.8$
	(-0.3,2.499)	0	1	-0.3	2.499	$M\left(\theta ;0,1\right)=0.85$
	(-0.2,1.666)	0	1	-0.2	1.666	$M\left(\theta ;0,1\right)=0.9$
C	(0,3.428)	0	1	0	3.428	$M\left(\theta ;0,1\right)=0.8$
	(0,2.571)	0	1	0	2.571	$M\left(\theta ;0,1\right)=0.85$
	(0,1.71)	0	1	0	1.71	$M\left(\theta ;0,1\right)=0.9$
D	(0,-3.428)	0	1	0	-3.428	$M\left(\theta ;0,1\right)=0.8$
	(0,-2.571)	0	1	0	-2.571	$M\left(\theta ;0,1\right)=0.85$
	(0,-1.71)	0	1	0	-1.71	$M\left(\theta ;0,1\right)=0.9$
E	(1.39,-0.067)	0	1	1.39	-0.067	$M\left(\theta ;0,1\right)=0.825$
	(1.175,-0.46)	0	1	1.175	-0.46	$M\left(\theta ;0,1\right)=0.85$
	(0.775,-0.408)	0	1	0.775	-0.408	$M\left(\theta ;0,1\right)=0.9$
F	(-1.39,-0.067)	0	1	-1.39	-0.067	$M\left(\theta ;0,1\right)=0.825$
	(-1.175,-0.46)	0	1	-1.175	-0.46	$M\left(\theta ;0,1\right)=0.85$
	(-0.775,-0.408)	0	1	-0.775	-0.408	$M\left(\theta ;0,1\right)=0.9$
G	(1.391,0)	0	1	1.391	0	$M\left(\theta ;0,1\right)=0.825$
	(1.19,0)	0	1	1.19	0	$M\left(\theta ;0,1\right)=0.85$
	(0.795,0)	0	1	0.795	0	$M\left(\theta ;0,1\right)=0.9$
H	(-1.391,0)	0	1	-1.391	0	$M\left(\theta ;0,1\right)=0.825$
	(-1.19,0)	0	1	-1.19	0	$M\left(\theta ;0,1\right)=0.85$
	(-0.795,0)	0	1	-0.795	0	$M\left(\theta ;0,1\right)=0.9$

Figure A1. PDF curves of the ES distribution for parameter values presented in Table A1.

Figure A1. PDF curves of the ES distribution for parameter values presented in Table A1.

Appendix A.2. Pearson Distribution

Let

$$a={\displaystyle \frac{2{\overline{\gamma }}_2-3{\gamma }_1^2}{10{\overline{\gamma }}_2-5{\gamma }_1^2+12}},b={\displaystyle \frac{\left|{\gamma }_1\right|\left({\overline{\gamma }}_2+6\right)}{10{\overline{\gamma }}_2-5{\gamma }_1^2+12}},c={\displaystyle \frac{4{\overline{\gamma }}_2-3{\gamma }_1^2+12}{10{\overline{\gamma }}_2-5{\gamma }_1^2+12}},\Delta =b^2-4ac,$$

then the PDF of the Pearson (P) distribution is given by (Pearson 1895)

$$f_P\left(x;{\gamma }_{1,},{\overline{\gamma }}_2\right)=\left\{\begin{array}{cc}{\displaystyle \frac{exp\left[\frac{2ab-b}{a\left(2ax+b\right)}\right]}{C_1{\left(2ax+b\right)}^{1/a}}}& \Delta =0\\ {\displaystyle \frac{exp\left[\frac{b-2ab}{a\sqrt{4ac-b^2}}{tan}^{-1}\left(\frac{2ax+b}{\sqrt{4ac-b^2}}\right)\right]}{C_2{\left(a{x}^2+bx+c\right)}^{1/\left(2a\right)}}}& \Delta <0\\ {\displaystyle \frac{{\left(\frac{2ax+b-\sqrt{b^2-4ac}}{2ax+b+\sqrt{b^2-4ac}}\right)}^{\frac{b-2ab}{2a\sqrt{b^2-4ac}}}}{C_3{\left(a{x}^2+bx+c\right)}^{1/\left(2a\right)}}}& \Delta >0\end{array}\right.$$

where $x\in R,{\gamma }_{1,}\in R,{\overline{\gamma }}_2\ge -2$ and $C_1$, $C_2$, $C_3$ are normalizing constants defined as

$$C_1={\int }_{-\infty }^{\infty }{\displaystyle \frac{exp\left[\frac{2ab-b}{a\left(2ax+b\right)}\right]}{{\left(2ax+b\right)}^{1/a}}}dx,C_2={\int }_{-\infty }^{\infty }{\displaystyle \frac{exp\left[\frac{b-2ab}{a\sqrt{4ac-b^2}}{tan}^{-1}\left(\frac{2ax+b}{\sqrt{4ac-b^2}}\right)\right]}{{\left(a{x}^2+bx+c\right)}^{1/\left(2a\right)}}}dx,$$

$$C_3={\int }_{-\infty }^{\infty }{\displaystyle \frac{{\left(\frac{2ax+b-\sqrt{\Delta }}{2ax+b+\sqrt{\Delta }}\right)}^{\frac{b-2ab}{2a\sqrt{\Delta }}}}{C_8{\left(a{x}^2+bx+c\right)}^{1/\left(2a\right)}}}dx.$$

A special case of the P distribution is the normal $N\left(0,1\right)$ for ${\gamma }_1={\overline{\gamma }}_2=0$.

Table A2. Vectors of the P parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups 0, A-H.

Group	$\mathit{\theta }=\left({\mathit{\gamma }}_{1,},{\overline{\mathit{\gamma }}}_2\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
0	(0,0)	0	1	0	0	$M(\theta ;0,1)=1$
A	(2.04,4.1)	0	1	2.04	4.1	$M(\theta ;0,1)=0.5$
	(1.62,3.845)	0	1	1.62	3.845	$M(\theta ;0,1)=0.75$
	(0.9,2)	0	1	0.9	2	$M(\theta ;0,1)=0.9$
B	(-2.04,4.1)	0	1	-2.04	4.1	$M(\theta ;0,1)=0.5$
	(-1.62,3.845)	0	1	-1.62	3.845	$M(\theta ;0,1)=0.75$
	(-0.9,2)	0	1	-0.9	2	$M(\theta ;0,1)=0.9$
C	(0,11.2)	0	1	0	11.2	$M(\theta ;0,1)=0.9$
	(0,3.65)	0	1	0	3.65	$M(\theta ;0,1)=0.925$
	(0,1.521)	0	1	0	1.521	$M(\theta ;0,1)=0.95$
D	(0,-1.695)	0	1	0	-1.695	$M(\theta ;0,1)=0.5$
	(0,-1.315)	0	1	0	-1.315	$M(\theta ;0,1)=0.75$
	(0,-0.89)	0	1	0	-0.89	$M(\theta ;0,1)=0.9$
E	(0.985,-0.5)	0	1	0.985	-0.5	$M(\theta ;0,1)=0.5$
	(0.715,-0.475)	0	1	0.715	-0.475	$M(\theta ;0,1)=0.75$
	(0.515,-0.2)	0	1	0.515	-0.2	$M(\theta ;0,1)=0.9$
F	(-0.985,-0.5)	0	1	-0.985	-0.5	$M(\theta ;0,1)=0.5$
	(-0.715,-0.475)	0	1	-0.715	-0.475	$M(\theta ;0,1)=0.75$
	(-0.515,-0.2)	0	1	-0.515	-0.2	$M(\theta ;0,1)=0.9$
G	(1.164,0)	0	1	1.164	0	$M(\theta ;0,1)=0.5$
	(0.879,0)	0	1	0.879	0	$M(\theta ;0,1)=0.75$
	(0.578,0)	0	1	0.578	0	$M(\theta ;0,1)=0.9$
H	(-1.164,0)	0	1	-1.164	0	$M(\theta ;0,1)=0.5$
	(-0.879,0)	0	1	-0.879	0	$M(\theta ;0,1)=0.75$
	(-0.578,0)	0	1	-0.578	0	$M(\theta ;0,1)=0.9$

Table A2. Vectors of the P parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups 0, A-H.

Group	$\mathit{\theta }=\left({\mathit{\gamma }}_{1,},{\overline{\mathit{\gamma }}}_2\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
0	(0,0)	0	1	0	0	$M(\theta ;0,1)=1$
A	(2.04,4.1)	0	1	2.04	4.1	$M(\theta ;0,1)=0.5$
	(1.62,3.845)	0	1	1.62	3.845	$M(\theta ;0,1)=0.75$
	(0.9,2)	0	1	0.9	2	$M(\theta ;0,1)=0.9$
B	(-2.04,4.1)	0	1	-2.04	4.1	$M(\theta ;0,1)=0.5$
	(-1.62,3.845)	0	1	-1.62	3.845	$M(\theta ;0,1)=0.75$
	(-0.9,2)	0	1	-0.9	2	$M(\theta ;0,1)=0.9$
C	(0,11.2)	0	1	0	11.2	$M(\theta ;0,1)=0.9$
	(0,3.65)	0	1	0	3.65	$M(\theta ;0,1)=0.925$
	(0,1.521)	0	1	0	1.521	$M(\theta ;0,1)=0.95$
D	(0,-1.695)	0	1	0	-1.695	$M(\theta ;0,1)=0.5$
	(0,-1.315)	0	1	0	-1.315	$M(\theta ;0,1)=0.75$
	(0,-0.89)	0	1	0	-0.89	$M(\theta ;0,1)=0.9$
E	(0.985,-0.5)	0	1	0.985	-0.5	$M(\theta ;0,1)=0.5$
	(0.715,-0.475)	0	1	0.715	-0.475	$M(\theta ;0,1)=0.75$
	(0.515,-0.2)	0	1	0.515	-0.2	$M(\theta ;0,1)=0.9$
F	(-0.985,-0.5)	0	1	-0.985	-0.5	$M(\theta ;0,1)=0.5$
	(-0.715,-0.475)	0	1	-0.715	-0.475	$M(\theta ;0,1)=0.75$
	(-0.515,-0.2)	0	1	-0.515	-0.2	$M(\theta ;0,1)=0.9$
G	(1.164,0)	0	1	1.164	0	$M(\theta ;0,1)=0.5$
	(0.879,0)	0	1	0.879	0	$M(\theta ;0,1)=0.75$
	(0.578,0)	0	1	0.578	0	$M(\theta ;0,1)=0.9$
H	(-1.164,0)	0	1	-1.164	0	$M(\theta ;0,1)=0.5$
	(-0.879,0)	0	1	-0.879	0	$M(\theta ;0,1)=0.75$
	(-0.578,0)	0	1	-0.578	0	$M(\theta ;0,1)=0.9$

Figure A2. PDF curves of the P distribution for parameter values presented in Table A2.

Figure A2. PDF curves of the P distribution for parameter values presented in Table A2.

Appendix A.3. Normal Mixture Distribution

PDF of the normal mixture (NM) distribution is given by

$$f_{NM}\left(x;\theta \right)=\omega \varphi \left(x;{\mu }_1,{\sigma }_1\right)+\left(1-\omega \right)\varphi \left(x;{\mu }_2,{\sigma }_2\right)\left(x\in R\right),$$

where $\theta =\left({\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,\omega \right)$ and ${\mu }_1,{\mu }_2\in R,{\sigma }_1,{\sigma }_2>0,\omega \in \left[0,1\right]$.

Special cases of the NM distribution are:

• normal $N\left({\mu }_1,{\sigma }_1\right)$ for $\omega =1$, $N\left({\mu }_2,{\sigma }_2\right)$ for $\omega =0$,
• location contaminated normal (LCN) $f_{LCM}\left(x;{\mu }_1,\omega \right)=f_{NM}\left(x;{\mu }_1,1,0,1,\omega \right)$,
• scale contaminated normal (SCN) $f_{SCN}\left(x;{\sigma }_1,\omega \right)=f_{NM}\left(x;0,{\sigma }_1,0,1,\omega \right)$.

Table A3. Vectors of the NM parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups 0, A-H.

Group	$\mathit{\theta }=\left({\mathit{\mu }}_1,{\mathit{\sigma }}_1,{\mathit{\mu }}_2,{\mathit{\sigma }}_2,\mathit{\omega }\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
0	$\left({\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,1\right)$	0	1	0	0	$M\left(\theta ;{\mu }_1,{\sigma }_1\right)=1$
	$\left({\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,0\right)$	0	1	0	0	$M\left(\theta ;{\mu }_2,{\sigma }_2\right)=1$
A	(0.572,2.472,5.614,3.454,0.787)	1.646	3.408	0.685	0.755	$M(\theta ;0,1)=0.5$
	(-0.215,1.254,1.979,1.99,0.639)	0.577	1.883	0.645	0.502	$M(\theta ;0,1)=0.75$
	(0.497,1.376,-0.268,0.884,0.612)	0.2	1.265	0.287	0.249	$M(\theta ;0,1)=0.9$
B	(0.502,2.019,1.708,0.953,0.36)	1.274	1.544	-0.748	1.502	$M(\theta ;0,1)=0.5$
	(0.06,1.437,1.004,0.609,0.634)	0.406	1.285	-0.5	0.499	$M(\theta ;0,1)=0.75$
	(0.709,0.368,-0.072,1.115,0.193)	0.079	1.06	-0.301	0.15	$M(\theta ;0,1)=0.9$
C	(0.519,6.599,0.519,1.058,0.665)	0.519	5.416	0	1.398	$M(\theta ;0,1)=0.5$
	(0.137,0.581,0.137,2.391,0.294)	0.137	2.034	0	1.054	$M(\theta ;0,1)=0.75$
	(0.1,0.988,0.1,1.543,0.532)	0.1	1.278	0	0.554	$M(\theta ;0,1)=0.9$
D	(-0.511,1.353,4.293,1.021,0.551)	1.645	2.681	0	-1.28	$M(\theta ;0,1)=0.5$
	(2.707,0.013,0.017,1.125,0.238)	0.657	1.509	0	-1.001	$M(\theta ;0,1)=0.75$
	(1.243,0.621,-0.39,0.811,0.347)	0.111	1.09	0	-0.63	$M(\theta ;0,1)=0.9$
E	(-0.475,2.22,5.318,2.427,0.721)	1.141	3.457	0.5	-0.204	$M(\theta ;0,1)=0.5$
	(-0.019,1.369,2.979,1.15,0.829)	0.494	1.748	0.339	-0.1	$M(\theta ;0,1)=0.75$
	(2.635,0.35,-0.015,1.166,0.038)	0.086	1.253	0.137	-0.075	$M(\theta ;0,1)=0.9$
F	(-0.692,0.705,2.1,0.679,0.324)	1.195	1.476	-0.542	-0.852	$M(\theta ;0,1)=0.5$
	(-0.055,1.277,1.781,0.443,0.775)	0.358	1.377	-0.3	-0.5	$M(\theta ;0,1)=0.75$
	(-0.09,1.08,-1.581,0.92,0.9)	-0.239	1.155	-0.071	-0.042	$M(\theta ;0,1)=0.9$
G	(2.686,3.099,-0.964,2.217,0.471)	0.755	3.232	0.4	0	$M(\theta ;0,1)=0.5$
	(-0.56,1.465,1.411,1.45,0.8)	-0.166	1.661	0.151	0	$M(\theta ;0,1)=0.75$
	(-0.286,1.114,0.984,1.105,0.801)	-0.033	1.222	0.101	0	$M(\theta ;0,1)=0.9$
H	(2.425,1.101,0.272,1.693,0.526)	1.404	1.775	-0.499	0	$M(\theta ;0,1)=0.5$
	(0.864,1.125,-1.339,1.241,0.735)	0.28	1.511	-0.386	0	$M(\theta ;0,1)=0.75$
	(0.429,1.078,-0.364,1.228,0.434)	-0.02	1.23	-0.1	0	$M(\theta ;0,1)=0.9$

Table A3. Vectors of the NM parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups 0, A-H.

Group	$\mathit{\theta }=\left({\mathit{\mu }}_1,{\mathit{\sigma }}_1,{\mathit{\mu }}_2,{\mathit{\sigma }}_2,\mathit{\omega }\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
0	$\left({\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,1\right)$	0	1	0	0	$M\left(\theta ;{\mu }_1,{\sigma }_1\right)=1$
	$\left({\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,0\right)$	0	1	0	0	$M\left(\theta ;{\mu }_2,{\sigma }_2\right)=1$
A	(0.572,2.472,5.614,3.454,0.787)	1.646	3.408	0.685	0.755	$M(\theta ;0,1)=0.5$
	(-0.215,1.254,1.979,1.99,0.639)	0.577	1.883	0.645	0.502	$M(\theta ;0,1)=0.75$
	(0.497,1.376,-0.268,0.884,0.612)	0.2	1.265	0.287	0.249	$M(\theta ;0,1)=0.9$
B	(0.502,2.019,1.708,0.953,0.36)	1.274	1.544	-0.748	1.502	$M(\theta ;0,1)=0.5$
	(0.06,1.437,1.004,0.609,0.634)	0.406	1.285	-0.5	0.499	$M(\theta ;0,1)=0.75$
	(0.709,0.368,-0.072,1.115,0.193)	0.079	1.06	-0.301	0.15	$M(\theta ;0,1)=0.9$
C	(0.519,6.599,0.519,1.058,0.665)	0.519	5.416	0	1.398	$M(\theta ;0,1)=0.5$
	(0.137,0.581,0.137,2.391,0.294)	0.137	2.034	0	1.054	$M(\theta ;0,1)=0.75$
	(0.1,0.988,0.1,1.543,0.532)	0.1	1.278	0	0.554	$M(\theta ;0,1)=0.9$
D	(-0.511,1.353,4.293,1.021,0.551)	1.645	2.681	0	-1.28	$M(\theta ;0,1)=0.5$
	(2.707,0.013,0.017,1.125,0.238)	0.657	1.509	0	-1.001	$M(\theta ;0,1)=0.75$
	(1.243,0.621,-0.39,0.811,0.347)	0.111	1.09	0	-0.63	$M(\theta ;0,1)=0.9$
E	(-0.475,2.22,5.318,2.427,0.721)	1.141	3.457	0.5	-0.204	$M(\theta ;0,1)=0.5$
	(-0.019,1.369,2.979,1.15,0.829)	0.494	1.748	0.339	-0.1	$M(\theta ;0,1)=0.75$
	(2.635,0.35,-0.015,1.166,0.038)	0.086	1.253	0.137	-0.075	$M(\theta ;0,1)=0.9$
F	(-0.692,0.705,2.1,0.679,0.324)	1.195	1.476	-0.542	-0.852	$M(\theta ;0,1)=0.5$
	(-0.055,1.277,1.781,0.443,0.775)	0.358	1.377	-0.3	-0.5	$M(\theta ;0,1)=0.75$
	(-0.09,1.08,-1.581,0.92,0.9)	-0.239	1.155	-0.071	-0.042	$M(\theta ;0,1)=0.9$
G	(2.686,3.099,-0.964,2.217,0.471)	0.755	3.232	0.4	0	$M(\theta ;0,1)=0.5$
	(-0.56,1.465,1.411,1.45,0.8)	-0.166	1.661	0.151	0	$M(\theta ;0,1)=0.75$
	(-0.286,1.114,0.984,1.105,0.801)	-0.033	1.222	0.101	0	$M(\theta ;0,1)=0.9$
H	(2.425,1.101,0.272,1.693,0.526)	1.404	1.775	-0.499	0	$M(\theta ;0,1)=0.5$
	(0.864,1.125,-1.339,1.241,0.735)	0.28	1.511	-0.386	0	$M(\theta ;0,1)=0.75$
	(0.429,1.078,-0.364,1.228,0.434)	-0.02	1.23	-0.1	0	$M(\theta ;0,1)=0.9$

Figure A3. PDF curves of the NM distribution for parameter values presented in Table A3.

Figure A3. PDF curves of the NM distribution for parameter values presented in Table A3.

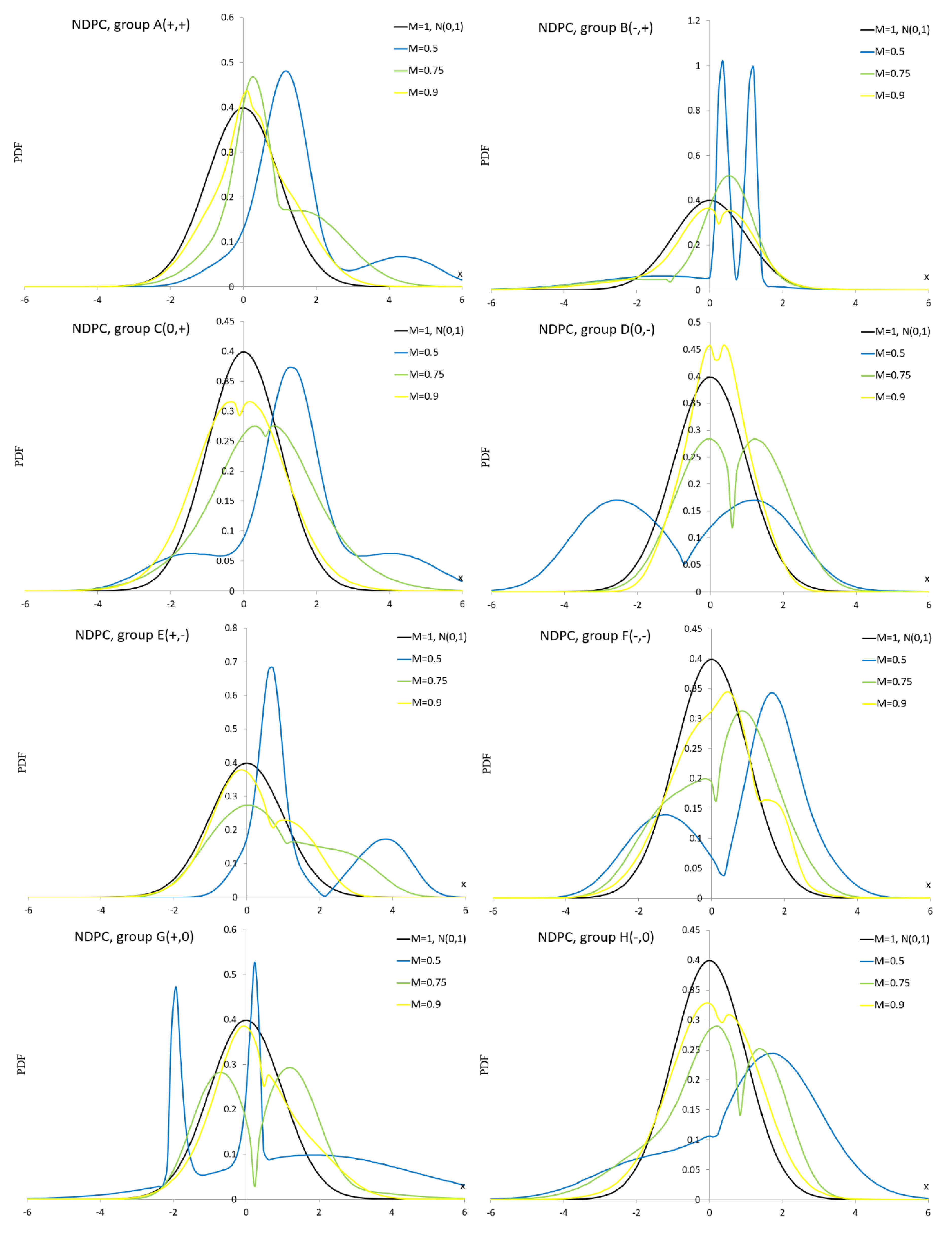
Appendix A.4. Normal Distribution with Plasticizing Component

PDF of the normal distribution with plasticizing component (NDPC) is given by [64]

$$f_{NDPC}\left(x;\theta \right)=\omega \varphi \left(x;{\mu }_1,{\sigma }_1\right)+\left(1-\omega \right){\displaystyle \frac{c_2}{{\sigma }_2}}{\left|{\displaystyle \frac{x-{\mu }_2}{{\sigma }_2}}\right|}^{c_2-1}\varphi \left({\left|{\displaystyle \frac{x-{\mu }_2}{{\sigma }_2}}\right|}^{c_2};0,1\right)\left(x\in R\right),$$

where $\theta =\left({\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,c_2,\omega \right)$ and ${\mu }_1,{\mu }_2\in R,{\sigma }_1,{\sigma }_2>0,c_2\ge 1,\omega \in \left[0,1\right]$.

Special cases of the NDPC distribution are: $N\left({\mu }_1,{\sigma }_1\right)$ for $\omega =1$; $N\left({\mu }_2,{\sigma }_2\right)$ for $c_2=1,\omega =0$ and plasticizing component for $\omega =0$.

Table A4. Vectors of NDPC parameter $\theta$, mean ${\mu }_a$,standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups 0, A-H.

Group	$\mathit{\theta }=\left({\mathit{\mu }}_1,{\mathit{\sigma }}_1,{\mathit{\mu }}_2,{\mathit{\sigma }}_2,{\mathit{c}}_2,\mathit{\omega }\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
0	(${\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,c_2,1$)	0	1	0	0	$M\left(\theta ;{\mu }_1,{\sigma }_1\right)=1$
	(${\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,1,0$)	0	1	0	0	$M\left(\theta ;{\mu }_2,{\sigma }_2\right)=1$
A	(1.194,0.601,2.186,2.592,2,0.666)	1.526	1.5	1.002	1.001	$M(\theta ;0,1)=0.5$
	(0.265,0.415,0.996,1.541,1.16,0.313)	0.767	1.288	0.426	0.152	$M(\theta ;0,1)=0.75$
	(0.173,0.358,0.289,1.268,1.132,0.198)	0.266	1.104	0.056	0.071	$M(\theta ;0,1)=0.9$
B	(-1.321,1.842,0.741,0.459,2.56,0.287)	0.15	1.4	-1.764	3.3	$M(\theta ;0,1)=0.5$
	(0.539,0.632,-1.078,2.061,1.174,0.741)	0.12	1.34	-1.499	2.986	$M(\theta ;0,1)=0.75$
	(-0.966,1.824,0.259,0.889,1.1,0.26)	-0.059	1.305	-0.899	1.999	$M(\theta ;0,1)=0.9$
C	(1.308,0.656,1.308,3.261,2,0.613)	1.308	1.884	0	0.504	$M(\theta ;0,1)=0.5$
	(0.571,1.023,0.571,1.962,1.15,0.505)	0.571	1.508	0	0.325	$M(\theta ;0,1)=0.75$
	(-0.097,1.332,-0.097,1.058,1.1,0.614)	-0.097	1.223	0	0.101	$M(\theta ;0,1)=0.9$
D	(-0.692,2.203,-0.692,2.544,1.759,0.25)	-0.692	2.265	0	-1	$M(\theta ;0,1)=0.5$
	(0.323,1.312,0.605,1.335,1.2,0.01)	0.602	1.266	0	-0.587	$M(\theta ;0,1)=0.75$
	(0.179,0.494,0.179,1.163,1.426,0.443)	0.179	0.862	0	-0.202	$M(\theta ;0,1)=0.9$
E	(0.675,0.284,2.122,1.968,2.104,0.374)	1.581	1.565	0.749	-0.849	$M(\theta ;0,1)=0.5$
	(0.423,1.032,1.058,2.077,1.815,0.494)	0.744	1.544	0.311	-0.667	$M(\theta ;0,1)=0.75$
	(-0.134,0.993,0.671,1.211,1.479,0.583)	0.202	1.115	0.115	-0.4	$M(\theta ;0,1)=0.9$
F	(1.609,0.59,0.322,2.194,1.609,0.309)	0.72	1.784	-0.491	-0.728	$M(\theta ;0,1)=0.5$
	(0.617,0.737,0.129,1.752,1.465,0.332)	0.291	1.395	-0.239	-0.526	$M(\theta ;0,1)=0.75$
	(-0.046,1.156,1.261,0.799,1.87,0.876)	0.116	1.191	-0.1	-0.2	$M(\theta ;0,1)=0.9$
G	(1.88,2.736,-0.848,1.122,6.437,0.679)	1.005	2.656	0.524	0	$M(\theta ;0,1)=0.5$
	(2.419,1.56,0.237,1.384,1.476,0.074)	0.398	1.409	0.35	0	$M(\theta ;0,1)=0.75$
	(0.055,0.702,0.474,1.586,1.328,0.473)	0.276	1.191	0.31	0	$M(\theta ;0,1)=0.9$
H	(1.642,1.247,0.202,2.681,1.428,0.554)	1	2.018	-0.594	0	$M(\theta ;0,1)=0.5$
	(-1.246,1.326,0.858,1.103,1.242,0.313)	0.2	1.496	-0.5	0	$M(\theta ;0,1)=0.75$
	(-0.115,1.286,0.306,1.091,1.093,0.465)	0.11	1.189	-0.1	0	$M(\theta ;0,1)=0.9$

Table A4. Vectors of NDPC parameter $\theta$, mean ${\mu }_a$,standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups 0, A-H.

Group	$\mathit{\theta }=\left({\mathit{\mu }}_1,{\mathit{\sigma }}_1,{\mathit{\mu }}_2,{\mathit{\sigma }}_2,{\mathit{c}}_2,\mathit{\omega }\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
0	(${\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,c_2,1$)	0	1	0	0	$M\left(\theta ;{\mu }_1,{\sigma }_1\right)=1$
	(${\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,1,0$)	0	1	0	0	$M\left(\theta ;{\mu }_2,{\sigma }_2\right)=1$
A	(1.194,0.601,2.186,2.592,2,0.666)	1.526	1.5	1.002	1.001	$M(\theta ;0,1)=0.5$
	(0.265,0.415,0.996,1.541,1.16,0.313)	0.767	1.288	0.426	0.152	$M(\theta ;0,1)=0.75$
	(0.173,0.358,0.289,1.268,1.132,0.198)	0.266	1.104	0.056	0.071	$M(\theta ;0,1)=0.9$
B	(-1.321,1.842,0.741,0.459,2.56,0.287)	0.15	1.4	-1.764	3.3	$M(\theta ;0,1)=0.5$
	(0.539,0.632,-1.078,2.061,1.174,0.741)	0.12	1.34	-1.499	2.986	$M(\theta ;0,1)=0.75$
	(-0.966,1.824,0.259,0.889,1.1,0.26)	-0.059	1.305	-0.899	1.999	$M(\theta ;0,1)=0.9$
C	(1.308,0.656,1.308,3.261,2,0.613)	1.308	1.884	0	0.504	$M(\theta ;0,1)=0.5$
	(0.571,1.023,0.571,1.962,1.15,0.505)	0.571	1.508	0	0.325	$M(\theta ;0,1)=0.75$
	(-0.097,1.332,-0.097,1.058,1.1,0.614)	-0.097	1.223	0	0.101	$M(\theta ;0,1)=0.9$
D	(-0.692,2.203,-0.692,2.544,1.759,0.25)	-0.692	2.265	0	-1	$M(\theta ;0,1)=0.5$
	(0.323,1.312,0.605,1.335,1.2,0.01)	0.602	1.266	0	-0.587	$M(\theta ;0,1)=0.75$
	(0.179,0.494,0.179,1.163,1.426,0.443)	0.179	0.862	0	-0.202	$M(\theta ;0,1)=0.9$
E	(0.675,0.284,2.122,1.968,2.104,0.374)	1.581	1.565	0.749	-0.849	$M(\theta ;0,1)=0.5$
	(0.423,1.032,1.058,2.077,1.815,0.494)	0.744	1.544	0.311	-0.667	$M(\theta ;0,1)=0.75$
	(-0.134,0.993,0.671,1.211,1.479,0.583)	0.202	1.115	0.115	-0.4	$M(\theta ;0,1)=0.9$
F	(1.609,0.59,0.322,2.194,1.609,0.309)	0.72	1.784	-0.491	-0.728	$M(\theta ;0,1)=0.5$
	(0.617,0.737,0.129,1.752,1.465,0.332)	0.291	1.395	-0.239	-0.526	$M(\theta ;0,1)=0.75$
	(-0.046,1.156,1.261,0.799,1.87,0.876)	0.116	1.191	-0.1	-0.2	$M(\theta ;0,1)=0.9$
G	(1.88,2.736,-0.848,1.122,6.437,0.679)	1.005	2.656	0.524	0	$M(\theta ;0,1)=0.5$
	(2.419,1.56,0.237,1.384,1.476,0.074)	0.398	1.409	0.35	0	$M(\theta ;0,1)=0.75$
	(0.055,0.702,0.474,1.586,1.328,0.473)	0.276	1.191	0.31	0	$M(\theta ;0,1)=0.9$
H	(1.642,1.247,0.202,2.681,1.428,0.554)	1	2.018	-0.594	0	$M(\theta ;0,1)=0.5$
	(-1.246,1.326,0.858,1.103,1.242,0.313)	0.2	1.496	-0.5	0	$M(\theta ;0,1)=0.75$
	(-0.115,1.286,0.306,1.091,1.093,0.465)	0.11	1.189	-0.1	0	$M(\theta ;0,1)=0.9$

Figure A4. PDF curves of the NDPC for parameter values presented in Table A4.

Figure A4. PDF curves of the NDPC for parameter values presented in Table A4.

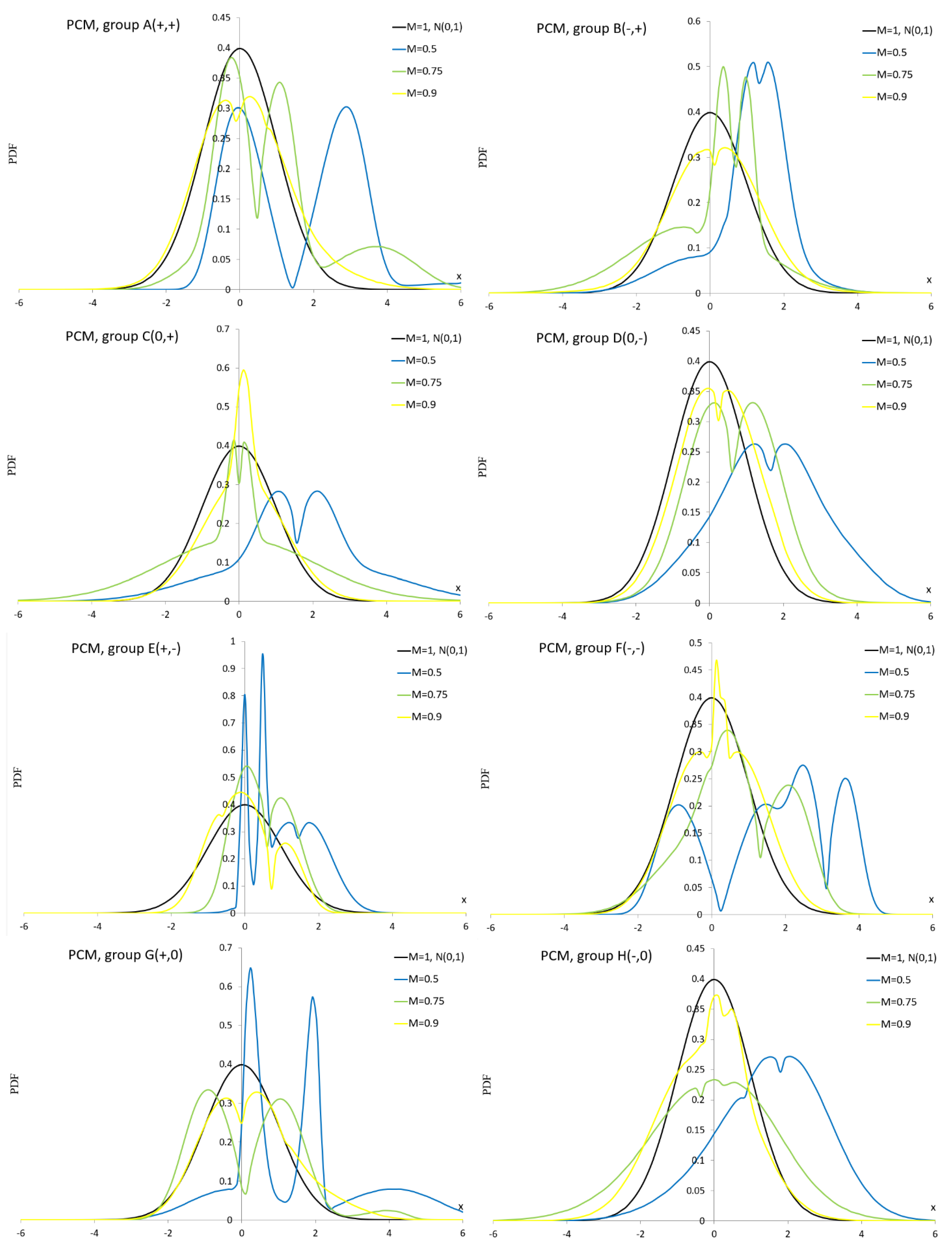
Appendix A.5. Plasticizing Component Mixture Distribution

PDF of the plasticizing component mixture distribution (PCM) is given by [64]

$$f_{PCM}\left(x;\theta \right)=\omega f_{PC}\left(x;{\mu }_1,{\sigma }_1,c_1\right)+\left(1-\omega \right)f_{PC}\left(x;{\mu }_2,{\sigma }_2,c_2\right)\left(x\in R\right),$$

where $f_{PC}\left(x;\mu ,\sigma ,c\right)={\displaystyle \frac{c}{\sigma }}{\left|{\displaystyle \frac{x-\mu }{\sigma }}\right|}^{c-1}\varphi \left({\left|{\displaystyle \frac{x-\mu }{\sigma }}\right|}^c;0,1\right)\left(x\in R\right)$ and $\theta =\left({\mu }_1,{\sigma }_1,c_1,{\mu }_2,{\sigma }_2,c_2,\omega \right)$,

$${\mu }_1,{\mu }_2\in R,{\sigma }_1,{\sigma }_2>0,c_1,c_2\ge 1,\omega \in \left[0,1\right].$$

Special cases of the PCM distribution are: $N\left({\mu }_1,{\sigma }_1\right)$ for $c_1=1,\omega =1$; $N\left({\mu }_2,{\sigma }_2\right)$ for $c_2=1,\omega =0$; plasticizing components $PC\left({\mu }_1,{\sigma }_1,c_1\right),$ and $PC\left({\mu }_2,{\sigma }_2,c_2\right)$ for $\omega =0,\omega =1$, respectively.

Table A5. Vectors of PCM parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups 0, A-H.

Group	$\mathit{\theta }=\left({\mathit{\mu }}_1,{\mathit{\sigma }}_1,{\mathit{c}}_1,{\mathit{\mu }}_2,{\mathit{\sigma }}_2,{\mathit{c}}_2,\mathit{\omega }\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
0	$({\mu }_1,{\sigma }_1,{1,\mu }_2,{\sigma }_2,c_2,1$)	0	1	0	0	$M\left(\theta ;{\mu }_1,{\sigma }_1\right)=1$
	(${\mu }_1,{\sigma }_1,{c_1,\mu }_2,{\sigma }_2,1,0$)	0	1	0	0	$M\left(\theta ;{\mu }_2,{\sigma }_2\right)=1$
A	(1.415,1.684,2.194,11.252,5.474,2.331,0.9)	2.399	3.622	2.647	7.663	$M(\theta ;0,1)=0.5$
	(0.444,0.899,1.602,1.653,2.506,1.876,0.64)	0.879	1.604	0.913	0.412	$M(\theta ;0,1)=0.75$
	(-0.076,1.056,1.1,0.701,1.646,1.095,0.71)	0.149	1.268	0.374	0.374	$M(\theta ;0,1)=0.9$
B	(1.366,0.572,1.11,0.502,1.669,1.253,0.658)	1.071	1.099	-0.978	1.565	$M(\theta ;0,1)=0.5$
	(0.67,0.425,1.576,-0.323,1.696,1.05,0.349)	0.024	1.444	-0.569	0.606	$M(\theta ;0,1)=0.75$
	(-0.204,2.209,1.205,0.133,1.139,1.05,0.076)	0.107	1.224	-0.122	0.457	$M(\theta ;0,1)=0.9$
C	(1.597,2.518,1.263,1.596,0.856,1.285,0.526)	1.597	1.797	0	0.601	$M(\theta ;0,1)=0.5$
	(0.012,0.274,1.256,0.012,2.046,1.01,0.183)	0.012	1.846	0	0.598	$M(\theta ;0,1)=0.75$
	(0.127,1.089,1.01,0.127,0.183,1.01,0.863)	0.127	1.01	0	0.401	$M(\theta ;0,1)=0.9$
D	(1.631,0.893,1.05,1.632,2.104,1.554,0.498)	1.632	1.488	0	-0.268	$M(\theta ;0,1)=0.5$
	(0.639,1.576,1.167,0.64,1.085,1.199,0.163)	0.64	1.12	0	-0.251	$M(\theta ;0,1)=0.75$
	(0.666,1.123,4.041,0.233,1.069,1.05,0.01)	0.237	1.052	0	-0.198	$M(\theta ;0,1)=0.9$
E	(1.472,0.782,1.11,0.236,0.291,3.203,0.692)	1.091	0.861	0.38	-0.8	$M(\theta ;0,1)=0.5$
	(-0.196,0.341,1.064,0.613,0.758,1.204,0.153)	0.489	0.734	0.201	-0.7	$M(\theta ;0,1)=0.75$
	(0.722,0.703,1.304,-0.57,0.598,1.05,0.455)	0.018	0.893	0.179	-0.617	$M(\theta ;0,1)=0.9$
F	(0.261,1.419,1.909,3.099,0.744,1.567,0.57)	1.481	1.757	-0.3	-1.107	$M(\theta ;0,1)=0.5$
	(0.037,1.295,1.076,1.316,1.171,1.654,0.485)	0.696	1.326	-0.204	-0.4	$M(\theta ;0,1)=0.75$
	(0.201,0.121,1.573,0.184,1.177,1.161,0.066)	0.185	1.087	-0.003	-0.331	$M(\theta ;0,1)=0.9$
G	(1.088,0.894,3.782,1.969,2.71,1.792,0.55)	1.484	1.793	0.6	0	$M(\theta ;0,1)=0.5$
	(1.515,2.553,3.55,0.07,1.328,1.619,0.07)	0.171	1.359	0.501	0	$M(\theta ;0,1)=0.75$
	(-0.034,1.072,1.159,1.146,1.51,1.301,0.756)	0.254	1.238	0.401	0	$M(\theta ;0,1)=0.9$
H	(0.816,1.867,1.24,1.787,1.272,1.05,0.278)	1.517	1.475	-0.302	0	$M(\theta ;0,1)=0.5$
	(-0.364,1.889,1.057,0.29,1.413,1.05,0.527)	-0.055	1.682	-0.154	0	$M(\theta ;0,1)=0.75$
	(0.286,0.405,1.27,-0.263,1.261,1.05,0.112)	-0.202	1.188	-0.128	0	$M(\theta ;0,1)=0.9$

Table A5. Vectors of PCM parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups 0, A-H.

Group	$\mathit{\theta }=\left({\mathit{\mu }}_1,{\mathit{\sigma }}_1,{\mathit{c}}_1,{\mathit{\mu }}_2,{\mathit{\sigma }}_2,{\mathit{c}}_2,\mathit{\omega }\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
0	$({\mu }_1,{\sigma }_1,{1,\mu }_2,{\sigma }_2,c_2,1$)	0	1	0	0	$M\left(\theta ;{\mu }_1,{\sigma }_1\right)=1$
	(${\mu }_1,{\sigma }_1,{c_1,\mu }_2,{\sigma }_2,1,0$)	0	1	0	0	$M\left(\theta ;{\mu }_2,{\sigma }_2\right)=1$
A	(1.415,1.684,2.194,11.252,5.474,2.331,0.9)	2.399	3.622	2.647	7.663	$M(\theta ;0,1)=0.5$
	(0.444,0.899,1.602,1.653,2.506,1.876,0.64)	0.879	1.604	0.913	0.412	$M(\theta ;0,1)=0.75$
	(-0.076,1.056,1.1,0.701,1.646,1.095,0.71)	0.149	1.268	0.374	0.374	$M(\theta ;0,1)=0.9$
B	(1.366,0.572,1.11,0.502,1.669,1.253,0.658)	1.071	1.099	-0.978	1.565	$M(\theta ;0,1)=0.5$
	(0.67,0.425,1.576,-0.323,1.696,1.05,0.349)	0.024	1.444	-0.569	0.606	$M(\theta ;0,1)=0.75$
	(-0.204,2.209,1.205,0.133,1.139,1.05,0.076)	0.107	1.224	-0.122	0.457	$M(\theta ;0,1)=0.9$
C	(1.597,2.518,1.263,1.596,0.856,1.285,0.526)	1.597	1.797	0	0.601	$M(\theta ;0,1)=0.5$
	(0.012,0.274,1.256,0.012,2.046,1.01,0.183)	0.012	1.846	0	0.598	$M(\theta ;0,1)=0.75$
	(0.127,1.089,1.01,0.127,0.183,1.01,0.863)	0.127	1.01	0	0.401	$M(\theta ;0,1)=0.9$
D	(1.631,0.893,1.05,1.632,2.104,1.554,0.498)	1.632	1.488	0	-0.268	$M(\theta ;0,1)=0.5$
	(0.639,1.576,1.167,0.64,1.085,1.199,0.163)	0.64	1.12	0	-0.251	$M(\theta ;0,1)=0.75$
	(0.666,1.123,4.041,0.233,1.069,1.05,0.01)	0.237	1.052	0	-0.198	$M(\theta ;0,1)=0.9$
E	(1.472,0.782,1.11,0.236,0.291,3.203,0.692)	1.091	0.861	0.38	-0.8	$M(\theta ;0,1)=0.5$
	(-0.196,0.341,1.064,0.613,0.758,1.204,0.153)	0.489	0.734	0.201	-0.7	$M(\theta ;0,1)=0.75$
	(0.722,0.703,1.304,-0.57,0.598,1.05,0.455)	0.018	0.893	0.179	-0.617	$M(\theta ;0,1)=0.9$
F	(0.261,1.419,1.909,3.099,0.744,1.567,0.57)	1.481	1.757	-0.3	-1.107	$M(\theta ;0,1)=0.5$
	(0.037,1.295,1.076,1.316,1.171,1.654,0.485)	0.696	1.326	-0.204	-0.4	$M(\theta ;0,1)=0.75$
	(0.201,0.121,1.573,0.184,1.177,1.161,0.066)	0.185	1.087	-0.003	-0.331	$M(\theta ;0,1)=0.9$
G	(1.088,0.894,3.782,1.969,2.71,1.792,0.55)	1.484	1.793	0.6	0	$M(\theta ;0,1)=0.5$
	(1.515,2.553,3.55,0.07,1.328,1.619,0.07)	0.171	1.359	0.501	0	$M(\theta ;0,1)=0.75$
	(-0.034,1.072,1.159,1.146,1.51,1.301,0.756)	0.254	1.238	0.401	0	$M(\theta ;0,1)=0.9$
H	(0.816,1.867,1.24,1.787,1.272,1.05,0.278)	1.517	1.475	-0.302	0	$M(\theta ;0,1)=0.5$
	(-0.364,1.889,1.057,0.29,1.413,1.05,0.527)	-0.055	1.682	-0.154	0	$M(\theta ;0,1)=0.75$
	(0.286,0.405,1.27,-0.263,1.261,1.05,0.112)	-0.202	1.188	-0.128	0	$M(\theta ;0,1)=0.9$

Figure A5. PDF curves of the PCM distribution for parameter values presented in Table A5.

Figure A5. PDF curves of the PCM distribution for parameter values presented in Table A5.

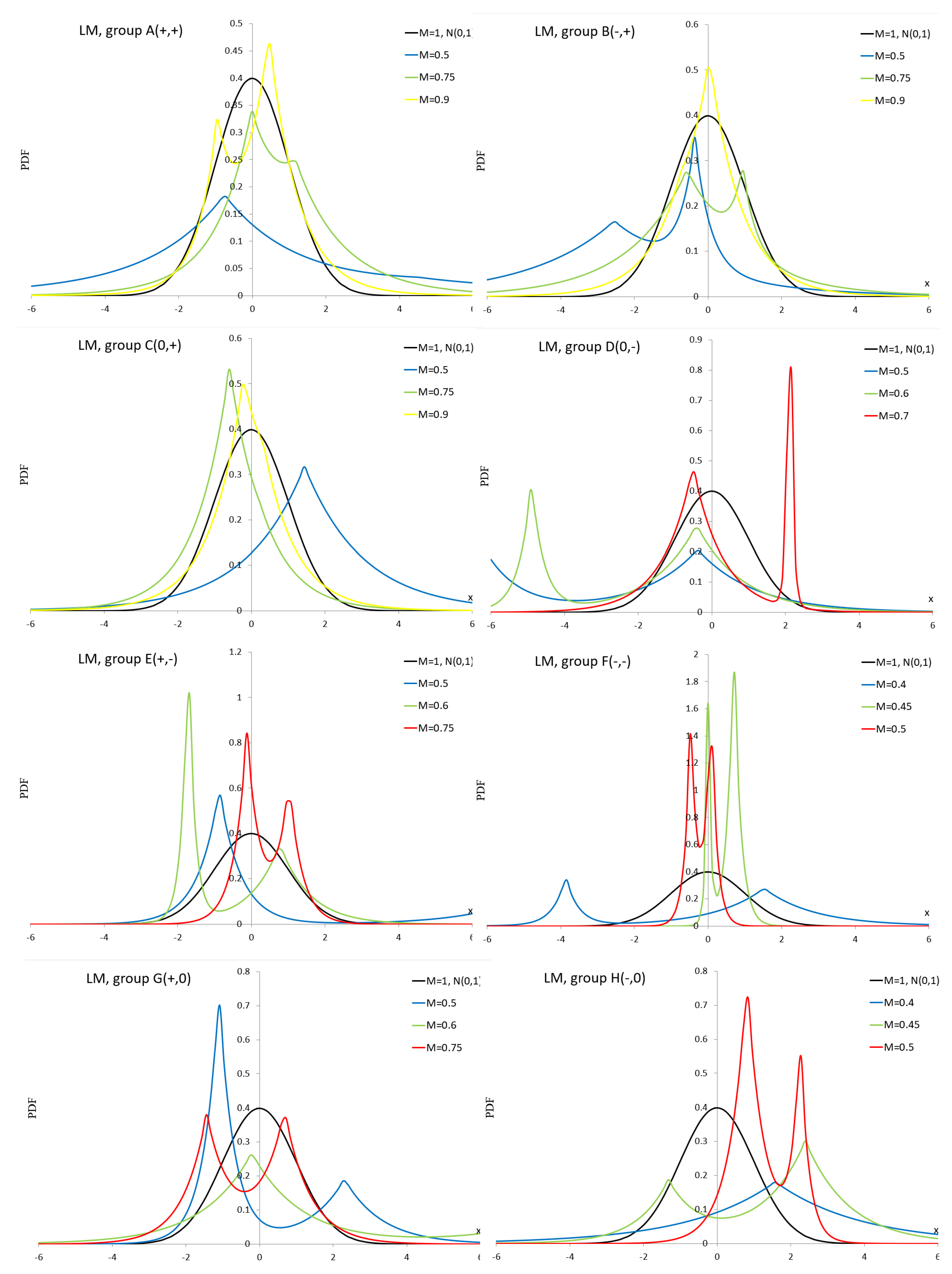
Appendix A.6. Laplace Mixture Distribution

PDF of the Laplace mixture (LM) distribution is given by

$$f_{LM}\left(x;\theta \right)=\omega {\displaystyle \frac{1}{2{\sigma }_1}}exp\left(-{\displaystyle \frac{\left|x-{\mu }_1\right|}{{\sigma }_1}}\right)+\left(1-\omega \right){\displaystyle \frac{1}{2{\sigma }_2}}exp\left(-{\displaystyle \frac{\left|x-{\mu }_2\right|}{{\sigma }_2}}\right),$$

where $\theta =\left({\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2,\omega \right)$ and $x\in R,{\mu }_1,{\mu }_2\in R,{\sigma }_1,{\sigma }_2>0,\omega \in \left[0,1\right]$.

Special cases of the LM distribution are Laplace (L) $L\left({\mu }_1,{\sigma }_1\right)$ for $\omega =1$ and $L\left({\mu }_2,{\sigma }_2\right)$ for $\omega =0$.

Table A6. Vectors of LM parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups A-H.

Group	$\mathit{\theta }=\left({\mathit{\mu }}_1,{\mathit{\sigma }}_1,{\mathit{\mu }}_2,{\mathit{\sigma }}_2,\mathit{\omega }\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
A	(4.521,7.174,-0.757,1.959,0.313)	0.895	6.594	1.172	9.074	$M(\theta ;0,1)=0.5$
	(1.169,1.491,-0.019,0.849,0.56)	0.646	1.863	0.4	3.454	$M(\theta ;0,1)=0.75$
	(0.452,0.818,-0.947,0.482,0.762)	0.119	1.219	0.224	1.644	$M(\theta ;0,1)=0.9$
B	(-0.358,0.405,-2.549,2.309,0.234)	-2.036	3.018	-0.407	3.5	$M(\theta ;0,1)=0.5$
	(0.94,0.335,-0.571,1.585,0.122)	-0.387	2.164	-0.202	3.136	$M(\theta ;0,1)=0.75$
	(-0.736,0.911,0.04,0.878,0.132)	-0.062	1.275	-0.034	2.773	$M(\theta ;0,1)=0.9$
C	(1.445,1.571,-2.516,1.87,1)	1.445	2.222	0	3	$M(\theta ;0,1)=0.5$
	(0.246,0.844,-0.59,0.905,0.043)	-0.554	1.287	0	2.894	$M(\theta ;0,1)=0.75$
	(0.319,0.86,-0.21,0.874,0.222)	-0.092	1.251	0	2.815	$M(\theta ;0,1)=0.9$
D	(-6.131,0.945,-0.386,1.54,0.366)	-2.487	3.364	0	-0.648	$M(\theta ;0,1)=0.5$
	(-4.898,0.343,-0.415,1.234,0.29)	-1.716	2.523	0	-0.597	$M(\theta ;0,1)=0.6$
	(2.115,0.07,-0.512,0.822,0.208)	0.034	1.486	0	-0.005	$M(\theta ;0,1)=0.7$
E	(7.186,1.509,-0.869,0.58,0.309)	1.62	3.966	1.005	-0.403	$M(\theta ;0,1)=0.5$
	(-1.711,0.177,0.773,0.823,0.421)	-0.274	1.522	0.5	-0.32	$M(\theta ;0,1)=0.6$
	(1.023,0.358,-0.118,0.348,0.428)	0.37	0.753	0.15	-0.014	$M(\theta ;0,1)=0.75$
F	(-3.863,0.348,1.522,1.359,0.248)	0.184	2.872	-0.18	-0.556	$M(\theta ;0,1)=0.4$
	(0.006,0.065,0.703,0.189,0.227)	0.545	0.378	-0.17	-0.286	$M(\theta ;0,1)=0.45$
	(-0.466,0.161,0.08,0.159,0.48)	-0.182	0.354	-0.05	-0.2	$M(\theta ;0,1)=0.5$
G	(2.309,1.022,-1.1,0.418,0.391)	0.233	1.949	0.85	0	$M(\theta ;0,1)=0.5$
	(-0.208,1.335,7.917,1.899,0.712)	2.132	4.261	0.839	0	$M(\theta ;0,1)=0.6$
	(0.679,0.702,-1.434,0.642,0.532)	-0.31	1.422	0.036	0	$M(\theta ;0,1)=0.75$
H	(-9.234,0.124,1.581,2.321,0.161)	-0.159	4.983	-0.556	0	$M(\theta ;0,1)=0.4$
	(-1.322,0.83,2.398,1.181,0.291)	1.317	2.287	-0.1	0	$M(\theta ;0,1)=0.45$
	(0.81,0.479,2.254,0.229,0.736)	1.191	0.878	-0.032	0	$M(\theta ;0,1)=0.5$

Table A6. Vectors of LM parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups A-H.

Group	$\mathit{\theta }=\left({\mathit{\mu }}_1,{\mathit{\sigma }}_1,{\mathit{\mu }}_2,{\mathit{\sigma }}_2,\mathit{\omega }\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
A	(4.521,7.174,-0.757,1.959,0.313)	0.895	6.594	1.172	9.074	$M(\theta ;0,1)=0.5$
	(1.169,1.491,-0.019,0.849,0.56)	0.646	1.863	0.4	3.454	$M(\theta ;0,1)=0.75$
	(0.452,0.818,-0.947,0.482,0.762)	0.119	1.219	0.224	1.644	$M(\theta ;0,1)=0.9$
B	(-0.358,0.405,-2.549,2.309,0.234)	-2.036	3.018	-0.407	3.5	$M(\theta ;0,1)=0.5$
	(0.94,0.335,-0.571,1.585,0.122)	-0.387	2.164	-0.202	3.136	$M(\theta ;0,1)=0.75$
	(-0.736,0.911,0.04,0.878,0.132)	-0.062	1.275	-0.034	2.773	$M(\theta ;0,1)=0.9$
C	(1.445,1.571,-2.516,1.87,1)	1.445	2.222	0	3	$M(\theta ;0,1)=0.5$
	(0.246,0.844,-0.59,0.905,0.043)	-0.554	1.287	0	2.894	$M(\theta ;0,1)=0.75$
	(0.319,0.86,-0.21,0.874,0.222)	-0.092	1.251	0	2.815	$M(\theta ;0,1)=0.9$
D	(-6.131,0.945,-0.386,1.54,0.366)	-2.487	3.364	0	-0.648	$M(\theta ;0,1)=0.5$
	(-4.898,0.343,-0.415,1.234,0.29)	-1.716	2.523	0	-0.597	$M(\theta ;0,1)=0.6$
	(2.115,0.07,-0.512,0.822,0.208)	0.034	1.486	0	-0.005	$M(\theta ;0,1)=0.7$
E	(7.186,1.509,-0.869,0.58,0.309)	1.62	3.966	1.005	-0.403	$M(\theta ;0,1)=0.5$
	(-1.711,0.177,0.773,0.823,0.421)	-0.274	1.522	0.5	-0.32	$M(\theta ;0,1)=0.6$
	(1.023,0.358,-0.118,0.348,0.428)	0.37	0.753	0.15	-0.014	$M(\theta ;0,1)=0.75$
F	(-3.863,0.348,1.522,1.359,0.248)	0.184	2.872	-0.18	-0.556	$M(\theta ;0,1)=0.4$
	(0.006,0.065,0.703,0.189,0.227)	0.545	0.378	-0.17	-0.286	$M(\theta ;0,1)=0.45$
	(-0.466,0.161,0.08,0.159,0.48)	-0.182	0.354	-0.05	-0.2	$M(\theta ;0,1)=0.5$
G	(2.309,1.022,-1.1,0.418,0.391)	0.233	1.949	0.85	0	$M(\theta ;0,1)=0.5$
	(-0.208,1.335,7.917,1.899,0.712)	2.132	4.261	0.839	0	$M(\theta ;0,1)=0.6$
	(0.679,0.702,-1.434,0.642,0.532)	-0.31	1.422	0.036	0	$M(\theta ;0,1)=0.75$
H	(-9.234,0.124,1.581,2.321,0.161)	-0.159	4.983	-0.556	0	$M(\theta ;0,1)=0.4$
	(-1.322,0.83,2.398,1.181,0.291)	1.317	2.287	-0.1	0	$M(\theta ;0,1)=0.45$
	(0.81,0.479,2.254,0.229,0.736)	1.191	0.878	-0.032	0	$M(\theta ;0,1)=0.5$

Figure A6. PDF curves of the LM distribution for parameter values presented in Table A6.

Figure A6. PDF curves of the LM distribution for parameter values presented in Table A6.

Appendix A.7. Johnson SB Distribution

PDF of the Johnson SB (SB) distribution is given by [65]

$$f_{SB}\left(x;a,b,c,d\right)={\displaystyle \frac{bd}{\left(x-c\right)\left(c+d-x\right)}}\Phi \left[a+bln\left({\displaystyle \frac{x-c}{c+d-x}}\right);0,1\right],x\in \left[c,c+d\right]$$

where$a,c\in R;b,d>0$.

Table A7. Vectors of the SB parameter $\theta$, mean ${\mu }_a$,standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups A –B, D –H.

Group	$\mathit{\theta }=\left({\mathit{\mu }}_1,{\mathit{\sigma }}_1,{\mathit{\mu }}_2,{\mathit{\sigma }}_2,\mathit{\omega }\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
A	(1.972,1.819,-0.45,4)	0.613	0.411	0.649	0.3	$M(\theta ;0,1)=0.5$
	(2.482,2.23,-1.665,7.423)	0.237	0.618	0.584	0.298	$M(\theta ;0,1)=0.75$
	(3.092,2.702,-2.908,12.271)	0.132	0.832	0.518	0.267	$M(\theta ;0,1)=0.9$
B	(-4.086,2.097,-5.424,6.348)	0.074	0.351	-1	1.488	$M(\theta ;0,1)=0.5$
	(-2.614,2.258,-5.722,7.58)	-0.021	0.611	-0.6	0.341	$M(\theta ;0,1)=0.75$
	(-1.992,2.198,-6.446,8.974)	-0.129	0.823	-0.485	0.099	$M(\theta ;0,1)=0.9$
D	(0,3.149,-2.116,4.115)	-0.059	0.319	0	-0.176	$M(\theta ;0,1)=0.5$
	(0,3.958,-4.707,9.414)	0	0.585	0	-0.117	$M(\theta ;0,1)=0.75$
	(0,4.304,-8.154,15.856)	-0.227	0.909	0	-0.1	$M(\theta ;0,1)=0.9$
E	(0.664,0.45,-0.027,4.679)	1.377	1.38	0.856	-0.558	$M(\theta ;0,1)=0.5$
	(0.834,0.754,-0.727,3.258)	0.26	0.726	0.788	-0.25	$M(\theta ;0,1)=0.75$
	(0.867,2.297,-4.627,10.828)	-0.18	1.095	0.2	-0.227	$M(\theta ;0,1)=0.9$
F	(-0.716,0.448,-0.622,1.618)	0.534	0.47	-0.931	-0.4	$M(\theta ;0,1)=0.5$
	(-1.044,1.22,-4.394,5.493)	-0.665	0.88	-0.603	-0.145	$M(\theta ;0,1)=0.75$
	(-1.202,1.515,-4.252,6.217)	-0.065	0.837	-0.522	-0.1	$M(\theta ;0,1)=0.9$
G	(1.64,2.044,-3.761,8.045)	-1.199	0.819	0.452	0	$M(\theta ;0,1)=0.5$
	(1.825,2.345,-1.984,6.623)	0.145	0.596	0.401	0	$M(\theta ;0,1)=0.75$
	(2.952,4.082,-5.487,16.27)	-0.135	0.87	0.24	0	$M(\theta ;0,1)=0.9$
H	(-1.357;1.565;-1.601;3.202)	0.605	0.41	-0.563	0	$M(\theta ;0,1)=0.5$
	(-2.046;2.695;-5.081;7.468)	-0.032	0.592	-0.354	0	$M(\theta ;0,1)=0.75$
	(-2.068;2.73;-7.098;10.398)	-0.07	0.814	-0.35	0	$M(\theta ;0,1)=0.9$

Table A7. Vectors of the SB parameter $\theta$, mean ${\mu }_a$,standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups A –B, D –H.

Group	$\mathit{\theta }=\left({\mathit{\mu }}_1,{\mathit{\sigma }}_1,{\mathit{\mu }}_2,{\mathit{\sigma }}_2,\mathit{\omega }\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
A	(1.972,1.819,-0.45,4)	0.613	0.411	0.649	0.3	$M(\theta ;0,1)=0.5$
	(2.482,2.23,-1.665,7.423)	0.237	0.618	0.584	0.298	$M(\theta ;0,1)=0.75$
	(3.092,2.702,-2.908,12.271)	0.132	0.832	0.518	0.267	$M(\theta ;0,1)=0.9$
B	(-4.086,2.097,-5.424,6.348)	0.074	0.351	-1	1.488	$M(\theta ;0,1)=0.5$
	(-2.614,2.258,-5.722,7.58)	-0.021	0.611	-0.6	0.341	$M(\theta ;0,1)=0.75$
	(-1.992,2.198,-6.446,8.974)	-0.129	0.823	-0.485	0.099	$M(\theta ;0,1)=0.9$
D	(0,3.149,-2.116,4.115)	-0.059	0.319	0	-0.176	$M(\theta ;0,1)=0.5$
	(0,3.958,-4.707,9.414)	0	0.585	0	-0.117	$M(\theta ;0,1)=0.75$
	(0,4.304,-8.154,15.856)	-0.227	0.909	0	-0.1	$M(\theta ;0,1)=0.9$
E	(0.664,0.45,-0.027,4.679)	1.377	1.38	0.856	-0.558	$M(\theta ;0,1)=0.5$
	(0.834,0.754,-0.727,3.258)	0.26	0.726	0.788	-0.25	$M(\theta ;0,1)=0.75$
	(0.867,2.297,-4.627,10.828)	-0.18	1.095	0.2	-0.227	$M(\theta ;0,1)=0.9$
F	(-0.716,0.448,-0.622,1.618)	0.534	0.47	-0.931	-0.4	$M(\theta ;0,1)=0.5$
	(-1.044,1.22,-4.394,5.493)	-0.665	0.88	-0.603	-0.145	$M(\theta ;0,1)=0.75$
	(-1.202,1.515,-4.252,6.217)	-0.065	0.837	-0.522	-0.1	$M(\theta ;0,1)=0.9$
G	(1.64,2.044,-3.761,8.045)	-1.199	0.819	0.452	0	$M(\theta ;0,1)=0.5$
	(1.825,2.345,-1.984,6.623)	0.145	0.596	0.401	0	$M(\theta ;0,1)=0.75$
	(2.952,4.082,-5.487,16.27)	-0.135	0.87	0.24	0	$M(\theta ;0,1)=0.9$
H	(-1.357;1.565;-1.601;3.202)	0.605	0.41	-0.563	0	$M(\theta ;0,1)=0.5$
	(-2.046;2.695;-5.081;7.468)	-0.032	0.592	-0.354	0	$M(\theta ;0,1)=0.75$
	(-2.068;2.73;-7.098;10.398)	-0.07	0.814	-0.35	0	$M(\theta ;0,1)=0.9$

Figure A7. PDF curves of the SB distribution for parameter values presented in Table A7.

Figure A7. PDF curves of the SB distribution for parameter values presented in Table A7.

Appendix A.8. Johnson SU Distribution

PDF of the Johnson SU (SU) distribution is given by [65]

$$f_{SU}\left(x;a,b,c,d\right)={\displaystyle \frac{b}{\sqrt{{\left(x-c\right)}^2+d^2}}}\varphi \left[a+b{sinh}^{-1}\left({\displaystyle \frac{x-c}{d}}\right);0,1\right]\left(x\in R\right)$$

where $b>0,a,c\in R,d\ne 0$.

Table A8. Vectors of the SU parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups A – C, E – H.

Group	$\mathit{\theta }=\left(\mathit{a},\mathit{b},\mathit{c},\mathit{d}\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
A	(-1.246,2.021,0.257,0.731)	0.800	0.501	1.014	2.911	$M(\theta ;0,1)=0.5$
	(-0.569,2.063,-1.301,2.625)	-0.477	1.499	0.493	1.720	$M(\theta ;0,1)=0.75$
	(-0.11,2.762,-0.069,3.319)	0.072	1.286	0.049	0.648	$M(\theta ;0,1)=0.9$
B	(2.502,2.889,2.029,3.828)	-1.949	2	-0.8	1.455	$M(\theta ;0,1)=0.5$
	(2.564,3.308,2.137,1.902)	0.435	0.8	-0.636	0.926	$M(\theta ;0,1)=0.75$
	(2.296,5.558,2.36,6.031)	-0.246	1.2	-0.218	0.2	$M(\theta ;0,1)=0.9$
C	(0,1.821,-1.617,3.096)	-1.617	1.992	0	2	$M(\theta ;0,1)=0.5$
	(0,1.829,-0.205,2.967)	-0.205	1.897	0	1.97	$M(\theta ;0,1)=0.75$
	(0,3.372,0.204,2.935)	0.204	0.91	0	0.403	$M(\theta ;0,1)=0.9$
E	(-22.518,45.262,-11.095,19.766)	-0.848	0.492	0.031	-0.007	$M(\theta ;0,1)=0.5$
	(1.29,40.539,-0.294,-17.564)	0.155	0.484	0.491	-0.784	$M(\theta ;0,1)=0.6$
	(0.244,21.027,-0.134,-12.383)	0.01	0.59	0.002	-0.007	$M(\theta ;0,1)=0.75$
F	(0.861,18.997,-1.158,14.674)	-1.824	0.774	-0.011	-0.005	$M(\theta ;0,1)=0.3$
	(0.756,3.676,0.166,0.819)	-0.010	0.236	-0.359	-0.450	$M(\theta ;0,1)=0.4$
	(13.843,36.36,4.174,11.623)	-0.360	0.343	-0.030	-0.077	$M(\theta ;0,1)=0.5$
G	(-9.342,11.021,-1.575,1.981)	0.32	0.25	0.207	0	$M(\theta ;0,1)=0.4$
	(-23.944,18.041,-8.486,5.409)	1.009	0.606	0.15	0	$M(\theta ;0,1)=0.5$
	(-9.349,85.071,-3.763,35.754)	0.174	0.423	0.004	0	$M(\theta ;0,1)=0.6$
H	(0.738,49.723,3.6,73.029)	2.516	1.469	-0.001	0	$M(\theta ;0,1)=0.3$
	(2.547,7.276,0.835,1.65)	0.24	0.243	-0.141	0	$M(\theta ;0,1)=0.4$
	(4.211,10.507,1.959,3.55)	0.491	0.367	-0.11	0	$M(\theta ;0,1)=0.5$

Table A8. Vectors of the SU parameter $\theta$, mean ${\mu }_a$, standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups A – C, E – H.

Group	$\mathit{\theta }=\left(\mathit{a},\mathit{b},\mathit{c},\mathit{d}\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
A	(-1.246,2.021,0.257,0.731)	0.800	0.501	1.014	2.911	$M(\theta ;0,1)=0.5$
	(-0.569,2.063,-1.301,2.625)	-0.477	1.499	0.493	1.720	$M(\theta ;0,1)=0.75$
	(-0.11,2.762,-0.069,3.319)	0.072	1.286	0.049	0.648	$M(\theta ;0,1)=0.9$
B	(2.502,2.889,2.029,3.828)	-1.949	2	-0.8	1.455	$M(\theta ;0,1)=0.5$
	(2.564,3.308,2.137,1.902)	0.435	0.8	-0.636	0.926	$M(\theta ;0,1)=0.75$
	(2.296,5.558,2.36,6.031)	-0.246	1.2	-0.218	0.2	$M(\theta ;0,1)=0.9$
C	(0,1.821,-1.617,3.096)	-1.617	1.992	0	2	$M(\theta ;0,1)=0.5$
	(0,1.829,-0.205,2.967)	-0.205	1.897	0	1.97	$M(\theta ;0,1)=0.75$
	(0,3.372,0.204,2.935)	0.204	0.91	0	0.403	$M(\theta ;0,1)=0.9$
E	(-22.518,45.262,-11.095,19.766)	-0.848	0.492	0.031	-0.007	$M(\theta ;0,1)=0.5$
	(1.29,40.539,-0.294,-17.564)	0.155	0.484	0.491	-0.784	$M(\theta ;0,1)=0.6$
	(0.244,21.027,-0.134,-12.383)	0.01	0.59	0.002	-0.007	$M(\theta ;0,1)=0.75$
F	(0.861,18.997,-1.158,14.674)	-1.824	0.774	-0.011	-0.005	$M(\theta ;0,1)=0.3$
	(0.756,3.676,0.166,0.819)	-0.010	0.236	-0.359	-0.450	$M(\theta ;0,1)=0.4$
	(13.843,36.36,4.174,11.623)	-0.360	0.343	-0.030	-0.077	$M(\theta ;0,1)=0.5$
G	(-9.342,11.021,-1.575,1.981)	0.32	0.25	0.207	0	$M(\theta ;0,1)=0.4$
	(-23.944,18.041,-8.486,5.409)	1.009	0.606	0.15	0	$M(\theta ;0,1)=0.5$
	(-9.349,85.071,-3.763,35.754)	0.174	0.423	0.004	0	$M(\theta ;0,1)=0.6$
H	(0.738,49.723,3.6,73.029)	2.516	1.469	-0.001	0	$M(\theta ;0,1)=0.3$
	(2.547,7.276,0.835,1.65)	0.24	0.243	-0.141	0	$M(\theta ;0,1)=0.4$
	(4.211,10.507,1.959,3.55)	0.491	0.367	-0.11	0	$M(\theta ;0,1)=0.5$

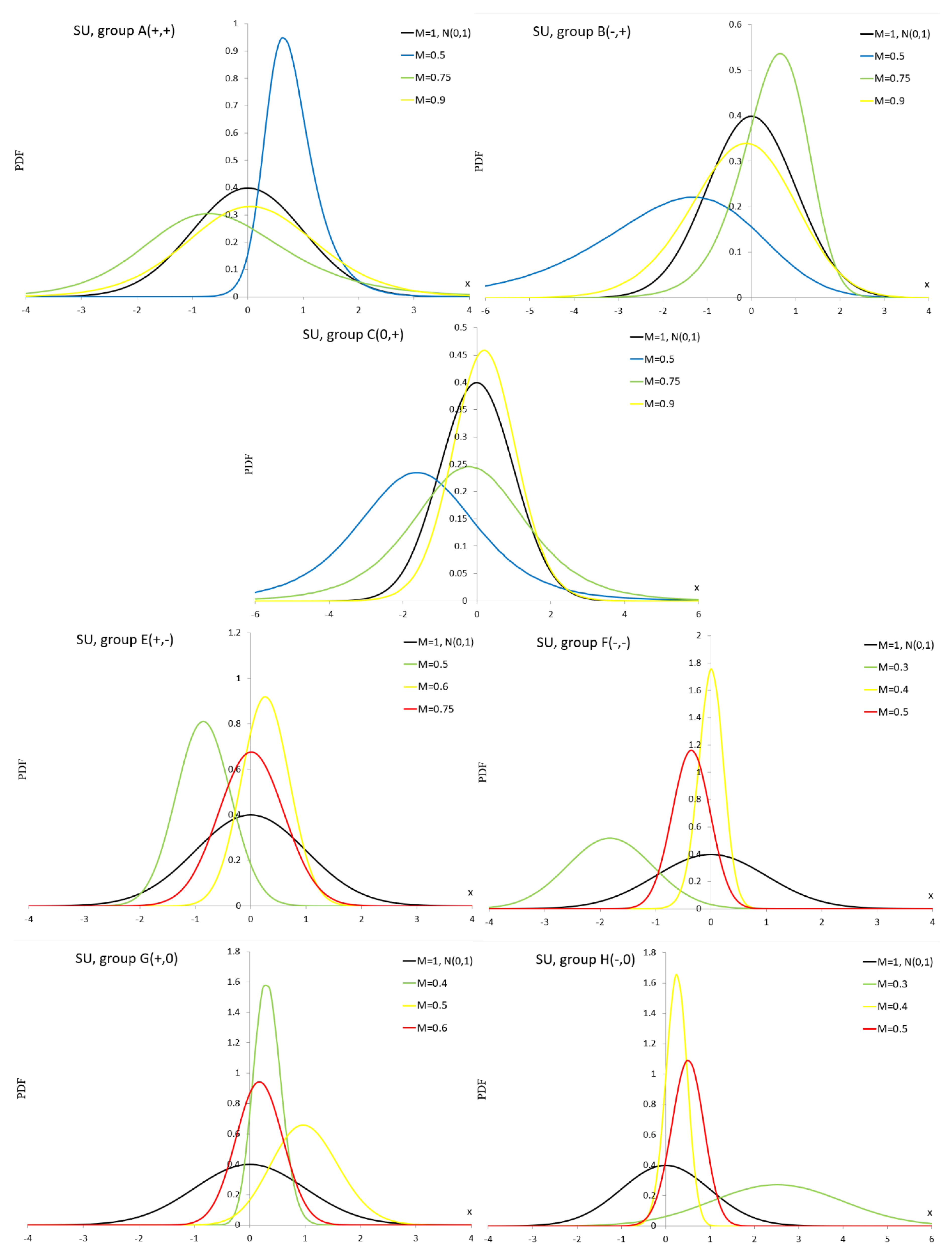
Figure A8. PDF curves of the SU distribution for parameter values presented in Table A8.

Figure A8. PDF curves of the SU distribution for parameter values presented in Table A8.

Appendix A.9. Extended Easily Changeable Kurtosis Distribution

PDF of the extended easily changeable kurtosis (EECK) distribution is given by [66]

$$f_{EECK}\left(x;\mathrm{a},\mathrm{b}\right)={\displaystyle \frac{{\left(1-{\left|x\right|}^b\right)}^a\Gamma \left(a+\frac{1}{b}+1\right)}{2\Gamma \left(a+1\right)\Gamma \left(\frac{1}{b}+1\right)}}\left(x\in \left[-1,1\right]\left(a\ge 0\right),x\in \left(-1,1\right)\left(1<a<0\right)\right),$$

where $a>-1,b>0$. Special cases of the EECK distribution are: uniform $U\left(-1,1\right)=EECK\left(0,\mathrm{b}\right)$, triangle $\left(\mathrm{a}=\mathrm{b}=1\right)$ and easily changeable kurtosis $\left(b=2\right)$ [67] distributions.

Table A9. Vectors of the EECK parameter $\theta$, mean ${\mu }_a$,standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups A-H.

Group	$\mathit{\theta }=\left(\mathit{a},\mathit{b}\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
C	(46.018,1.043)	0	0.032	0	2.256	$M(\theta ;0,0.096)=0.5$
	(40.914,1.366)	0	0.06	0	0.921	$M(\theta ;0,0.096)=0.75$
	(10.676,1.184)	0	0.128	0	0.912	$M(\theta ;0,0.096)=0.9$
D	(60.495,4.846)	0	0.244	0	-0.921	$M(\theta ;0,0.096)=0.5$
	(48.76,2.738)	0	0.15	0	-0.51	$M(\theta ;0,0.096)=0.75$
	(48.76,2.211)	0	0.115	0	-0.238	$M(\theta ;0,0.096)=0.9$

Table A9. Vectors of the EECK parameter $\theta$, mean ${\mu }_a$,standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M. Groups A-H.

Group	$\mathit{\theta }=\left(\mathit{a},\mathit{b}\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
C	(46.018,1.043)	0	0.032	0	2.256	$M(\theta ;0,0.096)=0.5$
	(40.914,1.366)	0	0.06	0	0.921	$M(\theta ;0,0.096)=0.75$
	(10.676,1.184)	0	0.128	0	0.912	$M(\theta ;0,0.096)=0.9$
D	(60.495,4.846)	0	0.244	0	-0.921	$M(\theta ;0,0.096)=0.5$
	(48.76,2.738)	0	0.15	0	-0.51	$M(\theta ;0,0.096)=0.75$
	(48.76,2.211)	0	0.115	0	-0.238	$M(\theta ;0,0.096)=0.9$

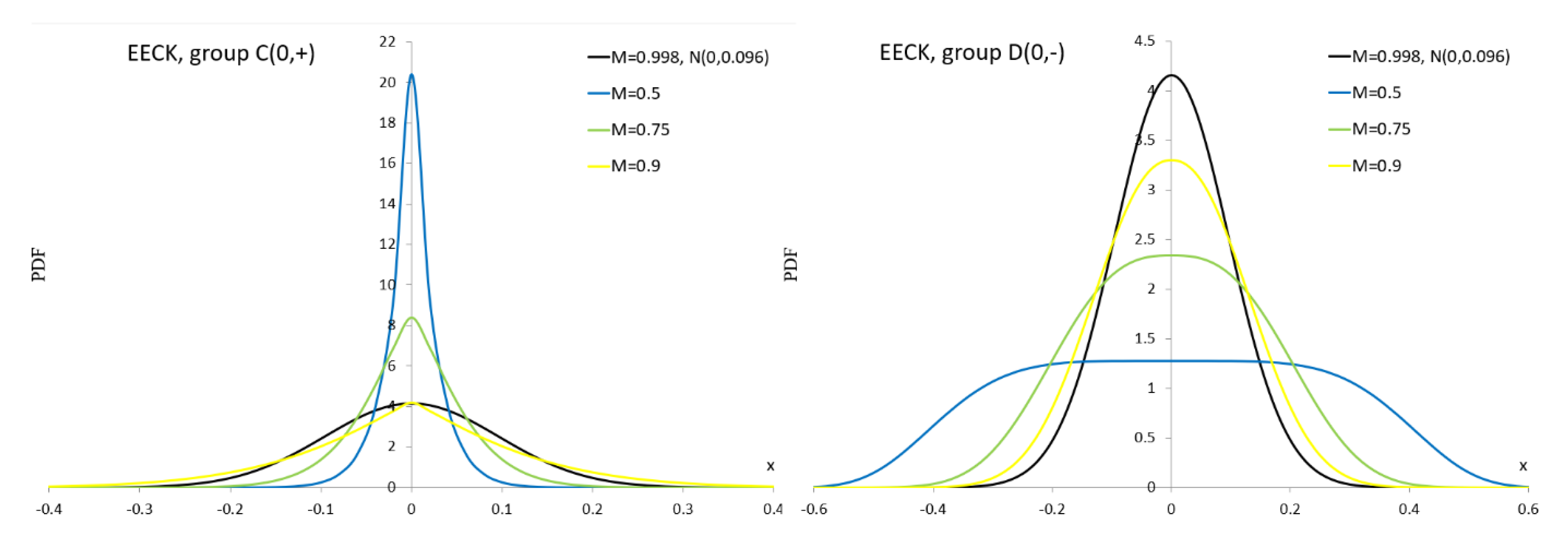
Figure A9. PDF curves of the EECK distribution for parameter values presented in Table A9.

Figure A9. PDF curves of the EECK distribution for parameter values presented in Table A9.

Appendix A.10. Exponential Power Distribution

PDF of the exponential power (EP) distribution is given by [68,70]

$$f_{EP}\left(x;a,b,c\right)={\displaystyle \frac{1}{2c\sqrt[c]{c}\Gamma \left(1+\frac{1}{c}\right)}}exp\left[-{\displaystyle \frac{1}{c}}{\left(\left|{\displaystyle \frac{x-a}{b}}\right|\right)}^c\right],x\in R\left(a\in R,b,c>0\right).$$

Special case of the EP distribution is the $N\left(a,b\right)$ for $c=2$.

Table A10. Vectors of the EP parameter $\theta$, mean ${\mu }_a$,standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M.

Group	$\mathit{\theta }=\left(\mathit{a},\mathit{b},\mathit{c}\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
C	(-0.796,2.985,1.609)	-0.796	3.257	0	0.536	$M(\theta ;0,1)=0.5$
	(90.611,1.385,1.695)	0.611	1.478	0	0.386	$M(\theta ;0,1)=0.75$
	(90.251,1.033,1.785)	0.251	1.079	0	0.253	$M(\theta ;0,1)=0.9$
D	(-0.611,3.71,28.792)	-0.611	2.368	0	-1.188	$M(\theta ;0,1)=0.5$
	(-0.673,1.198,3.828)	-0.673	0.994	0	-0.783	$M(\theta ;0,1)=0.75$
	(-0.05,1.272,3.117)	-0.05	1.11	0	-0.619	$M(\theta ;0,1)=0.9$

Table A10. Vectors of the EP parameter $\theta$, mean ${\mu }_a$,standard deviation ${\sigma }_a$, skewness ${\gamma }_1$, excess kurtosis ${\overline{\gamma }}_2$ and similarity measure M.

Group	$\mathit{\theta }=\left(\mathit{a},\mathit{b},\mathit{c}\right)$	${\mathit{\mu }}_{\mathit{a}}$	${\mathit{\sigma }}_{\mathit{a}}$	${\mathit{\gamma }}_1$	${\overline{\mathit{\gamma }}}_2$	$\mathit{M}\left(\mathit{\theta };\mathit{\mu },\mathit{\sigma }\right)$
C	(-0.796,2.985,1.609)	-0.796	3.257	0	0.536	$M(\theta ;0,1)=0.5$
	(90.611,1.385,1.695)	0.611	1.478	0	0.386	$M(\theta ;0,1)=0.75$
	(90.251,1.033,1.785)	0.251	1.079	0	0.253	$M(\theta ;0,1)=0.9$
D	(-0.611,3.71,28.792)	-0.611	2.368	0	-1.188	$M(\theta ;0,1)=0.5$
	(-0.673,1.198,3.828)	-0.673	0.994	0	-0.783	$M(\theta ;0,1)=0.75$
	(-0.05,1.272,3.117)	-0.05	1.11	0	-0.619	$M(\theta ;0,1)=0.9$

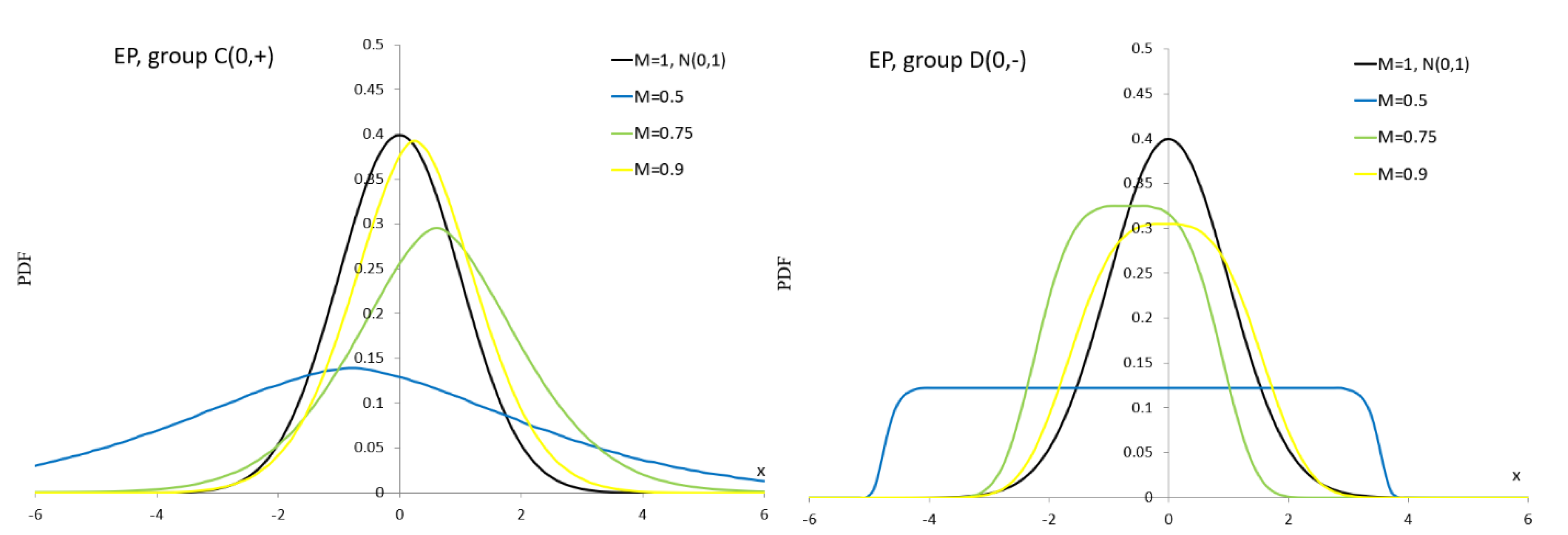
Figure A10. PDF curves of the EP distribution for parameter values presented in Table A10.

Figure A10. PDF curves of the EP distribution for parameter values presented in Table A10.