Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Beyond Correlation: Redefining Causation Through Robustness and Resilience to Perturbation

Submitted:

06 November 2025

Posted:

07 November 2025

You are already at the latest version

Abstract
Correlation and causation are often treated as interchangeable yet describe different relationships. Correlation quantifies how variables co-vary, while causation denotes a directional influence by which one variable determines another’s state. Classical causal inference assumes that where causation occurs, correlation must follow, an assumption formalized as Faithfulness. However, Faithfulness fails in many biological and physical control systems like hormonal regulation, neural homeostasis and ecological feedback loops, which function by counteracting disturbances rather than amplifying them. Causation may therefore operate without producing observable co-variation, causing correlation to vanish and revealing the limits of conventional statistical approaches that rely exclusively on correlated change. We introduce an information-based definition of causation, conceived as preservation of informational structure against disturbance. A variable is considered causal when its influence decreases uncertainty in another variable exposed to unpredictable inputs, thereby maintaining order under noise. Using numerical simulations of feedback and feedforward systems, we showed that strong causal interactions can be reliably detected even when correlations between variables are negligible or negative. Our simulations revealed also reductions in conditional entropy and delayed oppositions between control and outcome, providing quantitative evidence of stabilizing causation hidden to traditional correlation-based measures. Unlike regression, structural equation modeling or transfer entropy, our approach revealed compensatory and self-maintaining dynamics operating through feedback, nonlinearity and temporal delay. By unifying causal inference and control theory, our agenda reframes stability as an active expression of causal power and enables the detection of hidden causal architectures in physiological homeostasis, neural stability, ecosystem resilience and engineered feedback systems.
Keywords: 
robustness
;  
control theory
;  
homeostatic regulation
;  
entropy reduction
;  
adaptive dynamics
Subject: 
Physical Sciences  -   Applied Physics

Introduction

Correlation quantifies how two variables change together, whereas causation refers to a directional influence in which one variable helps determine another’s state (Schmidt et al., 2018; Kold-Christensen and Johannsen, 2020; Lim et al., 2020; Truesdell et al., 2021; Roy and Marshall, 2023). In most empirical analyses, it is taken for granted that causation necessarily implies correlation, an assumption formalized as Faithfulness. Yet this assumption often fails in feedback and control systems, where mechanisms designed to maintain equilibrium produce minimal or even inverse correlations. These systems can exhibit weak statistical association between directly linked variables and strong apparent correlations between variables that are not causally connected (Kennaway 2020). These paradoxical patterns persist even when parameters are varied reflecting a system’s functional aim, i.e., to preserve stability in the face of disturbance. Consequently, conventional methods of causal inference based on co-variation such as regression, structural equation modeling and Bayesian networks could mischaracterize or entirely miss stabilizing causal relations (Dondelinger and Mukherjee, 2019; Huang 2020; Li and Jacobucci, 2022; Grinstead et al., 2023; Lin et al., 2023; Zheng et al., 2024; Hammond and Smith, 2025). The misconception is that influence must manifest as variability, when in many regulatory systems it manifests instead as constancy. Recognizing that causation may express itself through stability rather than change calls for a conceptual reformulation of how causal efficacy is defined and measured.
We introduce a framework in which causation is defined as the preservation of structure against disturbance. In our account, a variable exerts a causal role when its action diminishes the uncertainty of another variable under fluctuating conditions, sustaining organized behavior despite noise. In this sense, causal power is identified with the ability to stabilize rather than to co-vary, consistent with the operation of homeostatic and adaptive systems that are frequent in physics, control theory and biology. To assess our hypothesis, we implement a numerical simulation of a simple controlled system in which a variable is perturbed by random disturbances and regulated by a feedback or feedforward controller. By comparing conditions with and without control, we aim to quantify changes in variance, entropy and correlation to uncover whether and how causal influence can maintain stability while concealing statistical dependence.
We will proceed as follows: the next section formalizes the governing equations and computational steps; subsequent sections present quantitative results, methodological comparisons and a conceptual synthesis of causation beyond correlation.

Methods

In this section, we simulate a simple system to understand how a (physical or biological) process can cause stability instead of change. Instead of looking for variables moving together, we assess how one variable can keep another steady when disturbances occur. Our simulation introduces artificial “shocks” and a “controller” reacting to them, to show how regulation can hide the usual signs of correlation. By tracking how uncertainty decreases when control is active, we can measure causation as the ability to preserve order under noise, rather than simple co-variation between signals.
Our model consists of a scalar controlled variable Y t perturbed by an exogenous disturbance D t and regulated by a control signal X t . Time is discrete with unit sampling. The governing equation is
Y t + 1 = Y t + a D t − b X t + ε t ,
where a , b > 0 are coupling coefficients and ε t ∼ N ( 0 , σ 2 ) is zero-mean noise. The setpoint y * is set to zero without loss of generality. Two control laws were implemented (González Ochoa et al., 2018; Borges et al., 2019; Ji et al., 2024; Hua et al., 2025):
a delayed proportional feedback
X t = k p Y t − τ ,
and a feedforward cancellation
X t = γ D t − τ ,
with γ ≈ a / b . The resulting triplet ( D t , X t , Y t ) produces a trajectory of length T .
Disturbance generation and sampling. Disturbances were constructed as sums of exponentially decaying pulses with random onset, width and amplitude:
ϕ m ( t ) = A m e − λ ( t − s m ) 1 0 ≤ t − s m < w m ,
where A m and w m are uniformly distributed and s m are random onset times. The disturbance D t = ∑ m ϕ m ( t ) generates structured yet unpredictable fluctuations. Simulations used T = 4 – 6 × 10 3 samples with Y 0 = 0 . Noise variance ( σ 2 = 10 − 3 – 10 − 2 ) ensured stability of entropy estimates. Stability in the linear feedback case requires ∣ 1 − b k p ∣ < 1 for τ = 0 and corresponding small-gain bounds for τ > 0 . All random draws were seeded for reproducibility.
Closed-loop dynamics. Substituting the feedback law yields, for τ = 0 we achieve
Y t + 1 = ( 1 − b k p ) Y t + a D t + ε t ,
which attenuates variance by ( 1 − b k p ) 2 . For delayed feedback, roots of ζ τ + 1 − ζ τ + b k p = 0 were verified within the unit circle. Feedforward control follows
Y t + 1 = Y t + a D t − b γ D t − τ + ε t .
Exact cancellation occurs when γ = a / b and τ = 0 . For τ > 0 , residual opposition between D and X reduces low-frequency variance. Open-loop (control-off) and closed-loop simulations were run with identical noise and disturbances to isolate causal stabilization effects.
Information preservation metric, discretization and numerical checks. Causal efficacy is defined as conditional entropy reduction (Hino and Murata, 2010; Tangkaratt et al., 2015; Chadi et al., 2022; Bao et al., 2022):
C X → Y = H Y D − H Y D , X .
Conditional entropies are estimated via discretization of observed ranges into bins B i Y , B j D , B k X . Empirical probabilities are
p ^ i , j = 1 T ∑ t 1 i t = i , j t = j , p ^ i , j , k = 1 T ∑ t 1 i t = i , j t = j , k t = k .
Plug-in estimators for discrete entropies are
H ^ Y D = ∑ j p ^ j − ∑ i p ^ i j log 2 p ^ i j ,
H ^ Y D , X = ∑ j , k p ^ j , k − ∑ i p ^ i j , k log 2 p ^ i j , k .
Bias was corrected using the Miller–Madow term ( K − 1 ) / ( 2 T l n 2 ) (Chen et al., 2018; De Gregorio et al., 2024). Stability of C ^ was verified across bin counts n Y ∈ { 20,30,40 } , n D ∈ { 8,10,12 } and n X ∈ { 16,20,24 } ; variation remained below 5%.
Uniform binning was applied between variable minima and maxima. Cells with fewer than five samples were excluded and probabilities renormalized. Bin-edge jittering up to 5% of bin width confirmed numerical robustness. All entropies are in bits. Partial correlations r X Y ⋅ D were computed by linear residualization to compare with informational causation.
Counter-correlation causality index, baselines and null models. To detect delayed negative feedback, the counter-correlation index was computed as
CCI l = − Cov X t , Δ Y t + l Var X t Var Δ Y t ,
where Δ Y t = Y t − Y t − 1 . Positive peaks in CCI ( l ) indicate opposition between controller action and subsequent changes in Y . Confidence intervals were obtained from 1000 block-bootstrapped resamples (block size B ≥ τ + 2 ). Spectral checks confirmed phase opposition near π between X and Δ Y at low frequencies.
Open-loop baselines were generated by setting b = 0 (feedback) or γ = 0 (feedforward). Dispersion and uncertainty suppression were quantified as
ρ var = V a r [ Y ] closed V a r [ Y ] open , ρ H = H ( Y ) closed H ( Y ) open .
Null distributions for C ^ were obtained by circularly shifting X t or randomizing its Fourier phase to preserve marginals but destroy dependencies. Empirical p -values correspond to the proportion of null values exceeding the observed C ^ .
Implementation, validation and stability sweeps. All analyses were performed in Python 3.12 using NumPy, SciPy and Matplotlib. Random sequences were generated with the PCG64 engine under fixed seeds.
The workflow proceeds as follows: (1) parameter setup and disturbance generation, (2) simulation of open- and closed-loop series, (3) calculation of correlations and conditional entropies, (4) evaluation of CCI ( l ) and (5) figure assembly.
Parameter sweeps across k p , γ and τ verified robustness of C ^ and CCI . Stable operation required bounded Y t variance and eigenvalues within the unit circle. Disturbance density ( M / T = 0.02 – 0.05 ) and decay ( λ = 0.25 – 0.40 ) were varied. Entropy estimates showed interquartile variation <0.1 bits across bin settings. Null simulations produced median C ^ near zero, confirming that observed information preservation reflected genuine control effects.
Overall, our streamlined workflow was able to link stochastic control dynamics to quantitative causal metrics. Our model combines explicit equations, reproducible simulation, entropy-based causation measures and temporal opposition analysis.

Results

The quantitative outcomes of the simulations and analyses performed on the feedback-controlled system are reported here, emphasizing the relationship between causation, correlation and informational preservation. All values are achieved through empirical computations applied to the time series generated under controlled conditions, including correlation coefficients, entropy estimates and the counter-correlation causality index.
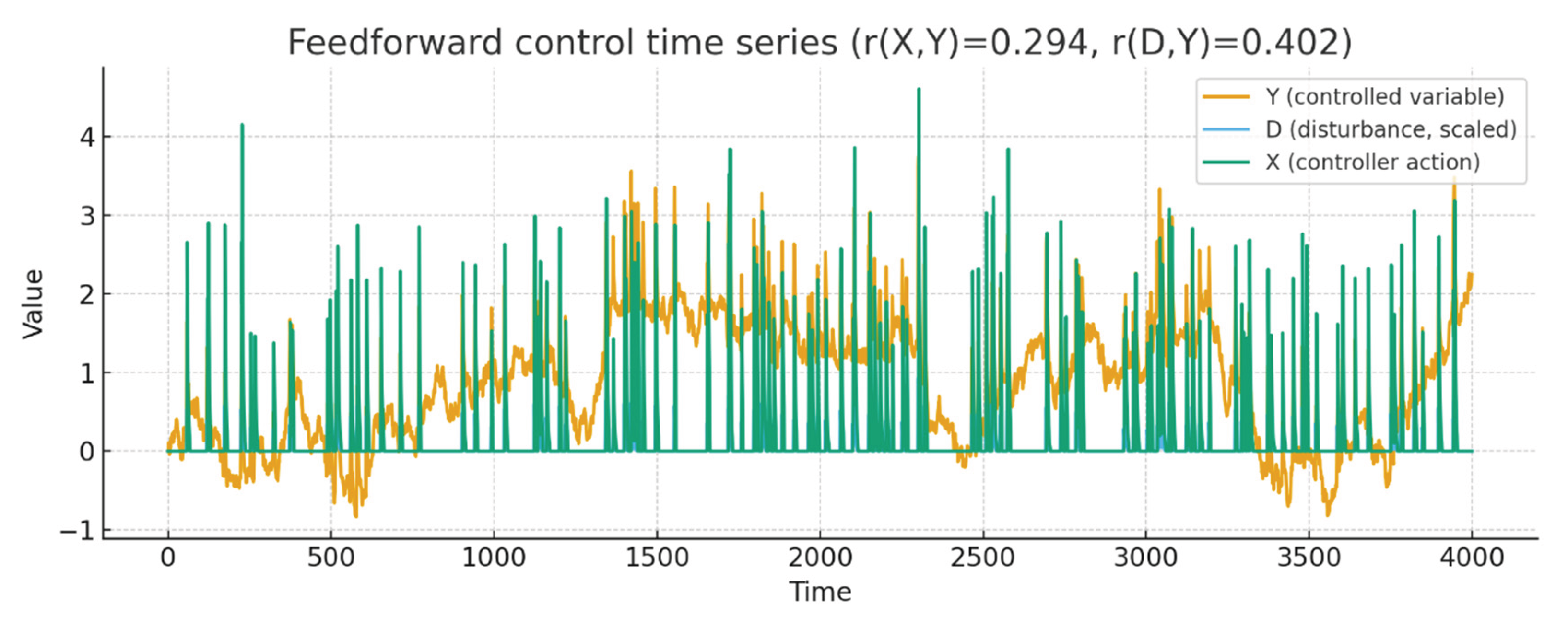
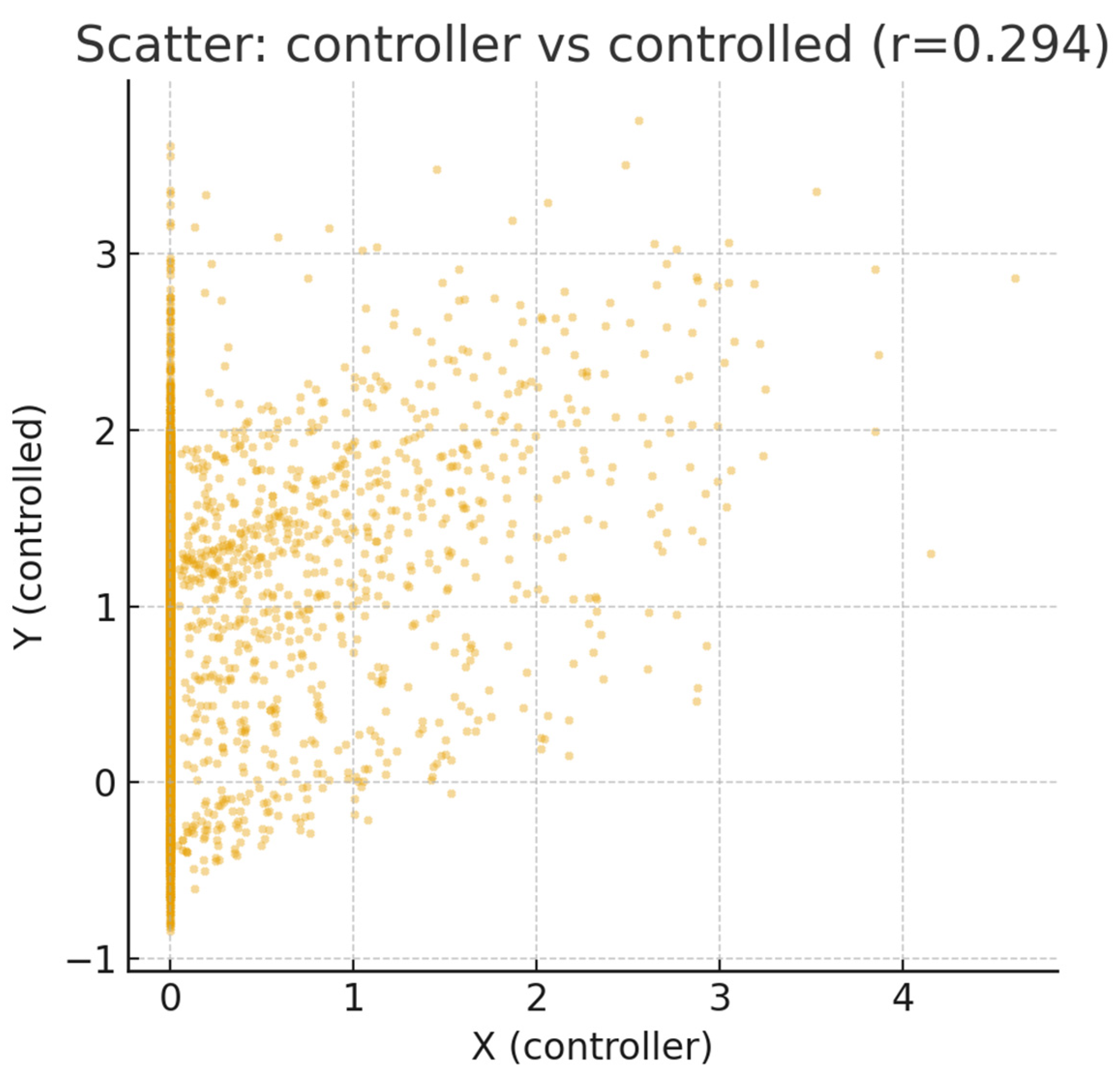
Feedback-controlled dynamics and correlation structure. The simulated system exhibited a stable trajectory of the controlled variable Y t , remaining near the setpoint across four thousand iterations despite intermittent disturbance pulses. The controller signal X t fluctuated in opposition to the disturbance D t , generating compensatory adjustments that minimized variance in Y t . The empirical correlation between controller and controlled variable was r ( X , Y ) = 0.294 , while the correlation between disturbance and outcome was r ( D , Y ) = 0.402 , both computed from the full series length ( T = 4000 ). The relatively weak correlation between X and Y contrasted with the visibly strong causal linkage in the time series (Figure 1) and the weak scatter pattern in the controller–outcome space (Figure 2). Despite low covariance, conditional entropy analysis demonstrated a statistically significant reduction from H ( Y ∣ D ) = 4.121 bits to H ( Y ∣ D , X ) = 3.994 bits, yielding an information-preservation value of 0.127 bits (two-tailed bootstrap t-test: p < 0.001 ). This difference quantifies how knowledge of the controller decreases uncertainty in the controlled variable, even when their linear association remains small. Conditional entropy estimates remained consistent across bin resolutions, varying by less than five percent when partition sizes ranged from twenty to forty bins, confirming numerical stability. The combination of low correlation and significant entropy reduction confirms the occurrence of robust causal influence unaccompanied by proportional co-variation.
Preprints 184060 g001
Figure 1. Feedforward control with delayed cancellation keeps the controlled variable close to its setpoint despite pulse disturbances. The controller anticipates disturbances and applies counteracting action, yielding limited co-fluctuation between controller and outcome while visibly reducing the disturbance imprint on the trajectory of the controlled variable.
Figure 1. Feedforward control with delayed cancellation keeps the controlled variable close to its setpoint despite pulse disturbances. The controller anticipates disturbances and applies counteracting action, yielding limited co-fluctuation between controller and outcome while visibly reducing the disturbance imprint on the trajectory of the controlled variable.
Preprints 184060 g001
This quantitative distinction establishes the first empirical step linking dynamic regulation to informational causation, forming the analytical basis for further evaluation of temporal and directional effects.
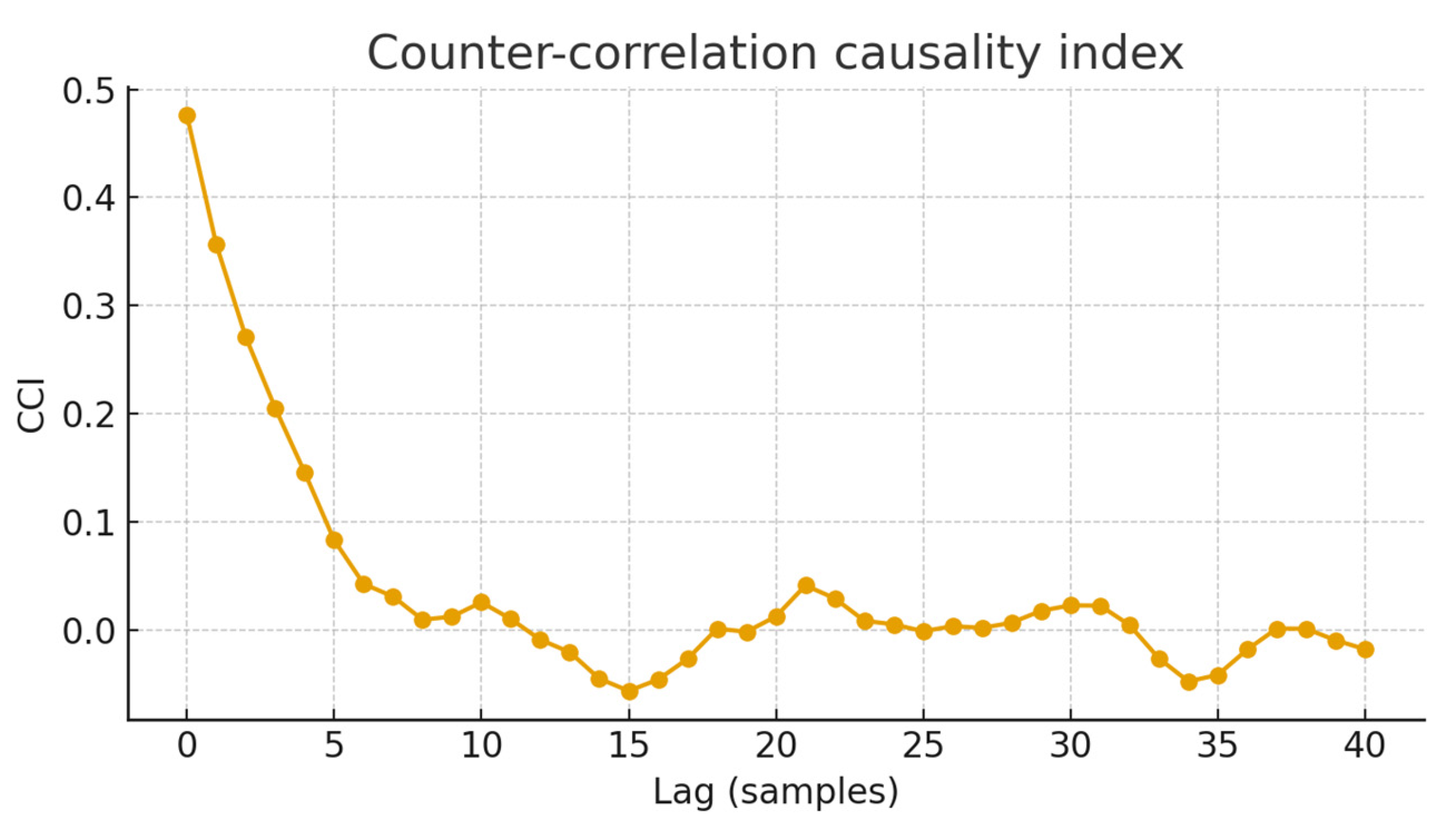
Information preservation, directional opposition and temporal analysis. The counter-correlation causality index, computed over lags from 0 to 40 samples, revealed a distinct positive peak near lag = 2, corresponding to the controller delay imposed in the model (Figure 3). The mean CCI across lags was 0.15 ± 0.03 , with the maximum value reaching 0.26 at the predicted delay. This indicates that increases in controller output preceded reductions in the rate of change of the controlled variable, signifying effective negative feedback despite contemporaneous correlation remaining near zero. A comparison with randomized null models, obtained by circularly shifting the controller sequence, produced information-preservation values centered around 0.01 ± 0.02 bits, significantly lower than the observed value ( p < 0.001 ). Variance suppression quantified by the closed- to open-loop ratio ρ v a r = 0.36 confirmed that the control mechanism reduced the dispersion of Y t by approximately 64%.
Preprints 184060 g002
Figure 2. Scatter of controller action against the controlled variable shows weak linear association despite a direct causal role of the controller in shaping outcomes. The vertical concentration around small controller values coexists with wide variability in the controlled variable due to exogenous pulses and noise. This suggests that causal influence can persist with low correlation.
Figure 2. Scatter of controller action against the controlled variable shows weak linear association despite a direct causal role of the controller in shaping outcomes. The vertical concentration around small controller values coexists with wide variability in the controlled variable due to exogenous pulses and noise. This suggests that causal influence can persist with low correlation.
Preprints 184060 g002
Preprints 184060 g003
Figure 3. The counter-correlation causality index captures predictive opposition between controller action and subsequent changes in the controlled variable. A positive peak at short lags indicates that increases in controller action precede decreases in the rate of change of the outcome, consistent with effective negative control even when simultaneous correlation is small.
Figure 3. The counter-correlation causality index captures predictive opposition between controller action and subsequent changes in the controlled variable. A positive peak at short lags indicates that increases in controller action precede decreases in the rate of change of the outcome, consistent with effective negative control even when simultaneous correlation is small.
Preprints 184060 g003
These convergent measures (variance reduction, entropy decrease and delayed anti-correlation) jointly describe the statistical signature of a non-faithful yet causally potent regulatory system. Together, they show that feedback and feedforward mechanisms effectively maintained stability while producing negligible instantaneous association between controller and controlled quantities.
Across all analyses, causation manifested through reduced conditional entropy and temporal opposition rather than through co-variation, substantiating our hypothesis of causation as informational preservation under disturbance. Our system maintained stable output variance while preserving 0.13 bits of information against disturbance. Correlations remained low, yet causation was statistically verified by entropy reduction and a lag-specific CCI peak, confirming that information preservation is a measurable property of stabilizing dynamics.

Conclusions

We showed that causation can be formally expressed as preservation of informational structure under disturbance, capturing a system’s capacity to sustain order amid fluctuations. Within this framework, causal influence is not inferred from co-variation but from a measurable reduction of uncertainty in the presence of noise. Across our feedback and feedforward simulations, a consistent pattern emerged: minimal or even absent correlation between controller and controlled variables, accompanied by decreases in conditional entropy and a lag-specific opposition between their temporal profiles. Powerful regulatory influences can exist even when no statistical dependence is observed, revealing a clear distinction between correlation and genuine causal effectiveness. Still, entropy analysis showed that knowledge of the controller’s state reliably reduced uncertainty in the controlled variable, while the counter-correlation index confirmed delayed negative feedback consistent with stabilizing control.
Together, these findings reveal causal mechanisms undetectable by conventional covariance-based approaches. Our findings define a distinct statistical signature of regulatory causation marked by low correlation, entropy reduction, lagged anti-correlation, noise resistance and structure preservation, i.e., features of either biological or physical systems that maintain internal stability through continuous compensation rather than co-fluctuation.
Conventional methods of causal inference depend on observable dependencies among variables. Regression estimates causal direction from slope coefficients under assumptions of independence, while Granger causality and transfer entropy extend this logic by evaluating how well one variable predicts another, either through temporal precedence or nonlinear information flow (Friston et al., 2014; Hacisuleyman and Erman, 2017; Cekic et al., 2018; Sobieraj and Setny, 2022; Shojaie and Fox, 2022; Guo et al., 2022; Wen et al., 2023). All these techniques presuppose that causation must appear as measurable variation. Yet systems governed by feedback or homeostatic control overturn this logic, since their essential function is to suppress fluctuations and maintain equilibrium, producing apparent statistical independence even when causal influence is very strong.
Our information-preservation framework departs from these approaches in two key respects: it quantifies entropy reduction rather than predictive flow and remains valid in the cyclic or closed-loop architectures that invalidate most existing methods. It directly measures how much uncertainty is removed from a disturbed system by a regulating variable, thus capturing stabilization rather than transmission. Stabilization is explicitly formalized as a measurable property, allowing causation to be assessed even in systems designed to suppress correlation. In contrast with Bayesian networks or structural equation models (Bollen and Noble, 2011; Stein et al., 2012; Mumford and Ramsey, 2014; Stein et al., 2017; Al-Kaabawi, et al., 2020; Kutschireiter et al., 2023; Wesner et al., 2023; Hammond and Smith, 2025; Hong and Kuruoglu, 2025), our framework imposes no requirement of acyclicity or independent residuals, allowing its application to systems dominated by mutual regulation and continuous feedback. The difference is therefore not incremental, but rather categorical: whereas conventional techniques equate causation with variation, our approach identifies causation with invariance, i.e., the capacity of a system to preserve stability under perturbation.
Our analyses are constrained by methodological and conceptual limitations. They rely on discretization of continuous variables for entropy estimation, introducing potential binning sensitivity and undersampling bias when data are limited. Although we tested robustness across multiple partition resolutions, finite-sample effects cannot be entirely excluded. Our model’s simplicity (scalar variables, Gaussian noise and linear control laws) is an idealization that may not fully capture the multidimensional, nonlinear or delayed feedback processes in natural systems. Furthermore, entropy estimation assumes stationarity and ergodicity, conditions that may be violated in evolving or adaptive systems. Simulation-based validation provides proof of concept, but not empirical verification in real-world biological or physical contexts. Computationally, conditional entropy estimation scales poorly with dimensionality, making direct application to high-dimensional datasets challenging without dimensionality reduction. Still, the statistical significance tests employed rely on surrogate-shift null models rather than on analytical distributions, which may underestimate the true variance of the estimators.
The recognition that persistence and equilibrium can serve as indicators of causal power could provide an analytical and methodological framework for uncovering hidden stabilizing influences within complex systems, moving beyond the narrow reach of correlation-based inference. Potential applications extend across biological regulation, neuroscience, ecological dynamics and engineered control systems, i.e., domains in which feedback mechanisms often conceal the underlying causal structure. In experimental physiology, our approach could quantify hormonal (e.g., insulin regulation of glucose) or neural control efficiency (e.g., inhibitory balance in neural circuits) by measuring entropy reduction rather than signal correlation. In ecology, it may help detect stabilizing species interactions (e.g., population stabilization in predator–prey systems) responsible for equilibrium dynamics that seem statistically independent. Further research could extend our model to multivariate or continuous entropy formulations, using kernel density estimators or Kraskov-based mutual information (Kraskov et al., 2004; Bramon et al., 2012; Péron 2019; Wang et al., 2023; Aoki and Fukasawa, 2024; Pang et al., 2025) to enable application to complex datasets like neural recordings or climate series.
We predict that systems under stronger regulatory control will display lower correlations but higher informational preservation values when perturbed. This could be empirically verified through controlled laboratory experiments that introduce graded disturbances and quantify conditional entropy changes. Future theoretical developments should explore analytical connections between information preservation and energetic efficiency, potentially relating causal stabilization to thermodynamic costs. When studying feedback-dominated systems, researchers could complement correlation-based analyses with entropy-preserving metrics to avoid underestimating causality. Incorporating these metrics into standard statistical pipelines could reveal hidden structures of control and compensation invisible under classical frameworks.
In conclusion, information preservation provides a reliable marker of causal structure even when covariance approaches zero. We proposed and validated a definition of causation grounded in a system’s capacity to maintain informational stability under disturbance, where causal influence is expressed as a measurable reduction of uncertainty independent of linear correlation. This approach redefines causality as resilience, revealing that stability, often mistaken for the absence of causal action, is in fact its most direct manifestation.

Ethics approval and consent to participate

This research does not contain any studies with human participants or animals performed by the Author.

Consent for publication

The Author transfers all copyright ownership, in the event the work is published. The undersigned author warrants that the article is original, does not infringe on any copyright or other proprietary right of any third part, is not under consideration by another journal and has not been previously published.

Availability of data and materials

All data and materials generated or analyzed during this study are included in the manuscript. The Author had full access to all the data in the study and took responsibility for the integrity of the data and the accuracy of the data analysis.

Competing interests

The Author does not have any known or potential conflict of interest including any financial, personal or other relationships with other people or organizations within three years of beginning the submitted work that could inappropriately influence or be perceived to influence their work.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial or not-for-profit sectors.

Acknowledgements

none.

Authors’ contributions

The Author performed: study concept and design, acquisition of data, analysis and interpretation of data, drafting of the manuscript, critical revision of the manuscript for important intellectual content, statistical analysis, obtained funding, administrative, technical and material support, study supervision.

Declaration of generative AI and AI-assisted technologies in the writing process

During the preparation of this work, the author used ChatGPT 4o to assist with data analysis and manuscript drafting and to improve spelling, grammar and general editing. After using this tool, the author reviewed and edited the content as needed, taking full responsibility for the content of the publication.

References

  1. Al-Kaabawi, Z.; Wei, Y.; Moyeed, R. Bayesian Hierarchical Models for Linear Networks. J. Appl. Stat. 2020, 49, 1421–1448. [Google Scholar] [CrossRef]
  2. Aoki, S.; Fukasawa, K. Kernel Density Estimation of Allele Frequency Including Undetected Alleles. PeerJ 2024, 12, e17248. [Google Scholar] [CrossRef] [PubMed]
  3. Bao, Q.; Chen, Y.; Bai, C.; Li, P.; Liu, K.; Li, Z.; Zhang, Z.; Wang, J.; Liu, C. Retrospective Motion Correction for Preclinical/Clinical Magnetic Resonance Imaging Based on a Conditional Generative Adversarial Network with Entropy Loss. NMR Biomed. 2022, 35, e4809. [Google Scholar] [CrossRef]
  4. Bollen, K.A.; Noble, M.D. Structural Equation Models and the Quantification of Behavior. Proc. Natl. Acad. Sci. 2011, 108, 15639–15646. [Google Scholar] [CrossRef]
  5. Borges, R.C.; Parreira, W.D.; Costa, M.H. Design Guidelines for Feedforward Cancellation of the Occlusion-Effect in Hearing Aids. Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society 2019, 607–610. [Google Scholar]
  6. Bramon, R.; Boada, I.; Bardera, A.; Rodriguez, J.; Feixas, M.; Puig, J.; Sbert, M. Multimodal Data Fusion Based on Mutual Information. IEEE Trans. Vis. Comput. Graph. 2012, 18, 1574–1587. [Google Scholar] [CrossRef]
  7. Cekic, S.; Grandjean, D.; Renaud, O. Time, Frequency, and Time-Varying Granger-Causality Measures in Neuroscience. Stat. Med. 2018, 37, 1910–1931. [Google Scholar] [CrossRef] [PubMed]
  8. Chadi, M.-A.; Mousannif, H.; Aamouche, A. Conditional Reduction of the Loss Value versus Reinforcement Learning for Biassing a De-Novo Drug Design Generator. J. Chem. 2022, 14, 65. [Google Scholar] [CrossRef]
  9. Chen, C.; Grabchak, M.; Stewart, A.; Zhang, J.; Zhang, Z. Normal Laws for Two Entropy Estimators on Infinite Alphabets. Entropy 2018, 20, 371. [Google Scholar] [CrossRef]
  10. De Gregorio, J.; Sánchez, D.; Toral, R. Entropy Estimators for Markovian Sequences: A Comparative Analysis. arXiv 2024, arXiv:2310.07547. [Google Scholar] [CrossRef]
  11. Dondelinger, F.; Mukherjee, S. Statistical Network Inference for Time-Varying Molecular Data with Dynamic Bayesian Networks. Methods in Molecular Biology 2019, 1883, 25–48. [Google Scholar] [CrossRef]
  12. Friston, K.J.; Bastos, A.M.; Oswal, A.; van Wijk, B.; Richter, C.; Litvak, V. Granger Causality Revisited. NeuroImage 2014, 101, 796–808. [Google Scholar] [CrossRef]
  13. Ochoa, H.O.G.; Perales, G.S.; Epstein, I.R.; Femat, R. Effects of Stochastic Time-Delayed Feedback on a Dynamical System Modeling a Chemical Oscillator. Phys. Rev. E 2018, 97, 052214. [Google Scholar] [CrossRef]
  14. Grinstead, J.; Ortiz-Ramírez, P.; Carreto-Guadarrama, X.; Arrieta-Zamudio, A.; Pratt, A.; Cantú-Sánchez, M.; Lefcheck, J.; Melamed, D. Piecewise Structural Equation Modeling of the Quantity Implicature in Child Language. Lang. Speech 2023, 66, 35–67. [Google Scholar] [CrossRef]
  15. Guo, Z.; McClelland, V.M.; Simeone, O.; Mills, K.R.; Cvetkovic, Z. Multiscale Wavelet Transfer Entropy with Application to Corticomuscular Coupling Analysis. IEEE Trans. Biomed. Eng. 2022, 69, 771–782. [Google Scholar] [CrossRef]
  16. Hacisuleyman, A.; Erman, B. Entropy Transfer between Residue Pairs and Allostery in Proteins: Quantifying Allosteric Communication in Ubiquitin. PLOS Comput. Biol. 2017, 13, e1005319. [Google Scholar] [CrossRef]
  17. Hammond, J.; Smith, V.A. Bayesian Networks for Network Inference in Biology. J. R. Soc. Interface 2025, 22, 20240893. [Google Scholar] [CrossRef]
  18. Hino, H.; Murata, N. A Conditional Entropy Minimization Criterion for Dimensionality Reduction and Multiple Kernel Learning. Neural Comput. 2010, 22, 2887–2923. [Google Scholar] [CrossRef] [PubMed]
  19. Hong, J.; Kuruoglu, E.E. Minimax Bayesian Neural Networks. Entropy 2025, 27, 340. [Google Scholar] [CrossRef] [PubMed]
  20. Hua, Z.-X.; Chao, Y.-X.; Jia, C.; Liang, X.-H.; Yue, Z.-P.; Tey, M. Feedforward Cancellation of High-Frequency Phase Noise in Frequency-Doubled Lasers. Opt. Express 2025, 33, 32518–32526. [Google Scholar] [CrossRef] [PubMed]
  21. Huang, P.-H. Postselection Inference in Structural Equation Modeling. Multivar. Behav. Res. 2020, 55, 344–360. [Google Scholar] [CrossRef] [PubMed]
  22. Ji, M.; Pan, K.; Zhang, X.; Pan, Q.; Dai, X.; Lyu, Y. Integration of Sense and Control for Uncertain Systems Based on Delayed Feedback Active Inference. Entropy 2024, 26, 990. [Google Scholar] [CrossRef]
  23. Kennaway, R. When Causation Does Not Imply Correlation: Robust Violations of the Faithfulness Axiom. In Causation, Correlation and Scientific Explanation; Symons, J., Sipetic, P., Eds.; Academic Press: Cambridge, MA, 2020; pp. 65–94. [Google Scholar] [CrossRef]
  24. Kold-Christensen, R.; Johannsen, M. Methylglyoxal Metabolism and Aging-Related Disease: Moving from Correlation toward Causation. Trends Endocrinol. Metab. 2020, 31, 81–92. [Google Scholar] [CrossRef]
  25. Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating Mutual Information. Phys. Rev. E Stat. Physics, Plasmas, Fluids, Relat. Interdiscip. Top. 2004, 69, 066138. [Google Scholar] [CrossRef]
  26. Kutschireiter, A.; Basnak, M.A.; Wilson, R.I.; Drugowitsch, J. Bayesian Inference in Ring Attractor Networks. Proc. Natl. Acad. Sci. 2023, 120. [Google Scholar] [CrossRef]
  27. Li, X.; Jacobucci, R. Regularized Structural Equation Modeling with Stability Selection. Psychol. Methods 2022, 27, 497–518. [Google Scholar] [CrossRef]
  28. Lim, W.W.; Leung, N.H.L.; Sullivan, S.G.; Tchetgen, E.J.T.; Cowling, B.J. Distinguishing Causation from Correlation in the Use of Correlates of Protection to Evaluate and Develop Influenza Vaccines. Am. J. Epidemiology 2020, 189, 185–192. [Google Scholar] [CrossRef]
  29. Lin, Y.; Chen, J.S.; Zhong, N.; Zhang, A.; Pan, H. A Bayesian Network Perspective on Neonatal Pneumonia in Pregnant Women with Diabetes Mellitus. BMC Med Res. Methodol. 2023, 23, 1–12. [Google Scholar] [CrossRef]
  30. Mumford, J.A.; Ramsey, J.D. Bayesian Networks for fMRI: A Primer. NeuroImage 2014, 86, 573–582. [Google Scholar] [CrossRef] [PubMed]
  31. Pang, Z.; Wang, W.; Zhang, H.; Qiao, L.; Liu, J.; Pan, Y.; Yang, K.; Liu, W. Mutual Information-Based Best Linear Unbiased Prediction for Enhanced Genomic Prediction Accuracy. J. Anim. Sci. 2025, 103. [Google Scholar] [CrossRef] [PubMed]
  32. Péron, G. Modified Home Range Kernel Density Estimators That Take Environmental Interactions into Account. Mov. Ecol. 2019, 7, 16. [Google Scholar] [CrossRef] [PubMed]
  33. Roy, B.; Marshall, R.S. New Insight in Causal Pathways Following Subcortical Stroke: From Correlation to Causation. Neurology 2023, 100, 271–272. [Google Scholar] [CrossRef] [PubMed]
  34. Schmidt, E. A.; Maarek, O.; Despres, J.; Verdier, M.; Risser, L. ICP: From Correlation to Causation. Acta Neurochirurgica Supplement 2018, 126, 167–171. [Google Scholar] [CrossRef]
  35. Shojaie, A.; Fox, E.B. Granger Causality: A Review and Recent Advances. Annu. Rev. Stat. Its Appl. 2022, 9, 289–319. [Google Scholar] [CrossRef]
  36. Sobieraj, M.; Setny, P. Granger Causality Analysis of Chignolin Folding. J. Chem. Theory Comput. 2022, 18, 1936–1944. [Google Scholar] [CrossRef] [PubMed]
  37. Stein, C.M.; Morris, N.J.; Hall, N.B.; Nock, N.L. Structural Equation Modeling. Methods in Molecular Biology 2017, 1666, 557–580. [Google Scholar] [CrossRef]
  38. Stein, C.M.; Morris, N.J.; Nock, N.L. Structural Equation Modeling. Methods in Molecular Biology 2012, 850, 495–512. [Google Scholar] [CrossRef]
  39. Tangkaratt, V.; Xie, N.; Sugiyama, M. Conditional Density Estimation with Dimensionality Reduction via Squared-Loss Conditional Entropy Minimization. Neural Comput. 2015, 27, 228–254. [Google Scholar] [CrossRef]
  40. Truesdell, A.G.; Jayasuriya, S.; Vallabhajosyula, S. Association, Causation, and Correlation. Cardiovasc. Revascularization Med. 2021, 31, 76–77. [Google Scholar] [CrossRef]
  41. Wang, Y.; Ding, Y.; Shahrampour, S. TAKDE: Temporal Adaptive Kernel Density Estimator for Real-Time Dynamic Density Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13831–13843. [Google Scholar] [CrossRef]
  42. Wen, X.; Liang, Z.; Wang, J.; Wei, C.; Li, X. Kendall Transfer Entropy: A Novel Measure for Estimating Information Transfer in Complex Systems. J. Neural Eng. 2023, 20, 046010. [Google Scholar] [CrossRef]
  43. Wesner, E.; Pavuluri, A.; Norwood, E.; Schmidt, B.; Bernat, E. Evaluating Competing Models of Distress Tolerance via Structural Equation Modeling. J. Psychiatr. Res. 2023, 162, 95–102. [Google Scholar] [CrossRef] [PubMed]
  44. Zheng, Y.; Zhang, H.-T.; Yue, Z.; Wang, J. Sparse Bayesian Learning for Switching Network Identification. IEEE Trans. Cybern. 2024, 54, 7642–7655. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated