CALM: Continual Associative Learning Model via Sparse Distributed Memory

1. Introduction

Modern large language models (LLMs) with transformer architecture revolutionized natural language understanding and generation. However, transformers lack persistent memory, continual learning capabilities, and are vulnerable to catastrophic forgetting. The reason for this is the encoding of information through dense vector spaces and positional embeddings. While powerful for static inference, they lack inherent memory and must be retrained or fine-tuned to learn new data. This situation led to the exploration of additional methods to integrate an online learning capabilities and dynamic memory processing to transformers. Since generalization and reasoning are possible only via stored associations, memory is interpretable as a substrate of intelligence. If comparisons to biological brains are used, transformers act as neocortex for reasoning. This is System 2 which needs time and energy and learns slowly to extract structured knowledge. It operates with quick and associative System 1 - functions driven by cortical ensemble of hippocampus, amygdala and basal ganglia.

Transformers apply a non-declarative (implicit) memory logic via probabilistic reconstructions although their behavior simulates declarative knowledge. An actual declarative (explicit) memory is formed from semantic memories (facts) and episodic memories (experiences and events) [1]. Although Retrieval-Augmented Generation (RAG) has been used as a complementary retriever, its lack of internalization does not satisfy declarative representation, which involves acquisition, consolidation (also online), and long-term retrieval. Episodic memory as a sub-component follows a similar workflow by involving encoding (acquisition), consolidation (storage), and recall (retrieval).

Explorations for declarative augmentation via episodic memory incorporated the study of Kanerva’s Sparse Distributed Memory (SDM) framework based on high-dimensional, associative, and distributed memory principles. Kanerva’s framework in 1988 [2] established SDM as both a model of human long-term memory and a practical associative memory system. SDM represents data in high-dimensional binary spaces where memory is spread across many storage locations instead of localization. Addresses are compared via Hamming distance, and memory retrieval uses weighted averaging from nearby locations. This approach yields robustness to noise and partial input [2,3].

These principles directly motivate SDM’s sparse binary representation and distributed storage mechanisms. The Continual Associative Learning Model (CALM) framework is introduced to fill the gap in the integration of lifelong learning in AI applications. Integrating SDM and a transformer was seen as an opportunity to explore online learning with associative memory in various application spaces. This hybrid network merges SDM module (System 1) that is always online with pair of asynchronous lightweight transformer modules for serving and training (System 2). The serving transformer is active (wake) and replaced periodically by forked shadow transformer performing training and consolidation of information. The research goals were set as follows:

• Establish evaluation system to configure optimal parameters for SDM devices
• Validate the behavior of SDM by computational tests from SDM benchmark
• Define and validate preliminary the hybrid architecture containing SDM module (System 1) and dual-transformer module (System 2)

2. Related Work

Subsequent research has developed sophisticated algorithms for high-dimensional pattern storage and retrieval [4,5]. Subsequent research in 1989 established practical parameters for memory operations [6]. The study of the foundations of SDM reveals how biological neural circuits inspired novel computational approaches, enabling modern applications such as a continual learning, neuromorphic computing, and artificial intelligence (AI) systems. The biological inspiration came from cerebellar cortex models by Marr and Albus, where the cerebellum was proposed as an associative learning device through sparsely distributed neural computations [7,8].

The fundamental difference between transformer and SDM representations lies in their vector encoding. Transformers typically operate on dense floating-point vectors (e.g., 768 or 1024 dimensions in BERT/GPT), requiring substantial compute for each token [9]. A dense floating-point vector may look like the following:

[0.12, -0.89, 1.4, 0.03, -0.55, 0.6, 0.0, 1.2]

In contrast, SDM leverages sparse binary vectors, often of size $n=1000$ or more, where each bit is either 0 or 1. These high-dimensional binary vectors facilitate associative recall by proximity (Hamming distance) without the need for exact matches or matrix multiplications. Interference is handled by multiple patterns stored at overlapping locations that form associative links. This characteristic allows memory access in $\mathcal{O}\left(1\right)$ time per hard location, significantly reducing the computational load for memory access while providing theoretical capacity that can scale exponentially with dimension for sparse patterns. A sparse binary vector may look like the following:

[0,0,0,1,0,0,1,0,0,0,0,0,0,0,0,1,0,0,0,0,...] (3/512 bits active)

The sparsity enables efficient bitwise operations and dramatically reduces memory requirements for embedded systems. Episodic memory could be achievable as an inherent feature for observer objects such as sensors and IoT devices. Characteristics of SDM highlight the efficiency required from the System 1 running initialization of explicit memory. The correspondence to cerebellar provides the primary neural inspiration with anatomical mappings from mossy fibers to address inputs, in addition to granule cells to hard locations and parallel fibers to distributed storage connections, and Purkinje cells to output neurons [7,10]. This biological architecture exhibits sparse activation patterns (only small percentages of granule cells active simultaneously) and massive parallelism enabling fast computation, as well as distributed storage with graceful degradation [11,12].

The sparse coding principles of widespread neuroscience research have influenced the SDM development. SDM has been extended through cortical coding models mapping mini- and macro-columnar structures [13] and recent continual-learning implementations [12]. Human hippocampus studies by Rutishauser et al. (2014) found direct evidence for sparse distributed coding in episodic memory, with only small percentages of neurons in hippocampus responding to any given memory target. Each neuron contributes to representations of only a few memories, providing “the most efficient way for neurons in hippocampus to encode episodic memories rapidly. [14]”. Cortical column theories have demonstrated connections between SDM principles and cortical organization through research by Rinkus (2010) showing macrocolumns functioning as sparse distributed coding fields. Minicolumns ( 20 L2/3 pyramidal cells) act as winner-take-all competitive modules enforcing sparseness, with sparse distributed codes consisting of 70 active L2/3 cells from much larger populations [13].

Since then, neuromorphic hardware implementations have achieved remarkable success on the SpiNNaker platform, with Steve Furber’s lab incorporating N-of-M rank codes into SDM variants for biologically plausible implementation [15,16,17]. The SpiNNaker2 chip (2024) supports 153 ARM cores with 19MB on-chip SRAM, dedicated ML and neuromorphic accelerators, and 10x increase in neural simulation capacity per watt [18,19]. Recent work demonstrates the first neuromorphic language model using Event-based Gated Recurrent Units (EGRU), achieving LSTM-equivalent performance with significant energy advantages [20]. In another study, XNOR-Net [21] demonstrated the practical advantages of binary representations, achieving 32× memory savings through binary weight approximations and 58× speedup in convolutional operations by using primarily bitwise operations rather than high-precision floating-point arithmetic. These binary approximations enable state-of-the-art deep networks to run on CPUs in real-time rather than requiring GPU acceleration, making them suitable for portable devices with limited computational resources. The success of XNOR-Net validates the fundamental principle underlying SDM that sparse binary representations can maintain accuracy while providing substantial computational and memory advantages over dense floating-point approaches. Achieved efficiency enables SDM to complement transformer models with declarative memory, but also provides a specialized method to deploy lightweight edge AI with episodic memory capabilities.

Continual learning breakthroughs emerged with Bricken et al.’s 2023 [12] work demonstrating that “Sparse Distributed Memory is a Continual Learner.” This modified Multi-Layered Perceptron exhibits strong continual learning capabilities without catastrophic forgetting, translating biological neural circuit principles into artificial networks [12]. The approach achieves continual learning performance comparable to biological systems through sparse activation patterns and biologically-inspired connectivity. In another study of Compressive Sensing SDM (CS-SDM) by Vdovychenko and Tulchinsky [22] integrated a compressive sensing theory with SDM to address classical limitations. This GPU-based implementation uses compressive sensing principles to achieve significantly better capacity and denoising capabilities compared to classical designs, particularly for semantic storage with enhanced noise tolerance [22,23]. In-memory computing implementations reported in Nature Electronics (2020) achieved breakthrough performance using 760,000 phase-change memory devices that perform analog in-memory computing. These systems demonstrate software-equivalent accuracy for language classification, news classification, and hand gesture recognition while providing massive parallel processing with a significant reduction in data movement and energy consumption [4].

Recent work in continual learning has explored Elastic Weight Consolidation (EWC) [24] and replay-based methods [25]. However, these approaches are based on retraining or storing of past data. In contrast, SDM allows for continual learning without parameter adjustment, supporting modular, fault-tolerant memory access.

The biological foundations established several key principles: metabolic efficiency through sparse coding, fault tolerance via the distributed storage, scalability through high-dimensional spaces allowing virtually unlimited memory capacity, computational speed through parallel processing, and generalization through similar representations for similar inputs supporting learning transfer.

Furthermore, sparse coding in neuroscience is related to biological neural networks that should exhibit sparse activation patterns. Only a few percent of neurons are simultaneously active in cortical areas [26,27,28]. Sparse codes maximize information capacity and energy efficiency [29,30]. Lateral inhibition mechanisms maintain sparsity constraints [29,31]. Population vector decoding enables robust pattern completion [32,33]

3. Materials and Methods

The primary objectives of this study are (1) to characterize the computational dynamics of SDM through the SDMPreMark benchmark, (2) to define a verifiable continual learning loop integrating SDM and transformers, and (3) to establish empirical baselines for System 1 (associative) and System 2 (reasoning) integration. The methodological approach contains five sections. The first section establishes evaluation methodology for SDM operations, according existing literature. The second section establishes SDM benchmark system, which converts SDM evaluation system to algorithmic system running as a computer program to measure SDM capabilities for different devices, aiding with parameter calibration. The third section involves mapping system for System 1 to explore feature integrations from existing biological mechanisms. The fourth section introduces CALM architecture that embeds calibrated SDM module to dual-transformer module. The fifth section studies validation of CALM integration logic.

3.1. SDM Evaluation Methodology

Unlike von Neumann architectures, SDM implements content-addressable memory based on Hamming distance and distributed storage. This section summarizes the key mathematical operations; full derivations follow Kanerva’s original formulation [2,11]. Hamming distance is defined as $H(x,y)$ and is used for SDM addressing for binary vectors $x,y\in {\{0,1\}}^n$; in bipolar form $x,y\in {\{-1,+1\}}^n$, this is simplified, as shown in Equation (1):

$$H(x,y)=\sum _{i=1}^n|x_i-y_i|=\sum _{i=1}^n(x_i\oplus y_i)\to H(x,y)={\displaystyle \frac{n-x·y}{2}}$$

(1)

where n is the vector dimensionality. Memory locations are activated when $H(A_m,x)\le r$, or equivalently $A_m·x\ge n-2r$. Write operation is implemented by storing each pattern $\mathbf{w}$ in all active locations within radius r:

$$\mathbf{C}:=\mathbf{C}+\mathbf{y}\otimes \mathbf{w},$$

(2)

where $\mathbf{y}$ is a binary activation mask ($y_m=1$ if $H(A_m,x)\le r$). Weighted writes use distance-dependent gains $\alpha \left(H\right)$ that decrease with radius. Read operation retrieves aggregates of all active counters and applies thresholding:

$$\mathbf{z}=\mathrm{sign}\left({\mathbf{C}}^T\mathbf{y}\right),$$

(3)

which reconstructs stored patterns even from incomplete inputs. Retrieval fidelity depends on the signal-to-noise ratio $\rho$ and the resulting bit accuracy $\varphi$, given by:

$$\rho ={\displaystyle \frac{\mu }{\sigma }},\mu =pM,{\sigma }^2\approx pM[1+pT(1+p^{2}M)],\varphi \approx \Phi \left(\rho \right)$$

(4)

where p is the activation probability of a memory location, M is the number of hard locations, T is the number of stored patterns, $\mu$ and ${\sigma }^2$ are the signal and noise components respectively, and $\Phi$ denotes the standard normal cumulative distribution function (CDF). Access radius is solved by the probability of activating a location p and its optimal value, following Kanerva’s rule:

$$p^{*}={\left(2MT\right)}^{-1/3},r\approx 0.4n,$$

(5)

where M is the number of hard locations and T the number of stored patterns. The radius controls the trade-off between generalization and interference. The Address generation uses uniform random N-bit addresses stored in matrix [16,34]:

$$\mathbf{A}\in {\{-1,+1\}}^{M\times N}$$

(6)

with each row representing one hard location’s address in random or structured address matrix. Jaeckel’s Selected-Coordinate Design optimizes this through sparse address matrices with $k\approx 10$ non-zero coordinates per address and activation condition:

$${\mathbf{A}}_m·\mathbf{x}=k$$

(7)

which provide exact match on selected coordinates. The use of Hyperplane applies k ones per hard address for skewed data distributions. Weighted retrieval applies similarity-based weighting functions such as

$$w_i\left(Q\right)=exp(-\alpha H(A_i,Q)),\mathrm{for}H(A_i,Q)\le r$$

(8)

and yield smooth recall probabilities:

$$P_{\mathrm{retrieval}}\left(\mathrm{BER}\right)=\sum _{k=0}^r\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\mathrm{BER}}^k{(1-\mathrm{BER})}^{n-k}$$

(9)

where $w_i\left(Q\right)$ is the weight assigned to location i for query Q, $H(A_i,Q)$ denotes the Hamming distance between the query and memory address $A_i$, r is the access radius that defines the activation threshold, and $\alpha$ is a decay coefficient controlling distance sensitivity. In the recall probability expression, n is the dimensionality of the binary vector space, k indexes the number of bit errors, and BER (bit-error rate) defines the fraction of corrupted bits in the query relative to the stored address. Further methods involve location activity probability $P_{activate}$ and expected number of activated locations $E\left[K\right]$ (Equation (10)):

$$P_{activate}=P(H({\mathbf{a}}_i,\mathbf{p})\le r)={\displaystyle \frac{{\sum }_{k=0}^r\left(\genfrac{}{}{0pt}{}{d}{k}\right)}{2^d}},E\left[K\right]=m·P_{activate}$$

(10)

where $H({\mathbf{a}}_i,\mathbf{p})$ is the Hamming distance between address ${\mathbf{a}}_i$ and probe $\mathbf{p}$, m is the total number of memory locations, d is the vector dimensionality, r is the access radius, and k is the summation index over bit differences. Interference coefficient $\gamma$ (patterns per location) and quality degradation due to interference $Q\left(\gamma \right)$ are defined as (Equation (11)):

$$\gamma ={\displaystyle \frac{N_{total}}{E\left[K\right]}},Q\left(\gamma \right)={\displaystyle \frac{1}{1+\beta {\gamma }^2}}$$

(11)

where $N_{total}$ is the sum of all patterns, $\beta$ is the interference sensitivity constant that determines how strongly overlapping pattern storage affects recall quality. Higher $\beta$ values correspond to higher sensitivity and faster degradation of the retrieval accuracy as $\gamma$ increases. Shannon-type capacity bound $C_{Shannon}$ defines the theoretical upper bound on SDM storage capacity per dimension for interference-free storage while empirical capacity $C_{empirical}$ measures actual storage efficiency and capacity to store unique patters per location before domination of recall errors (Equation (12)):

$$C_{Shannon}={\displaystyle \frac{2^d·{\sum }_{k=0}^r\left(\genfrac{}{}{0pt}{}{d}{k}\right)}{m·d}},C_{empirical}={\displaystyle \frac{N_{succ}}{m}}$$

(12)

where $N_{succ}$ measures successfully stored patterns. Having established the theoretical foundations for SDM evaluation, next section proceeds to examine how evaluation methodology is converted to benchmark design for real-life performance tests.

3.2. SDM Benchmark Design

LLM benchmarks assume continuous token embeddings, cosine similarity and dot products on continuous vectors, gradient-based learning with continuous optimization, and probabilistic next-token prediction. The combination of memory architecture in terms of address space (learned embeddings versus random binary addresses), storage (parameter matrices vs hard locations with binary counters) and retrieval (attention mechanisms vs Hamming distance-based associative recall) create distinct challenges to apply LLM benchmarks on SDM-based processes.

This study focused on implementing SDMPreMark as the first configuration phase to discover optimal parameters for different processing capabilities. It provides device-specific analysis to evaluate and optimize selection of suitable SDM configuration combinations, fingerprinting optimal parameter combinations (vector_dim, num_locations, access_radius, reinforce, match_ratio) across different hardware environments. This benchmark framework tests 1470 unique configurations, exploring the trade-offs between memory capacity, retrieval accuracy, and computational efficiency. Key parameter ranges include parameter-sweep coverage of vector dimension, memory locations, access radius factor, and reinforcement cycles. The parameters are listed in Table 1.

Vector dimension impacts memory footprint and computational complexity. Larger dimensions establish more precise representations but require proportionally more resources. Access radius is calculated as $r=max(1,\lfloor d\times \alpha \rfloor )$ where d is vector dimension and $\alpha$ is the radius factor, controlling the specificity-generalization issues in pattern matching. Memory locations determines storage capacity and potential interference patterns, where higher counts provide greater capacity at the cost of increased search complexity. Reinforcement cycles control pattern strengthening, with more cycles improving storage reliability but increasing training overhead.

The benchmark generates key performance indicators including match ratio (retrieval accuracy ranging 0-1), execution duration (computational efficiency in seconds), and sparsity ratio (input pattern density). Additional metrics capture input pattern characteristics (ones count), recalled pattern fidelity (recalled ones count), and derived measures such as the radius factor for systematic analysis. These metrics enable comprehensive evaluation of configuration performance across accuracy, efficiency, and pattern handling dimensions. The benchmark aims to identify parameter combinations that achieve high retrieval accuracy with minimal computational overhead for specific hardware environments.

Further optimization of SDM could involve a benchmark for evaluating episodic memory capacity, pattern completion accuracy, and interference resistance in long-context scenarios using binary distributed representations. Another benchmark design could be used for assessing temporal reasoning capabilities through binary vector binding/unbinding operations and chronological sequence reconstruction in high-dimensional space.

3.3. System 1 Methodology

According to Kahneman [35], System 1 in biological context involves plethora of mapped mechanisms applied for fast thinking. The most prevalent of those is associative activation, the core feature of SDM method. SDM also achieves stereotyping as category vectors naturally serve as prototypes via pattern matching. SDM also integrates mechanisms for availability heuristic as retrieval probability scales with memory frequency and recency. Similarity-based recall functions provides classification by resemblance and prototype matching, emerging as representativeness heuristic. Since SDM limit local view, it models partial-context reasoning, resembling the mechanism of “What You See Is All There is” (WYSIATI).

Questions were raised as to whether other mechanisms could be beneficial and implementable for CALM. The easiest mechanisms for integration were estimated to be substitution, anchoring, cognitive ease, halo effect, and framing effect.

Substitution simplifies difficult questions and favors intuition. Its use in the SDM framework adds fallback mechanism under uncertainty with incomplete data. Substitution requires addition of heuristic controller to fall back to nearest simpler query under high uncertainty. Risk of oversimplification (confident answers) is apparent, and therefore the mechanism should be used as probabilistic feedback to be triggered only in low confidence levels, marked as heuristic inference.

Anchoring provides stability and context persistence across iterative queries, and prevents erratic jumps in associative recall. Anchoring could operate by maintaining an initial retrieval with decay per distance or time. The risk of path fixation may occur during early states, requiring controller decay by using System 2 to reset anchor periodically.

Cognitive ease in SDM is the confidence estimator which signals for internal coherence by fast retrieval and low-conflict responses. Retrieval fluency drives confidence signal for cognitive ease. The overrating of effortless associations may ignore deeper associations. Consequently, this mechanism should be used to weight certainty estimates only, and not for logical validity or decision rule.

Halo effect (influence of overall impression to generalize positively all traits) may be used to propagate affective coherence such as consistent emotional stance or tone across related memory clusters. In practice, this could manifest as empathy, narrative consistency, and user alignment. This mechanism applies spread valence to nearby vectors for tone propagation. The risk of halo effect is the spread of undesired bias to overly positive or negative framing. Therefore, it should be applied only locally and allow the decay over distance. An additional module may be required to neutralize overgeneralization.

For stylistic purposes, framing effect can bring more sensitivity to linguistic context, helping the system to detect user framing adapt tone based on keyword frames. Acting as a stylistic modulation for the encoder, it could provide an additional record of framing tags separate from factual memory.

Mechanisms deemed not worth of feature integration include confirmation bias, the law of small numbers, and overconfidence. Confirmation bias is problematic due to its rejection of new or contradictory data, introducing riks of rigidity and echo-chamber effect. These are not interpreted as desirable features for adaptive, learning model. A law of small numbers (generalization based on small sample sizes) is neither desirable behavior; it may however manifest itself at the degree when adaptive memory radius is tuned. Likewise, overconfidence can occur during natural manifestation of SDM parameters. Consequently, these methods act more as emergent lag indicators of underlying SDM parameters, instead of driving mechanisms for memory processing.

Additionally, while intensity matching, affect heuristic, and causal thinking were estimated to be not integrated to System 1, although applicable when integrated with System 2. Intensity matching would enable along reasoning about degree and magnitude to form analogues, emotional scales and prioritization, but requires scalar extensions to binary SDM. Affect heuristic is critical for motivational steering, empathy, and adaptivity, but is difficult to ground safely without human-level affection. Furthermore, although causal thinking with predictive reasoning is useful for planning and behavior modeling, its implementation requires temporal reasoning beyond SDM module.

Mechanisms of System 1 in the context of SDM are represented in four categories: inherent, intuitive, emergent, and causal. Mirroring cognitive architectures, the inherent module act as reflexive neural wiring; the intuitive module applies heuristic reasoning; the emergent module displays adaptive biases; and the causal module is reflective cognition with abstractions (System 2 interface). This also clarifies evolutionary design priorities:

• Establish inherent System 1 mechanisms
• Integrate intuitive System 1 mechanisms
• Implement controller to detect emergent System 1 mechanisms
• Integrate System 2 dual transformers to System 1 (SDM and controller)

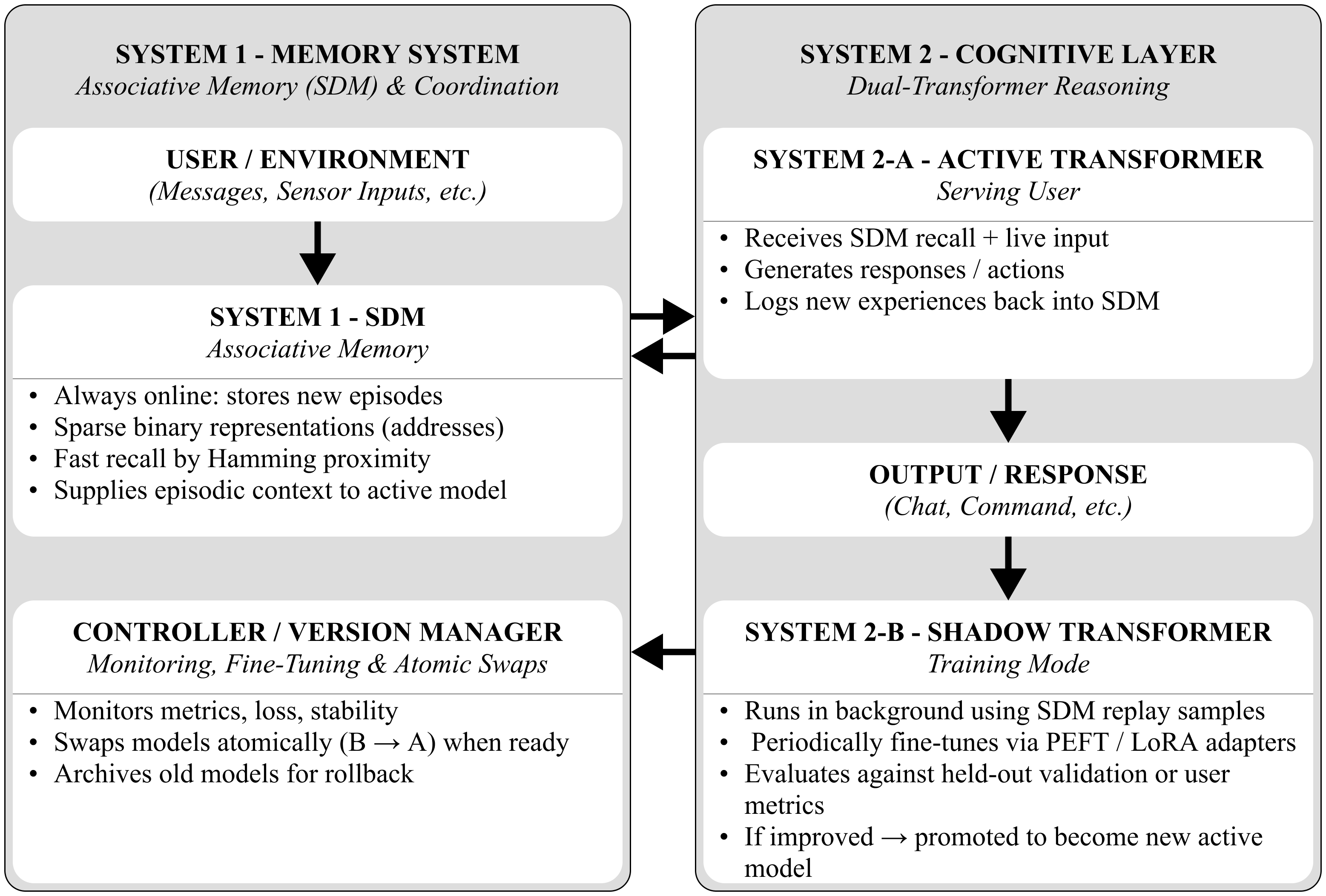
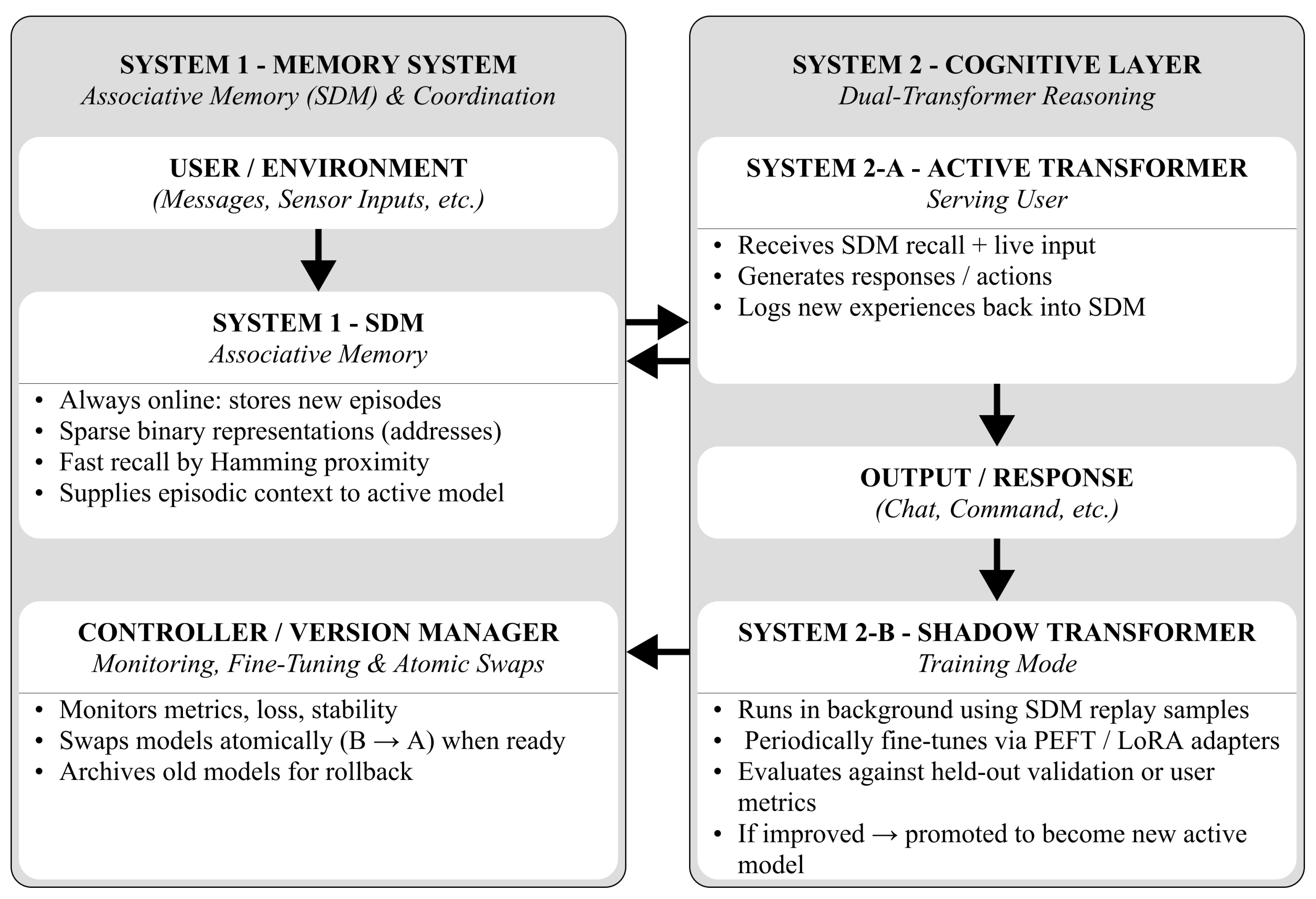
3.4. CALM Architecture

Building on limitations of conventional transformer systems and the continual learning capabilities of Sparse Distributed Memory (SDM), the proposed CALM framework integrates a dual-system architecture inspired by cognitive processes (Figure 1). This hybrid design was motivated by three key goals:

• Continual Adaptation: SDM is allowing rapid incorporation of new data without retraining.
• Memory Grounding: The system maintains an episodic trace of events, enabling structured recall and System 1 operations.
• Biological Plausibility: The modular memory structure aligns with the distributed intelligence of the cortical columns and sensorimotor integration.

System 1 encapsulates online associative memory (SDM), storing new experiences as sparse binary vectors, and providing rapid associative recall via Hamming proximity. It also provides episodic context for active models. System 2 comprises an Active Transformer (System 2-A) serving user interactions and a Shadow Transformer (System 2-B) training asynchronously using SDM replay samples and fine-tuning adapters (PEFT/LoRA). The shadow model replaces the active one atomically, when validated improvement occurs. The controller and version manager monitor metrics, stability, and loss, but also manage swaps and archives model versions for rollback or analysis.The model operates in three concurrent processes:

• Encoding & Acquisition: New input is encoded as high-dimensional binary vectors and stored in SDM.
• Retrieval & Reasoning: SDM provides associative recall to the Active Transformer, which generates responses and updates memory into the SDM.
• Consolidation: The Shadow Transformer fine-tunes asynchronously on SDM replay data, ensuring gradual learning without disrupting live performance.

This architecture enables continual adaptation, episodic recall, and stable long-term reasoning—bridging the gap between static transformer inference and dynamic memory-based cognition. Internally, CALM’s distributed SDM implementation mirrors cortical organization through modular associative units analogous to cortical columns. In local learning, each SDM module independently encodes local sensory or contextual input, enabling online adaptation without global retraining. The use of reference frames are implemented via spatial and temporal patterns that are represented as high-dimensional binary vectors, preserving relative relationships across inputs. Voting mechanism uses overlapping modules collaborating through similarity-based activation to resolve ambiguous or noisy inputs. Higher-level SDM layers integrate outputs from lower layers to form increasingly abstract episodic representations, representing hierarchical integration.

Transformer-to-binary encoding serves as a bridge between dense transformer embeddings and sparse SDM representations. Floating-point vectors are constrained by threshold to produce binary encoding, ensuring compatibility between systems while preserving semantic content:

$${\mathbf{v}}_{dense}=\mathrm{BERT}\left(\mathrm{tokenize}\left(s\right)\right)\in {\mathbb{R}}^{d_{model}}$$

(13)

$$b_i=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{v}_i>\theta \hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(14)

Here, BERT denotes a bidirectional transformer encoder that maps a tokenized input sequence s into a dense embedding space of dimensionality $d_{model}$. The vector ${\mathbf{v}}_{dense}$ represents the continuous embedding output of the transformer, $b_i$ is the i-th bit of the resulting binary vector after thresholding, and $\theta$ is the activation threshold controlling sparsity. Alternative mapping schemes such as locality-sensitive hashing (LSH) or learned quantization may be applied to balance sparsity and information retention.

The SDM maintains a fixed set of hard memory locations uniformly distributed in high-dimensional space. Stored patterns activate subsets of these locations within a Hamming radius r. Fixed locations simplify hardware access, though future work may explore dynamic expansion for scalability. An example of SDM association storage between high-dimensional addresses and their corresponding data is demonstrated in (Table 2).

Memory retrieval operates by computing Hamming distances between query and stored addresses and aggregating all locations within a threshold. SDM tolerates noisy or partial inputs through distributed representation and weighted recall, recovering nearest stored patterns even under corruption (Equation (15)).

$$\mathrm{BER}={\displaystyle \frac{\mathrm{corrupted}\text{\_}\mathrm{bits}}{d}},P_{retrieval}\left(\mathrm{BER}\right)=\sum _{k=0}^r\left({\displaystyle \genfrac{}{}{0pt}{}{d}{k}}\right){\mathrm{BER}}^k{(1-\mathrm{BER})}^{d-k}.$$

(15)

where d denotes the dimensionality of the binary address vectors, r is the Hamming distance threshold (access radius), and k indexes the number of bit errors tolerated during retrieval. $P_{retrieval}$ thus expresses the probability of successful recall under a Bernoulli noise model with bit error rate BER.

SDM tolerates noisy or partial inputs due to its distributed representation and weighted retrieval. For instance, a corrupted binary query averages activations over nearby locations, recovering the closest stored pattern. This contrasts with transformers that degrade under corrupted inputs unless retrained. Experimental results demonstrate this behavior (Section 4).

The CALM architecture unites the reasoning power of transformers with the continual memory and robustness of SDM. System 1 provides online associative learning and recall, while System 2 performs symbolic reasoning and long-term consolidation through dual transformer models. This design supports continual adaptation, structured episodic recall, and biologically plausible memory dynamics. Architectural trade-offs for the design are summarized in Table 3.

This hybrid approach is particularly suited for systems operating in dynamic or noisy environments, such as embedded agents and real-time anomaly detection tasks, where continual learning and long-term memory stability are critical.

In the following section, the experimental setup is defined for its use to validate this architecture, including integration with embedded sensors and benchmarks against conventional transformer models.

3.5. CALM Integration

The CALM framework integrates Sparse Distributed Memory (System 1) with dual-transformer reasoning modules (System 2-A and 2-B) to enable continual, online adaptation. While the SDMPreMark benchmark empirically validates the stability and efficiency of the System 1 memory substrate, the overall CALM architecture must also demonstrate provable capability for lifelong continual learning by satisfying three conditions. (1) Theoretical Sufficiency. The CALM architecture satisfies the three canonical operations required for continual learning:

$$\mathcal{E}\left(x_t\right)\stackrel{\mathrm{encode}}{\to }\mathrm{SDM},\mathcal{R}\left(C_t\right)\stackrel{\mathrm{recall}}{\to }\mathrm{Transformer},\mathcal{U}\left({\widehat{x}}_t\right)\stackrel{\mathrm{consolidate}}{\to }\mathrm{SDM}$$

(16)

where $\mathcal{E}$ denotes episodic encoding, $\mathcal{R}$ associative retrieval providing contextual recall to the active transformer, and $\mathcal{U}$ consolidation of newly generated representations back into memory. Together, these three transformations form a closed-loop continual learning cycle:

$${(\mathrm{Encode}\to \mathrm{Recall}\to \mathrm{Consolidate})}_t\Rightarrow {\left(\mathrm{Adaptive}\mathrm{Memory}\mathrm{Update}\right)}_{t+1}$$

This cycle ensures that every interaction (user input, environmental stimulus, or transformer output) is internalized into SDM and available for subsequent reasoning.

(2) Empirical Plausibility. Results from the SDMPreMark benchmark establish a deterministic critical radius threshold ($r\approx 0.4$–$0.6$ of vector dimensionality) defining stable associative recall. Above this threshold, SDM recall becomes error-free (match_ratio = 1.0) across all tested dimensions, satisfying the stability condition required for consistent transformer context generation. This empirical property guarantees that the memory subsystem feeding the reasoning layers operates deterministically and noise-tolerantly.

(3) Provability Condition. Functional provability of CALM is defined through measurable improvement of the active transformer following SDM-based consolidation. Given the shadow transformer $B_t$ trained asynchronously on replay samples ${\mathcal{M}}_{t-r:t}$ from SDM memory, promotion to active model $A_{t+1}$ occurs when:

$$\Delta {\mathcal{L}}_t=\mathcal{L}\left(A_t\right)-\mathcal{L}\left(B_t\right)>ϵ$$

(17)

where $\mathcal{L}$ is a task-specific loss (e.g., validation loss, accuracy, or user metric) and $ϵ$ is a minimal improvement threshold. This measurable criterion provides a falsifiable condition for continual learning: each update cycle must yield a quantifiable improvement in the active model’s performance without external retraining [24].

(4) Verification Roadmap. The provability of CALM can be established through a progressive evaluation sequence. At first, SDMPreMark benchmark confirms associative stability and computational efficiency (System 1 validation). Next verification component, CALMark benchmark measures $\Delta \mathcal{L}$ before and after atomic model swaps to verify memory-driven consolidation (System-2 validation). Third verification component involves continual reasoning tests employing long-term retention and adaptation benchmarks (e.g., GLUE, SQuAD) to validate stability over time. Verification roadmap is categorized in Table 4.

4. Preliminary Results

The SDMPreMark benchmark was executed as a controlled in silico experiment to map parameter sensitivities in high-dimensional associative memory operations. Each configuration was deterministically evaluated via the the sdm memory test routine, providing reproducible metrics (match ratio, sparsity ratio, runtime). Although these experiments do not involve learned datasets, they qualify as algorithmic characterization of SDM dynamics.

Critical Radius Threshold Behavior: The most striking finding is the existence of a sharp performance threshold around radius factor 0.2 (corresponding to access radius values of 6, 12, 25, 51, 102, 204, 307, 399, 460, 614, 798, and 921 for vector dimensions 32, 64, 128, 256, 512, and 1024 respectively). This transition corresponds to the empirical critical radius function $r_{critical}$ (Equation (5)) and performance transition function $P_{success}$ (Equation (10)), presented together in Equation (18).

$$r_{critical}\left(d\right)=\left\{\begin{array}{cc}0.375d,\hfill & \mathrm{if}d\le 64\hfill \\ 0.40d,\hfill & \mathrm{if}64<d\le 256\hfill \\ 0.60d,\hfill & \mathrm{if}d>256\hfill \end{array}\right.,P_{success}(r,d)=\left\{\begin{array}{cc}0.4-0.6,\hfill & \mathrm{if}r<r_{critical}\left(d\right)\hfill \\ 1.0,\hfill & \mathrm{if}r\ge r_{critical}\left(d\right)\hfill \end{array}\right.$$

(18)

Below this threshold, match ratios consistently remain under 0.7, while configurations at or above radius factor 0.2 achieve perfect recall (match_ratio = 1.0) across most parameter combinations. This threshold represents a fundamental transition point where the SDM system shifts from under-activation to reliable pattern retrieval.

Vector Dimension Scaling: Performance remains remarkably stable across vector dimensions from 32 to 1024 bits once the critical radius threshold is exceeded. Lower dimensions (32-128) show slightly more variability in the sub-threshold region, while higher dimensions (512-1024) demonstrate more consistent behavior. Notably, the M1 Pro’s unified memory architecture appears to handle even the largest vector dimensions efficiently, with execution times scaling predictably rather than experiencing memory bottlenecks.

Computational Efficiency Patterns: Empirical latency model $T_{empirical}$ was derived from time complexity equations to extend theoretical latency scaling ). Execution duration scales linearly with both memory locations and reinforcement cycles ($R^2=0.98$). The relationship follows: $T\approx 0.07\times {\displaystyle \frac{\mathrm{locations}}{1000}}+0.03$ milliseconds. The binary nature of retrieval success patterns creates distinct operating regimes, as show in Table 5. Latency was calculated according to the empirical relation (Equation (19):

$$T_{empirical}(d,m)=0.07·{\displaystyle \frac{m}{1000}}+0.03\mathrm{ms},E_{bit}={\alpha }_{switching}·V_{dd}^2+{\beta }_{leakage}·V_{dd}$$

(19)

Configurations with 500-1000 memory locations complete in under 0.1 seconds for most parameter combinations, while 8000 locations require 1-5 seconds. The reinforcement cycle impact is particularly pronounced, with 100 cycles taking approximately 10x longer than single-cycle operations. This suggests that for the M1 Pro platform, configurations with 1000-3000 memory locations and 10-30 reinforcement cycles provide an optimal balance between capacity and responsiveness.

Optimal Radius Selection: To minimize retrieval errors, the optimal radius $r^{*}$ is obtained by balancing miss and interference probabilities: Equation (20) contains methods for optimal radius selection $r^{*}$ and miss probability $P_{miss}\left(r\right)$ (derived from Equation (10)).

$$r^{*}=arg\underset{r}{min}\left[\alpha ·P_{miss}\left(r\right)+\beta ·P_{interference}\left(r\right)\right],P_{miss}\left(r\right)=P{(}_{idle})={\left(1-{\displaystyle \frac{{\sum }_{k=0}^r\left(\genfrac{}{}{0pt}{}{d}{k}\right)}{2^d}}\right)}^m$$

(20)

Capacity: Following Equation (12), practical efficiency was calculated with capacity utilization factor ${\alpha }_{capacity}$ (Equation (21)). Increasing memory locations shows minimal effect on match ratio but significant impact on processing time (Table 6).

$${\alpha }_{capacity}={\displaystyle \frac{C_{empirical}}{C_{Shannon}}}\approx 0.3-0.7$$

(21)

The M1 Pro’s performance characteristics reveal that this platform favors moderate memory locations (1000-5000) with radius factors between 0.4-0.6 for optimal efficiency. Configurations exceeding these parameters show diminishing returns in accuracy, while significantly increasing computational overhead. These findings establish a clear device-specific configuration profile that prioritizes the M1 Pro’s strengths in parallel processing while respecting its thermal and power constraints.

Analytical Resource Constraints: To quantify the stability of associative recall under concurrent storage, the interference probability $P_{interference}$ (Equation (22)) was derived from the expected number of activated locations $E\left[K\right]$. This metric captures how overlapping address activations degrade recall fidelity as memory utilization increases.

$$P_{interference}\left(r\right)=1-exp\left(-{\displaystyle \frac{N·E\left[K\right]}{m}}\right)$$

(22)

Memory requirements $M_{total}$ and $M_{memory}$ (Equation (23)) were evaluated to estimate storage scalability (Equation (12):

$$M_{total}=m·(d_{addr}+d_{data}+{log}_2\left(N_{max}\right)),M_{memory}(d,m)=m·(d+p)$$

(23)

Equation (24) dictates processing power (operations per second) $P_{ops}$ and time complexities ($T_{write}$, $T_{read}$) according to Equation (1):

$$P_{ops}={\displaystyle \frac{f_{cpu}}{d·m}},T_{write}(d,m)=O(m·d)T_{read}(d,m,k)=O(m·d+k·logk)$$

(24)

These formulations were used only to validate scalability trends observed empirically and were not directly benchmarked on hardware.

5. Discussion and Future Work

The results demonstrate SDM’s viability for real-time applications while highlighting the critical importance of proper sparsity control in the encoding pipeline. Recommendations for deploying SDM-based AI for different hardware setups include three recommendations. Firstly, sparsity problem arises from 50% bit activation which is too dense for efficient SDM operation, requiring larger radii and reducing specificity. Sparse encoding should be therefore implemented to encode schemes targeting 2-5% sparsity instead of 50%. Secondly, sharp transition between failure and success suggests sensitivity to parameter tuning based on access radius, contradicting assumptions of gradual degradation. Critical radius seems to grow faster than linear with dimension, challenging traditional SDM assumptions Thus, achieving sufficient binary performance requires adaptive radius that can be achieved by dynamic radius adjustment based on vector dimension and content. Thirdly, capacity optimization for embedded deployment with 500-1000 locations provides optimal trade-off for latency-accuracy.

Successful deployment of the CALM model could allow AI agents, Internet-of-Things (IoT) devices and cognitive robotics the lifelong learning and memory-augmented decision-making with high energy efficiency. One promising direction for extending CALM involves applying its associative memory and continual-learning capabilities to collective decision-making systems. Recent work in civic intelligence and smart-city governance is suggesting that integrating blockchain and AI can enhance participatory processes through transparent data flows and adaptive governance models [36]. CALM or similar frameworks could serve as the cognitive substrate for such civic intelligence frameworks by enabling persistent, decentralized memory and reasoning across distributed agents. This would allow communities and institutions to develop continual learning infrastructures for governance.

Existing smart device assistants respond to isolated prompts. In contrast, continuity of purpose in CALM handles prompts as storage of declarative knowledge. Progress mirrors, contextual nudges, and surface memory associations could create a meta-cognitive AI assistant set to grow with user’s goals. A next step is to project persistent goals in digital societies toward realizing autonomous, self-evolving Virtual Cities (VCs) and its smart citizens, integrated into continual adaptive learning architectures. By introducing sparse distributed memory consolidation, online updating, and self-referential feedback loops, AI entities mirror their goals and cognitive models in real time from context providers. Within the context of VCs, quantifying autonomy levels in AI entities and agents is challenging as they should transcend from simple digital replicas of real-world systems, and then evolve gradually toward more complex mirroring in socio-technical ecosystems [37]. Building on continual associative architecture, future research could extend the framework into large-scale digital twin ecosystems representing adaptive VCs. Agents within a hypernetwork would possess local SDM and reasoning capabilities learning from real-world IoT data and interactions while sharing cognitive substrate between each other [38].

An open direction is to explore distributed polynomial-time SDM and AI updates via the block-wise memory allocation, which could resemble polynomial proof-of-memory mechanisms from blockchain theory [39]. This would allow decentralized and scalable lifelong learning in edge environments. The stake of resources proven in this context involves a scalar measure of cognitive bandwidth for verifiable memory traces. Participants in such a network could exchange verified experience blocks, where each block encapsulates episodic data, update metadata, and a cryptographic certificate of associative gain. This could allow decentralized agents to share verified cognitive resources instead of raw computation, establishing an economy of useful learning in which value is derived from validated memory formation and recall performance. The distributed SDM network introduces a new staking resource method for decentralized economics, which presents an alternative to existing resource methods such as computation resources or energy expenditure.

6. Conclusion

Sparse Distributed Memory offers a promising path toward more adaptive, efficient, and human-like AI systems. By embracing distributed, continual memory, and biologically inspired computation, interactions with AI can surpass the static nature of current models. Empirical analysis reveals a critical radius threshold ($r\approx 0.4$–$0.6$) that defines stable associative recall and demonstrates near-linear computational scaling. The SDMPreMark benchmark introduced provided an initial phase to codify the evaluation methodology, allowing the discovery of optimal parameters per host. This confirms the associative stability and computational efficiency required from System 1.

The architecture for a hybrid LLM scheme with episodic memory capacities was introduced, containing System 1 (SDM) and System 2-A/B (dual-transformers). An evolutionary design of System 1 was introduced to map feature clusters for further behavioral optimizations. The next step involves adding intuitive models to SDM, and integrating lightweight transformer pair and synchronization of operations with existing SDM modules applied in SDMPreMark. The final deployment also requires that emergent mechanisms are trackable and causal linkages between System 1 and System 2 are established. An additional benchmark is planned as the method to verify memory-driven consolidations before and after atomic models, along with continual reasoning tests (e.g, GLUE, SQuAD) to validate stability over time.

Although SDMPreMark provides a deterministic evaluation, the absence of semantic data benchmarks limits the generalization assessment. Future CALMark experiments will address this by incorporating transformer-driven semantic replay.

The implication of the main findings establishes a biologically grounded framework for lifelong AI learning that maintains compatibility with standard transformer benchmarks and adjusts to different device configurations.