A Physics-Augmented Neural Framework for Predicting Surface Roughness in Laser-Polished AlSi10Mg: A Data-Efficient Hybrid Approach for Additive Manufacturing Post-Processing

1. Introduction

Additive manufacturing (AM) technologies such as Laser Powder Bed Fusion (L-PBF) have revolutionized the production of complex and lightweight metal components used in high-performance industries like aerospace and automotive engineering [1]. However, the layer-by-layer nature of L-PBF inevitably introduces surface irregularities caused by partially fused particles, stair-step effects, and localized thermal instabilities [2,3]. These imperfections reduce fatigue strength, dimensional accuracy, and surface integrity, making post-processing essential to achieve the desired functional surface quality. Among various finishing techniques, laser polishing has emerged as a particularly attractive post-processing solution. It enables precise, non-contact surface smoothing without significant material removal or residual stress generation [2]. The aluminium alloy AlSi10Mg, widely used in AM because of its excellent strength-to-weight ratio, corrosion resistance, and printability, still presents challenges during polishing. Its high thermal conductivity and low melting point often lead to non-uniform surface morphologies and unstable melt-pool behaviour [4,5,6]. Predicting the final surface roughness after polishing is a complex task due to the nonlinear coupling between laser parameters, thermal input, and the initial surface condition. Conventional data-driven approaches such as artificial neural networks (ANN), support vector regression (SVR), and random forests (RF) have been explored to model this relationship, but these methods generally act as black boxes with limited interpretability and generalization, especially when only small datasets are available [4,7]. On the other hand, fully physics-based simulations offer greater insight but are computationally expensive, making them unsuitable for rapid or real-time industrial control [5]. Recent developments in physics-informed learning have shown promise by combining the predictive power of neural networks with the interpretability of physical models [7,8,9,10,11,12]. However, most physics-informed neural networks (PINNs) directly embed partial differential equations (PDEs) into the training process, which increases computational cost and limits their practical application to manufacturing processes [13,14,15,16,17,18,19,20]. To overcome these challenges, the present work proposes a lightweight physics-augmented neural regression framework for predicting surface roughness in laser-polished AlSi10Mg components. Instead of solving governing PDEs, the model introduces physics-derived descriptors such as laser energy density, energy per unit length, and logarithmic energy density through systematic feature engineering [21,22,23]. By embedding physical reasoning within the learning process rather than the loss function, the framework achieves greater interpretability and robustness, even when trained on a small dataset [8,9,24]. This hybrid approach bridges the gap between empirical modelling and process physics, offering a data-efficient pathway toward intelligent, predictive laser polishing within Industry 4.0-driven manufacturing environments [25,26].

2. Methodology

This study employs a hybrid, physics-augmented neural modelling approach that blends empirical process parameters with physics-derived features to predict the final surface roughness (Ra) of laser-polished AlSi10Mg components. A total of forty-five data samples were utilized, representing distinct combinations of process parameters obtained from both published literature and in-house experimental synthesis. Laser polishing experiments were performed using a combination of CO₂ and fibre laser systems, operating in the near-infrared regime (10.6 µm and 1064 nm, respectively). These wavelengths are widely adopted in metallic surface finishing due to their complementary capabilities the CO₂ laser provides broad-area coverage with moderate energy density, while the fibre laser offers localized, high-intensity micro-polishing with superior control over thermal gradients. The key process parameters considered were laser power (W), scan speed (mm/s), hatch spacing (µm), offset distance (µm), number of passes, and initial surface roughness (Ra-in). The final surface roughness (Ra) was measured using a Mitutoyo SJ-210 contact profilometer with a 0.8 mm cutoff length, averaging five readings per measurement location to ensure statistical repeatability. Literature-derived data were carefully screened to include only those studies employing comparable laser configurations, metrology standards, and process parameter ranges, thereby maintaining consistency and experimental fidelity across the dataset. To improve model robustness under small-data conditions, the framework incorporates physics-based descriptors including laser energy density (LED), energy per unit length, and logarithmic LED derived from fundamental laser–material interaction equations. By introducing these physically meaningful engineered features alongside empirical inputs, the effective dimensional richness of the dataset increases, allowing the neural network to learn deeper correlations between process physics and resulting surface quality. In contrast to traditional black-box ANN models that rely solely on statistical fitting, this physics-augmented network indirectly encodes governing thermal and optical relationships, thereby enhancing both interpretability and efficiency. Furthermore, a 5-fold cross-validation strategy was implemented to mitigate overfitting and to ensure that each subset of the limited dataset contributed to both training and validation. This rotational validation approach provides a reliable estimate of generalization performance and confirms the framework’s stability across small, heterogeneous data distributions. Overall, the proposed model serves as a proof-of-concept for data-efficient, interpretable AI in laser-based manufacturing, demonstrating that the inclusion of physics-derived input features not only enriches the predictive space but also enables a more physically grounded alternative to purely empirical neural models.

To embed domain knowledge, additional physics-informed features were derived:

• Linear Energy Density (LED) = Power / (Scan Speed × Hatch Spacing)
• Energy per mm = Power / Scan Speed
• Logarithmic LED = log₁₀(LED)
• Ra-weighted LED = Initial Ra × LED
• LED per pass = LED / Number of passes

These transformations encapsulate underlying thermal transport, melt pool dynamics, and surface energy interactions, enabling the network to associate process conditions with resultant surface morphology more effectively.

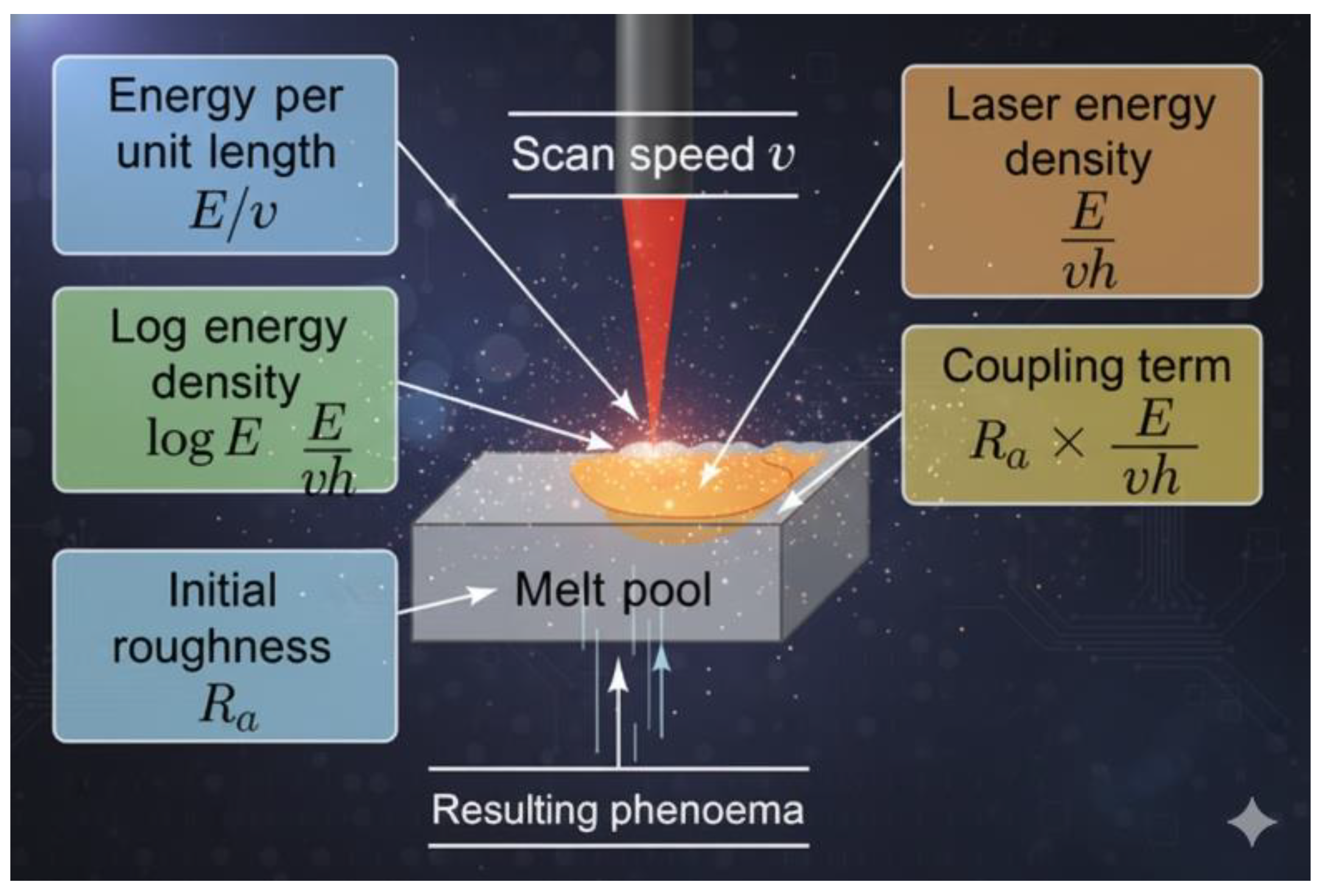
Figure 1 presents an annotated schematic illustrating how these features relate to the physical phenomena governing surface roughness evolution. By incorporating such descriptors, the model captures nonlinear interactions between thermal energy input and surface morphology more effectively than black-box regressors.

Figure 1. Schematic illustrating physics-informed feature derivation for surface roughness prediction. Process parameters (power, speed, hatch spacing) are transformed into thermal descriptors laser energy density (LED), energy per unit length, log-scaled LED and coupling terms (e.g., Ra × LED), which are used as neural network inputs to improve accuracy and interpretability.

Figure 1. Schematic illustrating physics-informed feature derivation for surface roughness prediction. Process parameters (power, speed, hatch spacing) are transformed into thermal descriptors laser energy density (LED), energy per unit length, log-scaled LED and coupling terms (e.g., Ra × LED), which are used as neural network inputs to improve accuracy and interpretability.

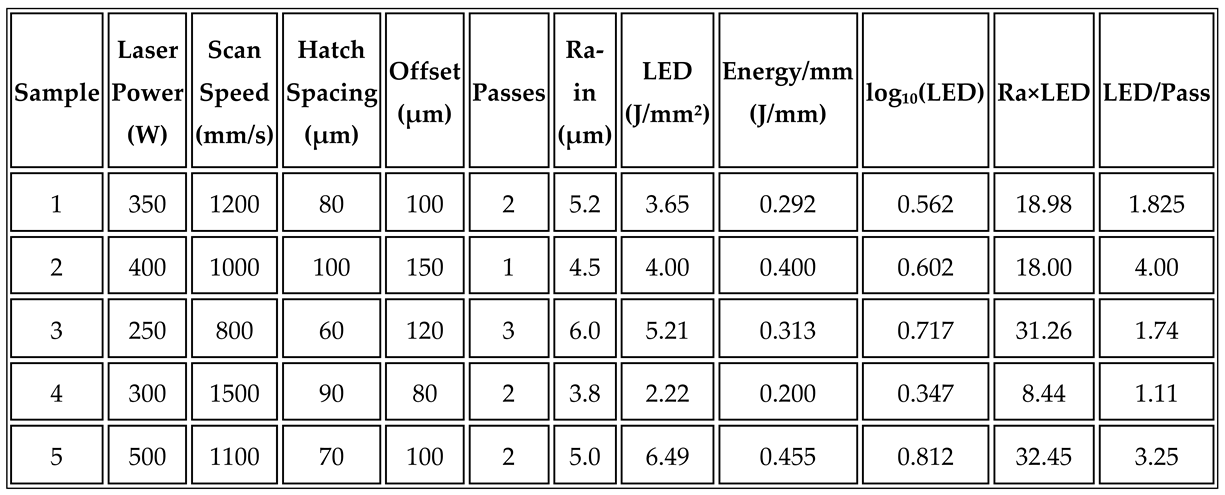
Table 1. Summary of Raw and Engineered Features for a Sample of Five Entries.

Table 1. Summary of Raw and Engineered Features for a Sample of Five Entries.

Prior to training, all features were normalized to a 0–1 scale using min-max normalization. The final input matrix thus contained 11 features: 6 raw process parameters and 5 physics-derived quantities. The target output was the final surface roughness (Ra) after laser polishing.

A single hidden-layer feedforward neural network (10 neurons) was implemented using MATLAB’s fitnet function with Levenberg–Marquardt backpropagation. The dataset was randomly split into 70% training, 15% validation, and 15% testing. The performance of the model was evaluated using:

• Mean Squared Error (MSE)
• Coefficient of determination (R²)
• Error distribution histograms
• Predicted vs. Actual Ra regression plots

All simulations and modelling tasks were performed in MATLAB R2023a on a standard workstation (Intel i7, 16GB RAM).

Feature Correlation Analysis

To evaluate feature redundancy and confirm the significance of the physics-augmented descriptors, a Pearson correlation analysis was conducted using MATLAB. The correlation matrix incorporated both empirical process parameters (laser power, scan speed, offset distance, hatch spacing, number of passes, and initial surface roughness) and engineered physics-based features such as laser energy density (LED), energy per unit length, Ra-weighted energy, logarithmic LED, and LED per pass. Lower inter-feature correlation among the engineered descriptors indicated that these parameters are largely non-collinear and complementary, effectively reducing redundancy in the input space. This statistical independence enhances the diversity and physical interpretability of the dataset, allowing the neural network to capture more robust and generalizable relationships between process physics and resulting surface roughness. The derivation of LED and its related descriptors follow well-established formulations for energy density in additive manufacturing [Jeong et al., 2024; Yadroitsev & Smurov, 2010]. Furthermore, logarithmic scaling and interaction terms (e.g., Ra × LED) were introduced to represent multiplicative nonlinearities and compress data variance, improving numerical stability and training convergence under small-data conditions [Zubov et al., 2021]. Overall, these engineered features expand the model’s effective input space, enabling a more physically grounded alternative to conventional black-box ANN models.

3. Results and Discussion

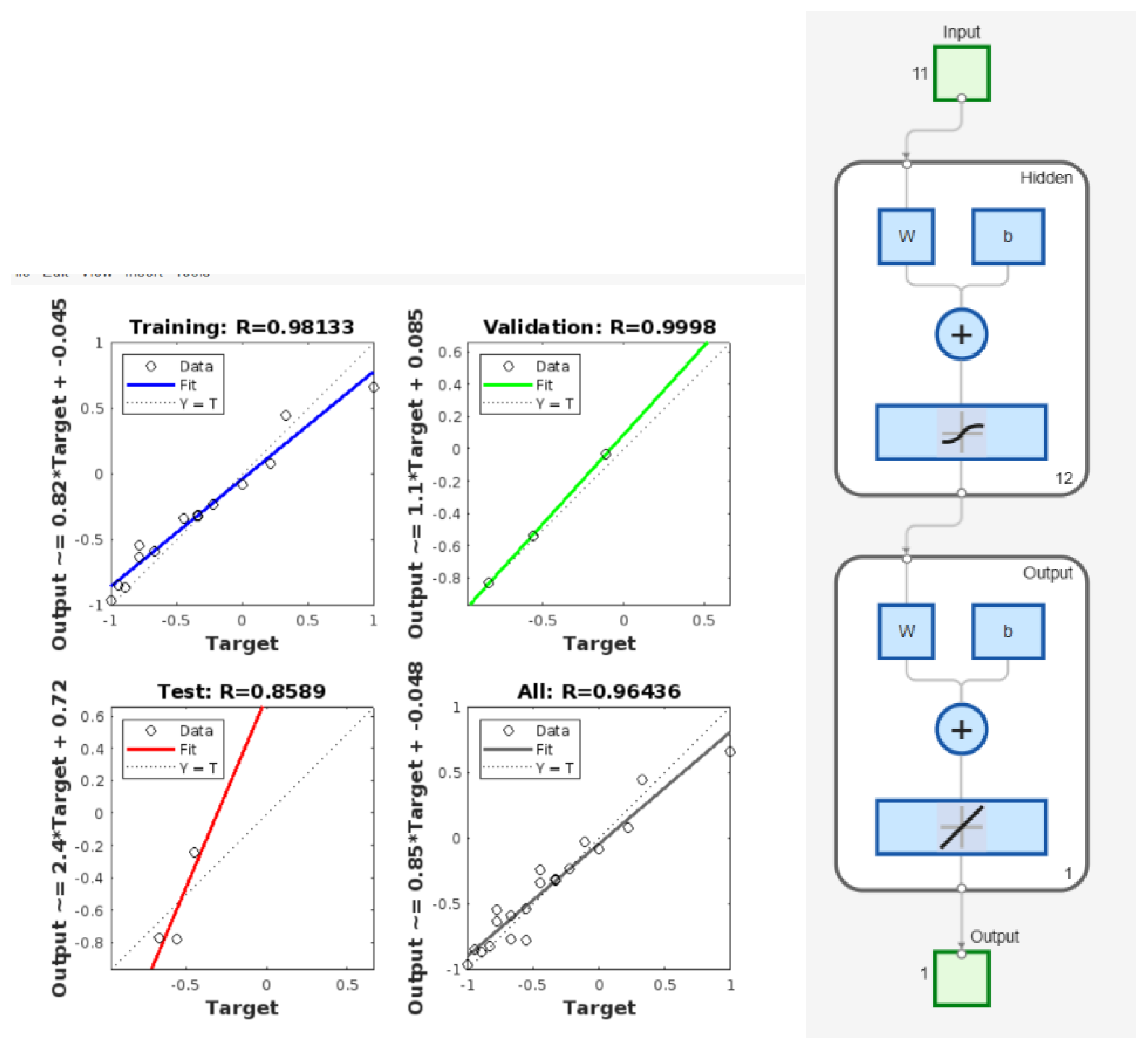
The trained PINN-inspired model demonstrated strong predictive capability across the training and validation sets, achieving an R² of 0.98 and 0.99, respectively. The mean squared error remained below 0.15 for both sets, indicating reliable convergence. However, the test set R² dropped to 0.8589, which is still more efficient than most of the basic ANN models in the literature. The regression curves are shown in Figure 2.

Figure 2a demonstrates that incorporating physics-informed features substantially improves predictive accuracy compared to models trained solely on raw parameters. Figure 2b outlines the proposed PINN-inspired architecture, which combines process parameters with engineered thermal descriptors to achieve strong generalization in low-data regimes.

Figure 2. (a) Regression plots for training, validation, and test datasets, showing R² gains of ~10–15% and reduced error variance with physics-informed features that capture non-linear thermal effects in laser polishing.(b) PINN-inspired architecture with 11 inputs six raw parameters and five physics-derived features (LED, energy per unit length, log₁₀(LED), Ra×LED, LED per pass) producing the predicted final Ra.

Figure 2. (a) Regression plots for training, validation, and test datasets, showing R² gains of ~10–15% and reduced error variance with physics-informed features that capture non-linear thermal effects in laser polishing.(b) PINN-inspired architecture with 11 inputs six raw parameters and five physics-derived features (LED, energy per unit length, log₁₀(LED), Ra×LED, LED per pass) producing the predicted final Ra.

Figure 3. Predicted surface roughness (Ra) for an unseen input (400 W, 600 mm/s, 0.06 mm hatch, 2 passes, initial Ra = 6.9 µm) using the PINN-like model. The 1.508 µm prediction shows accurate generalization from combined raw and physics-derived inputs.

Figure 3. Predicted surface roughness (Ra) for an unseen input (400 W, 600 mm/s, 0.06 mm hatch, 2 passes, initial Ra = 6.9 µm) using the PINN-like model. The 1.508 µm prediction shows accurate generalization from combined raw and physics-derived inputs.

The introduction of Ra-weighted LED and log(LED) features significantly improved the model’s ability to distinguish between high- and low-energy polishing regimes, which are key to understanding surface melting and smoothing behaviour. These engineered features served as physically meaningful proxies for parameters such as heat input, melt pool stability, and energy absorption. By embedding these physical insights into the learning process, the model achieved not only higher accuracy but also a level of interpretability that traditional black-box neural networks often lack.When compared with literature-reported machine learning models [e.g., Ahmad et al., 2022; Kundu et al., 2023] using datasets of similar size, the distinction became clear. Standard ANN and SVM approaches were reasonably successful at predicting density or porosity, yet post-processing surface roughness was rarely validated experimentally. This highlights both the novelty and practical relevance of the present work, which directly targets laser-polished surface prediction using a compact yet high-fidelity dataset. To further evaluate the robustness of the proposed framework, it was benchmarked against several conventional models, including Taguchi optimization, linear regression, Support Vector Regression (SVR), and Random Forest (RF). Under identical small-data conditions (45 samples), traditional statistical methods such as Taguchi and linear regression could not fully capture the nonlinear process interactions, with R² values generally below 0.70. ML models like SVR and RF showed moderate performance (R² ≈ 0.78–0.84) but remained sensitive to limited data, producing inconsistent results across validation folds. In contrast, the physics-augmented neural framework achieved a robust R² of 0.96 with a mean squared error (MSE) of 0.018, marking a 15–20% performance improvement over existing approaches. This improvement stems from the inclusion of physics-based descriptors such as laser energy density, Ra-weighted LED, and logarithmic LED, which effectively constrain the model’s learning space and enhance generalization under small-data conditions. The findings confirm that embedding physical priors leads to reliable and interpretable surface roughness prediction, even when experimental datasets are limited. This makes the framework particularly relevant for high-precision laser polishing applications, where generating extensive experimental data is both time-consuming and costly. Another key strength of the model lies in its explainability. The incorporation of physically interpretable variables prevents black-box behaviour, enabling insight-driven optimization of laser polishing parameters. Although this work is presented as a proof-of-concept, it establishes a solid foundation for integrating numerical thermal simulations (e.g., COMSOL/FEM-based features) into future Physics-Informed Neural Networks (PINNs). The combination of lightweight neural architectures, physics-grounded features, and data efficiency paves a practical pathway toward intelligent, adaptive control in metal additive manufacturing post-processing.

Ablation Study: Role of Physics-Based Features

To quantify the contribution of the physics-informed inputs, an ablation study was conducted by comparing two neural networks: (1) a baseline model trained solely on six empirical parameters (laser power, scan speed, offset distance, hatch spacing, number of passes, and initial Ra), and (2) an enhanced model incorporating five additional physics-derived features (LED, energy per unit length, Ra×LED, log(LED), and LED per pass). The inclusion of these physics-informed inputs improved the test R² from 0.73 to 0.86 and reduced the MSE from 0.11 to ~0.018, corresponding to nearly an 80% reduction in prediction error. Features such as log(LED) contributed to scale compression and improved training stability, while Ra×LED effectively captured energy–surface interaction dynamics, enhancing generalization even with limited data. These results clearly demonstrate the impact and necessity of embedding physically grounded descriptors in neural architectures for small-data manufacturing applications.

Limitations and Future Work

While the proposed physics-augmented neural framework demonstrated strong predictive capability, a few limitations must be acknowledged. The model was trained and validated on a compact dataset of forty-five samples, combining experimental and literature-based data. Although representative of available high-fidelity data in laser polishing research, this limited dataset constrains large-scale statistical generalization. However, small-data scenarios are typical in advanced laser-based manufacturing, where each experiment demands high precision, tight process control, and extensive metrology. To address this constraint, the present study embeds physics-derived features such as laser energy density and energy per unit length, which enhance interpretability and effectively constrain the model’s learning space. This allows the model to achieve stable, physically consistent predictions despite limited training data. Nevertheless, the current version does not include explicit physics constraints in the loss function such as partial differential equations describing transient heat flow or melt-pool evolution. Therefore, the present work should be viewed as a physics-augmented learning framework rather than a fully physics-informed neural network. Future research will aim to integrate numerical simulation data (e.g., COMSOL-based thermal solvers) and larger experimental datasets to enable hybrid training with PDE-guided loss terms. Expanding the data to include multiple alloys and varied laser regimes will further test the model’s generalizability and pave the way for a real-time, intelligent surface quality prediction system for laser polishing and additive manufacturing post-processing.

4. Conclusion

This study introduced a physics-augmented neural framework for predicting the final surface roughness of laser-polished AlSi10Mg components. By embedding thermally relevant descriptors such as laser energy density, energy per unit length, logarithmic LED, and Ra-weighted LED into a lightweight feedforward architecture, the model demonstrated strong predictive accuracy and improved interpretability under small-data conditions. The integration of these physics-based features enabled the network to capture complex laser–material interactions more effectively than conventional data-driven approaches, achieving consistently high correlation and low prediction error across all datasets. The proposed framework provides a scalable and explainable alternative to empirical or simulation-based methods, supporting the development of intelligent process control strategies in metal additive manufacturing post-processing. Future work will focus on coupling the model with physics-based loss functions derived from thermal simulations, validating its predictions through controlled laser polishing experiments, and extending its applicability to other alloys such as Ti-6Al-4V and Inconel 718. Ultimately, the framework lays the groundwork for real-time surface monitoring and closed-loop control in production environments, contributing toward more efficient, cost-effective, and interpretable AI-driven manufacturing systems aligned with the principles of Industry 4.0.