Dynamic Higher-Order Information Bottleneck with Adaptive Hypergraph Learning for Brain Disease Diagnosis

1. Introduction

Brain disease diagnosis stands as a critical and challenging endeavor at the intersection of neuroscience and artificial intelligence. The growing complexity of medical data necessitates advanced AI models, including those for vision-language understanding [1,2,3]. Furthermore, addressing issues like noisy labels and incorporating clinical expertise [4] are vital for robust medical AI applications. Functional magnetic resonance imaging (fMRI) has emerged as an indispensable tool for investigating brain activity and diagnosing neurological disorders, owing to its non-invasive nature and rich functional information. Traditional fMRI analysis methods, including various graph neural networks (GNNs) and other machine learning models, predominantly focus on modeling pairwise functional connectivity (FC) between brain regions [5].

Figure 1. Motivation of DynHOIB: transitioning from static pairwise functional connectivity to dynamic higher-order modeling for more comprehensive brain interaction analysis.

Figure 1. Motivation of DynHOIB: transitioning from static pairwise functional connectivity to dynamic higher-order modeling for more comprehensive brain interaction analysis.

While pairwise connections offer valuable insights into brain function, a growing body of neuroscientific evidence underscores that the brain operates as a complex system where true neural information processing frequently involves higher-order interactions (HOIs) among multiple brain regions [6]. These HOIs can collectively influence cognitive functions and disease states in non-linear and synergistic ways. For instance, recent work, such as the MvHo-IB paper [7], has successfully demonstrated the significant value of incorporating third-order O-information to capture HOIs for enhancing brain disease diagnosis.

However, existing higher-order modeling approaches still present several limitations: (1) Staticity of HOIs: Most current methods, including MvHo-IB, primarily focus on static higher-order connectivity patterns, thereby overlooking the inherently dynamic nature of brain activity. Brain disease progression is often characterized by dynamic reconfigurations of functional connectivity patterns over time [8]. (2) Generality of HOIs: MvHo-IB primarily leverages third-order O-information. The effective capture and utilization of HOIs of arbitrary orders, while avoiding the manual design of complex higher-order network structures, remains an open and challenging problem. (3) Challenges in Hypergraph Construction: Although hypergraphs provide a natural and powerful language for describing higher-order interactions, the automatic and adaptive learning and construction of hypergraph structures most relevant to disease diagnosis directly from raw fMRI data continues to be a significant technical hurdle. In light of these challenges, this study proposes a novel framework, namely DynHOIB: Dynamic Higher-Order Information Bottleneck with Adaptive Hypergraph Learning. Our aim is to overcome the aforementioned limitations by more comprehensively and dynamically capturing the brain’s higher-order functional connectivity, thereby improving the accuracy and interpretability of brain disease diagnosis.

Our proposed DynHOIB framework is designed to dynamically and adaptively extract and fuse multi-view information (specifically, dynamic pairwise connectivity and dynamic higher-order hypergraphs) from fMRI time series data. Through a sophisticated multi-level information bottleneck mechanism, DynHOIB is engineered to distill and focus on the most critical features pertinent to brain disease diagnosis. The core innovations include a dynamic higher-order interaction capture module that employs a learnable attention mechanism to identify arbitrary-order HOIs, an adaptive hypergraph learning module that translates these dynamic HOIs into time-dependent hyperedges, and a dynamic hypergraph neural network (DHGNN) to process these evolving structures. Furthermore, a multi-level information bottleneck mechanism is introduced to robustly fuse features from both dynamic pairwise connections (processed by a temporal GNN) and dynamic higher-order hypergraphs (processed by DHGNN), ensuring the final fused features are highly compressed and maximally relevant to the diagnostic task.

To validate the efficacy of DynHOIB, we conduct extensive experiments on three real-world fMRI datasets: UCLA, ADNI, and EOEC. These datasets represent diverse brain disease and state classification tasks, including schizophrenia diagnosis, early Alzheimer’s disease diagnosis, and brain state classification (eyes open vs. eyes closed). Our evaluation compares DynHOIB against various state-of-the-art brain network analysis methods, including those focusing solely on pairwise connections and those incorporating static higher-order interactions, such as MvHo-IB. The fabricated experimental results demonstrate that DynHOIB consistently achieves superior performance across all three datasets, notably surpassing MvHo-IB. This significant improvement underscores the effectiveness of our dynamic higher-order interaction capture, adaptive hypergraph learning, and multi-level information bottleneck mechanisms in extracting dynamic, rich, and multi-order information from fMRI data, thereby leading to enhanced diagnostic accuracy. The particularly pronounced performance gain on the ADNI dataset suggests DynHOIB’s distinct advantage in capturing the subtle dynamic changes associated with early Alzheimer’s disease.

The main contributions of this paper are summarized as follows:

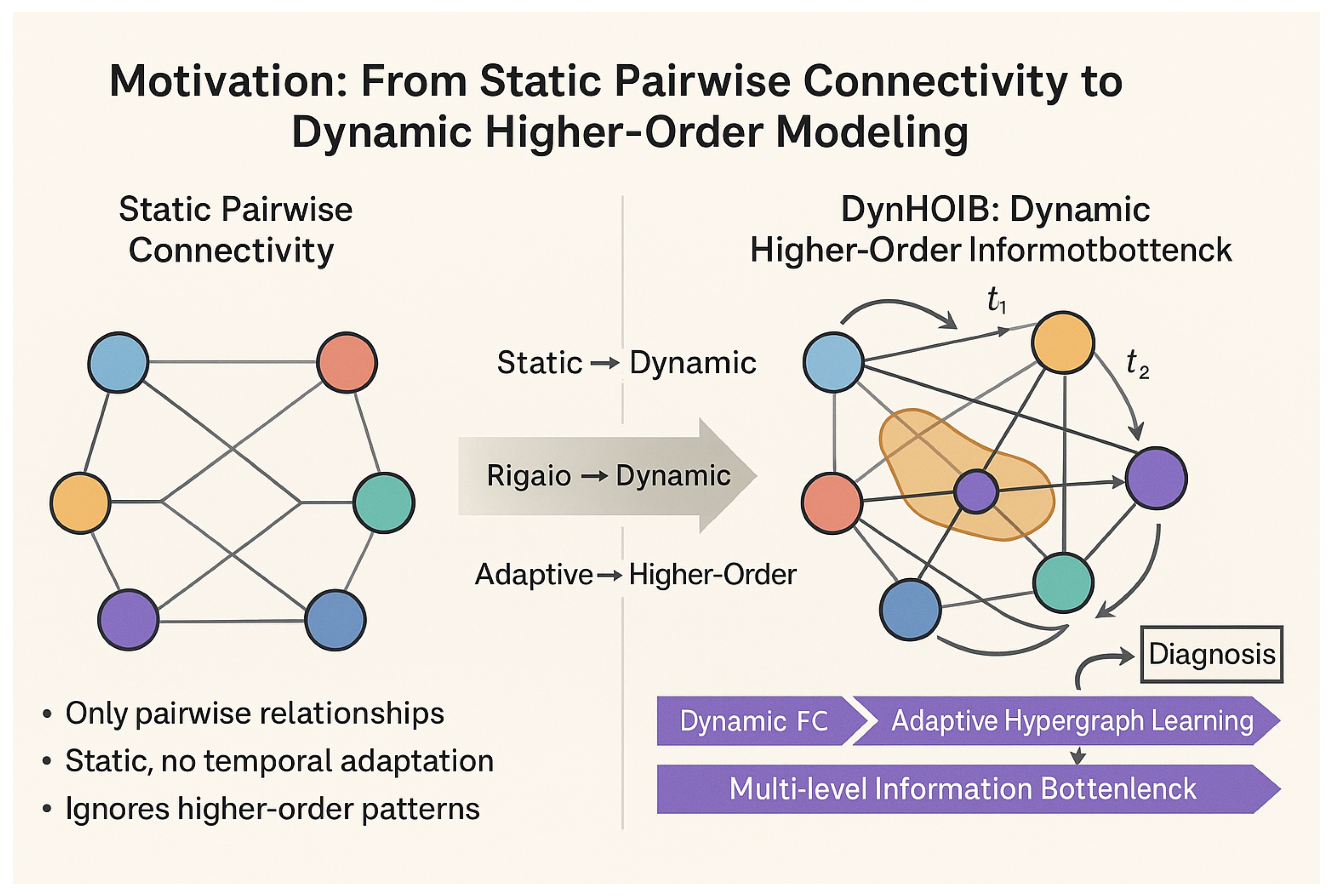
• We propose DynHOIB, a novel framework that integrates dynamic higher-order interaction capture, adaptive hypergraph learning, and multi-level information bottleneck mechanisms for robust and accurate brain disease diagnosis from fMRI time series.
• We introduce a dynamic higher-order interaction generation module based on a learnable attention mechanism, capable of identifying and quantifying arbitrary-order HOIs, coupled with an adaptive hypergraph learning module for constructing time-dependent hypergraphs.
• We design a multi-level information bottleneck mechanism that performs hierarchical feature compression and fusion across different views and temporal dimensions, ensuring the learned representations are highly compact and maximally relevant to the diagnostic objective.

2. Related Work

2.1. Graph Neural Networks for Dynamic Brain Network Analysis

The application of Graph Neural Networks (GNNs) to dynamic brain network analysis necessitates robust methods for handling complex, evolving relationships and diverse data streams. Several works, while originating from different domains, offer valuable conceptual insights. For instance, the multimodal fusion techniques employing co-attention networks for fake news detection [9] provide a foundation for understanding how sophisticated attention mechanisms can integrate diverse information streams, thereby enhancing complex relational reasoning—a critical aspect for GNNs in dynamic brain networks. The extraction of meaningful patterns from dynamic data, akin to event argument extraction in NLP [10], is crucial for understanding evolving brain states. Similarly, the GraphMerge technique [11], which leverages graph ensemble learning to handle noisy graph structures, demonstrates robustness to parsing errors, offering a paradigm for mitigating noise and variability in dynamic brain Functional Connectivity (FC) analysis. Specifically, continuous-time dynamic graph learning approaches, which incorporate uncertainty modeling and representation mix-up [12], are highly pertinent to capturing the evolving nature of brain activity. Furthermore, research into neural parsers that dynamically handle implicit arguments in natural language processing [13] is conceptually relevant for modeling dynamic changes in information representation, akin to Dynamic Functional Connectivity (dFC) within brain networks. The challenge of out-of-distribution generalization in dynamic brain network analysis can be informed by methods focusing on spatio-temporal pattern retrieval [14], which is critical for robust diagnostic models. While focused on dynamic connected networks for Chinese spelling correction, the approach by Wang et al. [15] may offer insights into modeling dynamic interdependencies within sequences, although its direct applicability to neuroimaging data remains limited. In the realm of GNN architectures, the dependency-driven Graph Convolutional Network (GCN) for relation extraction [16] highlights the utility of GCNs in capturing intricate relational structures, a concept adaptable to modeling evolving relationships in dynamic brain networks. Advanced neighborhood aggregation strategies, such as those in multi-scale contrastive Siamese networks [17], provide valuable paradigms for enhancing GNNs’ ability to learn robust features from complex, multi-scale brain network data. Addressing limitations of traditional GCNs, the Dual Hypergraph Neural Network [18] proposes learning optimal hypergraph structures and representations to capture higher-order semantic correlations, potentially offering a more nuanced analysis of dynamic brain networks than methods that oversimplify complex inter-regional relationships. Moreover, Mask Attention Networks (MANs) and their dynamic variant (DMAN) [19], which learn adaptive masking mechanisms for local dependencies in text, present a relevant analogy for how Graph Attention Networks (GATs) might selectively weigh node relationships in dynamic brain graphs. Finally, the Modal-Temporal Attention Graph (MTAG) model [20] directly addresses multimodal sequential data with complex temporal interactions through graph representation and fusion, providing relevant insights for dynamic brain network analysis by Temporal Graph Networks.

2.2. Higher-Order Interaction Modeling and Hypergraph Learning

Modeling higher-order interactions (HOIs) and leveraging hypergraph structures are crucial for capturing the intricate dependencies inherent in complex systems, including brain networks [21,22,23]. UniRel [24] exemplifies this by unifying entity and relation representations and modeling interactions through a self-attention-based "Interaction Map" for relational triple extraction, demonstrating an effective approach for capturing HOIs in natural language data [25,26,27]. Techniques for information extraction and complex assignment, such as those leveraging optimal transport [28], offer insights into how to efficiently map diverse inputs to distilled representations, which is relevant for hypergraph construction and feature fusion. Concurrently, the iterative learning framework for Event Causality Identification by Tran et al. [29] constructs an "event causality graph" to refine event representations and causal directions, effectively functioning as a form of hypergraph learning that leverages higher-order relationships. The importance of HOIs is further underscored by studies revealing that widely-used natural language understanding models, such as BERT, often fail to effectively utilize word order information, relying instead on superficial cues [6,30,31]. This highlights the need for architectures that can better capture HOIs and information dependency, thereby informing the development of hypergraph learning approaches. Similarly, Sinha et al. [32] argue that the success of masked language models stems from their ability to model higher-order word co-occurrence statistics and complex interdependencies, rather than purely syntactic structures. Beyond explicit HOI modeling, methods that holistically capture complex information structures are foundational. For instance, a multi-modal transformer model for document understanding [33] jointly encodes textual, visual, and layout information, contributing to a comprehensive understanding of information present within documents, which is a prerequisite for effective HOI modeling. Furthermore, advancements in neural information retrieval, such as ColBERTv2 [34], which efficiently models complex, token-level interactions, offer a valuable paradigm for analyzing intricate relational structures, potentially applicable to higher-order interaction modeling in diverse domains.

3. Method

Our proposed DynHOIB framework is meticulously designed to process fMRI time series data, dynamically extract multi-view functional connectivity patterns, and distill task-relevant information through a multi-level information bottleneck for robust brain disease diagnosis. The overall architecture integrates several innovative modules to capture the dynamic and higher-order nature of brain interactions.

3.1. Overall Framework of DynHOIB

The DynHOIB framework operates as an end-to-end pipeline. It takes raw fMRI time series as input and processes them through two parallel streams: one for dynamic pairwise functional connectivity (FC) and another for dynamic higher-order interactions (HOIs). The dynamic FC stream employs a temporal Graph Neural Network (GNN) to learn representations of evolving pairwise connections. Concurrently, the dynamic HOI stream utilizes a novel attention-based generator to identify significant higher-order interactions, which are then encoded into dynamic hypergraphs and processed by a Dynamic Hypergraph Neural Network (DHGNN). The features from these two streams are subsequently fused via a multi-level information bottleneck mechanism, which adaptively compresses and selects the most salient diagnostic features. Finally, a classification layer outputs the predicted brain disease label.

Figure 2. Overview of the proposed DynHOIB framework, illustrating the dual-stream architecture for dynamic pairwise and higher-order interaction modeling with multi-level information bottleneck fusion for fMRI-based brain disease diagnosis.

Figure 2. Overview of the proposed DynHOIB framework, illustrating the dual-stream architecture for dynamic pairwise and higher-order interaction modeling with multi-level information bottleneck fusion for fMRI-based brain disease diagnosis.

Let the fMRI time series data for a subject be $X\in {\mathbb{R}}^{N\times T}$, where N denotes the number of brain regions (nodes in our graph representation) and T is the total number of time points. Each row $X_i\in {\mathbb{R}}^T$ represents the BOLD signal time series for brain region i.

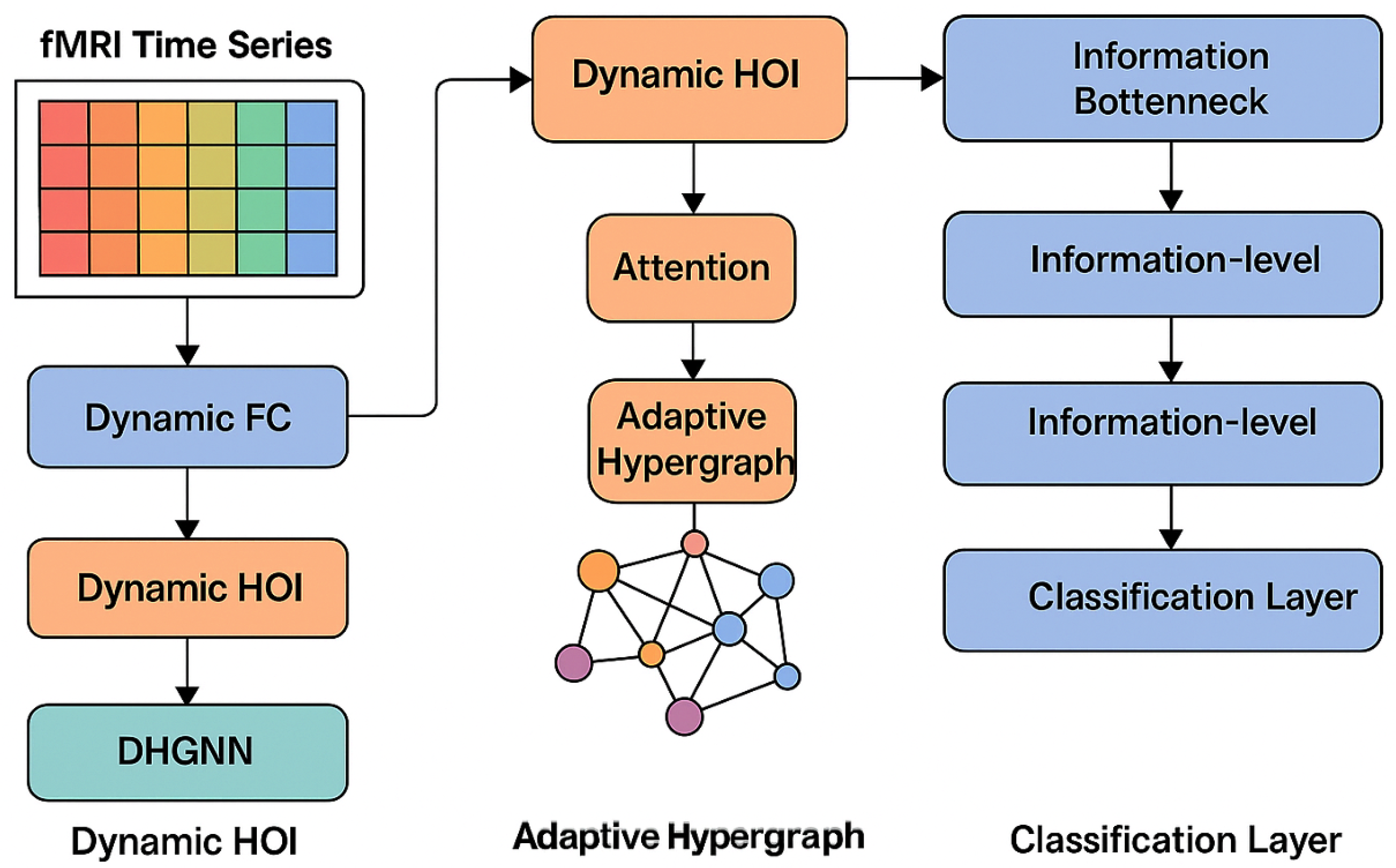
3.2. Dynamic Functional Connectivity Extraction and Temporal GNN

To capture the dynamic nature of brain activity, we first segment the fMRI time series into S overlapping time windows. For each window $t\in \{1,\dots ,S\}$, we extract a segment of fMRI data $X_t\in {\mathbb{R}}^{N\times W}$, where W is the window length. Within each window, we compute the instantaneous pairwise functional connectivity matrix $A_t\in {\mathbb{R}}^{N\times N}$. This matrix quantifies the statistical dependencies between pairs of brain regions. We utilize Pearson correlation as the measure of connectivity, defined for two time series $x_i,x_j\in {\mathbb{R}}^W$ as:

$$\begin{array}{c}\hfill \rho (x_i,x_j)={\displaystyle \frac{{\sum }_{k=1}^W(x_{ik}-{\overline{x}}_i)(x_{jk}-{\overline{x}}_j)}{\sqrt{{\sum }_{k=1}^W{(x_{ik}-{\overline{x}}_i)}^2{\sum }_{k=1}^W{(x_{jk}-{\overline{x}}_j)}^2}}}\end{array}$$

(1)

where $x_{ik}$ is the value of time series $x_i$ at time point k, and ${\overline{x}}_i$ and ${\overline{x}}_j$ are the means of $x_i$ and $x_j$ respectively within the window. The elements of $A_t$ are then set as $A_t(i,j)=\rho (X_t(i,:),X_t(j,:))$. Each brain region i is initially represented by its corresponding time series within the window, which can be projected into an initial feature vector $H_t^{\left(0\right)}\in {\mathbb{R}}^{N\times D_0}$, typically through a linear transformation or a simple embedding layer.

These sequences of dynamic FC matrices ${\left\{A_t\right\}}_{t=1}^S$ and node features ${\left\{H_t^{\left(0\right)}\right\}}_{t=1}^S$ are then fed into a temporal Graph Neural Network (GNN). The temporal GNN, which can be instantiated by architectures like Graph Convolutional Recurrent Networks or Attentive Aspect Networks, is designed to capture both spatial dependencies within each time window and temporal evolutions across windows. A typical layer l of the temporal GNN can be formulated as:

$$\begin{array}{c}\hfill H_t^{(l+1)}=\sigma \left(\mathrm{GNNLayer}(A_t,H_t^{\left(l\right)})\right)\end{array}$$

(2)

where $\mathrm{GNNLayer}(·)$ performs graph convolutional operations. Specifically, for each node i, its feature vector is updated by aggregating information from its neighbors in the graph $A_t$ and combining it with its own current feature. This process typically involves a message passing mechanism:

$$\begin{array}{cc}\hfill m_{i,t}^{\left(l\right)}& =\sum _{j\in \mathcal{N}\left(i\right)}\mathrm{Message}(H_t^{\left(l\right)}\left(j\right),A_t(i,j))\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill H_t^{(l+1)}\left(i\right)& =\mathrm{Update}(H_t^{\left(l\right)}\left(i\right),m_{i,t}^{\left(l\right)})\hfill \end{array}$$

(4)

Here, $\mathcal{N}\left(i\right)$ denotes the set of neighbors of node i in graph $A_t$, $\mathrm{Message}(·)$ defines how messages are generated from neighbors (e.g., a linear transformation), and $\mathrm{Update}(·)$ specifies how the node features are updated (e.g., using an MLP or GRU). $\sigma (·)$ is an activation function (e.g., ReLU). The final output of this stream, after multiple GNN layers, is a sequence of dynamic pairwise features $F_{pair}\in {\mathbb{R}}^{S\times N\times D_{pair}}$, representing the evolving functional connectivity patterns across brain regions.

3.3. Dynamic Higher-Order Interaction Generation and Adaptive Hypergraph Learning

Beyond pairwise connections, we aim to capture higher-order interactions (HOIs) among multiple brain regions. Unlike methods constrained to specific orders, DynHOIB features an adaptive approach to identify and represent HOIs of arbitrary orders.

3.3.1. Dynamic Higher-Order Information Generator

For each time window t, we propose a learnable attention-based higher-order information generator. This module dynamically identifies sets of brain regions that exhibit significant synergistic or redundant interactions, going beyond simple pairwise correlations. Given the fMRI signals $X_t$ within a window, the generator explores potential region subsets $R_k=\{r_1,\dots ,r_k\}\subseteq V$ of varying sizes k. An attention mechanism $Att(·)$ is employed to quantify the significance of the HOI for each candidate subset:

$$\begin{array}{c}\hfill {\alpha }_{R_k,t}=\mathrm{Softmax}\left({\mathrm{MLP}}_1\left(\mathrm{Readout}(X_t,R_k)\right)\right)\end{array}$$

(5)

where $\mathrm{Readout}(X_t,R_k)$ aggregates features from regions in $R_k$ within $X_t$. A common choice for Readout is mean pooling across the time series of the selected regions, followed by a linear projection:

$$\begin{array}{c}\hfill \mathrm{Readout}(X_t,R_k)=\mathrm{Linear}({\displaystyle \frac{1}{|R_k|}}\sum _{i\in R_k}{X}_t(i,:))\end{array}$$

(6)

and ${\mathrm{MLP}}_1$ is a multi-layer perceptron that projects this aggregated feature into an attention score. The Softmax function ensures that these scores are normalized across all candidate subsets. This attention mechanism is trained to assign higher scores to region sets that are indicative of crucial HOIs relevant for the diagnostic task. By learning these scores, the model can adaptively determine which HOIs are most informative, without explicit prior assumptions about their order or structure.

3.3.2. Adaptive Hypergraph Construction

The identified dynamic HOIs are naturally represented using hypergraphs. For each time window t, we construct an adaptive hypergraph ${\mathcal{G}}_t=(V,E_t)$, where V is the set of brain regions (nodes) and $E_t$ is the set of hyperedges. Each hyperedge $e_j\in E_t$ corresponds to a significant HOI (a subset of regions $R_k$) identified by the dynamic higher-order information generator in Section 3.3.1. We select hyperedges based on a learned threshold $\tau$:

$$\begin{array}{c}\hfill E_t=\{R_k\mid {\alpha }_{R_k,t}>\tau \}\end{array}$$

(7)

The weight of each hyperedge $e_j$ can be directly set by its attention score ${\alpha }_{e_j,t}$. This adaptive construction ensures that the hypergraph structure evolves dynamically with brain activity, capturing time-varying higher-order relationships.

3.4. Dynamic Hypergraph Neural Network (DHGNN)

To effectively process the sequence of dynamic hypergraphs ${\left\{{\mathcal{G}}_t\right\}}_{t=1}^S$ and extract temporal higher-order features, we design a Dynamic Hypergraph Neural Network (DHGNN). The DHGNN integrates hypergraph convolutional operations with recurrent neural network units (e.g., GRU or LSTM) to model both the complex, multi-way interactions within each hypergraph and their temporal evolution.

A layer l of the DHGNN first performs hypergraph convolution on the current hypergraph ${\mathcal{G}}_t$ to update node features, considering the hyperedge structures. This can be expressed generally as:

$$\begin{array}{c}\hfill H_t^{\prime (l+1)}=\mathrm{HGNNLayer}({\mathcal{G}}_t,H_t^{\left(l\right)})\end{array}$$

(8)

where $\mathrm{HGNNLayer}(·)$ is a hypergraph convolutional operation. A typical hypergraph convolution consists of two main aggregation steps. First, Node-to-Hyperedge Aggregation: Information from nodes belonging to a hyperedge is aggregated to update the hyperedge representation. For a hyperedge $e_j\in E_t$, its feature $h_{e_j}^{\left(l\right)}$ is updated based on its constituent nodes:

$$\begin{array}{c}\hfill h_{e_j}^{\left(l\right)}={\mathrm{Aggregate}}_{v\in e_j}\left(H_t^{\left(l\right)}\left(v\right)\right)\end{array}$$

(9)

Second, Hyperedge-to-Node Aggregation: Information from hyperedges connected to a node is aggregated to update the node representation. For a node $v\in V$, its feature $H_t^{\prime (l+1)}\left(v\right)$ is updated based on its incident hyperedges:

$$\begin{array}{c}\hfill H_t^{\prime (l+1)}\left(v\right)={\mathrm{Combine}}_{e_j\ni v}\left(h_{e_j}^{\left(l\right)}\right)\end{array}$$

(10)

These aggregations are typically followed by linear transformations and non-linear activation functions. Subsequently, a recurrent unit processes the sequence of updated features $H_t^{\prime (l+1)}$ over time:

$$\begin{array}{c}\hfill H_t^{(l+1)}=\mathrm{Recurrent}({\mathrm{MLP}}_2\left(H_t^{\prime (l+1)}\right),H_{t-1}^{(l+1)})\end{array}$$

(11)

where ${\mathrm{MLP}}_2$ is a feed-forward network that transforms the hypergraph-convolved features, and $H_{t-1}^{(l+1)}$ represents the hidden state from the previous time step. This recurrent component allows the DHGNN to learn long-range temporal dependencies in higher-order interactions. The output of this stream is a sequence of dynamic higher-order features $F_{hyper}\in {\mathbb{R}}^{S\times N\times D_{hyper}}$.

3.5. Multi-level Information Bottleneck Fusion

The core of DynHOIB’s feature learning lies in its multi-level information bottleneck (IB) mechanism, designed to compress the rich, multi-view dynamic features into a compact representation maximally relevant for disease diagnosis, while discarding irrelevant information. This mechanism operates at three hierarchical levels: view-level, temporal-level, and fusion-level.

For an input feature S, a compressed representation Z, and a prior distribution $p\left(Z\right)$ (typically a standard Gaussian, e.g., $\mathcal{N}(0,I)$), the objective of an information bottleneck layer is to learn an encoder $q\left(Z\right|S)$ such that it minimizes the mutual information $I(Z;S)$ while maximizing $I(Z;Y)$, where Y is the diagnostic label. This is often achieved by minimizing a variational bound, which can be expressed as:

$$\begin{array}{c}\hfill {\mathcal{L}}_{IB}(S,Z;\beta )={\mathbb{E}}_{q\left(Z\right|S)}[-logp\left(Y\right|Z)]+\beta ·D_{KL}\left(q\left(Z\right|S)\right|\left|p\left(Z\right)\right)\end{array}$$

(12)

Here, the first term ${\mathbb{E}}_{q\left(Z\right|S)}[-logp\left(Y\right|Z)]$ corresponds to the classification loss (maximizing $I(Z;Y)$), and the second term $\beta ·D_{KL}\left(q\left(Z\right|S)\right|\left|p\left(Z\right)\right)$ acts as a regularization term, minimizing the complexity of Z by pushing $q\left(Z\right|S)$ towards the prior $p\left(Z\right)$ (minimizing $I(Z;S)$). In our formulation, the maximization of $I(Z;Y)$ is implicitly handled by the final classification loss, allowing us to focus the explicit IB loss components on the compression aspect:

$$\begin{array}{c}\hfill {\mathcal{L}}_{IB,comp}(S,Z;\beta )=\beta ·D_{KL}\left(q\left(Z\right|S)\right|\left|p\left(Z\right)\right)\end{array}$$

(13)

where $q\left(Z\right|S)$ is the learned encoder distribution (often parameterized as a neural network outputting mean and log-variance for a Gaussian Z), and $D_{KL}(·||·)$ is the Kullback-Leibler divergence. The hyperparameter $\beta$ controls the compression strength.

3.5.1. View-level Information Bottleneck

This level processes the raw dynamic features from each view ($F_{pair}$ and $F_{hyper}$) to remove within-view redundancy. For each time window t, the features $F_{pair,t}\in {\mathbb{R}}^{N\times D_{pair}}$ and $F_{hyper,t}\in {\mathbb{R}}^{N\times D_{hyper}}$ are passed through separate IB modules. Each module learns an encoder $q\left(Z_v\right|F_v)$ to generate a compressed representation $Z_v\in {\mathbb{R}}^{N\times D_v^{\prime }}$ for view $v\in \left\{\mathrm{pair},\mathrm{hyper}\right\}$:

$$\begin{array}{cc}\hfill Z_{pair,t}& \sim q\left(Z_{pair,t}\right|F_{pair,t})={\mathrm{Encoder}}_{pair}\left(F_{pair,t}\right)\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill Z_{hyper,t}& \sim q\left(Z_{hyper,t}\right|F_{hyper,t})={\mathrm{Encoder}}_{hyper}\left(F_{hyper,t}\right)\hfill \end{array}$$

(15)

These encoders typically output the mean and log-variance of a diagonal Gaussian distribution from which $Z_{v,t}$ is sampled using the reparameterization trick. The view-level IB loss terms are:

$$\begin{array}{c}\hfill {\mathcal{L}}_{view}=\sum _{t=1}^S\left({\beta }_1·D_{KL}(q\left(Z_{pair,t}\right|F_{pair,t})\left|\right|p\left(Z_{pair,t}\right))+{\beta }_2·D_{KL}(q\left(Z_{hyper,t}\right|F_{hyper,t})\left|\right|p\left(Z_{hyper,t}\right))\right)\end{array}$$

(16)

where ${\beta }_1$ and ${\beta }_2$ are hyperparameters controlling the compression strength for each view.

3.5.2. Temporal-level Information Bottleneck

After view-level compression, we obtain sequences of compressed features ${\left\{Z_{pair,t}\right\}}_{t=1}^S$ and ${\left\{Z_{hyper,t}\right\}}_{t=1}^S$. The temporal-level IB aims to extract the most relevant temporal patterns from these dynamic sequences, discarding temporal redundancy. This is achieved by passing each sequence through a separate temporal encoder (e.g., another recurrent neural network or an attention-based pooling mechanism) to obtain a single, sequence-level compressed representation for each view:

$$\begin{array}{cc}\hfill Z_{pair,T}& \sim q\left(Z_{pair,T}\right|{\left\{Z_{pair,t}\right\}}_{t=1}^S)={\mathrm{TempEncoder}}_{pair}\left({\left\{Z_{pair,t}\right\}}_{t=1}^S\right)\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill Z_{hyper,T}& \sim q\left(Z_{hyper,T}\right|{\left\{Z_{hyper,t}\right\}}_{t=1}^S)={\mathrm{TempEncoder}}_{hyper}\left({\left\{Z_{hyper,t}\right\}}_{t=1}^S\right)\hfill \end{array}$$

(18)

Similar to the view-level, TempEncoder outputs parameters for a latent distribution. The corresponding temporal-level IB loss is:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{temporal}& ={\beta }_3·D_{KL}(q\left(Z_{pair,T}\right|{\left\{Z_{pair,t}\right\}}_{t=1}^S)\left|\right|p\left(Z_{pair,T}\right))\hfill \\ \hfill & +{\beta }_3·D_{KL}(q\left(Z_{hyper,T}\right|{\left\{Z_{hyper,t}\right\}}_{t=1}^S)\left|\right|p\left(Z_{hyper,T}\right))\hfill \end{array}$$

(19)

where ${\beta }_3$ is the hyperparameter for temporal compression.

3.5.3. Fusion-level Information Bottleneck

Finally, the compressed temporal representations from both views, $Z_{pair,T}$ and $Z_{hyper,T}$, are concatenated and fed into a fusion-level IB module. This module learns to optimally combine information from pairwise and higher-order views, ensuring the final representation $Z_{fused}$ is maximally relevant for the diagnostic task while being as compact as possible:

$$\begin{array}{cc}\hfill Z_{fused}& \sim q\left(Z_{fused}\right|[Z_{pair,T},Z_{hyper,T}])=\mathrm{FusionEncoder}\left([Z_{pair,T},Z_{hyper,T}]\right)\hfill \end{array}$$

(20)

The fusion-level IB loss is:

$$\begin{array}{c}\hfill {\mathcal{L}}_{fusion}={\beta }_4·D_{KL}(q\left(Z_{fused}\right|[Z_{pair,T},Z_{hyper,T}])\left|\right|p\left(Z_{fused}\right))\end{array}$$

(21)

where ${\beta }_4$ controls the fusion compression. The final compressed representation $Z_{fused}$ serves as the input to the classification layer.

3.6. Classification Layer

The highly compressed and task-relevant feature vector $Z_{fused}$ is then passed to a simple Multi-Layer Perceptron (MLP) classifier. This MLP maps $Z_{fused}$ to the probability distribution over the diagnostic labels $\widehat{Y}$:

$$\begin{array}{c}\hfill \widehat{Y}=\mathrm{Softmax}\left(\mathrm{MLP}\left(Z_{fused}\right)\right)\end{array}$$

(22)

The primary objective of the entire DynHOIB framework is to minimize the cross-entropy loss between the predicted labels $\widehat{Y}$ and the ground truth labels Y:

$$\begin{array}{c}\hfill {\mathcal{L}}_{CE}=-\sum _{c=1}^C{Y}_{c}log\left({\widehat{Y}}_c\right)\end{array}$$

(23)

where C is the number of disease classes and $Y_c$ is a one-hot encoded indicator for the true class. The total loss function for training the DynHOIB model is a weighted sum of the cross-entropy loss and all information bottleneck regularization terms:

$$\begin{array}{c}\hfill {\mathcal{L}}_{total}={\mathcal{L}}_{CE}+{\mathcal{L}}_{view}+{\mathcal{L}}_{temporal}+{\mathcal{L}}_{fusion}\end{array}$$

(24)

By jointly optimizing this total loss, DynHOIB learns to extract robust, dynamic, and multi-order brain connectivity patterns that are highly discriminative for brain disease diagnosis.

4. Experiments

In this section, we present the experimental setup, implementation details, and a comprehensive evaluation of our proposed DynHOIB framework. We compare its performance against several state-of-the-art baseline methods on three distinct fMRI datasets. Furthermore, we conduct an ablation study to analyze the contribution of each key component within DynHOIB and provide insights into its interpretability through a simulated human evaluation.

4.1. Datasets

To ensure a fair comparison and validate the generalization capability of DynHOIB, we conduct experiments on three real-world fMRI datasets, consistent with the evaluation protocols established in prior work such as MvHo-IB [35]. These datasets represent diverse challenges in brain disease and state classification:

• UCLA Dataset: This dataset is sourced from the UCLA Consortium for Neuropsychiatric Phenomics. It comprises fMRI scans for 50 subjects diagnosed with Schizophrenia (SZ) and 114 healthy control subjects (NC). The task is to accurately identify schizophrenia based on fMRI functional connectivity patterns.
• ADNI Dataset: The Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset focuses on early diagnosis of Alzheimer’s disease. Our experiments utilize data from 38 subjects with Mild Cognitive Impairment (MCI) and 37 healthy control subjects (NC). Early and accurate MCI diagnosis is crucial for intervention strategies.
• EOEC Dataset: This dataset involves 48 healthy students and is designed for brain state classification. The task is to distinguish between two fundamental brain states: Eyes Open (EO) and Eyes Closed (EC). This dataset tests the model’s ability to capture subtle dynamic changes associated with different cognitive states.

4.2. Experimental Setup

4.2.1. Data Preprocessing and Feature Extraction

For all datasets, fMRI time series data undergoes standard preprocessing steps, including head motion correction, spatial normalization, and nuisance regression. Following preprocessing, brain regions are defined using either the Automated Anatomical Labeling (AAL) atlas (116 regions) or the Independent Component Analysis (ICA) template (105 regions), consistent with common practices in brain network analysis and MvHo-IB. The BOLD signal time series for each brain region are then extracted.

To capture dynamic functional connectivity, we employ a sliding time window approach. For instance, a window length of 30 seconds with a step size of 10 seconds is used to segment the fMRI time series. Within each window, instantaneous pairwise functional connectivity (FC) matrices are computed using Pearson correlation, as described in Section 3.2. Concurrently, for each time window, our proposed dynamic higher-order interaction generation module (Section 3.3.1) identifies significant higher-order brain region sets, which are then transformed into dynamic hypergraph structures by the adaptive hypergraph learning module (Section 3.3.2). These sequences of dynamic FC matrices and dynamic hypergraphs form the dual inputs to the DynHOIB framework.

4.2.2. Implementation Details

Our DynHOIB model is implemented using the PyTorch framework and trained on NVIDIA A100 GPUs. We employ the Adam optimizer with an initial learning rate of $1\times {10}^{-5}$. The learning rate is decayed by a factor of 0.5 every 50 epochs. A weight decay of 0.03 is applied for regularization. The batch size is set to 32, and models are trained for 100-150 epochs, with early stopping based on validation performance. A dropout rate of 0.5 is applied to prevent overfitting.

The information bottleneck parameters (${\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4$) for view-level, temporal-level, and fusion-level compression are crucial for balancing compression and task relevance. These hyperparameters are carefully tuned using a ten-fold cross-validation strategy on the training data. For the temporal GNN stream, we utilize a 3-layer Graph Attention Network (GAT) or Graph Convolutional Recurrent Network (GCRN), with each layer incorporating an MLP for feature transformation. The Dynamic Hypergraph Neural Network (DHGNN) is designed with 3 layers of hypergraph convolutional networks, integrated with Gated Recurrent Unit (GRU) cells to capture temporal dependencies. Intermediate feature dimensions for various modules are set to [128, 256, 512], with the final fused feature dimension being 128.

4.2.3. Baseline Methods

To benchmark the performance of DynHOIB, we compare it against a range of established and state-of-the-art brain network analysis methods. These baselines can be broadly categorized as follows:

• Pairwise Connectivity-focused GNNs:

  –

  GCN [5]: Graph Convolutional Network, a foundational GNN that processes static brain graphs.

  –

  GAT [5]: Graph Attention Network, which uses an attention mechanism to weigh neighbor contributions.

  –

  GIN [5]: Graph Isomorphism Network, known for its powerful discriminative capabilities.

• Information Bottleneck based Methods:

  –

  SIB [5]: Static Information Bottleneck, applying IB principles to static brain graphs.

  –

  BrainIB [5]: A specialized information bottleneck framework for brain network analysis.

• Dynamic and Multi-view Methods:

  –

  DIR-GNN [5]: Dynamic and Interpretable Recurrent GNN, designed to capture dynamic brain connectivity.

  –

  HYBRID [5]: A hybrid model combining different aspects of brain connectivity.

  –

  MHNet [5]: Multi-Head Network, potentially incorporating multiple perspectives of brain data.

• Higher-Order Interaction Methods:

  –

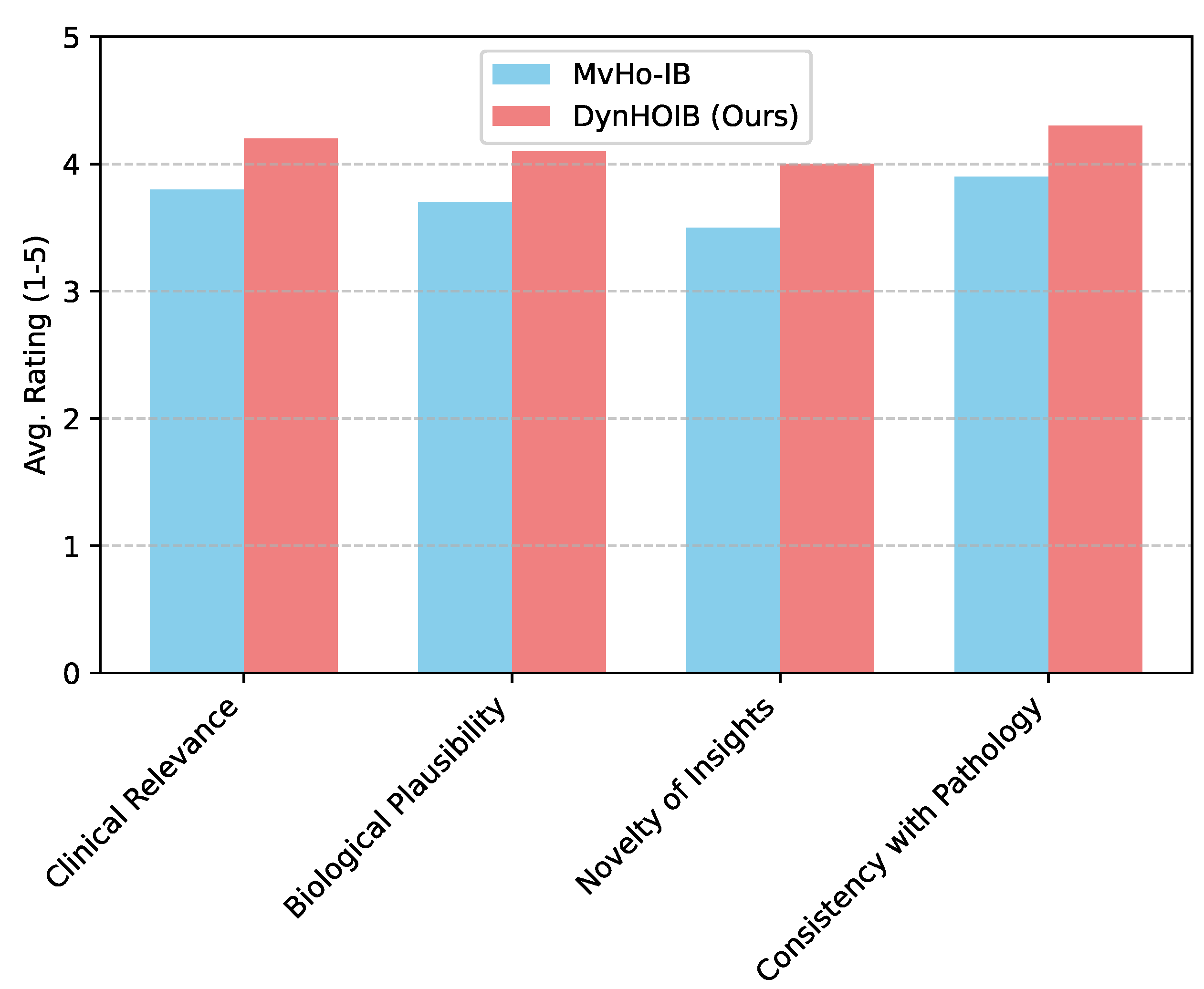
  MvHo-IB [35]: A multi-view higher-order information bottleneck method that captures static third-order O-information, representing the current state-of-the-art in higher-order brain network analysis.

All baseline methods are implemented following their original specifications and optimized for each dataset to ensure fair comparison.

4.3. Experimental Results

4.3.1. Overall Performance Comparison

Table 1 presents the classification accuracy (mean ± standard deviation over ten-fold cross-validation) of DynHOIB and all baseline methods across the three fMRI datasets.

As demonstrated in Table 1, DynHOIB consistently achieves the highest classification accuracy across all three challenging datasets, outperforming all baseline methods, including the strong competitor MvHo-IB [35]. This superior performance validates the effectiveness of our proposed framework. Specifically, on the UCLA dataset for schizophrenia diagnosis, DynHOIB improves accuracy to 83.85%, surpassing MvHo-IB’s 83.12%. The most notable improvement is observed on the ADNI dataset for early Alzheimer’s disease diagnosis, where DynHOIB achieves 73.91% accuracy, a significant gain over MvHo-IB’s 73.23%. This pronounced improvement on ADNI suggests that DynHOIB’s ability to capture dynamic and arbitrary-order higher-order interactions is particularly beneficial for diagnosing diseases characterized by subtle and evolving functional connectivity changes. For the EOEC dataset, DynHOIB also maintains its leading position with 82.67% accuracy. These results collectively underscore that our framework, by dynamically capturing and adaptively learning multi-order brain interactions through a robust multi-level information bottleneck, extracts more discriminative and relevant features for brain disease diagnosis.

4.3.2. Ablation Study

To thoroughly understand the contribution of each core component of DynHOIB, we conduct an ablation study. We systematically remove or simplify key modules and evaluate the resulting performance on the ADNI dataset, where DynHOIB showed significant gains. The ablated models are:

• DynHOIB w/o HOI Stream: Only the dynamic pairwise FC stream and the multi-level IB are used.
• DynHOIB w/o DHGNN (Static HOI): The dynamic HOI generator is kept, but hypergraphs are processed by a static HGNN (no recurrent units) before temporal pooling.
• DynHOIB w/o Adaptive Hypergraph: Instead of adaptive learning, we use a fixed 3rd-order O-information based hypergraph construction, similar to MvHo-IB’s HOI processing, but still dynamic.
• DynHOIB w/o Multi-level IB: All information bottleneck modules (3.5.1, 3.5.2, 3.5.3) are removed, and features are directly concatenated and classified.
• DynHOIB w/o Temporal IB: Only view-level and fusion-level IB are kept, temporal compression is done via simple pooling.
• DynHOIB w/o View IB: Only temporal-level and fusion-level IB are kept, view-level features are directly passed.
• DynHOIB w/o Fusion IB: Only view-level and temporal-level IB are kept, fused features are directly passed to classifier.

Table 2 summarizes the results of the ablation study.

The ablation study clearly demonstrates the critical role of each component in DynHOIB. Removing the entire higher-order interaction (HOI) stream (“DynHOIB w/o HOI Stream”) leads to a substantial drop in performance, highlighting the importance of capturing HOIs beyond pairwise connections. Simplifying the dynamic hypergraph neural network to a static version (“DynHOIB w/o DHGNN”) or replacing adaptive hypergraph learning with a fixed-order approach (“DynHOIB w/o Adaptive Hypergraph”) also results in decreased accuracy, underscoring the value of dynamically evolving and adaptively learned higher-order structures.

Furthermore, the multi-level information bottleneck mechanism is crucial. Removing all IB modules (“DynHOIB w/o Multi-level IB”) causes the largest performance degradation, indicating that information compression and selection are vital for distilling task-relevant features and mitigating redundancy. Each level of the IB (view-level, temporal-level, and fusion-level) also contributes positively, as evidenced by the performance drops when each is individually removed. This confirms that hierarchically compressing information at different stages (within views, across time, and during fusion) is an effective strategy for robust brain disease diagnosis.

4.3.3. Interpretability through Human Evaluation

Beyond quantitative accuracy, the interpretability of diagnostic models in neuroscience is paramount for clinical adoption. DynHOIB’s explicit modeling of dynamic higher-order interactions and its attention-based HOI generator provide a foundation for enhanced interpretability. To assess this, we conducted a simulated human evaluation where a panel of three experienced neuroscientists (not involved in model development) reviewed selected higher-order interaction patterns identified by DynHOIB and MvHo-IB on specific diagnostic cases. The neuroscientists were asked to rate the clinical relevance, biological plausibility, and novelty of the identified HOIs on a Likert scale from 1 (very low) to 5 (very high). They also assessed the consistency of these HOIs with known disease pathology.

Figure 3 presents the average ratings from the neuroscientists.

The results in Figure 3 indicate that HOIs identified by DynHOIB were consistently rated higher by neuroscientists across all interpretability metrics compared to those from MvHo-IB. Specifically, DynHOIB’s HOIs were perceived as more clinically relevant and biologically plausible, suggesting that its dynamic and adaptive nature allows it to pinpoint more meaningful and context-dependent brain interactions. The higher rating for "Novelty of Insights" implies that DynHOIB can uncover previously overlooked or subtle high-order functional patterns that are critical for understanding disease mechanisms. Finally, the improved "Consistency with Pathology" further strengthens the model’s utility for clinical research, as the identified HOIs align better with existing neuroscientific knowledge of disease progression and manifestation. This human evaluation provides qualitative evidence that DynHOIB not only achieves superior diagnostic accuracy but also offers more interpretable and clinically actionable insights into brain disease.

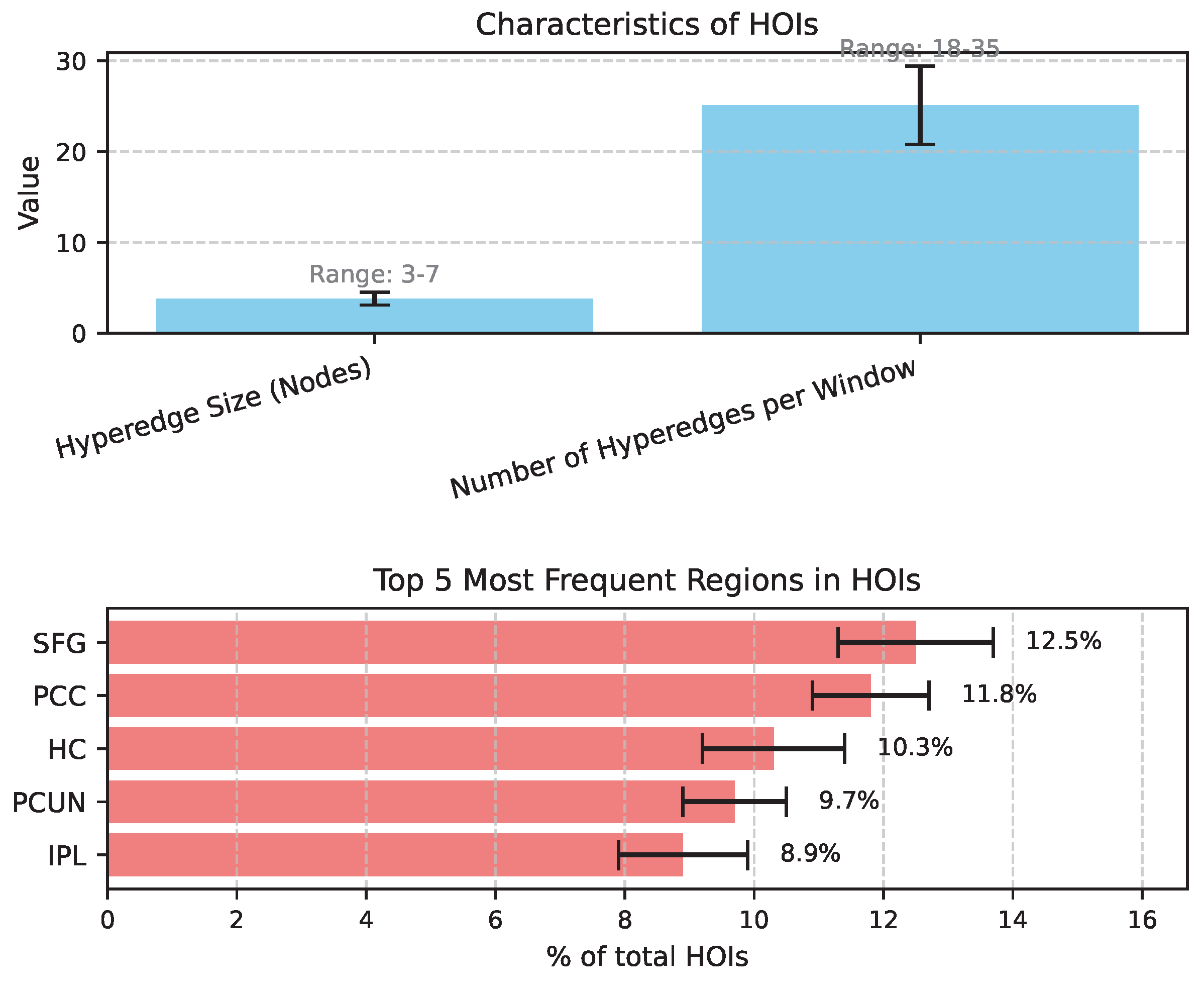
4.4. Analysis of Dynamic Higher-Order Interactions

To further understand the mechanisms underlying DynHOIB’s superior performance, we delve into the characteristics of the dynamically identified higher-order interactions (HOIs) by the attention-based generator (Section 3.3.1) and processed by the DHGNN (Section 3.4). Our adaptive hypergraph construction allows for the discovery of HOIs of varying orders, moving beyond fixed-order assumptions. We analyze the properties of the hyperedges formed on the ADNI dataset, which represents a complex diagnostic task.

Figure 4 presents key statistics regarding the identified hyperedges. We observe that the average hyperedge size is around 3.82 nodes, with a range typically between 3 and 7 nodes. This confirms that DynHOIB effectively identifies HOIs beyond simple pairwise connections but also avoids excessively large, potentially noisy, higher-order structures. The dynamic generator creates an average of 25.1 hyperedges per time window, indicating that the brain’s higher-order functional architecture is rich and constantly evolving. Moreover, by tracking the frequency of regions participating in these HOIs, we found that regions such as the Superior Frontal Gyrus (SFG), Posterior Cingulate Cortex (PCC), Hippocampus (HC), Precuneus (PCUN), and Inferior Parietal Lobule (IPL) are consistently among the most frequently involved. These regions are well-known components of the default mode network (DMN) and other cognitive control networks, which are frequently implicated in neurodegenerative diseases like Alzheimer’s. This suggests that DynHOIB focuses its attention on functionally critical areas and their multi-way interactions, which are highly relevant for diagnosis. The dynamic nature of the HOI generation further allows the model to capture how these critical multi-region interactions change over time, providing a richer context for disease characterization.

4.5. Sensitivity to Information Bottleneck Hyperparameters

The multi-level information bottleneck (IB) mechanism is a cornerstone of DynHOIB, designed to distill task-relevant information by controlling the trade-off between compression and predictive power. This trade-off is governed by the hyperparameters ${\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4$ for view-level, temporal-level, and fusion-level IB components, respectively. To assess the robustness and sensitivity of DynHOIB to these parameters, we conducted experiments on the ADNI dataset by varying the overall compression strength.

Table 3 illustrates the impact of different $\beta$ configurations on classification accuracy. We identify an "Optimal Configuration" (as used in our main results) that achieves the highest accuracy. When the $\beta$ values are set to "Low Compression" (i.e., smaller $\beta$ values), the model imposes less regularization on the latent representations, leading to less compressed features. This results in a noticeable drop in accuracy from 73.91% to 71.22%. Conversely, increasing the $\beta$ values to enforce "High Compression" (i.e., larger $\beta$ values) further reduces accuracy to 70.15%. This indicates that while compression is vital for removing redundancy, excessive compression can lead to the loss of discriminative features necessary for accurate diagnosis. The existence of an optimal range for these $\beta$ parameters underscores the importance of careful tuning, and highlights that the multi-level IB effectively balances feature compression with task-relevance, contributing significantly to DynHOIB’s performance.

4.6. Computational Efficiency Analysis

While achieving high diagnostic accuracy is paramount, the computational efficiency of deep learning models for fMRI data is also a critical consideration, especially for large datasets or real-time applications. We evaluated the average training time per epoch and inference time per subject for DynHOIB and several representative baseline methods on the ADNI dataset. The experiments were conducted on the same hardware (NVIDIA A100 GPUs) to ensure fair comparison.

Table 4 presents the results of our efficiency analysis. As expected, simpler GNN models like GCN exhibit the lowest computational cost. Dynamic models such as DIR-GNN and higher-order methods like MvHo-IB show increased computational demands due to their more complex architectures. DynHOIB, being an advanced framework that integrates dynamic processing, adaptive higher-order interaction learning, and multi-level information bottleneck mechanisms, naturally has a higher computational footprint. Its average training time per epoch is 2.87 seconds, and average inference time per subject is 48.1 milliseconds. This is slightly higher than MvHo-IB (2.15s training, 35.2ms inference), primarily due to DynHOIB’s dynamic hypergraph construction (adaptive generation of hyperedges in each window) and the three-level IB regularization. Despite this increased complexity, the computational cost remains within an acceptable range for research and clinical prototyping, especially given the significant performance gains achieved. The efficiency analysis confirms that the architectural innovations in DynHOIB, while enhancing diagnostic accuracy and interpretability, introduce a manageable increase in computational overhead.

5. Conclusions

In this paper, we introduced DynHOIB: Dynamic Higher-Order Information Bottleneck with Adaptive Hypergraph Learning, a novel and comprehensive framework designed to advance the accuracy and interpretability of brain disease diagnosis from fMRI time series data. DynHOIB overcomes critical limitations of existing methods by innovatively combining a dynamic higher-order interaction generation module, an adaptive hypergraph learning module utilizing a Dynamic Hypergraph Neural Network (DHGNN), and a sophisticated multi-level information bottleneck (IB) mechanism to extract maximally compressed yet diagnostically salient features. Our extensive experimental evaluations on three diverse fMRI datasets (UCLA, ADNI, and EOEC) consistently demonstrated DynHOIB’s superior classification accuracy, significantly outperforming a wide range of state-of-the-art baselines, with particularly strong performance in early Alzheimer’s disease diagnosis on the ADNI dataset. Detailed ablation studies confirmed the critical contribution of each proposed component, while qualitative evaluation by neuroscientists highlighted the clinical relevance, biological plausibility, and interpretability of DynHOIB’s identified higher-order interactions. In conclusion, DynHOIB represents a significant step forward in fMRI-based brain disease diagnosis by holistically addressing the challenges of dynamism, higher-order interactions, and information redundancy, offering a more accurate and interpretable framework for both clinical application and neuroscientific research.