Submitted:
29 October 2025
Posted:
30 October 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Review on Robust Estimators
2.1.1. The Huber Maximum Likelihood Estimator (HME)
2.1.2. James Stein Estimator (JSE)
2.1.3. The Robust Stein Estimator (RSE)
- are the ordered eigenvalues of the design information matrix (e.g., in linear models),
- are the components of the robust estimator ,
- are the diagonal entries of the variance-covariance matrix .
2.1.4. The Least Median of Squares Estimator (LMSE)
2.1.5. The Least Trimmed Squares Estimator (LTSE)
2.1.6. The S-Estimator (SE)
- (A1)
- is symmetric, continuously differentiable, and ;
- (A1)
- There exists such that is strictly increasing on and constant on .
2.1.7. The Modified Maximum Likelihood Estimator (MME)
Stage 1:
Stage 2:
Stage 3:
2.2. Criteria for Assessing the Estimator’s Performance
2.2.1. Bias Under the Bootstrap
2.2.2. RMSE Under the Bootstrap
3. Monte Carlo Simulation Study
3.1. Simulation Procedure
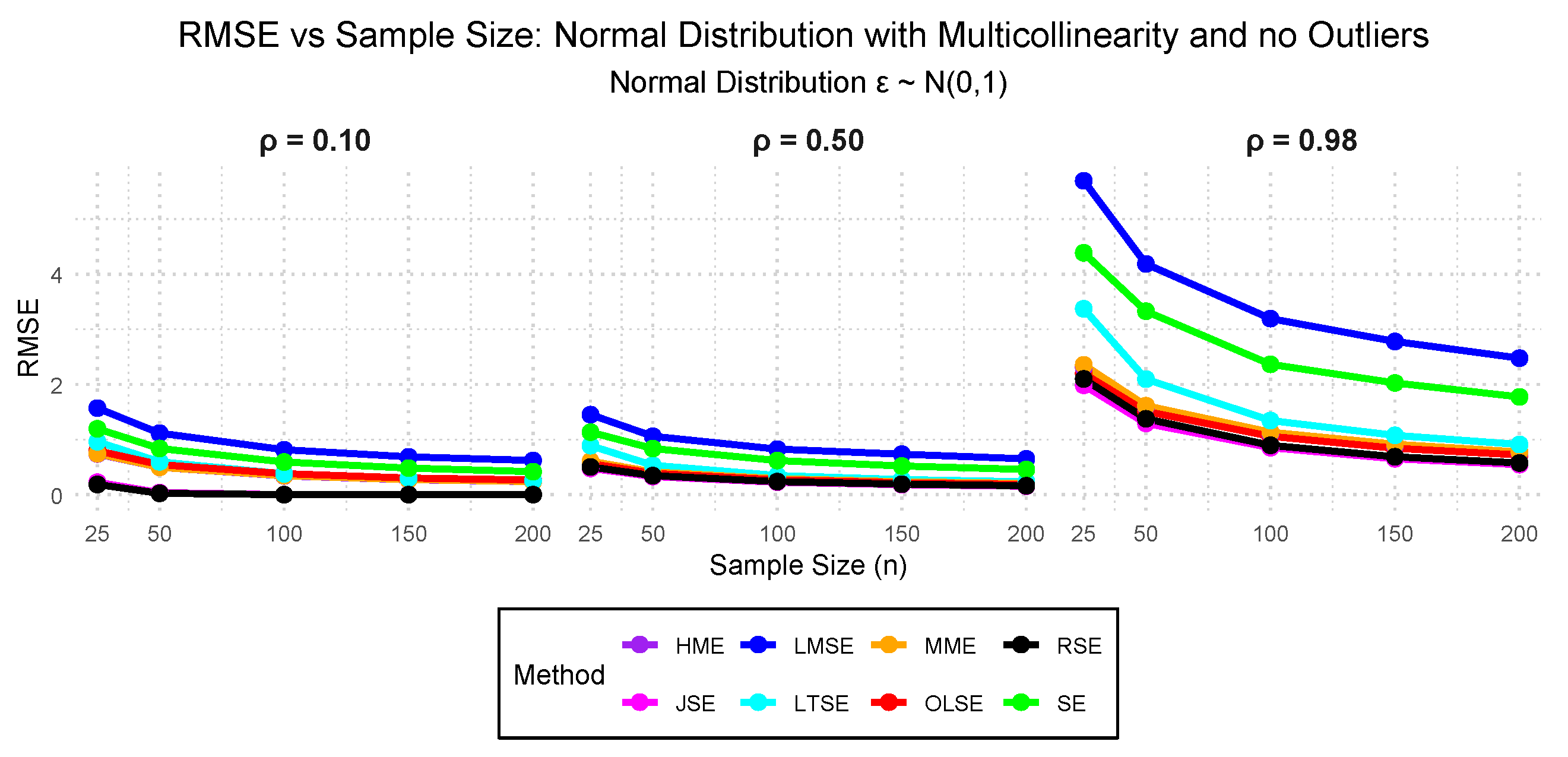
- Case I: - Standard normal distribution with 0.10, 0.50, and 0.98 multicollinearity and 0.00% outliers.
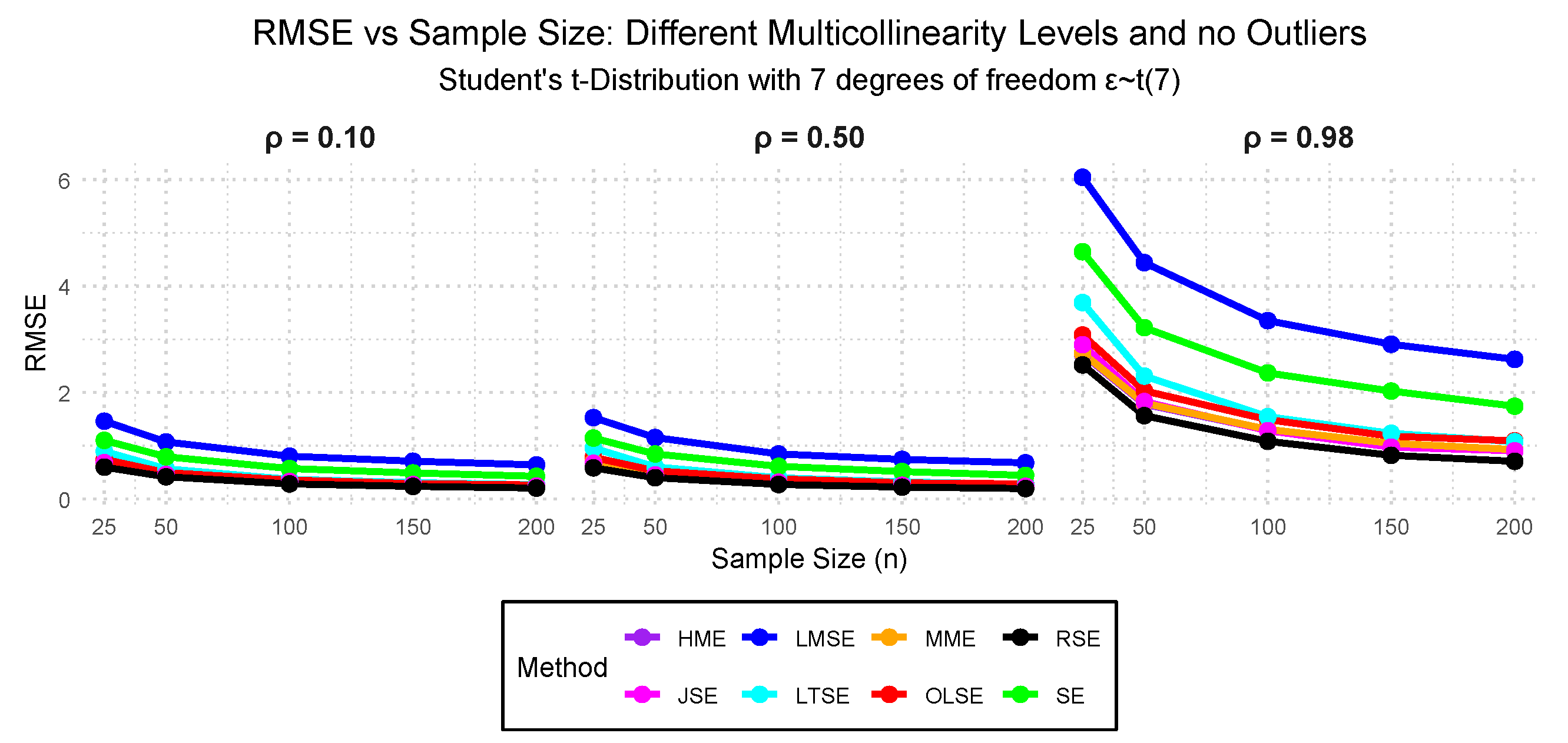
- Case II: — Student’s t-distribution with 7 degrees of freedom with 0.10, 0.50, and 0.98 multicollinearity and 0.00% outliers.
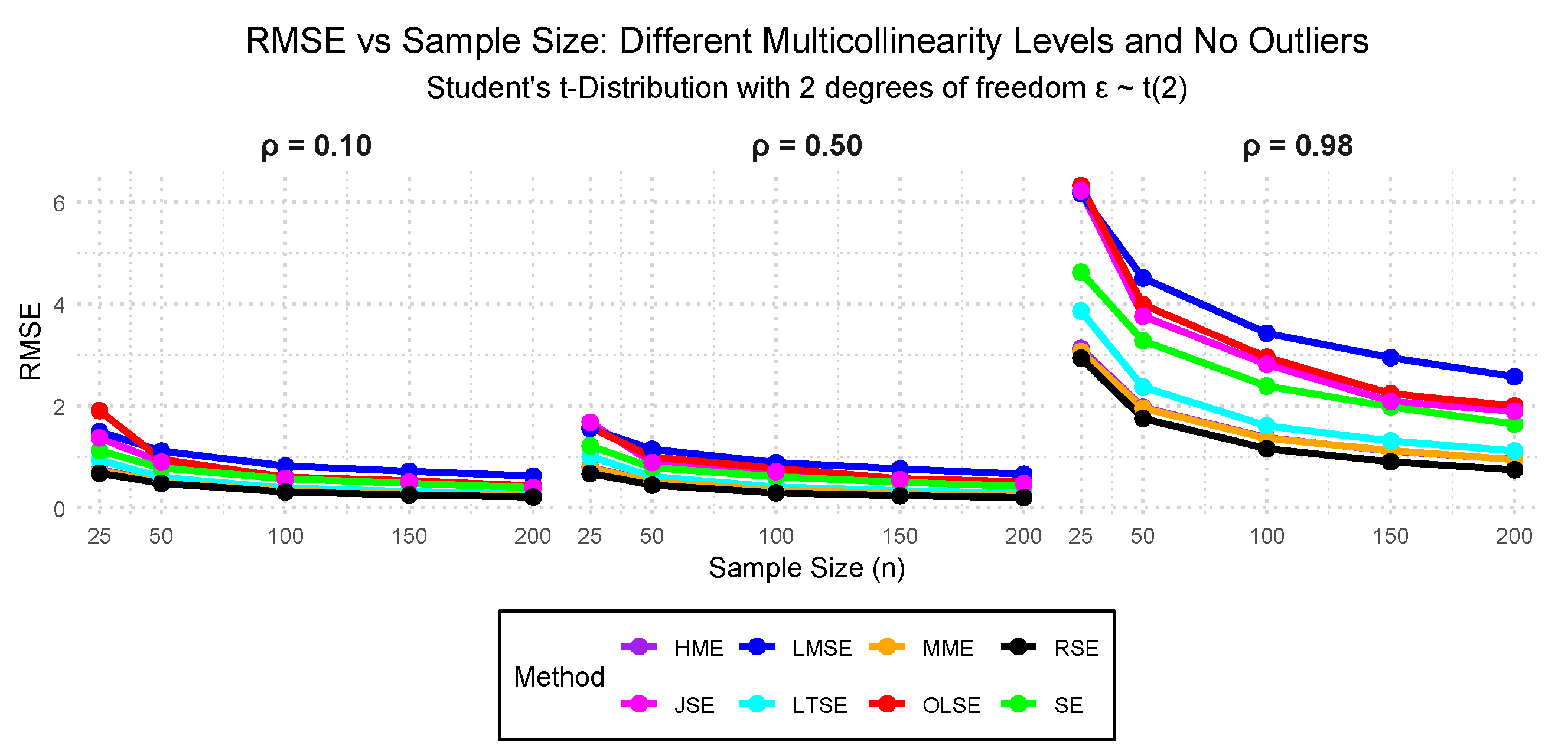
- Case III: — Student’s t-distribution with 2 degrees of freedom, 0.10, 0.50, and 0.98 multicollinearity and 0.00% outliers.
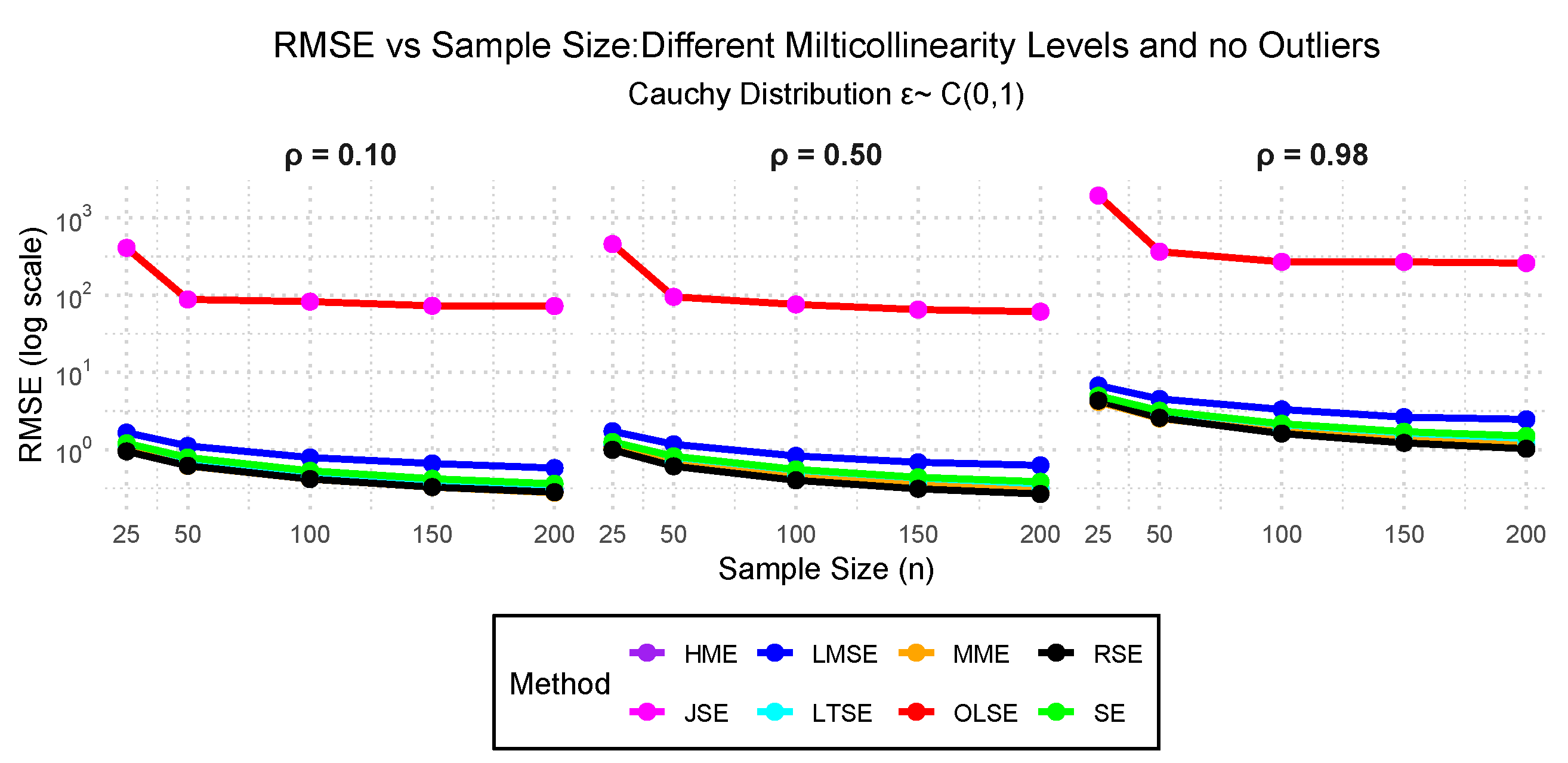
- Case IV: — Cauchy distribution errors with 0.10, 0.50, and 0.98 multicollinearity and 0.00% outliers.
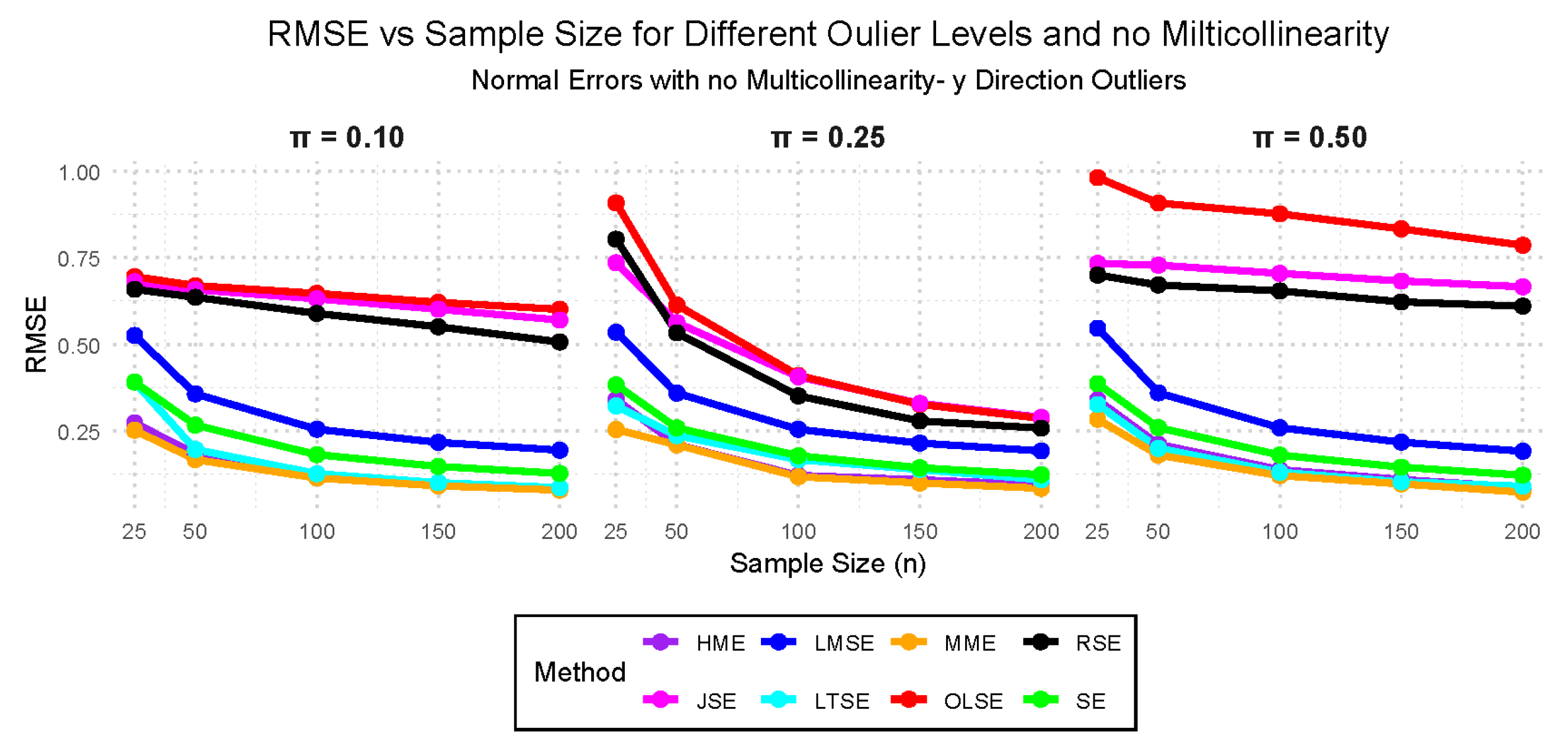
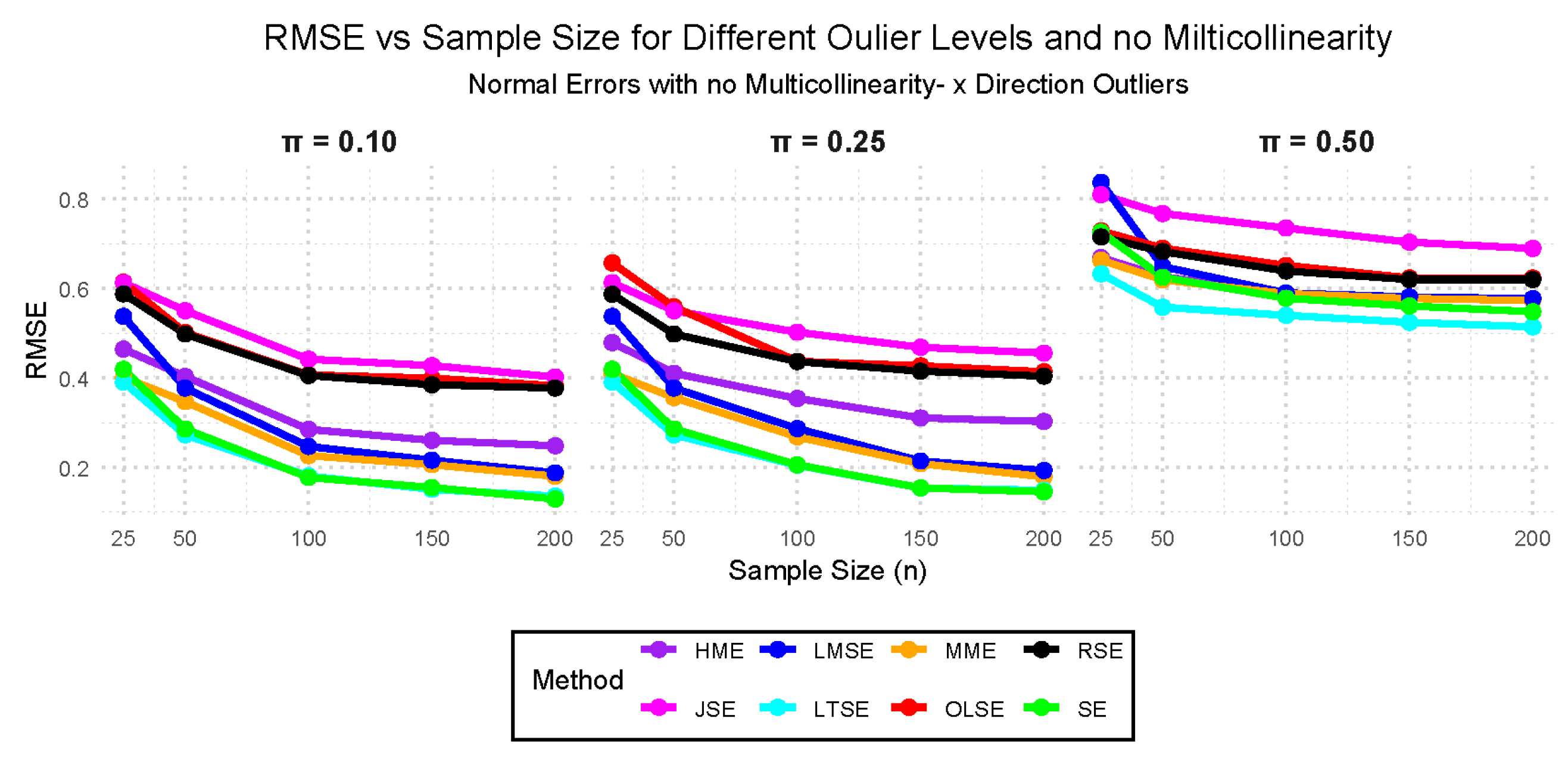
- Case V: — Standard normal distribution with 10%, 25%, and 50% outliers with no multicollinearity.
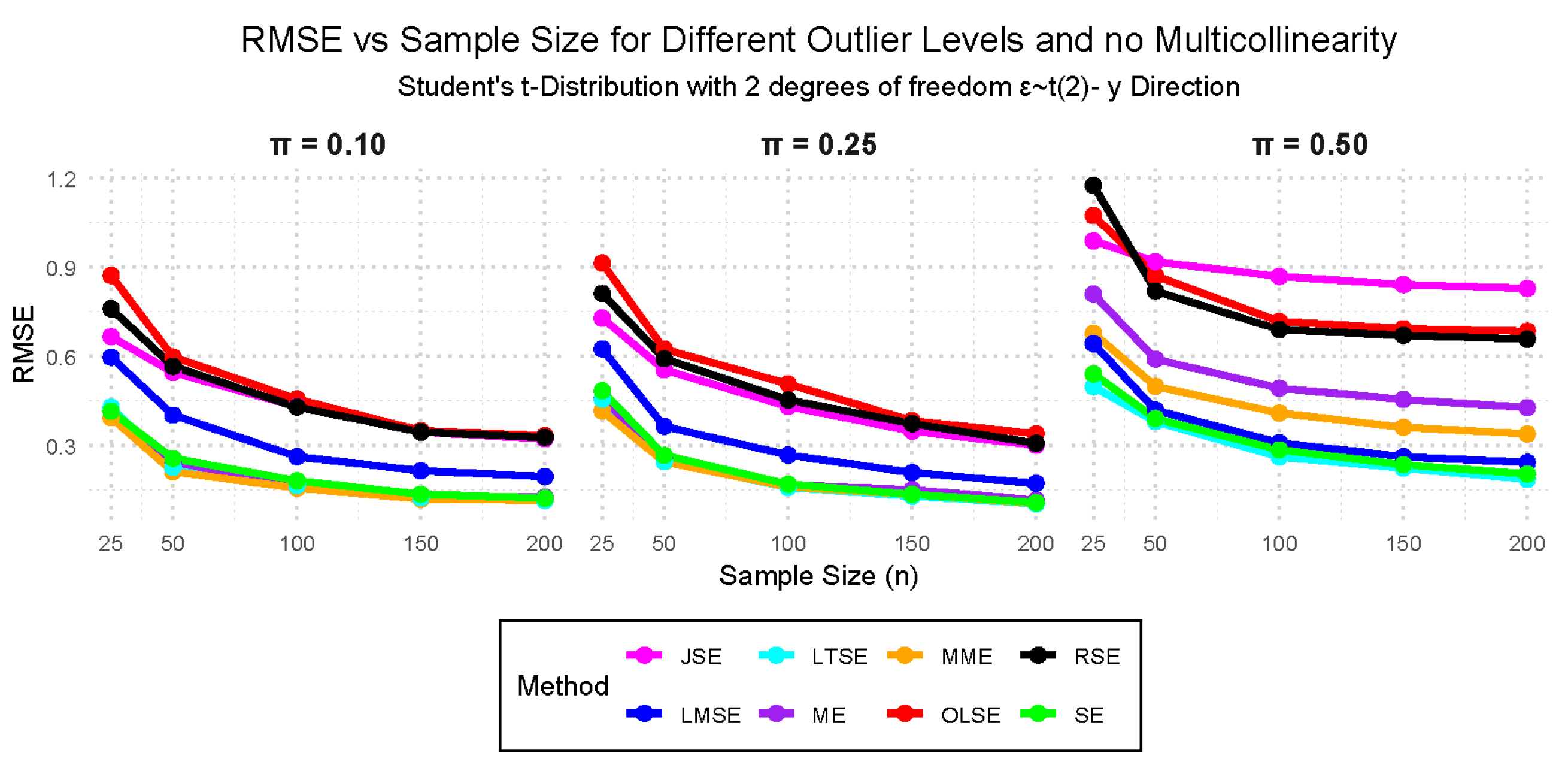
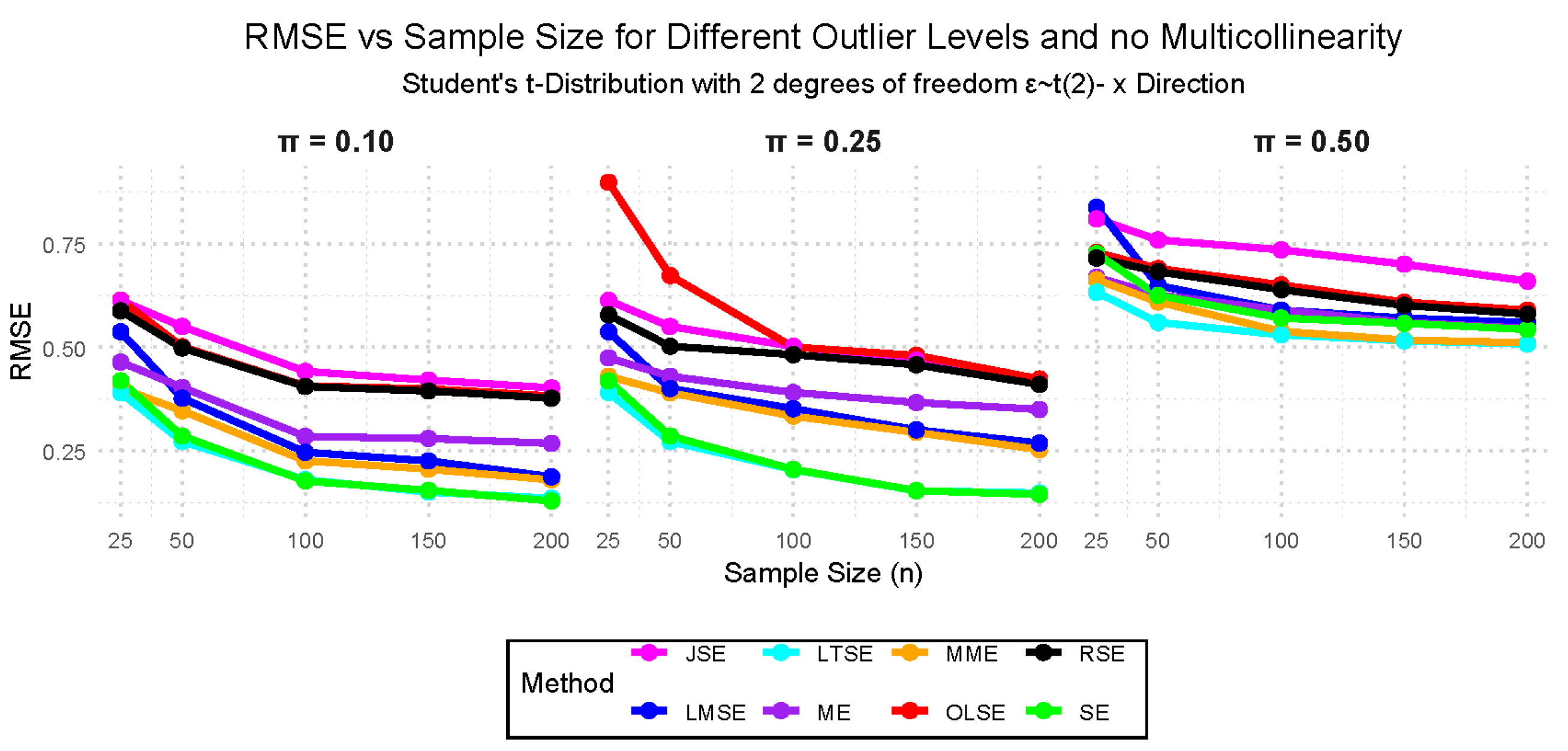
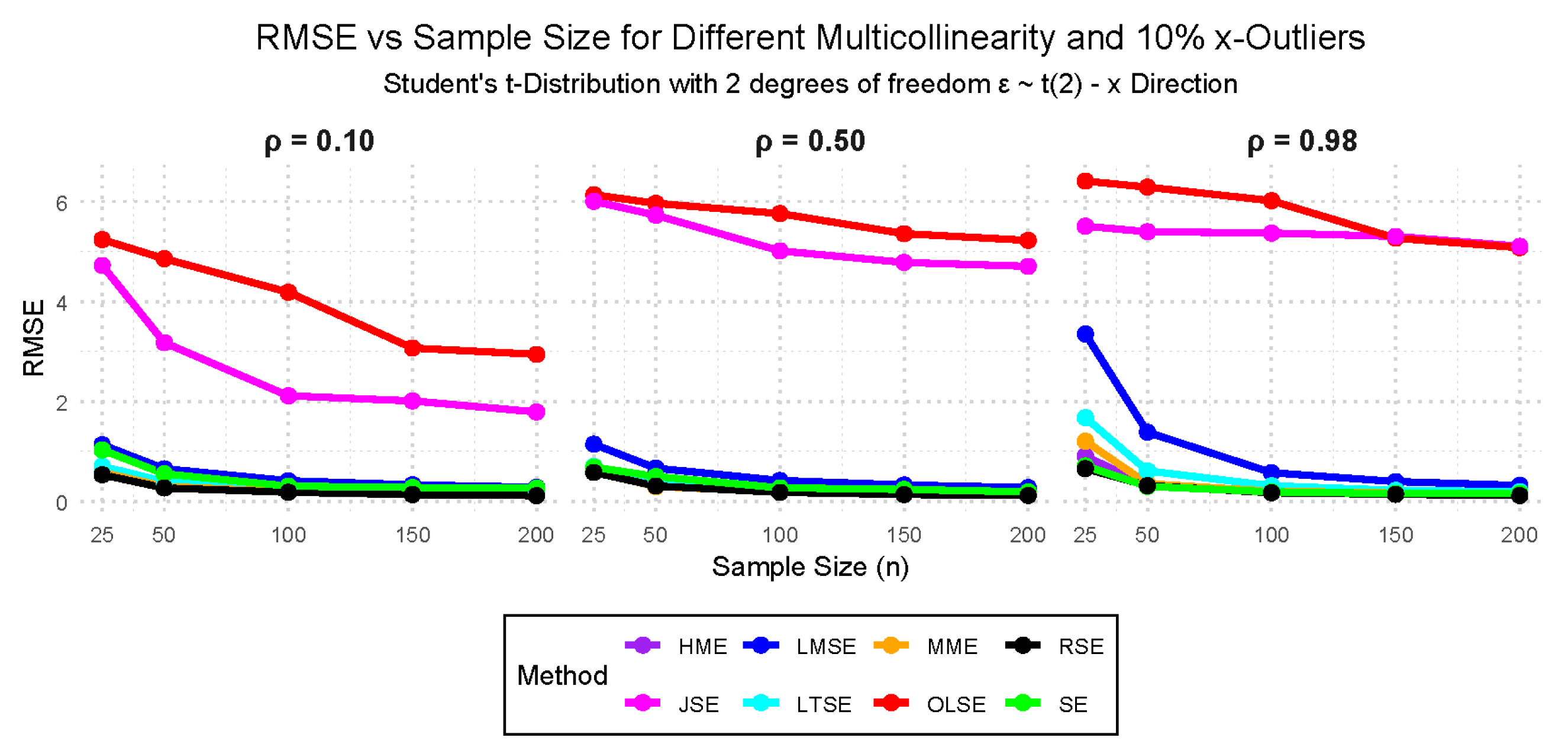
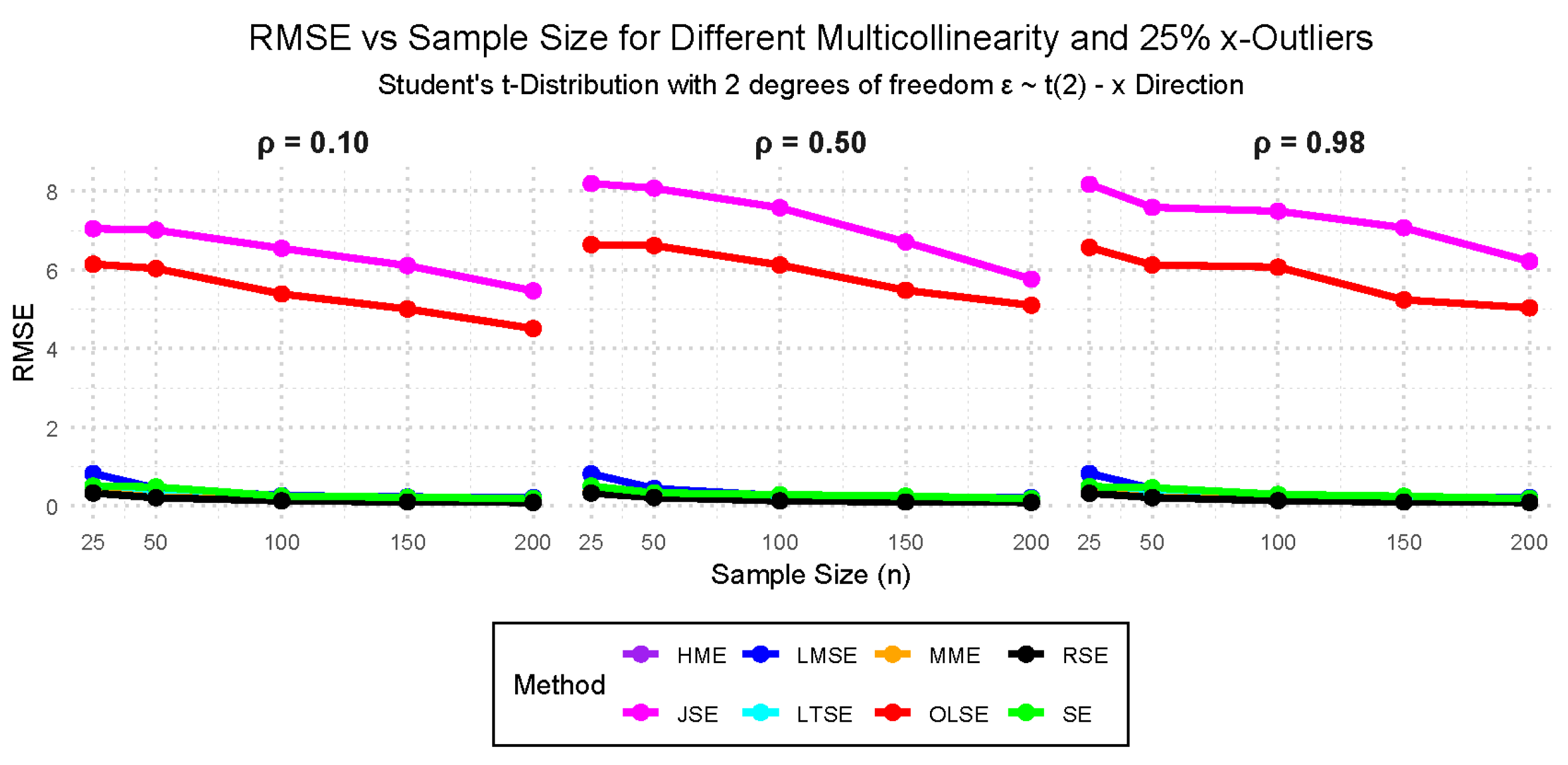
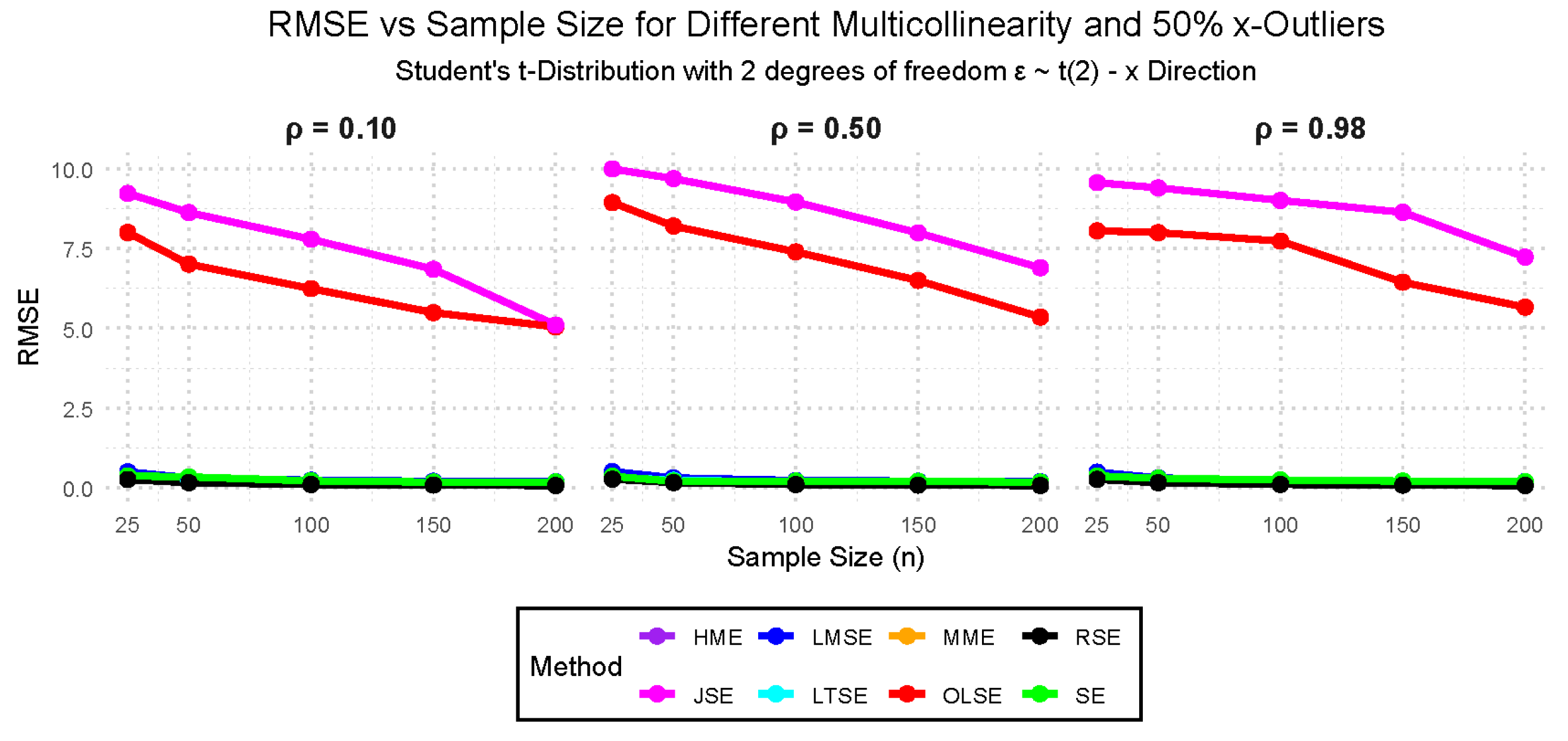
- Case VI: — Student’s t-distribution with 2 degrees of freedom, 10%, 25%, and 50% outliers with no multicollinearity.
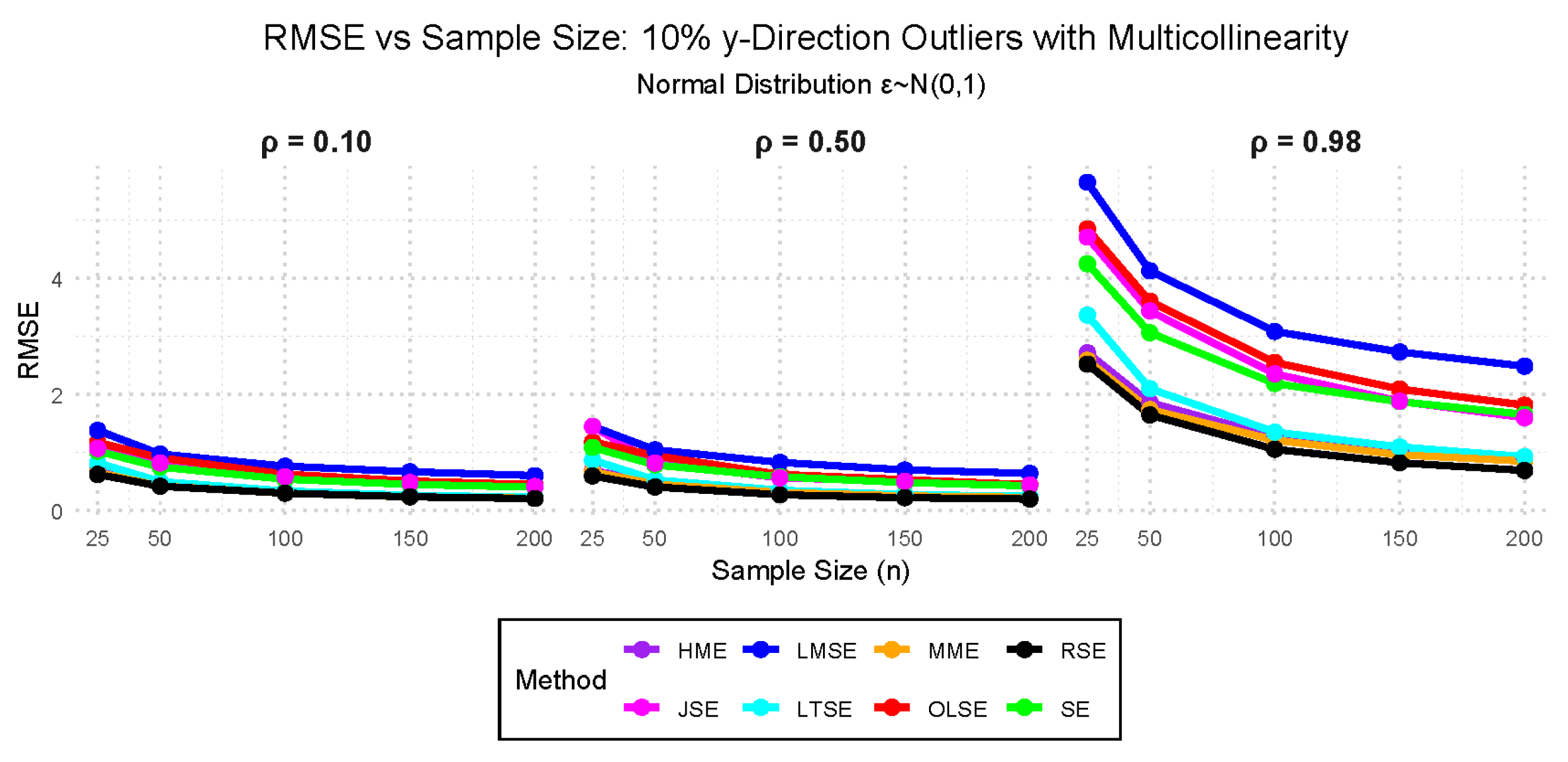
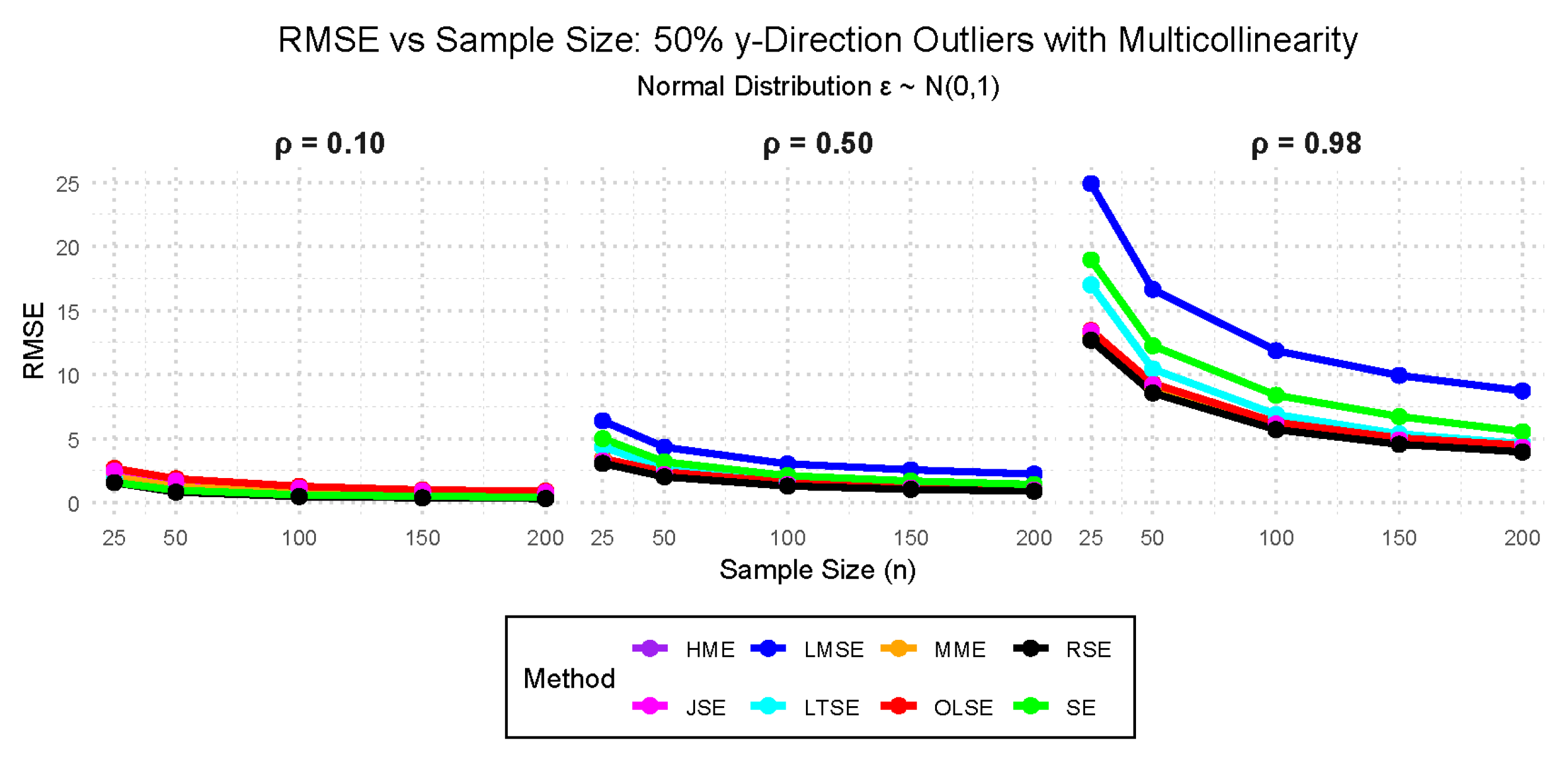
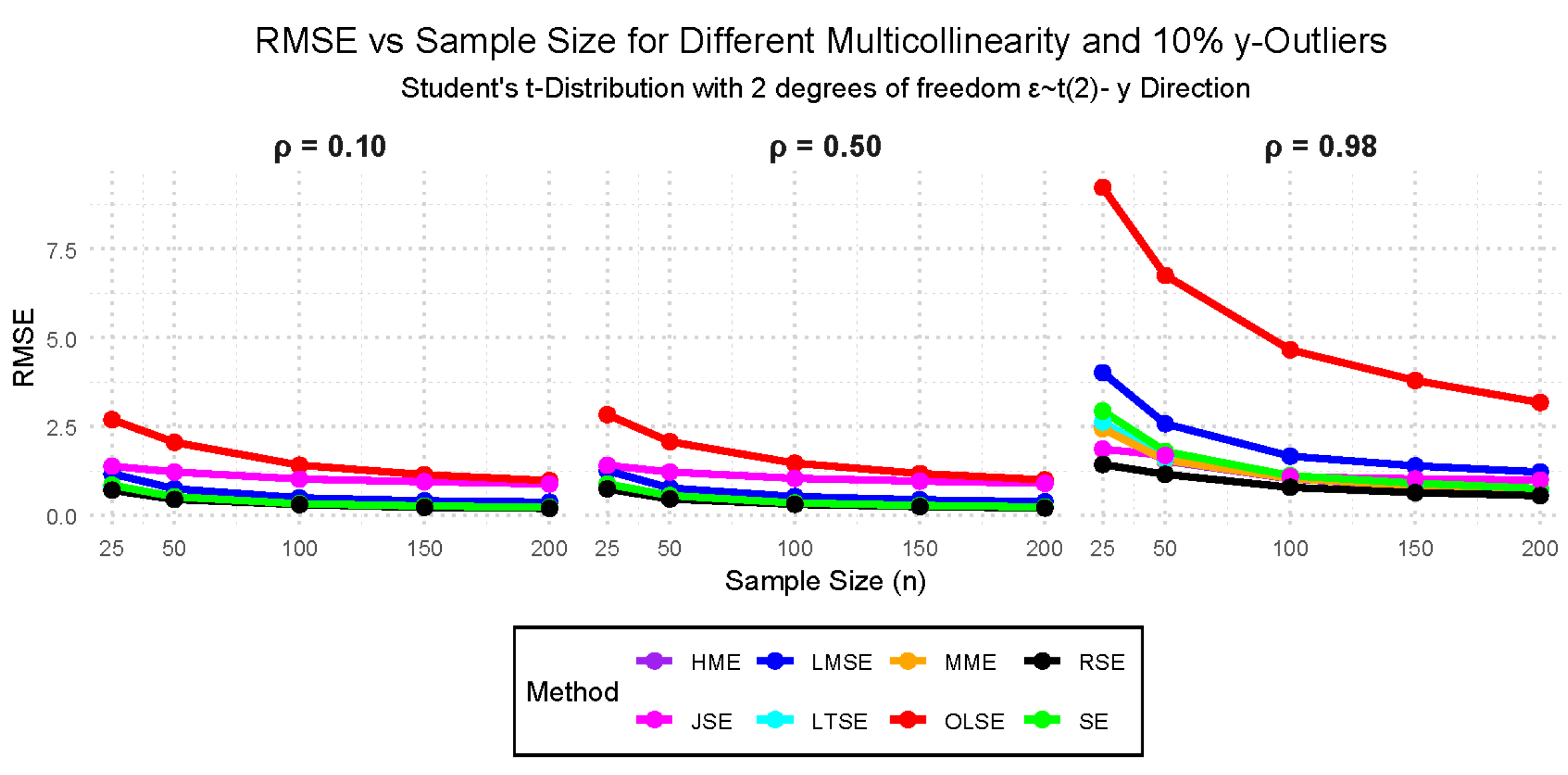
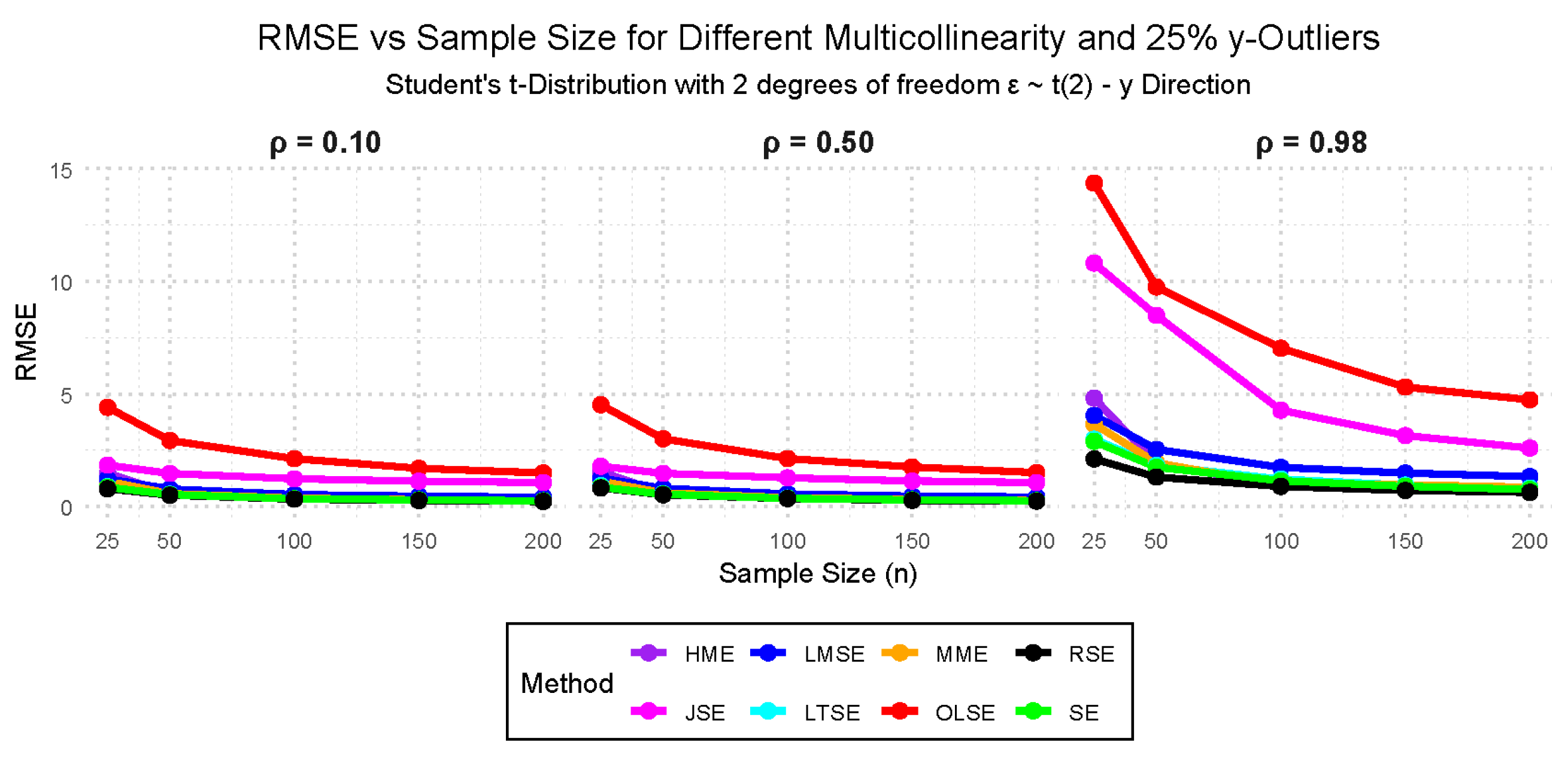
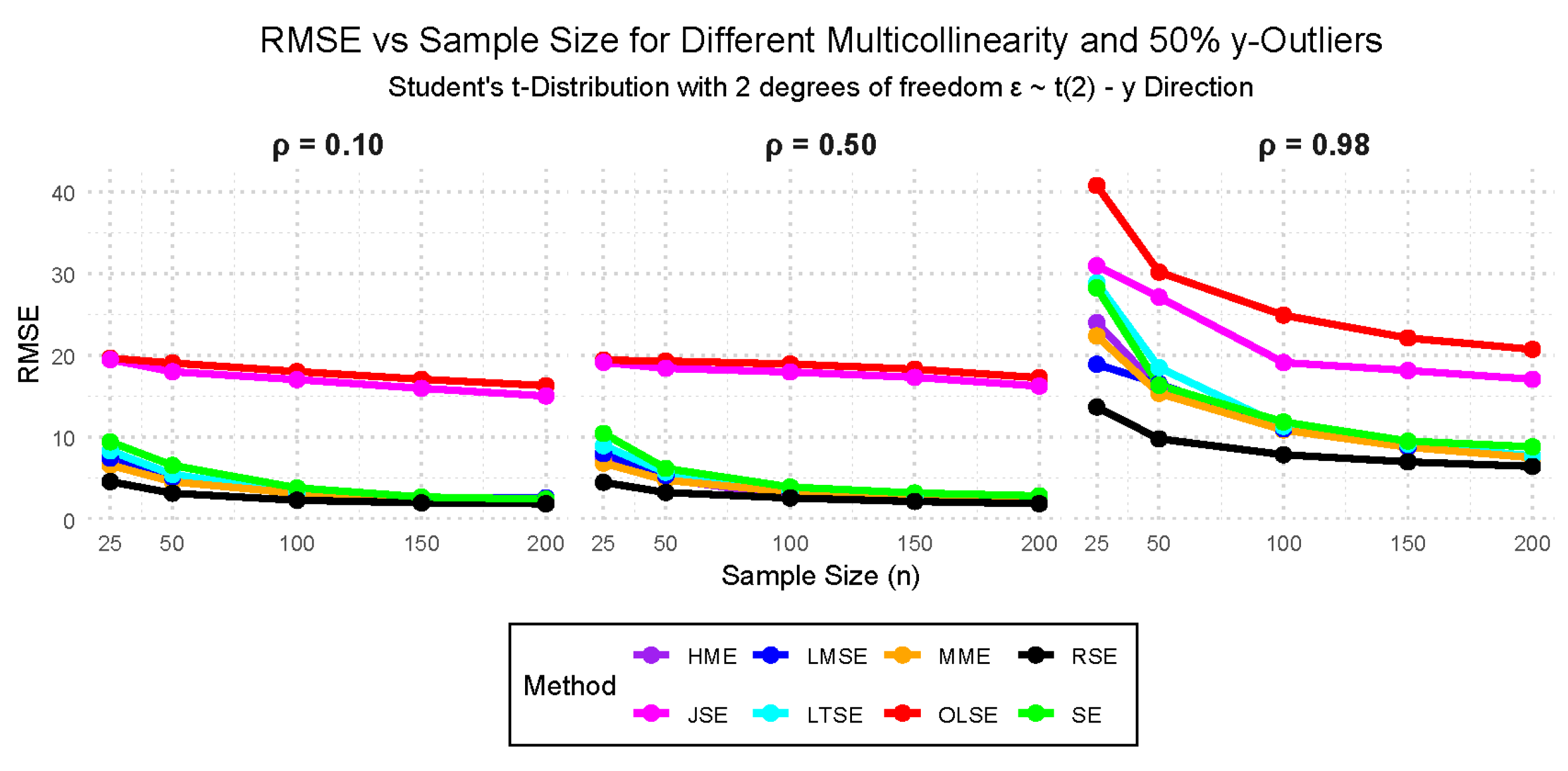
- Case VII: — 10%, 25%, and 50% outliers in the y-direction with 0.10, 0.50, and 0.98 multicollinearity.
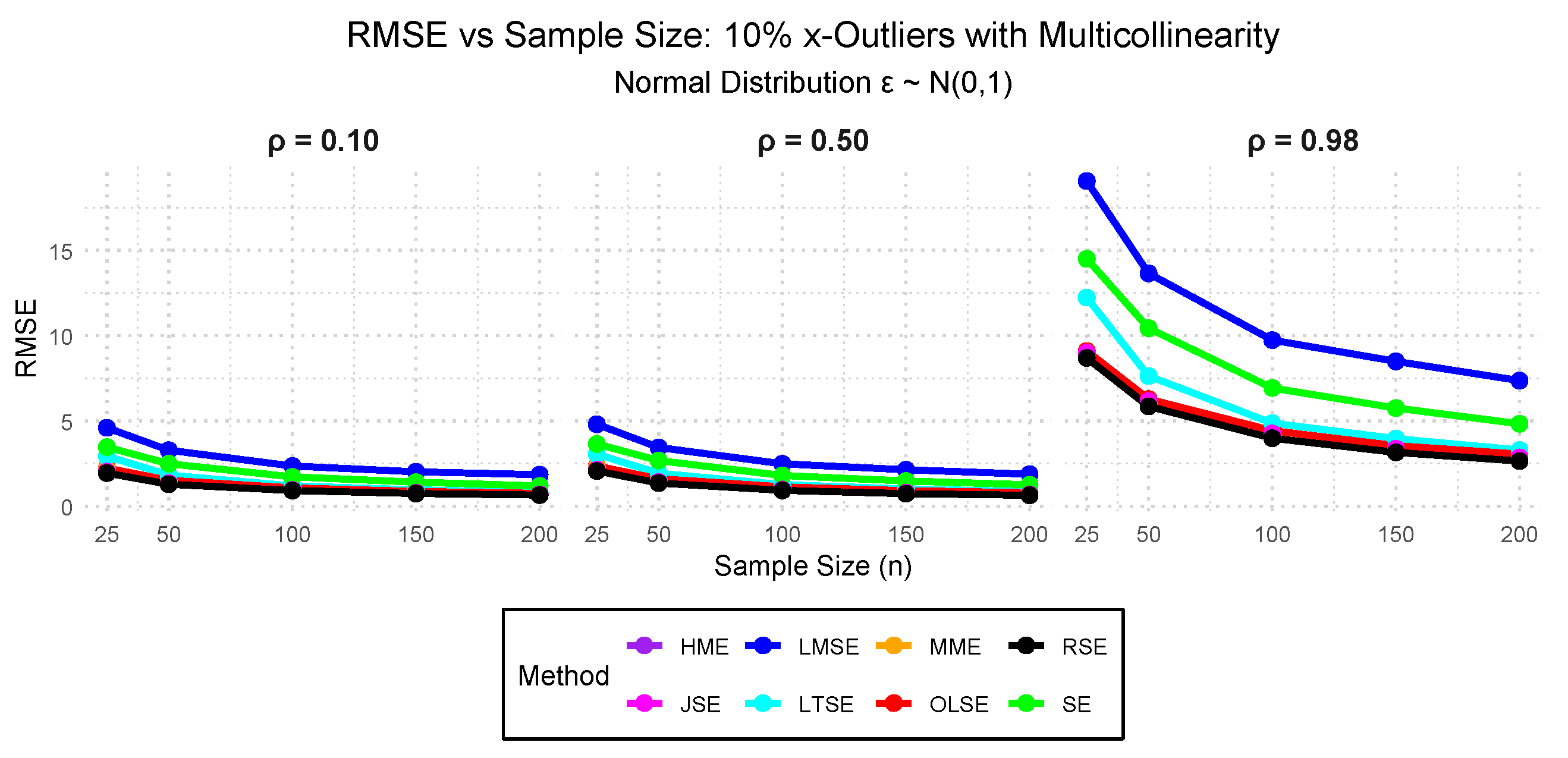
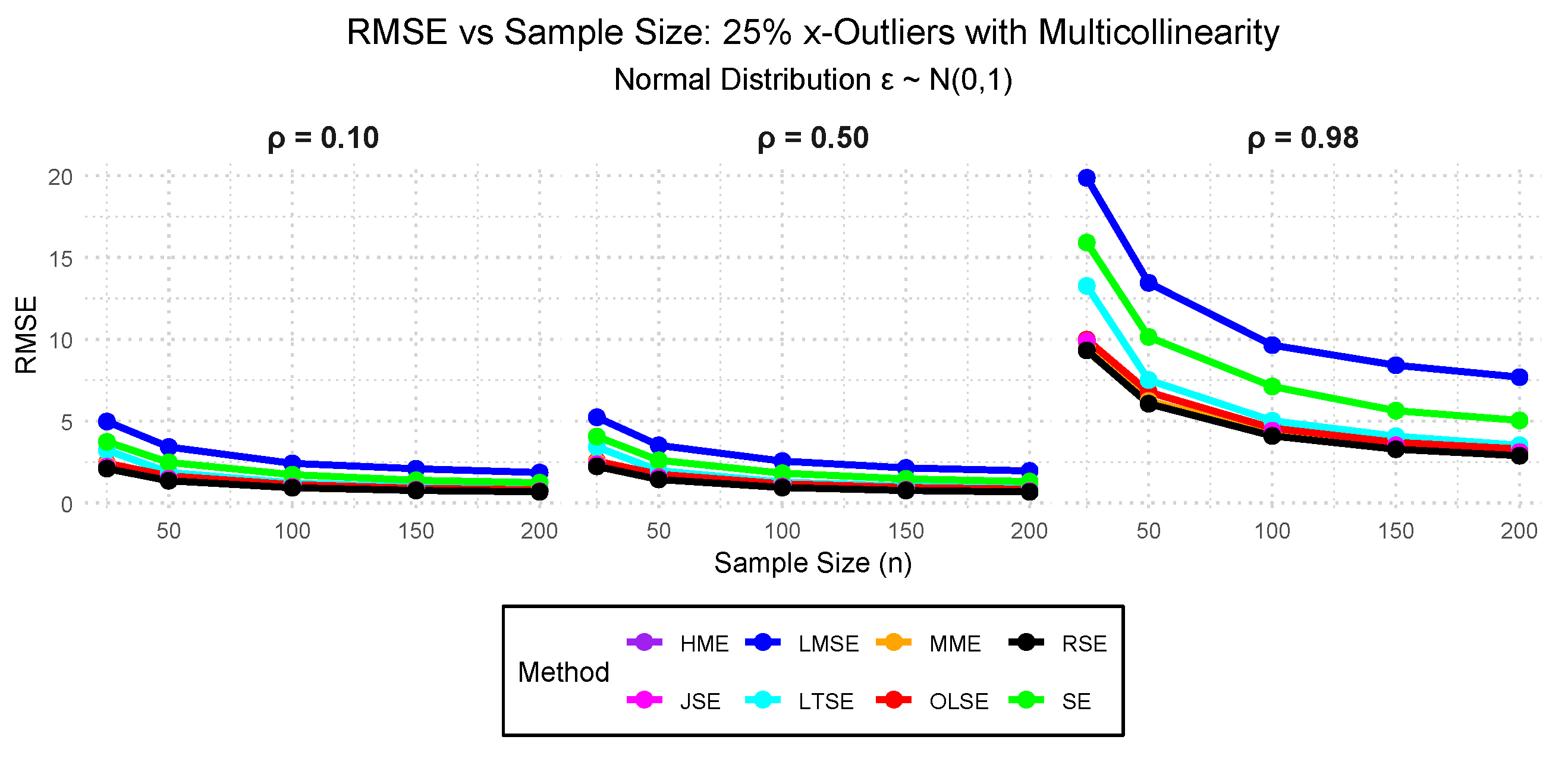
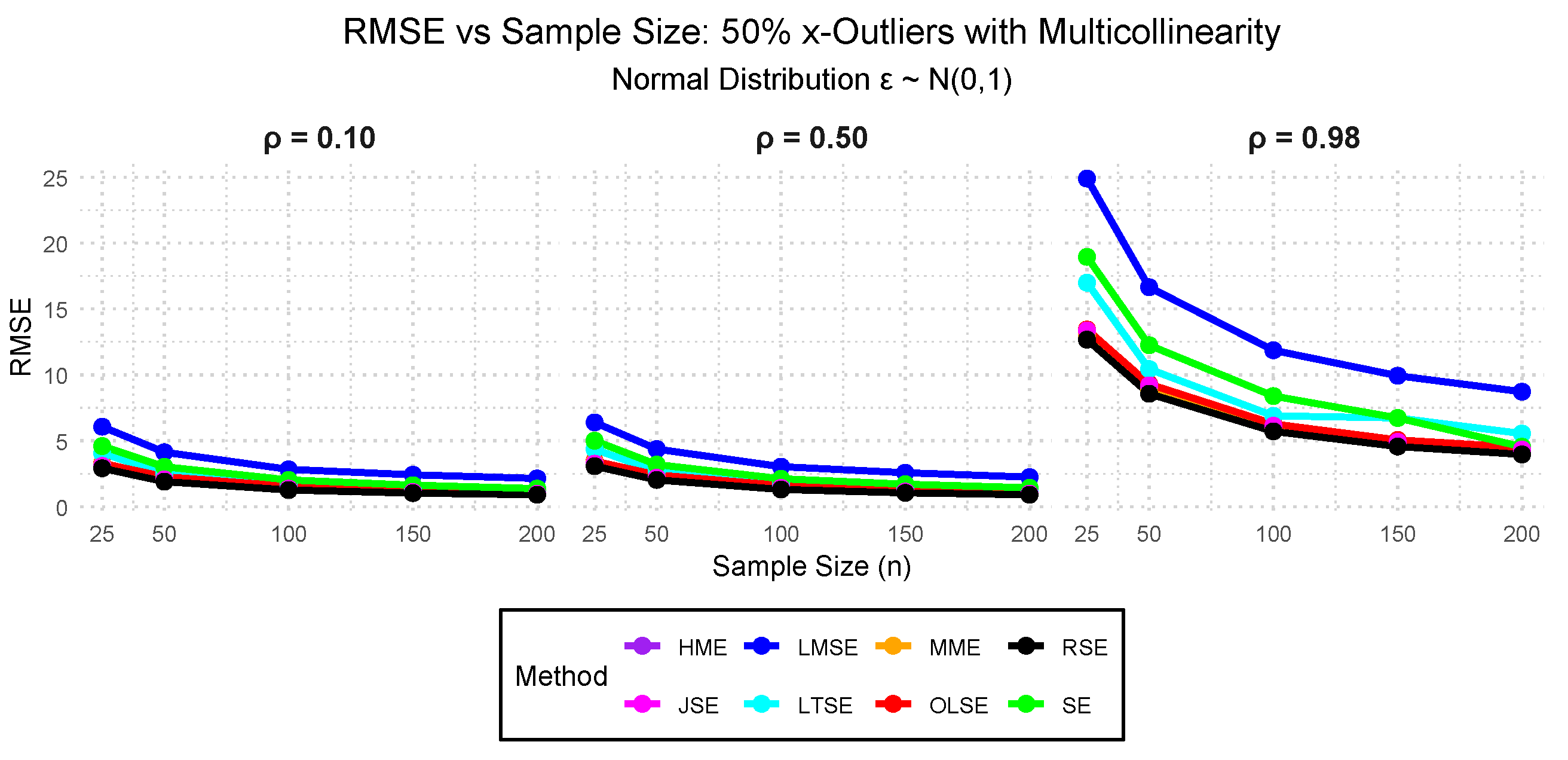
- Case VIII: — 10%, 25%, and 50% outliers in the x-direction with 0.10, 0.50, and 0.98 multicollinearity.
- Case IX: (Student’s t-distribution with 2 degrees of freedom), with multicollinearity levels of 0.10, 0.50, and 0.98, and outliers in the y-direction at 10%, 25%, and 50%.
- Case X: (Student’s t-distribution with 2 degrees of freedom), with multicollinearity levels of 0.10, 0.50, and 0.98, and outliers in the x-direction at 10%, 25%, and 50%.
| Sample size (n) | Multicollinearity () | Outlier () |
|---|---|---|
| 25 | 0.10 | 0.00 |
| 50 | 0.50 | 0.10 |
| 100 | 0.98 | 0.25 |
| 150 | 0.50 | |
| 200 |
3.2. Simulation Study Findings
3.2.1. Performance Evaluation Findings Across the Cases
4. Emprical Applications
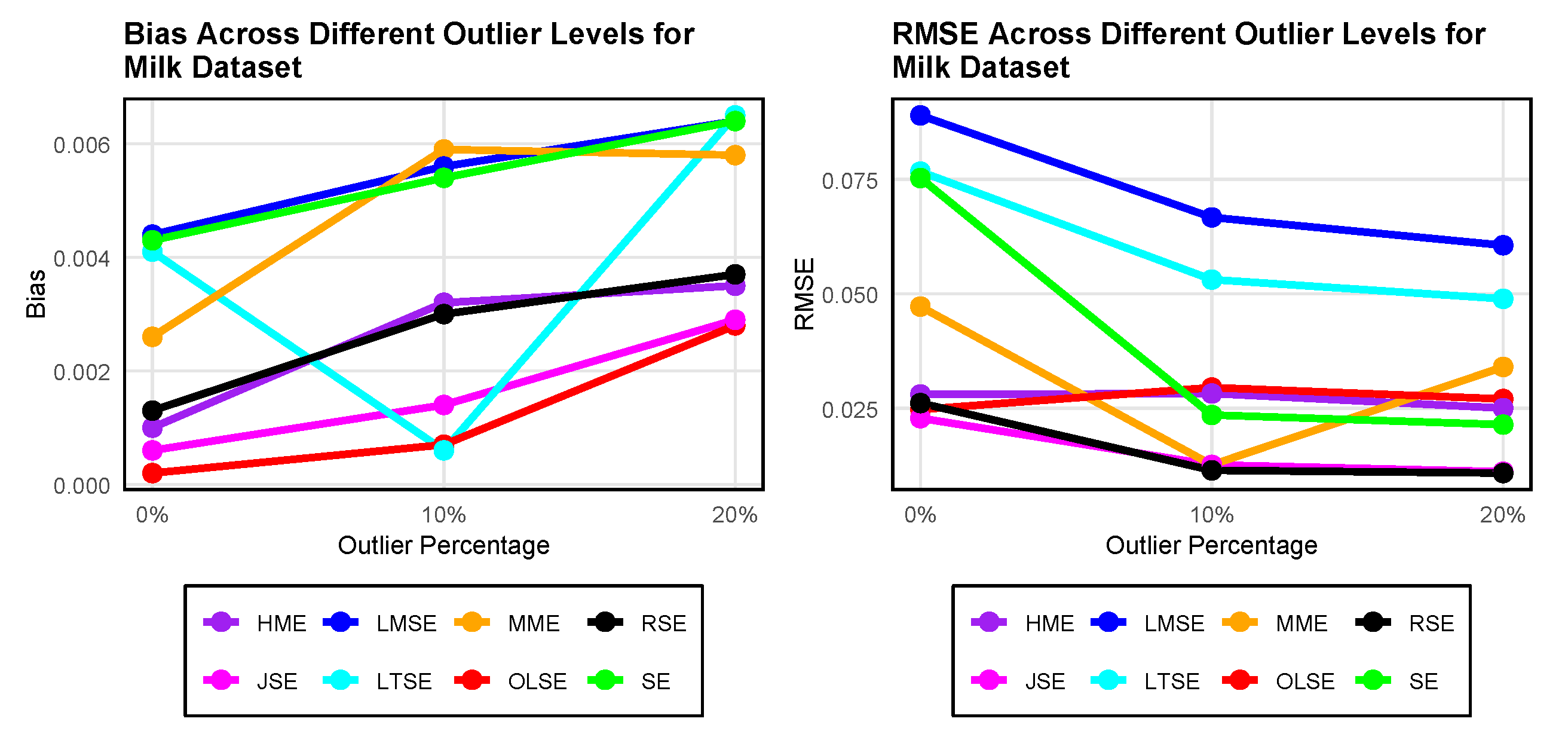
4.1. Exploratory Analysis for Milk Dataset
4.1.1. Multicollinearity Detection for Milk Dataset
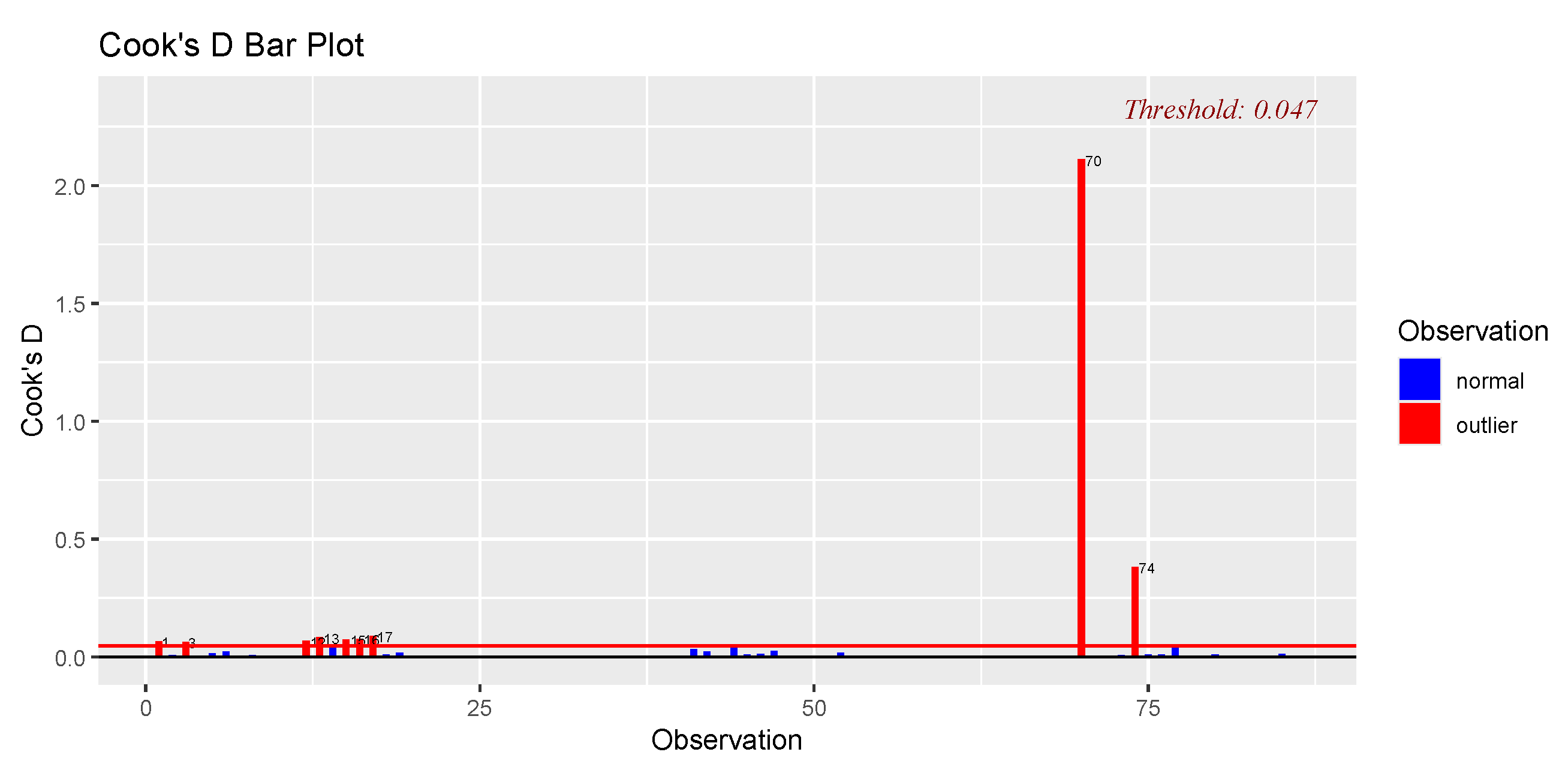
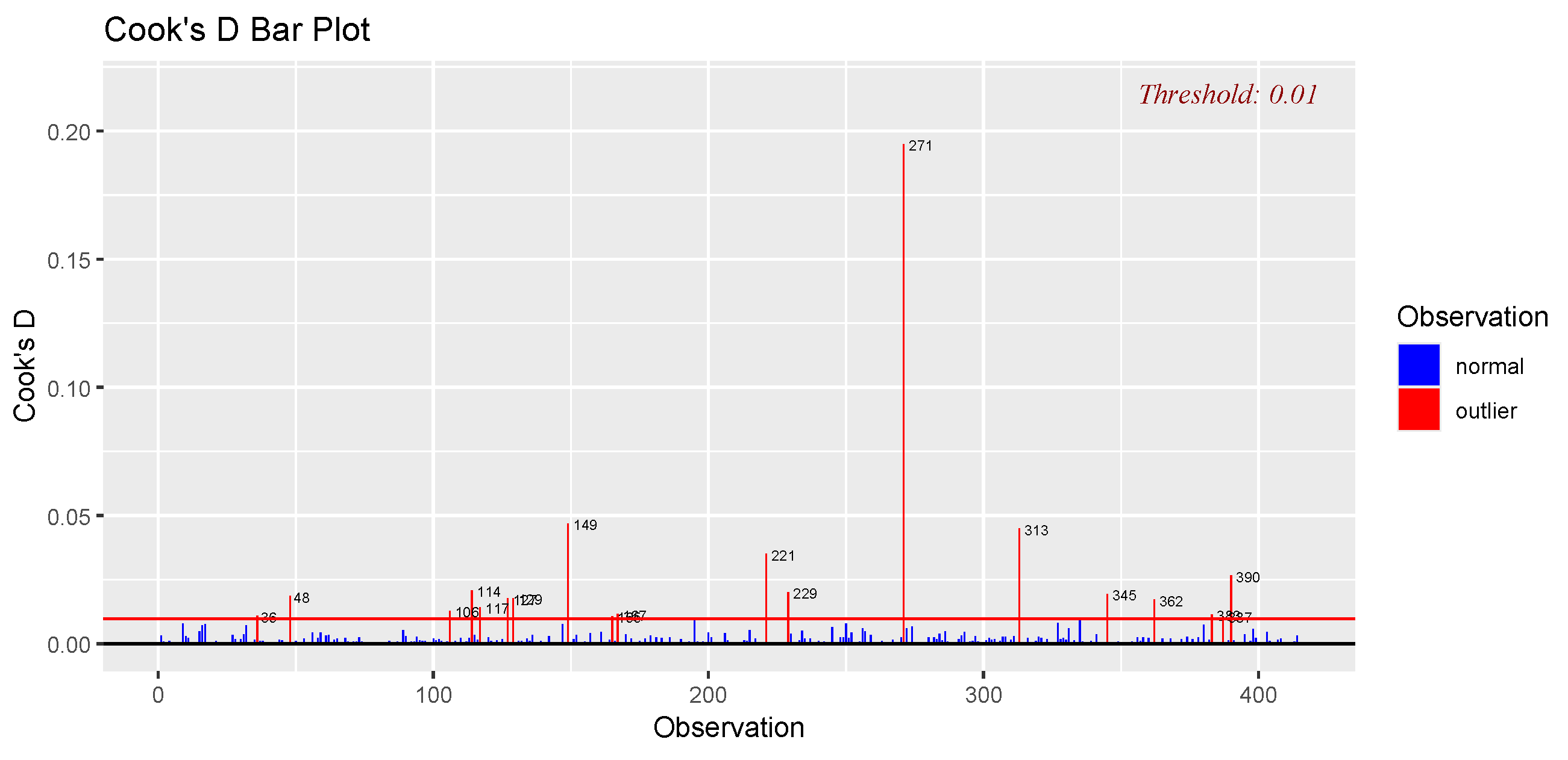
4.1.2. Outlier Detection Using Cook’s Distance for Milk Dataset
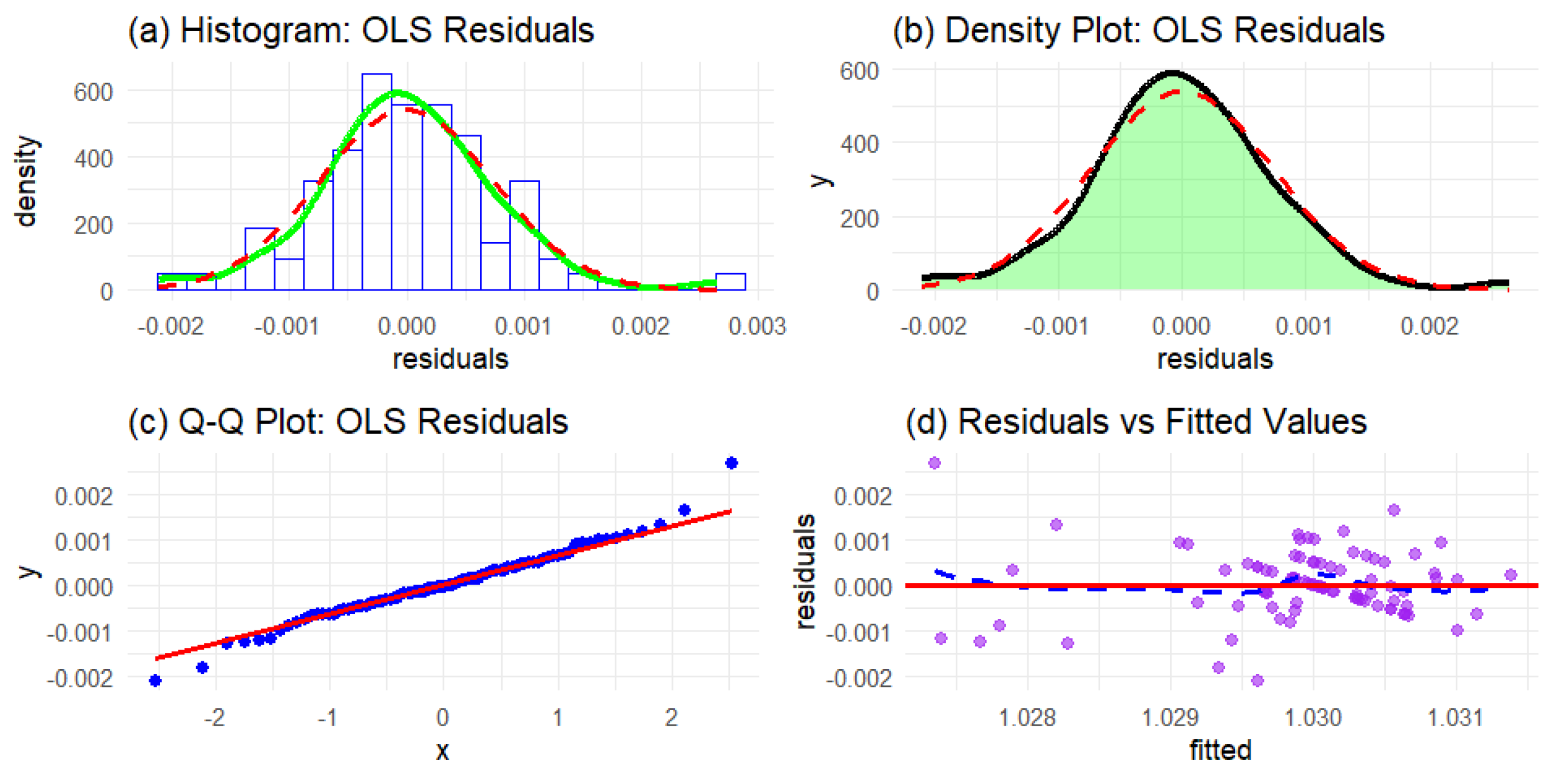
4.1.3. Testing for Normality for Milk Dataset
4.1.4. Model Fit and Evaluation for Milk Dataset
4.2. Exploratory Analysis for Real Estate Valuation
4.2.1. Multicollinearity Detection for Real Estate Valuation
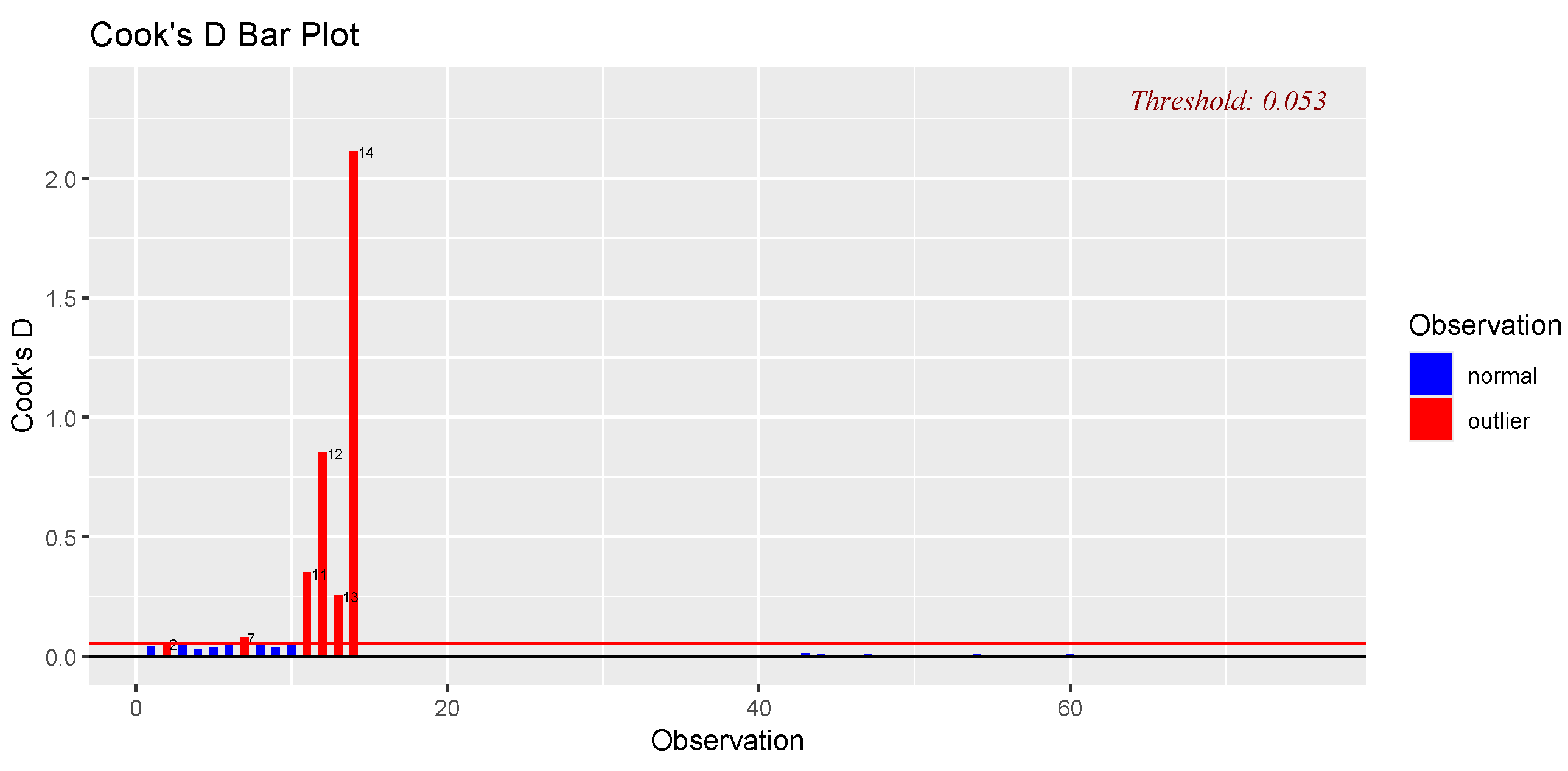
4.2.2. Outlier Detection Using Cook’s Distance for Real Estate Valuation Dataset
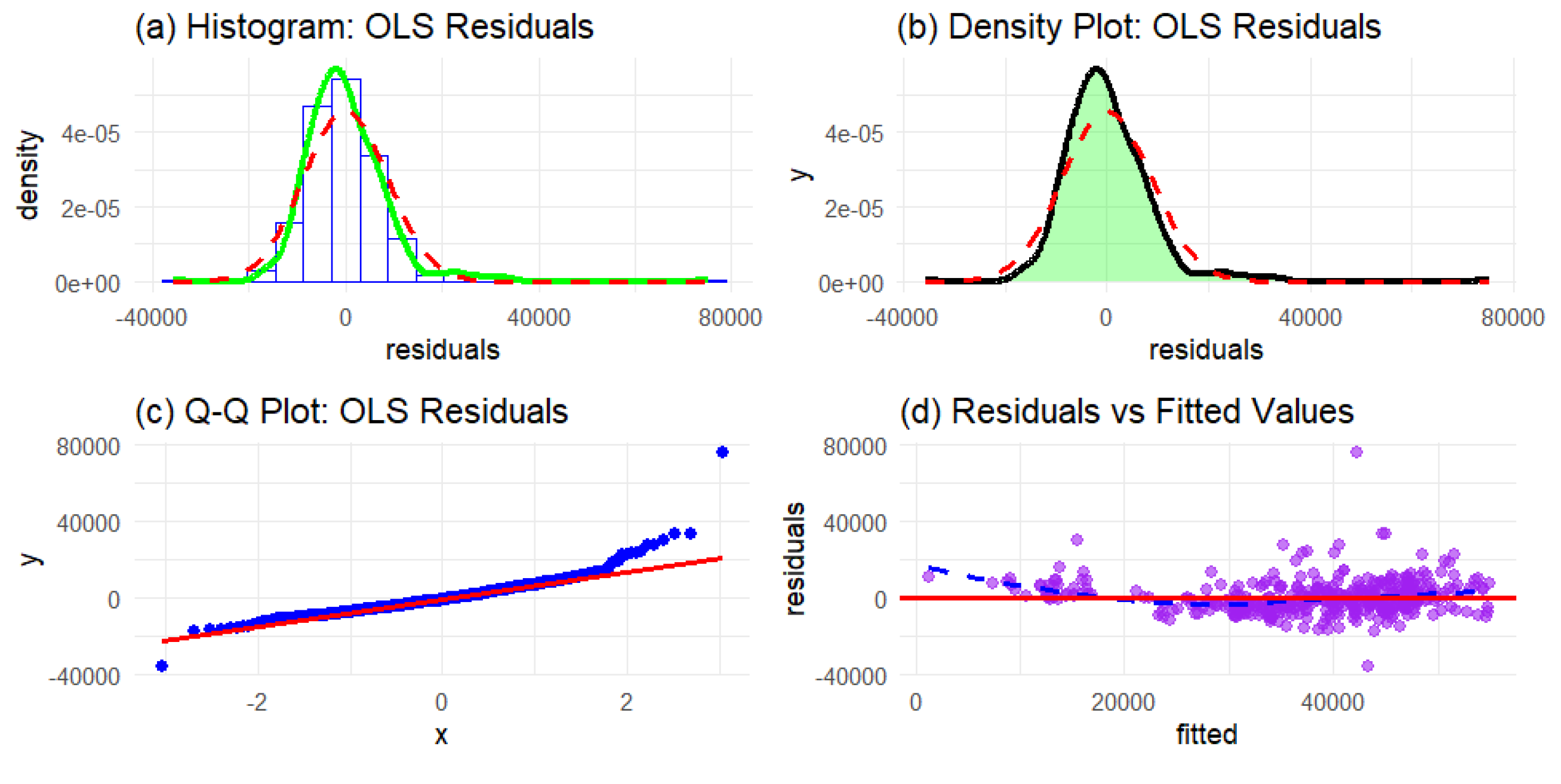
4.2.3. Testing for Normality for Real Estate Valuation Dataset
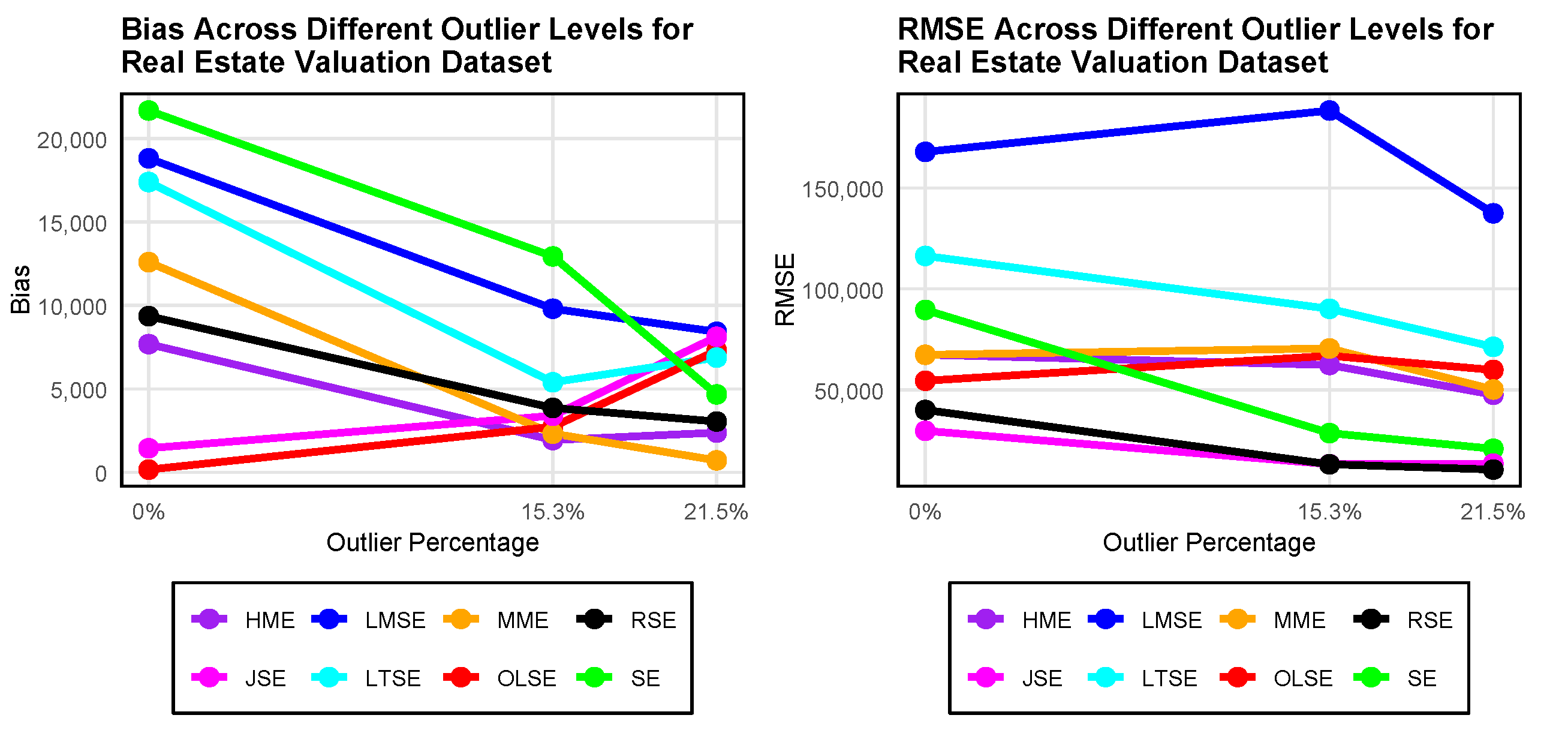
4.2.4. Model Fit and Evaluation for eal Estate Valuation Dataset
4.3. Exploratory Analysis for Hawkins Bradu Kass Dataset
4.3.1. Multicollinearity Detection for Hawkins Bradu Kass Dataset
4.3.2. Outlier Detection Using Cook’s Distance for Hawkins Bradu Kass Dataset
4.3.3. Testing for Normality for Hawkins Bradu Kass Dataset
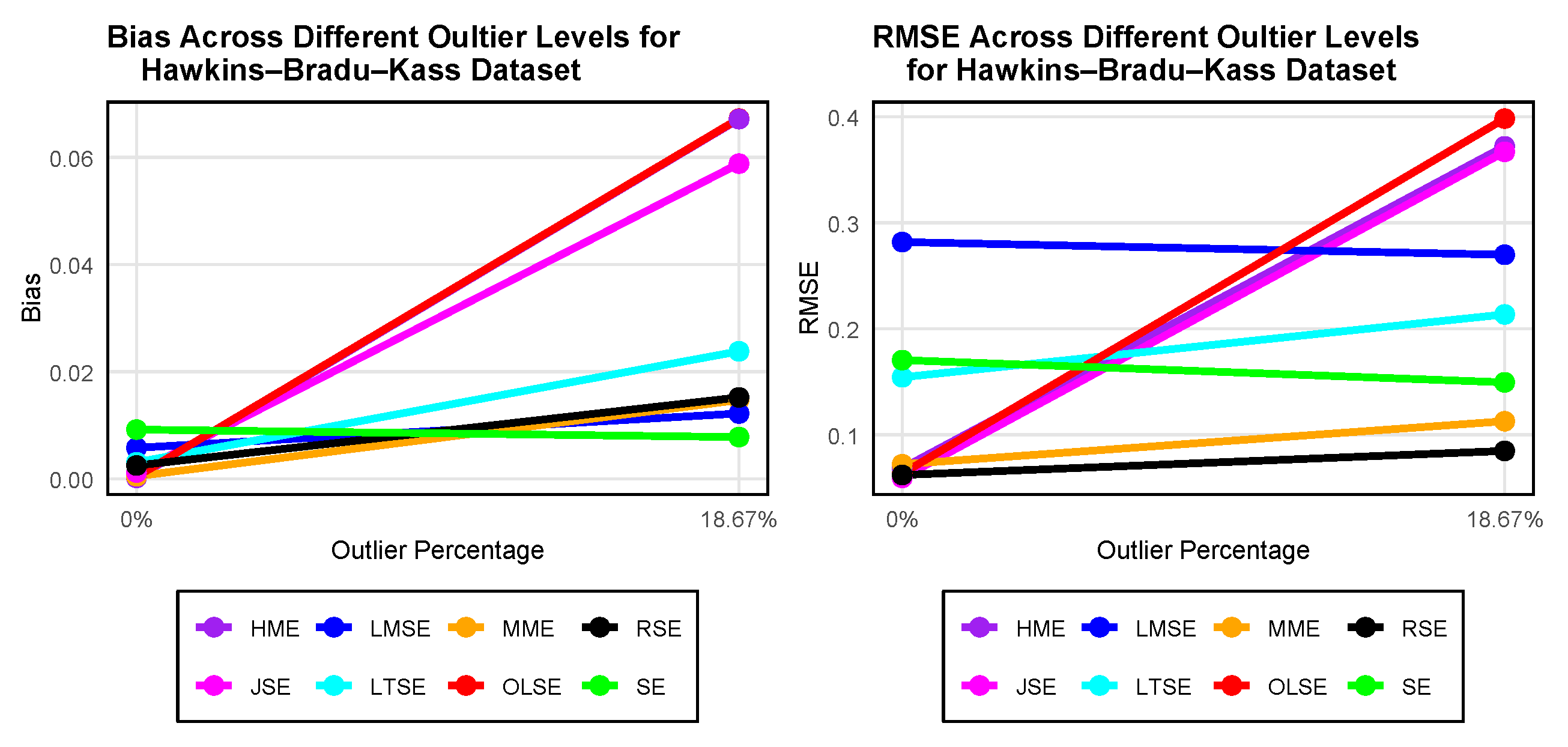
4.3.4. Model Fit and Evaluation for Hawkins Bradu Kass Dataset.
5. Discussion
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
| Study No. | Dataset | n | p | No. of Outliers | Outliers (%) |
|---|---|---|---|---|---|
| Milk dataset (original) | 86 | 8 | 20 | 20% | |
| 1 | Milk trimmed dataset | 62 | 8 | 0 | 0% |
| Milk trimmed dataset | 81 | 8 | 8 | 10% | |
| Real Estate Valuation (original) | 414 | 7 | 88 | 21.25% | |
| 2 | Real Estate Valuation trimmed dataset | 212 | 7 | 0 | 0% |
| Real Estate Valuation trimmed dataset | 268 | 7 | 41 | 15.3% | |
| Hawkins–Bradu–Kass dataset (original) | 75 | 4 | 14 | 18.67% | |
| 3 | Hawkins–Bradu–Kass trimmed dataset | 61 | 4 | 0 | 0% |
| Dataset | Variable | VIF | Variable | VIF |
|---|---|---|---|---|
| Milk dataset | 2.2007 | 24.7561 | ||
| 8.2865 | 3.2919 | |||
| 7.2187 | 2.1834 | |||
| 24.2253 | ||||
| Real Estate Valuation dataset | 1.0147 | 1.6023 | ||
| 1.0143 | 2.9263 | |||
| 4.3230 | ||||
| 1.6170 | ||||
| Hawkins Bradu Kass datase | 13.4320 | |||
| 23.8535 | ||||
| 33.4325 |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0048 | 0.7969 | 0.0071 | 0.5625 | 0.0080 | 2.1962 |
| 50 | 0.0031 | 0.5451 | 0.0064 | 0.3860 | 0.0173 | 1.5106 | |
| 100 | 0.0016 | 0.3808 | 0.0025 | 0.2692 | 0.0096 | 1.0585 | |
| 150 | 0.0019 | 0.3016 | 0.0010 | 0.2140 | 0.0036 | 0.8410 | |
| 200 | 0.0008 | 0.2651 | 0.0014 | 0.1833 | 0.0153 | 0.7204 | |
| HME | 25 | 0.0004 | 0.7367 | 0.0055 | 0.5905 | 0.0193 | 2.3061 |
| 50 | 0.0049 | 0.4955 | 0.0052 | 0.4067 | 0.0173 | 1.5944 | |
| 100 | 0.0021 | 0.3392 | 0.0009 | 0.2817 | 0.0050 | 1.1043 | |
| 150 | 0.0032 | 0.2705 | 0.0029 | 0.2245 | 0.0135 | 0.8834 | |
| 200 | 0.0027 | 0.2369 | 0.0016 | 0.1924 | 0.0152 | 0.7554 | |
| MME | 25 | 0.0048 | 0.7450 | 0.0065 | 0.6064 | 0.0160 | 2.3551 |
| 50 | 0.0034 | 0.4964 | 0.0064 | 0.4113 | 0.0191 | 1.6135 | |
| 100 | 0.0029 | 0.3450 | 0.0010 | 0.2885 | 0.0080 | 1.1326 | |
| 150 | 0.0032 | 0.2735 | 0.0029 | 0.2338 | 0.0181 | 0.9137 | |
| 200 | 0.0033 | 0.2377 | 0.0005 | 0.2031 | 0.0184 | 0.7736 | |
| LMSE | 25 | 0.0236 | 1.5696 | 0.0125 | 1.4520 | 0.0490 | 5.6943 |
| 50 | 0.0144 | 1.1159 | 0.0225 | 1.0589 | 0.0505 | 4.1858 | |
| 100 | 0.0114 | 0.8152 | 0.0045 | 0.8262 | 0.0335 | 3.1939 | |
| 150 | 0.0067 | 0.6859 | 0.0073 | 0.7339 | 0.0387 | 2.7792 | |
| 200 | 0.0087 | 0.6201 | 0.0094 | 0.6494 | 0.0063 | 2.4765 | |
| LTSE | 25 | 0.0076 | 0.9591 | 0.0033 | 0.8883 | 0.0473 | 3.3716 |
| 50 | 0.0038 | 0.5957 | 0.0080 | 0.5332 | 0.0150 | 2.0957 | |
| 100 | 0.0036 | 0.3777 | 0.0057 | 0.3466 | 0.0162 | 1.3443 | |
| 150 | 0.0043 | 0.3010 | 0.0013 | 0.2741 | 0.0124 | 1.0760 | |
| 200 | 0.0027 | 0.2567 | 0.0034 | 0.2336 | 0.0170 | 0.9105 | |
| SE | 25 | 0.0135 | 1.1950 | 0.0122 | 1.1329 | 0.0784 | 4.3873 |
| 50 | 0.0089 | 0.8378 | 0.0082 | 0.8368 | 0.0301 | 3.3277 | |
| 100 | 0.0099 | 0.5921 | 0.0028 | 0.6184 | 0.0254 | 2.3643 | |
| 150 | 0.0071 | 0.4814 | 0.0031 | 0.5198 | 0.0295 | 2.0266 | |
| 200 | 0.0027 | 0.4170 | 0.0037 | 0.4561 | 0.0173 | 1.7737 | |
| JSE | 25 | 0.0037 | 0.2250 | 0.0107 | 0.4773 | 0.0661 | 1.9841 |
| 50 | 0.0003 | 0.0370 | 0.0076 | 0.3276 | 0.0430 | 1.2924 | |
| 100 | 0.0000 | 0.0000 | 0.0046 | 0.2253 | 0.0434 | 0.8524 | |
| 150 | 0.0000 | 0.0000 | 0.0025 | 0.1809 | 0.0256 | 0.6505 | |
| 200 | 0.0000 | 0.0000 | 0.0024 | 0.1535 | 0.0194 | 0.5438 | |
| RSE | 25 | 0.0037 | 0.1838 | 0.0116 | 0.5022 | 0.0759 | 2.0991 |
| 50 | 0.0003 | 0.0235 | 0.0065 | 0.3444 | 0.0461 | 1.3762 | |
| 100 | 0.0000 | 0.0000 | 0.0055 | 0.2366 | 0.0425 | 0.8949 | |
| 150 | 0.0000 | 0.0000 | 0.0033 | 0.1896 | 0.0329 | 0.6874 | |
| 200 | 0.0000 | 0.0000 | 0.0028 | 0.1611 | 0.0233 | 0.5744 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0123 | 0.7426 | 0.0066 | 0.7806 | 0.0216 | 3.0798 |
| 50 | 0.0027 | 0.4939 | 0.0037 | 0.5268 | 0.0152 | 2.0303 | |
| 100 | 0.0054 | 0.3541 | 0.0062 | 0.3753 | 0.0169 | 1.4894 | |
| 150 | 0.0010 | 0.2870 | 0.0053 | 0.3012 | 0.0153 | 1.1769 | |
| 200 | 0.0058 | 0.2611 | 0.0045 | 0.2817 | 0.0069 | 1.0910 | |
| HME | 25 | 0.0061 | 0.6519 | 0.0154 | 0.6874 | 0.0306 | 2.7191 |
| 50 | 0.0035 | 0.4402 | 0.0072 | 0.4624 | 0.0192 | 1.7788 | |
| 100 | 0.0039 | 0.3065 | 0.0040 | 0.3260 | 0.0102 | 1.2931 | |
| 150 | 0.0018 | 0.2491 | 0.0035 | 0.2613 | 0.0236 | 1.0218 | |
| 200 | 0.0019 | 0.2184 | 0.0017 | 0.2308 | 0.0067 | 0.9018 | |
| MME | 25 | 0.0091 | 0.6554 | 0.0116 | 0.6922 | 0.0222 | 2.7395 |
| 50 | 0.0020 | 0.4447 | 0.0037 | 0.4656 | 0.0166 | 1.7988 | |
| 100 | 0.0051 | 0.3109 | 0.0046 | 0.3317 | 0.0031 | 1.3056 | |
| 150 | 0.0043 | 0.2569 | 0.0053 | 0.2669 | 0.0206 | 1.0457 | |
| 200 | 0.0019 | 0.2233 | 0.0019 | 0.2338 | 0.0051 | 0.9262 | |
| LMSE | 25 | 0.0018 | 1.4606 | 0.0085 | 1.5271 | 0.0909 | 6.0429 |
| 50 | 0.0074 | 1.0703 | 0.0124 | 1.1522 | 0.0852 | 4.4395 | |
| 100 | 0.0114 | 0.8019 | 0.0070 | 0.8446 | 0.0392 | 3.3496 | |
| 150 | 0.0104 | 0.7081 | 0.0064 | 0.7417 | 0.0163 | 2.9055 | |
| 200 | 0.0085 | 0.6387 | 0.0037 | 0.6779 | 0.0252 | 2.6226 | |
| LTSE | 25 | 0.0146 | 0.8923 | 0.0168 | 0.9548 | 0.0262 | 3.6888 |
| 50 | 0.0030 | 0.5645 | 0.0082 | 0.6011 | 0.0218 | 2.3083 | |
| 100 | 0.0034 | 0.3680 | 0.0056 | 0.3962 | 0.0154 | 1.5443 | |
| 150 | 0.0027 | 0.3054 | 0.0027 | 0.3190 | 0.0260 | 1.2319 | |
| 200 | 0.0029 | 0.2662 | 0.0029 | 0.2745 | 0.0049 | 1.0743 | |
| SE | 25 | 0.0149 | 1.0998 | 0.0063 | 1.1431 | 0.0280 | 4.6433 |
| 50 | 0.0047 | 0.7914 | 0.0065 | 0.8444 | 0.0129 | 3.2186 | |
| 100 | 0.0058 | 0.5706 | 0.0094 | 0.6112 | 0.0277 | 2.3669 | |
| 150 | 0.0090 | 0.4875 | 0.0083 | 0.5134 | 0.0304 | 2.0260 | |
| 200 | 0.0046 | 0.4245 | 0.0056 | 0.4416 | 0.0107 | 1.7412 | |
| JSE | 25 | 0.0234 | 0.6805 | 0.0246 | 0.6675 | 0.0777 | 2.8964 |
| 50 | 0.0116 | 0.4579 | 0.0152 | 0.4494 | 0.0745 | 1.8283 | |
| 100 | 0.0063 | 0.3252 | 0.0068 | 0.3130 | 0.0524 | 1.2813 | |
| 150 | 0.0080 | 0.2689 | 0.0044 | 0.2548 | 0.0417 | 0.9715 | |
| 200 | 0.0027 | 0.2399 | 0.0010 | 0.2360 | 0.0345 | 0.9034 | |
| RSE | 25 | 0.0157 | 0.5964 | 0.2093 | 0.5832 | 0.0781 | 2.5176 |
| 50 | 0.0120 | 0.4152 | 0.0123 | 0.3979 | 0.0585 | 1.5641 | |
| 100 | 0.0049 | 0.2813 | 0.0055 | 0.2705 | 0.0484 | 1.0821 | |
| 150 | 0.0042 | 0.2349 | 0.0032 | 0.2212 | 0.0290 | 0.8186 | |
| 200 | 0.0014 | 0.2036 | 0.0008 | 0.1939 | 0.0286 | 0.7053 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0108 | 1.9081 | 0.0363 | 1.5837 | 0.0343 | 6.3193 |
| 50 | 0.0083 | 0.9523 | 0.0063 | 0.9997 | 0.0226 | 3.9887 | |
| 100 | 0.0097 | 0.6049 | 0.0029 | 0.7770 | 0.0326 | 2.9553 | |
| 150 | 0.0068 | 0.5355 | 0.0029 | 0.5735 | 0.0283 | 2.2427 | |
| 200 | 0.0060 | 0.4347 | 0.0077 | 0.5177 | 0.0298 | 2.0001 | |
| HME | 25 | 0.0069 | 0.7556 | 0.0040 | 0.7981 | 0.0368 | 3.1272 |
| 50 | 0.0052 | 0.5005 | 0.0023 | 0.5157 | 0.0348 | 1.9727 | |
| 100 | 0.0036 | 0.3357 | 0.0036 | 0.3515 | 0.0179 | 1.3784 | |
| 150 | 0.0042 | 0.2731 | 0.0028 | 0.2860 | 0.0079 | 1.1151 | |
| 200 | 0.0024 | 0.2306 | 0.0031 | 0.2437 | 0.0014 | 0.9518 | |
| MME | 25 | 0.0048 | 0.7392 | 0.0075 | 0.7847 | 0.0241 | 3.0678 |
| 50 | 0.0067 | 0.4957 | 0.0030 | 0.5140 | 0.0348 | 1.9556 | |
| 100 | 0.0029 | 0.3305 | 0.0040 | 0.3492 | 0.0150 | 1.3666 | |
| 150 | 0.0026 | 0.2755 | 0.0019 | 0.2858 | 0.0109 | 1.1261 | |
| 200 | 0.0030 | 0.2283 | 0.0021 | 0.2438 | 0.0070 | 0.9481 | |
| LMSE | 25 | 0.0371 | 1.4968 | 0.0141 | 1.5585 | 0.0470 | 6.1612 |
| 50 | 0.0141 | 1.1147 | 0.0083 | 1.1513 | 0.0508 | 4.5106 | |
| 100 | 0.0085 | 0.8248 | 0.0105 | 0.8907 | 0.0191 | 3.4257 | |
| 150 | 0.0038 | 0.7199 | 0.0084 | 0.7672 | 0.0261 | 2.9467 | |
| 200 | 0.0042 | 0.6274 | 0.0075 | 0.6625 | 0.0196 | 2.5748 | |
| LTSE | 25 | 0.0174 | 0.9393 | 0.0158 | 1.0102 | 0.0448 | 3.8620 |
| 50 | 0.0033 | 0.6015 | 0.0092 | 0.6156 | 0.0173 | 2.3741 | |
| 100 | 0.0056 | 0.3893 | 0.0054 | 0.4122 | 0.0229 | 1.6104 | |
| 150 | 0.0054 | 0.3245 | 0.0042 | 0.3397 | 0.0138 | 1.3150 | |
| 200 | 0.0011 | 0.2687 | 0.0034 | 0.2872 | 0.0095 | 1.1192 | |
| SE | 25 | 0.0152 | 1.1244 | 0.0097 | 1.2179 | 0.0888 | 4.6215 |
| 50 | 0.0034 | 0.7851 | 0.0067 | 0.7939 | 0.0592 | 3.2794 | |
| 100 | 0.0048 | 0.5736 | 0.0075 | 0.6120 | 0.0133 | 2.3900 | |
| 150 | 0.0029 | 0.4841 | 0.0035 | 0.5061 | 0.0113 | 1.9832 | |
| 200 | 0.0018 | 0.3995 | 0.0048 | 0.4249 | 0.0141 | 1.6467 | |
| JSE | 25 | 0.0457 | 1.3759 | 0.0470 | 1.6786 | 0.0724 | 6.2188 |
| 50 | 0.0294 | 0.9000 | 0.0257 | 0.8909 | 0.0782 | 3.7598 | |
| 100 | 0.0118 | 0.5776 | 0.0199 | 0.7118 | 0.0897 | 2.8167 | |
| 150 | 0.0096 | 0.5067 | 0.0120 | 0.5562 | 0.0552 | 2.0879 | |
| 200 | 0.0056 | 0.4034 | 0.0130 | 0.4802 | 0.0643 | 1.8965 | |
| RSE | 25 | 0.0239 | 0.6831 | 0.0210 | 0.6786 | 0.0681 | 2.9392 |
| 50 | 0.0102 | 0.4820 | 0.0141 | 0.4488 | 0.0585 | 1.7551 | |
| 100 | 0.0040 | 0.3145 | 0.0105 | 0.2950 | 0.0537 | 1.1619 | |
| 150 | 0.0049 | 0.2565 | 0.0051 | 0.2422 | 0.0394 | 0.9057 | |
| 200 | 0.0018 | 0.2153 | 0.0018 | 0.2044 | 0.0307 | 0.7498 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 1.7105 | 410.0024 | 1.1075 | 458.8047 | 2.9021 | 1949.7800 |
| 50 | 7.4097 | 88.0969 | 8.0337 | 95.2352 | 32.8347 | 366.0479 | |
| 100 | 1.1715 | 72.3916 | 1.2518 | 75.8250 | 5.6827 | 270.3350 | |
| 150 | 1.1942 | 72.8678 | 1.2158 | 65.0286 | 4.0633 | 269.6116 | |
| 200 | 1.0946 | 82.4840 | 1.3290 | 61.1405 | 5.1978 | 260.7603 | |
| HME | 25 | 0.0202 | 1.0725 | 0.0131 | 1.1397 | 0.0682 | 4.4596 |
| 50 | 0.0027 | 0.6690 | 0.0040 | 0.7065 | 0.0227 | 2.7626 | |
| 100 | 0.0043 | 0.4428 | 0.0035 | 0.4679 | 0.0198 | 1.8232 | |
| 150 | 0.0043 | 0.3481 | 0.0047 | 0.3659 | 0.0224 | 1.4325 | |
| 200 | 0.0026 | 0.2999 | 0.0017 | 0.3154 | 0.0026 | 1.2351 | |
| MME | 25 | 0.0153 | 0.9846 | 0.0034 | 1.0397 | 0.0587 | 4.1478 |
| 50 | 0.0027 | 0.6136 | 0.0051 | 0.6459 | 0.0446 | 2.5230 | |
| 100 | 0.0021 | 0.4140 | 0.0050 | 0.4379 | 0.0256 | 1.7081 | |
| 150 | 0.0020 | 0.3261 | 0.0035 | 0.3471 | 0.0118 | 1.3298 | |
| 200 | 0.0051 | 0.2766 | 0.0026 | 0.2908 | 0.0094 | 1.1309 | |
| LMSE | 25 | 0.0167 | 1.6576 | 0.0167 | 1.7265 | 0.0770 | 6.7443 |
| 50 | 0.0102 | 1.1152 | 0.0102 | 1.1698 | 0.0990 | 4.5277 | |
| 100 | 0.0073 | 0.7885 | 0.0113 | 0.8272 | 0.0224 | 3.3110 | |
| 150 | 0.0041 | 0.6602 | 0.0030 | 0.6842 | 0.0299 | 2.6303 | |
| 200 | 0.0044 | 0.5764 | 0.0022 | 0.6247 | 0.0366 | 2.4631 | |
| LTSE | 25 | 0.0117 | 1.1359 | 0.0084 | 1.1692 | 0.0235 | 4.5503 |
| 50 | 0.0109 | 0.6670 | 0.0056 | 0.6998 | 0.0437 | 2.7133 | |
| 100 | 0.0032 | 0.4465 | 0.0061 | 0.4661 | 0.0118 | 1.8315 | |
| 150 | 0.0046 | 0.3569 | 0.0047 | 0.3711 | 0.0232 | 1.4465 | |
| 200 | 0.0046 | 0.3029 | 0.0041 | 0.3189 | 0.0127 | 1.2497 | |
| SE | 25 | 0.0097 | 1.2065 | 0.0132 | 1.2566 | 0.0738 | 4.9714 |
| 50 | 0.0149 | 0.7895 | 0.0098 | 0.8189 | 0.0270 | 3.1879 | |
| 100 | 0.0067 | 0.5307 | 0.0087 | 0.5537 | 0.0319 | 2.1612 | |
| 150 | 0.0102 | 0.4192 | 0.0070 | 0.4375 | 0.0333 | 1.7050 | |
| 200 | 0.0039 | 0.3603 | 0.0058 | 0.3829 | 0.0182 | 1.4984 | |
| JSE | 25 | 1.5931 | 409.9958 | 0.9673 | 458.8019 | 2.9194 | 1949.7800 |
| 50 | 7.3356 | 88.0764 | 7.9925 | 95.2344 | 32.7987 | 270.3315 | |
| 100 | 1.1244 | 82.4731 | 1.2966 | 75.8101 | 5.7051 | 366.0451 | |
| 150 | 1.1460 | 72.8492 | 1.1730 | 65.0195 | 4.0186 | 269.6087 | |
| 200 | 1.0538 | 72.3765 | 1.3648 | 61.1171 | 5.2656 | 260.7565 | |
| RSE | 25 | 0.0321 | 0.9482 | 0.0383 | 0.9908 | 0.0662 | 4.3078 |
| 50 | 0.0182 | 0.6170 | 0.0232 | 0.6077 | 0.0801 | 2.5756 | |
| 100 | 0.0037 | 0.4146 | 0.0126 | 0.4003 | 0.0822 | 1.6125 | |
| 150 | 0.0024 | 0.3266 | 0.0047 | 0.3100 | 0.0594 | 1.2199 | |
| 200 | 0.0049 | 0.2803 | 0.0092 | 0.2658 | 0.0444 | 1.0249 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0055 | 0.6950 | 0.0071 | 0.9077 | 0.0014 | 0.9806 |
| 50 | 0.0012 | 0.6690 | 0.0026 | 0.6134 | 0.0041 | 0.9072 | |
| 100 | 0.0019 | 0.6467 | 0.0003 | 0.4100 | 0.0031 | 0.8761 | |
| 150 | 0.0020 | 0.6210 | 0.0035 | 0.3268 | 0.0042 | 0.8328 | |
| 200 | 0.0010 | 0.6007 | 0.0020 | 0.2863 | 0.0042 | 0.7854 | |
| HME | 25 | 0.0031 | 0.2733 | 0.0035 | 0.3405 | 0.0041 | 0.3394 |
| 50 | 0.0009 | 0.1834 | 0.0007 | 0.2106 | 0.0002 | 0.2116 | |
| 100 | 0.0021 | 0.1246 | 0.0004 | 0.1218 | 0.0012 | 0.1384 | |
| 150 | 0.0005 | 0.0999 | 0.0001 | 0.1091 | 0.0002 | 0.1100 | |
| 200 | 0.0004 | 0.0863 | 0.0010 | 0.0948 | 0.0003 | 0.0876 | |
| MME | 25 | 0.0024 | 0.2521 | 0.0031 | 0.2543 | 0.0014 | 0.2838 |
| 50 | 0.0015 | 0.1675 | 0.0000 | 0.2099 | 0.0019 | 0.1807 | |
| 100 | 0.0004 | 0.1143 | 0.0002 | 0.1180 | 0.0018 | 0.1213 | |
| 150 | 0.0003 | 0.0917 | 0.0004 | 0.1001 | 0.0004 | 0.0974 | |
| 200 | 0.0007 | 0.0795 | 0.0080 | 0.0846 | 0.0003 | 0.0734 | |
| LMSE | 25 | 0.0024 | 0.5255 | 0.0004 | 0.5347 | 0.0013 | 0.5462 |
| 50 | 0.0004 | 0.3570 | 0.0012 | 0.3591 | 0.0078 | 0.3599 | |
| 100 | 0.0007 | 0.2549 | 0.0005 | 0.2547 | 0.0026 | 0.2594 | |
| 150 | 0.0016 | 0.2171 | 0.0007 | 0.2150 | 0.0013 | 0.2177 | |
| 200 | 0.0028 | 0.1946 | 0.0017 | 0.1924 | 0.0009 | 0.1914 | |
| LTSE | 25 | 0.0020 | 0.3909 | 0.0021 | 0.3222 | 0.0021 | 0.3264 |
| 50 | 0.0010 | 0.1966 | 0.0007 | 0.2367 | 0.0029 | 0.2000 | |
| 100 | 0.0005 | 0.1268 | 0.0007 | 0.1674 | 0.0018 | 0.1309 | |
| 150 | 0.0004 | 0.1008 | 0.0003 | 0.1388 | 0.0002 | 0.1033 | |
| 200 | 0.0007 | 0.0865 | 0.0004 | 0.1094 | 0.0005 | 0.0906 | |
| SE | 25 | 0.0020 | 0.3909 | 0.0008 | 0.3831 | 0.0020 | 0.3865 |
| 50 | 0.0006 | 0.2670 | 0.0015 | 0.2588 | 0.0049 | 0.2597 | |
| 100 | 0.0005 | 0.1817 | 0.0017 | 0.1786 | 0.0007 | 0.1805 | |
| 150 | 0.0004 | 0.1477 | 0.0009 | 0.1438 | 0.0006 | 0.1457 | |
| 200 | 0.0013 | 0.1277 | 0.0003 | 0.1239 | 0.0007 | 0.1224 | |
| JSE | 25 | 0.2602 | 0.6801 | 0.3516 | 0.7350 | 0.3477 | 0.7329 |
| 50 | 0.2062 | 0.6573 | 0.0263 | 0.5623 | 0.2685 | 0.7280 | |
| 100 | 0.0123 | 0.6312 | 0.0168 | 0.4063 | 0.1634 | 0.7044 | |
| 150 | 0.0004 | 0.6011 | 0.1233 | 0.3295 | 0.1242 | 0.6825 | |
| 200 | 0.0672 | 0.5698 | 0.0981 | 0.2892 | 0.0957 | 0.6657 | |
| RSE | 25 | 0.4704 | 0.6585 | 0.4667 | 0.8030 | 0.4757 | 0.6995 |
| 50 | 0.4905 | 0.6355 | 0.0487 | 0.5328 | 0.4881 | 0.6709 | |
| 100 | 0.0495 | 0.5889 | 0.0493 | 0.3510 | 0.4898 | 0.6538 | |
| 150 | 0.0493 | 0.5504 | 0.4951 | 0.2790 | 0.4943 | 0.6222 | |
| 200 | 0.4947 | 0.5065 | 0.4935 | 0.2581 | 0.4974 | 0.6098 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.1225 | 0.6138 | 0.3650 | 0.6569 | 0.5100 | 0.7285 |
| 50 | 0.2247 | 0.5014 | 0.3927 | 0.5589 | 0.5224 | 0.6899 | |
| 100 | 0.2599 | 0.4067 | 0.4165 | 0.4371 | 0.5259 | 0.6514 | |
| 150 | 0.2600 | 0.3993 | 0.4293 | 0.4270 | 0.5167 | 0.6235 | |
| 200 | 0.2769 | 0.3824 | 0.4227 | 0.4136 | 0.5269 | 0.6233 | |
| HME | 25 | 0.1103 | 0.4643 | 0.3445 | 0.4789 | 0.5015 | 0.6688 |
| 50 | 0.1681 | 0.4031 | 0.3641 | 0.4104 | 0.5229 | 0.6262 | |
| 100 | 0.1824 | 0.2849 | 0.3908 | 0.3541 | 0.5237 | 0.5897 | |
| 150 | 0.1872 | 0.2604 | 0.4029 | 0.3105 | 0.5169 | 0.5801 | |
| 200 | 0.1901 | 0.2482 | 0.3968 | 0.3025 | 0.5242 | 0.5755 | |
| MME | 25 | 0.0285 | 0.4011 | 0.1932 | 0.4098 | 0.4868 | 0.6631 |
| 50 | 0.0513 | 0.3470 | 0.2401 | 0.3560 | 0.5219 | 0.6192 | |
| 100 | 0.0567 | 0.2262 | 0.3271 | 0.2682 | 0.5213 | 0.5883 | |
| 150 | 0.0619 | 0.2060 | 0.3510 | 0.2083 | 0.5162 | 0.5775 | |
| 200 | 0.0646 | 0.1801 | 0.3523 | 0.1789 | 0.5242 | 0.5730 | |
| LMSE | 25 | 0.0078 | 0.5375 | 0.1014 | 0.5375 | 0.2804 | 0.8372 |
| 50 | 0.0173 | 0.3772 | 0.0688 | 0.3772 | 0.3846 | 0.6487 | |
| 100 | 0.0106 | 0.2467 | 0.0601 | 0.2867 | 0.3937 | 0.5898 | |
| 150 | 0.0127 | 0.2160 | 0.0571 | 0.2142 | 0.4303 | 0.5810 | |
| 200 | 0.0116 | 0.1877 | 0.0428 | 0.1930 | 0.4311 | 0.5770 | |
| LTSE | 25 | 0.0154 | 0.3907 | 0.1135 | 0.3907 | 0.3341 | 0.6326 |
| 50 | 0.0263 | 0.2727 | 0.0953 | 0.2727 | 0.4087 | 0.5581 | |
| 100 | 0.0245 | 0.1806 | 0.0964 | 0.2048 | 0.4324 | 0.5398 | |
| 150 | 0.0251 | 0.1508 | 0.1036 | 0.1539 | 0.4324 | 0.5242 | |
| 200 | 0.0271 | 0.1358 | 0.0884 | 0.1487 | 0.4424 | 0.5140 | |
| SE | 25 | 0.0129 | 0.4191 | 0.1048 | 0.4191 | 0.3425 | 0.7257 |
| 50 | 0.0170 | 0.2859 | 0.0757 | 0.2859 | 0.4262 | 0.6250 | |
| 100 | 0.0139 | 0.1775 | 0.0613 | 0.2056 | 0.4381 | 0.5781 | |
| 150 | 0.0128 | 0.1548 | 0.0591 | 0.1542 | 0.4823 | 0.5607 | |
| 200 | 0.0135 | 0.1294 | 0.0464 | 0.1453 | 0.4764 | 0.5479 | |
| JSE | 25 | 0.1912 | 0.6128 | 0.4938 | 0.6128 | 0.7283 | 0.8096 |
| 50 | 0.2693 | 0.5501 | 0.4705 | 0.5501 | 0.6711 | 0.7674 | |
| 100 | 0.2874 | 0.4417 | 0.4604 | 0.5021 | 0.6127 | 0.7350 | |
| 150 | 0.2874 | 0.4274 | 0.4605 | 0.4684 | 0.5777 | 0.7033 | |
| 200 | 0.2894 | 0.4020 | 0.4458 | 0.4554 | 0.5764 | 0.6893 | |
| RSE | 25 | 0.1303 | 0.5878 | 0.4913 | 0.5870 | 0.8224 | 0.7151 |
| 50 | 0.0528 | 0.4982 | 0.5671 | 0.4980 | 0.8589 | 0.6823 | |
| 100 | 0.1036 | 0.4054 | 0.6383 | 0.4365 | 0.8633 | 0.6389 | |
| 150 | 0.1213 | 0.3847 | 0.6688 | 0.4149 | 0.8607 | 0.6198 | |
| 200 | 0.1324 | 0.3772 | 0.6593 | 0.4039 | 0.8738 | 0.6198 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0457 | 0.8724 | 0.0108 | 0.9139 | 0.3930 | 1.0740 |
| 50 | 0.0267 | 0.5982 | 0.0230 | 0.6246 | 0.3705 | 0.8713 | |
| 100 | 0.0233 | 0.4566 | 0.0136 | 0.5075 | 0.4457 | 0.7181 | |
| 150 | 0.0188 | 0.3505 | 0.0276 | 0.3837 | 0.3872 | 0.6936 | |
| 200 | 0.0189 | 0.3341 | 0.0043 | 0.3400 | 0.4038 | 0.6850 | |
| ME | 25 | 0.0208 | 0.4170 | 0.0102 | 0.4597 | 0.1766 | 0.8102 |
| 50 | 0.0031 | 0.2449 | 0.0197 | 0.2570 | 0.1835 | 0.5907 | |
| 100 | 0.0141 | 0.1654 | 0.0059 | 0.1681 | 0.1964 | 0.4931 | |
| 150 | 0.0029 | 0.1322 | 0.0024 | 0.1516 | 0.2044 | 0.4554 | |
| 200 | 0.0021 | 0.1266 | 0.0037 | 0.1169 | 0.2053 | 0.4281 | |
| MME | 25 | 0.0022 | 0.3946 | 0.0113 | 0.4170 | 0.0299 | 0.6781 |
| 50 | 0.0008 | 0.2122 | 0.0235 | 0.2452 | 0.0475 | 0.4995 | |
| 100 | 0.0123 | 0.1573 | 0.0009 | 0.1612 | 0.0993 | 0.4100 | |
| 150 | 0.0044 | 0.1205 | 0.0007 | 0.1362 | 0.0906 | 0.3616 | |
| 200 | 0.0039 | 0.1158 | 0.0042 | 0.1057 | 0.0901 | 0.3397 | |
| LMSE | 25 | 0.0123 | 0.5972 | 0.0260 | 0.6250 | 0.0345 | 0.6433 |
| 50 | 0.0217 | 0.4033 | 0.0009 | 0.3650 | 0.0146 | 0.4197 | |
| 100 | 0.0028 | 0.2630 | 0.0049 | 0.2685 | 0.0317 | 0.3096 | |
| 150 | 0.0075 | 0.2153 | 0.0102 | 0.2092 | 0.0140 | 0.2627 | |
| 200 | 0.0053 | 0.1956 | 0.0122 | 0.1731 | 0.0033 | 0.2433 | |
| LTSE | 25 | 0.0081 | 0.4295 | 0.0103 | 0.4563 | 0.0157 | 0.4986 |
| 50 | 0.0032 | 0.2272 | 0.0203 | 0.2466 | 0.0226 | 0.3812 | |
| 100 | 0.0097 | 0.1658 | 0.0007 | 0.1595 | 0.0435 | 0.2623 | |
| 150 | 0.0069 | 0.1249 | 0.0036 | 0.1300 | 0.0199 | 0.2243 | |
| 200 | 0.0076 | 0.1155 | 0.0022 | 0.1046 | 0.0311 | 0.1865 | |
| SE | 25 | 0.0130 | 0.4157 | 0.0041 | 0.4847 | 0.0254 | 0.5413 |
| 50 | 0.0024 | 0.2574 | 0.0230 | 0.2676 | 0.0375 | 0.3912 | |
| 100 | 0.0061 | 0.1817 | 0.0040 | 0.1702 | 0.0580 | 0.2859 | |
| 150 | 0.0126 | 0.1366 | 0.0042 | 0.1362 | 0.0317 | 0.2358 | |
| 200 | 0.0055 | 0.1233 | 0.0027 | 0.1084 | 0.0493 | 0.2046 | |
| JSE | 25 | 0.2578 | 0.6665 | 0.3083 | 0.7295 | 0.6597 | 0.9887 |
| 50 | 0.2344 | 0.5465 | 0.2726 | 0.5550 | 0.7327 | 0.9186 | |
| 100 | 0.2220 | 0.4315 | 0.2031 | 0.4319 | 0.7492 | 0.8692 | |
| 150 | 0.1064 | 0.3455 | 0.0935 | 0.3493 | 0.6862 | 0.8416 | |
| 200 | 0.0805 | 0.3229 | 0.1119 | 0.3013 | 0.6758 | 0.8293 | |
| RSE | 25 | 0.0204 | 0.7605 | 0.0753 | 0.8116 | 0.2687 | 1.1759 |
| 50 | 0.0109 | 0.5665 | 0.0525 | 0.5923 | 0.4567 | 0.8200 | |
| 100 | 0.0487 | 0.4300 | 0.0482 | 0.4537 | 0.5525 | 0.6905 | |
| 150 | 0.0068 | 0.3458 | 0.0151 | 0.3743 | 0.6033 | 0.6707 | |
| 200 | 0.0091 | 0.3282 | 0.0136 | 0.3082 | 0.6156 | 0.6582 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | Bias | RMSE | ||
| OLSE | 25 | 0.2460 | 0.6138 | 0.2460 | 0.8977 | 0.5062 | 0.7285 |
| 50 | 0.3284 | 0.5014 | 0.3284 | 0.6730 | 0.5376 | 0.6899 | |
| 100 | 0.2551 | 0.4067 | 0.3381 | 0.5003 | 0.5133 | 0.6504 | |
| 150 | 0.2546 | 0.4000 | 0.3364 | 0.4804 | 0.5158 | 0.6086 | |
| 200 | 0.2783 | 0.3824 | 0.3544 | 0.4236 | 0.5260 | 0.5897 | |
| ME | 25 | 0.2329 | 0.4643 | 0.2329 | 0.4745 | 0.4999 | 0.6688 |
| 50 | 0.2970 | 0.4031 | 0.2970 | 0.4299 | 0.5360 | 0.6262 | |
| 100 | 0.2078 | 0.2849 | 0.2898 | 0.3909 | 0.5190 | 0.5897 | |
| 150 | 0.2336 | 0.2798 | 0.2886 | 0.3667 | 0.5216 | 0.5601 | |
| 200 | 0.2234 | 0.2682 | 0.3060 | 0.3500 | 0.5271 | 0.5455 | |
| MME | 25 | 0.1196 | 0.4011 | 0.1196 | 0.4299 | 0.4886 | 0.6631 |
| 50 | 0.1961 | 0.3470 | 0.1961 | 0.3902 | 0.5335 | 0.6092 | |
| 100 | 0.1135 | 0.2262 | 0.1969 | 0.3339 | 0.5159 | 0.5383 | |
| 150 | 0.1231 | 0.2060 | 0.2112 | 0.2945 | 0.5205 | 0.5175 | |
| 200 | 0.1286 | 0.1801 | 0.2439 | 0.2532 | 0.5249 | 0.5110 | |
| LMSE | 25 | 0.0158 | 0.5375 | 0.0158 | 0.5375 | 0.3637 | 0.8372 |
| 50 | 0.0639 | 0.3772 | 0.0639 | 0.4005 | 0.4210 | 0.6487 | |
| 100 | 0.0338 | 0.2467 | 0.0263 | 0.3519 | 0.3981 | 0.5898 | |
| 150 | 0.0139 | 0.2260 | 0.0238 | 0.3007 | 0.4402 | 0.5703 | |
| 200 | 0.0094 | 0.1877 | 0.0090 | 0.2689 | 0.4483 | 0.5598 | |
| LTSE | 25 | 0.0196 | 0.3907 | 0.0196 | 0.3907 | 0.3810 | 0.6326 |
| 50 | 0.0955 | 0.2727 | 0.0955 | 0.2727 | 0.4372 | 0.5599 | |
| 100 | 0.0363 | 0.1806 | 0.0601 | 0.2048 | 0.4448 | 0.5300 | |
| 150 | 0.0350 | 0.1508 | 0.0514 | 0.1539 | 0.4439 | 0.5156 | |
| 200 | 0.0371 | 0.1358 | 0.0622 | 0.1487 | 0.4658 | 0.5078 | |
| SE | 25 | 0.0059 | 0.4191 | 0.0059 | 0.4191 | 0.4574 | 0.7257 |
| 50 | 0.0652 | 0.2859 | 0.0652 | 0.2859 | 0.4620 | 0.6250 | |
| 100 | 0.0260 | 0.1775 | 0.0299 | 0.2056 | 0.4497 | 0.5705 | |
| 150 | 0.0204 | 0.1548 | 0.0333 | 0.1542 | 0.4946 | 0.5577 | |
| 200 | 0.0140 | 0.1294 | 0.0365 | 0.1453 | 0.5012 | 0.5429 | |
| JSE | 25 | 0.4444 | 0.6128 | 0.4444 | 0.6128 | 0.7679 | 0.8096 |
| 50 | 0.4666 | 0.5501 | 0.4666 | 0.5501 | 0.7722 | 0.7589 | |
| 100 | 0.3449 | 0.4417 | 0.4348 | 0.5021 | 0.7062 | 0.7350 | |
| 150 | 0.3477 | 0.4209 | 0.4115 | 0.4684 | 0.6812 | 0.7003 | |
| 200 | 0.3409 | 0.4020 | 0.4128 | 0.4109 | 0.6663 | 0.6593 | |
| RSE | 25 | 0.2650 | 0.5878 | 0.2650 | 0.5782 | 0.5192 | 0.7151 |
| 50 | 0.3363 | 0.4982 | 0.3363 | 0.5024 | 0.5473 | 0.6823 | |
| 100 | 0.2608 | 0.4054 | 0.3427 | 0.4822 | 0.5167 | 0.6389 | |
| 150 | 0.2751 | 0.3947 | 0.3426 | 0.4577 | 0.5207 | 0.6011 | |
| 200 | 0.2826 | 0.3772 | 0.3566 | 0.4104 | 0.5291 | 0.5800 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0161 | 1.1661 | 0.0267 | 1.1767 | 0.0859 | 4.8447 |
| 50 | 0.0104 | 0.9019 | 0.0146 | 0.9395 | 0.0823 | 3.5972 | |
| 100 | 0.0102 | 0.6200 | 0.0049 | 0.6164 | 0.0264 | 2.5442 | |
| 150 | 0.0075 | 0.5013 | 0.0039 | 0.5253 | 0.0245 | 2.0862 | |
| 200 | 0.0066 | 0.4414 | 0.0045 | 0.4400 | 0.0096 | 1.8097 | |
| HME | 25 | 0.0089 | 0.6654 | 0.0067 | 0.6856 | 0.0170 | 2.7112 |
| 50 | 0.0028 | 0.4462 | 0.0069 | 0.4787 | 0.0182 | 1.8527 | |
| 100 | 0.0038 | 0.3104 | 0.0003 | 0.3135 | 0.0257 | 1.2647 | |
| 150 | 0.0012 | 0.2425 | 0.0031 | 0.2661 | 0.0156 | 1.0221 | |
| 200 | 0.0024 | 0.2164 | 0.0047 | 0.2285 | 0.0083 | 0.8758 | |
| MME | 25 | 0.0022 | 0.6513 | 0.0054 | 0.6630 | 0.0297 | 2.5821 |
| 50 | 0.0007 | 0.4161 | 0.0023 | 0.4474 | 0.0148 | 1.7323 | |
| 100 | 0.0019 | 0.2932 | 0.0019 | 0.3061 | 0.0174 | 1.2065 | |
| 150 | 0.0023 | 0.2304 | 0.0052 | 0.2452 | 0.0072 | 0.9542 | |
| 200 | 0.0024 | 0.2049 | 0.0013 | 0.2196 | 0.0071 | 0.8440 | |
| LMSE | 25 | 0.0042 | 1.3739 | 0.0186 | 1.4445 | 0.0502 | 5.6464 |
| 50 | 0.0048 | 0.9668 | 0.0129 | 1.0399 | 0.0760 | 4.1230 | |
| 100 | 0.0069 | 0.7582 | 0.0155 | 0.8240 | 0.0185 | 3.0788 | |
| 150 | 0.0091 | 0.6626 | 0.0094 | 0.6933 | 0.0459 | 2.7251 | |
| 200 | 0.0060 | 0.5967 | 0.0010 | 0.6350 | 0.0252 | 2.4792 | |
| LTSE | 25 | 0.0071 | 0.8149 | 0.0092 | 0.8652 | 0.0275 | 3.3599 |
| 50 | 0.0046 | 0.4933 | 0.0080 | 0.5221 | 0.0095 | 2.0934 | |
| 100 | 0.0010 | 0.3309 | 0.0036 | 0.3435 | 0.0076 | 1.3464 | |
| 150 | 0.0052 | 0.2572 | 0.0015 | 0.2701 | 0.0092 | 1.0902 | |
| 200 | 0.0041 | 0.2228 | 0.0002 | 0.2390 | 0.0086 | 0.9219 | |
| SE | 25 | 0.0065 | 1.0166 | 0.0091 | 1.0819 | 0.0270 | 4.2438 |
| 50 | 0.0118 | 0.7430 | 0.0059 | 0.7808 | 0.0462 | 3.0566 | |
| 100 | 0.0035 | 0.5346 | 0.0047 | 0.5755 | 0.0378 | 2.1820 | |
| 150 | 0.0069 | 0.4442 | 0.0062 | 0.4766 | 0.0322 | 1.8690 | |
| 200 | 0.0060 | 0.3978 | 0.0060 | 0.4206 | 0.0118 | 1.6512 | |
| JSE | 25 | 0.0705 | 1.0623 | 0.0712 | 1.4445 | 0.0855 | 4.7029 |
| 50 | 0.0258 | 0.8135 | 0.0322 | 0.8125 | 0.1237 | 3.4315 | |
| 100 | 0.0101 | 0.5772 | 0.0303 | 0.5580 | 0.0744 | 2.3470 | |
| 150 | 0.0058 | 0.4759 | 0.0288 | 0.4987 | 0.0558 | 1.8779 | |
| 200 | 0.0020 | 0.4091 | 0.0119 | 0.4366 | 0.0604 | 1.5931 | |
| RSE | 25 | 0.0083 | 0.6170 | 0.0226 | 0.5898 | 0.0942 | 2.5164 |
| 50 | 0.0079 | 0.4132 | 0.0090 | 0.4003 | 0.0612 | 1.6407 | |
| 100 | 0.0033 | 0.2935 | 0.0051 | 0.2657 | 0.0500 | 1.0493 | |
| 150 | 0.0019 | 0.2310 | 0.0018 | 0.2155 | 0.0323 | 0.8170 | |
| 200 | 0.0029 | 0.2015 | 0.0015 | 0.1936 | 0.0359 | 0.6839 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0062 | 1.5543 | 0.0046 | 1.6247 | 0.0530 | 6.3331 |
| 50 | 0.0212 | 1.0810 | 0.0089 | 1.1396 | 0.0191 | 4.4080 | |
| 100 | 0.0137 | 0.7174 | 0.0154 | 0.7447 | 0.0368 | 2.8907 | |
| 150 | 0.0038 | 0.5801 | 0.0062 | 0.6160 | 0.0452 | 2.4116 | |
| 200 | 0.0057 | 0.5121 | 0.0029 | 0.5368 | 0.0291 | 2.1021 | |
| HME | 25 | 0.0100 | 0.7930 | 0.0035 | 0.8190 | 0.0139 | 3.1968 |
| 50 | 0.0021 | 0.4917 | 0.0063 | 0.5162 | 0.0092 | 1.9931 | |
| 100 | 0.0030 | 0.3281 | 0.0013 | 0.3415 | 0.0247 | 1.3352 | |
| 150 | 0.0030 | 0.2676 | 0.0023 | 0.2830 | 0.0123 | 1.1082 | |
| 200 | 0.0057 | 0.2380 | 0.0056 | 0.2501 | 0.0191 | 0.9796 | |
| MME | 25 | 0.0064 | 0.7174 | 0.0071 | 0.7441 | 0.0280 | 2.8945 |
| 50 | 0.0020 | 0.4460 | 0.0070 | 0.4675 | 0.0163 | 1.8181 | |
| 100 | 0.0019 | 0.3435 | 0.0046 | 0.3183 | 0.1093 | 1.2491 | |
| 150 | 0.0027 | 0.2773 | 0.0022 | 0.2609 | 0.0150 | 1.0299 | |
| 200 | 0.0029 | 0.2187 | 0.0024 | 0.2308 | 0.0145 | 0.9129 | |
| LMSE | 25 | 0.0218 | 1.4472 | 0.0095 | 1.4409 | 0.0370 | 5.9381 |
| 50 | 0.0122 | 1.0082 | 0.0089 | 1.0629 | 0.0320 | 4.0632 | |
| 100 | 0.0108 | 0.7533 | 0.0069 | 0.7914 | 0.0285 | 2.9913 | |
| 150 | 0.0034 | 0.6561 | 0.0024 | 0.7027 | 0.0321 | 2.7053 | |
| 200 | 0.0046 | 0.6061 | 0.0042 | 0.6359 | 0.0222 | 2.4734 | |
| LTSE | 25 | 0.0062 | 0.8854 | 0.0060 | 0.9104 | 0.0131 | 3.5050 |
| 50 | 0.0041 | 0.5026 | 0.0037 | 0.5218 | 0.0206 | 2.0321 | |
| 100 | 0.0026 | 0.3326 | 0.0022 | 0.3432 | 0.0239 | 1.3321 | |
| 150 | 0.0045 | 0.2677 | 0.0018 | 0.2782 | 0.0096 | 1.0861 | |
| 200 | 0.0022 | 0.2301 | 0.0012 | 0.2423 | 0.0055 | 0.9453 | |
| SE | 25 | 0.0127 | 1.0989 | 0.0099 | 1.0978 | 0.0512 | 4.3564 |
| 50 | 0.0048 | 0.8401 | 0.0057 | 0.7404 | 0.0092 | 2.8994 | |
| 100 | 0.0095 | 0.6323 | 0.0018 | 0.5428 | 0.0240 | 2.1071 | |
| 150 | 0.0066 | 0.5142 | 0.0052 | 0.4565 | 0.0158 | 1.7641 | |
| 200 | 0.0040 | 0.4505 | 0.0034 | 0.3906 | 0.0154 | 1.5235 | |
| JSE | 25 | 0.0786 | 1.3898 | 0.0726 | 1.4474 | 0.0525 | 6.2080 |
| 50 | 0.0515 | 0.9745 | 0.0477 | 1.0007 | 0.1046 | 4.2547 | |
| 100 | 0.0166 | 0.6572 | 0.0200 | 0.6375 | 0.1093 | 2.6981 | |
| 150 | 0.0143 | 0.5358 | 0.0192 | 0.5287 | 0.1118 | 2.2113 | |
| 200 | 0.0077 | 0.4776 | 0.0126 | 0.4550 | 0.0670 | 1.8900 | |
| RSE | 25 | 0.0086 | 0.6409 | 0.0226 | 0.7031 | 0.0942 | 3.0150 |
| 50 | 0.0079 | 0.4270 | 0.0090 | 0.4487 | 0.0612 | 1.7837 | |
| 100 | 0.0033 | 0.3202 | 0.0051 | 0.2902 | 0.0500 | 1.1195 | |
| 150 | 0.0019 | 0.2411 | 0.0018 | 0.2385 | 0.0323 | 0.9004 | |
| 200 | 0.0029 | 0.1902 | 0.0015 | 0.2102 | 0.0359 | 0.7816 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0361 | 2.6872 | 0.0391 | 3.4565 | 0.1435 | 13.4395 |
| 50 | 0.0207 | 1.8804 | 0.0137 | 2.4060 | 0.1291 | 9.2996 | |
| 100 | 0.0229 | 1.2856 | 0.0173 | 1.6108 | 0.0680 | 6.2748 | |
| 150 | 0.0054 | 1.0056 | 0.0135 | 1.2991 | 0.0646 | 5.0614 | |
| 200 | 0.0152 | 0.9050 | 0.0219 | 1.1438 | 0.0649 | 4.4912 | |
| HME | 25 | 0.0152 | 2.0393 | 0.0385 | 3.2750 | 0.2547 | 12.7506 |
| 50 | 0.0178 | 1.2846 | 0.0166 | 2.2399 | 0.0905 | 8.6701 | |
| 100 | 0.0107 | 0.8170 | 0.0108 | 1.4946 | 0.0923 | 5.8517 | |
| 150 | 0.0043 | 0.6205 | 0.0192 | 1.2080 | 0.1026 | 4.7199 | |
| 200 | 0.0055 | 0.5431 | 0.0188 | 1.0487 | 0.0344 | 4.1304 | |
| MME | 25 | 0.0123 | 2.0160 | 0.0502 | 3.3765 | 0.1710 | 12.9902 |
| 50 | 0.0119 | 1.2511 | 0.0190 | 2.2857 | 0.0689 | 8.8028 | |
| 100 | 0.0085 | 0.8068 | 0.0139 | 1.5218 | 0.0902 | 5.9529 | |
| 150 | 0.0056 | 0.6260 | 0.0097 | 1.2321 | 0.1193 | 4.8432 | |
| 200 | 0.0027 | 0.5310 | 0.0206 | 1.0664 | 0.0504 | 4.1981 | |
| LMSE | 25 | 0.0111 | 1.8804 | 0.0700 | 6.3924 | 0.2934 | 24.8944 |
| 50 | 0.0141 | 1.1249 | 0.0352 | 4.3369 | 0.1285 | 16.6505 | |
| 100 | 0.0033 | 0.7390 | 0.0336 | 3.0340 | 0.0672 | 11.8651 | |
| 150 | 0.0067 | 0.6363 | 0.0238 | 2.5743 | 0.0366 | 9.9337 | |
| 200 | 0.0056 | 0.5753 | 0.0365 | 2.2427 | 0.0476 | 8.7208 | |
| LTSE | 25 | 0.0126 | 1.8604 | 0.0447 | 4.3584 | 0.2164 | 16.9940 |
| 50 | 0.0069 | 1.1510 | 0.0124 | 2.6902 | 0.1171 | 10.4412 | |
| 100 | 0.0074 | 0.7537 | 0.0205 | 1.7371 | 0.1301 | 6.8903 | |
| 150 | 0.0089 | 0.6363 | 0.0113 | 1.3817 | 0.0520 | 5.3751 | |
| 200 | 0.0050 | 0.4968 | 0.0054 | 1.1846 | 0.0265 | 4.6208 | |
| SE | 25 | 0.0054 | 1.5971 | 0.0354 | 5.0033 | 0.1718 | 18.9508 |
| 50 | 0.0155 | 0.9831 | 0.0254 | 3.1914 | 0.0856 | 12.2507 | |
| 100 | 0.0080 | 0.6203 | 0.0418 | 2.1167 | 0.1493 | 8.3920 | |
| 150 | 0.0010 | 0.5092 | 0.0101 | 1.7027 | 0.0531 | 6.7311 | |
| 200 | 0.0016 | 0.4403 | 0.0184 | 1.4327 | 0.0516 | 5.5473 | |
| JSE | 25 | 0.1135 | 2.4747 | 0.1148 | 3.2656 | 0.1605 | 13.3709 |
| 50 | 0.0988 | 1.6975 | 0.0892 | 2.1964 | 0.0541 | 9.2018 | |
| 100 | 0.0749 | 1.1428 | 0.0778 | 1.4191 | 0.0462 | 6.1440 | |
| 150 | 0.0472 | 0.9173 | 0.0748 | 1.1416 | 0.0819 | 4.9121 | |
| 200 | 0.0328 | 0.8131 | 0.0387 | 0.9870 | 0.0584 | 4.3278 | |
| RSE | 25 | 0.0986 | 1.5785 | 0.1026 | 3.0745 | 0.2389 | 12.6750 |
| 50 | 0.0718 | 0.8309 | 0.0875 | 2.0285 | 0.0940 | 8.5669 | |
| 100 | 0.0245 | 0.4867 | 0.0564 | 1.3047 | 0.0169 | 5.7115 | |
| 150 | 0.0130 | 0.3892 | 0.0506 | 1.0478 | 0.1073 | 4.5634 | |
| 200 | 0.0102 | 0.3333 | 0.0408 | 0.9044 | 0.0529 | 3.9618 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0135 | 2.2325 | 0.0281 | 2.3509 | 0.1694 | 9.0955 |
| 50 | 0.0263 | 1.5163 | 0.0141 | 1.6087 | 0.0844 | 6.2819 | |
| 100 | 0.0101 | 1.0717 | 0.0084 | 1.1340 | 0.0381 | 4.4269 | |
| 150 | 0.0078 | 0.8638 | 0.0185 | 0.9072 | 0.0316 | 3.5486 | |
| 200 | 0.0127 | 0.7507 | 0.0129 | 0.7909 | 0.0288 | 3.0516 | |
| HME | 25 | 0.0144 | 2.1473 | 0.0092 | 2.2668 | 0.0867 | 8.7886 |
| 50 | 0.0344 | 1.4519 | 0.0249 | 1.5383 | 0.0609 | 5.9849 | |
| 100 | 0.0123 | 1.0188 | 0.0082 | 1.0696 | 0.0453 | 4.1529 | |
| 150 | 0.0095 | 0.8122 | 0.0089 | 0.8530 | 0.0302 | 3.3366 | |
| 200 | 0.0047 | 0.7005 | 0.0093 | 0.7376 | 0.0201 | 2.8468 | |
| MME | 25 | 0.0107 | 2.1610 | 0.0093 | 2.2880 | 0.0801 | 9.0087 |
| 50 | 0.0365 | 1.4752 | 0.0242 | 1.5452 | 0.0408 | 6.0579 | |
| 100 | 0.0170 | 1.0358 | 0.0058 | 1.0782 | 0.0595 | 4.1825 | |
| 150 | 0.0183 | 0.8209 | 0.0035 | 0.8702 | 0.0559 | 3.3697 | |
| 200 | 0.0046 | 0.7107 | 0.0105 | 0.7372 | 0.0416 | 2.8525 | |
| LMSE | 25 | 0.0205 | 4.5983 | 0.0626 | 4.8056 | 0.2446 | 19.0631 |
| 50 | 0.0381 | 3.2831 | 0.0553 | 3.4427 | 0.1216 | 13.6482 | |
| 100 | 0.0346 | 2.3554 | 0.0554 | 2.4843 | 0.1069 | 9.7381 | |
| 150 | 0.0204 | 2.0155 | 0.0385 | 2.1367 | 0.0515 | 8.4898 | |
| 200 | 0.0150 | 1.8472 | 0.0211 | 1.8739 | 0.0571 | 7.3646 | |
| LTSE | 25 | 0.0272 | 2.9346 | 0.0400 | 3.0534 | 0.1054 | 12.2296 |
| 50 | 0.0189 | 1.8234 | 0.0098 | 1.9280 | 0.0747 | 7.6308 | |
| 100 | 0.0194 | 1.1892 | 0.0067 | 1.2630 | 0.0460 | 4.8699 | |
| 150 | 0.0064 | 0.9607 | 0.0084 | 1.0068 | 0.0521 | 3.9624 | |
| 200 | 0.0043 | 0.8050 | 0.0114 | 0.8567 | 0.0224 | 3.2949 | |
| SE | 25 | 0.0533 | 3.4634 | 0.0468 | 3.6445 | 0.1537 | 14.5047 |
| 50 | 0.0244 | 2.4897 | 0.0347 | 2.6742 | 0.0834 | 10.4343 | |
| 100 | 0.0294 | 1.7188 | 0.0229 | 1.8000 | 0.0372 | 6.9285 | |
| 150 | 0.0215 | 1.4082 | 0.0176 | 1.4764 | 0.0661 | 5.7540 | |
| 200 | 0.0089 | 1.1880 | 0.0051 | 1.2568 | 0.0224 | 4.8324 | |
| JSE | 25 | 0.1058 | 2.0278 | 0.0689 | 2.1415 | 0.0877 | 8.9953 |
| 50 | 0.0684 | 1.3438 | 0.0585 | 1.4176 | 0.0926 | 6.1550 | |
| 100 | 0.0423 | 0.9539 | 0.0499 | 0.9805 | 0.0767 | 4.2635 | |
| 150 | 0.0217 | 0.7895 | 0.0265 | 0.7840 | 0.1009 | 3.3695 | |
| 200 | 0.0281 | 0.6973 | 0.0348 | 0.6879 | 0.0934 | 2.8600 | |
| RSE | 25 | 0.0949 | 1.9411 | 0.0778 | 2.0640 | 0.0336 | 8.6892 |
| 50 | 0.0494 | 1.2857 | 0.0664 | 1.3551 | 0.0386 | 5.8501 | |
| 100 | 0.0430 | 0.9164 | 0.0547 | 0.9267 | 0.0962 | 3.9854 | |
| 150 | 0.0150 | 0.7424 | 0.0255 | 0.7345 | 0.1059 | 3.1533 | |
| 200 | 0.0235 | 0.6516 | 0.0381 | 0.6387 | 0.0934 | 2.6459 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0281 | 2.4286 | 0.0247 | 2.5558 | 0.0960 | 9.9821 |
| 50 | 0.0326 | 1.6594 | 0.0078 | 1.7535 | 0.0437 | 6.7796 | |
| 100 | 0.0136 | 1.1247 | 0.0146 | 1.1722 | 0.0898 | 4.5734 | |
| 150 | 0.0103 | 0.9013 | 0.0171 | 0.9516 | 0.0493 | 3.7040 | |
| 200 | 0.0075 | 0.7997 | 0.0081 | 0.8411 | 0.0309 | 3.3035 | |
| HME | 25 | 0.0275 | 2.3096 | 0.0108 | 2.4388 | 0.0361 | 9.4162 |
| 50 | 0.0181 | 1.5310 | 0.0308 | 1.6133 | 0.0503 | 6.1978 | |
| 100 | 0.0091 | 1.0456 | 0.0143 | 1.0929 | 0.1120 | 4.2635 | |
| 150 | 0.0118 | 0.8415 | 0.0064 | 0.8870 | 0.0390 | 3.4689 | |
| 200 | 0.0066 | 0.7483 | 0.0098 | 0.7872 | 0.0170 | 3.0805 | |
| MME | 25 | 0.0349 | 2.3528 | 0.0125 | 2.4749 | 0.0507 | 9.5822 |
| 50 | 0.0203 | 1.5405 | 0.0272 | 1.6325 | 0.0503 | 6.2386 | |
| 100 | 0.0157 | 1.0569 | 0.0211 | 1.1076 | 0.1020 | 4.3226 | |
| 150 | 0.0059 | 0.8486 | 0.0060 | 0.8878 | 0.0290 | 3.5174 | |
| 200 | 0.0066 | 0.7566 | 0.0126 | 0.7982 | 0.0120 | 3.1332 | |
| LMSE | 25 | 0.0683 | 4.9767 | 0.0417 | 5.2389 | 0.1866 | 19.8633 |
| 50 | 0.0586 | 3.4244 | 0.0647 | 3.5244 | 0.3311 | 13.4509 | |
| 100 | 0.0313 | 2.4225 | 0.0572 | 2.5611 | 0.0303 | 9.6458 | |
| 150 | 0.0295 | 2.0941 | 0.0110 | 2.1461 | 0.0874 | 8.4162 | |
| 200 | 0.0024 | 1.8611 | 0.0328 | 1.9605 | 0.0901 | 7.6914 | |
| LTSE | 25 | 0.0260 | 3.2252 | 0.0309 | 3.4264 | 0.1217 | 13.2600 |
| 50 | 0.0071 | 1.8757 | 0.0271 | 1.9788 | 0.1588 | 7.5153 | |
| 100 | 0.0185 | 1.2288 | 0.0070 | 1.2818 | 0.0851 | 5.0267 | |
| 150 | 0.0063 | 0.9946 | 0.0084 | 1.0384 | 0.0529 | 4.0800 | |
| 200 | 0.0094 | 0.8717 | 0.0096 | 0.9133 | 0.0515 | 3.5295 | |
| SE | 25 | 0.0354 | 3.7383 | 0.0530 | 4.0627 | 0.0944 | 15.9112 |
| 50 | 0.0174 | 2.4830 | 0.0605 | 2.6136 | 0.2457 | 10.1470 | |
| 100 | 0.0102 | 1.7304 | 0.0191 | 1.8229 | 0.0568 | 7.1198 | |
| 150 | 0.0236 | 1.3918 | 0.0101 | 1.4741 | 0.0348 | 5.6401 | |
| 200 | 0.0185 | 1.2410 | 0.0301 | 1.3127 | 0.0663 | 5.0493 | |
| JSE | 25 | 0.0838 | 2.2172 | 0.1500 | 2.3635 | 0.0430 | 9.8877 |
| 50 | 0.0962 | 1.4831 | 0.0885 | 1.5707 | 0.0312 | 6.0673 | |
| 100 | 0.0434 | 0.9977 | 0.0552 | 1.0160 | 0.1486 | 4.4244 | |
| 150 | 0.0290 | 0.8187 | 0.0299 | 0.8197 | 0.0966 | 3.5270 | |
| 200 | 0.0191 | 0.7291 | 0.0371 | 0.7239 | 0.0727 | 3.1188 | |
| RSE | 25 | 0.0900 | 2.1028 | 0.0717 | 2.2381 | 0.0566 | 9.3223 |
| 50 | 0.0846 | 1.3616 | 0.0952 | 1.4390 | 0.1143 | 6.0673 | |
| 100 | 0.0521 | 0.9346 | 0.0482 | 0.9475 | 0.1295 | 4.1004 | |
| 150 | 0.0289 | 0.7667 | 0.0304 | 0.7642 | 0.0856 | 3.2875 | |
| 200 | 0.0163 | 0.6869 | 0.0270 | 0.6772 | 0.0723 | 2.8904 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0257 | 3.2900 | 0.0391 | 3.4565 | 0.1435 | 13.4395 |
| 50 | 0.0204 | 2.2706 | 0.0137 | 2.4060 | 0.1291 | 9.2996 | |
| 100 | 0.0120 | 1.5474 | 0.0173 | 1.6108 | 0.0680 | 6.2748 | |
| 150 | 0.0127 | 1.2354 | 0.0135 | 1.2991 | 0.0646 | 5.0614 | |
| 200 | 0.0123 | 1.0907 | 0.0219 | 1.1438 | 0.0649 | 4.4912 | |
| HME | 25 | 0.0311 | 3.1178 | 0.0385 | 3.2750 | 0.2547 | 12.7506 |
| 50 | 0.0172 | 2.1034 | 0.0166 | 2.2399 | 0.0905 | 8.6701 | |
| 100 | 0.0211 | 1.4313 | 0.0108 | 1.4946 | 0.0923 | 5.8517 | |
| 150 | 0.0149 | 1.1512 | 0.0192 | 1.2080 | 0.1026 | 4.7199 | |
| 200 | 0.0244 | 1.0038 | 0.0188 | 1.0487 | 0.0344 | 4.1304 | |
| MME | 25 | 0.0491 | 3.1932 | 0.0502 | 3.3765 | 0.1710 | 12.9902 |
| 50 | 0.0248 | 2.1431 | 0.0190 | 2.2857 | 0.0689 | 8.8028 | |
| 100 | 0.0204 | 1.4502 | 0.0139 | 1.5218 | 0.0902 | 5.9529 | |
| 150 | 0.0165 | 1.1734 | 0.0097 | 1.2321 | 0.1193 | 4.8432 | |
| 200 | 0.0244 | 1.0204 | 0.0206 | 1.0664 | 0.0504 | 4.1981 | |
| LMSE | 25 | 0.0645 | 6.0669 | 0.0700 | 6.3924 | 0.2934 | 24.8944 |
| 50 | 0.0437 | 4.1302 | 0.0352 | 4.3695 | 0.1285 | 16.6505 | |
| 100 | 0.0353 | 2.8316 | 0.0336 | 3.0340 | 0.0672 | 11.8651 | |
| 150 | 0.0203 | 2.4174 | 0.0238 | 2.5743 | 0.0366 | 9.9337 | |
| 200 | 0.0136 | 2.1420 | 0.0337 | 2.2427 | 0.0476 | 8.7208 | |
| LTSE | 25 | 0.0761 | 4.0590 | 0.0457 | 4.3584 | 0.2164 | 16.9940 |
| 50 | 0.0180 | 2.5061 | 0.0124 | 2.6902 | 0.1171 | 10.4412 | |
| 100 | 0.0214 | 1.6536 | 0.0205 | 1.7371 | 0.1301 | 6.8903 | |
| 150 | 0.0062 | 1.3165 | 0.0113 | 1.3817 | 0.0520 | 6.7311 | |
| 200 | 0.0110 | 1.1377 | 0.0054 | 1.1846 | 0.0265 | 5.5473 | |
| SE | 25 | 0.0337 | 4.5980 | 0.0354 | 5.0033 | 0.1718 | 18.9508 |
| 50 | 0.0206 | 3.0280 | 0.0254 | 3.1914 | 0.0856 | 12.2507 | |
| 100 | 0.0307 | 2.0286 | 0.0418 | 2.1167 | 0.1493 | 8.3920 | |
| 150 | 0.0246 | 1.6297 | 0.0101 | 1.7027 | 0.0531 | 6.7311 | |
| 200 | 0.0133 | 1.3705 | 0.0184 | 1.4327 | 0.0516 | 4.5473 | |
| JSE | 25 | 0.1499 | 3.0926 | 0.1148 | 3.2656 | 0.1605 | 13.3709 |
| 50 | 0.1395 | 2.0736 | 0.0875 | 2.1964 | 0.0541 | 9.2018 | |
| 100 | 0.0838 | 1.3648 | 0.0778 | 1.4191 | 0.0462 | 6.1440 | |
| 150 | 0.0664 | 1.1109 | 0.0748 | 1.1416 | 0.0819 | 4.9121 | |
| 200 | 0.0398 | 0.9737 | 0.0387 | 0.9870 | 0.0584 | 4.3278 | |
| RSE | 25 | 0.1312 | 2.9141 | 0.1026 | 3.0745 | 0.2389 | 12.6750 |
| 50 | 0.1123 | 1.8990 | 0.0875 | 2.0285 | 0.0940 | 8.5669 | |
| 100 | 0.0838 | 1.2641 | 0.0564 | 1.3057 | 0.0169 | 5.7115 | |
| 150 | 0.0538 | 1.0271 | 0.0506 | 1.0478 | 0.1073 | 4.5634 | |
| 200 | 0.0466 | 0.9041 | 0.0408 | 0.9044 | 0.0529 | 3.9618 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0355 | 2.6985 | 0.0653 | 2.8377 | 0.2089 | 9.2302 |
| 50 | 0.0320 | 2.0576 | 0.0495 | 2.0770 | 0.1682 | 6.7577 | |
| 100 | 0.0432 | 1.4167 | 0.0319 | 1.4718 | 0.1120 | 4.6603 | |
| 150 | 0.0193 | 1.1467 | 0.0397 | 1.1803 | 0.1703 | 3.7981 | |
| 200 | 0.0354 | 0.9816 | 0.0358 | 1.0025 | 0.0565 | 3.1780 | |
| HME | 25 | 0.0128 | 0.7385 | 0.0191 | 0.7786 | 0.0294 | 2.4807 |
| 50 | 0.0077 | 0.4569 | 0.0275 | 0.4823 | 0.0326 | 1.5343 | |
| 100 | 0.0099 | 0.3093 | 0.0030 | 0.3199 | 0.0089 | 1.0333 | |
| 150 | 0.0018 | 0.2471 | 0.0038 | 0.2575 | 0.0173 | 0.8176 | |
| 200 | 0.0039 | 0.2129 | 0.0094 | 0.2207 | 0.0171 | 0.6987 | |
| MME | 25 | 0.0158 | 0.7469 | 0.0195 | 0.7784 | 0.0311 | 2.4392 |
| 50 | 0.0077 | 0.4638 | 0.0300 | 0.4883 | 0.0375 | 1.5615 | |
| 100 | 0.0086 | 0.3129 | 0.0027 | 0.3233 | 0.0065 | 1.0473 | |
| 150 | 0.0016 | 0.2493 | 0.0038 | 0.2594 | 0.0190 | 0.8263 | |
| 200 | 0.0042 | 0.2152 | 0.0095 | 0.2230 | 0.0167 | 0.7059 | |
| LMSE | 25 | 0.0290 | 1.1745 | 0.0626 | 1.2612 | 0.1298 | 4.0206 |
| 50 | 0.0253 | 0.7511 | 0.0316 | 0.7720 | 0.1194 | 2.5813 | |
| 100 | 0.0116 | 0.4959 | 0.0168 | 0.5316 | 0.0427 | 1.6684 | |
| 150 | 0.0121 | 0.4128 | 0.0056 | 0.4416 | 0.0336 | 1.3965 | |
| 200 | 0.0115 | 0.3746 | 0.0096 | 0.3859 | 0.0415 | 1.2230 | |
| LTSE | 25 | 0.0252 | 0.7879 | 0.0193 | 0.8346 | 0.0366 | 2.6328 |
| 50 | 0.0072 | 0.4848 | 0.0269 | 0.5010 | 0.0346 | 1.6078 | |
| 100 | 0.0142 | 0.3152 | 0.0040 | 0.3235 | 0.0088 | 1.0657 | |
| 150 | 0.0012 | 0.2513 | 0.0031 | 0.2666 | 0.0148 | 0.8401 | |
| 200 | 0.0043 | 0.2158 | 0.0086 | 0.2244 | 0.0174 | 0.7055 | |
| SE | 25 | 0.0276 | 0.8549 | 0.0235 | 0.8870 | 0.0585 | 2.9387 |
| 50 | 0.0185 | 0.5267 | 0.0266 | 0.5610 | 0.0671 | 1.8034 | |
| 100 | 0.0099 | 0.3323 | 0.0085 | 0.3532 | 0.0227 | 1.1202 | |
| 150 | 0.0057 | 0.2680 | 0.0035 | 0.2835 | 0.0095 | 0.9089 | |
| 200 | 0.0088 | 0.2276 | 0.0086 | 0.2383 | 0.0127 | 0.7596 | |
| JSE | 25 | 0.7574 | 1.3869 | 0.7617 | 1.4108 | 0.7701 | 1.8679 |
| 50 | 0.6873 | 1.2240 | 0.7396 | 1.2222 | 0.7502 | 1.6907 | |
| 100 | 0.5537 | 1.0248 | 0.6130 | 1.0448 | 0.7646 | 1.0864 | |
| 150 | 0.4985 | 0.9498 | 0.5308 | 0.9672 | 0.7523 | 1.0285 | |
| 200 | 0.4551 | 0.8875 | 0.5165 | 0.9029 | 0.7547 | 0.9957 | |
| RSE | 25 | 0.1224 | 0.7129 | 0.1233 | 0.7489 | 0.2582 | 1.4354 |
| 50 | 0.1200 | 0.4517 | 0.1200 | 0.4631 | 0.2510 | 1.1576 | |
| 100 | 0.1123 | 0.3073 | 0.1130 | 0.3143 | 0.2413 | 0.7914 | |
| 150 | 0.1126 | 0.2284 | 0.1132 | 0.2495 | 0.2421 | 0.6433 | |
| 200 | 0.1164 | 0.2003 | 0.1159 | 0.2105 | 0.2397 | 0.5571 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.0851 | 4.4032 | 0.1041 | 4.5218 | 0.4094 | 14.3599 |
| 50 | 0.0658 | 2.9326 | 0.0482 | 3.0069 | 0.3181 | 9.7475 | |
| 100 | 0.1061 | 2.1240 | 0.0376 | 2.1299 | 0.3463 | 7.0300 | |
| 150 | 0.0412 | 1.6970 | 0.0381 | 1.7547 | 0.1705 | 5.3059 | |
| 200 | 0.0538 | 1.4902 | 0.0549 | 1.5066 | 0.1883 | 4.7391 | |
| HME | 25 | 0.0308 | 1.4874 | 0.0160 | 1.5534 | 0.2438 | 4.8113 |
| 50 | 0.0183 | 0.5697 | 0.0149 | 0.5926 | 0.0435 | 1.9026 | |
| 100 | 0.0115 | 0.3552 | 0.0117 | 0.3766 | 0.0294 | 0.9398 | |
| 150 | 0.0075 | 0.2912 | 0.0033 | 0.2994 | 0.0294 | 0.9398 | |
| 200 | 0.0058 | 0.2434 | 0.0066 | 0.2565 | 0.0235 | 0.7541 | |
| MME | 25 | 0.0157 | 1.1182 | 0.0193 | 1.1224 | 0.0734 | 3.6637 |
| 50 | 0.0157 | 0.5721 | 0.0118 | 0.6094 | 0.0330 | 1.9400 | |
| 100 | 0.0122 | 0.3691 | 0.0134 | 0.3909 | 0.0258 | 0.9677 | |
| 150 | 0.0080 | 0.3006 | 0.0032 | 0.3098 | 0.0258 | 0.9677 | |
| 200 | 0.0055 | 0.2507 | 0.0064 | 0.2638 | 0.0190 | 0.8570 | |
| LMSE | 25 | 0.0338 | 1.2257 | 0.0361 | 1.2559 | 0.1089 | 4.0461 |
| 50 | 0.0072 | 0.7788 | 0.0252 | 0.8096 | 0.0647 | 2.5366 | |
| 100 | 0.0081 | 0.5321 | 0.0176 | 0.5589 | 0.0429 | 1.7388 | |
| 150 | 0.0191 | 0.4592 | 0.0113 | 0.4624 | 0.0448 | 1.4856 | |
| 200 | 0.0075 | 0.4087 | 0.0086 | 0.4204 | 0.0120 | 1.3296 | |
| LTSE | 25 | 0.0268 | 0.8817 | 0.0122 | 0.9245 | 0.0879 | 2.9881 |
| 50 | 0.0119 | 0.5463 | 0.0140 | 0.5711 | 0.0339 | 1.8242 | |
| 100 | 0.0103 | 0.3505 | 0.0096 | 0.3767 | 0.0106 | 1.2141 | |
| 150 | 0.0079 | 0.2930 | 0.0054 | 0.2985 | 0.0324 | 0.9495 | |
| 200 | 0.0073 | 0.2445 | 0.0066 | 0.2566 | 0.0201 | 0.8194 | |
| SE | 25 | 0.0336 | 0.8569 | 0.0086 | 0.8580 | 0.1036 | 2.8933 |
| 50 | 0.0091 | 0.5331 | 0.0194 | 0.5448 | 0.0678 | 1.7469 | |
| 100 | 0.0084 | 0.3461 | 0.0077 | 0.3611 | 0.0160 | 1.1448 | |
| 150 | 0.0086 | 0.2966 | 0.0058 | 0.2981 | 0.0428 | 0.9002 | |
| 200 | 0.0079 | 0.2547 | 0.0074 | 0.2619 | 0.0235 | 0.7541 | |
| JSE | 25 | 0.7908 | 1.8380 | 0.7576 | 1.7894 | 0.7684 | 10.8075 |
| 50 | 0.7524 | 1.4694 | 0.7724 | 1.4720 | 0.7594 | 8.4858 | |
| 100 | 0.7156 | 1.2321 | 0.7597 | 1.2758 | 0.7571 | 4.2756 | |
| 150 | 0.6420 | 1.1254 | 0.7081 | 1.1349 | 0.7642 | 3.1536 | |
| 200 | 0.5570 | 1.0665 | 0.6444 | 1.0662 | 0.7670 | 2.5951 | |
| RSE | 25 | 0.1144 | 0.7906 | 0.1131 | 0.8281 | 0.2498 | 2.1158 |
| 50 | 0.1181 | 0.5053 | 0.1187 | 0.5235 | 0.2424 | 1.3083 | |
| 100 | 0.1241 | 0.3315 | 0.1168 | 0.3544 | 0.2384 | 0.8901 | |
| 150 | 0.1182 | 0.2685 | 0.1211 | 0.2755 | 0.2412 | 0.7147 | |
| 200 | 0.1116 | 0.2276 | 0.1144 | 0.2380 | 0.2428 | 0.6306 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.8488 | 19.6873 | 0.7906 | 19.4488 | 1.0191 | 40.7973 |
| 50 | 0.5346 | 19.0980 | 0.6276 | 19.3425 | 1.2897 | 30.2086 | |
| 100 | 0.7694 | 18.0536 | 0.7018 | 18.9754 | 0.8172 | 24.9392 | |
| 150 | 0.6870 | 17.1070 | 0.4330 | 18.3462 | 1.0011 | 22.1539 | |
| 200 | 0.5887 | 16.3318 | 0.4991 | 17.3047 | 0.7971 | 20.7615 | |
| HME | 25 | 0.3293 | 7.0647 | 0.1116 | 7.3974 | 0.4452 | 24.0466 |
| 50 | 0.1449 | 4.7746 | 0.1662 | 4.9250 | 0.5889 | 15.9805 | |
| 100 | 0.1303 | 3.2177 | 0.1267 | 2.8200 | 0.1635 | 11.1029 | |
| 150 | 0.1416 | 2.6552 | 0.1113 | 2.4335 | 0.1934 | 8.9369 | |
| 200 | 0.0943 | 2.3010 | 0.0537 | 2.0563 | 0.1468 | 7.5880 | |
| MME | 25 | 0.2795 | 6.6162 | 0.0981 | 6.8656 | 0.4049 | 22.4089 |
| 50 | 0.1324 | 4.5829 | 0.1512 | 4.7748 | 0.5941 | 15.3914 | |
| 100 | 0.1227 | 3.1681 | 0.1144 | 3.3225 | 0.1632 | 10.9061 | |
| 150 | 0.1379 | 2.6262 | 0.1059 | 2.7004 | 0.1905 | 8.8067 | |
| 200 | 0.0825 | 2.2941 | 0.0405 | 2.3425 | 0.1613 | 7.5240 | |
| LMSE | 25 | 0.1442 | 7.4609 | 0.1380 | 8.0187 | 0.3155 | 18.9403 |
| 50 | 0.0989 | 5.1311 | 0.1235 | 5.3363 | 0.2125 | 16.5584 | |
| 100 | 0.0634 | 3.2493 | 0.1848 | 3.3769 | 0.1479 | 11.0435 | |
| 150 | 0.0803 | 2.6496 | 0.0792 | 3.0367 | 0.0967 | 8.8498 | |
| 200 | 0.1008 | 2.6153 | 0.0984 | 2.6756 | 0.2632 | 7.7167 | |
| LTSE | 25 | 0.4722 | 8.3560 | 0.1881 | 8.9986 | 0.7007 | 28.8922 |
| 50 | 0.1518 | 5.4782 | 0.2335 | 5.7422 | 0.7990 | 18.5412 | |
| 100 | 0.1381 | 3.2822 | 0.1341 | 3.4588 | 0.2280 | 11.3549 | |
| 150 | 0.1360 | 2.6971 | 0.1302 | 2.7673 | 0.1870 | 9.1910 | |
| 200 | 0.1052 | 2.3156 | 0.0656 | 2.3916 | 0.1188 | 7.7337 | |
| SE | 25 | 2.8435 | 9.4556 | 3.7004 | 10.4928 | 5.4429 | 28.2871 |
| 50 | 0.8114 | 6.5779 | 1.2565 | 6.2095 | 2.0388 | 16.3748 | |
| 100 | 0.6504 | 3.8305 | 0.9445 | 3.9316 | 1.9139 | 11.8926 | |
| 150 | 0.9939 | 2.7156 | 0.7543 | 3.2098 | 5.5093 | 9.5507 | |
| 200 | 0.8905 | 2.4521 | 0.5439 | 2.8587 | 3.0965 | 8.8487 | |
| JSE | 25 | 0.7432 | 19.5232 | 0.6327 | 19.1775 | 0.9350 | 30.9780 |
| 50 | 0.5909 | 18.0380 | 0.9221 | 18.4486 | 0.3600 | 27.1521 | |
| 100 | 0.4665 | 17.0666 | 0.4645 | 18.0012 | 0.5687 | 19.1521 | |
| 150 | 0.4083 | 16.0001 | 0.7556 | 17.3483 | 1.1434 | 18.1797 | |
| 200 | 0.5706 | 15.0623 | 0.6031 | 16.2746 | 0.5111 | 17.1067 | |
| RSE | 25 | 0.3469 | 4.5985 | 0.1614 | 4.5109 | 0.1272 | 13.7179 |
| 50 | 0.0791 | 3.1763 | 0.1239 | 3.2625 | 0.7092 | 9.8212 | |
| 100 | 0.0890 | 2.3176 | 0.0884 | 2.5966 | 0.1543 | 7.8820 | |
| 150 | 0.1325 | 2.0001 | 0.0942 | 2.1660 | 0.1484 | 7.0053 | |
| 200 | 0.0768 | 1.8924 | 0.0263 | 1.8990 | 0.1324 | 6.4548 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.7944 | 5.2375 | 0.5017 | 6.1350 | 0.6275 | 6.4083 |
| 50 | 0.5521 | 4.8550 | 0.7120 | 5.9626 | 0.4389 | 6.2877 | |
| 100 | 0.8544 | 4.1828 | 0.4655 | 5.7585 | 0.6999 | 6.0153 | |
| 150 | 0.7160 | 3.0651 | 0.5376 | 5.3560 | 0.5693 | 5.2649 | |
| 200 | 0.5921 | 2.9390 | 0.5933 | 5.2213 | 0.6371 | 5.0758 | |
| HME | 25 | 0.0695 | 0.5643 | 0.0608 | 0.5857 | 0.0679 | 0.8973 |
| 50 | 0.0690 | 0.3065 | 0.0660 | 0.2964 | 0.0626 | 0.3229 | |
| 100 | 0.0623 | 0.2039 | 0.0598 | 0.2038 | 0.0604 | 0.2116 | |
| 150 | 0.0600 | 0.1724 | 0.0624 | 0.1757 | 0.0629 | 0.1757 | |
| 200 | 0.0614 | 0.1599 | 0.0619 | 0.1614 | 0.0601 | 0.1588 | |
| MME | 25 | 0.0562 | 0.5725 | 0.0457 | 0.5904 | 0.0489 | 1.2000 |
| 50 | 0.0562 | 0.2944 | 0.0548 | 0.2909 | 0.0484 | 0.3485 | |
| 100 | 0.0468 | 0.1900 | 0.0464 | 0.1906 | 0.0450 | 0.1981 | |
| 150 | 0.0458 | 0.1560 | 0.0484 | 0.1639 | 0.0481 | 0.1609 | |
| 200 | 0.0463 | 0.1433 | 0.0448 | 0.1420 | 0.0452 | 0.1447 | |
| LMSE | 25 | 0.0625 | 1.1280 | 0.0498 | 1.1404 | 0.0931 | 3.3462 |
| 50 | 0.0519 | 0.6491 | 0.0658 | 0.6595 | 0.0648 | 1.3806 | |
| 100 | 0.0548 | 0.4080 | 0.0576 | 0.4131 | 0.0598 | 0.5696 | |
| 150 | 0.0529 | 0.3264 | 0.0605 | 0.3239 | 0.0503 | 0.3914 | |
| 200 | 0.0566 | 0.2774 | 0.0519 | 0.2713 | 0.0580 | 0.3142 | |
| LTSE | 25 | 0.0973 | 0.6964 | 0.0647 | 0.6953 | 0.0736 | 1.6717 |
| 50 | 0.0780 | 0.3913 | 0.0783 | 0.3967 | 0.0724 | 0.6050 | |
| 100 | 0.0750 | 0.2562 | 0.0680 | 0.2529 | 0.0700 | 0.3075 | |
| 150 | 0.0673 | 0.2046 | 0.0731 | 0.2093 | 0.0706 | 0.2163 | |
| 200 | 0.0672 | 0.1781 | 0.0662 | 0.1813 | 0.0685 | 0.1867 | |
| SE | 25 | 0.1298 | 1.0254 | 0.0169 | 0.6801 | 0.3637 | 0.7047 |
| 50 | 0.0934 | 0.5478 | 0.0110 | 0.4933 | 0.1190 | 0.2945 | |
| 100 | 0.1629 | 0.3002 | 0.1485 | 0.2666 | 0.1052 | 0.1858 | |
| 150 | 0.1206 | 0.2731 | 0.0512 | 0.2351 | 0.0928 | 0.1529 | |
| 200 | 0.1736 | 0.2623 | 0.0736 | 0.1853 | 0.1457 | 0.1497 | |
| JSE | 25 | 0.3167 | 4.7204 | 0.4594 | 6.0041 | 0.4751 | 5.5051 |
| 50 | 0.1586 | 3.1748 | 0.1988 | 5.7254 | 0.3179 | 5.3947 | |
| 100 | 0.1965 | 2.1097 | 0.3427 | 5.0111 | 0.1710 | 5.3683 | |
| 150 | 0.1029 | 2.0062 | 0.2095 | 4.7791 | 0.2699 | 5.3016 | |
| 200 | 0.2396 | 1.7858 | 0.2952 | 4.7019 | 0.1746 | 5.1026 | |
| RSE | 25 | 0.0100 | 0.5285 | 0.0157 | 0.5742 | 0.0415 | 0.6514 |
| 50 | 0.0161 | 0.2630 | 0.0246 | 0.3027 | 0.0195 | 0.3105 | |
| 100 | 0.0236 | 0.1779 | 0.0211 | 0.1759 | 0.0182 | 0.1691 | |
| 150 | 0.0214 | 0.1315 | 0.0182 | 0.1328 | 0.0213 | 0.1359 | |
| 200 | 0.0190 | 0.1099 | 0.0214 | 0.1128 | 0.0204 | 0.1124 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.7197 | 6.1436 | 0.4972 | 6.6404 | 0.6248 | 6.5710 |
| 50 | 0.6168 | 6.0352 | 0.6490 | 6.6169 | 0.5822 | 6.1232 | |
| 100 | 0.6384 | 5.3854 | 0.6268 | 6.1234 | 0.5426 | 6.0692 | |
| 150 | 0.6185 | 5.0035 | 0.5820 | 5.4785 | 0.6485 | 5.2365 | |
| 200 | 0.7964 | 4.5073 | 0.5438 | 5.0980 | 0.5591 | 5.0336 | |
| HME | 25 | 0.0624 | 0.3609 | 0.0500 | 0.3594 | 0.0579 | 0.3638 |
| 50 | 0.0679 | 0.2331 | 0.0592 | 0.2360 | 0.0594 | 0.2316 | |
| 100 | 0.0604 | 0.1783 | 0.0564 | 0.1780 | 0.0620 | 0.1811 | |
| 150 | 0.0606 | 0.1604 | 0.0569 | 0.1595 | 0.0575 | 0.1577 | |
| 200 | 0.0629 | 0.1523 | 0.0601 | 0.1527 | 0.0627 | 0.1536 | |
| MME | 25 | 0.0510 | 0.3599 | 0.0474 | 0.3606 | 0.0449 | 0.3565 |
| 50 | 0.0530 | 0.2201 | 0.0519 | 0.2177 | 0.0513 | 0.2196 | |
| 100 | 0.0461 | 0.1625 | 0.0468 | 0.1615 | 0.0462 | 0.1618 | |
| 150 | 0.0477 | 0.1434 | 0.0471 | 0.1435 | 0.0449 | 0.1427 | |
| 200 | 0.0460 | 0.1335 | 0.0469 | 0.1348 | 0.0452 | 0.1334 | |
| LMSE | 25 | 0.0571 | 0.8234 | 0.0557 | 0.8147 | 0.0521 | 0.8229 |
| 50 | 0.0541 | 0.4482 | 0.0580 | 0.4417 | 0.0566 | 0.4412 | |
| 100 | 0.0537 | 0.2613 | 0.0540 | 0.2610 | 0.0550 | 0.2635 | |
| 150 | 0.0578 | 0.2292 | 0.0558 | 0.2290 | 0.0556 | 0.2292 | |
| 200 | 0.0543 | 0.2115 | 0.0564 | 0.2134 | 0.0559 | 0.2125 | |
| LTSE | 25 | 0.0744 | 0.4775 | 0.0732 | 0.4801 | 0.0670 | 0.4804 |
| 50 | 0.0741 | 0.3025 | 0.0734 | 0.3042 | 0.0713 | 0.3037 | |
| 100 | 0.0702 | 0.2001 | 0.0678 | 0.1998 | 0.0684 | 0.2009 | |
| 150 | 0.0665 | 0.1720 | 0.0687 | 0.1716 | 0.0697 | 0.1719 | |
| 200 | 0.0709 | 0.1635 | 0.0701 | 0.1639 | 0.0699 | 0.1644 | |
| SE | 25 | 0.1102 | 0.5024 | 0.1217 | 0.5035 | 0.0173 | 0.4901 |
| 50 | 0.2590 | 0.4799 | 0.1471 | 0.3330 | 0.1527 | 0.4601 | |
| 100 | 0.1934 | 0.2489 | 0.1479 | 0.2863 | 0.1231 | 0.2918 | |
| 150 | 0.1387 | 0.2201 | 0.1286 | 0.2488 | 0.1150 | 0.2446 | |
| 200 | 0.1072 | 0.1870 | 0.1130 | 0.1855 | 0.1092 | 0.1880 | |
| JSE | 25 | 0.2322 | 7.0444 | 0.2406 | 8.1936 | 0.2621 | 8.1735 |
| 50 | 0.2676 | 7.0099 | 0.1940 | 8.0740 | 0.2975 | 7.5860 | |
| 100 | 0.2418 | 6.5458 | 0.2174 | 7.5776 | 0.2899 | 7.4900 | |
| 150 | 0.2262 | 6.1071 | 0.3186 | 6.7061 | 0.3452 | 7.0690 | |
| 200 | 0.2661 | 5.4648 | 0.2850 | 5.7614 | 0.3689 | 6.2156 | |
| RSE | 25 | 0.0103 | 0.3262 | 0.0073 | 0.3252 | 0.0091 | 0.3206 |
| 50 | 0.0276 | 0.2069 | 0.0077 | 0.2121 | 0.0054 | 0.2102 | |
| 100 | 0.0214 | 0.1277 | 0.0082 | 0.1278 | 0.0062 | 0.1306 | |
| 150 | 0.0215 | 0.1008 | 0.0079 | 0.1000 | 0.0087 | 0.1005 | |
| 200 | 0.0188 | 0.0869 | 0.0079 | 0.0880 | 0.0073 | 0.0878 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| BIAS | RMSE | BIAS | RMSE | BIAS | RMSE | ||
| OLSE | 25 | 0.5657 | 7.9980 | 0.4434 | 8.9370 | 0.6042 | 8.0520 |
| 50 | 0.7596 | 7.0075 | 0.5667 | 8.2005 | 0.5769 | 7.9962 | |
| 100 | 0.8088 | 6.2413 | 0.5829 | 7.3920 | 0.5820 | 7.7281 | |
| 150 | 0.6682 | 5.4902 | 0.7837 | 6.4956 | 0.6723 | 6.4396 | |
| 200 | 0.7307 | 5.0436 | 0.8332 | 5.3495 | 0.5592 | 5.6593 | |
| HME | 25 | 0.0657 | 0.2953 | 0.0582 | 0.2969 | 0.0578 | 0.2917 |
| 50 | 0.0612 | 0.2139 | 0.0654 | 0.2124 | 0.0623 | 0.2131 | |
| 100 | 0.0651 | 0.1721 | 0.0580 | 0.1679 | 0.0612 | 0.1758 | |
| 150 | 0.0612 | 0.1567 | 0.0627 | 0.1582 | 0.0614 | 0.1559 | |
| 200 | 0.0645 | 0.1484 | 0.0615 | 0.1483 | 0.0593 | 0.1483 | |
| MME | 25 | 0.0479 | 0.2803 | 0.0449 | 0.2840 | 0.0449 | 0.2810 |
| 50 | 0.0480 | 0.1995 | 0.0512 | 0.1984 | 0.0479 | 0.1999 | |
| 100 | 0.0499 | 0.1552 | 0.0454 | 0.1518 | 0.0434 | 0.1575 | |
| 150 | 0.0496 | 0.1415 | 0.0455 | 0.1373 | 0.0473 | 0.1378 | |
| 200 | 0.0464 | 0.1283 | 0.0461 | 0.1263 | 0.0451 | 0.1296 | |
| LMSE | 25 | 0.0594 | 0.5024 | 0.0572 | 0.5109 | 0.0464 | 0.4924 |
| 50 | 0.0536 | 0.3142 | 0.0523 | 0.3122 | 0.0626 | 0.3105 | |
| 100 | 0.0548 | 0.2374 | 0.0546 | 0.2300 | 0.0526 | 0.2314 | |
| 150 | 0.0556 | 0.2082 | 0.0595 | 0.2112 | 0.0561 | 0.2105 | |
| 200 | 0.0541 | 0.1899 | 0.0557 | 0.1919 | 0.0562 | 0.1953 | |
| LTSE | 25 | 0.0713 | 0.3348 | 0.0669 | 0.3417 | 0.0678 | 0.3342 |
| 50 | 0.0733 | 0.2375 | 0.0690 | 0.2358 | 0.0676 | 0.2295 | |
| 100 | 0.0693 | 0.1848 | 0.0699 | 0.1838 | 0.0657 | 0.1865 | |
| 150 | 0.0706 | 0.1679 | 0.0708 | 0.1707 | 0.0684 | 0.1704 | |
| 200 | 0.0701 | 0.1584 | 0.0699 | 0.1608 | 0.0704 | 0.1616 | |
| SE | 25 | 0.0487 | 0.3743 | 0.1390 | 0.3623 | 0.0858 | 0.3725 |
| 50 | 0.1429 | 0.3441 | 0.1533 | 0.2081 | 0.0967 | 0.2990 | |
| 100 | 0.0755 | 0.2189 | 0.1182 | 0.2116 | 0.1140 | 0.2466 | |
| 150 | 0.1122 | 0.1808 | 0.1004 | 0.2062 | 0.1067 | 0.2130 | |
| 200 | 0.1100 | 0.1816 | 0.1044 | 0.1792 | 0.0577 | 0.1935 | |
| JSE | 25 | 0.2102 | 9.2222 | 0.2572 | 9.9901 | 0.1209 | 9.5601 |
| 50 | 0.0821 | 8.6237 | 0.2206 | 9.6870 | 0.1603 | 9.3979 | |
| 100 | 0.3418 | 7.7882 | 0.2696 | 8.9530 | 0.2304 | 9.0038 | |
| 150 | 0.3379 | 6.8491 | 0.1748 | 7.9881 | 0.3194 | 8.6317 | |
| 200 | 0.0998 | 5.1003 | 0.3074 | 6.8933 | 0.4819 | 7.2279 | |
| RSE | 25 | 0.0075 | 0.2611 | 0.0061 | 0.2718 | 0.0082 | 0.2668 |
| 50 | 0.0039 | 0.1622 | 0.0110 | 0.1645 | 0.0030 | 0.1593 | |
| 100 | 0.0051 | 0.1044 | 0.0039 | 0.1027 | 0.0057 | 0.1072 | |
| 150 | 0.0045 | 0.0854 | 0.0072 | 0.0843 | 0.0054 | 0.0828 | |
| 200 | 0.0062 | 0.0730 | 0.0042 | 0.0732 | 0.0051 | 0.0735 | |
References
- Lukman, A.F.; Farghali, R.A.; Kibria, B.G.; Oluyemi, O.A. Robust-stein estimator for overcoming outliers and multicollinearity. Scientific Reports 2023, 13, 9066. [CrossRef]
- Sani, M. Robust Diagnostic and Parameter Estimation for Multiple Linear and Panel Data Regression Models 2018.
- Algamal, Z.; Lukman, A.; Abonazel, M.R.; Awwad, F. Performance of the Ridge and Liu Estimators in the zero-inflated Bell Regression Model. Journal of Mathematics 2022, 2022, 9503460. [CrossRef]
- Fernandes, G.; Rodrigues, J.J.; Carvalho, L.F.; Al-Muhtadi, J.F.; Proença, M.L. A comprehensive survey on network anomaly detection. Telecommunication Systems 2019, 70, 447–489. [CrossRef]
- Hampel, F.R. Robust statistics: A brief introduction and overview. In Proceedings of the Research Report/Seminar für Statistik, Eidgenössische Technische Hochschule (ETH). Seminar für Statistik, Eidgenössische Technische Hochschule, 2001, Vol. 94.
- Huber, P.J. Robust regression: asymptotics, conjectures and Monte Carlo. The annals of statistics 1973, pp. 799–821.
- Draper, N.R. Applied regression analysis bibliography update 1992–93 1994.
- Hadi. A modification of a method for the detection of outliers in multivariate samples. Journal of the Royal Statistical Society Series B: Statistical Methodology 1994, 56, 393–396. [CrossRef]
- Neter, J.; Wasserman, W.; Kutner, M.H. Applied linear regression models; Richard D. Irwin, 1983.
- Fitrianto, A.; Xin, S.H. Comparisons between robust regression approaches in the presence of outliers and high leverage points. BAREKENG: Jurnal Ilmu Matematika dan Terapan 2022, 16, 243–252. [CrossRef]
- Arum.; Ugwuowo. Combining principal component and robust ridge estimators in linear regression model with multicollinearity and outlier. Concurrency and Computation: Practice and Experience 2022, 34, e6803. [CrossRef]
- Jegede, S.L.; Lukman, A.F.; Ayinde, K.; Odeniyi, K.A. Jackknife Kibria-Lukman M-estimator: Simulation and application. Journal of the Nigerian Society of Physical Sciences 2022, pp. 251–264.
- Dawoud, I.; Kibria, B.G. A new biased estimator to combat the multicollinearity of the Gaussian linear regression model. Stats 2020, 3, 526–541. [CrossRef]
- Dawoud, I.; Abonazel. Robust Dawoud–Kibria estimator for handling multicollinearity and outliers in the linear regression model. Journal of Statistical Computation and Simulation 2021, 91, 3678–3692. [CrossRef]
- Alma, Ö.G. Comparison of robust regression methods in linear regression. Int. J. Contemp. Math. Sciences 2011, 6, 409–421.
- Stein, C. Inadmissibility of the usual estimator for the mean of a multivariate normal distribution. In Proceedings of the Proceedings of the third Berkeley symposium on mathematical statistics and probability, volume 1: Contributions to the theory of statistics. University of California Press, 1956, Vol. 3, pp. 197–207.
- James, W.; Stein, C.; et al. Estimation with quadratic loss. In Proceedings of the Proceedings of the fourth Berkeley symposium on mathematical statistics and probability. University of California Press, 1961, Vol. 1, pp. 361–379.
- Siegel, A.F. Robust regression using repeated medians. Biometrika 1982, 69, 242–244. [CrossRef]
- Yohai. High breakdown-point and high efficiency robust estimates for regression. The Annals of statistics 1987, pp. 642–656.
- Rousseeuw.; Yohai. Robust regression by means of S-estimators. In Proceedings of the Robust and nonlinear time series analysis: Proceedings of a Workshop Organized by the Sonderforschungsbereich 123 “Stochastische Mathematische Modelle”, Heidelberg 1983. Springer, 1984, pp. 256–272.
- Yohai. High breakdown-point and high efficiency robust estimates for regression. The Annals of Statistics 1987, 15, 642–656. [CrossRef]
- Huber, P.J. The place of the L1-norm in robust estimation. Computational statistics & data Analysis 1987, 5, 255–262.
- Fitrianto, A.; Midi, H. Estimating bias and rmse of indirect effects using rescaled residual bootstrap in mediation analysis. WSEAS Transaction on Mathematics 2010, 9, 397–406.
- Bai, X. Robust linear regression 2012.
- Yahya. Performance of ridge estimator in inverse Gaussian regression model. Communications in Statistics-Theory and Methods 2019, 48, 3836–3849. [CrossRef]
- Suhail, M.; Chand, S.; Aslam, M. New quantile based ridge M-estimator for linear regression models with multicollinearity and outliers. Communications in Statistics-Simulation and Computation 2023, 52, 1417–1434. [CrossRef]
- Lee, B.K.; Lessler, J.; Stuart, E.A. Weight trimming and propensity score weighting. PloS one 2011, 6, e18174. [CrossRef]
- Mutalib, S.S.S.; Satari, S.Z.; Yusoff, W.N.S.W. Comparison of robust estimators for detecting outliers in multivariate datasets. In Proceedings of the Journal of Physics: Conference Series. IOP Publishing, 2021, Vol. 1988, p. 012095.
- Yeh, I.C.; Hsu, T.K. Building real estate valuation models with comparative approach through case-based reasoning. Applied Soft Computing 2018, 65, 260–271. [CrossRef]
- Ibrahim. Comparative study of some estimators of linear regression models in the presence of outliers. FUDMA Journal of Sciences 2022, 6, 368–376. [CrossRef]
- Rahayu, D.A.; Nursholihah, U.F.; Suryaputra, G.; Surono, S. Comparasion of the m, mm and s estimator in robust regression analysis on indonesian literacy index data 2018. EKSAKTA: Journal of Sciences and Data Analysis 2023, pp. 11–22.
- Gad, A.M.; Qura, M.E. Regression estimation in the presence of outliers: A comparative study. International Journal of probability and Statistics 2016, 5, 65–72.
- Affindi, A.; Ahmad, S.; Mohamad, M. A comparative study between ridge MM and ridge least trimmed squares estimators in handling multicollinearity and outliers. In Proceedings of the Journal of Physics: Conference Series. IOP Publishing, 2019, Vol. 1366, p. 012113.
- Almetwally, E.M.; Almongy, H. Comparison between M-estimation, S-estimation, and MM estimation methods of robust estimation with application and simulation. International Journal of Mathematical Archive 2018, 9, 1–9.


| 1.0000 | 0.4496 | 0.4055 | 0.3235 | 0.3588 | 0.6748 | 0.6480 | |
| 0.4496 | 1.0000 | 0.9248 | 0.6288 | 0.6382 | 0.7010 | 0.6380 | |
| 0.4055 | 0.9248 | 1.0000 | 0.5866 | 0.5959 | 0.6963 | 0.6380 | |
| 0.3235 | 0.6288 | 0.5866 | 1.0000 | 0.9782 | 0.5469 | 0.3897 | |
| 0.3588 | 0.6382 | 0.5959 | 0.9782 | 1.0000 | 0.5666 | 0.4292 | |
| 0.6748 | 0.7010 | 0.6963 | 0.5469 | 0.5666 | 1.0000 | 0.6827 | |
| 0.6480 | 0.6380 | 0.6380 | 0.3897 | 0.4292 | 0.6827 | 1.0000 |
| Estimator | 0% Outlier | 10% Outlier | 20% Outlier | |||
|---|---|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | Bias | RMSE | |
| OLSE | 0.0002 | 0.0247 | 0.0007 | 0.0295 | 0.0028 | 0.0270 |
| HME | 0.0010 | 0.0280 | 0.0032 | 0.0282 | 0.0035 | 0.0250 |
| MME | 0.0026 | 0.0472 | 0.0059 | 0.0126 | 0.0058 | 0.0340 |
| LMSE | 0.0044 | 0.0890 | 0.0056 | 0.0667 | 0.0064 | 0.0606 |
| LTSE | 0.0041 | 0.0767 | 0.0006 | 0.0531 | 0.0065 | 0.0489 |
| SE | 0.0043 | 0.0753 | 0.0054 | 0.0235 | 0.0064 | 0.0214 |
| JSE | 0.0006 | 0.0228 | 0.0014 | 0.0126 | 0.0029 | 0.0111 |
| RSE | 0.0013 | 0.0261 | 0.0030 | 0.0114 | 0.0037 | 0.0108 |
| 1.0000 | 0.0175 | 0.0609 | 0.0095 | 0.0350 | ||
| 0.0175 | 1.0000 | 0.0256 | 0.0496 | 0.0544 | ||
| 0.0609 | 0.0256 | 1.0000 | -0.6025 | -0.5911 | -0.8063 | |
| 0.0095 | 0.0496 | -0.6025 | 1.0000 | 0.4441 | 0.4491 | |
| 0.0350 | 0.0544 | -0.5911 | 0.4441 | 1.0000 | 0.4129 | |
| -0.8063 | 0.4491 | 0.4129 | 1.0000 |
| Estimator | 0% Outlier | 15.3% Outlier | 21.5% Outlier | |||
|---|---|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | Bias | RMSE | |
| OLSE | 168.2679 | 54504.9900 | 2732.8280 | 66897.1350 | 7291.0330 | 59865.6200 |
| HME | 7683.2360 | 67391.2100 | 1937.2760 | 62329.2885 | 2379.8690 | 47601.0400 |
| MME | 12588.7800 | 67391.2100 | 2322.3150 | 70523.8053 | 720.0933 | 50175.4500 |
| LMSE | 18806.2100 | 167922.3000 | 9802.2880 | 188380.7012 | 8417.1460 | 137477.5000 |
| LTSE | 17386.5200 | 116365.6000 | 5397.6670 | 90165.8498 | 6875.5230 | 71319.8900 |
| SE | 21667.5800 | 89613.2900 | 12931.5900 | 28573.5115 | 4669.2530 | 20823.2300 |
| JSE | 1446.8980 | 29700.3800 | 3393.4700 | 13195.9917 | 8122.0880 | 13441.6400 |
| RSE | 9355.8480 | 40048.4200 | 3861.2500 | 13122.0683 | 3046.3670 | 10501.8300 |
| 1.0000 | 0.9460 | 0.9618 | |
| 0.9460 | 1.0000 | 0.9787 | |
| 0.9618 | 0.9787 | 1.0000 |
| Estimator | 0% Outlier | 18.67% Outlier | ||
|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | |
| OLSE | 0.0004 | 0.0633 | 0.0672 | 0.3983 |
| HME | 0.0002 | 0.0683 | 0.0671 | 0.3721 |
| MME | 0.0005 | 0.0721 | 0.0147 | 0.1127 |
| LMSE | 0.0058 | 0.2818 | 0.0122 | 0.2698 |
| LTSE | 0.0031 | 0.1542 | 0.0238 | 0.2135 |
| SE | 0.0092 | 0.1704 | 0.0078 | 0.1494 |
| JSE | 0.0012 | 0.0593 | 0.0588 | 0.3669 |
| RSE | 0.0025 | 0.0620 | 0.0152 | 0.0847 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





