Fe(II)/Fe(III) Catalysed Peroxymonosulfate Modelling in the Presence of Protocatechuic Acid

1. Introduction

Advanced oxidation processes based on the simultaneous generation of hydroxyl and sulfate radicals have raised an increasing interest among researchers and water treatment practitioners. The escalation of studies on sulfate radical based technologies can be attributed to the higher redox potential compared to hydroxyl radical, handling and transport easiness of peroxymonosulfate (PMS) in solid form, safety reasons, etc. Activation of PMS can be carried out in different ways such as irradiation, sonication, homogeneous or heterogeneous catalysis and/or heat [1]. Apparently, from an economic point of view, homogenous catalytic activation is conceived as the cheapest option if the catalyst is economical. Co(II) has been demonstrated to be the most active cation in PMS decomposition, however, toxicity of this element advises against its use in water treatment facilities. Otherwise, Fe(II) is considered as a suitable alternative due to a number of advantages. Hence, iron is a cheap element which can be catalogued as environmentally harmless [2]. However, Fe(II) is not the panacea of PMS based systems. Hence, in some cases the system Fe(II)/H2O2 is more efficient than the combination Fe(II)/PMS [3]. In acidic conditions, regeneration of Fe(II) from Fe(III) by PMS is rather slow, as a consequence, the reaction normally comes to a halt [4]. Additionally, formation of Fe(III) involves the precipitation of ferric species at circumneutral pH (solubility constant of Fe(OH)3 = 2.8 10-39), removing, therefore, the catalyst from the media.

To overcome the previous drawbacks, some authors have suggested the utilization of reducing/complexing substances capable of accelerating Fe(II) regeneration simultaneously avoiding Fe(III) precipitation [5]. Hence, Shi and co-workers [2] investigated the elimination of ciprofloxacim by the Fe(II)/PMS system in the presence of protocatechuic acid (pCtchA), confirming the beneficial effect of the phenolic substance addition.

This work is focused to model the main features of the system PMS/Fe/pCtchA by considering a detailed reaction mechanism of elemental stages.

2. Results and Discussion

In order to establish a detailed reaction mechanism and validate its suitability and general use, the influence of a series of key variables was evaluated. Once, the mechanism of elemental reactions was proposed, the set of linear differential equations derived from the reactions carried out in a discontinuous batch reactor was numerically solved.

2.1. Effect of Fe(III) Concentration

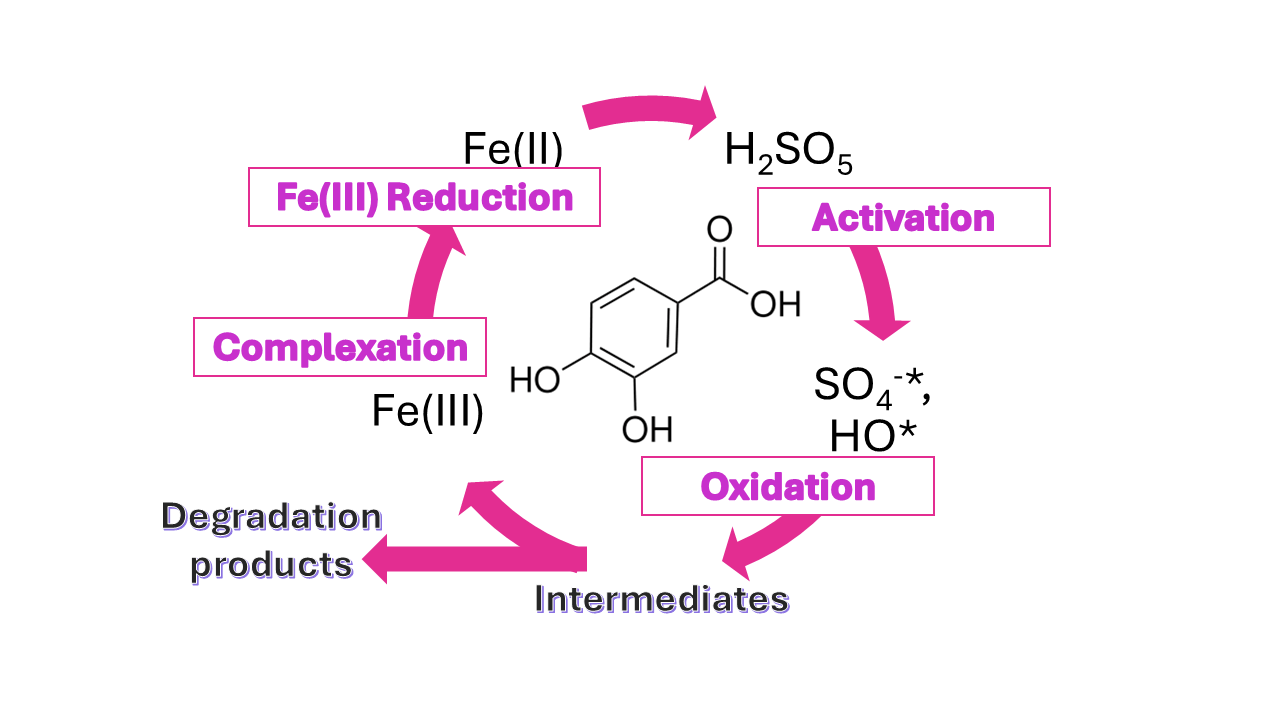
The system PMS/Fe(II) is believed to act in a similar way to Fenton´s chemistry [6], i.e. generation of highly reactive radicals is postulated to occur:

${\mathrm{Fe}\left(\mathrm{II}\right)+\mathrm{HSO}}_5^{-}\to \left\{\begin{array}{l}{\mathrm{SO}}_4^{-\text{•}}{+\mathrm{Fe}\left(\mathrm{III}\right)+\mathrm{HO}}^{-}\\ {\mathrm{SO}}_4^{2-}{+\mathrm{Fe}\left(\mathrm{III}\right)+\mathrm{HO}}^{•}\end{array}\right.$                 k=3x10⁴ M^-1s^-1         (1)

Additionally, some authors also claim the formation of Fe(IV) species, suggesting the absence of hydroxyl radicals [4]:

${\mathrm{Fe}\left(\mathrm{II}\right)+\mathrm{HSO}}_5^{-}\to {\mathrm{SO}}_4^{2-}{+\mathrm{FeO}}^{2+}{+\mathrm{H}}^{+}$                     k=2.2 x10⁴ M^-1s^-1         (2)

${\mathrm{Fe}\left(\mathrm{II}\right)+\mathrm{FeO}}^{2+}+2H^{+}\to 2Fe(III)+H_{2}O$                 k=9.0 x10⁴ M^-1s^-1         (3)

${4\mathrm{FeO}}^{2+}+4H^{+}\to 4Fe(III)+O_2+2H_{2}O$                 k=1.5 s^-1             (4)

${\mathrm{FeO}}^{2+}{+\mathrm{SO}}_4^{-•}\to {\mathrm{Fe}\left(\mathrm{III}\right)+\mathrm{SO}}_5^{-•}$                         k=1.2 x10⁶ M^-1s^-1         (5)

${\mathrm{FeO}}^{2+}{+\mathrm{HSO}}_5^{-}\to {\mathrm{Fe}\left(\mathrm{III}\right)+\mathrm{SO}}_5^{-•}+O{H}^{-}$                 k=2.8 x10⁵ M^-1s^-1         (6)

Formation of Fe(IV) species has also been reported to occur in the classical Fenton´s reaction under circumneutral pH conditions, while HO• radicals are generated at acidic pH [7].

If the reactivity of FeO²⁺, HO• and SO₄^-• with pCtchA is assumed to be similar, the nature of the reactive species generated in the PMS/Fe system is irrelevant in terms of simulation purposes (notice that peroxymonosulfate scavenging of the three oxidants is comparable). Accordingly, in this work it was decided to ignore FeO²⁺ formation, assuming that model results would not significantly change.

Together with the initiation reaction (eq. 1), the following mechanism was therefore adopted [1,2,4,8]:

HSO₅^- + Fe(III) → Fe(II) + H⁺ + SO₅^-•            k=unknown            (7)

SO₄^-• + Fe(II) → SO₄^2- + Fe(III)                k = 4.6 x10⁹ M^-1s^-1            (8)

HO^• + Fe(II) → HO^- + Fe(III)                    k = 3.2 x10⁸ M^-1s^-1            (9)

H₂O₂+ Fe(II)→ HO^• + Fe(III)+OH^-                k = 50-70 M^-1s^-1            (10)

SO₅^-• + Fe(II) +H⁺→ HSO₅^- + Fe(III)                k = 4.3 x10⁷ M^-1s^-1            (11)

Fe(III) + HO₂^• → Fe(II) + O₂ + H⁺                k = 7.8 x10⁵ M^-1s^-1            (12)

Fe(II) + HO₂^• → Fe(III) + H₂O₂                k = 1.3 x10⁶ M^-1s^-1            (13)

SO₄^-• + HSO₅^- → HSO₄^- + SO₅^-•                k < 1 x 10⁵ M^-1s^-1            (14)

HO^• + HSO₅^- → SO₅^-• + H₂O                    k = 1.7 x10⁷ M^-1s^-1            (15)

HO^• + SO₅^2- → SO₅^-• + OH^-                    k = 2.1 x10⁹ M^-1s^-1            (16)

${\mathrm{HO}}^{•}{+\mathrm{H}}_2{\mathrm{O}}_2\to {{\mathrm{HO}}_2}^{•}{+\mathrm{H}}_2\mathrm{O}$                        k = 2.7 x10⁷ M^-1s^-1            (17)

${\mathrm{HO}}^{•}{+\mathrm{HO}}_2^{ -}\to {\mathrm{HO}}_2^{ •}{+\mathrm{OH}}^{-}$                        k = 7.5 x10⁹ M^-1s^-1            (18)

${\mathrm{HO}}_2^{ •}{+\mathrm{H}}_2{\mathrm{O}}_2\to {\mathrm{HO}}^{•}{+\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O}$                    k = 3.0 M^-1s^-1            (19)

${\mathrm{O}}_2^{ -•}{+\mathrm{H}}_2{\mathrm{O}}_2\to {\mathrm{HO}}^{•}{+\mathrm{O}}_2+{\mathrm{OH}}^{-}$                    k = 0.13 M^-1s^-1            (20)

${\mathrm{SO}}_4^{-•}{+\mathrm{H}}_2\mathrm{O}\rightleftarrows {\mathrm{OH}}^{•}{+\mathrm{HSO}}_4^{-}$            k = 6.6 x10² s^-1 k- = 6.9x10⁵ M^-1s^-1        (21)

${\mathrm{SO}}_4^{-•}{+\mathrm{OH}}^{-}\to {\mathrm{OH}}^{•}{+\mathrm{SO}}_4^{2-}$                    k = 6.5x10⁷ M^-1s^-1            (22)

${2\mathrm{SO}}_5^{-•}\to {2\mathrm{SO}}_4^{-•}{+\mathrm{O}}_2$                        k = 2.15 x 10⁸ M^-1s^-1        (23)

${2\mathrm{SO}}_4^{-•}\to {\mathrm{S}}_2{\mathrm{O}}_8^{2-}$                        k = 7.5 x 10⁸-3.6 x 10⁹ M^-1s^-1        (24)

${2\mathrm{SO}}_5^{-•}\to {\mathrm{S}}_2{\mathrm{O}}_8^{2-}{+\mathrm{O}}_2$                        k = 3.5 x 10⁸ M^-1s^-1        (25)

2HO^• → H₂O₂                            k = 5.2 x 10⁹ M^-1s^-1        (26)

${\mathrm{SO}}_4^{-•}$+HO^• → HSO₅^-                        k = 1.0 x 10¹⁰ M^-1s^-1        (27)

${\mathrm{SO}}_4^{-•}{+\mathrm{S}}_2{\mathrm{O}}_8^{2-}\to {\mathrm{S}}_2{\mathrm{O}}_8^{-•}{+\mathrm{SO}}_4^{=}$                     k = 6.5 x 10⁵ M^-1s^-1            (28)

${\mathrm{HO}}^{•}{+\mathrm{S}}_2{\mathrm{O}}_8^{2-}\to {\mathrm{S}}_2{\mathrm{O}}_8^{-•}{+\mathrm{OH}}^{-}$                     k = 1.4 x 10⁷ M^-1s^-1            (29)

${\mathrm{HO}}_2^{•}+{\mathrm{HO}}_2^{•}\to {\mathrm{O}}_2+{\mathrm{H}}_2{\mathrm{O}}_2$                    k = 8.3 x 10⁵ M^-1s^-1        (30)

${\mathrm{HO}}_2^{•}+{\mathrm{O}}_2^{-•}\to {\mathrm{O}}_2+{\mathrm{HO}}_2^{-}$                        k = 9.7 x 10⁷ M^-1s^-1        (31)

${\mathrm{HO}}^{•}{+\mathrm{HO}}_2^{•}\to {\mathrm{H}}_2{\mathrm{O}+\mathrm{O}}_2$                        k = 6.6 x 10⁹ M^-1s^-1            (32)

${\mathrm{HO}}^{•}{+\mathrm{O}}_2^{-•}\to {\mathrm{OH}}^{-}{+\mathrm{O}}_2$                        k = 7.0 x 10⁹ M^-1s^-1            (33)

${\mathrm{S}}_2{\mathrm{O}}_8^{2-}{+\mathrm{H}}_2\mathrm{O}\to {\mathrm{HSO}}_5^{-}+{\mathrm{HSO}}_4^{-}$                    k = 7.5 x 10^-5 M^-1s^-1        (34)

${\mathrm{HSO}}_5^{-}\rightleftarrows {\mathrm{H}}^{+}{+\mathrm{SO}}_5^{2-}$                        pK_eq =    9.4            (35)

${\mathrm{H}}_2\mathrm{O}\rightleftarrows {\mathrm{H}}^{+}{+\mathrm{OH}}^{-}$                        pK_eq = 14                (36)

${\mathrm{HSO}}_4^{-}\to {\mathrm{H}}^{+}{+\mathrm{SO}}_4^{2-}$                            k = 0.012 s^-1            (37)

${\mathrm{H}}_2{\mathrm{O}}_2\rightleftarrows {\mathrm{H}}^{+}{+\mathrm{HO}}_2^{-}$                        pK_eq = 11.6            (38)

HO₂^•    $\rightleftarrows$ H⁺ + O₂^-•                     k = 3.2 x 10⁵, k- = 2.0 x 10¹⁰        (39)

pCtchA + SO₄^-•    $\to$ Intermediate + SO₄^2-         k = 1.2 x 10⁹ M^-1s^-1        (40)

pCtchA + HO^•    $\to$ Intermediate + HO^-            k = 2.2 x 10¹⁰ M^-1s^-1        (41)

pCtchA + HSO₅^-    $\to$ Intermediate            k = 0.02 M^-1s^-1            (42)

Intermediate + SO₄^-•    $\to$ Intermediate2 + HSO₄^2-    k = 10⁹-10¹⁰ M^-1s^-1            (43)

Intermediate + HO^•    $\to$ Intermediate2 + HO^-        k = 10⁹-10¹⁰ M^-1s^-1            (44)

Intermediate2 + SO₄^-•    $\to$ Product + HSO₄^2-        k = 10⁹-10¹⁰ M^-1s^-1            (45)

Intermediate2 + HO^•    $\to$ Product + HO^-        k = 10⁹-10¹⁰ M^-1s^-1            (46)

In the previous reaction mechanism, the following aspects have been considered. First, pCthA can be directly oxidized by peroxymonosulfate (eq. 42) through a non-radical pathway similarly to other reported compounds [1]. Additionally, two intermediates have been considered with assumed reactivity with radicals similar to that of the parent compound (eqs. 43-46).

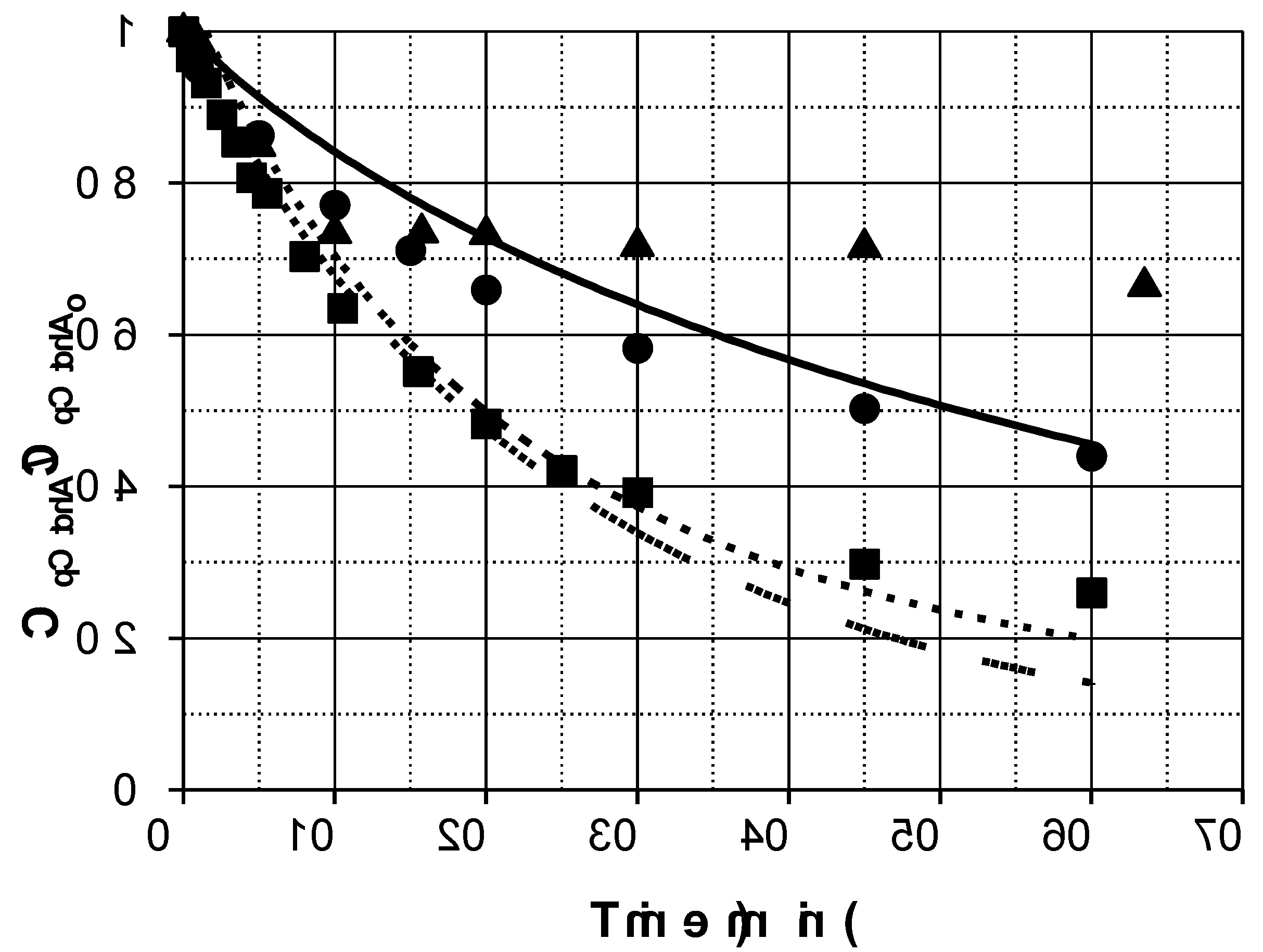
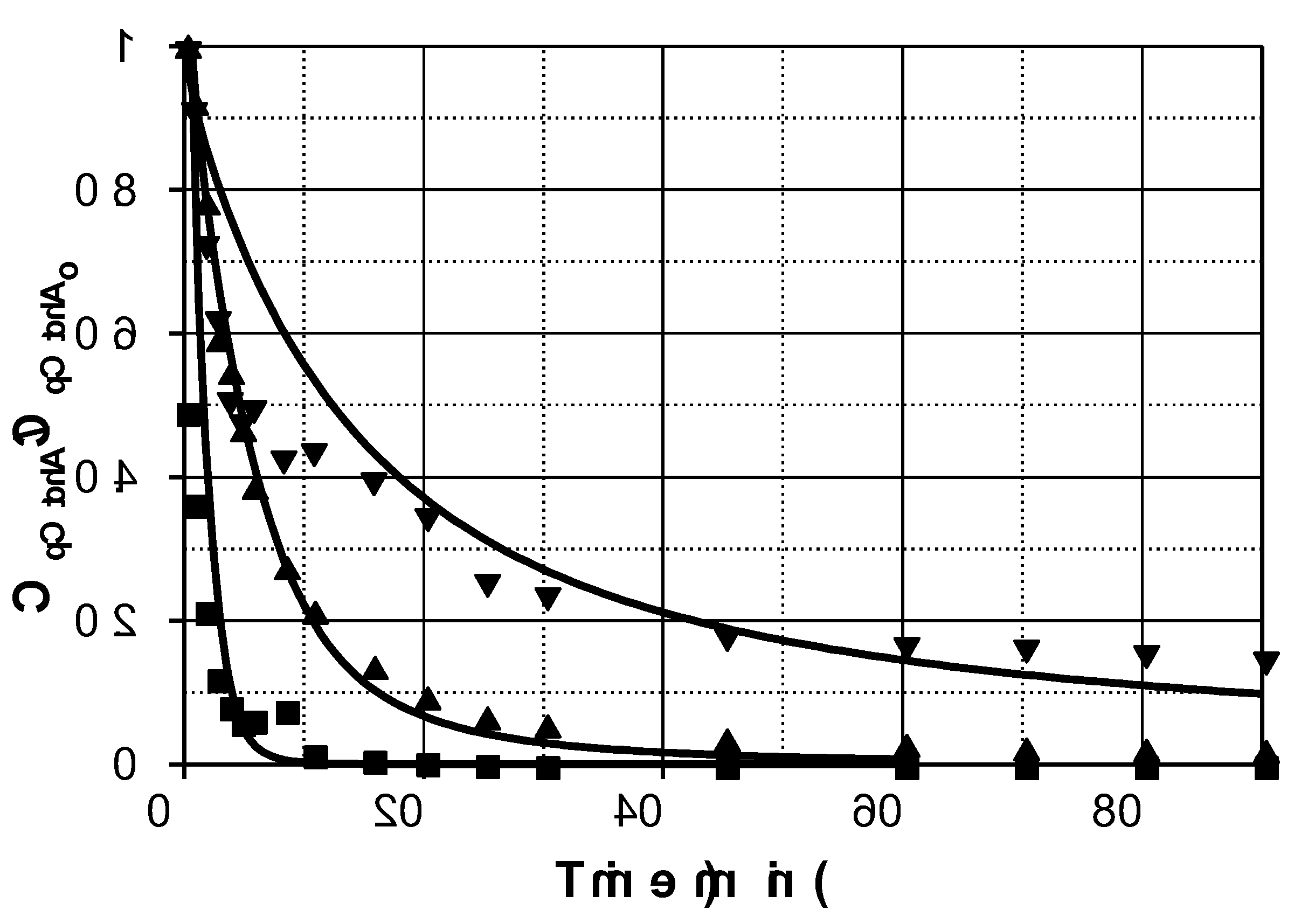
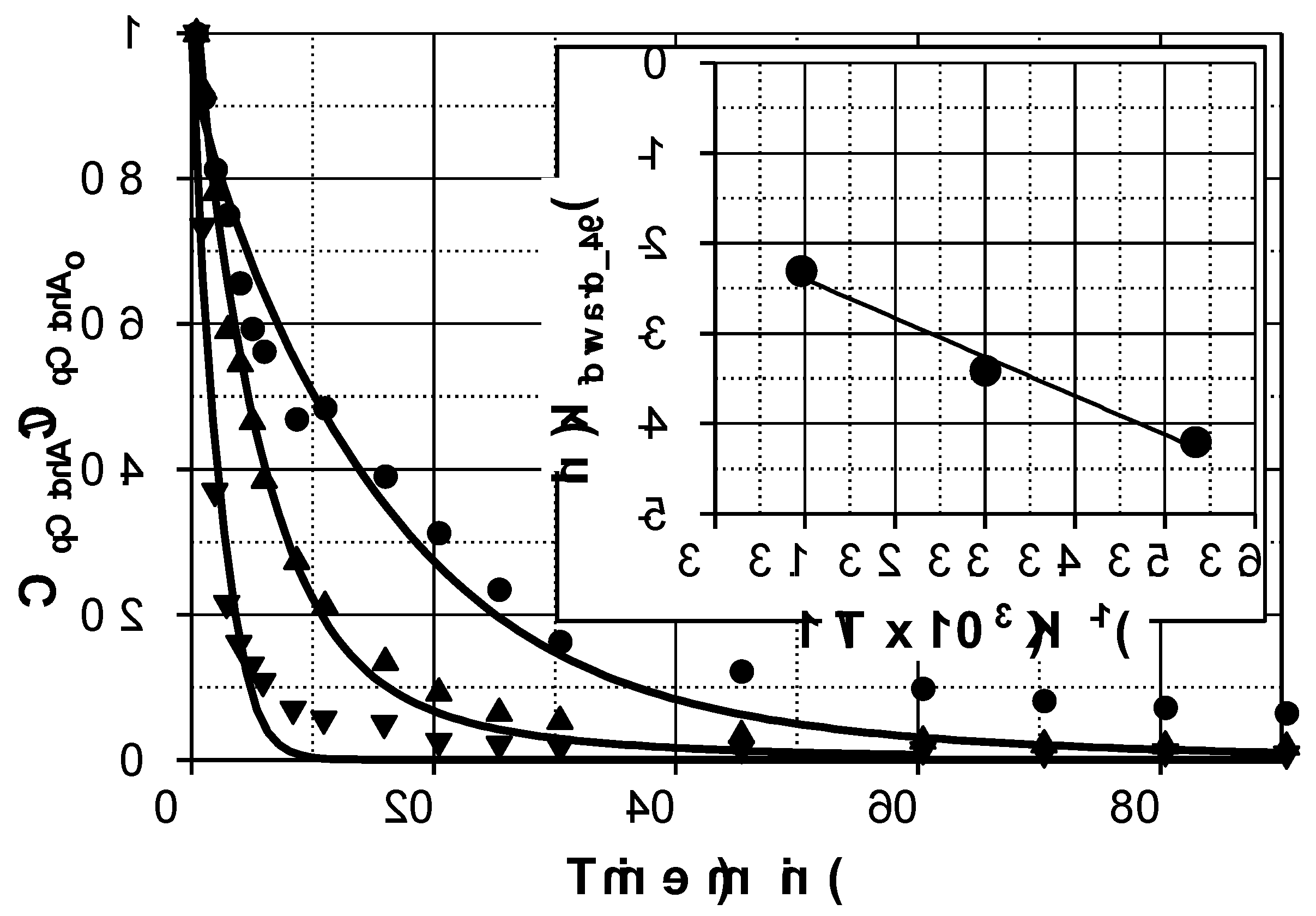
Development of direct pCtchA oxidation was confirmed in discontinuous runs in the presence of PMS at the pH obtained after reagents addition (pH around 3.4).

Figure 1 shows the results obtained at two different initial PMS concentrations. Hence, under the conditions investigated, for a discontinuous perfectly mixed reactor, in the absence of catalyst, pCtchA removal could be modelled by a simple second order reaction of the type:

$-{\displaystyle \frac{{\mathrm{dC}}_{\mathrm{pCtchA}}}{\mathrm{dt}}}{=\mathrm{kC}}_{\mathrm{pCtchA}}{\mathrm{C}}_{{\mathrm{HSO}}_5^{-}}$                            (47)

The direct rate constant k was estimated to be 0.02 + 0.003 M^-1s^-1, leading to a 25-30% conversion in 150 min when the highest PMS concentration was used.

Moreover, the interaction of polyphenols and iron species has also been reported in the literature. Hence, Pan and co-workers [5] claim that ortho-dihydroxy groups in polyphenols (as it is the case of pCtchA) can reduce Fe(III) to Fe(II) via a one-electron reaction leading to the formation of semiquinones. The previous assumption was corroborated in this work by conducting oxidation experiments of caffeic and p-coumaric acids. These experiments revealed a high conversion in the first case and no effect when p-coumaric acid was used (results not shown). Accordingly, the following reactions were incorporated to the overall mechanism to account for the Fe(III) reduction stage [8]:

$\mathrm{pCtchA}+\mathrm{Fe}\left(\mathrm{III}\right)\rightleftarrows \mathrm{pCtchA}\equiv \mathrm{Fe}\left(\mathrm{III}\right)$    K_eq = 1.18 x 10⁴ M^-1                (48)

$\mathrm{pCtchA}\equiv \mathrm{Fe}\left(\mathrm{III}\right)\rightleftarrows {\mathrm{Fe}\left(\mathrm{II}\right)+3,4\mathrm{SQ}}^{•}$         k = 3.3 x10^-2 s^-1 k- = 3.0 x10⁴ M^-1s^-1        (49)

${3,4\mathrm{SQ}}^{•}+\mathrm{Fe}\left(\mathrm{III}\right)\rightleftarrows {\mathrm{Fe}\left(\mathrm{II}\right)+\mathrm{BQ}+\mathrm{H}}^{+}$         k = 1.0 x10⁵ M^-1s^-1 k- = 1.0 x10¹ M^-1s^-1     (50)

Reactions 48 and 49 are key stages in the process. The forward rate constant of the complex formation (eq. 48) is reported to highly depend on pH. Hence, deprotonation of polyphenols is required for metal chelation [5], although some controversy is raised about this statement [9]. Hence, Mentasti et al. report a complex formation rate constant depending on proton concentration according to the mechanism [9]:

$\mathrm{pCtchA}+\mathrm{Fe}\left(\mathrm{III}\right)\rightleftarrows \mathrm{pCtchA}\equiv {\mathrm{Fe}\left(\mathrm{III}\right)}^{+}{+2\mathrm{H}}^{+}$                            (51)

${\mathrm{pCtchA}+\mathrm{Fe}\left(\mathrm{OH}\right)}^{2+}\rightleftarrows \mathrm{pCtchA}\equiv {\mathrm{Fe}\left(\mathrm{III}\right)}^{+}{+\mathrm{H}}^{+}{+\mathrm{H}}_2\mathrm{O}$                        (52)

${\mathrm{Fe}\left(\mathrm{III}\right)+\mathrm{H}}_2\mathrm{O}\rightleftarrows {\mathrm{Fe}\left(\mathrm{OH}\right)}^{2+}{+\mathrm{H}}^{+}$                                    (53)

From the mechanism 51-53 it is seen that an increase in protons concentration promotes the reverse reactions in equilibriums 51 and 52 while a decrease in H⁺ favours formation of Fe(OH)²⁺.

Based on the previous reasoning, a negative effect of H⁺ concentration (pH decrease) is assumed and accounted for in the kinetic analysis. A value of 1.7 x 10³ M^-1s^-1 is reported in the literature for the forward reaction in equilibrium 48. This value was randomly assigned to occur at pH 3 so the forward rate constant was supposed to inversely change with protons concentration according to k_{forward_48} =1.7/C_H+.

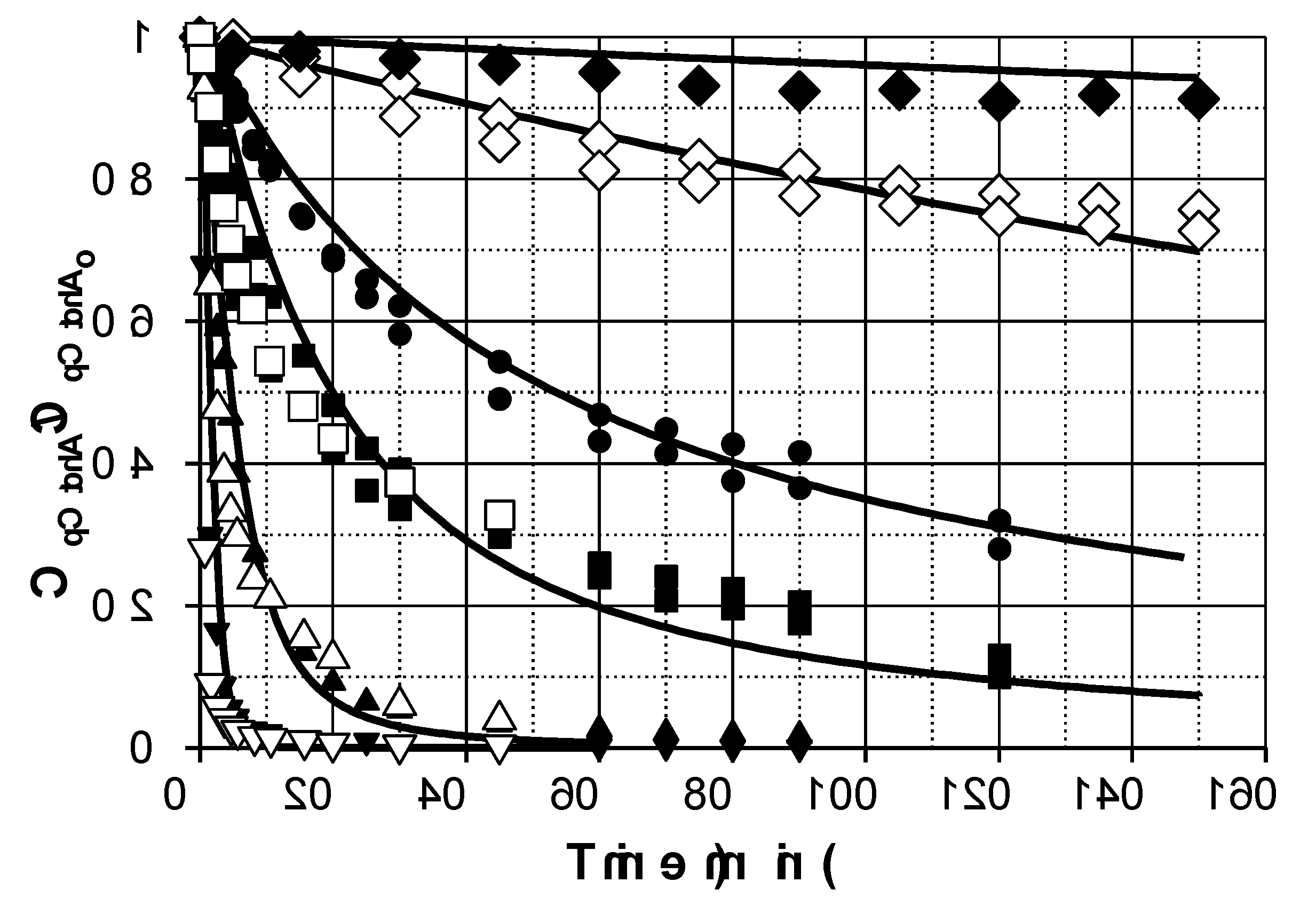
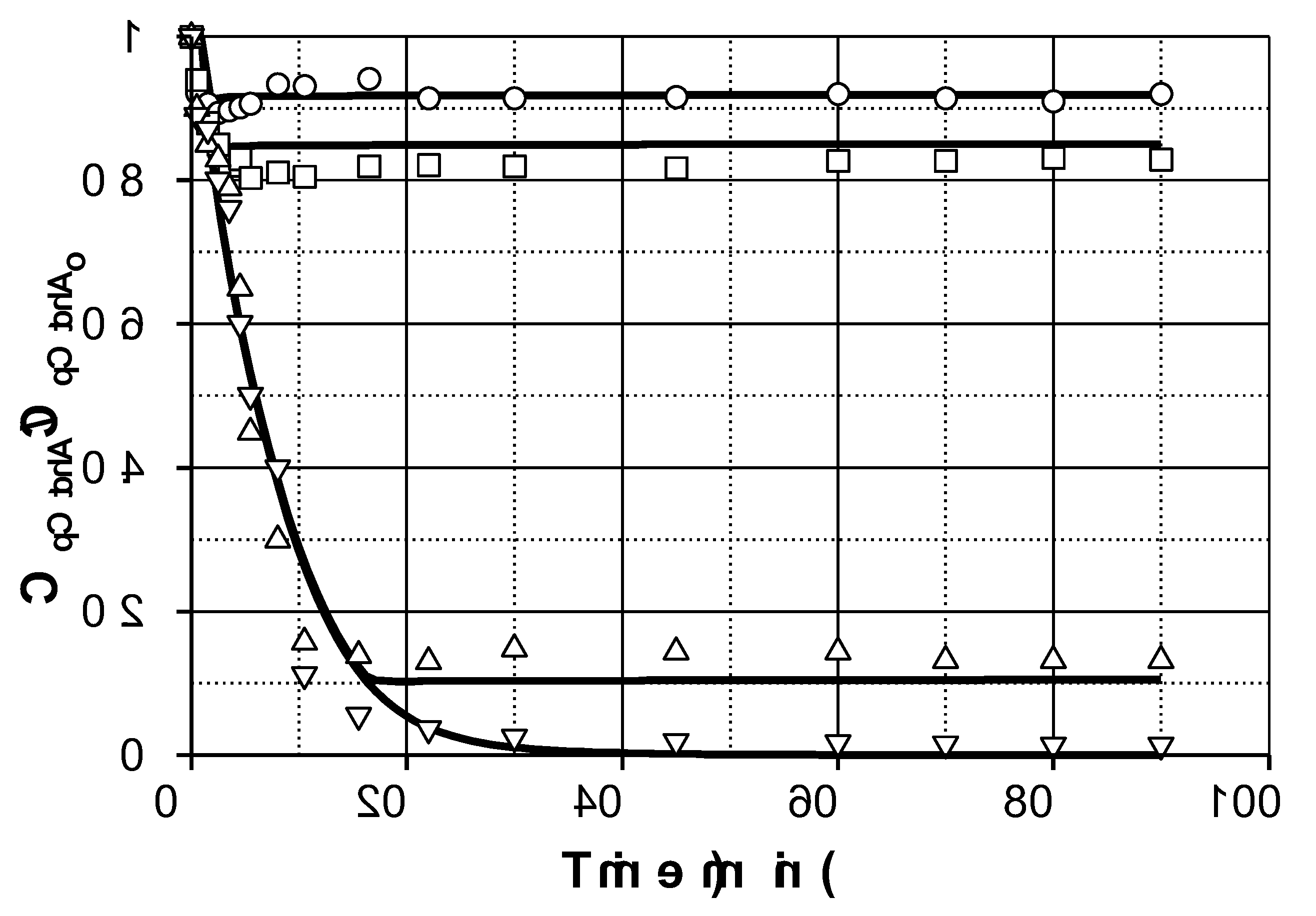
According to the previous statement, the presence of Fe(III) would be able to remove pCtchA when PMS is added due to iron reduction and formation of radicals through equation 1. Figure 1 shows the evolution profiles of pCtchA removal when different amounts of Fe(III) were added in the presence of PMS. As commented previously, pH evolution was taken into account since this parameter highly affects Fe(III) reduction. A linear decrease of pH was experienced in all the experiments from 3.5 to 1.7-2.0 depending on operating conditions.

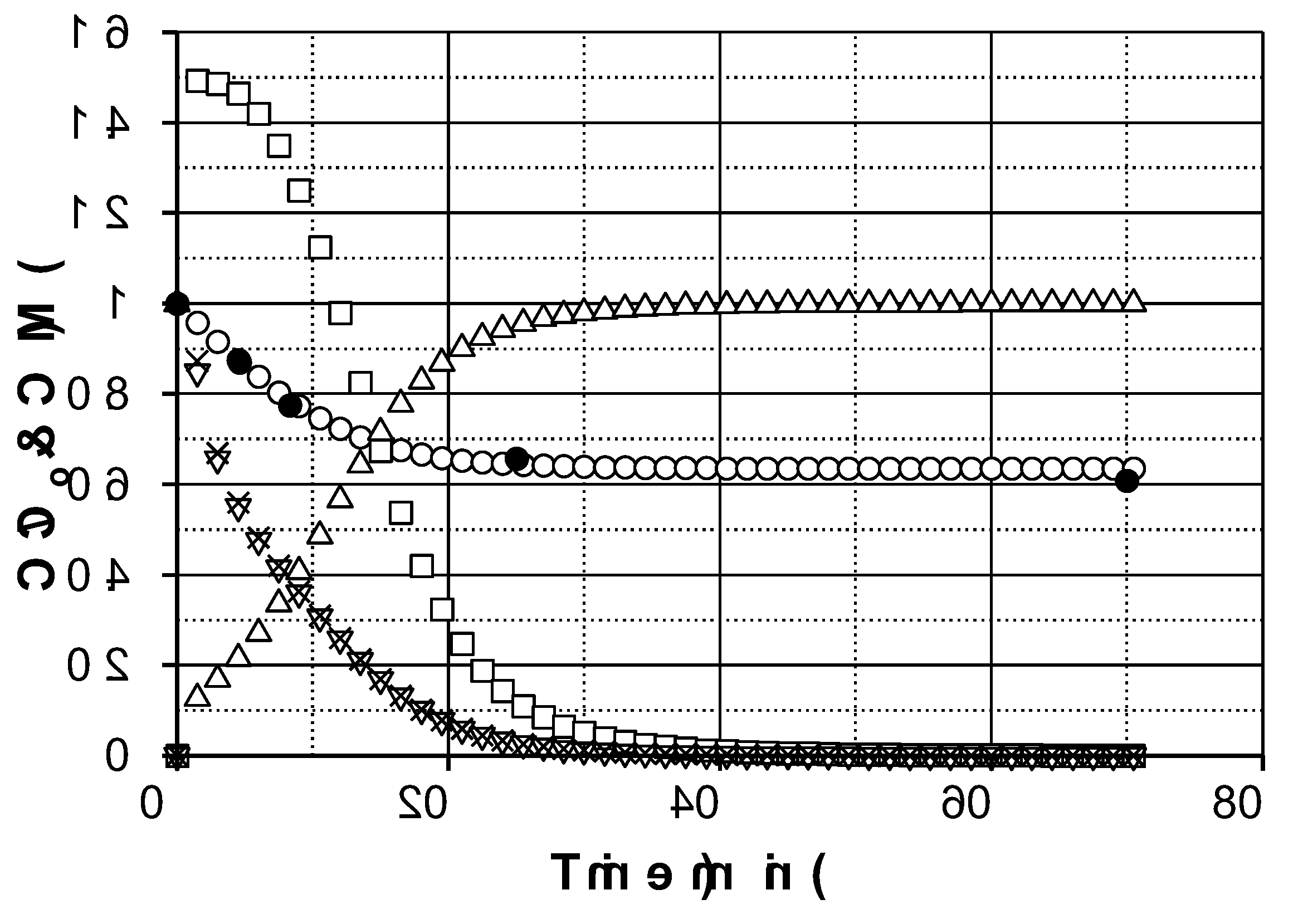
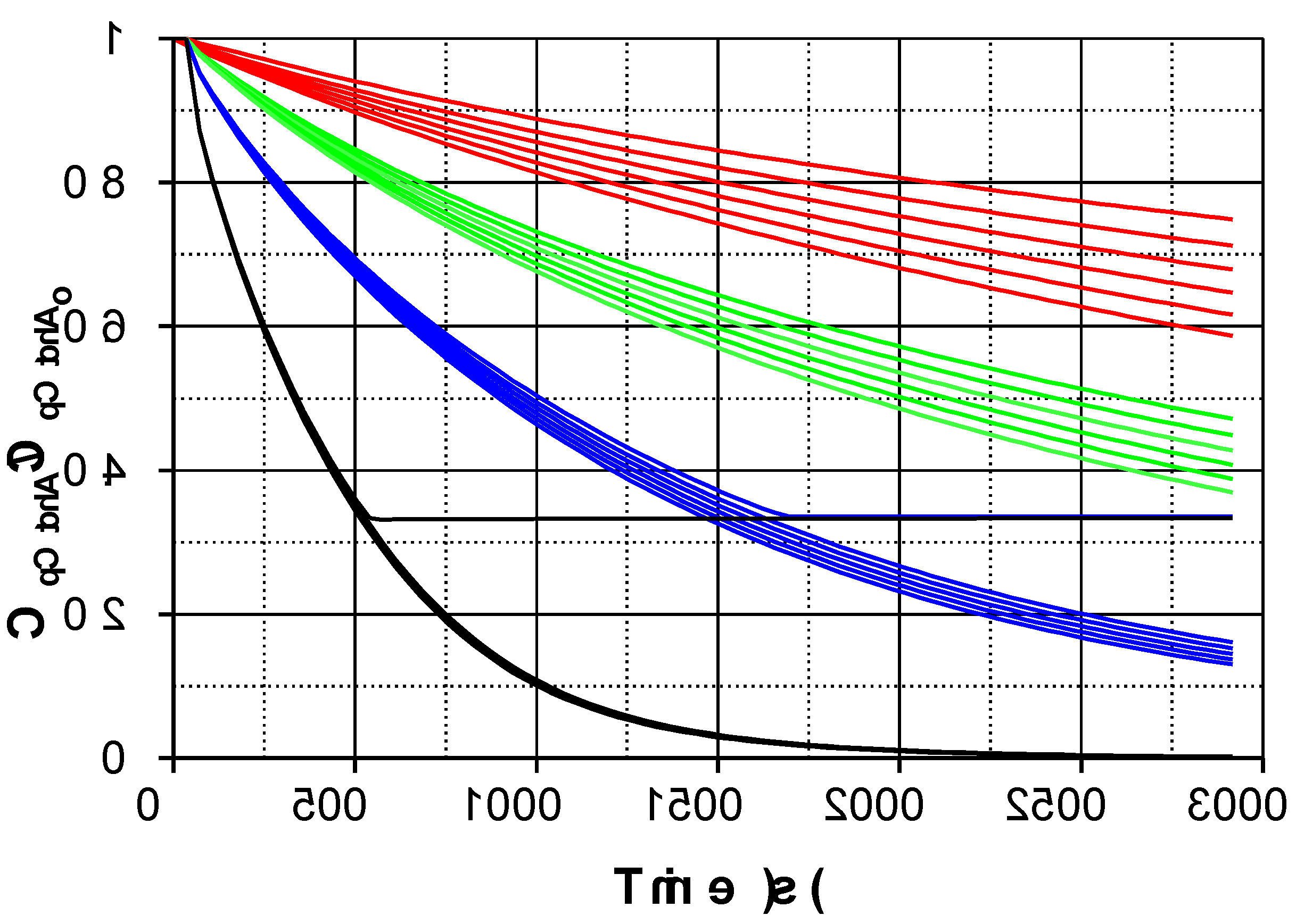
As inferred from Figure 1, addition of Fe(III) significantly accelerates pCtchA oxidation even when the ratio Fe(III):pCtchA is extremely low. The model is capable of acceptably simulate the influence of Fe(III) initial concentration not only on the pCtchA disappearance but also in the evolution of PMS. Peroxymonosulfate undergoes a relatively fast initial reduction coinciding with the decrease in Fe(III) concentration. Once pCtchA disappears, Fe(III) concentration recovers its initial value while PMS stabilizes in time. As an example, Figure 2 shows the evolution profiles of PMS (experimental and simulated), iron species and radicals in a typical experiment obtained from the model.

2.2. Effect of Fe(II) Concentration

To check the differences between the systems Fe(II)/PMS and Fe(III)/PMS, a series of experiments was carried out modifying the initial concentration of Fe(II) initially added with no pH control. As stated previously, variation of pH along the experiments was incorporated to the model due to its influence in the redox Fe(II)/Fe(III) cycle. Apparently, if reduction of Fe(III) to Fe(II) is not the controlling stage in the process, the systems PMS/Fe(II) and PMS/Fe(III) should lead to similar results. As inferred from Figure 1, no significant differences were observed when using Fe(II) instead of Fe(III), suggesting that the reduction of Fe(III) to Fe(II) is quite fast and does not control the pCtchA removal rate.

2.3. Effect of PMS Concentration

The influence of PMS initial concentration was assessed by completing an experimental series keeping constant the operating conditions but the initial PMS load in the approximated range 4 – 250 x 10^-5 M. Figure 3 shows the experimental and model calculated evolution of pCtchA in runs carried out at pH 3 in the presence of 2 x 10^-5 M in Fe(II). As observed, both experimental and model results indicate a roughly 1:1 stoichiometric ratio between PMS and pCtchA when low PMS concentrations are used. This stoichiometric factor slightly increases above 1 when an excess of PMS is applied. As inferred from the experiments completed with the highest PMS concentration in the presence of 20x 10^-5 M in Fe, the initial concentration of the oxidant affects the final conversion achieved but does not influence pCtchA removal rate. However, if the catalyst concentration is decreased, PMS initial load affects both the reaction rate and the final conversion. Figure 4 shows the theoretical influence of PMS concentration in the presence of varying amounts of Fe(II).

Figure 4 corroborates the influence of PMS (range 5x10^-4 – 5x10^-3 M) in the reaction rate when the iron concentration is low. Contrarily, when an excess of PMS and iron are used, no significant differences are appreciated in pCtchA conversion or removal rate.

2.4. pH Influence

pH significantly affects reactions involving homogeneous iron catalysts. In the case of the system PMS/Fe in the presence of pCtchA two opposite effects can be encountered. On one hand, dihydroxybenzenes (as it is the case of pCtchA) need to be deprotonated to form Fe complexes. Three types of chelates can be formed, depending on pH. Hence, mono, bis or tris complexes are formed at acidic, neutral and basic pH, respectively [5]. However, only monocomplexes are capable of reducing Fe(III) to Fe(II) [10]. In this sense, some works have reported that the optimum pH in Fenton like systems carried out in the presence of dihydroxybenzenes is located around 3.0-3.5 [10,11,12]. In this work, two more experiments were carried out at initial pH 2.0 and 7.0. As observed, the model acceptably simulated the effect of decreasing the initial pH to 2.0, however, when the initial pH was set to 7.0, the reaction mechanism failed after roughly 10 min of reaction. As commented previously, formation of bicomplexes is favoured at neutral pH while Fe(III) reduction is promoted by monocomplexes. The reaction mechanism used in this study has just considered the formation of the bidentate monocomplex so, pH effect above 3.0-3.5 is not adequately simulated.

Figure 5. PMS/iron removal of pCtchA. C_pCtchAo = 6.5 10^-4 M, T = 30 ºC, C_Fe 5.0 x 10^-6, C_PMSo: 2.45 x 10^-3, pH_o: ●, 2.0; !, 3.5; ▲, 7.0. Lines correspond to model calculations (solid = pH 2, dot line= pH 3.5, dashed = pH 7).

Figure 5. PMS/iron removal of pCtchA. C_pCtchAo = 6.5 10^-4 M, T = 30 ºC, C_Fe 5.0 x 10^-6, C_PMSo: 2.45 x 10^-3, pH_o: ●, 2.0; !, 3.5; ▲, 7.0. Lines correspond to model calculations (solid = pH 2, dot line= pH 3.5, dashed = pH 7).

2.5. Initial pCtchA Influence

Initial concentration of pCtchA was evaluated in the range 3.0-12.0 x 10^-4 M. The expected effect for this variable presents some uncertainty. On one hand, a higher amount of the parent compound competes for oxidant species likely leading to a decrease in conversion (do not confuse conversion with rate). Additionally, as the oxidation of pCtchA proceeds, the generation of low carboxylic acids increases leading to a decrease in pH. As commented previously, low pH values reduce the rate of Fe(III) reduction (eq. 48-50). However, on another hand, reduction of Fe(III) to Fe(II) may be favored by a higher concentration of the ligand. Figure 6 shows the results obtained.

As observed, the negative effect of the initial parent compound predominates being acidification the most probable cause of conversion rate reduction (the experiment conducted with the highest pCtchA concentration led to a final pH well below 2).

2.6. Temperature Effect

Given the number of reactions considered in this work, temperature may influence a high number of reaction rates, especially those considering the iron redox cycle (radical reactions have low activation energy values).

In this sense, a sensitivity analysis was completed by varying the rate constants involved in reactions 48, 49 and 50. Figure 7 left shows a change in the direct rate constant of reaction 48 from k_{forward_48} =0.1/C_H+ to 10/C_H+ (linear increase) showing a clear positive influence between the lowest values ant the rest, however, the effect of the highest values tested did not led to a significant increase in conversion, moreover, the initial pCtchA removal rate is similar regardless of the k_{forward_48} value. Figure 7 right depicts the influence of the forward rate constant in reaction 49 from 0.02 to 0.08 s^-1 (linear increase). In this case, this parameter exerts not only a positive effect on conversion rate but also in the initial parent compound removal. Finally, equilibrium in eq. 50 did not significantly alter the simulated results obtained.

Figure 8 shows the experimental results obtained in runs completed at 10, 30 and 50 ºC. As observed, initial rates of parent compound removal are affected by temperature, suggesting that equilibrium 49 is mainly responsible for the influence of temperature. This is just an hypothesis derived from modelling aspects, however, likely a number of stages are affected by temperature such as the direct pCtchA oxidation by PMS (eq. 42) and others. In any case, just from modelling purposes, the forward rate constant in reaction 49 was optimized to minimize differences between experimental and calculated results. Hence, values of 0.015, 0.033 and 0.1 s^-1 were obtained corresponding to runs completed at 10, 30 and 50 ºC, respectively. The activation energy obtained is located around 36 kJ/mol.

3. Materials and Methods

Experimental setup

A 2.25 L glass isothermal reactor was used in the experiments. Isothermal conditions were achieved by means of a water circulating Frigiterm-10 apparatus. Agitation was carried out by a Heidolph RZ-2050 mechanical agitator.

pCtchA was monitored by HPLC (Hewlett Packard serie 1100) with UV detection at 254 nm. A mixture of methanol water 35:65 was used as mobile phase (1.0 mL/min). A 250x4.6 mm silane octadecyl packed column was used in the separation. Monopersulfate was determined iodometrically.

Reagents were purchased from Sigma Aldrich and used as received.

4. Conclusions

The system PMS/Fe(II) can be applied to the elimination of phenolic compounds when Fe(II) is present at catalytic concentrations if regeneration of Fe(II) is warranted.

If the redox cycle Fe(II)/Fe(III) occurs at adequate rates, no significant differences are found when using ferrous iron or ferric iron in the presence of peroxymonopersulfate.

Fe(III) reduction is associated to the existence of two adjacent hydroxyl groups as it is the case of protocatechuic or caffeic acids. P-coumaric acid cannot be eliminated with the system PMS/Fe(II) due to the impossibility of Fe(II) regeneration.

pH exerts a significant influence affecting the formation of different complexes and the rate of Fe(III) reduction. Similarly, temperature positively impact on the parent compound removal, likely increasing the rate of Fe(III) reduction by decomposition of the Fe(III)-pCtchA complex.