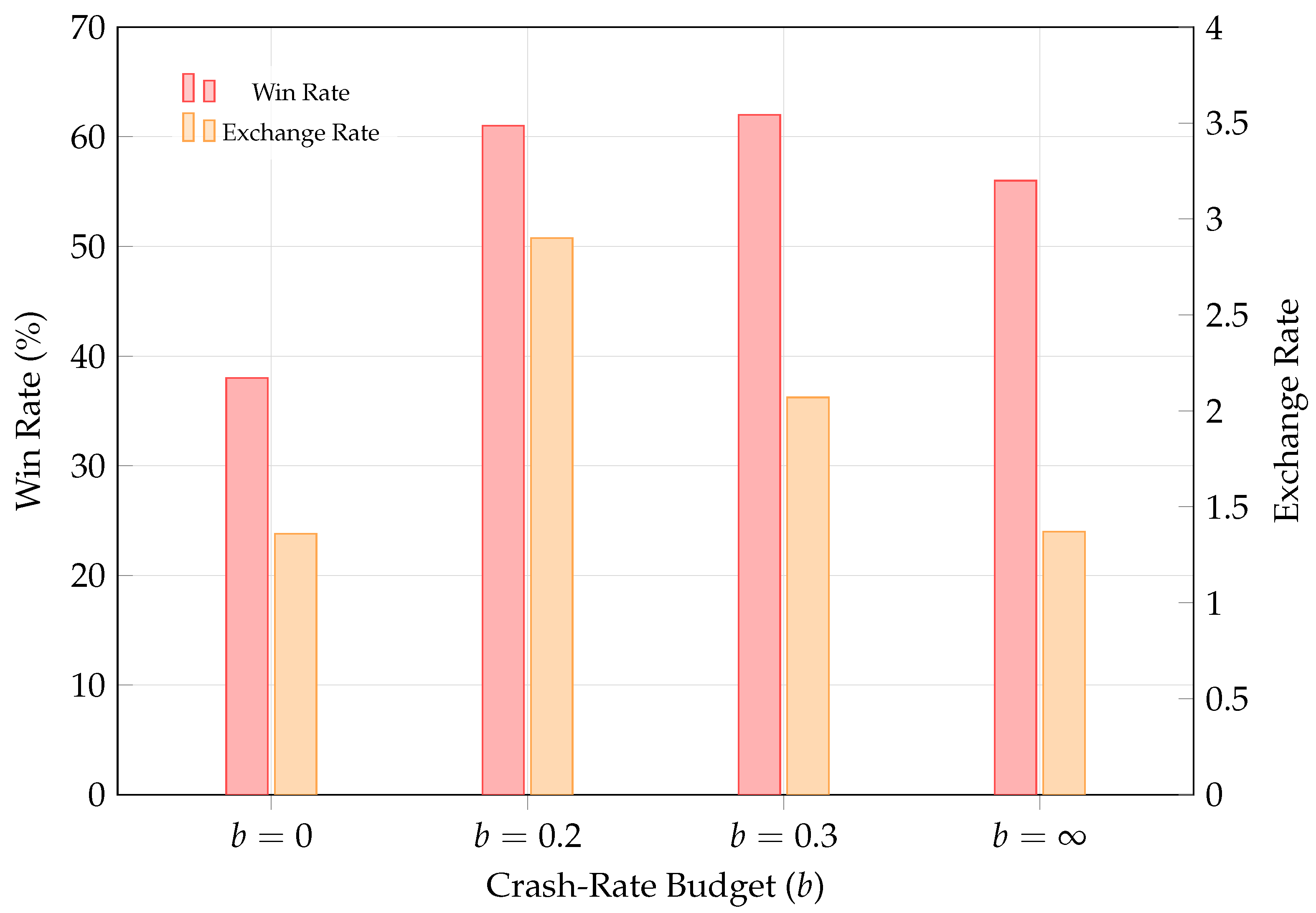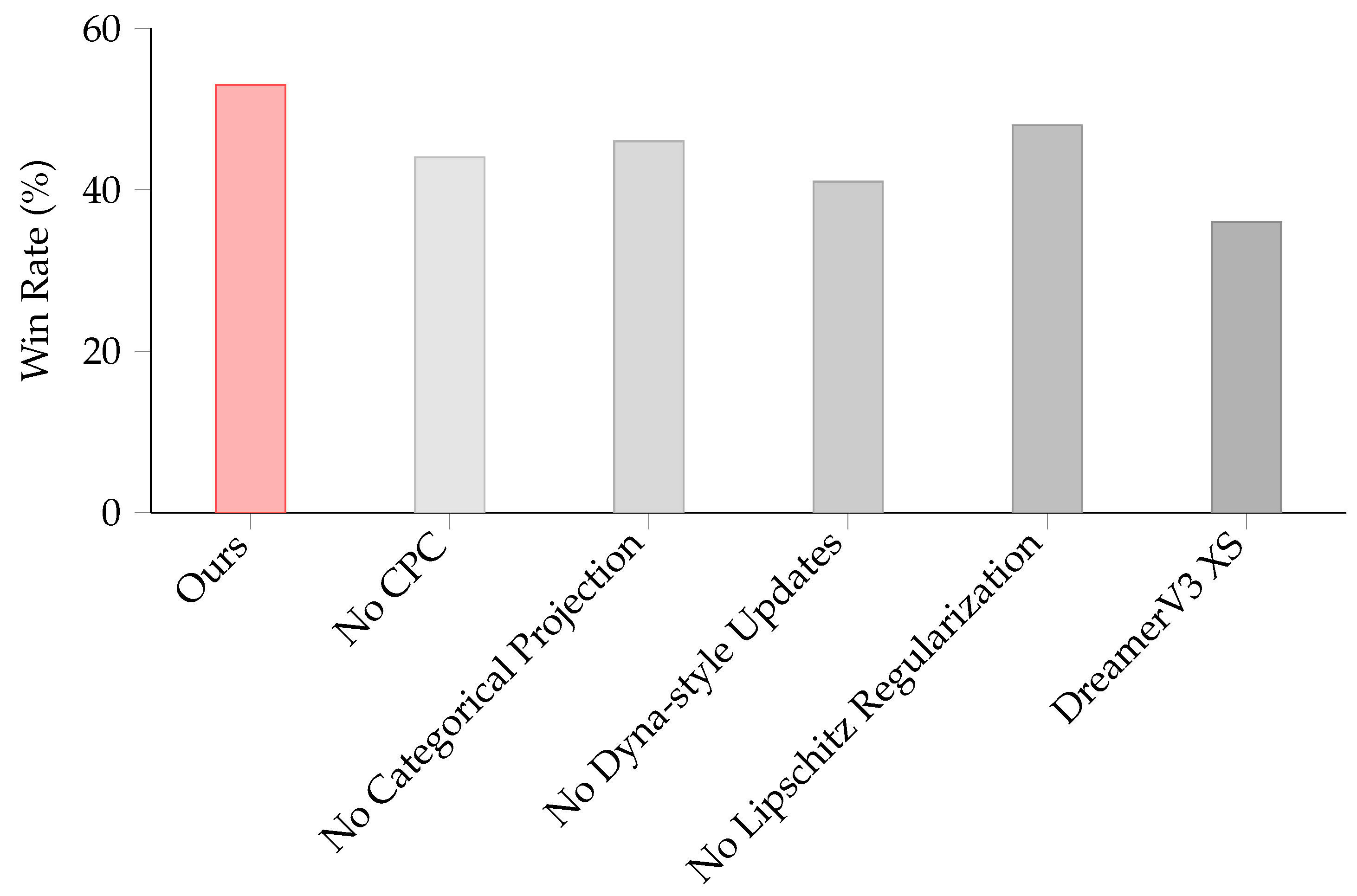Empowering Aerial Maneuver Games Through Model-Based Constrained Reinforcement Learning

1. Introduction

Advances in autonomous aerial systems have garnered considerable attention as both a practical engineering challenge and a domain of strategic importance. Realistic flight agents underpin next-generation flight simulators and serious video games. Despite this broad interest, most deployed autonomy solutions are rule-based, consisting of expert-designed state machines or hierarchical controllers that are adequate for auto cruise control or obstacle-avoidance tasks, but fall short in more complex engagements such as suppression of enemy air defenses, escorting, and point protection.

Within-Visual-Range (WVR) aerial maneuver game encompasses basic flight maneuvers and requires split-second decisions, and mastering it is a critical step toward fully autonomous flight agents. Recent work has explored Reinforcement Learning (RL) for WVR engagements [1], demonstrating that agents can learn basic tactics in simplified settings. However, many of these methods rely on handcrafted architectures that stitch learned sub-policies into high-level coordinators. Such designs lack scalability and generality, and they require substantial domain expertise, which has impeded broader research efforts.

In this work, we aim to train a single, end-to-end reinforcement learning policy to master a full one-on-one WVR engagement. Motivated by recent empirical findings of Model-Based Reinforcement Learning (MBRL) applied in competitive settings [2], we adopt the Dreamer framework as the foundation for our algorithm, given its state-of-the-art performance on a wide range of continuous control benchmarks. However, applying Dreamer out of the box in a full aerial maneuver game reveals several key challenges: first, the mutual influence between imagination-driven background planning and self-play dynamics remains understudied; second, abrupt terminations, coupled with the stochastic, discontinuous nature of aerial maneuver dynamics, undermine standard latent-rollout techniques that rely on smooth transitions. In addition, balancing aggression with survival through tuning of crash vs. kill rewards proves sensitive to reward scales. To address these issues, we design a Dreamer-style algorithm with enhanced termination sensitivity and robust self-play training. Our main contributions are threefold:

• We extend the Dreamer architecture and introduce a learning paradigm that improves the model’s predictive accuracy in the vicinity of rare crash events, and also the robustness of actor-critic learning.
• We derive a risk-aware learning objective that facilitates high-speed maneuver learning while bounding the overall crash rate, without extensive reward scale tuning.
• We design a pipeline that bootstraps learning with curriculum initialization, drives strategy discovery through self-play exploration, and finetunes against specific opponents for rapid adaptation.

We demonstrate that, with these modifications, a single Dreamer-style policy can learn effective aerial maneuver tactics from scratch, without relying on expert domain knowledge.

2. Related Works

Efforts to automate competitive air-to-air flight games began with rule-based expert systems, exemplified by TacAir-Soar in the late 1990s [3]. With regard to learning-based approaches, earlier studies [4,5] demonstrated that autonomous agents could learn basic WVR manuerver tactics through deep RL but were constrained by low-fidelity, 3-DoF environments and limited computational resources. In 2019–20, DARPA’s AlphaDogfight Trials saw a Heron Systems deep RL agent defeat a seasoned F-16 pilot 5-0 in a 6DoF simulated engagement [6], and academic teams using hierarchical RL architectures achieved top placements [1]. However, most recent deep RL approaches surveyed [7,8,9] still abstracted the action space to high-level behaviors or tactics, or employ complex hierarchies to cover the vast state space. In contrast, our work explores truly end-to-end model-based reinforcement learning of WVR high-speed maneuver techniques and tactics with a single policy and minimal domain priors.

Model-based reinforcement learning (MBRL) learns a World Model (WM) to simulate the true dynamics of the environment. This WM can be employed either for decision-time planning [10,11] or for background planning [12,13]. Decision-time planning methods(e.g., Model Predictive Control [14] or Monte Carlo Tree Search [15]) conduct online look-ahead by simulating candidate action sequences under the WM and selecting actions that maximize predicted returns at each step. In contrast, background-planning algorithms amortize model rollouts by generating imagined experiences to update actor and critic networks. A second, orthogonal axis of distinction is whether the WM is a generative observation model, capable of reconstructing raw sensory inputs [12], or a latent-only model(e.g., contrastive or predictive state representations), trained in self-supervised manners without an explicit decoder [10]. A third axis concerns how uncertainty is represented and managed within the WM. Classical approaches employ probabilistic ensembles [16] or Bayesian neural networks [17] to estimate epistemic uncertainty and mitigate its impact on planning explicitly; More recent methods leverage powerful generative architectures to holistically model both aleatoric and epistemic uncertainty without disentangling their sources. The Dreamer family of MBRL algorithms, which form the basis of our work, occupies the quadrant defined by background planning, generative WM(via a latent bottleneck), and holistic uncertainty modeling. Readers can refer to [18] for a more comprehensive review of MBRL.

Self-play has been explored extensively in the multi-agent reinforcement learning literature, ranging from simply matching against past versions of selves [19,20,21] to more complex, game-theoretic frameworks such as PSRO [20] and NeuPL [22]; Readers can refer to, e.g., [23] for a more comprehensive review. However, the majority of the empirical studies are based on model-free RL methods; efforts to couple MBRL with self-play remain scarce. WMs offer the promise of explicitly capturing opponent strategies and thereby improving generalization, but the non-stationarity induced by self-play poses a significant challenge for stable model learning. In this work, we take a first step toward bridging this gap by integrating a recurrent WM into a population-based self-play regime, showing that a single model-based policy can robustly master competitive senarios of highly specialized domains.

3. Preliminaries

3.1. Zero-Sum Stochastic Games & Neural Self-Play

One-on-one aerial maneuver game is an instance of a two-player zero-sum stochastic game, where both players interact with the environment simultaneously. Such a game can be formally defined by the tuple $(S,A^1,A^2,P,r,\gamma )$, where S is a finite set of states, $A^i$ is the finite action set for player i, $P:S\times A^1\times A^2\to \Delta \left(S\right)$ is the transition kernel, $r:S\times A^1\times A^2\to \mathbb{R}$ is the reward for player 1 (player 2 receives $-r$), and $\gamma \in [0,1)$ is the discount factor. At each step t, in state $s_t$, players sample actions $a_t^1\sim {\pi }^1(·\mid s_t)$ and $a_t^2\sim {\pi }^2(·\mid s_t)$; then the environment transitions to $s_{t+1}\sim P(·\mid s_t,a_t^1,a_t^2)$, and player 1 receives reward $r(s_t,a_t^1,a_t^2)$. The cumulative return is

$$G_0=\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t^1,a_t^2),$$

which player 1 seeks to maximize and player 2 to minimize. The corresponding state-value function under policies $({\pi }^1,{\pi }^2)$ is

$$V^{{\pi }^1,{\pi }^2}\left(s\right)=\mathbb{E}\left[G_0\mid s_0=s\right].$$

The minimax value

$$V^{*}\left(s\right)=\underset{{\pi }^1}{max}\underset{{\pi }^2}{min}{V}^{{\pi }^1,{\pi }^2}\left(s\right)=\underset{{\pi }^2}{min}\underset{{\pi }^1}{max}{V}^{{\pi }^1,{\pi }^2}\left(s\right)$$

characterizes the value of the game, and under standard compactness assumptions, there exists a stationary Nash equilibrium $({\pi }^{1*},{\pi }^{2*})$ achieving $V^{*}$ [24,25]. Exact dynamic-programming methods for solving stochastic games suffer from the “curse of dimensionality”. Self-play has therefore emerged as a scalable, model-free paradigm: the agent iteratively refines its policy by playing against itself or mixtures of past policies, using reinforcement-learning updates on the generated data. Variants of self-play (e.g., Neural Fictitious Self-Play [26]) have proven instrumental in developing superhuman agents in complex competitive zero-sum domains such as Go, chess [27], and StarCraft II [21].

3.2. The Dreamer Algorithm

Our approach branches from DreamerV3 [28], the latest heritage of the Dreamer family of model-based reinforcement learning algorithms. Dreamer utilizes a recurrent state-space model (RSSM) to learn a compact latent state $z_t$ that predicts future rewards/discounts and reconstructs raw observations via a variational decoder. At each training iteration, Dreamer:

• Learns the RSSM by minimizing a combined Evidence Lower Bound (ELBO):

  $$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{ELBO}}\left(t\right)& ={\mathbb{E}}_{q(z_t\mid h_t,o_t)}[\underset{{\mathcal{L}}_{\mathrm{recon}}}{\underbrace{-logp(o_t,r_t,{\gamma }_t\mid z_t)}}\hfill \\ \hfill & +\underset{{\mathcal{L}}_{\mathrm{KL}}}{\underbrace{\mathrm{KL}\left(q(z_t^{pos}\mid h_t,o_t)\parallel p(z_t^{pri}\mid h_t)\right)}}]\hfill \end{array}$$

  which includes the reconstruction loss and the prior–posterior KL-balancing.
• Imagines multi-step latent rollouts under the learned transition dynamics.
• Optimizes actor and value networks by backpropagating stochastic value gradients and/or REINFORCE [29] gradients of expected return through the imagined trajectories.

The learned decoder is not used at inference; the reconstructions serve solely as a self-supervision signal to regularize and stabilize learning of latent representation. This architecture yields a purely reactive policy at runtime and achieves state-of-the-art data efficiency and asymptotic performance on popular vision and proprietary benchmarks.

3.3. Constrained MDPs

In real-world flights, ensuring survival is indispensable, yet this imperative does not always align with maximizing offensive impact. To encode this dual objective, we employ the framework of Constrained Markov Decision Processes (CMDPs) [30]. A CMDP augments the standard MDP $(S,A,P,r,\gamma )$ with a cost function $c:S\times A\to {\mathbb{R}}_{\ge 0}$ and a cost budget $\delta$. The learning problem is

$$\underset{\pi }{max}{J}_R\left(\pi \right)\mathrm{s}.\mathrm{t}.J_C\left(\pi \right)=\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^{t}c(s_t,a_t)\right]\le b,$$

where $J_R$ is the usual discounted return and $J_C$ the expected discounted cost (e.g. crash probability). Solving for the CMDP fosters SafeRL [31], where one seeks policies that satisfy $J_C\le \delta$ while optimizing performance. A common approach is to form the augmented Lagrangian

$${\mathcal{L}}_{\mathrm{AL}}(\theta ,\lambda )=J_R\left(\theta \right)-\lambda \left(J_C\left(\theta \right)-b\right)-{\displaystyle \frac{\mu }{2}}{\left(J_C\left(\theta \right)-b\right)}^2,$$

where $\theta$ parameterizes the policy, $\lambda \ge 0$ is a Lagrange multiplier, and $\mu >0$ a penalty coefficient. By tuning b, one balances utility and safety. This methodology is shown to integrate seamlessly with model-based agents [32].

3.4. Aerial Manuever Game Environment

We investigate one-to-one (red versus blue) WVR pursuit-evasion games, as demonstrated in Figure 1. The physics of aircraft is simulated using JSBsim [33], an open-source, high-fidelity 6DoF flight dynamics model. We expose proprietary vector observations and a discrete action space. Details of the scenario, simulation parameters, and environment specifications are provided in Appendix A.

4. Learning Algorithm

Overview 

Dreamer-style algorithms typically consist of four components: the World Model (WM) predicts the outcomes of potential action sequences, the critic evaluates the expected return of each outcome, the actor chooses actions to reach the most valuable outcomes, and the replay buffer accumulates experiences for replay. Aerial manuever environments bring abrupt termination events, discontinuous dynamics, and aggressive-survival tradeoff; challenges largely absent from standard control benchmarks. First and foremost, we elucidate the major adaptations to vanilla Dreamer’s WM, critic, actor, and replay modules that accommodate the unique difficulties of learning aerial manuevers.

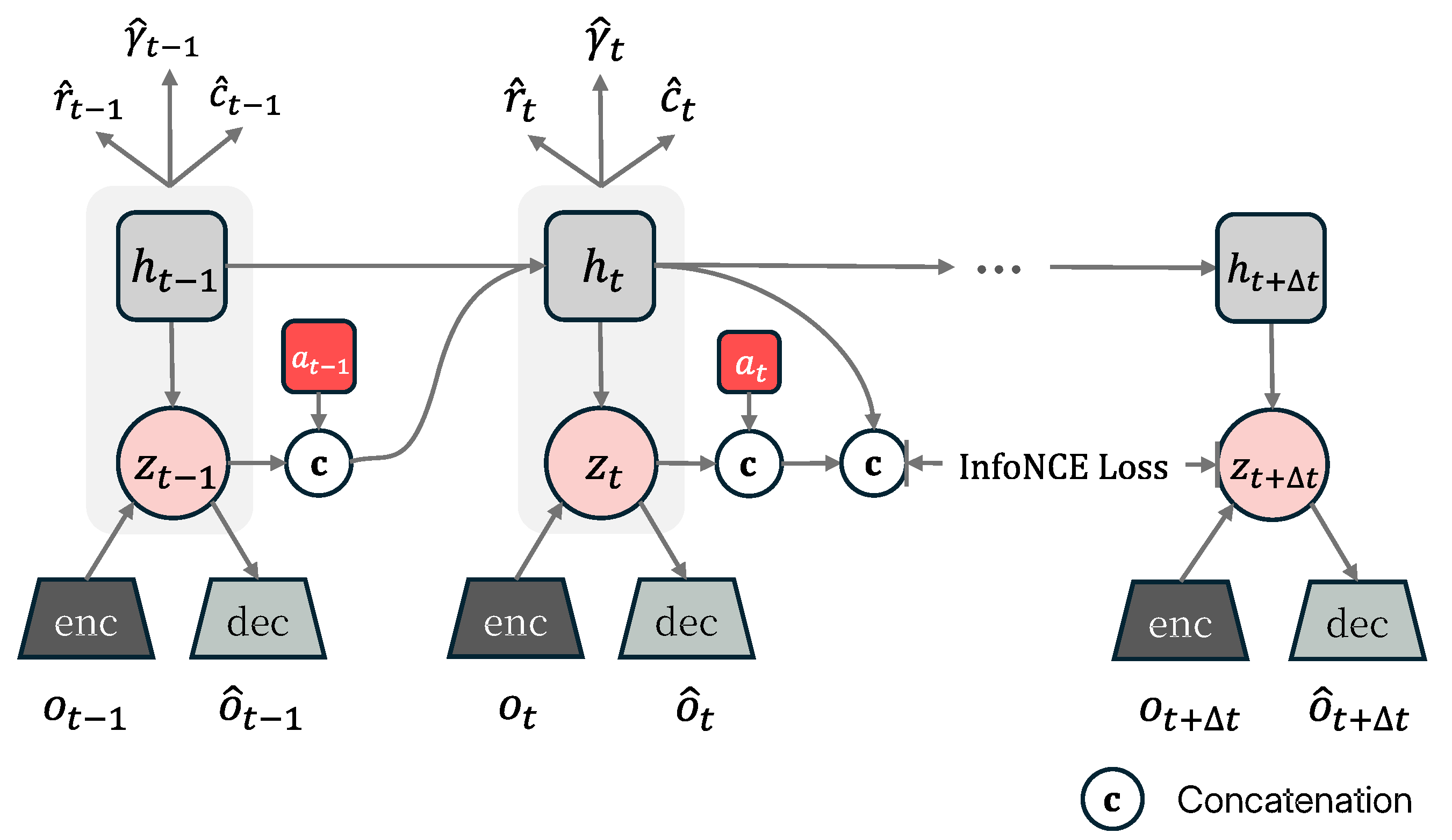
• World model architecture and objectives. We replace Dreamer’s GRU sequence model with an RWKV-style linear attention backbone, enabling parallelizable training via scan while preserving long-context credit assignment. Beyond the ELBO reconstruction objective, we add a termination-aware CPC loss: This explicitly biases the latent dynamics toward long-horizon, crash-relevant structure.
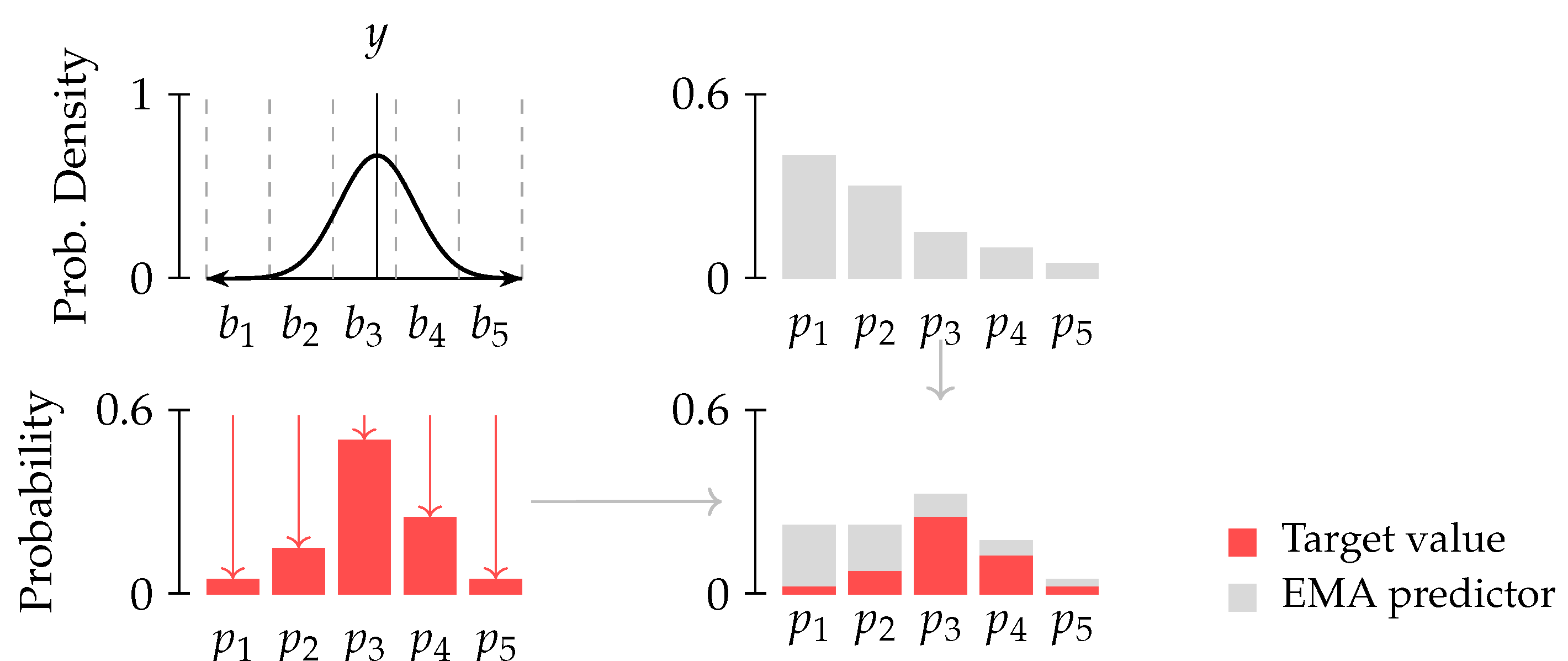
• Distributional parameterization of reward and value. Instead of scalar regression used in standard Dreamer heads, we model reward, return, and cost as categorical distributions on finite support with exponentially spaced bins. Targets are formed by fusing a Gaussian-smoothed histogram of the scalar label with an EMA teacher distribution, and optimized via cross-entropy.
• Constrained policy optimization under learned dynamics. Rather than tuning reward scales to break stalemates, we cast learning as a constrained MBRL problem: Maximizing expected return while constraining expected crash probability/cost under the learned model.
• Dyna-style actor–critic updates. In contrast to Dreamer’s purely imagined updates, we mix imagined rollouts with off-policy real updates computed via V-trace on replayed data.
• Value-aware robustness regularization. To mitigate value amplification of small model errors, we add a Lipschitz-consistency penalty on the critic’s output distribution.
• Multiagent Learning Pipline. Unlike single-agent Dreamer on control tasks, we use a three-phase scheme including cirriculum initailization, population self-play and few-shot adaptation.

4.1. World Model Learning

We denote by $o_t$ the symlog [28] transformed raw vector observation at time t, by $h_t$ the deterministic recurrent state of the sequence model, and by $z_t$ the stochastic states. $(h_t,z_t)$ constitutes the history-encoding model states. Each network within the WM models a conditional distribution:

$$\begin{array}{l}\mathrm{Sequence}\mathrm{model}:(h_t,z_t^{pri})=f_{\theta }(h_{t-1},z_{t-1},a_{t-1}),\\ \mathrm{Discount}\mathrm{predictor}:{\widehat{\gamma }}_t\sim p_{\theta }({\widehat{\gamma }}_t\mid h_t,z_t),\\ \mathrm{Representation}\mathrm{model}:z_t^{pos}\sim q_{\theta }(z_t\mid h_t,\mathbf{Enc}\left(o_t\right)),\\ \mathrm{Reward}\mathrm{predictor}:{\widehat{r}}_t\sim p_{\theta }({\widehat{r}}_t\mid h_t,z_t),\\ \mathrm{Decoder}(\mathrm{Obs}.\mathrm{Predictor}):{\widehat{o}}_t\sim p_{\theta }({\widehat{o}}_t\mid h_t,z_t),\\ \mathrm{Cos}\mathrm{t}\mathrm{predictor}:{\widehat{c}}_t\sim p_{\theta }({\widehat{c}}_t\mid h_t,z_t).\end{array}$$

Contrastive Predictive Coding 

The standard ELBO objective in Dreamer relies on a reconstruction term that only enforces next-step predictions, which exploit the local smoothness of the signal. This biases the Dreamer’s WM to generate locally plausible segments without a globally coherent structure, which exacerbates the difficulty in anticipating rare termination events. To remedy this, we incorporate a Contrastive Predictive Coding (CPC) [34] objective that encourages the latent representation to capture long-range dependencies and to be particularly sensitive to dynamics near termination, as shown in Figure 2.

Formally, we want to maximize the Mutual Information(MI) $I\left({\mathrm{c}}_{\mathrm{t}};o_{t+\Delta t}\right)$ between the context ${\mathrm{c}}_{\mathrm{t}}:(h_t,z_t,a_t)$ and some future observation $o_{t+\Delta t}$ that is both (i) not imminent, i.e., at least k steps ahead (ii) in the vicinity of a termination event i.e., within m steps of a termination flag. Directly modeling conditional distribution $p\left(o_{t+\Delta t}\right|{\mathrm{c}}_{\mathrm{t}})$ captures redundant local dependency in $o_t$. Instead, we estimate a density ratio using contrastive samples from $p\left(z_{t+\Delta t}\right|{\mathrm{c}}_{\mathrm{t}})$ and $p\left(z_t\right)$ and regularize the WM with the InfoNCE lower bound. We introduce a critic function $f_{\psi }\in \mathbb{R}$ and form one positive pair $({\mathrm{c}}_{\mathrm{t}},z_{t+\Delta t}^{+})$ (same trajectory, $\Delta t\ge k,L-m\le t+\Delta t\le L$) and negatives $\left\{z_t^{-}\right\}$ sampled from other time indices or trajectories. The InfoNCE loss is

$${\mathcal{L}}_{\mathrm{CPC}}\left(t\right)\doteq -\mathbb{E}\left[log{\displaystyle \frac{exp\left(f_{\psi }({\mathrm{c}}_{\mathrm{t}},z_{t+\Delta t}^{+})/\tau \right)}{{\sum }_{j=1}^{N}exp\left(f_{\psi }({\mathrm{c}}_{\mathrm{t}},z_j^{-})/\tau \right)}}\right],$$

where $\tau >0$ is a temperature parameter. Minimizing ${\mathcal{L}}_{\mathrm{CPC}}$ maximizes a lower bound on $I(c_t;z_{t+k})$. In practice, we integrate this into WM learning by augmenting the ELBO with weight $\beta =0.5$:

$${\mathcal{L}}_{\mathrm{WM}}=\sum _t\left[{\mathcal{L}}_{\mathrm{ELBO}}\left(t\right)+\beta {\mathcal{L}}_{\mathrm{CPC}}\left(t\right)\right],$$

Modeling Categorical Reward Distributions 

Training the reward model to predict a stochastic regression target is prone to outliers, especially when termination events correspond to large rewards. Instead, we model symlog transformed reward r as a categorical distribution supported on $[r_{min},r_{max}]$ with B bins. The predictor is trained to produce a probability vector $p_{\theta }\in {\Delta }^K$ that parameterizes this distribution, which is derived from the logits through the softmax function. The major hurdle here is to define a procedure to construct the target distribution and its associated projection onto the set of categorical distributions. We revise the approach in [35] and construct the target distribution as described below:

• Treat the observed scalar target r as a random variable $r^{\prime }\sim \mathcal{N}(r,{\sigma }^2)$, where $\sigma =0.3$ is a fixed hyperparameter. Define exponentially spaced bin boundaries $\{b_0,\dots ,b_K\}$ on $[r_{min},r_{max}]$. Compute the histogram $h_j$ of the Gaussian [36]:

  $$h_j={\int }_{b_{j-1}}^{b_j}\mathcal{N}(x\mid r,{\sigma }^2)\mathrm{d}x,j=1,\dots ,K,$$
• Form the target distribution by combining the histogram $h_j$ with the outputs of a target predictor $p_{\overline{\theta },j}$, whose parameters are the Exponential Moving Average (EMA) of the online predictor:

  $${\tilde{p}}_j=p_{\overline{\theta },j}+h_j,p_j^{*}={\displaystyle \frac{{\tilde{p}}_j}{{\sum }_{k=1}^K{\tilde{p}}_k}}.$$
  Finally, update the online predictor $p_{\theta }$ via the cross-entropy loss

  $${\mathcal{L}}_{\mathrm{CE}}=\mathrm{CE}(p^{*},p_{\theta })\doteq -\sum _{j=1}^K{p}_j^{*}log{p}_{\theta ,j}.$$

This process is visualized in Figure 3. At inference time, we recover a scalar estimate via the Conditional Value-at-Risk (CVaR) at level $\alpha$:

$$\widehat{r}={\mathrm{CVaR}}_{\alpha }\left(p_{\theta }\right)\doteq {\displaystyle \frac{1}{1-\alpha }}{\int }_{\alpha }^1{F}^{-1}\left(u\right)\mathrm{d}u,$$

where $F^{-1}$ is the quantile function of $p_{\theta }$ and we set $\alpha =0.8$.

Figure 3. Visualization of categorical target value projection for cross-entropy based learning. We distribute the probability mass to neighbouring locations (which is akin to smoothing the target value).

Figure 3. Visualization of categorical target value projection for cross-entropy based learning. We distribute the probability mass to neighbouring locations (which is akin to smoothing the target value).

Experience Replay 

We store full episodes in the replay buffer and sample fixed-length trajectories of $L=64$ steps (12.8 simulation seconds) for each WM update. To assemble a minibatch of size 16, we mix:

$$\underset{\begin{array}{c}\mathrm{uniformly}\mathrm{sampled}\\ \mathrm{starting}\mathrm{indices}\end{array}}{\underbrace{14}}:\underset{\begin{array}{c}\mathrm{episode}\text{-}\mathrm{terminal}\\ \mathrm{trajectory}\end{array}}{\underbrace{1}}:\underset{\mathrm{most}\mathrm{recent}\mathrm{trajectory}}{\underbrace{1}}$$

Trajectories shorter than T are padded to include the final transition. We store latent states into the replay buffer during data collection, and use burn-in [37] to initialize the WM on replayed trajectories.

Network Architecture 

DreamerV3’ original sequence model uses GRU recurrence to generate model states $(h_t,z_t)$, but GRUs’ sequential steps impede parallel training. We therefore replace them with an RWKV style linear-attention [38,39] with RMSNorm [40] and GELU activations [41], which can be parallelized via scan [42]. Other components are implemented as dense MLPs with LayerNorm [43] and GELU activations.

4.2. Actor-Critic Learning

Although our scenario is formally a zero-sum game, the allowance for draws introduces a practical challenge: once both agents master evasive maneuvers, matches often end in stalemate, diluting the learning signal. Hand-tuning kill rewards versus crash penalties to break these ties is brittle—small changes in their relative scale can tip the agent toward overly aggressive tactics causing crashes or extreme terminal states, or otherwise overly cautious, non-engaging behavior. To address this, we adopt a constrained model-based reinforcement learning formulation. We assign a cost of 1 only when the aircraft is destroyed by accident, i.e. crash and overload, and terminations due to reaching maximum episode duration incur zero cost. Accordingly, we optimize

$$\underset{{\pi }_{\theta }\in {\Pi }_{\theta }}{max}{J}_{\varphi }^R\left({\pi }_{\theta }\right)\mathrm{s}.\mathrm{t}.J_{\varphi }^C\left({\pi }_{\theta }\right)\le b,$$

(1)

where $J_{\varphi }^R$ is the expected reward, $J_{\varphi }^C$ the expected crash probability(or cumulative costs) under the learned dynamics $P_{\varphi }$, and b is a user-specified crash-rate budget. This constraint enforces a controllable aggression–survival trade-off: the agent maximizes its score while keeping the likelihood of being shot down below b. By adopting the relaxation technique of the Lagrangian method, the formulation above is transformed into an unconstrained optimization problem, where $\lambda$ is the Lagrangian multiplier:

$$\underset{{\pi }_{\theta }\in {\Pi }_{\theta }}{max}\underset{\lambda \ge 0}{min}{J}_{\varphi }^R\left({\pi }_{\theta }\right)-{\lambda }_C\left(J_{\varphi }^C\left({\pi }_{\theta }\right)-b\right).$$

To estimate cumulative costs, we additionally learns a cost critic $v_{{\psi }_c}$ along with the return critic $v_{\psi }$. The actor and critics operate on model states $s_t\doteq (z_t,h_t)$ and thus benefit from the Markovian representations learned by the WM. We use the REINFORCE estimator [29] and obtain the surrogate actor loss for the unconstrained policy objective:

$$\begin{array}{cc}\hfill \mathcal{L}\left(\theta \right)& =-\sum _{t=1}^{T}sg\left(R_t^{\lambda }-v_{\psi }\left(s_t\right)\right)log{\pi }_{\theta }(a_t\mid s_t)\hfill \\ \hfill & +\eta \mathrm{H}\left[{\pi }_{\theta }(a_t\mid s_t)\right]-\Psi \left(sg\left(C_t^{\lambda }\right),{\lambda }_C^k,{\mu }^k\right),\hfill \end{array}$$

where sg denotes the stop-gradient operator, $R_t^{\lambda }$ and $C_t^{\lambda }$ are bootstrapped $\lambda$-return and $\lambda$-cumulative costs, and $\Psi$ denotes the Augmented Lagrangian. Define $\Delta =\left(C_t^{\lambda }-b\right)$, and let the non-decreasing penalty term ${\mu }^k$ corresponds to current gradient step k, the update rules for $\Psi$ and $\lambda$ are as follows [44]:

$$\Psi ,{\lambda }_C^{k+1}=\left\{\begin{array}{cc}{\lambda }_C^k\Delta +{\displaystyle \frac{{\mu }^k}{2}}{\Delta }^2,{\lambda }_C^k+{\mu }^k\Delta \hfill & \mathrm{if}{\lambda }_C^k+{\mu }^k\Delta \ge 0,\hfill \\ -{\displaystyle \frac{{\left({\lambda }_C^k\right)}^2}{2{\mu }^k}},0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Modeling Categorical Return Distributions 

We adopt the same categorical-projection procedure as for rewards: each scalar target $R_t^{\lambda }$(or $C_t^{\lambda }$) is first transformed into a Gaussian distribution, then discretized into B bins to form a histogram $h_j$ on $[v_{min},v_{max}]$, then merged with the EMA-updated target critic output $p_{\overline{\psi },j}$ and finally normalized to $p_j^{*}$. The online critics are updated by minimizing the respective cross-entropy loss against this target distribution. At inference time, we recover the scalar return estimate ${\widehat{v}}_{\psi }\left(s_t\right)$ from CVaR with $\alpha =0.8$, and the cumulative cost estimate ${\widehat{v}}_{{\psi }_c}\left(s_t\right)$ from distribution mean.

Dyna-Style Actor-Critic Updates 

Most recent model-based methods (including Dreamer) perform actor-critic updates solely on imagined rollouts, risking over-reliance on an imperfect WM, especially near terminations. We instead adopt a Dyna-style scheme that mixes imagined trajectories with real experiences for policy learning. At each actor-critic update, we generate on-policy imagined rollouts of horizon $H=16$ starting from replayed states during WM learning, and compute the $\lambda$-returns $R_t^{\lambda }$ and advantages $A_t^{\lambda }=R_t^{\lambda }-v_{\psi }\left(s_t\right)$; Simultaneously, on the replayed real trajectories we compute off-policy V-trace [45] returns $R_t^{\mathrm{vt}}$ and advantages $A_t^{vt}=R_t^{\mathrm{vt}}-v_{\psi }\left(s_t\right)$. The combined surrogate actor loss and cross-entropy critic loss are formed as weighted sums of their imagined and real components.

Regulating Model-Aware Value Error 

Even when the learned WM is approximately accurate in terms of the ELBO, the prediction error can still be amplified by the value function updates. Value-aware model error [46] measures the difference between the simulated and true Bellman operator acting on a given value function, and can be made small by promoting the local smoothness of the value function. To this end, we add a Lipschitz-consistency regularizer [47]. For each model state $s_t$, We define a consistency loss:

$${\mathcal{L}}_{\mathrm{lip}}\left(s_t\right)=\underset{\parallel s^{\prime }-s_t{\parallel }_{\infty }\le \epsilon }{max}\mathrm{KL}\left[sg\left(v_{\psi }\left(R\right|s_t)\right),v_{\psi }\left(R\right|s^{\prime })\right]$$

with $\epsilon =0.01$. In practice, we approximate this maximum by a single FGSM [48] step in latent space, then add ${\lambda }_{\mathrm{reg}}{\mathcal{L}}_{\mathrm{lip}}\left(s\right)$ to the standard value loss.

Network Architecture 

Both actor and critic networks are implemented as MLPs with LayerNorm and GELU activations, and are trained concurrently with the WM. We alternate two WM gradient updates with one actor-critic update to ensure stable learning. Inspired by [49], we replaced each critic’s penultimate MLP layer with a soft-MoE block [50] and observed an incremental performance gain as the number of experts increases; applying the same modification to the actor network yielded no benefit.

4.3. Learning Curriculum & Self-Play

Pure self-play agents (using only a win–loss reward signal) learn slowly and are susceptible to converging on a single, easily countered offensive pattern. In this section, we outline a three-phase pipeline that (i) initializes learning via a curriculum of heuristic opponents, (ii) promotes strategic discovery through self-play exploration, and (iii) fine-tunes against specific adversaries for rapid adaptation. Throughout all phases, the WM is conditioned on learnable embeddings of the ego and opponent policy identities, accounting for the dynamics introduced by different ego-opponent policy pairs.

Curriculum initialization 

We design three rule-based bots to bootstrap training:

• Pursuit Agent: Seeks a pursuit position behind the opponent.
• Maneuver Agent: Does not actively pursue, but executes various escape maneuvers if engaged.
• Aggressive Agent: Adopts a risk-seeking policy that approaches the opponent frontally to induce high-intensity interactions.

These heuristics capture core pursuit-evasion tactics and serve as initial benchmarks. Our curriculum pool comprises the rule-based bots and under-trained PPO [51] self-play agents. In each episode, an opponent is sampled uniformly from this pool. During curriculum initialization, we employ handcrafted pseudo-rewards to encourage human-like flight behaviors, as described in [1].

Self-Play Exploration 

We employ a population-based self-play framework with Elo-based matchmaking to drive strategic discovery as shown in Figure 4. Rather than updating a single agent against static past versions as in fictitious self-play, we train a fixed population of N policies in parallel to introduce diversity and scalability [52]. Each member of the population is initialized with the curriculum-trained agent and participates in repeated self-play tournaments. During each self-play training cycle, we iterate over all N policies in sequence. For a given policy, we conduct a batch of 10 training episodes in which the opponent is sampled according to current Elo ratings, except that with probability ${\theta }_{\mathrm{bot}}$ a PPO-trained baseline with fixed Elo rating is selected instead. After each episode, we update the Elo ratings of the matched policies immediately, without dedicating separate evaluation sessions. If a policy’s Elo falls below a threshold $b_{\mathrm{elo}}$, it is evicted and replaced by a copy of a randomly chosen peer from the remaining $N-1$ policies. During self-play, $R_{\mathrm{damage}}$ and $R_{\mathrm{health}}$ remain active, while each other’s pseudo-reward is activated independently with probability $0.25$ to regulate policy behavior. To reduce computational overhead, all N policies share a single WM, which is trained on the aggregated replay buffer.

Finetuning 

During fine-tuning, the agent with the highest final Elo rating is matched against the designated target opponent, but with probability ${\theta }_{pop}$, the opponent is sampled from the population to maintain exposure to diverse strategies. Only $R_{\mathrm{damage}}$ and $R_{\mathrm{health}}$ are active during finetuning, and the opponent embedding is initialized as a random vector [11].

5. Experiments

We benchmark the performance of the proposed approach applied to each stage of the training pipeline as outlined in Section 4.3. Based on experiment results, we seek to answer the following core research questions: compared to the model-free pure self-play baselines,

• Policy Performance and Efficiency: Does a model-based approach produce stronger, more resilient policies, and do the reductions in sample complexity justify the additional computational cost?
• Agression/Survival Tradeoff: To what extent can a constrained learning objective be used to balance an agent’s tendency for aggression versus survival?
• Rapid Adaptation: Can the learned WM accelerate fine-tuning against novel opponents to a degree that is practical for real-world deployment?

We also perform an ablation study to assess the impact of each design choice in Section 5.4.

All experiments use a discount factor $\gamma =0.998$, which corresponds to a half-life of approximately 346 steps. Our agent includes a total of 10.7 M learnable parameters, matching the parameter count of a size XS DreamerV3 agent. As a model-free baseline, we choose a high-quality implementation of a PPO agent from the open-source CleanRL library [53].

5.1. Curriculum Learning

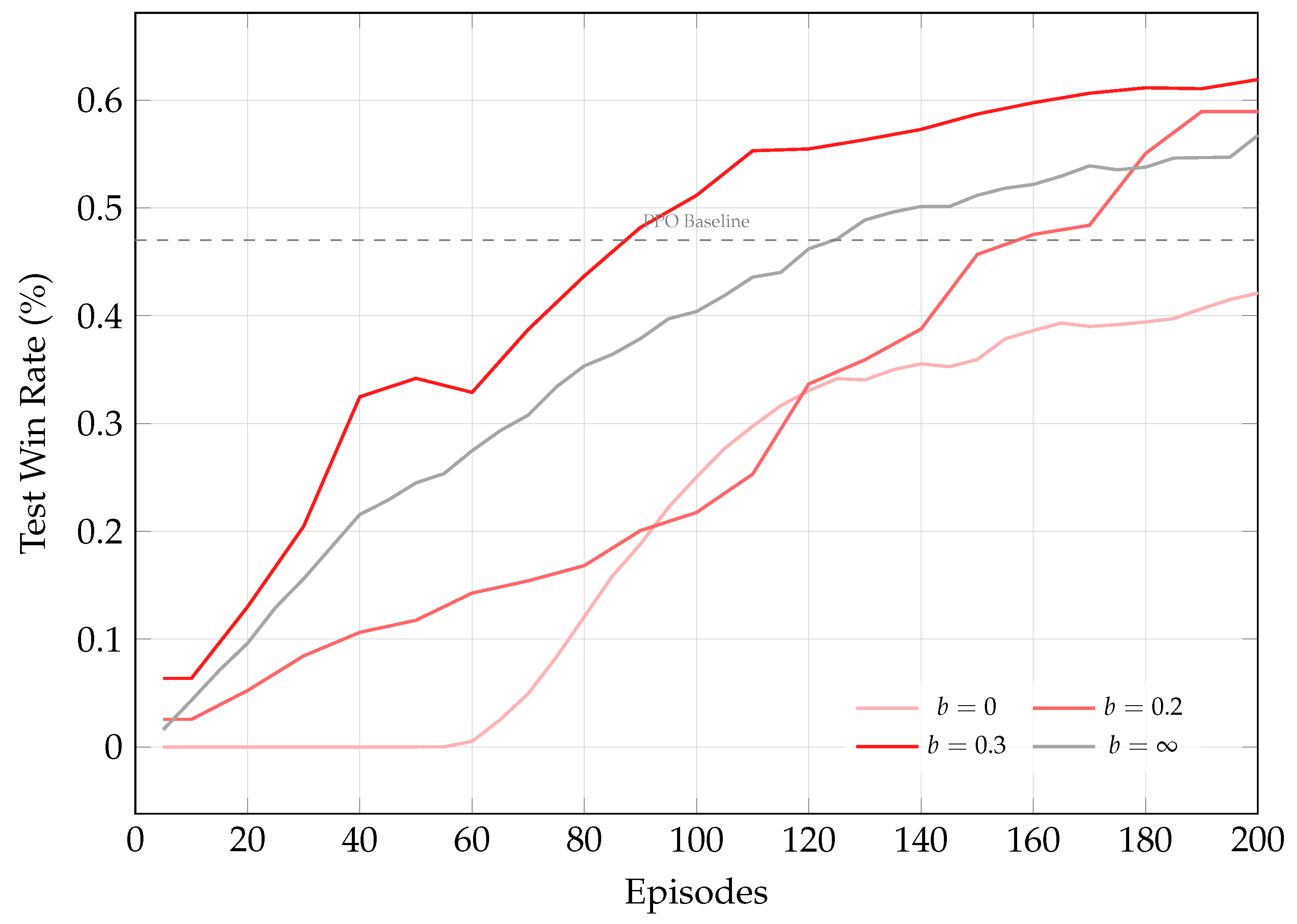
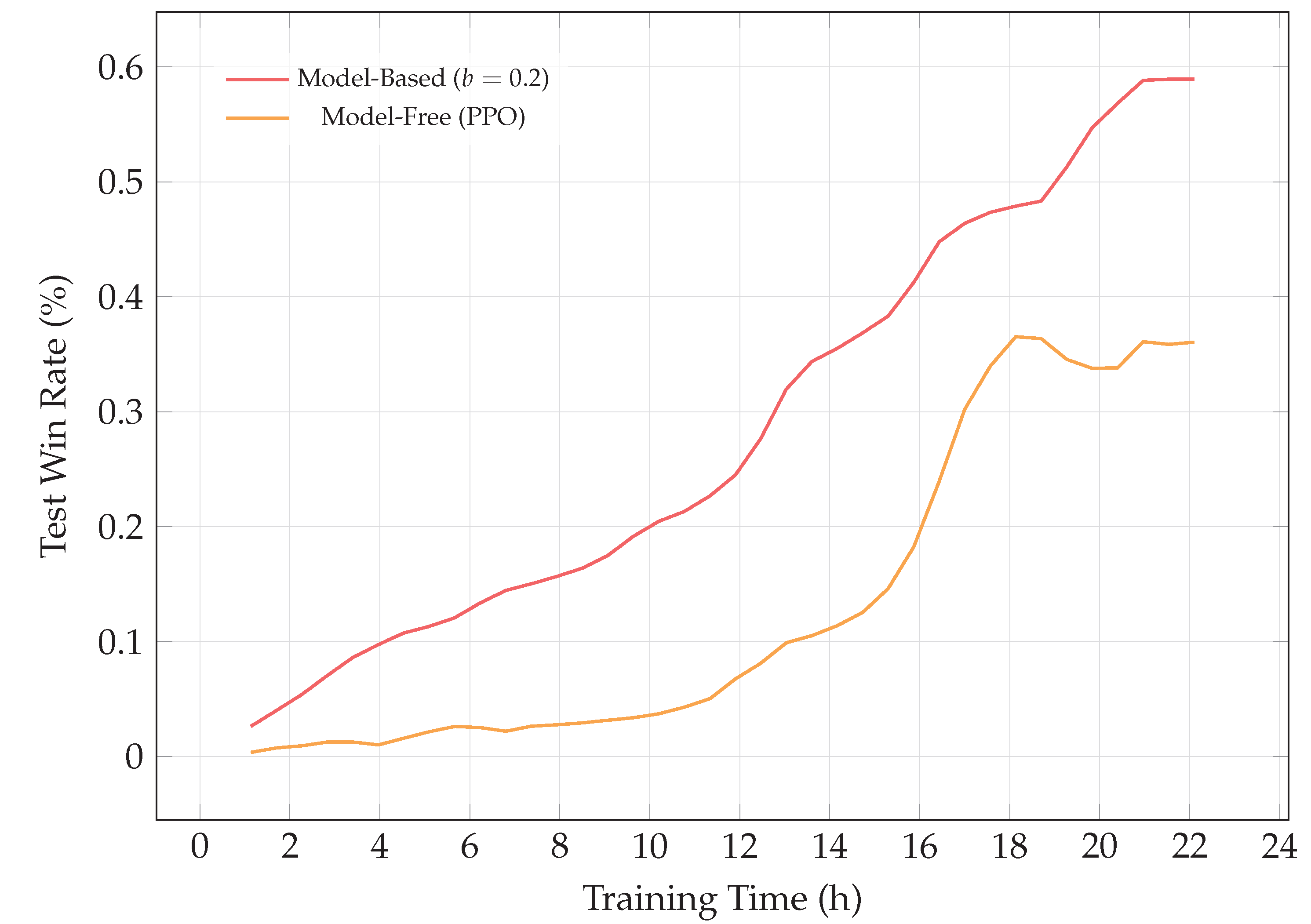
To shed light on the first and second research questions, we first evaluate curriculum initialization under varying crash rate budgets b and benchmark it against the PPO baseline, as shown in Figure 5. The training is paused after every 10000 environment steps, during which 30 test episodes are run with a randomly chosen opponent from the curriculum pool. At the extreme $b=0$, the agent adopts a passive strategy, yielding fewer wins and frequent draws, which is consistent with our expectations. For moderate crash rate budgets, the agent swiftly matches the performance of the heuristic and under-trained learning-based opponents within 200 episodes, resulting in significantly higher exchange rates than training with an unlimited crush budget, while dramatically outperforming PPO in sample efficiency. When measured in wall-clock time as shown in Figure 6, the margin narrows, but the model-based agent still outperforms PPO using a replay ratio of 512; lowering this ratio would further improve runtime at the cost of additional environment samples. The final performance of curriculum-trained agents are displayed in Figure 7. In light of the preliminary results, we opt for a crash rate budget of $b=0.2$ during self-play and fine-tuning, as it yields an agent with a satisfying win rate and the highest exchange rate.

5.2. Self-Play

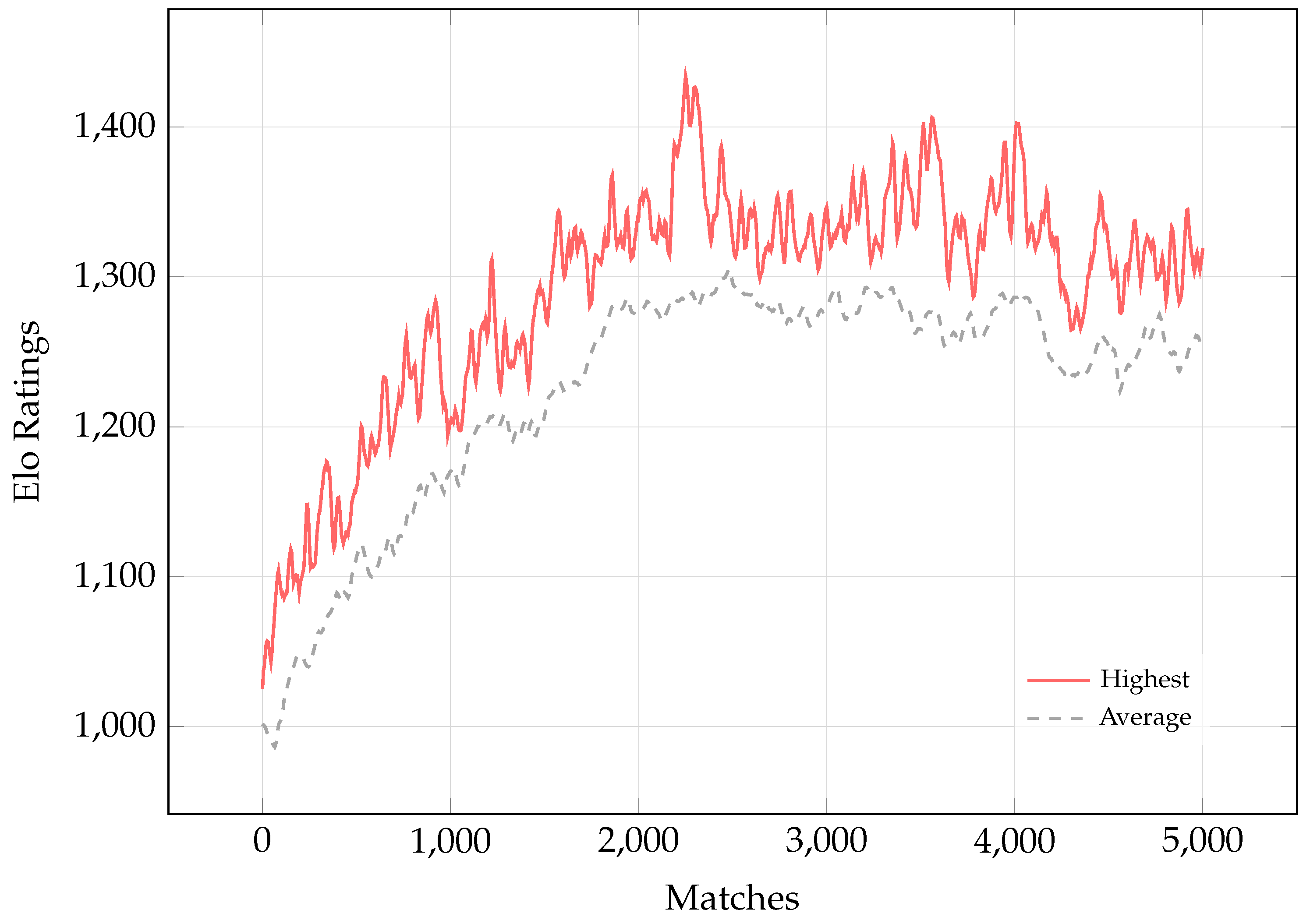
We employ a population of $N=5$ learning agents and inject three fixed PPO-trained opponents, all initialized at 1000 Elo. Figure 8 plots the maximum and mean Elo of the learning population over time. We observe a steady rise in Elo reaching a plateau around 1350. Beyond the limited rounds of self-play iterations, this stagnation likely stems from insufficient strategic diversity: lower-ranked agents tend to converge on diluted versions of the champion’s tactics, preventing further gains. We hypothesize that enforcing population diversity, so that agents discover non-transitive, complementary strategies, would sustain collective improvement. We leave the exploration of such diversity-promoting mechanisms to future work.

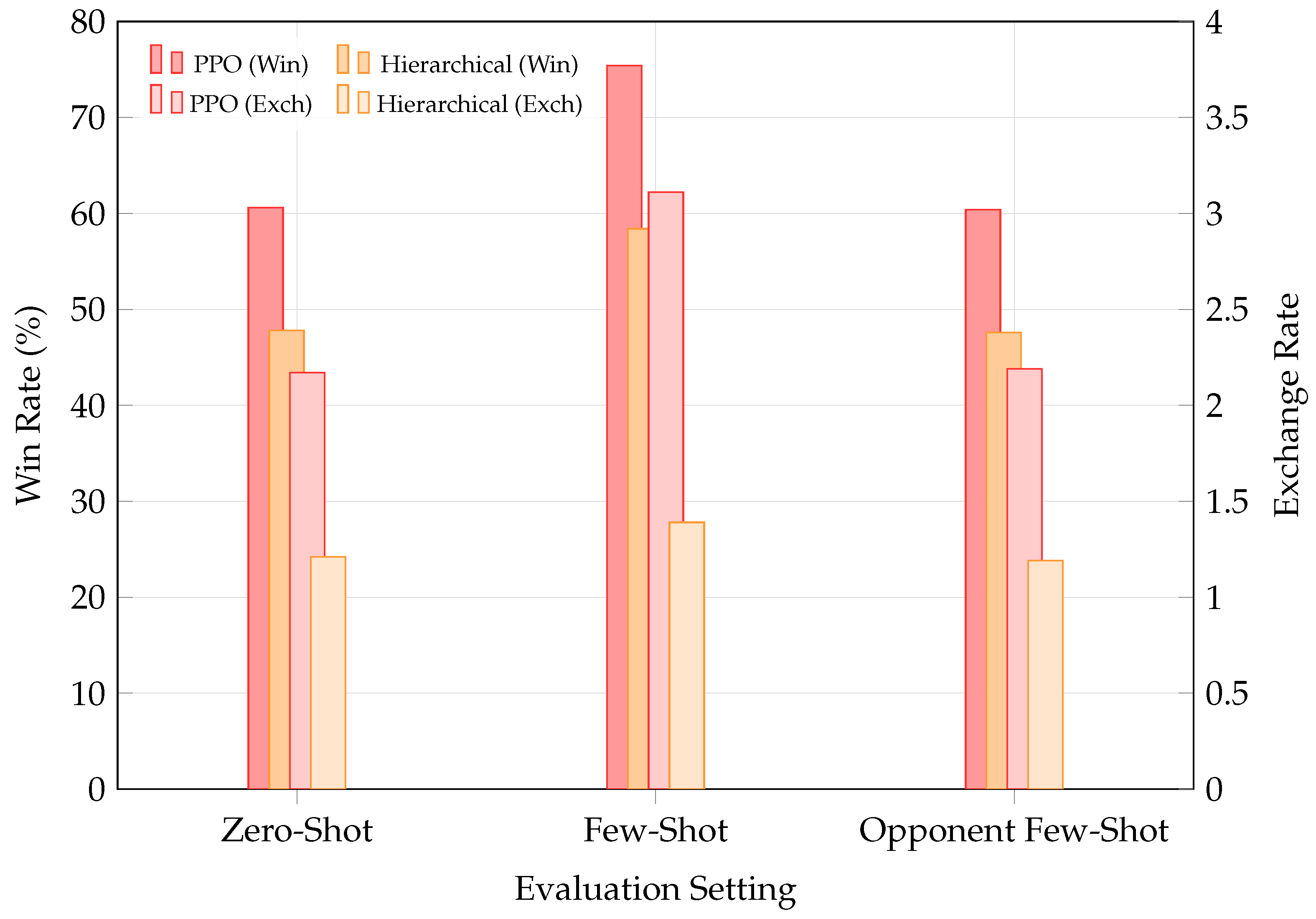
5.3. Zero-Shot Evaluation and Few-Shot Fine-Tuning

To address our final research question, we evaluate the pretrained model-based agent head-to-head against two benchmarks:

• PPO Baseline — A Proximal Policy Optimization agent trained with the identical training pipeline described in the preceding subsections.
• Hierarchical Baseline — A hierarchical agent following the architecture proposed by Li et al. [54].

In the zero-shot setting, each agent is tested against its opponent without any additional training. In the few-shot setting, either our agent or the benchmark is fine-tuned for up to 50,000 transitions (approximately three hours of real-world experience) before facing the unmodified opponent. Figure 9 reports the average win rate and exchange rate over 100 test episodes per opponent. Our agent demonstrates strong zero-shot performance against unseen opponents, and this performance improves substantially after a brief fine-tuning phase. In contrast, naive fine-tuning of the PPO baseline or the intra-option policy of the hierarchical agent [54] yields negligible improvement against our agent. These findings highlight the robustness of our pipeline and the WM’s ability to rapidly adapt to specific opponents, approaching the sample efficiency required for real-world deployment.

5.4. Ablation Studies

To validate our design choices, we conduct a series of ablation studies during the curriculum learning stage, systematically removing key components of our model to assess their impact on performance. The components evaluated include: contrastive predictive coding, categorical target projection, the Dyna-style mixing of real and imagined rollouts, and value-function Lipschitz regularization.

Figure 10 illustrates the win rates of the ablated models after 200 training episodes. The results unequivocally demonstrate that the removal of any single component leads to a degradation in performance. This confirms that each modification is integral to achieving the robustness and high performance of our single, monolithic policy.

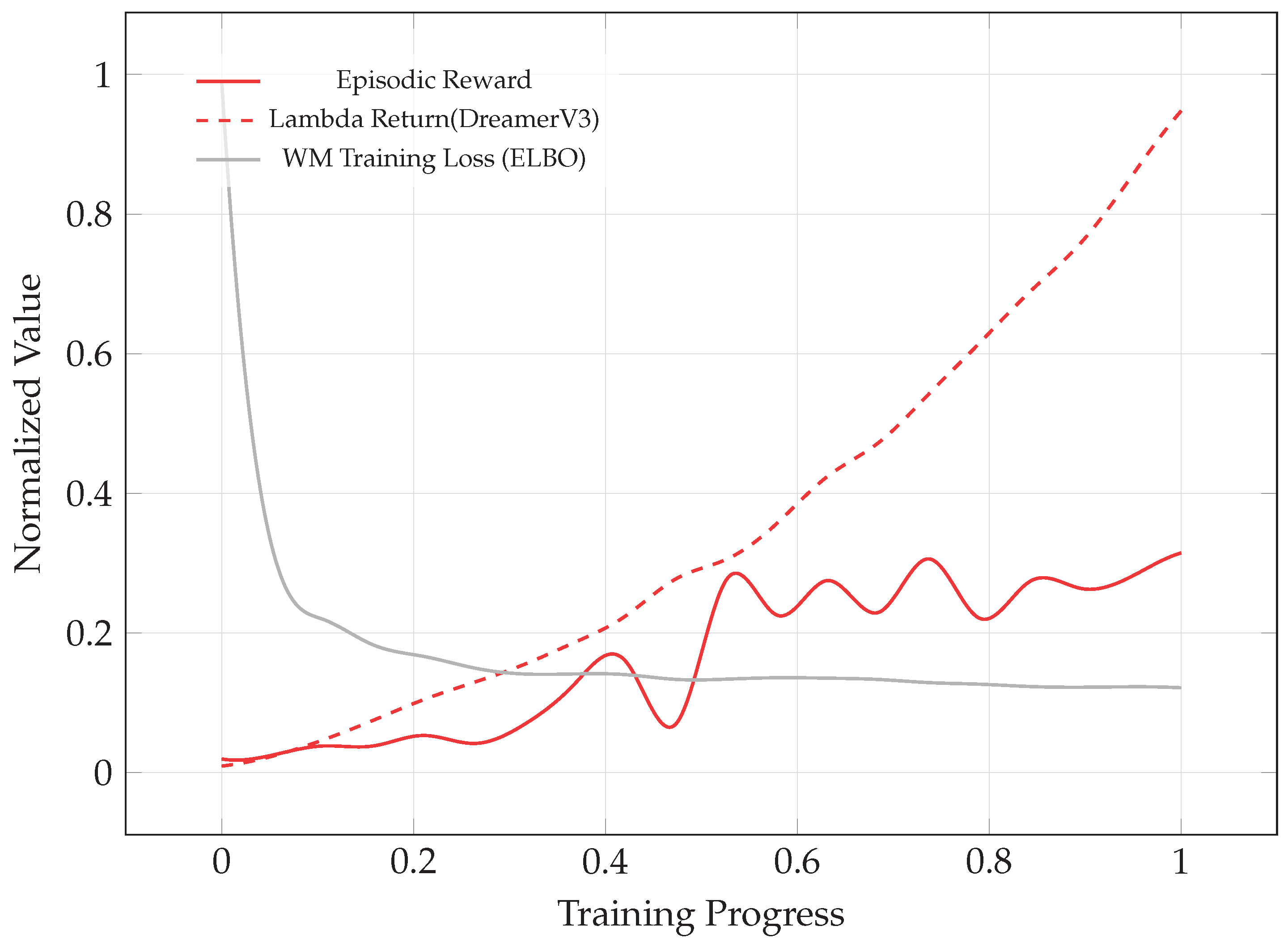
We further contextualize these findings by comparing our model to a vanilla DreamerV3-XS agent with a similar parameter count. The vanilla agent not only underperforms significantly but also falls behind a much simpler PPO baseline. This highlights a critical insight: state-of-the-art performance on standard benchmarks does not necessarily translate to robustness in complex, specialized domains. A common failure mode observed in the vanilla DreamerV3 agent is its tendency to settle on rudimentary tactics; for instance, it quickly learns basic evasion maneuvers in favorable scenarios but fails to discover more complex and effective tactics, such as the barrel roll or fake overshoot. Moreover, the agent sometimes exhibits a lack of sensitivity to imminent threats, often cruising idly into danger. We hypothesize that these shortcomings stem from the WM’s inaccuracy in predicting critical future states, which leads to value overestimation in dangerous situations.

A deeper investigation, illustrated in Figure 11, substantiates this hypothesis. We observe a significant mismatch between the model’s training error as measured by the ELBO and the actual deviation in value predictions along imagined trajectories. For the vanilla DreamerV3 agent, the model-aware value error remains substantial even when the ELBO, a reconstruction-based metric, is optimized. This discrepancy confirms that relying solely on reconstruction losses can be misleading, as they do not adequately capture errors in long-term value prediction. In contrast, our incorporated features directly mitigate this issue: CPC module improves the WM’s sensitivity to termination events, categorical value distribution paired with Lipschitz regularization promotes smoother and more reliable value landscapes, while the Dyna-style blending of real and imagined rollouts provides corrective learning signals from ground-truth trajectories.

It is worth noting that the design of the population-based self-play pipeline, i.e., population initialization, policy conditioning, and the opponent sampling strategy, could also impact the agent’s final performance. Regrettably, due to substantial resource constraints, a thorough ablation of these self-play mechanics is deferred to future work.

Figure 11. Discrepancy between imagined value and actual epsisodic return during curriculum learning of vanilla DreamerV3-XS agent. The lambda return of imagined trajectories serves as a proxy for the agent’s self-assessed performance. As the WM loss decreases, the model-based agent tends to overestimate its performance more rather than reduce this bias. Values are normalized for comparability.

Figure 11. Discrepancy between imagined value and actual epsisodic return during curriculum learning of vanilla DreamerV3-XS agent. The lambda return of imagined trajectories serves as a proxy for the agent’s self-assessed performance. As the WM loss decreases, the model-based agent tends to overestimate its performance more rather than reduce this bias. Values are normalized for comparability.

6. Discussions and Future Directions

This work has introduced a modified Dreamer algorithm, enhanced with a self-play mechanism, to develop a single, end-to-end monolithic policy for the complex domain of automating within-visual-range air manuevers. Our model-based agent not only demonstrates robust zero-shot performance against diverse opponents but also shows amenability to rapid, gradient-based fine-tuning with minimal domain-specific knowledge. A key contribution of this research is demonstrating that by integrating a WM with a meticulously designed self-play pipeline, the expressiveness and performance of a learning-based monolithic policy can be significantly extended, challenging the prevailing view that such policies lag behind hierarchical baselines in this context.

Nevertheless, this study has two principal limitations. First, the scarcity of open-source implementations of leading hierarchical automated aerial agents prevented a direct, fair comparative analysis against State-of-the-Art solutions. Second, the substantial computational resources required for our experiments constrained this investigation to a JSBSim-level simulator.

Future research will focus on overcoming these limitations by scaling our approach to higher-fidelity simulations and, eventually, real-world platforms. Such efforts will be crucial to validating whether the robustness of our architecture and training methodology persists in genuinely operational environments. Ultimately, this research represents a significant step toward making scalable, stable reinforcement learning more accessible to non-practitioners in specialized fields.

Appendix A.1. Game Scenario and Rules

We evaluate two autonomous aircraft (red vs. blue) engaged in a close-range aerial pursuit-evasion task. Both agents are initialized under randomized conditions, including relative separation, headings, attitudes, altitudes, and body-frame velocities, all sampled uniformly from feasible flight envelopes.

Both agents attempt to maintain positional advantage by minimizing the line-of-sight (LOS) angle and distance to the opponent agent. At each simulation step, a continuous reward is assigned based on relative geometry:

$$r_t=w_{d}exp(-\parallel p_{\mathrm{red}}-p_{\mathrm{blue}}\parallel /R)+w_{\theta }cos\left({\theta }_{\mathrm{LOS}}\right),$$

where $\parallel p_{\mathrm{red}}-p_{\mathrm{blue}}\parallel$ is the relative distance, ${\theta }_{\mathrm{LOS}}$ is the angle between the pursuer’s forward axis and the line of sight, and $(w_d,w_{\theta })$ are weighting coefficients. This encourages the pursuer to stay close and aligned, and the evader to escape alignment.

Each encounter terminates when (1) the distance between aircraft exceeds the disengagement threshold $R_{\max }$, (2) one aircraft departs from the valid flight envelope, or (3) the elapsed time exceeds 1000s. At the end of the encounter, the aircraft with the higher accumulated reward wins.

Appendix A.2. Action Space of Aircraft Agent

We define two action levels:

Raw Action Space The low-level control action, which feeds directly into the simulator control interface

$$\begin{array}{c}\hfill a\sim \mathrm{MultiDiscrete}\left(\right[41,41,41,30\left]\right)\end{array}$$

where $a_{\mathrm{ctrl}}=(a_{\mathrm{ail}},a_{\mathrm{ele}},a_{\mathrm{rud}},a_{\mathrm{thr}})$ indexes evenly spaced bins for aileron, elevator, rudder ($\{0,\dots ,40\}$) and throttle ($\{0,\dots ,29\}$).

Hierarchical Action Space Directly learning $a_{\mathrm{ctrl}}$ can be challenging due to its high dimensionality. Following [55], we introduce a coarse high-level action space used by the model-based policy:

$$\begin{array}{cc}\hfill a_{\mathrm{high}}& =\left(a_{\Delta \varphi },a_{\Delta \theta },a_{\Delta V}\right)\hfill \\ \hfill & \sim \mathrm{MultiDiscrete}\left(\right[3,5,3\left]\right)\hfill \end{array}$$

where $a_{\Delta \varphi }$, $a_{\Delta \theta }$, and $a_{\Delta V}$ select among roll angle, pitch angle, and velocity increments. These commands are concatenated with the ego-state and fed into a learned low-level policy network, which outputs $a_{\mathrm{ctrl}}$. The low-level controller is trained via Proximal Policy Optimization (PPO); The training recipe is provided in Appendix ??.