1. Introduction
The estimation of the postmortem interval (PMI) remains one of the most enduring and consequential challenges in forensic practice. Its determination underpins the reconstruction of events in suspicious deaths, supports or refutes alibis, and guides identification in cases of mass fatalities. Despite more than a century of intensive work, no single method has achieved universal reliability. Classic signs—body cooling, rigor mortis, and livor mortis—remain in routine use, yet their reliability is limited and their interpretive windows narrow [
1,
2]. Contemporary reviews confirm that decomposition is influenced not only by external factors such as temperature, humidity, and insect activity, but also by intrinsic characteristics including body mass, pathology, and microbiome composition, rendering PMI estimation an inherently complex and context-dependent task [
3,
4]. Attempts to refine early postmortem estimations have largely focused on temperature-based models, with the Henssge nomogram representing the most enduring effort to formalize algor mortis through parameters such as body weight and ambient temperature. While influential, this method assumes environmental stability rarely encountered in casework. Recent evaluations demonstrated only a 36.8% concordance with the actual time of death, with acceptable accuracy achievable only under controlled laboratory-like conditions [
5]. Subsequent exchanges between investigators and critics emphasized that the model was derived from limited case material and lacks the external validation required for forensic reliability [
5,
6]. Even under ideal conditions, confounding factors such as clothing, body surface area, and body mass index substantially reduce precision [
7]. Other classical indicators, such as rigor and livor mortis, have proven equally inconsistent. Rigor mortis, once considered a predictable sequence of stiffening and relaxation, is affected by temperature, exertion, and pathological status, and may even reappear outside its canonical window [
6]. Livor mortis is assessed qualitatively and shows high inter-observer variability, with progression strongly dependent on ambient conditions and body position [
4]. Supravital reactions—initially thought to provide precise temporal markers—are short-lived, variable, and resistant to standardization [
8]. To extend applicability beyond the early hours after death, anthropological models such as the Total Body Score (TBS) combined with Accumulated Degree-Days (ADD) sought to link decomposition with environmental energy input. These systems appeared attractive for their structured scoring and adaptability to fieldwork [
9]. Yet their limitations soon became evident: results vary across climates and ecological zones, undermining claims of universality. Field studies in South Africa demonstrated significant inaccuracies when ADD models were applied outside temperate regions [
10], and although improved mathematical formulations have been proposed [
11], systematic reviews and meta-analyses confirm that prediction intervals remain too broad for forensic or judicial certainty [
9,
12]. Parallel efforts have explored biochemical and imaging-based strategies. Vitreous humor analysis, once promising for its relative stability, has yielded variable results depending on storage conditions and cause of death. Studies on DNA and RNA degradation suggest temporal signatures, but their rates are highly dependent on temperature and tissue type [
4]. Proteomic markers such as creatine kinase or GAPDH have been investigated, yet findings are inconsistent and often based on small sample sets. Emerging imaging modalities—including postmortem computed tomography, magnetic resonance imaging, and optical coherence tomography—have provided proof-of-concept evidence that structural changes may carry chronological information [
13]. However, these remain fragmented innovations: each method illuminates only a narrow segment of the postmortem timeline, and none has matured into a universally accepted protocol. The fragility of PMI estimation methods is most clearly revealed in the legal domain. Courts demand that forensic techniques meet rigorous criteria of admissibility—such as those outlined under the Daubert standard—which emphasize reproducibility, peer review, known error rates, and general acceptance. Analyses of Dutch case law reveal that PMI methods, though frequently invoked, often fail to satisfy these requirements [
14]. The lack of standardized protocols, the sensitivity to uncontrollable variables, and the reliance on subjective interpretation diminish their credibility in adversarial contexts. Scholarly reviews echo these concerns, underscoring that dependence on narrow or poorly validated models risks overconfidence and misrepresentation in judicial proceedings [
4,
13]. Taken together, these limitations illustrate a paradox that defines forensic chronobiology: the demand for accuracy is greatest where uncertainty is most profound. Temperature-based models, stiffness and lividity, decomposition scores, biochemical assays, and imaging methods each provide valuable fragments of knowledge, but none offer a comprehensive solution. Their failures in reproducibility, generalizability, and legal robustness underscore the need for a unifying framework. These limitations illustrate a paradox that defines forensic chronobiology: the demand for accuracy is greatest where uncertainty is most profound. The present work proposes a unifying physical framework in which these heterogeneous phenomena are expressed through a single, dimensionless variable: entropy. By translating the results of virtually all established PMI estimation methods into entropic terms, we show that each describes a different projection of the same irreversible process—the progressive loss of order and the drift toward equilibrium. This empirical translatability gives the model its “theory of everything” character: not by explaining all things, but by encompassing the totality of measurable postmortem change within one quantitative law. Once normalized, this approach allows direct comparison between domains and time scales, potentially enabling the same physical quantity to describe both an individual dead for one hour and one dead for several days. In this sense, the model does not replace traditional techniques but integrates them within a single thermodynamic continuum, transforming PMI estimation from an empirical extrapolation into a physics-based inference problem.
1.1. Why “Theory of Everything”
The expression “Theory of Everything” is used here not in its cosmological sense, but as a shorthand for empirical completeness. In forensic science, the fragmentation of methods—thermal, biochemical, structural, and microbial—has long prevented a unified description of postmortem change. Each approach captures a different projection of the same irreversible process, yet their outputs remain confined to incompatible scales.
By translating the results of virtually all established PMI estimation techniques into a single quantitative variable—entropy—this framework achieves an operational form of totality: it allows every measurable manifestation of death to be expressed along the same physical continuum. The “everything” therefore refers to the scope of integration, not to metaphysical ambition. The model does not claim to explain all processes of decay, but to encompass the totality of reproducible observations through a single mathematical law.
Once normalized, entropy becomes a shared metric connecting different domains, body conditions, and temporal scales. It potentially enables the same physical quantity to describe both an individual dead for one hour and another dead for several days. In this sense, the theory aspires not to universality in the philosophical sense, but to interoperability in the scientific one—a bridge among all valid quantitative descriptions of dying.
2. Death as Rising Entropy
The search for a single law capable of encompassing all postmortem transformations naturally leads to the thermodynamic principle of entropy.
Entropy is not an abstract or metaphysical idea; it is a measurable property describing how any system evolves from order to disorder. Entropy (S) quantifies the number of microstates accessible to a system at a given energy level and thus its degree of disorder, according to Boltzmann’s definition:
where k is the Boltzmann constant and W is the number of possible microstates. While Boltzmann entropy quantifies physical microstates, Shannon entropy describes uncertainty in state distributions; both share the same mathematical form, linking energy dispersion to informational disorder
Every living organism represents an improbable pocket of order maintained by continuous energy flow, molecular coordination, and information control. When this regulation ceases, gradients flatten, correlations vanish, and entropy rises.
In thermodynamics, entropy quantifies the dispersion of energy—the degree to which heat or chemical potential becomes unavailable for work, a concept first formalized by Rudolf Clausius in 1864 and later extended to complex systems [
15,
16]. Living cells postpone this process through metabolism, exporting entropy to the environment to preserve internal structure [
17]. When metabolism stops, temperature and electrochemical gradients collapse, ATP breaks down, and ions diffuse freely. These macroscopic and microscopic transitions—cooling, ionic leakage, and rigor mortis—represent measurable manifestations of increasing thermodynamic entropy.
In information theory, entropy assumes a complementary meaning. Claude Shannon (1948) defined informational entropy as the average uncertainty of a system, formalized as H = −Σ p log p, expressing the number of possible states a system can occupy: the greater the unpredictability, the higher the entropy [
18]. Building upon Shannon’s framework, Machado and Lopes extended this concept to human mortality, demonstrating that the uncertainty of death itself can be described through Shannon and cumulative residual entropies [
19]. Their model shows that as survival probability declines, life progressively resolves its own unpredictability—an elegant bridge between informational and biological entropy.
In living organisms, predictable patterns—regular heartbeats, stable gene expression, and organized tissue morphology—reflect low informational entropy. After death, these regularities vanish: electrical rhythms flatten, macromolecules fragment, and tissue architecture disintegrates. The dissolution of predictable structure transforms biological information into statistical noise, marking the informational counterpart of thermodynamic decay. Recent advances in systems and computational biology have revealed that life itself can be described as a continuous exchange of information between molecular “senders” and “receivers” [
20]. Signal-transduction networks, feedback loops, and metabolic circuits transmit biochemical messages with finite “channel capacity.” As long as this internal communication remains intact, uncertainty remains low. When circulation stops, these informational channels fail, mutual information collapses, and randomness expands. Informational entropy thus rises in parallel with thermodynamic entropy, linking the physical and computational dimensions of biological order. From a theoretical perspective, biological systems persist by managing entropy flow: they maintain low internal entropy through metabolic coupling that exports disorder outward [
17]. Gladyshev described this through temporal hierarchies, where higher biological levels (organs, tissues) decay first after systemic regulation ceases, releasing lower levels (cells, molecules) to equilibrate independently [
21]. The loss of hierarchical coordination—rather than a single catastrophic event—marks the true beginning of death. At the statistical level, Aristov et al. demonstrated that cooperative correlations between subsystems minimize total entropy in living matter; when these correlations vanish, entropy rises abruptly [
22]. This observation captures Schrödinger’s notion of “feeding on negentropy” in measurable physical terms. Bailly and Longo introduced the concept of “anti-entropy” to describe biological organization as an active, self-regenerating order distinct from structural regularity; death thus represents the disappearance of anti-entropy—the irreversible loss of self-repair and self-prediction [
23]. Information-theoretic analyses reinforce this view. As emphasized by Chanda et al., biological systems are inherently noisy across molecular hierarchies—from gene expression to metabolomic networks—and entropy provides a unifying metric for quantifying that noise [
24]. Summers further argued that organisms survive by dynamically regulating uncertainty, reducing surprise through feedback, consistent with Friston’s free-energy principle [
25,
26]. When this regulatory loop fails, both thermodynamic and informational entropy accelerate in tandem. Natural systems, as shown by Martyushev and Seleznev, evolve to maximize entropy production until equilibrium is reached [
27]. Mitrokhin emphasized that thermodynamic and informational entropy coexist in biology and unravel simultaneously at death. The dying organism therefore follows a predictable entropic trajectory: residual metabolism briefly resists disorder, but once energy reserves are exhausted, gradients collapse and randomness dominates. Entropy, in this sense, is not merely an endpoint—it is the slope of dying itself [
28].
Forensic observation fits seamlessly into this framework. Every postmortem change—body cooling, hypostasis, rigor, cellular autolysis, and DNA fragmentation—represents a stage in the rise of entropy across biological scales. These processes can be quantified in physical units (J/K, bits) or statistical indices, linking molecular and macroscopic phenomena under one law. Entropy transforms the descriptive language of decomposition into a measurable continuum of disorder. Brooks and Wiley famously described life as a temporary negation of entropy, a fleeting improbability maintained through continuous work. When that work ceases, the improbability collapses [
29]. Thus, death as rising entropy is not metaphorical but physical: a trajectory from low to maximal entropy encompassing all observable signs of biological cessation. By framing the postmortem interval as a quantifiable entropic ascent, forensic science gains a unifying principle that bridges thermodynamics, information theory, and biology—turning the decay of order into a measurable chronometer of death [
30].
2.1. Entropy as Progressive Loss of Biological Order
The transition from metabolic order to thermodynamic equilibrium unfolds as a continuous loss of organization across physical and informational hierarchies.
From a physical perspective, death marks the interruption of the metabolic flow that kept a living organism far from thermodynamic equilibrium. When circulation and respiration cease, the continuous exchange of energy and information that sustains cellular order comes to an end, and all gradients—thermal, chemical, and electrical—begin to dissipate spontaneously. This transition represents a progressive increase in entropy, measurable as the loss of organization and the equalization of potential differences within the system. In the minutes following cardiac arrest, residual metabolic reactions persist transiently. Oxygen tension declines, ATP synthesis stops, and ionic pumps fail, leading to passive diffusion of ions across membranes. pH decreases, mitochondrial potential collapses, and body temperature begins to equilibrate with the environment. These processes correspond to an early thermodynamic drift: the energy once used to preserve structure and function becomes uniformly distributed, increasing systemic disorder. At the molecular level, enzymatic control deteriorates and macromolecules lose conformational stability. Proteins unfold, nucleic acids undergo hydrolysis, and the cytoskeleton disassembles. The selective compartmentalization of the living state gives way to unrestricted diffusion, allowing metabolites, ions, and water to move according to purely physical laws. Each of these transitions contributes to the rise of entropy, quantifiable either as energy dispersion (ΔS = Q/T) or as loss of informational order (Shannon entropy). As time progresses, the breakdown of regulatory hierarchies propagates to tissues and organs. Mechanical stiffness, osmotic balance, and optical properties—such as corneal transparency—change predictably as entropy increases. Structural coherence decays into homogeneity, and the gradients that defined the living architecture vanish. The organism approaches thermal and chemical equilibrium with its surroundings—the maximal entropic state. This continuum, rather than a discrete event, constitutes the physical basis for PMI estimation. Every measurable postmortem change—temperature decrease, biochemical drift, molecular degradation, or morphological alteration—represents a specific domain of the same entropic process. Quantifying this progression through diverse observable variables allows the PMI to be expressed as a function of entropy rather than as a purely empirical timeframe [
30].
3. Entropic Domains of Postmortem Transformation
The concept of death as rising entropy becomes fully tangible only when examined through the hierarchy of transformations that unfold from the moment biological order begins to fail. Entropy does not increase within a single domain but propagates through successive layers of organization, each governed by its own physical and biochemical principles.
Immediately after cardiac arrest, the body behaves as a closed thermodynamic system, still attempting to maintain internal equilibrium. During this phase, entropy rises internally across four interconnected domains—thermal, biochemical, microstructural, and macrostructural—each marking a measurable step in the collapse of organization and predictability. Heat dissipates, chemical gradients flatten, cellular architecture disintegrates, and tissue coherence vanishes.
At a later stage, the system ceases to be closed. Its boundaries dissolve, and the corpse merges with the surrounding environment. This marks the onset of a fifth, biological–ecological domain, in which external biological agents—microbes, insects, and decomposers—become active participants in entropy production. The once self-contained system opens to exchanges of matter, energy, and information with the ecosystem.
Together, these five domains describe a continuous thermodynamic trajectory in which the postmortem system evolves irreversibly toward equilibrium. The first four belong to the physics of a closed biological system (internal disorganization), while the fifth marks the transition to an open system where decomposition becomes ecological.
The five entropic domains can be summarized as follows:
- (1)
thermal entropy — dissipation of residual metabolic heat;
- (2)
biochemical entropy — biochemical entropy — diffusion and redistribution of metabolites and ions as metabolic gradients decay
- (3)
microstructural entropy — molecular and subcellular degradation (DNA, RNA, proteins);
- (4)
macrostructural entropy — loss of tissue and organ coherence observable through imaging;
- (5)
biological–ecological entropy — incorporation of the body into the environmental energy flow.
3.1. Methods: Deriving and Comparing Entropy Across Domains
To render the concept of rising entropy operational, each domain of the postmortem process must be expressed as a measurable function of disorder. Although the nature of the variables differs across physical, chemical, and structural scales, the same mathematical principle applies: entropy increases as gradients vanish and variability becomes maximal.
For the purposes of this framework, entropy in each domain (Si) is defined as a dimensionless index ranging from 0 (complete order) to 1 (maximum disorder).
- Thermal entropy (S1) — reduction of temperature differentials between body and environment, normalized by the initial gradient (ΔT0).
- Chemical entropy (S2) — equalization of metabolite and ion concentrations, e.g., vitreous potassium or lactate.
- Microstructural entropy (S3) — molecular disorganization quantified from fragment-size or conformational distributions.
- Macrostructural entropy (S4) — tissue-level disintegration measurable by radiomic or texture-based entropy.
- Biological–ecological entropy (S5) — microbial diversification and ecological succession describing the body’s integration into environmental energy flow.
Each S
i(t) increases monotonically with postmortem time
t. Mapping all indices onto a common 0–1 scale allows the construction of a composite trajectory:
where the weights w
i(t) represent the relative reliability of each domain as a function of time. In early postmortem phases, thermal and biochemical entropy dominate; in later intervals, structural and ecological components become more informative.
The calibration of wi(t) can, in principle, be achieved empirically by evaluating the predictive accuracy of each domain within distinct postmortem intervals. However, in this theoretical formulation, the weights remain conceptual placeholders for empirical confidence, representing the dynamic contribution of each domain to the total entropic rise.
This framework provides a universal procedure for converting any measurable postmortem variable into an entropic expression comparable across scales.
3.2. Thermal Domain: Dissipation of Residual Heat
The first and most fundamental manifestation of postmortem entropy is the dissipation of residual heat. With the cessation of metabolism, internal temperature gradients vanish as the organism moves toward equilibrium with its surroundings. According to the second law of thermodynamics, this spontaneous heat transfer corresponds to an entropy increase:
where T
0 and T
f denote the core temperature at death and at time t, respectively. Body cooling follows an exponential decay consistent with Newton’s law and its forensic adaptation by Henssge [
31,
32,
33]; simplified analytical models [
34] and validation studies [
35] show monotonic decay with rate constant
kt dependent on body mass, clothing, and ambient temperature. The normalized thermal entropy is defined as:
rising from 0 (complete order) to 1 (thermal equilibrium).
The entropic expression of the PMI is obtained by inversion of the same relationship:
Under constant conditions, kₜ typically ranges between 0.08 and 0.15 h⁻¹, producing an entropy rise that stabilizes within the first 24 hours. In this formulation, kₜ (h⁻¹) represents the thermal rate constant governing the exponential cooling process.
As shown in
Figure 1(a), the thermal entropy curves are adapted from the experimental dataset of Heinrich [
35], who validated the Henssge model [
1] using human cadavers stored at different ambient temperatures (≈10 °C and ≈20 °C). In that dataset, the measured temperature decay remains consistent with Newton’s exponential law, but when expressed as normalized entropy, it appears quasi-sigmoidal due to sampling resolution and limited temporal coverage, although the underlying physical model remains purely exponential. Entropy increases rapidly after death and gradually approaches equilibrium, with faster progression and higher asymptotic values at higher ambient temperatures, reflecting the modulatory effect of environmental heat exchange.
This thermal component represents the earliest and most deterministic contributor to the global entropic drift of the corpse. Its reproducibility and simplicity make it an ideal reference for normalizing the subsequent domains of postmortem entropy
3.3. Biochemical Domain: Collapse of Metabolic Equilibrium
The biochemical domain captures the molecular loss of order that follows circulatory arrest.
Residual ATP and phosphocreatine transiently sustain ion pumps; as these energy reserves are depleted, sodium–potassium gradients fail, metabolites diffuse, lactate and hypoxanthine accumulate, and pH decreases.
These transitions reflect the spontaneous equalization of chemical potentials and the monotonic rise of biochemical entropy [
36,
37].
Metabolomic investigations of vitreous humour, pericardial fluid, and skeletal muscle have shown reproducible temporal trajectories for amino acids, nucleotides, and oxidative-stress markers [
38,
39,
40,
41,
42].
Biochemical entropy can be expressed in two complementary ways.
The raw (empirical) biochemical entropy quantifies the logarithmic loss of molecular order relative to the concentration at death.
If M
0,i is the metabolites concentration at death and M
t the concentration at postmortem time
t, entropy increases as:
when normalized on a dimensionless 0–1 scale, biochemical entropy follows a logistic trajectory characterized by a rate constant k
b (h
-1) and an inflection point t
0:
The inverse of this function provides the entropic expression of the PMI, which allows the time since death to be estimated directly from the measured entropy value:
In this model,
k_b (h⁻¹) represents the biochemical rate constant describing the rate of metabolic equilibration after death. Experimental data reported by
Chighine et al. [
40] demonstrate that approximately 70–80% of biochemical entropy accumulation occurs within the first 24 hours after death, followed by a slower approach toward equilibrium as metabolite diffusion and chemical gradients flatten.
3.4 Microstructural Domain: Macromolecular Disorganization
At the microstructural level, the rise of entropy reflects the progressive collapse of macromolecular architecture.
Protein denaturation, aggregation, and fragmentation—together with nucleic-acid hydrolysis—dissolve the correlated conformations that sustain cellular integrity.
Proteomic studies have demonstrated reproducible degradation kinetics of cytoskeletal proteins such as titin, desmin, and vinculin [
43,
44,
45,
46,
47], indicating that the loss of molecular order proceeds in a consistent, time-dependent manner.
The raw (empirical) microstructural entropy quantifies the logarithmic decline in macromolecular order, expressed as:
where M
0,i represents the initial molecular integrity (e.g., intact protein fraction) and M
t the residual integrity at postmortem time
t.
When normalized between 0 (full order) and 1 (complete disorder), the normalized microstructural entropy follows a logistic progression:
where
km (h
-1)is the molecular degradation rate constant and
t0 the inflection point of maximal entropy gain.
The inverse form provides the entropic estimation of the PMI:
For human skeletal muscle, Battistini et al. reported km= 0.20 h−1 and t0=52.6 h.
Approximately 90% of total structural entropy accumulation occurs within 100–120 hours, defining the transitional molecular bridge between chemistry and morphology.
3.5. Macrostructural Domain: The Geometry of Disintegration
As molecular integrity collapses, visible tissue architecture progressively loses coherence. Histological and imaging analyses confirm this pattern: hepatic and lingual muscle fibers degrade predictably [
49,
50]; corneal optical coherence tomography (OCT) reveals a monotonic loss of transparency and microstructural order [
51,
52,
53]; and radiomic studies show flattening of contrast gradients and diffusion of texture [
54,
55,
56].
The morphological Shannon entropy describes the degree of form dispersion:
where
pi represents the probability distribution of pixel or voxel intensities, and
kB is a normalization constant.
In practical terms, the morphological entropy
H is first computed from image intensity distributions according to Shannon’s definition:
where p
i are the normalized probabilities of each pixel intensity. The resulting H values are then normalized within the [0–1] range to yield a dimensionless measure of disorder, which can subsequently be fitted to the exponential model:
The inverse form yields the entropic expression of the PMI:
Under controlled conditions, kr (h-1) typically ranges between 0.08 and 0.12 h⁻¹, with approximately 90% of morphological entropy accumulation occurring within 48 hours.
3.6. Biological Entropy: From Microbial Drift to Ecological Equilibrium
When the boundary between organism and environment dissolves, decomposition becomes an open, self-sustaining ecosystem. Microbial succession replaces internal order with ecological complexity. In human cadavers, microbial Shannon entropy increased from 1.85 to 3.15 between 24 and 432 hours, describing the shift from structured organ-specific microbiota to a homogeneous anaerobic community [
57].
The biological-ecological entropy can be expressed as:
where E
max=3.2 represents the equilibrium value and
ke = 0.0051 h
−1 the rate constant.
The normalized entropy function (independent of scale) becomes:
and the entropic PMI is obtained as:
Both microbial and entomological dynamics follow the same statistical law of entropy increase.
Microbial metabolism generates volatile compounds that attract necrophagous insects, initiating trophic succession [
58,
59,
60,
61,
62,
63,
64,
65].
The combined microbial–insect evolution can be formalized as ecological entropy:
At this stage, the cadaver ceases to be a discrete biological object and becomes part of a broader thermodynamic continuum—the irreversible diffusion of biological information into the environment. The quantitative parameters derived from each entropic domain are summarized in
Table 1, providing an overview of rate constants, temporal windows, and equilibrium values.
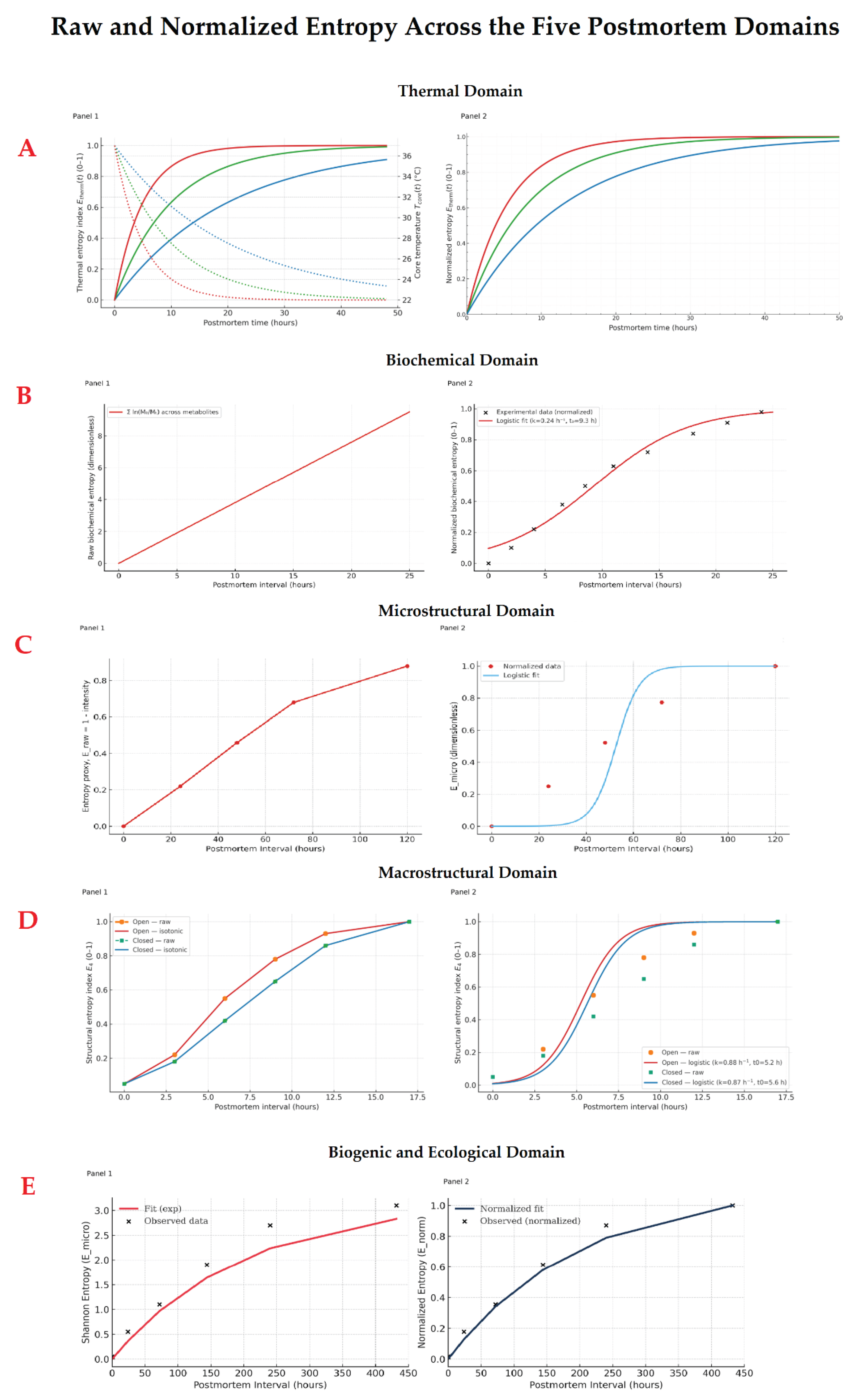
Figure 1 presents the five entropic domains in panels (a–e), each depicting the normalized rise of entropy over time. The uniform layout and progressive lettering emphasize the continuity of the entropic cascade—from thermal dissipation to ecological equilibrium A theoretical synthesis of total entropy weighted across domains (S_total(t)) is provided in
Supplementary Figure S1.
Figure 1.
Entropic progression across postmortem domains. Panels 1 show raw (empirical) entropy values derived from experimental datasets, while Panels 2 display their normalized fits (0–1 scale) for each postmortem domain. Together, these curves illustrate the theoretical and observed rise of entropy from molecular to ecological scales. (a)
Thermal domain. The curves reproduce experimental data from Heinrich et al. (2025) [
35], illustrating the increase of thermodynamic entropy (Eₜ) in corpses stored at different ambient temperatures (≈10 °C vs. ≈20 °C), modeled from temperature-decay data derived from the Henssge method. The trajectory shows a rapid early rise followed by asymptotic stabilization, with faster thermal equilibration and higher entropy rates at higher ambient temperatures. At lower ambient temperatures, entropy increases more slowly and reaches a lower plateau, highlighting how thermal conduction and environmental heat exchange modulate the entropic trajectory toward equilibrium. (b)
Biochemical domain. Based on metabolomic data from Chighine et al. [
40], entropy rises exponentially as metabolic homeostasis collapses after death. The two curves represent the progressive loss of biochemical order over time, reflecting ATP depletion, lactate accumulation, and diffusion-driven equalization of ionic and metabolite gradients. (c)
Macromolecular domain. The unfolding of proteins and the fragmentation of nucleic acids are expressed as a monotonic increase in molecular disorder, from Battistini et al., [
47]. The logistic form of the curves represents the transition from structured macromolecules to random degradation products as postmortem entropy increases. (d)
Macrostructural domain (OCT). Entropy derived from corneal texture analysis reveals a faster increase in the open eye, exposed to dehydration and oxidative stress, and a slower, smoother progression in the closed eye, where eyelid protection delays structural disorganization, from Nioi et al. [
52]. (e)
Bilogical–ecological domain. Microbial succession produces a rise in ecological entropy (Shannon index from ≈ 1.8 to ≈ 3.1 between 24 h and 432 h postmortem) as organ-specific microbiota are replaced by a uniform anaerobic community, from Lutz et al. [
57].
Figure 1.
Entropic progression across postmortem domains. Panels 1 show raw (empirical) entropy values derived from experimental datasets, while Panels 2 display their normalized fits (0–1 scale) for each postmortem domain. Together, these curves illustrate the theoretical and observed rise of entropy from molecular to ecological scales. (a)
Thermal domain. The curves reproduce experimental data from Heinrich et al. (2025) [
35], illustrating the increase of thermodynamic entropy (Eₜ) in corpses stored at different ambient temperatures (≈10 °C vs. ≈20 °C), modeled from temperature-decay data derived from the Henssge method. The trajectory shows a rapid early rise followed by asymptotic stabilization, with faster thermal equilibration and higher entropy rates at higher ambient temperatures. At lower ambient temperatures, entropy increases more slowly and reaches a lower plateau, highlighting how thermal conduction and environmental heat exchange modulate the entropic trajectory toward equilibrium. (b)
Biochemical domain. Based on metabolomic data from Chighine et al. [
40], entropy rises exponentially as metabolic homeostasis collapses after death. The two curves represent the progressive loss of biochemical order over time, reflecting ATP depletion, lactate accumulation, and diffusion-driven equalization of ionic and metabolite gradients. (c)
Macromolecular domain. The unfolding of proteins and the fragmentation of nucleic acids are expressed as a monotonic increase in molecular disorder, from Battistini et al., [
47]. The logistic form of the curves represents the transition from structured macromolecules to random degradation products as postmortem entropy increases. (d)
Macrostructural domain (OCT). Entropy derived from corneal texture analysis reveals a faster increase in the open eye, exposed to dehydration and oxidative stress, and a slower, smoother progression in the closed eye, where eyelid protection delays structural disorganization, from Nioi et al. [
52]. (e)
Bilogical–ecological domain. Microbial succession produces a rise in ecological entropy (Shannon index from ≈ 1.8 to ≈ 3.1 between 24 h and 432 h postmortem) as organ-specific microbiota are replaced by a uniform anaerobic community, from Lutz et al. [
57].
4. Bayesian Integration of Entropic Domains
The long-standing fragmentation of PMI estimation—where thermal, biochemical, molecular, and structural approaches have evolved in isolation—has hindered the emergence of a single predictive framework. Yet each method measures a distinct expression of the same underlying process: the irreversible drift of a once-living system toward thermodynamic equilibrium. From this standpoint, entropy provides a universal metric linking all domains of death, while the precision and temporal validity of each domain remain inherently unequal.
A Bayesian formalism offers a principled way to integrate these heterogeneous signals into a single, coherent equation. Every experimental domain yields an entropic observation—a measurable expression of disorder that evolves over time. Thermal diffusion, metabolite accumulation, DNA fragmentation, and corneal disorganization can all be represented as rising entropic functions. Their diagnostic reliability, however, varies: temperature-based models are highly accurate in the first hours after death; biochemical or radiomic indices dominate the intermediate interval; and ecological or microbial signals prevail over longer timescales. A unified model must therefore weight each observation not equally, but in proportion to its empirical precision and temporal relevance.
Following the classical interpretation of Bayesian inference as the rational updating of belief in light of new evidence [
66], probability represents a
state of knowledge rather than a frequency of occurrence. The posterior probability of a given PMI, conditioned on the observed entropic evidence, is therefore expressed as:
where Z is the normalization constant ensuring that the posterior integrates to one. Each entropic likelihood term P(Eᵢ | PMI) can be empirically modeled from regression fits to experimental datasets
Here, E
i denotes the entropy measurement from the
i-th domain, and w
i represents its adaptive weight—proportional to the confidence and temporal validity of that method. The prior probability P(PMI) encodes contextual knowledge such as ambient temperature, environment, and body characteristics, preserving the probabilistic rather than deterministic nature of the model. As Pearl emphasized in his causal framework [
67], such formulations extend Bayesian reasoning beyond description, allowing inference under uncertainty to become causal and predictive. In this context, the time-dependent weights w
i(PMI) act as causal modulators, encoding both reliability and domain-specific validity. Each new entropic observation refines the posterior distribution, progressively narrowing the uncertainty of the inferred time since death.
From a practical standpoint, this framework can be represented as a composite entropy function:
where S
i(PMI) is the entropy specific to each domain and w
i(PMI) its time-dependent reliability coefficient. The estimated PMI corresponds to the point that maximizes the posterior likelihood of observing the measured configuration:
4.1. Simplified Bayesian Formulation
For computational and interpretive clarity, the unified model can be expressed in its logarithmic form—mathematically equivalent but more stable and transparent:
Defining the domain-specific log-likelihood as L
i(PMI)=logP(S
i∣PMI), the formulation becomes:
For reference, the entire model can be summarized in an ultracompact functional form:
w(PMI): time-dependent reliability weights.
L(PMI)L(\mathrm{PMI})L(PMI): domain log-likelihoods; F: arg-max operator.
Here, w(PMI) is the time-dependent weight vector (method reliability/validity over PMI), L(PMI) the vector of domain log-likelihoods (thermal, biochemical, micro/macrostructural, ecological), and F denotes the maximization operator (arg max) yielding the PMI estimate.
This expression condenses the model into a form that directly parallels a weighted regression of entropic likelihoods, where each domain contributes according to its evidential strength. It preserves the Bayesian foundation while emphasizing interpretability: the estimated time since death corresponds to the point where the sum of prior knowledge and domain-specific information reaches maximal coherence.
In operational terms, the model continuously updates as new data are introduced, refining the posterior distribution of PMI through an adaptive weighting scheme. Early after death, thermal entropy dominates the inference; at intermediate intervals, biochemical and microstructural information prevail; and at extended timescales, ecological entropy becomes the primary driver.
The resulting framework is not a static equation but a living probability function—a continuously updated synthesis of all measurable forms of postmortem disorder. It quantifies uncertainty, integrates evidence across scales, and unifies previously separate forensic paradigms into a single probabilistic narrative of death.
By framing death as a continuous rise in system entropy and the PMI as a process of probabilistic inference rather than a fixed estimate, this Bayesian model offers a conceptual step toward the long-sought Equation of Death—a synthesis that respects empirical variability, quantifies uncertainty, and harmonizes the partial truths of every postmortem domain within one coherent mathematical language.
4.2. Computational Implementation
In practical terms, the Bayesian entropic model can be implemented using standard probabilistic programming frameworks such as PyMC, Stan, or TensorFlow Probability. These tools allow efficient sampling of the posterior PMI distribution through Markov chain Monte Carlo (MCMC) or variational inference methods. The algorithm iteratively updates the likelihoods of each entropic domain according to their reliability weights wᵢ(t), producing a posterior probability curve that reflects both measurement noise and inter-domain uncertainty. The resulting distribution provides not only the most probable PMI estimate but also a transparent quantification of its uncertainty, consistent with forensic reporting standards.
5. Perspectives and Future Directions
This work represents the first coherent attempt to outline what may be considered a theory of everything of death — a conceptual and quantitative framework capable of describing the entire postmortem process through a single physical principle: the spontaneous increase of entropy. Each established forensic method, whether based on temperature, metabolite concentration, molecular degradation, or tissue structure, has so far observed only a portion of this universal trajectory. The entropic approach reinterprets these phenomena as multiple projections of the same irreversible transition from order to disorder, from organized metabolism to thermodynamic equilibrium. In this sense, the estimation of the PMI is not a collection of techniques but an inference on a single, measurable law of decay that governs all systems once vital.
The appeal of this framework lies in its empirical transparency. The transition toward disorder is not an abstract construct: it is directly visible in all serious studies based on serial postmortem sampling. Temperature equalization, biochemical drift, RNA fragmentation, and morphological disorganization all describe the same underlying pattern — a progressive rise in entropy. By identifying this common axis, the model unites data that previously appeared unrelated, providing forensic science with a single quantitative dimension capable of accommodating every observable scale, from the molecular to the macroscopic. The theoretical strength of the model also translates into practical coherence. Through its Bayesian formulation, it allows the integration of heterogeneous signals according to their precision, stability, and temporal validity. The weighting system transforms complexity into proportion: early after death, thermal and ionic entropy dominate; at later intervals, biochemical and structural information prevail. The result is an adaptive inference process that updates itself as new evidence becomes available, replacing deterministic formulas with probabilistic reasoning grounded in physical law. Entropy thus becomes not only a metaphor of disorganization, but a measurable bridge connecting biological, physical, and informational domains of death. The advantages of this approach are manifold. It provides, for the first time, a universal unit of measure for postmortem change; it allows the simultaneous incorporation of multiple independent variables into a coherent probabilistic model; and it quantifies uncertainty in a transparent way, offering courts a more rigorous interpretative tool. Its architecture is flexible and evolutionary: new technologies — from high-resolution imaging to portable metabolomic sensors — can be incorporated without modifying its mathematical foundation. In this respect, the model is not a closed theory but an open system, capable of assimilating future evidence while preserving internal consistency. Nevertheless, the proposal remains at an early conceptual stage. The absence of large, prospective datasets remains the main obstacle to full validation. Empirical calibration of the model requires standardized multicentric sampling that simultaneously records thermal, biochemical, and structural data under controlled conditions. Only by applying the framework to unified cohorts will it be possible to assign precise weights to each domain and verify the reproducibility of the resulting entropy curves. These efforts will mark the transition from theoretical formulation to operational forensic tool. The next challenge is accessibility. If the entropic framework is to guide real-world practice, it must be compatible with the resources, time constraints, and technical capacities of ordinary forensic laboratories. Future research should aim to design simplified, robust, and affordable methods for entropy measurement — possibly through portable or semi-automated devices integrating spectroscopic, thermal, or optical data. Such instruments could provide rapid, field-ready estimates of the PMI, bridging the gap between scientific theory and judicial necessity. This transformation will require collective engagement. Interdisciplinary meetings among pathologists, physicists, engineers, and data scientists will be essential to define standardized protocols, shared databases, and validation metrics. Only through such collaboration can the forensic community move from parallel efforts to a unified scientific front. In practical terms, the first step toward implementation would be the creation of standardized reference datasets combining thermal, biochemical, and structural measures under controlled morgue conditions. Multicentric collaboration among a limited number of forensic laboratories—ideally equipped with comparable CT or OCT systems—could provide the calibration basis for domain-specific entropy curves. Harmonizing acquisition protocols and defining inter-scanner normalization coefficients would enable reproducible measurement of macrostructural entropy across instruments and institutions. Such pilot datasets, even on a small scale, would transform the entropic framework from a theoretical construct into an operational roadmap for empirical validation. The development of open repositories of postmortem entropy data, accessible worldwide, would accelerate progress and foster reproducibility across institutions. Ultimately, this framework aspires to more than methodological refinement. It proposes a general law of the postmortem state — a principle as simple as it is universal: entropy always rises, and the rate of its increase carries the imprint of time since death. By grounding the estimation of the PMI in this fundamental process, forensic science moves closer to a comprehensive, quantitative, and conceptually unified model of biological dissolution. If realized, the entropic paradigm could become not merely a tool for measuring time, but the foundational equation describing the very physics of dying — the moment when the organized improbability of life collapses, inevitably, into equilibrium.
l5.1. Limitations and Next Steps
Despite its conceptual consistency, the entropic framework remains in an early, primarily theoretical stage. Its validation will depend on the creation of large, prospective, multicentric datasets that integrate thermal, biochemical, and structural measurements under standardized and ecologically diverse conditions. Such harmonized sampling will be essential to derive empirical reliability weights (wᵢ) for each domain and to verify the reproducibility of entropy curves across laboratories. A further challenge lies in the standardization of entropic indices, which must be calibrated against reference materials or controlled decomposition models to ensure comparability across instruments, institutions, and environmental settings. The current absence of universally accepted calibration protocols represents a major limitation for inter-study reproducibility. From a translational standpoint, the framework must evolve into a rapid, field-operable system. Future development should aim toward portable or semi-automated devices capable of estimating entropy in real time, integrating optical, spectroscopic, or thermal sensors within a unified interface. Such instruments would transform the model from a conceptual paradigm into an operational forensic tool, usable during on-site investigations or early autopsy phases. Equally crucial is the selection of the measurement techniques used to quantify each entropic domain. These methods must be chosen not solely for analytical precision but also for accessibility, cost-effectiveness, and reproducibility, ensuring that the model remains applicable to a broad spectrum of forensic pathologists and laboratories. Without this practical inclusivity, the framework risks becoming a specialized construct rather than a universal standard. Finally, computational validation remains an open task. The Bayesian model must be empirically tested through simulation and real datasets using probabilistic inference methods such as Markov chain Monte Carlo or variational optimization. This step will determine whether the proposed weighting scheme (wᵢ) and likelihood structure can robustly handle real-world uncertainty and measurement noise. In summary, while the entropic theory of death provides an elegant unifying principle for postmortem transformations, its translation into an operational forensic instrument will require: (1) multicentric empirical calibration, (2) standardized computation of entropy metrics, (3) validation of portable and accessible measurement tools, (4) method selection compatible with widespread forensic practice, and (5) computational testing under real conditions. These steps mark the bridge between theoretical formulation and practical implementation—the necessary pathway for transforming a physical law into a reproducible forensic tool. Future work should also address the empirical calibration of the time-dependent weights wᵢ(t). These coefficients can be derived from large, multicentric datasets by analyzing the temporal decay of predictive accuracy for each domain—expressed, for example, through coefficients of determination (R²), area under the curve (AUC), or Bayesian information gain. This approach would allow the weighting system to evolve dynamically, giving higher influence to domains that retain predictive value at specific postmortem intervals and reducing the contribution of those that become unstable over time.
7. Concluding Remarks
This work proposes a unified physical description of death — a theory of everything for the postmortem state. Entropy, the universal measure of disorder, becomes the single variable capable of translating molecular decay, thermal diffusion, and structural collapse into one continuous law. Each observation, from the microscopic to the macroscopic, represents a fragment of the same irreversible drift toward equilibrium. By merging them into a single probabilistic equation, the postmortem interval ceases to be an estimate and becomes a physical inference. In this framework, death is not chaos but convergence: the final restoration of balance through the quiet rise of entropy — the mathematical signature of life returning to stillness.
Supplementary Materials
The following supporting information can be downloaded at website of this paper posted on Preprints.org.
Author Contributions
Conceptualization, M.N. and E.d.A.; methodology, M.N. and E.d.A.; software, M.N.; validation, M.N. and E.d.A.; formal analysis, M.N.; investigation, M.N.; resources, E.d.A.; data curation, M.N.; writing—original draft preparation, M.N.; writing—review and editing, M.N. and E.d.A.; visualization, M.N.; supervision, E.d.A.; project administration, E.d.A.; funding acquisition, E.d.A. All authors have read and agreed to the published version of the manuscript.
Funding
Please add: This research received no external funding.
Institutional Review Board Statement
Not applicable
Informed Consent Statement
Not applicable.
Data Availability Statement
Acknowledgments
During the preparation of this manuscript/study, the author(s) used ChatGPT5 OPENAI for the purposes of language adaption. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADD |
Accumulated Days-Degree |
| DNA |
Deoxyribonucleic Acid |
| OCT |
Optical Coherence Tomography |
| PMI |
Postmortem Interval |
| RNA |
Ribonucleic Acid |
| TBS |
Total Body Score |
References
- Henssge C, Madea B. Estimation of the time since death in the early post-mortem period. Forensic Science International. 2004;144(2–3):167–175. [CrossRef]
- Madea B, editor. Estimation of the Time Since Death. 4th ed. Boca Raton: CRC Press; 2023.
- Weisensee KE, Atwell MM. Human decomposition and time since death: Persistent challenges and future directions of postmortem interval estimation in forensic anthropology. American Journal of Biological Anthropology. 2024;186:e70011. [CrossRef]
- Ruiz López JL, Partido Navadijo M. Estimation of the post-mortem interval: a review. Forensic Science International. 2025;369:112412. [CrossRef]
- Henssge, C.; Madea, B. Estimation of the time since death. Forensic Sci. Int. 2007, 165(2–3), 182–184. [CrossRef]
- Madea, B.; Doberentz, E. Commentary on: “An Assessment of the Henssge Method for Forensic Death Time Estimation in the Early Post-Mortem Interval” by Heinrich et al. Int. J. Legal Med. 2025, 139, 1137–1138. [CrossRef]
- Hubig, M.; Muggenthaler, H.; Sinicina, I.; Mall, G. Temperature-Based Forensic Death Time Estimation: The Standard Model in Experimental Test. Leg. Med. 2015, 17(5), 381–387. [CrossRef]
- Cockle, D.L.; Bell, L.S. Human Decomposition and the Reliability of a ‘Universal’ Model for Post-Mortem Interval Estimations. Forensic Sci. Int. 2015, 253, 136.e1–136.e9. [CrossRef]
- López-Lázaro, S. & Castillo-Al onso, C. Accuracy of estimating postmortem interval using the relationship between total body score and accumulated degree-days: a systematic review and meta-analysis. Int. J. Legal Med. 138, 2659–2670 (2024). [CrossRef]
- Forbes, M.N.; Finaughty, D.A.; Miles, K.L.; Gibbon, V.E. Inaccuracy of Accumulated Degree Day Models for Estimating Terrestrial Post-Mortem Intervals in Cape Town, South Africa. Forensic Sci. Int. 2019, 296, 67–73. [CrossRef]
- Moffatt, C.; Simmons, T.; Lynch-Aird, J. An Improved Equation for TBS and ADD: Establishing a Reliable Postmortem Interval Framework for Casework and Experimental Studies. J. Forensic Sci. 2016, 61, S201–S207. [CrossRef]
- Marhoff, S.J.; Fahey, P.; Forbes, S.L.; Green, H. Estimating Post-Mortem Interval Using Accumulated Degree-Days and a Degree of Decomposition Index in Australia: A Validation Study. Aust. J. Forensic Sci. 2016, 48(1), 24–36. [CrossRef]
- Strete, G.; Sălcudean, A.; Cozma, A.A.; Radu, C.C. Current Understanding and Future Research Direction for Estimating the Postmortem Interval: A Systematic Review. Diagnostics 2025, 15(15), 1954. [CrossRef]
- Gelderman, T.; Stigter, E.; Krap, T.; Amendt, J.; Duijst, W. The Time of Death in Dutch Court: Using the Daubert Criteria to Evaluate Methods to Estimate the PMI Used in Court. Leg. Med. 2021, 53, 101970. [CrossRef]
- Clausius, R. Abhandlungen über die Mechanische Wärmetheorie; F. Vieweg und Sohn: Braunschweig, Germany, 1864.
- Zanchini, E.; Beretta, G.P. Recent Progress in the Definition of Thermodynamic Entropy. Entropy 2014, 16(3), 1547–1570. [CrossRef]
- Toussaint, O.; Schneider, E.D. The Thermodynamics and Evolution of Complexity in Biological Systems. Comp. Biochem. Physiol. A Mol. Integr. Physiol. 1998, 120(1), 3–9. [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423.
- Tenreiro Machado, J.A.; Lopes, A.M. Entropy Analysis of Human Death Uncertainty. Nonlinear Dyn. 2021, 104(4), 3897–3911. [CrossRef]
- Uda, S. Application of Information Theory in Systems Biology. Biophys. Rev. 2020, 12(2), 377–384. [CrossRef]
- Gladyshev, G.P. On Thermodynamics, Entropy and Evolution of Biological Systems: What Is Life from a Physical Chemist’s Viewpoint. Entropy 1999, 1(2), 9–20. [CrossRef]
- Aristov, V.V.; Buchelnikov, A.S.; Nechipurenko, Y.D. The Use of the Statistical Entropy in Some New Approaches for the Description of Biosystems. Entropy 2022, 24(2), 172. [CrossRef]
- Bailly, F.; Longo, G. Biological Organization and Anti-Entropy. J. Biol. Syst. 2009, 17(1), 63–96. [CrossRef]
- Chanda, P.; Costa, E.; Hu, J.; Sukumar, S.; Van Hemert, J.; Walia, R. Information Theory in Computational Biology: Where We Stand Today. Entropy 2020, 22(6), 627. [CrossRef]
- Summers, R.L. Entropic Dynamics in a Theoretical Framework for Biosystems. Entropy 2023, 25(3), 528 . [CrossRef]
- Friston, K. A Free Energy Principle for Biological Systems. Entropy 2012, 14(11), 2100–2121. [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum Entropy Production Principle in Physics, Chemistry and Biology. Phys. Rep. 2006, 426(1), 1–45. [CrossRef]
- Mitrokhin, Y. Two Faces of Entropy and Information in Biological Systems. J. Theor. Biol. 2014, 359, 192–198. [CrossRef]
- Brooks, D.R.; Wiley, E.O. Evolution as Entropy: Toward a Unified Theory of Biology; University of Chicago Press: Chicago, IL, USA, 1988.
- Madea, B.; Henssge, C.; Reibe, S.; Tsokos, M.; Kernbach-Wighton, G. Postmortem Changes and Time Since Death. In Handbook of Forensic Medicine; Madea, B., Ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2014; pp. 75–133. [CrossRef]
- Al-Alousi, L.M. A Study of the Shape of the Post-Mortem Cooling Curve in 117 Forensic Cases. Forensic Sci. Int. 2002, 125, 237–244. [CrossRef]
- Sharma, P.; Kabir, C.S. A Simplified Approach to Understanding Body Cooling Behavior and Estimating the Postmortem Interval. Forensic Sci. 2022, 2, 403–416. [CrossRef]
- Laplace, K.; Baccino, E.; Peyron, P.-A. Estimation of the Time Since Death Based on Body Cooling: A Comparative Study of Four Temperature-Based Methods. Int. J. Legal Med. 2021, 135, 2479–2487. [CrossRef]
- Henssge, C. Post-Mortem Body Cooling and Temperature-Based Methods. In Estimation of the Time Since Death; Madea, B., Ed.; CRC Press: Boca Raton, FL, USA, 2023; pp. 77–186.
- Heinrich, F.; Rimkus-Ebeling, F.; Dietz, E.; Raupach, T.; Ondruschka, B.; Anders-Lohner, S. An Assessment of the Henssge Method for Forensic Death Time Estimation in the Early Post-Mortem Interval. Int. J. Legal Med. 2025, 139, 99–111. [CrossRef]
- Donaldson, A.E.; Lamont, I.L. Biochemistry Changes That Occur after Death: Potential Markers for Determining Post-Mortem Interval. PLoS ONE 2013, 8(11), e82011. [CrossRef]
- Zavolskova, M.; Senko, D.; Bukato, O.; Troshin, S.; Stekolshchikova, E.; Kachanovski, M.; Khaitovich, P. Postmortem Stability Analysis of Lipids and Polar Metabolites in Human, Rat, and Mouse Brains. Biomolecules 2025, 15(9), 1288. [CrossRef]
- Locci, E.; Stocchero, M.; Gottardo, R.; Chighine, A.; De-Giorgio, F.; Ferino, G.; Nioi, M.; Demontis, R.; Tagliaro, F.; D’Aloja, E. PMI Estimation through Metabolomics and Potassium Analysis on Animal Vitreous Humour. Int. J. Legal Med. 2023, 137, 887–895. [CrossRef]
- Chighine, A.; Stocchero, M.; Ferino, G.; De-Giorgio, F.; Conte, C.; Nioi, M.; D’Aloja, E.; Locci, E. Metabolomics Investigation of Post-Mortem Human Pericardial Fluid. Int. J. Legal Med. 2023, 137, 1875–1885. [CrossRef]
- Chighine, A.; Stocchero, M.; De-Giorgio, F.; Nioi, M.; D’Aloja, E.; Locci, E. Translating Metabolomic Evidence Gathered from an Animal Model to a Real Human Scenario: The Post-Mortem Interval Issue. Metabolomics 2025, 21, 125. [CrossRef]
- Zelentsova, E.A.; Yanshole, L.V.; Melnikov, A.D.; Kudryavtsev, I.S.; Novoselov, V.P.; Tsentalovich, Y.P. Post-Mortem Changes in Metabolomic Profiles of Human Serum, Aqueous Humor and Vitreous Humor. Metabolomics 2020, 16, 80. [CrossRef]
- AlJuhani, A.A.; Desoky, R.M.; Binshalhoub, A.A.; Alzahrani, M.J.; Alraythi, M.S.; Alzahrani, F.F. Advances in Postmortem Interval Estimation: A Systematic Review of Machine Learning and Metabolomics across Various Tissue Types. Forensic Sci. Med. Pathol. 2025, 1–19.
- Wand, A.J.; Sharp, K.A. Measuring Entropy in Molecular Recognition by Proteins. Annu. Rev. Biophys. 2018, 47, 41–61. [CrossRef]
- Poór, V.S.; Lukács, D.; Nagy, T.; Rácz, E.; Sipos, K. The Rate of RNA Degradation in Human Dental Pulp Reveals Post-Mortem Interval. Int. J. Legal Med. 2016, 130, 615–619. [CrossRef]
- Pittner, S.; Ehrenfellner, B.; Monticelli, F.C.; Zissler, A.; Sänger, A.M.; Stoiber, W.; Steinbacher, P. Postmortem Muscle Protein Degradation in Humans as a Tool for PMI Delimitation. Int. J. Legal Med. 2016, 130, 1547–1555. [CrossRef]
- Pittner, S.; Gotsmy, W.; Zissler, A.; Ehrenfellner, B.; Baumgartner, D.; Schrüfer, A.; Steinbacher, P.; Monticelli, F. Intra- and Intermuscular Variations of Postmortem Protein Degradation for PMI Estimation. Int. J. Legal Med. 2020, 134, 1775–1782. [CrossRef]
- Battistini, A.; Capitanio, D.; Bailo, P.; Moriggi, M.; Tambuzzi, S.; Gelfi, C.; Piccinini, A. Proteomic Analysis by Mass Spectrometry of Postmortem Muscle Protein Degradation for PMI Estimation: A Pilot Study. Forensic Sci. Int. 2023, 349, 111774. [CrossRef]
- Wand, A.J.; Sharp, K.A. Measuring Entropy in Molecular Recognition by Proteins. Annu. Rev. Biophys. 2018, 47, 41–61. [CrossRef]
- Ceciliason, A.-S.; Andersson, M.G.; Nyberg, S.; Sandler, H. Histological Quantification of Decomposed Human Livers: A Potential Aid for Estimation of the Post-Mortem Interval. Int. J. Legal Med. 2021, 135, 253–267. [CrossRef]
- Guerrero-Urbina, C.; Fors, M.; Vásquez, B.; Fonseca, G.; Rodríguez-Guerrero, M. Histological Changes in Lingual Striated Muscle Tissue of Human Cadavers to Estimate the Postmortem Interval. Forensic Sci. Med. Pathol. 2023, 19, 16–23. [CrossRef]
- Nioi, M.; Napoli, P.E.; Demontis, R.; Locci, E.; Fossarello, M.; d’Aloja, E. Postmortem Ocular Findings in the Optical Coherence Tomography Era: A Proof of Concept Study Based on Six Forensic Cases. Diagnostics 2021, 11, 413. [CrossRef]
- Nioi, M.; Napoli, P.E.; Demontis, R.; Chighine, A.; De-Giorgio, F.; Grassi, S.; Scorcia, V.; Fossarello, M.; d’Aloja, E. The Influence of Eyelid Position and Environmental Conditions on the Corneal Changes in Early Postmortem Interval: A Prospective, Multicentric OCT Study. Diagnostics 2022, 12, 2169. [CrossRef]
- Napoli, P.E.; Nioi, M.; Gabiati, L.; Laurenzo, M.; De-Giorgio, F.; Scorcia, V.; Grassi, S.; d’Aloja, E.; Fossarello, M. Repeatability and Reproducibility of Post-Mortem Central Corneal Thickness Measurements Using a Portable Optical Coherence Tomography System in Humans: A Prospective Multicenter Study. Sci. Rep. 2020, 10, 14508. [CrossRef]
- Klein, W.M.; Kunz, T.; Hermans, K.; Bayat, A.R.; Koopmanschap, D.H.J.L.M. The Common Pattern of Postmortem Changes on Whole Body CT Scans. J. Forensic Radiol. Imaging 2016, 4, 47–52. [CrossRef]
- Wagensveld, I.M.; Blokker, B.M.; Wielopolski, P.A.; Renken, N.S.; Krestin, G.P.; Hunink, M.G.; Oosterhuis, J.W.; Weustink, A.C. Total-Body CT and MR Features of Postmortem Change in In-Hospital Deaths. PLoS ONE 2017, 12(9), e0185115. [CrossRef]
- Surat, P.; Meesilpavikkai, K.; Vongpaisarnsin, K.; Nathongchai, R. The Relationship between Postmortem Interval in Advanced Decomposed Bodies and the Settling Ratio of the Liver in Postmortem CT Scan. Forensic Imaging 2023, 33, 200545. [CrossRef]
- Lutz, H.; Vangelatos, A.; Gottel, N.; Osculati, A.; Visona, S.; Finley, S.J.; Gilbert, J.A.; Javan, G.T. Effects of Extended Postmortem Interval on Microbial Communities in Organs of the Human Cadaver. Front. Microbiol. 2020, 11, 569630. [CrossRef]
- Arnaldos, M.I.; García, M.D.; Romera, E.; Presa, J.J.; Luna, A. Estimation of Postmortem Interval in Real Cases Based on Experimentally Obtained Entomological Evidence. Forensic Sci. Int. 2005, 149, 57–65. [CrossRef]
- Franceschetti, L.; Pradelli, J.; Tuccia, F.; Giordani, G.; Cattaneo, C.; Vanin, S. Comparison of Accumulated Degree-Days and Entomological Approaches in Post Mortem Interval Estimation. Insects 2021, 12, 264. [CrossRef]
- Mohr, R.M.; Tomberlin, J.K. Environmental Factors Affecting Early Carcass Attendance by Four Species of Blow Flies (Diptera: Calliphoridae) in Texas. J. Med. Entomol. 2014, 51(3), 702–708. [CrossRef]
- Mohr, R.M.; Tomberlin, J.K. Development and Validation of a New Technique for Estimating a Minimum Postmortem Interval Using Adult Blow Fly (Diptera: Calliphoridae) Carcass Attendance. Int. J. Legal Med. 2015, 129, 851–859. [CrossRef]
- Johnson, H.R.; Trinidad, D.D.; Guzman, S.; Khan, Z.; Parziale, J.V.; DeBruyn, J.M.; Lents, N.H. A Machine Learning Approach for Using the Postmortem Skin Microbiome to Estimate the Postmortem Interval. PLoS ONE 2016, 11(12), e0167370. [CrossRef]
- Zapico, S.C.; Adserias-Garriga, J. Postmortem Interval Estimation: New Approaches by the Analysis of Human Tissues and Microbial Communities’ Changes. Forensic Sci. 2022, 2, 163–174. [CrossRef]
- Metcalf, J.L.; Xu, Z.Z.; Weiss, S.; Lax, S.; Van Treuren, W.; Hyde, E.R.; Knight, R.
- Microbial Community Assembly and Metabolic Function during Mammalian Corpse Decomposition.
- Science 2016, 351(6269), 158–162. [CrossRef]
- Burcham, Z.M.; Belk, A.D.; McGivern, B.B.; Bouslimani, A.; Ghadermazi, P.; Martino, C.; Metcalf, J.L.
- A Conserved Interdomain Microbial Network Underpins Cadaver Decomposition Despite Environmental Variables.
- Nat. Microbiol. 2024, 9(3), 595–613. [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003.
- Pearl, J. The Book of Why: The New Science of Cause and Effect; Basic Books: New York, NY, USA, 2018.
Table 1.
Entropic domains, experimental variables, curve models, and derived formulas for PMI estimation.
Table 1.
Entropic domains, experimental variables, curve models, and derived formulas for PMI estimation.
| Entropic Domain |
Experimental Variables (Study Used) |
Domain-Specific entropy Trend / Shape |
Entropy Growth Formula – E(t) |
PMI from Entropy – t(E) |
Thermal
(Heinrich et al.) |
Core temperature series: Tcore(t), Tenv, ΔT0 = T0 – Tenv; fitted cooling constant k. |
Increasing, exponential decay of temperature gradient. |
|
|
| Biochemical (Chighine et al.) |
Aqueous humour metabolomics: amino acids, nucleotides, and energy intermediates. |
Logarithmic → sigmoidal saturation (E_bio,raw = Σi ln(M0,i/Mt,i)). |
|
|
| Microstructural (Battistini et al.) |
Proteomic degradation kinetics (LC–MS/MS): titin, desmin, vinculin; fitted k_m, t0. |
Sigmoidal increase reflecting collapse of structural order. |
|
|
| Macrostructural (Nioi, et al.) |
Corneal OCT (open vs closed eyes): intensity histogram p_i; Shannon entropy H = –Σ pi log pi. |
Quasi-linear → exponential increase as image contrast decays. |
|
|
| Bio-ecological (Lutz et al.) |
Postmortem microbiome (Lutz dataset): Shannon diversity H′ vs time; fitted rate kb. |
Exponential growth toward equilibrium (diversity increase). |
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).






