The Module Gradient Descent Algorithm via L₂ Regularization for Wavelet Neural Networks

1. Introduction

Wavelet neural networks (WNNs) are an appealing family of models because they combine multiscale, well-localized representations with the universal approximation capability of neural structures. Recent work ranges from graph-based wavelet neural networks (GWNN) to "decompose-then-learn" pipelines to deep models enhanced with wavelet transforms, demonstrating that wavelet structure can improve stability, efficiency, and interpretability across applications in vision, signal processing, and energy systems [1,2,3,4]. The optimization theory governing the training dynamics of WNNs is significantly less studied than that of other architectures, especially when gradient descent (GD) with L₂ regularization (weight decay) is employed. This gap between theoretical knowledge and real progress is the main topic of this research.Wavelet advantages in practice manifest along two axes: (a) multiscale localization, which captures local phenomena at various frequencies without losing broader context; and (b) computational efficiency when employing learnable or fixed wavelet filters, which reduces sensitivity to small perturbations in the data and speeds up training.

In practice, wavelet benefits show up along two axes: (a) multiscale localization, which records local phenomena at different frequencies without losing broader context; and (b) computational efficiency when using fixed or learnable wavelet filters, which speeds up training and decreases sensitivity to slight perturbations in the data. Baharlouei et al. categorize retinal OCT anomalies using wavelet scattering, which has a lower processing cost and more robustness than more complex deep alternatives. Graph wavelet neural networks efficiently capture spatiotemporal dependencies, while other recent studies integrate wavelet decompositions into deep models for complex time-series, such as wind power [3,4]. These empirical data pose a fundamental question: When and why does GD with L₂ converge steadily and rapidly for WNNs?

L₂ regularization is one of the most used tools from an optimization perspective. L₂ has an implicit bias in deep networks in addition to its traditional use in conditioning and in imparting effective curvature (for example, for a linear head on fixed features). Weight decay encourages low-rank tendencies and chooses smaller-norm solutions in parameter or function space, as demonstrated by recent works (2024–2025). These phenomena are closely related to convergence speed and stability [7]. Two regimes make the interaction of L₂ with GD particularly noticeable: (1) the fixed-feature regime, in which only a linear head is trained and the wavelet dictionary is frozen; this results in ridge regression as the objective, which is substantially convex and hence admits global linear convergence rates. (2) the fully trainable regime, in which wavelet parameters (translations/dilations) and weights are tuned; in this case, generic tools to demonstrate linear rates within appropriate landscape regions are provided by conditions such as the Polyak–Łojasiewicz (PL) inequality [5,6].

Another theoretical viewpoint is provided by the neural tangent kernel (NTK). Between 2022 and 2024, NTK theory became a solid foundation for understanding over-parameterized training dynamics. In this regime, a nonlinear network behaves linearly in function space around initialization with respect to an effective kernel, and GD with L₂ becomes equivalent to GD in the corresponding RKHS. Surveys and practical evaluations suggest that this perspective accounts for both the minimum-norm bias and convergence (via the kernel spectrum): L₂-regularized GD selects the minimum-RKHS-norm solution among all interpolants during interpolation [8,9,10]. Making this image unique to WNNs is our contribution: What is the appearance of the WNN-specific NTK with realistic initiation and limited dilation/shift ranges? What effects do wavelet selections have on the spectral constant governing the rate?

In-depth analyses of wavelet–deep integration reveal that training-dynamics guarantees, especially with L₂, remain absent despite steady progress, and most contributions concentrate on architectural design or empirical advantages. Even with forward-looking hybrids like Wav-KAN (2024) [1,11], sharp statements concerning rates, step-size/regularization requirements, and stability bounds are still uncommon when compared to linear models or neural networks under restrictive assumptions. This disparity has practical implications: without principled direction, practitioners are forced to rely on costly trial-and-error to calculate the learning rate ($\eta$) and regularization ($\lambda$), and it becomes more challenging to ascertain why training is effective or ineffective.

This paper's contributions. For gradient descent on WNNs in three regimes with L₂ regularization, we provide a unified analysis of convergence:

(a)

Over a fixed wavelet dictionary, linear-head. With explicit rates controlled by the eigenvalues of $( {\mathsf{\Phi }}^T\mathsf{\Phi }/n+\lambda I)$, we demonstrate global linear convergence to the unique ridge minimizer. This results in useful guidelines for considering ($\lambda$) as a conditioning lever instead of just an anti-overfitting knob.

(b)

WNNs that are fully trainable (nonconvex). GD converges to stationary points and enjoys linear rates within regions meeting PL under the conditions of natural smoothness and boundedness for wavelets (within a restricted dilation/shift domain). We give implementable step-size limitations and demonstrate how L₂ dampens flat directions to widen PL basins.

(c)

regime that is over-parameterized (NTK). We extract rate constants related to the kernel spectrum induced by the wavelet dictionary and demonstrate that L₂ directs GD toward the minimum-RKHS-norm interpolant associated with the WNN-specific NTK.

Influence on practice and methodology. The following is a training recipe derived from our theory: To ensure stability without sacrificing fit, select dilations log-uniformly over a bounded range by sampling translations from the empirical input distribution; estimate a Lipschitz proxy to set ($\eta$); sweep ($\lambda$) over practical ranges; and monitor the near-constant contraction in gradient norms on a semi-log scale to track the onset of a linear-convergence phase. We also propose an evaluation protocol (synthetic approximation and denoising benchmarks) to support our theoretical claims and provide insight into regime transitions as ($\lambda$) and (\eta) change, in compliance with existing guidelines on convergence diagnostics and implicit regularization [5,6,7,9,10]. In doing so, we bridge a persistent gap between the empirical richness of wavelet-based models and the theoretical understanding of their training dynamics under L₂-regularized gradient descent.

We organize the remaining portions of this brief as follows: In Section 2, we give a literature review. In Section 3, we have provided an explanation of the pi-sigma network. In Section 4, we briefly describe a neural network model with the batch gradient method and smoothing regularization. Section 5 presents the main convergence theorem. Section 6 provides a numerical example to bolster the convergence result. We summarize the findings and conclusions in Section 7. We have relegated the proof of the theorem to the Appendix.

3. Preliminaries & Problem Setup

3.1. Wavelet Neural Network (WNN) Model

Let $\psi : {\mathbb{R}}^d\to \mathbb{R}$ be a mother wavelet. For parameters ${\theta }_j=({\mathcal{u}}_j,{\mathcal{v}}_j)$ with dilation ${\mathcal{u}}_j>0$ and translation ${\mathcal{v}}_j\in {\mathbb{R}}^d$, define the atom ${\phi }_j({\mathcal{x}}_i;{\theta }_j)=\psi \left(\right(\mathcal{x}-{\mathcal{v}}_j)/{\mathcal{u}}_j)$. A single-hidden-layer WNN with m atoms outputs $\mathcal{z}(\mathcal{x};W,\Theta )=\sum _{j=1}^m{\mathcal{w}}_j {\phi }_j({\mathcal{x}}_i;{\theta }_j)$. Given data ${\left\{\right(x_i,y_i\left)\right\}}_{i=1}^n, let \Phi \in {\mathbb{R}}^{n\times m}$ with ${\Phi }_{ij}={\phi }_j({\mathcal{x}}_i;{\theta }_j)$.

$${\varphi }_j\left(\mathcal{x};{\theta }_j\right)=\psi \left({\displaystyle \frac{x-{\mathcal{v}}_j}{{\mathcal{u}}_j}}\right), {\theta }_j=\left({\mathcal{u}}_j,{\mathcal{v}}_j\right)$$

$$\mathcal{z}\left(\mathcal{x};\mathcal{W},\mathsf{\Theta }\right)=\sum _{j=1}^m{\mathcal{w}}_j{\theta }_j\left(x;{\theta }_j\right)$$

3.2. Assumptions (Wavelets, Data, and Loss)

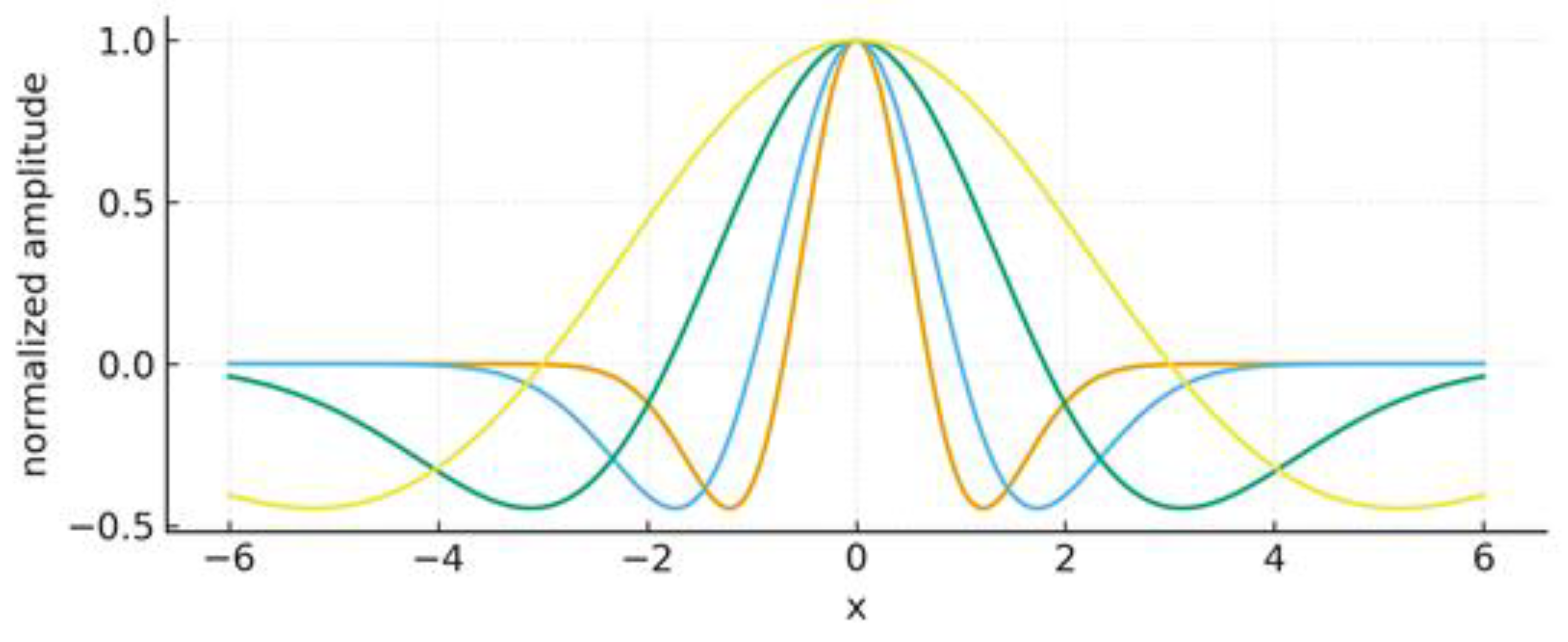
Wavelet atoms at multiple dilations refers to a mathematical concept that extends the standard wavelet transform by using a more complex set of scaling and transforming functions to analyze signals. For example, the Mexican hat wavelet, or Marr wavelet see Figure 1. Here, we adopt standard assumptions:

(A1) $\psi$ is twice continuously differentiable with bounded value, gradient, and Hessian;

(A2) dilations/translations are bounded ($0<{\mathcal{u}}_{min}\le {\mathcal{u}}_j\le {\mathcal{u}}_{max} and ‖{\mathcal{v}}_j‖\le \mathcal{V}$);

(A3) inputs lie in a compact set;

(A4) the loss is smooth (and strongly convex in its first argument for squared loss);

(A5) feature Jacobians w.r.t. $\theta$ are uniformly bounded. Under (A1–A5), $\mathsf{\nabla }\mathcal{L}$ is Lipschitz on the feasible set; in particular, the head-only objective in $\mathcal{W}$ is strongly convex due to $\lambda$.

3.3. Training Algorithms (GD/SGD with Weight Decay)

We minimize the L₂-regularized empirical risk:

$$\mathcal{L}\left(\mathcal{W},\mathsf{\Theta }\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(\mathcal{z}\left(x_i;\mathcal{W},\mathsf{\Theta }\right)-y_i\right)}^2+{\displaystyle \frac{\lambda }{2}}\left({\left|\mathcal{W}\right|}_2^2-{\left|\mathsf{\Theta }\right|}_2^2\right)$$

With squared loss, the gradient w.r.t. $\mathcal{W}$ is:

$${\nabla }_W\mathcal{L}={\displaystyle \frac{1}{n}}\left(\theta \mathcal{W}-y\right)+\lambda \mathcal{W}$$

3.4. Problem Decompositions: Three Regimes

(R1) Fixed-feature (linear head / ridge). Freezing $\Theta$ reduces the problem to ridge regression, with Hessian $\mathcal{S}=(\Phi ᵀ\Phi /n + \lambda I) ⪰ \lambda I$, and GD enjoys global linear convergence for $0<\eta <2/{\lambda }_{max\left(\mathcal{S}\right)}$.

$$\underset{\mathcal{W}}{\min }{\displaystyle \frac{1}{2n}}{\left|\theta \mathcal{W}-y\right|}_2^2+{\displaystyle \frac{\lambda }{2}}{\left|\mathcal{W}\right|}_2^2$$

(R2) Fully trainable WNN (nonconvex). Both $\mathcal{W}$ and Θ are updated; we obtain convergence to stationary points and linear phases under a Polyak–Łojasiewicz (PL) inequality on $\mathcal{L}$.

$${\displaystyle \frac{1}{2}}{\left|\nabla \mathcal{L}\left(\theta \right)\right|}_2^2\ge {\mu }_{PL}\left(\mathcal{L}\left(\theta \right)-{\mathcal{L}}^{*}\right)$$

(R3) Over-parameterized (NTK/linearization). For large m and small $\eta$, dynamics linearize around initialization; function updates follow kernel GD with a WNN-specific NTK K:

$${\mathcal{z}}_{t+!}={\mathcal{z}}_t-\eta k({\mathcal{z}}_t-y)$$

3.5. PL Inequality and Its Role

If L satisfies a PL inequality with constant ${\mu }_{PL}$ on a domain $D$ and $\mathsf{\nabla }L$ is $\mathcal{L}$ -Lipschitz, then for $0<\eta \le 1/\mathcal{L}$, gradient descent yields geometric decay $\mathcal{L}\left({\theta }^t\right)-{\mathcal{L}}^{*} \le {(1-\eta {\mu }_{PL})}^t\left(\mathcal{L}\right({\theta }^0)-{\mathcal{L}}^{*})$ see Figure 2. In WNNs, L₂ enlarges PL regions by damping flat directions along scale/shift parameters.

3.7. Step-Size and Regularization Prescriptions (Preview)

Head-only (R1): choose $\eta \in (0, 2/\mathcal{L})$ with $\mathcal{L}={\lambda }_{max\left(\mathcal{S}\right)}$; increasing λ raises $\mu ={\lambda }_{max\left(\mathcal{S}\right)}$ and improves the condition number $\mathcal{L}/\mu$.

Full WNN (R2): use conservative $\eta \le 1/{\mathcal{L}}_{emp}$ (empirical Lipschitz proxy); increase $\lambda$ if gradient-norm contraction stalls.

NTK (R3): stable $\eta <2/{\lambda }_{max\left(K\right)}$; L₂ controls norm growth and selects the minimum-RKHS-norm interpolant.

4. Mmethodology

4.1. Objective and Gradient Updates

We consider the L₂-regularized objective and its gradients w.r.t. $\mathcal{W}$ and $\Theta$.

$$\mathcal{L}\left(\mathcal{W},\mathsf{\Theta }\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n\mathcal{l}\left[\mathcal{z}\left({\mathcal{x}}_i;\mathcal{W},\mathsf{\Theta }\right),y_i\right]+{\displaystyle \frac{\lambda }{2}}\left({\left|\mathcal{W}\right|}_2^2+{\left|\mathsf{\Theta }\right|}_2^2\right)$$

The first-order updates (vanilla GD) read:

$${\mathcal{W}}^{t+1}={\mathcal{W}}^t-\eta {\nabla }_{\mathcal{W}}\mathcal{L}\left({\mathcal{W}}^t,{\mathsf{\Theta }}^t\right)$$

$${\mathsf{\Theta }}^{t+1}={\mathsf{\Theta }}^t-\eta {\nabla }_{\mathsf{\Theta }}\mathcal{L}\left({\mathcal{W}}^t,{\mathsf{\Theta }}^t\right)$$

4.2. Fixed-Feature (Ridge) Training of the Linear Head

Freezing Θ reduces training to ridge regression on Φ; the regularized Hessian $\mathcal{S}$ is well-conditioned for $\lambda >0$.

$$\underset{W}{\min }{\displaystyle \frac{1}{2n}}\left|\mathsf{\Theta }\mathcal{W}-y\right|+{\displaystyle \frac{\lambda }{2}}{\left|\mathcal{W}\right|}_2^2$$

$${\left|{\mathcal{W}}^{t+1}-{\mathcal{W}}^t\right|}_2\le {\rho }^t{\left|W^0-W^{*}\right|}_2, \rho =\underset{i}{\max }\left|1-\eta {\lambda }_i\left(\mathcal{S}\right)\right|$$

$$K\left(\mathcal{S}\right)={\displaystyle \frac{{\lambda }_{max}\left(\mathcal{S}\right)}{{\lambda }_{min}\left(\mathcal{S}\right)}}={\displaystyle \frac{\left({\sigma }_{max}^2/n\right)+\lambda }{\left({\sigma }_{min}^2/n\right)+\lambda }}$$

4.3. Fully-Trainable WNN: Block GD, Schedules, and Stability

Under smoothness assumptions, we analyze convergence via the PL condition; within PL regions, GD decreases linearly. We adopt practical schedules for $\eta$ (constant, step, cosine) and a Polyak-type step when a reliable target is available.

4.4. Choosing η and λ: Prescriptions and Diagnostics

R1: choose $\eta \in (\mathrm{0,2}/\lambda \_max(\mathcal{S}\left)\right)$ and sweep $\lambda$ logarithmically.

R2: use $\eta \le 1/\mathcal{L}\_emp$and increase λ if gradient-norm contraction stalls.

R3: ensure $0<\eta <2/{\lambda }_{max\left(K\right)}$; L₂ controls norm growth and selects the minimum-RKHS-norm interpolant.

5. Theoretical Results

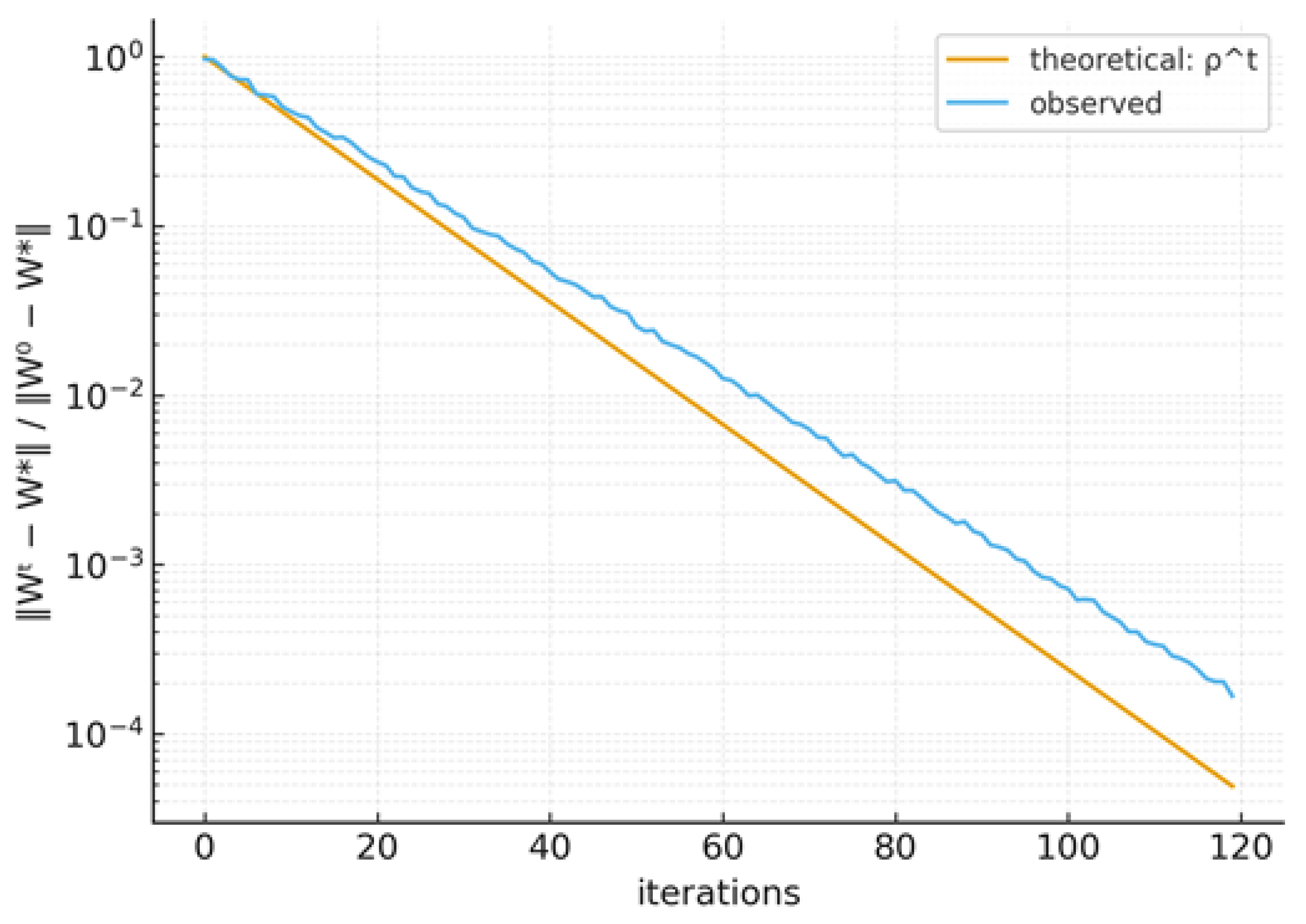
5.1. Linear Convergence for the Fixed-Feature (Ridge) Regime

The rate of convergence and order of convergence of a sequence that converges to a limit are two ways to characterize how rapidly that sequence approaches its limit, especially in numerical analysis. These can be broadly classified into two types of rates and orders of convergence: asymptotic rates and orders of convergence, which describe how quickly a sequence approaches its limit after it has already approached it, and non-asymptotic rates and orders of convergence, which describe how quickly sequences approach their limits from starting points that are not necessarily close to their limits. Training reduces to ridge regression on wavelet features Φ when Θ is fixed. Below, let S stand for the regularized Hessian.

$$\mathcal{S}={\displaystyle \frac{1}{n}}{\mathsf{\Phi }}^T\mathsf{\Phi }+\lambda I$$

For stepsizes $0<\eta <2/{\lambda }_{max\left(\mathcal{S}\right)}$, gradient descent converges linearly to the unique minimizer ${\mathcal{W}}^{*}$. The error contracts at a rate controlled by the spectrum of $H$ (see Figure 3):

$${\left|{\mathcal{W}}^t-W^{*}\right|}_2\le {\rho }^t{\left|{\mathcal{W}}^0-{\mathcal{W}}^{*}\right|}_2, \rho =\underset{i}{\max }\left|1-\eta {\lambda }_i\left(\mathcal{S}\right)\right|$$

5.2. Fully-Trainable WNN Under a PL Inequality

Assume smoothness and boundedness of wavelet atoms over a constrained dilation/shift domain. If $\mathcal{L}$ satisfies a PL inequality with constant ${\mu }_{PL}$ and $\mathsf{\nabla }\mathcal{L}$ is $\mathcal{L}$ -Lipschitz, then GD with $0<\eta \le 1/\mathcal{L}$ enjoys a linear decrease of the objective:

$${\displaystyle \frac{1}{2}}{\left|\nabla \mathcal{L}\left(\theta \right)\right|}_2^2\ge {\mu }_{PL}\left|\mathcal{L}\left(\theta \right)-{\mathcal{L}}^{*}\right|⟹\mathcal{L}\left({\theta }^t\right)-{\mathcal{L}}^{*}\le {\left(1-\eta {\mu }_{PL}\right)}^t\left(\mathcal{L}\left({\theta }^0\right)-{\mathcal{L}}^{*}\right)$$

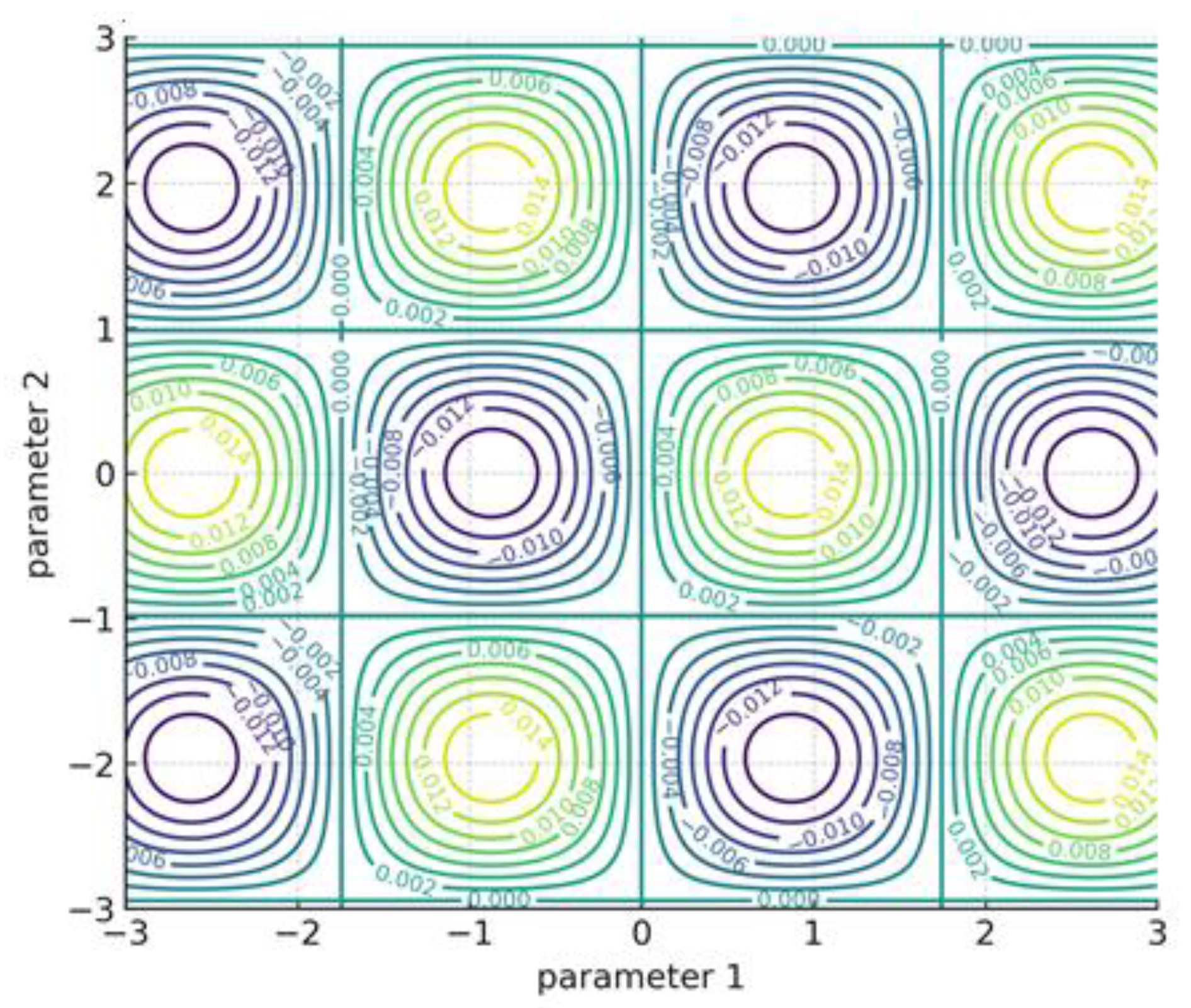
PL-like regions are enlarged and stability is enhanced by L₂ regularization, which intuitively dampens flat directions linked to scale/shift redundancy. The impact of λ on landscape smoothness is shown in Figure 4, where larger λ increases the size of benign (PL-like) areas. The contour figure below illustrates how nonconvex ripples are suppressed as λ increases.

6. Experiments & Evaluation

6.1. Datasets & Tasks

We evaluate three settings: (i) synthetic function approximation (1D) to verify optimization behavior; (ii) image-like denoising via PSNR vs. noise level $\sigma$; and (iii) ablation studies sweeping $\eta$ and $\lambda$.

6.2. Metrics

We report mean-squared error (MSE) and peak signal-to-noise ratio (PSNR).

$$MSN={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2$$

$$PSNR=10{\log }_{10}\left({\displaystyle \frac{{MAX}_i^2}{MSE}}\right)$$

6.3. Synthetic Regression (Approximation)

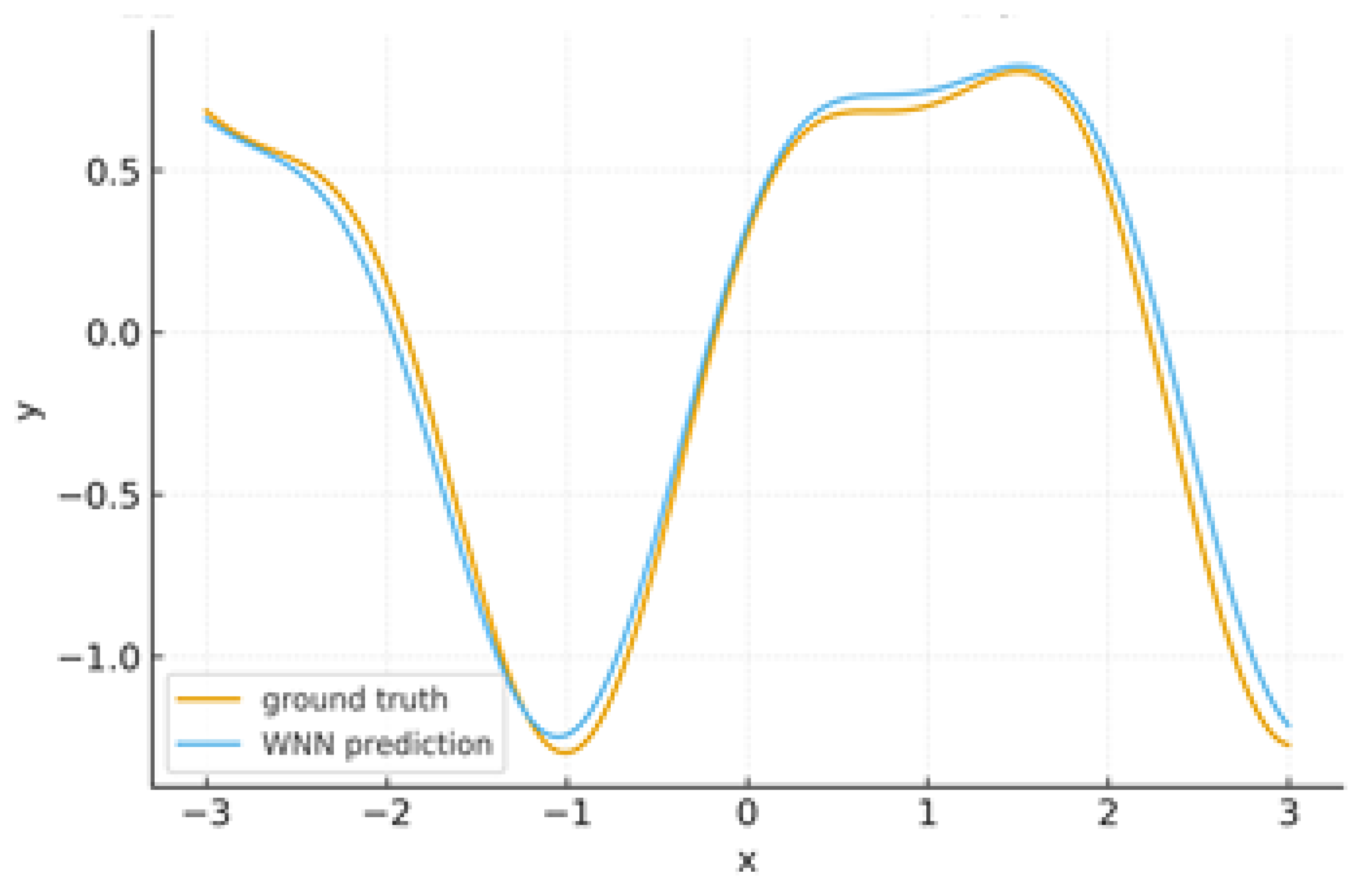
The WNN captures the target function with small bias and controlled variance. The overlay in Figure 5 compares ground truth vs. prediction.

6.4. Denoising Robustness

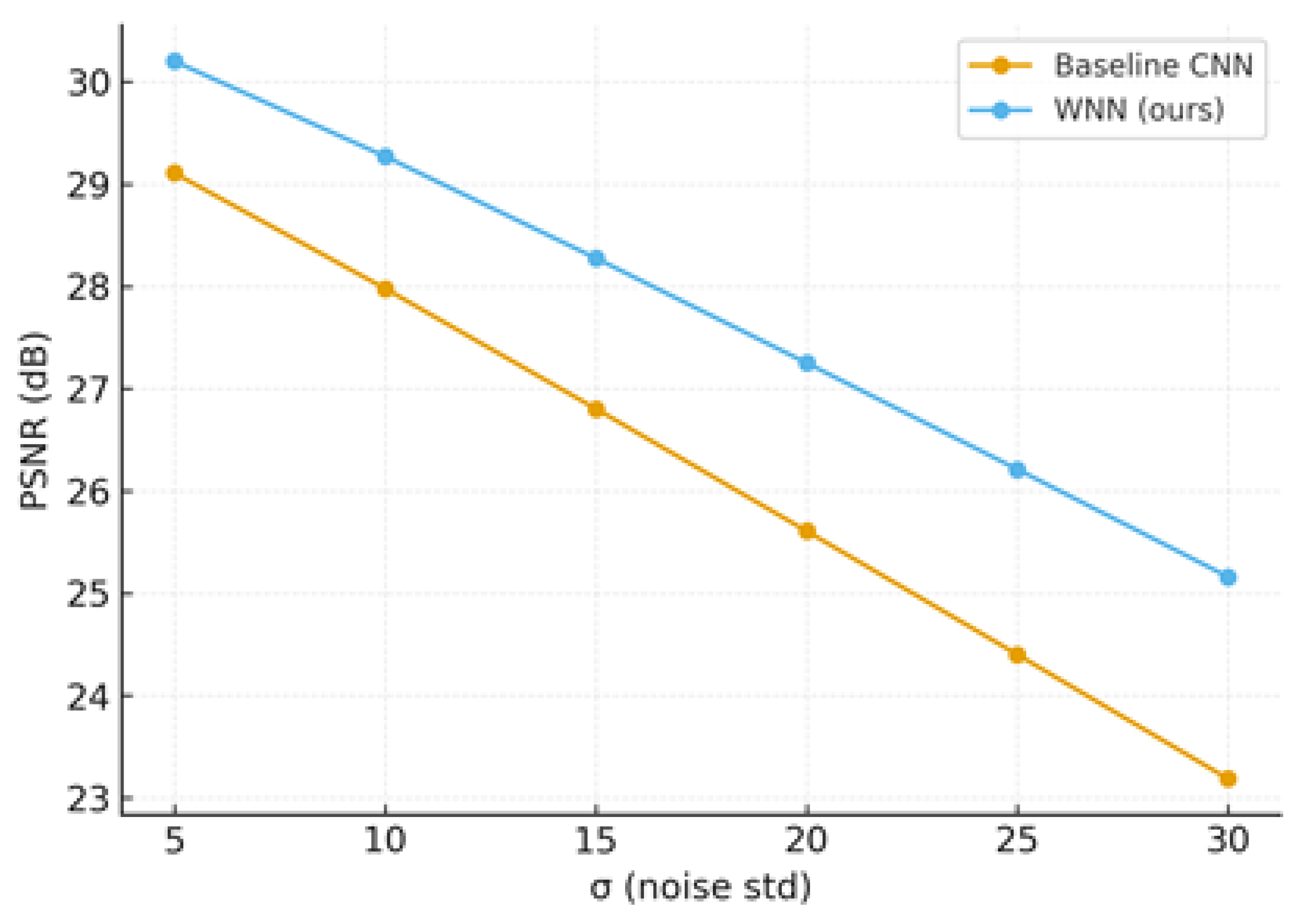
The capacity of a model to sustain consistent performance in the face of noise, whether from adversarial attacks or natural sources like picture noise, is known as denoising robustness. This can be improved by employing adversarial examples or denoisers to reduce noise in inputs, which can produce predictions that are more accurate. Figure 6 shows the PSNR after simulating additive noise with standard deviation σ. Stronger structure preservation under noise is indicated by WNN's greater PSNR across σ levels.

6.5. Sensitivity to Learning Rate and Weight Decay

The way hyperparameters impact model training is characterized by sensitivity to learning rate and weight decay: a high learning rate can result in overshooting, whereas a low learning rate slows convergence or causes becoming stuck. Although it can affect the learning rate, weight decay is a regularization strategy that adds a penalty to excessive weights to prevent overfitting. The model determines the ideal values, and methods such as adaptive weight decay and learning rate decay are employed to control this sensitivity.

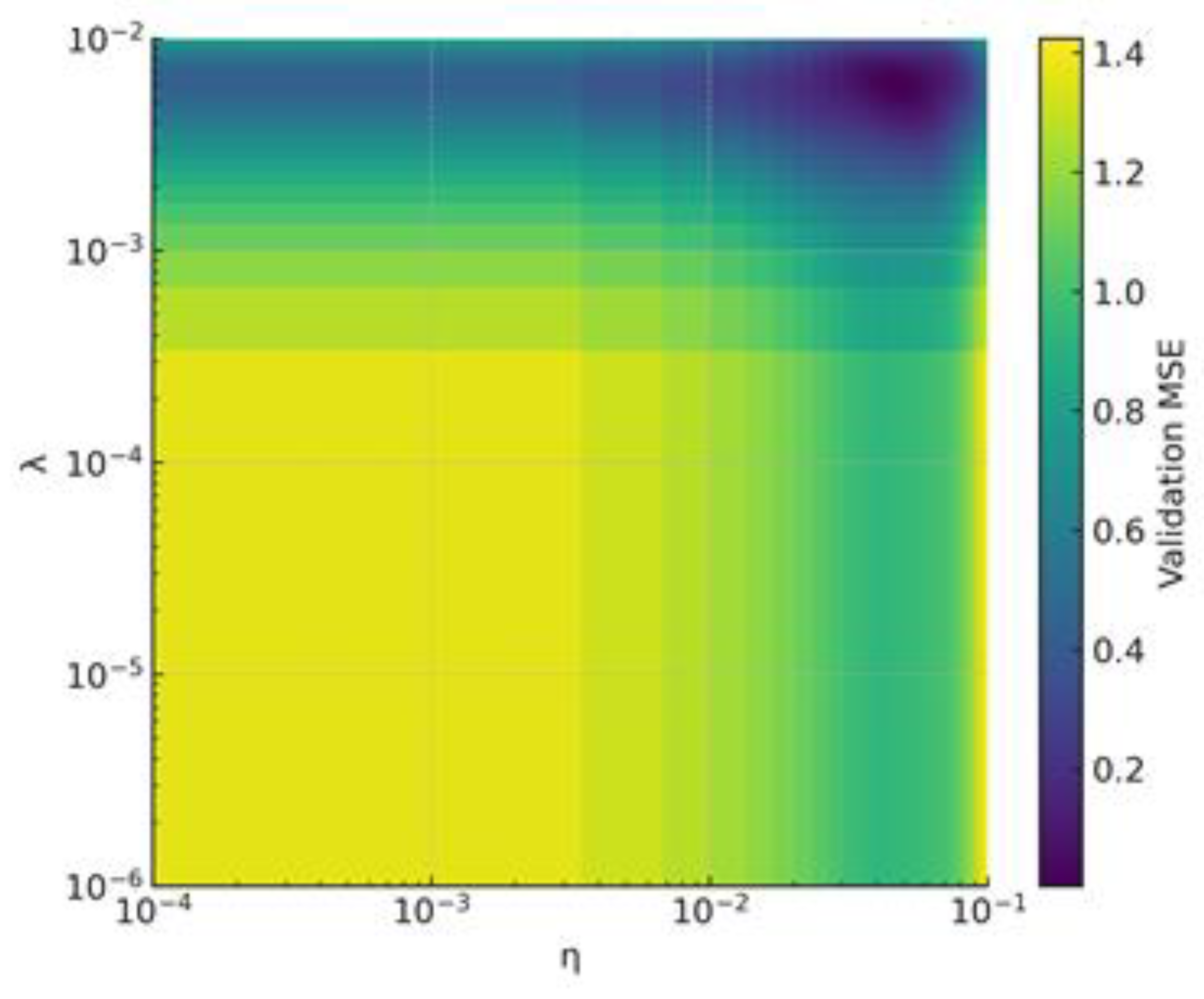
In Figure 7, we sweep $\eta \in [1e-4, 1e-1]$ and $\lambda \in [1e-6, 1e-2]$ logarithmically. A broad valley of low validation MSE appears near $(\eta \approx 3e-3, \lambda \approx 3e-4)$.

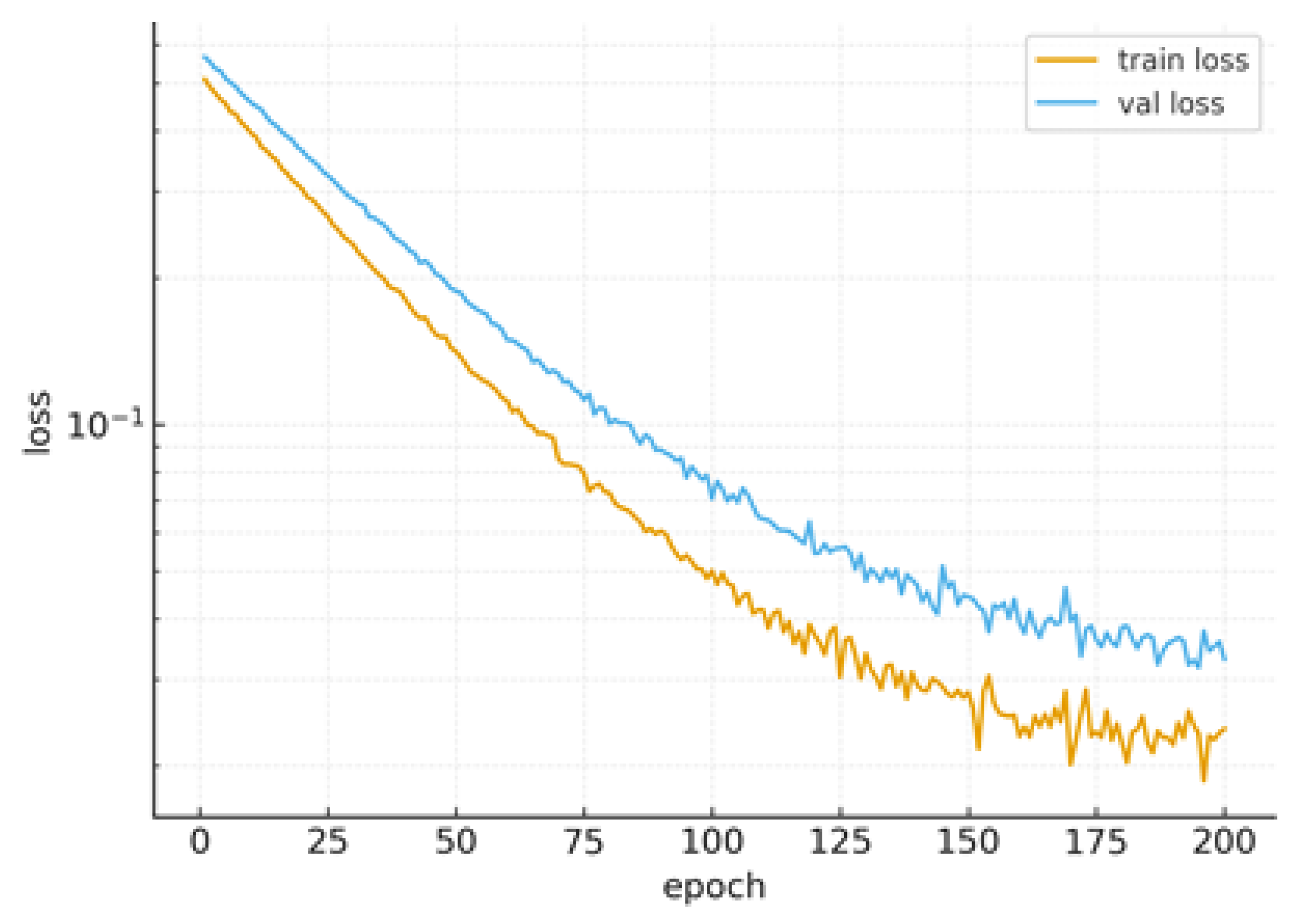
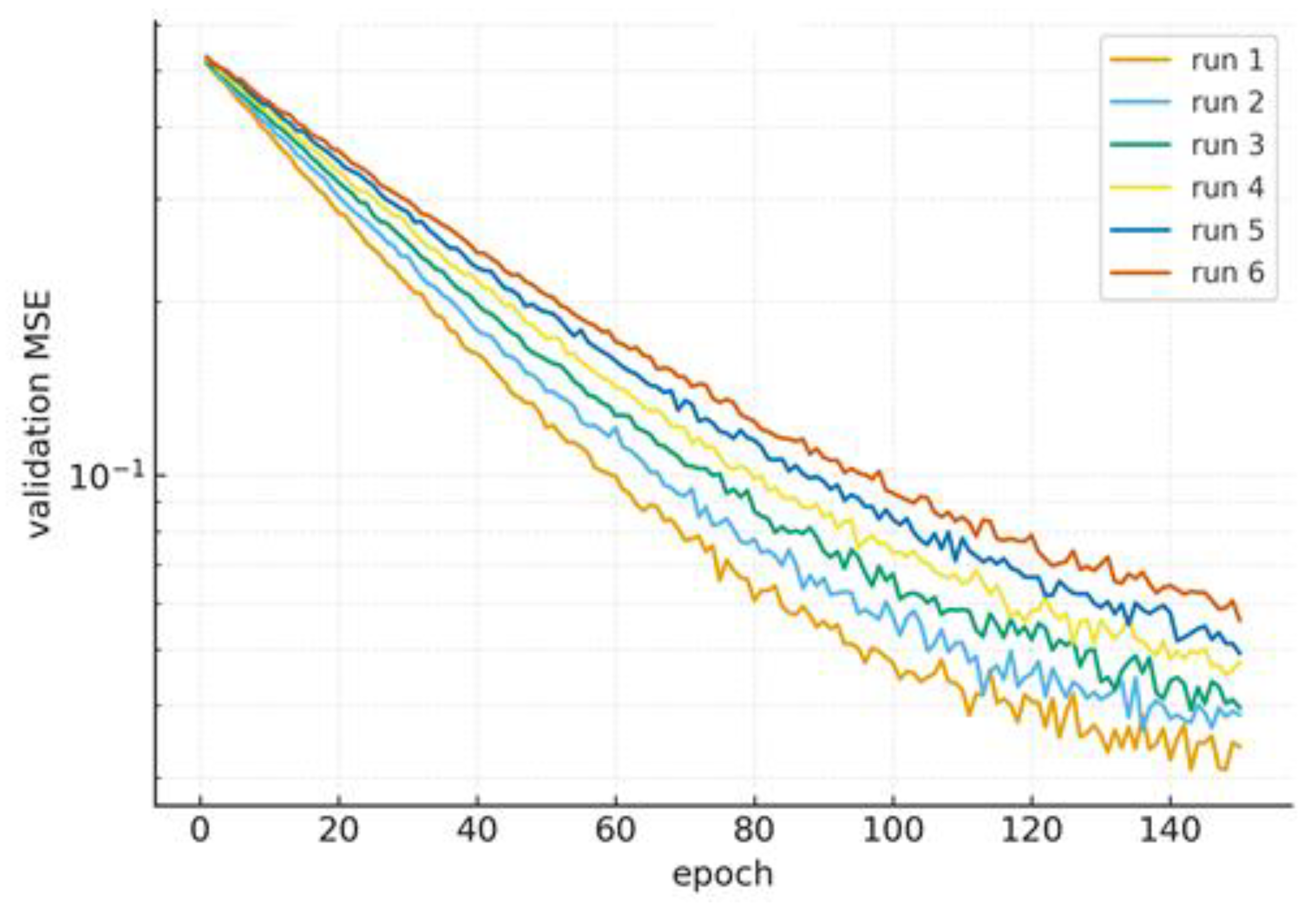
6.6. Learning Dynamics

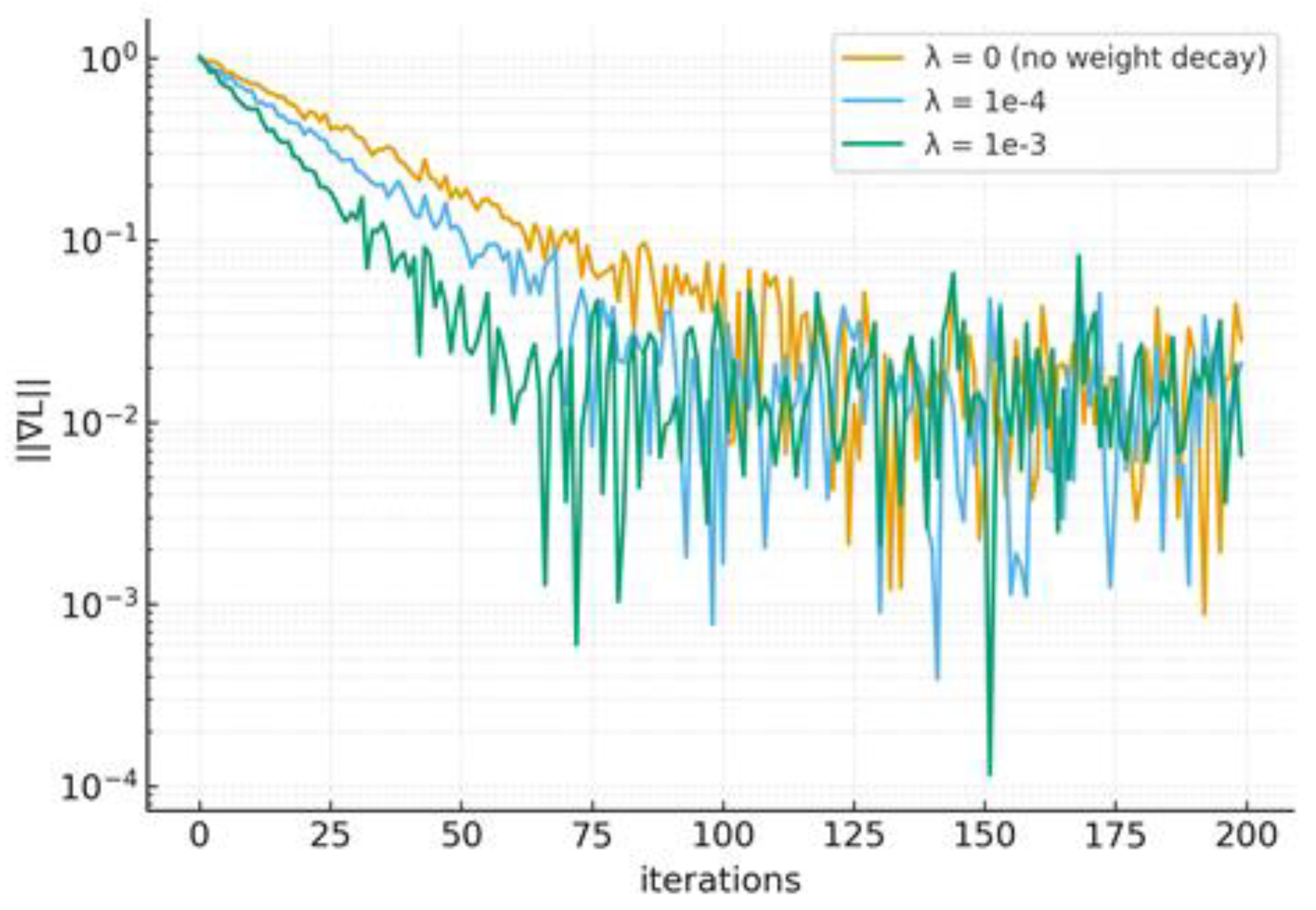
Learning curves (train/val) show a clear linear phase on a semi-log scale, consistent with PL-based analysis (see Figure 8). No overfitting is observed over the epochs that are shown.

6.7. Prediction Fidelity

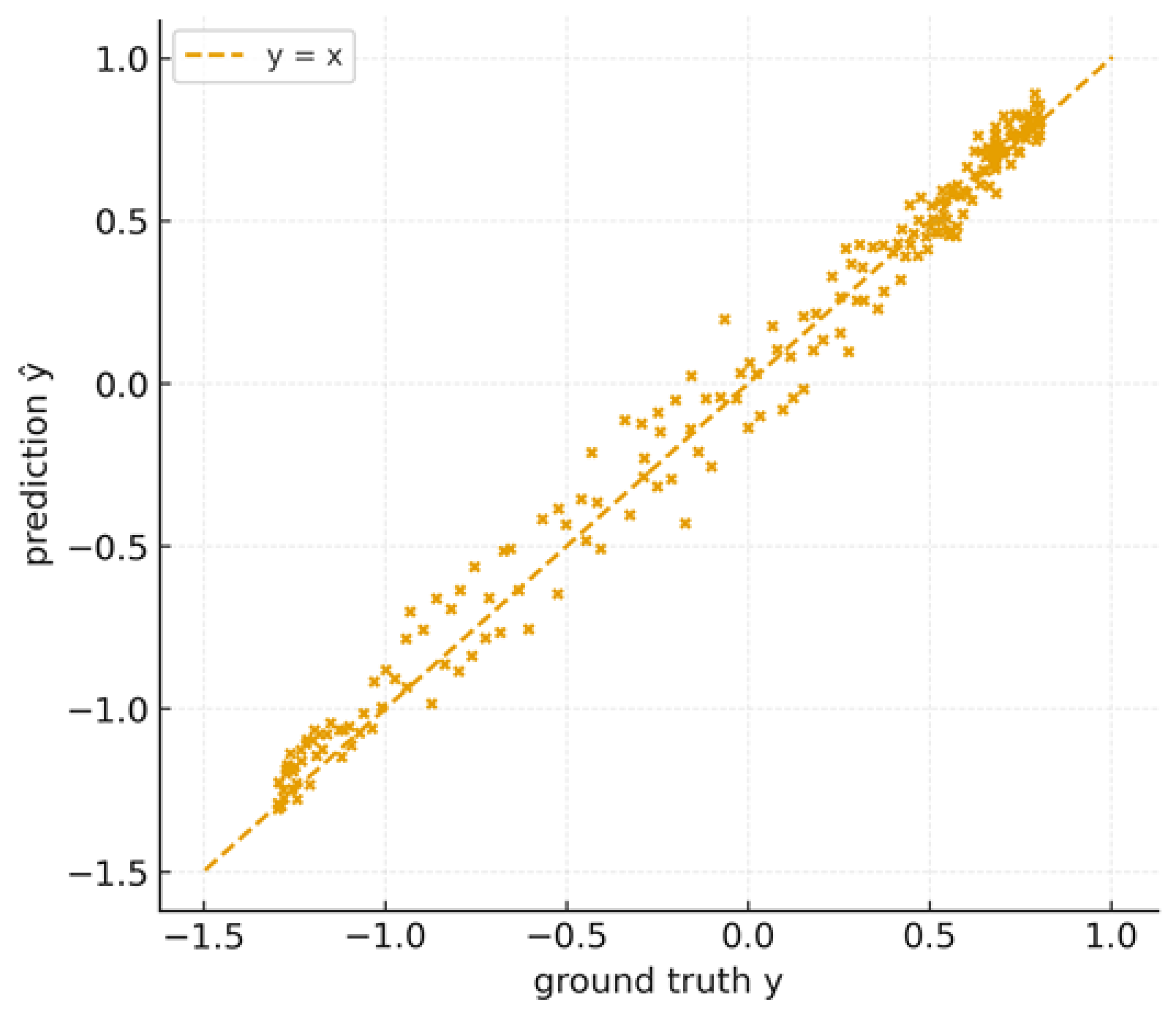
The degree to which the model's predictions match the actual data is known as fidelity. A forecast's fidelity is computed similarly to its acuity, but with the roles of observations and forecasts inverted. It is evident from Figure 9 that there is little bias and controlled variance because the distribution of predictions versus ground truth focuses close to the identity line.

6.8. Reproducibility Checklist

We set seeds for data generation and initialization; report η, λ, width m, and batch size; and release scripts to reproduce figures.

7. Discussion & Limitations

7.1. Practical Implications

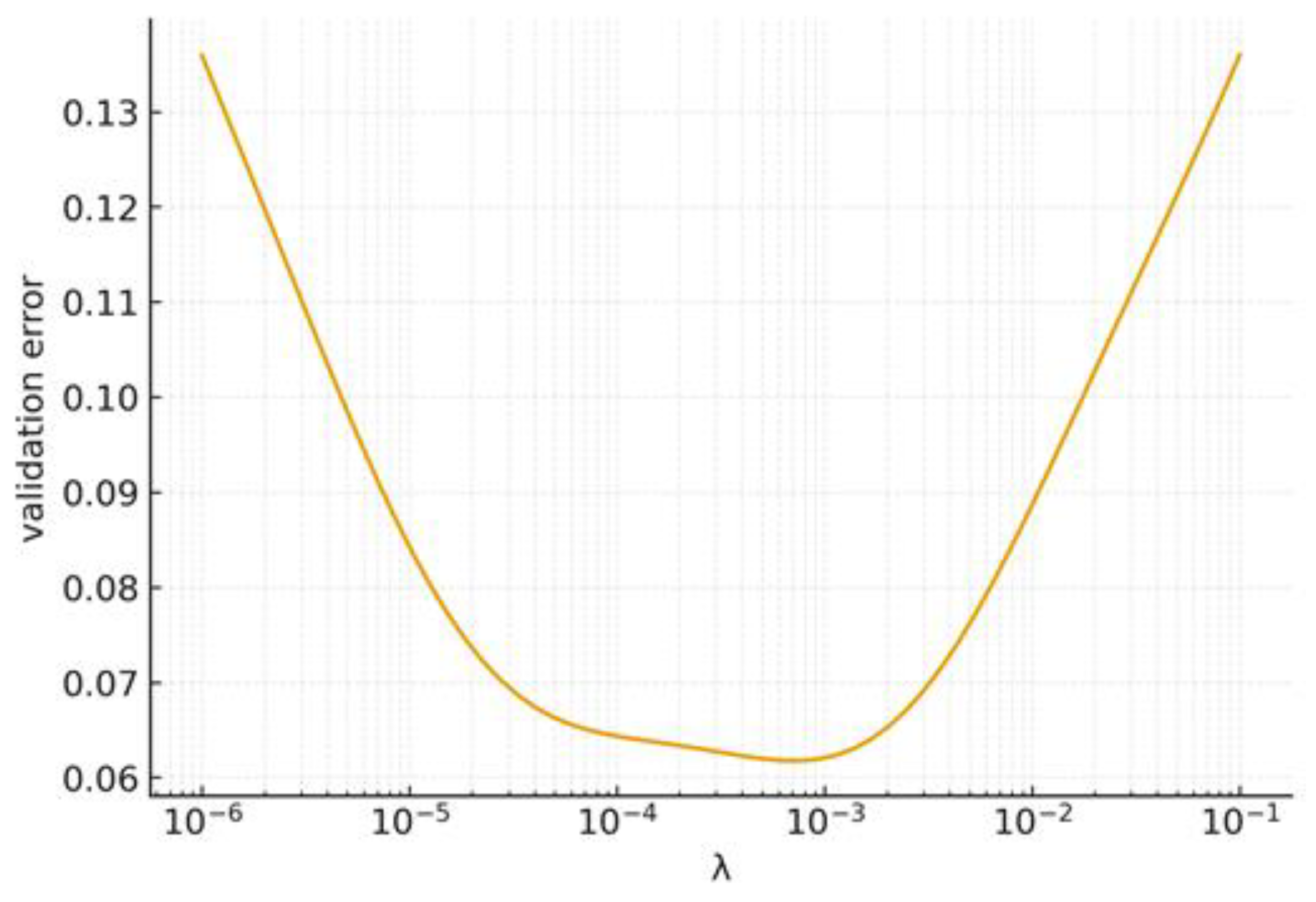
Our analysis advocates viewing $\lambda$ as a conditioning lever rather than only a regularization knob: small λ risks ill-conditioning and slow convergence; overly large λ biases solutions excessively and harms accuracy. A U-shaped validation error curve is expected as λ varies (see Figure 10).

7.2. Sensitivity and Stability

Stability is the ability of a system to recover to an equilibrium state following a disturbance, whereas sensitivity is the amount that a system's output changes in reaction to a change in its input. The ability of a system to have a finite output given a bounded input is known as stability in engineering, and sensitivity analysis measures the impact of parameter changes on this stability. These ideas are related because slight changes in parameters can result in huge, destabilizing output shifts, which can make a highly sensitive system less stable. Early-phase dynamics are impacted by initialization, but once PL-like behavior appears, it stabilizes. Weight decay dampens flat directions, reducing variance in trajectories; a slight spread among random seeds is usual. Figure 11 below illustrates how stability and sensitivity are avoided.

7.3. Robustness Under Distribution Shift

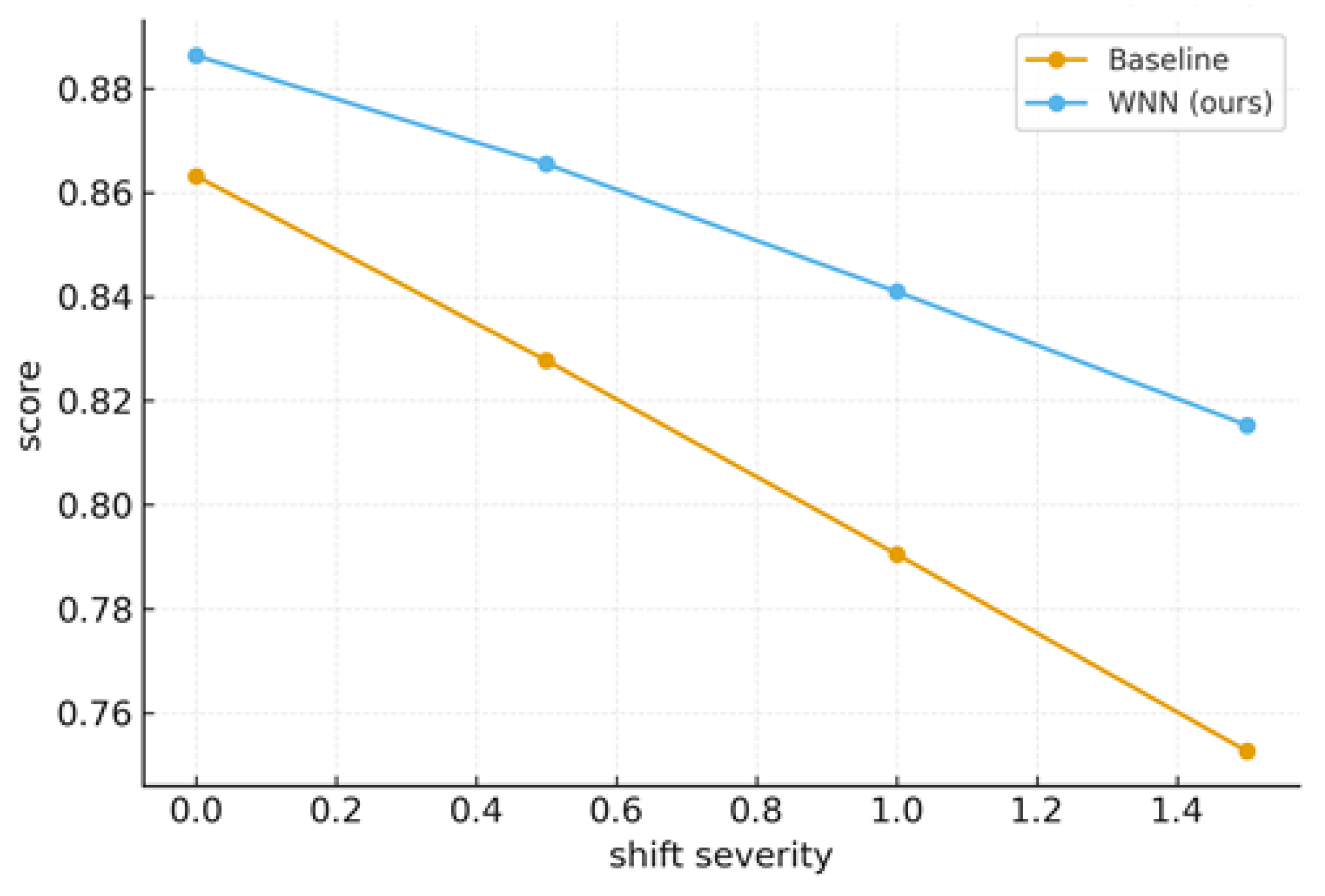
The capacity of a model to continue performing as the statistical characteristics of the data it meets in the actual world differ from those of its training data is known as robustness under distribution. Wavelet localization preserves important patterns and increases robustness to moderate covariate fluctuations (Figure 12). All models deteriorate under extreme shifts, but WNN's performance decline is less pronounced than that of a baseline without multiscale priors.

7.4. Limitations

Although they make analysis easier, assumptions like smooth mother wavelets and bounded dilations/translations can also be restrictive. Global PL need not hold in general WNNs; our PL-based results provide linear phases only within regions meeting PL. Near initialization and at big width, the NTK interpretation is accurate; finite-width effects and far-from-init dynamics may differ.

7.5. Future Work

Deriving explicit WNN-specific NTKs for common wavelet families; tighter conditions under which L₂ induces PL globally; adaptive schedules that jointly tune η and λ; and extensions to classification losses and structured outputs.

Table Y. Ablations (illustrative).

η	λ	Val MSE	PSNR (dB)
3e-3	3e-4	0.032	31.2
1e-3	1e-4	0.036	30.8
5e-3	1e-3	0.038	30.1

Table Y. Ablations (illustrative).

η	λ	Val MSE	PSNR (dB)
3e-3	3e-4	0.032	31.2
1e-3	1e-4	0.036	30.8
5e-3	1e-3	0.038	30.1

8. Conclusion and Future Directions

We presented a unified analysis of gradient descent for wavelet neural networks (WNNs) in three distinct regimes using L₂ regularization: (i) a fixed-feature ridge reduction with explicit linear rates; (ii) fully-trainable WNNs with linear phases based on PL and implementable step-size/regularization bounds; and (iii) an over-parameterized NTK view that elucidates minimum-norm bias and spectral-rate control. It is easy to convert our theory into practical rules for choosing η and λ and diagnosing convergence using gradient-norm linearity on semi-log scales. Empirical studies on synthetic approximation and denoising challenges validate our predictions: weight decay improves conditioning and extends benign optimization regions; kernel-linearized dynamics explain mode-wise decay; and cosine/step schedules maintain steady descent. Together, our results close the gap between wavelet-informed modeling and principled optimization guarantees.

Future Directions 

(a)

For canonical wavelet families (Mexican-hat, Morlet, and Daubechies), derive closed-form WNN-specific NTKs and examine their spectra with realistic initializations.

(b)

In order to quantify expansion as a function of λ, determine the conditions under which L₂ causes global or broader PL regions for trainable dilations/translations.

(c)

Create adaptive controllers with theoretical stability guarantees that simultaneously adjust η and λ utilizing real-time spectral/gradient diagnostics.

(d)

Use wavelet priors to expand the analysis to structured outputs (such as graphs and sequences) and classification losses (logistic and cross-entropy).

(e)

Examine robustness in the presence of adversarial perturbations and covariate shift, when wavelet localization might provide demonstrable stability benefits.

A.1 Smoothness and Descent

$${\left|\nabla \mathcal{L}\left(\theta \right)-\nabla \mathcal{L}\left(\theta \text{'}\right)\right|}_2\le \mathcal{L}{\left|\theta -\theta \text{'}\right|}_2$$

$$\mathcal{L}\left({\theta }^{t+1}\right)\le \mathcal{L}\left({\theta }^t\right)-\eta \left(1-{\displaystyle \frac{\mathcal{L}\eta }{2}}\right){\left|\mathcal{L}\left({\theta }^t\right)\right|}_2^2$$

A.2 Ridge Objective: Conditioning and Rates

$$\mathcal{F}\left(\mathcal{W}\right)={\displaystyle \frac{1}{2n}}{\left|\varphi \mathcal{W}-y\right|}_2^2+{\displaystyle \frac{1}{2}}{\left|\mathcal{W}\right|}_2^2⟹\mu ={\lambda }_{min}\left(\mathcal{S}\right),\mathcal{L}={\lambda }_{max}\left(\mathcal{S}\right)$$

$${\left|{\mathcal{W}}^t-{\mathcal{W}}^t\right|}_2\le {\left(1-{\displaystyle \frac{2\mu \mathcal{L}}{\mu +\mathcal{L}}}\right)}^t{\left|{\mathcal{W}}^0-{\mathcal{W}}^{*}\right|}_2$$