Second Order L1 Schemes for Fractional Differential Equations

1. Introduction

Fractional differentiation extends integer-order differentiation and integration to arbitrary orders. There is a growing interest in developing numerical methods for fractional differential equations due to their wide applicability in various branches of science [2,3,4]. Finite difference schemes provide a powerful approach for the numerical solution of fractional differential equations and the study of their properties. The Caputo fractional derivative of order $\alpha$, where $0<\alpha <1$, is defined as

$$f^{\left(\alpha \right)}\left(x\right)=D^{\alpha }f\left(x\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}{\int }_0^x{\displaystyle \frac{f^{\prime }\left(\xi \right)}{{(x-\xi )}^{\alpha }}}d\xi .$$

(1)

The power function $x^p$ and the functions $e^x$, $sinx$, and $cosx$ have fractional derivatives.

$$D^{\alpha }{x}^p={\displaystyle \frac{\mathsf{\Gamma }(p+1)}{\mathsf{\Gamma }(p+1-\alpha )}}{x}^{p-\alpha },D^{\alpha }{e}^x=x^{1-\alpha }{E}_{1,2-\alpha }\left(x\right),$$

$$D^{\alpha }sinx=x^{1-\alpha }{E}_{2,2-\alpha }(-x^2),D^{\alpha }cosx=-x^{2-\alpha }{E}_{2,3-\alpha }(-x^2),$$

where $p>0$ and $E_{\alpha ,\beta }\left(x\right)$ is the Mittag-Leffler function

$$E_{\alpha ,\beta }\left(x\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{x^k}{\mathsf{\Gamma }(\alpha x+\beta )}}.$$

The lower limit of fractional differentiation may be an arbitrary number. The kernel of the fractional derivative has a singularity of order $\alpha$. A direct application of numerical integration methods for discretizations of the fractional derivative leads to reduced accuracy and a lower order of approximation. Therefore, the construction of high-order approximations of fractional derivatives requires additional considerations.

Fractional calculus is a rapidly developing scientific field that extends and generalizes differential calculus. Other definitions of fractional derivatives and integrals include the Riemann–Liouville and Grünwald–Letnikov derivatives, introduced in the 19^th century. The Riemann–Liouville derivative is the first known generalization of integer-order derivatives and is a widely used definition in fractional calculus. The three definitions of the fractional derivative are directly related and share similar properties. The main difference between fractional and integer-order derivatives lies in their nonlocal properties. Fractional derivatives have a strong dependence on the previous values of the function according to the power law, or exhibit memory-influenced dynamics. The definition of integer-order derivatives depends only on the local behavior of the function in a small neighborhood around the point of differentiation. The definitions of integer-order derivatives imply an exponential dependence on previous values, and this effect may be negligible or minimal. The choice of a particular definition of the fractional derivative and its advantages depend on the problem under consideration. The Caputo fractional derivative, defined in 1967, has the advantage that when solving differential equations, it allows the use of initial conditions expressed in terms of integer-order derivatives, which often have direct physical meaning. In addition to the most commonly used definitions of the fractional derivative, such as those of Riemann–Liouville and Caputo, there exist other important and widely applicable definitions in the theory of fractional calculus. Among them are the fractional derivatives of Weyl, Hadamard, Marchaud, and Riesz. The recently introduced fractional derivatives, the Caputo–Fabrizio derivative (2015), the Atangana–Baleanu–Caputo (ABC) fractional derivative (2016), have also proven their significance in modeling various time-dependent complex processes. These derivatives, provide improved accuracy in describing memory effects in physical, biological, and engineering phenomena [5,6,7].

Fractional Differential Equations (FDEs) are a generalization of ordinary and partial differential equations and provide powerful tools for modeling complex systems with memory, hereditary properties, or anomalous diffusion. Due to the complexity of fractional differential equations and their corresponding models, numerical methods are the main and, in many cases, the only approach for solving them. Numerical methods could be applied to a much wider class of fractional differential equations compared to analytical methods. Many of the properties and approaches used for solving ordinary and partial differential equations are also applicable to the corresponding fractional differential equations. The development of numerical methods is based on the growing number and diversity of the considered models, as well as on the improvement of the technical means for their solution. The main types of approaches for solving differential and fractional differential equations include the Finite Difference Methods [8,9,10,11], Spectral Methods [12,13,14,15], Finite Element Methods [16,17], and Predictor–Corrector Methods [18,19].

Finite difference schemes for the numerical solution of fractional differential equations are widely used because of their simplicity, flexibility, and consistency of the numerical results. The difference schemes for fractional differential equations use discretizations of the fractional derivative on uniform or nonuniform grids over the interval of fractional differentiation. These approximations involve the previous values of the function, which leads to a more complex analysis of the difference schemes and increases the computational time required for their solution. Constructions of fast difference schemes for fractional differential equations that achieve optimal computational complexity using sum of exponentials approximation of the kernel function are presented in [20,21,22,23]. To improve the efficiency of difference schemes and achieve high computational accuracy, high-order approximations of the fractional derivative are used. The development of high-order approximations of the fractional derivative and the investigation of their properties are important problems in the construction and analysis of difference schemes for fractional differential equations. Constructions of second-order approximations are discussed in [24,25,26,27,28]. High-order approximations of the fractional derivative are constructed in [29,30,31,32,33,34].

The Grünwald–Letnikov difference approximation and the L1 approximation are important and widely used discretizations of fractional derivatives[35,36,37,38,39]. The Grünwald–Letnikov approximation has first-order accuracy and a generating function ${(1-x)}^{\alpha }$. The L1 approximation has an accuracy of order $2-\alpha$ and a generating function

$$G\left(x\right)={\displaystyle \frac{{(1-x)}^2{\mathrm{Li}}_{\alpha -1}\left(x\right)}{x}},$$

where ${\mathrm{Li}}_{\nu }\left(x\right)$ is the polylogarithm function. The generating function of an approximation of the fractional derivative satisfies

$$G\left(1\right)=0,\underset{x\to 1^{-}}{lim}G\left(x\right){(1-x)}^{-\alpha }=1.$$

The present paper continues the study in [1] and focuses on the properties of the L1 approximation and on methods for extending it to higher-order approximations while preserving the properties of the weights. Consider fractional differentiation on the interval $[0,X]$ and a uniform net with a step size $h=X/N$, where N is a positive integer. Denote $f_n=f\left(x_n\right)=f\left(nh\right)$. L1 approximation of the Caputo derivative has an order $2-\alpha$ and is defined as:

$${\mathcal{L}}_{n}f={\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\sigma }_k^{\left(\alpha \right)}{f}_{n-k}=f_n^{\left(\alpha \right)}+\mathcal{O}\left(h^{2-\alpha }\right),$$

where ${\sigma }_0^{\left(\alpha \right)}=1,{\sigma }_n^{\left(\alpha \right)}={(n-1)}^{1-\alpha }-n^{1-\alpha }$ and

$${\sigma }_k^{\left(\alpha \right)}={(k-1)}^{1-\alpha }-2k^{1-\alpha }+{(k+1)}^{1-\alpha },(1\le k<n).$$

The weights of L1 and Grünwald–Letnikov approximations have properties:

$${\sigma }_0^{\left(\alpha \right)}>0,{\sigma }_k^{\left(\alpha \right)}<0(1\le k\le n),\sum _{k=0}^n{\sigma }_k^{\left(\alpha \right)}=0.$$

(2)

The properties of the weights of Grünwald–Letnikov and L1 approximations enable an efficient analysis of the stability and convergence of difference schemes for fractional differential equations.

In section 4 we obtain the second order expansion formula of the L1 approximation

$${\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\sigma }_k^{\left(\alpha \right)}{f}_{n-k}=f_n^{\left(\alpha \right)}+{\displaystyle \frac{s_n}{\mathsf{\Gamma }(2-\alpha )}}{f}_n^{″}{h}^{2-\alpha }+\mathcal{O}\left(h^2\right),$$

(3)

where

$$s_n=\sum _{k=1}^{n-1}{k}^{1-\alpha }+{\displaystyle \frac{n^{1-\alpha }}{2}}-{\displaystyle \frac{n^{2-\alpha }}{2-\alpha }}.$$

One approach to constructing discretizations of the fractional derivative is by specifying the generating function. This method also applies to the construction of approximations for integer-order derivatives. In [1], we constructed a parameter-dependent approximation of the first derivative and applied it to obtain a discretization of the fractional derivative of order $2-\alpha$.

$${\mathcal{A}}_{n}f={\displaystyle \frac{1-b}{h}}\left(f_n-(1-b)\sum _{k=1}^{n-2}{b}^{k-1}{f}_{n-k}-{\displaystyle \frac{b^{n-2}(1-2b)}{1-b}}{f}_1-{\displaystyle \frac{b^{n-1}}{1-b}}{f}_0\right)=f_n^{\prime }+\mathcal{O}\left(h\right),$$

(4)

where $\left|b\right|<1$. Approximation (4) has a generating function

$$G_1\left(x\right)={\displaystyle \frac{(1-b)(1-x)}{1-bx}},$$

where b is a parameter, $\left|b\right|<1$.The generating function $G_1\left(x\right)$ has properties

$$G_1\left(1\right)=0,G_1^{\prime }\left(1\right)=-1.$$

In the present paper we use the method from [1,41] for constructing a parameter-dependent approximation of the second derivative

$$\begin{array}{cc}\hfill {\mathcal{B}}_{n}f={\displaystyle \frac{1-b}{h^2}}& (f_n-(2-b)f_{n-1}+{(1-b)}^2\sum _{k=1}^{n-3}{b}^{k-2}{f}_{n-k}\hfill \\ \hfill & +{\displaystyle \frac{1-3b+3b^2}{1-b}}{b}^{n-4}{f}_2+{\displaystyle \frac{1-3b}{1-b}}{b}^{n-3}{f}_1+{\displaystyle \frac{1}{1-b}}{b}^{n-2}{f}_0)=f_n^{\prime \prime }+\mathcal{O}\left(h\right).\hfill \end{array}$$

(5)

In Section 4, we use (5) to construct second-order approximations of the fractional derivative. By substituting the second derivative in the expansionn formula of the L1 approximation (3) with its approximation ${\mathcal{B}}_{n-1}f$ and choosing the parameter value $b=1-\alpha +{\alpha }^2$, we obtain a second-order approximation of the Caputo derivative

$${\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\gamma }_k^{\left(\alpha \right)}{f}_{n-k}=f_n^{\left(\alpha \right)}+\mathcal{O}\left(h^2\right),$$

(6)

where ${\gamma }_0^{\left(\alpha \right)}=1-\alpha (1-\alpha )s_n,{\gamma }_1^{\left(\alpha \right)}=2^{1-\alpha }-2+\alpha (1-\alpha )(1+\alpha -{\alpha }^2)s_n$, and

$$\begin{array}{cc}& {\gamma }_k^{\left(\alpha \right)}={(k-1)}^{1-\alpha }-2k^{1-\alpha }+{(k+1)}^{1-\alpha }-{\alpha }^3{(1-\alpha )}^3{(1-\alpha +{\alpha }^2)}^{k-2}{s}_n,(2\le k\le n-4),\hfill \\ & {\gamma }_{n-3}^{\left(\alpha \right)}={(n-4)}^{1-\alpha }-2{(n-3)}^{1-\alpha }+{(n-2)}^{1-\alpha }-(1-3\alpha +6{\alpha }^2-6{\alpha }^3+3{\alpha }^4){(1-\alpha +{\alpha }^2)}^{n-5}{s}_n,\hfill \\ & {\gamma }_{n-2}^{\left(\alpha \right)}={(n-3)}^{1-\alpha }-2{(n-2)}^{1-\alpha }+{(n-1)}^{1-\alpha }+(2-3\alpha +3{\alpha }^2){(1-\alpha +{\alpha }^2)}^{n-4}{s}_n,\hfill \\ & {\gamma }_{n-1}^{\left(\alpha \right)}={(n-2)}^{1-\alpha }-2{(n-1)}^{1-\alpha }+n^{1-\alpha }-{(1-\alpha +{\alpha }^2)}^{n-3}{s}_n,{\gamma }_n^{\left(\alpha \right)}={(n-1)}^{1-\alpha }-n^{1-\alpha }.\hfill \end{array}$$

From the formula for the sum of the zeta sequence, we obtain that the numbers $s_n$ converge to the value of the zeta function $\zeta (a-1)$. By substituting $s_n$ with $\zeta (a-1)$ in (3) and (6), we obtain the second-order asymptotic expansion formula of the L1 approximation.

$${\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\omega }_k^{\left(\alpha \right)}{f}_{n-k}=f_n^{\left(\alpha \right)}+{\displaystyle \frac{\zeta (\alpha -1)}{\mathsf{\Gamma }(2-\alpha )}}{f}_n^{″}{h}^{2-\alpha }+\mathcal{O}\left(h^2\right)$$

(7)

and a second order asymptotic approximation

$${\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\omega }_k^{\left(\alpha \right)}{f}_{n-k}=f_n^{\left(\alpha \right)}+\mathcal{O}\left(h^2\right),$$

(8)

where ${\omega }_0^{\left(\alpha \right)}=1-\alpha (1-\alpha )\zeta (\alpha -1),{\omega }_1^{\left(\alpha \right)}=2^{1-\alpha }-2+\alpha (1-\alpha )(1+\alpha -{\alpha }^2)\zeta (\alpha -1)$, and

$$\begin{array}{cc}& {\omega }_k^{\left(\alpha \right)}={(k-1)}^{1-\alpha }-2k^{1-\alpha }+{(k+1)}^{1-\alpha }-{\alpha }^3{(1-\alpha )}^3{(1-\alpha +{\alpha }^2)}^{k-2}\zeta (\alpha -1),\hfill \\ & {\omega }_{n-3}^{\left(\alpha \right)}={(n-4)}^{1-\alpha }-2{(n-3)}^{1-\alpha }+{(n-2)}^{1-\alpha }\hfill \\ & -(1-3\alpha +6{\alpha }^2-6{\alpha }^3+3{\alpha }^4){(1-\alpha +{\alpha }^2)}^{n-5}\zeta (\alpha -1),\hfill \\ & {\omega }_{n-2}^{\left(\alpha \right)}={(n-3)}^{1-\alpha }-2{(n-2)}^{1-\alpha }+{(n-1)}^{1-\alpha }+(2-3\alpha +3{\alpha }^2){(1-\alpha +{\alpha }^2)}^{n-4}\zeta (\alpha -1),\hfill \\ & {\omega }_{n-1}^{\left(\alpha \right)}={(n-2)}^{1-\alpha }-2{(n-1)}^{1-\alpha }+n^{1-\alpha }-{(1-\alpha +{\alpha }^2)}^{n-3}\zeta (\alpha -1),{\omega }_n^{\left(\alpha \right)}={\gamma }_n^{\left(\alpha \right)}={\sigma }_n^{\left(\alpha \right)}.\hfill \end{array}$$

The value of the parameter $b=1-\alpha +{\alpha }^2$ is chosen so that the weights of discretizations (6) and (8) satisfy properties (2). One difference between the two approximations is that, while approximation (6) has second-order accuracy for every $n>4$, the order of approximation in (7) and(8) varies from $2-\alpha$ when $n=1$ to second order when $n=N$. In Section 5, we prove that the difference schemes for fractional differential equations using both approximations achieve second-order accuracy. The results of the paper are summarized below.

In Section 2, we derive an approximation (5) of the second derivative. In Section 3, we consider applications of approximation (4) and its corresponding right-side approximation to the numerical solution of initial value and boundary value ordinary differential equations. These two approximations are related to two-point approximations and lead to efficient numerical methods whose performance and accuracy are comparable to standard finite difference methods. A convergence and error analysis of the numerical solution of a first-order ordinary differential equation is presented, with respect to the values of the parameter.

In Section 4, we derive the second-order expansion formula (3) of the L1 approximation and construct second-order approximations (6) and (8) of the fractional derivative. In Section 5, we consider applications of approximations (6) and (8) to the construction of difference schemes for the two-term ordinary fractional differential equation and the fractional subdiffusion equation. The difference schemes based on approximations (6) and (8) achieve second-order accuracy, and the proof of their convergence and order relies on the magnitude of the last weight of the L1 approximation.

2. Approximation of the Second Derivative

In paper [1], we constructed an approximation (4) of the first derivative with generating function $G_1\left(x\right)=(1-b)(1-x)/(1-bx)$. Constructions of approximations of the first and second derivatives whose generating functions are based on the exponential and logarithmic functions are discussed in [40,41]. In this section, we derive a parameter-dependent approximation of the second derivative and its second-order asymptotic expansion formula which has a generating function

$$G_2\left(x\right)={\displaystyle \frac{(1-b){(1-x)}^2}{1-bx}}.$$

The function $G_2\left(x\right)$ has properties $G_2\left(1\right)=G_2^{\prime }\left(1\right)=0,G_2^{″}\left(1\right)=2$. Denote

$$H_2\left(x\right)=G_2\left(e^{-x}\right)={\displaystyle \frac{(1-b){(1-e^{-x})}^2}{1-b{e}^{-x}}}.$$

The functions $G_2\left(x\right)$ and $H_2\left(x\right)$ have Maclaurin series

$$\begin{array}{cc}\hfill & G_2\left(x\right)=(1-b)\left(1-(2-b)x+{(1-b)}^2\sum _{k=2}^{n-3}{b}^{k-1}{x}^k\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & H_2\left(x\right)=x^2-{\displaystyle \frac{x^3}{1-b}}+{\displaystyle \frac{(7+4b+b^2)x^4}{12{(1-b)}^2}}+\mathcal{O}\left(x^4\right).\hfill \end{array}$$

(10)

Formulas (9) and (10) lead to the following asymptotic approximation of the second derivative and its second-order expansion formula.

$$\begin{array}{c}\hfill {\displaystyle \frac{1-b}{h^2}}\left(f_n-(2-b)f_{n-1}+{(1-b)}^2\sum _{k=1}^{n-3}{b}^{k-2}{f}_{n-k}\right)=f_n^{\prime \prime }-{\displaystyle \frac{1}{1-b}}{f}_n^{\prime \prime \prime }h+\mathcal{O}\left(h^2\right),\end{array}$$

where the function $f\in C^3[0,X]$ and satisfies the condition $f\left(0\right)=f^{\prime }\left(0\right)=f^{″}\left(0\right)=0$. Now we extend the approximation to all functions in the class $C^3[0,X]$. Let

$$\begin{array}{cc}\hfill {\mathcal{B}}_{n}f={\displaystyle \frac{1-b}{h^2}}(f_n-(2-b)f_{n-1}+{(1-b)}^2& \sum _{k=1}^{n-3}{b}^{k-2}{f}_{n-k}\hfill \\ \hfill & +c_2{b}^{n-4}{f}_2+c_1{b}^{n-3}{f}_1+c_0{b}^{n-2}{f}_0).\hfill \end{array}$$

The coefficients $c_0,c_1$ and $c_2$ are determined from the right expansion formula of the approximation. From Taylor’s formula, we obtain

$$f_{n-k}=f_n-kh{f}_n^{\prime }+{\displaystyle \frac{1}{2}}{k}^2{h}^2{f}_n^{″}-{\displaystyle \frac{1}{6}}{k}^3{h}^3{f}^{\left(3\right)}\left({\theta }_k\right),$$

where ${\theta }_k\in \left((n-k)h,x_n\right)$. Approximation ${\mathcal{B}}_n$ has a right expansion formula

$${\mathcal{B}}_{n}f=K_0{f}_n+K_1{f}_n^{\prime }+K_2{f}_n^{″}+E_n^{1}h,$$

where

$$\begin{array}{cc}\hfill & K_0={\displaystyle \frac{1-b}{h^2}}\left(1-(2-b)+{(1-b)}^2\sum _{k=2}^{n-3}{b}^{k-2}+\sum _{i=0}^2{b}^{n-i-2}{c}_i\right),\hfill \\ \hfill & K_1={\displaystyle \frac{1-b}{h}}\left(-(2-b)+{(1-b)}^2\sum _{k=2}^{n-3}k{b}^{k-2}+\sum _{i=0}^2(n-i)b^{n-i-2}{c}_i\right),\hfill \\ \hfill & K_2={\displaystyle \frac{1-b}{2}}\left(-(2-b)+{(1-b)}^2\sum _{k=2}^{n-3}{k}^2{b}^{k-2}+\sum _{i=0}^2{(n-i)}^2{b}^{n-i-2}{c}_i\right),\hfill \end{array}$$

and

$$E_n^1={\displaystyle \frac{1-b}{6}}\left({(1-b)}^2\sum _{k=2}^{n-3}{k}^3{b}^{k-2}{f}^{\left(3\right)}\left({\theta }_k\right)-(2-b)f^{\left(3\right)}\left({\theta }_1\right)+\sum _{i=0}^2{(n-i)}^3{b}^{n-i-2}{c}_i{f}^{\left(3\right)}\left({\theta }_{n-i}\right)\right).$$

The following formulas for the finite geometric series are used.

$$\sum _{k=2}^{n-3}{b}^{k-2}={\displaystyle \frac{1-b^{n-4}}{1-b}},\sum _{k=2}^{n-3}k{b}^{k-2}={\displaystyle \frac{2-b+b^{n-4}(2-3b+nb-n)}{{(1-b)}^2}},$$

$$\sum _{k=2}^{n-3}{k}^2{b}^{k-2}={\displaystyle \frac{4-3b+b^2-b^{n-4}\left(4-11b+9b^2-4n+10bn-6b^{2}n+n^2-2b{n}^2+b^2{n}^2\right)}{{(1-b)}^3}}.$$

Therefore

$$K_0={\displaystyle \frac{1-b}{h^2}}\left(c_0{b}^{n-2}+c_1{b}^{n-3}+c_2{b}^{n-4}-(1-b)b^{n-4}\right),$$

$$K_1={\displaystyle \frac{1-b}{h}}\left(c_{0}n{b}^{n-2}+c_1(n-1)b^{n-3}+c_2(n-2)b^{n-4}+b^{n-4}(2+bn-n-3b)\right),$$

$$\begin{array}{cc}\hfill K_2& ={\displaystyle \frac{1-b}{2}}\left(c_0{n}^2{b}^{n-2}+c_1{(n-1)}^2{b}^{n-3}+c_2{(n-2)}^2{b}^{n-4}+b^{n-4}(2+bn-n-3b)\right)\hfill \\ & +{\displaystyle \frac{2-b^{n-4}\left(4-11b+9b^2-4n+10bn-6b^{2}n+n^2-2b{n}^2+b^2{n}^2\right)}{2}}.\hfill \end{array}$$

A system of equations for the coefficients $c_0,c_1,c_2$ is obtained by setting $K_0=K_1=0$ and the coefficient of the second derivative $K_2=1$.

$$\left\{\begin{array}{cc}\hfill c_2+c_{1}b+& c_0{b}^2=1-b,\hfill \\ \hfill c_2(n-2)+& c_1(n-1)b+c_{0}n{b}^2=R1,\hfill \\ \hfill {c_2(n-2)}^2+& c_1{(n-1)}^{2}b+c_0{n}^2{b}^2=R2,\hfill \end{array}\right.$$

where

$$R1=n+3b-2-b,R2={\displaystyle \frac{4-11b+9b^2-4n+10bn-6b^{2}n+n^2-2b{n}^2+b^2{n}^2}{1-b}}.$$

The system of equations has a solution.

$$c_0={\displaystyle \frac{1}{1-b}},c_1={\displaystyle \frac{1-3b}{1-b}},c_2={\displaystyle \frac{1-3b+3b^2}{1-b}}.$$

Therefore

$$\begin{array}{cc}\hfill {\mathcal{B}}_{n}f={\displaystyle \frac{1}{h^2}}& ((1-b)f_n-(1-b)(2-b)f_{n-1}+{(1-b)}^3\sum _{k=1}^{n-3}{b}^{k-2}{f}_{n-k}\hfill \\ \hfill & +(1-3b+3b^2)b^{n-4}{f}_2+(1-3b)b^{n-3}{f}_1+b^{n-2}{f}_0)=f_n^{\prime \prime }+E_n^{1}h.\hfill \end{array}$$

Denote

$$M_i=\underset{0\le x\le X}{max}\left|f^{\left(i\right)}\left(x\right)\right|.$$

In the following claim, we obtain an error estimate for the approximation ${\mathcal{B}}_n$.

Claim 1.

Let $f\in C^3[0,X]$. Then

$$|E_n^1|<{\displaystyle \frac{2M_3}{1-b}}.$$

Proof. 

From the formula for the coefficient $E_n^1$, we obtain

$$\begin{array}{cc}\hfill |E_n^1|\le {\displaystyle \frac{1-b}{6}}((2-b)\left|f^{\left(3\right)}\left({\theta }_1\right)\right|+{(1-b)}^2& \sum _{k=2}^{n-3}{k}^3{b}^{k-2}\left|f^{\left(3\right)}\left({\theta }_k\right)\right|\hfill \\ \hfill & +\sum _{i=0}^2{(n-i)}^3{b}^{n-i-2}{c}_i\left|f^{\left(3\right)}\left({\theta }_{n-i}\right)\right|),\hfill \end{array}$$

$$|E_n^1|\le {\displaystyle \frac{(1-b)M_3}{6}}\left((2-b)+{(1-b)}^2\sum _{k=2}^{n-3}{k}^3{b}^{k-2}+\sum _{i=0}^2{(n-i)}^3{b}^{n-i-2}{c}_i\right),$$

$$|E_n^1|\le {\displaystyle \frac{2\left(5-5b+4b^2-b^3-3b^{n-1}\right)M_3}{6(1-b)}}<{\displaystyle \frac{2\left(5-5b+4b^2-b^3\right)M_3}{6(1-b)}}.$$

Let $f\left(b\right)=5-5b+4b^2-b^3$. Then

$$f^{\prime }\left(b\right)=-5+8b-3b^2=-(1-b)(5-3b)<0.$$

The function f is decreasing on the interval $[0,1]$ and has a maximum at zero, $f\left(0\right)=5$.

$$|E_n^1|<{\displaystyle \frac{5M_3}{3(1-b)}}<{\displaystyle \frac{2M_3}{1-b}}.$$

□

3. Numerical Solutions of Ordinary Differential Equations

The weights of the approximations (4) and (5) contain powers of the parameter b, which makes it possible to use them in constructions of approximations of the fractional derivative satisfying property (2). Both approximations can be derived from two-point approximations and are suitable for numerical solution of differential equations. In [1] we showed that, with an appropriate choice of the parameter, the numerical methods using approximation (4) attain an arbitrary order in $(0,2]$, and that their performance is comparable to standard difference schemes with respect to accuracy and computational time. Depending on the values of the parameters, the numerical solutions of initial- and boundary-value ordinary differential equations have different properties and regions of convergence [42,43,44,45,46,47]. In this section, we consider applications of (4) and the corresponding right-hand approximation to the numerical solution of initial- and boundary-value ordinary differential equations. In the following we derive a two-point approximation corresponding to approximation ${\mathcal{A}}_{n}f$.

$$\begin{array}{cc}\hfill {\mathcal{A}}_{n}f={\displaystyle \frac{1-b}{h}}& \left(f_n-(1-b)\sum _{k=1}^{n-2}{b}^{k-1}{f}_{n-k}-{\displaystyle \frac{1-2b}{1-b}}{b}^{n-2}{f}_1-{\displaystyle \frac{b^{n-1}}{1-b}}{f}_0\right)\hfill \\ \hfill & =f_n^{\prime }+{\displaystyle \frac{1+b}{2(1-b)}}{f}_n^{\prime \prime }h+\mathcal{O}\left(h^2\right).\hfill \end{array}$$

(11)

Express the formula in the form

$$\begin{array}{cc}\hfill {\mathcal{A}}_{n}f={\displaystyle \frac{1}{h}}& \left(b(1-b)f_{n-1}-{(1-b)}^{2}b\left(\sum _{k=2}^{n-2}{b}^{k-2}{f}_{n-k}-(1-2b)b^{n-3}{f}_1-b^{n-2}{f}_0\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{h}}\left((1-b)f_n-{(1-b)}^2{f}_{n-1}-b(1-b)f_{n-1}\right).\hfill \end{array}$$

Hence

$${\mathcal{A}}_{n}f=b{\mathcal{A}}_{n-1}f+{\displaystyle \frac{1}{h}}\left[(1-b)f_n-(1-b)f_{n-1}\right].$$

From (11) we obtain the two-point approximation

$$f_n^{\prime }=b{f}_{n-1}^{\prime }+{\displaystyle \frac{1-b}{h}}(f_n-f_{n-1})+\mathcal{O}\left(h\right).$$

(12)

Approximation (4) follows from successive applications of (12). When $b=-1$ two-point approximation (12) has a second order accuracy

$${\displaystyle \frac{2}{h}}(f_n-f_{n-1})-f_{n-1}^{\prime }-f_n^{\prime }=\mathcal{O}\left(h^2\right).$$

From Taylor’s theorem we obtain an estimate for the error

$$2(f_n-f_{n-1})-h{f}_{n-1}^{\prime }-h{f}_n^{\prime }=E_n^2{h}^3,$$

(13)

where $|E_n^2|<M_3/3$. We consider an application of (13) to the numerical solution of first-order ordinary differential equation

$$y^{\prime }\left(t\right)+Ly\left(t\right)=F\left(t\right),y\left(0\right)=y_0.$$

(14)

By substituting the first derivatives from the equation into (13), we obtain

$$2(y_n-y_{n-1})+h(L{y}_{n-1}-F_{n-1})+h(L{y}_n-F_n)=E_n^2{h}^3,$$

$$y_n(2+hL)-y_{n-1}(2-hL)=h(F_n+F_{n-1})+E_n^2{h}^3.$$

(15)

Canceling the error term yields a second-order numerical solution of equation (14).

$$u_n={\displaystyle \frac{2-hL}{2+hL}}{u}_{n-1}+{\displaystyle \frac{h(F_n+F_{n-1})}{2+hL}},u_0=y_0.$$

(16)

Example 1.

Consider the following ordinary differential equation

$$y^{\prime }\left(t\right)+Ly\left(t\right)=(1+L)e^t,y\left(0\right)=1,0\le t\le 1.$$

(17)

Equation (17) has a solution $y\left(t\right)=e^t$. The experimental results for the maximum error and the order of the numerical solution (16) of equation (17) are presented in Table 1 and Table 2. The experiments are carried out using Mathematica 13 and the orders of the numerical methods are computed by formula ${\mathrm{Order}}_h={log}_2|{\mathrm{Error}}_{h/2}/{\mathrm{Error}}_h|$.

The experimental results in Table 1 and Table 2 indicate that (16) is of second order, and the error of the numerical solution is less than ${10}^{-6}$ when the parameter $L>-10$. The error increases for decreasing values of the parameter $L<-10$. The results in Table 2 show that the error of the method becomes very large for $L<-50$, exceeding ${10}^{10}$ for $h={10}^{-4}$. Denote by $e_n=y_n-u_n$ the error of (16) at the point $t_n$. From (15) and (16) the sequence of the errors ${\left\{e_n\right\}}_{n=0}^N$ satisfies the recursive formula

$$e_n={\displaystyle \frac{2-hL}{2+hL}}{e}_{n-1}+{\displaystyle \frac{E_n^2{h}^3}{2+hL}},e_0=0.$$

(18)

In the following we establish the convergence of numerical solution (16) and obtain an estimate for the error.

Claim 2.

Let $h\left|L\right|<2$. Then

$$|e_n|<{\displaystyle \frac{M_3{h}^2}{6\left|L\right|}}\left|{\left({\displaystyle \frac{2-hL}{2+hL}}\right)}^n-1\right|,(1\le n\le N).$$

(19)

Proof. 

Denote

$$c={\displaystyle \frac{2-hL}{2+hL}},d_n={\displaystyle \frac{E_n^2{h}^3}{2+hL}}.$$

Formula (18) for the errors $e_n$ takes the form

$$e_n=c{e}_{n-1}+d_n.$$

(20)

Then

$$\begin{array}{cc}\hfill e_n& =c^2{e}_{n-2}+c{d}_{n-1}+d_n=c^3{e}_{n-3}+c^2{d}_{n-2}+c{d}_{n-1}+d_n.\hfill \end{array}$$

Applying (20) recursively $n-1$ times yields

$$\begin{array}{cc}\hfill e_n& =c^n{e}_0+c^{n-1}{d}_1+\dots +c^2{d}_{n-2}+c{d}_{n-1}+d_n,\hfill \\ \hfill |e_n|& \le c^{n-1}|d_1|+\dots +c^2|d_{n-2}|+c|d_{n-1}|+|d_n|.\hfill \end{array}$$

The numbers $d_i$ satisfy the estimate

$$d_i\le {\displaystyle \frac{|E_i^2|h^3}{2+hL}}={\displaystyle \frac{M_3{h}^3}{3(2+hL)}}.$$

Therefore

$$|e_n|<{\displaystyle \frac{M_3{h}^3}{3(2+hL)}}\left(c^{n-1}+\dots +c^2+c+1\right)={\displaystyle \frac{M_3{h}^3}{3(2+hL)}}\left|{\displaystyle \frac{1-c^n}{1-c}}\right|.$$

Using the equality

$$1-c=1-{\displaystyle \frac{2-hL}{2+hL}}={\displaystyle \frac{(2+hL)-(2-hL)}{2+hL}}={\displaystyle \frac{2hL}{2+hL}}$$

we obtain

$$|e_n|<{\displaystyle \frac{M_3{h}^3}{3(2+hL)}}·{\displaystyle \frac{1-c^n}{\frac{2hL}{2+hL}}}={\displaystyle \frac{M_3{h}^2}{6L}}|1-c^n|,$$

$$|e_n|<{\displaystyle \frac{M_3{h}^2}{6\left|L\right|}}\left|{\left({\displaystyle \frac{2-hL}{2+hL}}\right)}^n-1\right|.$$

□

Denote

$$g\left(x\right)=xln\left({\displaystyle \frac{2x+L}{2x-L}}\right).$$

Claim 3.

Let $L>0$ and $x>L/2$. Then the function $g\left(x\right)$ is decreasing.

Proof. 

$$g\left(x\right)=xln\left({\displaystyle \frac{2x+L}{2x-L}}\right)=x\left(ln(2x+L)-ln(2x-L)\right),$$

$$g^{\prime }\left(x\right)=ln(2x+L)-ln(2x-L)+{\displaystyle \frac{2x}{2x+L}}-{\displaystyle \frac{2x}{2x-L}},$$

$$g^{\prime \prime }\left(x\right)={\displaystyle \frac{2}{2x+L}}-{\displaystyle \frac{2}{2x-L}}+{\displaystyle \frac{2L}{{(L+2x)}^2}}+{\displaystyle \frac{2L}{{(2x-L)}^2}},$$

$$g^{\prime \prime }\left(x\right)={\displaystyle \frac{8L^3}{{(2x-L)}^2{(L+2x)}^2}}>0.$$

Since $g^{\prime }\left(x\right)$ is increasing and

$$\underset{n\to \infty }{lim}{g}^{\prime }\left(x\right)=0,$$

it follows that $g^{\prime }\left(x\right)<0$ for all x. Hence, $g\left(x\right)$ is decreasing. □

Lemma 4.

Let $L>0$ and $Lh<2$. Then

$$|e_n|<{\displaystyle \frac{M_3{h}^2}{6}},(1\le n\le N).$$

Proof. 

From Claim 2

$$|e_n|<{\displaystyle \frac{M_3{h}^2}{6L}}\left(1-{\left({\displaystyle \frac{2-hL}{2+hL}}\right)}^N\right)={\displaystyle \frac{M_3{h}^2}{6L}}\left(1-{\left({\displaystyle \frac{2N-L}{2N+L}}\right)}^N\right).$$

The function $1-{\left({\displaystyle \frac{2N-L}{2N+L}}\right)}^N=1-e^{-g\left(N\right)}$ is decreasing and has a maximum at $N=1$.

$$|e_n|<{\displaystyle \frac{M_3{h}^2}{6L}}\left(1-{\displaystyle \frac{2-L}{2+L}}\right)={\displaystyle \frac{M_3{h}^2}{6L}}·{\displaystyle \frac{2L}{2+L}}={\displaystyle \frac{M_3{h}^2}{3}}·{\displaystyle \frac{1}{2+L}}<{\displaystyle \frac{M_3{h}^2}{6}}.$$

□

Lemma 5.

Let $L<0$ and $h\left|L\right|<0.1$. Then

$$|e_n|<{\displaystyle \frac{2.{73}^{\left|L\right|}-1}{6\left|L\right|}}{M}_3{h}^2,(1\le n\le N).$$

(21)

Proof. 

$$|e_n|<{\displaystyle \frac{M_3{h}^2}{6\left|L\right|}}\left({\left({\displaystyle \frac{2-hL}{2+hL}}\right)}^n-1\right)\le {\displaystyle \frac{M_3{h}^2}{6\left|L\right|}}\left({\left({\displaystyle \frac{2-L/N}{2+L/N}}\right)}^N-1\right).$$

The function ${\left({\displaystyle \frac{2N-L}{2N+L}}\right)}^N=e^{g\left(N\right)}$ is decreasing with respect to N and

$${\left({\displaystyle \frac{2-L/N}{2+L/N}}\right)}^N<{\left({\displaystyle \frac{2+0.1}{2-0.1}}\right)}^{-10L}<2.{73}^{-L}.$$

Therefore

$$|e_n|\le {\displaystyle \frac{M_3{h}^2}{6\left|L\right|}}\left({\left({\displaystyle \frac{2-L/N}{2+L/N}}\right)}^N-1\right)<{\displaystyle \frac{2.{73}^{\left|L\right|}-1}{6\left|L\right|}}{M}_3{h}^2.$$

□

Corollary 6.

Let $-10<L<0$. Then

$$|e_n|<400M_3{h}^2.$$

(22)

Proof. 

The function ${\displaystyle \frac{2.{73}^{\left|L\right|}-1}{6\left|L\right|}}$ is increasing because its derivative is positive. Then

$$|e_n|<{\displaystyle \frac{2.{73}^{\left|L\right|}-1}{6\left|L\right|}}{M}_3{h}^2<{\displaystyle \frac{2.{73}^{10}-1}{60}}{M}_3{h}^2<400M_3{h}^2.$$

□

In most practical applications, it is sufficient to compute the solution of a differential equation with an error less than ${10}^{-5}$. The estimate (6) for the error of the numerical method (16) guarantees that, for $h={10}^{-6}$ and ${max}_{1\le t\le 1}\left|y^{\prime \prime \prime }\left(t\right)\right|<25000$ , the error of the solution is less than ${10}^{-5}$ for parameter values $-10<L<0$.

We consider the case $L<-10$. The results in Table 2, as well as estimate (21), show that in this case the error of the numerical solution (16) of equation (14) can become very large, exceeding ${10}^{10}$ for $L<-50$ and $h={10}^{-4}$. We use the following approach to solve equation (14) numerically: Consider the boundary-value ODE, which is obtained from equation (14) by converting the initial condition into a boundary condition.

$$z^{\prime }\left(t\right)+Lz\left(t\right)=F\left(t\right),z\left(2\right)=y_0,0\le t\le 2.$$

(23)

Equation (23) is chosen so that its numerical solution can also serve as a numerical solution of equation (14). This is justified because the difference between the solutions of the two equations is negligible for $L<-10$. Note that the boundary condition may be specified at a different point, e.g., $z\left(3\right)=y_0$. In the following claim, we provide an estimate of the difference between the solutions of equations (14) and (23) on the interval $[0,1]$.

Claim 7.

Let $L<0$ and $t\in [0,1]$. Then the difference of the solutions of equations (14) and (23) satisfies the estimate

$$|y\left(t\right)-z\left(t\right)|<2M_0{e}^{L(2-t)}$$

where ${\displaystyle M_0=\underset{0\le t\le 2}{max}\left|y\left(t\right)\right|}$.

Proof. 

The function $w\left(t\right)=y\left(t\right)-z\left(t\right)$ satisfies the equation

$$w^{\prime }\left(t\right)+Lw\left(t\right)=0,w\left(2\right)=y\left(2\right)-y\left(0\right).$$

Therefore

$$w\left(t\right)=c{e}^{-Lt}.$$

Applying the condition $w\left(2\right)=y\left(2\right)-y\left(0\right)$:

$$w\left(2\right)=c{e}^{-2L}=y\left(2\right)-y\left(0\right),c=(y\left(2\right)-y\left(0\right))e^{2L}.$$

Substituting back:

$$w\left(t\right)=(y\left(2\right)-y\left(0\right))e^{2L}·e^{-Lt}=(y\left(2\right)-y\left(0\right))e^{L(2-t)},$$

$$\left|w\left(t\right)\right|\le \left(\right|y\left(2\right)|+\left|y\left(0\right)\right|)e^{L(2-t)}\le 2M_0{e}^{L(2-t)}.$$

□

The numerical solutions of the boundary value ordinary differential equation (23) exhibit high accuracy for negative values of the parameter L. In Claim 7, it was demonstrated that for negative values of the parameter, $L<-10$ the difference between the solutions of equations (14) and (23) is insignificant. These properties enable us to compute a numerical solution of equation (23) on the interval $[0,2]$ and employ this solution for equation (14) on the interval $[0,1]$. In the following we compute the numerical solution of boundary value problem (23) using the right approximation of (11). Let $h=2/L$. The right-hand approximation corresponding to (11) is obtained by the substitution $g\left(x\right)=f(2t_n-x)$.

$${\displaystyle \frac{1-b}{h}}\left(-g_n+(1-b)\sum _{k=1}^{N-n-2}{b}^{k-1}{g}_{n+k}+{\displaystyle \frac{1-2b}{1-b}}{b}^{N-n-2}{g}_{N-1}+{\displaystyle \frac{b^{N-n-1}}{1-b}}{g}_N\right)=g_n^{\prime }+\mathcal{O}\left(h\right).$$

and has a related two-point approximation

$${\displaystyle \frac{1-b}{h}}(g_{n+1}-g_n)-g_n^{\prime }+b{g}_{n+1}^{\prime }=h\left({\displaystyle \frac{1+b}{2}}\right)g^{″}\left(\theta \right).$$

(24)

When $b=-1$ and $b=1-h$ approximation (24) has a second order accuracy. We use the two-point approximation (24) to obtain a numerical solution of equation (23).

$$(1-b)(z_{n+1}-z_n)-h{z}_n^{\prime }+bh{z}_{n+1}^{\prime }=h^2\left({\displaystyle \frac{1+b}{2}}\right)f^{″}\left(\theta \right),$$

$$(1-b)(z_{n+1}-z_n)-h(F_n-L{z}_n)+bh(F_{n+1}-L{z}_{n+1})=h^2\left({\displaystyle \frac{1+b}{2}}\right)f^{″}\left(\theta \right).$$

The numerical solution (${\mathrm{NS}}_v$) satisfies

$$(1-b)v_{n+1}-(1-b)v_n-h{F}_n+Lh{v}_n+bh{F}_{n+1}-bhL{v}_{n+1}=0,$$

$$v_n={\displaystyle \frac{(1-b-bhL)v_{n+1}-h{F}_n+bh{F}_{n+1}}{1-b-Lh}},v_N=y_0.$$

The numerical solution ${\mathrm{NS}}_v$ converges when $L<0$, since the modulus of the coefficient in front of $v_{n+1}$ is less than one

$$\left|{\displaystyle \frac{1-b-bhL}{1-b-Lh}}\right|<1.$$

Denote by ${\mathrm{NS}}_u$ the first half of the values of ${\mathrm{NS}}_v$, which are used as a numerical solution of equation (14) on the interval $[0,1]$. The numerical solution ${\mathrm{NS}}_u$ consists of ${\left\{v_i\right\}}_{i=0}^{N/2}$ and has accuracy $\mathcal{O}(ϵ+h)$, where $\left|b\right|<1$ and $ϵ<2M_0{e}^L$. The accuracy of ${\mathrm{NS}}_u$ is $\mathcal{O}(ϵ+h^2)$ when the parameter $b=-1+h$.

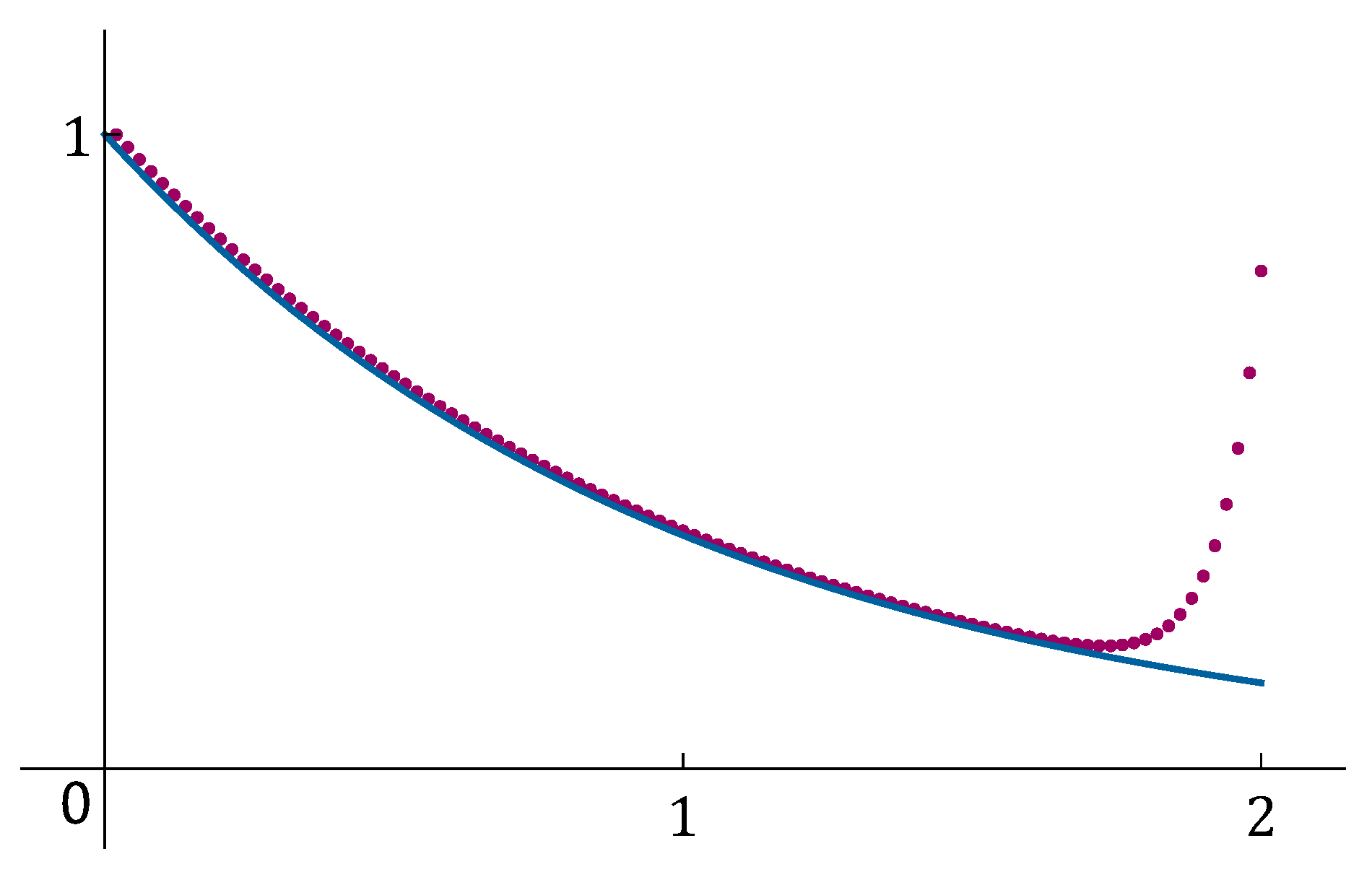
Example 2.

Consider the following boundary value ODE

$$z^{\prime }\left(t\right)+Lz\left(t\right)=(1+L)e^t,z\left(2\right)=1.$$

(25)

The numerical results for the error and order of numerical solution ${\mathrm{NS}}_u$ of equation (17) and values of the parameter $L=-10,L=-50$ and $L=-100$ are presented in Table 3.

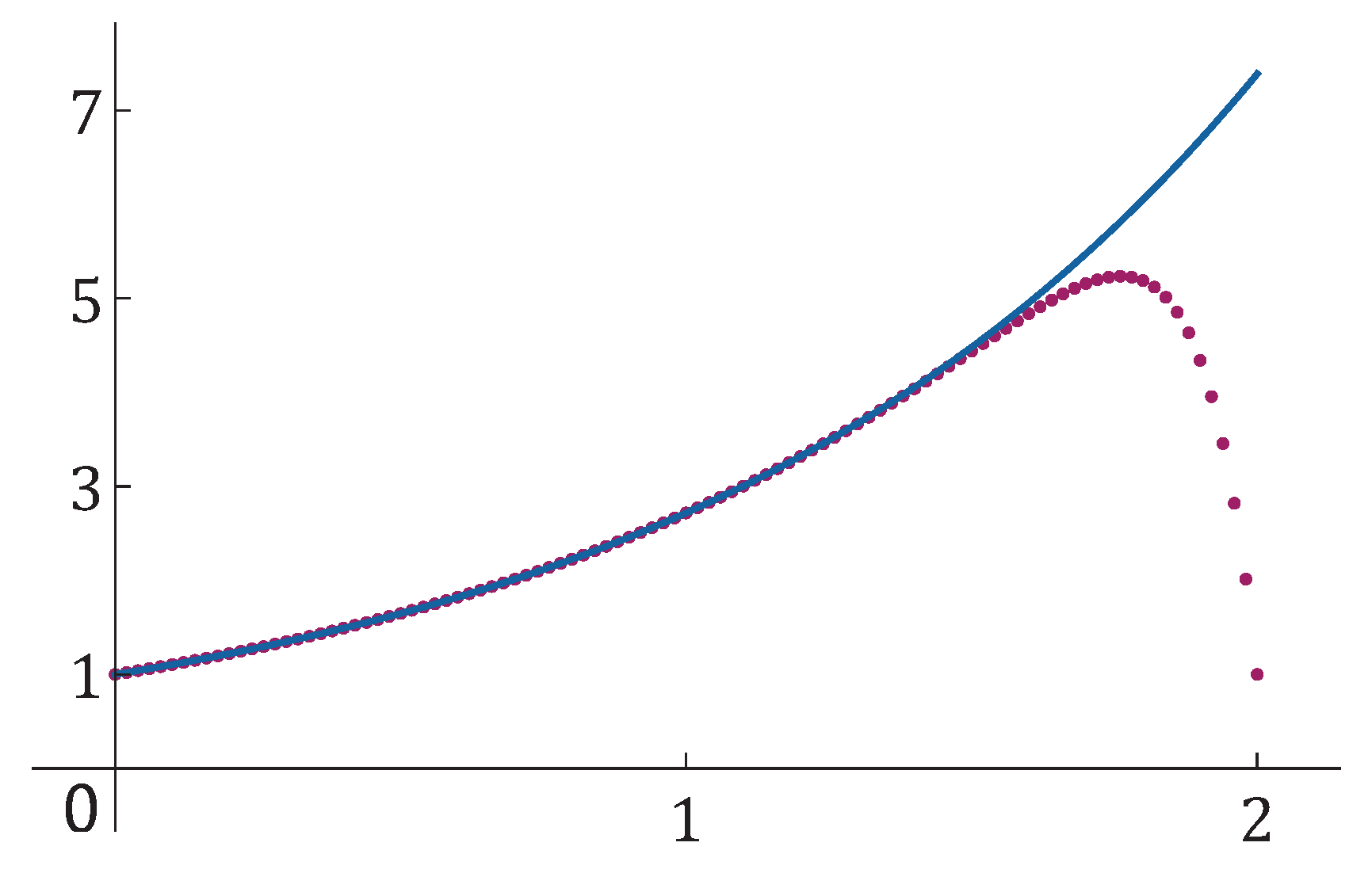
The experimental results in Table 3 show that the error of the numerical method ${\mathrm{NS}}_u$ is less than ${10}^{-5}$. The results in Table 3 represent a significant improvement over those in Table 3 for the numerical method (16). The graphs of the exact solution of equation (17) on the interval $[0,2]$ and numerical solution ${\mathrm{NS}}_u$ are given in Figure 3.

Figure 1. Graphs of the exact solution of equation (17) and of the numerical solution ${\mathrm{NS}}_v$ for $L=-10$ and $h=0.02$.

Figure 1. Graphs of the exact solution of equation (17) and of the numerical solution ${\mathrm{NS}}_v$ for $L=-10$ and $h=0.02$.

Example 3.

Consider the ordinary differential equation

$$y^{\prime }\left(t\right)-(20+t^2)y\left(t\right)=F\left(t\right),y\left(0\right)=1$$

(26)

for $t\in [0,1]$, and the corresponding boundary value ordinary differential equation

$$z^{\prime }\left(t\right)-(20+t^2)z\left(t\right)=F\left(t\right),z\left(2\right)=1,$$

(27)

where

$$F\left(t\right)=3cos3t-sint-(20+t^2)(cost+sin3t).$$

□

Equation (26) has a solution $y\left(t\right)=cost+sin3t$. The numerical solution of the initial value ordinary differential equation

$$y^{\prime }\left(t\right)+G\left(t\right)y\left(t\right)=F\left(t\right),y\left(0\right)=y_0$$

which uses 2-point approximation (24) is computed as

$$u_n={\displaystyle \frac{h{F}_n-bh{F}_{n-1}+\left(1-b+bh{G}_{n-1}\right)u_{n-1}}{1-b+h{G}_n}},u_0=y_0.$$

(28)

The numerical solution of the boundary value ordinary differential equation

$$z^{\prime }\left(t\right)+g\left(t\right)z\left(t\right)=F\left(t\right),z\left(2\right)=y_0,$$

which uses two-point approximation (24) is computed as

$$v_{n-1}={\displaystyle \frac{bh{F}_{n-1}-h{F}_n+\left(1-b+h{G}_n\right)v_n}{1-b+bh{g}_{n-1}}},v_N=y_0.$$

(29)

Denote by ${\mathrm{NS}}_{\overline{u}}$ the numerical solution (28) of equation (26), and by ${\mathrm{NS}}_{\overline{v}}$ the first half of the values ${\left\{v_i\right\}}_{i=0}^{N/2}$ of (29), regarded as a numerical solution of equation (26). The second column of Table 4 contains the numerical results for the error and order of numerical solution ${\mathrm{NS}}_{\overline{u}}$. The third and fourth columns contain the results for the error and order of numerical solution ${\mathrm{NS}}_{\overline{v}}$.

The graphs of the solution of equation (26) and numerical solution (29) of boundary value ordinary differential equation (27) are given on Figure 2. While the numerical results in the second column of Table 4 show that the numerical solution ${\mathrm{NS}}_{\overline{u}}$ is of first order, its error is quite large, making this method impractical for real applications. The applied approach for computing the numerical solutions of the ordinary differential equations (17) and (26), which uses the numerical solutions of the boundary value problems (25) and (27), allows one to obtain solutions with an error smaller than ${10}^{-5}$, which is sufficient for real-life problems.

Shifted approximations are employed for the solution of nonlinear ordinary differential equations. In order to derive the shifted approximation of (11), we make use of the two-point approximation (24).

$$(1-c)(f_n-f_{n-1})+ch{f}_n^{\prime }-h{f}_{n-1}^{\prime }=\mathcal{O}\left(h^2\right),$$

$$f_n+{\displaystyle \frac{ch{f}_n^{\prime }}{1-c}}=f_{n-1}+{\displaystyle \frac{h{f}_{n-1}^{\prime }}{1-c}}+\mathcal{O}\left(h^2\right).$$

When $c=(1+b)/(3-b)$ we obtain

$$f_n^{\prime }-{\displaystyle \frac{1+b}{2(1-b)}}h{f}_n^{″}=f_{n-1}^{\prime }+{\displaystyle \frac{1-3b}{2(1-b)}}h{f}_{n-1}^{″}+\mathcal{O}\left(h^2\right)$$

(30)

From (11) and (30) we obtain the shifted approximation of the first derivative

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{h}}\left((1-b)f_n-{(1-b)}^2\sum _{k=1}^{n-2}{b}^{k-1}{f}_{n-k}-(1-2b)b^{n-2}{f}_1-b^{n-1}{f}_0\right)\hfill \\ \hfill & =f_{n-1}^{\prime }+{\displaystyle \frac{1-3b}{2(1-b)}}{f}_{n-1}^{\prime \prime }h+\mathcal{O}\left(h^2\right).\hfill \end{array}$$

(31)

Consider the nonlinear ordinary differential equation

$$y^{\prime }\left(t\right)+g\left(t\right)y\left(t\right)=y^2\left(t\right)+F\left(t\right),y\left(0\right)=y_0.$$

(32)

By approximating the first derivative at $t_{n-1}$ with (31) we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{h}}\left((1-b)y_n-{(1-b)}^2\sum _{k=1}^{n-2}{b}^{k-1}{y}_{n-k}-(1-2b)b^{n-2}{y}_1-b^{n-1}{y}_0\right)\hfill \\ \hfill & +g_{n-1}{y}_{n-1}=y_{n-1}^2+F_{n-1}+\mathcal{O}\left(h^2\right).\hfill \end{array}$$

The numerical solution of equation (32) satisfies

$$\begin{array}{cc}\hfill u_n={\displaystyle \frac{h}{1-b}}\left(u_{n-1}^2-g_{n-1}{u}_{n-1}+F_{n-1}\right)+(1-b)\sum _{k=1}^{n-2}& b^{k-1}{u}_{n-k}\hfill \\ \hfill & +{\displaystyle \frac{1-2b}{1-b}}{b}^{n-2}{u}_1+{\displaystyle \frac{b^{n-1}}{1-b}}{u}_0\hfill \end{array}$$

(33)

and has initial conditions

$$u_0=y_0,u_1=y_0+h\left(y_0^2+F_0-g_0{y}_0\right).$$

The numerical solution (33) is computed with $\mathcal{O}\left(n^2\right)$ operations. The number of computations can be reduced to $\mathcal{O}\left(n\right)$ in the following way [1]: Let

$$S_n=(1-b)\sum _{k=1}^{n-2}{b}^{k-1}{u}_{n-k}+{\displaystyle \frac{1-2b}{1-b}}{b}^{n-2}{u}_1+{\displaystyle \frac{b^{n-1}}{1-b}}{u}_0.$$

The sequence $S_n$ is computed recursively as

$$S_n=(1-b)u_{n-1}+b{S}_{n-1}.$$

The sequence $S_n$ and the numerical solution (33) are computed with $\mathcal{O}\left(n\right)$ operations by means of the following pseudocode.

Initialization:$u_0=y_0,u_1=y_0+h\left(y_0^2+F_0-g_0{y}_0\right),$

$$S_2={\displaystyle \frac{b}{1-b}}{u}_0+{\displaystyle \frac{1-2b}{1-b}}{u}_1,u_2={\displaystyle \frac{h}{1-b}}\left(u_1^2-g_1{u}_1+F_1\right)+S_2.$$

Loop: for n from 3 to N do

$$S_n=(1-b)u_{n-1}+b{S}_{n-1},$$

$$u_n={\displaystyle \frac{h}{1-b}}\left(u_{n-1}^2-g_{n-1}{u}_{n-1}+F_{n-1}\right)+S_n.$$

The computational time of the numerical method (33) is comparable to that of standard difference methods. The numerical solution (33) has first-order accuracy, and second-order accuracy when $b=\frac{1}{3}$. When the parameter $b=1-h^p$, the numerical solution (33) has an accuracy of order $1-p$.

Example 4.

Consider the following nonlinear ordinary differential equation

$$y^{\prime }\left(t\right)+(20+t^2)y\left(t\right)=y^2\left(t\right)+(21+t^2)e^t-e^{2t},y\left(0\right)=1,0\le t\le 1.$$

(34)

Equation (34) has the solution $y\left(t\right)=e^t$. The experimental results for the error and the order of the numerical solution (33) of equation (34) are presented in Table 5.

4. Second-Order Approximations of the Fractional Derivative

In this section, we derive the second-order expansion formula for the L1 approximation. Second-order approximations of the fractional derivative, whose weights satisfy properties (2), are constructed using the expansion formula and the approximation (11) of the second derivative.

4.1. Second Order Expansion Formula

In the next claim, we express the L1 approximation in terms of the values of the second derivative.

Claim 8.

Let $f\in C^4[0,x_n]$. Then

$${\mathcal{L}}_{n}f={\displaystyle \frac{h^{2-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\sum _{k=1}^{n-1}{k}^{1-\alpha }{f}_{n-k}^{\prime \prime }+{\displaystyle \frac{\left(f_1-f_0\right)n^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}+E_n^3{h}^2,$$

(35)

where

$$|E_n^3|<{\displaystyle \frac{M_4{x}_n^{2-\alpha }}{12\mathsf{\Gamma }(3-\alpha )}}.$$

Proof. 

By rearranging the terms, the formula of the L1 approximation can be written in the form

$${\mathcal{L}}_{n}f={\displaystyle \frac{h^{-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\sum _{k=1}^{n-1}{k}^{1-\alpha }(f_{n-k+1}-2f_{n-k}+f_{n-k-1})+{\displaystyle \frac{n^{1-\alpha }(f_1-f_0)}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}.$$

The central difference approximation of the second derivative is given by

$$f_{m+1}-2f_m+f_{m-1}=h^2{f}_m^{\prime \prime }+E_m^4{h}^4,$$

where $|E_m^4|\le M_4/12$. Then

$${\mathcal{L}}_{n}f={\displaystyle \frac{h^{-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\sum _{k=1}^{n-1}{k}^{1-\alpha }\left(h^2{f}_{n-k}^{\prime \prime }+E_{n-k}^4{h}^4\right)+{\displaystyle \frac{n^{1-\alpha }(f_1-f_0)}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}},$$

$${\mathcal{L}}_{n}f={\displaystyle \frac{h^{2-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\sum _{k=1}^{n-1}{k}^{1-\alpha }{f}_{n-k}^{\prime \prime }+{\displaystyle \frac{h^{4-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\sum _{k=1}^{n-1}{E}_{n-k}^4{k}^{1-\alpha }+{\displaystyle \frac{\left(f_1-f_0\right)n^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}.$$

From the formula for the sum of zeta sequence

$$\sum _{k=1}^{n-1}{k}^{1-\alpha }=\zeta (\alpha -1)+{\displaystyle \frac{n^{2-\alpha }}{2-\alpha }}\sum _{k=0}^{\infty }\left({\displaystyle \genfrac{}{}{0pt}{}{2-\alpha }{k}}\right){\displaystyle \frac{B_k}{n^k}},$$

(36)

$$\sum _{k=1}^{n-1}{k}^{1-\alpha }={\displaystyle \frac{n^{2-\alpha }}{2-\alpha }}-{\displaystyle \frac{n^{1-\alpha }}{2}}+\zeta (\alpha -1)+{\displaystyle \frac{1-\alpha }{12n^{\alpha }}}+\mathcal{O}\left({\displaystyle \frac{1}{n^{2+a}}}\right).$$

Therefore

$$\sum _{k=1}^{n-1}{k}^{1-\alpha }<{\displaystyle \frac{n^{2-\alpha }}{2-\alpha }}.$$

The error of (35) satisfies

$$E_n^3{h}^2={\displaystyle \frac{h^{4-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\sum _{k=1}^{n-1}{E}_{n-k}^4{k}^{1-\alpha },$$

$$|E_n^3|\le {\displaystyle \frac{h^{2-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\sum _{k=1}^{n-1}\left|E_{n-k}^4\right|k^{1-\alpha }<{\displaystyle \frac{M_4{h}^{2-\alpha }}{12\mathsf{\Gamma }(2-\alpha )}}\sum _{k=1}^{n-1}{k}^{1-\alpha },$$

$$|E_n^3|<{\displaystyle \frac{M_4{h}^{2-\alpha }{n}^{2-\alpha }}{12\mathsf{\Gamma }(3-\alpha )}}={\displaystyle \frac{M_4{x}_n^{2-\alpha }}{12\mathsf{\Gamma }(3-\alpha )}}.$$

□

Let $G\left(t\right)={(x-t)}^{\beta }(g\left(t\right)-g\left(x\right))$, where $g\in C^2[0,x]$ and $x=x_n$. Denote

$${\overline{M}}_i=\underset{0\le t\le x}{max}\left|g^{\left(i\right)}\left(t\right)\right|.$$

The trapezoidal rule of the function G on the interval $[0,x]$ is defined as:

$${\mathcal{T}}_{n}G=h\left({\displaystyle \frac{G\left(0\right)}{2}}+\sum _{k=1}^{n-1}G\left(kh\right)+{\displaystyle \frac{G\left(x\right)}{2}}\right).$$

Claim 9.

Let $0<\beta <1$. Then

$${\int }_0^{x}G\left(x\right)dx={\mathcal{T}}_{n}G+E_n^4{h}^2,$$

where

$$|E_n|<{\displaystyle \frac{{\overline{M}}_1{x}^{\beta }}{3}}+{\displaystyle \frac{{\overline{M}}_2{x}^{\beta +1}}{12(\beta +1)}}.$$

Proof. 

The function G has first and second derivatives

$$G^{\prime }\left(t\right)=\beta {(x-t)}^{\beta -1}\left(g\left(x\right)-g\left(t\right)\right)+{(x-t)}^{\beta }{g}^{\prime }\left(t\right),$$

$$G^{\prime \prime }\left(t\right)=(1-\beta )\beta {(x-t)}^{\beta -2}\left(g\left(x\right)-g\left(t\right)\right)-2\beta {(x-t)}^{\beta -1}{g}^{\prime }\left(t\right)+{(x-t)}^{\beta }{g}^{\prime \prime }\left(t\right).$$

From the Mean Value Theorem

$$G^{\prime \prime }\left(t\right)=(1-\beta )\beta {(x-t)}^{\beta -1}{g}^{\prime }\left({\theta }_t\right)-2\beta {(x-t)}^{\beta -1}{g}^{\prime }\left(t\right)+{(x-t)}^{\beta }{g}^{\prime \prime }\left(t\right),$$

where ${\theta }_t\in (t,x)$. Hence

$$|G^{\prime \prime }{\left(t\right)|\le (1-\beta )\beta (x-t)}^{\beta -1}|g^{\prime }\left({\theta }_t\right)|+2\beta {(x-t)}^{\beta -1}|g^{\prime }\left(t\right)|+{(x-t)}^{\beta }\left|g^{\prime \prime }\left(t\right)\right|,$$

$$|G^{\prime \prime }\left(t\right)|\le (3-\beta )\beta {\overline{M}}_1{(x-t)}^{\beta -1}+{\overline{M}}_2{(x-t)}^{\beta }.$$

The error of the trapezoidal rule satisfies

$$E_n^4={\displaystyle \frac{1}{12}}\left(G^{\prime }\left(0\right)-G^{\prime }\left(x\right)\right)+{\displaystyle \frac{1}{2}}\sum _{k=0}^{n-1}{\int }_{kh}^{(k+1)h}{B}_2\left({\displaystyle \frac{t}{h}}-k\right)G^{\prime \prime }\left(t\right)dt,$$

where $B_2\left(t\right)$ is the second Bernoulli polynomial

$$B_2\left(t\right)={\displaystyle \frac{1}{6}}-t+t^2={\displaystyle \frac{1}{6}}-t(1-t).$$

The polynomial $B_2$ satisfies $|B_2\left(t\right)|\le 1/6$ for $t\in [0,1]$. Therefore

$$|E_n^4|={\displaystyle \frac{G^{\prime }\left(0\right)}{12}}+{\displaystyle \frac{1}{2}}\sum _{k=0}^{n-1}{\int }_{kh}^{(k+1)h}\left|B_2\left({\displaystyle \frac{t}{h}}-k\right)G^{\prime \prime }\left(t\right)\right|dt<{\displaystyle \frac{|G^{\prime }\left(0\right)|}{12}}+{\displaystyle \frac{1}{12}}{\int }_0^x\left|G^{\prime \prime }\left(t\right)\right|dt$$

because $G^{\prime }\left(x\right)=0$. The first derivative $G^{\prime }$ has a value at zero

$$G^{\prime }\left(0\right)=\beta x^{\beta -1}\left(g\left(x\right)-g\left(0\right)\right)+x^b{g}^{\prime }\left(0\right)=\beta x^{\beta }{g}^{\prime }\left({\phi }_t\right)+x^{\beta }{g}^{\prime }\left(0\right),$$

where ${\phi }_t\in (0,x)$, which implies that

$$|G^{\prime }\left(0\right)|\le (\beta +1)x^{\beta }{\overline{M}}_1.$$

The coefficient $E_n^4$ of the trapezoidal approximation error satisfies the estimate

$$|E_n^4|<{\displaystyle \frac{(\beta +1)x^{\beta }{\overline{M}}_1}{12}}+{\displaystyle \frac{1}{12}}\left((3-\beta )\beta {\overline{M}}_1{\int }_0^x{(x-t)}^{\beta -1}dt+{\overline{M}}_2{\int }_0^x{(x-t)}^{\beta }dt\right),$$

$$|E_n^4|<{\displaystyle \frac{(\beta +1)x^{\beta }{\overline{M}}_1}{12}}+{\displaystyle \frac{1}{12}}\left((3-\beta )x^{\beta }{\overline{M}}_1+{\displaystyle \frac{{\overline{M}}_2{x}^{\beta +1}}{\beta +1}}\right)={\displaystyle \frac{{\overline{M}}_1{x}^{\beta }}{3}}+{\displaystyle \frac{{\overline{M}}_2{x}^{\beta +1}}{12(\beta +1)}}.$$

□

Let

$$g\left(t\right)={\displaystyle \frac{f\left(x\right)-f\left(t\right)}{x-t}}.$$

Claim 10.

Let $f\in C^3[0,x]$. Then

$${\overline{M}}_1\le {\displaystyle \frac{M_2}{2}},{\overline{M}}_2\le {\displaystyle \frac{M_3}{3}}.$$

Proof. 

From Taylor’s theorem

$$g^{\prime }\left(t\right)={\displaystyle \frac{f\left(x\right)-f\left(t\right)-f^{\prime }\left(t\right)(x-t)}{{(x-t)}^2}}={\displaystyle \frac{f^{\prime \prime }\left({\theta }_t\right)}{2}},$$

$$g^{\prime \prime }\left(t\right)={\displaystyle \frac{2f\left(x\right)-2f\left(t\right)-2(x-t)f^{\prime }\left(t\right)-{(x-t)}^2{f}^{\prime \prime }\left(t\right)}{{(x-t)}^3}}={\displaystyle \frac{f^{\prime \prime \prime }\left({\phi }_t\right)}{3}},$$

where $t<{\theta }_t,{\phi }_t<x$. Therefore

$$|g^{\prime }\left(t\right)|\le {\displaystyle \frac{|f^{\prime \prime }\left({\theta }_t\right)|}{2}}\le {\displaystyle \frac{M_2}{2}},\left|g^{\prime \prime }\left(t\right)\right|\le {\displaystyle \frac{|f^{\prime \prime \prime }\left({\phi }_t\right)|}{3}}\le {\displaystyle \frac{M_3}{3}}.$$

□

By integrating by parts the formula in the definition of Caputo derivative we find

$$\begin{array}{cc}\hfill f^{\left(\alpha \right)}\left(x\right)& ={\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}{\int }_0^x{\displaystyle \frac{f^{\prime }\left(t\right)}{{(x-t)}^{\alpha }}}dt=-{\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}{\int }_0^x{f}^{\prime }\left(t\right)d{\displaystyle \frac{{(x-t)}^{1-\alpha }}{1-\alpha }}\hfill \\ \hfill & =-{\left.{\displaystyle \frac{f^{\prime }\left(t\right){(x-t)}^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\right|}_0^x+{\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )}}{\int }_0^x{(x-t)}^{1-\alpha }d{f}^{\prime }\left(t\right),\hfill \end{array}$$

$$f^{\left(\alpha \right)}\left(x\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )}}{\int }_0^x{(x-t)}^{1-\alpha }{f}^{\prime \prime }\left(t\right)dt+{\displaystyle \frac{f^{\prime }\left(0\right)x^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}.$$

(37)

In the following theorem, we obtain the second-order expansion formula of the L1 approximation and derive an error estimate.

Theorem 11.

Let $f\in C^5[0,x_n]$. Then

$${\mathcal{L}}_{n}f=f_n^{\left(\alpha \right)}+{\displaystyle \frac{s_n{f}_n^{\prime \prime }{h}^{2-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}+C_n{h}^2,$$

(38)

where

$$|C_n|<{\displaystyle \frac{36M_3{x}_n^{1-\alpha }+45M_4{x}_n^{2-\alpha }+2M_5{x}_n^{3-\alpha }}{36\mathsf{\Gamma }(4-\alpha )}}.$$

Proof. 

By adding and subtracting $f_n^{\prime \prime }$ in (37) we get

$$f_n^{\left(\alpha \right)}={\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )}}{\int }_0^{x_n}{(x_n-t)}^{1-\alpha }\left(f^{\prime \prime }\left(t\right)-f_n^{\prime \prime }\right)dt+{\displaystyle \frac{f_n^{\prime \prime }}{\mathsf{\Gamma }(2-\alpha )}}{\int }_0^{x_n}{(x_n-t)}^{1-\alpha }dt+{\displaystyle \frac{x_n^{1-\alpha }{f}_0^{\prime }}{\mathsf{\Gamma }(2-\alpha )}},$$

$$f_n^{\left(\alpha \right)}={\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )}}{\int }_0^{x_n}{(x_n-t)}^{1-\alpha }\left(f^{\prime \prime }\left(t\right)-f_n^{\prime \prime }\right)dt+{\displaystyle \frac{x_n^{2-\alpha }{f}_n^{\prime \prime }}{\mathsf{\Gamma }(3-\alpha )}}+{\displaystyle \frac{x^{1-\alpha }{f}_0^{\prime }}{\mathsf{\Gamma }(2-\alpha )}}.$$

From Claim 9 and Claim 10 the trapezoidal rule for the function

$${(x_n-t)}^{1-\alpha }\left(f^{\prime \prime }\left(t\right)-f_n^{\prime \prime }\right)={(x_n-t)}^{2-\alpha }g\left(t\right),g\left(t\right)={\displaystyle \frac{f^{\prime \prime }\left(t\right)-f_n^{\prime \prime }}{t-x_n}}$$

has a second order accuracy

$$\begin{array}{cc}\hfill f_n^{\left(\alpha \right)}={\displaystyle \frac{x_n^{2-\alpha }{f}_n^{\prime \prime }}{\mathsf{\Gamma }(3-\alpha )}}+{\displaystyle \frac{x_n^{1-\alpha }{f}_0^{\prime }}{\mathsf{\Gamma }(2-\alpha )}}+{\displaystyle \frac{h^{2-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}& \sum _{k=1}^{n-1}{k}^{1-\alpha }\left(f_{n-k}^{\prime \prime }-f_n^{\prime \prime }\right)\hfill \\ \hfill & +{\displaystyle \frac{h^{2-\alpha }{n}^{1-\alpha }(f_0^{\prime \prime }-f_n^{\prime \prime })}{2\mathsf{\Gamma }(2-\alpha )}}+E_n^5{h}^2,\hfill \end{array}$$

where

$$|E_n^5|<{\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )}}\left({\displaystyle \frac{{\overline{M}}_3{x}_n^{2-\alpha }}{3}}+{\displaystyle \frac{{\overline{M}}_4{x}_n^{3-\alpha }}{12(3-\alpha )}}\right)<{\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )}}\left({\displaystyle \frac{M_4{x}_n^{2-\alpha }}{6}}+{\displaystyle \frac{M_5{x}_n^{3-\alpha }}{36(3-\alpha )}}\right).$$

From Claim 8

$$\begin{array}{cc}\hfill f_n^{\left(\alpha \right)}={\mathcal{L}}_{n}f-& {\displaystyle \frac{n^{1-\alpha }(f_1-f_0)}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}+{\displaystyle \frac{x_n^{2-\alpha }{f}_n^{\prime \prime }}{\mathsf{\Gamma }(3-\alpha )}}+{\displaystyle \frac{x_n^{1-\alpha }{f}_0^{\prime }}{\mathsf{\Gamma }(2-\alpha )}}\hfill \\ \hfill & +{\displaystyle \frac{h^{2-\alpha }{n}^{1-\alpha }(f_0^{\prime \prime }-f_n^{\prime \prime })}{2\mathsf{\Gamma }(2-\alpha )}}-{\displaystyle \frac{h^{2-\alpha }{f}_n^{\prime \prime }}{\mathsf{\Gamma }(2-\alpha )}}\sum _{k=1}^{n-1}{k}^{1-\alpha }+E_n^6{h}^2,\hfill \end{array}$$

where $E_n^6=E_n^5+E_n^3$,

$$\begin{array}{cc}\hfill |E_n^6|<|E_n^5|+|E_n^3|& <{\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )}}\left({\displaystyle \frac{M_4{x}_n^{2-\alpha }}{6}}+{\displaystyle \frac{M_5{x}_n^{3-\alpha }}{36(3-\alpha )}}\right)+{\displaystyle \frac{M_4{x}_n^{2-\alpha }}{12\mathsf{\Gamma }(3-\alpha )}}\hfill \\ \hfill & ={\displaystyle \frac{x_n^{2-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\left({\displaystyle \frac{M_4}{6}}+{\displaystyle \frac{M_5{x}_n}{36(3-\alpha )}}+{\displaystyle \frac{M_4}{12(2-\alpha )}}\right)\hfill \\ \hfill & ={\displaystyle \frac{x_n^{2-\alpha }}{36\mathsf{\Gamma }(4-\alpha )}}\left(3(3-\alpha )(5-2\alpha )M_4+(2-\alpha )M_5{x}_n\right),\hfill \end{array}$$

$$|E_n^6|<{\displaystyle \frac{45M_4{x}_n^{2-\alpha }+2M_5{x}_n^{3-\alpha }}{36\mathsf{\Gamma }(4-\alpha )}}.$$

Therefore

$$\begin{array}{cc}\hfill {\mathcal{L}}_{n}f=f^{\left(\alpha \right)}\left(x\right)+& {\displaystyle \frac{n^{1-\alpha }(f_1-f_0-h{f}_0^{\prime }-h^2{f}_0^{\prime \prime }/2)}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\hfill \\ \hfill & -{\displaystyle \frac{h^{2-\alpha }{f}_n^{\prime \prime }}{\mathsf{\Gamma }(2-\alpha )}}\left({\displaystyle \frac{n^{2-\alpha }}{2-\alpha }}-{\displaystyle \frac{n^{1-\alpha }}{2}}-\sum _{k=1}^{n-1}{k}^{1-\alpha }\right)+E_n^6{h}^2.\hfill \end{array}$$

From Taylor’s theorem

$$(f_1-f_0-h{f}_0^{\prime }-h^2{f}_0^{\prime \prime }/2)n^{1-\alpha }{h}^{-\alpha }=E_n^7{h}^2,$$

where

$$|E_n^7|\le n^{1-\alpha }{h}^{1-\alpha }{\displaystyle \frac{M_3}{6}}={\displaystyle \frac{M_3{x}_n^{1-\alpha }}{6}}$$

L1 approximation has a second-order expansion formula

$$\begin{array}{c}\hfill {\mathcal{L}}_{n}f=f_n^{\left(\alpha \right)}+{\displaystyle \frac{s_n{f}_n^{\prime \prime }{h}^{2-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}+C_n{h}^2,\end{array}$$

where

$$s_n=\sum _{k=1}^{n-1}{k}^{1-\alpha }+{\displaystyle \frac{n^{1-\alpha }}{2}}-{\displaystyle \frac{n^{2-\alpha }}{2-\alpha }}$$

and

$$\begin{array}{cc}\hfill |C_n|<|E_n^6|+|E_n^7|/\mathsf{\Gamma }(2-\alpha )& <{\displaystyle \frac{M_3{x}_n^{1-\alpha }}{6\mathsf{\Gamma }(2-\alpha )}}+{\displaystyle \frac{45M_4{x}_n^{2-\alpha }+2M_5{x}_n^{3-\alpha }}{36\mathsf{\Gamma }(4-\alpha )}}\hfill \\ \hfill & <{\displaystyle \frac{6(2-\alpha )(3-\alpha )M_3{x}_n^{1-\alpha }+45M_4{x}_n^{2-\alpha }+2M_5{x}_n^{3-\alpha }}{36\mathsf{\Gamma }(4-\alpha )}},\hfill \end{array}$$

$$|C_n|<{\displaystyle \frac{36M_3{x}_n^{1-\alpha }+45M_4{x}_n^{2-\alpha }+2M_5{x}_n^{3-\alpha }}{36\mathsf{\Gamma }(4-\alpha )}}.$$

□

Corollary 12.

Let $f\in C^5[0,x_n]$. Then

$$\begin{array}{c}\hfill {\mathcal{L}}_{n}f=f_n^{\left(\alpha \right)}+{\displaystyle \frac{\zeta (\alpha -1)f_n^{\prime \prime }{h}^{2-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}+B_n{\displaystyle \frac{h^{2-\alpha }}{n^{\alpha }}}+C_n{h}^2,\end{array}$$

where

$$|B_n|<{\displaystyle \frac{M_2}{12\mathsf{\Gamma }(1-\alpha )}},\left|C_n\right|<{\displaystyle \frac{36M_3{x}_n^{1-\alpha }+45M_4{x}_n^{2-\alpha }+2M_5{x}_n^{3-\alpha }}{36\mathsf{\Gamma }(4-\alpha )}}.$$

Proof. 

From (36) the numbers $s_n$ converge to $\zeta (\alpha -1)$ and

$$s_n=\zeta (\alpha -1)+{\displaystyle \frac{1-\alpha }{12n^{\alpha }}}-{\displaystyle \frac{(1+\alpha )(1-\alpha )\alpha }{720n^{2+\alpha }}}+\mathcal{O}\left({\displaystyle \frac{1}{n^{3+a}}}\right),$$

$$0<s_n-\zeta (\alpha -1)<{\displaystyle \frac{1-\alpha }{12n^{\alpha }}}.$$

Therefore the coefficient $B_n$ satisfies

$$B_n={\displaystyle \frac{n^{\alpha }(s_n-\zeta (\alpha -1))}{\mathsf{\Gamma }(2-\alpha )}}{f}_n^{\prime \prime },$$

$$|B_n|=n^{\alpha }(s_n-\zeta (a-1))\left|f_n^{\prime \prime }\right|<{\displaystyle \frac{M_2(1-\alpha )}{12\mathsf{\Gamma }(2-\alpha )}}={\displaystyle \frac{M_2}{12\mathsf{\Gamma }(1-\alpha )}}.$$

□

By approximating the second derivative $f_n^{\left(\alpha \right)}$ in the expansion formula (38) of the L1 approximation with ${\mathcal{B}}_{n-1}f$ we obtain a second order approximation of the fractional derivative

$${\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\gamma }_k^{\left(\alpha \right)}{f}_{n-k}=f_n^{\left(\alpha \right)}+\mathcal{O}\left(h^2\right),$$

(39)

where

$$\begin{array}{cc}& {\gamma }_0^{\left(\alpha \right)}=1-s_n(1-b),{\gamma }_1^{\left(\alpha \right)}=2^{1-\alpha }-2+s_n(1-b)(2-b),\hfill \\ & {\gamma }_k^{\left(\alpha \right)}={(k-1)}^{1-\alpha }-2k^{1-\alpha }+{(k+1)}^{1-\alpha }-s_n{(1-b)}^3{b}^{k-2},\mathrm{for}2\le k\le n-4,\hfill \\ & {\gamma }_{n-3}^{\left(\alpha \right)}={(n-4)}^{1-\alpha }-2{(n-3)}^{1-\alpha }+{(n-2)}^{1-\alpha }-s_n(1-3b+3b^2)b^{n-5},\hfill \\ & {\gamma }_{n-2}^{\left(\alpha \right)}={(n-3)}^{1-\alpha }-2{(n-2)}^{1-\alpha }+{(n-1)}^{1-\alpha }-s_n(1-3b)b^{n-4},\hfill \\ & {\gamma }_{n-1}^{\left(\alpha \right)}={(n-2)}^{1-\alpha }-2{(n-1)}^{1-\alpha }+n^{1-\alpha }-s_n{b}^{n-3},{\gamma }_n^{\left(\alpha \right)}={(n-1)}^{1-\alpha }-n^{1-\alpha }.\hfill \end{array}$$

By substituting $s_n$ with the value of the zeta function $\zeta (\alpha -1)$ we obtain a second order asymptotic approximation of the fractional derivative

$${\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\omega }_k^{\left(\alpha \right)}{f}_{n-k}=f_n^{\left(\alpha \right)}+B_n{\displaystyle \frac{h^{2-\alpha }}{n^{\alpha }}}+\mathcal{O}\left(h^2\right),$$

(40)

where

$$\begin{array}{cc}\hfill & {\omega }_0^{\left(\alpha \right)}=1-\zeta (\alpha -1)(1-b),{\omega }_1^{\left(\alpha \right)}=2^{1-\alpha }-2+\zeta (\alpha -1)(1-b)(2-b),\hfill \\ \hfill & {\omega }_k^{\left(\alpha \right)}={(k-1)}^{1-\alpha }-2k^{1-\alpha }+{(k+1)}^{1-\alpha }-\zeta (\alpha -1){(1-b)}^3{b}^{k-2},\mathrm{for}2\le k\le n-4,\hfill \\ \hfill & {\omega }_{n-3}^{\left(\alpha \right)}={(n-4)}^{1-\alpha }-2{(n-3)}^{1-\alpha }+{(n-2)}^{1-\alpha }-\zeta (\alpha -1)(1-3b+3b^2)b^{n-5},\hfill \\ \hfill & {\omega }_{n-2}^{\left(\alpha \right)}={(n-3)}^{1-\alpha }-2{(n-2)}^{1-\alpha }+{(n-1)}^{1-\alpha }-\zeta (\alpha -1)(1-3b)b^{n-4},\hfill \\ \hfill & {\omega }_{n-1}^{\left(\alpha \right)}={(n-2)}^{1-\alpha }-2{(n-1)}^{1-\alpha }+n^{1-\alpha }-\zeta (\alpha -1)b^{n-3},{\omega }_n^{\left(\alpha \right)}={(n-1)}^{1-\alpha }-n^{1-\alpha }.\hfill \end{array}$$

The errors of approximations (39) and (40) satisfy the following estimates.

Corollary 13.

Let $b=1-\alpha +{\alpha }^2$. Then

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\gamma }_k^{\left(\alpha \right)}{f}_{n-k}=f_n^{\left(\alpha \right)}+A_n{h}^2,\end{array}$$

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\omega }_k^{\left(\alpha \right)}{f}_{n-k}=f_n^{\left(\alpha \right)}+B_n{\displaystyle \frac{h^{2-\alpha }}{n^{\alpha }}}+A_n{h}^2,\end{array}$$

where $|B_n|<{\displaystyle \frac{M_2}{12\mathsf{\Gamma }(1-\alpha )}}$ and

$$|A_n|<\left({\displaystyle \frac{x_n^{1-\alpha }}{(3-\alpha )(2-\alpha )}}+{\displaystyle \frac{2\left|\zeta \right(\alpha -1\left)\right|}{(1-\alpha )\alpha }}\right){\displaystyle \frac{M_3}{\mathsf{\Gamma }(2-\alpha )}}+{\displaystyle \frac{45M_4{x}_n^{2-\alpha }+2M_5{x}_n^{3-\alpha }}{36\mathsf{\Gamma }(4-\alpha )}}.$$

Proof. 

The zeta function is decreasing on $[-1,0]$ and takes values between $\zeta (-1)=-1/12$ and $\zeta \left(0\right)=-1/2$. Therefore

$$\zeta (\alpha -1)<s_n<\zeta (\alpha -1)+{\displaystyle \frac{1-\alpha }{12n^{\alpha }}}<0.$$

The estimates for $A_n$ and $B_n$ follow from Claim 1, Theorem 11 and Corollary 12. □

4.2. Properties of the Approximations

Now we prove that, when the parameter $b=1-\alpha +{\alpha }^2$, the weights of of approximations (39) and (40) satisfy properties (2). The values $s_n$ and $\zeta (\alpha -1)$ are negative, while the weights ${\gamma }_0^{\left(\alpha \right)}$ and ${\omega }_0^{\left(\alpha \right)}$ are positive; ${\gamma }_1^{\left(\alpha \right)}$ and ${\omega }_1^{\left(\alpha \right)}$ are negative. In the following we show that the remaining weights ${\omega }_n^{\left(\alpha \right)}$ and ${\gamma }_n^{\left(\alpha \right)}$ are negative. The proof relies on the inequalities from the claims below.

Claim 14.

Let $0<b<1$. Then

$$x^2{b}^x\le {\displaystyle \frac{4}{e^2{(lnb)}^2}}.$$

Proof. 

Let $f\left(x\right)=x^2{b}^x$. Then

$$f^{\prime }\left(x\right)=2x{b}^x+x^2{b}^{x}lnb=x(2+xlnb)b^x.$$

The function f has a maximum when $x=-2/lnb$.

$$f\left(-{\displaystyle \frac{2}{lnb}}\right)={\displaystyle \frac{4}{e^2{(lnb)}^2}}.$$

□

Claim 15.

Let $0<x<1/3$. Then

$$ln(1+x)>{\displaystyle \frac{2x}{2+x}}.$$

Proof. 

$$g\left(x\right)=ln(1+x)-{\displaystyle \frac{2x}{2+x}},$$

$$g^{\prime }\left(x\right)={\displaystyle \frac{x^2}{(1+x){(2+x)}^2}}>0.$$

The function g is positive because it is increasing and $g\left(0\right)=0$. □

Lemma 16.

Let $b=1-\alpha +{\alpha }^2$. Then

$${\omega }_n^{\left(\alpha \right)}<0,(1<n<N-3).$$

Proof. 

When $n\ge 2$, approximation (40) has weights

$${\omega }_n^{\left(\alpha \right)}={(n+1)}^{1-\alpha }-2n^{1-\alpha }+{(n-1)}^{1-\alpha }-\zeta (\alpha -1){\alpha }^3{(1-\alpha )}^3{b}^{n-2}.$$

The zeta function is decreasing on $(-1,0)$ and $\zeta (\alpha -1)>\zeta \left(0\right)=-0.5$. It is sufficient to prove that

$$|{(n+1)}^{1-\alpha }-2n^{1-\alpha }+{(n-1)}^{1-\alpha }|>0.5{\alpha }^3{(1-\alpha )}^3{b}^{n-2}.$$

(41)

Let $f\left(x\right)=x^{1-\alpha }$. From Mean Value Theorem

$${(n+1)}^{1-\alpha }-2n^{1-\alpha }+{(n-1)}^{1-\alpha }=f^{\prime \prime }\left(\theta \right)=-{\displaystyle \frac{\alpha (1-\alpha )}{{\theta }^{1+\alpha }}}$$

for some $\theta \in (n-1,n+1)$. Therefore

$$|{(n+1)}^{1-\alpha }-2n^{1-\alpha }+{(n-1)}^{1-\alpha }|>{\displaystyle \frac{\alpha (1-\alpha )}{{(n+1)}^{1+\alpha }}}>{\displaystyle \frac{\alpha (1-\alpha )}{{(n+1)}^2}}.$$

Inequality (41) follows from

$${\displaystyle \frac{\alpha (1-a)}{{(n+1)}^2}}>0.5{\alpha }^3{(1-\alpha )}^3{b}^{n-2},{\displaystyle \frac{2}{{\alpha }^2{(1-\alpha )}^2}}>{(n+1)}^2{b}^{n-2},$$

$${(n+1)}^2{b}^{n+1}<{\displaystyle \frac{2b^3}{{(1-b)}^2}}.$$

From Claim 14

$${(n+1)}^2{b}^{n+1}<{\displaystyle \frac{4}{e^2{(lnb)}^2}}<{\displaystyle \frac{2b^3}{{(1-b)}^2}}.$$

It is sufficient to prove that

$${(lnb)}^2>{\displaystyle \frac{{(1-b)}^2}{2b^3}}.$$

Substitute $b={\displaystyle \frac{1}{1+r}}$.

$${ln}^2(1+r)>{\displaystyle \frac{r^2(1+r)}{2}}.$$

When $\alpha \in (0,1)$, the parameter $b\in \left[{\displaystyle \frac{3}{4}},1\right)$, because $b=1-\alpha (1-\alpha )$. Then $r=1/b-1$ and $r\in \left(0,{\displaystyle \frac{1}{3}}\right]$. From Claim 15

$${ln}^2(1+r)>{\displaystyle \frac{4r^2}{{(2+r)}^2}}>{\displaystyle \frac{r^2(1+r)}{2}},$$

$$8>(1+r){(2+r)}^2.$$

The function $g\left(r\right)=(1+r){(2+r)}^2$ is increasing, because

$$g^{\prime }\left(r\right)=(2+r)(4+3r)>0.$$

The function g has a maximum at $r=1/3$.

$$g\left(r\right)\le g\left(1/3\right)={\displaystyle \frac{4}{3}}·{\displaystyle \frac{49}{9}}=7.259<8.$$

□

From the properties of the L1-approximation and the constructions of (39) and (40), their weights satisfy ${\sum }_{n=0}^N{\gamma }_n^{\left(\alpha \right)}={\sum }_{n=0}^N{\omega }_n^{\left(\alpha \right)}=0$. Therefore, approximation (40) satisfies properties (2). The weights of approximation (39) also satisfy the properties in (2), since $\zeta (\alpha -1)<s_n<0$. In the following claim, we establish a lower bound for the last weight of both approximations.

Claim 17.

$$|{\gamma }_N^{\left(\alpha \right)}|=|{\omega }_N^{\left(\alpha \right)}|>{\displaystyle \frac{1-\alpha }{N^{\alpha }}}.$$

Proof. 

From the binomial formula

$${\gamma }_N^{\left(\alpha \right)}={\omega }_N^{\left(\alpha \right)}={(N-1)}^{1-\alpha }-N^{1-\alpha }=\sum _{k=1}^{\infty }{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{1-\alpha }{k}}\right){\displaystyle \frac{1}{N^{k-1+\alpha }}}.$$

The values of ${(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{1-\alpha }{k}}\right)$ are negative. Hence

$${\gamma }_N^{\left(\alpha \right)}={\omega }_N^{\left(\alpha \right)}<-{\displaystyle \frac{1-\alpha }{N^{\alpha }}}.$$

□

4.3. Shifted Approximations for the Fractional Derivative

Now we derive shifted approximations of the fractional derivative on the first two-point and three-point stencils of the uniform mesh. These shifted approximations are used to specify the initial conditions in the numerical solutions of fractional differential equations that employ approximations (39) and (40) of the fractional derivative. From Taylor’s theorem

$$f^{\prime }\left(t\right)=f_0^{\prime }+t{f}_0^{\prime \prime }+{\displaystyle \frac{t^2}{2}}{f}_0^{\prime \prime \prime }+\mathcal{O}\left(t^3\right).$$

By substituting the first derivative in the definition of the Caputo fractional derivative (1) with the second Taylor polynomial, we obtain

$$f^{\left(\alpha \right)}\left(x\right)=f_0^{\prime }{D}^{\alpha }x+{\displaystyle \frac{f_0^{\prime \prime }}{2}}{D}^{\alpha }{x}^2+{\displaystyle \frac{f_0^{\prime \prime \prime }}{6}}{D}^{\alpha }{x}^3+\mathcal{O}\left(x^{4-\alpha }\right),$$

$$f^{\left(\alpha \right)}\left(x\right)={\displaystyle \frac{\mathsf{\Gamma }\left(2\right)x^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}{f}_0^{\prime }+{\displaystyle \frac{\mathsf{\Gamma }\left(3\right)x^{2-\alpha }}{\mathsf{\Gamma }(3-\alpha )}}{\displaystyle \frac{f_0^{\prime \prime }}{2}}+{\displaystyle \frac{\mathsf{\Gamma }\left(4\right)x^{3-\alpha }}{\mathsf{\Gamma }(4-\alpha )}}{\displaystyle \frac{f_0^{\prime \prime \prime }}{6}}+\mathcal{O}\left(x^{4-\alpha }\right),$$

$$f^{\left(\alpha \right)}\left(x\right)={\displaystyle \frac{x^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\left(f_0^{\prime }+{\displaystyle \frac{x{f}_0^{\prime \prime }}{2-\alpha }}+{\displaystyle \frac{x^2{f}_0^{\prime \prime \prime }}{(2-\alpha )(3-\alpha )}}\right)+\mathcal{O}\left(x^{4-\alpha }\right).$$

Substitute $x=rh$.

$$f^{\left(\alpha \right)}\left(rh\right)={\displaystyle \frac{{\left(rh\right)}^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\left(f_0^{\prime }+{\displaystyle \frac{rh{f}_0^{\prime \prime }}{2-\alpha }}+{\displaystyle \frac{r^2{h}^2{f}_0^{\prime \prime \prime }}{(2-\alpha )(3-\alpha )}}\right)+\mathcal{O}\left(h^{4-\alpha }\right).$$

(42)

Now we obtain a shifted approximation of the fractional derivative on the two-point stencil $0,h$ from the approximation

$$f^{\left(\alpha \right)}\left(rh\right)={\displaystyle \frac{{\left(rh\right)}^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\left(f_0^{\prime }+{\displaystyle \frac{rh}{2-\alpha }}{f}_0^{\prime \prime }\right)+E_n^8,$$

where $|E_n^8|<M_3{\left(rh\right)}^{3-\alpha }/\mathsf{\Gamma }(4-\alpha )$. Let

$$F_1\left(h\right)=c_0{f}_0+c_1{f}_1-f_0^{\prime }-{\displaystyle \frac{rh}{2-\alpha }}{f}_0^{\prime \prime }.$$

The function $F_1$ has a Taylor expansion of order two at the origin; that is,

$$F_1\left(h\right)=(c_0+c_1)f_0+\left(c_{1}h-1\right)f_0^{\prime }+\left({\displaystyle \frac{c_1{h}^2}{2}}-{\displaystyle \frac{bh}{2-\alpha }}\right)f_0^{\prime \prime }+\mathcal{O}\left(h^2\right).$$

By setting the coefficients equal to zero, we obtain the system of equations

$$\left\{\begin{array}{c}{c}_0+c_1=0,\hfill \\ c_{1}h-1=0,\hfill \\ {\displaystyle \frac{c_1{h}^2}{2}}-{\displaystyle \frac{rh}{2-\alpha }}=0.\hfill \end{array}\right.$$

The system of equations has a solution

$$c_1={\displaystyle \frac{1}{h}},c_0=-{\displaystyle \frac{1}{h}},r={\displaystyle \frac{2-\alpha }{2}}=1-{\displaystyle \frac{\alpha }{2}}.$$

From Taylor’s theorem and the values of the coefficients given above, we obtain

$$F_1\left(h\right)=E_n^9{h}^2,$$

where $|E_n^9|\le M_3/6$. Therefore

$$f_{1-\alpha /2}^{\left(\alpha \right)}={\displaystyle \frac{{\left(1-\frac{\alpha }{2}\right)}^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\left(f_1-f_0\right)+E_n^{10}{h}^{3-\alpha },$$

(43)

where

$$E_n^{10}<{\displaystyle \frac{r^{3-\alpha }{M}_3}{\mathsf{\Gamma }(4-\alpha )}}+{\displaystyle \frac{r^{1-\alpha }{M}_3}{6\mathsf{\Gamma }(2-\alpha )}}<{\displaystyle \frac{2M_3}{\mathsf{\Gamma }(4-\alpha )}}.$$

A shifted approximation on the three-point stencil $0,h,2h$ is obtained from (42) for $r=1$.

$$f^{\left(\alpha \right)}\left(h\right)={\displaystyle \frac{h^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\left(f_0^{\prime }+{\displaystyle \frac{h}{2-\alpha }}{f}_0^{\prime \prime }+{\displaystyle \frac{h^2{f}_0^{\prime \prime \prime }}{(2-\alpha )(3-\alpha )}}\right)+E_n^{11}{h}^{4-\alpha },$$

where $|E_n^{11}|<M_4/\mathsf{\Gamma }(5-\alpha )$. Let

$$F_2\left(h\right)={\displaystyle \frac{1}{h}}\left(c_{0}f\left(0\right)+c_{1}f\left(h\right)+c_{2}f\left(2h\right)\right)-f^{\prime }\left(0\right)-{\displaystyle \frac{h}{2-\alpha }}{f}^{\prime \prime }\left(0\right)-{\displaystyle \frac{h^2{f}_0^{\prime \prime \prime }}{(2-\alpha )(3-\alpha )}}.$$

The function $F_1$ has a Taylor expansion of order two at the origin; that is,

$$F_2\left(h\right)={\displaystyle \frac{f_0}{h}}(c_0+c_1+c_2)+f_0^{\prime }(c_1+2c_2-1)+\left({\displaystyle \frac{1}{2}}{c}_1+2c_2-{\displaystyle \frac{1}{2-\alpha }}\right)f_0^{\prime \prime }h+\mathcal{O}\left(h^2\right).$$

By setting the coefficients equal to zero, we obtain the system of equations

$$\left\{\begin{array}{c}{c}_0+c_1+c_2=0,\hfill \\ c_1+2c_2=1,\hfill \\ {\displaystyle \frac{c_1}{2}}+2c_2={\displaystyle \frac{1}{2-\alpha }},\hfill \end{array}\right.$$

which has a solution

$$c_0={\displaystyle \frac{3\alpha -4}{2(2-\alpha )}},c_1={\displaystyle \frac{2(1-\alpha )}{2-\alpha }}={\displaystyle \frac{4(1-\alpha )}{2(2-\alpha )}},c_2={\displaystyle \frac{\alpha }{2(2-\alpha )}}.$$

From Taylor’s theorem and the values of the coefficients given above, we obtain

$$F_2\left(h\right)=E_n^{12}{h}^2,$$

where

$$|E_n^{12}|<{\displaystyle \frac{\alpha M_3}{3(3-\alpha )}}.$$

Hence

$$f^{\left(\alpha \right)}\left(h\right)={\displaystyle \frac{h^{-\alpha }}{2\mathsf{\Gamma }(3-\alpha )}}\left((3\alpha -4)f\left(0\right)+4(1-\alpha )f\left(h\right)+\alpha f\left(2h\right)\right)+E_n^{13}{h}^{3-\alpha },$$

(44)

where

$$|E_n^{13}|<{\displaystyle \frac{\alpha M_3}{3(3-\alpha )\mathsf{\Gamma }(2-\alpha )}}+{\displaystyle \frac{M_{4}h}{\mathsf{\Gamma }(5-\alpha )}}<{\displaystyle \frac{8\alpha M_3+M_4}{3\mathsf{\Gamma }(5-\alpha )}}.$$

5. Numerical Solutions of Fractional Differential Equations

Difference schemes are the main approach for the numerical solution of ordinary and partial fractional differential equations [52,53,54,55,56,57,58]. In paper [1], we construct difference schemes for the two-term ordinary fractional differential equation and the fractional subdiffusion equation, which use approximations of the fractional derivative of order $2-\alpha$, obtained in a manner similar to the construction of approximations (6) and (8). In this section, we study the difference schemes that use approximations (6) and (8). The convergence and order of the difference schemes based on the second-order asymptotic approximation (8) are proved. Consider the two-term ordinary fractional differential equation

$$y^{\left(\alpha \right)}\left(t\right)+Ly\left(t\right)=F\left(t\right),y\left(0\right)=y_0.$$

(45)

Suppose that

$${\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\lambda }_k^{\left(\alpha \right)}{f}_{n-k}=f_n^{\left(\alpha \right)}+E_n^{\lambda }$$

(46)

is an approximation of the fractional derivative that has an error term $E_n^{\lambda }$. By substituting the fractional derivative $y_n$ in equation (45) with (46), we obtain

$${\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\sum _{k=0}^n{\lambda }_k^{\left(\alpha \right)}{y}_{n-k}+L{y}_n=F_n+E_n^{\lambda },$$

$$({\lambda }_0^{\left(\alpha \right)}+L\mathsf{\Gamma }(2-\alpha )h^{\alpha })y_n=\mathsf{\Gamma }(2-\alpha )h^{\alpha }{F}_n-\sum _{k=1}^n{\lambda }_k^{\left(\alpha \right)}{y}_{n-k}+\mathsf{\Gamma }(2-\alpha )E_n^{\lambda }{h}^{\alpha }.$$

The numerical solution of equation (45) obtained using approximation (46) is computed as

$$u_m={\displaystyle \frac{1}{{\lambda }_0^{\left(\alpha \right)}+L\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\left(\mathsf{\Gamma }(2-\alpha )h^{\alpha }{F}_m-\sum _{k=1}^m{\lambda }_k^{\left(\alpha \right)}{u}_{m-k}\right).$$

(47)

The initial values of $u_1,u_2,u_3$ and $u_4$ are computed using the L1 approximation, where ${\lambda }_k^{\left(\alpha \right)}={\sigma }_k^{\left(\alpha \right)}$ for $1\le n\le 4$. Denote by $N{S}_{\gamma }$ the numerical solution (47) of equation (45) that uses approximation (6), where ${\lambda }_k^{\left(\alpha \right)}={\gamma }_k^{\left(\alpha \right)}$, and by $N{S}_{\omega }$ the numerical solution that uses approximation (8), where ${\lambda }_k^{\left(\alpha \right)}={\omega }_k^{\left(\alpha \right)}$.

Example 5.

Consider the following boundary value OFDE

$$y^{\left(\alpha \right)}\left(t\right)+Ly\left(t\right)=-t^{1-\alpha }{E}_{1,2-\alpha }(-t)+L{e}^{-t},y\left(0\right)=1.$$

(48)

Equation (48) has a solution $y\left(t\right)=e^{-t}$. The numerical results for the error and order of numerical solutions $N{S}_{\gamma }$ and $N{S}_{\omega }$ on the interval $[0,1]$ are given in Table 6 and Table 7. The error of numerical solution $N{S}_{\gamma }$ is smaller than the error of $N{S}_{\omega }$ because approximation (6) has a smaller truncation error than (8). The computational time of $N{S}_{\gamma }$ is longer that that of $N{S}_{\omega }$ because on every iteration the weights of approximation (6) are recomputed.

In the following, we prove the convergence of the numerical solution $N{S}_{\omega }$ and obtain an estimate for the error. Denote by $e_n=y_n-u_n$ the error of $N{S}_{\omega }$ at the point $t_n$. The errors $e_1,e_2,e_3$ and $e_4$ are computed as $e_0=0$ and

$$e_n={\displaystyle \frac{1}{1+L\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\left(\mathsf{\Gamma }(2-\alpha )E_n{h}^2-\sum _{k=1}^{n-1}{\sigma }_k^{\left(\alpha \right)}{e}_{n-k}\right),(1\le n\le 4),$$

where $E_n{h}^{2-\alpha }$ is the truncation error of the L1 approximation [48]. Therefore, the numerical solution $N{S}_{\omega }$ has second-order accuracy for the first four iterations. Let

$$C_4={\displaystyle \frac{1}{h^2}}max\left\{\right|e_1|,|e_2|,|e_3|,|e_4\left|\right\}.$$

The sequence of the errors of numerical solution $N{S}_{\omega }$, for $n\ge 4$ satisfies

$$e_n={\displaystyle \frac{1}{{\omega }_0^{\left(\alpha \right)}+L\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\left(\mathsf{\Gamma }(2-\alpha )A_n{h}^{2+\alpha }+\mathsf{\Gamma }(2-\alpha ){\displaystyle \frac{B_n}{n^{\alpha }}}{h}^2-\sum _{k=1}^{n-1}{\omega }_k^{\left(\alpha \right)}{e}_{n-k}\right).$$

Theorem 18.

Suppose that $L>-{\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}$. Then

$$|e_n|\le C{h}^2,$$

(49)

where $n=1,\dots ,N$ and

$$C=max\left\{C_4,{\displaystyle \frac{M_2}{12}},{\displaystyle \frac{6M_2+252M_3+45M_4+2M_5}{72(1-\alpha +L\mathsf{\Gamma }(2-a\left)\right)}}\right\}.$$

Proof. 

We prove the statement by induction on n. The estimate holds for $n\le 4$. Assume that (49) holds for all $k=1,2,\dots ,m-1$.

$$|e_m|\le {\displaystyle \frac{1}{{\omega }_0^{\left(\alpha \right)}+L\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\left(-\sum _{k=1}^{m-1}{\omega }_k^{\left(\alpha \right)}|e_{m-k}|+\mathsf{\Gamma }(2-\alpha )|B_m|{\displaystyle \frac{h^2}{m^{\alpha }}}+\mathsf{\Gamma }(2-\alpha )\left|A_m\right|h^{2+\alpha }\right).$$

Applying the induction assumption

$$|e_m|\le {\displaystyle \frac{1}{{\omega }_0^{\left(\alpha \right)}+L\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\left(C{h}^2({\omega }_0^{\left(\alpha \right)}-|{\omega }_m^{\left(\alpha \right)}\left|\right)+\mathsf{\Gamma }(2-\alpha )|B_m|{\displaystyle \frac{h^2}{m^{\alpha }}}+\mathsf{\Gamma }(2-\alpha )\left|A_m\right|h^{2+\alpha }\right).$$

From Corollary 13 and Claim 17

$$|e_m|\le {\displaystyle \frac{1}{{\omega }_0^{\left(\alpha \right)}+L\mathsf{\Gamma }(2-\alpha )h^{\alpha }}}\left(C{h}^2\left({\omega }_0^{\left(\alpha \right)}-{\displaystyle \frac{1-\alpha }{m^{\alpha }}}\right)+{\displaystyle \frac{\mathsf{\Gamma }(2-\alpha )M_2}{12\mathsf{\Gamma }(1-\alpha )}}{\displaystyle \frac{h^2}{m^{\alpha }}}+\mathsf{\Gamma }(2-\alpha )A{h}^{2+\alpha }\right).$$

Factoring out $C{h}^2$ we write

$$|e_m|\le \left({\displaystyle \frac{{\omega }_0^{\left(\alpha \right)}+\frac{\mathsf{\Gamma }(2-a)A}{C{N}^a}-\frac{1-a}{m^a}\left(1-\frac{M_2}{12C}\right)}{{\omega }_0^{\left(\alpha \right)}+{\displaystyle \frac{L\mathsf{\Gamma }(2-a)}{N^a}}}}\right)C{h}^2.$$

When $C>{\displaystyle \frac{M_2}{12}}$, the number $1-{\displaystyle \frac{M_2}{12C}}>0$. Hence

$$|e_m|\le \left({\displaystyle \frac{{\omega }_0^{\left(\alpha \right)}{N}^{\alpha }+\frac{\mathsf{\Gamma }(2-\alpha )A}{C}-(1-\alpha )\left(1-\frac{M_2}{12C}\right)}{{\omega }_0^{\left(\alpha \right)}{N}^{\alpha }+L\mathsf{\Gamma }(2-\alpha )}}\right)C{h}^2.$$

To ensure $|e_m|<C{h}^2$, it suffices to show that the coefficient is at most one:

$${\displaystyle \frac{\mathsf{\Gamma }(2-\alpha )A}{C}}-(1-\alpha )\left(1-{\displaystyle \frac{M_2}{12C}}\right)\le L\mathsf{\Gamma }(2-\alpha ),$$

$${\displaystyle \frac{\mathsf{\Gamma }(2-\alpha )A}{C}}+{\displaystyle \frac{(1-\alpha )M_2}{12C}}\le (1-\alpha +L\mathsf{\Gamma }(2-\alpha )),$$

$$C\ge {\displaystyle \frac{12\mathsf{\Gamma }(2-\alpha )A+(1-\alpha )M_2}{12(1-\alpha +L\mathsf{\Gamma }(2-\alpha \left)\right)}}.$$

(50)

From Corollary 13 and $x_m\in [0,1]$, we obtain

$$A<\left({\displaystyle \frac{1}{(3-\alpha )(2-\alpha )}}+{\displaystyle \frac{2\left|\zeta \right(\alpha -1\left)\right|}{(1-\alpha )\alpha }}\right){\displaystyle \frac{M_3}{\mathsf{\Gamma }(2-\alpha )}}+{\displaystyle \frac{45M_4+2M_5}{36\mathsf{\Gamma }(4-\alpha )}},$$

$$A<{\displaystyle \frac{7M_3}{\mathsf{\Gamma }(4-\alpha )}}+{\displaystyle \frac{45M_4+2M_5}{36\mathsf{\Gamma }(4-\alpha )}}={\displaystyle \frac{252M_3+45M_4+2M_5}{36\mathsf{\Gamma }(4-\alpha )}}.$$

Combining (50) with the bound for A, we obtain that when

$$C>{\displaystyle \frac{6M_2+252M_3+45M_4+2M_5}{72(1-\alpha +L\mathsf{\Gamma }(2-\alpha \left)\right)}}$$

estimate (49) holds, $|e_m|<C{h}^2$, completing the induction. □

In Theorem 18, we proved that when the parameter $L>-1/\mathsf{\Gamma }(1-\alpha )$ numerical solution $N{S}_{\omega }$ has second-order accuracy. The proof of the convergence and order of $N{S}_{\gamma }$ is similar. When the parameter L is negative, the errors of the two numerical solutions become large. Experimental results for the error and order of $N{S}_{\gamma }$ and $N{S}_{\omega }$ for negative values of the parameter L are presented in Table 8 and Table 9. The errors of the numerical solutions in Table 8 and Table 9 are greater than ${10}^{14}$ for $L=-4$, $L=-10$, and $L=-20$.

The numerical methods $N{S}_{\gamma }$ and $N{S}_{\omega }$ exhibit behavior similar to that of numerical method (16) for equation (14) To compute the numerical solution of equation (48) with an accuracy not exceeding ${10}^{-5}$, we use the approach from Example 2. We consider the corresponding boundary value fractional ordinary differential equation whose boundary condition coincides with the initial condition of equation (48). Its numerical solution, obtained using the L1 approximation of the fractional derivative, is used as the numerical solution of equation (48), and it has an accuracy of $\mathcal{O}\left(h^{2-\alpha }\right)$, which is sufficient to solve both equations with an error smaller than ${10}^{-5}$. The accuracy of the numerical solution can be improved by using higher-order approximations of the fractional derivative and boundary conditions at different points.

Example 6.

Consider the following boundary value OFDE

$$z^{\left(a\right)}\left(t\right)+Lz\left(t\right)=F\left(t\right)=-t^{1-a}{E}_{1,2-a}(-t)+L{e}^{-t},z\left(2\right)=1.$$

(51)

Let $h=2/N$. By approximating the fractional derivative using the L1 approximation we obtain

$${\displaystyle \frac{h^{-\alpha }}{\mathsf{\Gamma }(2-\alpha )}}\sum _{k=0}^n{\sigma }_k^{\left(\alpha \right)}{z}_n+L{z}_n=F_n+\mathcal{O}\left(h^{2-\alpha }\right).$$

The numerical solution satisfies

$$(1+\mathsf{\Gamma }(2-\alpha )L{h}^{\alpha })u_n+\sum _{k=1}^n{\sigma }_k^{\left(\alpha \right)}{u}_{n-k}=\mathsf{\Gamma }(2-\alpha )h^{\alpha }{F}_n,u_N=1,$$

(52)

where $1\le n\le N$. The numerical solution is computed with the system of $N+1$ equations, which consists of equations (52) and the boundary condition $u_N=1$. The coefficient matrix of the system has entries $1+\mathsf{\Gamma }(2-\alpha )L{h}^{\alpha }$ on the diagonal above the main diagonal and is reduced to a lower-triangular form, using $N-1$ row operations. The graphs of the exact solution of equation (48) and numerical solution (52) for $L=-10,h=0.01,\alpha =0.9$ are given on Figure 3. The experimental results for the error of the numerical solution (52) are presented in Table 10, where all errors are smaller than ${10}^{-5}$. The results in Table 8, Table 9, and Table 10 demonstrate that the numerical method (52) for equation (48) represents a significant improvement over $N{S}_{\gamma }$ and $N{S}_{\omega }$ for negative values of the parameter L.

The fractional subdiffusion equation is a fractional partial differential equation of the following form

$${\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}u(x,t)=L{u}_{xx}+F(x,t),$$

where L is the diffusion coefficient and has initial and boundary conditions

$$u(0,t)=u_0\left(t\right),u(x,0)=v\left(x\right),u(1,t)=u_1\left(t\right).$$

Let $\tau =1/M$ and $h=1/N$, where M and N are integers. Denote $u_n^m=u(nh,m\tau )$ and by $\mathcal{J}$ the rectangular grid on $[0,1]\times [0,1]$

$$\mathcal{J}=\left\{\right(nh,m\tau \left)\right|0\le n\le N,0\le m\le M\}.$$

By substituting the fractional derivative at the point $(nh,m\tau )$ with approximation (8) and the second-order partial derivative with the second-order central difference formula, we obtain

$${\displaystyle \frac{1}{\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }}}\sum _{k=0}^m{\omega }_k^{\left(\alpha \right)}{u}_n^{m-k}=L{\displaystyle \frac{u_{n-1}^m-2u_n^m+u_{n+1}^m}{h^2}}+F_n^m+A_n{\tau }^2+B_n{\displaystyle \frac{{\tau }^{2-\alpha }}{n^{\alpha }}}+D_n{h}^2,$$

$$\begin{array}{cc}\hfill {\omega }_0^{\left(\alpha \right)}{u}_n^m+\sum _{k=1}^m{\omega }_k^{\left(\alpha \right)}{u}_n^{m-k}={\displaystyle \frac{L\mathsf{\Gamma }(2-\alpha ){\tau }^a}{h^2}}(u_{n-1}^m& -2u_n^m+u_{n+1}^m)+\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }{F}_n^m\hfill \\ \hfill & +\mathsf{\Gamma }(2-\alpha )\left(A_n^m{\tau }^{2+\alpha }+B_n^m{\displaystyle \frac{{\tau }^2}{n^{\alpha }}}+D_n^m{\tau }^{\alpha }{h}^2\right),\hfill \end{array}$$

where $A_n^m$ and $B_n^m$ are the coefficients of the error of approximation (8) and $D_n^m{h}^2$ is the error of central difference approximation. Denote $\eta ={\displaystyle \frac{L\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }}{h^2}}$.

$$\begin{array}{cc}\hfill -\eta u_{n-1}^m+(2\eta +{\omega }_0^{\left(\alpha \right)})u_n^m-\eta u_{n+1}^m=\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }& F_n^m-\sum _{k=1}^m{\omega }_k^{\left(\alpha \right)}{u}_n^{m-k}\hfill \\ \hfill & +\mathsf{\Gamma }(2-\alpha )\left(A_n{\tau }^{2+\alpha }+B_n{\displaystyle \frac{{\tau }^2}{n^{\alpha }}}+D_n{\tau }^{\alpha }{h}^2\right).\hfill \end{array}$$

The numerical solution ${\left\{U_n^m\right\}}_{n=0}^N$ on row m of the grid $\mathcal{J}$ is computed as

$$-\eta U_{n-1}^m+(2\eta +{\omega }_0^{\left(\alpha \right)})U_n^m-\eta U_{n+1}^m=\mathsf{\Gamma }(2-a){\tau }^a{F}_n^m-\sum _{k=1}^m{\omega }_k^{\left(\alpha \right)}{U}_n^{m-k},$$

(53)

where $5\le n\le N-1$ and has boundary conditions $U_0^m=u_0\left(m\tau \right),U_N^m=u_1\left(m\tau \right)$.

The numerical solution for the first row is obtained using shifted approximation (43)

$${\displaystyle \frac{{(1-\frac{\alpha }{2})}^{1-\alpha }}{\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }}}\left(u_n^1-u_n^0\right)={\displaystyle \frac{L(1-\frac{\alpha }{2})}{h^2}}\left(u_{n+1}^1-2u_n^1+u_{n-1}^1\right)+{\displaystyle \frac{L\alpha }{2}}{v}^{″}\left(x\right)+F_n^{1-\alpha /2}+\mathcal{O}\left(h^2+{\tau }^2\right),$$

$$\begin{array}{cc}\hfill u_n^1-u_n^0={\displaystyle \frac{L{(1-\frac{\alpha }{2})}^{\alpha }\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }}{h^2}}& \left(u_{n+1}^1-2u_n^1+u_{n-1}^1\right)\hfill \\ \hfill & +{\displaystyle \frac{\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }}{{(1-\frac{\alpha }{2})}^{1-\alpha }}}\left({\displaystyle \frac{L\alpha }{2}}{u}_0^{\prime \prime }\left(x\right)+F_n^{1-\alpha /2}\right)+\mathcal{O}\left({\tau }^{\alpha }\left(h^2+{\tau }^2\right)\right).\hfill \end{array}$$

Let ${\eta }_1={\displaystyle \frac{L{(1-\frac{\alpha }{2})}^{\alpha }\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }}{h^2}}$. The numerical solution ${\left\{U_n^1\right\}}_{n=0}^N$ satisfies

$$-{\eta }_1{U}_{n+1}^1+(1+2{\eta }_1)U_n^1-{\eta }_1{U}_{n-1}^1={\displaystyle \frac{\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }}{{(1-\frac{\alpha }{2})}^{1-\alpha }}}\left({\displaystyle \frac{L\alpha }{2}}{u}_0^{\prime \prime }\left(x\right)+F_n^{1-\alpha /2}\right)$$

(54)

and has boundary conditions boundary conditions $U_0^1=u_0\left(\tau \right),U_N^1=u_1\left(\tau \right)$. The coefficient matrix for the system of equations of the first row is a diagonally dominant matrix of size $N+1$. The $L_{\infty }$ (maximum) norm of a vector is the maximum of the absolute values of its elements and the $L_{\infty }$ norm of a matrix is the maximum of the absolute row sums. The norm of the inverse coefficient matrix of (54) is smaller than one [49,50]. Therefore, the numerical solution on the first row of the grid $\mathcal{J}$ has an error of order $\mathcal{O}\left({\tau }^{\alpha }\left(h^2+{\tau }^2\right)\right)$. The numerical solution for the second row of the grid $\mathcal{J}$ is computed explicitly using the shifted approximation (44)

$${\displaystyle \frac{\alpha u_n^2+4(1-\alpha )u_n^1+(3\alpha -4)u_n^0}{2\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }}}={\displaystyle \frac{L}{h^2}}\left(u_{n+1}^1-2u_n^1+u_{n-1}^1\right)+F_n^1+\mathcal{O}\left(h^2+{\tau }^{3-\alpha }\right).$$

The numerical solution satisfies

$$\alpha U_n^2+4(1-\alpha )U_n^1+(3\alpha -4)U_n^0={\displaystyle \frac{2L\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }}{h^2}}\left(U_{n+1}^1-2U_n^1+U_{n-1}^1\right)+2\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }{F}_n^1,$$

$$U_n^2={\displaystyle \frac{1}{\alpha }}\left({\displaystyle \frac{2\eta }{{(1-\frac{\alpha }{2})}^{\alpha }}}\left(U_{n+1}^1-2U_n^1+U_{n-1}^1\right)-4(1-\alpha )U_n^1-(3\alpha -4)U_n^0+2\mathsf{\Gamma }(2-\alpha ){\tau }^{\alpha }{F}_n^1\right).$$

The error of the numerical solution in the second row of $\mathcal{J}$ is also of order $\mathcal{O}\left({\tau }^{\alpha }\left(h^2+{\tau }^2\right)\right)$. The numerical solutions for the third and fourth rows are computed explicitly using the third order approximations

$$u_n^3=3u_n^2-3u_n^1+u_n^0+\mathcal{O}\left({\tau }^3\right),u_n^4=3u_n^3-3u_n^2+u_n^1+\mathcal{O}\left({\tau }^3\right),$$

$$U_n^3=3U_n^2-3U_n^1+U_n^0,U_n^4=3U_n^3-3U_n^2+U_n^1.$$

The errors for the third and fourth rows also have accuracy of $\mathcal{O}\left({\tau }^{\alpha }(h^2+{\tau }^2)\right)$.

Example 7.

Consider the following fractional subdiffusion equation

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}u(x,t)=u_{xx}+{\displaystyle \frac{\mathsf{\Gamma }(3+\alpha )}{2}}(1-2x+x^{3-\alpha })t^2-(3-\alpha )(2-\alpha )x^{1-\alpha }(1+t^{2+\alpha });\hfill \\ u(0,t)=1+t^{2+\alpha },u(x,0)=1-2x+x^{3-\alpha },u(1,t)=0.\hfill \end{array}\right.$$

(55)

Equation (55) has the solution

$$u(x,t)=(1+t^{2+\alpha })(1-2x+x^{3-\alpha }).$$

The numerical results for the error and order of the difference scheme (53) for the subdiffusion equation (55) with $\alpha =0.5$ and $\alpha =0.75$ are presented in the third and fourth columns of Table 11. The graphs for $\alpha =0.5$, $L=1$, $h=0.02$, and $\tau =0.005$ are shown in Figure 4.

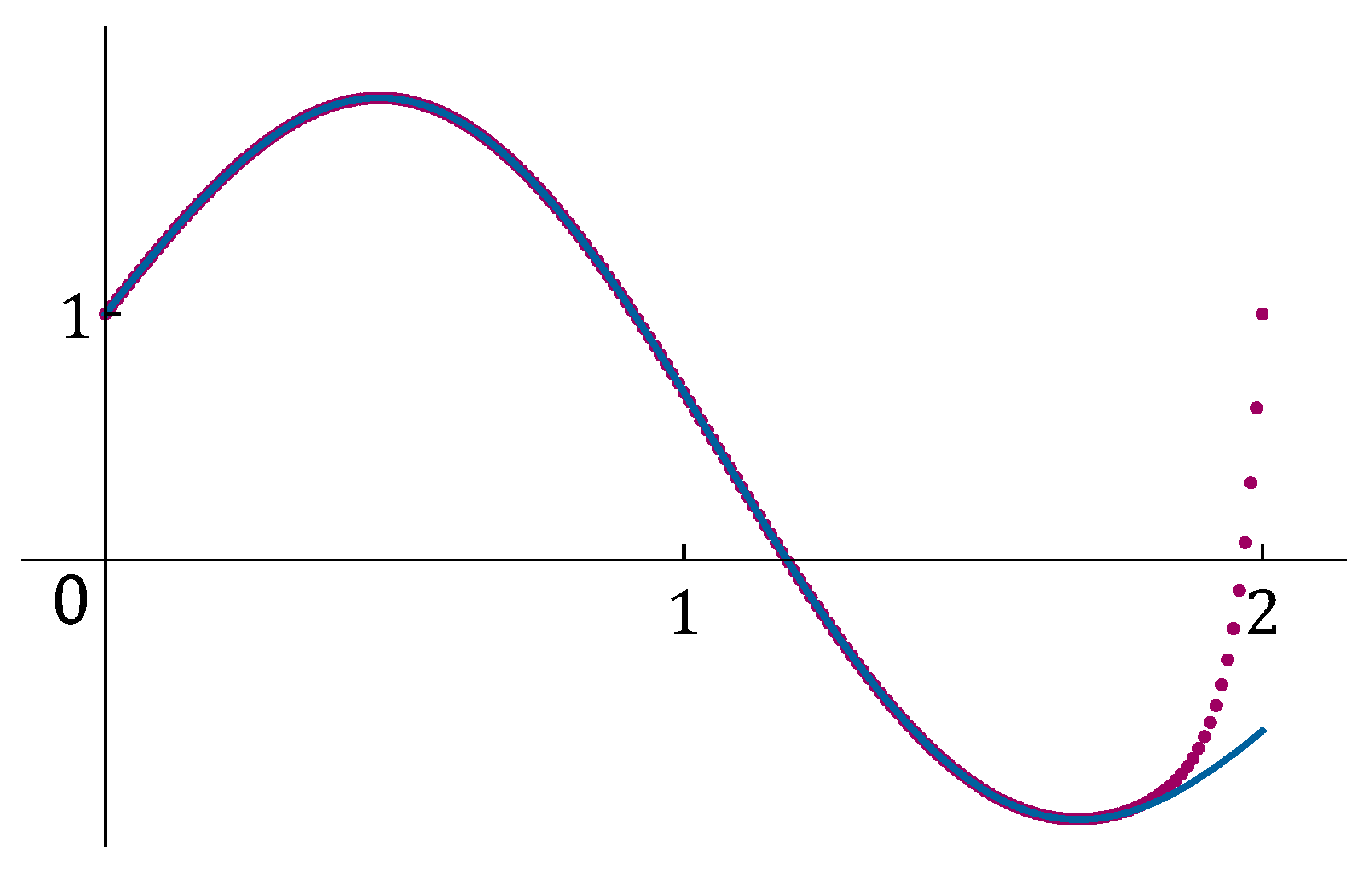
Example 8.

Consider the following fractional subdiffusion equation

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}}u(x,t)=3u_{xx}-e^x\left(3e^t+t^{1-\alpha }{E}_{1,2-\alpha }(-t)\right);\hfill \\ u(0,t)=e^t,u(x,0)=e^x,u(1,t)=e^{1+t}.\hfill \end{array}\right.$$

(56)

Equation (56) has the solution $u(x,t)=e^{x+t}$. The results of the numerical experiments for the error and order of the difference scheme (53) for the subdiffusion equation (56) with $\alpha =0.25$ are presented in the second column of Table 11. The graphs of numerical solution (53) and its error for $\alpha =0.5$, $L=3$, $h=0.02$, and $\tau =0.005$ are shown in Figure 5.

In the following, we prove that the difference scheme (53) for the fractional subdiffusion equation converges with second-order accuracy. The errors $E_n^m=u_n^m-U_n^m$ on the first four rows of the grid $\mathcal{J}$ have accuracy of $\mathcal{O}\left({\tau }^{\alpha }(h^2+{\tau }^2)\right)$. Therefore

$$|E_n^m|<C_1({\tau }^2+h^2),$$

where $C_1$ is a positive constant. The errors on row $m>4$ of the grid $\mathcal{J}$ are the solutions of the system of equations

$$-\eta E_{n-1}^m+(2\eta +{\omega }_0^{\left(\alpha \right)})E_n^m-\eta E_{n+1}^m={\mathcal{R}}_n^m,$$

where $E_0^m=E_N^m=0$ and

$${\mathcal{R}}_n^m=-\sum _{k=1}^{m-1}\left({\omega }_k^{\left(\alpha \right)}{E}_n^{m-k}\right)+\mathsf{\Gamma }(2-\alpha )\left(A_n^m{\tau }^{2+\alpha }+B_n^m{\displaystyle \frac{{\tau }^2}{m^{\alpha }}}+D_n^m{\tau }^{\alpha }{h}^2\right).$$

(57)

Denote

$$M_i=max\left|{\displaystyle \frac{{\partial }^i}{\partial t^i}}u(x,t)\right|,{\tilde{M}}_4=max\left|{\displaystyle \frac{{\partial }^4}{\partial x^4}}u(x,t)\right|,$$

where the maximums are taken for all $(x,t)\in [0,1]\times [0,1]$ and the coefficients $A_n^m,B_n^m$ and $D_n^m$ satisfy the bounds

$$|A_n^m|<{\displaystyle \frac{252M_3+45M_4+2M_5}{36\mathsf{\Gamma }(4-\alpha )}},|B_n|<{\displaystyle \frac{M_2}{12\mathsf{\Gamma }(1-\alpha )}},\left|D_n^m\right|<{\displaystyle \frac{{\tilde{M}}_4}{12}}.$$

Let ${\mathcal{E}}_m$ be an $(N+1)$-dimensional vector whose entries are the errors $E_n^m$ of difference scheme (53) on row m of the grid $\mathcal{J}$, and let ${\mathcal{R}}_m$ be the vector of truncation errors (57). The system of equations for the errors of difference scheme (53) in row m of the grid $\mathcal{J}$ can be written in matrix form as

$$\mathcal{M}{\mathcal{E}}_m={\mathcal{R}}_m,$$

where $\mathcal{M}=\left(a_{i,j}\right)$ is a tridiagonal square matrix with nonzero entries $a_{1,1}=a_{N,N}=1$ and

$$a_{i,i}=2\eta +w_0,a_{i-1,i}=a_{i+1,i}=\eta ,(2\le i\le N-1).$$

(58)

Theorem 19.

The errors of difference scheme (53) satisfy

$$\parallel {\mathcal{E}}_m\parallel <C\left({\tau }^2+h^2\right)$$

(59)

for all $m=1,\dots ,M$, where

$$C=max\left\{C_1,{\displaystyle \frac{6M_2+252M_3+45M_4+2M_5}{72(1-\alpha )}},{\displaystyle \frac{{\tilde{M}}_4}{12(1-\alpha )}}\right\}.$$

Proof. 

We prove the statement by induction. The estimate (59) holds for $M\le 4$. Assume that (59) holds for all rows $1,2,\dots ,m-1$ of the grid $\mathcal{J}$. From formula (57)

$$|{\mathcal{R}}_n^m|<-\sum _{k=1}^{m-1}{\omega }_k^{\left(\alpha \right)}\left|E_n^{m-k}\right|+\mathsf{\Gamma }(2-a)\left(|A_n^m|{\tau }^{2+\alpha }+|B_n^m|{\displaystyle \frac{{\tau }^2}{m^{\alpha }}}+\left|D_n^m\right|{\tau }^{\alpha }{h}^2\right).$$

When $0<\alpha <1$ the gamma function satisfies $0.88<\mathsf{\Gamma }(2-\alpha )<1$ (see [51]). Applying the induction assumption

$$|{\mathcal{R}}_n^m|\le -\sum _{k=1}^{m-1}{\omega }_k^{\left(\alpha \right)}C({\tau }^2+h^2)+\mathsf{\Gamma }(2-\alpha )|A_n^m|{\tau }^{2+\alpha }+\mathsf{\Gamma }(2-\alpha )|B_n^m|{\displaystyle \frac{{\tau }^2}{m^{\alpha }}}+\left|D_n^m\right|{\tau }^2{h}^2,$$

$$|{\mathcal{R}}_n^m|<({\omega }_0^{\left(\alpha \right)}-|{\omega }_m^{\left(\alpha \right)}\left|\right)C({\tau }^2+h^2)+A{\tau }^{2+\alpha }+{\displaystyle \frac{M_2(1-\alpha )}{12}}{\displaystyle \frac{{\tau }^2}{m^{\alpha }}}+{\displaystyle \frac{{\tilde{M}}_4}{12}}{\tau }^{\alpha }{h}^2,$$

where $A<(252M_3+45M_4+2M_5)/72$. From Claim 17

$$|{\mathcal{R}}_n^m|<{\omega }_0^{\left(\alpha \right)}C({\tau }^2+h^2)-{\displaystyle \frac{1-a}{m^{\alpha }}}C({\tau }^2+h^2)+A{\displaystyle \frac{{\tau }^2}{m^{\alpha }}}+{\displaystyle \frac{M_2(1-\alpha )}{12}}{\displaystyle \frac{{\tau }^2}{m^{\alpha }}}+{\displaystyle \frac{{\tilde{M}}_4}{12}}{\displaystyle \frac{h^2}{m^{\alpha }}},$$

$$|{\mathcal{R}}_n^m|<{\omega }_0^{\left(\alpha \right)}C({\tau }^2+h^2)-{\displaystyle \frac{(1-\alpha ){\tau }^2}{m^{\alpha }}}\left(C-{\displaystyle \frac{A}{1-\alpha }}-{\displaystyle \frac{M_2}{12}}\right)-{\displaystyle \frac{(1-\alpha )h^2}{m^{\alpha }}}\left(C-{\displaystyle \frac{{\tilde{M}}_4}{12(1-\alpha )}}\right).$$

When C satisfies the conditions of the theorem, the two coefficients $C-A/(1-\alpha )-M_2/12$ and $C-{\tilde{M}}_4/\left(12(1-\alpha )\right)$ are positive.Therefore

$$|{\mathcal{R}}_n^m|<{\omega }_0^{\left(\alpha \right)}C({\tau }^2+h^2).$$

From (58) the infinity norm of the inverse matrix satisfies [49,50]

$$\parallel {\mathcal{M}}^{-1}\parallel \le {\displaystyle \frac{1}{w_0^{\left(\alpha \right)}}}.$$

Hence

$${\mathcal{E}}_m={\mathcal{M}}^{-1}{\mathcal{R}}_m,$$

$$\parallel {\mathcal{E}}_m\parallel \le \parallel {\mathcal{M}}^{-1}\parallel \parallel {\mathcal{R}}_m\parallel <C({\tau }^2+h^2).$$

The error estimate (59) holds for the m-th row of the grid $\mathcal{J}$, completing the induction. □

6. Conclusions

In the present paper, we have studied the construction and properties of parameter-dependent approximations for the first and second derivatives, denoted by (4), (5), and for the Caputo fractional derivative, denoted by (6) and (8) and their applications for numerical solution of differential and fractional differential equations. The approximations of the fractional derivative are developed using the second-order expansion formula of the L1 approximation together with an approximation (5) of the second derivative. The weights of the two obtained approximations of the fractional derivative satisfy property (2) when the parameter takes the value $1-\alpha +{\alpha }^2$, where $\alpha$ is the order of the fractional derivative. Approximation (6) of the fractional derivative has second-order accuracy, while the order of approximation (8) depends on the mesh size and increases from $2-\alpha$ to 2. We provide examples demonstrating the application of the derived approximations to the construction of finite difference schemes for the numerical solution of fractional differential equations, and we analyze the convergence and order of these numerical solutions. In Theorem 18 and Theorem 19, we prove that the difference schemes based on both approximations (6) and (8) achieve second-order accuracy. The proofs rely on the properties (2) of the approximation weights and on the magnitude of the last weights. The theoretical results for the order and accuracy of the proposed numerical methods are confirmed by the presented numerical experiments.

In future work, we will continue the investigations initiated in this paper. We plan to address questions related to high-order expansion formulas and to the construction of approximations of the fractional derivative based on these formulas. We will also consider the development of high-order finite difference schemes for the numerical solution of fractional differential equations and analyze their performance and convergence.