Submitted:
19 October 2025
Posted:
20 October 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Bilinear Bäcklund Transformation and the Nonlinear Superposition Formula
3. One-Periodic Wave Solution of the sdKP Equation and Its Asymptotic Property
3.1. One-Periodic Wave Solution
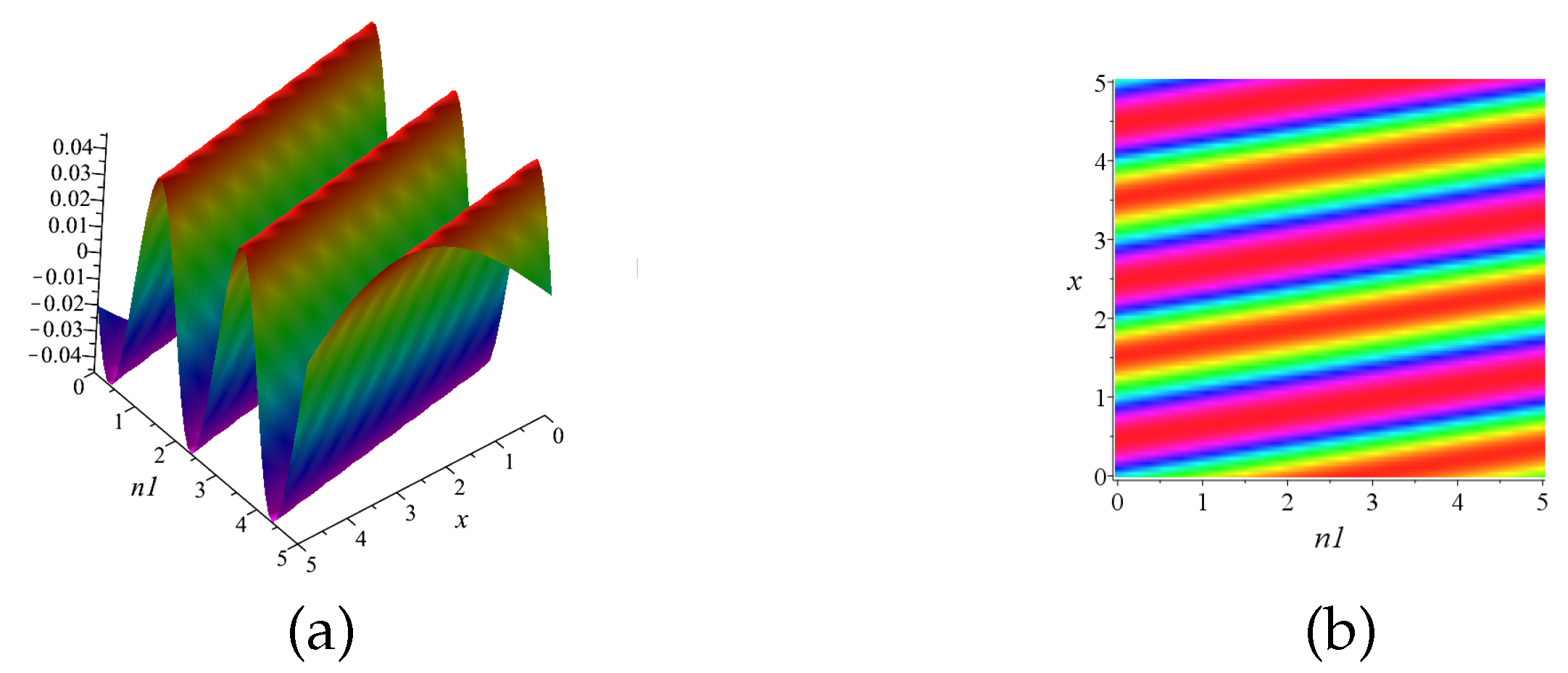
3.2. Asymptotic Properties of the One-Periodic Wave Solution
4. Two-Periodic Wave Solution of the sdKP Equation and Its Asymptotic Property
4.1. Two-Periodic Wave Solution
4.2. Asymptotic Properties of the Two-Periodic Wave Solution
5. Conclusions and Discussions
Author Contributions
Funding
Conflicts of Interest
References
- Bruschi, M.; Manakov, S. V.; Ragnisco, O.; Levi, D. The nonabelian Toda lattice-discrete analogue of the matrix Schrödinger spectral problem. J. Math. Phys. 1980, 21(2), 2749–2753. [Google Scholar] [CrossRef]
- Levi, D.; Ragnisco, O.; Bruschi, M. Extension of the Zakharov-Shabat generalized inverse method to solve differential-difference and difference-difference equations. Nuovo Cimento A 1980, 58(1), 56–66. [Google Scholar] [CrossRef]
- Takahashi, D. ; Matsukidaira,J. On discrete soliton equations related to cellular automata, Phys. Lett. A, 1995, 209, 184–188. [Google Scholar]
- Hirota, R.; Ohta, Y. Discretization of the new type of soliton equations, J. phys. Soc. Jpn., 2007, 76, 034001. [Google Scholar] [CrossRef]
- Nagai, H.; Ohta, Y.; Hirota, R. Discrete and ultradiscrete periodic phase soliton equations, 2019, 88, 034001.
- Hirota, R. Discrete analogue of a generalized Toda equation. J. Phys. Soc. Jpn., 1981, 50, 3785–3791. [Google Scholar] [CrossRef]
- Amjad, Z.; Haider, B.; Ma, W.X. Integrable discretization and multi-soliton solutions of negative order AKNS equation, 2024, 23(suppl.1), 280.
- Miwa, T. On Hirota’s difference equations. Proc. Japan Acad. A Math. Sci., 1982, 58(1), 9-12.
- Date, E.; Jimbo, M.; Miwa, T. Method for generating discrete solution equations. J. Phys. Soc. Jpn., 1982, 51, 4116–4124. [Google Scholar] [CrossRef]
- Li, C.X.; Lafortune, S.; Shen, S.F. A semi-discrete Kadomtsev-Petviashvili equation and its coupled integrable system. J. Math. Phys. 2017, 57, 053503:1–9. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory. Cambridge University Press, 2004.
- Nakamura, A. A direct method of calculating periodic wave solutions to nonlinear evolution equations. I. exact two-periodic wave solution. J.Phy.Soc.Jpn, 1979, 47(5), 1701-1705.
- Nakamura, A. A direct method of calculating periodic-wave solutions to nonlinear evolution equations. II. exact I-periodic and 2-periodic wave solutions of the coupled bilinear equations, J. Phys. Soc. Jpn. 1980, 48, 1365–1370. [Google Scholar]
- Whittaker, E.T.; Watson, G.N. Acourse of modern analysis. (Cambridge Univ. Press, Cambride), 1935.
- Bellman, R. A brief introduction to theta functions. (Rinehart,R; Winston), Newyork, 1961.
- Hirota, R.; Masaaki, I. A direct approach to multi-periodic wave solutions to nonlinear evolution equations. J. Phys. Soc. Jpn. 1981, 50(1), 338–342. [Google Scholar] [CrossRef]
- Fan, E.G. Quasi-periodic waves and an asymptotic property for the asymmetrical Nizhnik-Novikov-Veselov equation, J. Phys. A: Math. Theor. 2009, 42, 095206. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhou, R.G.; Gao, L. Exact one-periodic and two-periodic wave solutions to Hirota bilinear equations in (2+1)dimensions, Modern Phys. Lett. A 2009, 24, 1677–1688. [Google Scholar]
- Zhang, Y.N.; Hu, X.B.; Sun, J.Q. A numerical study of the 3-periodic wave solutions to KdV-type equations. J. Comp. Phys. 2018, 355, 566–581. [Google Scholar] [CrossRef]
- Wei, L. Multiple periodic-soliton solutions to Kadomtsev-Petviashvili equation, Appl. Math. Comp., 2011, 218, 368–375. [Google Scholar]
- Hon, Y.C.; Fan, E.G.; Qin, Z.Y. A kind of explicit quasi-periodic solution and its limit for the Toda lattice equation, Modern Phys. Lett. B, 2008, 22, 547–553. [Google Scholar]
- Luo, L. Exact periodic wave solutions for the differntial-difference KP equation, Reports on mathematical physics, 2010, 66(3), 403-417.
- Wu, G.C.; Xia, T.C. Uniformly constructing exact discrete soliton solutions and periodic solutions to differential-difference equations, Comput. Math. Appl., 2009, 58, 2351–2354. [Google Scholar]
- Wan, L.S. Nonlinear superposition formula of a semi-discrete KP equation and its exact solutions (master’s thesis), Capital Normal University, Beiing, China, 2024.
- Zhang, Y.N.; Hu, X.B.; Sun, J.Q. A numerical study of the 3-periodic wave solutions to Toda-type equations, Comm. Comp. Phys. 2019, 26(2), 579–598. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




