Submitted:
25 August 2023
Posted:
30 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- 1.
-
Scattering data The minimal sets of scattering data are determined by the asymptotics ofHere and are the factors of the Gauss decompositions of the scattering matrix .
- 2.
- Resolvent The FAS determine the kernel of the resolvent of L. Applying contour integration method on one can derive the spectral expansions for L, i.e. the completeness relation of FAS.
- 3.
- Dressing method Zakharov-Shabat dressing method is a very effective and convenient method to construct the class of reflectionless potentials of L and to derive the soliton solutions of the NLEE. The simplest dressing factor has pole singularities at , which determine the new discrete eigenvalues that are added to the spectrum of the initial Lax operator.
- 4.
- Generalized Fourier transforms Here we start with GZSh system related to a simple Lie algebra with Cartan-Weyl basis , [67] and construct the so-called 'squared solutions'where is the projector onto the image of the operator . It is known that the 'squared solution' are complete set of functions in the space of allowed potentials [30]. In particular, if we expand the potential over the 'squared solutions' the expansion coefficients will provide the minimal set of scattering data. Similarly, the expansion coefficients of are the variations of the minimal set of scattering data. Therefore the 'squared solutions' can be viewed as FAS in the adjoint representation of , see [2,12,30,45,59,62,63,64,78,108,121] as well as [12,24,39,65].
- 5.
- Hierarchies of Hamiltonian structures The GFT described above allow one to prove that each of the NLEE related to L allows a hierarchy of Hamiltonian structures. More precisely, each NLEE allows a hierarchy of Hamiltonians and a hierarchy of symplectic forms (or a hierarchy of Poisson brackets) such that for any n they produce the relevant NLEE. [30,81,86]
- 6.
- Complete integrability and action-angle variables. Starting from the famous paper by Zakharov and Faddeev [137] it is known that some of the NLEE allow action-angle variables. The difficulty here is that these NLEE are Hamiltonian system with infinitely many degrees of freedom. Therefore the strict derivation of the proof must be based on the completeness relation for the 'squared solutions'. In fact VG and E. Khristov [45,59] (see also [63]) proposed the so-called 'symplectic basis' of squared solutions, which maps the variation of the potential of the AKNS system to the variation of the action-variables. Unfortunately for many multi-component systems such bases are not yet known.
2. From the Lax representation to the RHP
2.1. N-waves according to Manakov and Zakharov
- C.1
- By we mean that possesses smooth derivatives of all orders and falls off to zero for faster than any power of x:
- C.2
- is such that the corresponding operator L has only a finite number of simple discrete eigenvalues.
2.2. MNLS equations according to Manakov, Fordy and Kulish
2.3. Generic Lax representation
2.4. Jost solutions and FAS of L
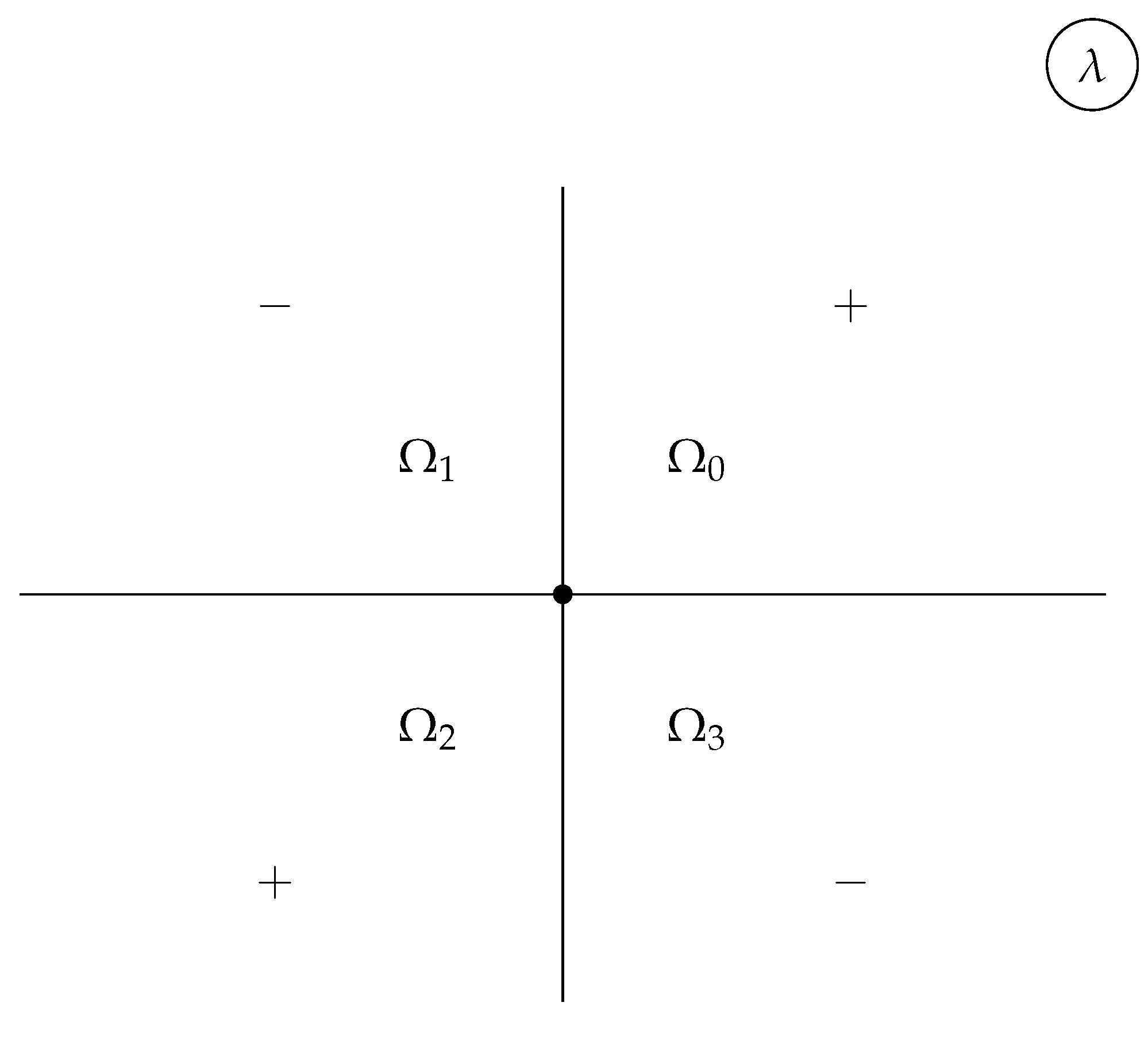
2.5. The time-dependence of
3. RHP and integrable NLEE
3.1. Uniqueness of the regular solution of RHP
3.2. Zakharov-Shabat theorem
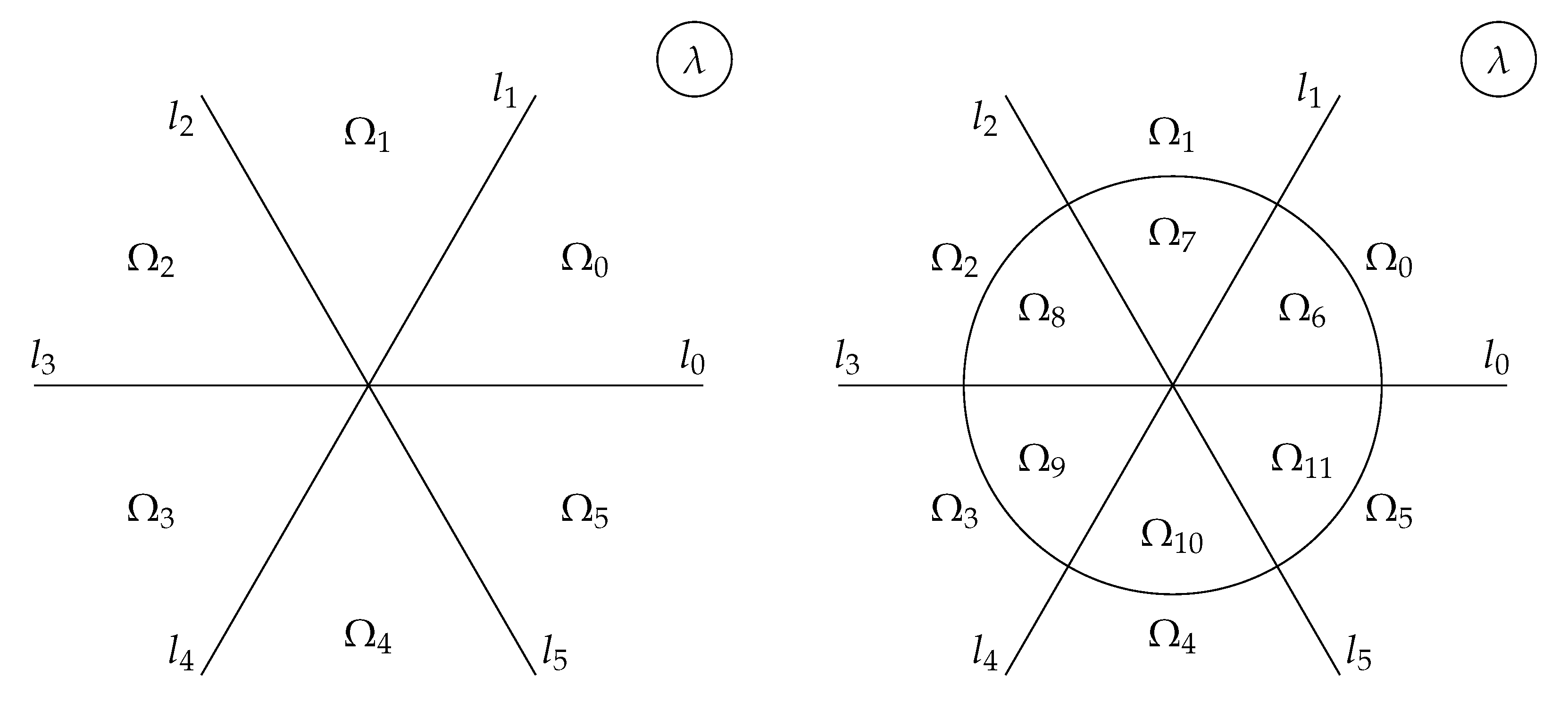
4. Mikhailov’s reduction groups and the contours of RHP
4.1. General theory
4.2. Involutive reductions
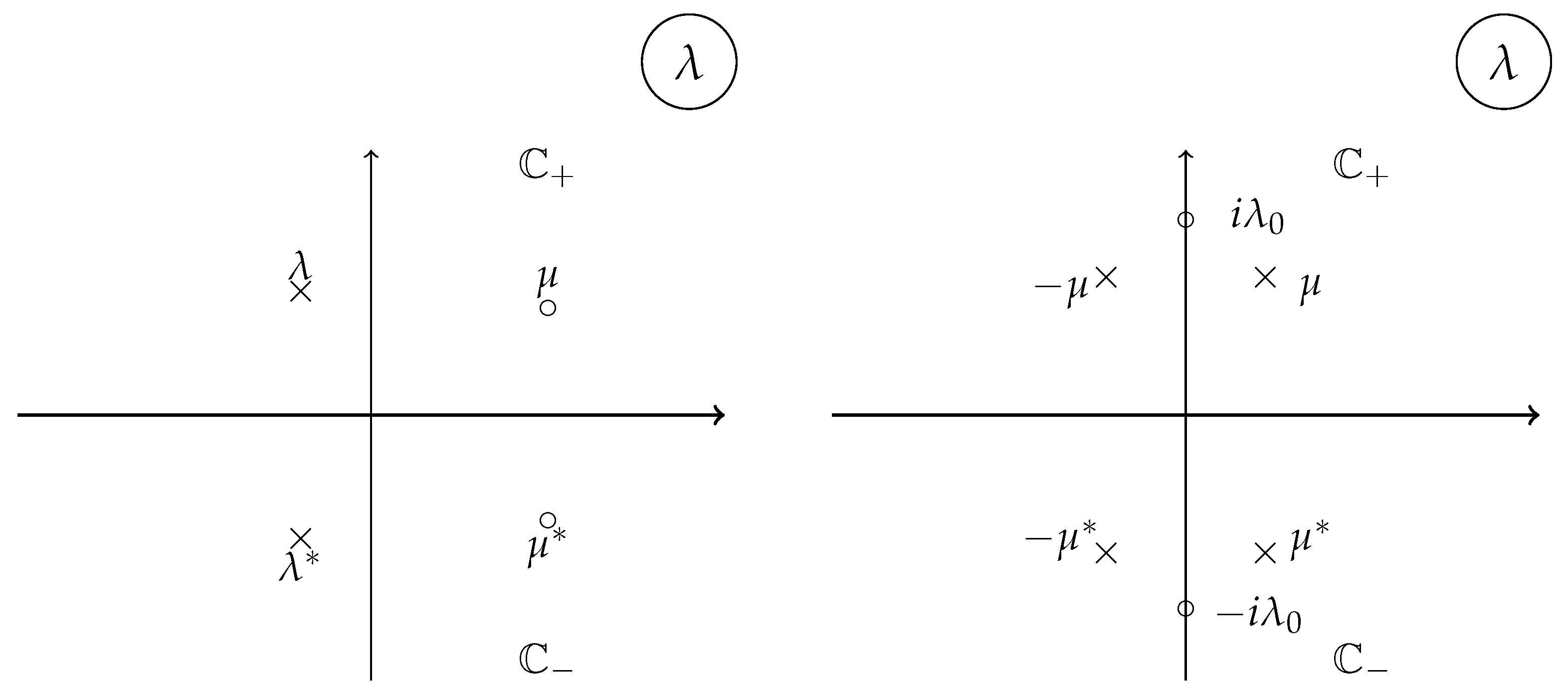
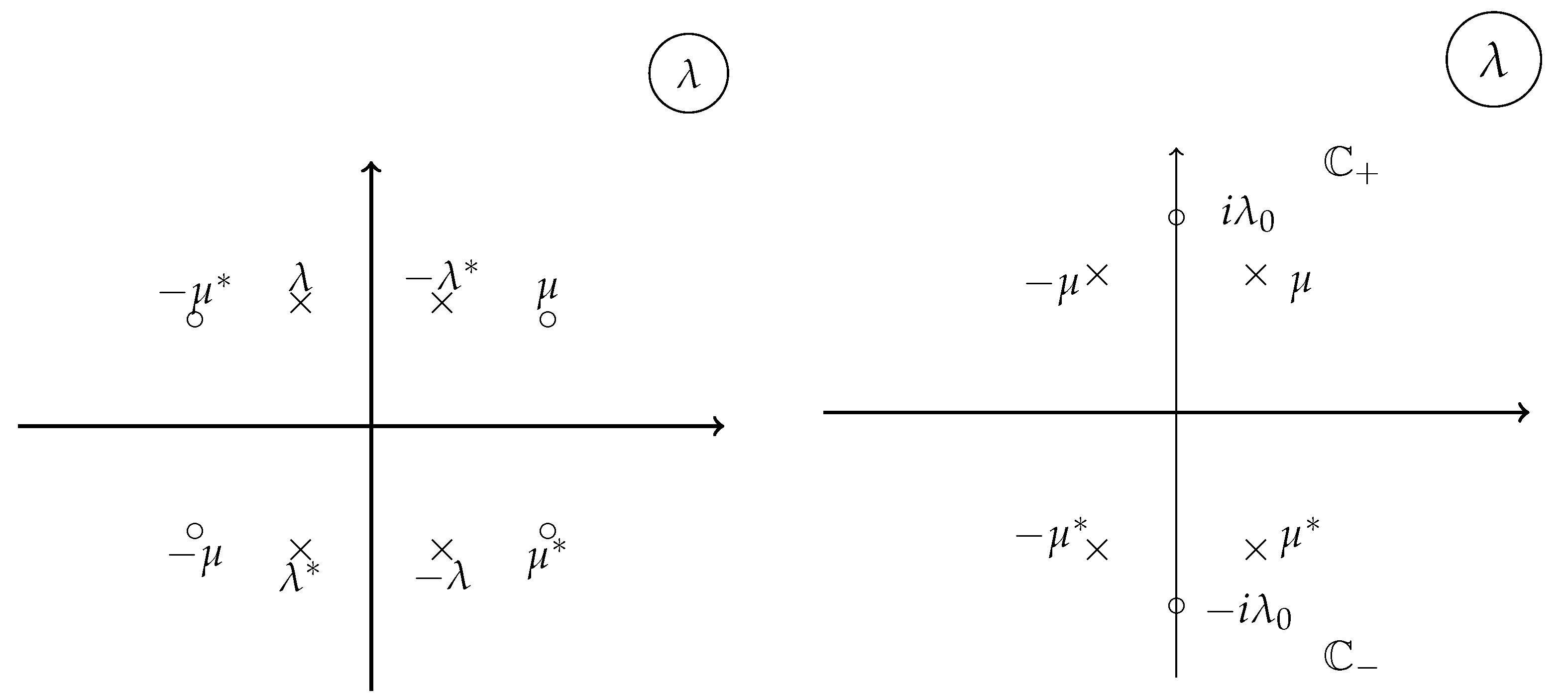
4.3. reduction groups
4.4. reduction groups
5. Parametrizing the RHP with canonical normalization
5.1. Generic parametrization of the RHP with canonical normalization
5.2. The family of N-wave equations with cubic nonlinearities
5.3. The main idea of the dressing method
5.4. Dressing of N-wave equations: two involutions
5.5. Dressing of N-wave equations: three involutions
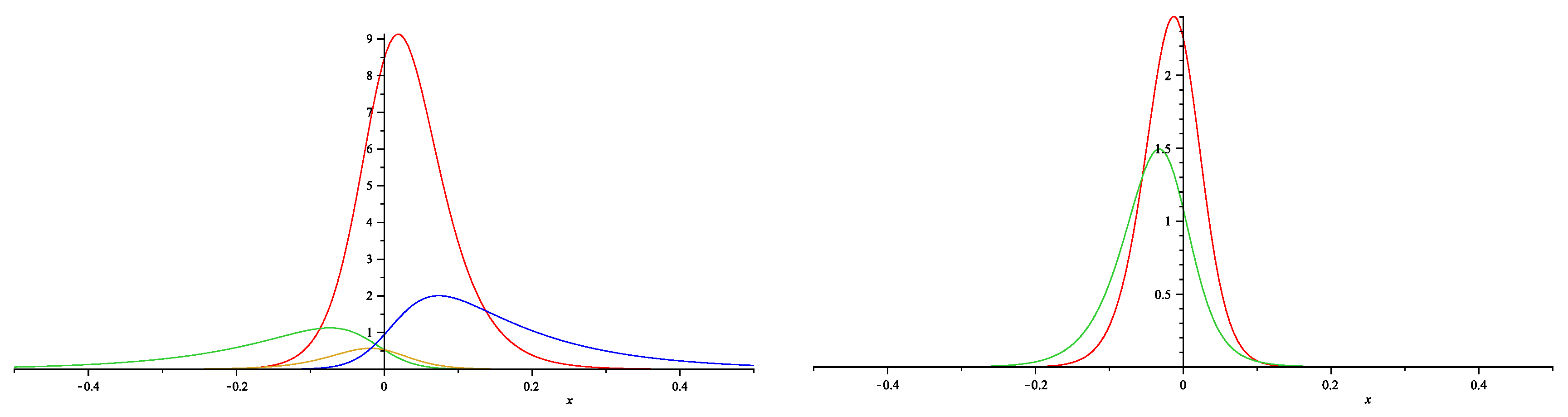
6. MNLS family and symmetric spaces
6.1. Lax pairs on symmetric spaces. Generic case
6.2. NLEE on symmetric spaces: A.III
6.3. MNLS equations related to D.III and C.I symmetric spaces
6.4. MNLS related to BD.I-type symmetric spaces
7. Soliton solutions of the MNLS equations
7.1. Dressing for NLEE on symmetric spaces: A.III case
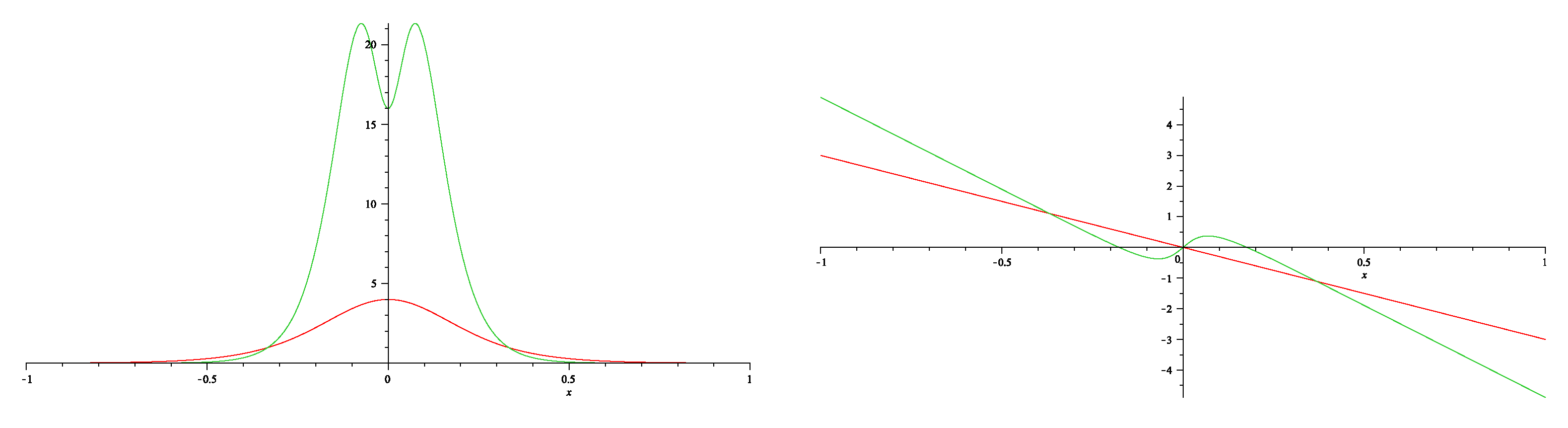
7.2. Dressing for NLEE on symmetric spaces: C.I and D.III cases
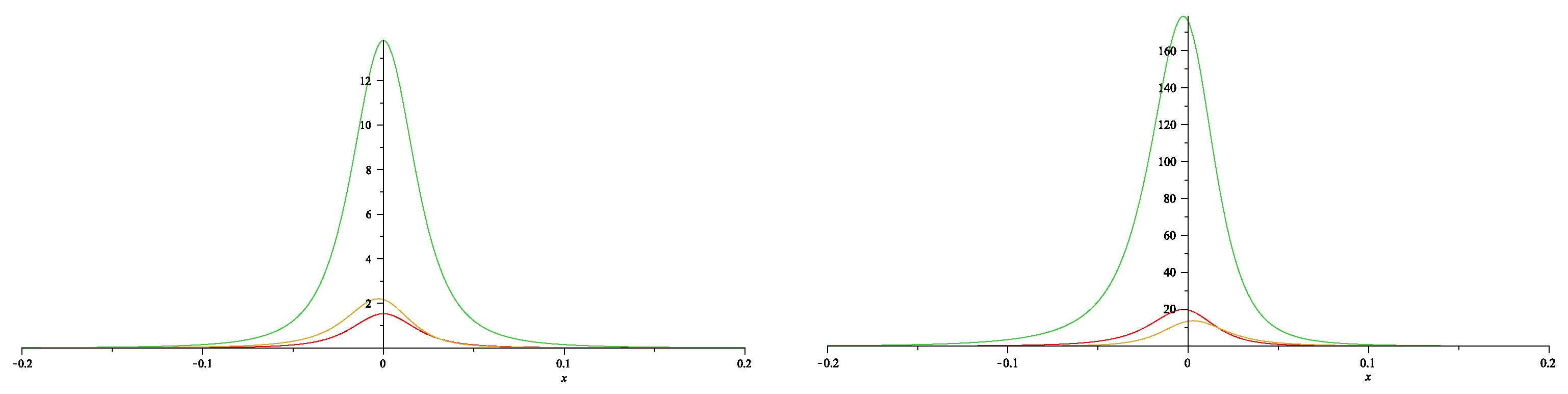
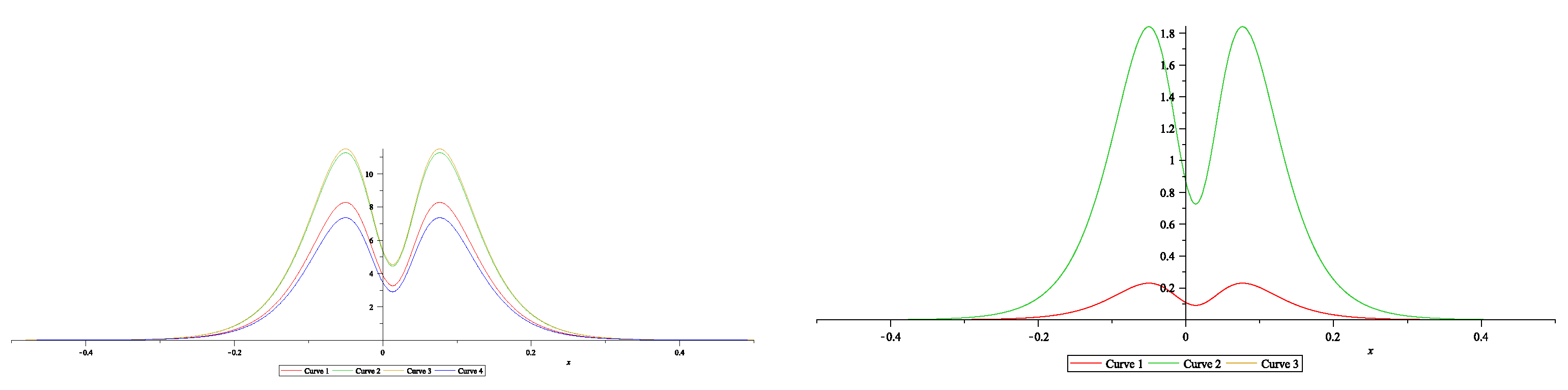
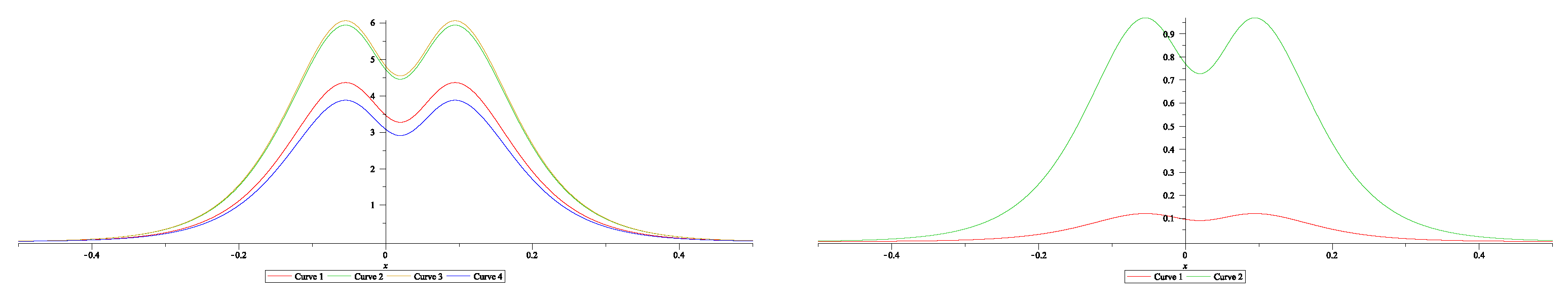
7.3. Dressing for NLEE on symmetric spaces: BD.I cases
7.4. N-soliton solutions and soliton interactions of MNLS equations
8. Multi-soliton solutions
9. The resolvent and spectral properties of Lax operators
- C.1
- possesses smooth derivatives of all orders with respect to x and falls off to zero for faster than any power of x:
- C.2
- is such that the corresponding RHP has finite index. For the class of RHP that we have been dealing with this means that the solution of the RHP must have finite number of simple zeroes and pole singularities.
- 1.
- if is a zero or pole of , then there must exist which is also a zero or pole of ;
- 2.
- if is a zero or pole of , then there must exist which is also zero or pole of .
- 3.
- if is a zero or pole of , then there must exist which is a zero or pole of .
- i) the continuous spectrum of consists of all points for which is an unbounded integral operator;
- ii) the discrete spectrum of consists of all points for which develops pole singularities.
- 1.
- will be FAS of a quadratic pencil of the form (5.11) whose coefficients will be expressed through as in (5.15).
- 2.
- is a kernel of a bounded integral operator for ;
- 3.
- is uniformly bounded function for and provides a kernel of an unbounded integral operator;
- 4.
- satisfy the equation:
- is obvious from the fact that are the FAS of (5.11). It is also easy to see that if satisfies conditions (C.1) and (C.2) then and will also satisfy condition C1. In addition obviously will satisfy condition C2 and will have poles and zeroes at the points , see Remark 9.
-
Assume that and consider the asymptotic behavior of for . From equations (5.11) we find thatWe use the fact that has triangular asymptotics for and (see eq. (2.38)). With the choice of (9.5) we check that the right hand side of (9.7) falls off exponentially for and arbitrary choice of y. All other possibilities are treated analogously.
- For the arguments of 2) can not be applied because the exponentials in the right hand side of (9.7) only oscillate. Thus we conclude that for is only a bounded function of x and thus the corresponding operator is an unbounded integral operator.
- The proof of eq. (9.6) follows from the fact that and
10. Discussion and conclusions
Acknowledgments
Appendix A. Root systems of simple Lie algebras
- The Cartan subalgebras of all simple Lie algebras can be represented by diagonal matrices;
- There is an one-to-one mapping between the elements of and the vectors in r-dimensional Euclidean space ;
- The Weil generators are defined as eigenvectors of all the elements of , i.e.where . Here is the vector corresponding to H, and is a root of the algebra belonging to its system of roots .
- Root systems
- Dynkin diagrams
- Cartan-Weyl basis
- Automorphisms of finite order
- If then is also a root, .
- Each roots system is split into positive and negative roots:
- In each root systems one can introduce a basis, known as system of simple roots. By definition , are simple roots if: i) they are linearly independent and form a basis in ; ii) they are positive roots such that ;
- Each positive root can be expressed as sum of simple roots where all are integers;
- There is a maximal (resp. minimal) root (resp ) such that (resp. ) is not a root;
-
Symmetry properties of and Weyl group. Introduce the Weyl reflections by:The Weyl reflections form a finite group, which preserves , i.e. .
Appendix A.1. The root system of A r ≃sl(r+1) algebras

Appendix A.2. The root system of B r ≃so(2r+1) algebras

Appendix A.3. The root system of C r ≃sp(2r) algebras

Appendix A.4. The root system of D r ≃so(2r) algebras
Appendix B. Gauss decompositions
References
- M. A. Ablowitz and P. A. Clarkson. Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, 1991. [CrossRef]
- M. J. Ablowitz, D. J. Kaup, A. C. Newell, and H. Segur. The inverse scattering transform- Fourier analysis for nonlinear problems. Studies in Appl. Math., 53(4):249–315, 1974. [CrossRef]
- M. J. Ablowitz and J. F. Ladik. Nonlinear differential–difference equations and fourier analysis. Journal of Mathematical Physics, 17(6):1011–1018, 1976. [CrossRef]
- M. Adler. On a trace functional for pseudo-differential operators and the symplectic structure of the Korteweg-de Vries equation. Invent. Math, 50:219–248, 1979.
- N. I. Akhiezer and I. M. Glazman. Theory of Linear operators in Hilbert space. Dover Publications, New York, (1961-1963). Translated from Russian.
- Dubrovin B. A. Matrix finite-zone operators. J. Soviet Math., 28(1):20–50, 1985. [CrossRef]
- R. Beals and R. R. Coifman. Scattering and inverse scattering for first order systems. Commun. Pure & Appl. Math., 37:39, 1984. [CrossRef]
- N. Bourbaki. Elements of mathematics. Lie Groups and Lie Algebras.Chapters 4-6. Springer, Berlin, Heidelberg, New York, 2002.
- R.T. Bury. Automorphic Lie Algebras, Corresponding Integrable Systems and Their Soliton Solutions. PhD thesis, University of Leeds, 2010.
- F. Calogero and A. Degasperis. Spectral transform and solitons. i. In Studies in Mathematics and its Applications, volume 13. Elsevier, North Holland, 1982.
- Q.U. Changzheng, Junfeng Song, and Ruoxia Yao. Multi-component integrable systems and invariant curve flows in certain geometries. SIGMA, 9:1–20, 2013. [CrossRef]
- A. Constantin, V. S. Gerdjikov, and R. I. Ivanov. Generalized fourier transform for the camassa-holm equation. Inverse Problems, 23:1565–1597, 2007.
- H. Coxeter and W Moser. Generators and relations for discrete groups (3ed). Springer, 1972.
- H. H. Dai and E. G. Fan. Variable separation and algebro-geometric solutions of the Gerdjikov-Ivanov equation. Chaos, Solitons, Fractals, 22:93–101, 2004. [CrossRef]
- L. A. Dickey. Soliton Equations and Hamiltonian Systems. World scientific, 2003.
- V. G. Drinfel’d and V. V. Sokolov. Lie algebras and equations of korteweg-de vries type. Sov. J. Math., 30:1975–2036, 1985. [CrossRef]
- N. Dunford and J. T. Schwartz. Spectral theory. Self-adjoint operators in Hilbert space, volume 2 of Linear operators. Interscience Publishers, Inc., NY, 1963.
- L. D. Faddeev and L. A. Takhtadjan. Hamiltonian Methods in the Theory of Solitons. Springer Verlag, Berlin, 1987.
- E.G. Fan. Darboux transformation and solion-like solutions for the gerdjikov-ivanov equation. J. Phys. A, 33:6925–6933, 2000.
- E.G. Fan. A family of completely integrable multi-hamiltonian systems explicitly related to some celebrated equations. J. Math. Phys., 42:4327–4344, 2001. [CrossRef]
- A. P. Fordy and P. P. Kulish. Nonlinear schrödinger equations and simple lie algebras. Commun. Math. Phys., 89:427–443, 1983. [CrossRef]
- A. V. Mikhailov G. Berkeley and P. Xenitidis. Darboux transformations with tetrahedral reduction group and related integrable systems. Journal of Mathematical Physics, 57:092701, 2016.
- S. Gaiarin, A. M. Perego, E. P. da Silva, F. Da Ros, and D. Zibar. Experimental demonstration of dual polarization nonlinear frequency division multiplexed optical transmission system. In 2017 European Conference on Optical Communication (ECOC), pages 1–3, 2017. [CrossRef]
- S. Gaiarin, A. M. Perego, E. P. da Silva, F. Da Ros, and D. Zibar. Dual-polarization nonlinear fourier transform-based optical communication system. Optica, 5(3):263–270, Mar 2018. [CrossRef]
- I. M. Gel’fand and L. A. Dikii. Fractional powers of operators and hamiltonian systems. Funct. Anal. Appl., 10(4):259–273, 1976. [CrossRef]
- I. M. Gel’fand and L. A. Dikii. The resolvent and hamiltonian systems. Funct. Anal. Appl., 11(2):93–105, 1977.
- I. M. Gel’fand and L. A. Dikii. The calculus of jets and nonlinear hamiltonian systems. Funct. Anal. Appl., 12(2):81–94, 1978. [CrossRef]
- I. M. Gel’fand and L. A. Dikii. Integrable nonlinear equations and the liouville theorem. Funct. Anal. Appl., 13(1):6–15, 1979. [CrossRef]
- V. S. Gerdjikov. On the spectral theory of the integro-differential operator λ, generating nonlinear evolution equations. Lett. Math. Phys., 6(6):315–324, 1982.
- V. S. Gerdjikov. Generalised fourier transforms for the soliton equations. gauge covariant formulation. Inverse Problems, 2(1):51–74, 1986. [CrossRef]
- V. S. Gerdjikov. zn–reductions and new integrable versions of derivative nonlinear schrödinger equations. In M. Lakshmanan A. P. Fordy, A. Degasperis, editor, Nonlinear evolution equations: integrability and spectral methods, pages 367–379. Manchester University Press, 1991.
- V. S. Gerdjikov. Algebraic and analytic aspects of n-wave type equations. Contemporary Mathematics, 301:35–68, 2002.
- V. S. Gerdjikov. Basic aspects of soliton theory. In A. C. Hirshfeld. I. M. Mladenov, editor, Geometry, Integrability and Quantization, pages 78–125. Sortex, Sofia, 2005.
- V. S. Gerdjikov. Bose-einstein condensates and spectral properties of multicomponent nonlinear schrödinger equations. Discrete and Continuous Dynamical Systems, 4(5):1181–1197, 2011. [CrossRef]
- V. S. Gerdjikov. On soliton interactions of vector nonlinear schrödinger equations. In AMITANS conference, AIP 1404, pages 57–67, 2011.
- V. S. Gerdjikov. Riemann-hilbert problems with canonical normalization and families of commuting operators. Pliska Stud. Math. Bulgar, 21:201–216, 2012.
- V. S. Gerdjikov. Derivative nonlinear schrödinger equations with Zn and Dn–reductions. Romanian Journal of Physics, 58:573–582, 2013.
- V. S. Gerdjikov. Kulish-sklyanin type models: integrability and reductions. Theoretical and Mathematical Physics, 192(2):1097–1114, 2017. [CrossRef]
- V. S. Gerdjikov. On nonlocal models of kulish-sklyanin type and generalized fourier transforms. In K. Georgiev, M. Todorov, and I. Georgiev, editors, Advanced Computing in Industrial Mathematics. Studies in Computational Intelligence, volume 681, pages 37–52. springer, 2017.
- V. S. Gerdjikov and G.G. Grahovski. Multi-component nls models on symmetric spaces: Spectral properties versus representations theory. SIGMA, 6:44–73, 2010. [CrossRef]
- V. S. Gerdjikov and G.G. Grahovski. Two soliton interactions of bd.i multicomponent nls equations and their gauge equivalent. AIP Conf. Proc., 1301:561–572, 2010. [CrossRef]
- V. S. Gerdjikov and M. I. Ivanov. The quadratic bundle of general form and the nonlinear evolution equations. i. expansions over the “squared” solutions are generalized fourier transforms. Bulgarian J. Phys, 10:13–26, 1983.
- V. S. Gerdjikov, M. I. Ivanov, and P. P. Kulish. Expansions over the "squared” solutions and difference evolution equations. J. Math. Phys., 25(1):25–34, 1984.
- V. S. Gerdjikov and R. I. Ivanov. Multicomponent fokas-lenells equations on hermitian symmetric spaces. Nonlinearity, 34:939, 2021. [CrossRef]
- V. S. Gerdjikov and E. Kh. Khristov. On the evolution equations solvable with the inverse scattering problem. i. the spectral theory. Bulgarian J. Phys., 7(1):28–41, 1979.
- V. S. Gerdjikov and P. P. Kulish. Complete integrable hamiltonian systems related to the non–self–adjoint dirac operator. Bulgarian J. Phys., 5(4):337–349, 1978.
- V. S. Gerdjikov and P. P. Kulish. The generating operator for the n×n linear system. Physica D, 3D(3):549–564, 1981.
- V. S. Gerdjikov, Nianhua Li, V. B. Matveev, and A. O. Smirnov. On soliton solutions and soliton interactions of kulish-sklyanin and hirota-ohta systems. Theoretical and Mathematical Physics, 213(1):1331–1347, 2022. [CrossRef]
- V. S. Gerdjikov, D. M. Mladenov, A. A. Stefanov, and S. K. Varbev. Mkdv-type of equations related to b2(1) and a4(2). In Mihaela Kouteva-Guentcheva Boyka Aneva, editor, Nonlinear Mathematical Physics and Natural Hazards. Springer Proceedings in Physics 163, pages 59–69. Springer, 2015.
- V. S. Gerdjikov, D. M. Mladenov, A. A. Stefanov, and S. K. Varbev. On mkdv equations related to the affine kac-moody algebra a5(2). J. Geom. Sym. Phys, 39:17–31, 2015. [CrossRef]
- V. S. Gerdjikov, D. M. Mladenov, A. A. Stefanov, and S. K. Varbev. Soliton equations related to the affine kac-moody algebra d4(1). Eur. Phys. J. Plus, 130:106–123, 2015. [CrossRef]
- V. S. Gerdjikov and A. A. Stefanov. New types of two component nls-type equations. Pliska Studia Mathematica, 26:53–66, 2016.
- V. S. Gerdjikov and A. A. Stefanov. On an example of derivative nonlinear schrödinger equation with D2 reduction. Pliska Stud. Math., 30:99–108, 2019.
- V. S. Gerdjikov, A. A. Stefanov, I. D. Iliev, G. P. Boyadjiev, A. O. Smirnov, V. B. Matveev, and M. V. Pavlov. Recursion operators and the hierarchies of mkdv equations related to d4(1), d4(2) and d4(3) kac-moody algebras. Theoretical and Mathematical Physics, 204(3):1110–1129, 2020.
- V. S. Gerdjikov and A. B. Yanovski. On soliton equations with Zh and Dh reductions: conservation laws and generating operators. J. Geom. Symmetry Phys, 31:57–92, 2013.
- V. S. Gerdjikov and A. B. Yanovski. Riemann-hilbert problems, families of commuting operators and soliton equations. Journal of Physics: Conference Series, 482:012017, 2014. [CrossRef]
- V. S. Gerdjikov and A. B. Yanovski. Cbc systems with mikhailov reductions by coxeter automorphism. i. spectral theory of the recursion operators. Studies in Applied Mathematics, 134:145–180, 2015. [CrossRef]
- V.S. Gerdjikov and M.I. Ivanov. The quadratic bundle of general form and the nonlinear evolution equations. ii. hierarchies of hamiltonian structures. Bulgarian J. Phys, 10:130–143, 1983.
- V.S. Gerdjikov and E.Kh. Khristov. On the evolution equations solvable with the inverse scattering problem. ii. hamiltonian structures and backlund transformations. Bulgarian J. Phys., 7(2):119–133, 1979.
- V.S. Gerdjikov, N.A. Kostov, and T.I. Valchev. Bose-einstein condensates with f=1 and f=2. reductions and soliton interactions of multi-component nls models. In Solomon M. Saltiel, Alexander A. Dreischuh, and Ivan P. Christov, editors, Proceedings of SPIE, volume 7501. SPIE, 2009.
- V.S. Gerdjikov, N.A. Kostov, and T.I. Valchev. Solutions of multi-component nls models and spinor bose-einstein condensates. Physica D, 238:1306–1310, 2009. [CrossRef]
- V.S. Gerdjikov, A.O. Smirnov, and V.B. Matveev. From generalized fourier transforms to spectral curves for the manakov hierarchy. i. generalized fourier transforms. Eur. Phys. J. Plus, 135(8):659, 2020.
- V.S. Gerdjikov, G. Vilasi, and A. B. Yanovski. Integrable Hamiltonian Hierarchies. Spectral and Geometric Methods, volume 748 of Lecture Notes in Physics. Springer Verlag, Berlin, Heidelberg, New York, 2008.
- V.S. Gerdjikov and A.B. Yanovski. Completeness of the eigenfunctions for the caudrey–beals–coifman system. J. Math. Phys., 35(7):3687–3725, 1994.
- J.V. Goossens, M. Yousefi, Y. Jaouën, and H. Haffermann. Polarization-division multiplexing based on the nonlinear Fourier transform. Optic Express, 25(22):437–462, 2017.
- J. Haberlin and T. Lyons. Solitons of shallow-water models from energy-dependent spectral problems. Eur. Phys. J. Plus, 133:16, 2018. [CrossRef]
- S. Helgasson. Differential geometry, Lie groups and symmetric spaces, volume 34 of Graduate Studies in Mathematics. AMS, Providence, Rhode Island, 2012.
- D. Holm and R. Ivanov. Smooth and peaked solitons of the ch equation. J. Phys. A: Math. Theor, 43:434003–434003–, 2010.
- D. Holm and R. Ivanov. Two-component ch system: Inverse scattering, peakons and geometry. Inverse Problems, 27:045013–045032, 2011. [CrossRef]
- D. D. Holm. Geometric Mechanics Part I: Dynamics and Symmetry. Imperial College Press, London, 2011.
- D. D. Holm. Geometric Mechanics Part II: Rotating, Translating and Rolling. Imperial College Press, London, 2011.
- J. Ieda, T. Miyakawa, and M. Wadati. Exact analysis of soliton dynamics in spinor bose-einstein condensates. Phys. Rev Lett., 93:194102, 2004. [CrossRef]
- J. Ieda, T. Miyakawa, and M. Wadati. Matter-wave solitons in an f=1 spinor bose-einstein condensate. J. Phys. Soc. Jpn, 73:2996, 2004.
- R. Ivanov. On the dressing method for the generalised zakharov-shabat system. Nuclear Physics B, 694:509–524, 2004. [CrossRef]
- R. Ivanov and T. Lyons. Integrable models for shallow water with energy dependent spectral problems. Journal of Nonlinear Mathematical Physics, 19:1240008–12400025, 2012. [CrossRef]
- R. I. Ivanov. Nls-type equations from quadratic pencil of lax operators: Negative flows. Chaos, Solitons & Fractals, 161:112299, 2022. [CrossRef]
- V. Z. Enol’skii J. C. Eilbeck and N. A. Kostov. Quasiperiodic and periodic solutions for vector nonlinear schrödinger equations. J. Math. Phys., 41(12):8236, 2000.
- D. J. Kaup. Closure of the squared zakharov–shabat eigenstates. J. Math. Annal. Appl., 54(3):849–864, 1976. [CrossRef]
- D. J. Kaup. The three-wave interaction - a nondispersive phenomenon. Stud. Appl. Math, 55:9–44, 1976. [CrossRef]
- D. J. Kaup. On the inverse scattering problem for cubic eigenvalue problems of the class ψxxx+6qψx+6rψ=λψ. Stud. Appl. Math, 62:189–216, 1980.
- D. J. Kaup and A. C. Newell. An exact solution for a derivative nonlinear schr6dinger equation. J. Math. Phys., 19(4):798–801, 1978.
- V. Knibbeler, S. Lombardo, and J. A. Sanders. Higher-dimensional automorphic lie algebras. Found. Comput. Math, 17:987–1035, 2017. [CrossRef]
- B.G. Konopelchenko. Solitons in Multidimensions. Inverse Spectral Transform Method. World Scientific, Singapore, 1993. [CrossRef]
- N. A. Kostov, V. A. Atanasov, V. S. Gerdjikov, and G. G. Grahovski. On the soliton solutions of the spinor bose-einstein condensate. In Peter A. Atanasov, Tanja N. Dreischuh, Sanka V. Gateva, and Lubomir M. Kovachev, editors, Proceedings of SPIE 6604, 2007.
- P. P. Kulish and E.K. Sklyanin. O(N)-invariant nonlinear Schrodinger equation – A new completely integrable system. Phys. Lett. A, 84(7):349–352, 1981. [CrossRef]
- P.P. Kulish and A.G. Reiman. Hamiltonian structure of polynomial bundles. Journal of Soviet Mathematics, 28(4):505–513, 1985. [CrossRef]
- A. N. Leznov and M. V. Saveliev. Two-dimensional nonlinear equations of the string type and their complete integration. Theoret. and Math. Phys., 54(3):323–337, 1983.
- S. Lombardo and A. V. Mikhailov. Reductions of integrable equations: Dihedral group. J. Phys. A, 37:7727–7742, 2004. [CrossRef]
- S. Lombardo and A. V. Mikhailov. Reduction groups and automorphic lie algebras. Communication in Mathematical Physics, 258:179–202, 2005. [CrossRef]
- Jinghua Luo and Engui Fan. ∂¯-dressing method for the coupled gerdjikov?ivanov equation. Applied Mathematics Letters, 110:106589, 2020.
- B. Prinari M. J. Ablowitz and A. D. Trubach. Discrete and Continuous Nonlinear Schrödinger Systems. London Mathematical Society Lecture Note Series. Cambridge University press, 2004.
- S. V. Manakov. On the theory of two-dimensional stationary self-focusing of electromagnetic waves. Sov. Phys. JETP, 38:248, 1974.
- S. V. Manakov and V. E. Zakharov. Soliton theory. In I. M. Khalatnikov, editor, Sov.Sci.Rev.A, volume 1, pages 133–190, London, 1979.
- V.B. Matveev and A.O. Smirnov. AKNS hierarchy, MRW solutions, Pn breathers, and beyond. J. Math. Phys., 59(9):091419, 2018.
- A. V. Mikhailov. Reductions in integrable systems. the reduction group. JETP Lett., 32(2):187–192, 1980. [CrossRef]
- A. V. Mikhailov. The reduction problem and the inverse scattering problem. Physica D, 3D:73–117, 1981. [CrossRef]
- A. V. Mikhailov, M. A. Olshanetsky, and A. M. Perelomov. Two-dimensional generalized toda lattice. Comm. Math. Phys, 79:473–488, 1981. [CrossRef]
- A. V. Mikhailov, A. B. Shabat, and R. I. Yamilov. The symmetry approach to the classification of non-linear equations. complete lists of integrable systems. Russian Math. Surveys, 42:3–53, 1987. [CrossRef]
- A. V. Mikhailov, A. B. Shabat, and R. I. Yamilov. Extension of the module of invertible transformations. classification of integrable systems. Commun. Math. Phys, 115:1–19, 1988. [CrossRef]
- A. V. Mikhailov and V. E. Zakharov. On the integrability of classical spinor models in two-dimensional space–time. Commun. Math. Phys, 74:21–40, 1980. [CrossRef]
- A.V. Mikhailov, A.B. Shabat, and V.V. Sokolov. The symmetry approach to classification of integrable equations. In V.E. Zakharov, editor, What Is Integrability? Springer Series in Nonlinear Dynamics, pages 115–184. Springer, Berlin, 1991.
- R. Constantinescu N. C. Babalic and V. Gerdjikov. On the solutions of a family of tzitzeica equations. J. Geom. Symm. Physics, 37:1–24, 2015.
- R. Constantinescu N. C. Babalic and V. S. Gerdjikov. On tzitzeica equation and spectral properties of related lax operators. Balkan Journal of Geometry and Its Applications, 19:11–22, 2014.
- S. Novikov, S. Manakov, L. Pitaevskii, and V. Zakharov. Theory of Solitons: The Inverse Scattering Method. Plenum, Consultants Bureau, New York, 1984. [CrossRef]
- T. Ohmi and K. Machida. Bose-einstein condensation with internal degrees of freedom in alkali atom gases. J. Phys. Soc. Jpn, 67:1822, 1998.
- A. B. Shabat. A one-dimensional scattering theory. i. Differ. Uravn., 8:164–178, 1972. [CrossRef]
- A. B. Shabat. The inverse scattering problem for a system of differential equations. Funkts. Anal. Prilozhen, 9:75–78, 1975.
- A. O. Smirnov, V. S. Gerdjikov, and V. B. Matveev. From generalized fourier transforms to spectral curves for the manakov hierarchy. ii. spectral curves for the manakov hierarchy. Eur. Phys. J. Plus, 135(7):561, 2020. [CrossRef]
- A.O. Smirnov. Spectral curves for the derivative nonlinear Schrodinger equations. Symmetry, 13(7):1203, 2021. [CrossRef]
- A.O. Smirnov, E.A. Frolov, and V.S. Gerdjikov. Spectral curves for the multi-phase solutions of manakov system. In IOP Conf Ser: Mater. Sci. Eng., volume 862, page 052041. IOP, 2020. [CrossRef]
- A.O. Smirnov, V.S. Gerdjikov, and E.E. Aman. The kulish-sklyanin type hierarchy and spectral curves. In IOP Conf. Ser.: Mater. Sci. Eng. 1047, page 012114, 2021. [CrossRef]
- A.O. Smirnov and A.S. Kolesnikov. Dubrovin’s method and ablowitz-kaup-newell-segur hierarchy. In IOP Conf. Ser.: Mat. Sci. Eng. 1181, page 012028, 2021.
- A. Streche-Pauna, A. Florian, and V. S. Gerdjikov. On generalized kulish-sklyanin models. Physics AUC, 30(2):175–195, 2020.
- M. Uchiyama, J. Ieda, and M. Wadati. Dark solitons in f=1 spinor bose–einstein condensate. J. Phys. Soc. Jpn, 75:064002, 2006.
- M. Uchiyama, J. Ieda, and M. Wadati. Multicomponent bright solitons in f=2 spinor bose-einstein condensates. J. Phys. Soc. Japan, 76(7):74005, 2007. [CrossRef]
- M. Ueda and M. Koashi. Theory of spin-2 bose-einstein condensates: Spin correlations, magnetic response, and excitation spectra. Phys. Rev. A, 65:063602, 2002. [CrossRef]
- G. G. Grahovski V. A. Atanasov, V. S. Gerdjikov and N. A. Kostov. Fordy-kulish models and spinor bose-einstein condensates. J. Nonlinear Math. Phys., 15(3):291–298, 2008.
- R. Ivanov V. Gerdjikov and G. Grahovski. On integrable wave interactions and lax pairs on symmetric spaces. Wave Motion, 71:53–70, 2017.
- R. Ivanov V. Gerdjikov and A. Stefanov. Riemann-hilbert problem, integrability and reductions. Journal of Geometric Mechanics, 11:167–185, 2019.
- G. G. Grahovski V. S. Gerdjikov, A. V. Mikhailov, and T. I. Valchev. On soliton interactions for the hierarchy of a generalised heisenberg ferromagnetic model on su(3)/s(u(1)× u(2)) symmetric space. Journal of Geometry and Symmetry in Physics, 25:23–55, 2012.
- M. I. Ivanov V. S. Gerdzhikov and P. P. Kulish. Quadratic bundle and nonlinear equations. Theoretical and Mathematical Physics, 44(3):784–795, 1980.
- T. I. Valchev. On certain reductions of integrable equations on symmetric spaces. AIP Conference Proceedings, 1340:154–164, 2011. [CrossRef]
- T. I. Valchev. Dressing method and quadratic bundles related to symmetric spaces. vanishing boundary conditions. Journal of Mathematical Physics, 57:021508, 2016.
- N.A. Kostov V.S. Gerdjikov and T.I. Valchev. Solutions of multi-component NLS models and Spinor Bose-Einstein condensates. Physica D, 238:1306–1310, 2009.
- M. Wadati. The exact solution of the modified Korteweg de Vries equation. J. Phys. Soc. Japan, 1972. [CrossRef]
- O.H. Warren and J.N. Elgin. The vector nonlinear Schrödinger hierarchy. Physica D, 228:166–171, 2007.
- A. B. Yanovski and T. I. Valchev. Pseudo-hermitian reduction of a generalized heisenberg ferromagnet equation. i. auxiliary system and fundamental properties. Journal of Nonlinear Mathematical Physics, 25:324–350, 2018.
- Norman J. Zabusky. Fermi–pasta–ulam, solitons and the fabric of nonlinear and computational science: History, synergetics, and visiometrics. Chaos, 15:015102, 2005. [CrossRef]
- V. E. Zakharov. The inverse scattering method. In R. K. Bullough and P. J. Caudrey, editors, Solitons, pages 243–286. Springer-Verlag, Berlin, 1980.
- V. E. Zakharov. Integrable systems in multidimensional spaces. In Mathematical Problems in Theoretical Physics, Lecture Notes in Phys. 153, pages 190–216. Springer-Verlag, Berlin, 1982.
- V. E. Zakharov and S. V. Manakov. On the theory of resonance interactions of wave packets in nonlinear media. Zh. Exp. Teor. Fiz, 69:1654–1673, 1975.
- V. E. Zakharov and A. B. Shabat. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Soviet Physics-JETP, 34:62–69, 1972.
- V. E. Zakharov and A. B. Shabat. Interaction between solitons in a stable medium. Sov. Phys. JETP, 37(5):823–828, 1973.
- V. E. Zakharov and A. B. Shabat. A scheme for integrating nonlinear evolution equations of mathematical physics by the inverse scattering method. i. Funkts. Anal. Prilozhen., 8:43–53, 1974.
- V. E. Zakharov and A. B. Shabat. Integration of the nonlinear equations of mathematical physics by the inverse scattering method. Funkts. Anal. Prilozhen, 13:13–22, 1979.
- V.E. Zakharov. Exact solutions of the problem of parametric interaction of wave packets. Dokl. Akad. Nauk SSSR, 228:1314–1316, 1976.
- V.E. Zakharov and L.D. Faddeev. Korteweg-de vries equation: A completely integrable hamiltonian system. Functional Analysis and Its Applications, 5(4):280–287, 1971. [CrossRef]
- Guangxiu Zhao. Integrability of Two-component Systems of Partial Differential Equations. PhD thesis, Loughborough University, 2020.
| 1 | Manakov proposed the first vector NLS equation with only 2 components [92]. The reason was that he wanted to treat a special case of VNLS which described the propagation of birefringent optical pulses in optical fibers. Since our Lax operator above is a quadratic pencil, the equation (6.30) we derived is a vector generalization of GI equation. Of course the method of solution of the VNLS is easily generalized to p-component vectors. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




