Submitted:
10 October 2025
Posted:
15 October 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental and Theoretical Methods
3. Experimental Results
3.1. Structure-Phase Composition: Results and Interpretation
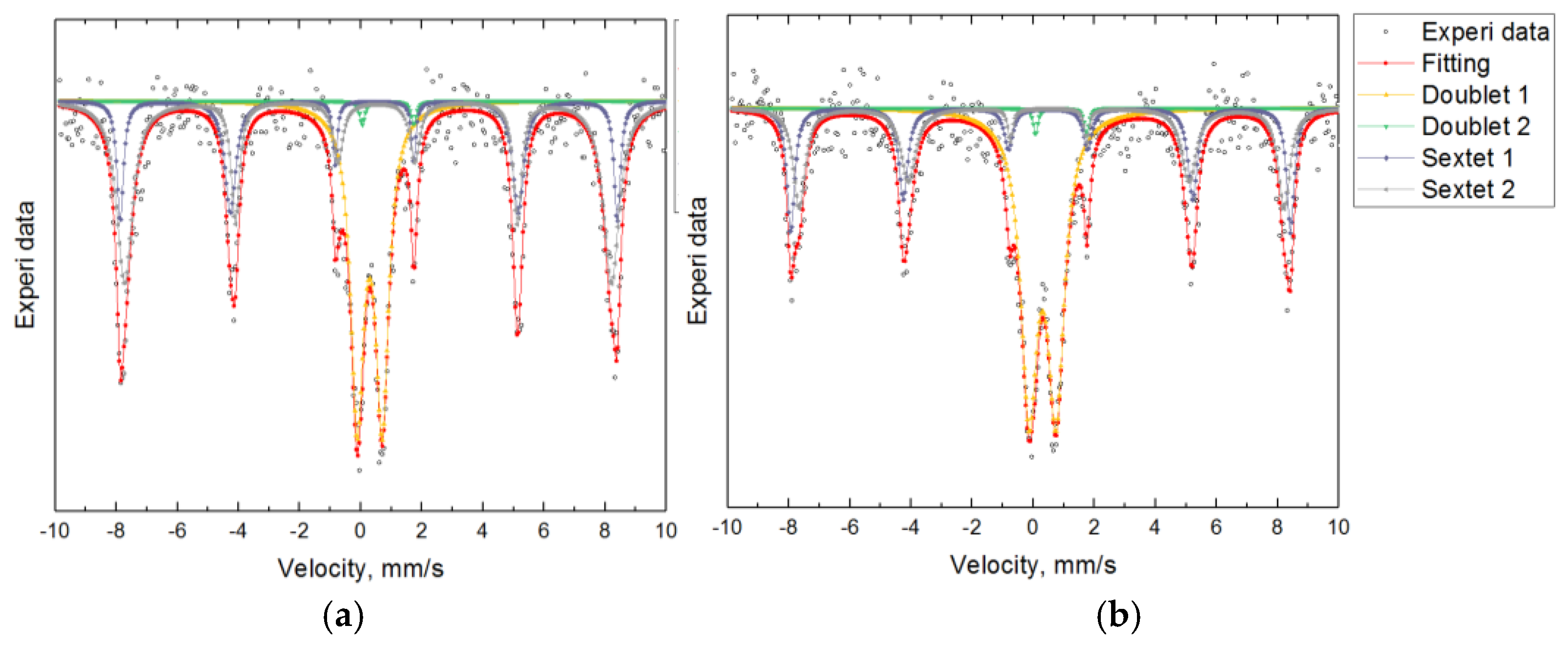
3.2. Mössbauer Spectroscopy: Fe Valence and Magnetic Ordering
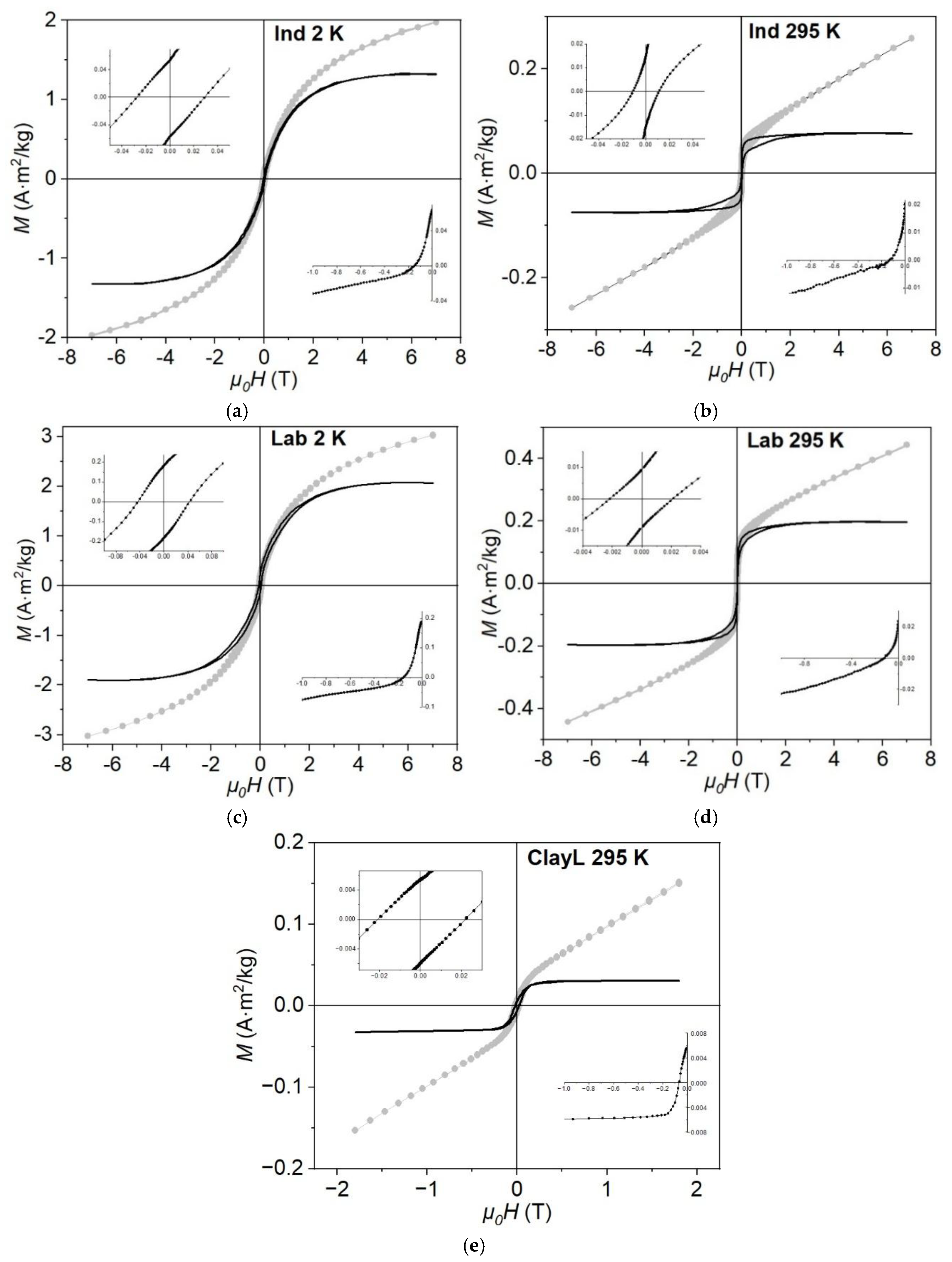
3.3. Field Dependencies of Magnetization
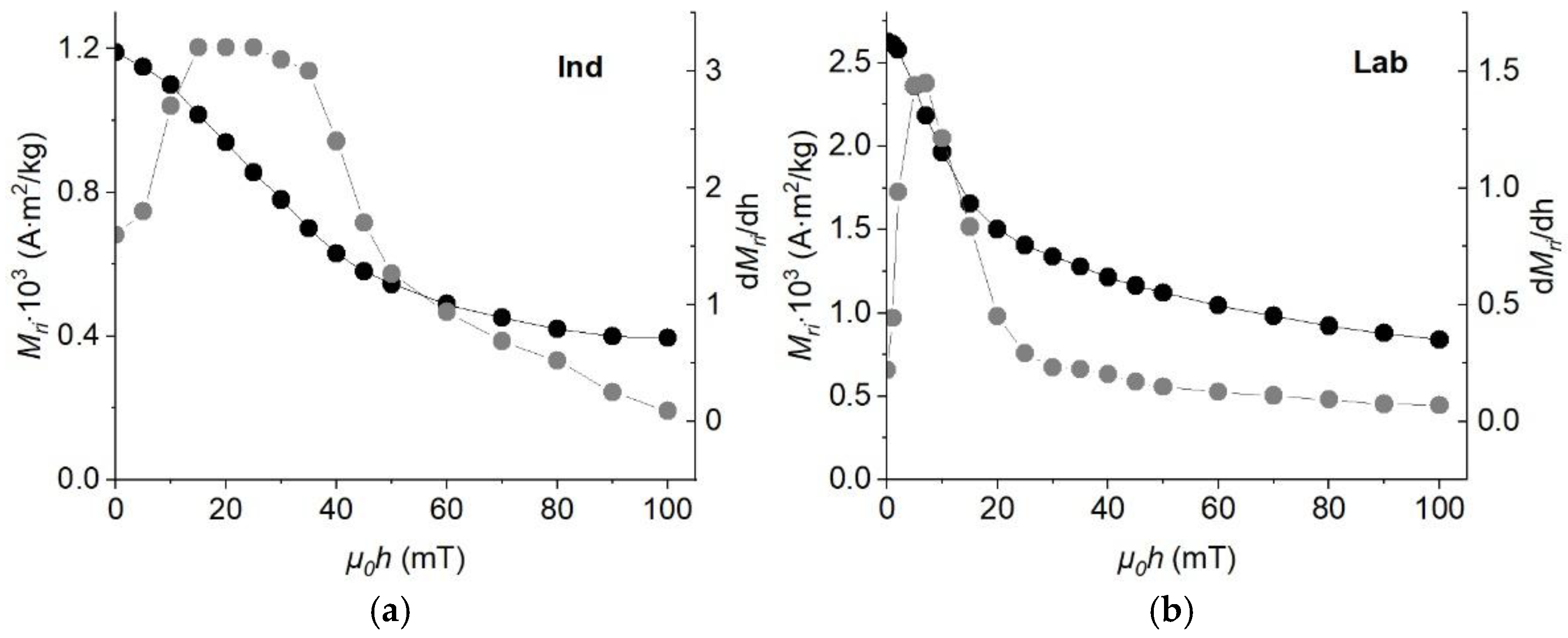
3.4. Coercivity Spectra and Remanent Magnetization
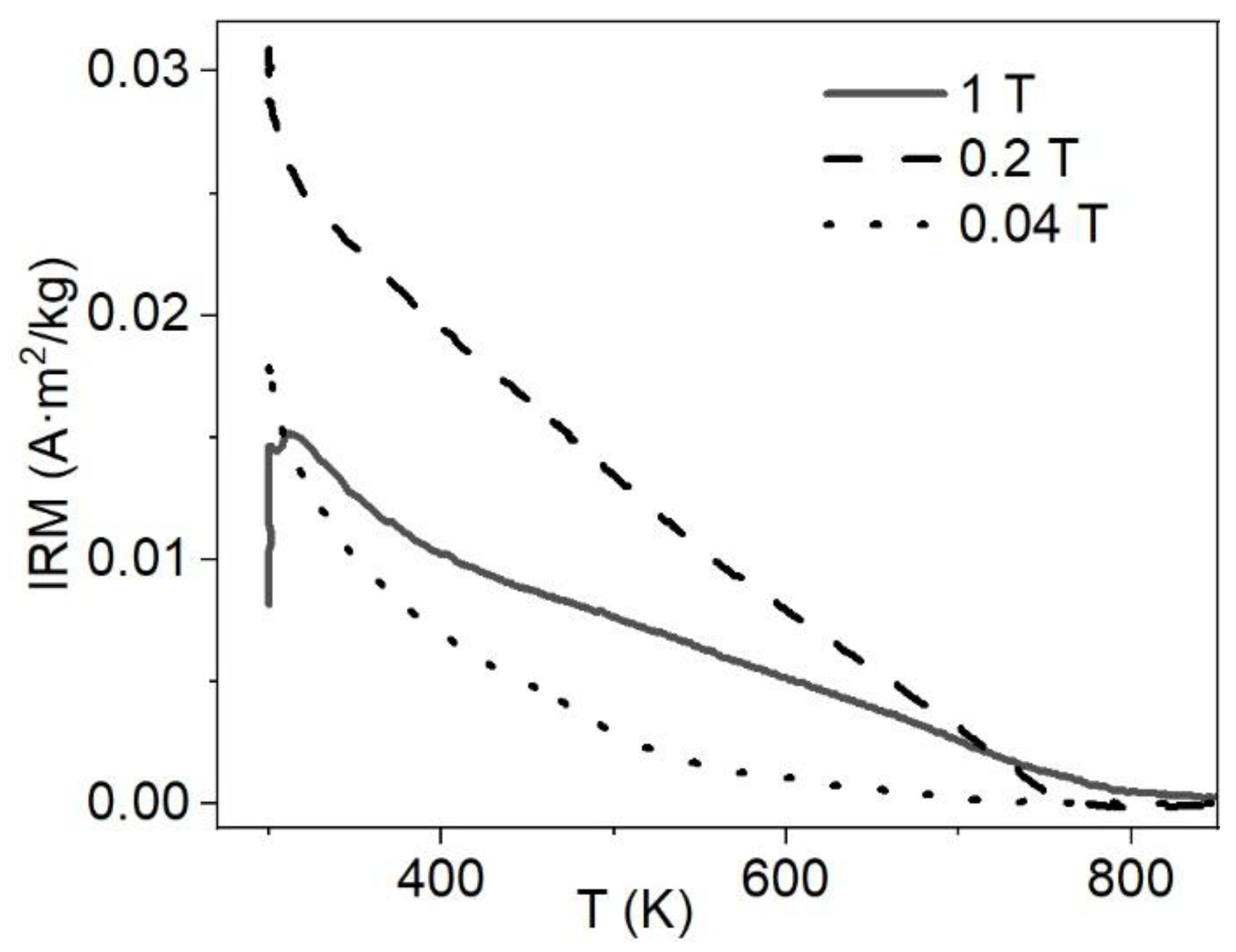
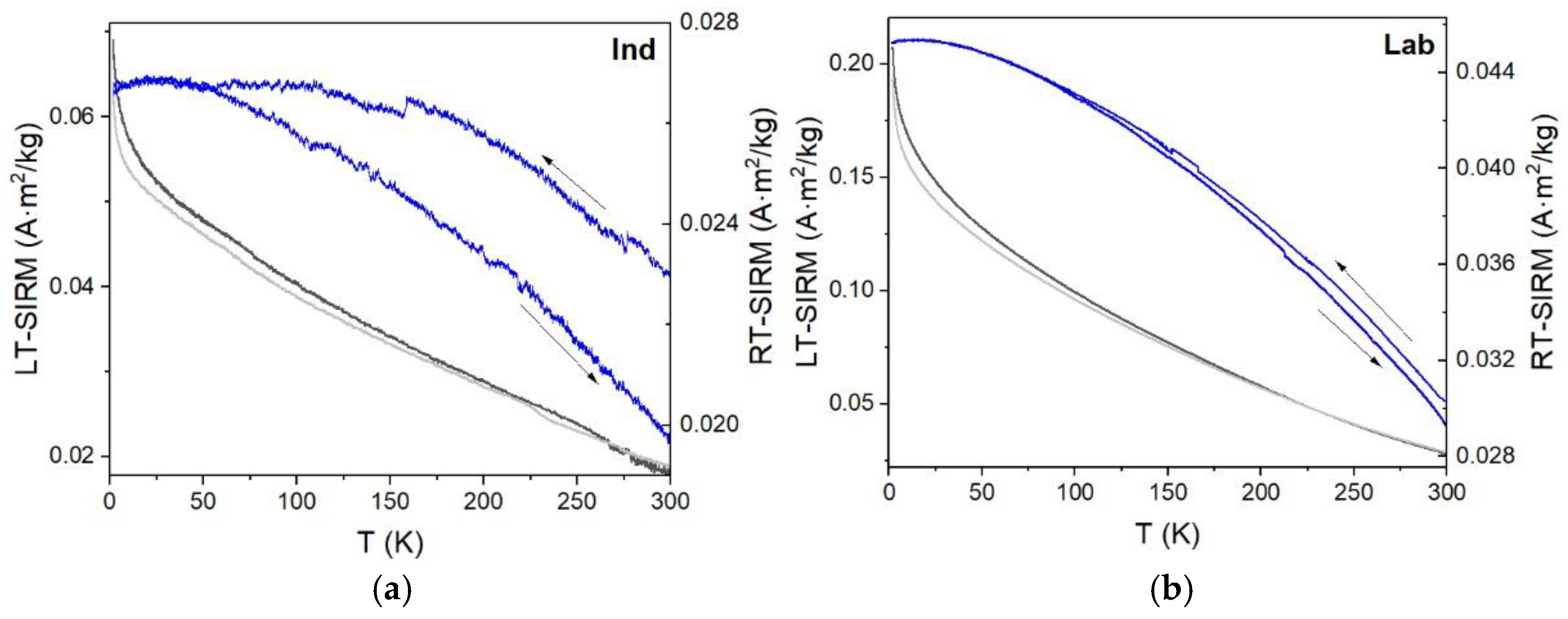
3.5. Low-Temperature Magnetization
3.6. Impulse and Frequency Characteristics of Susceptibility
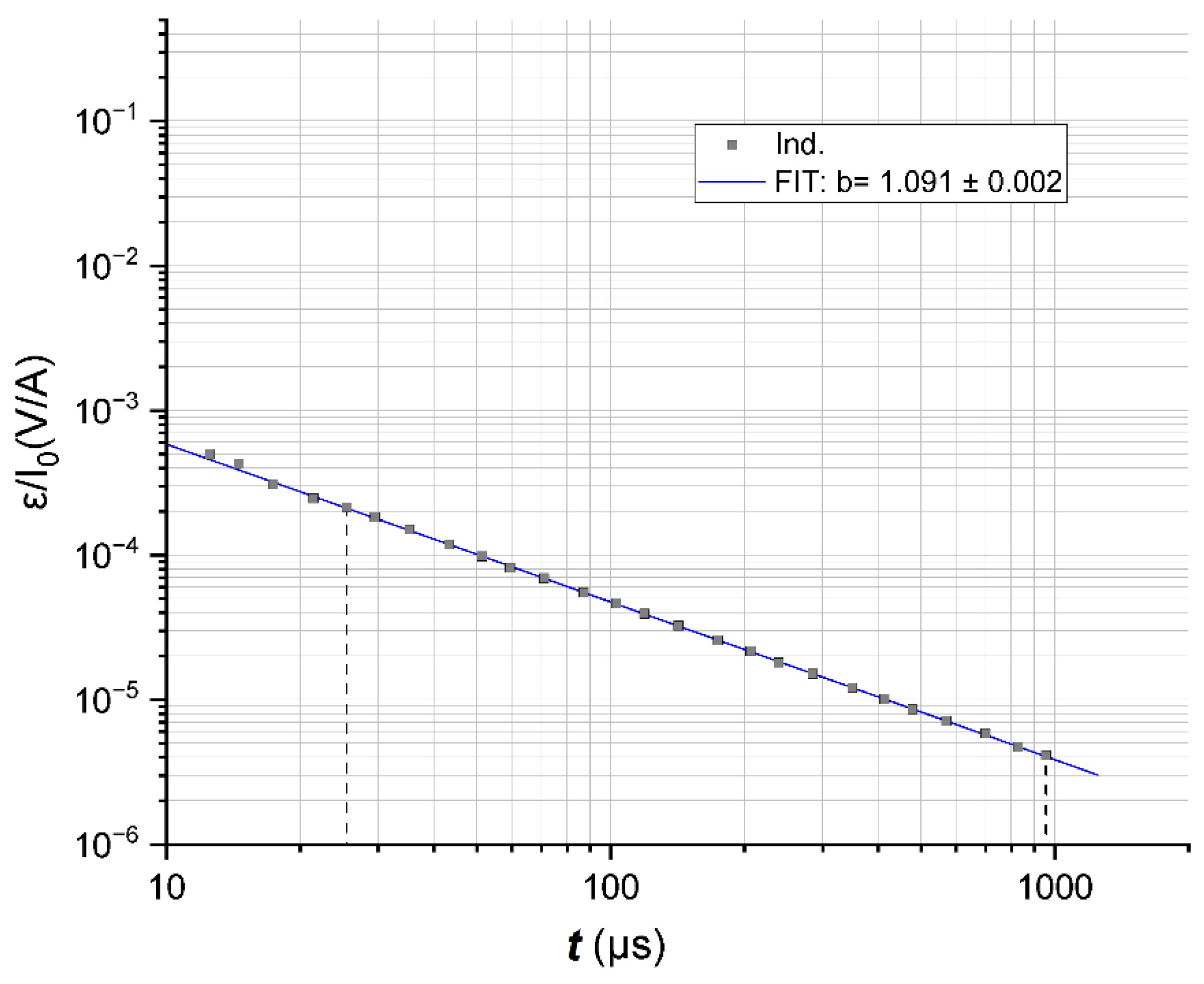
3.6.1. Impulse Characteristics
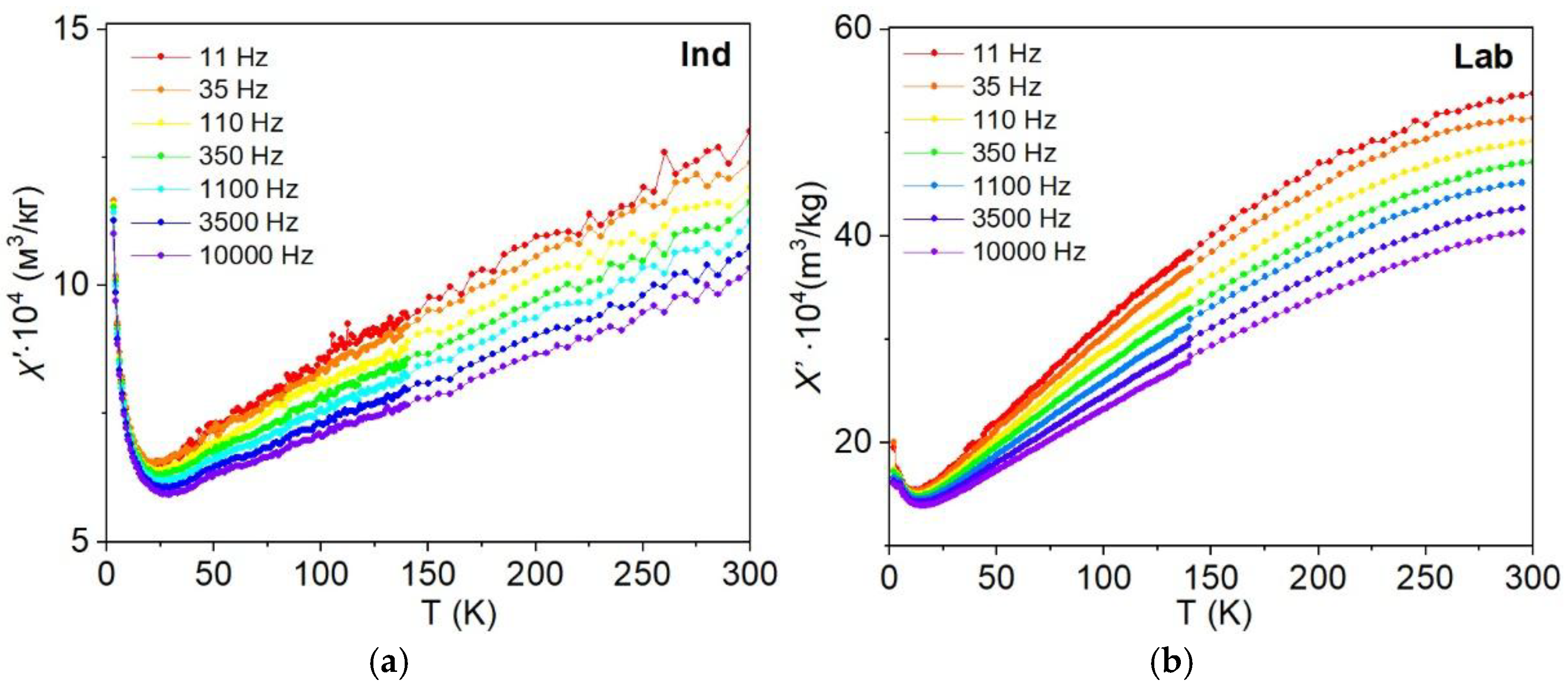
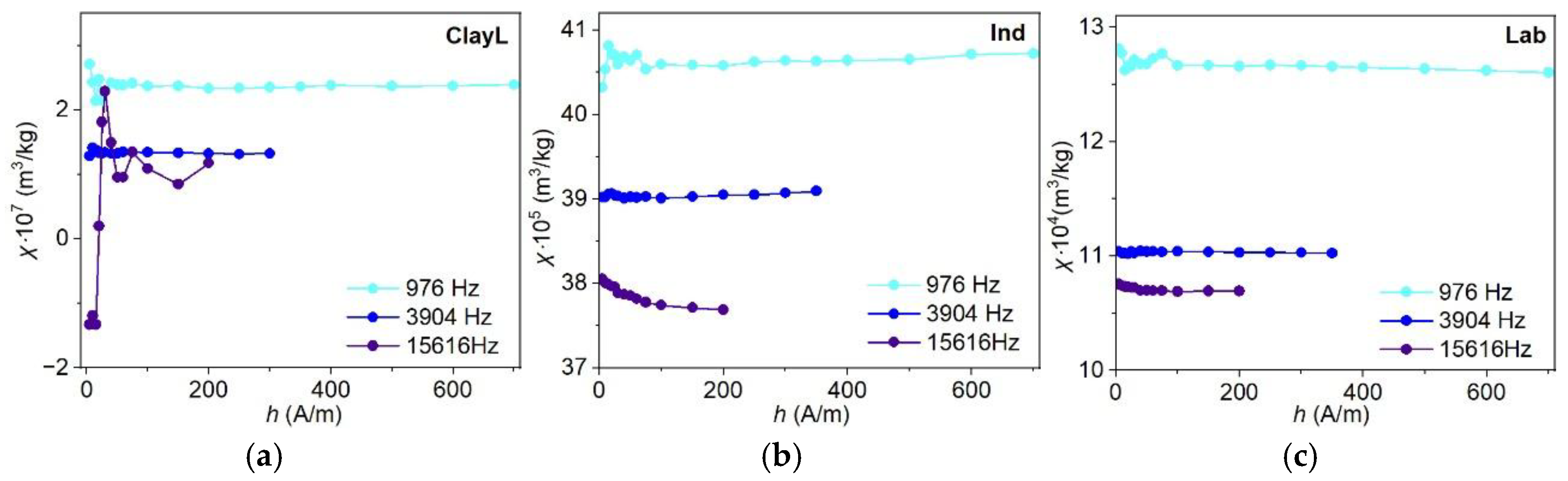
3.6.2. Frequency-Temperature and Frequency-Field Dependencies of Magnetic Susceptibility
3.7. FD Factor and SP Contributions
4. Discussion of the Experimental Results
4.1. Structure-Phase Basis of Magnetic Microheterogeneity
4.2. Magnetic Parameters as Indicators of Multicomponent Ensemble of Particles
4.3. Temperature Dependencies of ARM and IRM Coercivity
4.4. Low-Temperature Magnetic Behavior
4.5. Frequency-Dependent and Transient Susceptibility Signatures of SP Particles
5. Theoretical Modeling
| Sample | Δ1, % | cf, 10-3 | Ieff rs, kA/m | Ieff rs1, kA/m | δ1, % | δ2, % | δ3, % |
|---|---|---|---|---|---|---|---|
| Lab | 76–84 | 0.80–0.93 | 37–43 | 33–41 | 67.4–78.3 | 31.9–21.2 | 0.7–0.5 |
| Ind | 52–63 | 0.42–0.50 | 66–79 | 82–102 | 65.8–76.4 | 33.4–23.0 | 0.8–0.6 |
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rancourt, D.G. Magnetism of Earth, Planetary, and Environmental Nanomaterials. Rev. Mineral. Geochemistry 2001, 44, 217–292. [CrossRef]
- Evans, M.E.; Heller, F. Environmental Magnetism: Principles and Applications of Enviromagnetics; Academic Press: San Diego, 2003; ISBN 0122438515.
- Jordanova, N. Soil Magnetism: Applications in Pedology, Environmental Science and Agriculture; Elsevier Science: Amsterdam, 2016; ISBN 0128092394.
- Peters, C.; Thompson, R. Supermagnetic Enhancement, Superparamagnetism, and Archaeological Soils. Geoarchaeology - An Int. J. 1999, 14, 401–413. [CrossRef]
- Jordanova, N.; Petrovsky, E.; Kovacheva, M.; Jordanova, D. Factors Determining Magnetic Enhancement of Burnt Clay from Archaeological Sites. J. Archaeol. Sci. 2001, 28. [CrossRef]
- Maher, B.A. Palaeoclimatic Records of the Loess/Palaeosol Sequences of the Chinese Loess Plateau. Quat. Sci. Rev. 2016, 154, 23–84. [CrossRef]
- Kermenidou, M.; Balcells, L.; Martinez-Boubeta, C.; Chatziavramidis, A.; Konstantinidis, I.; Samaras, T.; Sarigiannis, D.; Simeonidis, K. Magnetic Nanoparticles: An Indicator of Health Risks Related to Anthropogenic Airborne Particulate Matter. Environ. Pollut. 2021, 271. [CrossRef]
- Néel, L. Théorie Du Traînage Magnétique Des Ferromagnétiques En Grains Fins Avec Application Aux Terres Cuites. Ann. Geophys. 1949, 5, 99–136.
- Kharitonskiǐ, P. V. Magnetostatic Interaction of Superparamagnetic Particles Dispersed in a Thin Layer. Phys. Solid State 1997, 39, 162–163. [CrossRef]
- Kharitonskii, P. V.; Gareev, K.G.; Ionin, S.A.; Ryzhov, V.A.; Bogachev, Y. V.; Klimenkov, B.D.; Kononova, I.E.; Moshnikov, V.A. Microstructure and Magnetic State of Fe3O4-SiO2 Colloidal Particles. J. Magn. 2015, 20, 221–228. [CrossRef]
- Barsukov, P.; Soupios, P.; Gorokhovich, Y. Application of Special SPM Loop in Archaeological Prospection. In Proceedings of The 20th International Geophysical Congress and Exhibition of Turkey, Antalya, Turkey, 25–27 November 2013; pp. 90–93.
- Kozhevnikov, N.O.; Antonov, E.Y. The Magnetic Relaxation Effect on TEM Responses of a Uniform Earth. Russ. Geol. Geophys. 2008, 49, 197–205. [CrossRef]
- Cowan, D.C.; Song, L.P.; Oldenburg, D.W. Transient VRM Response From a Large Circular Loop Over a Conductive and Magnetically Viscous Half-Space. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3669–3678. [CrossRef]
- Barsukov, P.O.; Fainberg, E.B. Study of the Environment by the Transient Electromagnetic Method Using the Induced Polarization and Superparamagnetic Effects. Izv. Phys. Solid Earth 2002, 38, 981–984.
- Thiesson, J.; Tabbagh, A.; Flageul, S. TDEM Magnetic Viscosity Prospecting Using a Slingram Coil Configuration. Near Surf. Geophys. 2007, 5, 363–374. [CrossRef]
- McNeill, J.D. The magnetic susceptibility of soils is definitely complex. Geonix Limited, Technical Note TN-36. 2013. 27 p.
- Tabbagh, A.; Dabas, M. Absolute Magnetic Viscosity Determination Using Time-Domain Electromagnetic Devices. Archaeol. Prospect. 1996, 3, 199–208. [CrossRef]
- Kozhevnikov, N.O.; Kharinsky, A. V.; Kozhevnikov, O.K. An Accidental Geophysical Discovery of an Iron Age Archaeological Site on the Western Shore of Lake Baikal. J. Appl. Geophys. 2001, 47, 107–122. [CrossRef]
- Cornell, R.M.; Schwertmann, U. The Iron Oxides: Structure, Properties, Reactions, Occurences and Uses; Wiley, 2004; ISBN 9783527602094.
- Machala, L.; Tuček, J.; Zbořil, R. Polymorphous Transformations of Nanometric Iron(III) Oxide: A Review. Chem. Mater. 2011, 23, 3255–3272. [CrossRef]
- Tuçek, J.; Kemp, K.C.; Kim, K.S.; Zboŗil, R. Iron-Oxide-Supported Nanocarbon in Lithium-Ion Batteries, Medical, Catalytic, and Environmental Applications. ACS Nano 2014, 8, 7571–7612. [CrossRef]
- Kharitonskii, P.; Kamzin, A.; Gareev, K.; Valiullin, A.; Vezo, O.; Sergienko, E.; Korolev, D.; Kosterov, A.; Lebedev, S.; Gurylev, A.; et al. Magnetic Granulometry and Mössbauer Spectroscopy of FemOn–SiO2 Colloidal Nanoparticles. J. Magn. Magn. Mater. 2018, 461, 30–36. [CrossRef]
- Gurylev, A.; Kharitonskii, P.; Kosterov, A.; Berestnev, I.; Sergienko, E. Magnetic Properties of Fired Clay (Bricks) Possibly Containing Epsilon Iron (III) Oxide. In Proceedings of the Journal of Physics: Conference Series; 2019; Vol. 1347. [CrossRef]
- Kharitonskii, P.; Bobrov, N.; Gareev, K.; Kosterov, A.; Nikitin, A.; Ralin, A.; Sergienko, E.; Testov, O.; Ustinov, A.; Zolotov, N. Magnetic Granulometry, Frequency-Dependent Susceptibility and Magnetic States of Particles of Magnetite Ore from the Kovdor Deposit. J. Magn. Magn. Mater. 2022, 553, 169279. [CrossRef]
- Bobrov, N.; Sergienko, E.; Yanson, S.; Kosterov, A.; Karpinsky, V.; Kharitonskii, P.; Ralin, A. Magnetic Viscosity of Suevites from the Zhamanshin Impact Crater. In Springer Proceedings in Earth and Environmental Sciences; 2023; Vol. 2023, pp. 85–109. [CrossRef]
- Kharitonskii, P.; Sergienko, E.; Ralin, A.; Setrov, E.; Sheidaev, T.; Gareev, K.; Ustinov, A.; Zolotov, N.; Yanson, S.; Dubeshko, D. Superparamagnetism of Artificial Glasses Based on Rocks: Experimental Data and Theoretical Modeling. Magnetochemistry 2023, 9. [CrossRef]
- Doebelin, N.; Kleeberg, R. Profex: A Graphical User Interface for the Rietveld Refinement Program BGMN. J. Appl. Crystallogr. 2015, 48. [CrossRef]
- Lowrie, W. Identification of Ferromagnetic Minerals in a Rock by Coercivity and Unblocking Temperature Properties. Geophys. Res. Lett. 1990, 17. [CrossRef]
- Applied Electromagnetic Research. Applied Electromagnetic Research. Available online: http://www.aemr.net/ (accessed 4th March 2025).
- Kharitonskii, P. V.; Setrov, E.A.; Ralin, A.Y. Modeling of Hysteresis Characteristics of a Dilute Magnetic with Dipole-Dipole Interaction of Particles. Mater. Phys. Mech. 2024, 52, 142–150. [CrossRef]
- Abert, C. Micromagnetics and Spintronics: Models and Numerical Methods. Eur. Phys. J. B 2019, 92. [CrossRef]
- Leliaert, J.; Mulkers, J. Tomorrow’s Micromagnetic Simulations. J. Appl. Phys. 2019, 125. [CrossRef]
- Donnelly, C.; Hierro-Rodríguez, A.; Abert, C.; Witte, K.; Skoric, L.; Sanz-Hernández, D.; Finizio, S.; Meng, F.; McVitie, S.; Raabe, J.; et al. Complex Free-Space Magnetic Field Textures Induced by Three-Dimensional Magnetic Nanostructures. Nat. Nanotechnol. 2022, 17, 136–142. [CrossRef]
- Kharitonskii, P.; Zolotov, N.; Kirillova, S.; Gareev, K.; Kosterov, A.; Sergienko, E.; Yanson, S.; Ustinov, A.; Ralin, A. Magnetic Granulometry, Mössbauer Spectroscopy, and Theoretical Modeling of Magnetic States of FemOn–Fem-XTixOn Composites. Chinese J. Phys. 2022, 78, 271–296. [CrossRef]
- Olin, M.; Anttila, T.; Dal Maso, M. Using a Combined Power Law and Log-Normal Distribution Model to Simulate Particle Formation and Growth in a Mobile Aerosol Chamber. Atmos. Chem. Phys. 2016, 16, 7067–7090. [CrossRef]
- Fujihara, A.; Tanimoto, S.; Yamamoto, H.; Ohtsuki, T. Log-Normal Distribution in a Growing System with Weighted and Multiplicatively Interacting Particles. J. Phys. Soc. Japan 2018, 87, 034001. [CrossRef]
- Hrouda, F. Models of Frequency-Dependent Susceptibility of Rocks and Soils Revisited and Broadened. Geophys. J. Int. 2011, 187, 1259–1269. [CrossRef]
- Kostadinova-Avramova, M.; Kovacheva, M. The Magnetic Properties of Baked Clays and Their Implications for Past Geomagnetic Field Intensity Determinations. Geophys. J. Int. 2013, 195. [CrossRef]
- Putnis, A.; McConnell, J.D.C. Principles of Mineral Behaviour; Blackwell Scientific Publications: Oxford, UK, 1980; 257 pp.
- Murad, E.; Wagner, U. The Mössbauer Spectrum of Illite. Clay Miner. 1994, 29, 1–10. [CrossRef]
- López-Sánchez, J.; Palencia-Ortas, A.; del Campo, A.; McIntosh, G.; Kovacheva, M.; Martín-Hernández, F.; Carmona, N.; Rodríguez de la Fuente, O.; Marín, P.; Molina-Cardín, A.; et al. Further Progress in the Study of Epsilon Iron Oxide in Archaeological Baked Clays. Phys. Earth Planet. Inter. 2020, 307. [CrossRef]
- McIntosh, G.; Kovacheva, M.; Catanzariti, G.; Donadini, F.; Lopez, M.L.O. High Coercivity Remanence in Baked Clay Materials Used in Archeomagnetism. Geochemistry, Geophys. Geosystems 2011, 12. [CrossRef]
- Kosterov, A.; Kovacheva, M.; Kostadinova-Avramova, M.; Minaev, P.; Salnaia, N.; Surovitskii, L.; Yanson, S.; Sergienko, E.; Kharitonskii, P. High-Coercivity Magnetic Minerals in Archaeological Baked Clay and Bricks. Geophys. J. Int. 2021, 224, 1256–1271. [CrossRef]
- Vandenberghe, R.E.; De Grave, E. Application of Mössbauer Spectroscopy in Earth Sciences. In Mössbauer Spectroscopy; Springer Berlin Heidelberg: Berlin, Germany, 2013; pp. 91–185.
- Maher, B.A.; Ahmed, I.A.M.; Karloukovski, V.; MacLaren, D.A.; Foulds, P.G.; Allsop, D.; Mann, D.M.A.; Torres-Jardón, R.; Calderon-Garciduenas, L. Magnetite Pollution Nanoparticles in the Human Brain. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 10797–10801. [CrossRef]
- Shokanov, A.; Manakova, I.; Vereshchak, M.; Migunova, A. Characterization of Kazakhstan’s Clays by Mössbauer Spectroscopy and X-ray Diffraction. Minerals 2024, 14, 713. [CrossRef]
- Tuček, J.; Zbořil, R.; Namai, A.; Ohkoshi, S.I. ε-Fe2O3: An Advanced Nanomaterial Exhibiting Giant Coercive Field, Millimeter-Wave Ferromagnetic Resonance, and Magnetoelectric Coupling. Chem. Mater. 2010, 22, 6483–6505.
- López-Sánchez, J.; McIntosh, G.; Osete, M.L.; del Campo, A.; Villalaín, J.J.; Pérez, L.; Kovacheva, M.; Rodríguez de la Fuente, O. Epsilon Iron Oxide: Origin of the High Coercivity Stable Low Curie Temperature Magnetic Phase Found in Heated Archeological Materials. Geochemistry, Geophys. Geosystems 2017, 18, 2646–2656. [CrossRef]
- Thompson, R.; Oldfield, F. Environmental magnetism; Springer: Dordrecht, Germany; 2012. ISBN 978-94-011-8038-2.
- Nogués, J.; Sort, J.; Langlais, V.; Doppiu, S.; Dieny, B.; Muñoz, J.S.; Suriñach, S.; Baró, M.D.; Stoyanov, S.; Zhang, Y. Exchange Bias in Ferromagnetic Nanoparticles Embedded in an Antiferromagnetic Matrix. Int. J. Nanotechnol. 2005, 2, 23–42. [CrossRef]
- López-Ortega, A.; Estrader, M.; Salazar-Alvarez, G.; Roca, A.G.; Nogués, J. Applications of Exchange Coupled Bi-Magnetic Hard/Soft and Soft/Hard Magnetic Core/Shell Nanoparticles. Phys. Rep. 2015, 553, 1–32. [CrossRef]
- Balaev, D.A.; Krasikov, A.A.; Dubrovskiy, A.A.; Popkov, S.I.; Stolyar, S. V.; Iskhakov, R.S.; Ladygina, V.P.; Yaroslavtsev, R.N. Exchange Bias in Nano-Ferrihydrite. J. Appl. Phys. 2016, 120. [CrossRef]
- Thi, T.N.; Van, P.C.; Artavazd, K.; Hwang, C.; Choi, J.; Kim, H.; Jeong, J.R. Effect of Heat-Treatment Temperature on the Formation of ε-Fe2O3 Nanoparticles Encapsulated by SiO2. J. Magn. 2023, 28. [CrossRef]
- Tauxe, L.; Mullender, T.A.T.; Pick, T. Potbellies, Wasp-Waists, and Superparamagnetism in Magnetic Hysteresis. J. Geophys. Res. Solid Earth 1996, 101. [CrossRef]
- Özdemir, Ö.; Dunlop, D.J. Hysteresis and Coercivity of Hematite. J. Geophys. Res. Solid Earth 2014, 119, B02101. [CrossRef]
- Roberts, A.P.; Yulong Cui; Verosub, K.L. Wasp-Waisted Hysteresis Loops: Mineral Magnetic Characteristics and Discrimination of Components in Mixed Magnetic Systems. J. Geophys. Res. 1995, 100, 17909–17924. [CrossRef]
- Dunlop, D.J. Theory and application of the Day plot (Mrs/Ms versus Hcr/Hc) 2. Application to data for rocks, sediments, and soils. J. Geophys. Res. Solid Earth 2002, 107. [CrossRef]
- Fabian, K. Some Additional Parameters to Estimate Domain State from Isothermal Magnetization Measurements. Earth Planet. Sci. Lett. 2003, 213, 337–345. [CrossRef]
- Muxworthy, A.R.; Williams, W. Critical Superparamagnetic/Single-Domain Grain Sizes in Interacting Magnetite Particles: Implications for Magnetosome Crystals. J. R. Soc. Interface 2009, 6, 1207–1212. [CrossRef]
- Liu, Q.; Roberts, A.P.; Torrent, J.; Horng, C.S.; Larrasoaña, J.C. What Do the HIRM and S-Ratio Really Measure in Environmental Magnetism? Geochemistry, Geophys. Geosystems 2007, 8. [CrossRef]
- Gehring, A.U.; Fischer, H.; Louvel, M.; Kunze, K.; Weidler, P.G. High Temperature Stability of Natural Maghemite: A Magnetic and Spectroscopic Study. Geophys. J. Int. 2009, 179, 1361–1371. [CrossRef]
- Dunlop, D. J.; Özdemir, Ö. Rock Magnetism. Fundamentals and Frontiers. Cambridge Studies in Magnetism Series. Cambridge University Press: Cambridge, UK; 1997. ISBN 978-0521000987.
- Özdemir, Ö.; Banerjee, S.K. High Temperature Stability of Maghemite (γ-Fe2O3). Geophys. Res. Lett. 1984, 11, 161–164. [CrossRef]
- Moskowitz, B.M.; Frankel, R.B.; Bazylinski, D.A. Rock Magnetic Criteria for the Detection of Biogenic Magnetite. Earth Planet. Sci. Lett. 1993, 120, 283–300. [CrossRef]
- Housen, B.A.; Banerjee, S.K.; Moskowitz, B.M. Low-Temperature Magnetic Properties of Siderite and Magnetite in Marine Sediments. Geophys. Res. Lett. 1996, 23, 2843–2846. [CrossRef]
- Smirnov, A. V.; Tarduno, J.A. Low-Temperature Magnetic Properties of Pelagic Sediments (Ocean Drilling Program Site 805C): Tracers of Maghemitization and Magnetic Mineral Reduction. J. Geophys. Res. Solid Earth 2000, 105. [CrossRef]
- Özdemir, Ö.; Dunlop, D.J. Hallmarks of Maghemitization in Low-Temperature Remanence Cycling of Partially Oxidized Magnetite Nanoparticles. J. Geophys. Res. 2010, 115. [CrossRef]
- Dearing, J.A.; Dann, R.J.L.; Hay, K.; Lees, J.A.; Loveland, P.J.; Maher, B.A.; O’Grady, K. Frequency-Dependent Susceptibility Measurements of Environmental Materials. Geophys. J. Int. 1996, 124, 228–240. [CrossRef]
- Khurshid, H.; Lampen-Kelley, P.; Iglesias, Ò.; Alonso, J.; Phan, M.H.; Sun, C.J.; Saboungi, M.L.; Srikanth, H. Spin-Glass-like Freezing of Inner and Outer Surface Layers in Hollow γ-Fe2O3 Nanoparticles. Sci. Rep. 2015, 5. [CrossRef]
- Mugiraneza, S.; Hallas, A.M. Tutorial: A Beginner’s Guide to Interpreting Magnetic Susceptibility Data with the Curie-Weiss Law. Commun. Phys. 2022, 5. [CrossRef]
- Kumar, P.; Gupta, P. Halloysite-Based Magnetic Nanostructures for Diverse Applications: A Review. ACS Appl. Nano Mater. 2023, 6, 13824–13868. [CrossRef]
- Balaev, D.A.; Semenov, S.V.; Dubrovskiy, A.A.; Knyazev, Y.V.; Kirillov, V.L.; Shaykhutdinov, K.A.; Martyanov, O.N. Size Effect and Temperature of Magnetic Ordering in ε-Fe2O3 Nanoparticles. Journal of Superconductivity and Novel Magnetism 2025, 38, 184. [CrossRef]
- Sakurai, S.; Namai, A.; Hashimoto, K.; Ohkoshi, S. First Observation of Phase Transformation of All Four Fe2O3 Phases (γ → ε → β → α-Phase). J. Am. Chem. Soc. 2009, 131, 18299–18303. [CrossRef]
- Kneller, E.F.; Luborsky, F.E. Particle Size Dependence of Coercivity and Remanence of Single-Domain Particles. J. Appl. Phys. 1963, 34, 656–658. [CrossRef]
- Stoner, E.C.; Wohlfarth, E.P. A Mechanism of Magnetic Hysteresis in Heterogeneous Alloys. Philos. Trans. R. Soc. London. Ser. A, Math. Phys. Sci. 1948, 240, 599–642. [CrossRef]
- Roberts, A.P.; Almeida, T.P.; Church, N.S.; Harrison, R.J.; Heslop, D.; Li, Y.; Li, J.; Muxworthy, A.R.; Williams, W.; Zhao, X. Resolving the Origin of Pseudo-Single Domain Magnetic Behavior. J. Geophys. Res. Solid Earth 2017, 122, 9534–9558. [CrossRef]

| ClayL | Ind | Lab | |
|---|---|---|---|
| Quartz | 40 | 44 | 49 |
| Feldspar (microcline + plagioclase) | 23 | 39 | 41 |
| Mica | 20 | 3 | 4 |
| Amphibole | 2 | 1 | 1 |
| Hematite | — | 5 | 5 |
| Spinel | — | 8 | — |
| Kaolinite | 9 | — | — |
| Pyroxene | 2 | — | — |
| Chlorite | 5 | — | — |
| Dolomite | 1 | — | — |
| Rp(*) (%) | 4.4 | 5.9 | 5.4 |
| (*) convergence factor of the calculated and experimental X-ray profiles, yi-intensity at each experimental point of the X-ray image. | |||
| Sample | Component | Fe | IS (mm/s) | QS (mm/s) | BHf (T) | % |
|---|---|---|---|---|---|---|
| Lab | Doublet Fe(1) | Fe3+ | 0.305±0.009 | 0.882±0.016 | — | 50.11 |
| Doublet Fe(2) | Fe2+ | 0.910±0.044 | 1.663±0.089 | — | 1.29 | |
| Sextet Fe(3) | Fe3+ | 0.363±0.012 | 0.241±0.023 | 50.796±0.097 | 22.82 | |
| Sextet Fe(4) | Fe3+ | 0.388±0.017 | 0.228±0.034 | 49.285±0.205 | 25.78 | |
| Ind | Doublet Fe(1) | Fe3+ | 0.293±0.007 | 0.819±0.012 | — | 36.92 |
| Doublet Fe(2) | Fe2+ | 0.895±0.057 | 1.675±0.115 | — | 1.13 | |
| Sextet Fe(3) | Fe3+ | 0.353±0.010 | 0.183±0.021 | 50.543±0.085 | 20.84 | |
| Sextet Fe(4) | Fe3+ | 0.372±0.010 | 0.274±0.021 | 49.496±0.132 | 41.11 |
| Sample | Ms, A⋅m2/kg | Mrs, A⋅m2/kg | Mrs/ Ms | μ0Hc, mT | μ0Hcr, mT | Hcr/ Hc |
|---|---|---|---|---|---|---|
| ClayL (Lake Shore 295) | 0.03 | 0.005 | 0.17 | 17 | 64 | 3.8 |
| Ind (MPMS 2) | 1.30 | 0.060 | 0.05 | 28 | 150 | 5.4 |
| Ind (MPMS 295) | 0.08 | 0.020 | 0.25 | 10 | 139 | 13.9 |
| Lab (MPMS 2) | 2.00 | 0.190 | 0.10 | 45 | 150 | 3.3 |
| Lab (MPMS 295) | 0.20 | 0.020 | 0.10 | 2 | 119 | 59.5 |
| Sample | fd, % | ||
|---|---|---|---|
| MFK1-FA | PPMS-9 | Average value | |
| Ind | 5.2 | 7.8 | 6.5 |
| Lab | 12.5 | 8.5 | 10.5 |
| ClayL | 50 (estimation) | – | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





