KOS: Kernel-based Optimal Subspaces Method for Data Classification

1. Introduction

Machine Learning (ML), a branch of Artificial Intelligence (AI), is the science of designing algorithms that can automatically improve by learning from data (see, for instance, [1]). This multidisciplinary field has a wide range of applications, including handwriting recognition, automated disease detection, robotics, and others.

Among the core problems in AI is data classification, which relies heavily on ML techniques. Kernel methods are one of the most popular subsets of data classifiers, with the Support Vector Machine (SVM) being among the most widely used. The SVM algorithm is grounded in statistical learning theory, originating from Vapnik’s work on the Structural Risk Minimization principle [2,3,4].

The fundamental idea of kernel methods is to map the original data,referred to as attributes, into a higher-dimensional space, known as the feature space, where the data can be more easily separated. While SVM was originally designed for linear separation, this mapping enables it to handle data that is non-linearly separable in the original space by achieving linear separation in the feature space. Note that, the mapping function is not explicitly defined, which is a tedious task, instead a suitable kernel function is used, as long as all operations can be expressed using dot products. The existence of such kernels is guaranteed under certain conditions by Mercer’s theorem [4,5].

SVM is widely recognized for its high performance (see [6,7,8,9,10,11,12,13] for recent improvements). However, despite significant advancements, it still has several limitations:

• As an optimization problem, SVM may fail, particularly in high-dimension, even though the cost function is convex (quadratic).
• Extending SVM to multiclass classification is not straightforward and becomes computationally expensive in high dimensions or when the number of classes is large. For instance, a common approach combining one-against-one and one-against-all strategies requires computing a total of $n+{\displaystyle \frac{n(n-1)}{2}}$ separating hyperplanes (i.e., solving n optimization problems), where n is the number of classes.
• Imbalanced classes poses another challenge. A popular approach to addressing this involves adding synthetic attributes to underrepresented classes. While effective, the process is not straightforward, and can alter the structure of the original class data.
• In dynamic classification, where classes may be added or removed, all separating hyperplanes must be recalculated, which can be prohibitively expensive for real-time applications.

To address these issues, a preliminary version of a novel method,proposed as an alternative to Support Vector Machines (SVMs), was introduced in a recent conference paper [30], along with basic initial results. In this extended journal version, we provide the complete formulation of the method for centered data, which offers more efficiency, along with a thorough theoretical analysis and corresponding proofs. Furthermore, we propose an effective strategy to tackle the inherent imbalanced classes problem. Extensive experiments are conducted on large, multi-class datasets for a thorough evaluation evaluation of the method’s performance. In addition, a detailed analysis of time efficiency is included. Finally, when using the radial basis function (RBF) kernel, we introduce a robust learning procedure for selecting the parameter $\sigma$.

In this work, the new method is referred to as Kernel-based Optimal Subspaces (KOS). The approach relies on computing a minimum distance between an unseen feature vector and a set of optimal subspaces, in a sense that will be defined, in the feature space. It will be shown that subspaces constructed using Proper Orthogonal Decomposition (POD) are optimal.

For classification, the method projects an unseen feature vector onto each feature subspace, claculate the distnace, and then assigns the attribute vector to the class achieving a minimum distance. Fundamentally, this requires only the computation of the eigenpairs of the Mercer kernel matrix for each training class independently, and no optimization is involved, making the method simple to implement, significantly faster than SVM (with linear complexity), and robust.

KOS is highly parallelizable and well-suited for dynamic and real-time classification, as only the eigenpairs for new classes need to be computed. If a class is removed, no further computation is required.

The issue of imbalanced classes is handled naturally by splitting large attribute classes into balanced subclasses, then labeling all corresponding feature subspaces as belonging to a single class. An unseen feature vector is classified into a given class if it is close to any of the subspaces generated by that class’s subclasses.

The performance of the proposed method is demonstrated through both 2D and high-dimensional, multi-class test cases. The results are compared against those of the Support Vector Machine (SVM), using the popular LIBSVM software package [21]. The findings show that KOS performs comparably to SVM, while offering several significant advantages as discussed earlier, making it a strong alternative to SVM.

The experiments use the Radial Basis Function (RBF) kernel, which, as is well known in the context of SVM, involves tuning two key parameters: the standard deviation $\sigma$ (in the Gaussian form) or $\gamma$ (in the RBF form), and the penalty parameter C. The most widely used method for selecting these parameters is cross-validation-based grid search, as described in [14,15,16,17,18], including both automated and manual search approaches.

In contrast, the KOS method does not require the penalty parameter C. Only one parameter, $\sigma$ or $\gamma$, needs to be learned. Through a class-wise re-scaling process, this parameter is learned in a robust and effective manner, contributing to the overall performance of the method.

In Section 2, a short overview of the proper orthogonal decomposition (POD) is provided. In Section 3, details of the proposed KOS method are developed. Tests to validate the proposed method by comparison to SVM results are performed and reported in Section 4. Conclusions are drawn in Section 5.

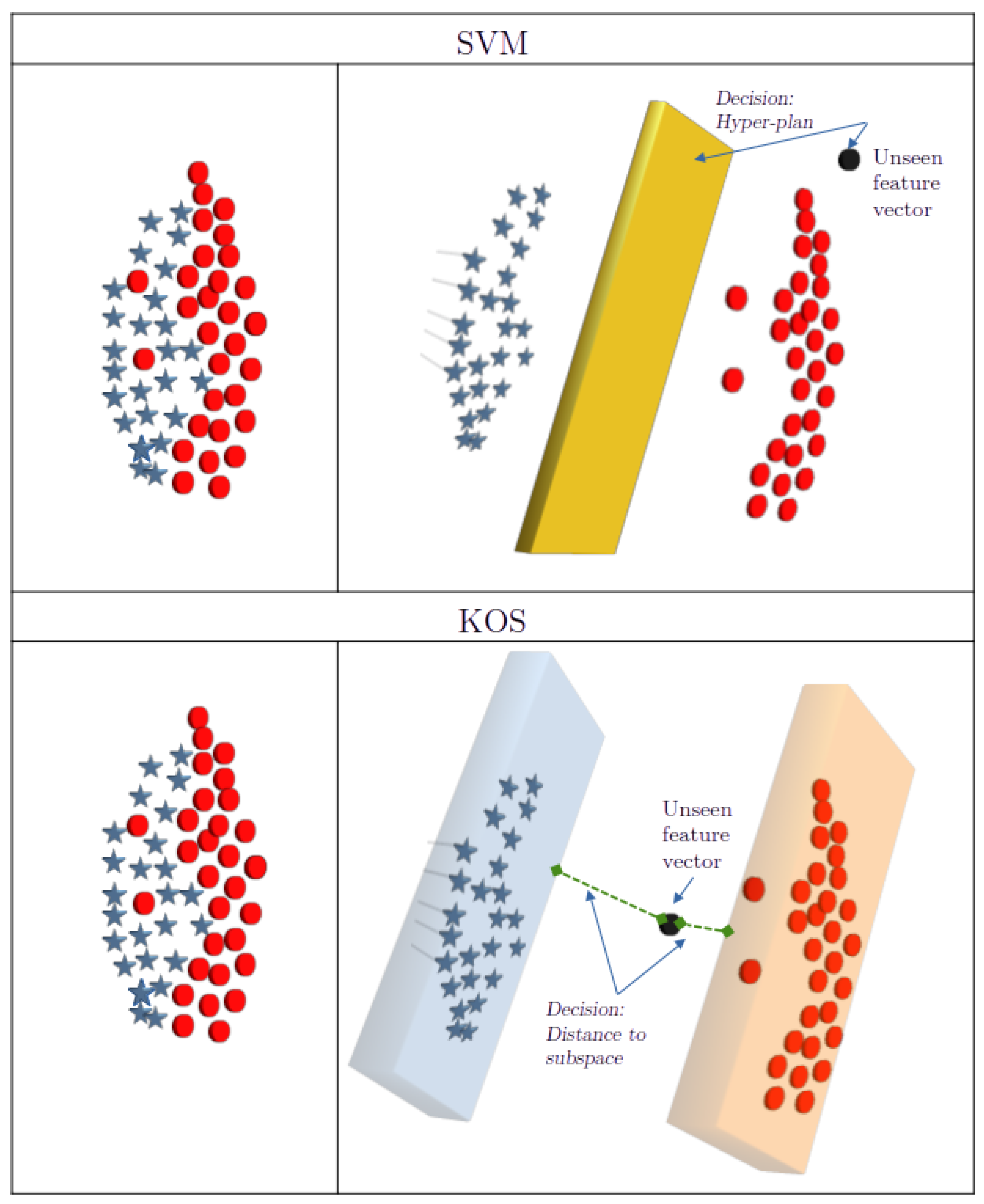
2. KOS: Kernel-Based Optimal Subspaces Method

Before detailing the proposed method, we first present a brief overview of the proper orthogonal decomposition technique, which is a crucial component of the new approach.

2.1. Proper Orthogonal Decomposition (POD): Overview

Proper Orthogonal Decomposition (POD) [19], known as well as Karhunen-Loeve’s expansion (KLE) [19], popular in data analysis field, is a technique that aims to represent a big amount of data by a reduced number of basis elements built from the data. More precisely, if the data are stored in a $m\times N$ matrix A with N being a large number, is it possible to represent the N columns of A by a p orthonormal vectors with p very small compared to N. The mathematical formulation can be summarized as follows, let $A=\left[Y_1,Y_2,...,Y_N\right]$, the problem is to find $B=\left[V^1,V^2,...,V^p\right]$ an orthonormal set of p vectors that better represent the N columns A in the following sense,

$V^1$ satisfying the optimization problem,

$$\begin{array}{c}\hfill V^1=Arg[Ma{x}_{V\in I{R}^m}\left(\sum _{i=1}^N{\left(〈V,Y_i〉\right)}^2\right)\\ \hfill {\mathit{subject}\mathit{to}\parallel V\parallel }^2=1].\end{array}$$

(1)

$$\begin{array}{c}\hfill V^2=Arg[Ma{x}_{V\in I{R}^m}\left(\sum _{i=1}^N{\left|〈V,Y_i〉\right|}^2\right)\\ \hfill {\mathit{subject}\mathit{to}\parallel V\parallel }^2=1\mathit{and}〈V,V^1〉=0].\end{array}$$

(2)

⋮

$$\begin{array}{c}\hfill V^k=Arg[Ma{x}_{v\in I{R}^m}\left(\sum _{i=1}^N{\left|〈V,Y_i〉\right|}^2\right)\\ \hfill {\mathit{subject}\mathit{to}\parallel V\parallel }^2=1\\ \hfill \mathit{and}〈V,V^1〉=0,〈V,V^2〉=0,...,〈V,V^{k-1}〉=0].\end{array}$$

(3)

The vectors $V^k,k=1,p$ are the eigenvectors of $A{A}^T$. A simplified proof is provided in Appendix (A) for self-content. For more details, see [19].

2.1.1. POD Basis System

The POD basis system is built as follows:

(1)

: if $n\le m$, let M be the correlation matrix $M_{i,j}={\left(A^{T}A\right)}_{i,j}$ where $(,)$ is any inner product. Let V the matrix of eigenvectors of M, then the basis functions ${\Psi }_i$, called modes, are given by:

$${\Psi }_i=\sum _{j=1}^N{v}_j^i{Y}_j$$

(4)

where $v_j^i$ are the components of the $i^{th}$ eigenvector of M

(2)

: if $n>m$, the POD basis is defined by the eigenvectors of the matrix ${\overline{M}}_{i,j}={\left(A{A}^T\right)}_{i,j}$

This paper will use the first definition since the original data will be mapped into an infinite dimension vector space.

Now calculate the inner product $({\Psi }_i,{\Psi }_j)$

$$\begin{array}{c}\hfill ({\Psi }_i,{\Psi }_j)=\\ \hfill (\sum _{l=1}^N{v}_l^i{Y}_l,\sum _{k=1}^N{v}_k^j,Y_k)=\sum _{l,k}{v}_l^i{v}_k^j(Y_l,Y_k)=\sum _{l,k}{v}_l^i{v}_k^j{M}_{l,k}=\\ \hfill M{V}^i.V^j={\lambda }_i{V}^i.V^j\end{array}$$

(5)

This shows that the functions ${\Psi }_i,1\le i\le N$ are orthogonal if and only the eigenvectors $V^i,1\le i\le N$ are, which is generally the case. For $i=j$ we get the norm $\parallel {\Psi }_i\parallel =\sqrt{{\lambda }_i}$, which shows that the norm of each mode represents part of the energy of the system. In conclusion, modes with low energy (small eigenvalues) can be neglected, reducing the POD basis to only modes with significant energy. Practically, the ratio of the modeled to the total energy contained in the system given by:

$$\epsilon \left(l\right)={\displaystyle \frac{{\sum }_{i=1}^l{\lambda }_i}{{\sum }_{i=1}^N{\lambda }_i}}$$

(6)

is calculated to decide if l modes are enough to describe the system.

This is an example of a quote.

2.2. KOS: Global Description and Some Theoretical Aspects

Similar to SVM, the first step in KOS is to map the original data (attributes) into a higher-dimensional feature space using a kernel function. For each class in the feature space, an optimal subspace, defined as the smallest and best fit subspace that contains the feature vectors of that class, is then constructed. The main difference

To classify an unseen attribute vector, its corresponding feature vector is projected onto each class subspace, and the class is determined based on the minimum distance to these subspaces. The fundamental difference from SVM is that the hyperplanes, responsible for many of the issues encountered with SVM, are removed and replaced by optimal subspaces that contain the feature data, as illustrated in Figure 1.

Note that, in some cases, different classes may be mapped to the same feature subspace, leading to a misclassification. Therefore, it is desirable for the subspaces to be as distinct as possible to reduce this risk. In theory, as proved later in the paper, it is always possible to construct subspaces that are even completely disjoint. However, in practice, this is cannot be guaranteed or controlled. For optimal performance, the kernel should be chosen such that the resulting feature space is of infinite dimension, which increases the likelihood of separability between class subspaces. It is well established, for example, that the RBF kernel meets this requirement.

Theorem 1.

There exist Mercer kernels such that the attribute classes can be mapped into disjoint feature subspaces.

Proof. 

For simplicity, the proof is given for the two-class case; the result can then be extended recursively to the multiclass case. Let $\chi$ denote the attribute (original) space and let $\mathit{H}$ be the feature space obtained through a mapping $\Phi$ associated with a Mercer kernel $K(x,y)$. Suppose that $K(x,y)$ is such that $\mathit{H}$ is of infinite-dimensional.

$$\Phi :\chi ⟶\mathit{H}$$

(7)

Let $C_1$ and $C_2$ be two classes, and let $\mathit{E}$ and $\mathit{F}$ be two finite-dimensional subspaces of the feature space $\mathit{H}$ such that $\Phi \left(C_1\right)\subset E$ and $\Phi \left(C_2\right)\subset F$. Let ${\mathit{E}}^T$ denote the orthogonal complement of $\mathit{E}$ in $\mathit{H}$. Since $\mathit{H}$ is infinite-dimensional and $\mathit{E}$ is finite-dimensional, $\mathit{E}$ is also infinite-dimensional.

Let $\mathit{G}\subset {\mathit{E}}^T$ be any subspace with the same dimension as $\mathit{F}$. Then there exist a one-to-one mapping $\varphi :\mathit{F}\to \mathit{G}$.

Now,define a new mapping $\psi :\chi ⟶\mathit{H}$ as follows:

$$\psi \left(x\right)=\left\{\begin{array}{c}\varphi \left(\Phi \left(x\right)\right)ifx\in C_2\hfill \\ \Phi \left(x\right)ifnot\hfill \end{array}\right.$$

(8)

We have $\Phi \left(C_1\right)\subset E$ and $\Phi \left(C_2\right)\subset G$ with E and G orthogonal then disjoint. The kernel defined by $\overline{K}(x,y)=\psi \left(x\right)*\psi \left(y\right)$ is a Mercer kernel by construction and satisfies the theorem, which ends the proof. □

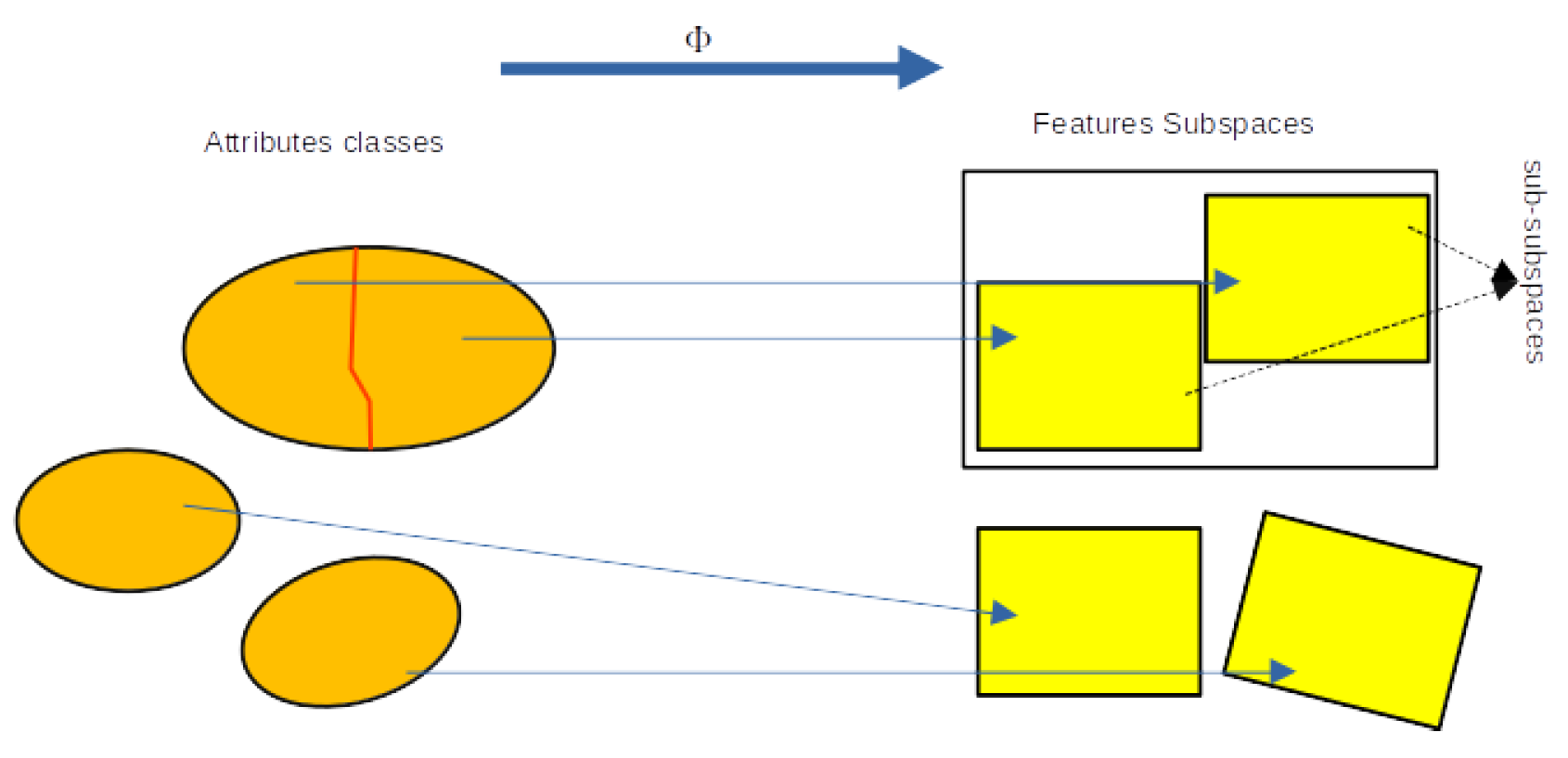
2.3. POD Feature Subspaces

The POD technique is proposed to build the optimal subspaces in the feature vector space. Note that similar techniques, such as PCA (Principal Component Analysis), are commonly used in kernel theory for data classification, typically as a pre-processing step for feature extraction and enhancement [22]. The optimality of the POD feature subspaces will be discussed later.

Assume a suitable kernel $K(x,y)$ is given, and let $\varphi$ be the associated mapping function. It is important to note that choosing a kernel such that the feature space $\mathit{H}$ is of infinite dimension is highly recommended, as it helps map data into subspaces with minimal or no overlap.. Let $C_{l,l=1,P}$ denote the P attributes classes. Denote by $X_i^l$ the $i^{th}$ element of class $C_l$ and by $Y_i^l=\varphi \left(X_i^l\right)$ its corresponding mapped feature vector. To construct the POD feature subspaces, we only need to build the POD basis, also known as the modes, as described in Section 2.1.

In general, it is well established that centering the data is recommended when applying the POD method. Therefore, we provide formulations of the POD basis for both non-centered centered and centered data.

To lighten the notations, the superscript l , which refers to a specific class, is omitted and will be reintroduced as needed. In the following, we use $K_{i,j}$ to denote the Mercer’ kernel K matrix, namely $K_{i,j}=Y_i{Y}_j=\varphi \left(X_i\right)\varphi \left(X_j\right)$, and $K(X,Y)$ when X or Y does not belong to the training dataset.

1.

None-Centered data formulation: In this case, the data in the feature space are used without centering. Let $Y_i=\varphi \left(X_i\right),i=1,N$ be the mapped data points of a selected class of size N. First, we construct the correlation matrix:

$$M(i,j)=Y_i{Y}_j=\varphi \left(X_i\right)\varphi \left(X_j\right)=K(i,j),$$

(9)

where $K(i,j)$ denotes the kernel function evaluated at $Y_i$ and $Y_j$. As seen, the POD correlation matrix is equivalent to the kernel matrix derived from the mapping.

The normalized POD modes are then given by:

$${\psi }_i={\displaystyle \frac{1}{{\sqrt{\sigma }}_i}}\sum _{k=1}^N{V}_k^i{Y}_k,$$

(10)

where $V^i$ is the $i^{th}$ eigenvector of the kernel matrix M and ${\sigma }_i$ the associated eigenvalue.

2.

Centered data formulation: In this case, the feature vectors $Y_i$ are centered. Let $\overline{Y}={\displaystyle \frac{1}{N}}{\sum }_{k=1}^N{Y}_k$ be the mean vector, and $Z_i=Y_i-\overline{Y}$ be the centered data. The correlation matrix is then given by:

$$M(i,j)=Z_i{Z}_j=(Y_i-\overline{Y})(Y_j-\overline{Y})=Y_i{Y}_j-Y_i\overline{Y}-Y_j\overline{Y}+\overline{Y}\overline{Y}.$$

(11)

Each of the inner products can be expressed in terms of the kernel function:

$$Y_i\overline{Y}=Y_i{\displaystyle \frac{1}{N}}\sum _{k=1}^N{Y}_k={\displaystyle \frac{1}{N}}\sum _{k=1}^N{Y}_i{Y}_k={\displaystyle \frac{1}{N}}\sum _{k=1}^{N}K(i,k),$$

(12)

$$\overline{Y}\overline{Y}={\displaystyle \frac{1}{N}}\sum _{k=1}^N{Y}_k{\displaystyle \frac{1}{N}}\sum _{l=1}^N{Y}_l={\displaystyle \frac{1}{N^2}}\sum _{k=1}^N\sum _{l=1}^{N}K(l,k).$$

(13)

Substituting back into the expression for $M(i,j)$, the centered correlation matrix becomes:

$$M(i,j)=K(i,j)-{\displaystyle \frac{1}{N}}\sum _{k=1}^N(K(i,k)+K(j,k))+{\displaystyle \frac{1}{N^2}}\sum _{k=1}^N\sum _{l=1}^{N}K(l,k).$$

(14)

As in the non-centered case, the correlation matrix can be entirely expressed using the kernel matrix.

The normalized POD modes for centered data are then given by:

$${\psi }_i={\displaystyle \frac{1}{{\sqrt{\sigma }}_i}}\sum _{k=1}^N{V}_k^i(Y_k-\overline{Y})$$

(15)

where $V^i$ is the $i^{th}$ eigenvector of the correlation matrix M defined by 14 and ${\sigma }_i$ the associated eigenvalue

Note that for calculating the minimum distance in classification (as will be shown later), it is not necessary to explicitly compute the feature vectors $Y_k$ or the POD modes.

2.4. Optimality of the POD Feature Subspaces

The optimality of the feature subspaces is considered from both geometric and algebraic perspectives.

From a geometric standpoint, the basis elements of the subspace should be as close as possible to the original feature vectors. This ensures maximum representativeness and preserves the structure of the data within the feature space.

From an algebraic standpoint, the feature subspace should be of minimal dimension while still containing the feature vectors. This dimensional compactness guarantees maximum discrimination between different feature subspaces and, consequently, between the associated attribute classes.

In essence, the POD method provides a set of orthonormal basis functions that span the most "informative" subspace, allowing for an efficient and discriminative representation of each class in the feature space.

• Geometrical Optimality of POD Feature Spaces:
  As shown in [19], if $\Psi$ is the POD basis matrix constructed to represent the columns of a matrix $A=\left[Y_1,Y_2,...,Y_N\right]$, and $\overline{\Psi }$ is any other basis of a same size constructed for the same purpose, then the following inequality holds:

  $${\parallel A-\Psi \parallel }_F\le {\parallel A-\overline{\Psi }\parallel }_F,$$

  (16)

  where ${\parallel .\parallel }_F$ is the Frobenius norm, defined by:

  $${\parallel A\parallel }_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^N\left|A_{i,j}\right|}=\sqrt{\mathit{Trace}\left(A^{T}A\right)}$$

  (17)
  This result demonstrates the geometric optimality of the POD basis: among all possible orthonormal bases of the same dimension, the POD basis provides the best approximation (in the least-squares sense) of the original data matrix A. Therefore, the POD basis vectors are the closest possible representatives of the original feature vectors, ensuring maximum fidelity in capturing the data structure.
• Algebraic Optimality of POD Feature Spaces:
  Lemma: The POD subspace is algebraically optimal; it is the smallest subspace containing the mapped data.
  Proof: The proof is straightforward. To show that the POD subspace is the smallest subspace containing the mapped (feature) data, it is sufficient to show that any subspace containing the feature data must also contain the POD subspace.
  Let F be a subspace that contains the given feature data. To prove that F also contains the POD subspace, it suffices to show that F ontains the POD modes (i.e., the basis of the POD subspace). Since the POD modes are linear combinations of the feature data, and F s a subspace (i.e., closed under linear combinations), the modes necessarily lie in F. Hence, the POD subspace is contained in a ny subspace that contains the mapped data, proving its algebraic optimality.

2.5. Decision Criterion

The decision criterion for an unseen element $\widehat{X}$, as introduced at the beginning of this section, is based on the minimum distance of the feature vector $\widehat{Y}=\varphi \left(\widehat{X}\right)$ to the POD feature subspaces.To achieve this, the POD coordinates of $\widehat{Y}$ within each subspace are computed. The details for both non-centered and centered data are provided.

1.

None-Centered data formulation: The coordinates ${\alpha }_i,i=1,N$ are given by the projection of the element on the POD modes

$${\alpha }_i=<{\psi }_i,\widehat{Y}>$$

(18)

with

$${\psi }_i={\displaystyle \frac{1}{{\sqrt{\sigma }}_i}}\sum _{k=1}^N{V}_k^i{Y}_k,$$

(19)

Then

$${\alpha }_i={\displaystyle \frac{1}{{\sqrt{\sigma }}_i}}<\sum _{k=1}^N{V}_k^i{Y}_k,\widehat{Y}>={\displaystyle \frac{1}{{\sqrt{\sigma }}_i}}\sum _{k=1}^N{V}_k^i\left(Y_k\widehat{Y}\right)={\displaystyle \frac{1}{{\sqrt{\sigma }}_i}}\sum _{k=1}^N{V}_k^{i}K(X_k,\widehat{X})$$

(20)

Using the Pythagoras rule, the distance of $\overline{Y}$ to the POD subspace F, is given by

$$dis(\widehat{Y},F)=\sqrt{\parallel \widehat{Y}{\parallel }^2-\sum _{i=1}^N{\alpha }_i^2}.$$

(21)

With

$$\parallel \widehat{Y}{\parallel }^2=\widehat{Y}\widehat{Y}=\varphi \left(\widehat{X}\right)\varphi \left(\widehat{X}\right)=K(\widehat{X},\widehat{X}).$$

(22)

2.

Centered data formulation: For the centered case, $\widehat{Y}$ and $Y_i$ are replaced by $\widehat{Y}-\overline{Y}$ and $Y_i-\overline{Y}$ respectively. That is,

$${\alpha }_i=<{\psi }_i,(\widehat{Y}-\overline{Y})>,$$

(23)

with

$${\psi }_i={\displaystyle \frac{1}{{\sqrt{\sigma }}_i}}\sum _{k=1}^N{V}_k^i(Y_k-\overline{Y}),$$

(24)

Then

$$\begin{array}{c}\hfill {\alpha }_i={\displaystyle \frac{1}{{\sqrt{\sigma }}_i}}<\sum _{k=1}^N{V}_k^i(Y_k-\overline{Y}),(\widehat{Y}-\overline{Y})>=\\ \hfill {\displaystyle \frac{1}{{\sqrt{\sigma }}_i}}[\sum _{k=1}^N{V}_k^i\left(Y_k\widehat{Y}\right)-\sum _{k=1}^N{V}_k^i\left(Y_k\overline{Y}\right)\\ \hfill -\sum _{k=1}^N{V}_k^i\overline{Y}\widehat{Y}+\sum _{k=1}^N{V}_k^i\overline{Y}\overline{Y}].\end{array}$$

(25)

Substituting $\overline{Y}={\displaystyle \frac{1}{N}}{\sum }_{j=1}^N{Y}_j$ we obtain

$$\begin{array}{c}\hfill {\alpha }_i={\displaystyle \frac{1}{{\sqrt{\sigma }}_i}}[\sum _{k=1}^N{V}_k^{i}K(X_k,\widehat{X})-{\displaystyle \frac{1}{N}}\sum _{k=1}^N\sum _{j=1}^N{V}_k^i{K}_{k,j}\\ \hfill -\left({\displaystyle \frac{1}{N}}\sum _{j=1}^{N}K(X_j,\widehat{X})\right)\sum _{k=1}^N{V}_k^i+\left({\displaystyle \frac{1}{N^2}}\sum _{k=1}^N\sum _{j=1}^N{K}_{k,j}\right)\sum _{k=1}^N{V}_k^i].\end{array}$$

(26)

Then

$$dis(\widehat{Y},F)=\sqrt{\parallel \widehat{Y}-\overline{Y}{\parallel }^2-{\sum }_{i=1}^N{\alpha }_i^2}.$$

(27)

With

$$\parallel \widehat{Y}-\overline{Y}{\parallel }^2={\widehat{Y}}^2-2\widehat{Y}\overline{Y}+{\overline{Y}}^2=K(\widehat{X},\widehat{X})-{\displaystyle \frac{2}{N}}\sum _{j=1}^{N}K(\widehat{X},X_j)+{\displaystyle \frac{1}{N^2}}\sum _{k=1}^N\sum _{j=1}^N{K}_{k,j}.$$

(28)

The unseen attribute vector is assigned to the class that corresponds to the minimum distance calculated above.

2.6. Imbalanced Classes

The issue of imbalanced classes is commonly encountered in many classifiers, including SVM. Several techniques address this problem, with the two most popular being weight adjustment between large and small classes (as used in LIBSVM) and the SMOTE (Synthetic Minority Over-Sampling Technique) algorithm [20], which generates synthetic data to augment smaller classes. Both methods yield acceptable results; however, there is no systematic approach for defining the weight distribution or the positioning of synthetic vectors, which may alter the data structure.

The proposed KOS method naturally handles this problem by subdividing large attribute classes into smaller subclasses of similar sizes. These subclasses will share the same class label. Specifically, a reference size is defined, which can be the size of the smallest class in the attribute space. Any class with a size at least double the reference size can be split into subsets, each roughly equal in size to the reference class. For the classification decision, if the minimum distance is obtained from one of the POD subspaces of a subdivided class, the unseen element is assigned to that class. This strategy is schematized in Figure 2 and will be validated in the test section.

2.7. RBF Parameter Learning

As previously mentioned, when using the RBF kernel, only the parameter $\sigma$ (equivalently $\gamma$) must be learned, as in the case of hard-margin SVM. There is need to the penality parameter. We propose a strategy to learn $\sigma$ that significantly reduces the range of values to be tested. The key idea is to scale $\sigma$ according to the size of each attribute class.

The RBF kernel (also known as the Gaussian kernel) is widely used in multi-scale image analysis, where small $\sigma$ values correspond to fine image details, and larger values capture more global structures. This makes it natural to scale $\sigma$ according to the size of the input set. We decompose $\sigma$ as follows:

$$\sigma =\omega D,$$

(29)

where D is the diameter of the set, computed as the maximum distance between any two elements in the set. The scaling factor $\omega$ is then varied from $0.1$ to 1 in steps of $0.1$. This approach significantly reduces the complexity of the parameter search. For comparison, in standard SVM, approximately $250\times 250$ grid searches are typically required to determine the optimal pair $(\sigma ,C)$, where C is the penalty parameter.

2.8. Summary of the Algorithm

Let $C_{k,k=1,P}$, denote P attributes sets representing P different classes used during the learning stage. Let $B_{k=1,P}$, denote the corresponding mapped sets in the feature space. The KOS classification procedure is as follows:

1.

Check whether the classes $C_k$ are imbalanced. If so, split the larger classes into smaller subclasses according to procedure described in Section 2.6.

2.

Select a Mercer kernel K, then compute the kernel matrices $K_k$ for each feature class $C_k$ (of feature subclasses if applicable).

3.

Compute the POD correlation matrices $M_k$ for each feature class (or subclass) $C_k$ using either the non-centered formulation 9 or the centred formulation 14.

4.

Compute the eigenvalues and eigenvectors of each matrix $M_{k,k=1,P}$.

5.

For each unseen vector $\widehat{X}$, compute its coordinates ${\alpha }_i^k,i=1,size\left(C_k\right)$ in each POD feature subspace using Formula (20) for non-centered case or 26 for centered case.

6.

Compute the distance of $\widehat{X}$ to each POD feature subspace using Formula (21) for non-centered case or 27 for centered case.

7.

Decision: Assign $\widehat{X}$ to the class corresponding to the minimum computed distance.

3. Results: Validation and Discussion

The proposed KOS method is verified and validated using the RBF kernel. Initial tests are conducted on 2D cases to visually assess its ability to handle non-linear classification. Subsequently, KOS is tested on selected real-world datasets from the LIBSVM repository [21], and the results are compared against those obtained using SVM implemented in the widely used LIBSVM software.

It is important to note that no specific preprocessing is applied to the data for KOS, apart from rescaling the input features to the interval $[-1,1]$.

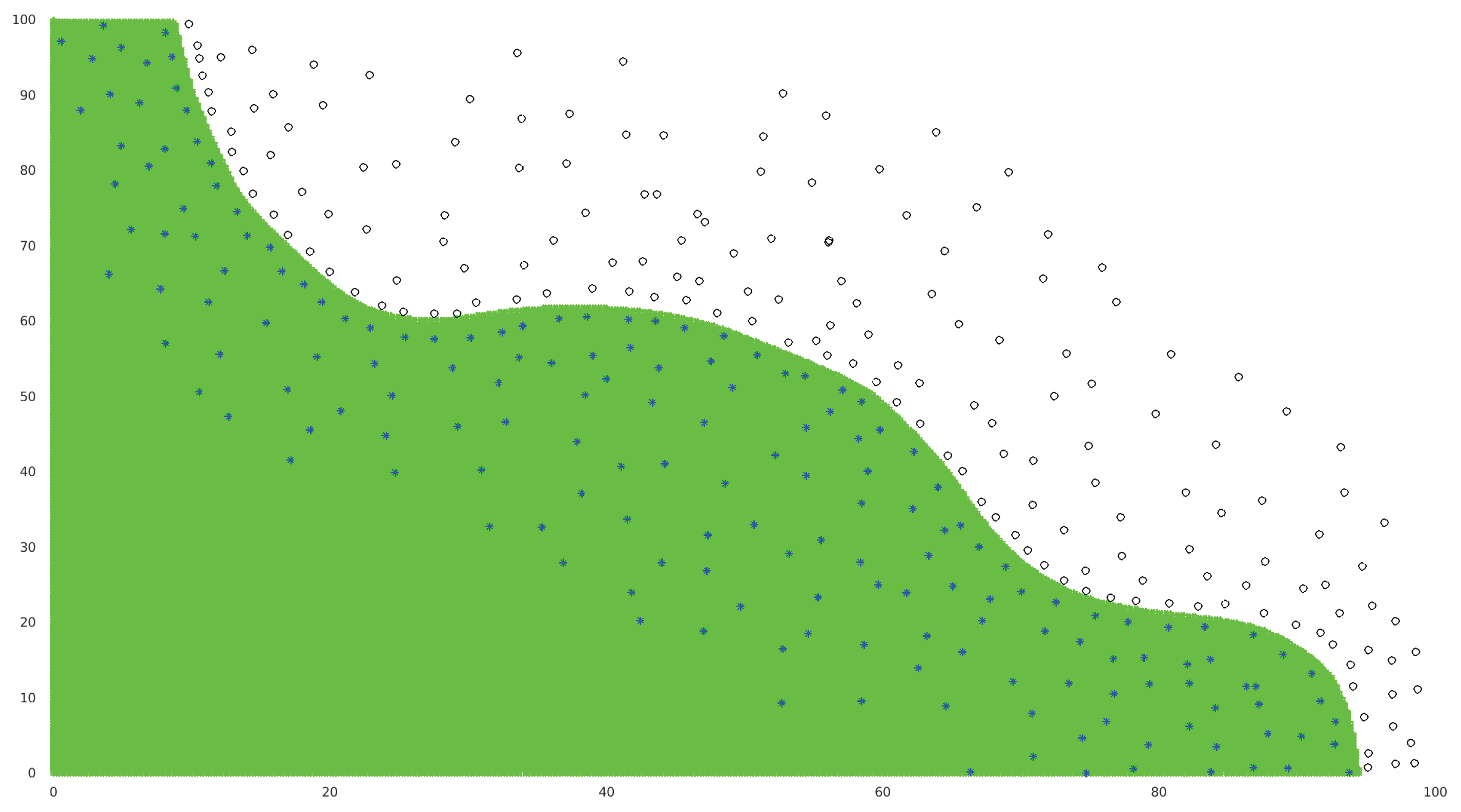
3.1. 2D Test Cases

To evaluate KOS’s capability in separating non-linearly separable data, three increasingly challenging scenarios are tested: (i) connected sets, (ii) non-connected sets, and (iii) a spiral configuration. Figure 3, Figure 4 and Figure 5 demonstrate that KOS successfully separates the data in all cases. A fixed kernel parameter value of $\sigma =1.2$ is used for all three tests.

3.2. Higher-Dimension Test Cases

Two-classes and multi-class test cases are selected from the database [21]. The proposed KOS and SVM (using LIBSVM software) are then tested, and their performances compared. Note that for KOS, there is no penalty parameter C; only the standard deviation $\sigma$ is learned. This is done by splitting the training set into two parts: $2/3^{rd}$ for building the KOS model (eigenpairs of the correlation matrices) and $1/3^{rd}$ for validation. The value of $\sigma$ is varied from $\sigma =0.1$, to $\sigma =1.4$ in increments of $0.1$. Once the optimal $\sigma$ is found, the entire training set is used to build the KOS model. The tests are briefly described in Table 1, and Table 2. Table 3 compares the performance of KOS and SVM. Overall, the table shows that KOS performs comparably to SVM, while offering significant advantages outlined in the next subsection.

The effectiveness of the proposed imbalanced strategy is demonstrated, for instance, in the Leukemia and Shuffle tests, which contain the most imbalanced classes. Specifically, the performance without splitting the classes was $67.64\%$ and $80.6\%$, respectively. After applying the splitting strategy, these scores improved to $82.35\%$ and $99.9\%$, respectively.

3.3. KOS main Advantages Compared to SVM

As shown by the tests, KOS is performing similarly to SVM, with many significant advantages that can be listed as:

1.

The KOS algorithm is easier to implement: it only requires the computation of the correlation matrix eigenpairs (9 or 14), followed by a direct application of formulas (20, 21 or 26, 27).

2.

Robustness: KOS algorithm is robust and faster; No optimization process is required that can slow down the algorithm in high dimensions and can fail even if the cost function is quadratic because of rounding-off errors as in the case of SVM.

3.

Complexity: SVM complexity grows quadratically with the number of classes (requiring $n+{\displaystyle \frac{n(n-1)}{2}}$ hyperplanes), while KOS scales linearly, needing only n sets of eigenpairs.

4.

Time efficiency: As a result of the two previous proprieties, KOS is significantly faster than SVM, up to more than 60 times faster in certain tests as shown in Table 4.

5.

Parallelization: KOS is highly parallelizable since all subspaces are independent..

6.

Dynamic classification: In the case of class creation or cancellation, SVM requires recalculating all feature-space hyperplanes. By contrast, KOS only requires computing eigenpairs of the Mercer kernel matrix for the new class, with no update needed for canceled classes.

7.

Imbalanced classes: In KOS, this issue is naturally handled by subdividing large classes into smaller, balanced subclasses (Section 2.6). This avoids the need for artificial attributes, which may distort the data structure, or the use of balancing weights, which often lack a clear and systematic procedure.

4. Conclusions

In this paper, a novel classification method is proposed, referred to as KOS (kernel-based optimal subspaces). The approach involves constructing optimal subspaces in the feature space, and classifying an unseen attribute vector based on its minimum distance to these subspaces. Some theoretical foundations are discussed, and proofs provided. The POD subspaces are proved to be optimal in the sense of being the smallest subspaces containing the feature classes, and the basis systems being the best features data representatives. All necessary formulations for practical implementation were derived.

The issue of imbalanced classes is addtressed a simple and intuitive mechanism, eliminating the need for additional preprocessing or resampling techniques. Experimental results on both 2D and high-dimensional multiclass datasets drawn from real-world scenarios show that KOS achieves performance comparable to optimized SVMs using LIBSVM. Beyond accuracy, KOS offers several practical advantages: it is easier to implement, significantly faster, more robust, imbalanced classes issue is systematically handled, suitable for dynamic classification tasks, and highly parallelizable. These strengths make KOS a promising alternative to traditional kernel-based classifiers in a variety of applications.