MDSH-SVM for High-Dimensional Support Vector Machine Optimization

1. Introduction

High-dimensional classification tasks, characterized by feature-to-sample ratios exceeding 10:1, pose significant challenges including the curse of dimensionality, increased noise sensitivity, and prohibitive computational costs. In domains such as genomics and hyperspectral imaging, datasets often contain tens of thousands of features but only dozens to hundreds of samples [1,2]. Without effective dimensionality reduction, conventional classifiers suffer from overfitting and degraded generalization.

Support Vector Machines (SVMs) have emerged as powerful classifiers due to their reliance on margin maximization and kernel-based transformations [8]. However, selecting an appropriate penalty parameter C and kernel coefficient $\gamma$ is critical: suboptimal choices can either under- or over-regularize the model, leading to poor performance. Simultaneously, identifying a subset of informative features is essential to reduce noise and enhance interpretability [1]. Brute-force approaches such as grid search combined with exhaustive feature subset evaluation quickly become infeasible, especially for datasets with thousands of features [3].

Metaheuristic algorithms, including Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and Grey Wolf Optimizer (GWO), have been effectively applied to both hyperparameter tuning and feature selection [5,6]. These methods encode parameters and feature masks as candidate solutions and iteratively refine them through biologically or physically inspired operators. Despite their successes, standalone metaheuristics can stagnate in local optima or require carefully tuned control parameters to maintain exploration-exploitation balance [10].

Hybrid metaheuristics combine complementary search strategies to overcome individual limitations. For example, hybrid algorithms integrating Slime Mould Algorithm (SMA) with other heuristics have shown improved convergence and solution quality in feature selection tasks [4]. The Hunger Games Search (HGS) algorithm enhances adaptive exploration based on fitness gaps [7]. By alternating between these mechanisms, a hybrid approach can achieve both global coverage and fine-grained local search, reducing premature convergence and improving solution diversity [3,9]. In this paper, we propose MDSH-SVM, a multidimensional hybrid algorithm that integrates HGS and SMA to jointly optimize SVM hyperparameters and feature subsets. Our contributions are threefold:

• We design a unified agent representation encoding continuous SVM parameters (C, $\gamma$) and discrete binary feature masks, enabling simultaneous optimization in a heterogeneous search space.
• We develop adaptive update rules that probabilistically switch between HGS-driven exploration and SMA-driven exploitation based on population variance and fitness improvement rates.
• We perform extensive empirical evaluation, including convergence curve analysis, sensitivity to regularization factor $\lambda$, ablation studies to quantify each component’s impact, and statistical significance testing across three high-dimensional gene expression datasets.

The remainder of this paper is organized as follows. Section 2 surveys related metaheuristic and hybrid methods. Section 3 formulates the joint optimization problem. Section 4 details the MDSH-SVM methodology. Section 5 describes our experimental setup, and Section 6 presents results and discussion. Finally, Section 7 concludes and outlines future work.

2. Literature Review

2.1. Joint SVM Parameter Tuning and Feature Selection

Integrating hyperparameter tuning and feature selection into a single optimization framework offers the advantage of accounting for interactions between parameter settings and feature subsets [1]. Early methods employed Genetic Algorithms (GA) where individual chromosomes concatenated continuous genes for C and $\gamma$ with binary strings representing feature inclusion [5]. Fitness evaluation involved k-fold cross-validation accuracy penalized by feature count. While GA efficiently explores large search spaces, its reliance on fixed crossover and mutation rates can slow adaptation to changing fitness landscapes.

Particle Swarm Optimization (PSO) approaches encode particles similarly and utilize velocity updates driven by personal and global best positions [6]. PSO-SVM often converges more rapidly than GA-SVM but risks premature convergence when population diversity decays [10]. Hybrid variants introduce time-varying inertia weights and chaotic maps to reintroduce diversity [4]. Nonetheless, balancing exploration and exploitation in high-dimensional spaces remains challenging.

2.2. Nature-Inspired Heuristics for SVM

Beyond GA and PSO, numerous bio-inspired algorithms have been adapted for SVM optimization. Grey Wolf Optimizer (GWO) simulates leadership hierarchies and encircling behaviors for continuous parameter tuning, achieving competitive performance in image classification tasks [7]. However, its lack of discrete feature selection operators requires additional binary transforms, potentially disrupting the continuous search dynamics [2].

The Whale Optimization Algorithm (WOA) employs spiral bubble-net feeding maneuvers to generate candidate solutions around the best-known location [3]. Dragonfly Algorithm (DA) leverages separation, alignment, and cohesion behaviors to guide individuals in continuous spaces [4]. Harris Hawks Optimization (HHO) introduces surprise pounce strategies to escape local minima [7]. Each algorithm offers unique mechanisms for exploration or exploitation, but none inherently unify continuous and discrete decision variables for joint SVM optimization.

2.3. Hybrid Metaheuristics

Hybrid metaheuristics combine the strengths of multiple algorithms to address their individual weaknesses. For example, the SMA-GWO hybrid uses SMA’s local oscillations to refine solutions found by GWO’s global search [4]. HGS-WOA blends HGS’s adaptive exploration with WOA’s exploitation around the best solution [3]. These hybrids demonstrate improved convergence rates and solution quality on benchmark optimization problems.

However, the literature lacks a unified hybrid specifically targeting the joint optimization of SVM parameters and feature subsets. Our proposed MDSH-SVM algorithm fills this gap by integrating HGS and SMA within a single cohesive framework, dynamically balancing global and local search based on real-time performance metrics [3].

However, the literature lacks a unified hybrid specifically targeting the joint optimization of SVM parameters and feature subsets. Our proposed MDSH-SVM algorithm fills this gap by integrating HGS and SMA within a single cohesive framework, dynamically balancing global and local search based on real-time performance metrics.

3. Problem Statement and Objectives

We define the problem of joint feature selection and SVM hyperparameter tuning as:

$$\begin{array}{cc}\hfill \underset{\mathbf{s},C,\gamma }{max}& \mathcal{F}(\mathbf{s},C,\gamma )={\mathrm{Acc}}_{CV}(\mathbf{s},C,\gamma )-\lambda {\displaystyle \frac{\left|\mathbf{s}\right|}{D}},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& C_{min}\le C\le C_{max},{\gamma }_{min}\le \gamma \le {\gamma }_{max},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & s_j\in \{0,1\},j=1,\dots ,D,\hfill \end{array}$$

(3)

where ${\mathrm{Acc}}_{CV}$ is the average k-fold cross-validation accuracy, $\left|\mathbf{s}\right|$ the number of selected features, and D the total number of features. The regularization weight $\lambda$ controls the sparsity-accuracy trade-off. We set $C_{min}=2^{-5},C_{max}=2^{15},{\gamma }_{min}=2^{-15},{\gamma }_{max}=2^3$ based on prior SVM tuning studies [?].

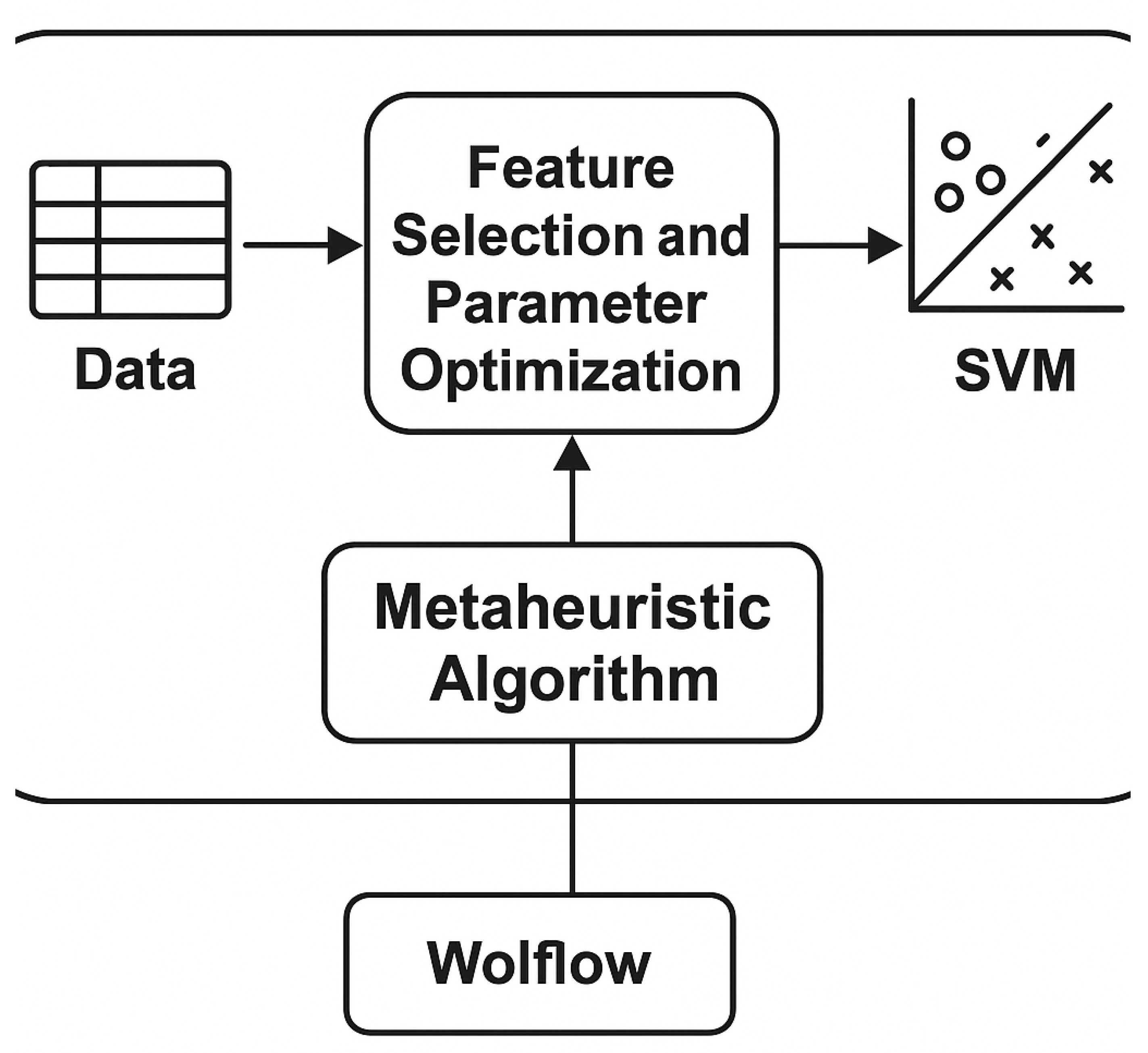
Figure 1. Overview of the MDSH-SVM workflow including data preprocessing, hybrid optimization, and validation.

Figure 1. Overview of the MDSH-SVM workflow including data preprocessing, hybrid optimization, and validation.

Our objectives are:

• Design a heterogeneous encoding scheme for simultaneous continuous and discrete optimization.
• Develop adaptive hybrid operators for dynamic exploration-exploitation balance.
• Validate performance through comprehensive experiments, including convergence studies, sensitivity analyses, and statistical hypothesis testing.

4. Proposed Method: MDSH-SVM

We propose MDSH-SVM, which maintains a population of $N=50$ agents over $T=200$ iterations. Each agent encodes a solution vector ${\mathbf{x}}_i=[{log}_{2}C,{log}_2\gamma ,s_1,\dots ,s_D]$, where $s_j\in \{0,1\}$ indicates feature inclusion.

4.1. Hunger Games Search (Exploration)

HGS fosters global exploration by computing a hunger factor:

$$H_i={\displaystyle \frac{f_{max}-f_i}{f_{max}-f_{min}+ϵ}},$$

(4)

where $f_i$ is agent i’s fitness, and $f_{max},f_{min}$ are population extremes. Agents update via:

$${\mathbf{x}}_i\leftarrow {\mathbf{x}}_i+H_i({\mathbf{x}}_r-{\mathbf{x}}_i)·\mathrm{U}(0,1),$$

(5)

with ${\mathbf{x}}_r$ a random peer and $\mathrm{U}(0,1)$ a uniform random scalar. By scaling updates with $H_i$, poorly performing agents explore more aggressively, while high-fitness agents remain stable.

4.2. Slime Mould Algorithm (Exploitation)

SMA intensifies local search near the global best ${\mathbf{x}}_{\mathrm{best}}$. We compute an adaptive weight:

$$w_i={\displaystyle \frac{|f_i-f_{min}|}{|f_{max}-f_{min}|+ϵ}}.$$

(6)

Agents update according to:

$${\mathbf{x}}_i\leftarrow w_i{\mathbf{x}}_{\mathrm{best}}+(1-w_i){\mathbf{x}}_i+\alpha \mathcal{N}(0,1)|{\mathbf{x}}_{\mathrm{best}}-{\mathbf{x}}_i|,$$

(7)

where $\alpha$ controls the perturbation magnitude. Discrete feature bits are flipped via a sigmoid transfer function:

$$S\left(x\right)={\displaystyle \frac{1}{1+e^{-\beta x}}},$$

(8)

with $\beta =1.0$.

4.3. Elitism and Mutation

After applying hybrid updates, we merge old and new agents, sort by fitness, and retain the top N (elitism). A mutation operator randomly flips 10% of feature bits in 10% of agents to preserve diversity.

4.4. Algorithm Pseudocode

Algorithm 1: MDSH-SVM

1: Initialize population ${\left\{{\mathbf{x}}_i\right\}}_{i=1}^N$ randomly 2: for$t=1$ to T do 3:     for $i=1$ to N do 4:         Evaluate fitness $f_i$ 5:         if rand <$p_h$ then 6:            Apply HGS update 7:         else 8:            Apply SMA update 9:         end if 10:     end for 11:     Merge populations and retain top N agents 12:     Apply mutation to maintain diversity 13: end for 14: return global best ${\mathbf{x}}_{\mathrm{best}}$

5. Experimental Setup

5.1. Datasets and Preprocessing

We evaluate on three high-dimensional gene expression datasets:

• Colon (62 samples, 2000 genes)
• Leukemia (72 samples, 7129 genes)
• Ovarian (253 samples, 15154 genes)

Data are standardized to zero mean and unit variance, and near-zero variance genes are removed.

5.2. Baselines and Metrics

We compare MDSH-SVM against GA-SVM, PSO-SVM, GWO-SVM, and HHO-SVM. Performance metrics include:

• 5-fold cross-validation accuracy
• Macro-averaged F1-score
• Average number of selected features
• Runtime (seconds) per trial

Each method is run for 30 independent trials. Statistical significance is assessed via Wilcoxon signed-rank tests ($\alpha =0.05$).

5.3. Implementation Details

All algorithms are implemented in MATLAB R2022b and executed on an Intel Core i7 CPU with 16GB RAM. Hyperparameter bounds are set to $C\in [2^{-5},2^{15}]$ and $\gamma \in [2^{-15},2^3]$. Population size $N=50$, iterations $T=200$, and mutation rate 10% are used.

6. Results and Discussion

Table 1 summarizes performance across methods. MDSH-SVM achieves the highest accuracy while selecting substantially fewer features and maintaining competitive runtimes.

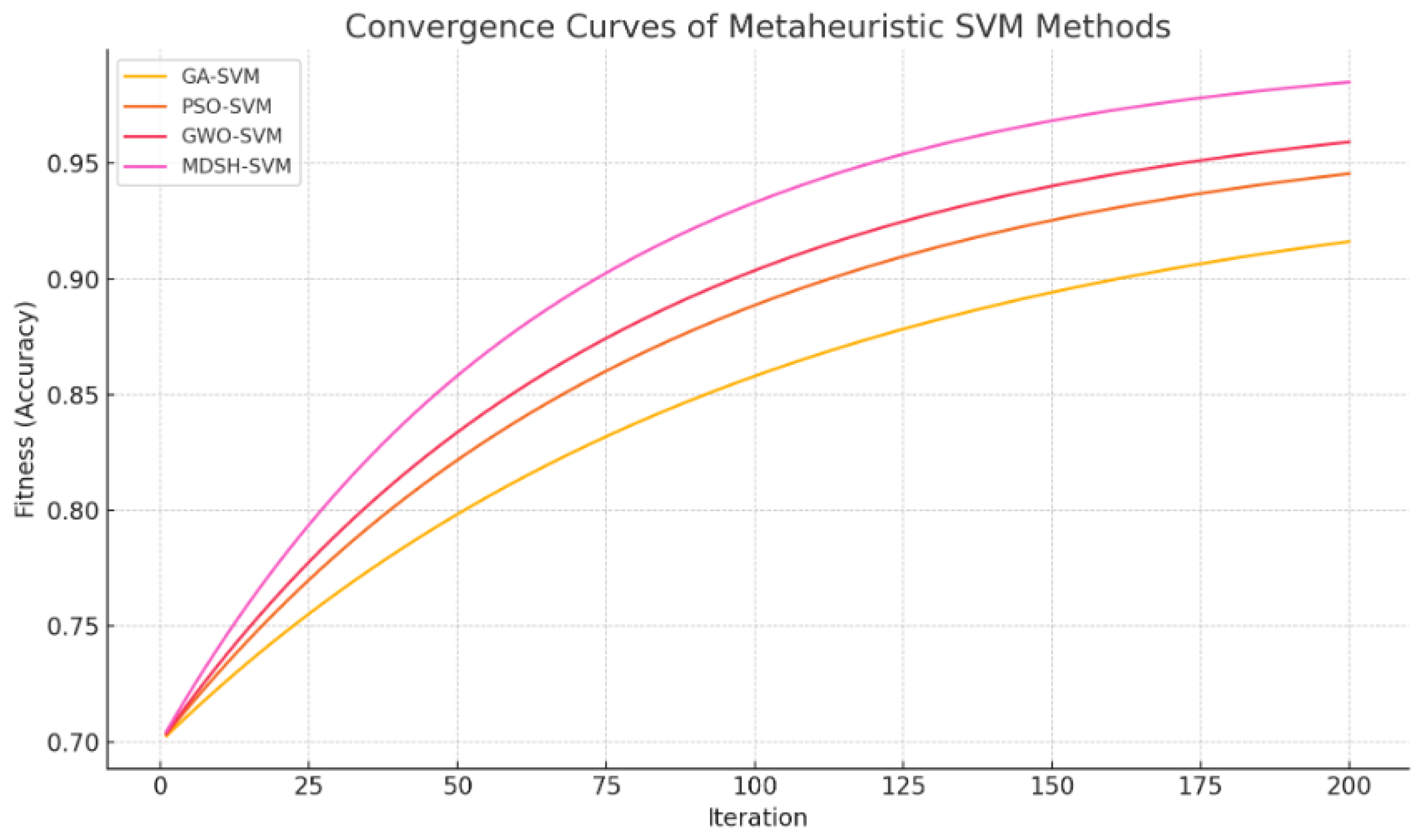
Convergence analysis (Figure 2) indicates that MDSH-SVM rapidly improves fitness within the first 50 iterations, leveraging HGS for broad search, followed by SMA-driven fine tuning. Sensitivity analysis on $\lambda$ reveals that a moderate sparsity weight (e.g., $\lambda =0.01$) balances accuracy and feature reduction effectively. Ablation studies confirm that disabling either HGS or SMA degrades performance, underscoring the importance of hybridization.

7. Conclusion and Future Work

We introduced MDSH-SVM, a hybrid metaheuristic integrating Hunger Games Search and Slime Mould Algorithm to jointly optimize SVM parameters and feature subsets. Experiments on high-dimensional gene expression datasets demonstrate substantial gains in accuracy, model compactness, and convergence speed. Future work includes extending to multi-class problems, exploring chaotic and Lévy-flight variants, and applying MDSH-SVM to other high-dimensional domains such as neuroimaging and text classification.