Intrinsically Optimal Equivariant Estimator for the Univariate Linear Normal Models

1. Introduction

The Fisher information matrix of a regular parametric family of probability distributions induces a natural Riemannian structure on the parameter space [1,2,3]. This structure provides the foundation for the intrinsic analysis of statistical estimation, see [4,5] and, beyond statistics, it has also been shown to reveal connections with physical laws [6].

In this intrinsic framework, estimators are assessed through tools that do not depend on any particular parametrization of the model. Consequently, non-intrinsic criteria such as the squared error loss should be replaced by intrinsic measures. A natural choice is the squared Riemannian (Rao) distance, which serves as an intrinsic loss function. The associated risk can behave very differently from that based on squared error loss, especially in small-sample regimes. Similarly, the classical definition of bias must be reformulated in terms of a vector field determined by the geometry of the model, whose squared norm provides a natural intrinsic bias measure.

The estimator itself should also be intrinsic, i.e., independent of parametrization. Consider, for instance, the exponential distribution under two parametrizations,

$$f(x,\theta )=\theta \exp (-\theta x){\mathbb{1}}_{{\mathbb{R}}^{+}}\left(x\right)\mathrm{and}f(x,\lambda )={\displaystyle \frac{1}{\lambda }}\exp (-x/\lambda ){\mathbb{1}}_{{\mathbb{R}}^{+}}\left(x\right)$$

where ${\mathbb{1}}_{{\mathbb{R}}^{+}}\left(x\right)$ is the positive real numbers indicator. The UMVU estimator computed under each parametrization $\widehat{\theta }$ and $\widehat{\lambda }$ are not related by $\widehat{\theta }=1/\widehat{\lambda }$. This apparent inconsistency arises because UMVU estimators rely on non-intrinsic notions such as unbiasedness and variance. As a result, the UMVU estimator is parametrization-dependent and cannot be regarded as intrinsically defined.

When the statistical model is invariant under the action of a transformation group on the sample space, it is natural to restrict attention to equivariant estimators, i.e., estimators U satisfying

$$U\left(g\left(x\right)\right)=\overline{g}\left(U\left(x\right)\right)\mathrm{for}\mathrm{all}g\in {\mathcal{G}}_n$$

where ${\mathcal{G}}_n$ is the transformation group acting on the space of all samples of size n and $\overline{g}\in \overline{\mathcal{G}}$ is the induced transformation on the parameter space $\Theta$. This restriction ensures logical consistency: only equivariant estimators remain coherent under data transformations. It is therefore a requirement that should be imposed prior to any attempt to minimize an intrinsic risk function.

As an illustration, consider the estimation of the unconstrained mean $\mu$ of a p–variate normal distribution. The MLE of $\mu$ (which really defines and intrinsic estimator) based on a sample of size n, is just the sample mean vector ${\overline{X}}_n$. However, for $p\ge 3$, the James–Stein estimator is known to have smaller quadratic risk [7]. In our view, this does not undermine the MLE. Although the James–Stein estimator enjoys a lower risk under the non-intrinsic quadratic loss, it lacks the essential property of equivariance, which is crucial from the intrinsic perspective.

In this work we focus on classical statistical estimation, as is standard in the absence of prior knowledge. Nonetheless, intrinsic Bayesian approaches based on non-informative priors are also possible [5,8], and represent an interesting avenue for future research. Here, we adopt the squared Rao distance as a natural loss function, since it is the conceptually simplest intrinsic analogue of the quadratic loss, despite potential computational challenges. For a broader background on statistical estimation and its intrinsic developments, see [9,10,11,12].

Specifically, we consider the univariate linear normal model with a fixed design matrix. First, we explicitly characterize the class of equivariant estimators under the action of a suitable subgroup of the affine group–namely, those affine transformations of the data that leave the column space of the design matrix unchanged. This subgroup is the largest one that preserves the model’s structure. Next, we prove the existence and uniqueness of the estimator within this class that minimizes intrinsic risk, i.e., the equivariant estimator that minimizes the mean squared Rao distance. We also derive an explicit expression for the intrinsic bias of any equivariant estimator.

Furthermore, we compare the intrinsic bias and risk of the proposed estimator with those of the MLE, highlighting their differences in small samples and showing how these differences diminish as the sample size grows. Finally, we propose a computable approximation of the optimal estimator, which mitigates most of the intrinsic bias and risk issues that affect the MLE in finite samples.

2. Equivariant estimators for linear models

Let us consider the univariate linear normal model,

$$\mathit{y}=\mathit{X}\mathit{\beta }+\mathit{e}$$

(1)

where $\mathit{y}$ is a $n\times 1$ random vector, $\mathit{X}$ is a $n\times m$ matrix of known constants with $0<\mathrm{rank}\left(\mathit{X}\right)=m\le n$, $\beta$ is a $m\times 1$ vector of unknown parameters to be estimated and $\mathit{e}$ is the fluctuation or error of $\mathit{y}$ about $\mathit{X}\mathit{\beta }$. We assume that the errors are unbiased, independent, with the same variance ${\sigma }^2$ and following a n–variate normal distribution, that is $\mathit{e}\sim N_n(\mathit{0},{\sigma }^2{\mathit{I}}_n)$, where ${\mathit{I}}_n$ is the $n\times n$ identity matrix. Therefore $\mathit{y}$ distributes according to an element of the parametric family of probability distributions $\mathcal{P}=\left\{N_n(\mathit{X}\mathit{\beta },{\sigma }^2{\mathit{I}}_n)\right|(\mathit{\beta },\sigma )\in \Theta \}$ with parameter space $\Theta ={\mathbb{R}}^m\times {\mathbb{R}}_{+}$, a $(m+1)$ – dimensional simply connected real manifold. Hereafter, we shall identify the elements of ${\mathbb{R}}^m$ with $m\times 1$ column vectors, when necessary.

Denote by

$$O_E\left(n\right)=\{\mathit{H}\in O\left(n\right)|\mathit{y}\in E\Rightarrow \mathit{Hy}\in E\}$$

where E is a subspace of ${\mathbb{R}}^n$ and $O\left(n\right)$ is the group of $n\times n$ orthogonal matrices with entries from $\mathbb{R}$. Define F as the subspace of ${\mathbb{R}}^n$ spanned by the columns of $\mathit{X}$, that is $F=\mathrm{Col}\left(\mathit{X}\right)$. Observe that $O_F\left(n\right)=O_{F^{\perp }}\left(n\right)$, ${\mathit{I}}_n\in O_F\left(n\right)$, $\mathrm{Col}\left(\mathit{X}\right)=\mathrm{Col}\left(\mathit{HX}\right)\forall \mathit{H}\in O_F\left(n\right)$ and if $\mathit{H}\in O_F\left(n\right)$ then ${\mathit{H}}^t\in O_F\left(n\right)$. Moreover, every $\mathit{H}\in O_F\left(n\right)$ induces, in F and $F^{\perp }$, two isomorphisms isomorphisms preserving the Euclidean norm in each subspace.

$\mathcal{P}$ is invariant under the action of the subgroup of the affine group in ${\mathbb{R}}^n$ given by the family of transformations

$$g_{(a,\mathit{H},\mathit{c})}\left(\mathit{y}\right)=a\mathit{H}\mathit{y}+\mathit{c},\mathit{y}\in {\mathbb{R}}^n$$

(2)

where $a>0,\mathit{H}\in O_F\left(n\right),\mathit{c}\in F$.

Observe that $\mathcal{G}=\left\{g_{(a,\mathit{H},\mathit{c})}\right|a>0,\mathit{H}\in O_F\left(n\right),\mathit{c}\in F\}$ induces an action on the parameter space $\theta$ given by

$$\begin{array}{ccc}\hfill \overline{g_{(a,\mathit{H},\mathit{c})}}(\mathit{\beta },\sigma )& =& \left(a{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\mathit{H}\mathit{X}\mathit{\beta }+{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\mathit{c},a\sigma \right)\hfill \end{array}$$

(3)

where this result is obtained taking into account that $\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}$ is the projection matrix into F and thus, if $\mathit{w}\in F$ there exists a unique $\mathit{\eta }$ such that $\mathit{w}=\mathit{X}\mathit{\eta }$ and $\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\mathit{w}=\mathit{w}$.

Since the family $\mathcal{P}$ is invariant under the action of $\mathcal{G}$, it is natural to restrict our attention to the class of equivariant estimators $\mathit{U}=({\mathit{U}}_1,U_2)$ of $(\mathit{\beta },\sigma )$ i.e. an estimator satisfying $\mathit{U}\left(g_{(a,\mathit{H},\mathit{c})}\left(\mathit{y}\right)\right)=\overline{g_{(a,\mathit{H},\mathit{c})}}\left(\mathit{U}\left(\mathit{y}\right)\right)$ for all $g_{(a,\mathit{H},\mathit{c})}\in \mathcal{G}$.

Proposition 1.  

Let $\mathit{U}$ be an equivariant estimator of $(\mathit{\beta },\sigma )$. Then $\mathit{U}$ belongs to the family $\{{\mathit{U}}_{\lambda },\lambda \in {\mathbb{R}}_{+}\}$ where,

$${\mathit{U}}_{\lambda }\left(\mathit{y}\right)=\left({\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\mathit{y},\lambda {\left\{{\mathit{y}}^{\mathsf{t}}\left({\mathit{I}}_n-\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\right)\mathit{y}\right\}}^{1/2}\right)$$

Proof. Let $\mathit{U}=({\mathit{U}}_1,U_2)$. The equivariance condition for $\mathit{U}$ involves,

$$\begin{array}{ccc}{\mathit{U}}_1(a\mathit{Hy}+\mathit{c})\hfill & =\hfill & a{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}{\mathit{H}\mathit{X}\mathit{U}}_1\left(\mathit{y}\right)+{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\mathit{c}\hfill \\ U_2(a\mathit{Hy}+\mathit{c})\hfill & =\hfill & a{U}_2\left(\mathit{y}\right)\hfill \end{array}$$

for any $a>0,\mathit{H}\in O_F\left(n\right),\mathit{c}\in F$.

Any $\mathit{y}\in {\mathbb{R}}^n$ can be written in a unique form as $\mathit{y}={\mathit{y}}_F+{\mathit{y}}_{F^{\perp }}$ where ${\mathit{y}}_F\in F$ and ${\mathit{y}}_{F^{\perp }}\in F^{\perp }$. Specifically

$${\mathit{y}}_F=\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\mathit{y}and{\mathit{y}}_{F^{\perp }}=({\mathit{I}}_n-\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}})\mathit{y}$$

(4)

If we choose $\mathit{c}=-a{\mathit{Hy}}_F$ in the previous expressions, we obtain

$$\begin{array}{ccc}\hfill {\mathit{U}}_1\left(a{\mathit{Hy}}_{F^{\perp }}\right)& =& a{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}{\mathit{H}\mathit{X}\mathit{U}}_1\left(\mathit{y}\right)-a{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}{\mathit{H}\mathit{y}}_F\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill U_2\left(a{\mathit{Hy}}_{F^{\perp }}\right)& =& a{U}_2\left(\mathit{y}\right)\hfill \end{array}$$

(6)

First we focus on ${\mathit{U}}_1$. If we let ${\mathit{H}}^{*}=({\mathit{I}}_n-2\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}})$, we have ${\mathit{H}}^{*}\in O_F\left(n\right)$ with

$${\mathit{H}}^{*}\mathit{v}=-\mathit{v}\forall \mathit{v}\in Fand{\mathit{H}}^{*}\mathit{v}=\mathit{v}\forall \mathit{v}\in F^{\perp }$$

Now observe that (5) is satisfied for any $a>0$ and $\mathit{H}$ in $O_F\left(n\right)$, in particular for ${\mathit{I}}_n$ and ${\mathit{H}}^{*}$. Therefore

$$\begin{array}{ccc}{\mathit{U}}_1\left(a{\mathit{y}}_{F^{\perp }}\right)\hfill & =\hfill & \hfill a{\mathit{U}}_1\left(\mathit{y}\right)-a{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}{\mathit{y}}_F\\ {\mathit{U}}_1\left(a{\mathit{H}}^{*}{\mathit{y}}_{F^{\perp }}\right)\hfill & =\hfill & \hfill -a{\mathit{U}}_1\left(\mathit{y}\right)+a{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}{\mathit{y}}_F\end{array}$$

But $a{\mathit{H}}^{*}{\mathit{y}}_{F^{\perp }}=a{\mathit{y}}_{F^{\perp }}$ which leads to

$$0={\mathit{U}}_1\left(\mathit{y}\right)-{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}{\mathit{y}}_F$$

From (4),

$${\mathit{U}}_1\left(\mathit{y}\right)={\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\mathit{y},\mathit{y}\in {\mathbb{R}}^n$$

Next, we consider $U_2$. Let $a=1$ and $\mathit{H}={\mathit{I}}_n$ in (), it follows

$$U_2\left({\mathit{y}}_{F^{\perp }}\right)=U_2\left(\mathit{y}\right)$$

(7)

Accordingly, it is enough to determine $U_2$ on $F^{\perp }$. Let us take a unit vector $\mathit{z}\in F^{\perp }$ such that $U_2\left(\mathit{z}\right)=\lambda >0$. Then ().

$$U_2\left(\mathit{Hz}\right)=U_2\left(\mathit{z}\right)$$

for any $\mathit{H}\in O_F\left(n\right)$. Observe that any arbitrary unit vector in $F^{\perp }$ can be written as $\mathit{Hz}$ for a proper $\mathit{H}\in O_F\left(n\right)$. Therefore, for any ${\mathit{y}}_{F^{\perp }}\in F^{\perp }$, ${\mathit{y}}_{F^{\perp }}\ne \mathit{0}$, we have

$$U_2\left({\mathit{y}}_{F^{\perp }}\right)=\parallel {\mathit{y}}_{F^{\perp }}\parallel U_2\left({\displaystyle \frac{{\mathit{y}}_{F^{\perp }}}{\parallel {\mathit{y}}_{F^{\perp }}\parallel }}\right)=\parallel {\mathit{y}}_{F^{\perp }}\parallel U_2\left(\mathit{Hz}\right)=\parallel {\mathit{y}}_{F^{\perp }}\parallel U_2\left(\mathit{z}\right)=\lambda \parallel {\mathit{y}}_{F^{\perp }}\parallel$$

Observe also that if $\mathit{y}=\mathit{0}$ then ${\mathit{y}}_{F^{\perp }}=0$ and, choosing $\mathit{c}=\mathit{0}$, we have that $U_2\left(\mathit{0}\right)=a{U}_2\left(\mathit{0}\right),\forall a\in {\mathbb{R}}_{+}$. This implies $U_2\left(\mathit{0}\right)=0$.

Finally, from (7) and (4) we have

$$U_2\left(\mathit{y}\right)=\lambda {\left\{{\mathit{y}}^{\mathsf{t}}\left({\mathit{I}}_n-\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\right)\mathit{y}\right\}}^{1/2}$$

□

Observe that the standard maximum likelihood estimator, MLE, for the present model is an equivariant estimator, with $\lambda ={\displaystyle \frac{1}{\sqrt{n}}}$.

3. Minimum Riemannian risk estimators

In the framework of intrinsic analysis, where the loss function is the square of the Rao distance, the Riemannian distance induced by the information metric in the parameter space $\Theta$, once the class of the equivariant estimators has been determined a natural question arises: which is the equivariant estimator that minimizes the risk?

First of all, we summarize the basic geometric results corresponding to the model (1) which are going to be used hereafter. We are going to use a standardized version of the information metric, given by the usual information metric corresponding to this linear model divided by a constant factor n, i.e. the number of rows of matrix $\mathit{X}$. This metric is given by

$$d{s}^2={\displaystyle \frac{1}{n{\sigma }^2}}\left(d{\mathit{\beta }}^{\mathsf{t}}{\mathit{X}}^{\mathsf{t}}\mathit{X}d\mathit{\beta }+2n{\left(d\sigma \right)}^2\right),$$

(8)

which is, up to a linear coordinate change, the Poincaré hyperbolic metric of the upper half space ${\mathbb{R}}^m\times {\mathbb{R}}^{+}$, see [13]. The Riemannian curvature $\kappa =-{\displaystyle \frac{1}{2}}$ is constant and negative and the unique geodesic, parameterized by the arc–length, which connects two points ${\theta }_1=({\mathit{\beta }}_1,{\sigma }_1)$ and ${\theta }_2=({\mathit{\beta }}_2,{\sigma }_2)\in \Theta$, when ${\mathit{\beta }}_1\ne {\mathit{\beta }}_2$, is given by:

$$\begin{array}{ccc}\hfill \mathit{\beta }\left(s\right)& =& 2n{K}^{-2}tanh\left({\displaystyle \frac{s}{\sqrt{2}}+ϵ}\right){\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1/2}\mathit{C}+\mathit{D}\hfill \\ \hfill \sigma \left(s\right)& =& K^{-1}sech\left({\displaystyle \frac{s}{\sqrt{2}}+ϵ}\right)\hfill \end{array}$$

(9)

where s is the arc–length, $\mathit{C}$ and $\mathit{D}$ are $m\times 1$ vectors whose components, and also $ϵ$, are convenient real integration constants, such that $\mathit{\beta }\left(0\right)={\mathit{\beta }}_1$, $\mathit{\beta }\left({\rho }_{12}\right)={\mathit{\beta }}_2$, $\sigma \left(0\right)={\sigma }_1$, $\sigma \left({\rho }_{12}\right)={\sigma }_2$ being ${\rho }_{12}$ the Riemannian distance between ${\theta }_1$ and ${\theta }_2$. Finally, K is given by $K^2=2n{\mathit{C}}^{\mathsf{t}}\mathit{C}$. When ${\mathit{\beta }}_1={\mathit{\beta }}_2$, the geodesic is given by

$$\mathit{\beta }\left(s\right)=\mathit{D}\sigma \left(s\right)=B{e}^{\pm {\displaystyle \frac{s}{\sqrt{2}}}}$$

(10)

where B is a positive integration constant.

The Rao distance $\rho$ between the points ${\theta }_1$ and ${\theta }_2$ is

$${\rho }_{12}\equiv \rho \left({\theta }_1,{\theta }_2\right)=\sqrt{2}ln\left({\displaystyle \frac{1+\delta ({\theta }_1,{\theta }_2)}{1-\delta ({\theta }_1,{\theta }_2)}}\right)=2\sqrt{2}arctanh\left(\delta ({\theta }_1,{\theta }_2)\right)$$

(11)

where

$$\delta ({\theta }_1,{\theta }_2)={\left({\displaystyle \frac{d_M^2({\mathit{\beta }}_{\mathit{1}},{\mathit{\beta }}_{\mathit{2}})+2{\displaystyle \frac{{({\sigma }_1-{\sigma }_2)}^2}{{\sigma }_1{\sigma }_2}}}{d_M^2({\mathit{\beta }}_{\mathit{1}},{\mathit{\beta }}_{\mathit{2}})+2{\displaystyle \frac{{({\sigma }_1+{\sigma }_2)}^2}{{\sigma }_1{\sigma }_2}}}}\right)}^{1/2}$$

(12)

and

$$d_M^2({\mathit{\theta }}_{\mathit{1}},{\mathit{\theta }}_{\mathit{2}})={\displaystyle \frac{1}{n{\sigma }_1{\sigma }_2}}{({\mathit{\beta }}_1-{\mathit{\beta }}_2)}^{\mathsf{t}}{\mathit{X}}^{\mathsf{t}}\mathit{X}({\mathit{\beta }}_1-{\mathit{\beta }}_2)$$

(13)

or, equivalently,

$$\rho \left({\theta }_1,{\theta }_2\right)=\sqrt{2}arccosh\left({\displaystyle \frac{1}{4}}{d}_M^2({\mathit{\theta }}_{\mathit{1}},{\mathit{\theta }}_{\mathit{2}})+{\displaystyle \frac{{\sigma }_1^2+{\sigma }_2^2}{2{\sigma }_1{\sigma }_2}}\right)$$

(14)

Let ${exp}_{{\theta }_1}^{-1}\left({\theta }_2\right)$ be the inverse of the exponential map corresponding to Levi-Civita connection and $W^1,\dots ,W^m,W^{m+1}$ its components corresponding to the basis field ${(\partial /\partial {\beta }^1)}_{{\theta }_1},$$\dots ,$${(\partial /\partial {\beta }^m)}_{{\theta }_1},{(\partial /\partial \sigma )}_{{\theta }_1}$. Then, we have

$$\begin{array}{ccc}{W}^i\hfill & =& {\displaystyle \frac{{\rho }_{12}/\sqrt{2}}{sinh({\rho }_{12}/\sqrt{2})}({\beta }_2^i-{\beta }_1^i)\frac{{\sigma }_1}{{\sigma }_2},i=1,\dots ,m}\hfill \\ W^{m+1}\hfill & =& {\displaystyle \frac{{\rho }_{12}/\sqrt{2}}{sinh({\rho }_{12}/\sqrt{2})}\left(cosh({\rho }_{12}/\sqrt{2})-\frac{{\sigma }_1}{{\sigma }_2}\right){\sigma }_1}\hfill \end{array}$$

(15)

It is well know that the Riemannian distance induced by the information metric is invariant under equivariant estimator transformations. We shall supply a direct and alternative proof for the linear model setting.

Proposition 2.  

The Rao distance ρ given by (11) is invariant under the action of the induced group by $\mathcal{G}$ on the parameter space, $\overline{\mathcal{G}}$. In other words

$$\rho (\overline{g_{(a,\mathit{H},\mathit{c})}}{\theta }_1,\overline{g_{(a,\mathit{H},\mathit{c})}}{\theta }_2)=\rho ({\theta }_1,{\theta }_2)$$

Proof: Observe that

$$\mathit{HX}({\mathit{\beta }}_1-{\mathit{\beta }}_2)\in F,\forall \mathit{H}\in O_F\left(n\right)$$

and taking into account that $\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}$ is the projection matrix into F, we have

$$\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\mathit{HX}({\mathit{\beta }}_1-{\mathit{\beta }}_2)=\mathit{HX}({\mathit{\beta }}_1-{\mathit{\beta }}_2)$$

Therefore

$${({\mathit{\beta }}_1-{\mathit{\beta }}_2)}^{\mathsf{t}}{\mathit{X}}^{\mathsf{t}}{\mathit{H}}^{\mathsf{t}}\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\mathit{HX}({\mathit{\beta }}_1-{\mathit{\beta }}_2)={({\mathit{\beta }}_1-{\mathit{\beta }}_2)}^{\mathsf{t}}{\mathit{X}}^{\mathsf{t}}\mathit{X}({\mathit{\beta }}_1-{\mathit{\beta }}_2)$$

and the invariance of $\delta$ and $\rho$ trivially follows. □

Proposition 3.  

$\overline{\mathcal{G}}$ acts transitively on Θ.

Proof: The transitivity follows observing that a is an arbitrary positive real number and $\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}$ is the projection matrix into F with $\mathrm{rank}\mathit{X}=m$. □

Since $\rho$, and thus ${\rho }^2$, is invariant under the action of $\overline{\mathcal{G}}$ and $\overline{\mathcal{G}}$ acts transitively on $\Theta$, the distribution of ${\rho }^2\left({\mathit{U}}_{\lambda }\left(\mathit{y}\right),\theta \right)$ does not depend on $\theta$, and therefore, the risk of any equivariant estimator remains constant and independent of the target parameter provided that this risk is finite. More precisely, observe that if we let

$$\mathit{z}={\displaystyle \frac{1}{\sigma }}({\mathit{y}}_F-\mathit{X}\mathit{\beta }),\mathcal{V}=\parallel \mathit{z}\parallel and\mathcal{W}={\displaystyle \frac{1}{\sigma }}\parallel {\mathit{y}}_{F^{\perp }}\parallel$$

(16)

from (1) and (4) we clearly have that $\mathit{z}\sim N_n(\mathit{0},\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}})$ with a rank m idempotent covariance matrix, and ${\mathcal{V}}^2$ and ${\mathcal{W}}^2$ are independent random variables following a chi-square distribution with m and $(n-m)$ degrees of freedom, equal to the dimensions of F and $F^{\perp }$ since ${\mathcal{V}}^2$ and ${\mathcal{W}}^2$ are quadratic forms based on the projection matrices on these subspaces of ${\mathbb{R}}^n$ and ${\mathit{y}}_F$ (or $\mathit{z}$) and ${\mathit{y}}_{F^{\perp }}$ are independent random vectors. Therefore, since $\mathit{X}{\mathit{U}}_{\lambda 1}\left(\mathit{y}\right)={\mathit{y}}_F$ and $U_{\lambda 2}\left(\mathit{y}\right)=\lambda \parallel {\mathit{y}}_{F^{\perp }}\parallel$, we have that

$$d_M^2({\mathit{U}}_{\lambda }\left(\mathit{y}\right),\theta )={\displaystyle \frac{1}{n{U}_{\lambda 2}\left(\mathit{y}\right)\sigma }}{({\mathit{U}}_{\lambda 1}\left(\mathit{y}\right)-\mathit{\beta })}^{\mathsf{t}}{\mathit{X}}^{\mathsf{t}}\mathit{X}({\mathit{U}}_{\lambda 1}\left(\mathit{y}\right)-\mathit{\beta })={\displaystyle \frac{{\mathcal{V}}^2}{n\lambda \mathcal{W}}}$$

(17)

$$\delta ({\mathit{U}}_{\lambda }\left(\mathit{y}\right),\theta )={\left({\displaystyle \frac{{\displaystyle \frac{{\mathcal{V}}^2}{n\lambda \mathcal{W}}}+2{\displaystyle \frac{{(\lambda \mathcal{W}-1)}^2}{\lambda \mathcal{W}}}}{{\displaystyle \frac{{\mathcal{V}}^2}{n\lambda \mathcal{W}}}+2{\displaystyle \frac{{(\lambda \mathcal{W}+1)}^2}{\lambda \mathcal{W}}}}}\right)}^{1/2}$$

(18)

and

$$\rho ({\mathit{U}}_{\lambda }\left(\mathit{y}\right),\theta )=2\sqrt{2}arctanh\left({\left({\displaystyle \frac{{\mathcal{V}}^2+2n{(\lambda \mathcal{W}-1)}^2}{{\mathcal{V}}^2+2n{(\lambda \mathcal{W}+1)}^2}}\right)}^{1/2}\right)$$

(19)

or

$$\rho \left({\mathit{U}}_{\lambda }\left(\mathit{y}\right),\theta \right)=\sqrt{2}arccosh\left({\displaystyle \frac{1}{4}}{\displaystyle \frac{{\mathcal{V}}^2}{n\lambda \mathcal{W}}}+{\displaystyle \frac{1}{2}}\left(\lambda \mathcal{W}+{\displaystyle \frac{1}{\lambda \mathcal{W}}}\right)\right)$$

(20)

which have a distribution which depend only on ${\mathcal{V}}^2$ and ${\mathcal{W}}^2$, independent random variables with fixed distribution, whatever the value of $\theta$.

Since the risk of any equivariant estimator remains constant on the parameter space, it’s enough to examine it at one point, for instance at the point $(\mathit{0},1)\in \Theta$. Let us denote the expectation with respect to the n–variate linear normal model $N_n(\mathit{X}\mathit{\beta },{\sigma }^2{\mathit{I}}_n)$ by $E_{(\mathit{\beta },\sigma )}$ and by E the $E_{(\mathit{0},1)}$. We can prove the following propositions.

Proposition 4.  

If $n\ge m+1$ we have:

$$E_{(\mathit{\beta },\sigma )}\left({\rho }^2\left({\mathit{U}}_{\lambda }\left(\mathit{y}\right),(\mathit{\beta },\sigma )\right)\right)=E\left({\rho }^2\left({\mathit{U}}_{\lambda }\left(\mathit{y}\right),(\mathit{0},1)\right)\right)<\infty ,\forall \lambda >0$$

for any $(\mathit{\beta },\sigma )\in \Theta$.

Proof: From (14) and (13), since

$$1+{\displaystyle \frac{1}{2!}}{\displaystyle \frac{{\rho }^2}{2}}+{\displaystyle \frac{1}{4!}}{\displaystyle \frac{{\rho }^4}{4}}\le cosh\left({\displaystyle \frac{\rho }{2}}\right)={\displaystyle \frac{1}{4}}{d}_M^2({\mathit{\theta }}_{\mathit{1}},{\mathit{\theta }}_{\mathit{2}})+{\displaystyle \frac{{\sigma }_1^2+{\sigma }_2^2}{2{\sigma }_1{\sigma }_2}}$$

(21)

we have

$$0\le {\rho }^2\left({\theta }_1,{\theta }_2\right)\le 12\left(\sqrt{1+{\displaystyle \frac{d_M^2({\mathit{\theta }}_{\mathit{1}},{\mathit{\theta }}_{\mathit{2}})}{6}}+{\displaystyle \frac{1}{3}}{\displaystyle \frac{{({\sigma }_1-{\sigma }_2)}^2}{{\sigma }_1{\sigma }_2}}}-1\right)$$

(22)

developing the square of the difference and taking into account that the standard Euclidean norm of a vector is less or equal to the absolute value of the sum of its components, we obtain

$$0\le {\rho }^2\left({\theta }_1,{\theta }_2\right)\le 2\sqrt{6}{d}_M({\mathit{\theta }}_{\mathit{1}},{\mathit{\theta }}_{\mathit{2}})+4\sqrt{3}\left(\sqrt{{\displaystyle \frac{{\sigma }_1}{{\sigma }_2}}}+\sqrt{{\displaystyle \frac{{\sigma }_2}{{\sigma }_1}}}\right)+4\sqrt{3}-12$$

(23)

Notice that both bounds (22) and (23) are invariant under the action of the induced group on the parameter space.

As we mentioned before, from [14], it is enough to prove that the risk is finite at $(\mathit{0},1)\in \Theta$. Taking into account (16) it follows, from (23), that

$$0\le {\rho }^2({\mathit{U}}_{\lambda }\left(\mathit{y}\right),(\mathit{0},1))\le 2\sqrt{6}\sqrt{{\displaystyle \frac{{\mathcal{V}}^2}{\lambda \mathcal{W}n}}}+4\sqrt{3}\left(\sqrt{\lambda \mathcal{W}}+{\displaystyle \frac{1}{\sqrt{\lambda \mathcal{W}}}}\right)+4\sqrt{3}-12$$

(24)

Observe that if Q has a chi-square distribution with k degrees of freedom

$$E\left(Q^{\alpha }\right)=2^{\alpha }{\displaystyle \frac{\Gamma (\frac{k}{2}+\alpha )}{\Gamma \left(\frac{k}{2}\right)}}\mathrm{providedthat}{\displaystyle \frac{k}{2}}+\alpha >0$$

Therefore, since ${\mathcal{V}}^2$ and ${\mathcal{W}}^2$ are independent random variables following a central chi-square distribution with m and $(n-m)$ degrees of freedom, we have

$$E\left(\mathcal{V}\right)=\sqrt{2}{\displaystyle \frac{\Gamma \left(\frac{m+1}{2}\right)}{\Gamma \left(\frac{m}{2}\right)}},E\left(\sqrt{\mathcal{W}}\right)=\sqrt[4]{2}{\displaystyle \frac{\Gamma \left(\frac{2(n-m)+1}{4}\right)}{\Gamma \left(\frac{n-m}{2}\right)}}providedthatn-m>-1/2$$

and

$$E\left({\displaystyle \frac{1}{\sqrt{\mathcal{W}}}}\right)={\displaystyle \frac{1}{\sqrt[4]{2}}}{\displaystyle \frac{\Gamma \left(\frac{2(n-m)-1}{4}\right)}{\Gamma \left(\frac{n-m}{2}\right)}}providedthatn-m>1/2$$

Then, taking the average, it follows that

$$\begin{array}{ccc}\hfill {\displaystyle E\left({\rho }^2({\mathit{U}}_{\lambda }\left(\mathit{y}\right),(0,1))\right)}& <& {\displaystyle \frac{2\sqrt{6}}{\sqrt{\lambda n}}E\left(\mathcal{V}\right)E\left(\frac{1}{\sqrt{\mathcal{W}}}\right)+}\hfill \\ & & {\displaystyle +4\sqrt{3}\left(\sqrt{\lambda }E\left(\sqrt{\mathcal{W}}\right)+\frac{1}{\sqrt{\lambda }}E\left(\frac{1}{\sqrt{\mathcal{W}}}\right)\right)+4\sqrt{3}-12}\hfill \\ \hfill {\displaystyle }& <& +\infty ,\forall \lambda >0\mathrm{and}n-m>1/2\hfill \end{array}$$

Since n and m are positive integers being $n>m$, we conclude that the risk is finite if $n\ge m+1$. □

Proposition 4 is a sufficient condition for the existence of the Riemannian risk of the equivariant estimator ${\mathit{U}}_{\lambda }$, thus

$$\Phi \left(\lambda \right)=E\left({\rho }^2({\mathit{U}}_{\lambda }\left(\mathit{y}\right),(\mathit{0},1))\right),\lambda >0,$$

(25)

is well defined for $n\ge m+1$, which we shall assume hereafter.

Proposition 5.  

There exists a unique minimizer ${\lambda }_{nm}>0$ of the Riemannian risk given by Φ.

Proof:

Let us consider the Riemannian risk at $\lambda =e^{{\displaystyle \frac{s}{2\sqrt{2}}}}$ as a function of s, that is

$$F\left(s\right)=\Phi \left(e^{{\displaystyle \frac{s}{2\sqrt{2}}}}\right),s\in \mathbb{R}$$

The particular selection of $\lambda$, from which F follows, relies on the Riemannian structure of $\Theta$ induced by the information metric. The Riemannian curvature is constant and equal to $-{\displaystyle \frac{1}{2}}$ and taking into account (10) we have that

$$\gamma \left(s\right)=\left({\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\mathit{y},e^{{\displaystyle \frac{s}{\sqrt{2}}}}{\left\{{\mathit{y}}^{\mathsf{t}}\left({\mathit{I}}_n-\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\right)\mathit{y}\right\}}^{1/2}\right)$$

is a geodesic in $\Theta$; precisely a geodesic parameterized by the arc–length, see [13] for further details.

Then, following [15], the real valued function

$$s\mapsto {\rho }^2(\gamma \left(s\right),(\mathit{0},1))$$

is strictly convex. Since almost surely convexity of a stochastic process carries over the mean of a process, the map F is strictly convex as well.

On the other hand, from Fatou’s Lemma $F\left(s\right)\to +\infty$ as $s\to -\infty$ or $s\to \infty$. This, together with the strict convexity of F yield the existence of a unique minimizer $s^{*}$ of the function F, which depends on n and m.

Finally, since the map $s\mapsto e^{{\displaystyle \frac{s}{2\sqrt{2}}}}$ is a strictly monotonous function; must exist a unique ${\lambda }_{nm}$, namely ${\lambda }_{nm}=e^{{\displaystyle \frac{s^{*}}{2\sqrt{2}}}}$, such that $\Phi \left({\lambda }_{nm}\right)={min}_{\lambda >0}\Phi \left(\lambda \right)$. □

In fact, this result guarantees the unicity of the MIRE, although a numerical analysis is required to obtain it explicitly (see next section). It could be useful to develop a simple approximate estimator, that shall be referred hereafter a-MIRE, obtained, luckily, minimizing a convenient upper bound of $\Phi \left(\lambda \right)$. Since

$$1+{\displaystyle \frac{1}{2!}}{\displaystyle \frac{{\rho }^2}{2}}\le cosh\left({\displaystyle \frac{\rho }{2}}\right)={\displaystyle \frac{1}{4}}{d}_M^2({\mathit{\theta }}_{\mathit{1}},{\mathit{\theta }}_{\mathit{2}})+{\displaystyle \frac{{\sigma }_1^2+{\sigma }_2^2}{2{\sigma }_1{\sigma }_2}}$$

(26)

we shall have

$$0\le {\rho }^2({\mathit{U}}_{\lambda }\left(\mathit{y}\right),(\mathit{0},1))\le {\displaystyle \frac{1}{n\lambda }}{\displaystyle \frac{{\mathcal{V}}^2}{\mathcal{W}}}+2{\left(\sqrt{\lambda \mathcal{W}}-{\displaystyle \frac{1}{\sqrt{\lambda \mathcal{W}}}}\right)}^2$$

(27)

and therefore

$$0\le \Phi \left(\lambda \right)\le H\left(\lambda \right)={\displaystyle \frac{1}{\lambda }}{\displaystyle \frac{\Gamma (\frac{n-m}{2}-\frac{1}{2})}{\sqrt{2}\Gamma \left(\frac{n-m}{2}\right)}}\left({\displaystyle \frac{m}{n}}+2\right)+2\sqrt{2}{\displaystyle \frac{\Gamma (\frac{n-m}{2}+\frac{1}{2})}{\Gamma \left(\frac{n-m}{2}\right)}}$$

(28)

the upper bound $H\left(\lambda \right)$ it is clearly a convex functions with an absolute minimum attained when $\lambda$ satisfy

$$\widetilde{{\lambda }_{nm}}=\left(\sqrt{1+{\displaystyle \frac{m}{2n}}}\right){\displaystyle \frac{1}{\sqrt{n-m-1}}}$$

(29)

Furthermore, given an arbitrary m, we have

$$\underset{n\to \infty }{lim}{\left(\widetilde{{\lambda }_{nm}}\right)}^{2}n=1$$

(30)

and, therefore, a-MIRE is very close to MLE for large values of n. Observe also that it is possible to compute a-MIRE for $n>m+1$, a condition which is slightly stronger that the result required for the existence of MIRE in proposition (4).

A further aspect is the intrinsic bias of the equivariant estimators. In fact connections between minimum risk, bias and invariance have been established, see [14]. Since the action of the group G is not commutative, we cannot guarantee the unbiasedness of the MIRE and an additional analysis must be performed. First of all we are going to compute the vector bias, see [4], a quantitative measure of the bias which is compatible with Lehmann results.

Let ${\mathit{A}}_{\theta }\left(\lambda \right)={exp}_{\theta }^{-1}\left({\mathit{U}}_{\lambda }\left(\mathit{y}\right)\right)$ and $A_{\theta }^1\left(\lambda \right),\dots ,A_{\theta }^m\left(\lambda \right),A_{\theta }^{m+1}\left(\lambda \right)$ be the components of ${\mathit{A}}_{\theta }\left(\lambda \right)$ corresponding to the basis field ${(\partial /\partial {\beta }^1)}_{\theta },\dots ,$${(\partial /\partial {\beta }^m)}_{\theta }$, ${(\partial /\partial \sigma )}_{\theta }$. With matrix notation, ${\mathit{A}}_{\theta 1}\left(\lambda \right)={(A_{\theta }^1\left(\lambda \right),\dots ,A_{\theta }^m\left(\lambda \right))}^{\mathsf{t}}$. Furthermore, let us define $h\left(x\right)\equiv x/sinhx$ for $x\ne 0$ and $h\left(0\right)\equiv 0$; taking into account (16), (19) and from (11) and (15) we have

$$\begin{array}{ccc}\hfill {\mathit{XA}}_{\theta 1}\left(\lambda \right)& =& {\displaystyle f_{\lambda }(\mathcal{V},\mathcal{W}))\mathit{z}\frac{\sigma }{\lambda \mathcal{W}}}\hfill \\ \hfill A_{\theta }^{m+1}\left(\lambda \right)& =& {\displaystyle f_{\lambda }(\mathcal{V},\mathcal{W})g_{\lambda }(\mathcal{V},\mathcal{W})\sigma }\hfill \end{array}$$

(31)

where

$$f_{\lambda }(\mathcal{V},\mathcal{W})\equiv h\left(\rho ({\mathit{U}}_{\lambda }\left(\mathit{y}\right),\theta )/\sqrt{2}\right)$$

and

$$g_{\lambda }(\mathcal{V},\mathcal{W})\equiv cosh\left(\rho ({\mathit{U}}_{\lambda }\left(\mathit{y}\right),\theta )/\sqrt{2}\right)-{\displaystyle \frac{1}{\lambda \mathcal{W}}}$$

Let ${\mathit{B}}_{\theta }\left(\lambda \right)=E_{\theta }\left({exp}_{\theta }^{-1}\left({\mathit{U}}_{\lambda }\left(\mathit{y}\right)\right)\right)$ be the intrinsic bias vector corresponding to an equivariant estimator ${\mathit{U}}_{\lambda }\left(\mathit{y}\right)=({\mathit{U}}_{\lambda 1}\left(\mathit{y}\right),U_{\lambda 2}\left(\mathit{y}\right))$ evaluated at the point $\theta =(\mathit{\beta },\sigma )$ and let $B_{\theta }^1\left(\lambda \right),$$\dots ,$$B_{\theta }^m\left(\lambda \right),$$B_{\theta }^{m+1}\left(\lambda \right)$ be their components. In matrix notation, ${\mathit{B}}_{\theta 1}\left(\lambda \right)={(B_{\theta }^1\left(\lambda \right),\dots ,B_{\theta }^m\left(\lambda \right))}^{\mathsf{t}}$. We have

Proposition 6.  

If $n\ge m+1$, the bias vector is finite and

$$\begin{array}{ccc}{\mathit{B}}_{\theta 1}\left(\lambda \right)\hfill & =& \mathit{0}\hfill \\ B_{\theta }^{m+1}\left(\lambda \right)\hfill & =& {\displaystyle E\left(f_{\lambda }(\mathcal{V},\mathcal{W})g_{\lambda }(\mathcal{V},\mathcal{W})\right)\sigma }\hfill \end{array}$$

(32)

where ${\mathcal{V}}^2$ and ${\mathcal{W}}^2$ are independent random variables following a chi-square distribution with m and $n-m$ degrees of freedom respectively.

Moreover, the square of the norm of the bias vector is constant and given by

$$\parallel {\mathit{B}}_{\theta }{\left(\lambda \right)\parallel }_{\theta }^2=2{\left(E\left(f_{\lambda }(\mathcal{V},\mathcal{W})g_{\lambda }(\mathcal{V},\mathcal{W})\right)\right)}^2$$

(33)

Proof: Observe that if $n\ge m+1$ we have

$$\begin{array}{ccc}\hfill \parallel {\mathit{B}}_{\theta }{\left(\lambda \right)\parallel }_{\theta }^2& \le & E_{\theta }(\parallel {exp}_{\theta }^{-1}\left({\mathit{U}}_{\lambda }\left(\mathit{y}\right)\right){\parallel }_{\theta }{)}^2\le E_{\theta }(\parallel {exp}_{\theta }^{-1}\left({\mathit{U}}_{\lambda }\left(\mathit{y}\right)\right){\parallel }_{\theta }^2)\hfill \\ & =& E_{\theta }\left({\rho }^2({\mathit{U}}_{\lambda }\left(\mathit{y}\right),\theta )\right)<\infty \hfill \end{array}$$

where ${\parallel ·\parallel }_{\theta }$ denotes the Riemannian norm at the tangent space at $\theta$.

On the other hand taking into account (31) and defining $\mathit{z}$ as in (16) observe that $\mathcal{V}=\parallel \mathit{z}\parallel =\parallel -\mathit{z}\parallel$, $\mathit{z}$ is independent of $\mathcal{W}$ and $\mathit{z}$ and $-\mathit{z}$ has the same distribution. Then we have

$$\begin{array}{ccc}\hfill \mathit{X}{\mathit{B}}_{\theta 1}\left(\lambda \right)& =& {\displaystyle E_{\theta }\left(f_{\lambda }(\mathcal{V},\mathcal{W})\mathit{z}\frac{\sigma }{\lambda \mathcal{W}}\right)}\hfill \\ & =& {\displaystyle E_{\theta }\left(f_{\lambda }(\mathcal{V},\mathcal{W})(-\mathit{z})\frac{\sigma }{\lambda \mathcal{W}}\right)=-E_{\theta }\left(f_{\lambda }(\mathcal{V},\mathcal{W})\mathit{z}\frac{\sigma }{\lambda \mathcal{W}}\right)=\mathit{0}}\hfill \end{array}$$

and since $rank\left(\mathit{X}\right)=m$ it follows that ${\mathit{B}}_{\theta 1}\left(\lambda \right)=\mathit{0}$.

$B_{\theta }^{m+1}\left(\lambda \right)$ is obtained directly from (31). The distribution of $\mathit{z}$ and ${\mathcal{W}}^2$ follow from basic properties of multivariate normal distribution. Finally, the norm of the bias vector field follows from (32) and (8).

□

We may remark, finally, that the norm of the bias vector field of any equivariant estimator, $\parallel {\mathit{B}}_{\theta }{\left(\lambda \right)\parallel }_{\theta }$, is invariant under the action of the induced group, $\overline{\mathcal{G}}$, on the parameter space and since this group acts transitively on $\Theta$, this quantity must be constant, which is clear from (33).

4. Numerical Evaluation

In this section we are going to compare, numerically, the MIRE estimator with the standard MLE. Observe that both estimators only differ in the estimation of the parameter $\sigma$ (or ${\sigma }^2$). Precisely, the MIRE and the MLE of ${\sigma }^2$ are, respectively,

$$\widehat{{\sigma }^2}={\lambda }_{nm}^2{\mathit{y}}^{\mathsf{t}}\left({\mathit{I}}_n-\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\right)\mathit{y}{{\sigma }^2}^{*}={\displaystyle \frac{1}{n}}{\mathit{y}}^{\mathsf{t}}\left({\mathit{I}}_n-\mathit{X}{\left({\mathit{X}}^{\mathsf{t}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{t}}\right)\mathit{y}$$

(34)

namely, they only differ by the factor ${\xi }_{nm}={\lambda }_{nm}^{2}n$, since $\widehat{{\sigma }^2}={\xi }_{nm}{{\sigma }^2}^{*}$.

In order to compare MLE with the MIRE we have computed the factor ${\xi }_{nm}$, the intrinsic risk and the square of the norm of the bias vector for each estimators. All the computations have been performed using Mathematica 10.2.

Moreover, we have suggested a rather simple approximation for ${\xi }_{nm}$, or ${\lambda }_{nm}$, which allow us to approximate MIRE estimator through (29), i.e.

$$\widetilde{{\xi }_{nm}}=\left(1+{\displaystyle \frac{m}{2n}}\right){\displaystyle \frac{n}{n-m-1}}$$

(35)

The corresponding estimator, that shall be referred hereafter as a-MIRE, has been also compared with MLE and MIRE in terms of intrinsic risk.

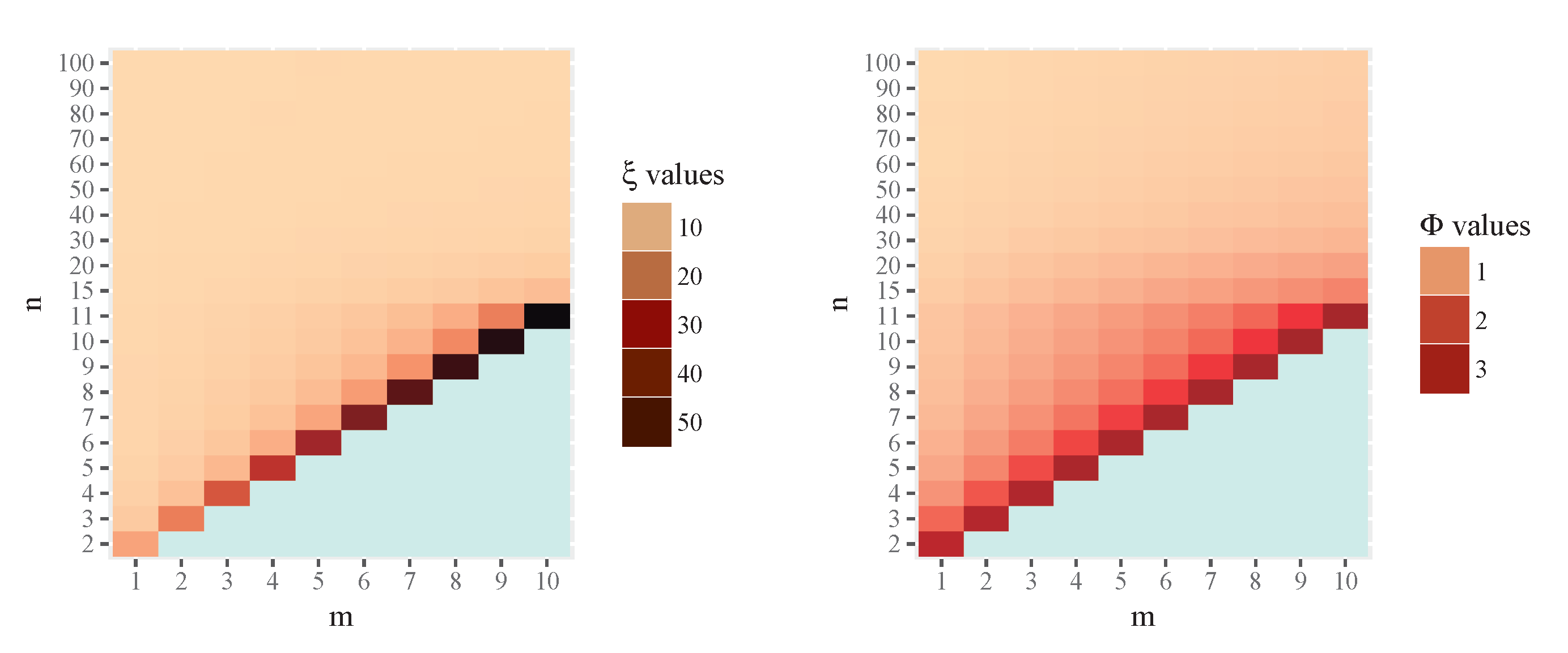
The results are summarized in the following figures which summarize the tables given in the Appendix, see [16] for a convincing argument for the use of plots over tables. In Figure 1 numerical results of ${\xi }_{nm}$ (left) and $\Phi \left({\lambda }_{nm}\right)=\Phi \left(\sqrt{{\xi }_{nm}/n}\right)$ (right) are displayed graphically. Observe that, for m fixed, as n increases $\Phi \left(\sqrt{{\xi }_{nm}/n}\right)$ goes to zero and ${\xi }_{nm}$ goes to one. The exact numerical values are given in the Appendix, Table 1.

Figure 1. Numerical results for ${\xi }_{nm}$ (left) and $\Phi \left({\lambda }_{nm}\right)$ (right), with ${\xi }_{nm}={\lambda }_{nm}^{2}n$.

Figure 1. Numerical results for ${\xi }_{nm}$ (left) and $\Phi \left({\lambda }_{nm}\right)$ (right), with ${\xi }_{nm}={\lambda }_{nm}^{2}n$.

Figure 2. Numerical results for ${\xi }_{nm}$ (left) and $\Phi \left({\lambda }_{nm}\right)$ (right), with ${\xi }_{nm}={\lambda }_{nm}^{2}n$.

Figure 2. Numerical results for ${\xi }_{nm}$ (left) and $\Phi \left({\lambda }_{nm}\right)$ (right), with ${\xi }_{nm}={\lambda }_{nm}^{2}n$.

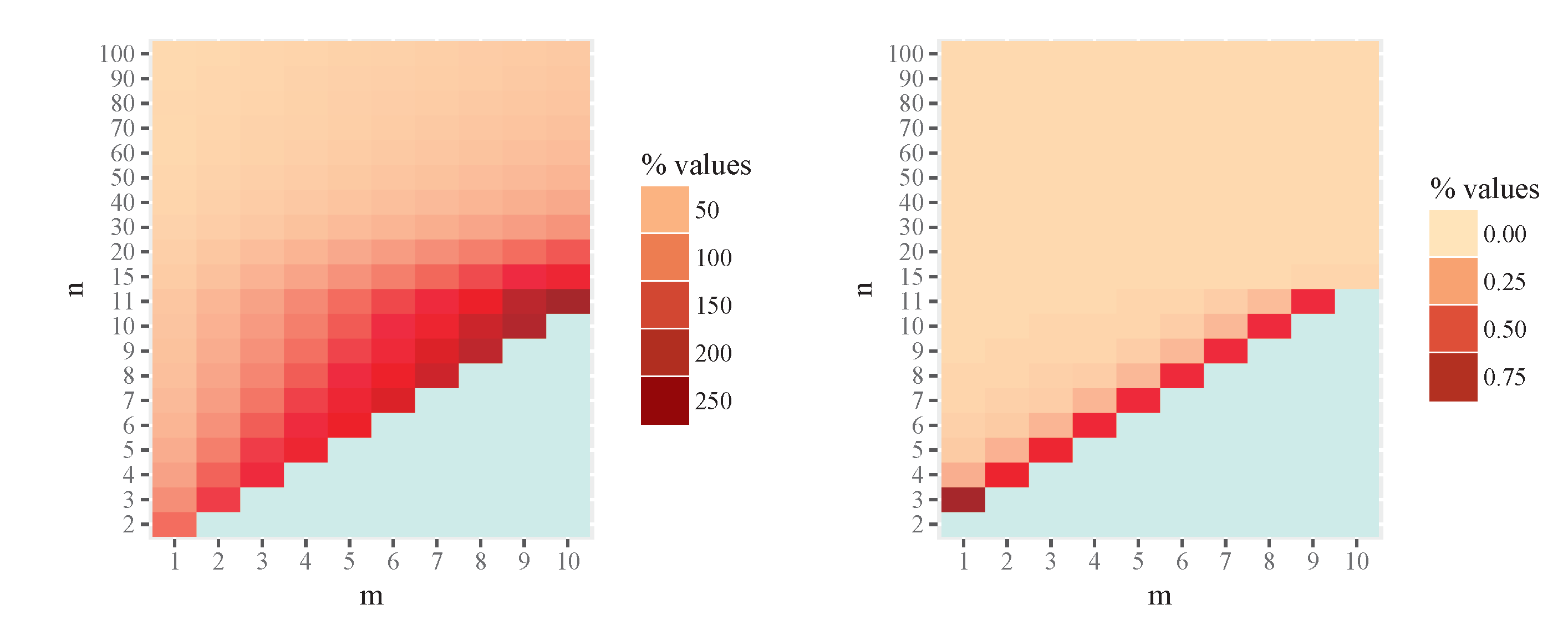
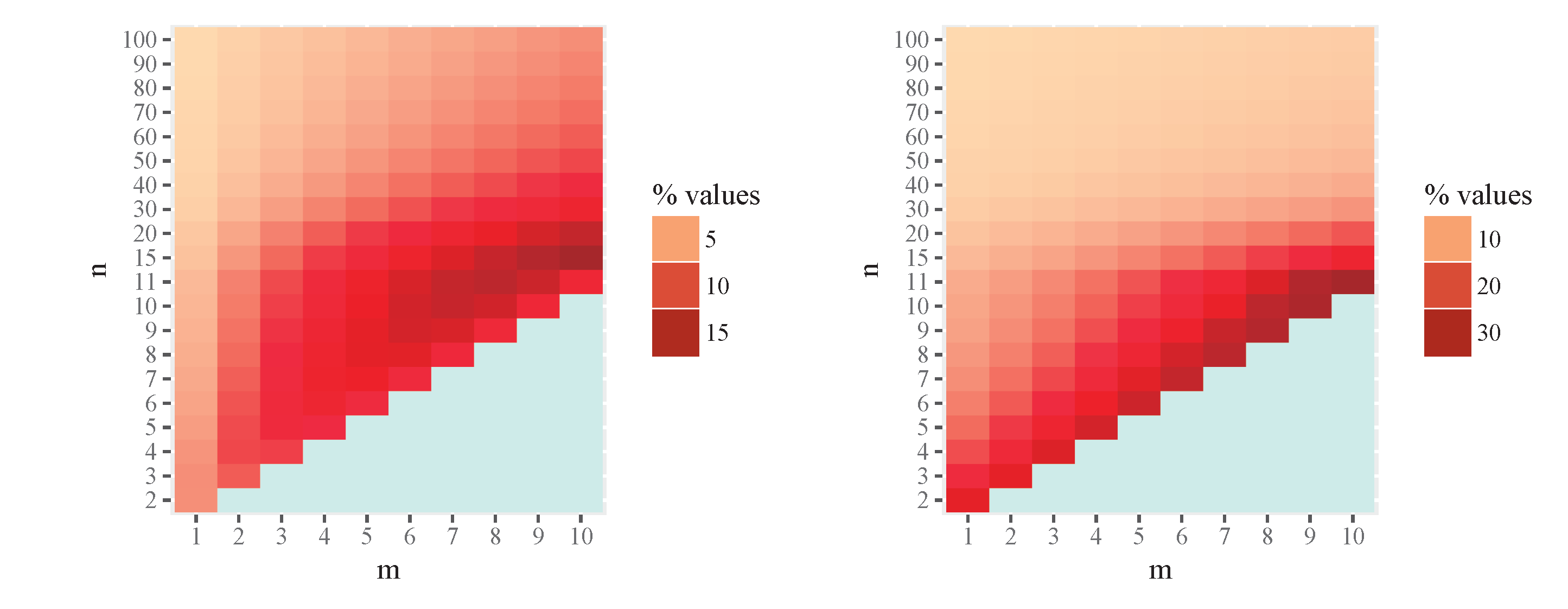
Figure 3 shows graphically the percentage of intrinsic risk increment for MLE (left) and a-MIRE (right), that is

$$100{\displaystyle \frac{\left(\Phi \left(\frac{1}{\sqrt{n}}\right)-\Phi \left({\lambda }_{nm}\right)\right)}{\Phi \left({\lambda }_{nm}\right)}}\mathrm{and}100{\displaystyle \frac{\left(\Phi \left(\widetilde{{\lambda }_{nm}}\right)-\Phi \left({\lambda }_{nm}\right)\right)}{\Phi \left({\lambda }_{nm}\right)}}$$

(36)

respectively, for some values of n and m. The exact numerical results are given in the Appendix, Table 2.

Observe that if we approximate the MIRE by the MLE for a certain value of m, the relative difference of risk decreases as n increases. Notice that these relative differences of risks are rather moderate or small (about 10-15%) only if $n>10m$. Let us remark also the non appropriate behavior of the MLE for small values of $n-m$. This regards to the intrinsic risk increment: when we use MLE instead of MIRE this increment oscillates between $80,5\%$ and $251,1\%$ when $n-m=1$ with m from 1 to 10. On the other hand, the behavior of the a-MIRE is reasonably good, with its intrinsic risk very similar to the risk of the MIRE estimator: here the percentage on risk increment is less than $1\%$ for all studied cases and also this percentage decreases as n increases. In fact this percentage is lower than 1‰ when $n-m\ge 4$, which indicates the extraordinary degree of approximation, being therefore the a-MIRE a reasonable and useful approximation of MIRE. In particular as an example, for a two way analysis of variance, with a and b levels for factors A and B respectively, with a single replicate for treatment we shall have

$$\tilde{\lambda }=\left(\sqrt{1+{\displaystyle \frac{a+b-1}{2ab}}}\right){\displaystyle \frac{1}{\sqrt{ab-a-b}}}$$

(37)

with $a>1$ and $b>1$, while the corresponding quantity for MLE is ${\lambda }^{*}={\displaystyle \frac{1}{\sqrt{ab}}}$.

In particular if $a=3$ and $b=5$ we shall have

$$\tilde{\lambda }=\left(\sqrt{1+{\displaystyle \frac{7}{30}}}\right){\displaystyle \frac{1}{\sqrt{7}}}=0,419750$$

and ${\lambda }^{*}={\displaystyle \frac{1}{\sqrt{15}}}=0,258199$, which is sensibly different. At this moment, it could be useful to recall that the quadratic loss and the squared of the Riemannian distance behaves very different, see [5].

Figure 3. Percentage of intrinsic risk increment for MLE (left) and a-MIRE (right).

Figure 3. Percentage of intrinsic risk increment for MLE (left) and a-MIRE (right).

Figure 4. Percentage of intrinsic risk increment for MLE (left) and a-MIRE (right).

Figure 4. Percentage of intrinsic risk increment for MLE (left) and a-MIRE (right).

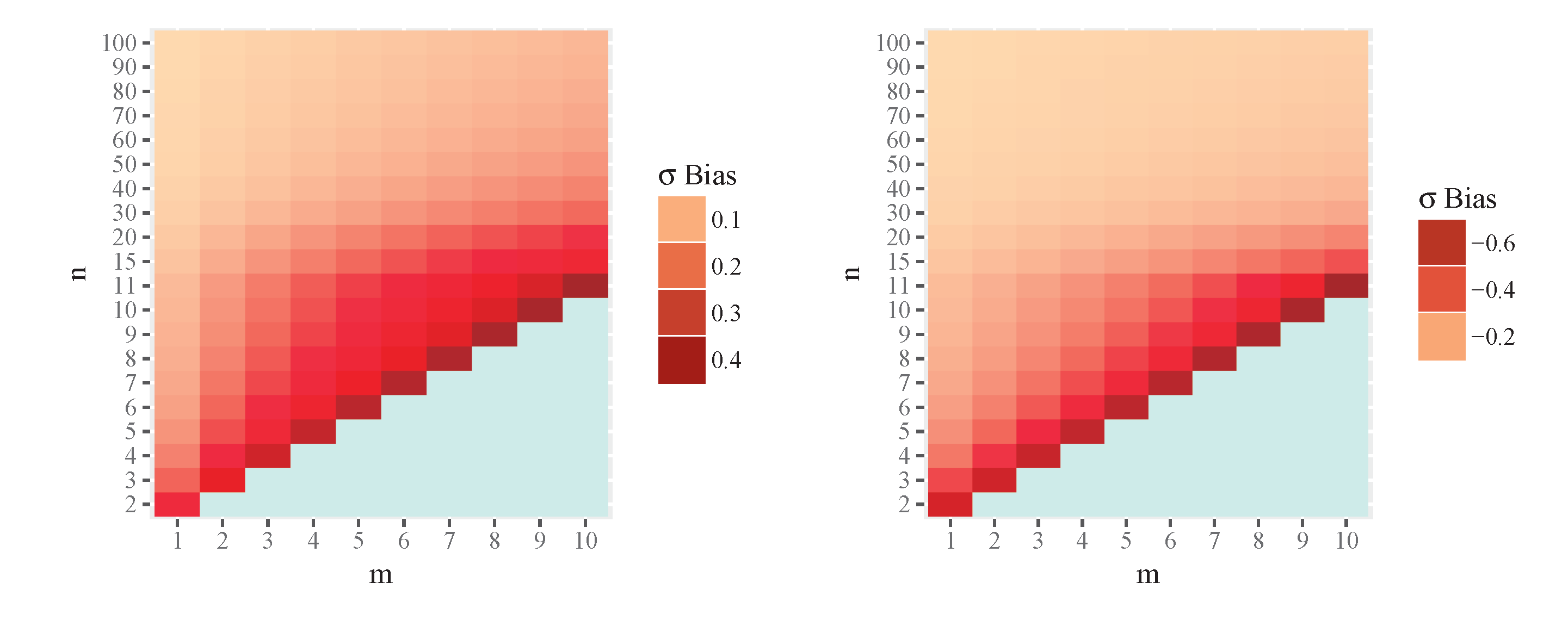
Figure 5 displays graphically the numerical results of the $m+1$ component of the bias vector divided by $\sigma$, i.e. the unique non zero physical component of this vector field, for MIRE (left) and MLE (right), ${\displaystyle \frac{1}{\sigma }}{B}_{\theta }^{m+1}\left({\lambda }_{nm}\right)$ and ${\displaystyle \frac{1}{\sqrt{n}\sigma }}{B}_{\theta }^{m+1}\left({\displaystyle \frac{1}{\sqrt{n}}}\right)$ respectively, for some values of n and m. Observe the sign differences, meaning that MIRE overestimates, in average, $\sigma$ while MLE underestimates this quantity, in average as well. This follows from the equation of the geodesics of the present model (9). The exact numerical values are given in the Appendix, Table 3.

Figure 5. Numerical results for the unique non–null physical component of bias vector field ${\displaystyle \frac{1}{\sigma }}{B}_{\theta }^{m+1}\left(\lambda \right)$, for MIRE (left, with $\lambda ={\lambda }_{nm}$) and MLE (right, with $\lambda =1/\sqrt{n}$).

Figure 5. Numerical results for the unique non–null physical component of bias vector field ${\displaystyle \frac{1}{\sigma }}{B}_{\theta }^{m+1}\left(\lambda \right)$, for MIRE (left, with $\lambda ={\lambda }_{nm}$) and MLE (right, with $\lambda =1/\sqrt{n}$).

Figure 6. Numerical results for the unique non–null physical component of bias vector field ${\displaystyle \frac{1}{\sigma }}{B}_{\theta }^{m+1}\left(\lambda \right)$, for MIRE (left, with $\lambda ={\lambda }_{nm}$, positive values) and MLE (right, with $\lambda =1/\sqrt{n}$, negative values).

Figure 6. Numerical results for the unique non–null physical component of bias vector field ${\displaystyle \frac{1}{\sigma }}{B}_{\theta }^{m+1}\left(\lambda \right)$, for MIRE (left, with $\lambda ={\lambda }_{nm}$, positive values) and MLE (right, with $\lambda =1/\sqrt{n}$, negative values).

Figure 7 shows graphically the numerical results of the percentage of intrinsic risk due to bias for MIRE and MLE, that is

$$100{\displaystyle \frac{{\parallel \mathit{B}\parallel }_{\theta }^2\left({\lambda }_{nm}\right)}{\Phi \left({\lambda }_{nm}\right)}}and100{\displaystyle \frac{{\parallel \mathit{B}\parallel }_{\theta }^2\left(\frac{1}{\sqrt{n}}\right)}{\Phi \left({\lambda }_{nm}\right)}}$$

(38)

respectively, for some values of n and m. Observe that the bias is moderate, with respect the intrinsic risk, in both estimators. The bias of MIRE estimator is smaller than the bias of MLE for small values of m and the opposite for large values. The exact numerical results are given in the Appendix, Table 4.

Figure 7. Percentage of intrinsic risk due to bias for MIRE (left) and MLE (right), referred to the risk of MIRE.

Figure 7. Percentage of intrinsic risk due to bias for MIRE (left) and MLE (right), referred to the risk of MIRE.

Figure 8. Percentage of intrinsic risk due to bias for MIRE (left) and MLE (right), referred to the risk of MIRE.

Figure 8. Percentage of intrinsic risk due to bias for MIRE (left) and MLE (right), referred to the risk of MIRE.

Acknowledgements: We have to thank the referees and the editor comments and suggestions for the improvement of this paper.