1. Introduction
Entropy traditionally quantifies uncertainty over random variables or states, with classical measures relying on probability distributions [
1]. Complex combinatorial structures, such as simplicial complexes and hypergraphs, lack intrinsic information measures independent of probability. We introduce
Combinatorial-Topological Entropy (CTE), a structural measure capturing the intrinsic complexity of topological arrangements. Unlike Shannon or Rényi entropy, CTE is a property of the combinatorial-topological object itself, invariant under isomorphism and sensitive to adjacency and hierarchy.
CTE provides a unified approach bridging combinatorics, topology, and information theory. Potential applications include quantifying complexity in AI latent spaces, feature analysis, network robustness, and topological data analysis.
2. Materials and Methods
2.1. Preliminaries
We consider:
Simplicial Complexes K: sets of vertices, edges, triangles, and higher-dimensional simplices closed under inclusion.
Hypergraphs H: collections of hyperedges connecting multiple vertices.
Chains, Betti numbers, and Euler characteristic: standard combinatorial-topological invariants.
2.2. CTE Definition
For a simplicial complex
K, each simplex
has dimension
and adjacency
, the number of higher-dimensional simplices containing it. We define the
CTE:
where
For hypergraphs
H, we define:
where
is the number of overlapping hyperedges.
2.3. Computation and Parameter Exploration
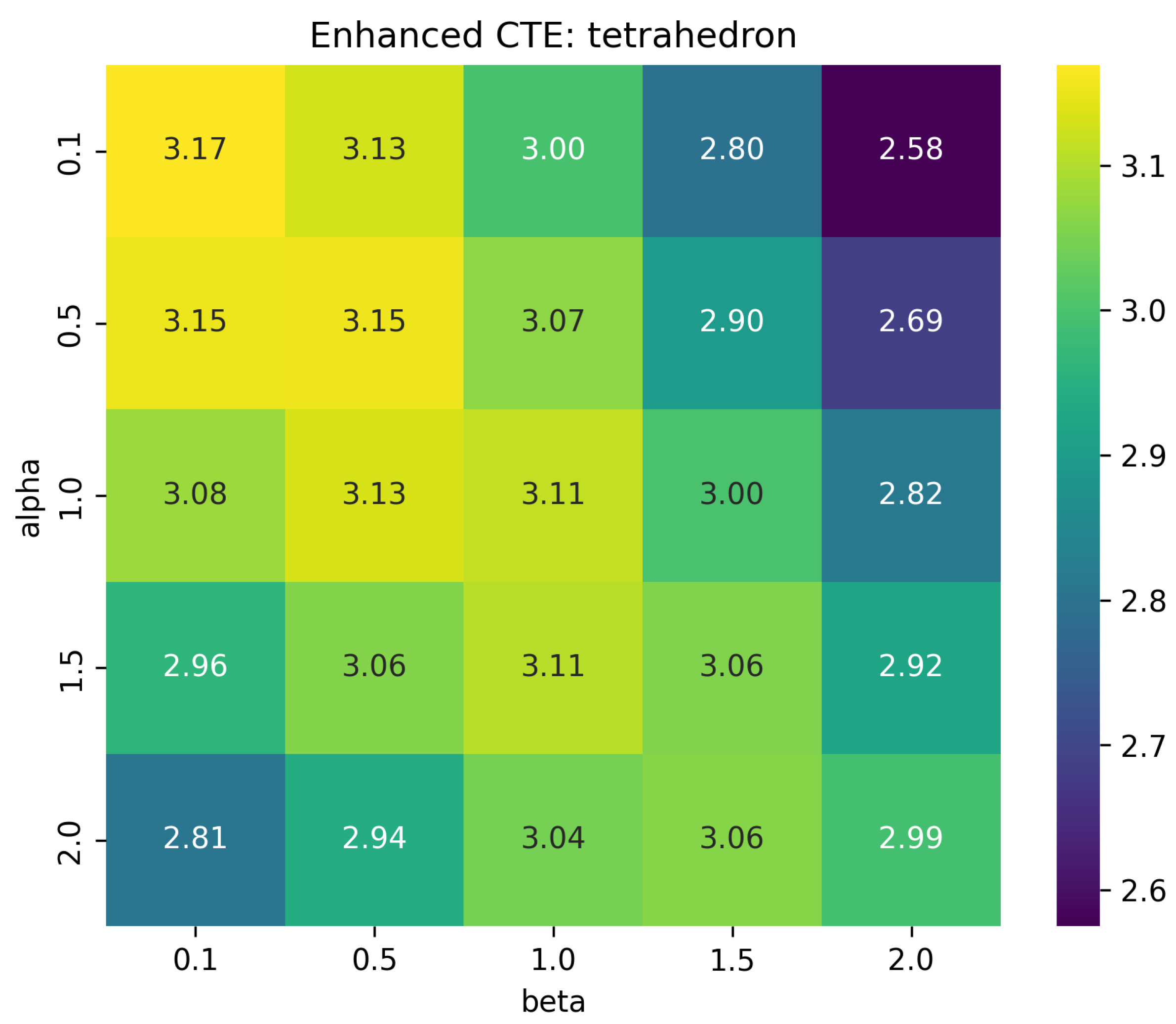
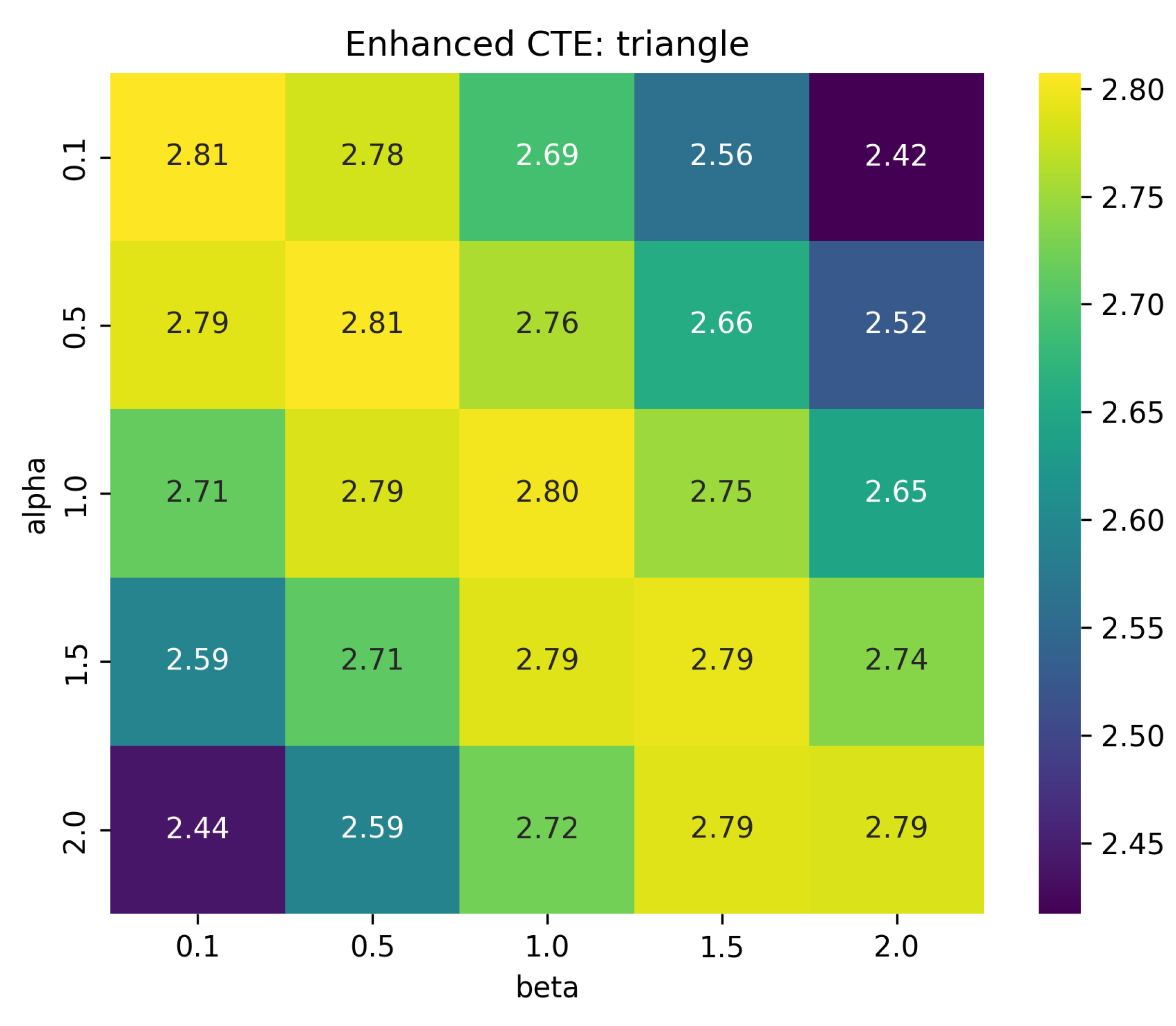
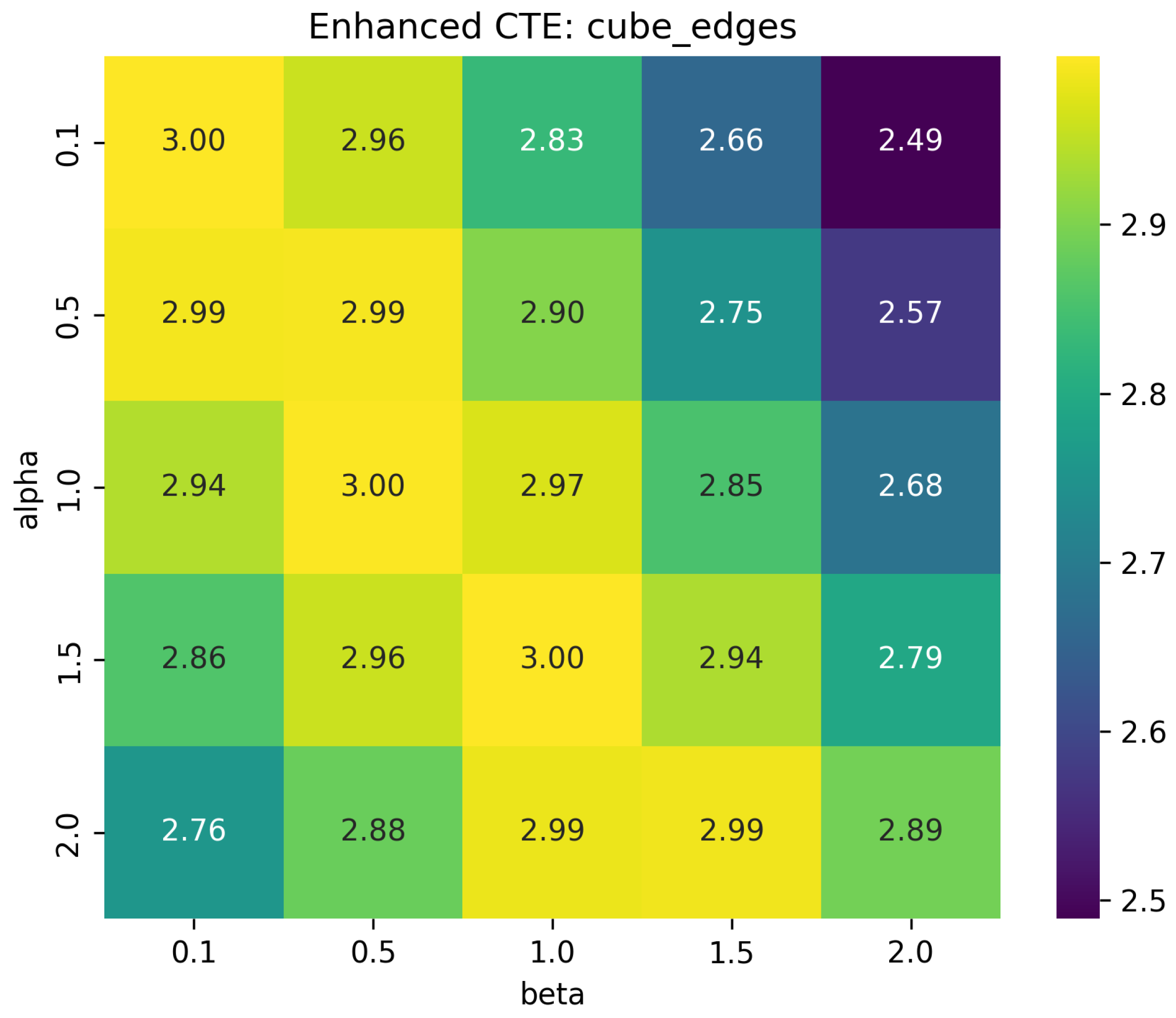
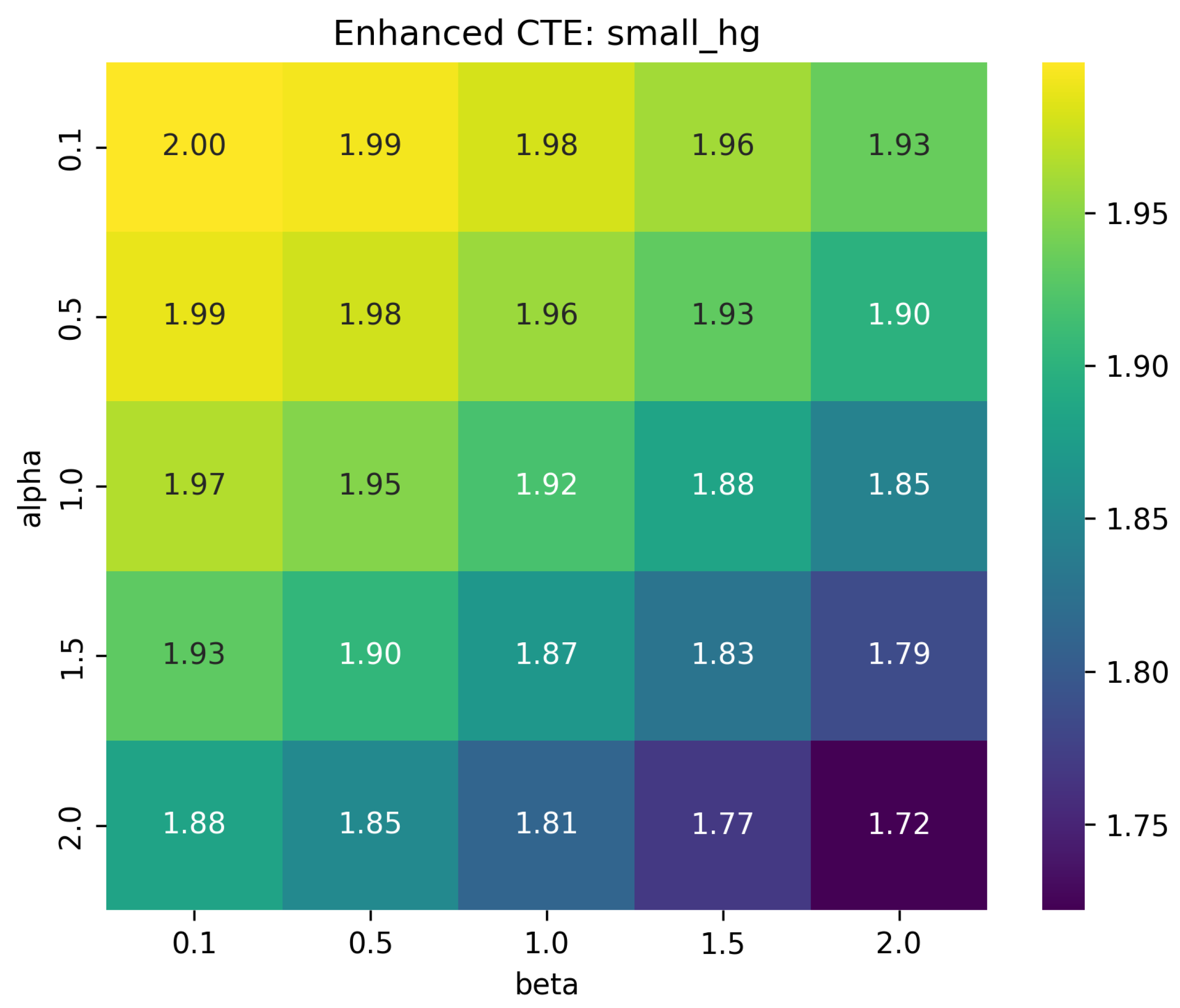
CTE was computed in Python for varying and over multiple combinatorial structures (tetrahedron, triangle, cube edges, small and dense hypergraphs). Heatmaps were generated to visualize how CTE changes with parameters.
2.4. Theoretical Properties of CTE
Theorem 1. (Permutation Invariance). CTE is invariant under any reordering of simplices in a simplicial complex or hyperedges in a hypergraph.
Proof. Let K be a simplicial complex with simplices . CTE depends only on the multiset . Reordering the simplices does not change this multiset; hence the normalized probabilities and resulting entropy remain unchanged. □
Theorem 2. (Isomorphism Invariance). CTE is invariant under combinatorial isomorphisms of simplicial complexes or hypergraphs.
Proof. Any bijection between vertex sets preserving adjacency ensures that each simplex or hyperedge retains its dimension and adjacency/degree. Since CTE depends only on these values, its computation yields the same result after isomorphism. □
Theorem 3. (Scale Invariance). Multiplying all dimensions or degrees by a constant factor does not change the relative CTE ranking of structures.
Proof. Let and consider modified weights . The normalization constant , giving . Thus, the probabilities in the entropy formula remain unchanged, leaving CTE invariant under scaling. □
3. Results
Table 1 presents example computed CTE values for the tetrahedron simplicial complex.
3.2. Comparison with Existing Complexity Measures
To evaluate the effectiveness of Combinatorial-Topological Entropy (CTE) relative to established measures, we computed **graph entropy** [
4] and **motif complexity** [
5] on the same set of simplicial complexes and hypergraphs used for CTE. Parameters
and
were varied as in
Section 2.3 to ensure consistent comparisons.
Table 2 presents representative results at
and
, using
and
in the PDF string to avoid warnings with hyperref. The table demonstrates that CTE captures both simplex size and adjacency, whereas graph entropy and motif complexity often fail to distinguish structurally distinct objects.
Several key observations emerge from these results:
Structural sensitivity: CTE exhibits meaningful variation across different simplicial complexes and hypergraphs, capturing both simplex size and adjacency information.
Parameter responsiveness: Adjusting and modifies CTE values predictably, reflecting the influence of simplex size and adjacency in the measure.
Limitations of existing measures: Graph entropy often remains unchanged across topologically distinct structures, while motif complexity can yield zero or indistinguishable values (e.g., cube edges), failing to detect nuanced combinatorial differences.
These results illustrate that CTE offers a more flexible and informative metric for combinatorial complexity than traditional graph-theoretic or motif-based approaches, particularly when assessing higher-dimensional simplicial and hypergraph structures.
4. Discussion
The heatmaps illustrate that CTE captures intrinsic structural properties independent of probability distributions. Parameter strongly influences adjacency weighting, decreasing CTE with higher adjacency sensitivity. Parameter moderately scales contributions from simplex size. Differences between simplicial complexes and hypergraphs demonstrate structural discrimination, validating CTE as a structural invariant.
Potential applications include quantifying AI latent space complexity, analyzing high-dimensional features, and assessing network robustness in complex systems.
4.1. Limitations
CTE requires selection of parameters and to weight simplex size and adjacency influence. While our heatmaps explore a broad range, optimal parameter choices may vary across applications. Computational complexity grows with the number of simplices/hyperedges, although vectorized or parallel implementations can mitigate this. Future work will focus on automatic parameter selection strategies and large-scale efficiency.
4.2. Future Directions
Potential applications of CTE include:
Quantifying latent-space complexity in AI models
Measuring robustness and heterogeneity in complex networks
Multi-layer topologies and higher-dimensional combinatorial structures
Automated feature selection using topological invariants
5. Conclusions
CTE is a novel structural entropy measure for combinatorial-topological objects. Computations and heatmap visualizations show sensitivity to simplex dimension and adjacency hierarchy. This framework provides a new approach where entropy is a topological-combinatorial invariant, independent of probabilistic assumptions.
Supplementary Materials
The CTE framework code is available at
https://github.com/Reyence/cte-entropy. This repository provides all functions needed to compute combinatorial-topological entropy for arbitrary simplicial complexes and hypergraphs.
Author Contributions
R.C. conducted all aspects of this work.
Funding
No external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The author thanks the open-source Python community for libraries facilitating computations. Python 3.11 was used for all simulations.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Hatcher, A. Algebraic Topology; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Edelsbrunner, H.; Harer, J. Computational Topology: An Introduction; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Mowshowitz, A. Entropy and the Complexity of Graphs. Bulletin of Mathematical Biophysics 1968, 30, 175–204. [Google Scholar] [CrossRef] [PubMed]
- Milo, R.; Shen-Orr, S.; Itzkovitz, S.; Kashtan, N.; Chklovskii, D.; Alon, U. Network motifs: Simple building blocks of complex networks. Science 2002, 298, 824–827. [Google Scholar] [CrossRef] [PubMed]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).