Neural Operator-Based Prediction of Temperature Dynamics in Lithium Iron Phosphate Batteries for Electric Vehicles

1. Introduction

The global automotive industry is undergoing a transformative shift driven by the convergence of environmental imperatives, depletion of fossil fuels, and aggressive policy mandates aimed at decarbonization. At the forefront of this evolution are electric vehicles (EVs), which are becoming viable and scalable alternatives to traditional internal combustion engine (ICE) vehicles. Among the critical components that determine the performance and viability of EVs are the energy storage systems—most notably lithium-ion batteries.

Lithium Iron Phosphate (LiFePO₄), a subclass of lithium-ion chemistries, has garnered significant attention in recent years due to its superior safety, thermal stability, and longevity. Compared to traditional Li-ion cells (e.g., NMC or LCO types), LiFePO₄ batteries exhibit:

• Enhanced thermal tolerance: Operate reliably across a wider temperature range without thermal runaway.
• Superior safety characteristics: Due to their chemical composition and robust phosphate framework, they are less prone to overheating or combustion.
• Longer lifecycle: Capable of sustaining thousands of charge-discharge cycles with minimal capacity fade.
• Cost-effectiveness and sustainability: Use of non-cobalt materials reduces environmental impact and material scarcity issues.

For instance, Tesla’s Model 3 uses LiFePO₄ cells to optimize for both economic scalability and operating safety.

Despite these advantages, LiFePO₄ batteries still face critical challenges, particularly related to temperature sensitivity. Battery temperature influences electrochemical kinetics, internal resistance, energy efficiency, and long-term degradation. Hence, precise prediction and management of temperature dynamics are essential for ensuring safe and optimal battery operation.

Traditional modeling approaches employ physics-based thermal models rooted in energy balance equations. While these offer interpretability, they often suffer from limited scalability in dynamic and uncertain real-world environments due to computational overhead and the need for accurate parameter estimation.

In contrast, this work introduces a neural operator-based approach for learning the temperature evolution of LiFePO₄ battery cells. Unlike conventional neural networks or recurrent models, neural operators learn mappings between function spaces. This makes them uniquely suited for modeling continuous spatiotemporal dynamics under varying inputs. Neural operators generalize better across unseen driving conditions and support fast inference suitable for embedded applications.

Figure 1 illustrates the proposed training architecture. A novel time-stability loss ensures consistency across successive temporal predictions, thereby preventing divergence—a common issue in autoregressive sequence models. This is especially beneficial in modeling battery behavior during highly transient driving scenarios, such as stop-and-go traffic or sudden temperature shifts.

In summary, this paper contributes a neural operator-based framework for accurate, stable, and generalizable prediction of temperature dynamics in EV batteries. By leveraging real-world telemetry from Tesla Model 3 vehicles, the model is designed to operate in noisy, variable conditions and lays the groundwork for future adaptive thermal management systems.

2. Methodology

This section delineates the experimental design, neural operator modeling approach, and the various enhancements introduced to improve robustness, generalizability, and interpretability of the proposed battery temperature modeling framework. Additionally, we detail the development of a surrogate model for estimating charging characteristics from predicted thermal states.

2.1. Experimental Setup and Data Acquisition

The experimental configuration is illustrated in Figure 3 (Appendix A), which provides a schematic overview of sensor placement and data logging mechanisms. Thermal readings were continuously captured using an Inkbird IBS-TH1 Bluetooth thermometer placed directly beneath the driver’s seat of a Tesla Model 3, a configuration selected to approximate the internal cabin temperature and infer subsurface battery heating effects.

The Tesla Model 3 employed in this study was equipped with a CATL-manufactured lithium iron phosphate (LiFePO₄) battery pack. This specific chemistry was selected due to its known stability and temperature sensitivity, which make it a compelling candidate for thermal modeling. Alongside thermal data, auxiliary driving telemetry was gathered via Tesla’s onboard API, including vehicle velocity, energy consumption, battery percentage, and ambient environmental conditions such as temperature, humidity, and elevation gradient. These parameters were recorded at 1 Hz intervals and were aligned temporally to ensure consistent feature synchronization.

2.2. Neural Operator Modeling Framework

To capture the dynamic evolution of the battery temperature during real-world driving conditions, we employ a neural operator-based parametric ordinary differential equation (ODE) framework. The model assumes the following continuous-time formulation:

$${\displaystyle \frac{du(\tau ,\mathbf{e})}{d\tau }}={\varphi }_{\theta }(\tau ,\mathbf{e}),u({\tau }_0,{\mathbf{e}}_0)=u_0$$

(1)

Here, $u(\tau ,\mathbf{e})$ denotes the temperature state at a relative time $\tau$ under environmental features $\mathbf{e}\in {\mathbb{R}}^d$, which include telemetry-based variables such as speed, SoC, and ambient temperature. The function ${\varphi }_{\theta }$, parameterized by learnable weights $\theta$, approximates the unknown temporal derivative of the temperature. This formulation allows the system to generalize beyond fixed-length sequences and model continuous trajectories effectively.

The model is trained by minimizing a discrete approximation of the temporal residual error, expressed as:

$${\mathcal{L}}_{\mathrm{NO}}=\sum _{i=0}^{N-1}{∥{\displaystyle \frac{u_{i+1}-u_i}{{\tau }_{i+1}-{\tau }_i}}-{\varphi }_{\theta }({\tau }_i,{\mathbf{e}}_i)∥}^2$$

(2)

This loss function penalizes divergence between the observed temporal gradient and the neural operator’s predicted evolution rate. The temporal propagation of temperature is computed through explicit Euler integration:

$$u_{i+1}=u_i+\delta ·{\varphi }_{\theta }({\tau }_i,{\mathbf{e}}_i)$$

(3)

where $\delta$ denotes the time step interval. This forward Euler method is computationally efficient and enables deployment in embedded or real-time inference settings.

2.3. Comparison with Traditional Modeling Approaches

Traditional thermal models such as equivalent circuit models (ECMs), empirical regression, and partial differential equations (PDEs) provide structured, physics-based insights but struggle under stochastic real-world conditions due to high computational overhead and parameter sensitivity. While recurrent neural networks (RNNs) and long short-term memory (LSTM) architectures offer temporal modeling capabilities, they typically require fixed-length sequences and exhibit vanishing gradient issues.

In contrast, neural operator methods operate in function space, enabling them to generalize across varying temporal trajectories and environmental configurations. This property makes them especially well-suited for systems where the input-output relationship evolves over time, such as battery thermal dynamics in electric vehicles. Furthermore, operator-based models inherently support continuous-time forecasting and can integrate domain constraints directly into their architecture, enhancing interpretability and physical coherence.

2.4. Smoothing Regularization for Stability

Although powerful, neural operators are prone to overfitting transient patterns and may exhibit erratic predictions when exposed to minor fluctuations in environmental inputs. To combat this, we introduce a smoothness regularization term that penalizes sharp gradients in the output with respect to the input feature space:

$${\mathcal{L}}_{\mathrm{smooth}}={\displaystyle \frac{1}{M}}\sum _{j=1}^M{∥{\displaystyle \frac{\partial {\varphi }_{\theta }(\tau ,\mathbf{e})}{\partial e_j}}∥}^2$$

(4)

Here, $e_j$ represents the j-th component of the environmental feature vector. This term encourages the model to learn smoother, more physically plausible transitions and reduces sensitivity to sensor noise. The total training loss is thus:

$${\mathcal{L}}_{\mathrm{reg}}={\mathcal{L}}_{\mathrm{NO}}+\lambda {\mathcal{L}}_{\mathrm{smooth}}$$

(5)

where $\lambda$ is a tunable regularization coefficient that balances model fidelity with generalization.

2.5. Time-Consistency Augmentation for Multi-Step Forecasting

Real-world driving scenarios demand stability across multi-step predictions. A common issue in autoregressive inference is compounding error. To alleviate this, we integrate a time-consistency augmentation loss that enforces agreement between true and recursively predicted thermal states:

$${\mathcal{L}}_{\mathrm{TS}}=\sum _{i=1}^{N-1}{∥u_i^{\mathrm{true}}-\left({\varphi }_{\theta }({\tau }_{i-1},{\mathbf{e}}_{i-1})·\delta +{\widehat{u}}_{i-1}\right)∥}^2$$

(6)

This term minimizes the deviation between the ground truth and the rolling forecast estimate over a sequence of time steps. It plays a critical role in preventing divergence during long-horizon simulations, as visualized in Figure 1.

2.6. Surrogate Modeling for Charging Characteristics

Beyond thermal prediction, a secondary objective is to infer charging characteristics from the modeled temperature profile. Toward this, we define a linear surrogate model that estimates charging metrics as a function of both thermal and SoC-derived features:

$$\begin{array}{cc}\hfill p_c& ={\beta }_{1}C+{\beta }_2{u}_i+\gamma \hfill \\ \hfill t_c& ={\delta }_1{C}_s+{\delta }_2{C}_e+{\delta }_3{u}_i+\eta \hfill \end{array}$$

(7)

Here, $p_c$ denotes peak charging power and $t_c$ represents estimated charging time. Variables C, $C_s$, and $C_e$ correspond to instantaneous SoC, SoC start, and SoC end respectively, while $u_i$ is the inferred battery temperature at time i. Coefficients $({\beta }_1,{\beta }_2,\gamma )$ and $({\delta }_1,{\delta }_2,{\delta }_3,\eta )$ are learned via ordinary least squares regression.

This auxiliary model helps quantify the downstream impact of thermal dynamics on EV charging performance and provides interpretable outputs that can inform battery management strategies. This surrogate mapping is grounded in the empirical observation that thermal stress directly influences charge acceptance and internal resistance. By using predicted temperature trajectories from the neural operator, we obtain a reliable intermediate feature that captures system-level state, enabling downstream applications like adaptive charging control or thermal-aware scheduling for fleet vehicles.

2.7. Implementation and Training Details

The neural operator ${\varphi }_{\theta }$ is implemented using a multilayer perceptron (MLP) architecture with ReLU activations, batch normalization, and dropout layers for regularization. Feature scaling was performed using z-score normalization. The model was trained using the Adam optimizer with a learning rate of $1\times {10}^{-4}$ for 300 epochs. Hyperparameters $\lambda$ and $\delta$ were tuned via cross-validation.

All experiments were conducted using PyTorch on an NVIDIA RTX 3090 GPU. Inference time per trajectory was under 20 ms, indicating suitability for deployment in low-latency environments such as EV onboard systems.

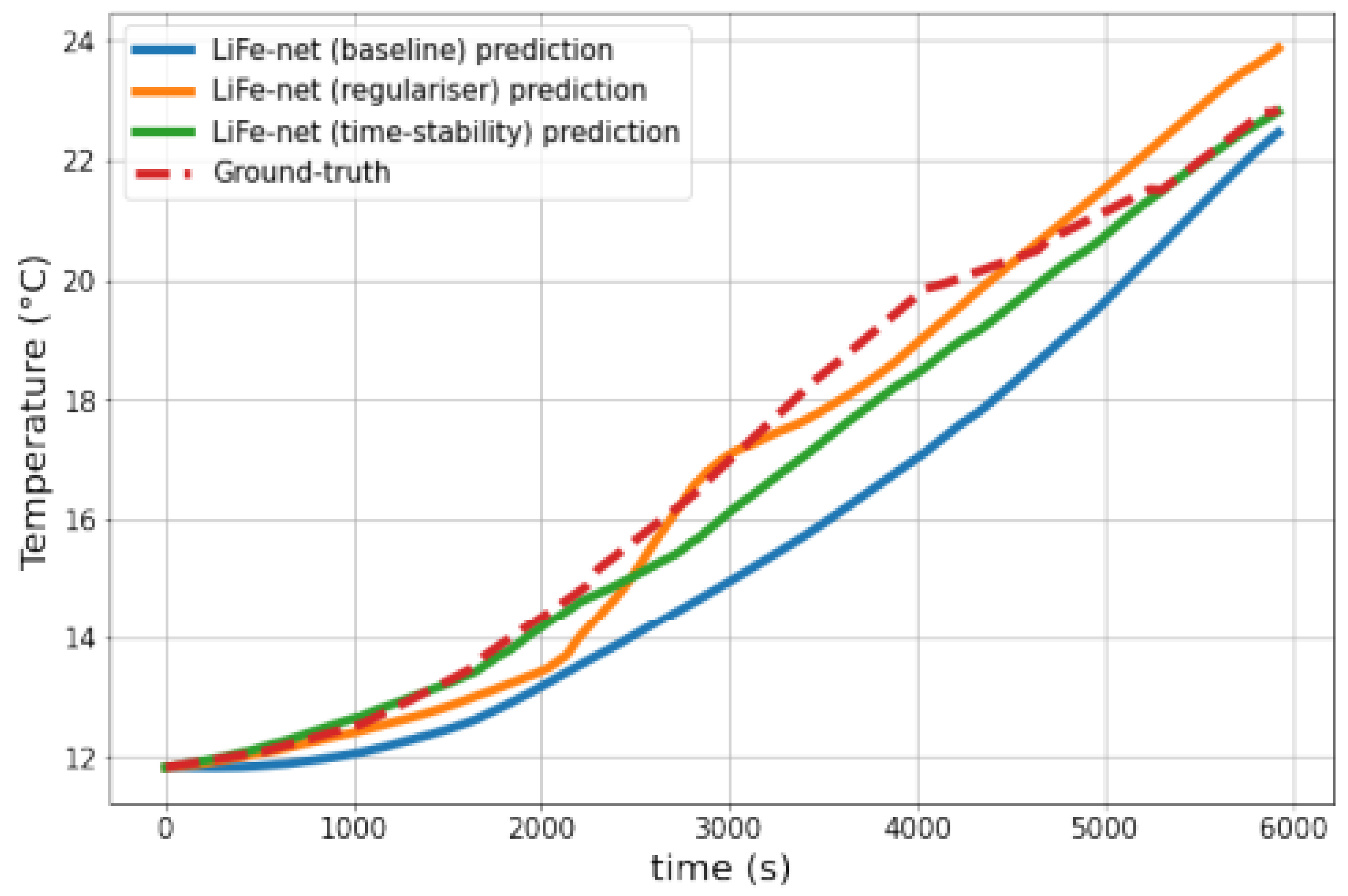
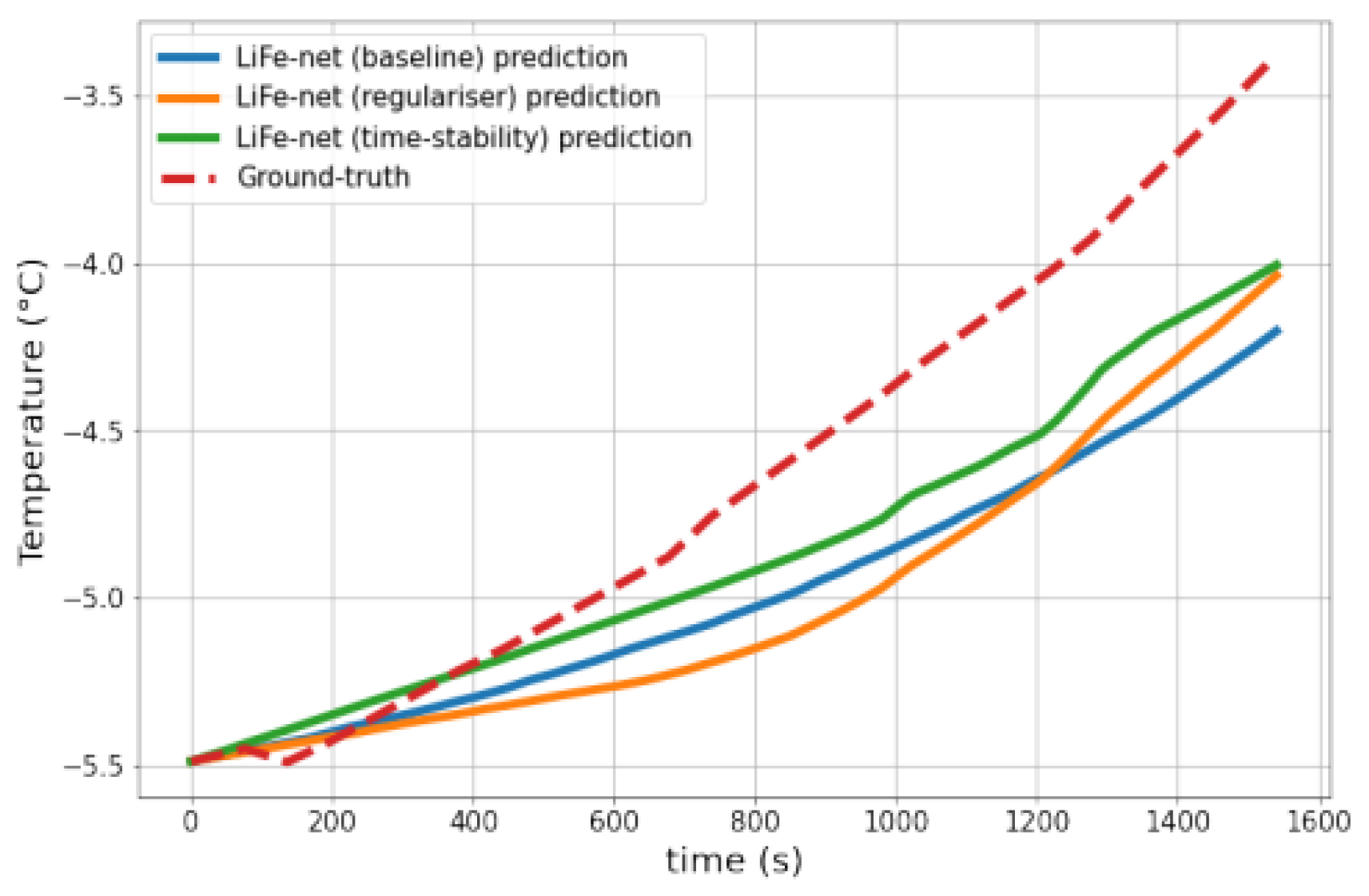
Figure 2. All models perform well on test data that is well represented by our training data.

Figure 2. All models perform well on test data that is well represented by our training data.

3. Evaluation and Results

To rigorously assess the efficacy of the proposed neural operator-based framework, a dataset comprising 445,000 timestamped entries was compiled from 99 distinct driving events. These drives were conducted under diverse environmental conditions, including varying ambient temperatures, humidity levels, and driving velocities. Data collection included not only thermal sensor readings from beneath the driver’s seat but also system-level telemetry such as energy draw, state-of-charge (SoC), and external climate variables obtained via the Tesla onboard interface.

The dataset was partitioned into a training subset consisting of 92 driving instances and an evaluation set of 7 unseen drives to assess generalizability. Several model variants were trained using this dataset and benchmarked using Mean Absolute Error (MAE), Mean Squared Error (MSE), and Relative Percentage Error (RPE). These metrics collectively provide insight into both the magnitude and variance of prediction deviations. In addition to accuracy, the computational overhead (epoch training time) was monitored to evaluate model scalability and suitability for real-time deployment scenarios.

Table 1 presents the quantitative outcomes across three principal model configurations: a baseline neural ODE model, a regularized version incorporating smoothness constraints, and a time-consistent model featuring temporal stability augmentation.

The baseline model demonstrated acceptable performance with moderate error margins; however, its prediction variance was sensitive to abrupt changes in environmental inputs. The regularized variant reduced both MAE and MSE significantly by enforcing local smoothness in the learned temporal dynamics, thereby improving stability in transitional phases such as acceleration or sudden braking.

The most advanced variant, incorporating time-consistency penalties, achieved the best performance across all three accuracy metrics. Despite its longer epoch time (an order of magnitude greater due to multi-step backpropagation), it maintained superior alignment between predicted and actual temperature profiles. This highlights the value of incorporating higher-order dynamics and recursive correction into temporal modeling tasks for electric vehicle systems.

3.1. Interpreting Charging Characteristics

Following temperature prediction, inferred thermal readings were employed in a linear regression framework as described in Equation (7) to estimate two key charging metrics: peak charging power ($p_c$) and total charging duration ($t_c$). Regression was performed using a standard least-squares approach across the evaluation set.

The resulting regression coefficients demonstrated strong correlation between thermal states and charging behaviors. Specifically, the R² coefficient for $p_c$ was found to be 0.726, indicating a moderately strong relationship between predicted thermal levels and peak charging power. In contrast, the R² score for $t_c$ was 0.884, suggesting a very strong association with thermal state and other SoC-derived features. These findings validate the hypothesis that thermal evolution profiles derived from the neural operator can serve as viable surrogates for estimating charging behavior in real time.

Moreover, this mapping opens avenues for closed-loop control systems that dynamically modulate charging profiles based on inferred thermal stress, enabling smarter energy management and improved battery longevity.

4. Conclusions

In this work, we introduced a neural operator-driven approach for learning and forecasting the thermal evolution of lithium iron phosphate (LiFePO₄) battery cells in electric vehicles, leveraging real-world telemetry collected from a Tesla Model 3. By treating the temporal temperature profile as a solution to a learned parametric ODE, our methodology encapsulates complex dependencies between environmental conditions and internal thermal dynamics.

Three variants of the neural architecture were compared: a baseline model, a regularized model with environmental input smoothing, and a time-stable model incorporating temporal consistency across multi-step forecasts. The time-stable variant significantly outperformed others in terms of prediction accuracy, demonstrating the utility of multi-step penalization in learning temporally coherent dynamics. The inclusion of smoothing and stability regularizers ensured generalizability and resilience against spurious environmental fluctuations.

Furthermore, we demonstrated that these temperature predictions could be effectively used as inputs to a secondary regression model to estimate peak charging power and total charging duration. The high correlation values obtained in this stage affirm the potential for integrated diagnostics, whereby thermal evolution acts as an intermediate signal bridging telemetry with power system management.

Looking ahead, this framework can be extended to incorporate uncertainty quantification through Bayesian neural operators, or fused with spatial sensors to enable full 3D thermal mapping. Additionally, adaptive integration schemes could further improve long-range predictive fidelity without incurring high computational costs. Ultimately, the presented approach contributes toward more intelligent, thermal-aware energy systems in next-generation electric vehicles.